Influence of the Three-Dimensional Effect of Pile-Soil System on the Vertical Dynamic Response of Large-Diameter Piles in Low-Strain Integrity Testing
Abstract
1. Introduction
2. Mathematical Model and Assumptions
- (1)
- The pile surrounding the soil is homogenous, and its top surface is free. Meanwhile, the pile surrounding the soil is infinite in the radial direction, and the displacement and stress of the soil at infinity are zero.
- (2)
- During the vibration, only the vertical displacement of the hammer-pile-soil system is taken into account, and the radial displacement is ignored. Both the vertical and radial differentials of the vertical displacement are considered in this paper.
- (3)
- There is no big deformation in the hammer-pile-soil system; thus, the stress and displacement at the interface between the pile and the surrounding soil are equal. Obviously, pile I also remains in perfect contact with pile II. The hammer-pile-soil system is located on rigid rock.
- (4)
- The hammer-pile-soil system is static at the beginning.
3. Vibration Equations and Their Solutions
3.1. Vertical Vibration Equation of Pile Surrounding Soil and Its Solution
- (1)
- The stress at the surface of the pile surrounding the soil top is zero:
- (2)
- The vertical displacement of the pile surrounding soil at the top of the rigid rock is zero:
- (3)
- The stress and displacement of the pile surrounding soil are zero at infinity:
- (4)
- The stress and displacement of the pile surrounding the soil are zero at the beginning:
3.2. Vertical Vibration Equations of the Pile
- (1)
- The boundary condition of the pile top:
- (2)
- The pile bottom is fixed:
- (3)
- The interface between the pile and the surrounding soil is continuous:
- (4)
- The interface between Pile I and Pile II is continuous:
- (5)
- The pile is static at the beginning:
3.3. The Solution for Pile I
3.4. The Solution for Pile II
4. Comparison
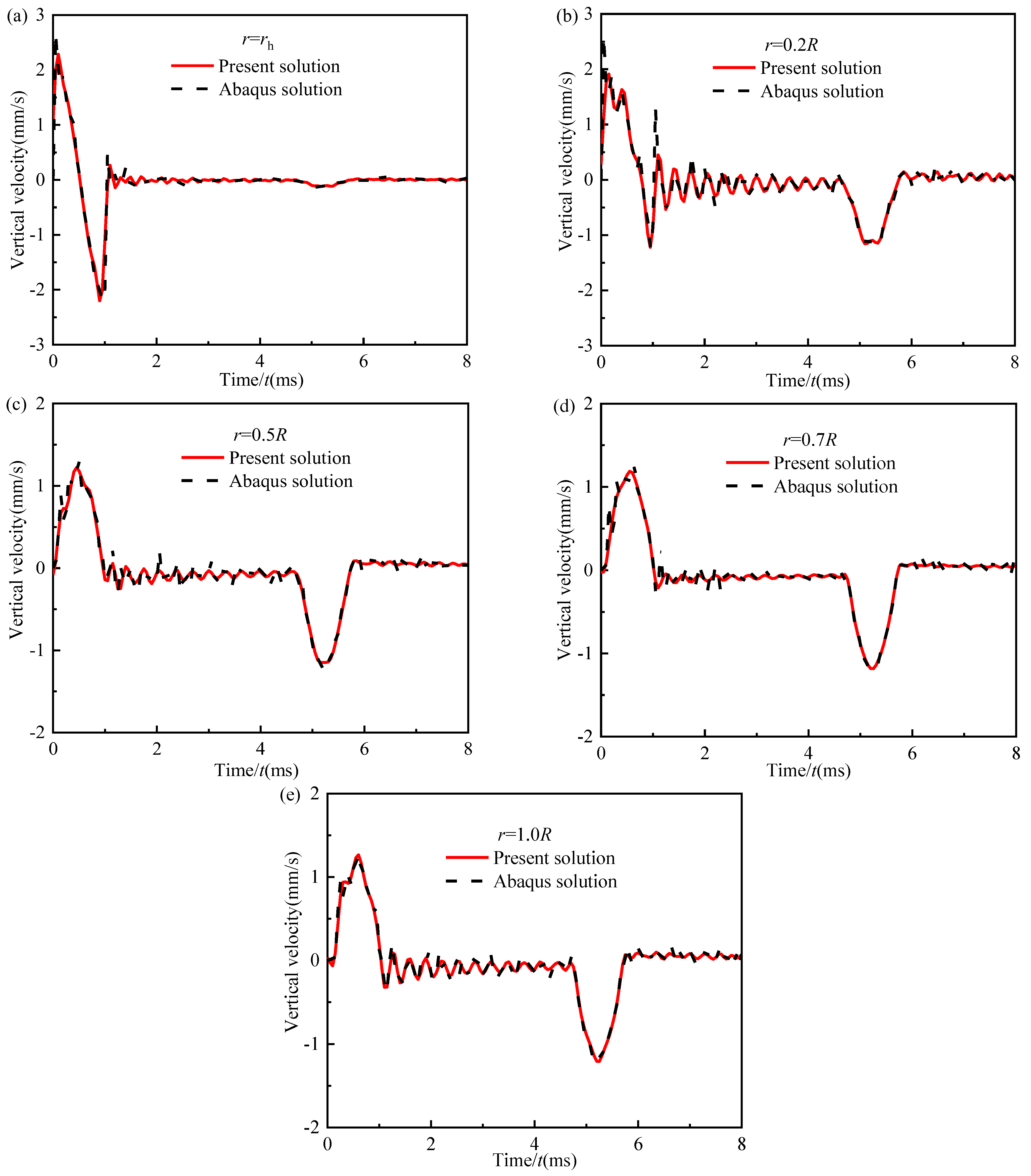
4.1. Comparison with Finite Element Model
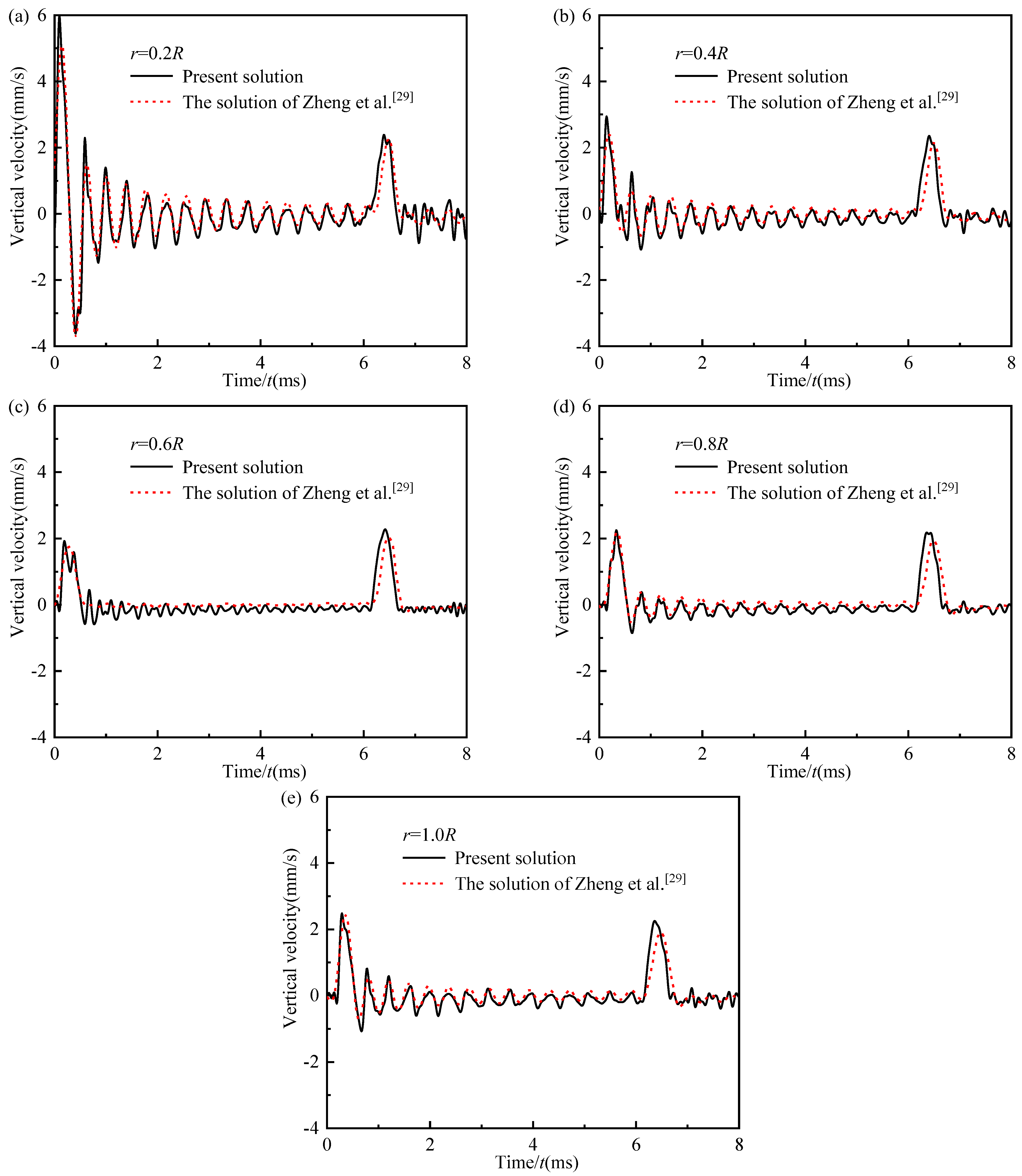
4.2. Comparison with Other Existing Solutions
5. Parametric Study
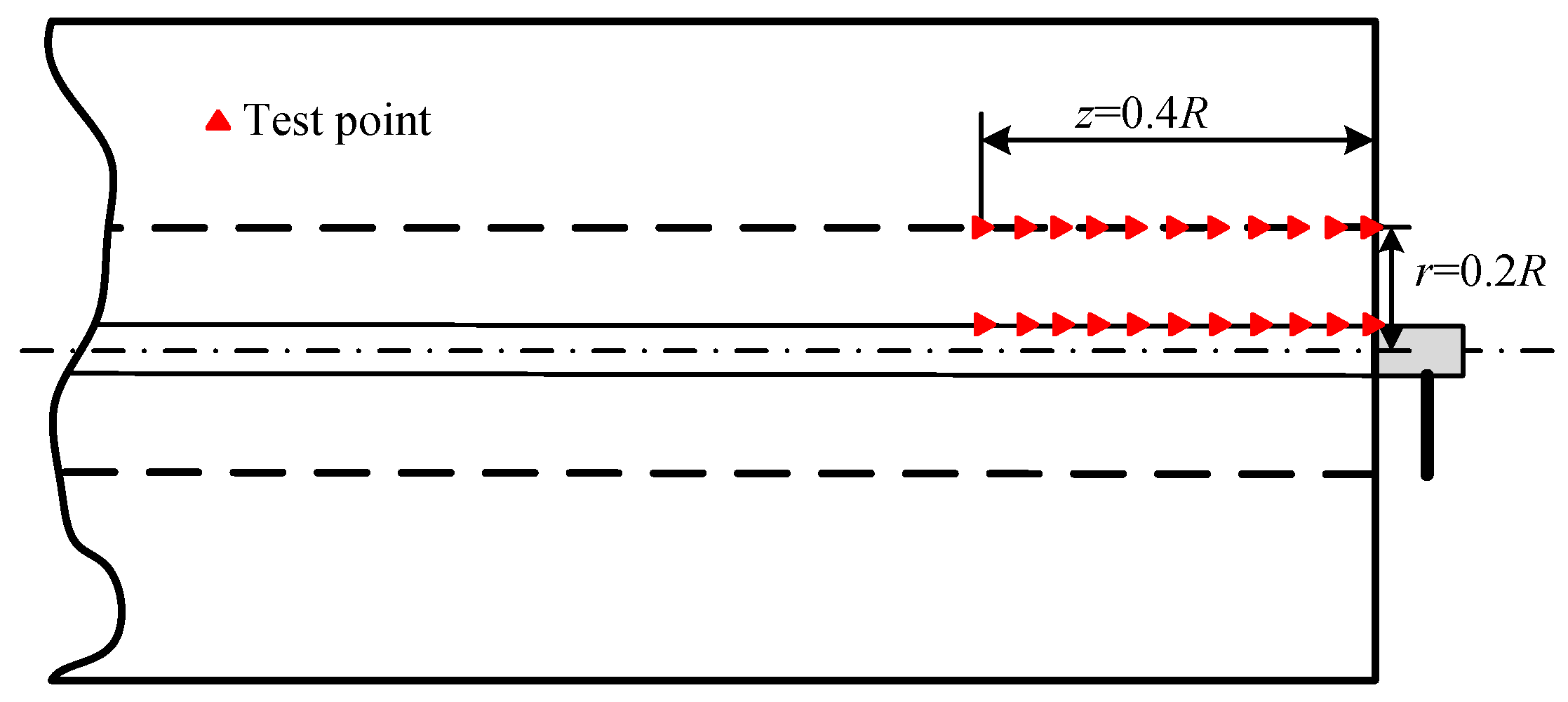
5.1. The Influence of the 3D Effect of the Pile-Soil System
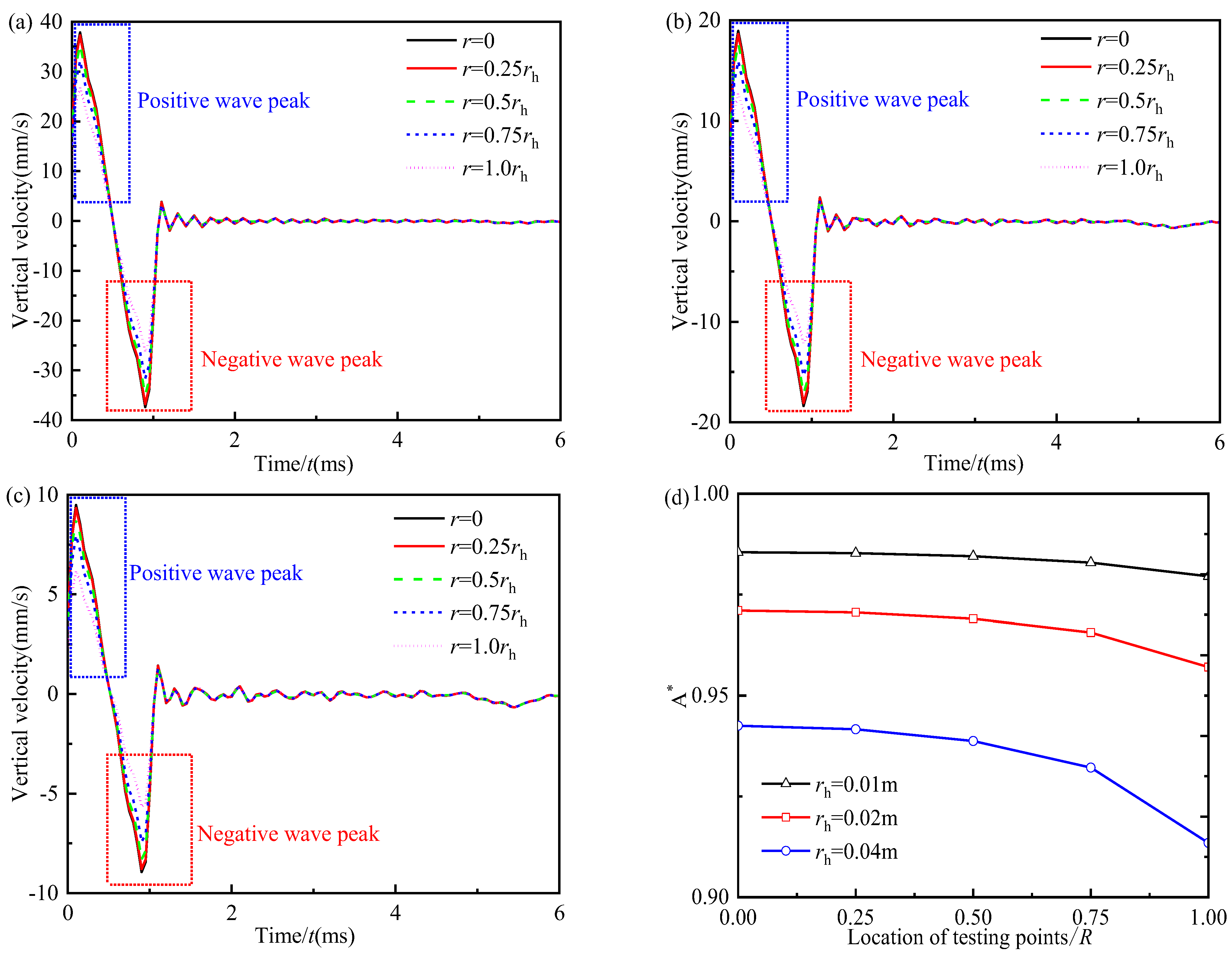
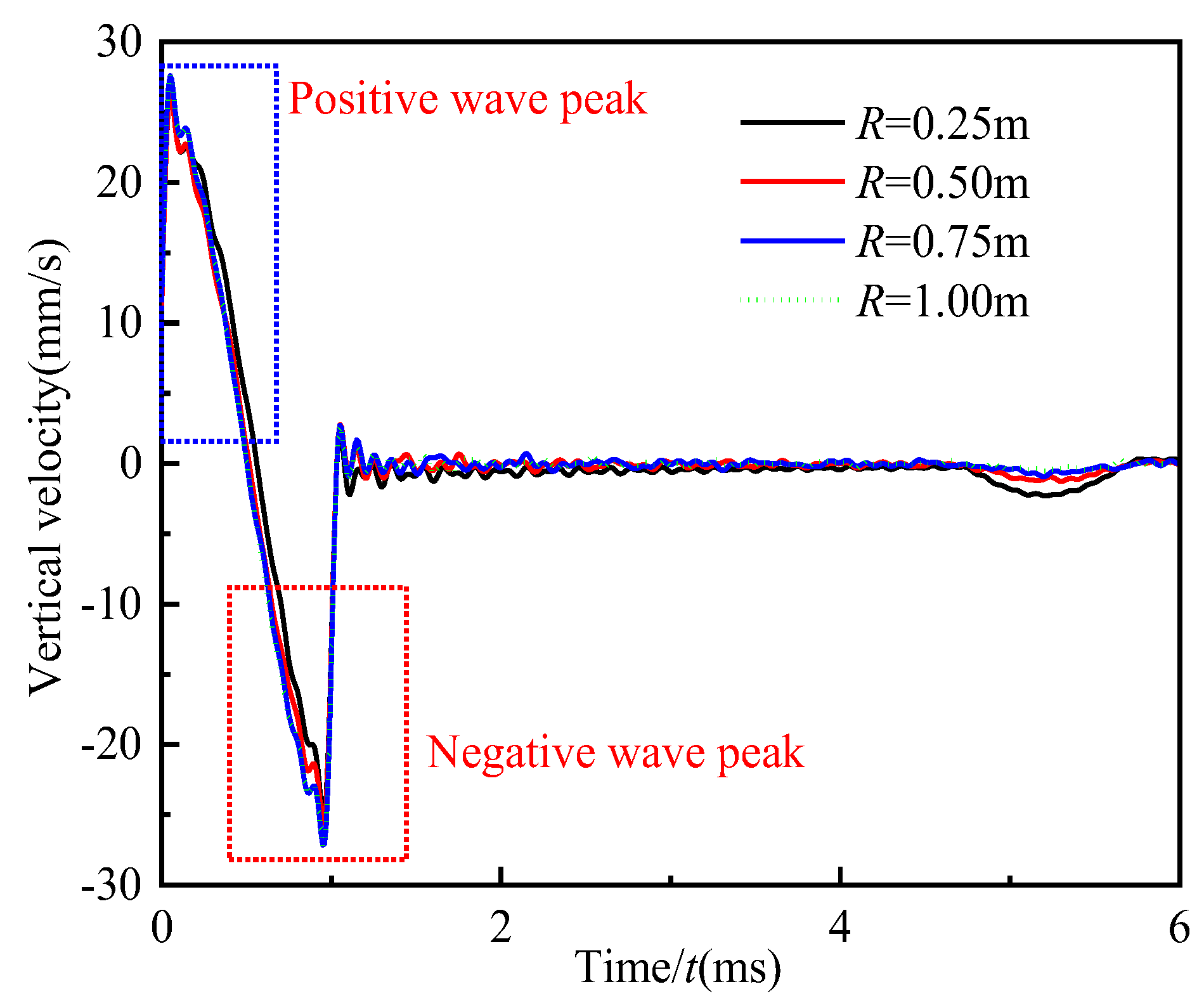
5.1.1. Within the Excitation Region
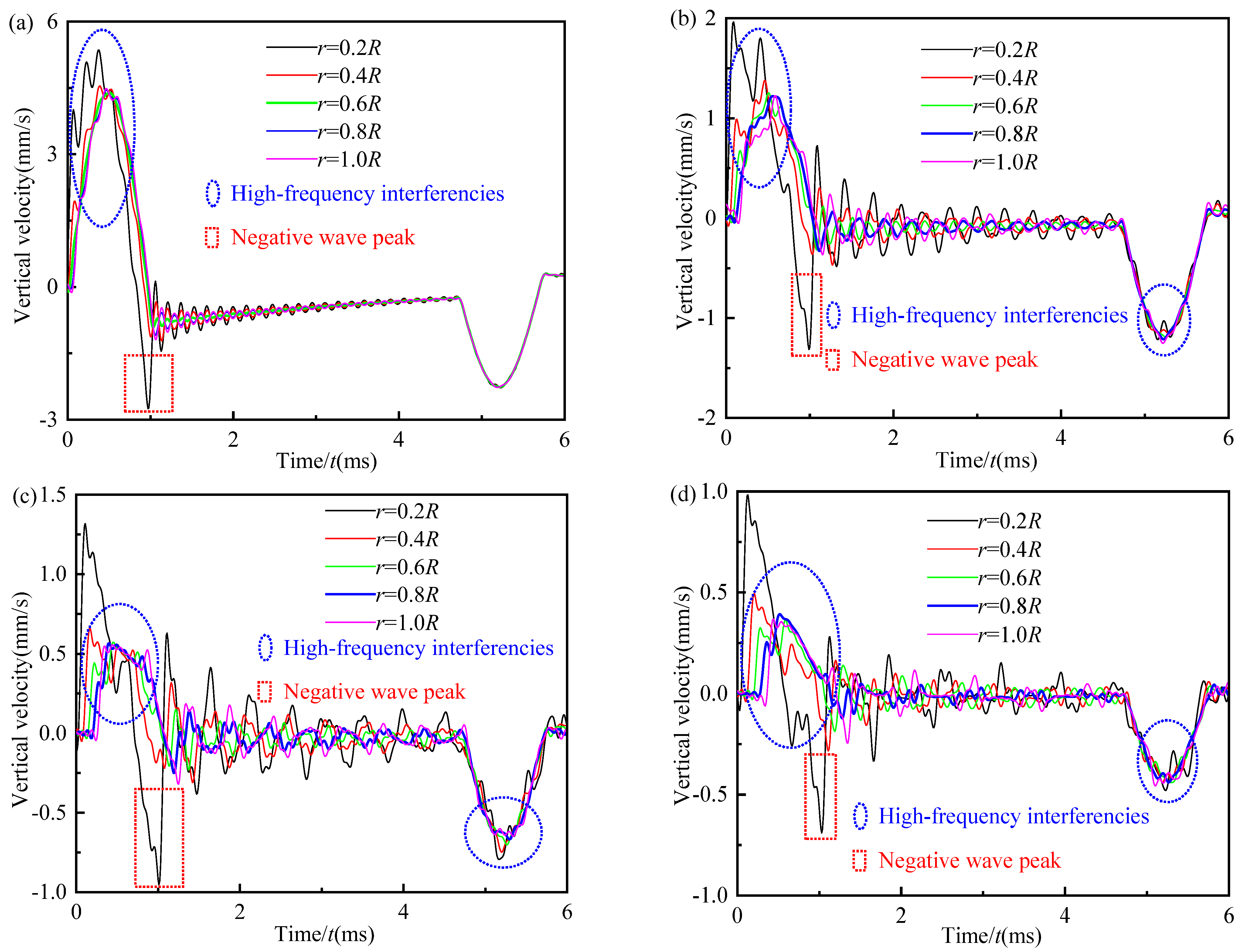
5.1.2. At the Edge of the Excitation Region
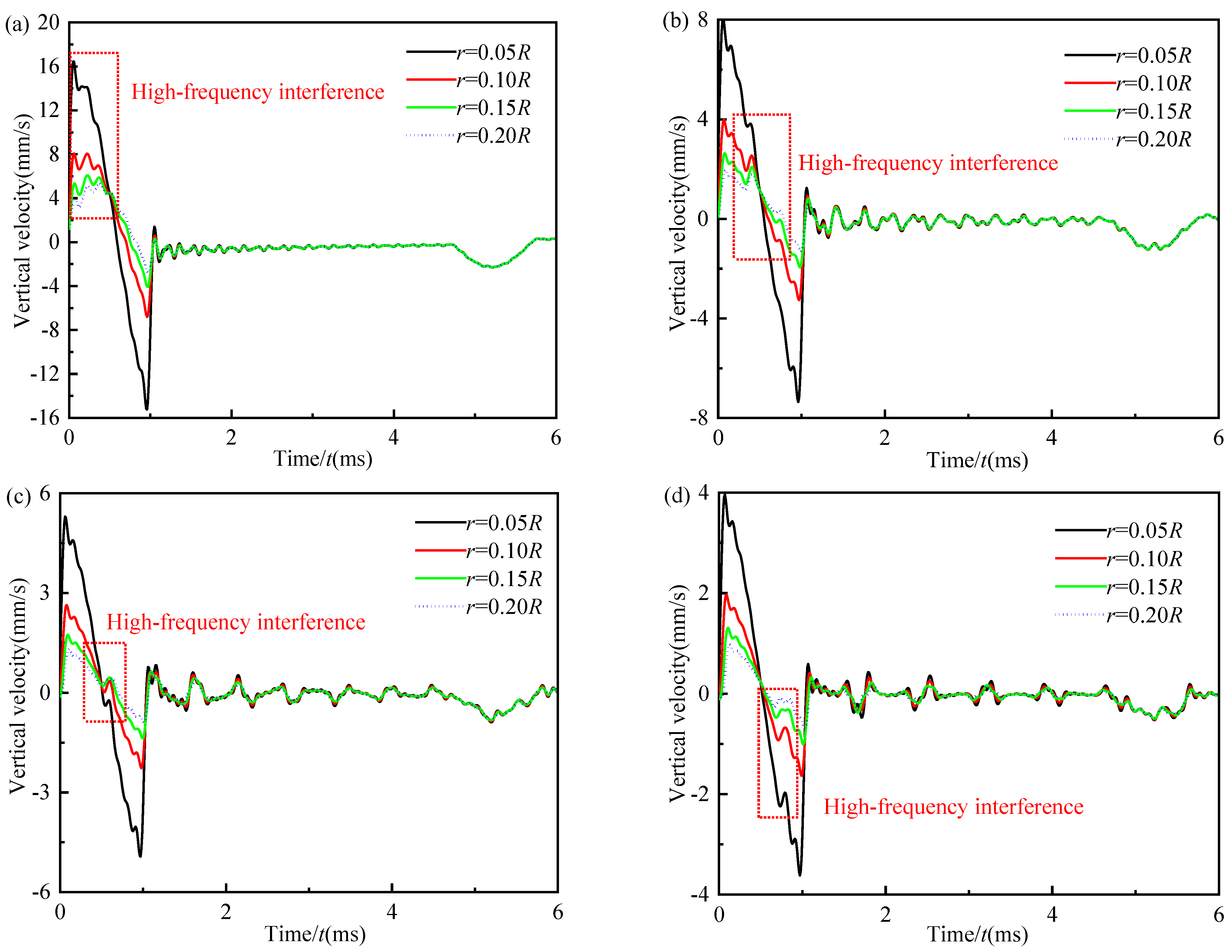
5.1.3. Outside the Excitation Region
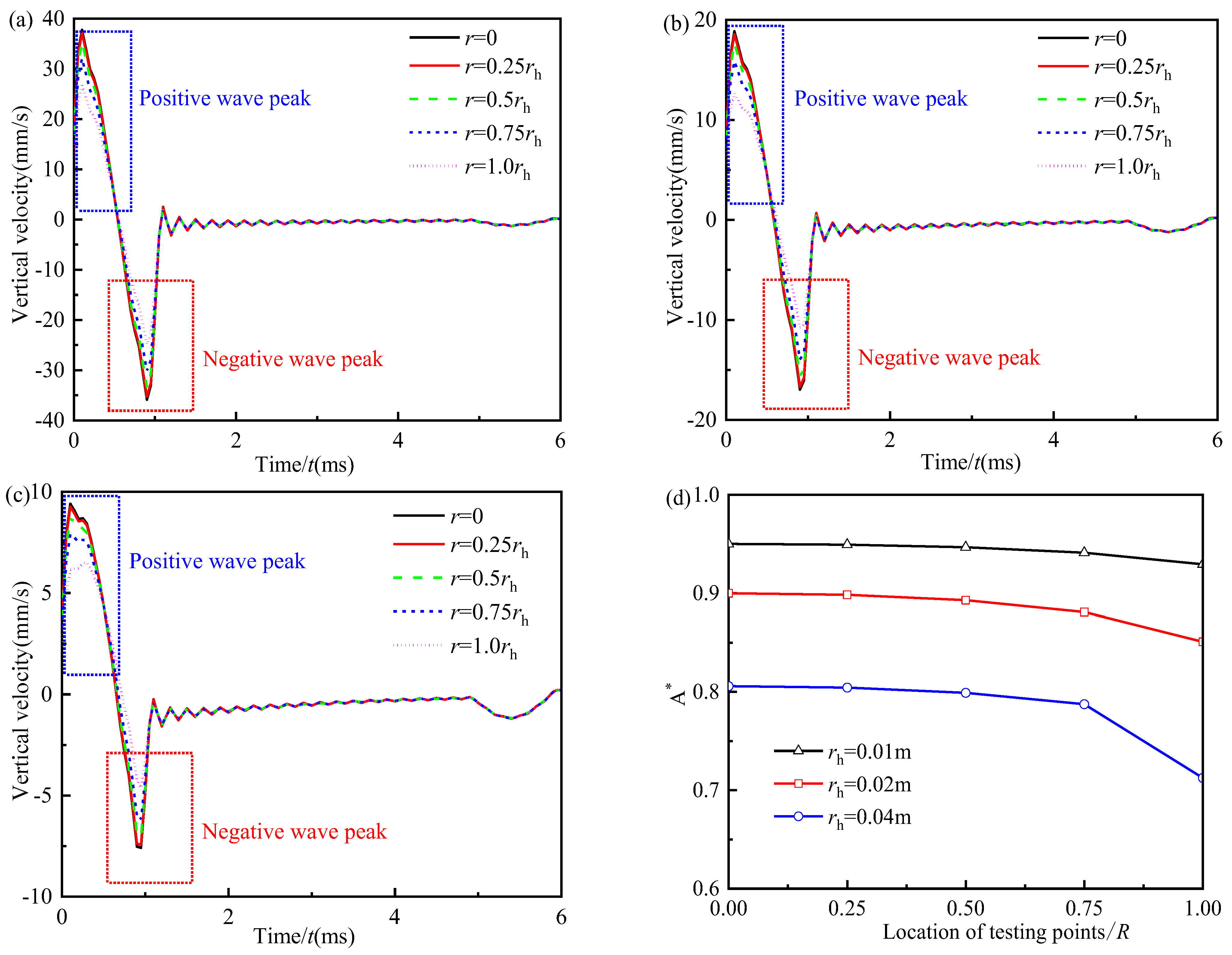
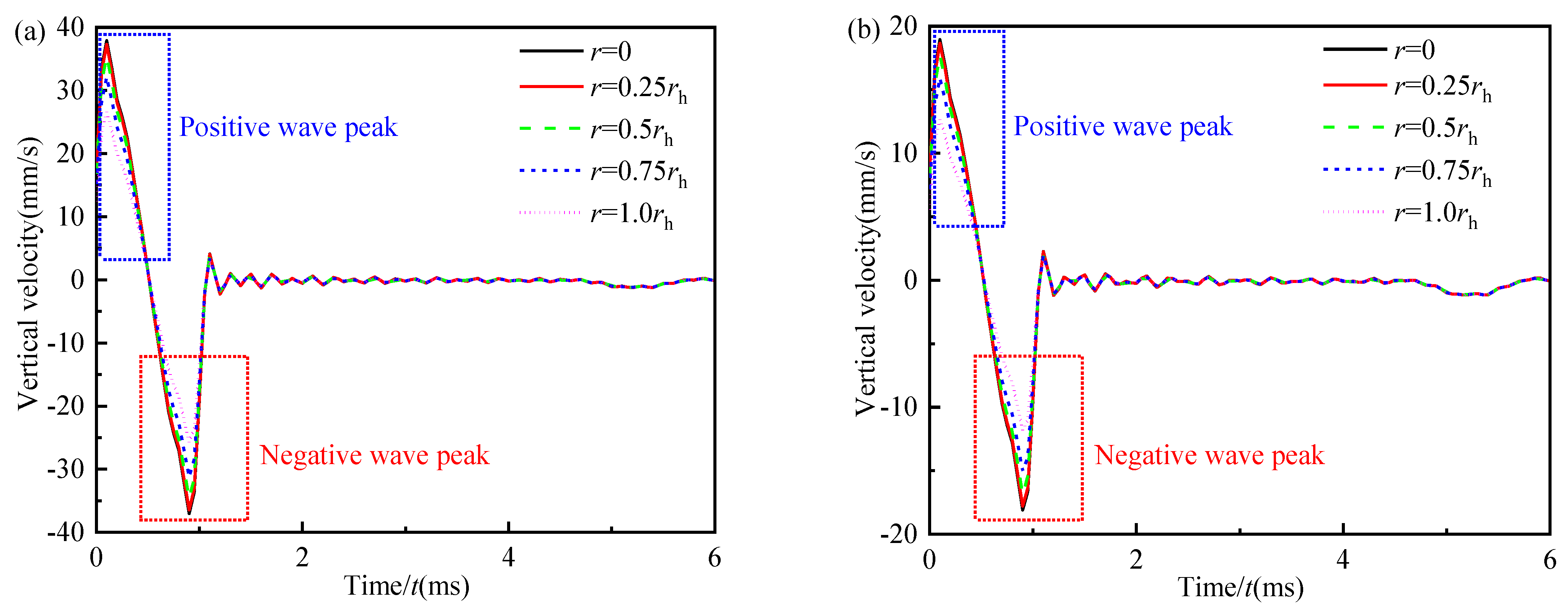
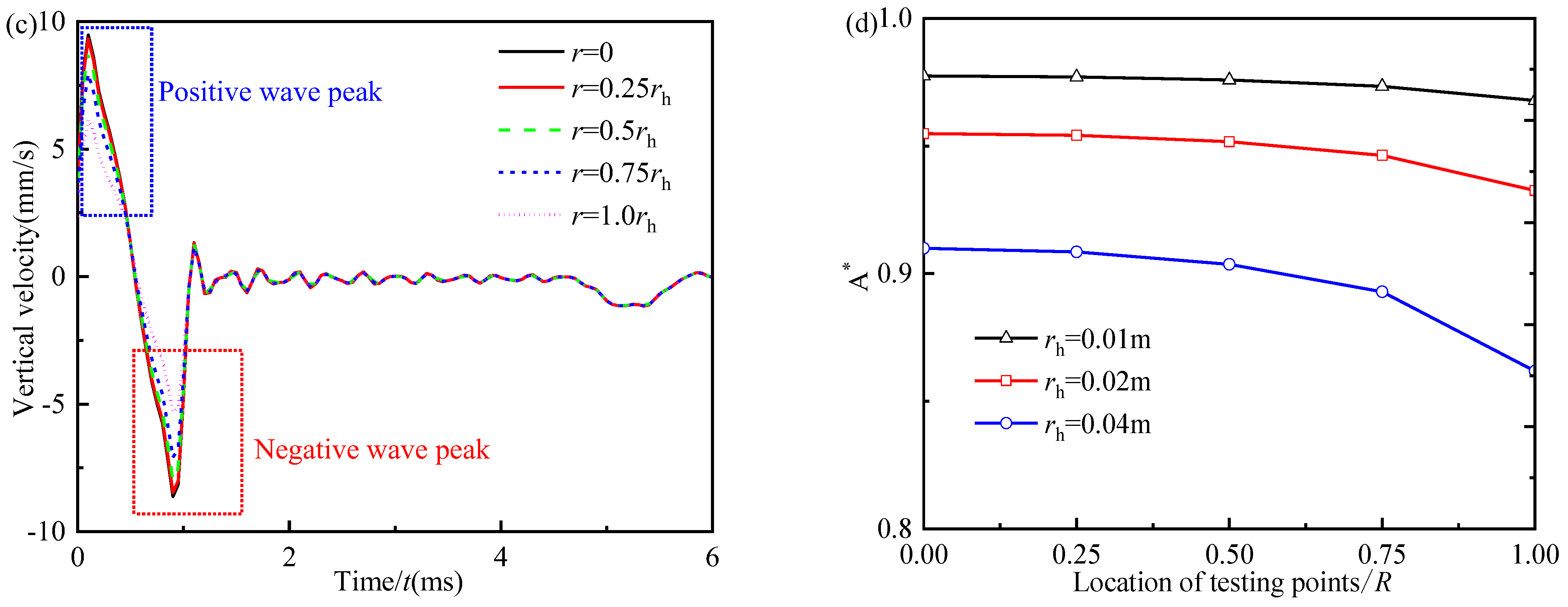
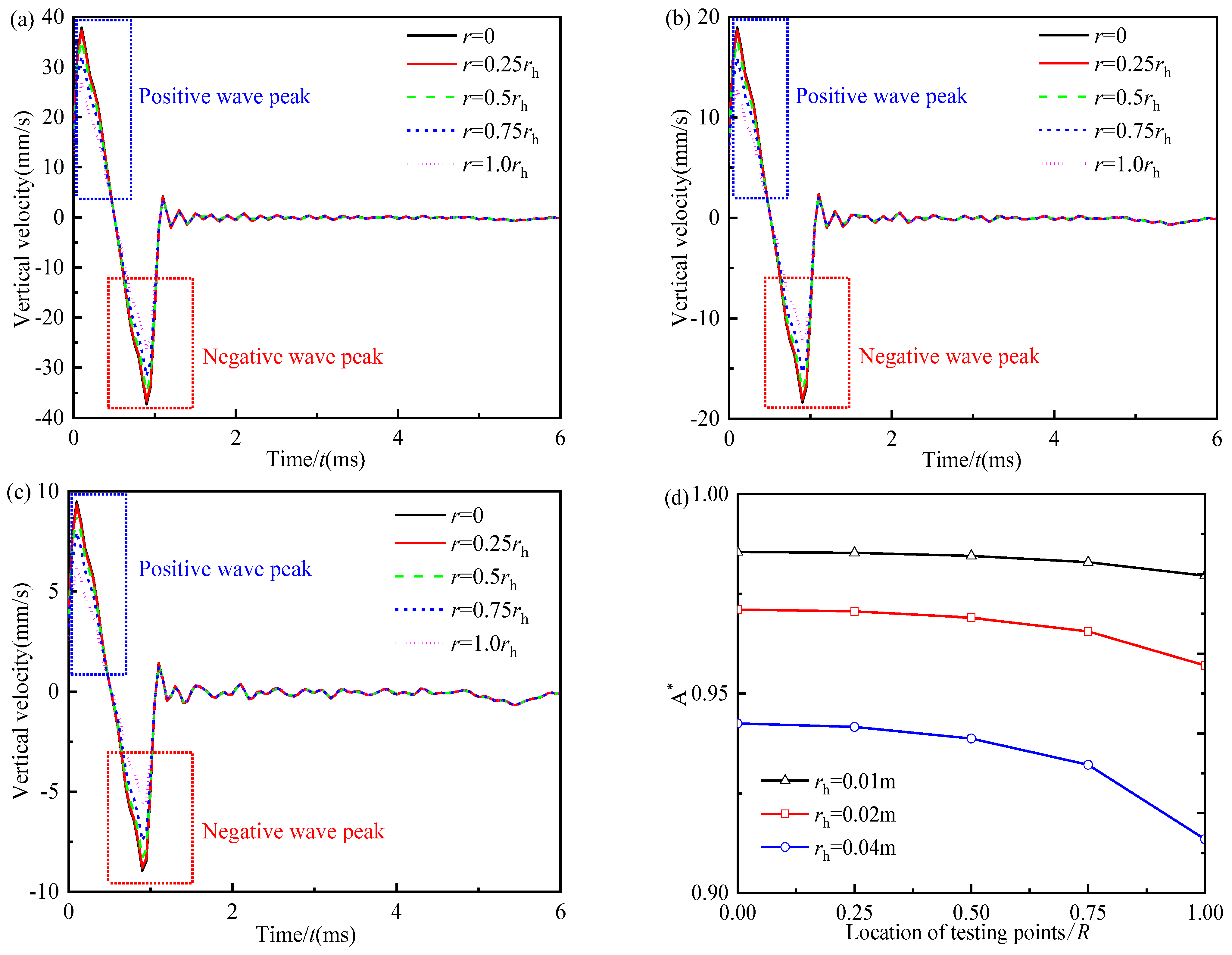
5.2. The Mechanism of the Negative Wave Signal in the Incident Wave Signal during Low-Strain Integrity Testing
5.2.1. Influence of the Ratio of Pile Radius to the Radius of Hammer
5.2.2. From the Perspective of Wave Propagation
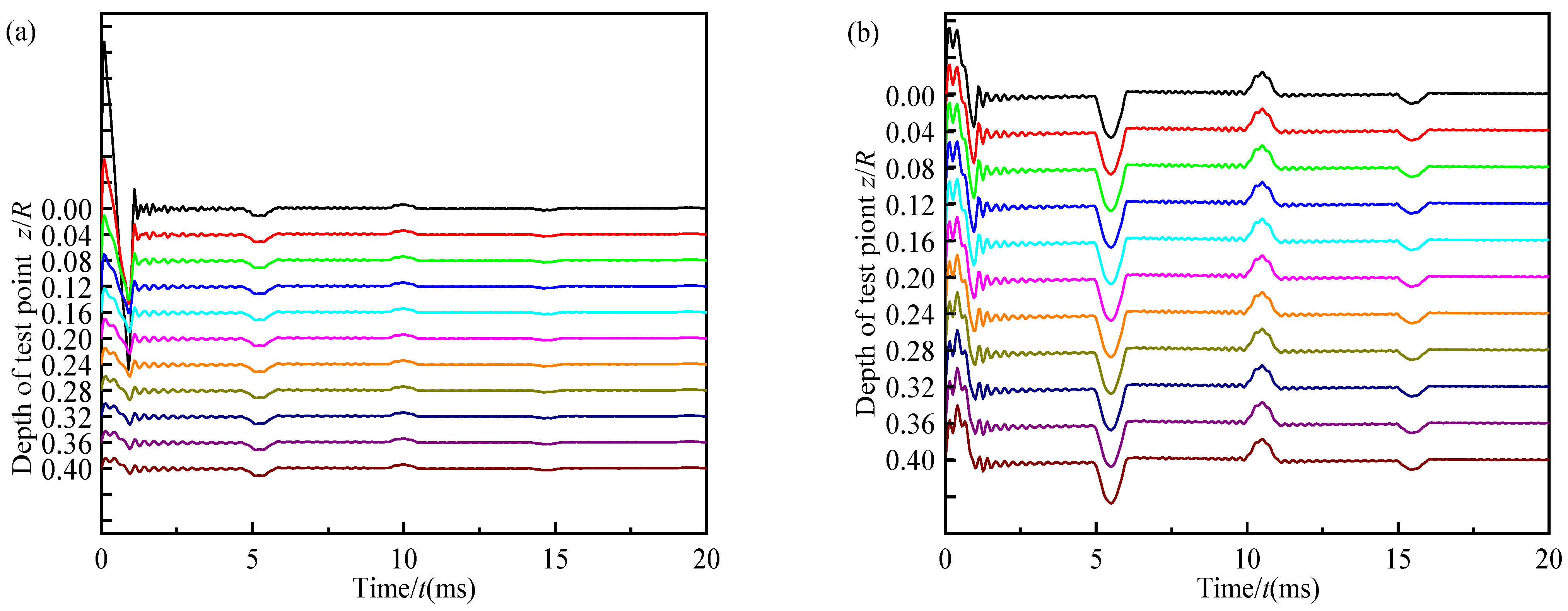
5.2.3. The Vertical Velocity Response in Time Domain along the Depth of the Pile
6. Conclusions
- The rationality of the present solution is verified by comparing it with the FEM results obtained using Abaqus software. Meanwhile, the reasonableness and advantages of the present solution in evaluating the 3D effect of the pile-soil system are verified by comparing it with the other existing solutions.
- It is reasonable to assume pile I (impacting area) as a 1D rod in the research of the low-strain integrity testing of large-diameter piles.
- In the time-domain velocity curves of different test points at the pile top along the radial direction, the negative wave signal in the incident wave signal only occurs at the test point inside and near the excitation region. Meanwhile, the negative wave signal at the edge of the excitation region is almost unaffected by the variation in the radius of the general engineering pile.
- During the low-strain integrity testing, the test point should be located near 0.6R–0.8R, which can reduce the high-frequency interference of the large-diameter pile top.
- In the time-domain velocity curves of the test points inside and near the excitation region, the negative wave signal in the incident wave signal is influenced by the pile-hammer-ratio and is caused by the larger pile-hammer-ratio. There is a critical value of the pile-hammer-ratio: when the pile-hammer-ratio is smaller than 3, that negative wave signal will totally vanish.
- From the perspective of wave propagation, in the time-domain velocity curves of the test points inside and near the excitation region, the negative wave signal in the incident wave signal is caused by the superposition of the direct R-wave on the direct S-wave. It is suggested to filter the R wave signal in the detection signal to eliminate the negative wave peak by adding a device to filter the R wave signal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, W.B.; Liu, H.; Yang, X.Y.; Jiang, G.S.; El Naggar, M.H.; Mei, G.X.; Liang, R.Z. New method to calculate apparent phase velocity of open-ended pipe pile. Can. Geotech. J. 2020, 57, 127–138. [Google Scholar] [CrossRef]
- Yang, X.Y.; Wang, L.X.; Wu, W.B.; Liu, H.; Jiang, G.S.; Wang, K.H.; Mei, G.X. Vertical dynamic impedance of a viscoelastic pile in arbitrarily layered soil based on the fictitious soil pile model. Energies 2022, 15, 2087. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Jiang, G.S.; Wu, W.B.; El Naggar, M.H.; Liu, H.; Wen, M.J.; Wang, K.H. Analytical solution for distributed torsional low strain integrity test for pipe pile. Int. J. Numer. Anal. Meth. Geomech. 2022, 46, 47–67. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.J.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Yang, X.Y.; Jiang, G.S.; Liu, H.; Wu, W.B.; Mei, G.X.; Yang, Z.J. Horizontal vibration characteristics of a tapered pile in arbitrarily layered soil. Energies 2022, 15, 3193. [Google Scholar] [CrossRef]
- Yang, Z.J.; Wu, W.B.; Liu, H.; Zhang, Y.P.; Liang, R.Z. Flexible support of a pile embedded in unsaturated soil under Rayleigh waves. Earthq. Eng. Struct. Dyn. 2022, 52, 226–247. [Google Scholar] [CrossRef]
- Wu, J.T.; El Naggar, M.H.; Wang, K.H.; Wu, W.B. Lateral vibration characteristics of an extended pile shaft under low-strain integrity test. Soil Dyn. Earthq. Eng. 2019, 126, 105812. [Google Scholar] [CrossRef]
- Meng, K.; Cui, C.Y.; Liang, Z.M.; Li, H.J.; Pei, H.F. A new approach for longitudinal vibration of a large-diameter floating pipe pile in visco-elastic soil considering the three-dimensional wave effects. Comput. Geotech. 2020, 128, 103840. [Google Scholar] [CrossRef]
- Wu, W.B.; Wang, Z.Q.; Zhang, Y.P.; El Naggar, M.H.; Wu, T.; Wen, M.J. Semi-analytical solution for negative skin friction development on deep foundations in coastal reclamation areas. Int. J. Mech. Sci. 2022, 241, 107981. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.X.; Yang, X.Y.; Chen, L.B.; Wu, W.B.; Wen, M.J.; Jiang, M.J.; Guo, C.J. Lateral dynamic response of offshore pipe piles considering effect of superstructure. Energies 2022, 15, 6759. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, G.K.; Zhu, S.Y.; Gu, Q.; Ke, S.T.; Lin, J.H. Seismic analysis of 10 MW offshore wind turbine with large-diameter monopile in consideration of seabed liquefaction. Energies 2022, 15, 2539. [Google Scholar] [CrossRef]
- Chen, L.B.; Li, J.X.; Wu, W.B.; Liu, H.; Yao, Y.; Zhang, P. New method to calculate the kinematic response of offshore pipe piles under seismic S-waves. Soil Dyn. Earthq. Eng. 2023, 165, 107651. [Google Scholar] [CrossRef]
- Zhang, Y.P.; El Naggar, M.H.; Wu, W.B.; Wang, Z.Q.; Yang, X.Y.; Jiang, G.S. Dynamic torsional impedance of large-diameter pipe pile for offshore engineering: 3D analytical solution. Appl. Math. Model. 2022, 111, 664–680. [Google Scholar] [CrossRef]
- Cui, C.Y.; Meng, K.; Xu, C.S.; Wang, B.L.; Xin, Y. Vertical vibration of a floating pile considering the incomplete bonding effect of the pile-soil interface. Comput. Geotech. 2022, 150, 104894. [Google Scholar] [CrossRef]
- Pasqual, R.P.S.; Kormann, A.C.M. Low strain integrity tests in piles –1-D and 3-D numerical modeling and comparisons with results obtained in the field. Multi-Sci. J. 2020, 2, 1–8. [Google Scholar] [CrossRef]
- Ding, W.; Chai, H.Y.; Liu, S.H.; Chen, C.; Nie, T.; Hu, Z. Analysis of influence of source and pile-soil interaction in low strain pile integrity testing. J. Civil Environ. Eng. 2020, 42, 73–79. [Google Scholar]
- Smith, E.A.L. Pile driving analysis by the wave equation. J. Soil Mech. Found. Div. 1960, 86, 35–64. [Google Scholar] [CrossRef]
- Ni, S.H.; Lehmann, L.; Charng, J.J.; Lo, K.F. Low-strain integrity testing of drilled piles with high slenderness ratio. Comput. Geotech. 2006, 33, 283–293. [Google Scholar] [CrossRef]
- Wang, K.H.; Wu, W.B.; Zhang, Z.Q.; Leo, C.J. Vertical dynamic response of an inhomogeneous viscoelastic pile. Comput. Geotech. 2010, 37, 536–544. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, P.; Huang, Y.H.; Gan, Y. Analysis of 3D effect of dynamic test along pile tip. Chin. J. Rock Mech. Eng. 2007, 26, 3209–3214. [Google Scholar]
- Steinbach, J.; Vey, E. Caisson evaluation by stress wave propagation method. J. Geotech. Geoenviron. Eng. Div. 1975, 101, 361–368. [Google Scholar] [CrossRef]
- Wu, W.B.; Wang, K.H.; Zhang, Z.Q.; Leo, C.J. Soil-pile interaction in the pile vertical vibration considering true three-dimensional wave effect of soil. Int. J. Num. Anal. Meth. Geomech. 2013, 37, 2860–2876. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Wang, Z.Q.; El Naggar, M.H.; Wu, W.B.; Wang, L.X.; Jiang, G.S. Three-dimensional wave propagation in a solid pile during torsional low strain integrity test. Int. J. Num. Anal. Meth. Geomech. 2022, 46, 2398–2411. [Google Scholar] [CrossRef]
- Fukuhara, T.; Kakurai, M.; Sugimoto, M. Analytical evaluation of defective piles. In Application of Stress-Wave Theory to Piles; Barends, Frans, B.J., Eds.; Routledge: London, UK, 1992; pp. 563–569. [Google Scholar]
- Chen, F.; Wang, R.J. Dimension effect on low strain integrity testing of piles. Chin. J. Geotech. Eng. 1998, 20, 92–96. [Google Scholar]
- Chow, Y.K.; Phoon, K.K.; Chow, W.F.; Wong, K.Y. Low strain integrity testing of piles: Three-dimensional effects. J. Geotech. Geoenviron. Eng. 2003, 129, 1057–1062. [Google Scholar] [CrossRef]
- Li, L.C.; Liu, X.; Liu, H.; Wu, W.B.; Lehane, B.M.; Jiang, G.S.; Xu, M.J. Experimental and numerical study on the static lateral performance of monopile and hybrid pile foundation. Ocean Eng. 2022, 255, 111461. [Google Scholar] [CrossRef]
- Wu, W.B.; Yang, Z.J.; Liu, X.; Zhang, Y.P.; Liu, H.; El Naggar, M.H.; Xu, M.J.; Mei, G.X. Horizontal dynamic response of pile in unsaturated soil considering its construction disturbance effect. Ocean Eng. 2022, 245, 110483. [Google Scholar] [CrossRef]
- Zheng, C.J.; Kouretzis, G.P.; Ding, X.M.; Liu, H.L.; Poulos, H.G. Three-dimensional effects in low-strain integrity testing of piles: Analytical solution. Can. Geotech. J. 2016, 53, 225–235. [Google Scholar] [CrossRef]
- Zheng, C.J.; Liu, H.L.; Ding, X.M.; Kouretzis, G.P.; Sloan, S.W.; Poulos, H.G. Non-axisymmetric response of piles in low-strain integrity testing. Geotechnique 2017, 67, 181–186. [Google Scholar] [CrossRef]
- Zheng, C.J.; Ding, X.M.; Kouretzis, G.P.; Liu, H.L.; Sun, Y. Three-dimensional propagation of waves in piles during low-strain integrity tests. Geotechnique 2018, 68, 358–363. [Google Scholar] [CrossRef]
- Liu, X.; El Naggar, M.H.; Wang, K.H.; Wu, J.T. Three-dimensional axisymmetric analysis of pile vertical vibration. J. Sound Vib. 2021, 494, 115881. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Di, T.Y.; El Naggar, M.H.; Wu, W.B.; Liu, H.; Jiang, G.S. Modified Rayleigh-Love rod model for 3D dynamic analysis of large-diameter thin-walled pipe pile embedded in multilayered soils. Comput. Geotech. 2022, 149, 104853. [Google Scholar] [CrossRef]
- Chai, H.Y.; Liu, M.G.; Li, Q.; Chen, X.Y. Propagation of stress waves in a plate-pile system: Experimental studies. Rock Soil Mechan. 2002, 23, 459–464. [Google Scholar]
- Chai, H.Y.; Liu, M.G.; Bai, S.W.; Li, Q. Numerical analysis of wave propagation in platform-pile system. Chin. J. Geotech. Eng. 2003, 25, 624–628. [Google Scholar]
- Chai, H.Y.; Phoon, K.K.; Zhang, D.J. Effects of the Source on Wave Propagation in Pile Integrity Testing. J. Geotech. Geoenviron. Eng. 2010, 136, 1200–1208. [Google Scholar] [CrossRef]
- Chai, H.Y.; Li, Q.; Liu, M.G.; He, H.J. Analysis of wave propagation on pile top. In Proceedings of the Second National Geotechnical and Engineering Academic Conference, Wuhan, China, 28 October–November 2006. [Google Scholar]
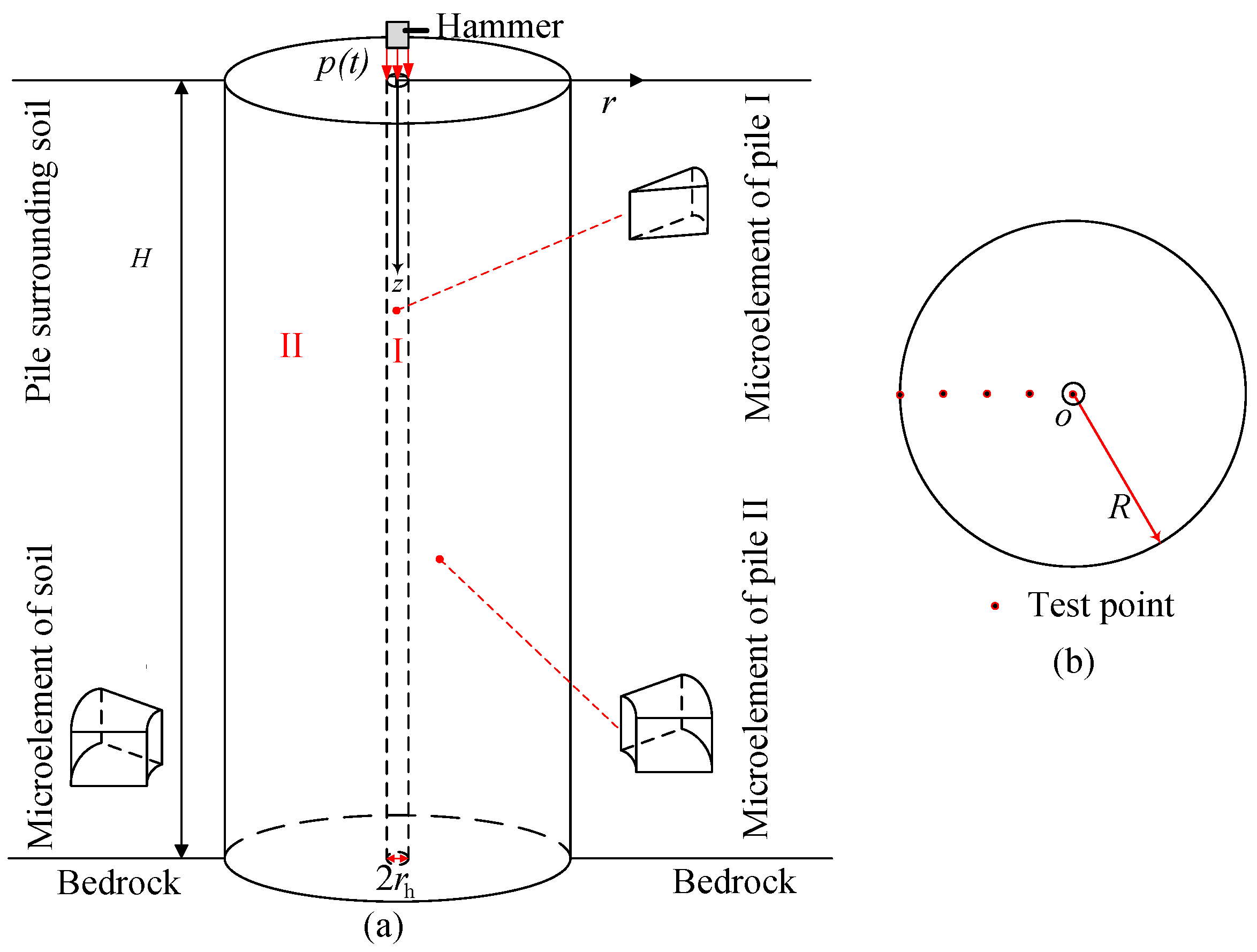
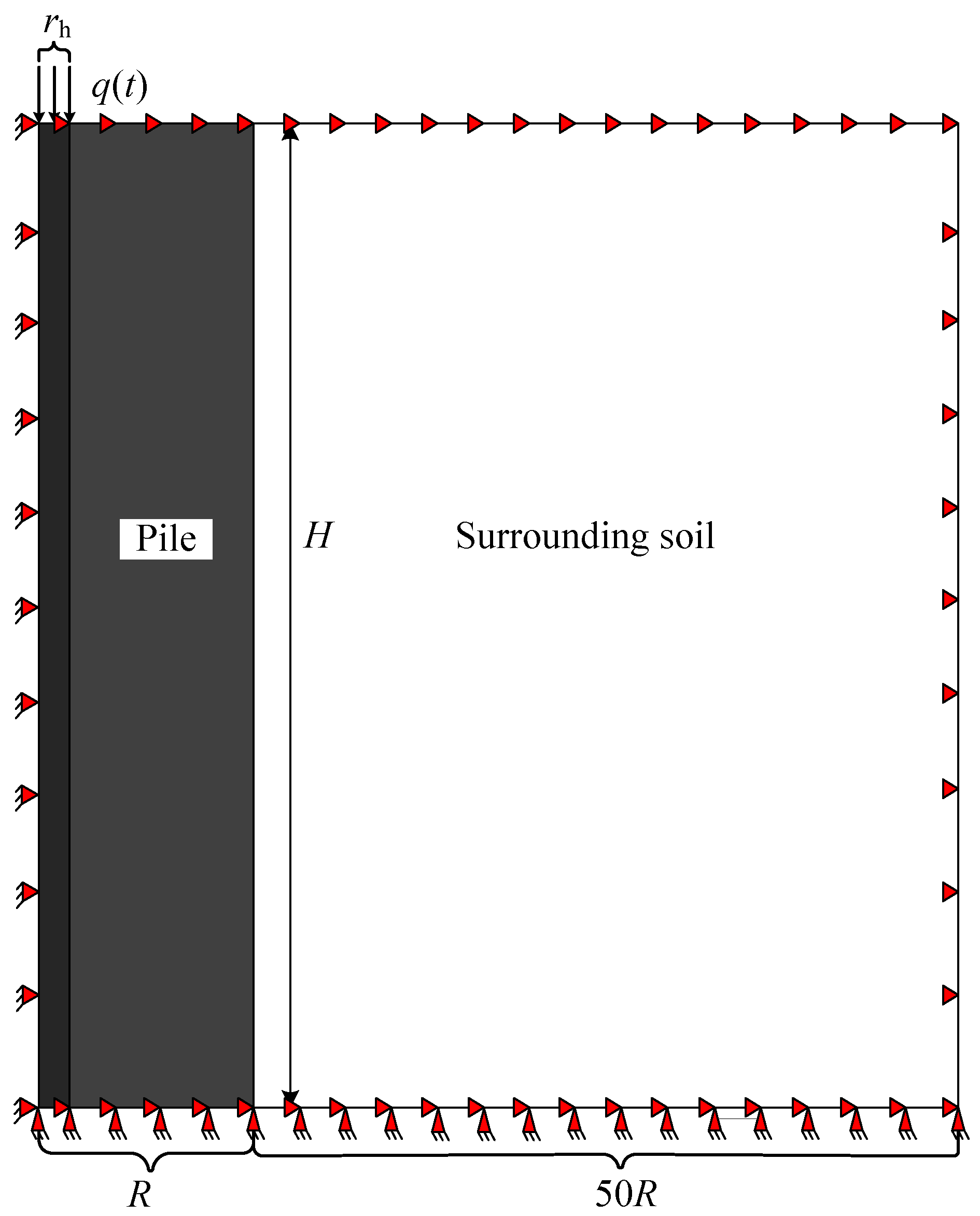

| Pile (I, II) | (GPa) | (kg/m3) | H (m) | |
| 40 | 2500 | 0.2 | 10 | |
| Surrounding soil | Es (Mpa) | (kg/m3) | ||
| 54 | 1800 | 0.35 |
| Pile (I, II) | (GPa) | (kg/m3) | H (m) | |
| 25 | 2500 | 0.15 | 10 | |
| Surrounding soil | Es (MPa) | (kg/m3) | ||
| 6 | 1800 | 0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, W.; Zhang, M.; Wang, Z.; Jiang, G.; Liu, W.; Cao, S.; Leo, C.J.; An, E.; Gao, X.; Wu, W. Influence of the Three-Dimensional Effect of Pile-Soil System on the Vertical Dynamic Response of Large-Diameter Piles in Low-Strain Integrity Testing. Energies 2022, 15, 9548. https://doi.org/10.3390/en15249548
Guan W, Zhang M, Wang Z, Jiang G, Liu W, Cao S, Leo CJ, An E, Gao X, Wu W. Influence of the Three-Dimensional Effect of Pile-Soil System on the Vertical Dynamic Response of Large-Diameter Piles in Low-Strain Integrity Testing. Energies. 2022; 15(24):9548. https://doi.org/10.3390/en15249548
Chicago/Turabian StyleGuan, Wenjie, Meixia Zhang, Zekun Wang, Guosheng Jiang, Wenqi Liu, Sheng Cao, Chin Jian Leo, Elieen An, Xiaodong Gao, and Wenbing Wu. 2022. "Influence of the Three-Dimensional Effect of Pile-Soil System on the Vertical Dynamic Response of Large-Diameter Piles in Low-Strain Integrity Testing" Energies 15, no. 24: 9548. https://doi.org/10.3390/en15249548
APA StyleGuan, W., Zhang, M., Wang, Z., Jiang, G., Liu, W., Cao, S., Leo, C. J., An, E., Gao, X., & Wu, W. (2022). Influence of the Three-Dimensional Effect of Pile-Soil System on the Vertical Dynamic Response of Large-Diameter Piles in Low-Strain Integrity Testing. Energies, 15(24), 9548. https://doi.org/10.3390/en15249548







