Study on Heat Transfer Characteristics and Performance of the Full Premixed Cauldron Stove with Porous Media
Abstract
1. Introduction
2. Theoretical Model
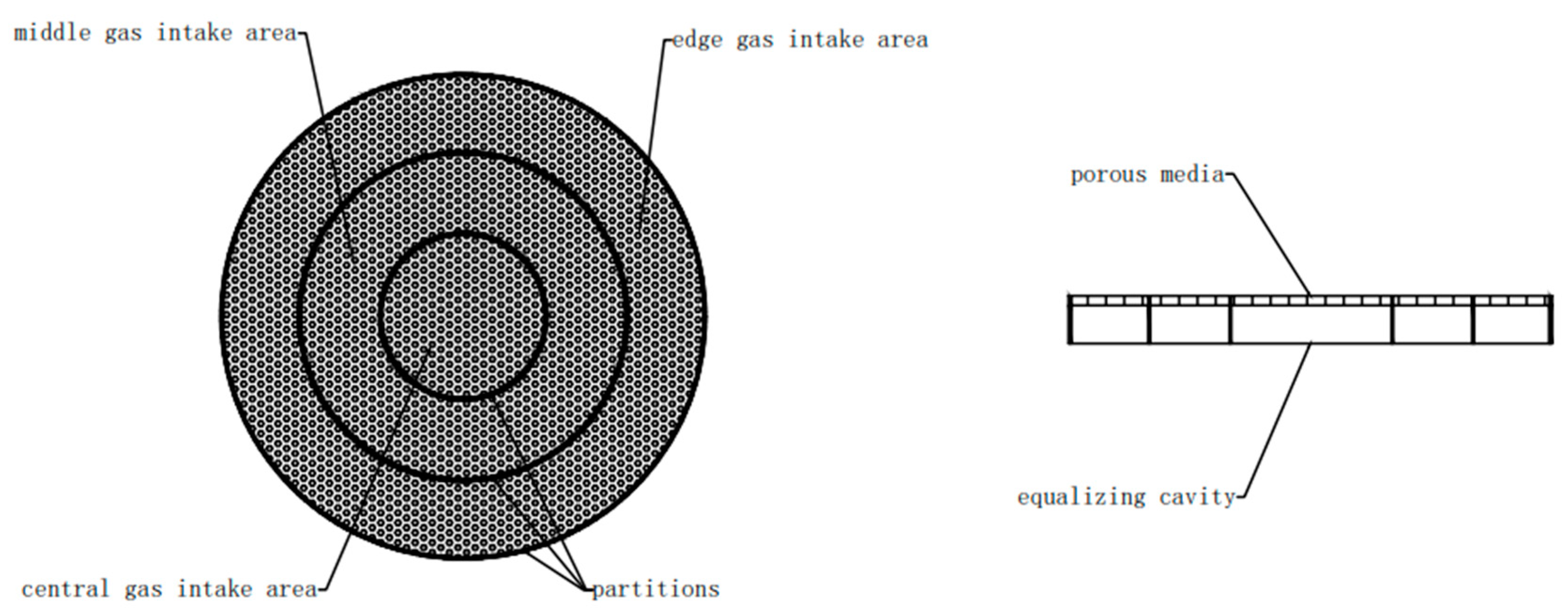
2.1. Structure and Working Principle of Fully Premixed Porous Media Cauldron Stove
2.2. Theoretical Model
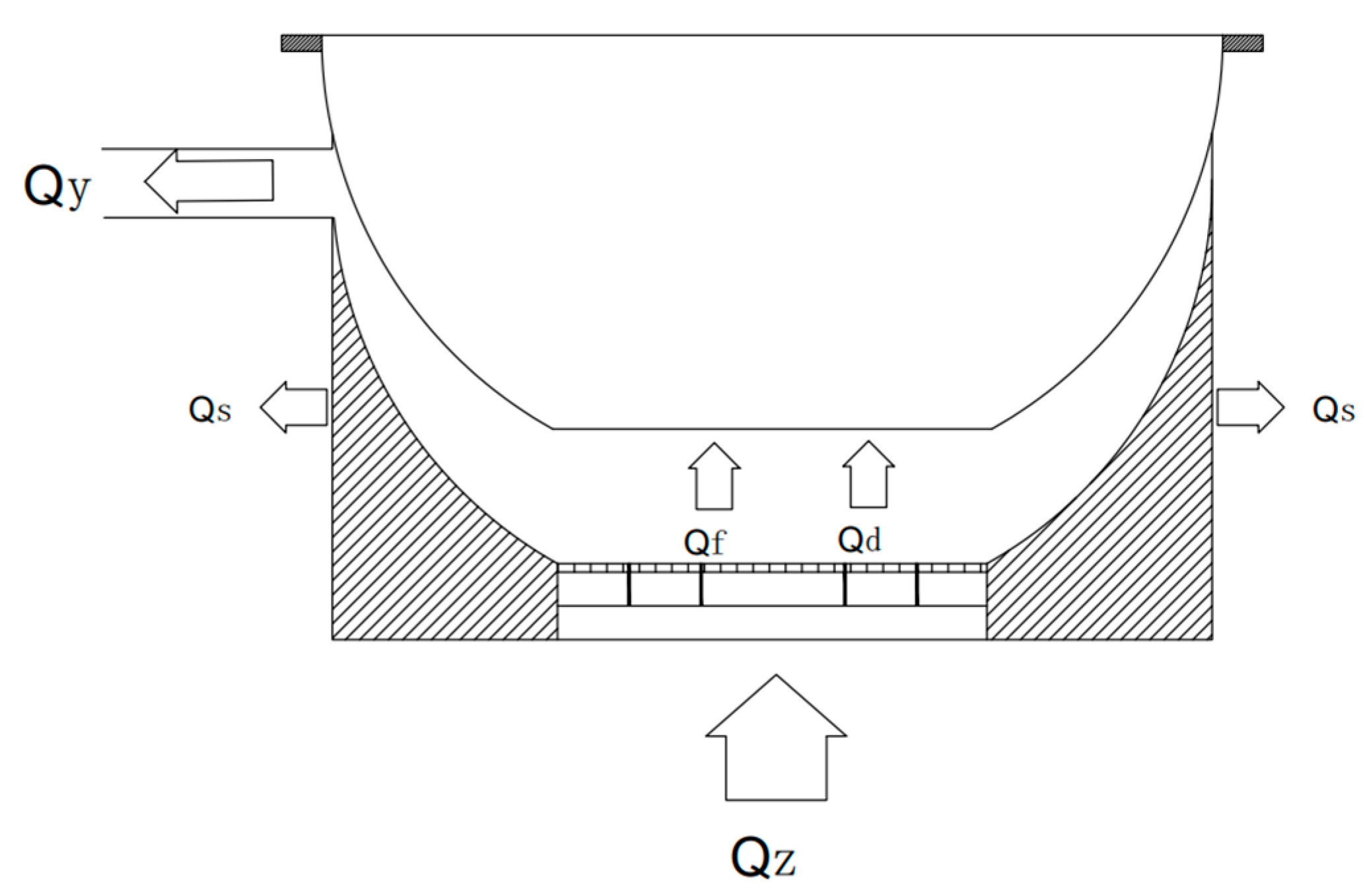
2.2.1. Heat Balance Equation of the Stove Chamber
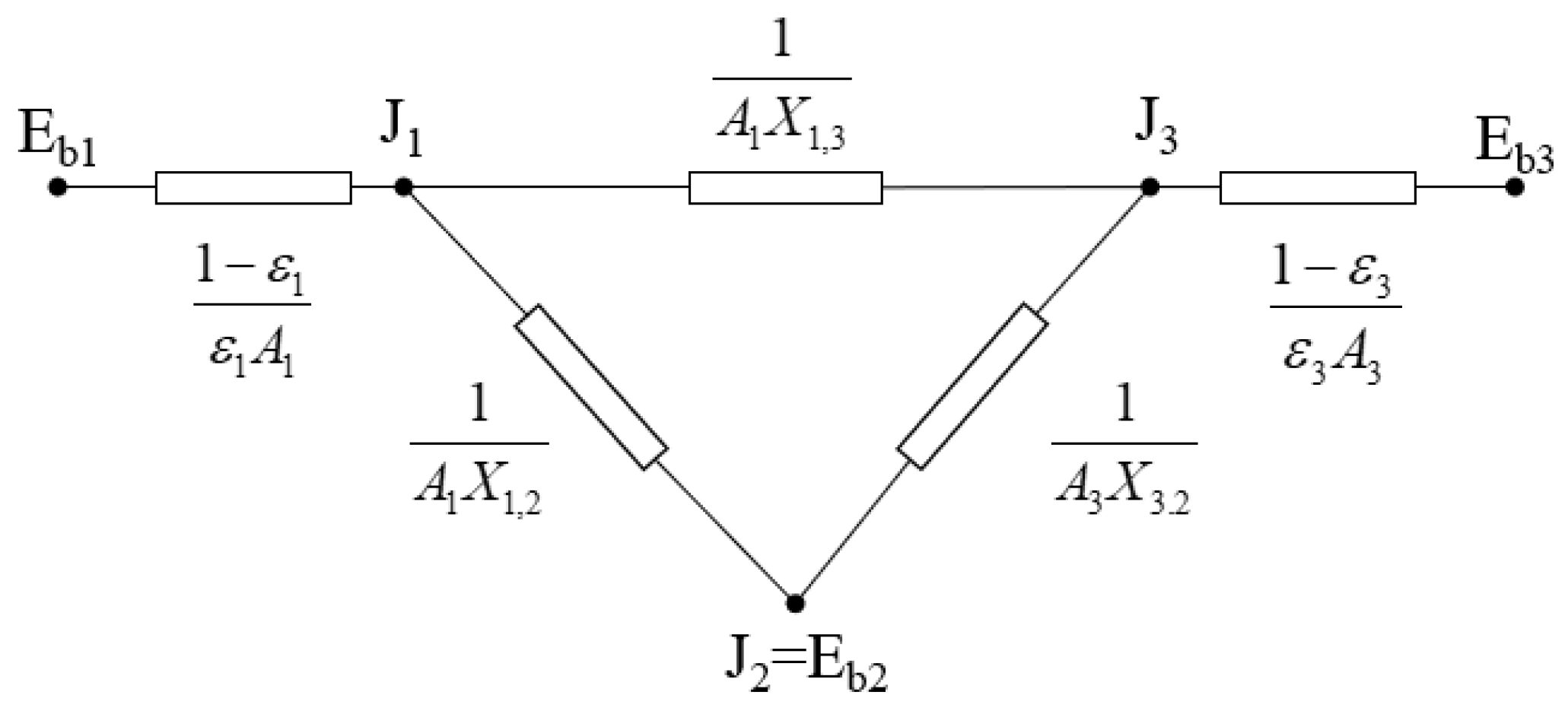
2.2.2. Heat Transfer Model Inside the Porous Media:
2.3. Numerical Simulation of Heat Transfer Characteristics of the Stove
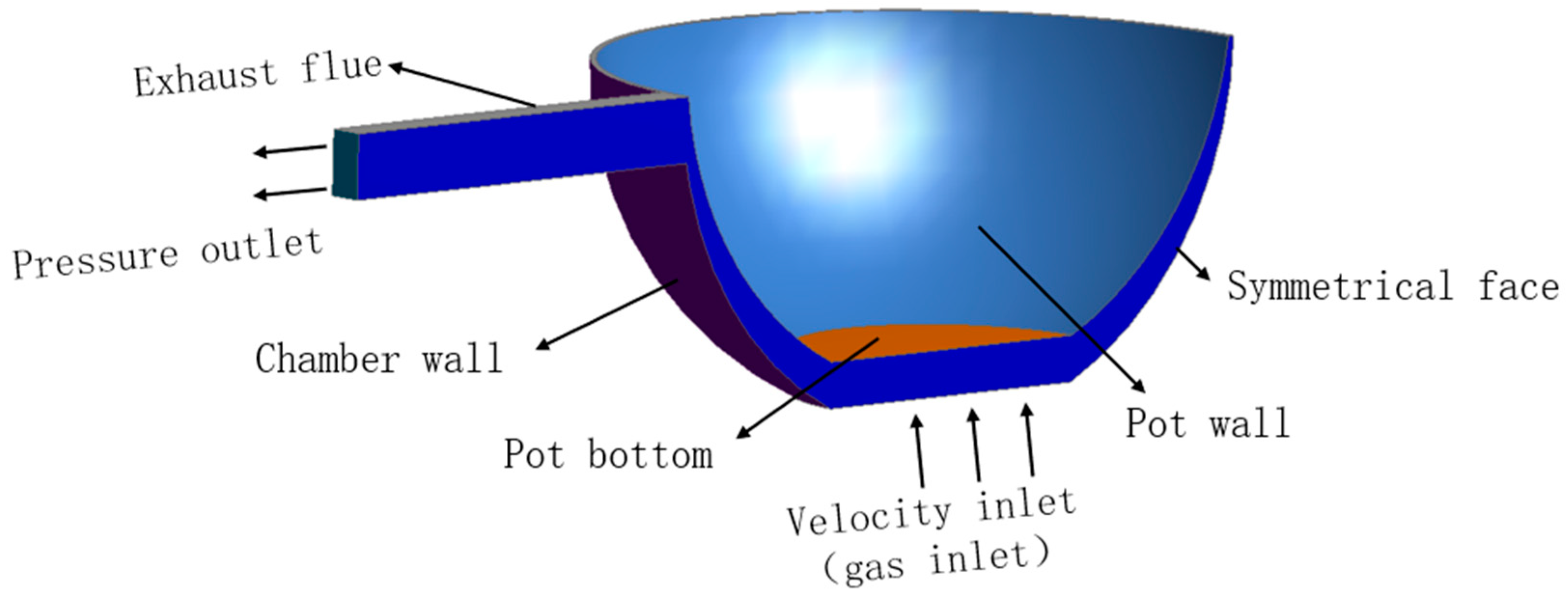
2.3.1. Physical Model
2.3.2. Model Assumptions
2.3.3. Control Equations and Boundary Conditions
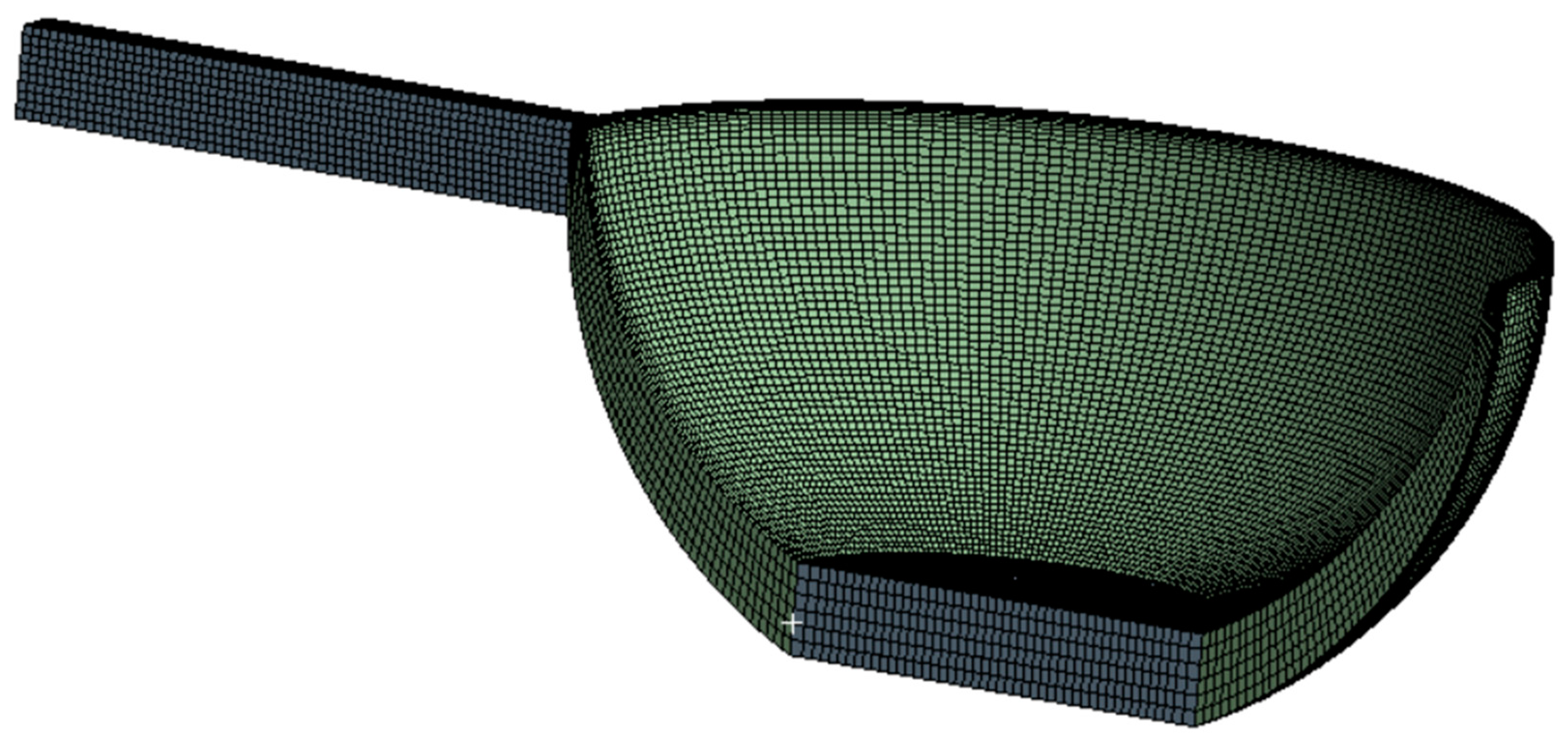
2.3.4. Meshing and Grid Independence Verification
3. Theoretical Analysis
3.1. Study on Performance of Fully Premixed Porous Stove at Rated Power
3.2. Analysis on Influencing Factors and Characteristics of the Fully Premixed Porous Stove
3.3. Performance Analysis
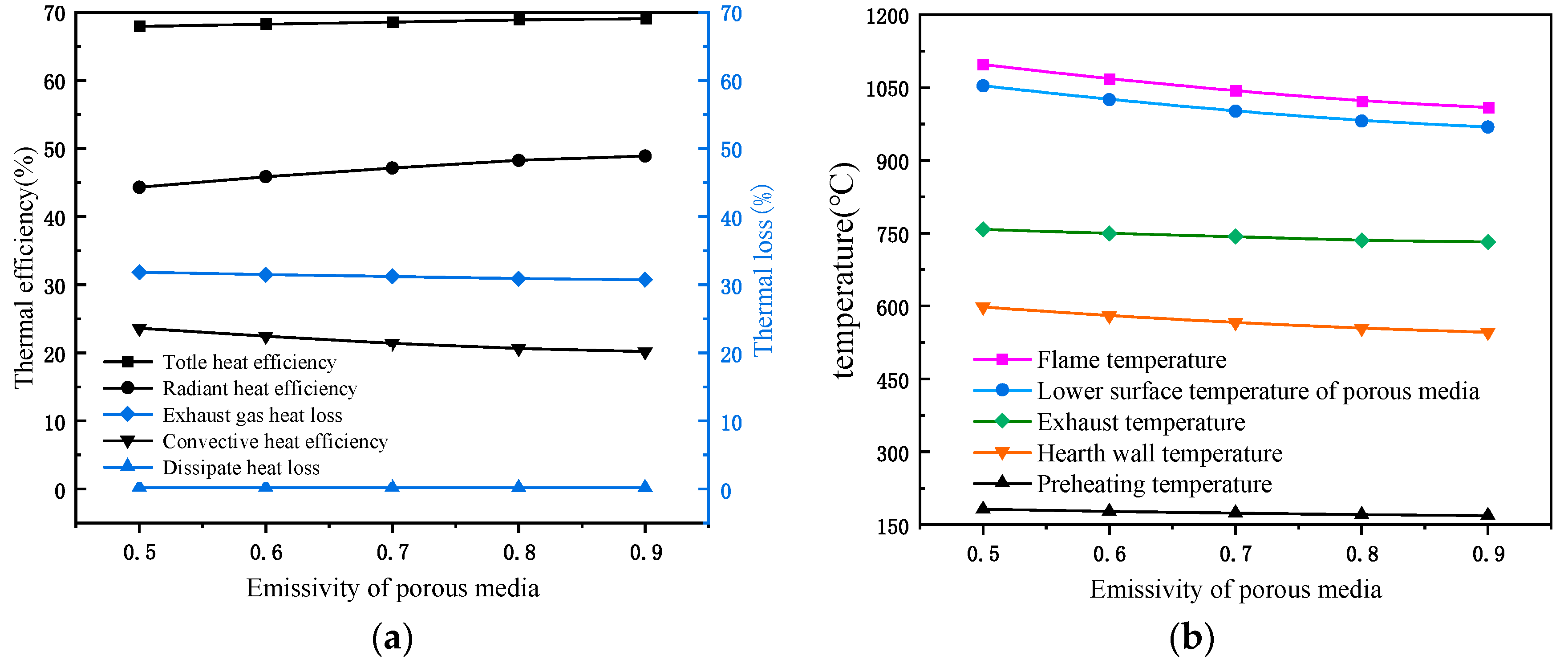
3.3.1. Influence of the Porous Media Emissivity on Stove Performance
3.3.2. Influence of the Porosity on Stove Performance
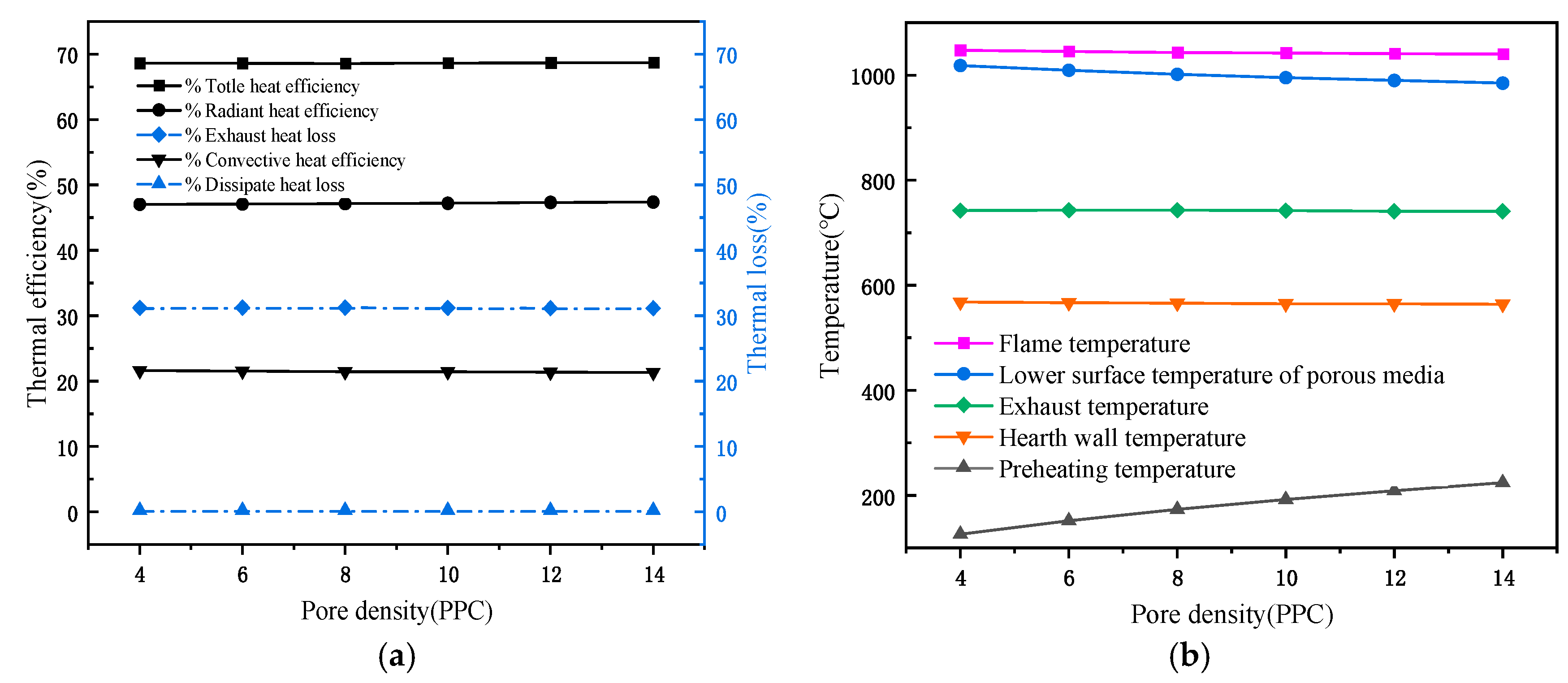
3.3.3. Influence of the Pore Density on Stove Performance
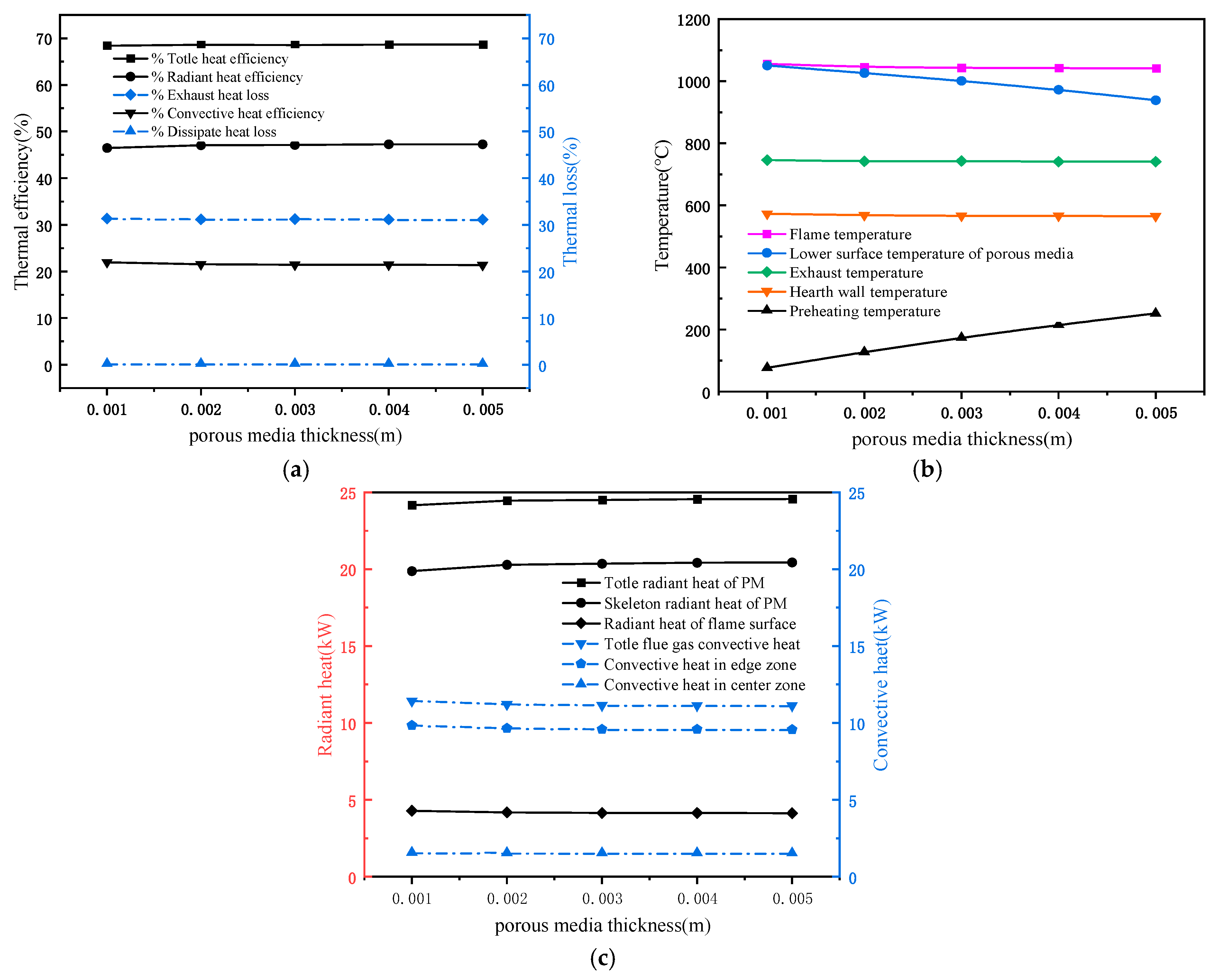
3.3.4. Influence of Porous Media Thickness on Stove Performance
3.3.5. Influence of the Porous Media Diameter on Stove Performance
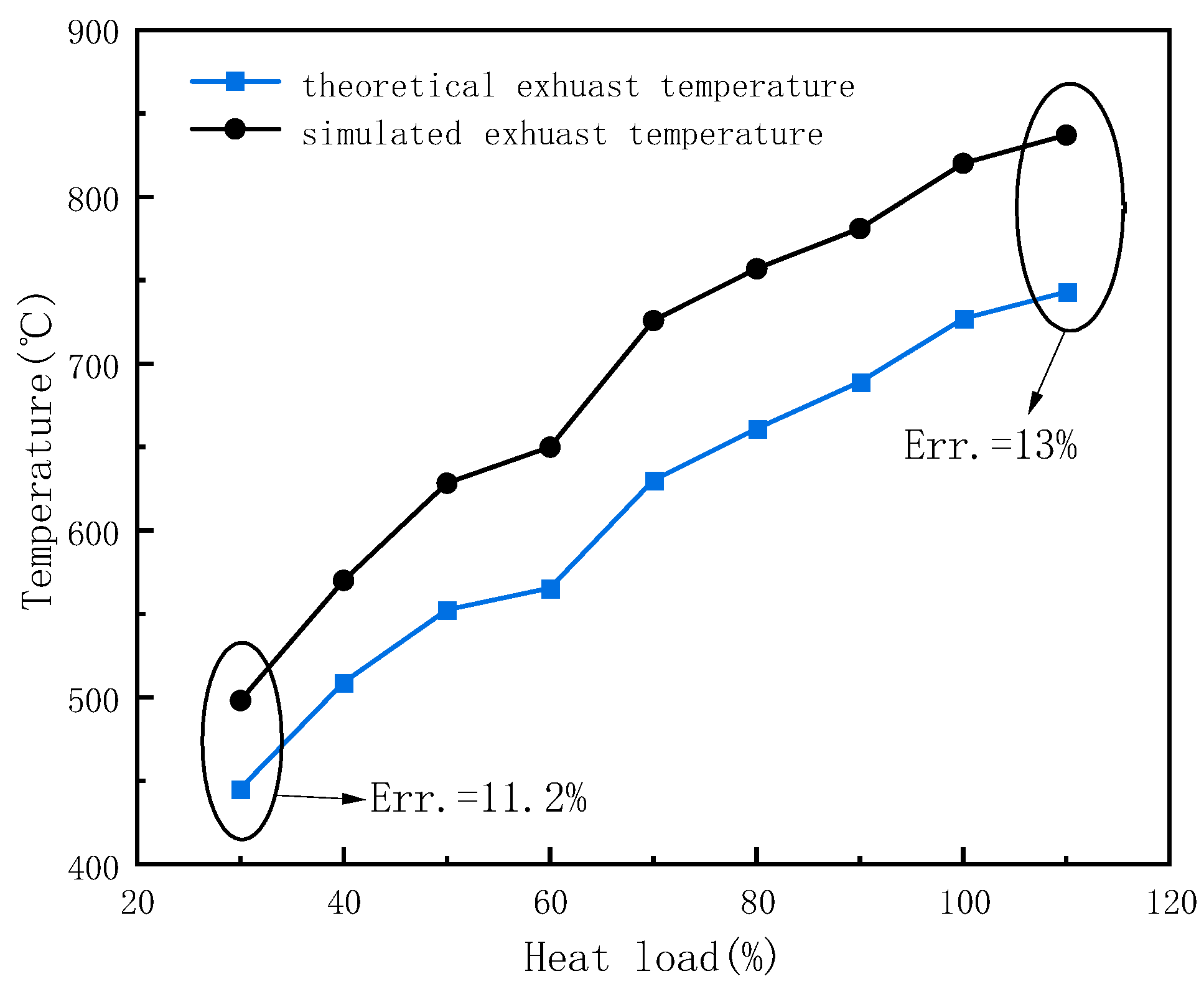
3.4. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | smoke blackness | W/(m2·K4) |
| ag | blackness of pot bottom | W/(m2·K4) |
| cpm | average constant pressure specific heat of premixed gas | kJ/(kg·K) |
| dk | diameter of the pores | m |
| h | convection heat transfer coefficient | W/(m2·K) |
| hz | distance from the porous media to the bottom of the pot | m |
| k | flue gas attenuation coefficient | 1/(m·MPa) |
| l | thickness of the stove | m |
| n | number of pores | |
| qv | volume flow of premixed gas | Nm3/s |
| r | volume share of triatomic gas | |
| rh | volume share of water vapor | |
| A1 | surface area of porous media | m2 |
| A3 | surface area of pot bottom | m2 |
| F | surface area of the chamber wall | m2 |
| P | pressure in the stove | Pa |
| Qc | low calorific value of natural gas | kJ/kg |
| Qd | flue gas convection heat | kW |
| Qd1 | convective heat transfer between the flue gas and the central area of the pot bottom | kW |
| Qd2 | convective heat transfer between the flue gas and marginal zone of the pot bottom | kW |
| Qf | radiant heat of the stove | kW |
| Qf2 | radiant heat transfer of the flue gas to the pot bottom | kW |
| Qs | heat dissipation of the chamber wall | kW |
| Qw | heat absorption of high-temperature flue gas at flame surface | kW |
| Qy | heat emitted by flue gas | kW |
| QZ | heat release of gas combustion | kW |
| Rz | total thermal resistance of space radiation | m2·K/W |
| Sd1 | area of the impinging jet area at the center of the pot bottom | m2 |
| Sd2 | heat exchange area between flue gas and pot bottom | m2 |
| Sn | total inner surface area of the pores | m2 |
| Tg | pot bottom temperature | °C |
| Th | flame temperature | °C |
| Tx | lower surface temperature of the porous media | °C |
| Ty | average temperature of flue gas in the stove | °C |
| Tyr | preheating temperature of premixed gas | °C |
| V | effective volume of the area in the stove except the flame jet | m3 |
| X1,2 | angle coefficients between porous media and chamber wall | |
| X1,3 | angle coefficients between porous media and pot bottom | |
| X3,2 | angle coefficients between pot bottom and chamber wall | |
| σ | blackbody radiation constant | W/(m2·K4) |
| ε1 | equivalent emissivity of the porous media | |
| ε3 | emissivity of the lower surface of the pot bottom | |
| ηq | flue gas dynamic viscosity calculated by the flue gas temperature | Pa·s |
| ηp | flue gas dynamic viscosity calculated by the boiler bottom temperature | Pa·s |
| η | total thermal efficiency of stove | |
| δ | thickness of porous media | m |
| λ | thermal conductivity of flue gas | W/m2·K−1 |
References
- Ren, Z. Combustion Simulation of Mixed Air Light Hydrocarbon Gas in Domestic Gas Stove; Xi’an Shiyou University: Xi’an, China, 2020. [Google Scholar]
- Ghosh, S.S.; Biswas, P.K.; Neogi, S. Thermal performance of solar cooker with special cover glass of low-e antimony doped indium oxide (IAO) coating. Appl. Therm. Eng. 2017, 113, 103–111. [Google Scholar] [CrossRef]
- Ongar, B.; Iliev, I.K.; Nikoli, V.; Milainovi, A.; Bulbul, O. The study and the mechanism of nitrogen oxides’ formation in combustion of fossil fuels udc 691.141. Facta Univ. Ser. Electron. Energetics 2018, 16, 273–283. [Google Scholar]
- Zhao, X. Application of full premixed combustion technology in gas appliances. Mod. Manuf. Technol. Equip. CNKI:SUN:SDJI.0.2019-01-075. 2019, 142+144. [Google Scholar]
- Cheng, L. Theory and Technology of Combustion in Porous Media; Chemical Industry Press: Beijing, China, 2013. [Google Scholar]
- Durst, F.; Weclas, M. A new type of internal combustion engine based on the porous media combustion technique. Proceedings of the Institute Mechanical Engineers. Part D. J. Automob. Eng. 2001, 215, 63–81. [Google Scholar] [CrossRef]
- Wang, E.; Cheng, L.; Luo, Z.; Xing, S.; Cen, K. Stability of Flames in the Gradually-varied Porous Media. Proc. Int. Conf. Energy Environ. 2003, 977–982. [Google Scholar]
- Deng, Z.; Liu, X.; Huang, Y.; Zhang, C.; Chen, Y. Heat Conduction in Porous Media Characterized by Fractal Geometry. Energies 2017, 10, 1230. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Fu, J.L.; Zhang, T.C.; Li, M.H.; Li, S.; Zhong, X.L.; Liu, X.R. Study on Flow and Heat Transfer Characteristics of Porous Media in Engine Particulate Filters Based on Lattice Boltzmann Method. Energies 2019, 12, 3319. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Z.; Yu, W.; Liu, M.; Chen, S. In vitro and in vivo evaluation of MgF2 coated AZ31 magnesium alloy porous scaffolds for bone regeneration. Colloids Surf. B Biointerfaces 2017, 149, 330–340. [Google Scholar]
- Gohil, P.P.; Dwivedi, G.; Shukla, A.K.; Verma, P. Experimental investigation of heat conservation through novel flame shield arrangement for domestic LPG gas stove. Mater. Today Proc. 2021, 49, 223–229. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Yang, T.; Yu, Y.; Liu, C.; Li, B. Numerical and experimental investigation on heat transfer enhancement by adding fins on the pot in a domestic gas stove. Energy 2021, 239, 122439. [Google Scholar] [CrossRef]
- Pantangi, V.K.; Mishra, S.C.; Muthukumar, P. Studies on porous radiant burners for LPG (liquefied petroleum gas) cooking applications. Energy 2011, 36, 6074–6080. [Google Scholar] [CrossRef]
- Kaushik, L.K.; Muthukumar, P. Life cycle Assessment (LCA) and Techno-economic Assessment (TEA) of media scale (5–10 kW) LPG cooking stove with two-layer porous radiant burner. Appl. Therm. Eng. 2018, 133, 316–326. [Google Scholar]
- Mishra, N.K. Development of Self-Aspirated Two-Layer Porous Radiant Burners for LPG Cooking Applications. Ph.D. Thesis, Department of Mechanical Engineering, IIT, Guwahati, India, 2015. [Google Scholar]
- Yang, S.; Tao, W. Heat Transfer, 4th ed.; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single spheres, and flow in packed bids and tube bundles. AIChE J. 1972, 18, 361–372. [Google Scholar] [CrossRef]
- Chen, G. Principle of Boiler; Huazhong University of Science and Technology Press: Wuhan, China, 2012. [Google Scholar]
- Kennedy, L.A.; Bingue, J.P.; Saveliev, A.V.; Fridman, A.A.; Foutko, S.I. Chemical structures of methane-air filtration combustion waves for fuel-lean and fuel-rich conditions. Proc. Combust. Inst. 2000, 28, 1431–1438. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, W.; Jia, Y.; Tang, J. Numerical simulation of combustion performance of porous metal plate gas stove. Gas. Heat 2021, 41, 18–25+42–43. [Google Scholar]
- Wu, C.; Chen, K.; Yang, S. Experimental study of porous metal burners for domestic stove applications. Energy Convers. Manag. 2014, 77, 380–388. [Google Scholar] [CrossRef]
- He, Y. Study on Thermal Performance and Energy Saving Technology of Infrared Gas Stove. Master’s Thesis, Chongqing University, Chongqing, China, 2020. [Google Scholar]
- Keramiotis, C.; Stelzner, B.; Trimis, D.; Founti, M. Porous burners for low emission combustion: An experimental investigation. Energy 2012, 45, 213–219. [Google Scholar] [CrossRef]




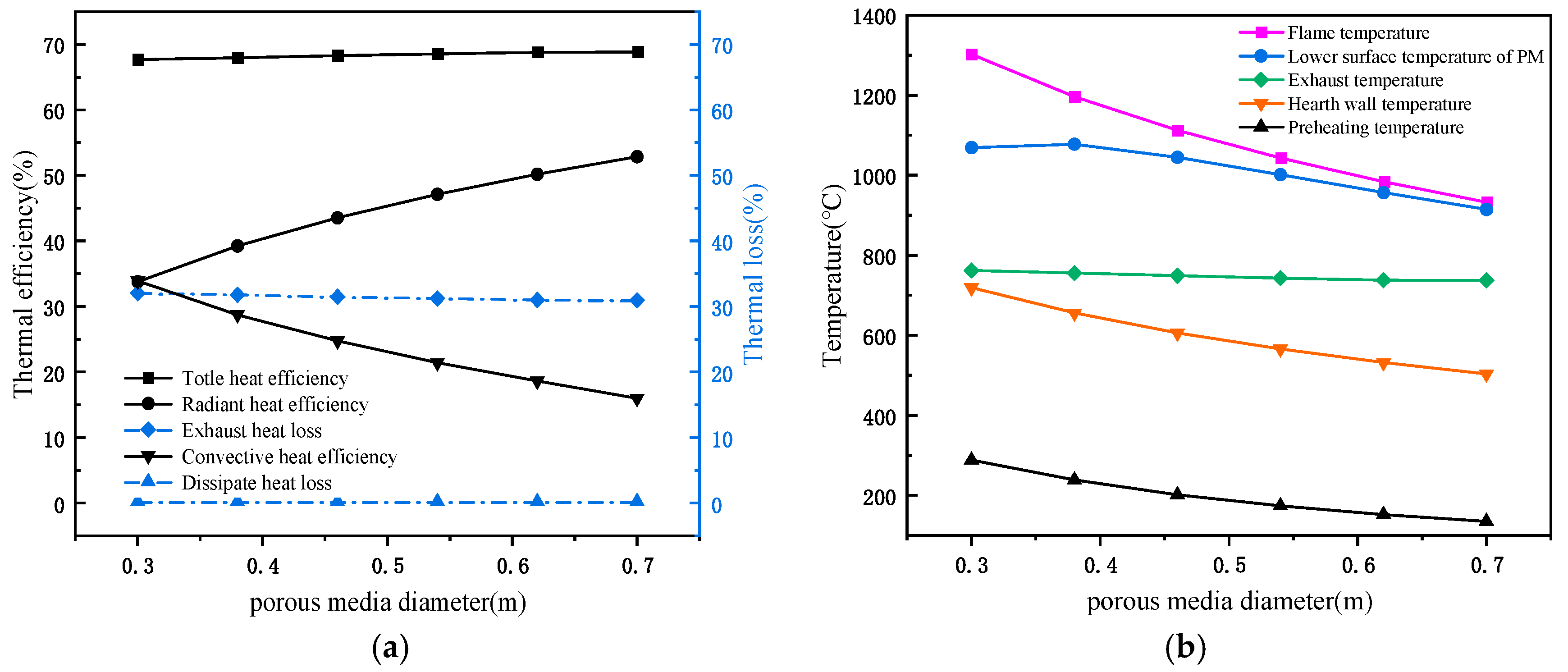
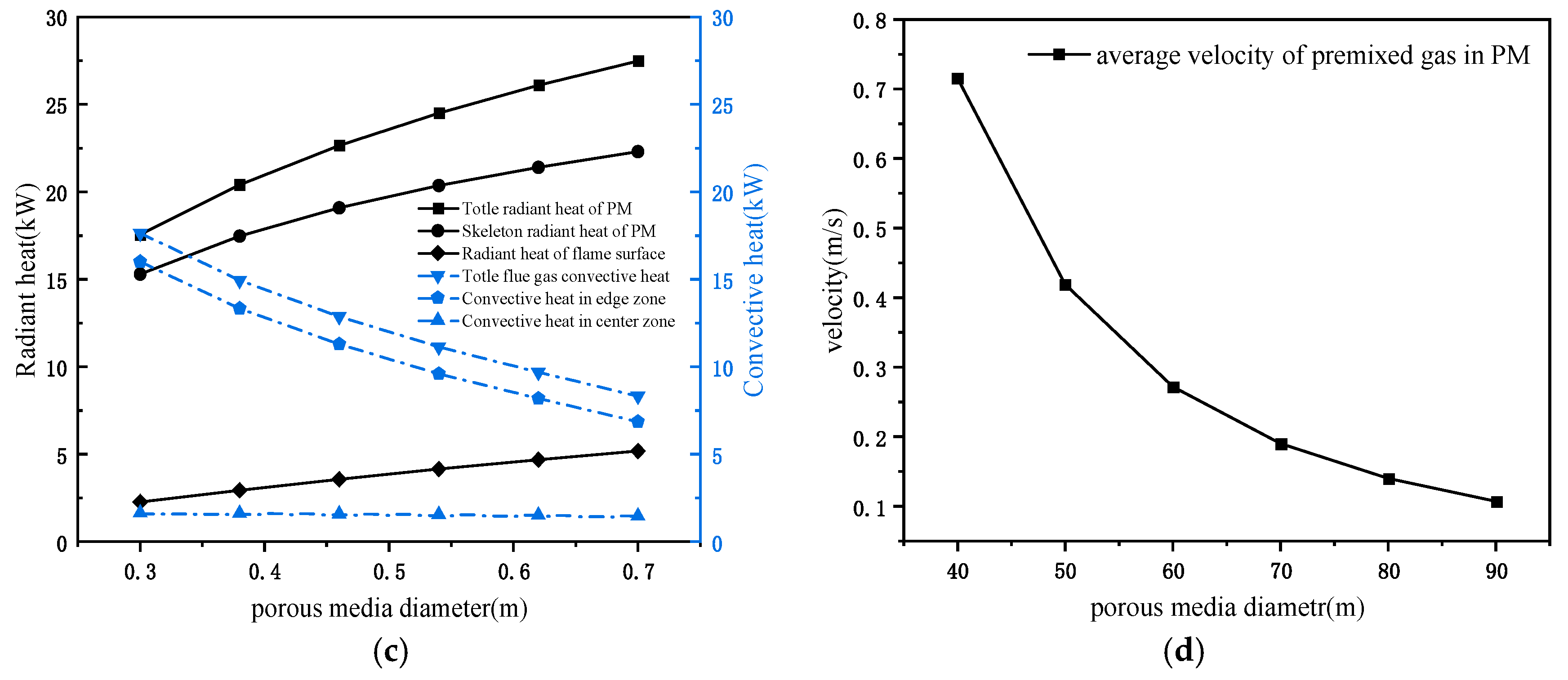
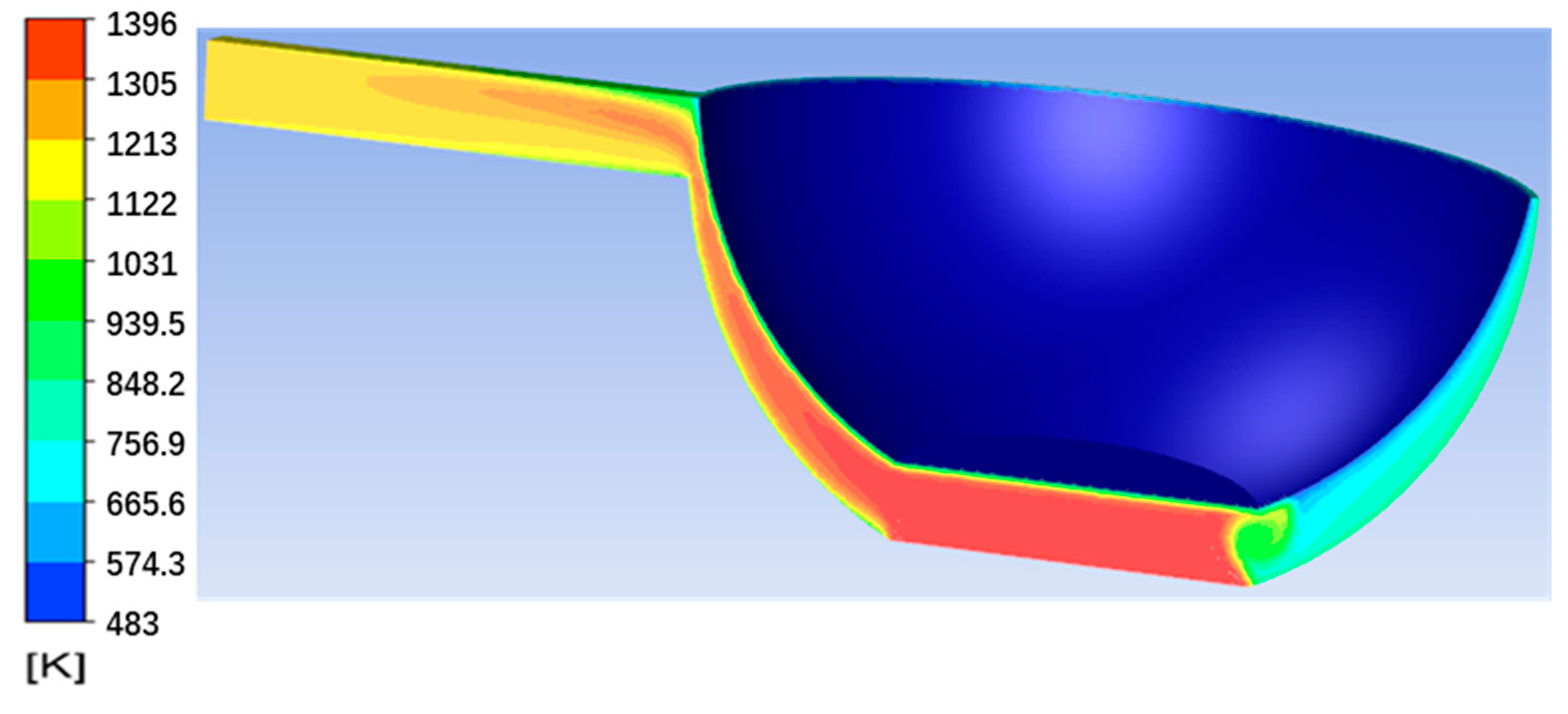
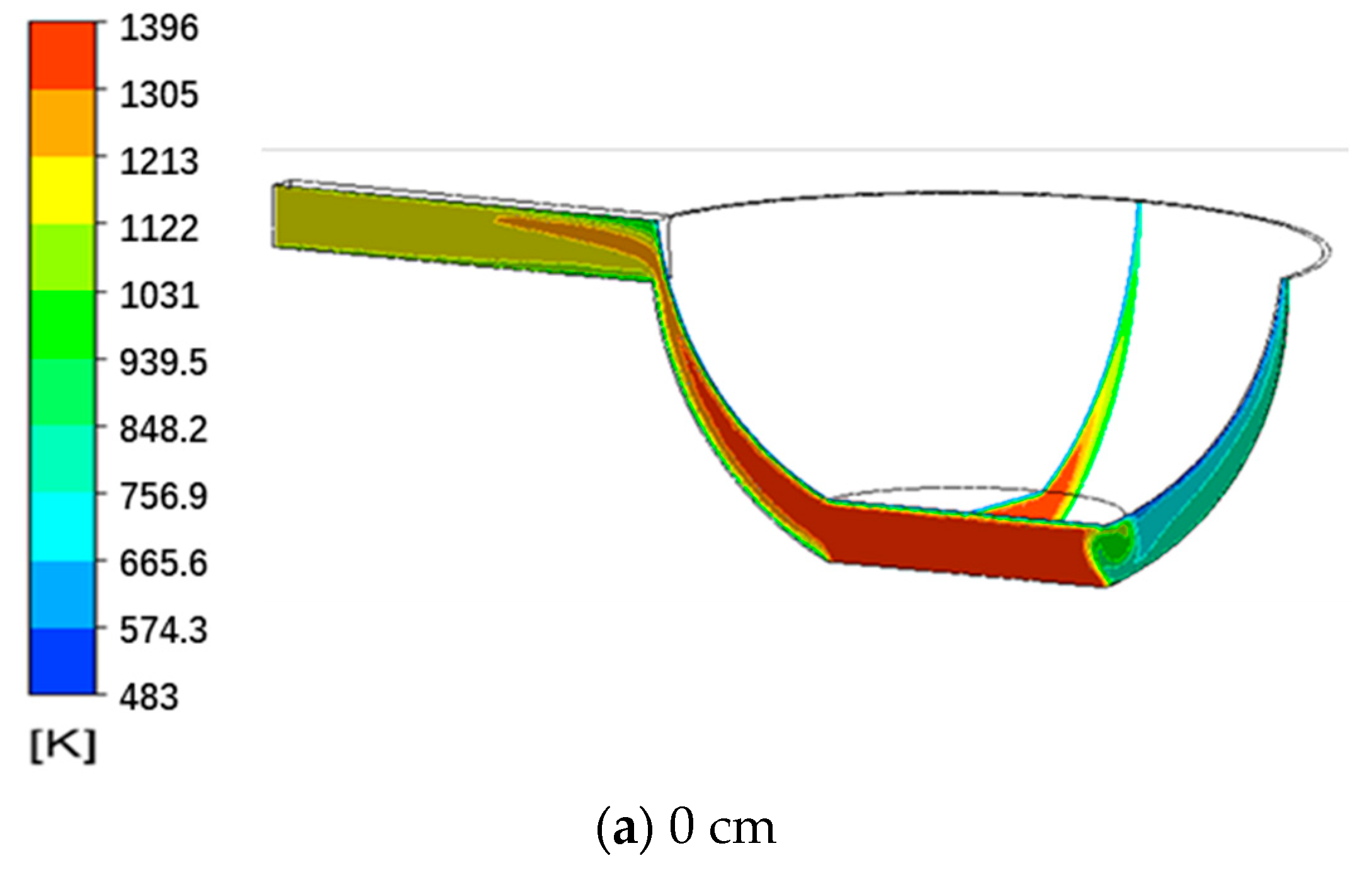


| Parameters of PM | Parameters of Stove Chamber | ||
|---|---|---|---|
| material | Cordierite | rated power | 52 kW |
| emissivity | 0.7 | chamber depth | 0.48 m |
| porosity | 60% | height between PM and pot bottom | 0.05 m |
| pore density | 8 PPC | ||
| average pore diameter | 0.0011 m | chamber volume | 0.0458 m3 |
| diameter of PM | 0.54 m | pot bottom temperature | 210 °C |
| thickness of PM | 0.003 m | ambient temperature | 20 °C |
| Item | Thermal Power, kW | Proportion, % | |||
|---|---|---|---|---|---|
| Effective heat | Radiant heat | Radiant heat of PM skeleton | 20.362 | 24.513 | 47.14 |
| Radiant heat of the flame surface | 4.151 | ||||
| Convective heat | Convective heat in the central region | 1.542 | 11.133 | 21.41 | |
| Convective heat in the edge zone | 9.591 | ||||
| Total effective heat | 35.646 | 68.55 | |||
| Heat loss item | Heat loss of exhaust gas | 16.229 | 31.21 | ||
| Heat loss of chamber wall | 0.171 | 0.24 | |||
| Total heat loss | 16.4 | 31.45 | |||
| Item | Influencing Factor | Original Value | Value Range |
|---|---|---|---|
| Influencing factors of PM | porosity | 60% | 40–90% |
| pore density | 8 PPC | 4–14 PPC | |
| emissivity | 0.7 | 0.5–0.9 | |
| thickness | 0.003 m | 0.001–0.005 m | |
| Influencing factors of chamber | diameter | 0.54 m | 0.3–0.7 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, D.; Su, L.; Ou, H.; Ruan, S. Study on Heat Transfer Characteristics and Performance of the Full Premixed Cauldron Stove with Porous Media. Energies 2022, 15, 9523. https://doi.org/10.3390/en15249523
Zheng D, Su L, Ou H, Ruan S. Study on Heat Transfer Characteristics and Performance of the Full Premixed Cauldron Stove with Porous Media. Energies. 2022; 15(24):9523. https://doi.org/10.3390/en15249523
Chicago/Turabian StyleZheng, Dingming, Lei Su, Haoyu Ou, and Shijie Ruan. 2022. "Study on Heat Transfer Characteristics and Performance of the Full Premixed Cauldron Stove with Porous Media" Energies 15, no. 24: 9523. https://doi.org/10.3390/en15249523
APA StyleZheng, D., Su, L., Ou, H., & Ruan, S. (2022). Study on Heat Transfer Characteristics and Performance of the Full Premixed Cauldron Stove with Porous Media. Energies, 15(24), 9523. https://doi.org/10.3390/en15249523







