Co-Operative Optimization Framework for Energy Management Considering CVaR Assessment and Game Theory
Abstract
:1. Introduction
- The master–slave game model can take into account the interest demands of each participant, while the direct P2P energy-sharing behavior among MGs can reduce the market power of leaders and improve social welfare. In terms of coalition cost sharing, this paper proposes an allocation method that considers the contribution of cooperation and adopts asymmetric Nash bargaining theory to allocate the co-operation surplus to make the allocation result fairer and more reasonable.
- In the proposed energy management model, MAs integrate social welfare and risk levels in order to determine price discrimination behavior for the whole process of coordinated electricity trading.
2. Problem Description
3. System Modelling
3.1. Caculation of the CVaR Value
3.2. Microgrid Aggregator
3.3. Multi-Microgrids
3.3.1. Energy Balance Constraints
3.3.2. Transmission Power Constraints
3.3.3. Battery Energy Storage System Operating Constraints
3.3.4. Micro Gas Turbines Operating Constraints
3.3.5. Constraints on Interruptible Loads
4. Bi-Level Optimization Model Based on Stackelberg Game and Solution Methodology
4.1. Stackelberg Game
4.2. Benefit Allocation Based on Nash Bargaining Theory
4.3. Solution Methodology
5. Case Study
5.1. Basic Parameters
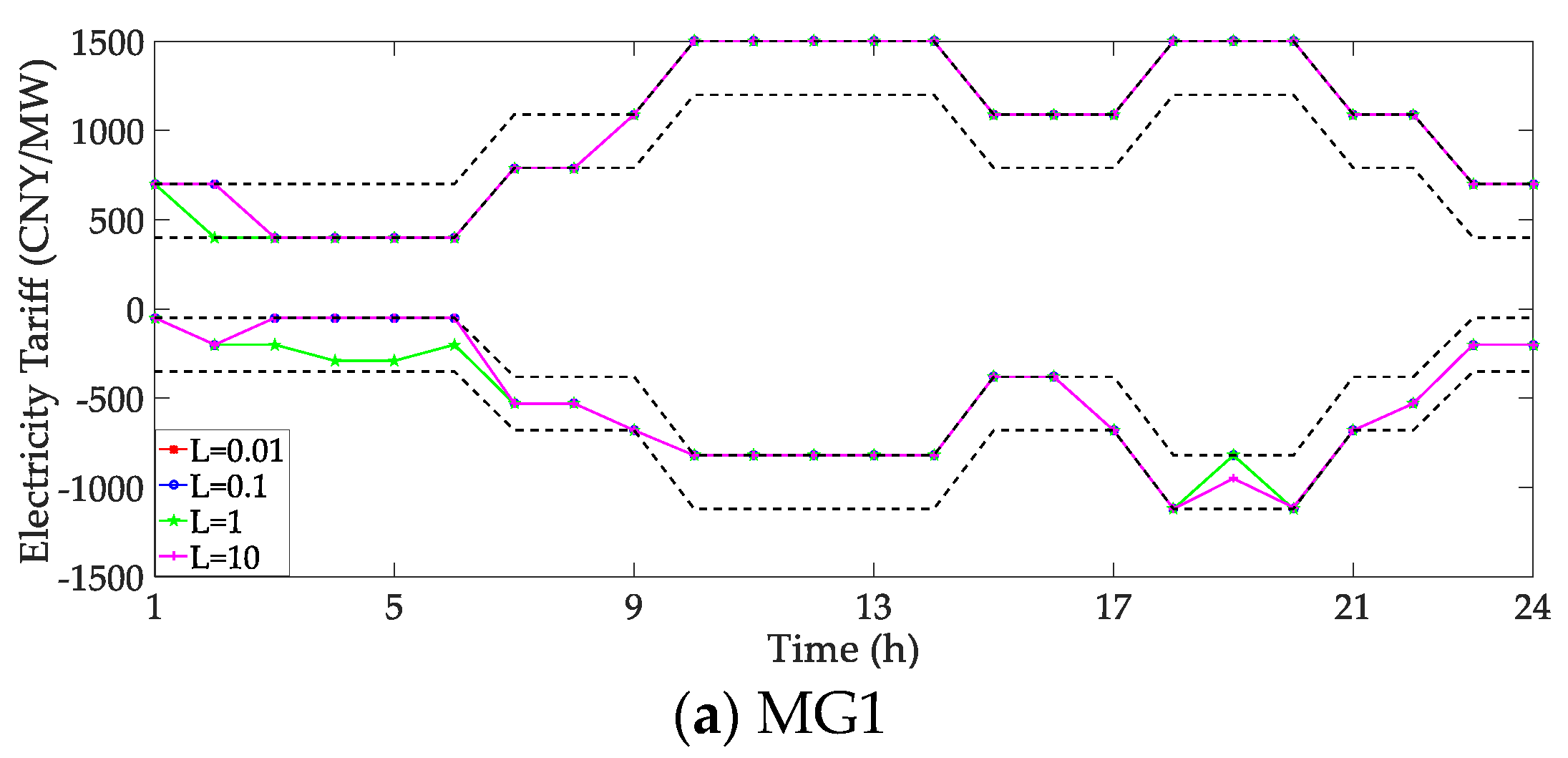
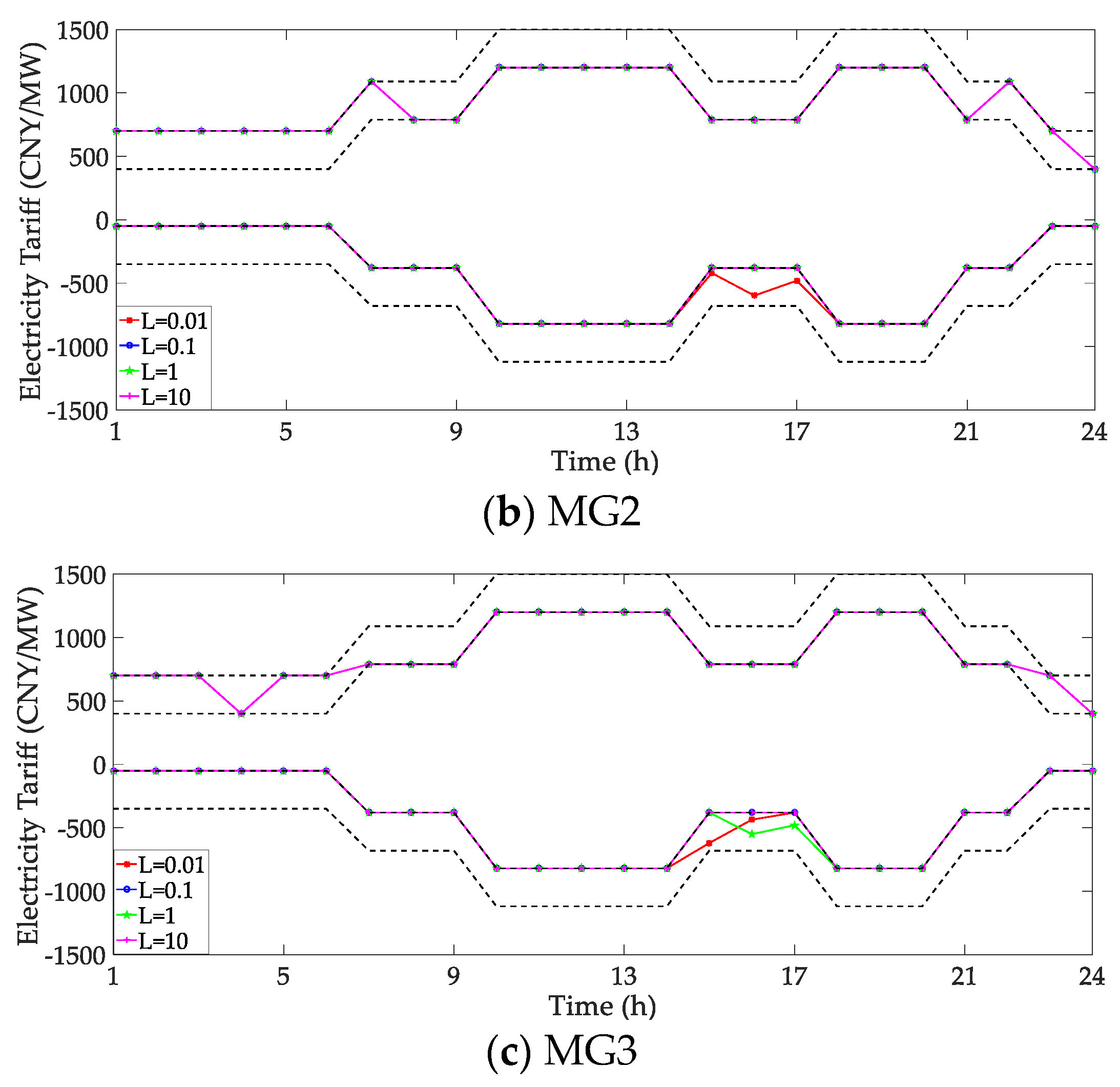
5.2. Impact of Parameter L on Electricity Sales Retail Price Decisions
5.3. Impact of Parameter L on the Operating State of MMGS
6. Conclusions
- The energy management framework based on the master–slave game proposed in this paper can take into account the mutual influence of MAs and each MG’s decision, which is in accordance with the actual interests of multiple subjects. The proposed bi-level optimization model in this paper can effectively improve the ability of the energy management system to cope with risks and improve the ability of the expected benefits of MAs under different risk levels.
- In the energy management framework proposed in this paper, the P2P energy sharing mode among MGs has the advantage of reducing the cost of electricity. In the model example of this paper, the cost of electricity consumption of MMGS was about 23% lower than the cost in the non-co-operative mode with complete competition among communities, thus achieving win–win co-operation.
- In the energy management framework proposed in this paper, the MA can enhance its ability to cope with risks to improve the expected revenue under different risk aversion levels.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Alotaibi, I.; Abido, M.A.; Khalid, M.; Savkin, A.V. A Comprehensive Review of Recent Advances in Smart Grids: A Sustainable Future with Renewable Energy Resources. Energies 2020, 13, 6269. [Google Scholar] [CrossRef]
- Jiaqi, S.; Liya, M.; Chenchen, L.; Nian, L.; Jianhua, Z. A comprehensive review of standards for distributed energy resource grid-integration and microgrid. Renew. Sust. Energ. Rev. 2022, 170, 112957. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, J.; Zhang, W. An Effective Operation Strategy for CCHP System Integrated with Photovoltaic/Thermal Panels and Thermal Energy Storage. Energies 2020, 13, 6418. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Tajik, E.; Awwad, E.M.; El-Sherbeeny, A.M.; Elmeligy, M.A.; Ali, Z.M. A two-stage stochastic framework for effective management of multiple energy carriers. Energy 2020, 197, 117170. [Google Scholar] [CrossRef]
- López-Prado, J.L.; Vélez, J.I.; Garcia-Llinás, G.A. Reliability Evaluation in Distribution Networks with Microgrids: Review and Classification of the Literature. Energies 2020, 13, 6189. [Google Scholar] [CrossRef]
- Yunshou, M.; Jiekang, W.; Zhihong, C.; Ruidong, W.; Ran, Z.; Lingmin, C. Cooperative Operation Framework for a Wind-Solar-CCHP Multi-Energy System Based on Nash Bargaining Solution. IEEE Access 2021, 9, 119987–120000. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Tang, L.; Sun, W.; Zhao, H. A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs. Energies 2019, 12, 3983. [Google Scholar] [CrossRef] [Green Version]
- Fan, S.; Ai, Q.; Piao, L. Bargaining-based cooperative energy trading for distribution company and demand response. Appl. Energy 2018, 226, 469–482. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.-W.; Shi, Y.; Xiao, J.-W. An Efficient Peer-to-Peer Energy-Sharing Framework for Numerous Community Prosumers. IEEE Trans. Ind. Inform. 2020, 16, 7402–7412. [Google Scholar] [CrossRef]
- Kumar, A.; He, X.; Deng, Y.; Singh, A.R.; Sah, B.; Kumar, P.; Bansal, R.C.; Bettayeb, M.; Rayudu, R. A sustainable rural electrification based on a socio-techno-economic-environmental-political microgrid design framework. Energy Environ. Sci. 2022, 15, 4213–4246. [Google Scholar] [CrossRef]
- Lan, T.; Jermsittiparsert, K.; Alrashood, S.T.; Rezaei, M.; Al-Ghussain, L.; Mohamed, A.M. An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand. Energies 2021, 14, 569. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Hajjiah, A.; Alnowibet, K.A.; Alrasheedi, A.F.; Awwad, E.M.; Muyeen, S.M. A Secured Advanced Management Architecture in Peer-to-Peer Energy Trading for Multi-Microgrid in the Stochastic Environment. IEEE Access 2021, 9, 92083–92100. [Google Scholar] [CrossRef]
- Davarzani, S.; Pisica, I.; Taylor, G.A.; Munisami, K.J. Residential Demand Response Strategies and Applications in Active Distribution Network Management. Renew. Sust. Energ. Rev. 2020, 138, 110567. [Google Scholar] [CrossRef]
- Patil, G.S.; Mulla, A.; Dawn, S.; Ustun, T.S. Profit Maximization with Imbalance Cost Improvement by Solar PV-Battery Hybrid System in Deregulated Power Market. Energies 2022, 15, 5290. [Google Scholar] [CrossRef]
- Li, G.; Li, Q.; Liu, Y.; Liu, H.; Song, W.; Ding, R. A cooperative Stackelberg game based energy management considering price discrimination and risk assessment. Int. J. Electr. Power 2022, 135, 107461. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.-W.; Liu, X.-K.; Wang, Z.; Xiao, J.-W. Economic Storage Sharing Framework: Asymmetric Bargaining-Based Energy Cooperation. IEEE Trans. Ind. Inform. 2021, 17, 7489–7500. [Google Scholar] [CrossRef]
- Ma, T.; Pei, W.; Xiao, H.; Kong, L.; Mu, Y.; Pu, T. The energy management strategies based on dynamic energy pricing for community integrated energy system considering the interactions between suppliers and users. Energy 2020, 211, 118677. [Google Scholar] [CrossRef]
- Pan, X.; Yang, F.; Ma, P.; Xing, Y.; Zhang, J.; Cao, L. A Game-Theoretic Approach of Optimized Operation of AC/DC Hybrid Microgrid Clusters. Energies 2022, 15, 5537. [Google Scholar] [CrossRef]
- Shandilya, S.; Szymanski, Z.; Shandilya, S.K.; Izonin, I.; Singh, K.K. Modeling and Comparative Analysis of Multi-Agent Cost Allocation Strategies Using Cooperative Game Theory for the Modern Electricity Market. Energies 2022, 15, 2352. [Google Scholar] [CrossRef]
- Yi, Z.; Xin-gang, Z.; Xin, M.; Yu-zhuo, Z. Research on tradable green certificate benchmark price and technical conversion coefficient: Bargaining-based cooperative trading. Energy 2020, 208, 376. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.-W.; Shi, Y.; Xiao, J.-W. A New and Fair Peer-to-Peer Energy Sharing Framework for Energy Buildings. IEEE Trans. Smart Grid 2020, 11, 3817–3826. [Google Scholar] [CrossRef]
- Wen, Y.; Chen, Y.; Wu, J.; Mao, X.; Huang, H.; Yang, L. Research on Risk Assessment and Suppression Measures for Ice-Shedding on 500 kV Compact Overhead Lines. Energies 2022, 15, 8005. [Google Scholar] [CrossRef]
- Wu, J.; Wu, Z.; Wu, F.; Tang, H.; Mao, X. CVaR risk-based optimization framework for renewable energy management in distribution systems with DGs and EVs. Energy 2018, 143, 323–336. [Google Scholar] [CrossRef]

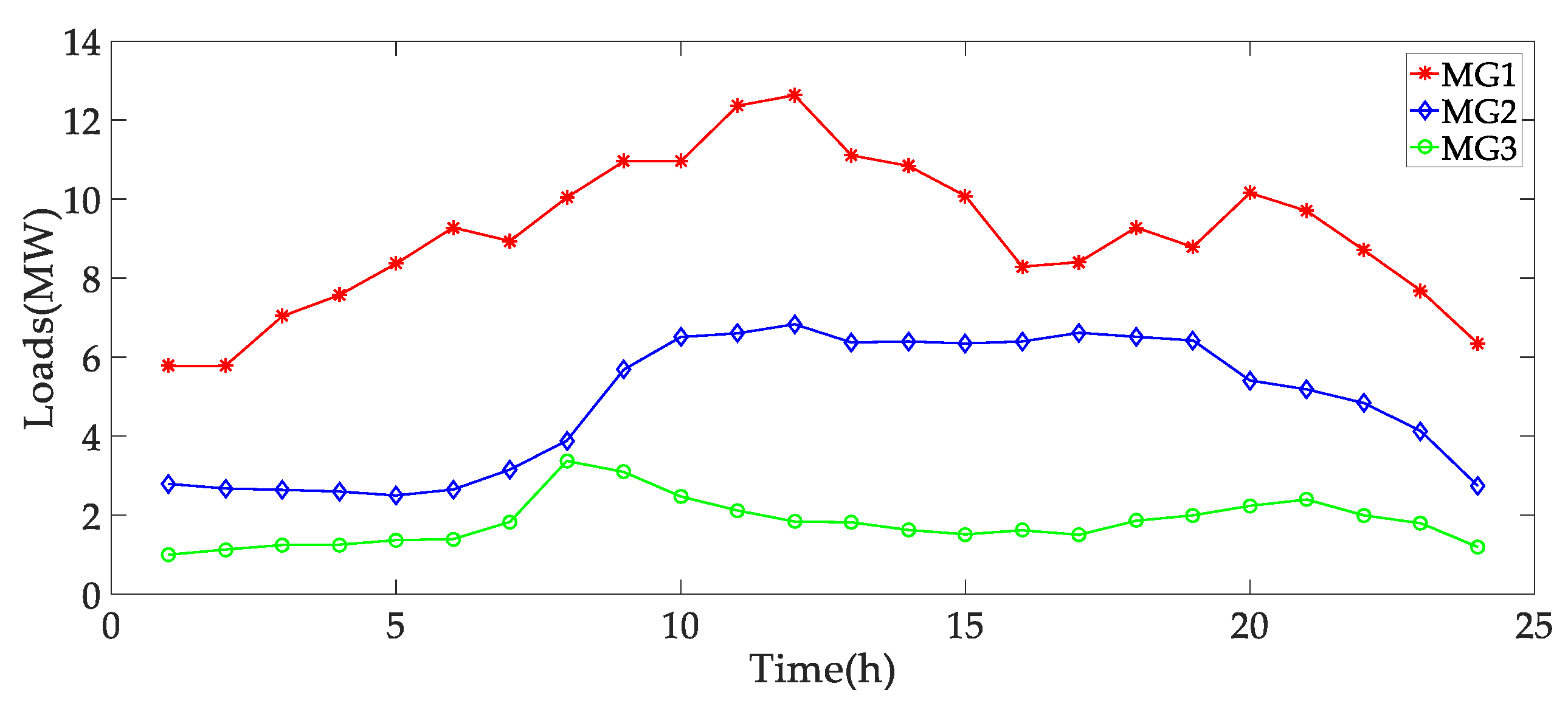


| Item | Parameter | Value | ||
|---|---|---|---|---|
| MG 1 | MG 2 | MG 3 | ||
| MT | 2 MW | 1 MW | 4 MW | |
| 1 MW | 0.5 MW | 2 MW | ||
| BESS | 8 MWh | 6 MWh | 10 MWh | |
| 0.33 | 0.33 | 0.33 | ||
| 0.2 | 0.2 | 0.2 | ||
| 0.85 | 0.85 | 0.85 | ||
| 2.4 MW | 1.8 MW | 3 MW | ||
| 2.4 MW | 1.8 MW | 3 MW | ||
| 0.95 | 0.95 | 0.95 | ||
| 0.95 | 0.95 | 0.95 | ||
| Interruptible load | 0.1 | 0.15 | 0.1 | |
| Power Interaction | 10 MW | 10 MW | 10 MW | |
| 10 MW | 10 MW | 10 MW | ||
| Time Period | Selling Tariff | Purchasing Tariff |
|---|---|---|
| Valley (1:00–7:00, 23:00–24:00) | 350 CNY/MW | 400 CNY/MW |
| Peak (7:00–10:00, 15:00–18:00, 21:00–23:00) | 680 CNY/MW | 790 CNY/MW |
| Flat (1:00–7:00, 23:00–24:00) | 1120 CNY/MW | 1200 CNY/MW |
| Risk Aversion Factor | P2P Energy Sharing Mode between MGs | Total Power Purchased by MGs from MA (MW) | Total Power Sold by MGs from MA (MW) |
|---|---|---|---|
| L = 0.01 | Yes | 54.01 | 369.76 |
| NO | 139.64 | 406.09 | |
| L = 0.1 | Yes | 54.19 | 380.14 |
| NO | 132.26 | 405.77 | |
| L = 1 | Yes | 53.43 | 370.63 |
| NO | 127.71 | 404.86 | |
| L = 10 | Yes | 50.23 | 350.32 |
| NO | 120.24 | 398.21 |
| Risk Aversion Factor | Items | MG1 | MG2 | MG3 | Total Cost |
|---|---|---|---|---|---|
| L = 0.01 | Total cost not in P2P mode (CYN) | −18,157.02 | −14,762.25 | 70,578.95 | 37,659.68 |
| O&M cost in P2P mode (CYN) | −10,218.26 | −10,878.88 | 41,092.57 | 19,995.43 | |
| Transfer payments of Nash bargaining (CYN) | −13,708.70 | −7143.23 | 20,851.92 | 0 | |
| Total cost in P2P mode (CYN) | −23,926.96 | −18,022.10 | 61,944.50 | 19,995.43 | |
| Benefit (CYN) | −5769.94 | −3259.85 | −8634.45 | −17,664.25 | |
| Shared Power (MWh) | −10.84 | −7.69 | 18.52 | 0 | |
| L = 0.1 | Total cost not in P2P mode (CYN) | −18,132.40 | −14,747.67 | 69,875.03 | 36,994.96 |
| O&M cost in P2P mode (CYN) | −10,634.68 | −10,247.81 | 40,714.18 | 19,831.69 | |
| Transfer payments of Nash bargaining (CYN) | −12,629.04 | −8187.94 | 20,816.98 | 0 | |
| Total cost in P2P mode (CYN) | −23,263.73 | −18,435.74 | 61,531.16 | 19,831.69 | |
| Benefit (CYN) | −5131.33 | −3688.07 | −8343.87 | −17,163.27 | |
| Shared Power (MWh) | −10.63 | −8.80 | 19.43 | 0 | |
| L = 1 | Total cost not in P2P mode (CYN) | −18,151.99 | −14,773.03 | 69,746.12 | 36,821.10 |
| O&M cost in P2P mode (CYN) | −10,955.28 | −9523.04 | 40,162.93 | 19,684.61 | |
| Transfer payments of Nash bargaining (CYN) | −11,621.84 | −10,471.39 | 22,093.23 | 0 | |
| Total cost in P2P mode (CYN) | −22,577.12 | −19,994.42 | 62,256.16 | 19,684.61 | |
| Benefit (CYN) | −4425.13 | −5221.39 | −7489.96 | −17,136.49 | |
| Shared Power (MWh) | −10.17 | −8.59 | 18.76 | 0 | |
| L = 10 | Total cost not in P2P mode (CYN) | −18,145.22 | −16,360.33 | 69,843.54 | 35,337.99 |
| O&M cost in P2P mode (CYN) | −11,259.75 | −9620.55 | 40,005.04 | 19,124.74 | |
| Transfer payments of Nash bargaining (CYN) | −11,740.75 | −9334.74 | 21,075.49 | 0 | |
| Total cost in P2P mode (CYN) | −23,000.50 | −18,955.29 | 61,080.53 | 19,124.74 | |
| Benefit (CYN) | −4855.28 | −2594.96 | −8763.01 | −16,213.25 | |
| Shared Power (MWh) | −11.75 | −6.32 | 18.06 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Fang, J. Co-Operative Optimization Framework for Energy Management Considering CVaR Assessment and Game Theory. Energies 2022, 15, 9483. https://doi.org/10.3390/en15249483
Xiong Y, Fang J. Co-Operative Optimization Framework for Energy Management Considering CVaR Assessment and Game Theory. Energies. 2022; 15(24):9483. https://doi.org/10.3390/en15249483
Chicago/Turabian StyleXiong, Yan, and Jiakun Fang. 2022. "Co-Operative Optimization Framework for Energy Management Considering CVaR Assessment and Game Theory" Energies 15, no. 24: 9483. https://doi.org/10.3390/en15249483
APA StyleXiong, Y., & Fang, J. (2022). Co-Operative Optimization Framework for Energy Management Considering CVaR Assessment and Game Theory. Energies, 15(24), 9483. https://doi.org/10.3390/en15249483






