Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation
Abstract
1. Introduction
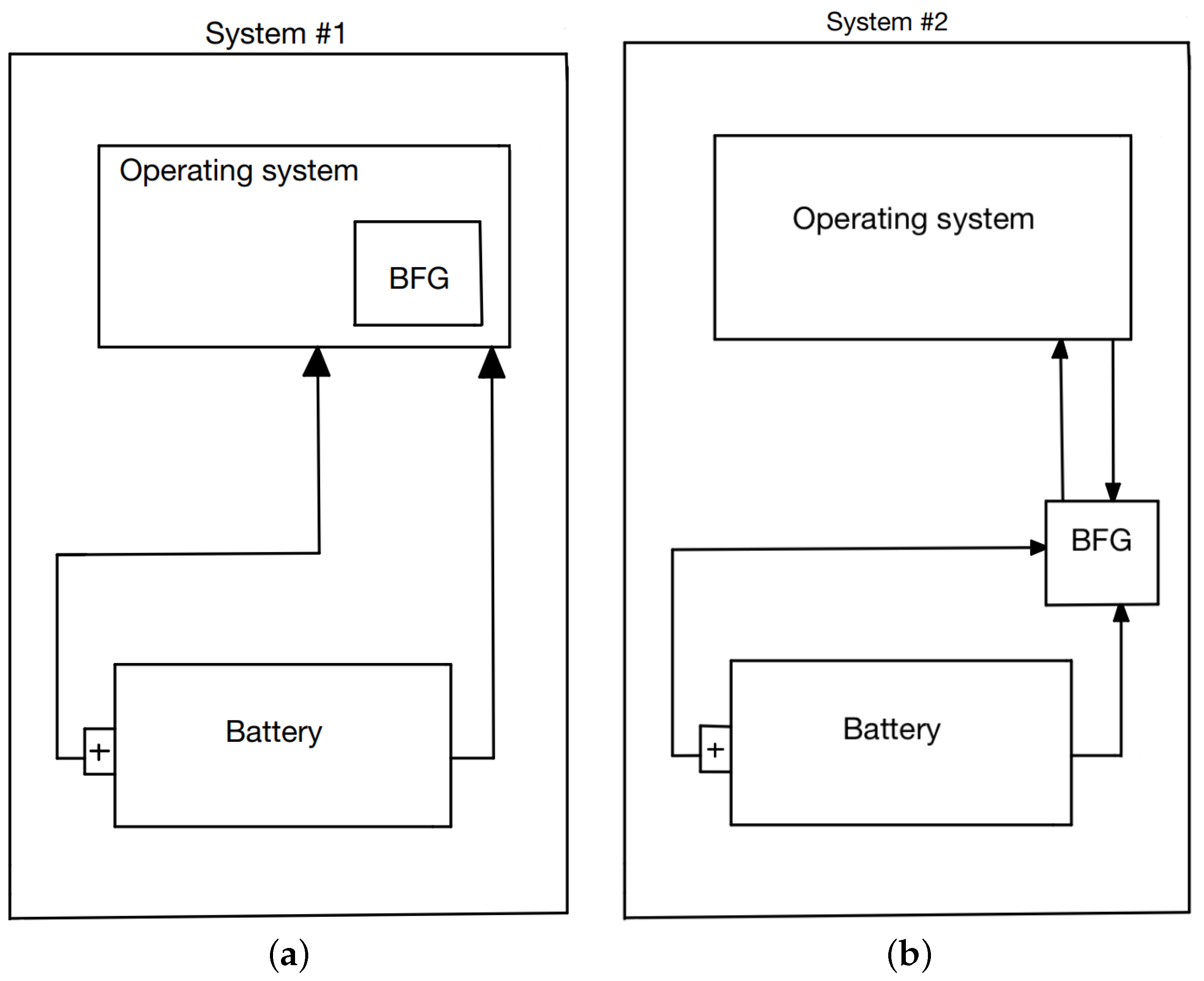
1.1. Computing System Requirements
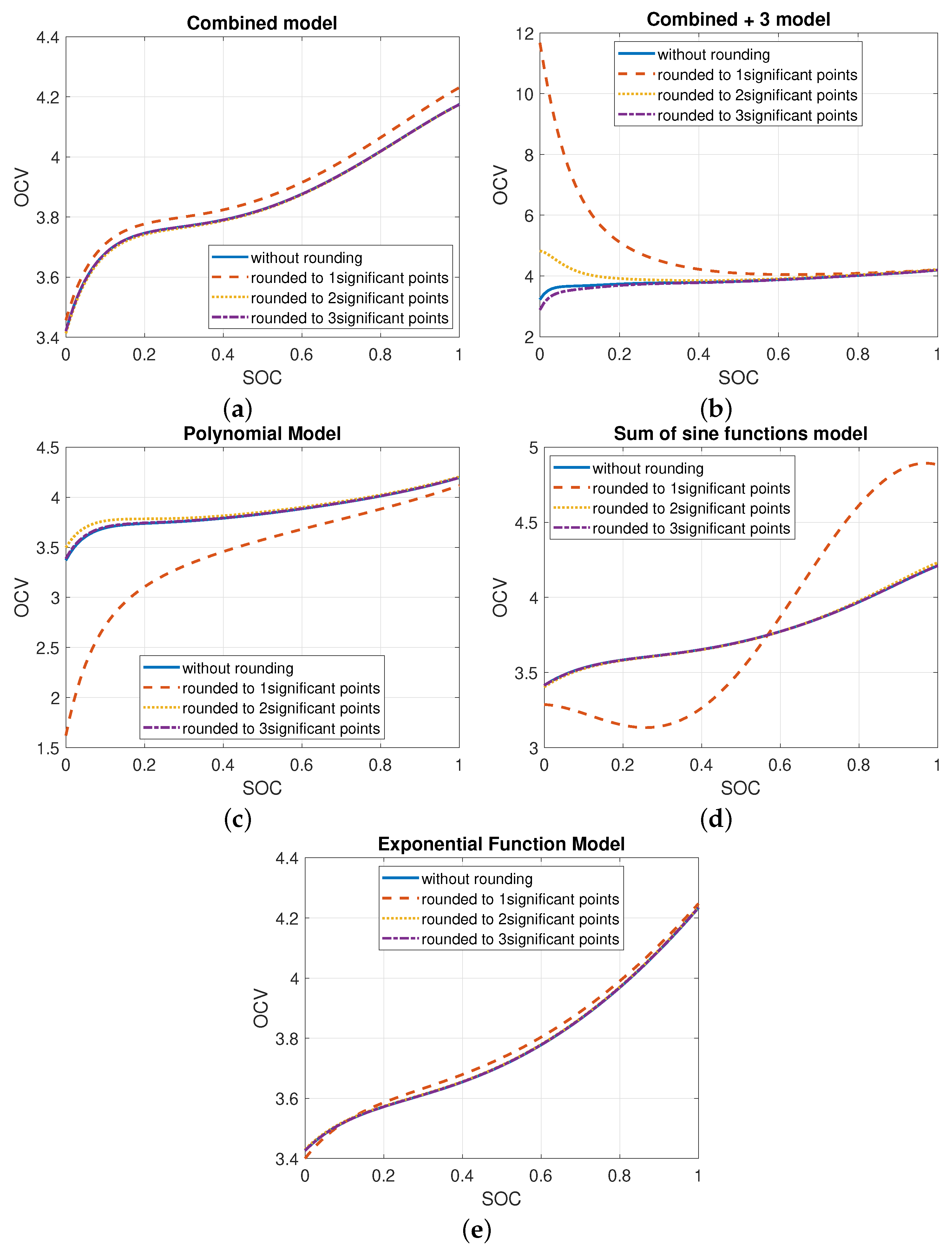
1.2. Rounding Errors
- (a)
- Existing OCV-SOC models require high-bit computing resources for parameter storage and processing, and
- (b)
- Existing model predictions are susceptible to significant errors when the model parameters are rounded.
1.3. Contribution of the Paper
- For the first time, this paper relates the accuracy of SOC estimation to the numerical stability of the estimated OCV-SOC parameters due to a very common practice: rounding.
- The OCV-SOC table formulation is introduced as an objectively defined optimization problem.
- An approach is presented to formally quantify the performance of an OCV-SOC table: similarity metrics between a tabular OCV model and a hi-fidelity model is proposed as the performance metric of a particular tabular OCV model.
- Three new approaches are presented to create OCV-SOC tables based on hi-fidelity models.
- The resulting three tables are evaluated based on the metrics developed in this paper.
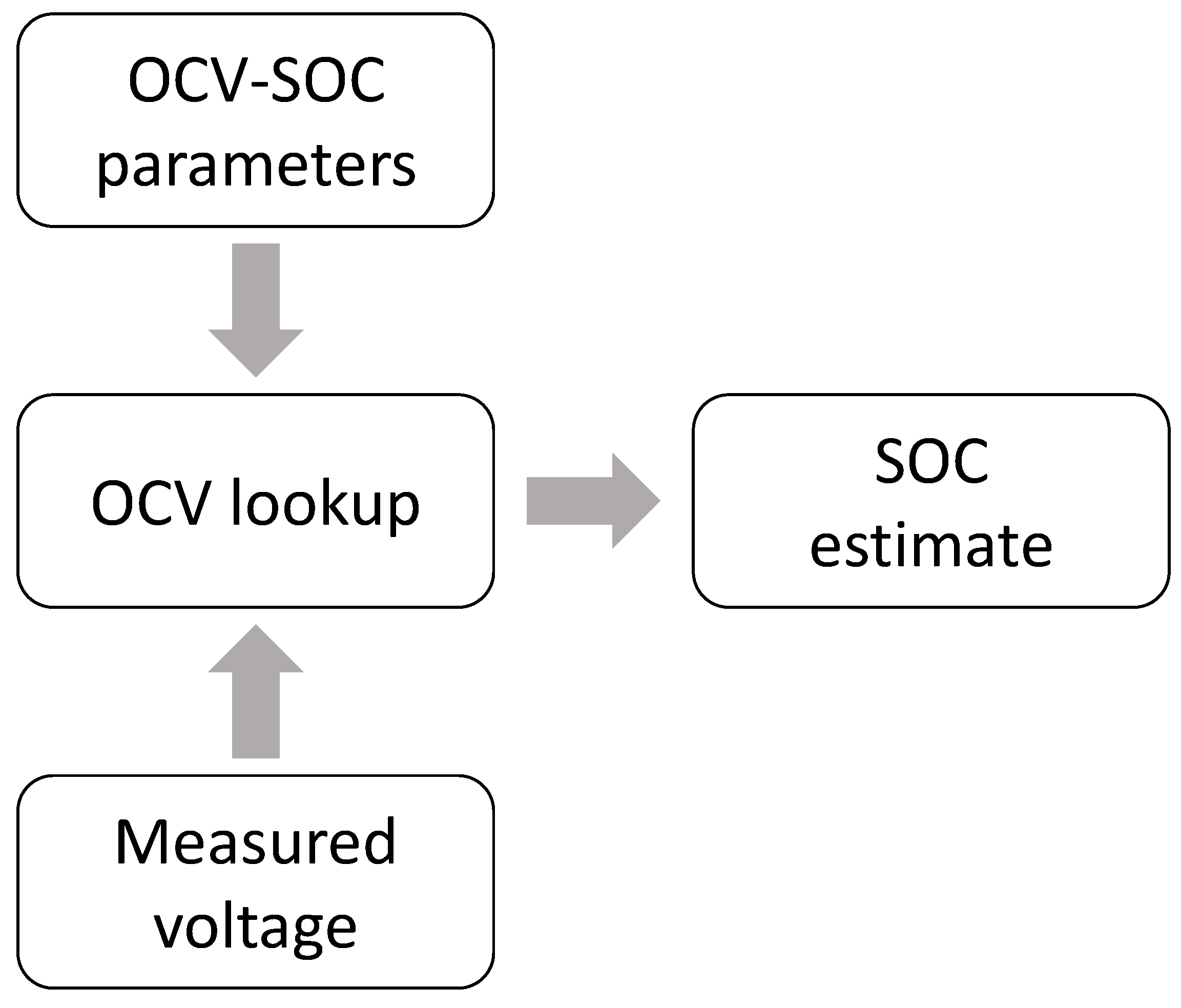
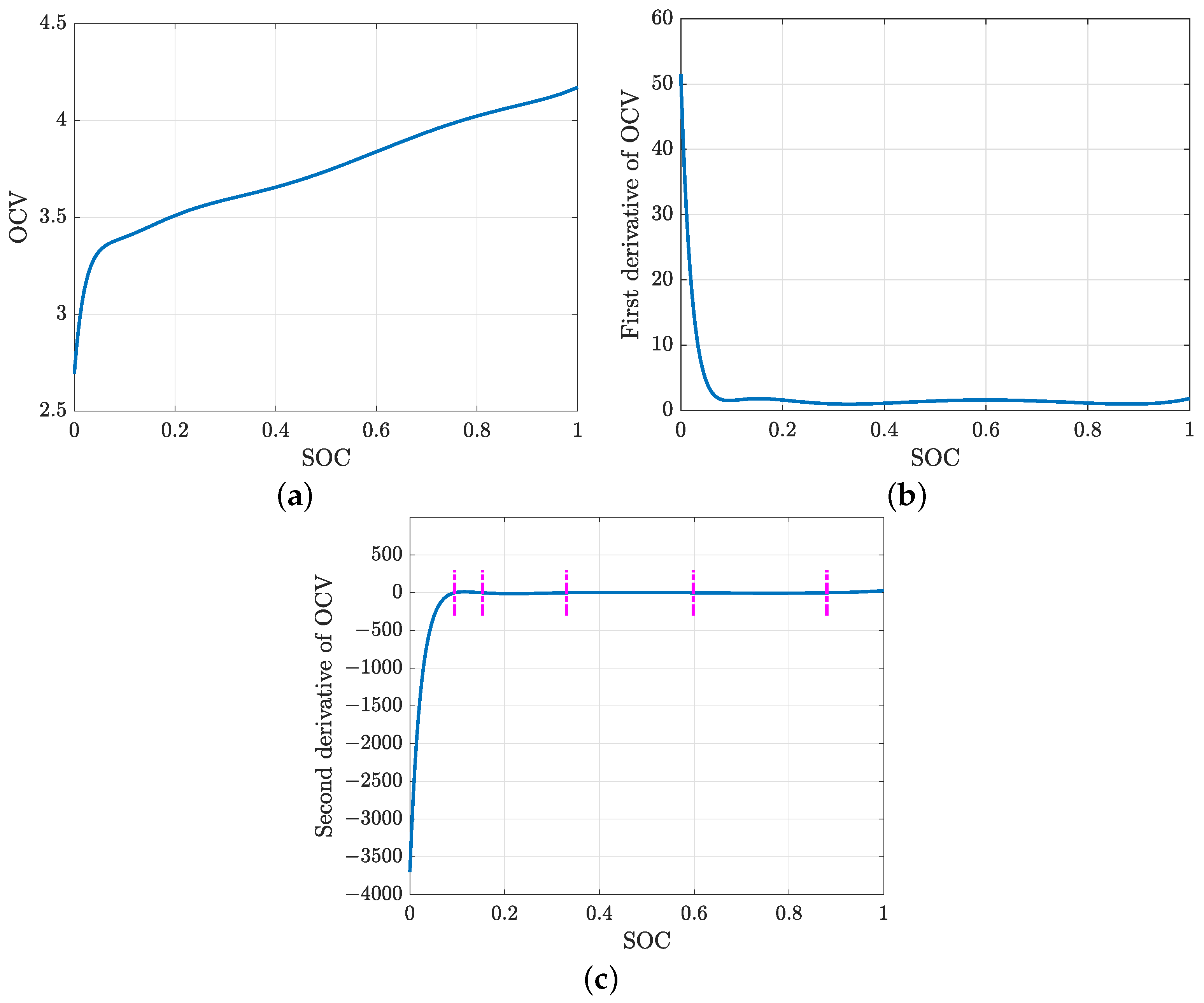
2. Problem Description
3. Solution Approaches
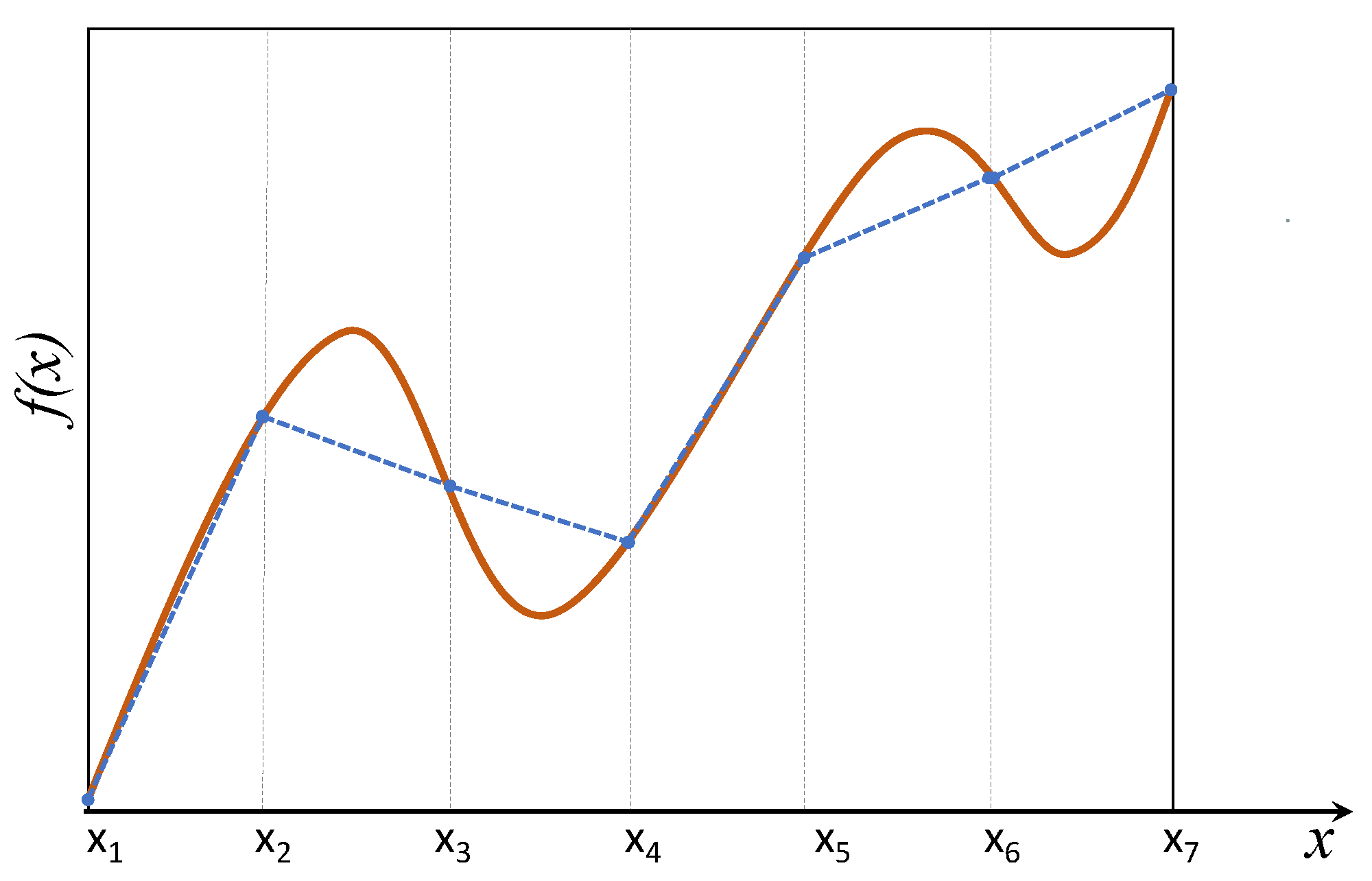
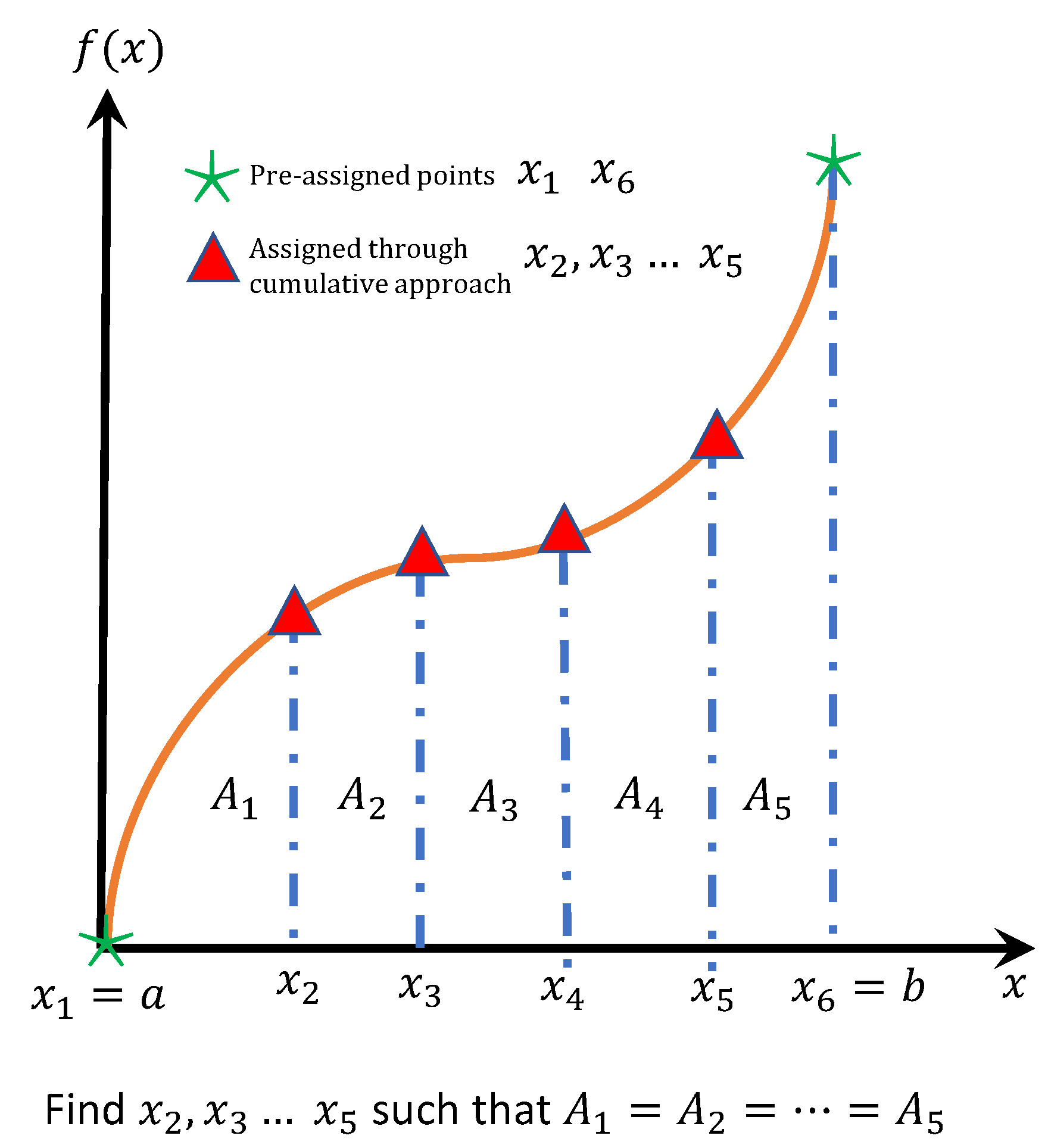
3.1. Cumulative Approach
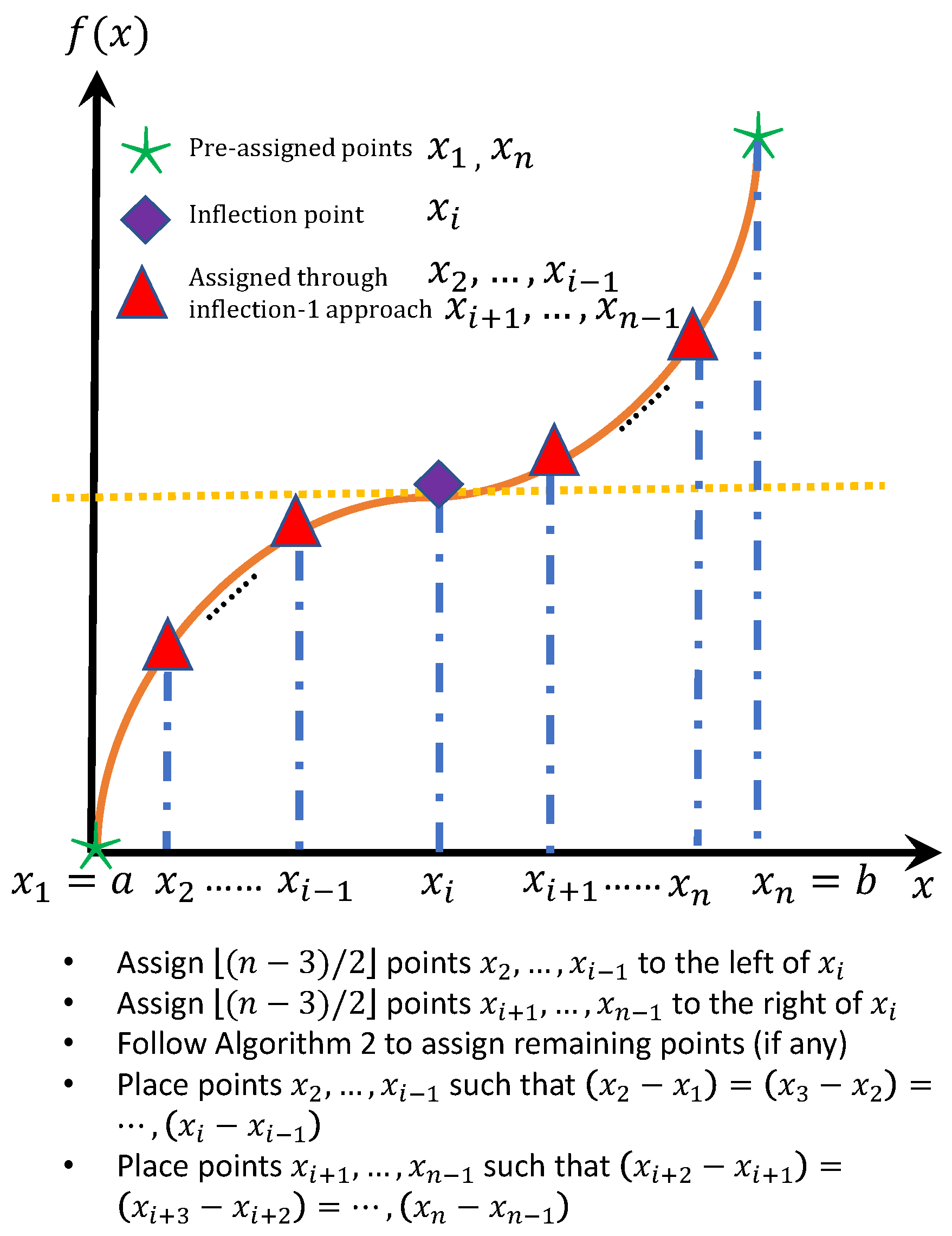
3.2. Inflection Point Approach
- (a)
- Find number of support points to be allocated to each of the sections created by the k inflection points.
- (b)
- Placement of support points in each section.
3.2.1. Approach-1 Based on Equal Distance in Each Section
- Each section gets r support points.
- The remaining m support points are allocated as follows:If , the m support points are assigned to section j such thatOtherwise, if and m is even, support points are assigned to each of section and section such thatOtherwise, if and m is odd, support points are assigned to section such thatsupport points are assigned to section such that
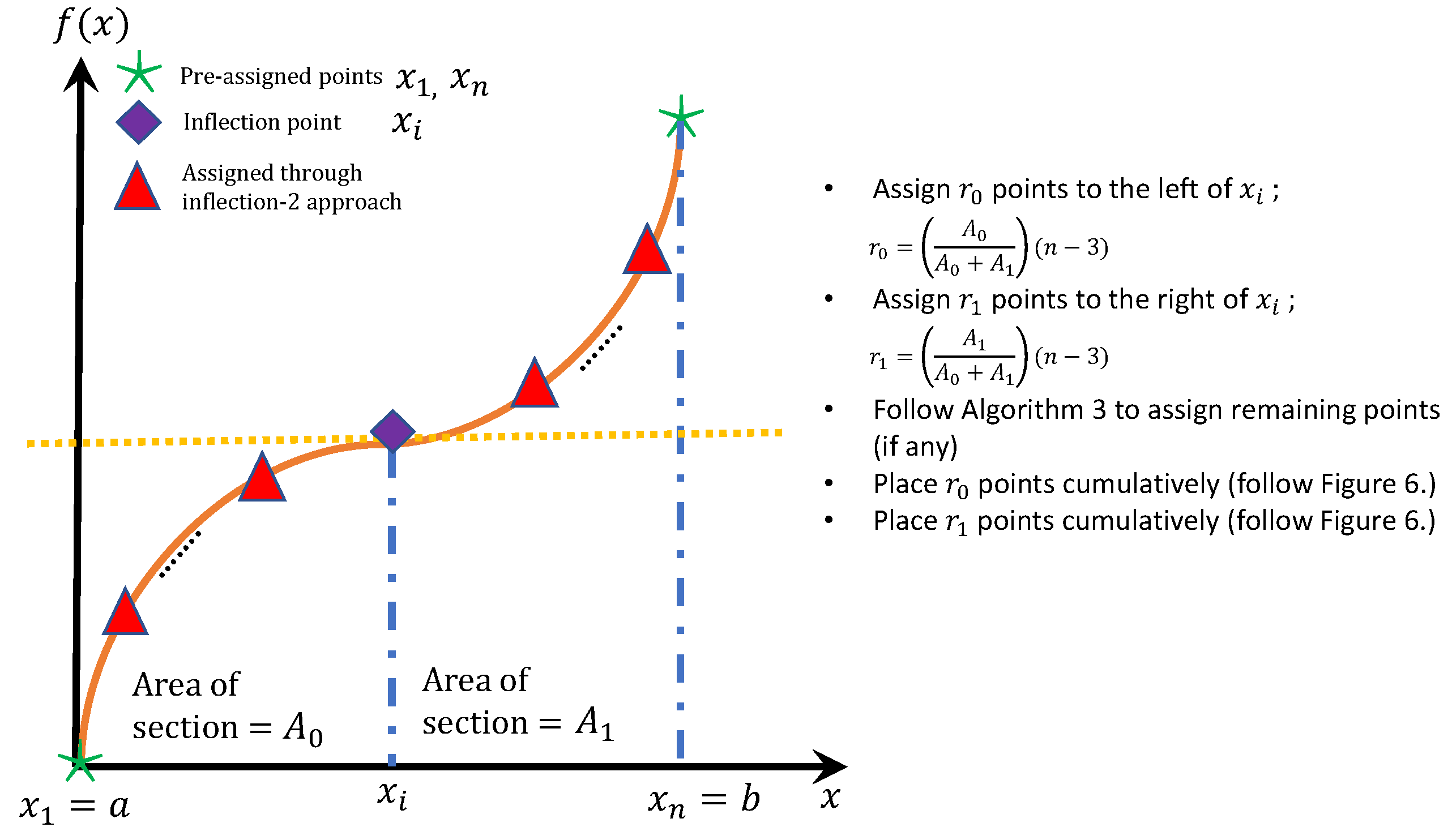
3.2.2. Approach-2 Based on Equal Area in Each Section
- Each section j gets support points as followswhere and the remaining number of points m is given by
- The remaining m support points are allocated as follows: The section with the highest area under the curvature gets one point; next, the section with the second highest area under the curvature gets one point; this is continued until all the remaining m points are assigned to a section.
| Algorithm 2 Inflection-1 approach. |
(I) Allocation of support points
(II) Placement of support points
|
| Algorithm 3 Inflection-2 approach. |
(I) Allocation of support points
(II) Placement of support points
|
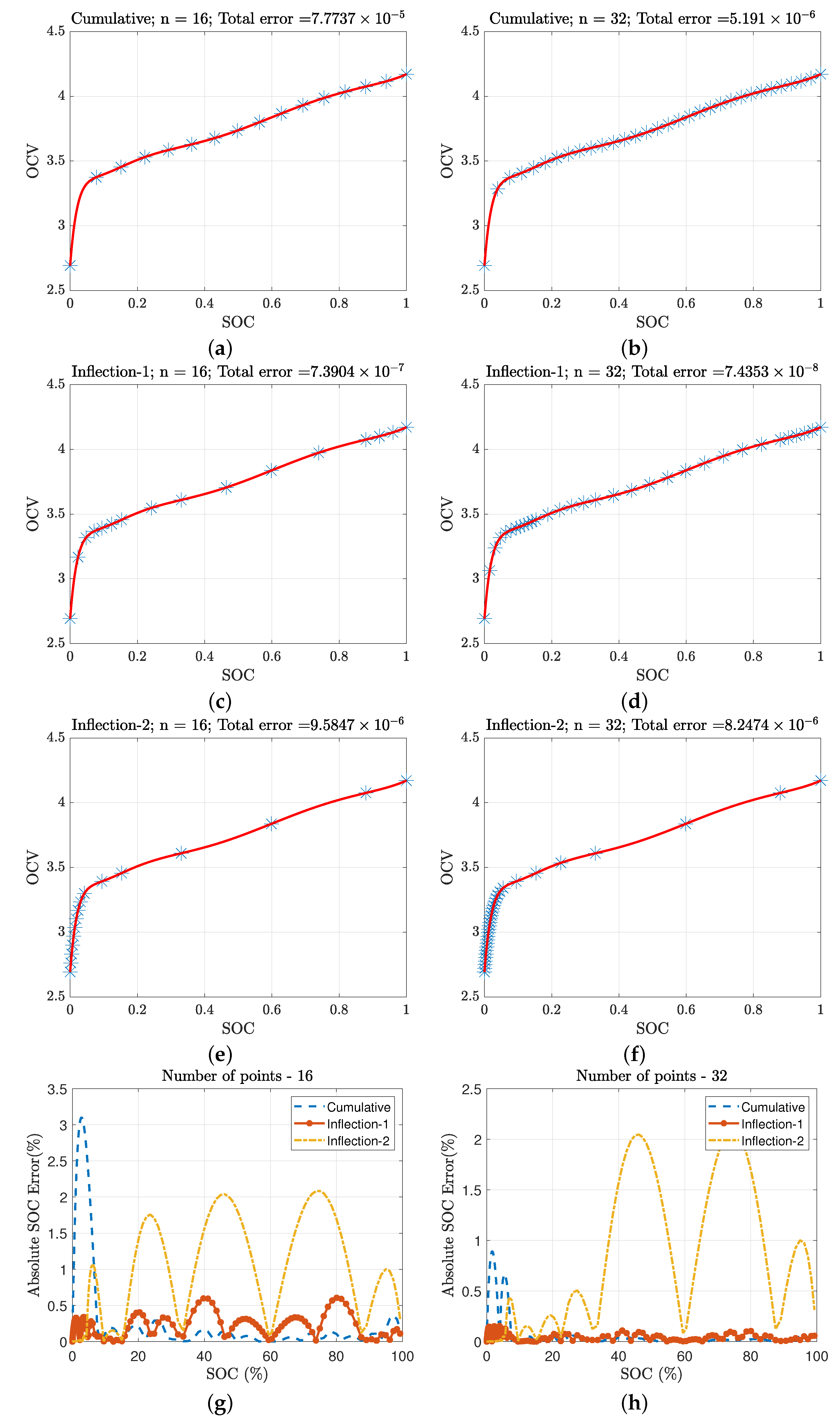
4. Implementation on OCV Model
4.1. Cumulative Approach
4.2. Inflection Point Approach
4.2.1. Approach-1 Based on Equal Distance
- The first step is to allocate the number of points to each of the four sections, given the total number of support points, n. Denote the number of points allocated to each section by an array, saywhere each is determined by the logic discussed in Section 3.2.1.
- The distance between the points in each section is then the difference between the preassigned points of that section divided by the number of points plus one of the corresponding section, which is
- Points in the first section are then placed at,where , while in the second section, points are placed at,where .
- Similarly, points in the third and fourth section are placed accordingly.
- Thus, and the corresponding OCV at those points form the support (SOC, OCV) pairs of the tabular OCV model.
4.2.2. Approach-2 Based on Equal Area
- The first step is to allocate the number of points to each of the four sections, given the total number of support points, n. Denote the number of points allocated to each section as in (31).
- The absolute area of each of the sections is determined as in (14). Denote the absolute area of each of the sections as .
- The points in the first section can thus be determined aswhile in the second section, points are determined as
- Similarly, points in the third and fourth section are placed accordingly.
- Thus, and the corresponding OCV at those points form the support (SOC, OCV) pairs of the tabular OCV model.
5. Experimental Details
5.1. Batteries Tested
5.2. Testing Equipment
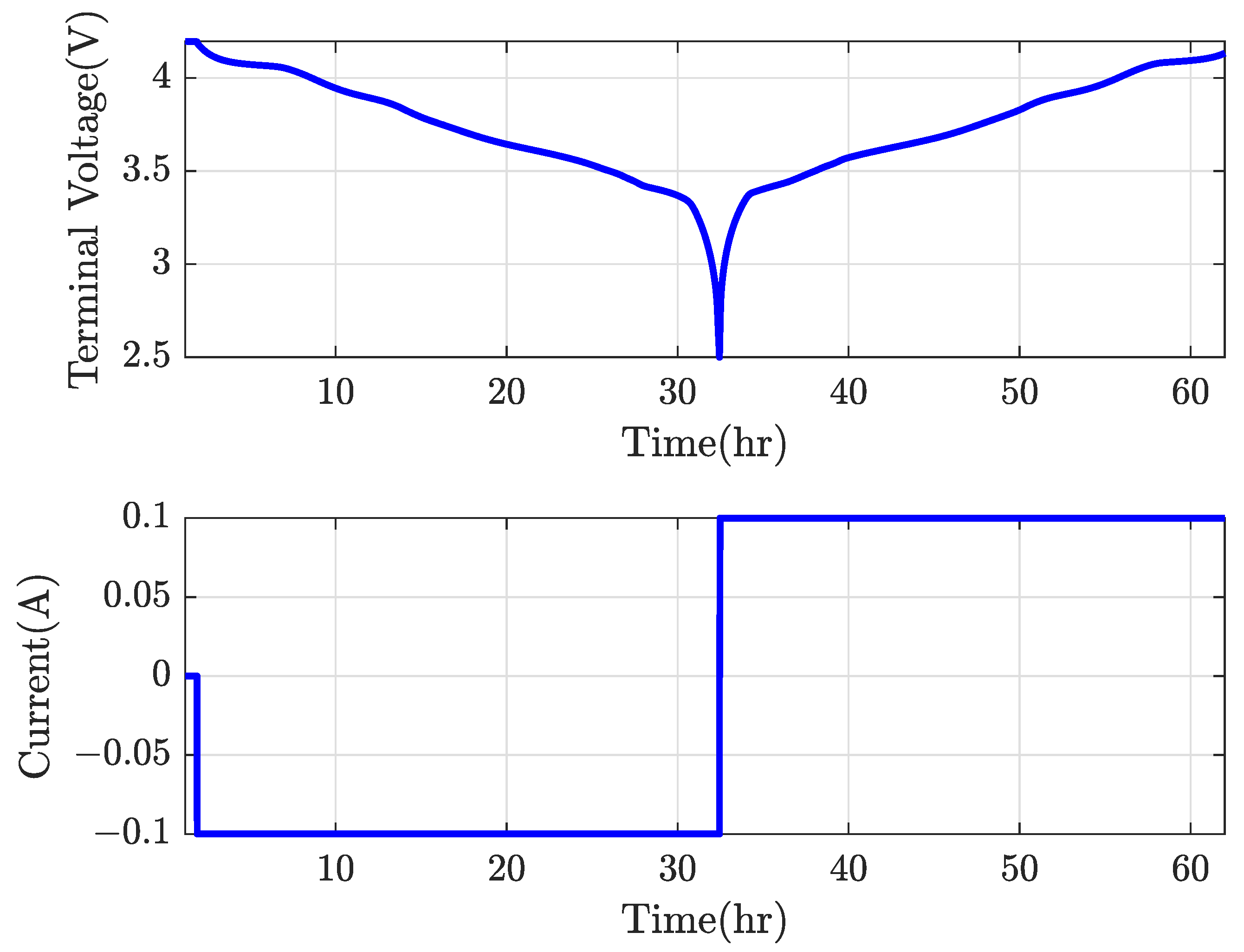
5.3. OCV-SOC Characterization Test
- A constant current is supplied to the battery until the terminal voltage reaches 4.2 V.
- The terminal voltage is maintained at 4.2 V for constant voltage charging until the current drops to 0.01 A.
- The battery is rested for one hour.
- A constant current of is supplied to slowly discharge the battery for thirty hours until the SOC reaches 0%. A rest of 1 h follows, before the battery is charged back again by for thirty hours until the SOC reaches 100%.
5.4. OCV Parameter Estimation
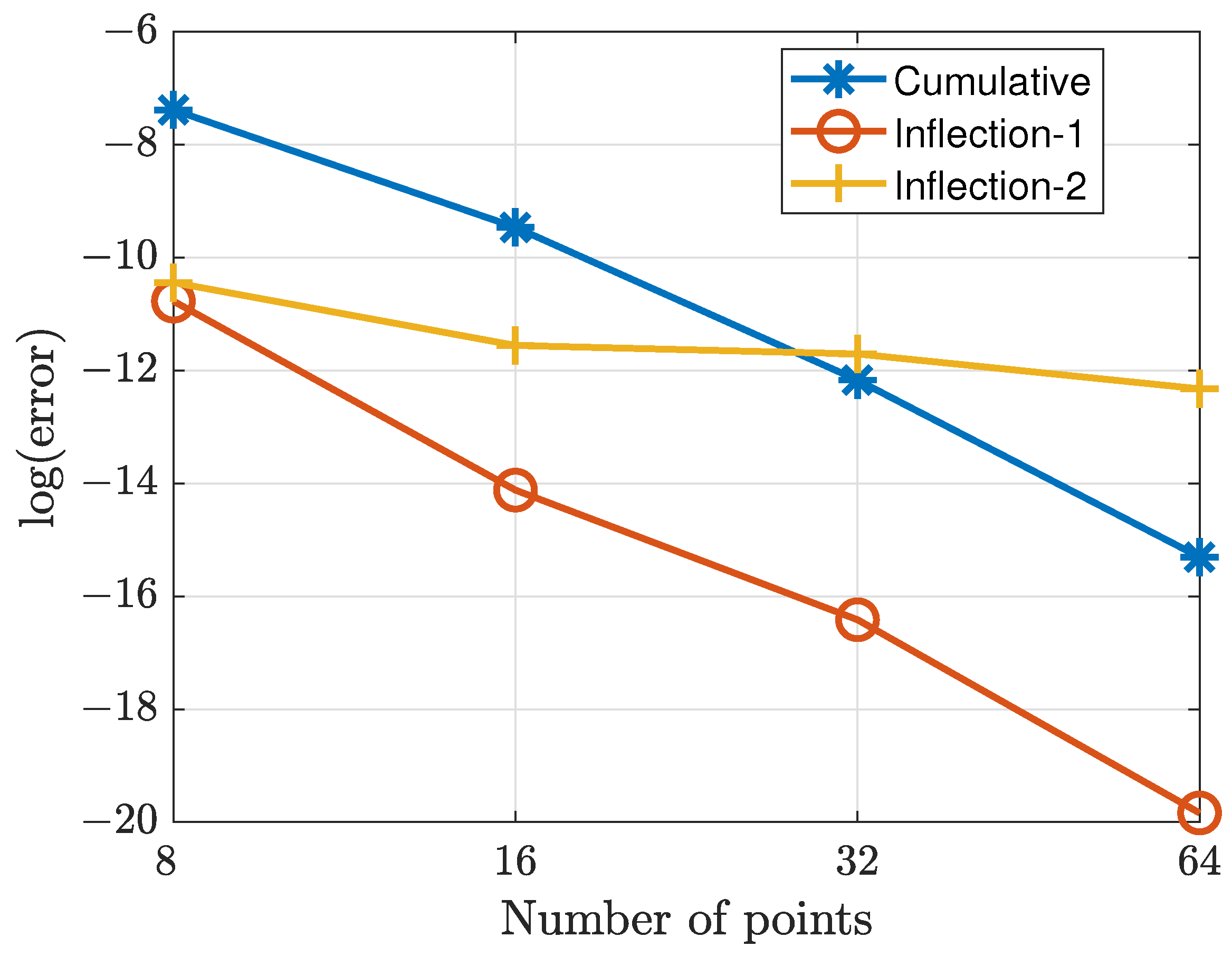
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hasan, M.K.; Mahmud, M.; Ahasan Habib, A.; Motakabber, S.; Islam, S. Review of electric vehicle energy storage and management system: Standards, issues, and challenges. J. Energy Storage 2021, 41, 102940. [Google Scholar] [CrossRef]
- Balasingam, B.; Ahmed, M.; Pattipati, K. Battery management systems—Challenges and some solutions. Energies 2020, 13, 2825. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Hussain, A.; Yusof, Y.; Ker, P.J. State-of-the-art and energy management system of lithium-ion batteries in electric vehicle applications: Issues and recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2021, 7, 100093. [Google Scholar] [CrossRef]
- Balasingam, B.; Pattipati, K.R. On the identification of electrical equivalent circuit models based on noisy measurements. IEEE Trans. Instrum. Meas. 2021, 70, 1–16. [Google Scholar] [CrossRef]
- Zhou, Z.; Cui, Y.; Kong, X.; Li, J.; Zheng, Y. A fast capacity estimation method based on open circuit voltage estimation for linixcoymn1-xy battery assessing in electric vehicles. J. Energy Storage 2020, 32, 101830. [Google Scholar] [CrossRef]
- Pan, W.; Luo, X.; Zhu, M.; Ye, J.; Gong, L.; Qu, H. A health indicator extraction and optimization for capacity estimation of li-ion battery using incremental capacity curves. J. Energy Storage 2021, 42, 103072. [Google Scholar] [CrossRef]
- Zheng, Y.; Cui, Y.; Han, X.; Dai, H.; Ouyang, M. Lithium-ion battery capacity estimation based on open circuit voltage identification using the iteratively reweighted least squares at different aging levels. J. Energy Storage 2021, 44, 103487. [Google Scholar] [CrossRef]
- Movahedi, H.; Tian, N.; Fang, H.; Rajamani, R. Hysteresis compensation and nonlinear observer design for state-of-charge estimation using a nonlinear double-capacitor li-ion battery model. IEEE/ASME Trans. Mechatron. 2021, 27, 594–604. [Google Scholar] [CrossRef]
- Ni, Z.; Yang, Y. A combined data-model method for state-of-charge estimation of lithium-ion batteries. IEEE Trans. Instrum. Meas. 2021, 71, 1–11. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Che, Y.; Hu, L. General discharge voltage information enabled health evaluation for lithium-ion batteries. IEEE/ASME Trans. Mechatron. 2020, 26, 1295–1306. [Google Scholar] [CrossRef]
- Bian, X.; Liu, L.; Yan, J.; Zou, Z.; Zhao, R. An open circuit voltage-based model for state-of-health estimation of lithium-ion batteries: Model development and validation. J. Power Sources 2020, 448, 227401. [Google Scholar] [CrossRef]
- Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; Islam, M.R.; et al. A comprehensive review of available battery datasets, rul prediction approaches, and advanced battery management. IEEE Access 2021, 9, 86166–86193. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the battery model and soc estimation method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A critical look at coulomb counting approach for state of charge estimation in batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Pattipati, B.; Balasingam, B.; Avvari, G.; Pattipati, K.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.P.; Park, J.W. On-line optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion battery using dual neural network fusion battery model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, Z.-F.; Wang, C.-H. The open-circuit voltage characteristic and state of charge estimation for lithium-ion batteries based on an improved estimation algorithm. J. Test. Eval. 2018, 48, 1712–1730. [Google Scholar] [CrossRef]
- Susanna, S.; Dewangga, B.R.; Wahyungoro, O.; Cahyadi, A.I. Comparison of simple battery model and thevenin battery model for soc estimation based on ocv method. In Proceedings of the 2019 International Conference on Information and Communications Technology, Yogyakarta, Indonesia, 24–25 July 2019; pp. 738–743. [Google Scholar]
- Wang, Q.; Qi, W. New soc estimation method under multi-temperature conditions based on parametric-estimation ocv. J. Power Electron. 2020, 20, 614–623. [Google Scholar] [CrossRef]
- Jibhkate, U.N.; Mujumdar, U.B. Development of low complexity open circuit voltage model for state of charge estimation with novel curve modification technique. Electrochim. Acta 2022, 429, 140944. [Google Scholar] [CrossRef]
- Plett, G.L. Extended kalman filtering for battery management systems of lipb-based hev battery packs: Part 2. modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Fathoni, G.; Widayat, S.A.; Topan, P.A.; Jalil, A.; Cahyadi, A.I.; Wahyunggoro, O. Comparison of state-of-charge (soc) estimation performance based on three popular methods: Coulomb counting, open circuit voltage, and kalman filter. In Proceedings of the 2017 2nd International Conference on Automation, Cognitive Science, Optics, Micro Electro-Mechanical System, and Information Technology, Jakarta, Indonesia, 23–24 October 2017; pp. 70–74. [Google Scholar]
- Xu, X.; Wu, D.; Yang, L.; Zhang, H.; Liu, G. State estimation of lithium batteries for energy storage based on dual extended kalman filter. Math. Probl. Eng. 2020, 2020, 6096834. [Google Scholar] [CrossRef]
- Gismero, A.; Schaltz, E.; Stroe, D.-I. Recursive state of charge and state of health estimation method for lithium-ion batteries based on coulomb counting and open circuit voltage. Energies 2020, 13, 1811. [Google Scholar] [CrossRef]
- Amifia, L.K.; Riansyah, M.; Muttaqin, B.I.A.; Ratri, A.P.; Rifansyah, F.A.; Prakoso, B.W. Optimization of battery management system with soc estimation by comparing two methods. In Proceedings of the 2nd International Conference on Electronics, Biomedical Engineering, and Health Informatics, Surabaya, Indonesia, 3–4 November 2021; Springer: Singapore, 2022; pp. 445–457. [Google Scholar]
- Adafruit. Adafruit LC709203F LiPoly/LiIon Fuel Gauge and Battery Monitor. Available online: https://www.adafruit.com/product/4712 (accessed on 20 April 2022).
- Yu, Q.-Q.; Xiong, R.; Wang, L.-Y.; Lin, C. A comparative study on open circuit voltage models for lithium-ion batteries. Chin. J. Mech. Eng. 2018, 31, 65. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A study on the open circuit voltage and state of charge characterization of high capacity lithium-ion battery under different temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Essoukri Ben Amara, N. Improved ocv model of a li-ion nmc battery for online soc estimation using the extended kalman filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Lazreg, M.B.; Jemmali, S.; Baccouche, I.; Manai, B.; Hamouda, M. Lithium-ion battery pack modeling using accurate ocv model: Application for soc and soh estimation. In Proceedings of the 2020 IEEE 4th International Conference on Intelligent Energy and Power Systems (IEPS), Istanbul, Turkey, 7–11 September 2020; pp. 175–179. [Google Scholar]
- Zhang, Q.; Cui, N.; Li, Y.; Duan, B.; Zhang, C. Fractional calculus based modeling of open circuit voltage of lithium-ion batteries for electric vehicles. J. Energy Storage 2020, 27, 100945. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and iv performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A generalized soc-ocv model for lithium-ion batteries and the soc estimation for lnmco battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.; Stone, D. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Elmahdi, F.; Ismail, L.; Noureddine, M. Fitting the ocv-soc relationship of a battery lithium-ion using genetic algorithm method. E3S Web Conf. 2021, 234, 00097. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B. Electro-thermal battery model identification for automotive applications. J. Power Sources 2011, 196, 449–457. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Raihan, S.A.; Balasingam, B. A scaling approach for improved state of charge representation in rechargeable batteries. Appl. Energy 2020, 267, 114880. [Google Scholar] [CrossRef]





| Reference | Model | Parameters | Lowest Parameter Value | Highest Parameter Value | System Requirement (Bits) |
|---|---|---|---|---|---|
| Combined [24] | 25 | ||||
| Combined + 3 [17] | 30 | ||||
| Polynomial [30] | 26 | ||||
| Sum of sine functions [31] | 16 | ||||
| Double exponential & quadratic [31,32,33] | 17 | ||||
| Fractional [34] | 16 | ||||
| Polynomial & exponential [35] | 16 | ||||
| Linear, logarithmic & exponential [36] | 18 | ||||
| 8th order polynomial [37,38] | 19 | ||||
| Weng’s model [39] | 17 | ||||
| [40] | Not available | - | - | - |
| Specification | Value (Unit) |
|---|---|
| Nominal capacity | 3000 mAh |
| Max. continuous discharge current | 35 A |
| Nominal voltage | 3.6 V |
| Height | 70 mm |
| Diameter | 21 mm |
| Weight | 70 g |
| Internal resistance | 15 m |
| C1202 | C1203 | C1204 | C1205 | |
|---|---|---|---|---|
| −7.583571 | −7.97819289 | −8.066393564 | −8.958403863 | |
| 167.937349 | 163.9771372 | 162.9340579 | 142.8466347 | |
| −28.707024 | −28.0994585 | −27.93066927 | −24.66098891 | |
| 3.179598 | 3.119518894 | 3.101048887 | 2.753908717 | |
| −0.154205 | −0.151625024 | −0.150700733 | −0.13454535 | |
| −136.082267 | −132.0073615 | −130.9737274 | −111.5824628 | |
| 239.483802 | 233.2027873 | 231.5789098 | 201.0624577 | |
| −1.939093 | −1.842637102 | −1.825728052 | −1.337800859 |
| C1202 | C1203 | C1204 | C1205 | ||||
|---|---|---|---|---|---|---|---|
| SOC | OCV | SOC | OCV | SOC | OCV | SOC | OCV |
| 0 | 2.6929 | 0 | 2.6902 | 0 | 2.7003 | 0 | 2.7296 |
| 0.0236 | 3.1683 | 0.0238 | 3.1678 | 0.0236 | 3.1692 | 0.0246 | 3.1836 |
| 0.0473 | 3.3177 | 0.0476 | 3.3175 | 0.0472 | 3.3171 | 0.0492 | 3.3247 |
| 0.0709 | 3.3668 | 0.0714 | 3.3667 | 0.0708 | 3.3658 | 0.0738 | 3.3725 |
| 0.0945 | 3.3923 | 0.0951 | 3.3923 | 0.0944 | 3.3910 | 0.0984 | 3.3991 |
| 0.1238 | 3.4225 | 0.1245 | 3.4226 | 0.1242 | 3.4216 | 0.1254 | 3.4270 |
| 0.1530 | 3.4561 | 0.1539 | 3.4562 | 0.1539 | 3.4557 | 0.1523 | 3.4570 |
| 0.2417 | 3.5478 | 0.2428 | 3.5481 | 0.2432 | 3.5479 | 0.2416 | 3.5469 |
| 0.3303 | 3.6094 | 0.3318 | 3.6103 | 0.3325 | 3.6101 | 0.3308 | 3.6099 |
| 0.4644 | 3.7059 | 0.4660 | 3.7075 | 0.4673 | 3.7073 | 0.4706 | 3.7129 |
| 0.5985 | 3.8368 | 0.6003 | 3.8384 | 0.6021 | 3.8384 | 0.6103 | 3.8511 |
| 0.7391 | 3.9740 | 0.7418 | 3.9760 | 0.7425 | 3.9748 | 0.7618 | 3.9999 |
| 0.8798 | 4.0759 | 0.8833 | 4.0784 | 0.8829 | 4.0773 | 0.9132 | 4.1080 |
| 0.9199 | 4.1018 | 0.9222 | 4.1036 | 0.9219 | 4.1029 | 0.9421 | 4.1260 |
| 0.9599 | 4.1315 | 0.9611 | 4.1321 | 0.9610 | 4.1319 | 0.9711 | 4.1453 |
| 1.0000 | 4.1710 | 1.0000 | 4.1693 | 1.0000 | 4.1696 | 1.0000 | 4.1676 |
| Parametric Combined + 3 Model | Tabular Inflection-1 Model | ||||||
|---|---|---|---|---|---|---|---|
| Rounded to 1 Digit | Rounded to 2 Digits | Rounded to 3 Digits | Without Rounding | Rounded to 1 Digit | Rounded to 2 Digits | Rounded to 3 Digits | |
| KL divergence | 0.044608 | 0.002606 | 0.000167 | 2.41 × 10 | 4.13 × 10 | 2.54 × 10 | 2.76 × 10 |
| Cosine distance | 0.058112 | 0.00275 | 0.000147 | 2.49 × 10 | 3.77 × 10 | 2.54 × 10 | 2.85 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sundaresan, S.; Devabattini, B.C.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation. Energies 2022, 15, 9142. https://doi.org/10.3390/en15239142
Sundaresan S, Devabattini BC, Kumar P, Pattipati KR, Balasingam B. Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation. Energies. 2022; 15(23):9142. https://doi.org/10.3390/en15239142
Chicago/Turabian StyleSundaresan, Sneha, Bharath Chandra Devabattini, Pradeep Kumar, Krishna R. Pattipati, and Balakumar Balasingam. 2022. "Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation" Energies 15, no. 23: 9142. https://doi.org/10.3390/en15239142
APA StyleSundaresan, S., Devabattini, B. C., Kumar, P., Pattipati, K. R., & Balasingam, B. (2022). Tabular Open Circuit Voltage Modelling of Li-Ion Batteries for Robust SOC Estimation. Energies, 15(23), 9142. https://doi.org/10.3390/en15239142







