An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting
Abstract
1. Introduction
- A novel feature selection technique was employed to investigate the feature patterns;
- A novel hybrid algorithm was explored for PV power forecasting;
- A fair evaluation was presented by showing the numerical and graphical performances of the proposed hybrid model.
2. Background and Proposed Architecture
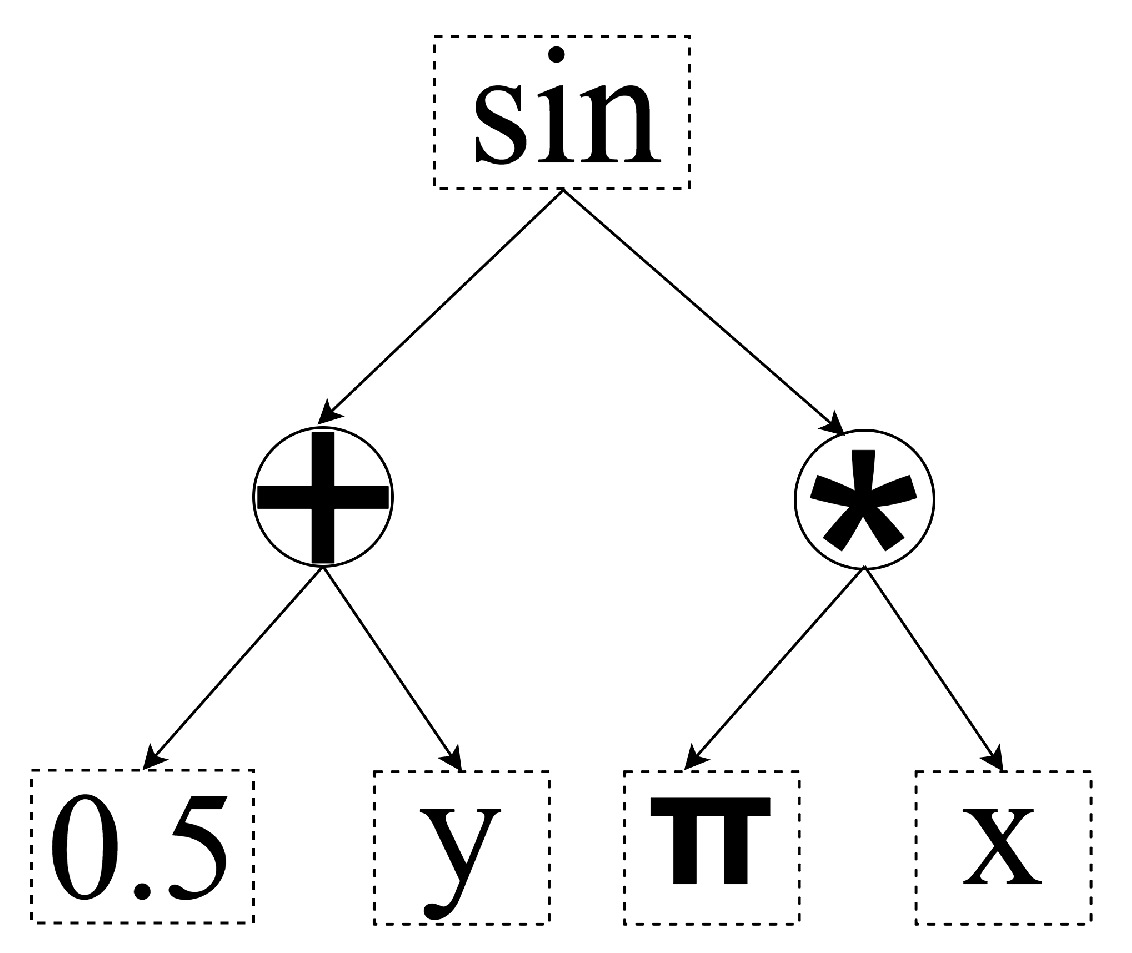
2.1. Symbolic Regression
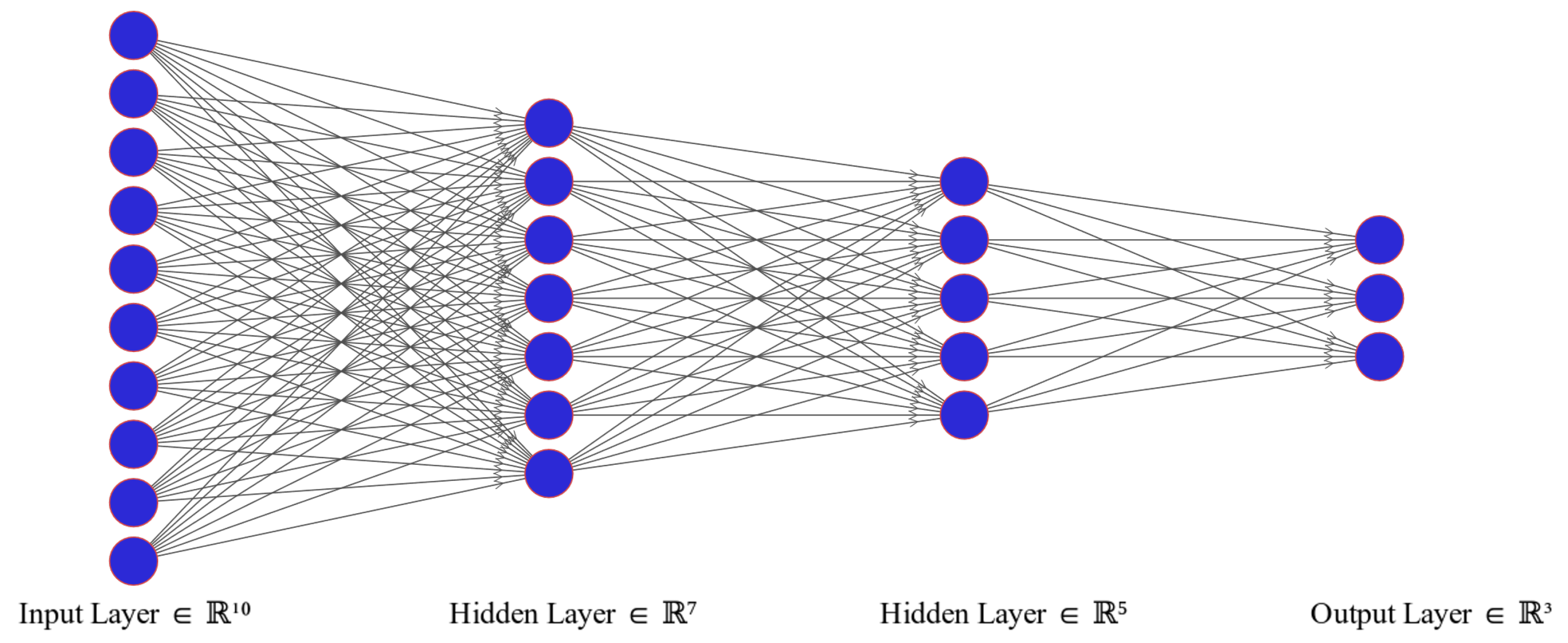
2.2. Deep Multi-Layer Perceptron
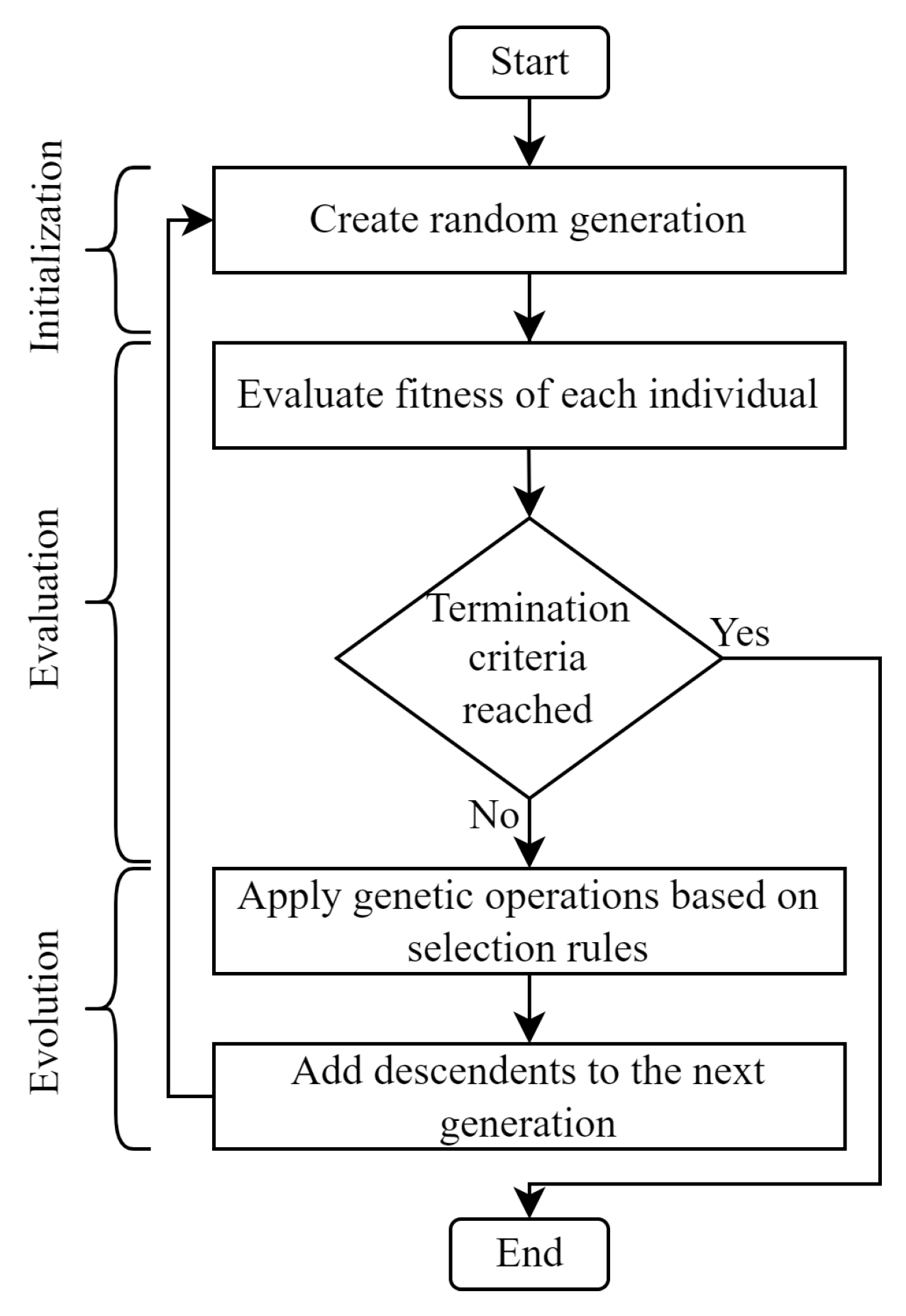
2.3. Genetic Programming
2.4. Problem Formulation
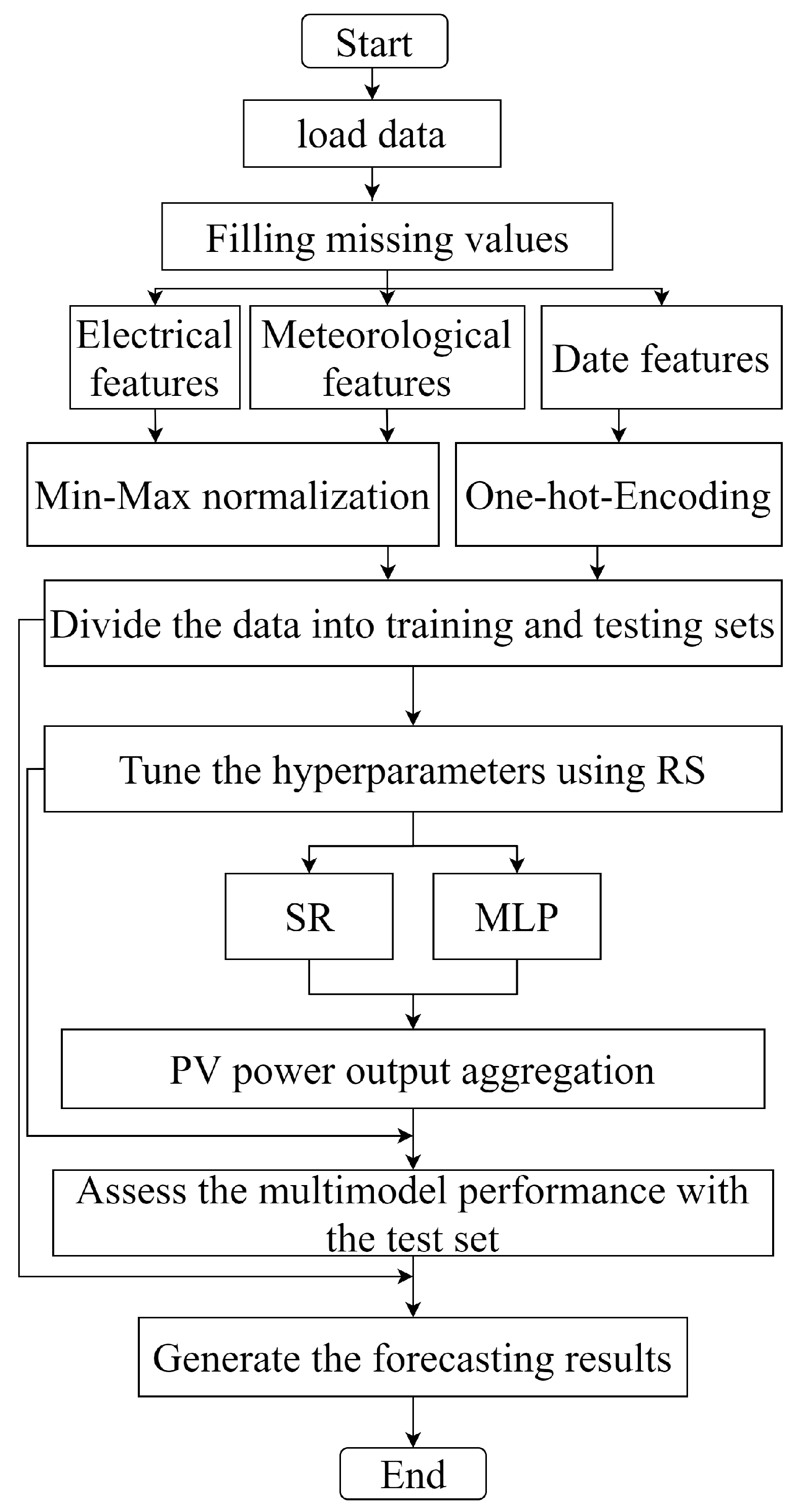
3. Hybrid Model
4. Case Study
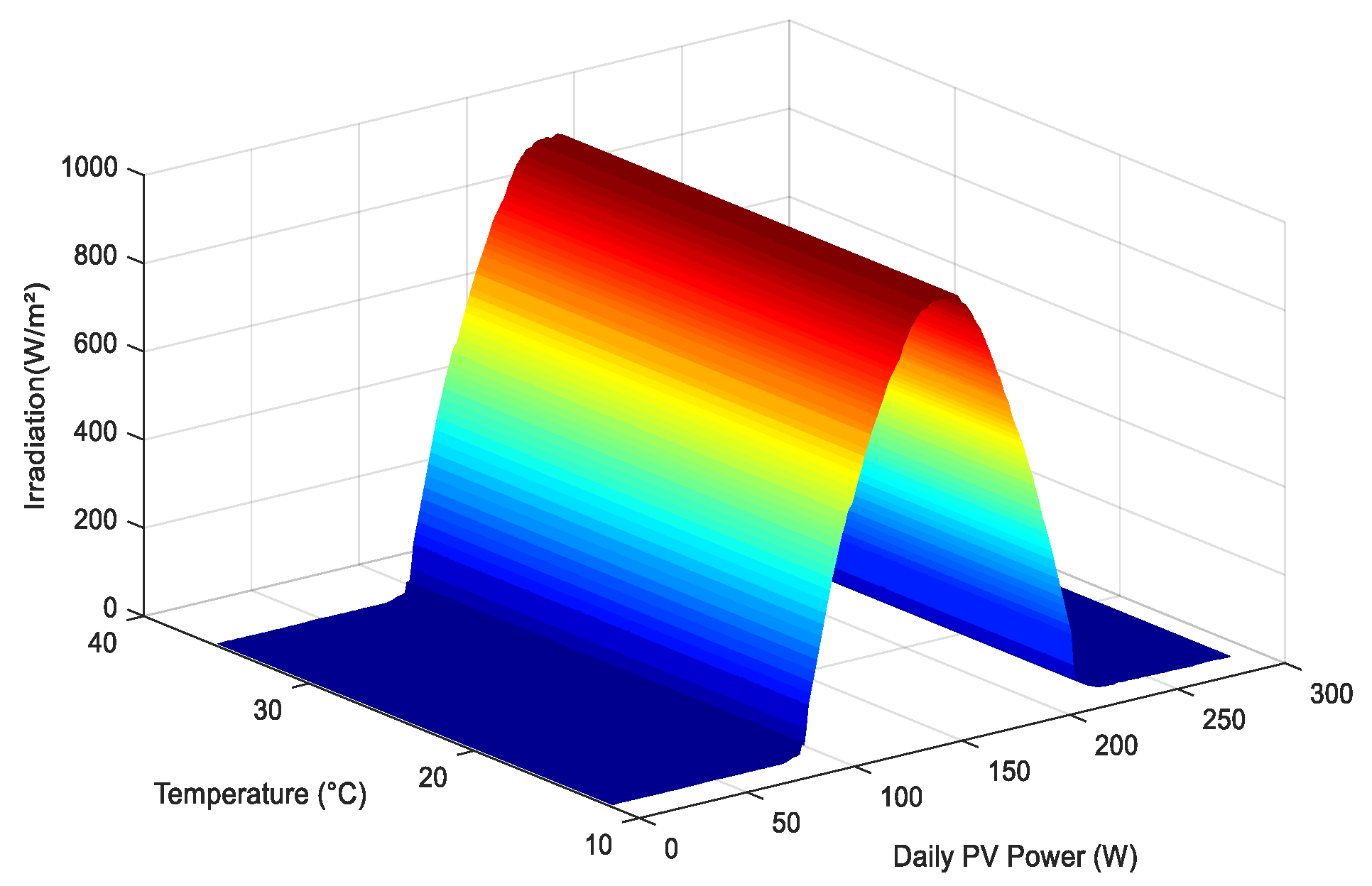
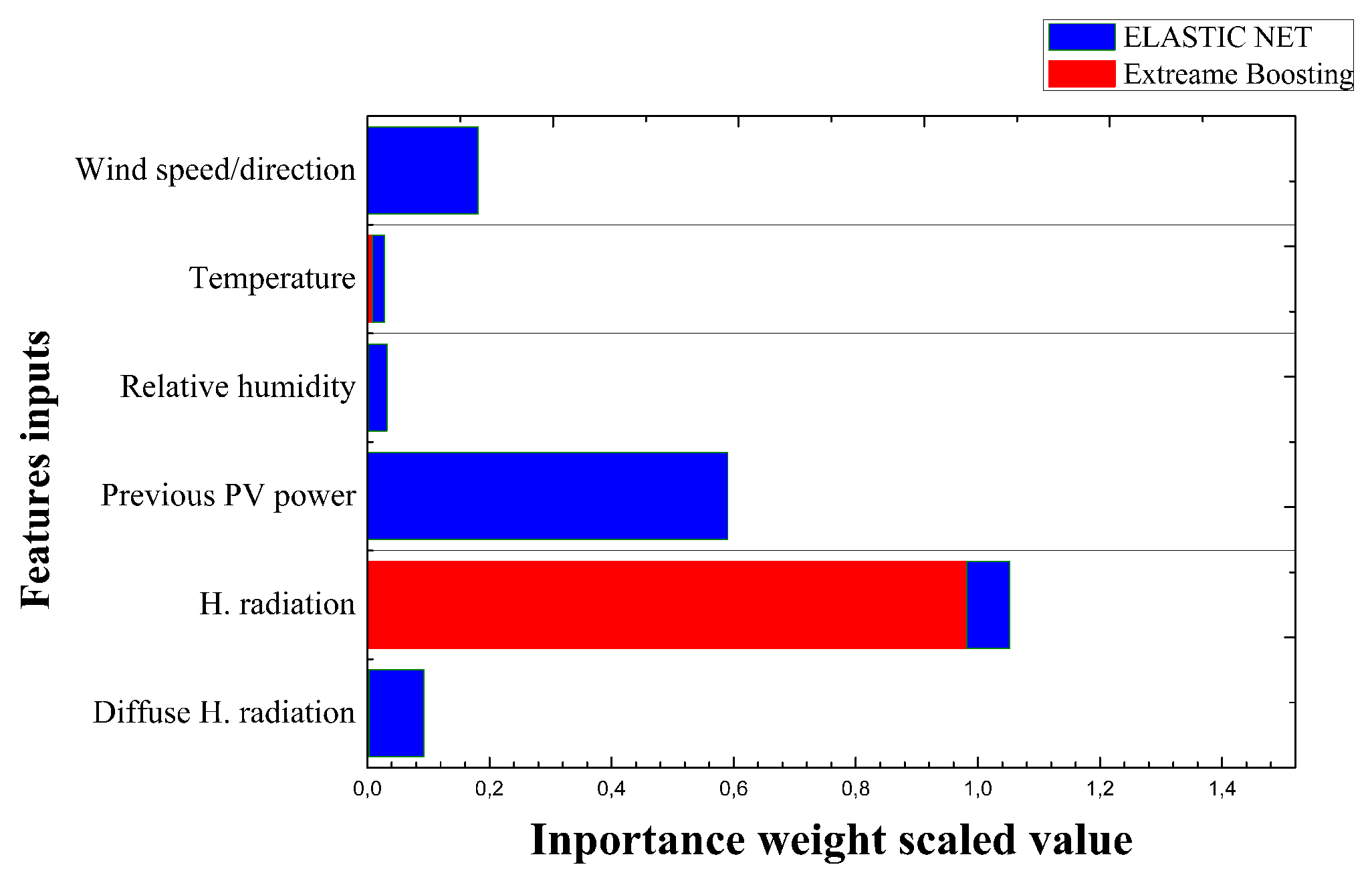
4.1. Features Selection
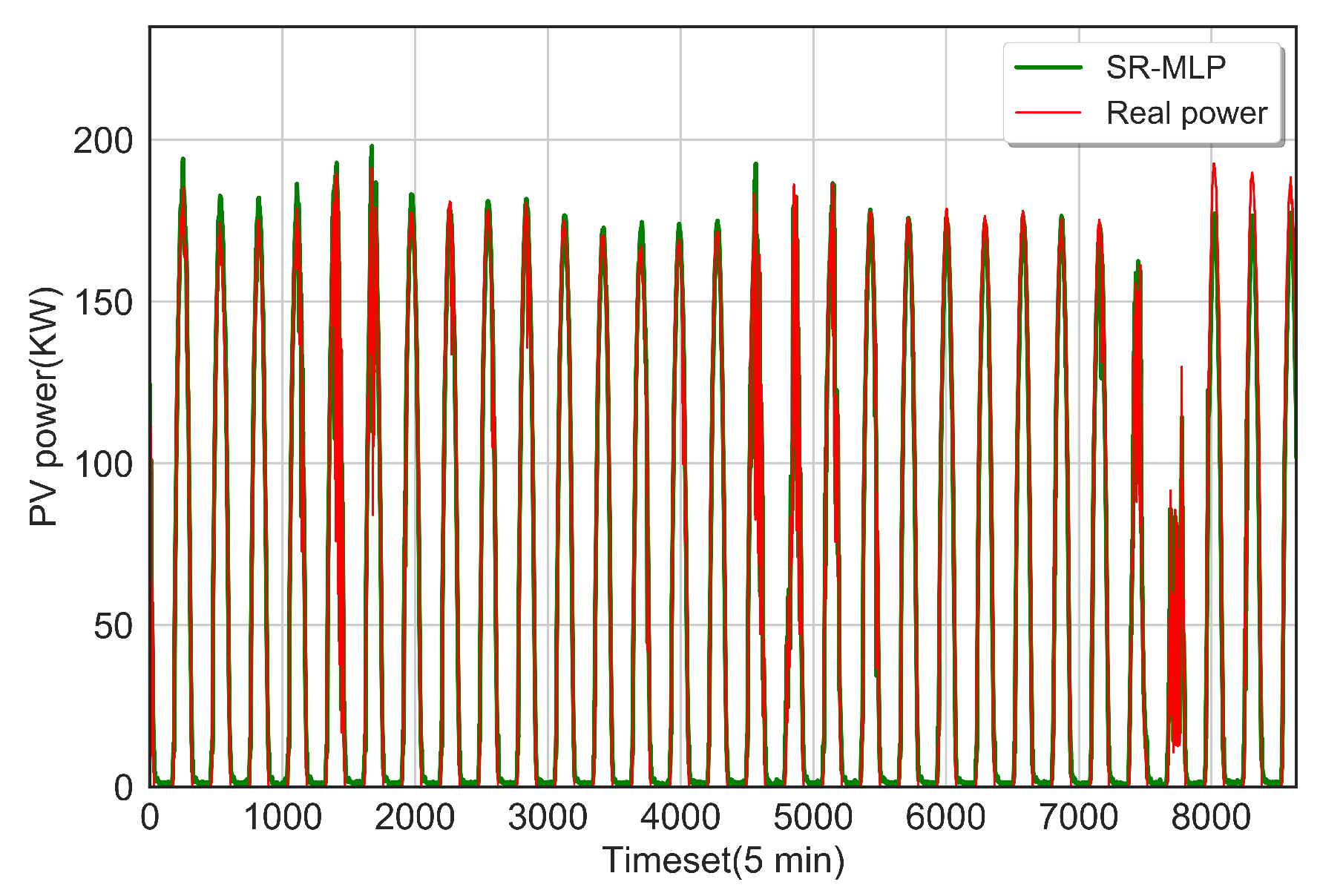
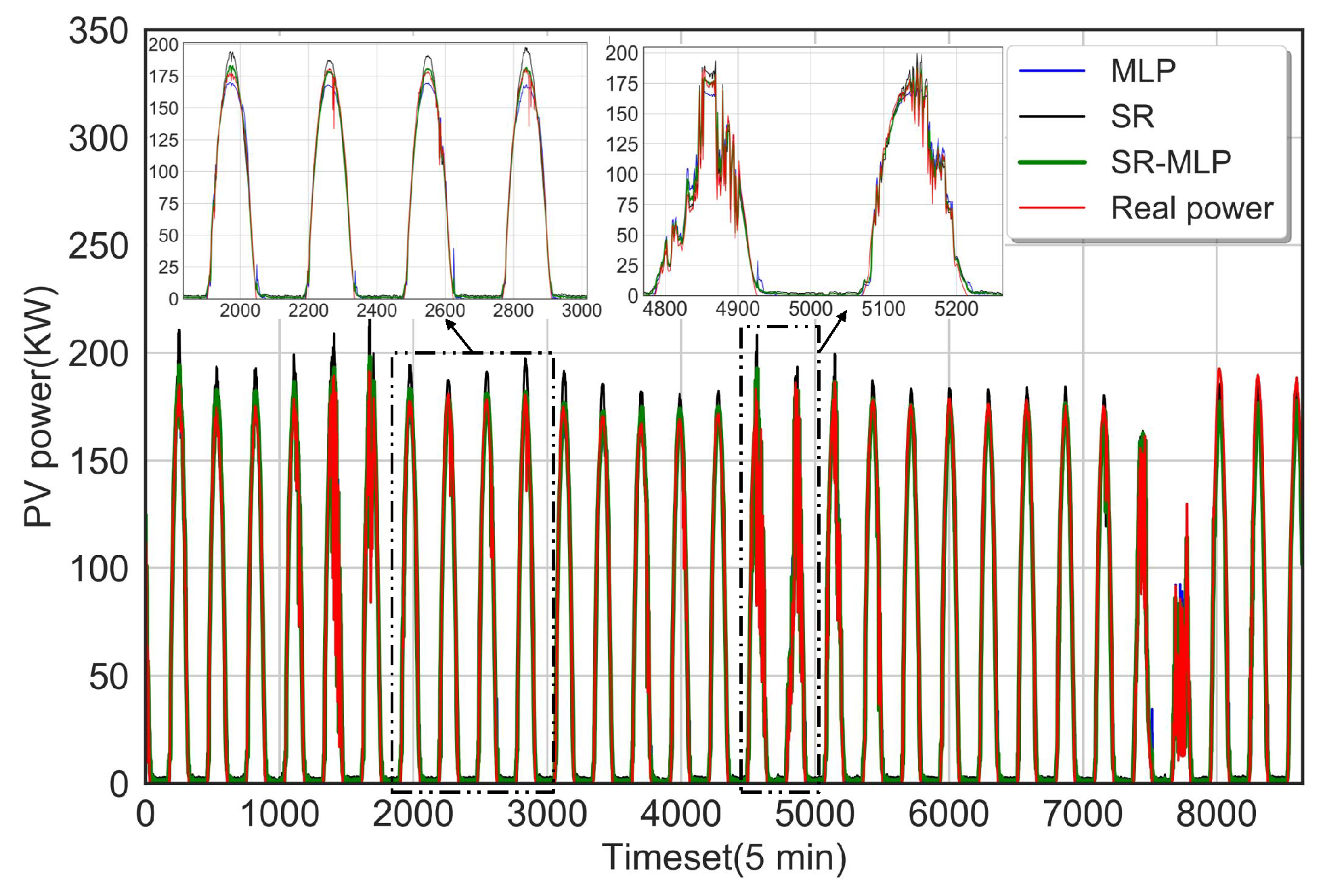
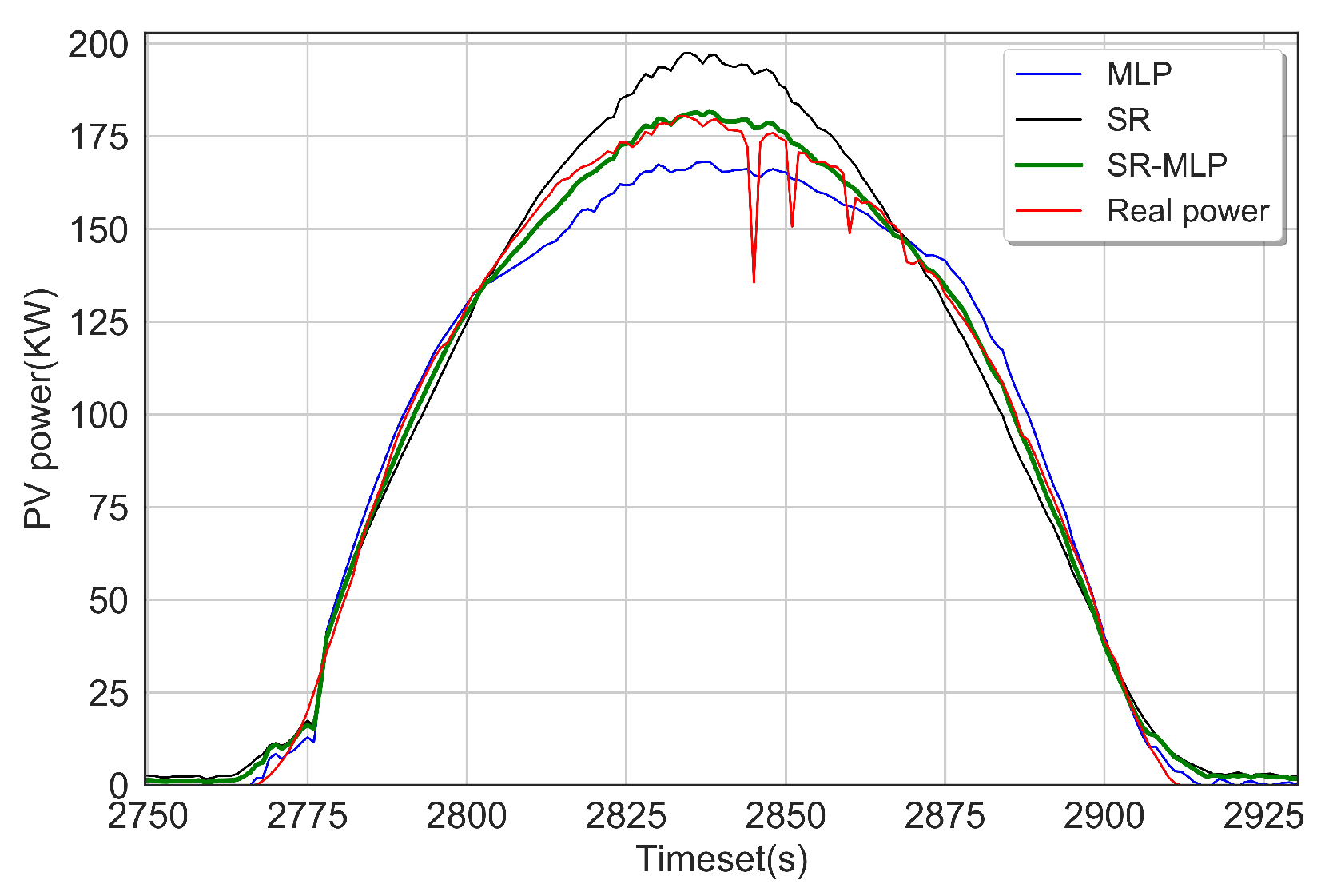
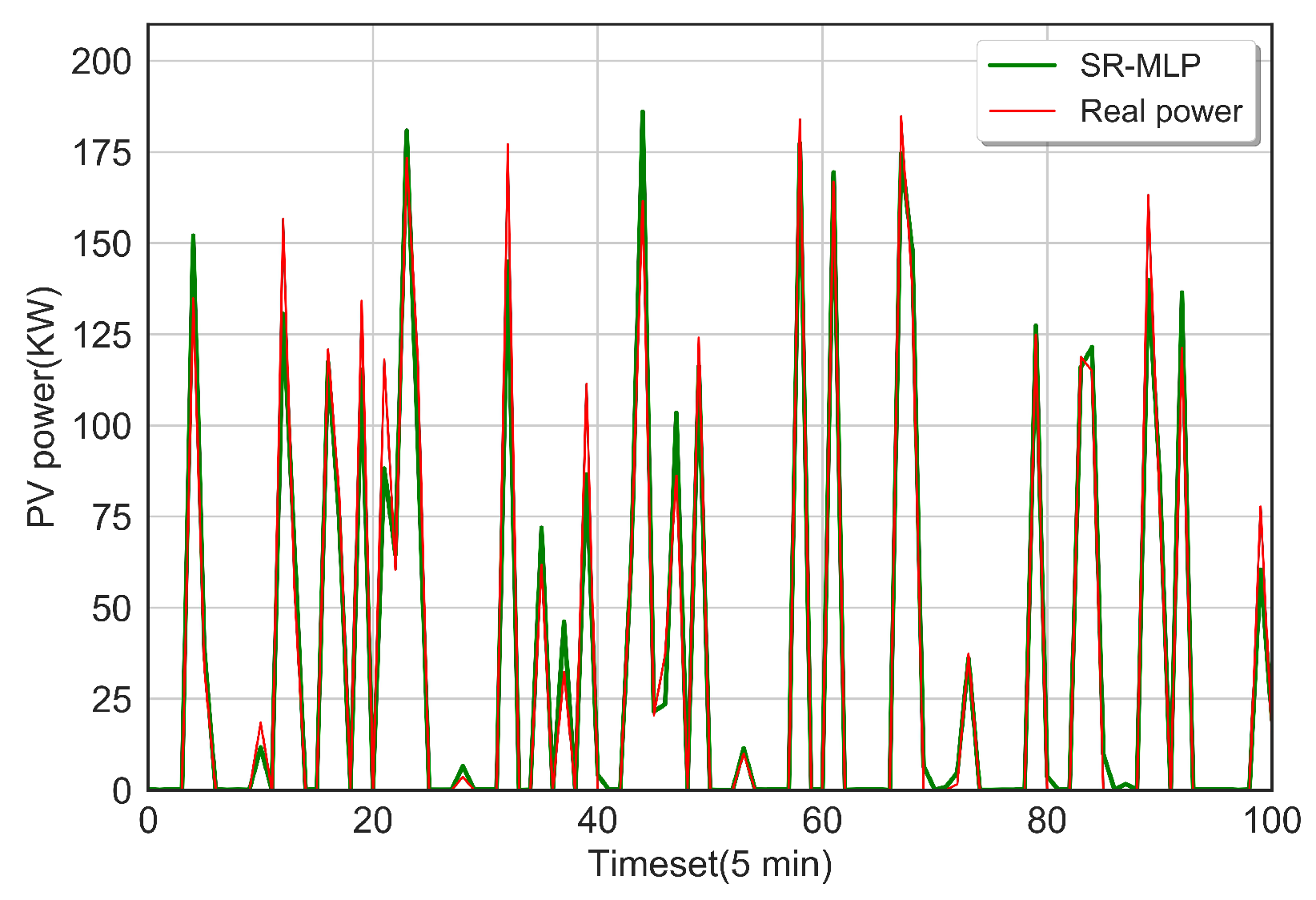
4.2. Training and Simulation Results
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feldman, D.J.; Margolis, R.M. Q4 2018/Q1 2019 Solar Industry Update; Technical report; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2019. [Google Scholar]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Guo, B.; Javed, W.; Figgis, B.; Mirza, T. Effect of dust and weather conditions on photovoltaic performance in Doha, Qatar. In Proceedings of the 2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 22–23 March 2015; pp. 1–6. [Google Scholar]
- Chaichan, M.T.; Kazem, H.A. Experimental analysis of solar intensity on photovoltaic in hot and humid weather conditions. Int. J. Sci. Eng. Res. 2016, 7, 91–96. [Google Scholar]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Massaoudi, M.; Chihi, I.; Sidhom, L.; Trabelsi, M.; Refaat, S.S.; Abu-Rub, H.; Oueslati, F.S. An effective hybrid NARX-LSTM model for point and interval PV power forecasting. IEEE Access 2021, 9, 36571–36588. [Google Scholar] [CrossRef]
- Massaoudi, M.; Chihi, I.; Sidhom, L.; Trabelsi, M.; Refaat, S.S.; Oueslati, F.S. Performance Evaluation of Deep Recurrent Neural Networks Architectures: Application to PV Power Forecasting. In Proceedings of the 2019 2nd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 19–21 November 2019; pp. 1–6. [Google Scholar]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Yadav, H.K.; Pal, Y.; Tripathi, M.M. Photovoltaic power forecasting methods in smart power grid. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Thevenard, D.; Pelland, S. Estimating the uncertainty in long-term photovoltaic yield predictions. Sol. Energy 2013, 91, 432–445. [Google Scholar] [CrossRef]
- Wolff, B.; Kühnert, J.; Lorenz, E.; Kramer, O.; Heinemann, D. Comparing support vector regression for PV power forecasting to a physical modeling approach using measurement, numerical weather prediction, and cloud motion data. Sol. Energy 2016, 135, 197–208. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Ogliari, E.; Dolara, A.; Manzolini, G.; Leva, S. Physical and hybrid methods comparison for the day ahead PV output power forecast. Renew. Energy 2017, 113, 11–21. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of different physical models for PV power output prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Zheng, D.; Semero, Y.K.; Zhang, J.; Wei, D. Short-term wind power prediction in microgrids using a hybrid approach integrating genetic algorithm, particle swarm optimization, and adaptive neuro-fuzzy inference systems. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1561–1567. [Google Scholar] [CrossRef]
- Fentis, A.; Bahatti, L.; Tabaa, M.; Mestari, M. Short-term nonlinear autoregressive photovoltaic power forecasting using statistical learning approaches and in-situ observations. Int. J. Energy Environ. Eng. 2019, 10, 189–206. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Shah, N.M. Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques. IET Renew. Power Gener. 2019, 13, 1009–1023. [Google Scholar] [CrossRef]
- Kuo, W.C.; Chen, C.H.; Chen, S.Y.; Wang, C.C. Deep Learning Neural Networks for Short-Term PV Power Forecasting via Sky Image Method. Energies 2022, 15, 4779. [Google Scholar] [CrossRef]
- Hussain, M.; Al-Aqrabi, H.; Hill, R. Statistical Analysis and Development of an Ensemble-Based Machine Learning Model for Photovoltaic Fault Detection. Energies 2022, 15, 5492. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Aslfattahi, N.; Ghodbane, M. Experimental analysis of novel ionic liquid-MXene hybrid nanofluid’s energy storage properties: Model-prediction using modern ensemble machine learning methods. J. Energy Storage 2022, 52, 104858. [Google Scholar] [CrossRef]
- Jamii, J.; Trabelsi, M.; Mansouri, M.; Mimouni, M.F.; Shatanawi, W. Non-Linear Programming-Based Energy Management for a Wind Farm Coupled with Pumped Hydro Storage System. Sustainability 2022, 14, 11287. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Extreme gradient boosting and deep neural network based ensemble learning approach to forecast hourly solar irradiance. J. Clean. Prod. 2021, 279, 123285. [Google Scholar] [CrossRef]
- Ramsami, P.; Oree, V. A hybrid method for forecasting the energy output of photovoltaic systems. Energy Convers. Manag. 2015, 95, 406–413. [Google Scholar] [CrossRef]
- Acharya, S.K.; Wi, Y.M.; Lee, J. Day-Ahead Forecasting for Small-Scale Photovoltaic Power Based on Similar Day Detection with Selective Weather Variables. Electronics 2020, 9, 1117. [Google Scholar] [CrossRef]
- Son, N.; Jung, M. Analysis of Meteorological Factor Multivariate Models for Medium-and Long-Term Photovoltaic Solar Power Forecasting Using Long Short-Term Memory. Appl. Sci. 2021, 11, 316. [Google Scholar] [CrossRef]
- Kim, Y.; Seo, K.; Harrington, R.J.; Lee, Y.; Kim, H.; Kim, S. High accuracy modeling for solar PV power generation using Noble BD-LSTM-based neural networks with EMA. Appl. Sci. 2020, 10, 7339. [Google Scholar] [CrossRef]
- Gigoni, L.; Betti, A.; Crisostomi, E.; Franco, A.; Tucci, M.; Bizzarri, F.; Mucci, D. Day-ahead hourly forecasting of power generation from photovoltaic plants. IEEE Trans. Sustain. Energy 2017, 9, 831–842. [Google Scholar] [CrossRef]
- Semero, Y.K.; Zhang, J.; Zheng, D. PV power forecasting using an integrated GA-PSO-ANFIS approach and Gaussian process regression based feature selection strategy. CSEE J. Power Energy Syst. 2018, 4, 210–218. [Google Scholar] [CrossRef]
- Yang, H.T.; Huang, C.M.; Huang, Y.C.; Pai, Y.S. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Wang, G.; Su, Y.; Shu, L. One-day-ahead daily power forecasting of photovoltaic systems based on partial functional linear regression models. Renew. Energy 2016, 96, 469–478. [Google Scholar] [CrossRef]
- Shuvho, M.B.A.; Chowdhury, M.A.; Ahmed, S.; Kashem, M.A. Prediction of solar irradiation and performance evaluation of grid connected solar 80KWp PV plant in Bangladesh. Energy Rep. 2019, 5, 714–722. [Google Scholar] [CrossRef]
- Yang, M.; Huang, X. Ultra-short-term prediction of photovoltaic power based on periodic extraction of PV energy and LSH algorithm. IEEE Access 2018, 6, 51200–51205. [Google Scholar] [CrossRef]
- Lee, W.; Kim, K.; Park, J.; Kim, J.; Kim, Y. Forecasting solar power using long-short term memory and convolutional neural networks. IEEE Access 2018, 6, 73068–73080. [Google Scholar] [CrossRef]
- Asrari, A.; Wu, T.X.; Ramos, B. A hybrid algorithm for short-term solar power prediction—Sunshine state case study. IEEE Trans. Sustain. Energy 2016, 8, 582–591. [Google Scholar] [CrossRef]
- Wang, F.; Pang, S.; Zhen, Z.; Li, K.; Ren, H.; Shafie-Khah, M.; Catalão, J.P. Pattern classification and pso optimal weights based sky images cloud motion speed calculation method for solar pv power forecasting. In Proceedings of the 2018 IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–9. [Google Scholar]
- Hokoi, S.; Matsumoto, M.; Ihara, T. Statistical time series models of solar radiation and outdoor temperature—Identification of seasonal models by Kalman filter. Energy Build. 1990, 15, 373–383. [Google Scholar] [CrossRef]
- Cohen, I.R. Updating Darwin: Information and entropy drive the evolution of life. F1000Research 2016, 5, 2808. [Google Scholar] [CrossRef]
- Massaoudi, M.; Abu-Rub, H.; Refaat, S.S.; Chihi, I.; Oueslati, F.S. Deep learning in smart grid technology: A review of recent advancements and future prospects. IEEE Access 2021, 9, 54558–54578. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Abd Elaziz, M.; Kabeel, A.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Isa, I.S.; Omar, S.; Saad, Z.; Noor, N.M.; Osman, M.K. Weather forecasting using photovoltaic system and neural network. In Proceedings of the 2010 2nd International Conference on Computational Intelligence, Communication Systems and Networks, Liverpool, UK, 28–30 July 2010; pp. 96–100. [Google Scholar]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Koza, J.R.; Poli, R. Genetic programming. In Search Methodologies; Springer: Berlin/Heidelberg, Germany, 2005; pp. 127–164. [Google Scholar]
- Brabazon, A.; O’Neill, M.; McGarraghy, S. Natural Computing Algorithms; Springer: Berlin/Heidelberg, Germany, 2015; Volume 554. [Google Scholar]
- Bhuvaneswari, G.; Annamalai, R. Development of a solar cell model in MATLAB for PV based generation system. In Proceedings of the 2011 Annual IEEE India Conference, Hyderabad, India, 16–18 December 2011; pp. 1–5. [Google Scholar]
- DKA Solar Centre. Available online: http://dkasolarcentre.com (accessed on 23 September 2019).
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting; R package version 0.4-2. 2015. Available online: https://cran.microsoft.com/snapshot/2017-12-11/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 23 September 2019).
- Shah, I.; Iftikhar, H.; Ali, S. Modeling and Forecasting Electricity Demand and Prices: A Comparison of Alternative Approaches. J. Math. 2022, 2022, 3581037. [Google Scholar] [CrossRef]
- Shah, I.; Jan, F.; Ali, S. Functional data approach for short-term electricity demand forecasting. Math. Probl. Eng. 2022, 2022, 6709779. [Google Scholar] [CrossRef]
- Lisi, F.; Shah, I. Forecasting next-day electricity demand and prices based on functional models. Energy Syst. 2020, 11, 947–979. [Google Scholar] [CrossRef]
| Model | Reference | Score Metrics | Lowest Score | Dataset |
|---|---|---|---|---|
| XGBF -DNN | [24] | RMSE, MBE , FS | RMSE = 51.35 W | PV data in Limberg, Belgium |
| SR-FFNN | [25] | RMSE, MBE , MAE, | = 0.932 | Solar power in Flanders, Belgium |
| LSTM | [26] | NMAE, RMSE | RMSE = 38.13 kWh | 1 MW PV site in Goheung, Korea |
| Modified LSTM | [27] | MAE, RMSE | RMSE = 0.55 kW | Ansan, Gyeonggi-do, Korea |
| LSTM-EMA | [28] | RMSE, , MAPE | = 0.96 | Yeonseong-gun, Gyeonggi-do, South Korea |
| ENS | [29] | NRMSE, nMBE, MAE, nMAE | MAE = 74.1 kW | 32 PV plants installed at different latitudes in Italy |
| GA-PSO-ANFIS | [30] | RMSE, MAE, NMAE, FS | RMSE = 2.08 kW | Goldwind microgrid system found in Beijing |
| SOM , LVQ , SVR | [31] | MRE and RMSE | MRE = 1.79% | Taiwan Central Weather Bureau |
| PFLRM | [32] | RMSE, MAD , MAPE | RMSE = 59.38 kW | Coloane island of Macau |
| ANN | [33] | RMSE, | = 0.999 | Solar power plant in Dhaka |
| LSH | [34] | RMSE, MRE, QR | RMSE = 4.23 kW | PV power station in Ashland |
| AE -LSTM | [35] | MAPE, RMSE, MAE | RMSE = 0.14 kW | PV inverter installed in Haenam, South Korea |
| SFLA -ANN | [36] | MAPE | MAPE = 5.38% | PV sites in Florida |
| PCPOW | [37] | = 0.938 | Yunnan Electric Power Research Institute |
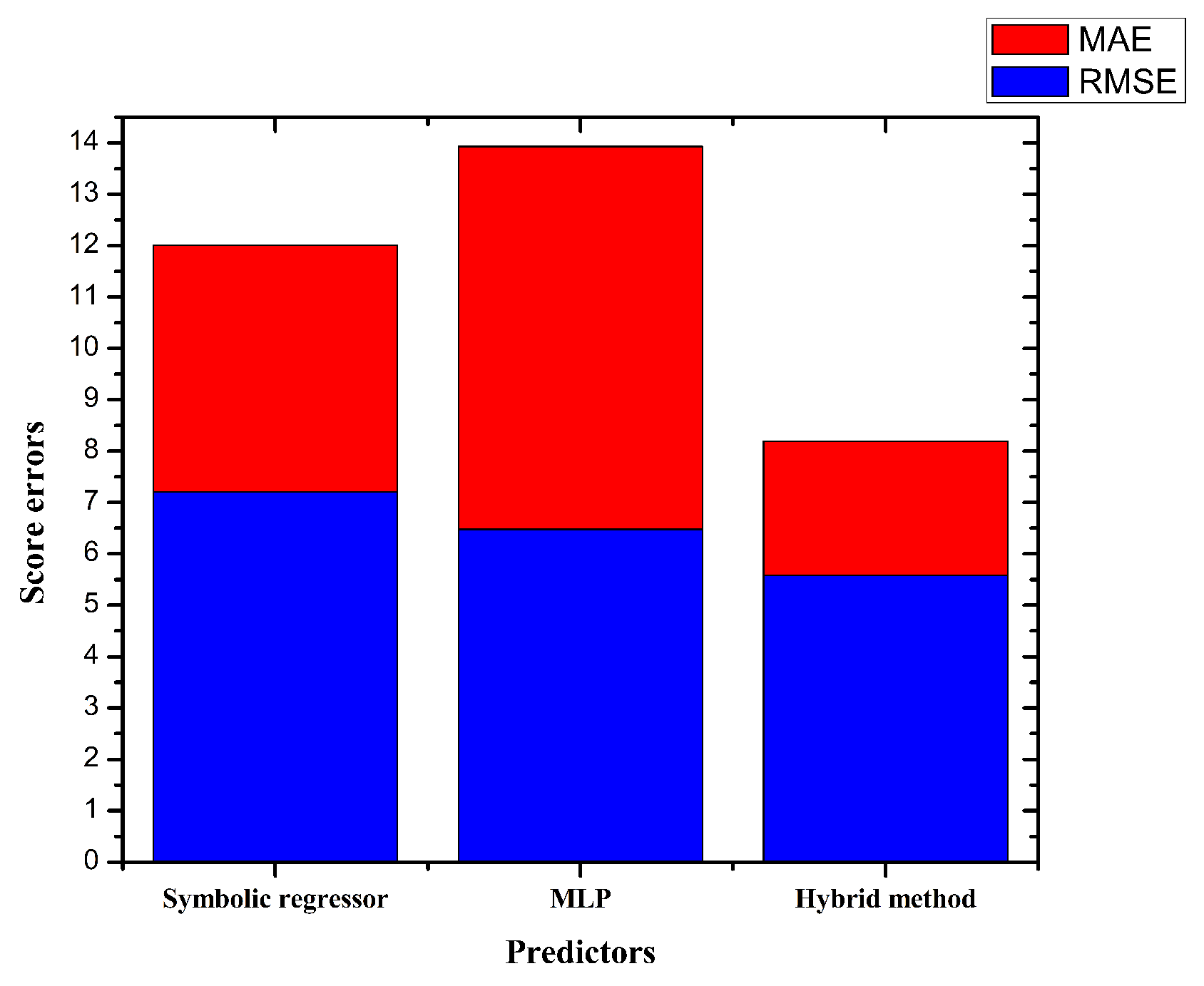
| Errors | SR | MLP | SR-MLP |
|---|---|---|---|
| RMSE (kW) | 7.21 | 6.48 | 5.58 |
| MAE (kW) | 4.92 | 3.81 | 3.3 |
| 0.988 | 0.990 | 0.993 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trabelsi, M.; Massaoudi, M.; Chihi, I.; Sidhom, L.; Refaat, S.S.; Huang, T.; Oueslati, F.S. An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting. Energies 2022, 15, 9008. https://doi.org/10.3390/en15239008
Trabelsi M, Massaoudi M, Chihi I, Sidhom L, Refaat SS, Huang T, Oueslati FS. An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting. Energies. 2022; 15(23):9008. https://doi.org/10.3390/en15239008
Chicago/Turabian StyleTrabelsi, Mohamed, Mohamed Massaoudi, Ines Chihi, Lilia Sidhom, Shady S. Refaat, Tingwen Huang, and Fakhreddine S. Oueslati. 2022. "An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting" Energies 15, no. 23: 9008. https://doi.org/10.3390/en15239008
APA StyleTrabelsi, M., Massaoudi, M., Chihi, I., Sidhom, L., Refaat, S. S., Huang, T., & Oueslati, F. S. (2022). An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting. Energies, 15(23), 9008. https://doi.org/10.3390/en15239008









