Improved Thermal Performance of a Serpentine Cooling Channel by Topology Optimization Infilled with Triply Periodic Minimal Surfaces
Abstract
1. Introduction
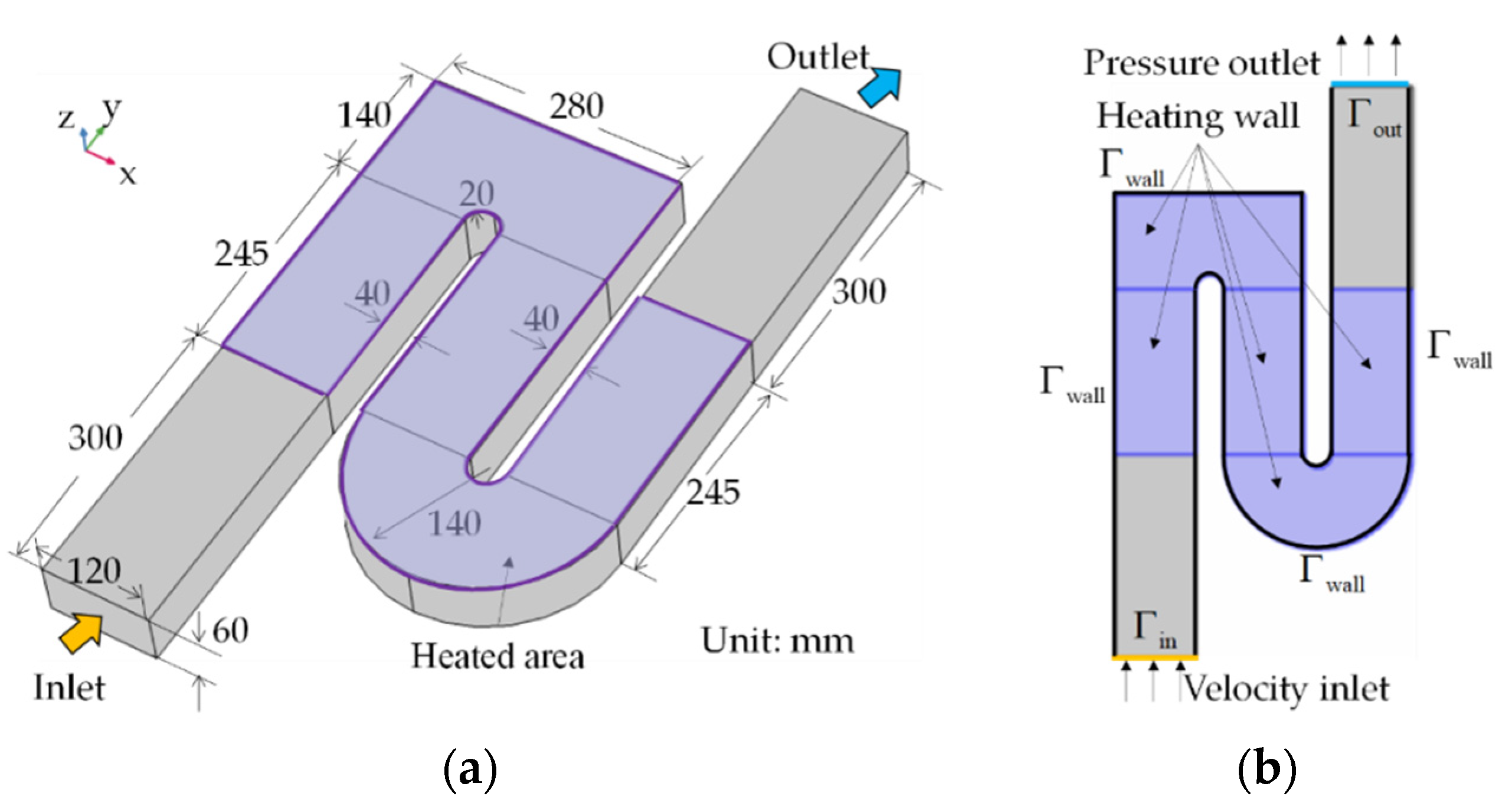
2. Serpentine Model
2.1. Model Description
2.2. Thermofluid Modeling
2.2.1. Fluid-Flow Modeling
2.2.2. Turbulence Modeling
2.2.3. Heat Transfer Modeling
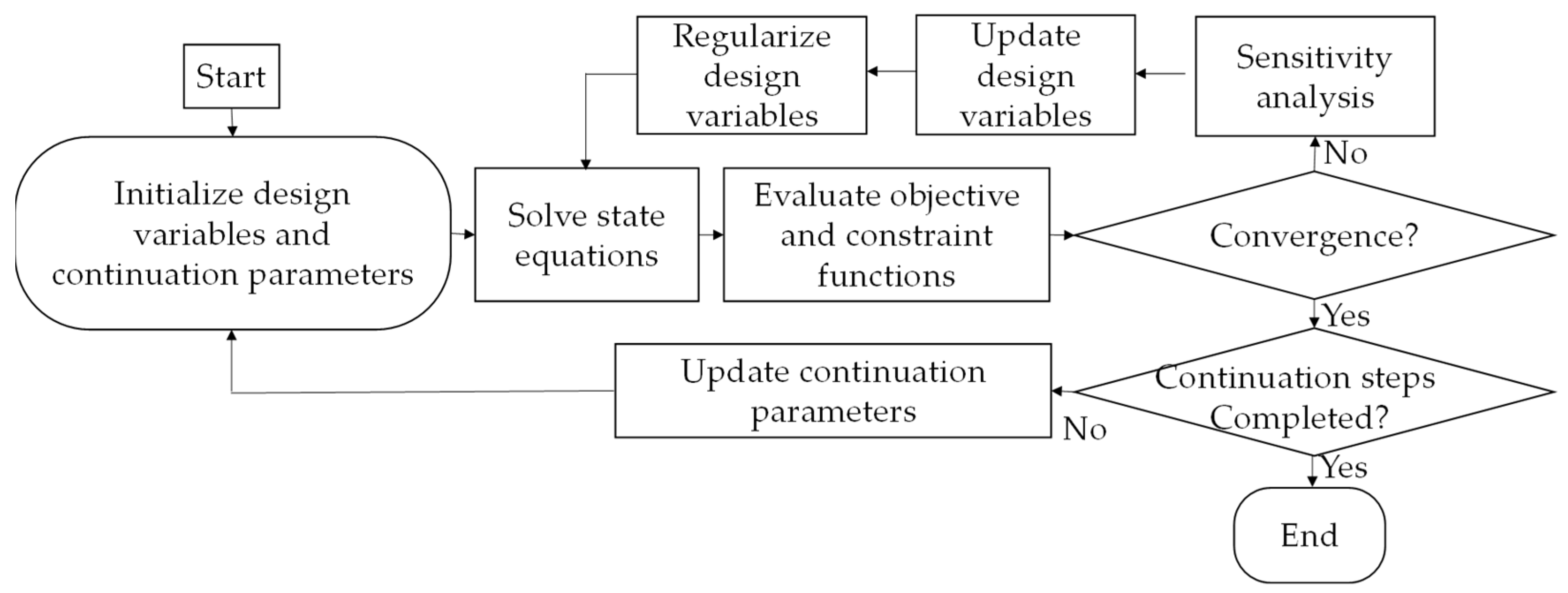
3. Optimization Procedures
3.1. Topology Optimization
3.1.1. Material Distribution
3.1.2. Problem Formulation
3.1.3. Density Filter and Projection
3.1.4. Summary of Topology Optimization Process
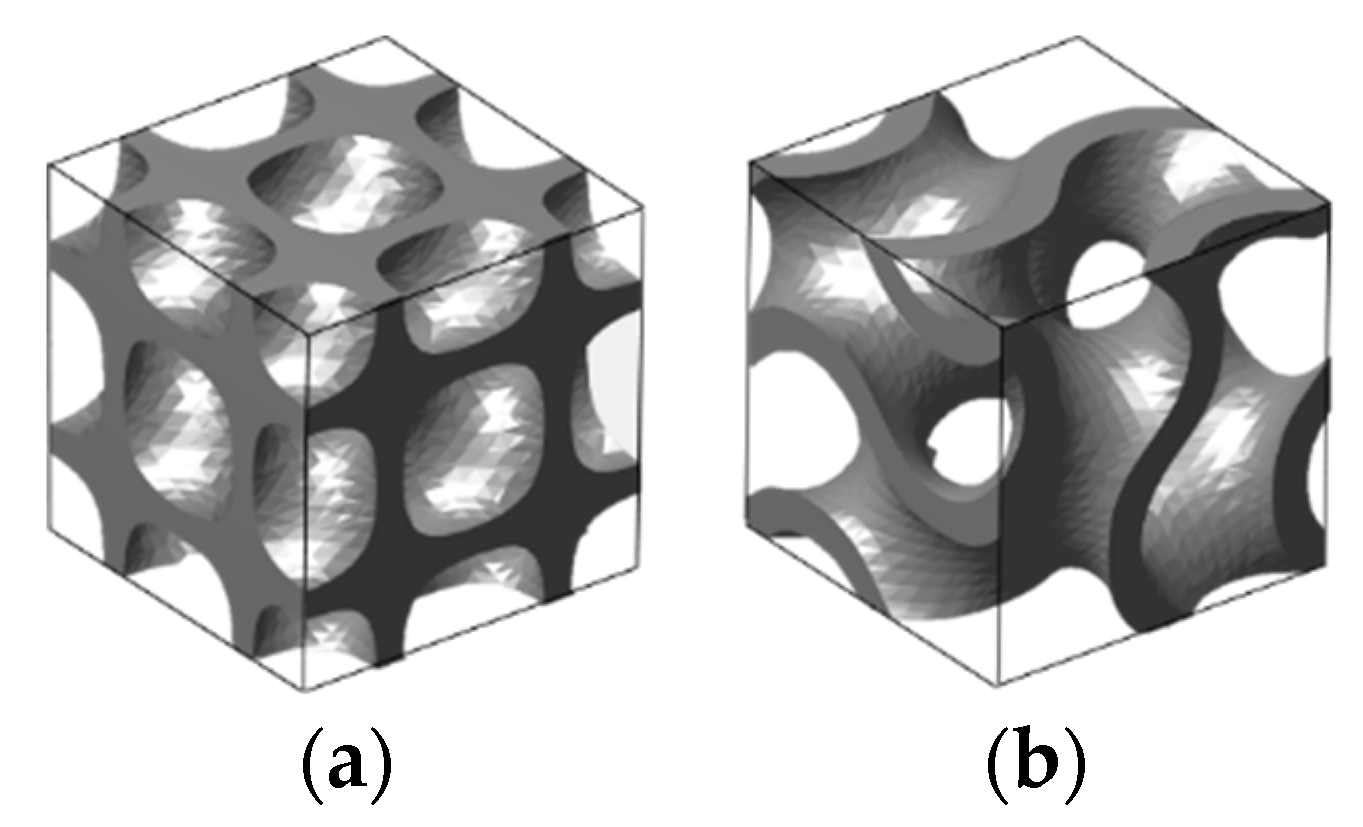
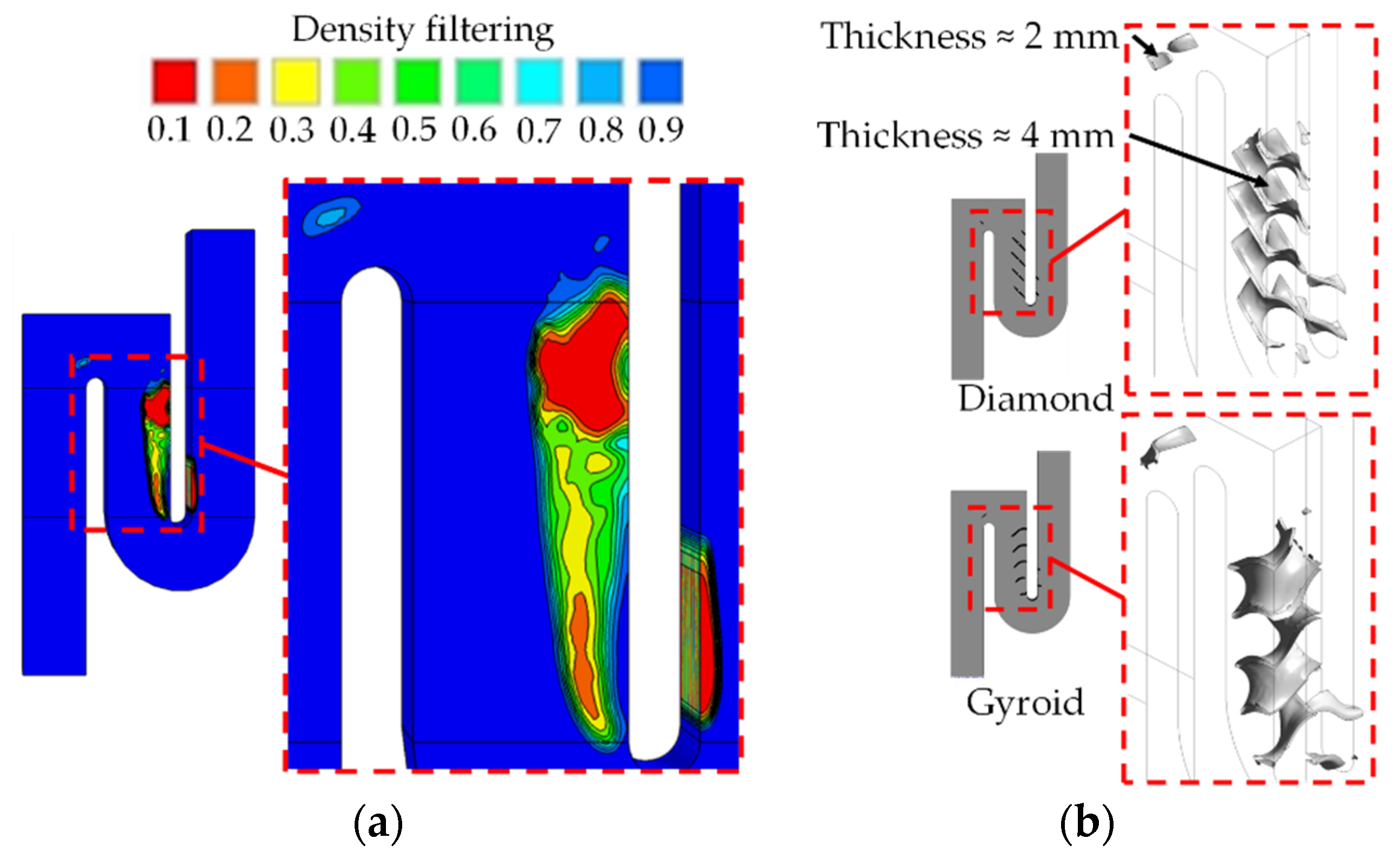
3.2. Infilling Lattice Structures
4. Results and Discussion
4.1. 2D Optimization
4.1.1. Validation of the 2D Model
4.1.2. Optimized Structure
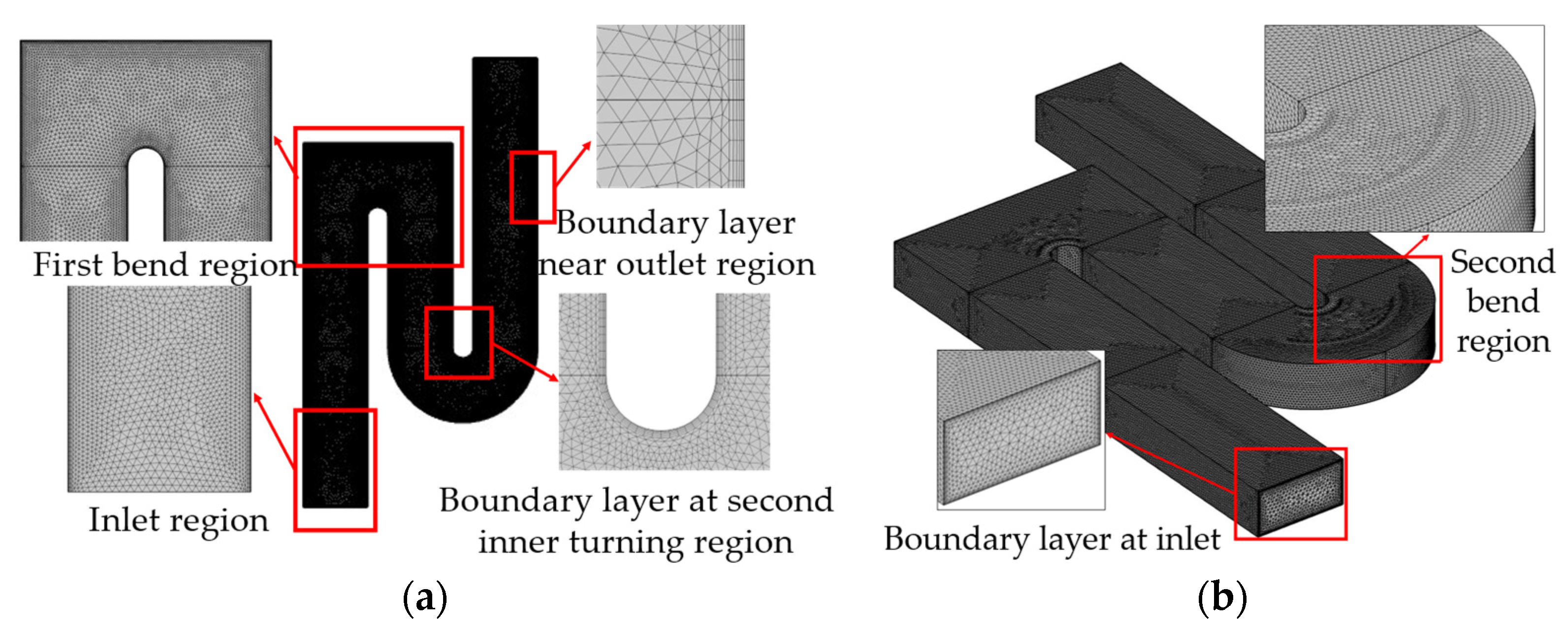
4.2. 3D Model Comparisons
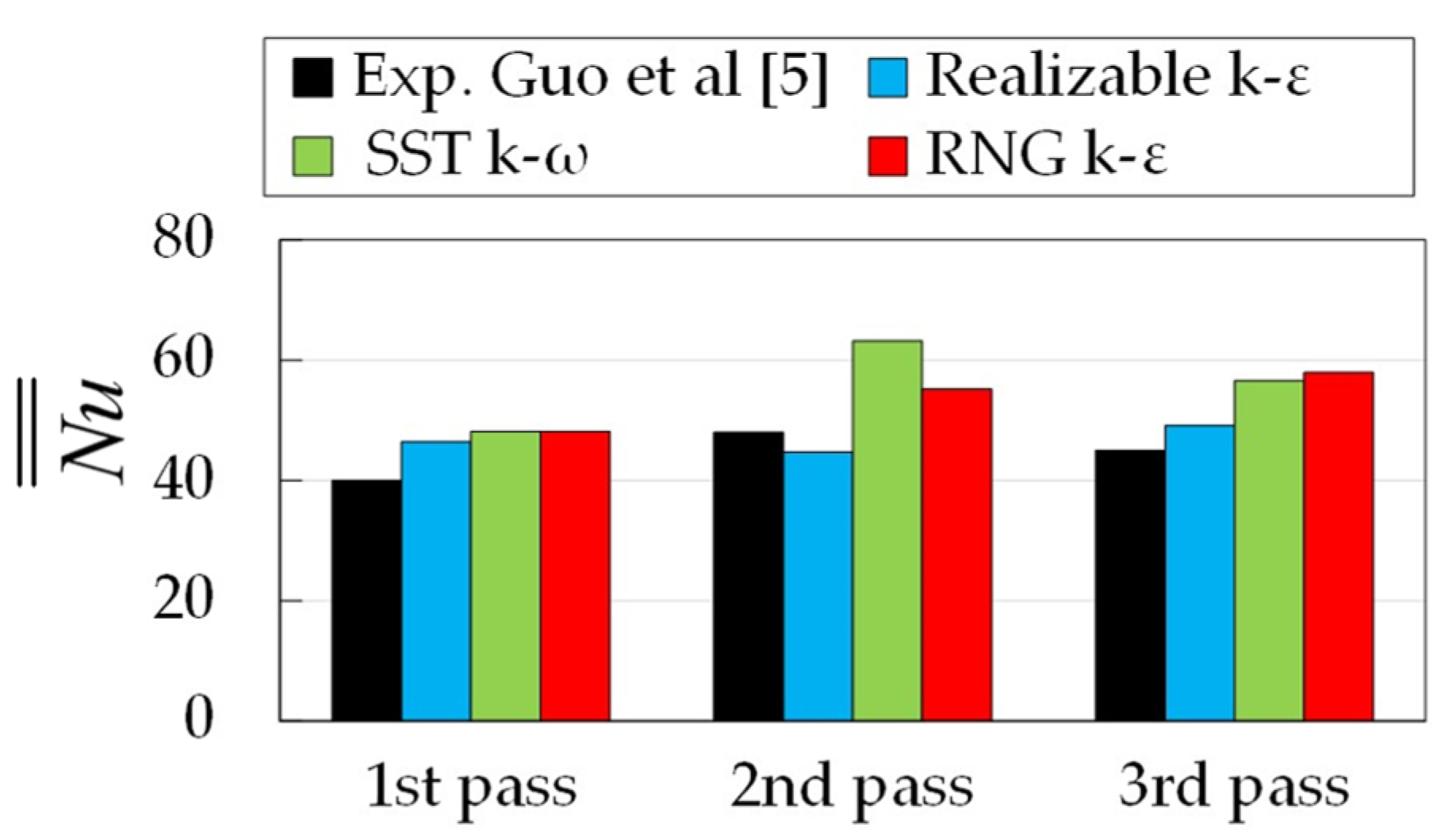
4.2.1. 3D Model Validation
4.2.2. Pressure Loss
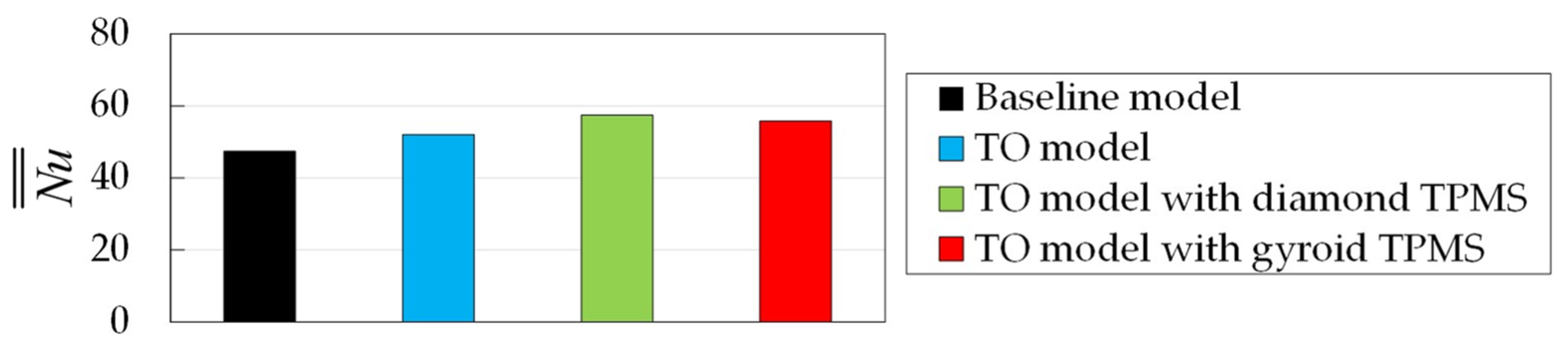
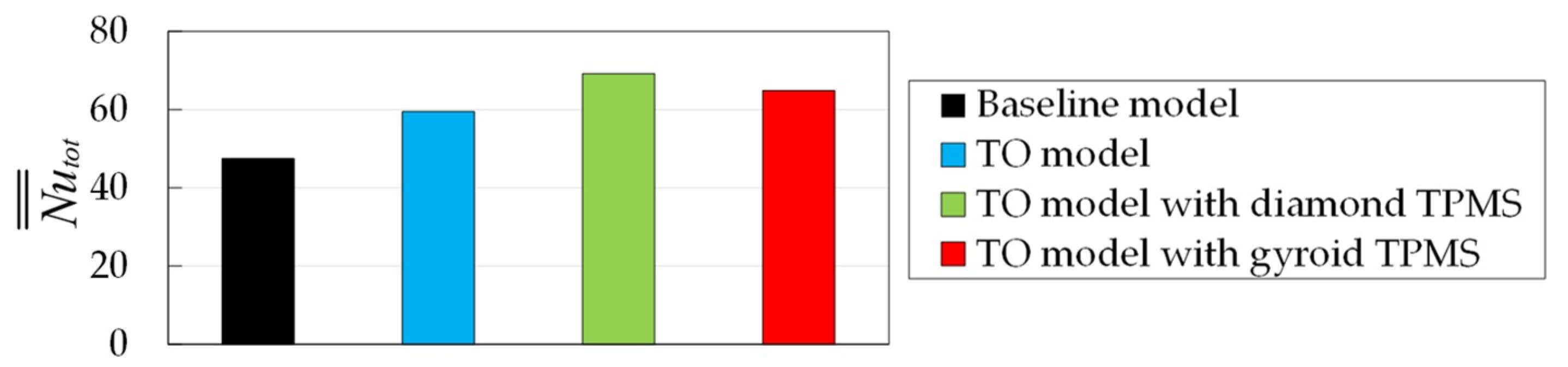
4.2.3. Heat Transfer
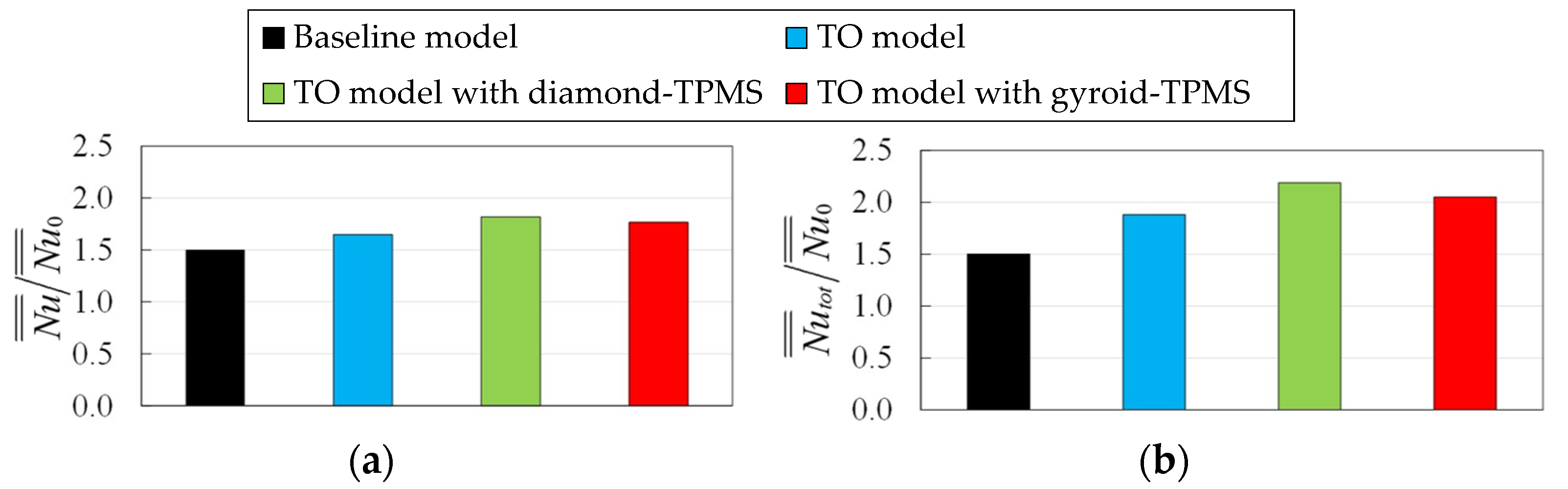
4.2.4. Thermal Performance
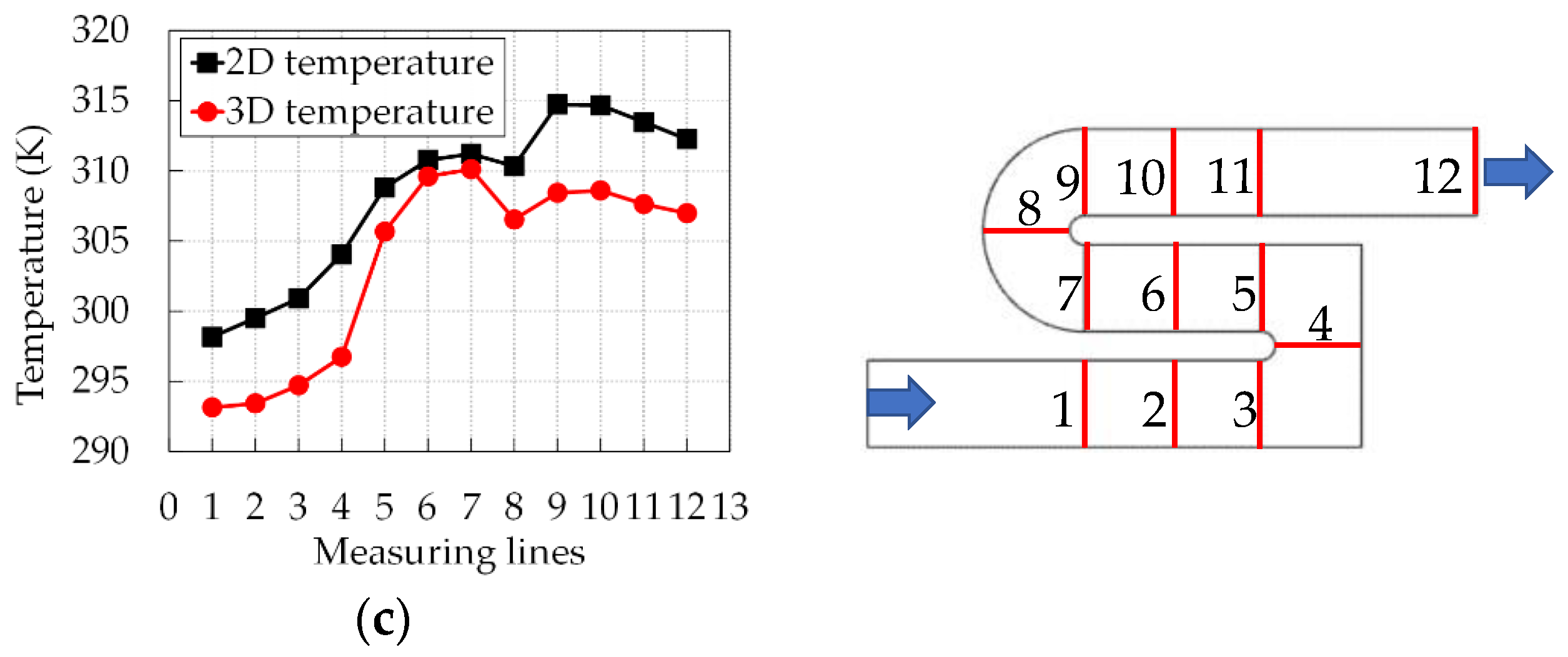
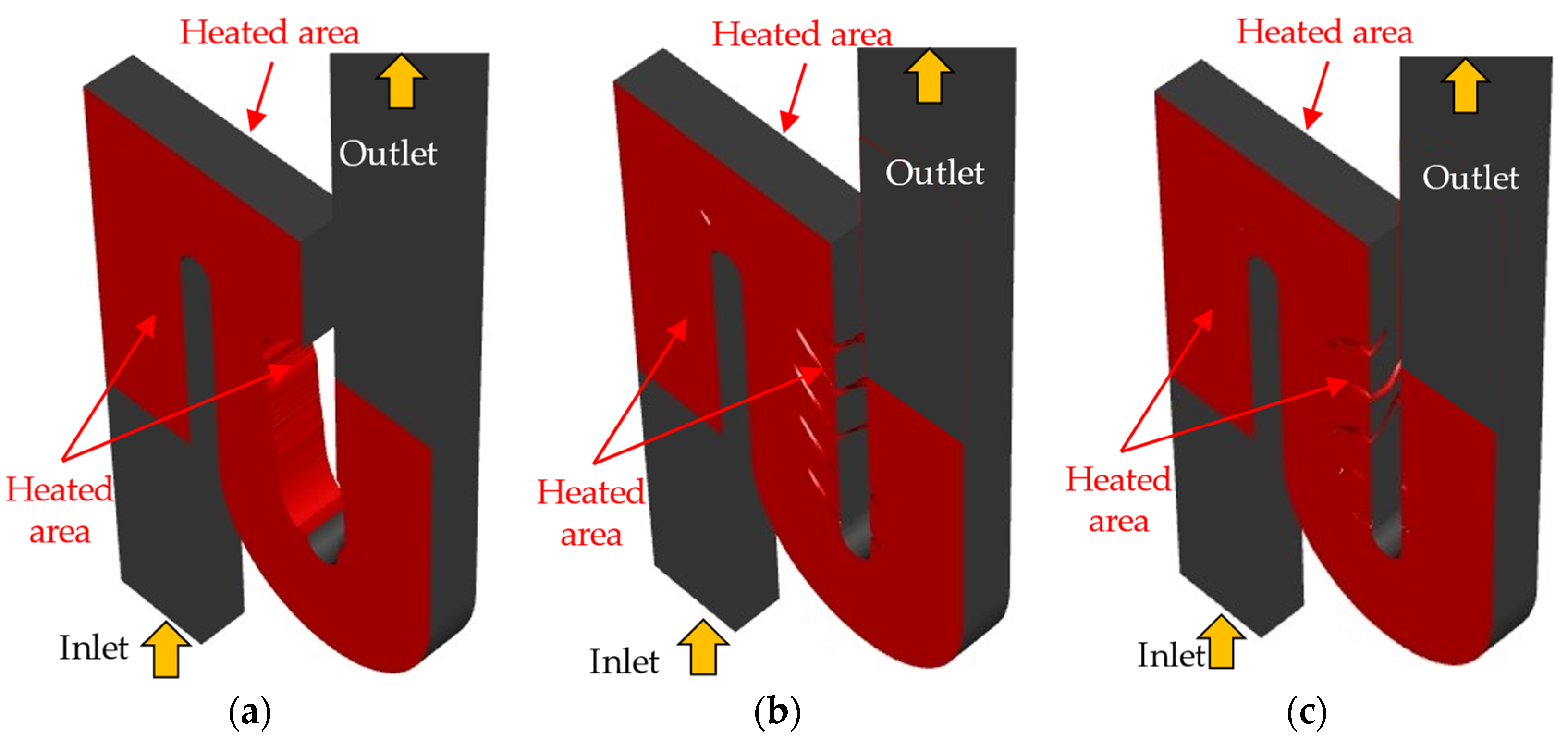
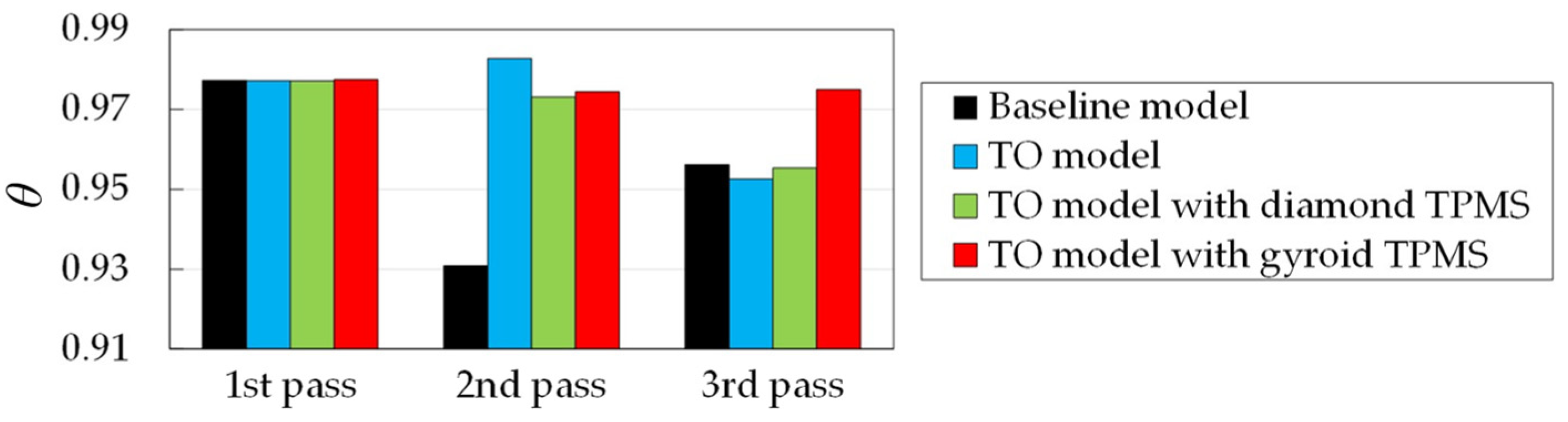
4.2.5. Temperature Uniformity
4.3. Detailed Flow and Heat Transfer Characteristics of the Optimal Serpentine Channel
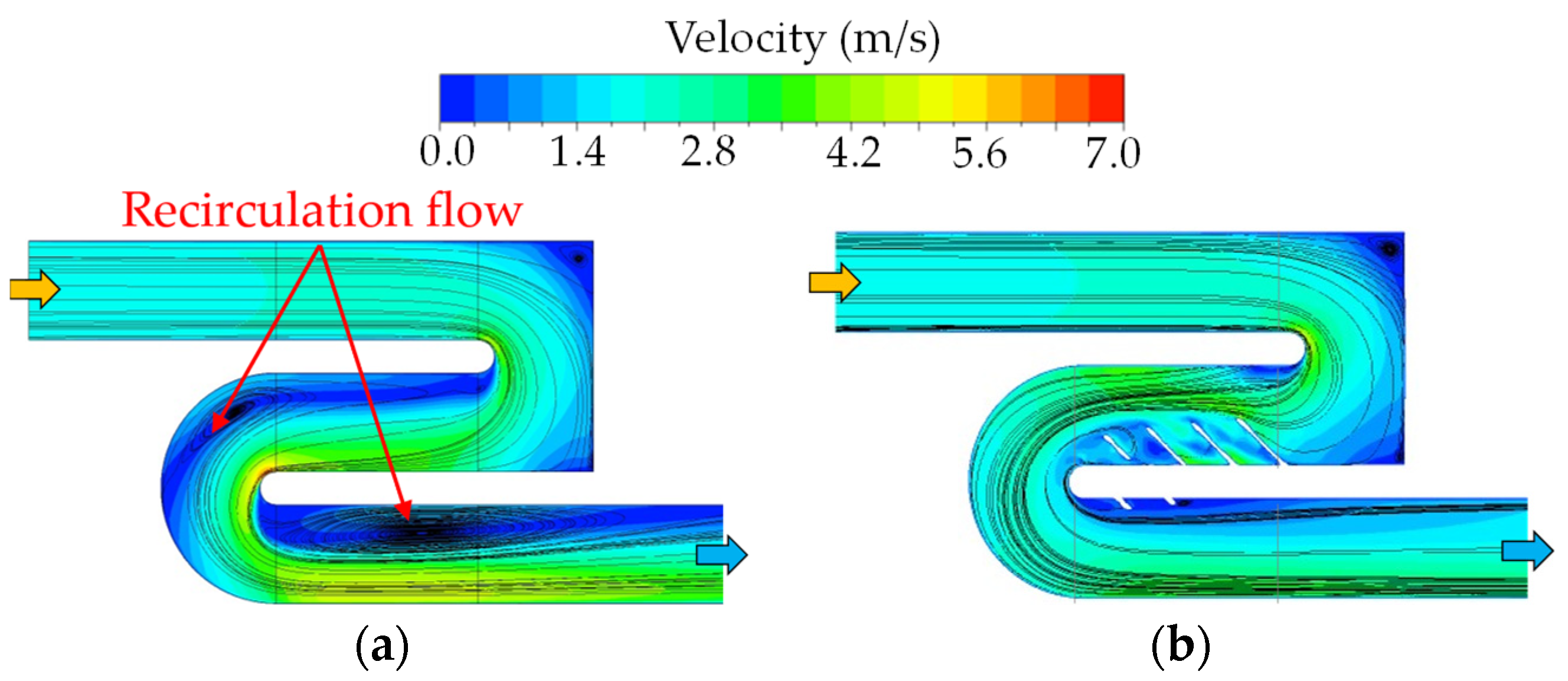
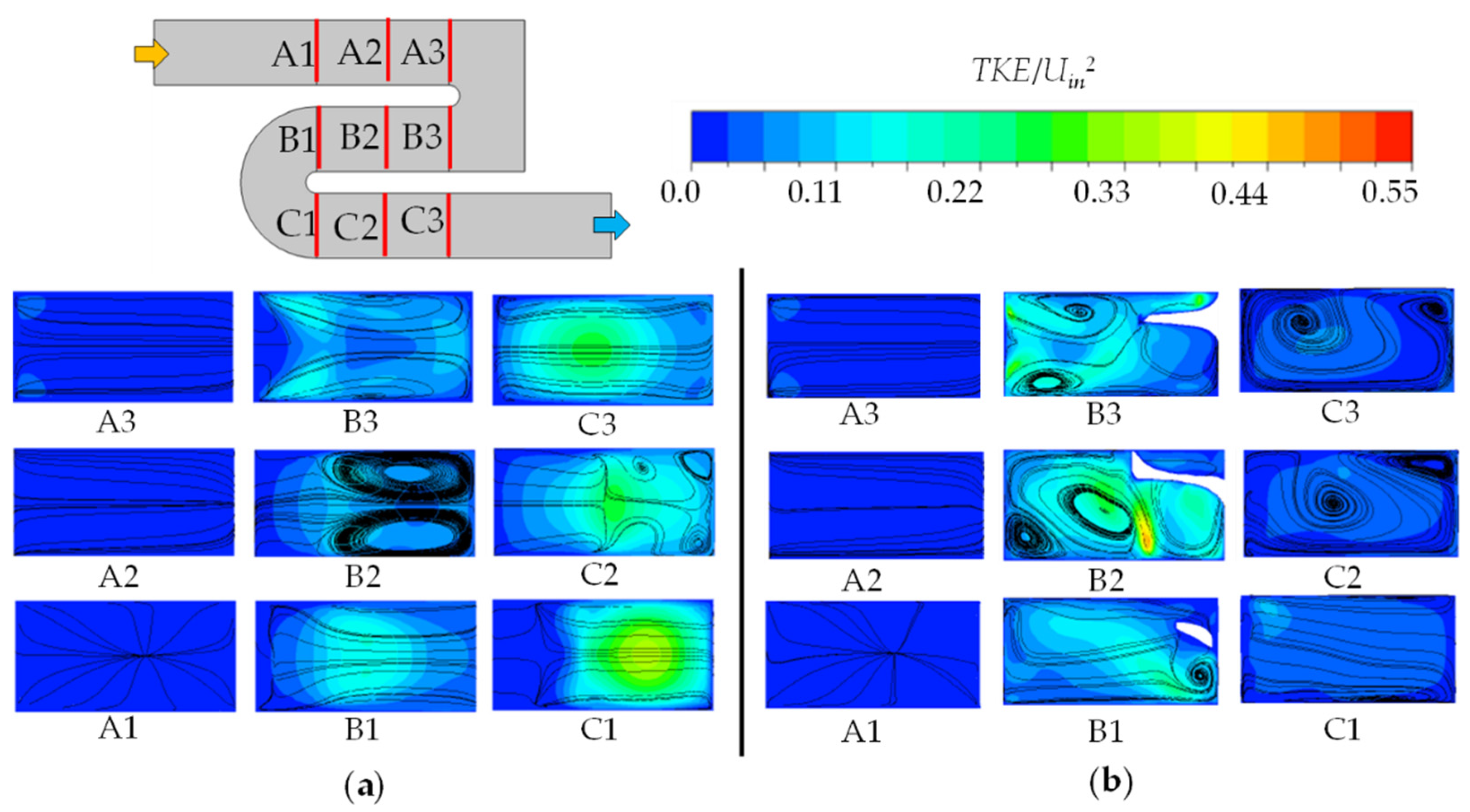
4.3.1. Flow Characteristics
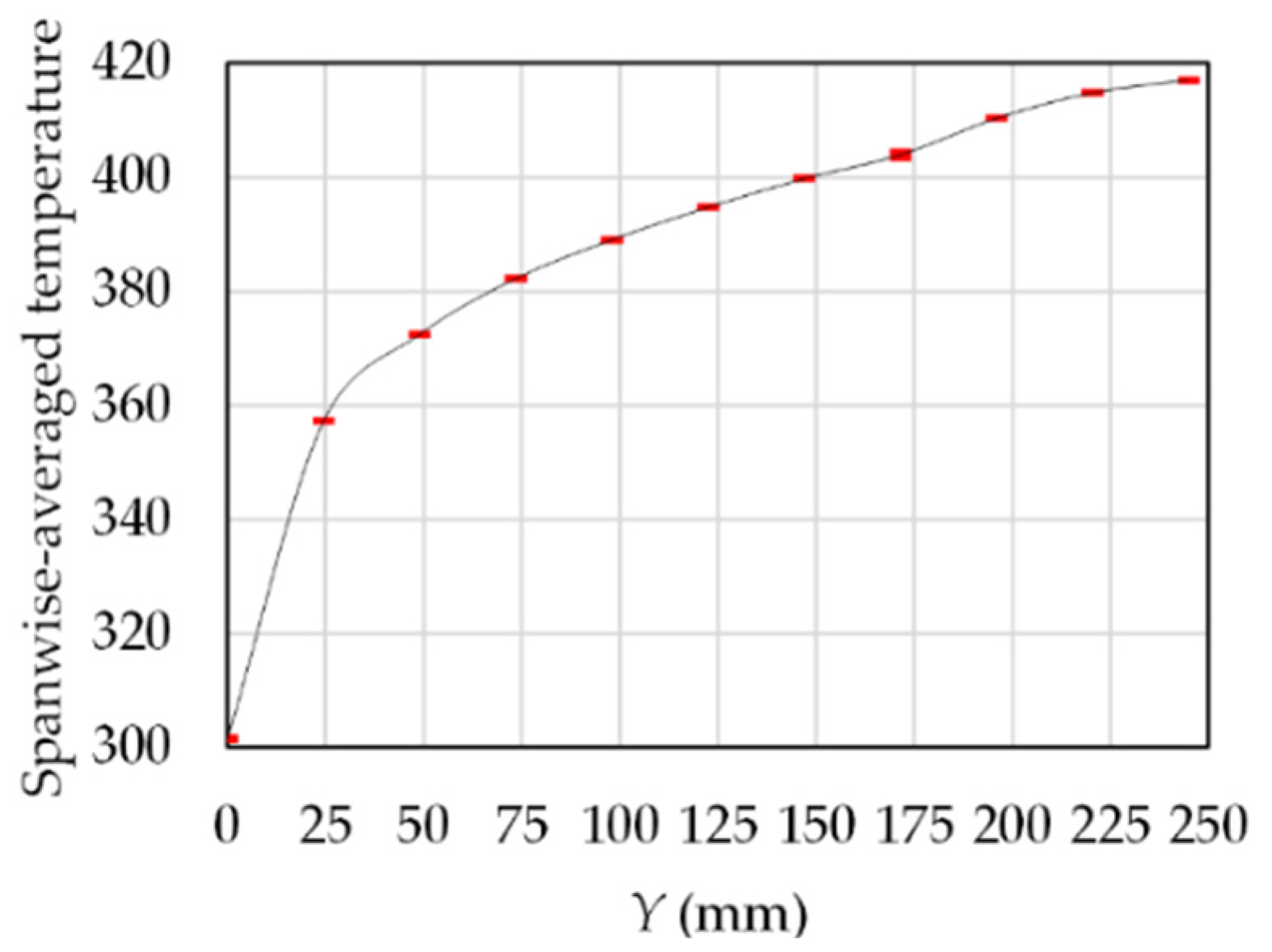
4.3.2. Heat Transfer Characteristics
5. Conclusions
- The conventional topology optimization model achieves a lower pressure loss and provides higher heat transfer than the baseline channel. Infilling the diamond- and gyroid-sheet structures in the optimal solution, including the intermediate results of the conventional topology optimization model, further enhance high heat transfer and maintains lower pressure loss than the baseline channel.
- The 3D optimized models with the TPMS structures provide lower pressure loss by about 19.0%–30.8% and higher total heat transfer by 36.6%–45.8%, compared to the 3D baseline channel. The optimized mode infilled with the diamond-TPMS structure is selected as the optimal serpentine channel in this study since it provides the best thermal performance, up to 64.8%, superior to the baseline channel. The temperature uniformity on the surface is also improved, particularly in the second passage.
- The 3D optimized model with the diamond-TPMS structure significantly eliminates the recirculation flow and the low heat transfer regions at the second and third passages. This model also reduces the influence of Dean’s vortices but maintains high turbulence kinetic energy, leading to better uniform flow and heat transfer distributions.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ah | Flat heated area (m2) |
| Ai | Local area (m) |
| Aw | Wetted area (m2) |
| AR | Aspect ratio of the channel |
| C | Constraint function |
| cf | Fluid heat capacity (J/(kg K)) |
| Cp | Relative pressure coefficient |
| Cref | Reference value in constraint function |
| Da | Darcy number |
| Dh | Hydraulic diameter of the channel (m) |
| F | Fictitious body-force (N/m3) |
| f | Friction factor |
| f0 | Blasius correlation |
| g | Inequality constraints |
| Iu, Ik, Iε, Ic, IK | Material interpolated functions |
| J | Objective function |
| k, k0 | Turbulent kinetic energy of the fluid and solid domains (m2/s2) |
| kf, ks | Thermal conductivity of the fluid and solid (W/(m K)) |
| L | Total length of the serpentine channel (m) |
| n | Normal vector |
| nc, nK | Penalization power coefficients in material interpolated functions |
| , | Globally and total Nusselt numbers |
| Dittus–Boelter equation | |
| Pk | Turbulent kinetic energy source term (W/m3) |
| p0 | Zero static pressure (Pa) |
| ploc | Local static pressure at measuring points (Pa) |
| pref | Pressure value at the channel inlet (Pa) |
| Pr | Prandtl number |
| Qtot | Total heat transfer (W) |
| q0 | Uniform heat flux (W/m2) |
| qu, qk, qε | Tuning parameters in material interpolated functions |
| R | Residual vector function |
| Re | Reynolds number |
| Rmin | Filter radius (m) |
| S | Vectors with discrete state fields |
| TP | Thermal performance of cooling channels |
| Tavg | Average temperature of the considered surface (m2) |
| Ti | Local temperature at the consider area (K) |
| Tin, Tout | Inlet and outlet temperatures (K) |
| Tw | Average wall temperature (K) |
| u | Fluid velocity vector |
| Uin | Inlet velocity (m/s) |
| x | Design variable vector |
| y+ | Nondimensional distance from the endwall to the first element node |
| Greek Letters | |
| αu,max, αu,min | Maximum and minimum inverse permeabilities of the porous medium (Pa s/m) |
| β | Projection slope |
| γ | Design variable |
| γf, γp | Smoothed and projected design variables |
| ε, ε0 | Turbulent energy dissipation for fluid and solid regions (m2/s3) |
| μ | Dynamic viscosity (N s/m2) |
| μT | Turbulent dynamic viscosity (N s/m2) |
| ρ | Fluid density (kg/m3) |
| η | Projection threshold |
| θ | Uniformity index of temperature |
| ω | Specific rate of dissipation in the k–ω turbulence model (1/s) |
| Γin, Γout | Inlet and outlet boundary conditions |
| Γwall | No-slip boundary conditions |
| Ωid, Ωod | Inside and outside design domains |
References
- Yeranee, K.; Rao, Y. A Review of Recent Studies on Rotating Internal Cooling for Gas Turbine Blades. Chin. J. Aeronaut. 2021, 34, 85–113. [Google Scholar] [CrossRef]
- Ekkad, S.; Singh, P. Detailed Heat Transfer Measurements for Rotating Turbulent Flows in Gas Turbine Systems. Energies 2021, 14, 39. [Google Scholar] [CrossRef]
- Rao, Y.; Guo, Z.; Wang, D. Experimental and Numerical Study of Heat Transfer and Turbulent Flow Characteristics in Three-Short-Pass Serpentine Cooling Channels with Miniature W-Ribs. J. Heat Transfer. 2020, 142, 121901. [Google Scholar] [CrossRef]
- Schüler, M.; Zehnder, F.; Weigand, B.; von Wolfersdorf, J.; Neumann, S. The Effect of Turning Vanes on Pressure Loss and Heat Transfer of a Ribbed Rectangular Two-Pass Internal Cooling Channel. J. Turbomach. 2011, 133, 021017. [Google Scholar] [CrossRef]
- Guo, Z.; Rao, Y.; Li, Y.; Wang, W. Experimental and Numerical Investigation of Turbulent Flow Heat Transfer in a Serpentine Channel with Multiple Short Ribbed Passes and Turning Vanes. Int. J. Therm. Sci. 2021, 165, 106931. [Google Scholar] [CrossRef]
- Lei, J.; Su, P.; Xie, G.; Lorenzini, G. The Effect of a Hub Turning Vane on Turbulent Flow and Heat Transfer in a Four-Pass Channel at High Rotation Numbers. Int. J. Heat Mass Transf. 2016, 92, 578–588. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, L.; Hu, C.; Zhao, J.; Tang, D.; Song, Y. Forced Convective Heat Transfer in Optimized Kelvin Cells to Enhance Overall Performance. Energy 2022, 242, 122995. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology Optimization Approaches: A Comparative Review. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Li, H.; Yamada, T.; Jolivet, P.; Kondoh, T.; Furuta, K.; Nishiwaki, S. Full-Scale 3D Structural Topology Optimization Using Adaptive Mesh Refinement Based on the Level-Set Method. Finite Elem. Anal. Des. 2021, 194, 103561. [Google Scholar] [CrossRef]
- Li, H.; Kondoh, T.; Jolivet, P.; Furuta, K.; Yamada, T.; Zhu, B.; Zhang, H.; Izui, K.; Nishiwaki, S. Optimum Design and Thermal Modeling for 2D and 3D Natural Convection Problems Incorporating Level Set-Based Topology Optimization with Body-Fitted Mesh. Int. J. Numer. Methods Eng. 2022, 123, 1954–1990. [Google Scholar] [CrossRef]
- Ghasemi, A.; Elham, A. A Novel Topology Optimization Approach for Flow Power Loss Minimization across Fin Arrays. Energies 2020, 13, 1987. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y.; Yang, L.; Li, H. Enhanced Thermal Performance of a Pin-Fin Cooling Channel for Gas Turbine Blade by Density-Based Topology Optimization. Int. J. Therm. Sci. 2022, 181, 107783. [Google Scholar] [CrossRef]
- Behrou, R.; Pizzolato, A.; Forner-Cuenca, A. Topology Optimization as a Powerful Tool to Design Advanced PEMFCs Flow Fields. Int. J. Heat Mass Transf. 2019, 135, 72–92. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, L. Topology Optimization of Convective Heat Transfer Problems for Non-Newtonian Fluids. Struct. Multidiscip. Optim. 2019, 60, 1821–1840. [Google Scholar] [CrossRef]
- Alexandersen, J.; Andreasen, C. A Review of Topology Optimisation for Fluid-Based Problems. Fluids 2020, 5, 29. [Google Scholar] [CrossRef]
- Manuel, M.C.E.; Lin, P.T. Heat Exchanger Design with Topology Optimization. In Heat Exchangers-Design, Experiment and Simulation; InTechOpen: London, UK, 2017. [Google Scholar]
- Alexandersen, J.; Sigmund, O.; Aage, N. Large Scale Three-Dimensional Topology Optimisation of Heat Sinks Cooled by Natural Convection. Int. J. Heat Mass Transf. 2016, 100, 876–891. [Google Scholar] [CrossRef]
- Dilgen, S.; Dilgen, C.; Fuhrman, D.; Sigmund, O.; Lazarov, B. Density Based Topology Optimization of Turbulent Flow Heat Transfer Systems. Struct. Multidiscip. Optim. 2018, 57, 1905–1918. [Google Scholar] [CrossRef]
- Haertel, J.; Engelbrecht, K.; Lazarov, B.; Sigmund, O. Topology Optimization of a Pseudo 3D Thermofluid Heat Sink Model. Int. J. Heat Mass Transf. 2018, 121, 1073–1088. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Meng, F.; Jing, D.; Xiong, M. Optimal Design and Thermal Modelling for Liquid-Cooled Heat Sink Based on Multi-Objective Topology Optimization: An Experimental and Numerical Study. Int. J. Heat Mass Transf. 2019, 144, 118638. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Jing, D.; Xiong, M.; Meng, F. Experimental and Numerical Investigation of Liquid-Cooled Heat Sinks Designed by Topology Optimization. Int. J. Therm. Sci. 2019, 146, 106065. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, J.; Gao, L. Topology Optimization Design of Nanofluid-Cooled Microchannel Heat Sink with Temperature-Dependent Fluid Properties. Appl. Therm. Eng. 2020, 176, 115354. [Google Scholar] [CrossRef]
- Othmer, C. A Continuous Adjoint Formulation for the Computation of Topological and Surface Sensitivities of Ducted Flows. Int. J. Numer. Methods Fluids 2008, 58, 861–877. [Google Scholar] [CrossRef]
- Ghosh, S.; Fernandez, E.; Kapat, J. Fluid-Thermal Topology Optimization of Gas Turbine Blade Internal Cooling Ducts. J. Mech. Des. 2021, 144, 051703. [Google Scholar] [CrossRef]
- Dilgen, C.; Dilgen, S.; Fuhrman, D.; Sigmund, O.; Lazarov, B. Topology Optimization of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 2018, 331, 363–393. [Google Scholar] [CrossRef]
- Yoon, G. Topology Optimization Method with Finite Elements Based on the K-ε Turbulence Model. Comput. Methods Appl. Mech. Eng. 2020, 361, 15–18. [Google Scholar] [CrossRef]
- Alkebsi, E.A.A.; Ameddah, H.; Outtas, T.; Almutawakel, A. Design of Graded Lattice Structures in Turbine Blades Using Topology Optimization. Int. J. Comput. Integr. Manuf. 2021, 34, 370–384. [Google Scholar] [CrossRef]
- Wang, N.; Meenashisundaram, G.K.; Chang, S.; Fuh, J.Y.H.; Dheen, S.T.; Senthil Kumar, A. A Comparative Investigation on the Mechanical Properties and Cytotoxicity of Cubic, Octet, and TPMS Gyroid Structures Fabricated by Selective Laser Melting of Stainless Steel 316L. J. Mech. Behav. Biomed. Mater. 2022, 129, 105151. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. Flow and Thermal Transport Characteristics of Triply-Periodic Minimal Surface (TPMS)-Based Gyroid and Schwarz-P Cellular Materials. Numer. Heat Transf. Part A Appl. 2021, 79, 553–569. [Google Scholar] [CrossRef]
- Pires, T.; Santos, J.; Ruben, R.B.; Gouveia, B.P.; Castro, A.P.G.; Fernandes, P.R. Numerical-Experimental Analysis of the Permeability-Porosity Relationship in Triply Periodic Minimal Surfaces Scaffolds. J. Biomech. 2021, 117, 110263. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, D.J. 3D Printed Compact Heat Exchangers with Mathematically Defined Core Structures. J. Comput. Des. Eng. 2020, 7, 527–550. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Ali, M.; Khalil, M.; Rowshan, R.; Khan, K.A.; Abu Al-Rub, R.K. Forced Convection Computational Fluid Dynamics Analysis of Architected and Three-Dimensional Printable Heat Sinks Based on Triply Periodic Minimal Surfaces. J. Therm. Sci. Eng. Appl. 2021, 13, 021010. [Google Scholar] [CrossRef]
- Li, W.; Yu, G.; Yu, Z. Bioinspired Heat Exchangers Based on Triply Periodic Minimal Surfaces for Supercritical CO2 Cycles. Appl. Therm. Eng. 2020, 179, 115686. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology Optimization of Fluids in Stokes Flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Lazarov, B.; Sigmund, O. Filters in Topology Optimization Based on Helmholtz-Type Differential Equations. Int. J. Numer. Methods Eng. 2011, 86, 765–781. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Winterton, R.H.S. Where Did the Dittus and Boelter Equation Come From? Int. J. Heat Mass Transf. 1998, 41, 809–810. [Google Scholar] [CrossRef]









| Author | Flow Regime | Structure | Discretization | Optimizer |
|---|---|---|---|---|
| Alexandersen et al. [17] | Laminar | 2D and 3D | FEM 1 | MMA 3 |
| Dilgen et al. [18] | Turbulent | 2D and 3D | FVM 2 | MMA |
| Haertel et al. [19] | Laminar | 2D | FEM | GCMMA 4 |
| Li et al. [20,21] | Laminar | 2D | FEM | SNOPT 5 |
| Zhang et al. [22] | Laminar | 2D | FEM | GCMMA |
| Parameter | Da | β | η | qu | qk | qε | nc | nK |
|---|---|---|---|---|---|---|---|---|
| Value | 10−4–10−6 | 1.5–16.0 | 0.5 | 0.1–10 | 0.001 | 0.1 | 3–5 | 3–5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeranee, K.; Rao, Y.; Yang, L.; Li, H. Improved Thermal Performance of a Serpentine Cooling Channel by Topology Optimization Infilled with Triply Periodic Minimal Surfaces. Energies 2022, 15, 8924. https://doi.org/10.3390/en15238924
Yeranee K, Rao Y, Yang L, Li H. Improved Thermal Performance of a Serpentine Cooling Channel by Topology Optimization Infilled with Triply Periodic Minimal Surfaces. Energies. 2022; 15(23):8924. https://doi.org/10.3390/en15238924
Chicago/Turabian StyleYeranee, Kirttayoth, Yu Rao, Li Yang, and Hao Li. 2022. "Improved Thermal Performance of a Serpentine Cooling Channel by Topology Optimization Infilled with Triply Periodic Minimal Surfaces" Energies 15, no. 23: 8924. https://doi.org/10.3390/en15238924
APA StyleYeranee, K., Rao, Y., Yang, L., & Li, H. (2022). Improved Thermal Performance of a Serpentine Cooling Channel by Topology Optimization Infilled with Triply Periodic Minimal Surfaces. Energies, 15(23), 8924. https://doi.org/10.3390/en15238924









