Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review
Abstract
1. Introduction
- –
- Thermodynamic properties, i.e., specific heat cp, linear thermal expansion (not considered in the present review), and density (dependent on this last property);
- –
- Transport properties, i.e., transport of heat (thermal conductivity k), transport of momentum (thermal viscosity, not handled in the present review), transport of electromagnetic radiation (radiative properties, not handled here).
- Theoretically, through specific models (e.g., inverse problems);
- Experimentally, with properly designed devices and experimental procedures;
- Analytically, from the knowledge of other properties (such as thermal diffusivity or thermal effusivity).
2. Specific Heat
3. Thermal Conductivity
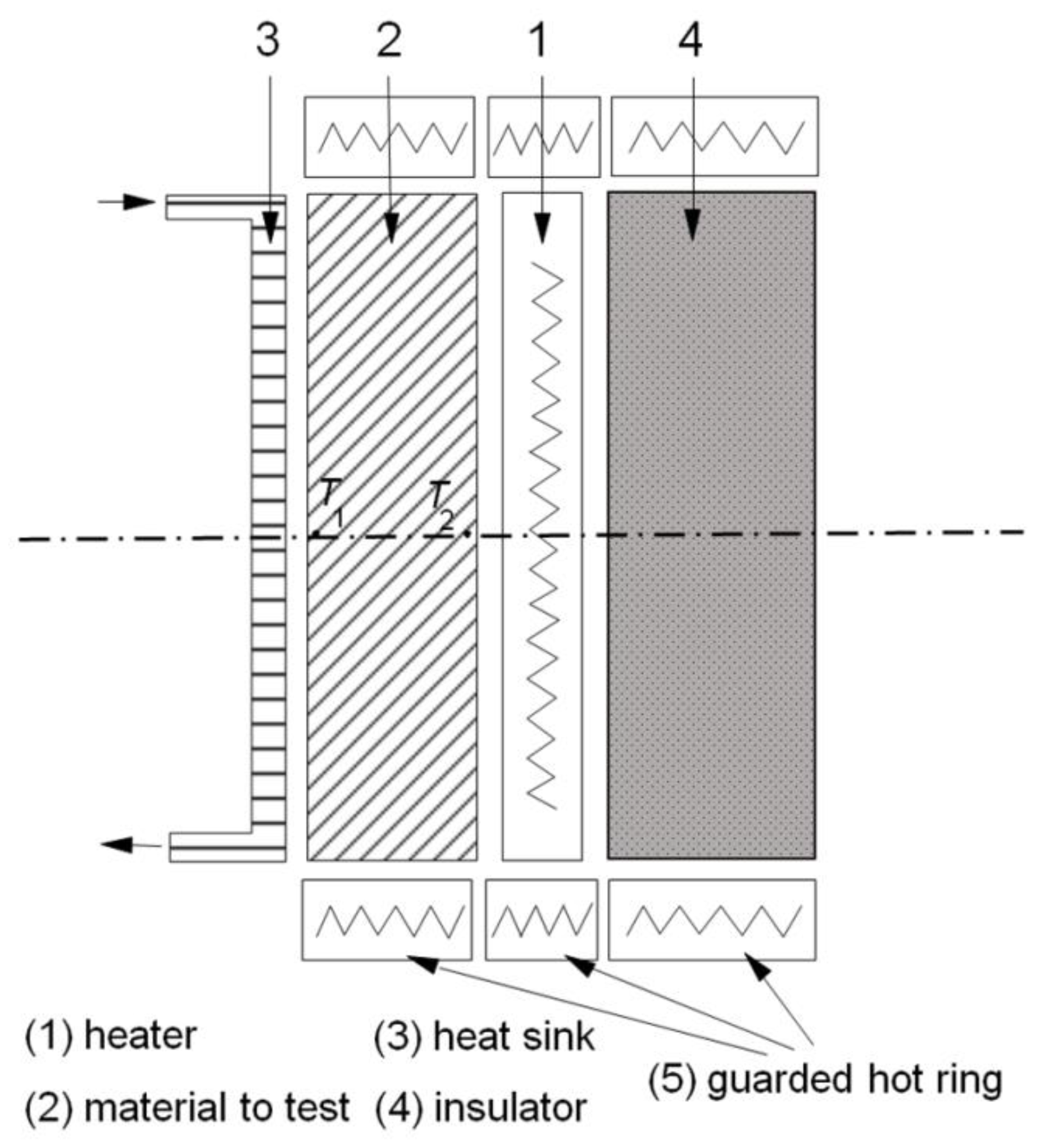
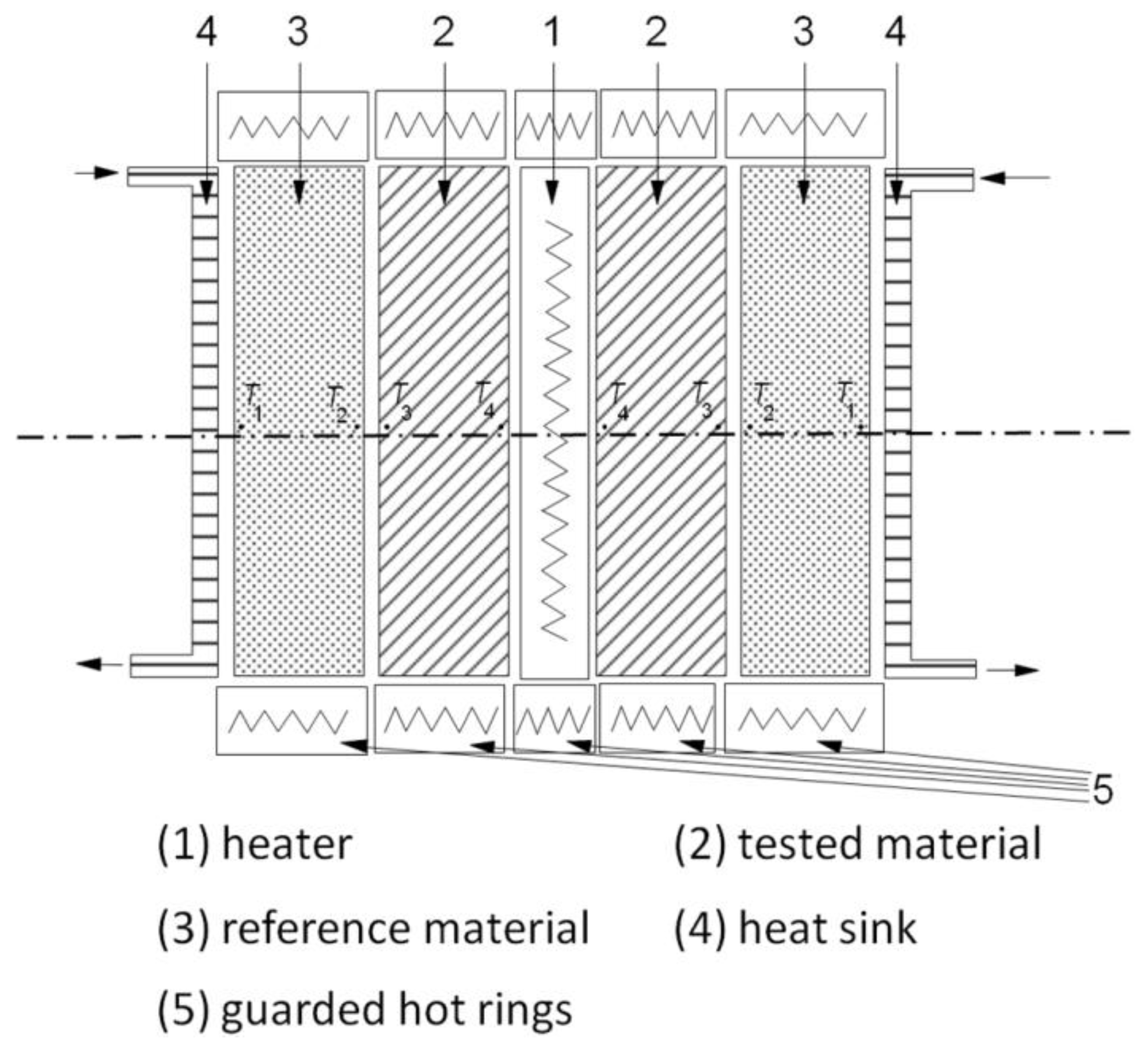
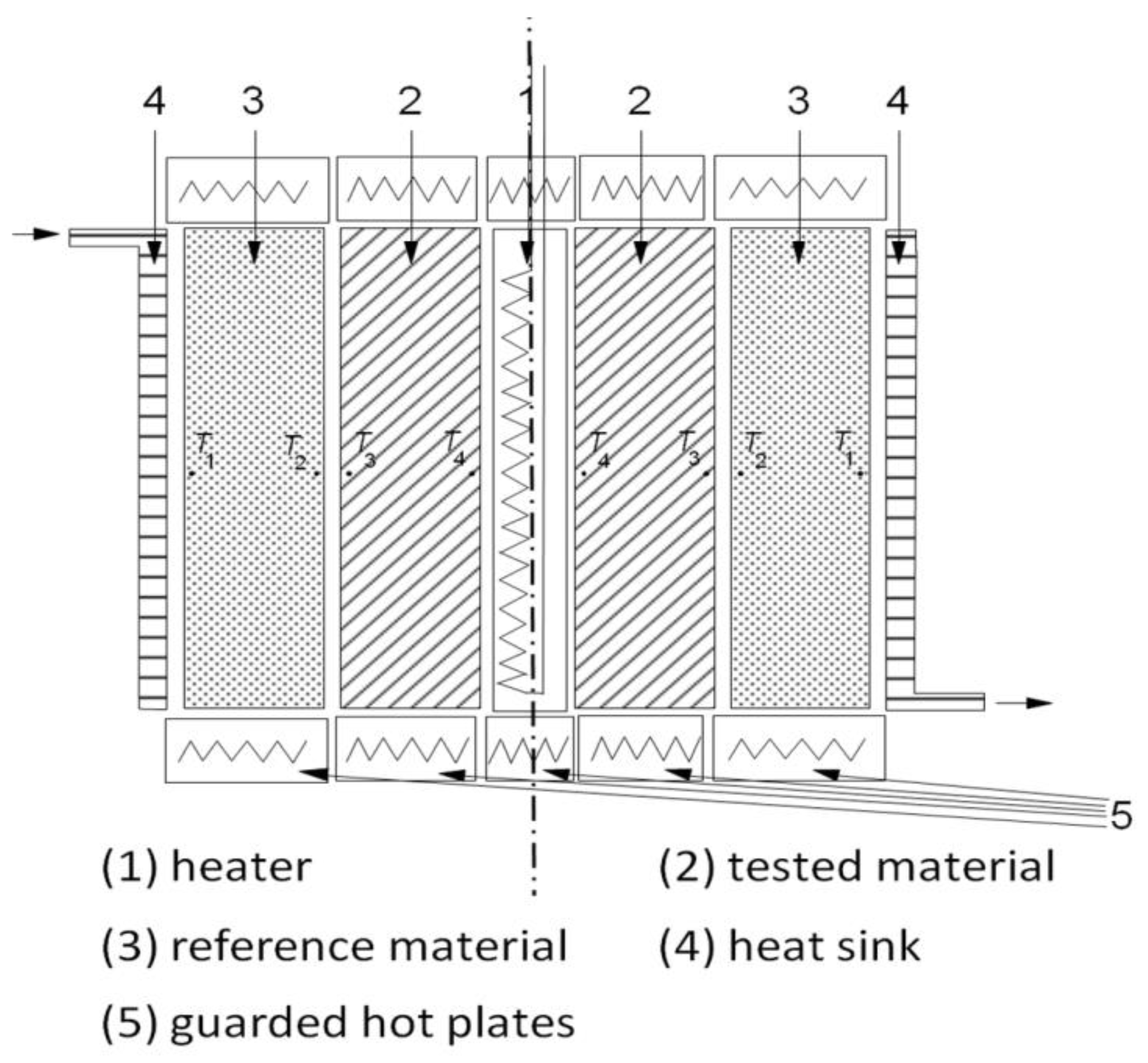
3.1. Guarded Hot Ring and Guarded Hot Plate
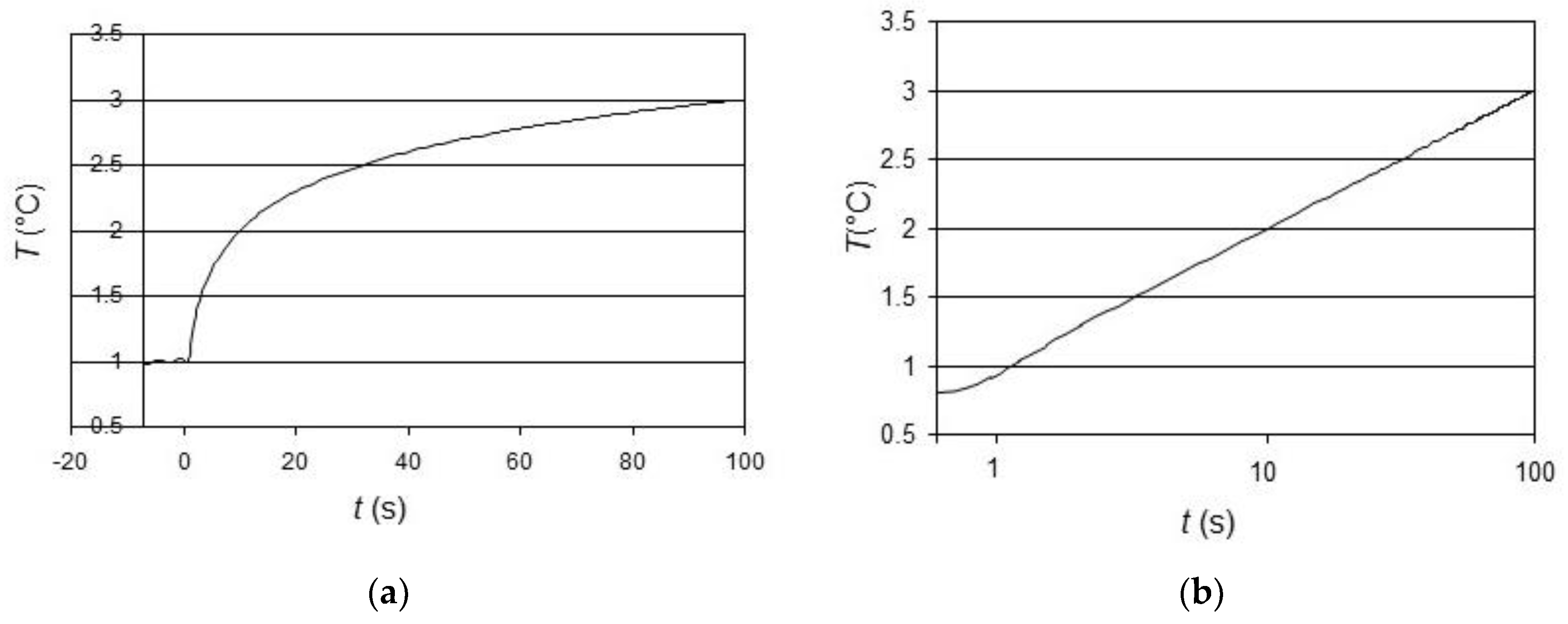
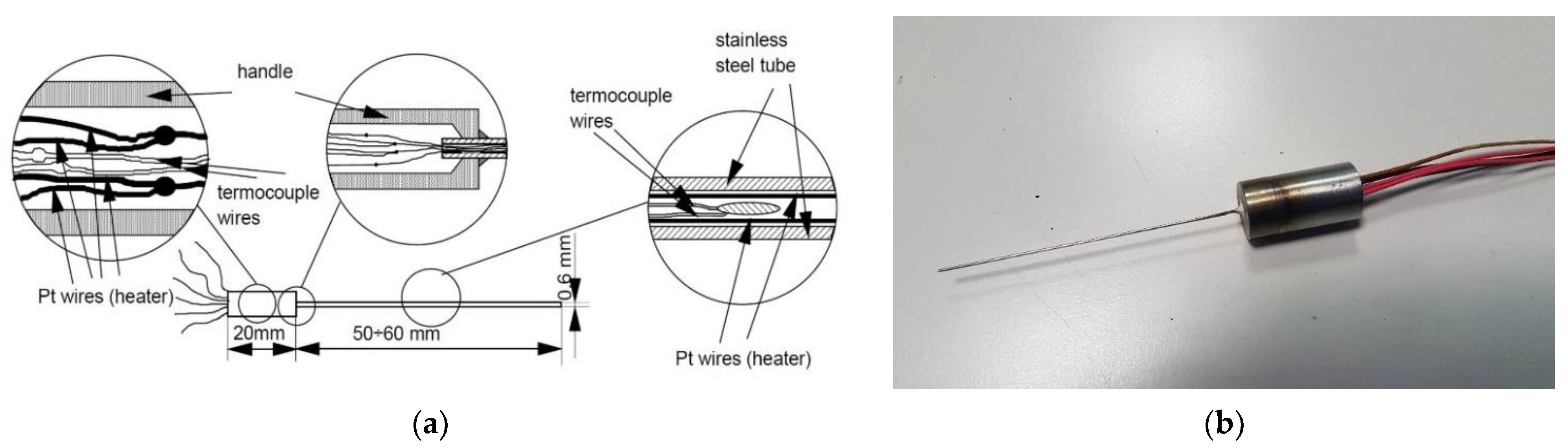
3.2. Transient Hot Wire
- At the beginning, immediately after the power is switched on, the series expansion is not yet valid, so temperature gradually increases. Theoretically, this part of the trend could be used to measure the thermal capacity of the sample, but often it is much more influenced by the thermal capacity of the wire, or the thermal resistance between the sample and the wire in the case of solid samples. Moreover, this thermal resistance can often be neglected because the wire plus the fluid between the wire and the sample simply behaves as a wider wire, at least when the contact resistance is uniform along the wire length.
- At the end of the test, often the linear trend bends until it reaches a constant value. This is mainly due the beginning of convection in the sample (if fluid) or at the sample border. Clearly, only the linear portion of the curve must be considered in the data processing. In the case of solid samples, it is advisable to locate a temperature sensor (e.g., a thermocouple) at the border sample that indicates when the thermal wave reaches the end of the sample, and to neglect the data after this point. Additionally, some precautions can be taken, e.g., to expand the linear range in special cases. For example, [19] applied different magnetic fields to increase the linear range and delay the natural convection start.
- Inhomogeneous samples can exhibit a waving trend due to different heat transfer velocities in different zones of the sample.
- The so-called “wall effect” occurs when a porous medium is measured, providing the sizes of the particles of the medium are greater than the wire diameter. In this case, the method will possibly supply the value of the interstitial fluid rather than the whole porous medium.
3.3. Thermal Conductivity Probe
4. Thermal Diffusivity Measurement
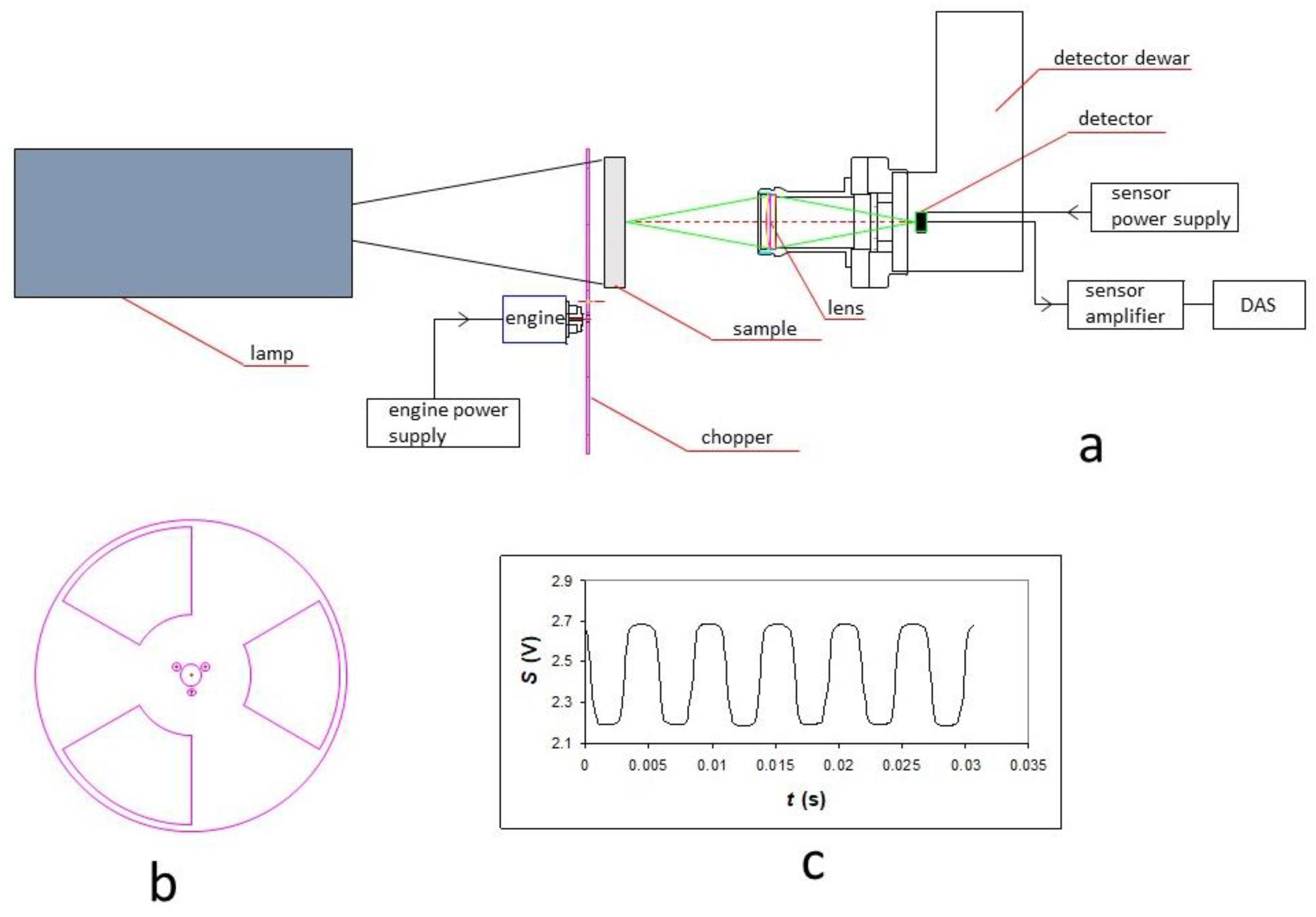
4.1. Laser Flash Method

4.2. Different Experimental Configurations in Applying the Flash Method
4.3. Dual-Probe Thermal Diffusivity Measurement
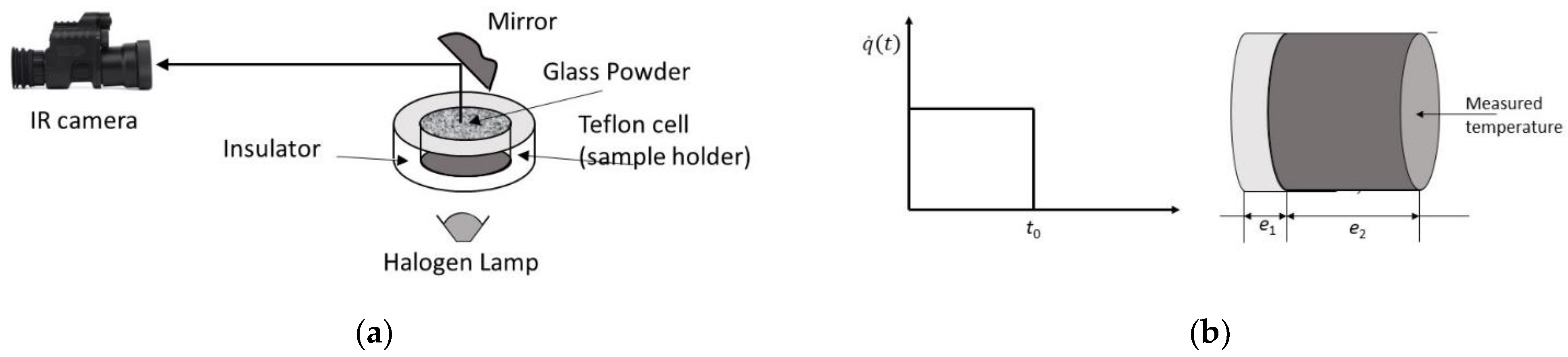
4.4. Photothermal Methods
4.5. Thermal Waving Source
5. Contemporary Measurement of Different Properties
5.1. Multiple Property Measurement with the Flash Method
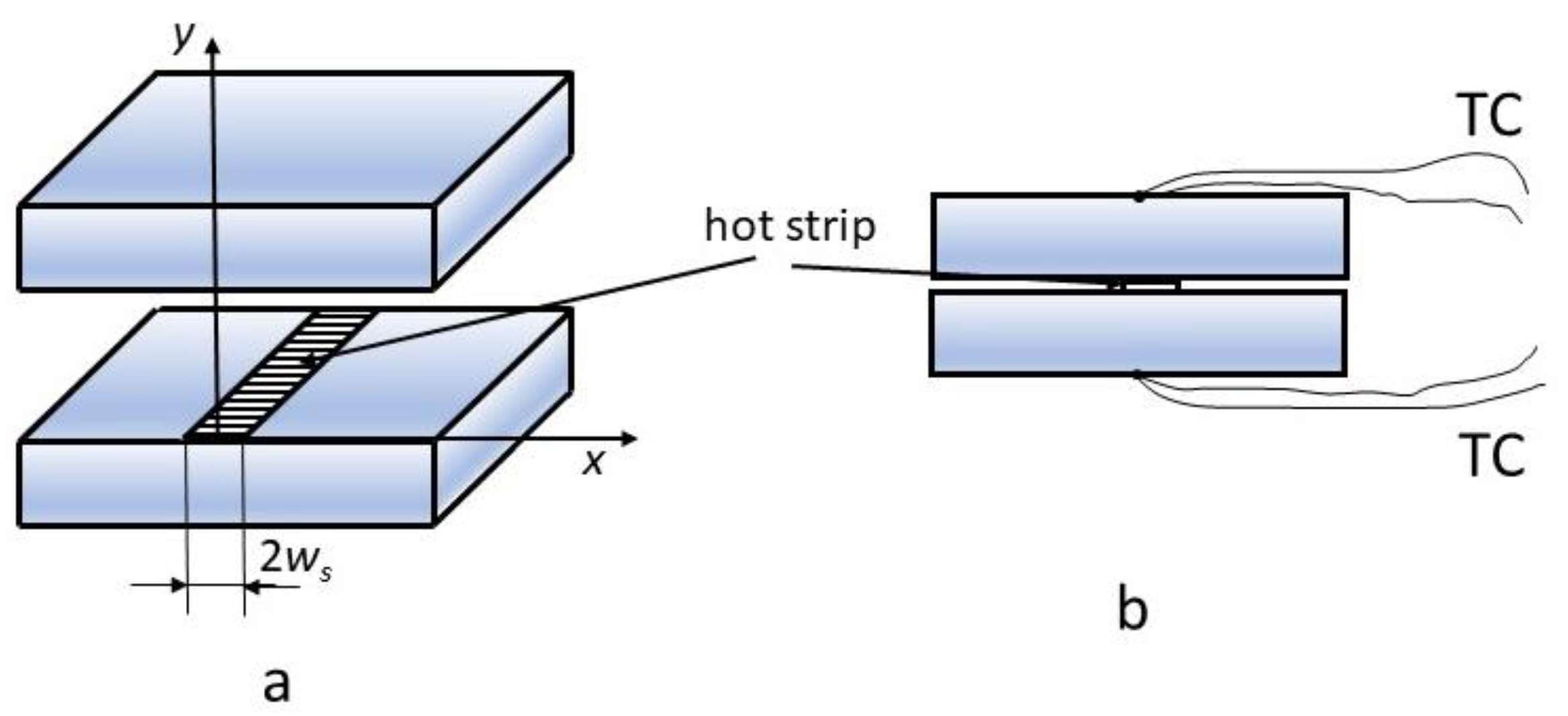
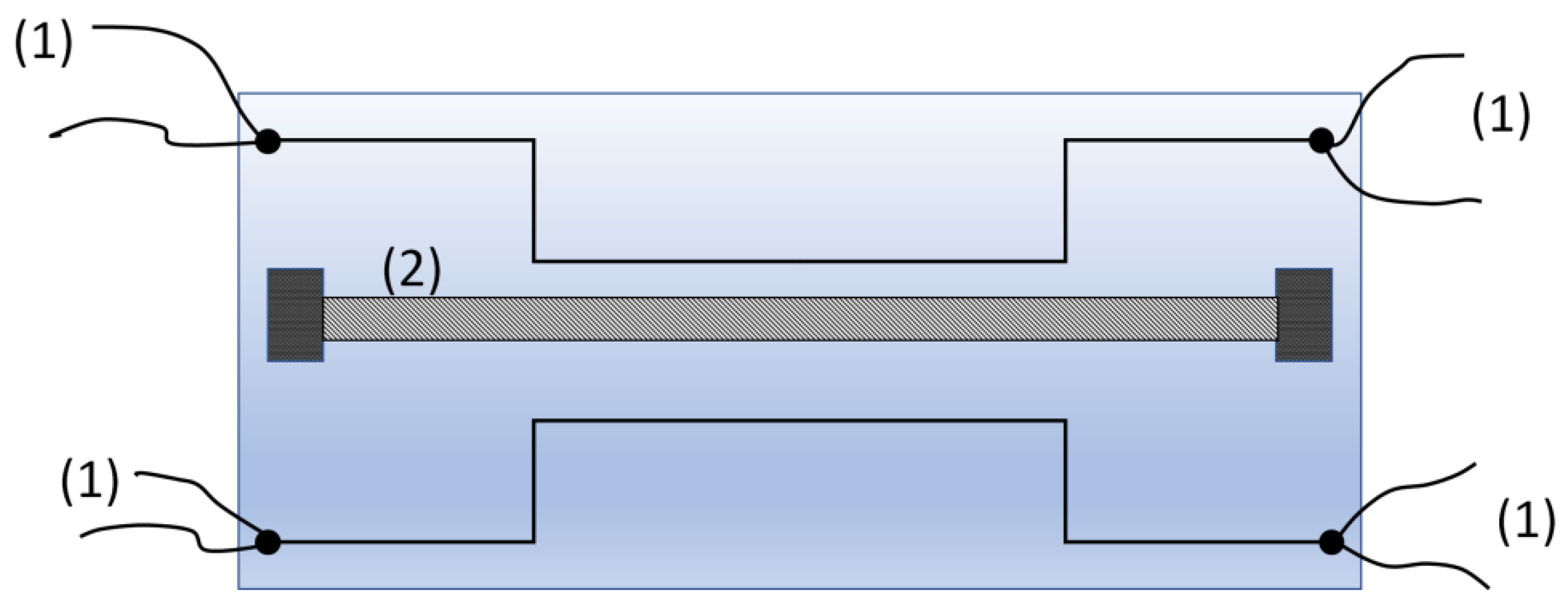
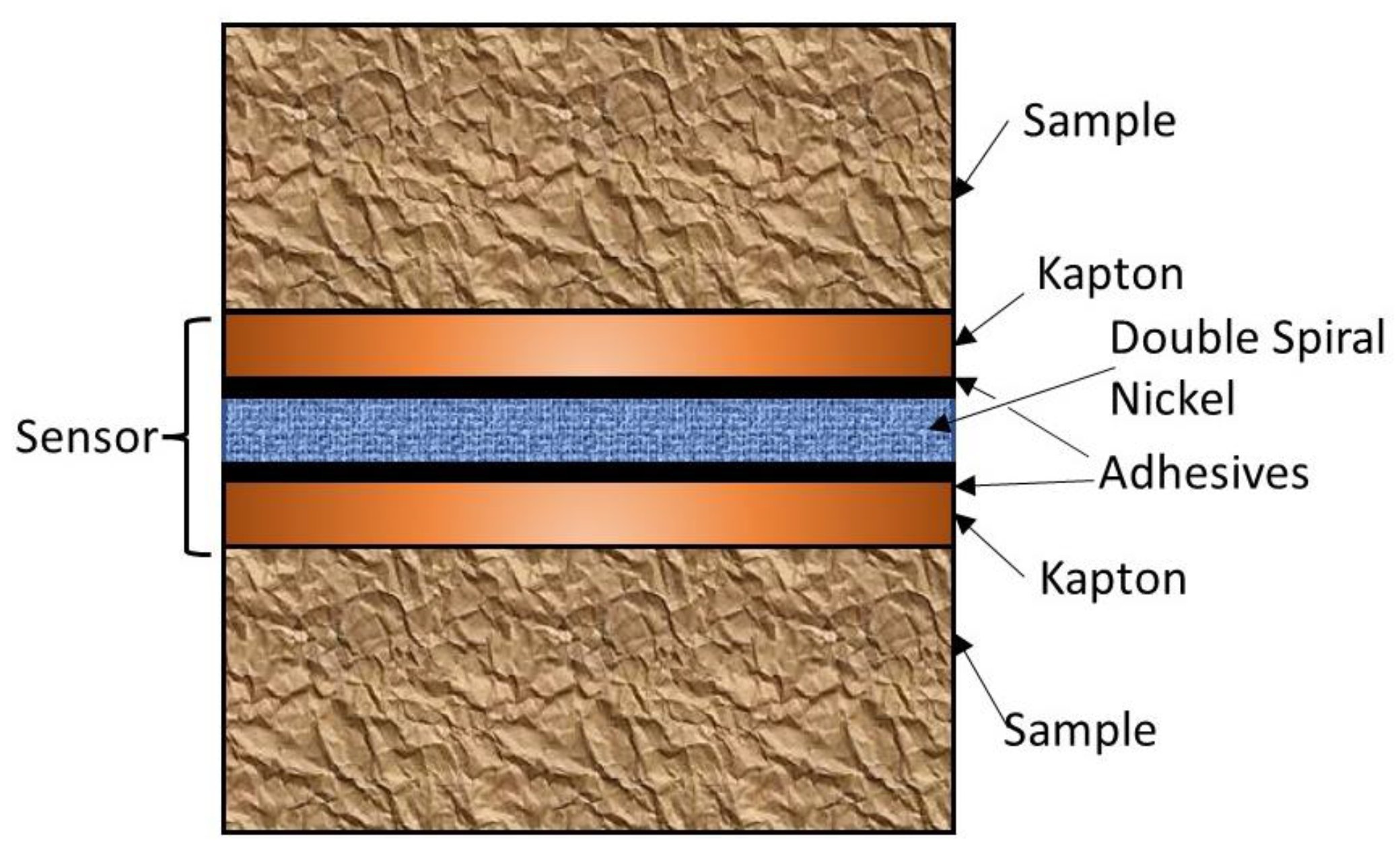
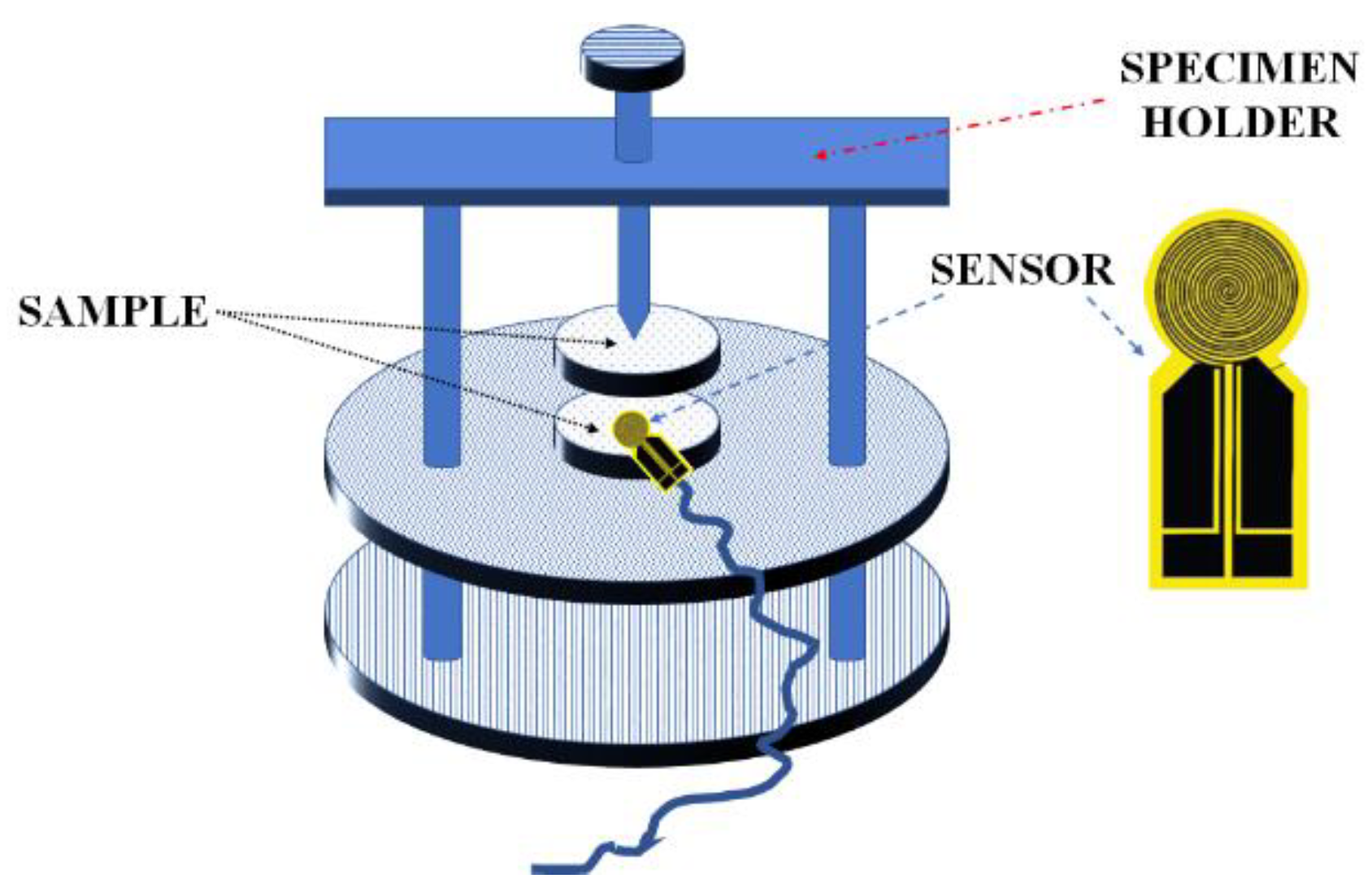
5.2. Transient Hot Strip
5.3. Transient Plane Source Method
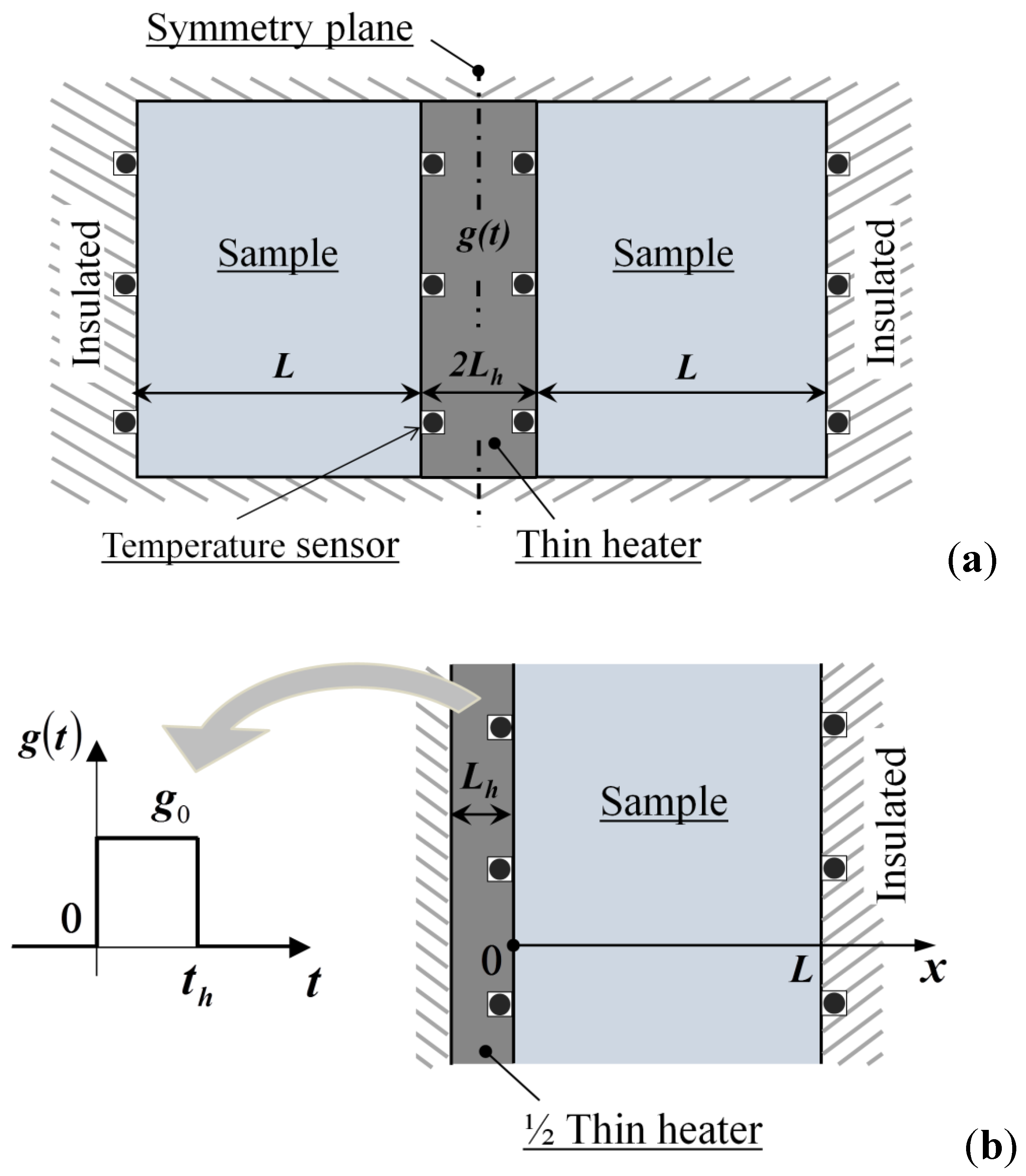
5.4. Modeling Inverse Transient Techniques
5.4.1. One-Dimensional Models
5.4.2. Multidimensional Models
5.5. Optimum Experiment Design
6. Conclusions
- –
- Transient hot wire or thermal conductivity probe, for measuring thermal conductivity.
- –
- Differential thermal analysis or differential scanning calorimetry, for thermal capacitance.
- –
- Laser flash method, for thermal diffusivity of samples in the shape of slabs.
- –
- Dual-probe method, for thermal diffusivity in bulk samples.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bud, R.; Warner, D.J. Instruments of Science; Routledge: New York, NY, USA, 1998; pp. 170–171. ISBN 9780815315612. [Google Scholar]
- Höhne, G.; Hemminger, W.F.; Flammersheim, H.J. Differential Scanning Calorimetry; Springer: Heidelberg/Berlin, Germany, 2003; ISBN 978-3-540-00467-7. [Google Scholar]
- Corsan, J.M. Axial heat flow methods of thermal conductivity measurement for good conducting materials. In Compendium of Thermophysical Property Measurement Methods: Recommended Measuring Techniques and Practices; Maglić, K.D., Cezairliyan, A., Peletsky, V.E., Eds.; Springer: Boston, MA, USA, 1992; Volume 2, pp. 3–31. [Google Scholar]
- Wang, Q.; Dai, J.M.; Coppa, P. Thermophysical property measurement of thermal protective material by guarded plane source method. J. Tianjin Univ. Sci. Technol. 2010, 43, 1086–1092. [Google Scholar]
- Flynn, D.R. Thermal conductivity of loose-fill materials by a radial-heat-flow method. In Compendium of Thermophysical Property Measurement Methods: Recommended Measuring Techniques and Practices; Maglić, K.D., Cezairliyan, A., Peletsky, V.E., Eds.; Springer: Boston, MA, USA, 1992; Volume 2, pp. 33–75. [Google Scholar]
- De Ponte, F.; Langlais, C.; Klarsfeld, S. Reference guarded hot plate apparatus for the determination of steady-state thermal transmission properties. In Compendium of Thermophysical Property Measurement Methods: Recommended Measuring Techniques and Practices; Maglić, K.D., Cezairliyan, A., Peletsky, V.E., Eds.; Springer: Boston, MA, USA, 1992; Volume 2, pp. 99–131. [Google Scholar]
- Healy, J.J.; de Groot, J.J.; Kestin, J. The theory of the transient hot-wire method for measuring thermal conductivity. Physica B+C 1976, 82, 392–408. [Google Scholar] [CrossRef]
- Hong, S.W.; Kang, Y.T.; Kleinstreuer, C.; Koo, J. Impact analysis of natural convection on thermal conductivity measurements of nanofluids using the transient hot-wire method. Int. J. Heat Mass Transf. 2011, 54, 3448–3456. [Google Scholar] [CrossRef]
- Turgut, A.; Sauter, C.; Chirtoc, M.; Henry, J.F.; Tavman, S.; Tavman, I.; Pelzl, J. AC hot wire measurement of thermophysical properties of nanofluids with 3ω method. Eur. Phys. J. Spec. Top. 2008, 153, 349–352. [Google Scholar] [CrossRef]
- Yoo, D.; Lee, J.; Lee, B.; Kwon, S.; Koo, J. Further elucidation of nanofluid thermal conductivity measurement using a transient hot-wire method apparatus. Heat Mass Transf. 2018, 54, 415–424. [Google Scholar] [CrossRef]
- Lee, J.; Lee, H.; Baik, Y.J.; Koo, J. Quantitative analyses of factors affecting thermal conductivity of nanofluids using an improved transient hot-wire method apparatus. Int. J. Heat Mass Transf. 2015, 89, 116–123. [Google Scholar] [CrossRef]
- Ahadi, M.; Andisheh-Tadbir, M.; Tam, M.; Bahrami, M. An improved transient plane source method for measuring thermal conductivity of thin films: Deconvoluting thermal contact resistance. Int. J. Heat Mass Transf. 2016, 96, 371–380. [Google Scholar] [CrossRef]
- Wechsler, A.E. The probe method for measuring thermal conductivity. In Compendium of Thermophysical Property Measurement Methods: Recommended Measuring Techniques and Practices; Maglić, K.D., Cezairliyan, A., Peletsky, V.E., Eds.; Springer: Boston, MA, USA, 1992; Volume 2, pp. 161–185. [Google Scholar]
- Gross, U.; Tran, L.T.S. Radiation effects on transient hot-wire measurements in absorbing and emitting porous media. Int. J. Heat Mass Transf. 2004, 47, 3279–3290. [Google Scholar] [CrossRef]
- Coquard, R.; Baillis, D.; Quenard, D. Experimental and theoretical study of the hot-wire method applied to low-density thermal insulators. Int. J. Heat Mass Transf. 2006, 49, 4511–4524. [Google Scholar] [CrossRef]
- Castán-Fernández, C.; Marcos-Robredo, G.; Ángel Rey-Ronco, M.; Alonso-Sánchez, T. Design, construction and commissioning of an apparatus for measuring the thermal conductivity of geothermal grouting materials based on the transient hot wire method. Proceedings 2018, 2, 1496. [Google Scholar]
- Carlslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford Univ. Press: London, UK, 1959. [Google Scholar]
- Bovesecchi, G.; Coppa, P.; Pistacchio, S. A new thermal conductivity probe for high temperature tests for the characterization of molten salts. Rev. Sci. Instrum. 2018, 89, 055107. [Google Scholar] [CrossRef] [PubMed]
- Fukuyama, H.; Yoshimura, T.; Yasuda, H.; Ohta, H. Thermal conductivity measurements of liquid mercury and gallium by a transient hot wire method in a static magnetic field. Int. J. Thermophys. 2006, 27, 1760–1777. [Google Scholar] [CrossRef]
- Coppa, P.; Pasquali, G. Thermal conductivity of lipidic emulsions and its use for production and quality control. In Proceedings of the 2nd International Symposium on Instrumentation Science and Technology, Jinan, China, 18–22 August 2002. [Google Scholar]
- Hopper, F.C.; Lepper, F.R. Transient heat flow apparatus for determination of thermal conductivities. ASHVE Trans. 1950, 56, 309. [Google Scholar]
- Zhang, Y.P.; Liang, X.G.; Wang, Z.; Ge, X.S. A method of determining the thermophysical properties and calorific intensity of the organ or tissue of a living body. Int. J. Thermophys. 2000, 21, 207–215. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbot, G.L. Flash method of determining thermal diffusivity heat capacity and thermal conductivity. J. App. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Maillet, D.; Moyne, C.; Remy, B. Effect of a thin layer on the measurement of the thermal diffusivity of a material by a flash method. Int. J. Heat Mass Transf. 2000, 43, 4057–4060. [Google Scholar] [CrossRef]
- Matteis, P.; Campagnoli, E.; Firrao, D.; Ruscica, G. Thermal diffusivity measurements of metastable austenite during continuous cooling. Int. J. Therm. Sci. 2008, 47, 695–708. [Google Scholar] [CrossRef]
- Brandt, S. Statistical and Computational Methods in Data Analysis; North Holland Pub: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Thermitus, M.A.; Laurent, M. New logarithmic technique in the flash method. Int. J. Heat Mass Transf. 1977, 40, 4183–4190. [Google Scholar] [CrossRef]
- Milosevic, N.; Raynaud, M.; Maglic, K. Estimation of thermal contact resistance between the materials of double-layer sample using the laser flash method. Inverse Probl. Eng. 2002, 10, 85–103. [Google Scholar] [CrossRef]
- Potenza, M.; Cataldo, A.; Bovesecchi, G.; Corasaniti, S.; Coppa, P.; Bellucci, S. Graphene nanoplatelets: Thermal diffusivity and thermal conductivity by the flash method. AIP Adv. 2017, 7, 075214. [Google Scholar] [CrossRef]
- Taylor, R.E. Thermal-property and contact-conductance measurements of coatings and thin films. Int. J. Thermophys. 1998, 19, 931–939. [Google Scholar] [CrossRef]
- Bocchini, G.F.; Bovesecchi, G.; Coppa, P.; Corasaniti, S.; Montanari, R.; Varone, A. Thermal diffusivity of sintered steels with flash method at ambient temperature. Int. J. Thermophys. 2016, 37. [Google Scholar] [CrossRef]
- Li, N.; Wang, Y.; Liu, Q.; Peng, H. Evaluation of thermal-physical properties of novel multicomponent molten nitrate salts for heat transfer and storage. Energies 2022, 15, 6591. [Google Scholar] [CrossRef]
- Bison, P.; Cernuschi, F.; Grinzato, E. Ageing evaluation of thermal barrier coating: Comparison between pulsed thermography and thermal wave interferometry. Quant. InfraRed Thermogr. J. 2006, 3, 169–181. [Google Scholar] [CrossRef]
- Cape, J.A.; Lehman, G.W. Temperature and finite pulse time effects in the flash method for measuring thermal diffusivity. J. Appl. Phys. 1963, 34, 1909. [Google Scholar] [CrossRef]
- Bellucci, S.; Bovesecchi, G.; Cataldo, A.; Coppa, P.; Corasaniti, S.; Potenza, M. Transmittance and reflectance effects during thermal diffusivity measurements of GNP samples with the flash method. Materials 2019, 12, 696. [Google Scholar] [CrossRef]
- Potenza, M.; Coppa, P.; Corasaniti, S.; Bovesecchi, G. Numerical simulation of thermal diffusivity measurements with the laser-flash method to evaluate the effective property of composite materials. J. Heat Transf. (ASME) 2021, 143, 072102. [Google Scholar] [CrossRef]
- Bison, P.; Cernuschi, F.; Capelli, S. A thermographic technique for the simultaneous estimation of in-plane and in-depth thermal diffusivities of TBCs. Surf. Coat. Technol. 2011, 205, 3128–3133. [Google Scholar] [CrossRef]
- Azumi, T.; Takahashi, Y. Novel finite pulse-width correction in flash thermal diffusivity measurement. Rev. Sci. Instrum. 1981, 52, 1411–1413. [Google Scholar] [CrossRef]
- dell’Avvocato, G.; Palumbo, D.; Palmieri, M.E.; Galietti, G. Evaluation of effectiveness of heat treatments in boron steel by laser thermography. Eng. Proc. 2021, 8, 8. [Google Scholar]
- Sfarra, S.; Cicone, A.; Yousefi, B.; Perilli, S.; Robol, L.; Maldague, X.P.V. Maximizing the detection of thermal imprints in civil engineering composites via numerical and thermographic results pre-processed by a groundbreaking mathematical approach. Int. J. Therm. Sci. 2022, 177, 107553. [Google Scholar] [CrossRef]
- Pawar, S.S.; Vavilov, V.P. A novel one-sided diffusivity evaluation technique versus Parker’s method in application to carbon/epoxy composite. In Proceedings of the 12th International Conference on Quantitative Infrared Thermography (QIRT 2015), Mahabalipuram, India, 6–10 July 2015. [Google Scholar]
- Heckman, R.C. Finite pulse-time and heat-loss effects in pulse thermal diffusivity measurements. J. Appl. Phys. 1973, 44, 1465–1470. [Google Scholar] [CrossRef]
- Clark, L.M., III; Taylor, R.E. Radiation loss in the flash method for thermal diffusivity. J. Appl. Phys. 1975, 46, 714–719. [Google Scholar] [CrossRef]
- Degiovanni, A. Diffusivité et méthode flash. Rev. Gén. Therm. 1977, 185, 420–442. [Google Scholar]
- Balageas, D.L. Nouvelle méthode d’interprétation des thermogrammes pour la détermination de la diffusivité thermique par la méthode impulsionnelle (méthode flash). Rev. Phys. Appl. 1982, 17, 227–237. [Google Scholar] [CrossRef]
- Degiovanni, A.; Laurent, M. Une nouvelle technique d’identification de la diffusivité thermique pour la méthode “flash”. Rev. Phys. Appl. 1986, 21, 229–237. [Google Scholar] [CrossRef]
- Pech-May, N.W.; Mendioroz, A.; Agustín Salazar, A. Generalizing the flash technique in the front-face configuration to measure the thermal diffusivity of semitransparent solids. Rev. Sci. Instrum. 2014, 85, 104902. [Google Scholar] [CrossRef]
- Salazar, A.; Mendioroz, A.; Apiñaniz, E.; Pradere, C.; Noël, F.; Batsale, J.-C. Extending the flash method to measure the thermal diffusivity of semitransparent solids. Meas. Sci. Technol. 2014, 25, 035604. [Google Scholar] [CrossRef]
- Bison, P.; Grinzato, E.; Marinetti, S. Local thermal diffusivity measurement. Quant. InfraRed Thermogr. J. 2004, 1, 241–250. [Google Scholar] [CrossRef]
- Hay, B.; Filtz, J.R.; Hameury, J.; Rongione, L. Uncertainty of thermal diffusivity measurements by laser flash method. Int. J. Thermophys. 2005, 26, 1883. [Google Scholar] [CrossRef]
- Bison, P.; Ferrarini, G.; Glorieux, C. Pulsed thermography in the assessment of in-plane thermal diffusivity: Aperiodic, periodic and random patterns. In Proceedings of the ICPPP21—International Conference on Photoacoustic and Photothermal Phenomena, Bled, Slovenia, 19–24 June 2022. [Google Scholar]
- Cernuschi, F.; Russo, A.; Lorenzoni, L.; Figari, A. In-plane thermal diffusivity evaluation by infrared thermography. Rev. Sci. Instrum. 2001, 72, 3988–3995. [Google Scholar] [CrossRef]
- Kalogiannakis, G.; Van Hemelrijck, D.; Longuemart, S.; Ravi, J.; Okasha, A.; Glorieux, C. Thermal characterization of anisotropic media in photothermal point, line, and grating configuration. J. Appl. Phys. 2006, 100, 063521. [Google Scholar] [CrossRef]
- Krapez, J.C. Diffusivity measurement by using a grid-like mask. In Proceedings of the Journée SFT “Thermographie Infrarouge”, Chatillon, France, 31 March 1999. [Google Scholar]
- Batsale, J.-C.; Battaglia, J.-L.; Fudym, O. Autoregressive algorithms and spatially random flash excitation for 2D non-destructive evaluation with infrared cameras. Quant. InfraRed Thermogr. J. 2004, 1, 5–20. [Google Scholar] [CrossRef]
- Duquesne, L.; Lorrette, C.; Pradère, C.; Vignoles, G.L.; Batsale, J.-C. A flash characterization method for thin cylindrical multilayered composites based on the combined front and rear faces thermograms. Quant. Infrared Thermogr. J. 2016, 13, 182–194. [Google Scholar] [CrossRef]
- Legaie, D.; Pron, H.; Bissieux, C. Resolution of an inverse heat conduction problem with a non-linear least square method in the Hankel space. Application to photothermal infrared thermography. J. Phys. Conf. Ser. 2008, 135, 012061. [Google Scholar] [CrossRef]
- Chudzik, S. Thermal diffusivity measurement of insulating material using infrared thermography. Opto-Electron. Rev. 2011, 20, 40–46. [Google Scholar] [CrossRef]
- Wrobel, G.; Rdzawski, Z.; Muzia, G.; Pawlak, S. Determination of thermal diffusivity of carbon/epoxy composites with different fiber content using transient thermography. J. Achiev. Mater. Manuf. Eng. 2009, 37, 518–525. [Google Scholar]
- Bristow, K.L.; Kluitenberg, G.J.; Horton, R. Measurement of soil thermal properties with a dual-probe heat-pulse technique. Soil Sci. Soc. Am. J. 1994, 58, 1288–1294. [Google Scholar] [CrossRef]
- Lubimova, H.A.; Lusova, L.M.; Firsov, F.V.; Starikova, G.N.; Shushpanov, A.P. Determination of surface heat flow. Maz. Ann. Geophys. 1961, 14, 157–167. [Google Scholar]
- Jaeger, J.C. Application of the theory of heat conduction to geothermal measurements. In Terrestrial Heat Flow, Geophysical Monograph Series; Lee, W.H.K., Ed.; American Geophysical Union: Washington, DC, USA, 1965; Volume 8, pp. 7–23. [Google Scholar]
- Campbell, G.S.; Calissendorff, K.; Williams, J.H. Probe for measuring soil specific heat using a heat pulse method. Soil Sci. Soc. Am. J. 1991, 55, 291–293. [Google Scholar] [CrossRef]
- Bovesecchi, G.; Coppa, P.; Corasaniti, S.; Potenza, M. Critical analysis of dual-probe heat-pulse technique applied to measuring thermal diffusivity. Int. J. Thermophys. 2018, 39, 82. [Google Scholar] [CrossRef]
- Bittle, R.R.; Taylor, R.E. Step-heating technique for thermal diffusivity measurements of large-grained heterogeneous materials. J. Am. Ceram. Soc. 1984, 67, 186–190. [Google Scholar] [CrossRef]
- Vozar, L.; Sramkova, T. Two data reduction methods for evaluating of thermal diffusivity from step-heating measurements. Int. J. Heat Mass Transf. 1997, 40, 1647–1655. [Google Scholar] [CrossRef]
- Griesinger, A.; Hurler, W.; Pietralla, M. A photothermal method with step heating for measuring the thermal diffusivity of anisotropic solids. Int. J. Heat Mass Transf. 1997, 40, 3049–3058. [Google Scholar] [CrossRef]
- Albouchi, F.; Fetoui, M.; Rigollet, F.; Sassi, M.; Nasrallah, S.B. Optimal design and measurement of the effective thermal conductivity of a powder using a crenel heating excitation. Int. J. Therm. Sci. 2005, 44, 1090–1097. [Google Scholar] [CrossRef]
- Bennis, G.L.; Vyas, R.; Gupta, R.; Ang, S.; Brown, W.D. Thermal diffusivity measurement of solid materials by the pulsed photothermal displacement technique. J. Appl. Phys. 1998, 84, 3602–3610. [Google Scholar] [CrossRef]
- Olmstead, M.A.; Amer, N.M.; Kohn, S.; Fournier, D.; Boccara, A.C. Photothermal displacement spectroscopy: An optical probe for solids and surfaces. Appl. Phys. A 1983, 32, 141–154. [Google Scholar] [CrossRef]
- Karner, C.; Mandel, A.; Trager, F. Pulsed laser photothermal displacement spectroscopy for surface studies. Appl. Phys. A 1985, 38, 19–21. [Google Scholar] [CrossRef]
- Elperin, T.; Rudin, G. Theory of photothermal displacement method for determining physical properties of multilayered coatings. Int. J. Thermophys. 2009, 30, 1598–1615. [Google Scholar] [CrossRef]
- Lopez-Baeza, E.; de la Rubia, J.; Goldsmid, H. Angstrom’s thermal diffusivity method for short samples. J. Phys. D Appl. Phys. 1987, 20, 1156. [Google Scholar] [CrossRef]
- Vargas, H.; Miranda, L.C. Photoacoustic effect and related photothermal techniques. Phys. Rep. 1988, 161, 43–101. [Google Scholar] [CrossRef]
- Tam, A.C. Applications of photoacoustic techniques. Rev. Mod. Phys. 1986, 58, 381–431. [Google Scholar] [CrossRef]
- Almond, D.P.; Patel, P.M. Photothermal Sciences and Techniques; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Mercuri, F.; Marinelli, M.; Paoloni, S.; Zammit, U.; Scudieri, F. Latent heat investigation by photopyroelectric calorimetry. Appl. Phys. Lett. 2008, 92, 251911. [Google Scholar] [CrossRef]
- Corasaniti, S.; Potenza, M.; Coppa, P.; Bovesecchi, G. Comparison of different approaches to evaluate the equivalent thermal diffusivity of building walls under dynamic conditions. Int. J. Thermal Sci. 2020, 150, 106232. [Google Scholar] [CrossRef]
- Mercuri, F.; Paoloni, S.; Zammit, U.; Marinelli, M. Dynamics at the nematic-isotropic phase transition in aerosil dispersed liquid crystal. Phys. Rev. Lett. 2005, 94, 247801. [Google Scholar] [CrossRef]
- Marinelli, M.; Mercuri, F.; Paoloni, S.; Zammit, U. Dynamics of nematic liquid crystal with quenched disorder in the random dilution and random field regimes. Phys. Rev. Lett. 2005, 95, 237801. [Google Scholar] [CrossRef] [PubMed]
- Luc, A.M.; Balageas, D.L. Non-stationary thermal behavior of reinforced composites—A better evaluation of wall energy balance for convective conditions. In Proceedings of the 1st International Joint Conferences on Thermophysical Properties, Gaithersburg, MD, USA, 15–18 June 1981. [Google Scholar]
- Luc-Bouhali, A.M.; Pujolà, R.M.; Balageas, D.L. Thermal diffusivity in situ measurements of carbon/carbon composite reinforcements. In Thermal Conductivity; Ashworth, T., Smith, D.R., Eds.; Plenum: London, UK, 1984; Volume 18, pp. 613–624. [Google Scholar]
- Pujolà, R.M.; Balageas, D.L. Derniers développements de la méthode flash adaptée aux matériaux composites à renforcement orienté. High Temp.-High Press. 1985, 17, 623–632. (In French) [Google Scholar]
- Bardon, J.-P.; Balageas, D.; Degiovanni, A.; Vuiiliermes, J. Thermics of composites and interfaces: Current status and perspectives. La Rech. Aérosp. 1989, 6, 37–45. [Google Scholar]
- Balageas, D.; Déom, A.; Boscher, D. Composite thermal properties measurements by pulse photothermal radiometry. In Proceedings of the Eurotherm IV Conference Thermal Transfer in Composite Materials and Solid-Solid Interface, Nancy, France, 28 June–1 July 1988. [Google Scholar]
- da Fonseca, H.M.; Barreto Orlande, H.R.; Fudym, O.; Sepúlveda, F. A statistical inversion approach for local thermal diffusivity and heat flux simultaneous estimation. Quant. Infrared Thermogr. J. 2014, 11, 170–189. [Google Scholar] [CrossRef][Green Version]
- Wawrzynek, A.; Nowak, A.J.; Bartoszek, M.; Delpak, R.; Hu, C.W. Theoretical analysis of applying thermography and inverse solutions to determine thermal properties of cementitious materials. Inverse Probl. Sci. Eng. 2005, 13, 23–46. [Google Scholar] [CrossRef]
- Vavilov, V.; Burleigh, D.; Shiryaev, V. IR thermographic evaluation of thermal diffusivity anisotropy: Comparative analysis of some algorithms. Quant. InfraRed Thermogr. J. 2007, 4, 187–200. [Google Scholar] [CrossRef]
- Malheiros, F.A.; Figueiredo, A.A.A.; da S. Ignacio, L.H.; Fernandes, H.C. Estimation of thermal properties using only one surface by means of infrared thermography. Appl. Therm. Eng. 2019, 157, 113696. [Google Scholar] [CrossRef]
- Chaffar, K.; Chauchois, A.; Defer, D.; Zalewski, L. Thermal characterization of homogeneous walls using inverse method. Energy Build. 2014, 78, 248–255. [Google Scholar] [CrossRef]
- Halloua, H.; Obbadi, A.; Errami, Y.; Sahnoun, S.; Elhassnaoui, A. Nondestructive inverse approach for determinign thermal and geometrical properties of internal defects in CFRP composites by lock-in thermography. In Proceedings of the 2016 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Marrakesh, Morocco, 26–28 October 2016. [Google Scholar]
- Krankenhagen, R.; Jonietz, F.; Zirker, S. Determination of thermal parameters of concrete by active thermographic measurements. J. Nondestruct. Eval. 2022, 41, 25. [Google Scholar] [CrossRef]
- Kooshki, S.; Mandelis, A.; Khodadad, M.; Khosravifard, A.; Melnikov, A. Determination of thermophysical properties and density volume fractions of Al2O3/Y-ZrO2 layered composite materials using transient thermography and two-stage inverse nonlinear heat conduction analysis. J. Appl. Phys. 2020, 127, 045110. [Google Scholar] [CrossRef]
- Florez-Ospina, J.F.; Ospina-Borras, J.E.; Benitez-Restrepo, H.D. Non-destructive infrared evaluation of thermo-physical parameters in bamboo specimens. Appl. Sci. 2017, 7, 1253. [Google Scholar] [CrossRef]
- Pavlov, T.R.; Staicu, D.; Vlahovic, L.; Konings, R.J.M.; van Uffelen, P.; Wenman, M.R. A new method for the characterization of temperature-dependent thermo-physical properties. Int. J. Therm. Sci. 2018, 124, 98–109. [Google Scholar] [CrossRef]
- Groz, M.M.; Sommier, A.; Abisset-Chavanne, E.; Batsale, J.-C.; Pradere, C. Flash method and Bayesian inference for measurement of thermophysical fields. AIP Adv. 2021, 11, 105009. [Google Scholar] [CrossRef]
- Pech-May, N.W.; Cifuentes, A.; Mendioroz, A.; Oleaga, A.; Salazar, A. Simultaneous measurement of thermal diffusivity and effusivity of solids using the flash technique in the front-face configuration. Meas. Sci. Technol. 2015, 26, 085017. [Google Scholar] [CrossRef]
- Gustafsson, S.E.; Karawacki, E.; Khan, M.N. Transient hot-strip method for simultaneously measuring thermal conductivity and thermal diffusivity of solids and fluids. J. Phys. D Appl. Phys. 1979, 12, 1411–1421. [Google Scholar] [CrossRef]
- Singh, R.; Saxena, N.S.; Chaudhary, D.R. Simultaneously measurement of thermal conductivity and thermal diffusivity of some building materials using the transient hot strip method. J. Phys. D Appl. Phys. 1985, 18, 1–8. [Google Scholar] [CrossRef]
- Gustavsson, M.; Wang, H.; Trejo, R.M.; Lara-Curzio, E. On the use of the transient hot-strip method for measuring the thermal conductivity of high-conductivity thin bars. Int. J. Thermophys. 2006, 27, 1816–1825. [Google Scholar] [CrossRef]
- Hu, R.; Ma, A.; Li, Y. Transient hot strip measures thermal conductivity of organic foam thermal insulation materials. Exp. Therm. Fluid Sci. 2018, 91, 443–450. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, X.; Yu, F. Thermal conductivity measurements on xonotlite-type calcium silicate by the transient hot-strip method. J. Univ. Sci. Technol. Beijing Miner. Metall. Mater. 2008, 15, 791–795. [Google Scholar] [CrossRef]
- Lourenco, M.J.; Rosa, S.C.S.; Nieto de Castro, C.A.; Albuquerque, C.; Erdmann, B.; Lang, J.; Roitzsch, R. Simulation of the transient heating in an unsymmetrical, coated, hot-strip sensor with a self-adaptive finite-element method (SAFEM). Int. J. Thermophys. 2000, 21, 377–384. [Google Scholar] [CrossRef]
- Gobbé, C.; Iserna, S.; Ladevie, B. Hot strip method: Application to thermal characterization of orthotropic media. Int. J. Therm. Sci. 2004, 43, 951–958. [Google Scholar] [CrossRef]
- Hammerschmidt, U.; Sabuga, W. Transient Hot Strip (THS) Method: Uncertainty Assessment. Int. J. Thermophys. 2000, 21, 217–248. [Google Scholar] [CrossRef]
- Hammerschmidt, U. A new pulse hot strip sensor for measuring thermal conductivity and thermal diffusivity of solids. Int. J. Thermophys. 2003, 24, 675–682. [Google Scholar] [CrossRef]
- Gustavsson, M.; Nagai, H.; Okutani, T. Measurements of the thermal effusivity of a drop-size liquid using the pulse transient hot-strip technique. Int. J. Thermophys. 2005, 26, 1803–1813. [Google Scholar] [CrossRef]
- Hammerschmidt, U.; Mayer, V. New transient hot-bridge sensor to measure thermal conductivity, thermal diffusivity, and volumetric specific heat. Int. J. Thermophys. 2006, 27, 840–865. [Google Scholar] [CrossRef]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Kalaprasad, G.; Pradeep, P.; Mathew, G.; Pavithran, C.; Thomas, S. Thermal conductivity and thermal diffusivity analyses of low-density polyethylene composites reinforced with sisal, glass and intimately sisal/glass fibres. Compos. Sci. Technol. 2000, 60, 2967–2977. [Google Scholar] [CrossRef]
- Bouguerra, A.; Ait-Mokhtar, A.; Amiri, O.; Diop, M.B. Measurement of thermal conductivity, thermal diffusivity and heat capacity of highly porous building materials using transient plane source technique. Int. Commun. Heat Mass Transf. 2001, 28, 1065–1078. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Tao, W. Effect of radiative heat transfer on determining thermal conductivity of semi-transparent materials using transient plane source method. Appl. Therm. Eng. 2017, 114, 337–345. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.S. Simultaneous determination of thermal conductivity and thermal diffusivity of food and agricultural materials using a transient plane-source method. J. Food Eng. 2009, 95, 179–185. [Google Scholar] [CrossRef]
- Boning, T.; Chuanqing, Z.; Nansheng, Q.; Yue, C.; Sasa, G.; Xin, L.; Baoshou, Z.; Kunyu, L.; Wenzheng, L.; Xiaodong, F. Analyzing and estimating thermal conductivity of sedimentary rocks from mineral composition and pore property. Geofluids 2021, 2021, 6665027. [Google Scholar]
- Elkholy, A.; Sadek, H.; Kempers, R. An improved transient plane source technique and methodology for measuring the thermal properties of anisotropic materials. Int. J. Therm. Sci. 2019, 135, 362–374. [Google Scholar] [CrossRef]
- Karawacki, E.; Suleiman, B.M. Dynamic plane source technique for simultaneous determination of specific heat, thermal conductivity and thermal diffusivity of metallic samples. Meas. Sci. Technol. 1991, 2, 744–750. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.M.; Tao, W.Q. Theoretical accuracy of anisotropic thermal conductivity determined by transient plane source method. Int. J. Heat Mass Transf. 2017, 108, 1634–1644. [Google Scholar] [CrossRef]
- Zheng, Q.; Kaur, S.; Dames, C.; Prasher, R.S. Analysis and improvement of the hot disk transient plane source method for low thermal conductivity materials. Int. J. Heat Mass Transf. 2020, 151, 119331. [Google Scholar] [CrossRef]
- Malinaric, S.; Elkholy, A. Comparison of the new plane source method to the step wise transient method for thermal conductivity and diffusivity measurement. Int. J. Therm. Sci. 2021, 164, 106901. [Google Scholar] [CrossRef]
- Dowding, K.; Beck, J.V.; Ulbrich, A.; Blackwell, B.; Hayes, J. Estimation of thermal properties and surface heat flux in carbon-carbon composite. J. Thermophys. Heat Transf. 1995, 9, 345–351. [Google Scholar] [CrossRef]
- D’Alessandro, G.; de Monte, F. Optimal experiment design for thermal property estimation using a boundary condition of the fourth kind with a time-limited heating period. Int. J. Heat Mass Transf. 2019, 134, 1268–1282. [Google Scholar] [CrossRef]
- D’Alessandro, G.; de Monte, F.; Gasparin, S.; Berger, J. Comparison of uniform and stepwise-uniform heatings when estimating thermal properties of high-conductivity materials. Int. J. Heat Mass Transf. 2022, in press. [CrossRef]
- D’Alessandro, G.; de Monte, F. Sensitivity coefficients for thermal property measurements using a boundary condition of the 4th kind. In Proceedings of the 34th UIT Heat Transf. Conference 2016, Ferrara, Italy, 4–6 July 2016; Volume 796. [Google Scholar]
- Dowding, K.J.; Blackwell, B.F.; Cochran, R.J. Application of sensitivity coefficients for heat conduction problems. Numer. Heat Transf. Part B 1999, 36, 33–55. [Google Scholar]
- Taktak, R.; Beck, J.V.; Scott, E.P. Optimal experimental design for estimating thermal properties of composite materials. Int. J. Heat Mass Transf. 1993, 36, 2977–2986. [Google Scholar] [CrossRef]
- Cole, K.D.; Beck, J.V.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Function, 2nd ed.; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bovesecchi, G.; Coppa, P. High temperature (till 1500 °C) contemporary thermal conductivity and thermal diffusivity measurements with the step flat heat source. In Proceedings of the 5th International Symposium on Instrumentation Science and Technology 2008, Shenyang, China, 15–18 September 2008; Society of Photo-Optical Instrumentation Engineers SPIE: Bellingham, WA, USA, 2009; Volume 7133. [Google Scholar]
- D’Alessandro, G.; de Monte, F.; Amos, D.E. Effect of heat source and imperfect contact on simultaneous estimation of thermal properties of high-conductivity materials. Math. Probl. Eng. 2019, 2019, 5945413. [Google Scholar] [CrossRef]
- D’Alessandro, G.; de Monte, F. Multi-layer transient heat conduction involving perfectly-conducting solids. Energies 2020, 13, 6484. [Google Scholar] [CrossRef]
- Al-Nimr, M.A.; Alkam, M.K. A Generalized Thermal Boundary Condition. Heat Mass Transf. 1997, 33, 157–161. [Google Scholar] [CrossRef]
- D’Alessandro, G.; de Monte, F. On the optimum experiment and heating times when estimating thermal properties through the plane source method. Heat Transf. Eng. 2022, 43, 257–269. [Google Scholar] [CrossRef]
- Monde, M.; Kosaka, M.; Mitsutake, Y. Simple measurement of thermal diffusivity and thermal conductivity using inverse solution for one-dimensional heat conduction. Int. J. Heat Mass Transf. 2010, 53, 5343–5349. [Google Scholar] [CrossRef]
- Kubičár, L.; Bohác, V. A step-wise method for measuring thermophysical parameters of materials. Meas. Sci. Technol. 2000, 11, 252–258. [Google Scholar]
- Malinarič, S.; Dieška, P. Stepwise and pulse transient methods of thermophysical parameters measurement. Int. J. Thermophys. 2016, 37, 114. [Google Scholar] [CrossRef]
- Dowding, K.J.; Beck, J.V.; Blackwell, B.F. Estimation of directional-dependent thermal properties in a carbon-carbon composite. Int. J. Heat Mass Transf. 1996, 39, 3157–3164. [Google Scholar] [CrossRef]
- Rodrigues, F.A.; Orlande, H.R.B.; Mejias, M.M. Use of a single heated surface for the estimation of thermal conductivity components of orthotropic 3D solids. Inverse Probl. Sci. Eng. 2004, 12, 501–517. [Google Scholar] [CrossRef]
- Somasundharam, S.; Reddy, K.S. Simultaneous estimation of thermal properties of orthotropic material with non-intrusive measurement. Int. J. Heat Mass Transf. 2018, 126, 1162–1177. [Google Scholar] [CrossRef]
- El Rassy, E.; Billaud, Y.; Saury, D. Simultaneous and direct identification of thermophysical properties for orthotropic materials. Measurement 2019, 135, 199–212. [Google Scholar] [CrossRef]
- de Monte, F.; Beck, J.V. Eigen-periodic-in-space surface heating in conduction with application to conductivity measurement of thin films. Int. J. Heat Mass Transf. 2009, 52, 5567–5576. [Google Scholar] [CrossRef]
- Wouwer, A.V.; Point, N.; Porteman, S.; Remy, M. An approach to the selection of optimal sensor locations in distributed parameter systems. J. Process Control 2000, 10, 291–300. [Google Scholar] [CrossRef]
- Ranjbar, A.A.; Ezzati, M.; Famouri, M. Optimization of experimental design for an inverse estimation of the metal-mold heat transfer coefficient in the solidification of Sn-10% Pb. J. Mater. Process. Tech. 2009, 209, 5611–5617. [Google Scholar] [CrossRef]
- Karalashvili, M.; Marquardt, W.; Mhamdi, A. Optimal experimental design for identification of transport coefficient models in convection-diffusion equations. Comput. Chem. Eng. 2015, 80, 101–113. [Google Scholar] [CrossRef]
- Berger, J.; Dutykh, D.; Mendes, N. On the optimal experiment design for heat and moisture parameter estimation. Exp. Therm. Fluid Sci. 2017, 81, 109–122. [Google Scholar] [CrossRef]
- Videcoq, E.; Petit, D. Model reduction for the solution of multidimensional inverse heat conduction problems. Int. J. Heat Mass Transf. 2001, 44, 1899–1911. [Google Scholar] [CrossRef]
- Mzali, F.; Sassi, L.; Jemmi, A.; Nasrallah, S.B.; Petit, D. Optimal experiment design for the identification of thermo-physical properties of orthotropic solids. Inverse Probl. Sci. Eng. 2004, 12, 193–209. [Google Scholar] [CrossRef]
- Ucinski, D. Optimal Measurement Methods for Distributed Parameter System Identification; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ruffio, E.; Saury, D.; Petit, D. Robust experiment design for the estimation of thermophysical parameters using stochastic algorithms. Int. J. Heat Mass Transf. 2012, 55, 2901–2915. [Google Scholar] [CrossRef]
- Dieb, T.M.; Tsuda, K. Machine learning-based experimental design in materials science. In Nanoinformatics; Tanaka, I., Ed.; Springer: Singapore, 2018; pp. 65–74. [Google Scholar]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Gasparin, S.; Berger, J.; D’Alessandro, G.; de Monte, F.; Ucinski, D. Optimal experimental design for the assessment of thermophysical properties in existing building walls. Heat Transf. Eng. 2022, in press.


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Alessandro, G.; Potenza, M.; Corasaniti, S.; Sfarra, S.; Coppa, P.; Bovesecchi, G.; de Monte, F. Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review. Energies 2022, 15, 8807. https://doi.org/10.3390/en15238807
D’Alessandro G, Potenza M, Corasaniti S, Sfarra S, Coppa P, Bovesecchi G, de Monte F. Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review. Energies. 2022; 15(23):8807. https://doi.org/10.3390/en15238807
Chicago/Turabian StyleD’Alessandro, Giampaolo, Michele Potenza, Sandra Corasaniti, Stefano Sfarra, Paolo Coppa, Gianluigi Bovesecchi, and Filippo de Monte. 2022. "Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review" Energies 15, no. 23: 8807. https://doi.org/10.3390/en15238807
APA StyleD’Alessandro, G., Potenza, M., Corasaniti, S., Sfarra, S., Coppa, P., Bovesecchi, G., & de Monte, F. (2022). Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review. Energies, 15(23), 8807. https://doi.org/10.3390/en15238807








