Prototyping and Experimental Investigation of Digital Hydraulically Driven Knee Exoskeleton
Abstract
1. Introduction
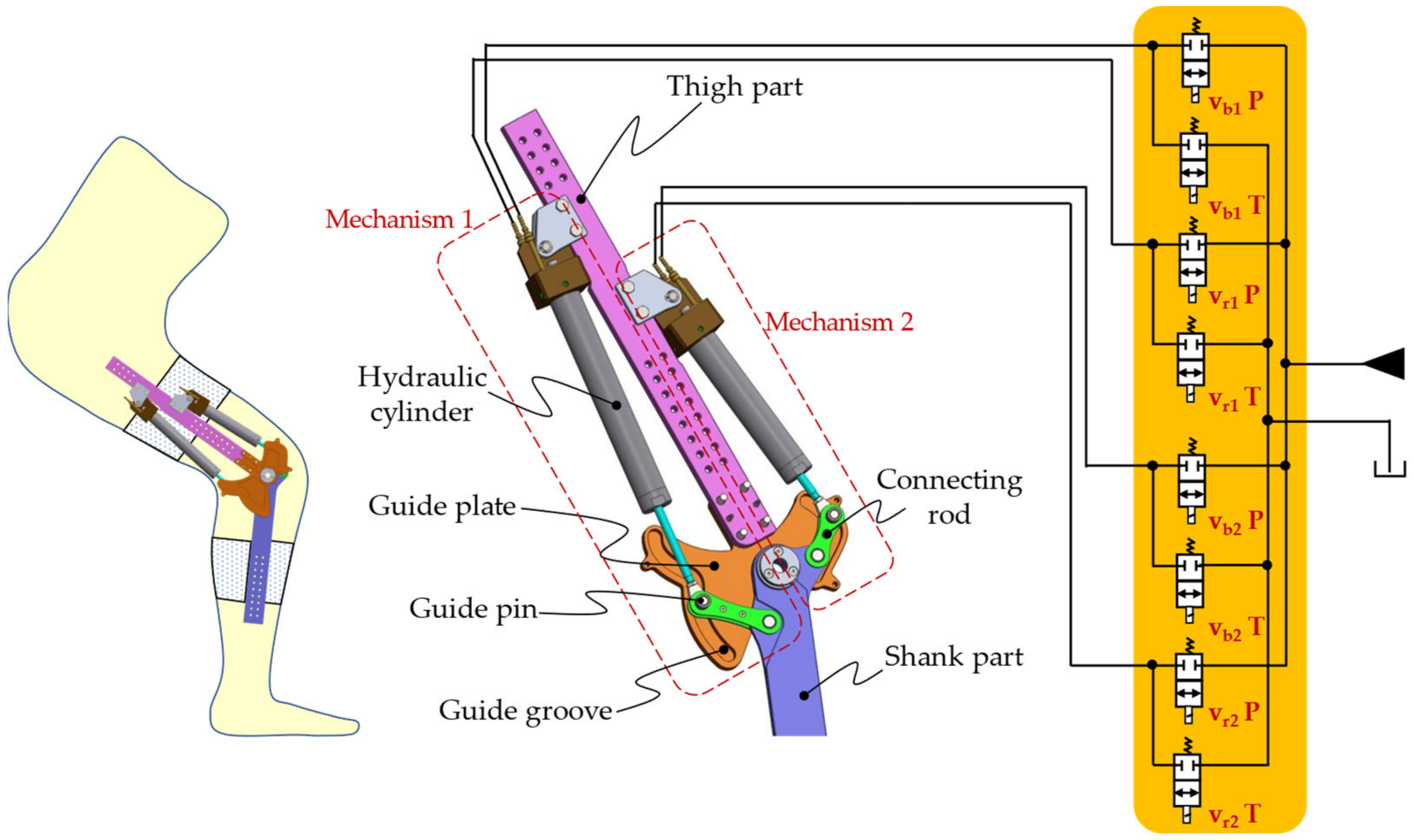
2. Knee Exoskeleton Design
2.1. Hydraulic Drive
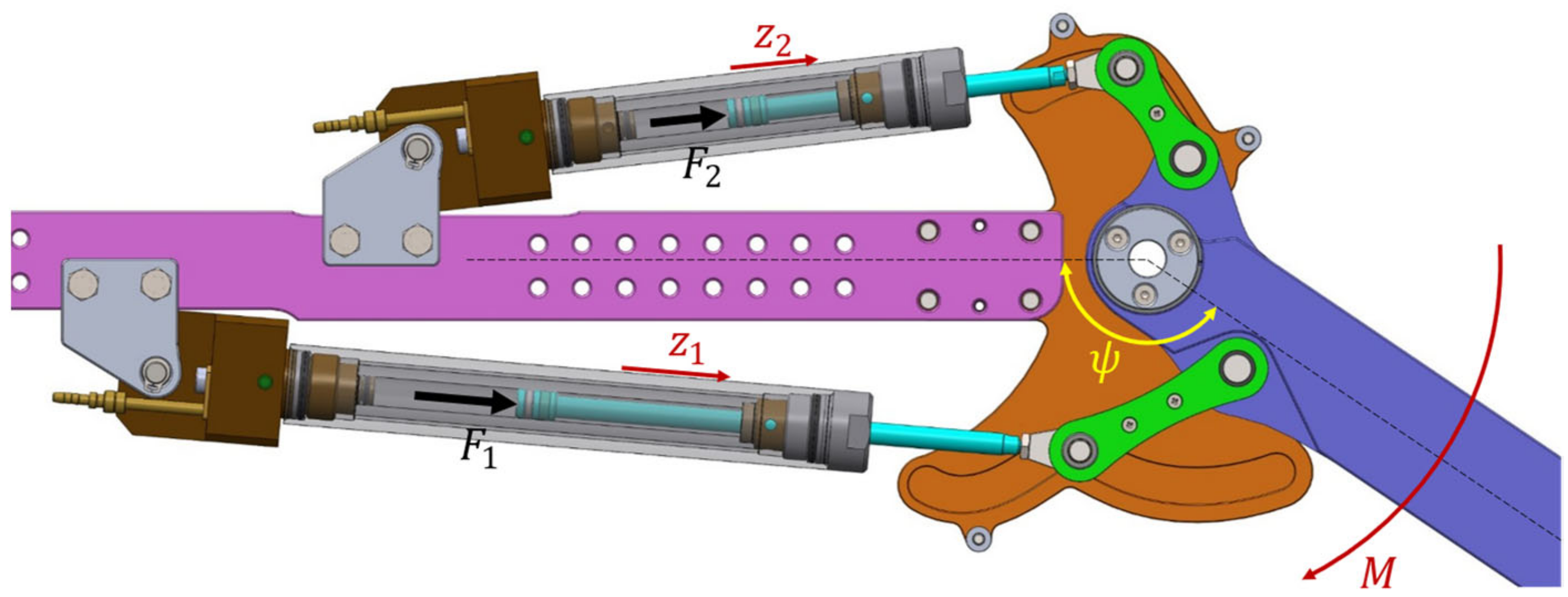
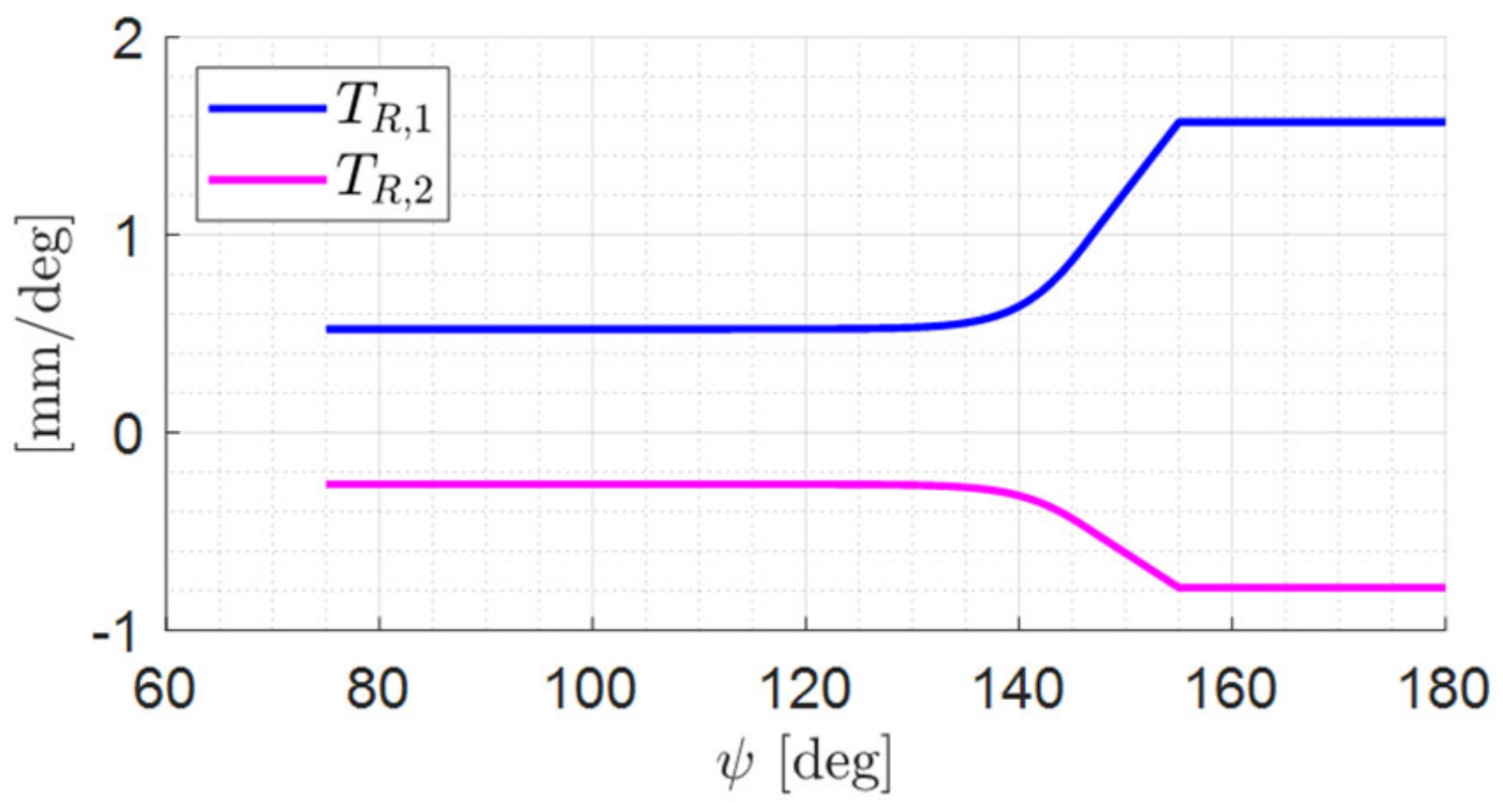
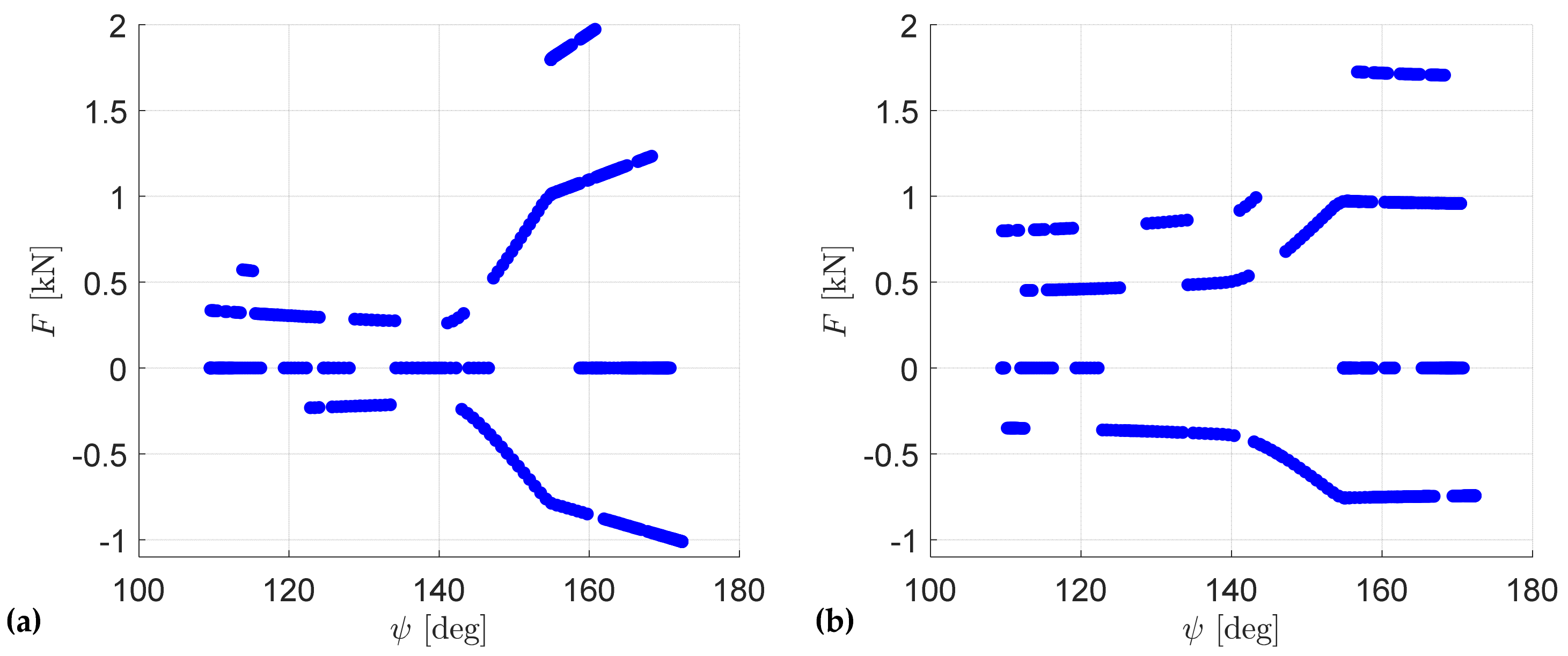
2.2. Transmission Ratio
3. Design Optimization Study
3.1. Objective Functions
3.2. Optimization Variables
3.3. Optimization Constraints
- The design must satisfy the transmission ratio requirements described in Section 2.2.
- The design must be kinematically feasible for the full range of knee motion.
- During the full range of knee motion, interference between different parts of the exoskeleton device must be avoided.
- It can be observed that the groove for mechanism 1 has a relatively sharp peak near the middle. If the curvature of the groove at this peak becomes too high, the knee motion may experience jerky behavior when the guide pin passes through this region. To avoid this, the curvature of the groove must be smaller than a certain value (170 m−1 is considered as an appropriate limit).
3.4. Optimization Procedure and Results
4. Prototype Development
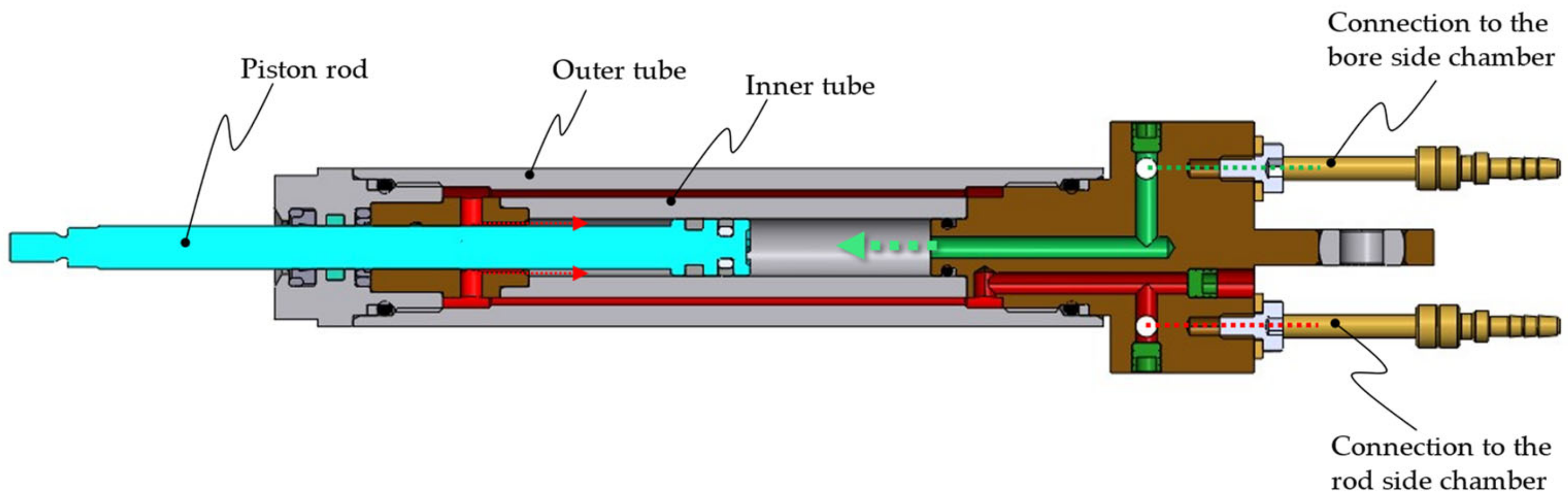
4.1. Hydraulic Cylinders
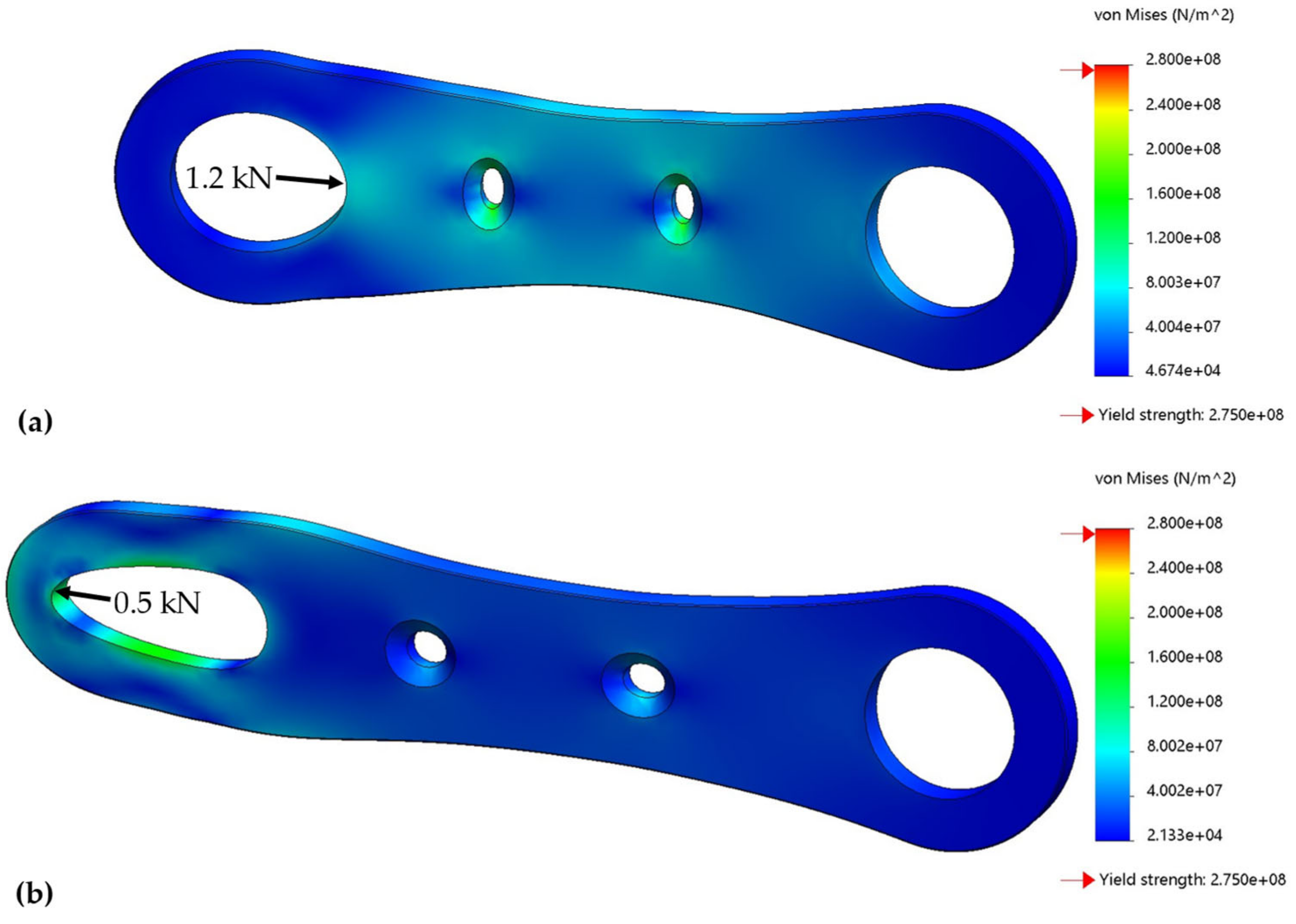
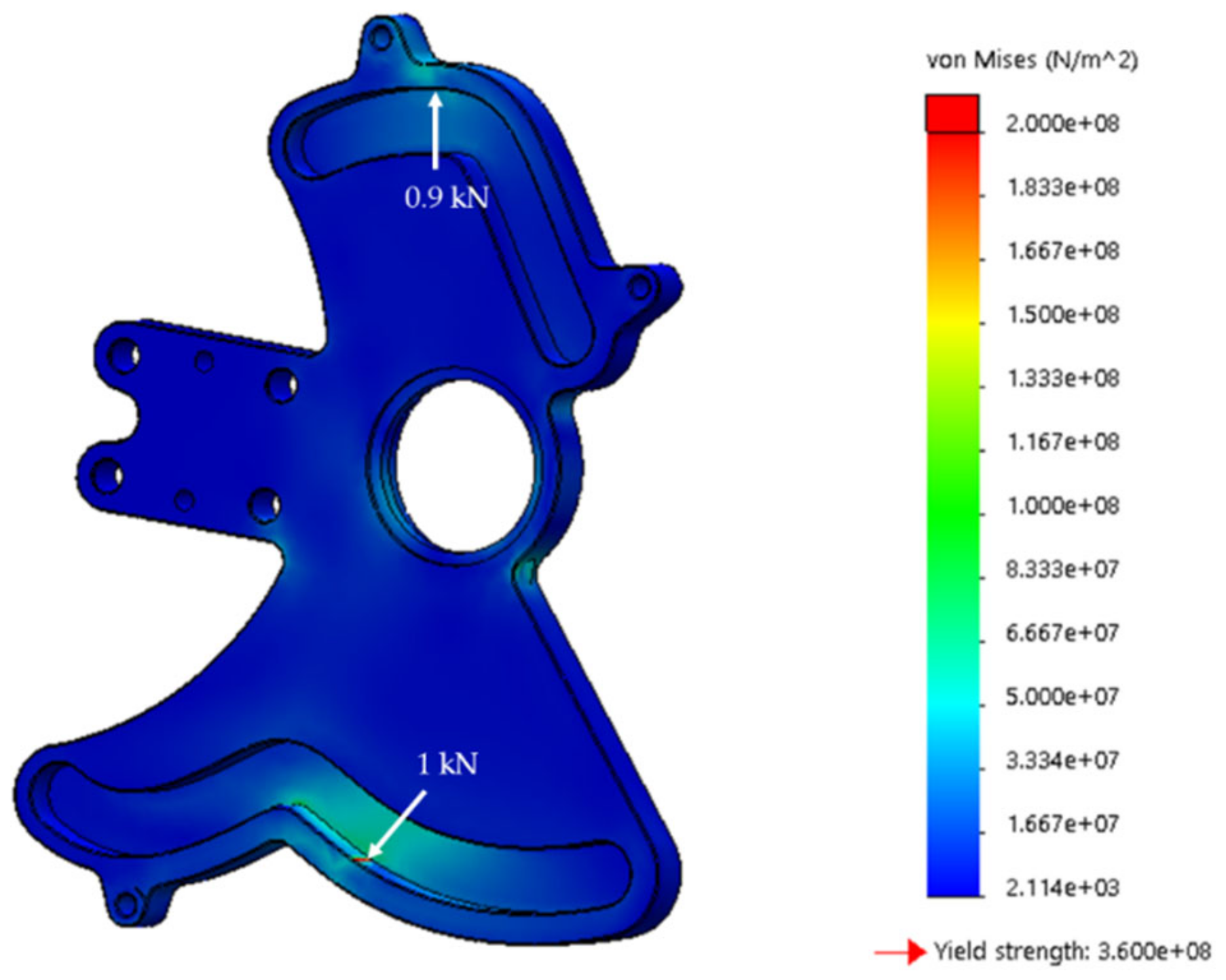
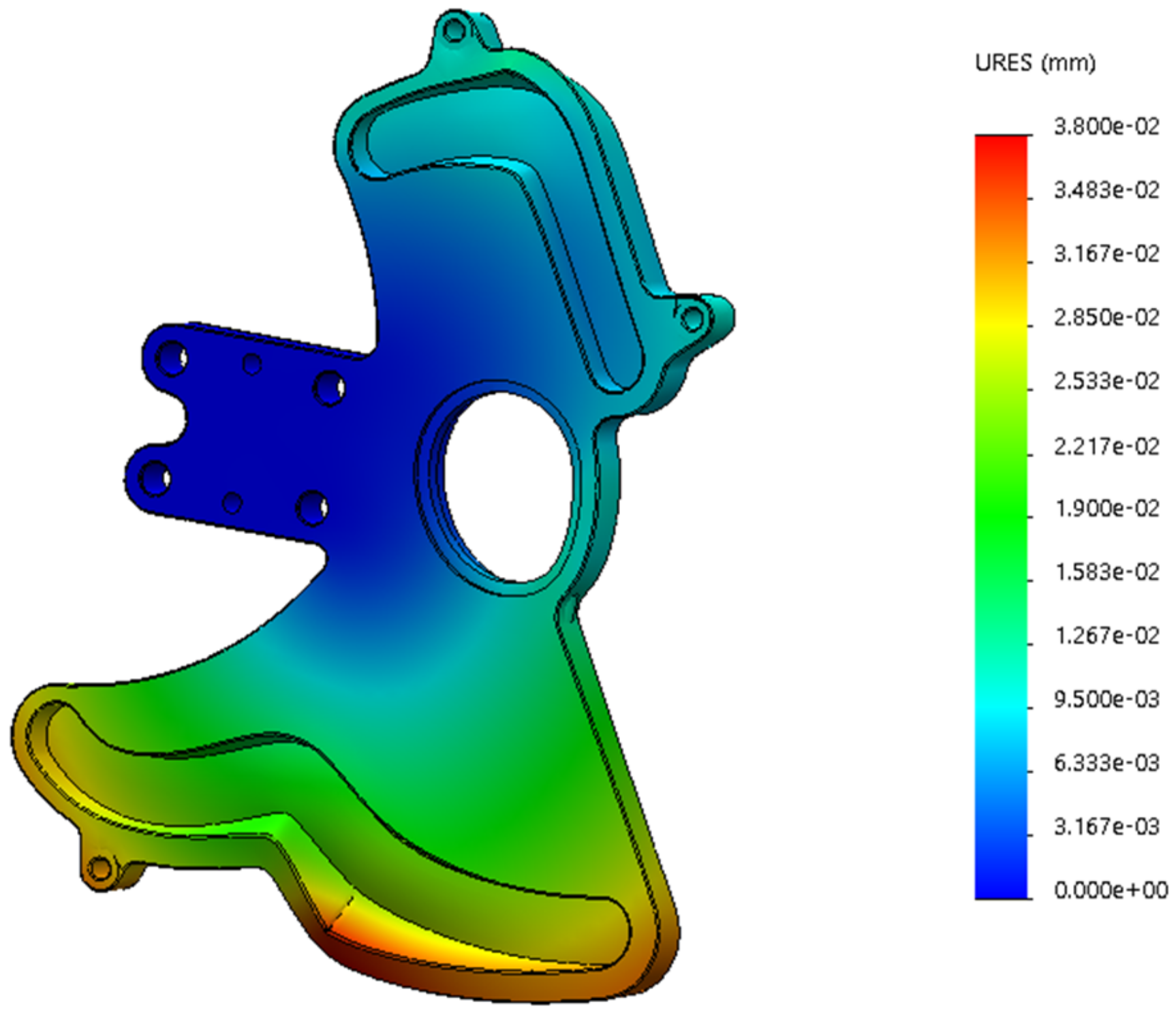
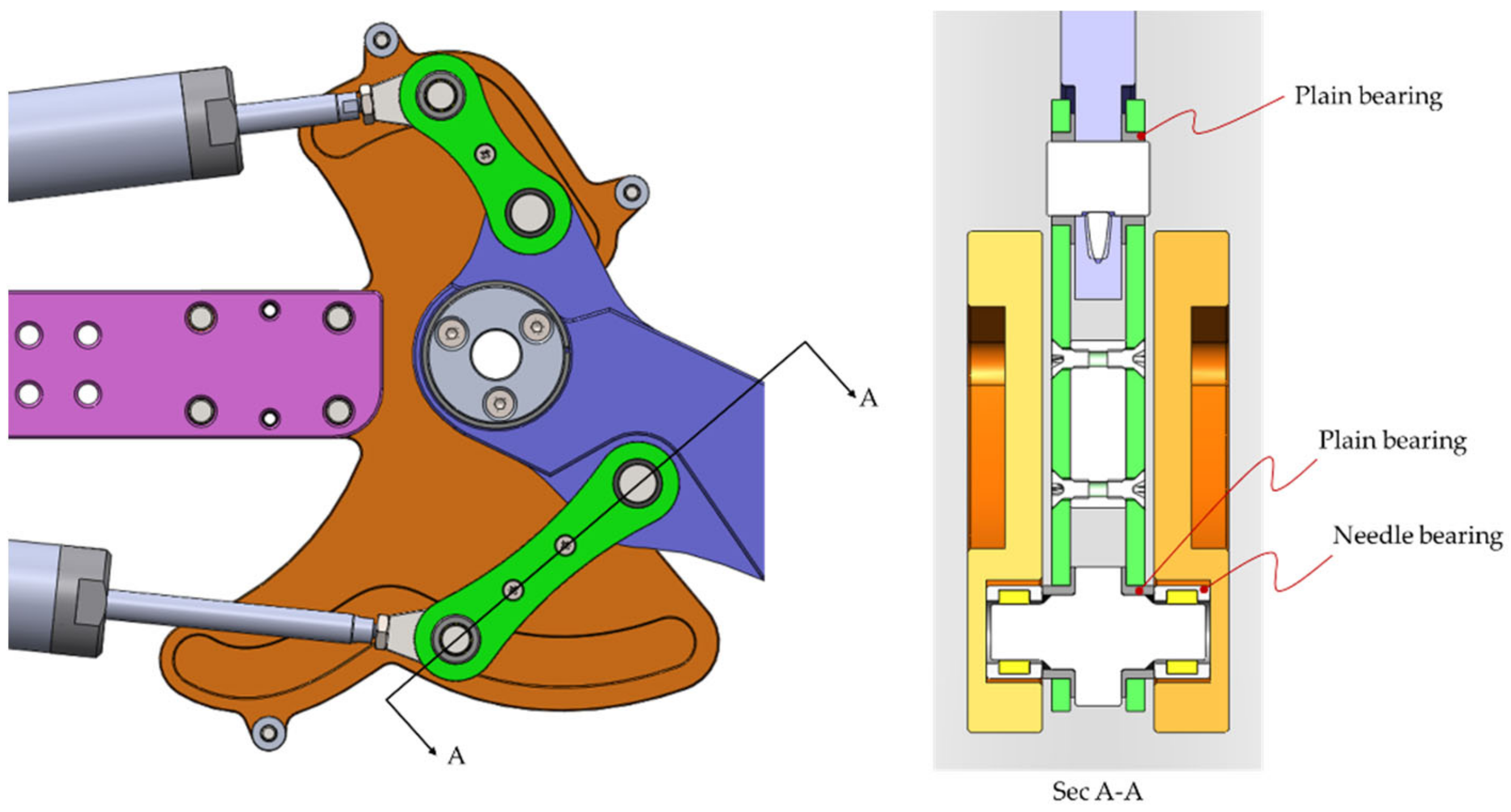
4.2. Linkage Parts and Guide Plates
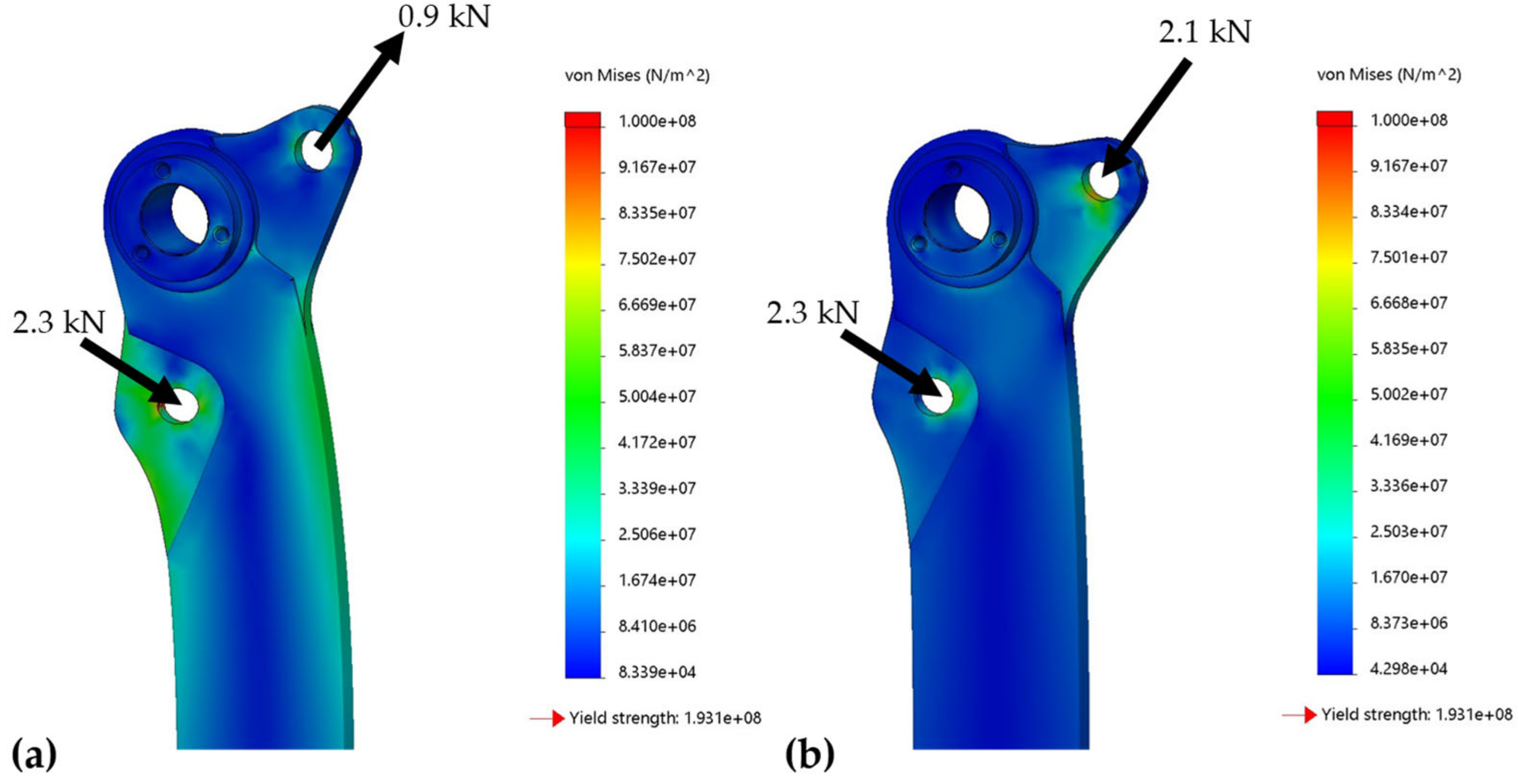
4.2.1. Connecting Rod Linkage
4.2.2. Guide Plates
4.2.3. Shank Part
4.2.4. Bearings
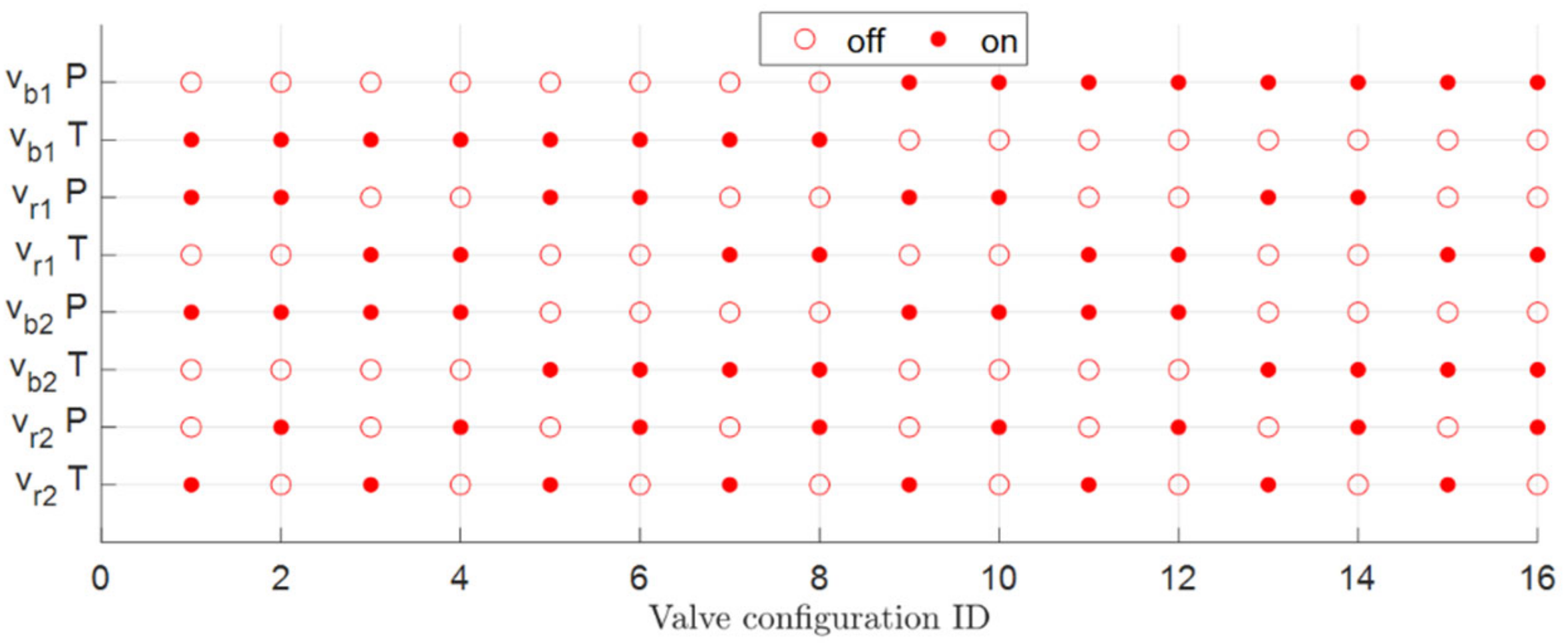
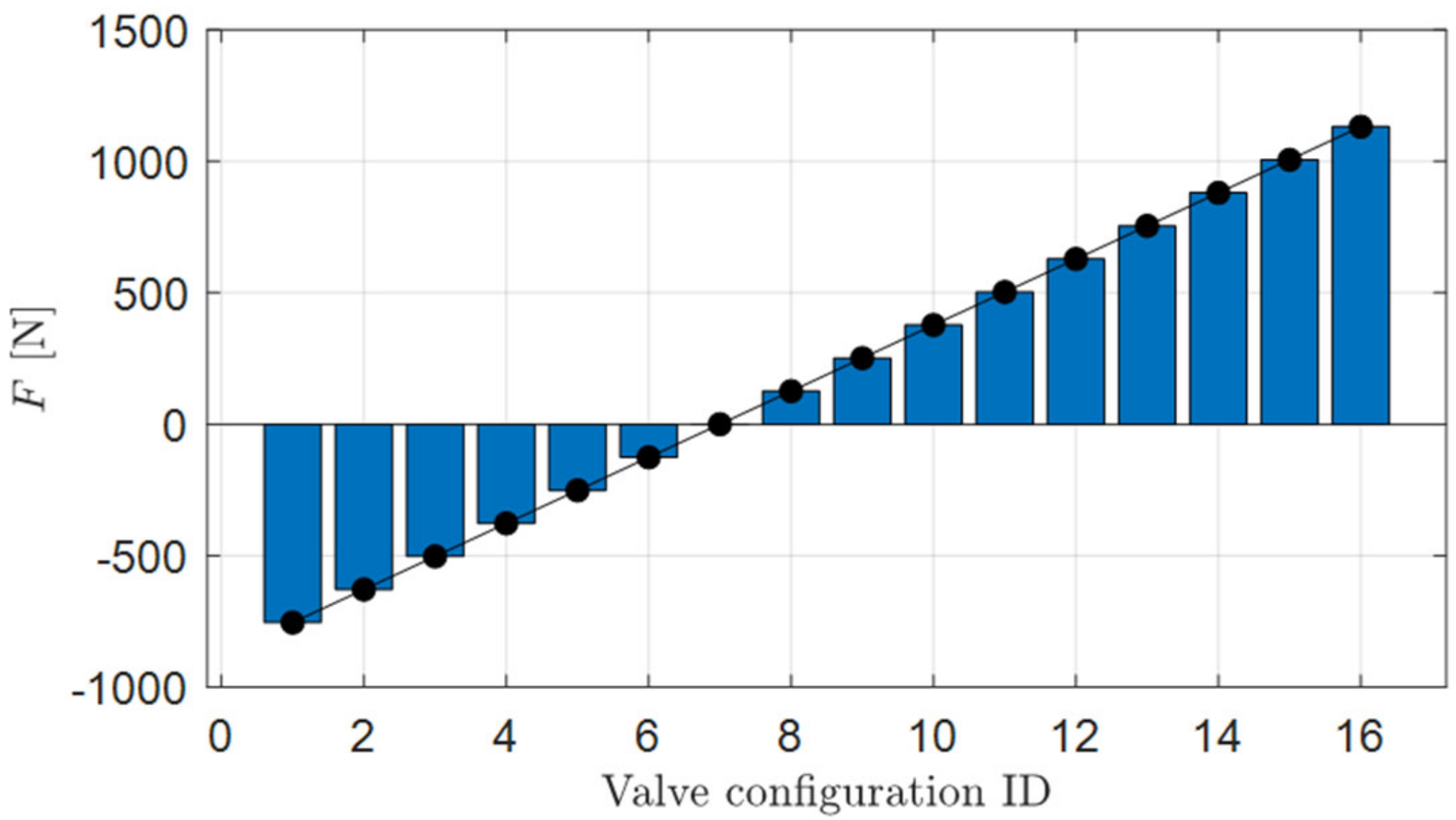
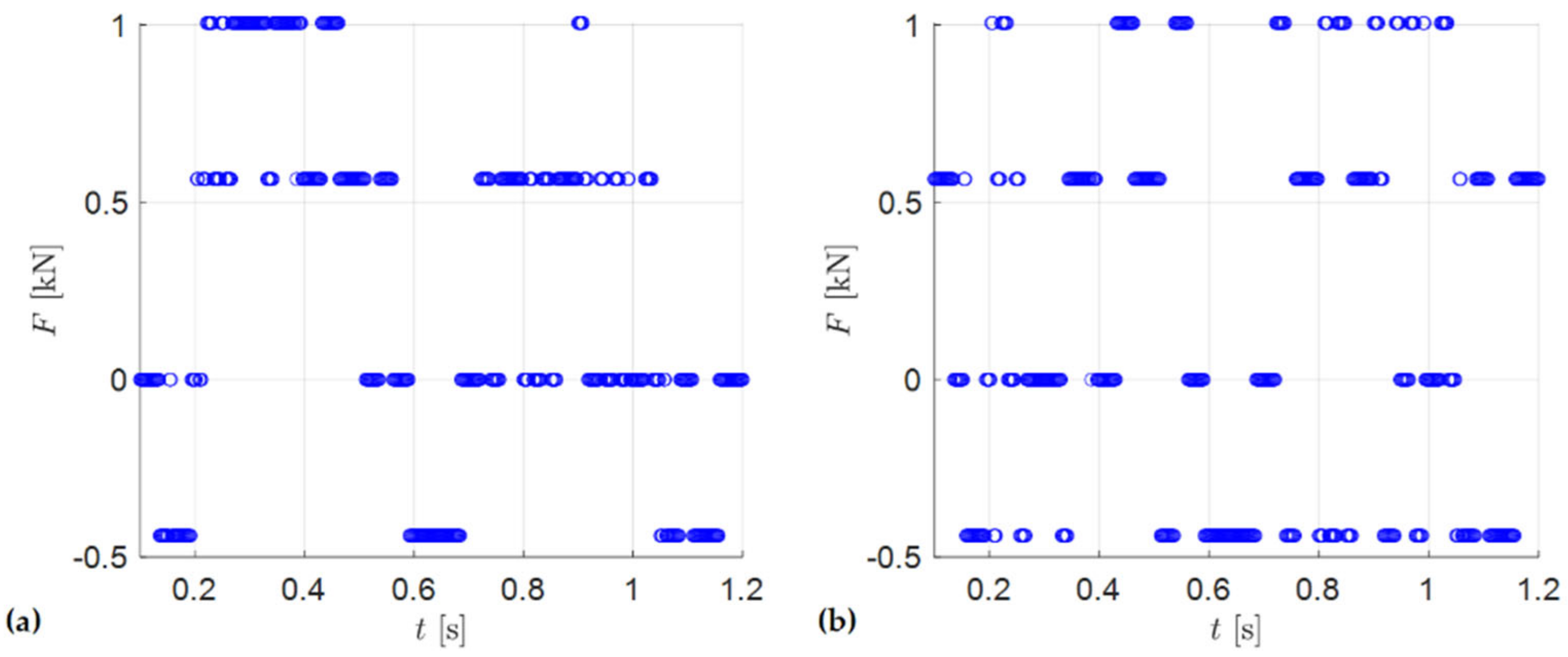
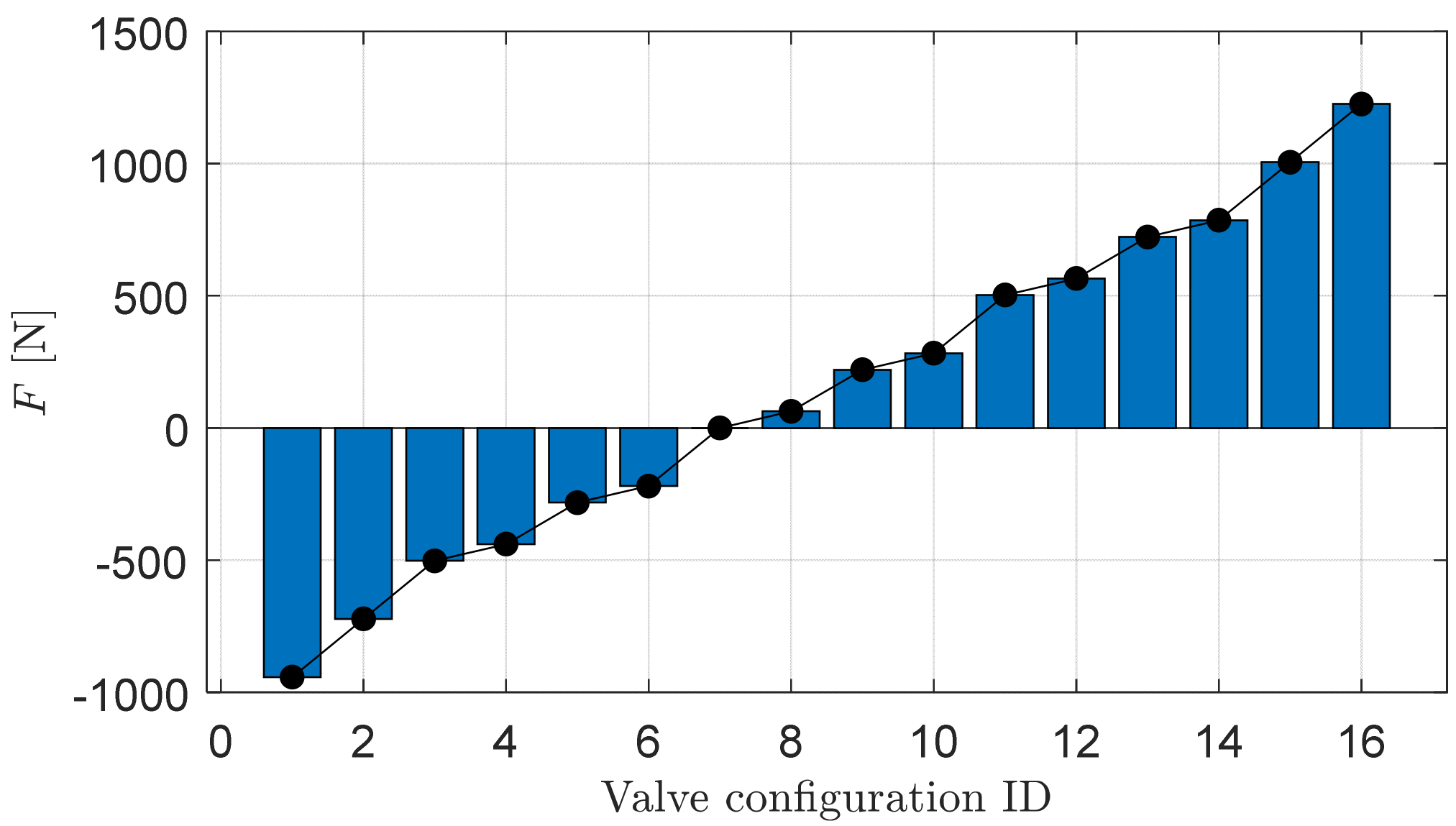
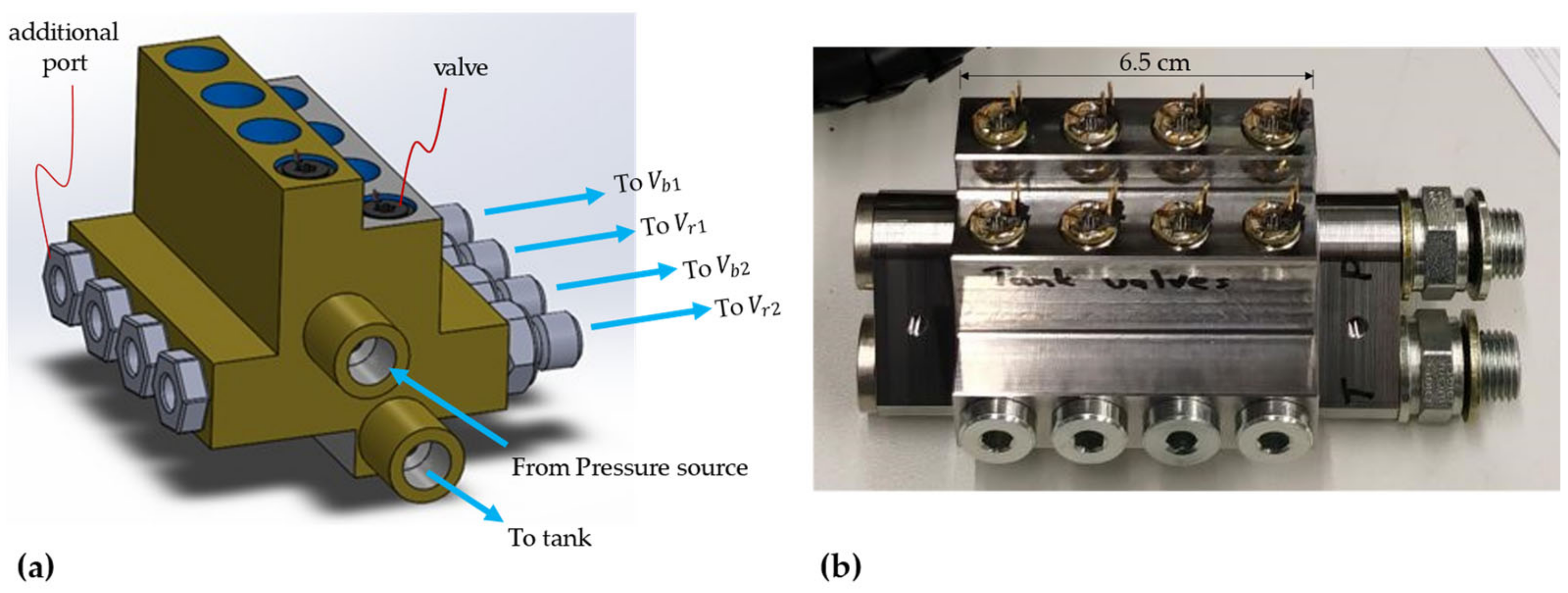
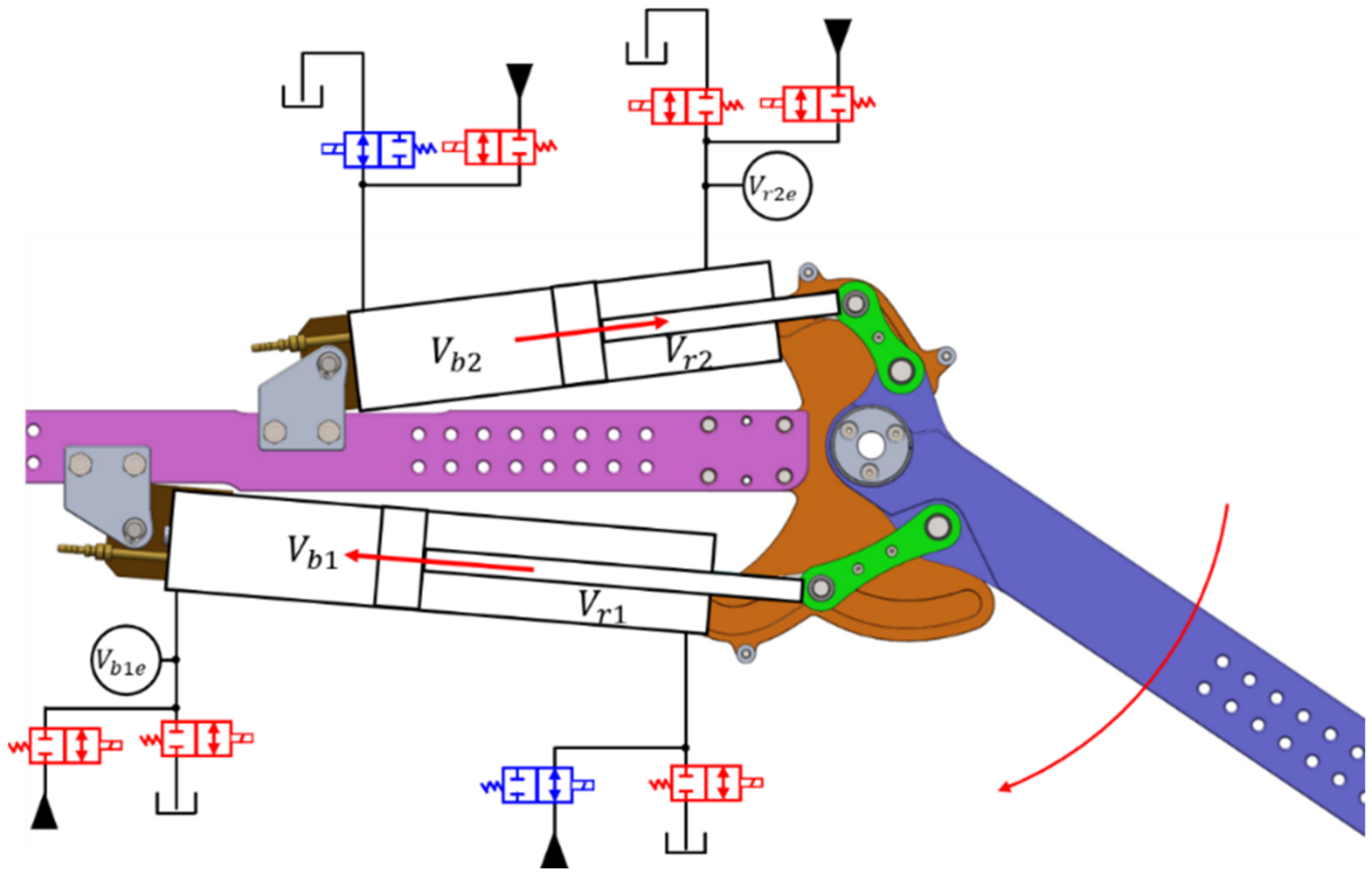
4.3. Valves
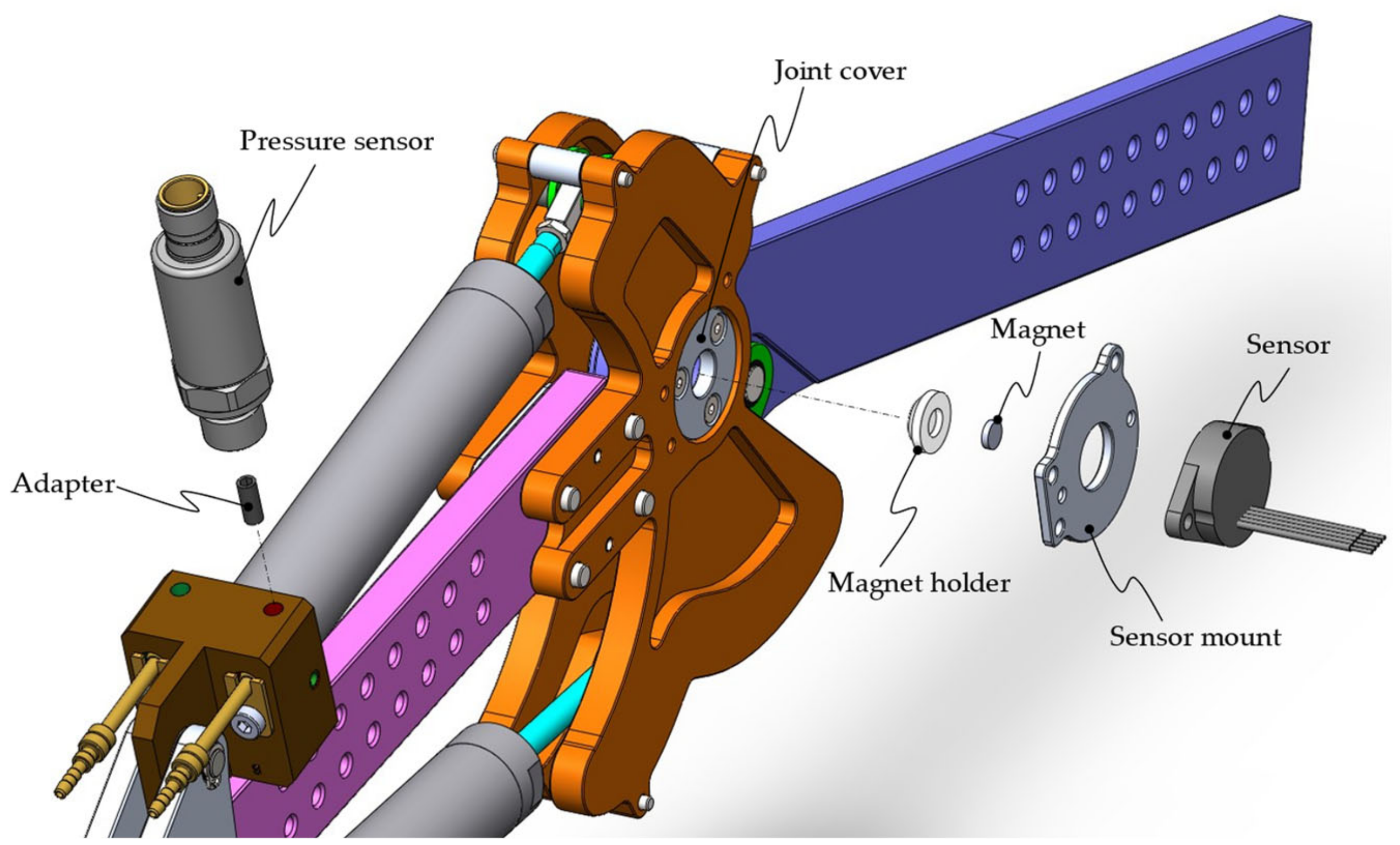
4.4. Sensors
5. Exoskeleton Control Strategy
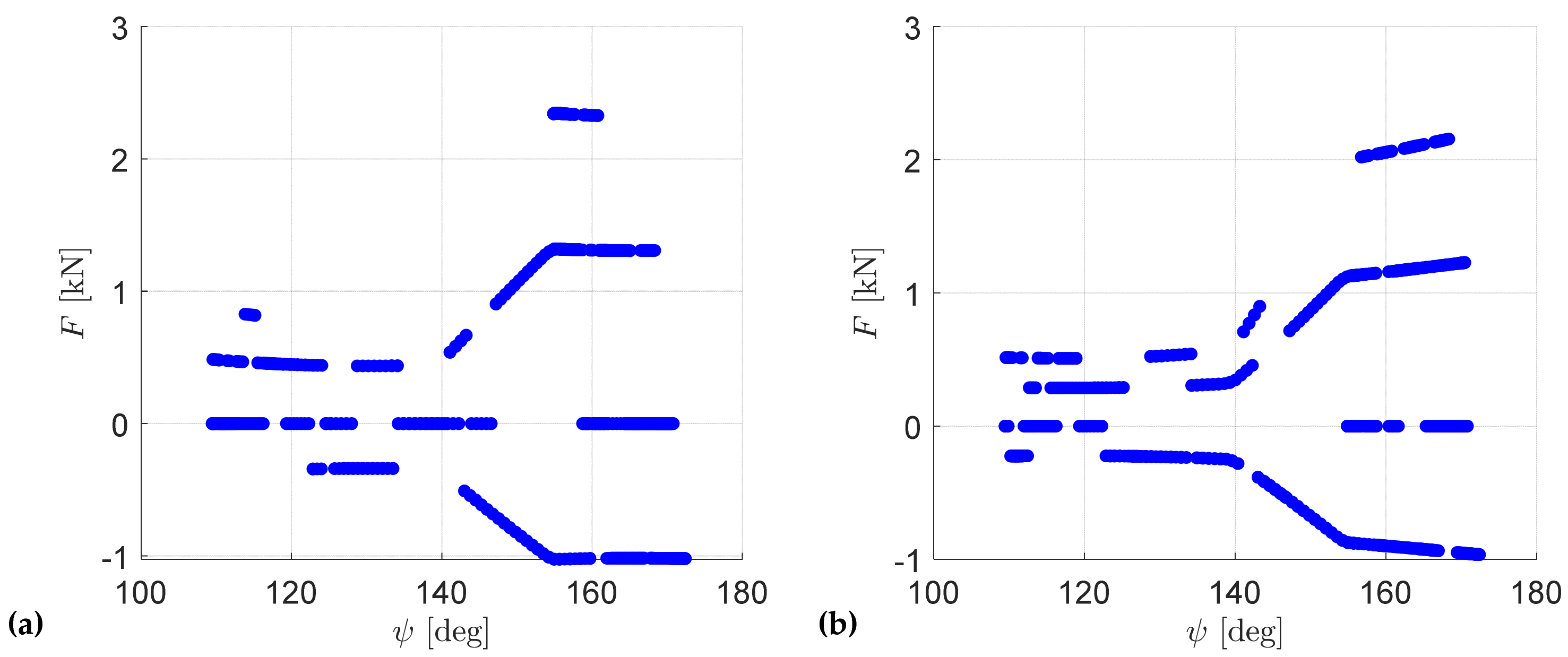
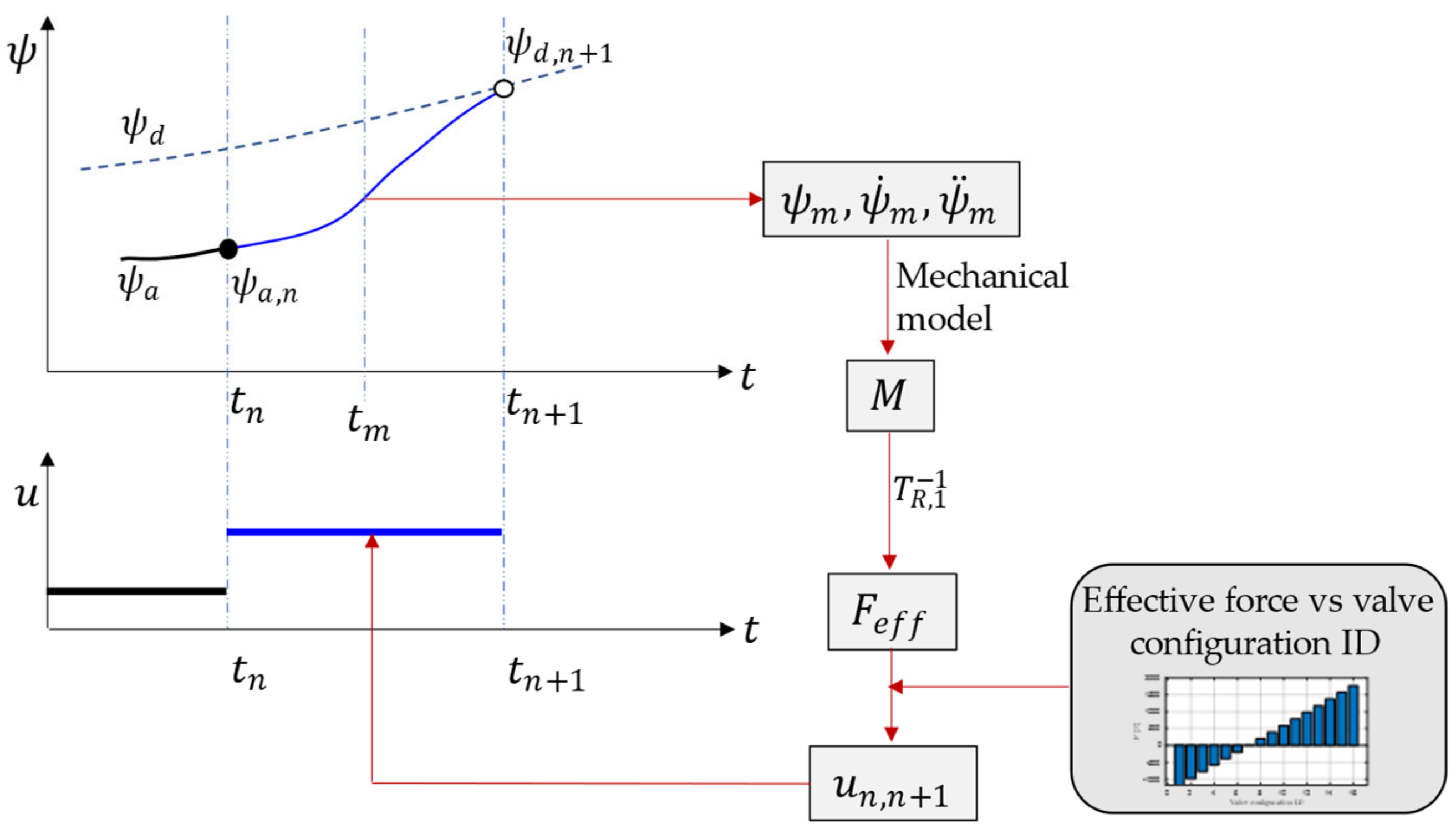
5.1. Passive Control in the Stance Phase
5.2. Model Predictive Control in the Swing Phase
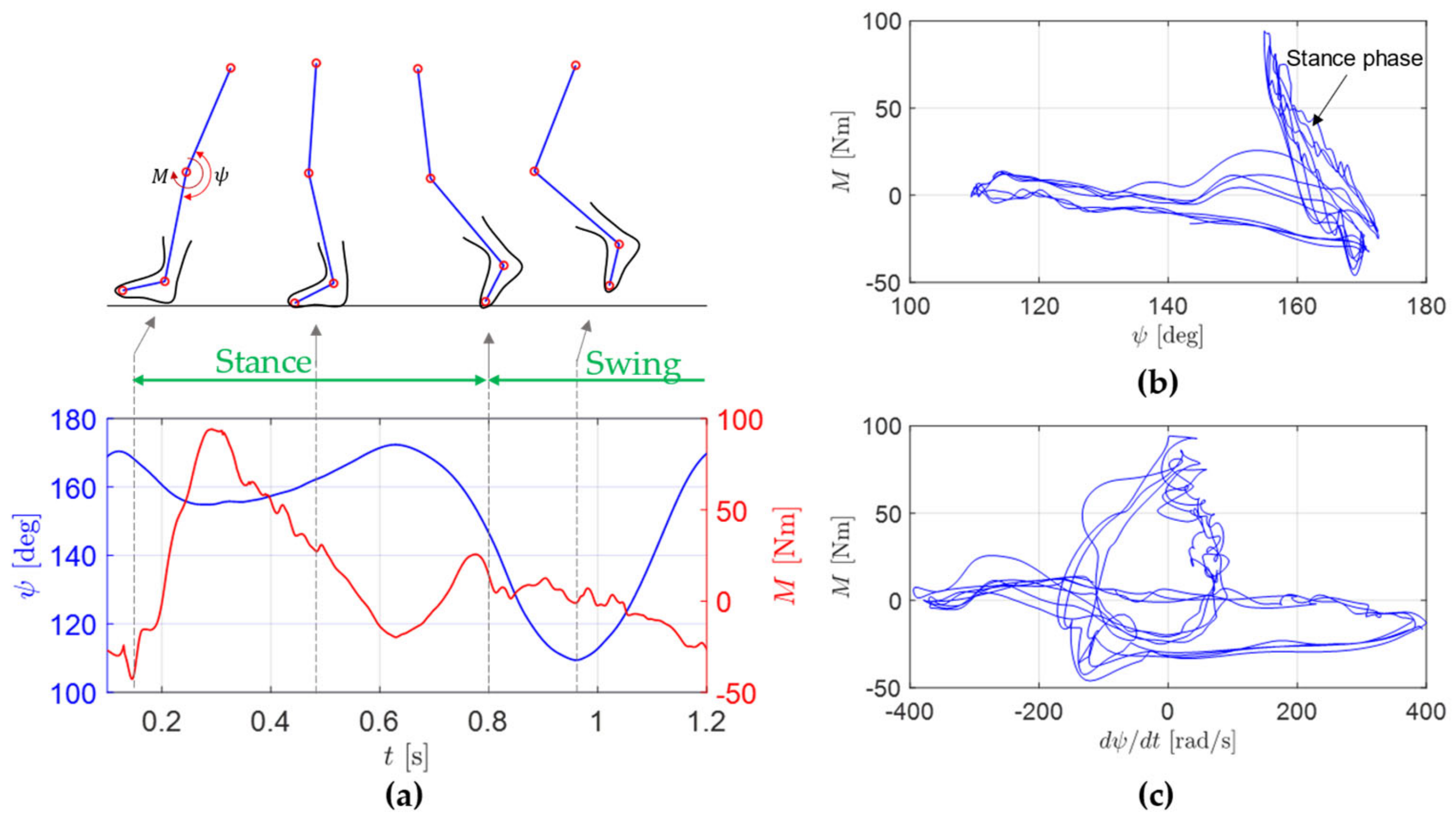
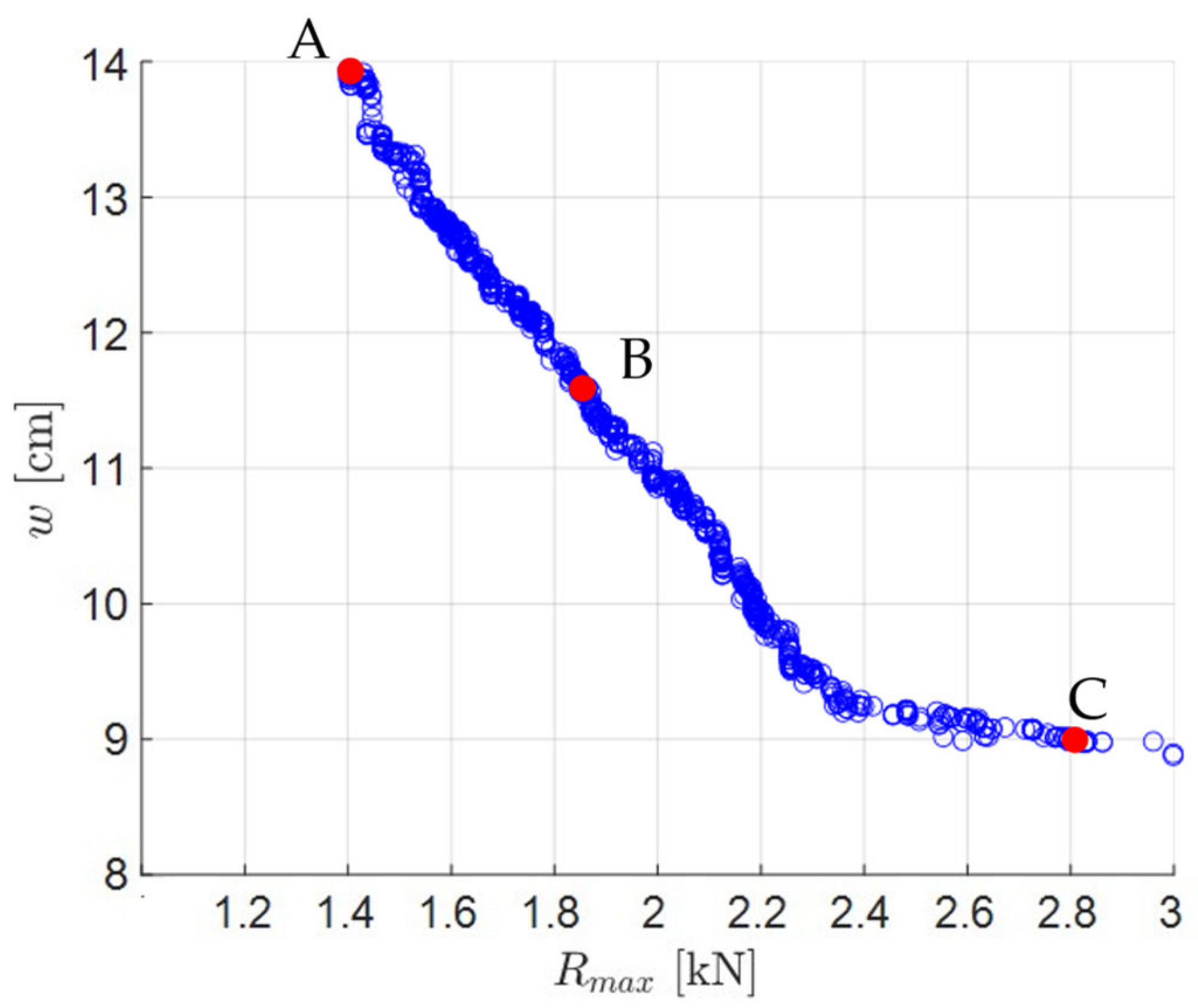
6. Experimental Tests
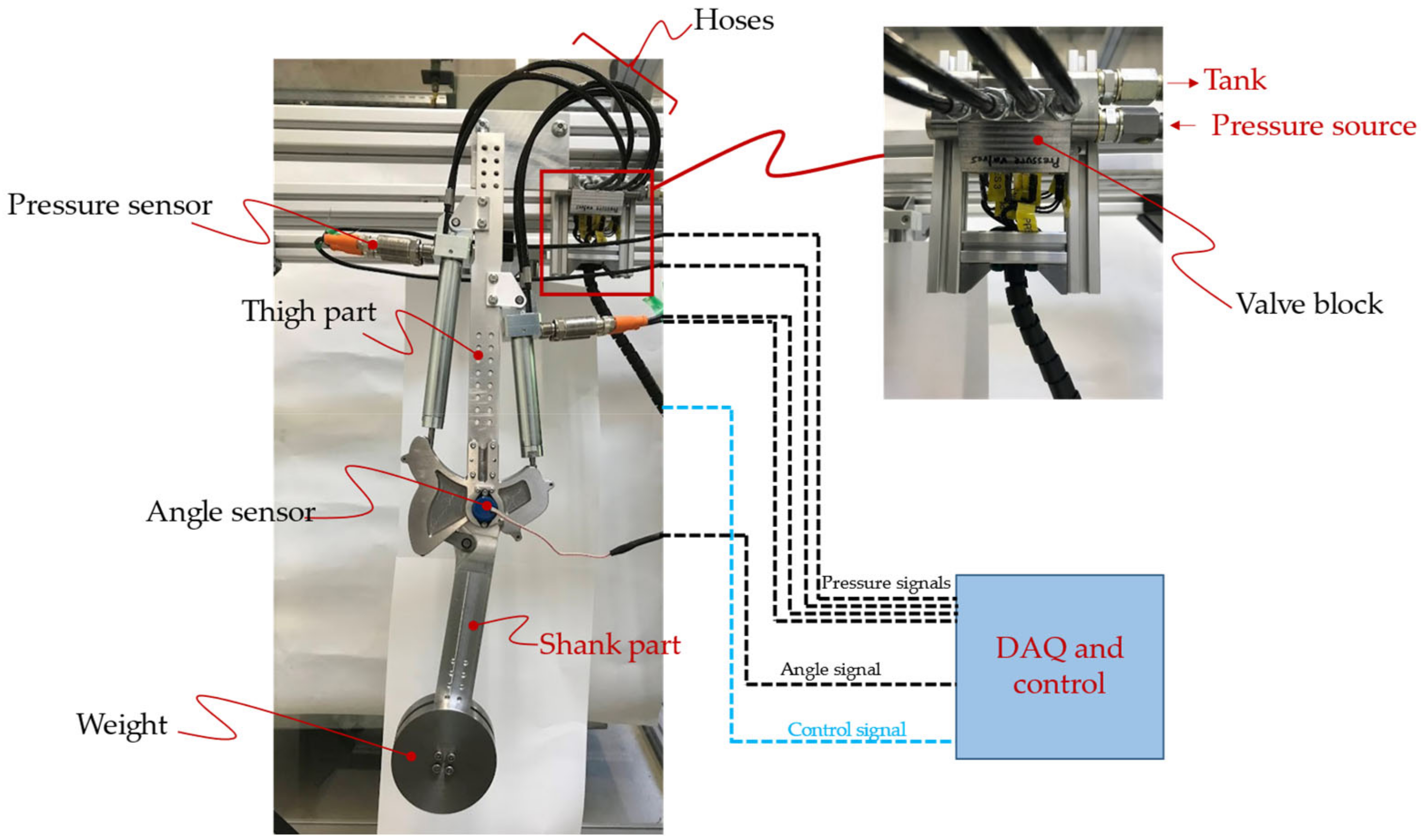
6.1. Experimental Setup
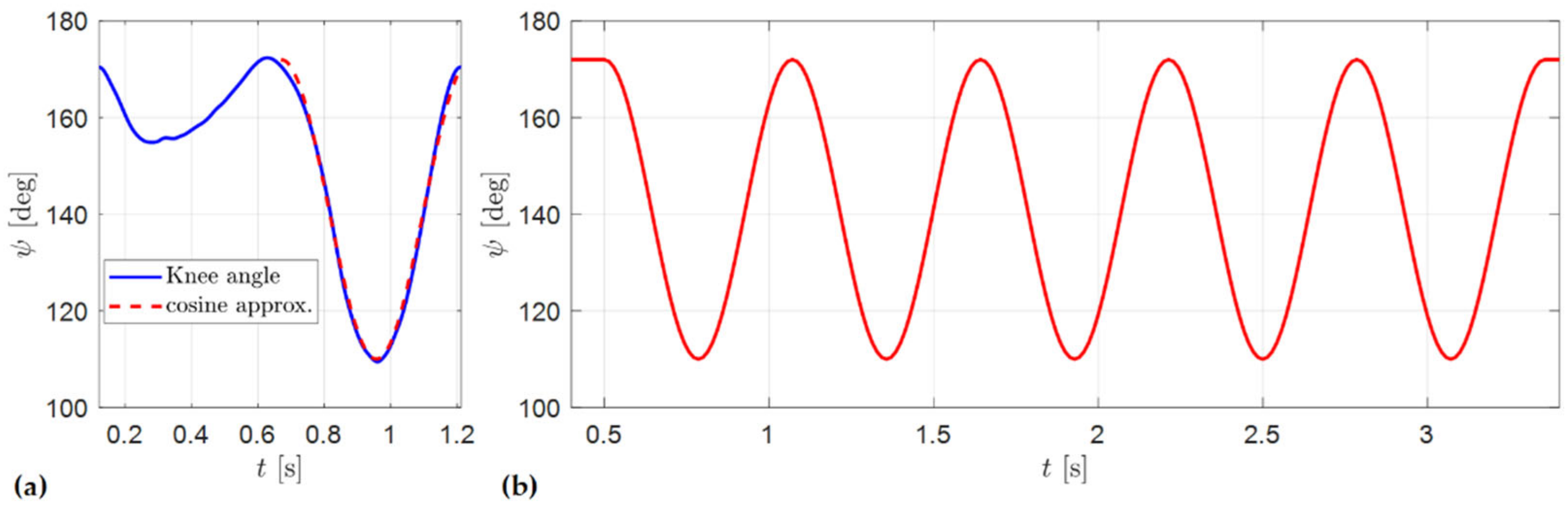
6.2. Test Trajectory
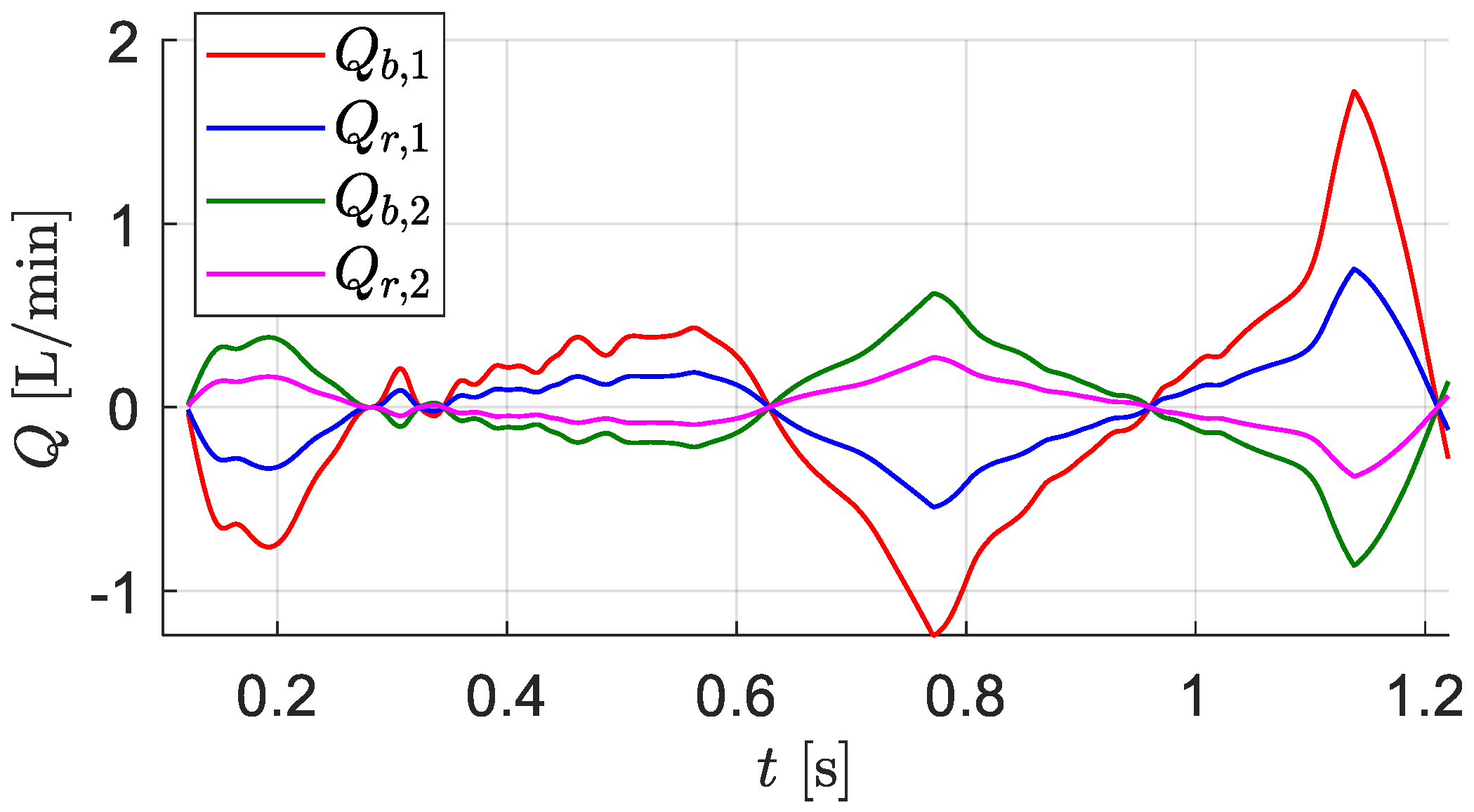
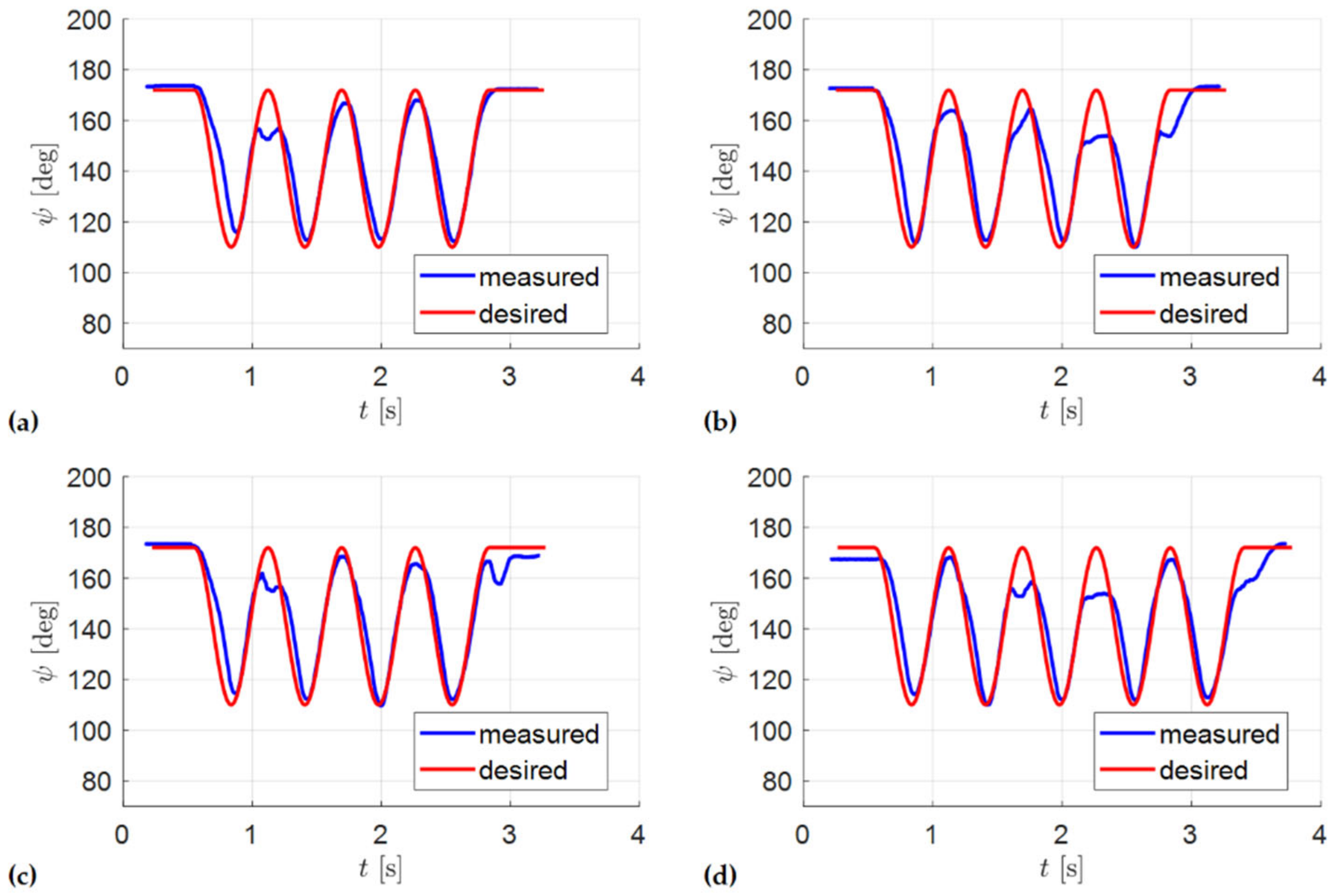
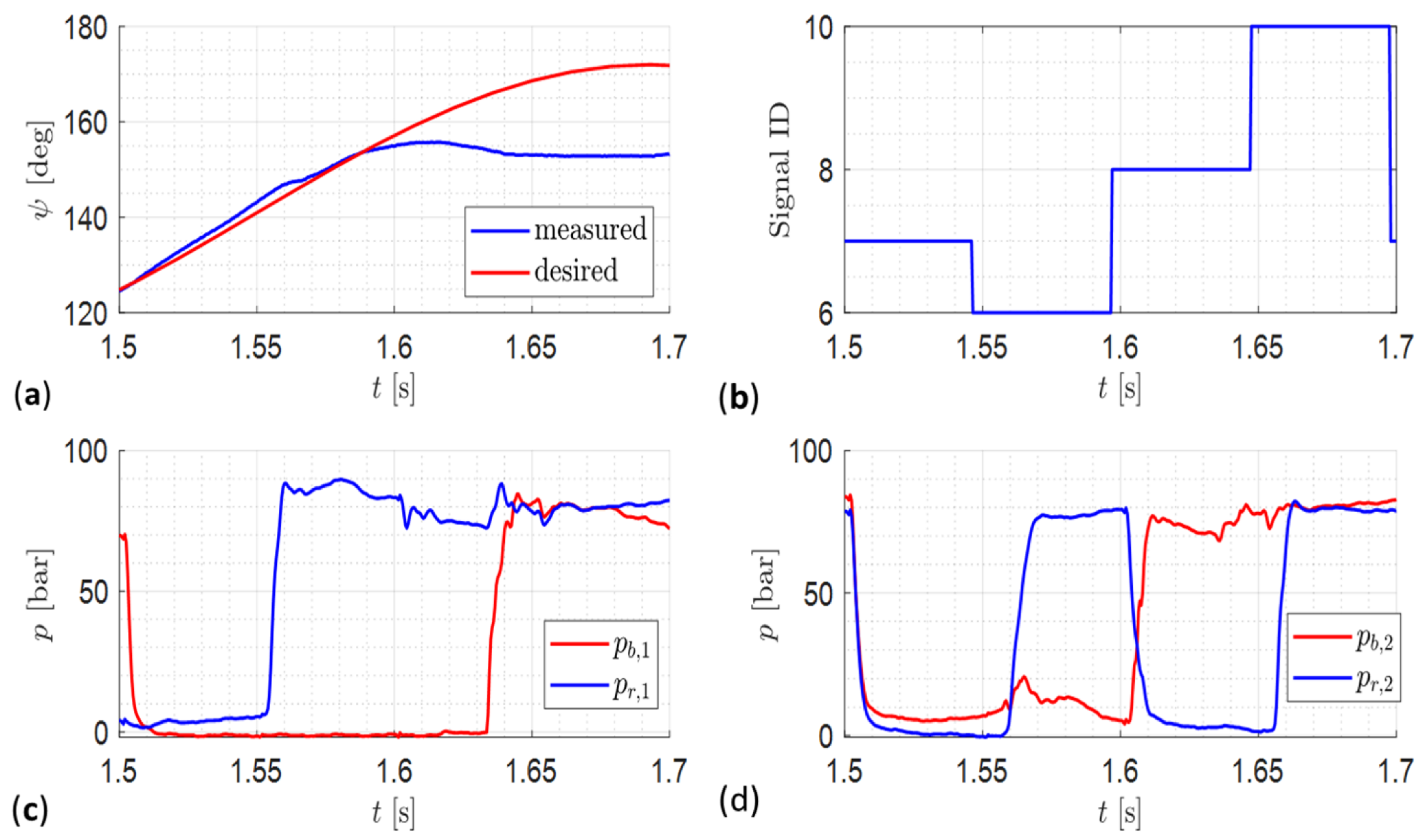
6.3. Test Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Area | |
| Guide curve | |
| Force | |
| Acceleration due to gravity | |
| Moment of inertia | |
| Bulk modulus of the fluid | |
| Kinetic energy of the system | |
| Length of the connecting rod | |
| Knee torque | |
| Mass | |
| P | Pressure source |
| Potential energy | |
| Flow rate | |
| Contact force at the guide curve | |
| Crank length | |
| T | Tank |
| Time | |
| Transmission ratio | |
| Valve configuration | |
| V | Volume |
| v | Valve |
| W | Work |
| w | Lateral width of the exoskeleton device |
| x, y | Coordinate positions |
| z | Piston position in the cylinder |
| Greek letters | |
| α | Angle between the connecting rod and the tangent to the guide curve |
| γ | Angle between the hydraulic cylinder rod and the tangent to the guide curve |
| Angle between the crank and the shank | |
| Yield strength | |
| Angular position of limb part | |
| Knee angle | |
| Subscripts | |
| 1,2 | Mechanism identifier |
| Actual | |
| Bore side of hydraulic cylinder | |
| Connecting rod | |
| Desired | |
| Friction | |
| Middle | |
| Measured | |
| Time step | |
| Rod side of hydraulic cylinder | |
| Source | |
| Abbreviations | |
| Effective | |
| Hydraulic |
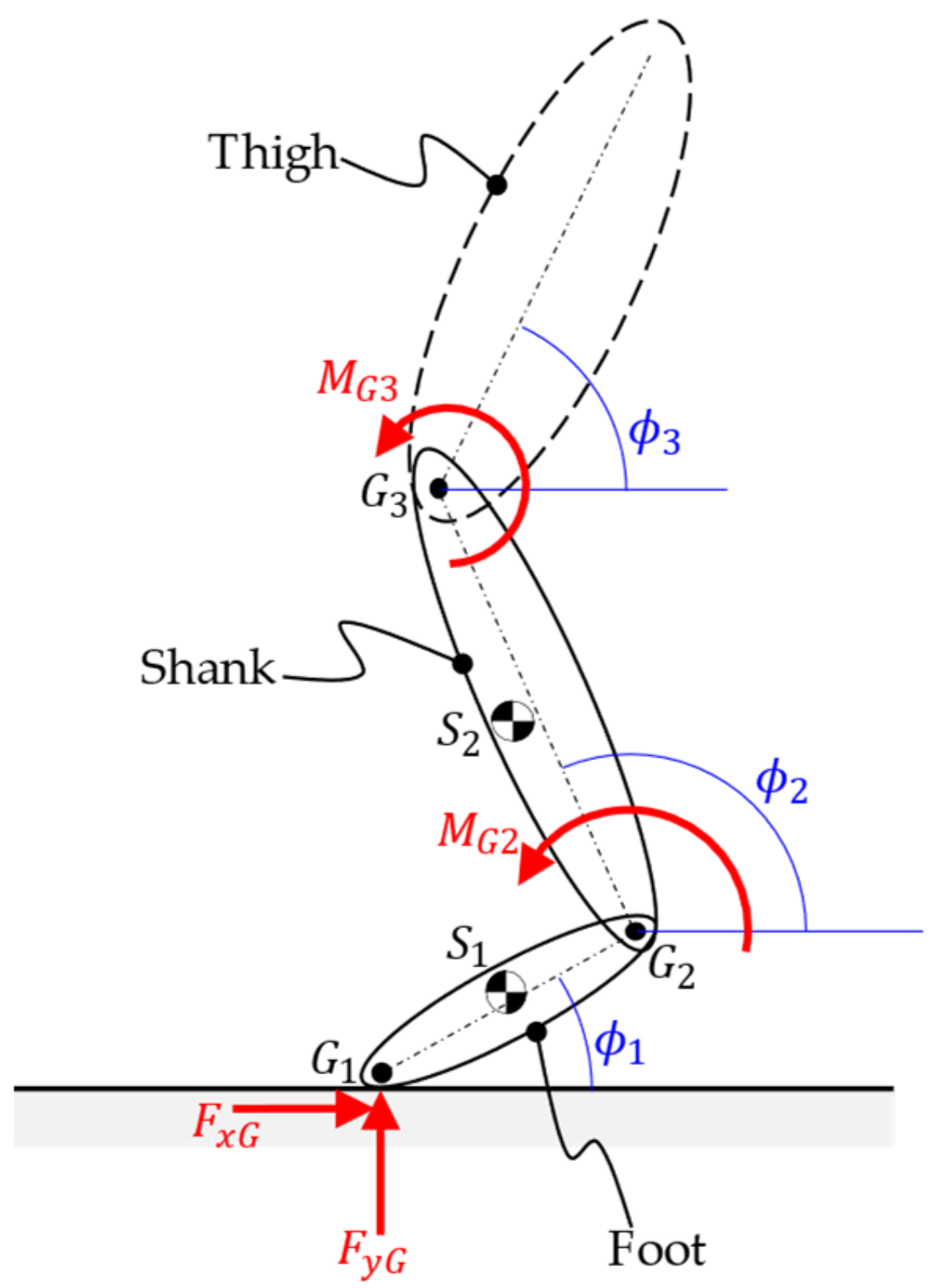
Appendix A. Mechanical Model of Lower Limb Motion
References
- Li, S.; Francisco, G.E.; Zhou, P. Post-stroke hemiplegic gait: New perspective and insights. Front. Physiol. 2018, 9, 1021. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, A.; Vreede, K.S.; Häglund, V.; Kawamoto, H.; Sankai, Y.; Borg, J. Gait training early after stroke with a new exoskeleton—The hybrid assistive limb: A study of safety and feasibility. J. NeuroEng. Rehabil. 2014, 11, 92. [Google Scholar] [CrossRef] [PubMed]
- Voilqué, A.; Masood, J.; Fauroux, J.C.; Sabourin, L.; Guezet, O. Industrial Exoskeleton Technology: Classification, Structural Analysis, and Structural Complexity Indicator. In Proceedings of the 2019 Wearable Robotics Association Conference (WearRAcon), Scottsdale, AZ, USA, 25–27 March 2019; pp. 13–20. [Google Scholar]
- Proud, J.K.; Lai, D.T.H.; Mudie, K.L.; Carstairs, G.L.; Billing, D.C.; Garofolini, A.; Begg, R.K. Exoskeleton application to military manual handling tasks. Hum. Factors 2022, 64, 527–554. [Google Scholar] [CrossRef] [PubMed]
- Osipov, A. Fire exoskeleton to facilitate the work of the fireman. E3S Web. Conf. 2019, 126, 00015. [Google Scholar] [CrossRef]
- De la Tejera, J.A.; Bustamante-Bello, R.; Ramirez-Mendoza, R.A.; Izquierdo-Reyes, J. Systematic review of exoskeletons towards a general categorization model proposal. Appl. Sci. 2021, 11, 76. [Google Scholar] [CrossRef]
- Scheidl, R. Digital Fluid Power for Exoskeleton Actuation—Guidelines, Opportunities, Challenges. In Proceedings of the Ninth Workshop on Digital Fluid Power, Aalborg, Denmark, 7–8 September 2017. [Google Scholar]
- Zoss, A.; Kazerooni, H.; Chu, A. On the Mechanical Design of the Berkeley Lower Extremity Exoskeleton (BLEEX). In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3465–3472. [Google Scholar]
- Zoss, A.B.; Kazerooni, H.; Chu, A. Biomechanical design of the Berkeley Lower Extremity Exoskeleton (BLEEX). IEEE/ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Kazerooni, H.; Racine, J.-L.; Huang, L.; Steger, R. On the Control of the Berkeley Lower Extremity Exoskeleton (BLEEX). In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 4353–4360. [Google Scholar]
- Xie, H.; Li, X.; Li, W.; Li, X. The Proceeding of the Research on Human Exoskeleton. In Advances in Intelligent Systems Research; Atlantis Press: Amsterdam, The Netherlands, 2014; pp. 754–758. [Google Scholar]
- Karlin, S. Raiding Iron Man’s Closet [Geek Life]. IEEE Spectr. 2011, 48, 25. [Google Scholar] [CrossRef]
- Huo, W.; Mohammed, S.; Moreno, J.C.; Amirat, Y. Lower limb wearable robots for assistance and rehabilitation: A state of the art. IEEE Syst. J. 2016, 10, 1068–1081. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Z.; Yao, B.; Zhu, X.; Zhu, S.; Wang, Q.; Song, Y. Adaptive robust cascade force control of 1-DOF hydraulic exoskeleton for human performance augmentation. IEEE/ASME Trans. Mechatron. 2017, 22, 589–600. [Google Scholar] [CrossRef]
- Kim, H.; Shin, Y.J.; Kim, J. Design and locomotion control of a hydraulic lower extremity exoskeleton for mobility augmentation. Mechatronics 2017, 46, 32–45. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, X.; Liu, X.; Huang, D. Robust repetitive learning-based trajectory tracking control for a leg exoskeleton driven by hybrid hydraulic system. IEEE Access 2020, 8, 27705–27714. [Google Scholar] [CrossRef]
- Chen, S.; Han, T.; Dong, F.; Lu, L.; Liu, H.; Tian, X.; Han, J. Precision interaction force control of an underactuated hydraulic stance leg exoskeleton considering the constraint from the wearer. Machines 2021, 9, 96. [Google Scholar] [CrossRef]
- Ouyang, X.; Ding, S.; Fan, B.; Li, P.Y.; Yang, H. Development of a novel compact hydraulic power unit for the exoskeleton robot. Mechatronics 2016, 38, 68–75. [Google Scholar] [CrossRef]
- Kosaki, T.; Li, S. A water-hydraulic upper-limb assistive exoskeleton system with displacement estimation. J. Robot. Mechatron. 2020, 30, 149–156. [Google Scholar] [CrossRef]
- Kaminaga, H.; Ono, J.; Nakashima, Y.; Nakamura, Y. Development of Backdrivable Hydraulic Joint Mechanism for Knee Joint of Humanoid Robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1577–1582. [Google Scholar]
- Kaminaga, H.; Amari, T.; Niwa, Y.; Nakamura, Y. Electro-Hydrostatic Actuators with Series Dissipative Property and Their Application to Power Assist Devices. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 76–81. [Google Scholar]
- Kaminaga, H.; Tanaka, H.; Nakamura, Y. Mechanism and Control of Knee Power Augmenting Device with Backdrivable Electro-Hydrostatic Actuator. In Proceedings of the 13th World Congress in Mechanism and Machine Science, Guanajuato, Mexico, 19–23 June 2011. [Google Scholar]
- Kaminaga, H.; Amari, T.; Niwa, Y.; Nakamura, Y. Development of Knee Power Assist Using Backdrivable Electro-Hydrostatic Actuator. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5517–5524. [Google Scholar]
- Tanaka, H.; Kaminaga, H.; Nakamura, Y. Pressure feedback control based on singular perturbation method of an electro-hydrostatic actuator for an exoskeletal power-assist system. J. Robot. Mechatron. 2012, 24, 354–362. [Google Scholar] [CrossRef]
- Kurosawa, H.; Walker, P.S.; Abe, S.; Garg, A.; Hunter, T. Geometry and motion of the knee for implant and orthotic design. J. Biomech. 1985, 18, 487–499. [Google Scholar] [CrossRef]
- Lee, D.; Song, B.; Park, S.Y.; Baek, Y.S. Development and control of an electro-hydraulic actuator system for an exoskeleton robot. Appl. Sci. 2019, 9, 4295. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Y.; Cao, H.; Zhu, J.; Zhang, X. A novel pump-valve coordinated controlled hydraulic system for the lower extremity exoskeleton. Trans. Inst. Meas. Control 2020, 42, 2872–2884. [Google Scholar] [CrossRef]
- Lee, T.; Lee, D.; Song, B.; Baek, Y.S. Design and control of a polycentric knee exoskeleton using an electro-hydraulic actuator. Sensors 2020, 20, 211. [Google Scholar] [CrossRef]
- Sun, M.; Ouyang, X.; Mattila, J.; Chen, Z.; Yang, H.; Liu, H. Lightweight electrohydrostatic actuator drive solution for exoskeleton robots. IEEE/ASME Trans. Mechatron. 2022, 1–12. [Google Scholar] [CrossRef]
- Scheidl, R.; Linjama, M.; Schmidt, S. Is the future of fluid power digital? Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2012, 226, 721–723. [Google Scholar] [CrossRef]
- Cao, H.; Ling, Z.; Zhu, J.; Wang, Y.; Wang, W. Design Frame of a Leg Exoskeleton for Load-Carrying Augmentation. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangxi, China, 13–19 December 2009; pp. 426–431. [Google Scholar]
- Holl, E.; Scheidl, R.; Eshkabilov, S. Simulation Study of a Digital Hydraulic Drive for a Knee Joint Exoskeleton. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 4 December 2017. [Google Scholar]
- Rituraj, R.; Scheidl, R.; Ladner, P.; Lauber, M. A Novel Design Concept of Digital Hydraulic Drive for Knee Exoskeleton. In Proceedings of the ASME/BATH 2021 Symposium on Fluid Power and Motion Control, Virtual, 13 December 2021. [Google Scholar]
- Rituraj, R.; Scheidl, R. Advancements in the Control Strategy for Digital Hydraulically Driven Knee Exoskeleton. In Proceedings of the ASME/BATH 2022 Symposium on Fluid Power and Motion Control, Bath, UK, 19 September 2022. [Google Scholar]
- HuMoD. Available online: https://www.sim.informatik.tu-darmstadt.de/res/ds/humod/ (accessed on 30 March 2022).
- Wojtusch, J.; Von Stryk, O. HuMoD—A Versatile and Open Database for the Investigation, Modeling and Simulation of Human Motion Dynamics on Actuation Level. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Republic of Korea, 3–5 November 2015; pp. 74–79. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- HAWE Micro Fluid GmbH. Available online: www.hawe.com (accessed on 22 February 2022).
- SOLIDWORKS Simulation. Available online: https://www.solidworks.com/domain/simulation (accessed on 1 June 2022).
- Igus. Available online: https://www.igus.co.uk/ (accessed on 3 July 2022).
- Iglidur. Available online: https://www.igus.co.uk/info/plain-bearings-x-material-data (accessed on 3 July 2022).
- Linjama, M.; Paloniitty, M.; Tiainen, L.; Huhtala, K. Mechatronic design of digital hydraulic micro valve package. Procedia Eng. 2015, 106, 97–107. [Google Scholar] [CrossRef]
- Megatron Kit Encoder Etx25K. Available online: https://www.megatron.de/en/products/angle-sensors/encoder-etx25k-with-3d-hall-as-kit-versions.html (accessed on 30 July 2022).
- Autosen AP019 Pressure Sensor. Available online: https://autosen.com/en/Process-Sensors/Pressure-sensors/Electronic-pressure-sensor-G1-4M-AP019 (accessed on 7 August 2022).
- B&R X20 System. Available online: https://www.br-automation.com/en/products/plc-systems/x20-system/ (accessed on 7 August 2022).
- Yang, J.; He, Y.; Shi, P.; Yu, H. A review on human intent understanding and compliance control strategies for lower limb exoskeletons. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2022, 236, 1067–1086. [Google Scholar] [CrossRef]




| 20 | 20 | 20 | 180 | 30 | 130 | 30 | 0 | 30 | ||
| 60 | 60 | 60 | 60 | 350 | 40 | 300 | 40 | 80 | 190 |
| 38.9 | 29.6 | 48.7 | 30.2 | 281.7 | 31.3 | 210.0 | 30.0 | 55.4 | 174.2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| Sensor | Model | Accuracy | Measuring Range | Resolution |
|---|---|---|---|---|
| Angle sensor | Megatron ETx25K | |||
| Pressure sensor | Autosen AP019 | bar | - |
| Error Statistics | (a) | (b) | (c) | (d) |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rituraj, R.; Scheidl, R.; Ladner, P.; Lauber, M.; Plöckinger, A. Prototyping and Experimental Investigation of Digital Hydraulically Driven Knee Exoskeleton. Energies 2022, 15, 8695. https://doi.org/10.3390/en15228695
Rituraj R, Scheidl R, Ladner P, Lauber M, Plöckinger A. Prototyping and Experimental Investigation of Digital Hydraulically Driven Knee Exoskeleton. Energies. 2022; 15(22):8695. https://doi.org/10.3390/en15228695
Chicago/Turabian StyleRituraj, Rituraj, Rudolf Scheidl, Peter Ladner, Martin Lauber, and Andreas Plöckinger. 2022. "Prototyping and Experimental Investigation of Digital Hydraulically Driven Knee Exoskeleton" Energies 15, no. 22: 8695. https://doi.org/10.3390/en15228695
APA StyleRituraj, R., Scheidl, R., Ladner, P., Lauber, M., & Plöckinger, A. (2022). Prototyping and Experimental Investigation of Digital Hydraulically Driven Knee Exoskeleton. Energies, 15(22), 8695. https://doi.org/10.3390/en15228695








