Microgrid Energy Management and Methods for Managing Forecast Uncertainties
Abstract
1. Introduction
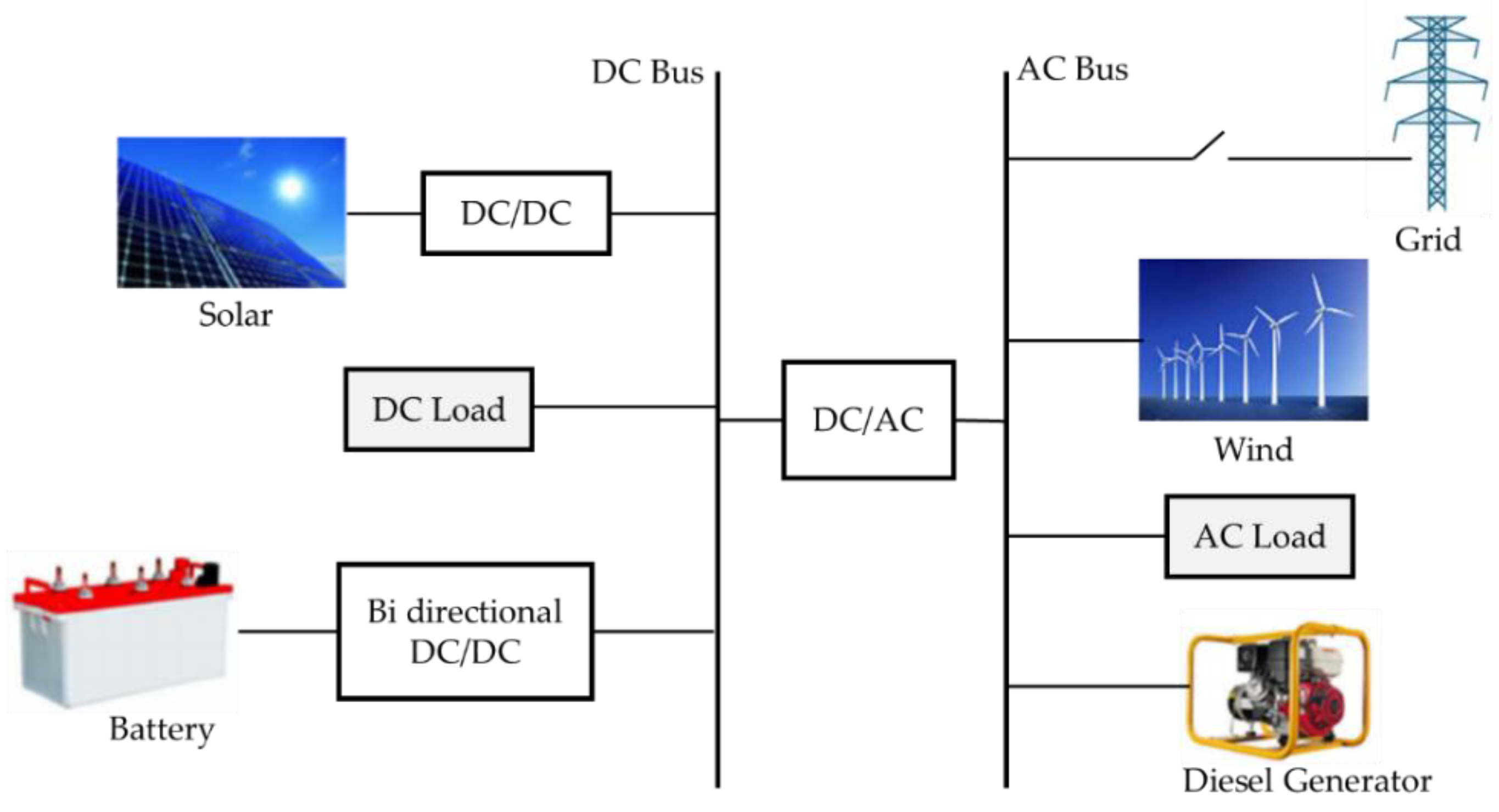
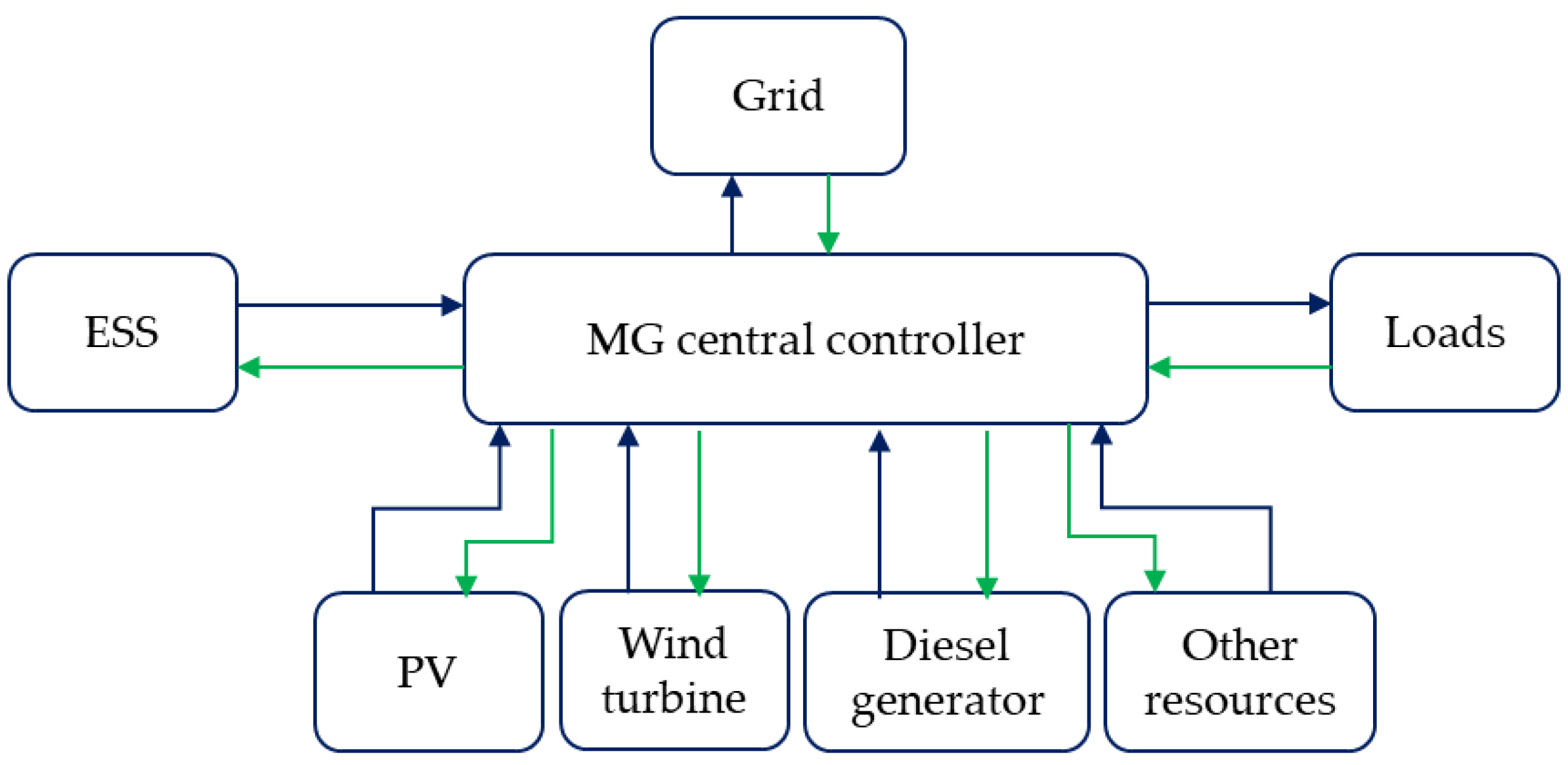
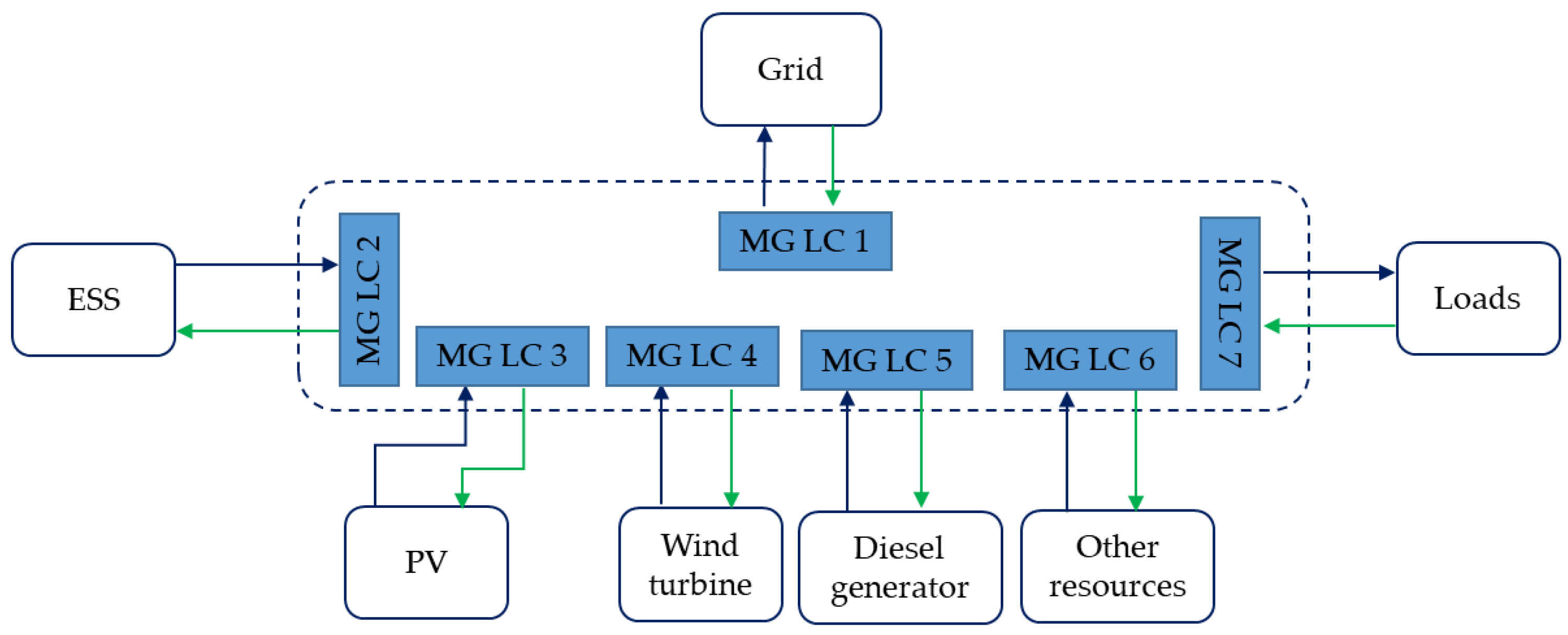
2. Microgrid Energy Management System (MG EMS): The Concept
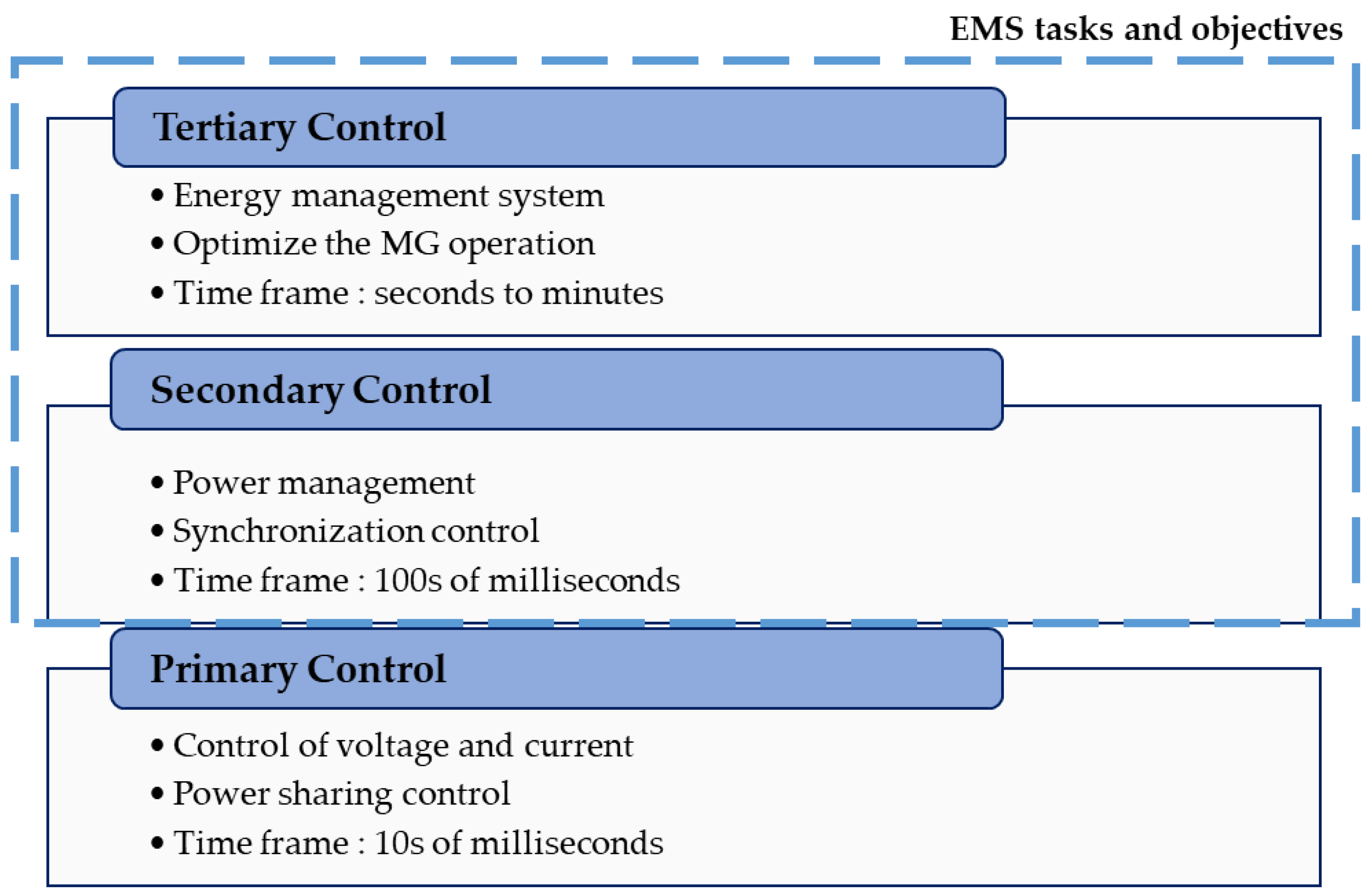
Control Systems Used in EMS
3. Microgrid Energy Management: Problem Formulation
- Operational cost = fuel cost + maintenance cost + startup cost of the thermal unit + shutdown cost of the thermal unit + cost of buying and selling power to the main grid + load shedding penalty cost + losses cost
- Environmental cost = carbon emission + penalties for emissions
- Energy storage cost = charging cost + discharging cost + degradation cost
- Constraints:
- Power balance: load demand at each time must be equal to the summation of power from microgrid resources and receiving/sending power from the main grid.
- Emission constraints: emissions caused by each fossil-fueled thermal generators cannot exceed the maximum limits at each time.
- Capacity limits: each RESs, ESS, and interconnection has a maximum and minimum capacity during the operating mode.
- Limit of ESS: charging and discharging power rates for batteries during operation mode and the operating SOC range must be limited as it may affect battery life time.
- Operating reserve: extra storage and generation capacity
- Generator start/stop limits: the number of generator starts/stops cannot exceed a certain number.
- Ramp rate power limit: the maximum power fluctuation of each unit is defined.
- System variables:
- Load profile: the demand forecast varies according to time, geographical location, season, weather, and other factors.
- PV and wind sources: the wind and PV power availability depends on wind speed forecasts and solar irradiation forecasts, respectively. Seasonal and local weather impacts these forecasts, and there is always some uncertainty associated with the forecasts.
- Electricity price: it is related to the price of the buying/selling power to the main grid. Prices may be time-sensitive.
4. Microgrid Energy Management: Solution Approaches
4.1. Mixed Integer Linear and Non-Linear Programming Methods
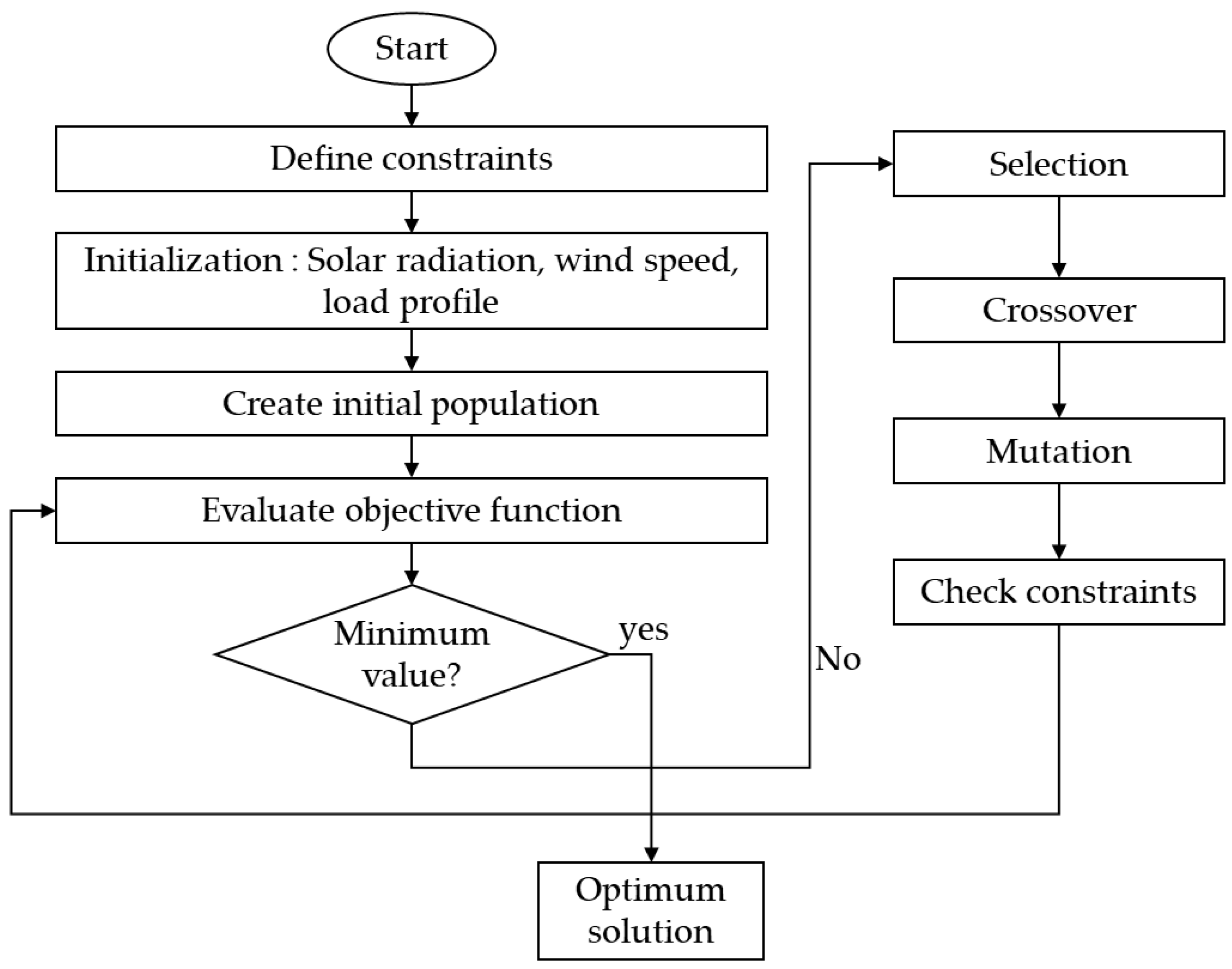
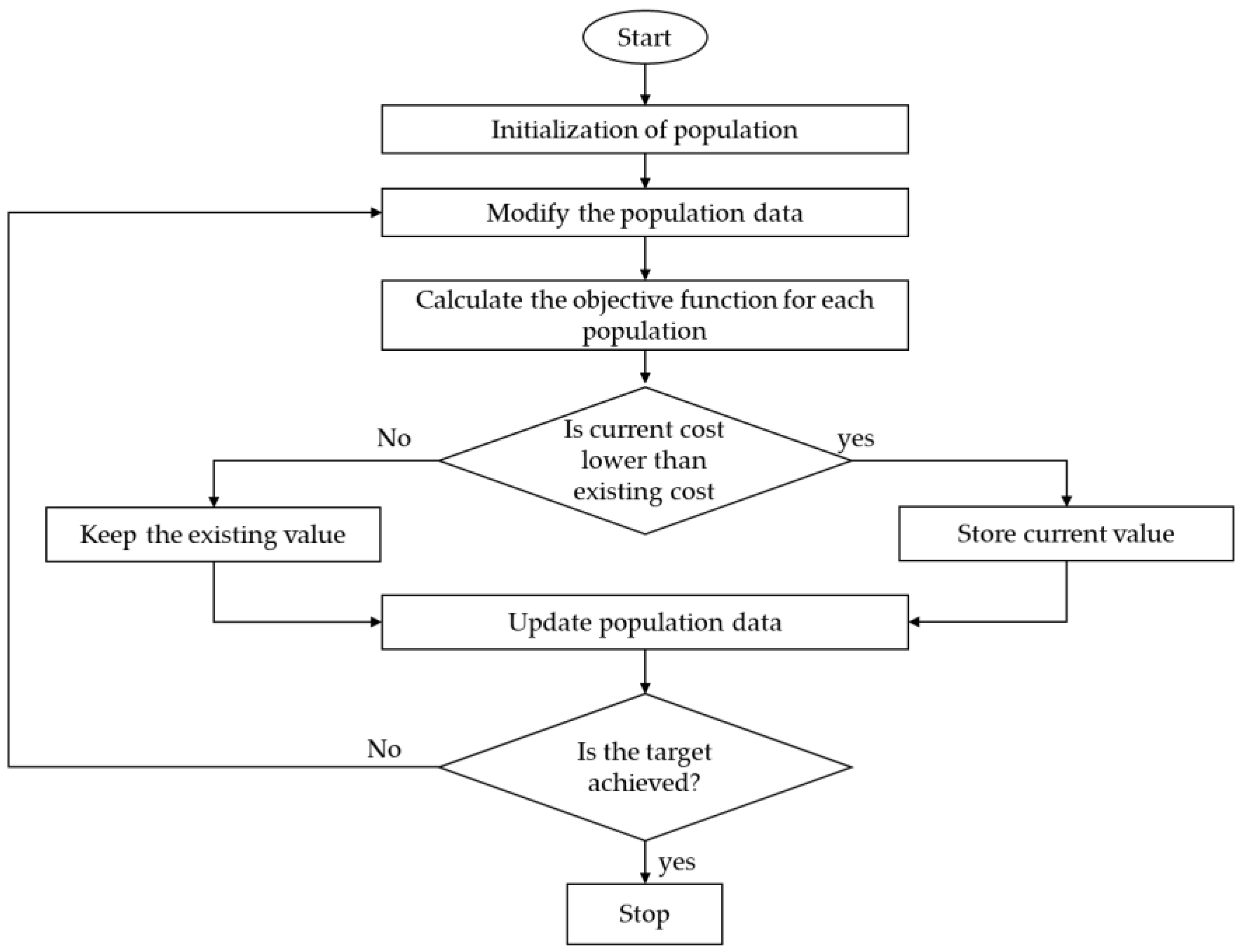
4.2. Heuristic Optimization Methods
- a.
- Genetic Algorithm
- b.
- Particle Swarm Optimization
4.3. Rule-Based Methods
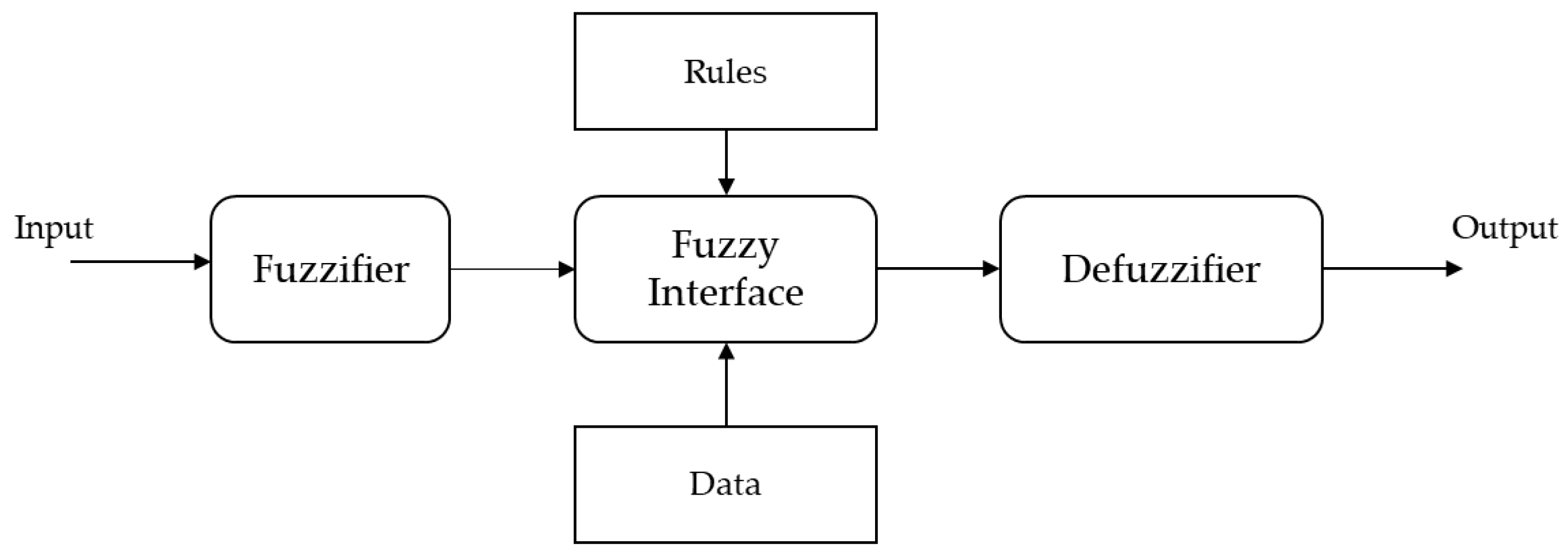
4.4. Fuzzy Logic Control Methods
5. Uncertainties in Microgrid Energy Management
- a.
- Monte Carlo Simulation (MCS)
- b.
- Worst Case Scenario Method
- c.
- Point Estimate Method (PEM)
- d.
- Fuzzy Method
- e.
- Autoregressive Moving Average
5.1. Stochastic Optimization
5.2. Robust Optimization (RO)
5.3. Chance Constrained Programming (CCP)
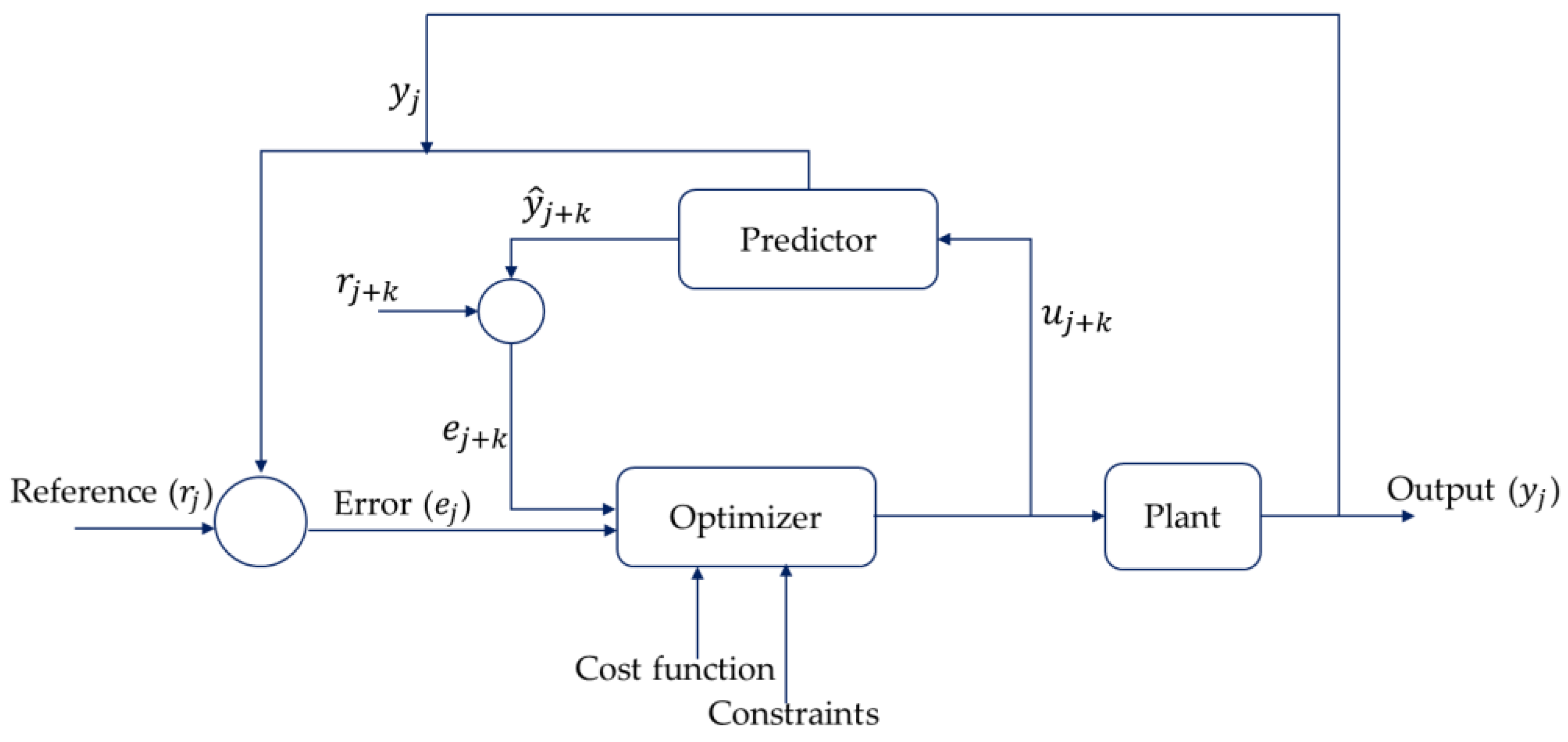
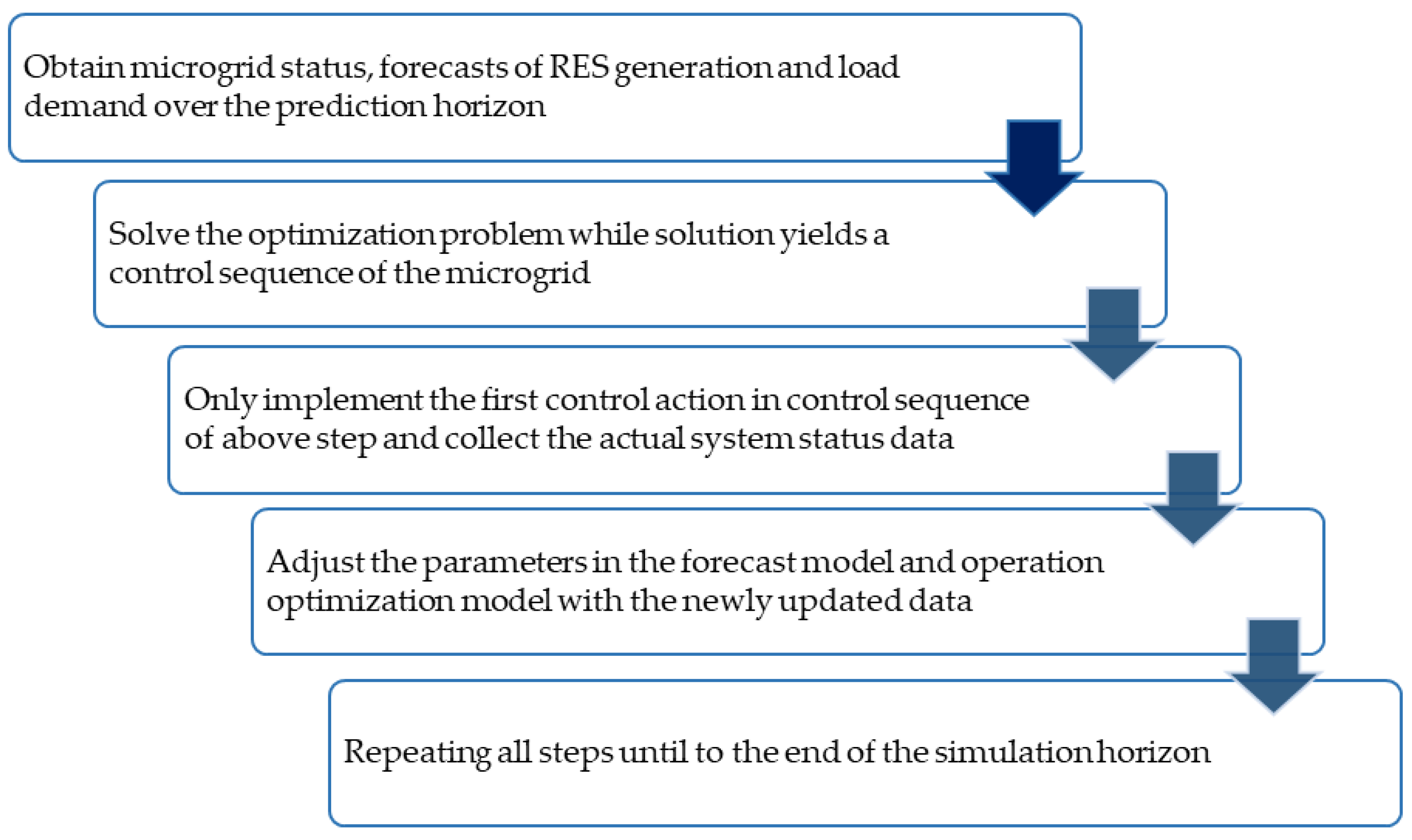
5.4. Model Predictive Control
6. Application of Artificial Intelligence and Machine Learning
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternative Current |
| AI | Artificial Intelligence |
| BESS | Battery Energy Storage System |
| CCP | Change Constrained Programming |
| DC | Direct Current |
| DER | Distributed Energy Resources |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| EV | Electric Vehicles |
| FLC | Fuzzy Logic Controller |
| GA | Generic Algorithm |
| IEC | International Electrotechnical Commission |
| MCS | Monte Carlo Simulation |
| MG | Microgrid |
| MG LC | Microgrid Local Controller |
| MG EMS | Microgrid Energy Management System |
| MILP | Mixed Integer Linear Programming |
| MINLP | Mixed Integer Non-Linear Programming |
| ML | Machine Learning |
| MPC | Model Predictive Control |
| PCC | Point of Common Coupling |
| Probability Density function | |
| PEM | Point Estimate Method |
| PI | Prediction Interval |
| PSO | Particle Swarm Optimization |
| PV | Photo Voltaic |
| RES | Renewable Energy Sources |
| RO | Robust Optimization |
| SOC | State of Charge |
| SOWGP | Sparse Online Warped Gaussian Process |
References
- Su, W.; Yuan, Z.; Chow, M.-Y. Microgrid Planning and Operation: Solar Energy and Wind Energy. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
- Elsied, M.; Oukaour, A.; Gualous, H.; Hassan, R.; Amin, A. An Advanced Energy Management of Microgrid System Based on Genetic Algorithm. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014. [Google Scholar] [CrossRef]
- Radosavljević, J.; Jevtić, M.; Klimenta, D. Energy and Operation Management of a Microgrid Using Particle Swarm Optimization. Eng. Optim. 2015, 48, 811–830. [Google Scholar] [CrossRef]
- Chen, Y.-K.; Wu, Y.-C.; Song, C.-C.; Chen, Y.-S. Design and Implementation of Energy Management System With Fuzzy Control for DC Microgrid Systems. IEEE Trans. Power Electron. 2012, 28, 1563–1570. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Rahman, M.S.U.; Sunni, F.M.A.L. Review of Microgrid Architectures—A System of Systems Perspective. IET Renew. Power Gener. 2015, 9, 1064–1078. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids Energy Management Systems: A Critical Review on Methods, Solutions, and Prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Arunkumar, A.P.; Kuppusamy, S.; Muthusamy, S.; Pandiyan, S.; Panchal, H.; Nagaiyan, P. An Extensive Review on Energy Management System for Microgrids. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 4203–4228. [Google Scholar] [CrossRef]
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.-P.; Péra, M.-C.; Hissel, D. A Review of DC Microgrid Energy Management Systems Dedicated to Residential Applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; Kamoun, N.E.; Khaidar, M.; Zine-Dine, K. Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 2020, 14, 168. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shahryari, E.; Moradzadeh, M.; Siano, P. A Survey on Microgrid Energy Management Considering Flexible Energy Sources. Energies 2019, 12, 2156. [Google Scholar] [CrossRef]
- Kumar, K.P.; Saravanan, B. Recent Techniques to Model Uncertainties in Power Generation from Renewable Energy Sources and Loads in Microgrids—A Review. Renew. Sustain. Energy Rev. 2017, 71, 348–358. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Apolinario, G.F.D. Uncertainty in Unit Commitment in Power Systems: A Review of Models, Methods, and Applications. Energies 2021, 14, 6658. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A Comprehensive Review on Uncertainty Modeling Techniques in Power System Studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Soroudi, A.; Amraee, T. Decision Making under Uncertainty in Energy Systems: State of the Art. Renew. Sustain. Energy Rev. 2013, 28, 376–384. [Google Scholar] [CrossRef]
- Meng, L.; Sanseverino, E.R.; Luna, A.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Microgrid Supervisory Controllers and Energy Management Systems: A Literature Review. Renew. Sustain. Energy Rev. 2016, 60, 1263–1273. [Google Scholar] [CrossRef]
- Lefort, A.; Bourdais, R.; Ansanay-Alex, G.; Guéguen, H. Hierarchical Control Method Applied to Energy Management of a Residential House. Energy Build. 2013, 64, 53–61. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.; de Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Kaluthanthrige, R.; Rajapakse, A. Demand Response Integrated Day-Ahead Energy Management Strategy for Remote off-Grid Hybrid Renewable Energy Systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106731. [Google Scholar] [CrossRef]
- Haider, Z.M.; Mehmood, K.K.; Khan, S.U.; Khan, M.O.; Wadood, A.; Rhee, S.-B. Optimal Management of a Distribution Feeder During Contingency and Overload Conditions by Harnessing the Flexibility of Smart Loads. IEEE Access 2021, 9, 40124–40139. [Google Scholar] [CrossRef]
- Zaree, N.; Vahidinasab, V. An MILP Formulation for Centralized Energy Management Strategy of Microgrids. In Proceedings of the Smart Grids Conference (SGC), Kerman, Iran, 21–22 December 2016. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-Economic Optimization of Hybrid Photovoltaic/Wind Generation Together with Energy Storage System in a Stand-Alone Micro-Grid Subjected to Demand Response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Tenfen, D.; Finardi, E.C. A Mixed Integer Linear Programming Model for the Energy Management Problem of Microgrids. Electr. Power Syst. Res. 2015, 122, 19–28. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Thesiya, D.K.; Esmat, A.; Jangir, P. A Multiple Environment Dispatch Problem Solution Using Ant Colony Optimization for Microgrids. In Proceedings of the International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12–14 August 2015. [Google Scholar] [CrossRef]
- Tran, H.G.; Thao, N.G.M.; TonThat, L. Energy Management and Optimization Method Based on Lagrange Multiplier for Microgrid with Considerations of Electricity Price and Vehicle. In Proceedings of the 10th Global Conference on Consumer Electronics (GCCE), Kyoto, Japan, 12–15 October 2021. [Google Scholar] [CrossRef]
- Papari, B.; Edrington, C.S.; Vu, T.V.; Diaz-Franco, F. A Heuristic Method for Optimal Energy Management of DC Microgrid. In Proceedings of the IEEE Second International Conference on DC Microgrids (ICDCM), Nuremburg, Germany, 27–29 June 2017. [Google Scholar] [CrossRef]
- Angelim, J.H.; Affonso, C.M. Energy Management on University Campus with Photovoltaic Generation and BESS Using Simulated Annealing. In Proceedings of the IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018. [Google Scholar] [CrossRef]
- Provata, E. Development of Optimization Algorithms for a Smart Grid Community. Master’s Thesis, Technical University of Crete, Chania, Greece, 2014. [Google Scholar]
- Grisales-Noreña, L.F.; Montoya, D.G.; Ramos-Paja, C.A. Optimal Sizing and Location of Distributed Generators Based on PBIL and PSO Techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Okhuegbe, S.N.; Mwaniki, C.; Akorede, M.F. Optimal Sizing of Hybrid Energy Systems in a Microgrid: A Review. In Proceedings of the Sustainable Research and Innovation Conference, Nairobi, Kenya, 5–6 October 2022. [Google Scholar]
- Bukar, A.L.; Tan, C.W.; Yiew, L.K.; Ayop, R.; Tan, W.-S. A Rule-Based Energy Management Scheme for Long-Term Optimal Capacity Planning of Grid-Independent Microgrid Optimized by Multi-Objective Grasshopper Optimization Algorithm. Energy Convers. Manag. 2020, 221, 113161. [Google Scholar] [CrossRef] [PubMed]
- Moghimi, M.; Leskarac, D.; Bennett, C.; Lu, J.; Stegen, S. Rule-Based Energy Management System in an Experimental Microgrid with the Presence of Time of Use Tariffs. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 70. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Optimal Energy Management System for Stand-Alone Wind Turbine/Photovoltaic/Hydrogen/Battery Hybrid System with Supervisory Control Based on Fuzzy Logic. Int. J. Hydrog. Energy 2013, 38, 14146–14158. [Google Scholar] [CrossRef]
- Aviles, D.A.; Pascual, J.; Marroyo, L.; Sanchis, P.; Guinjoan, F.; Marietta, M.P. Optimal Fuzzy Logic EMS Design for Residential Grid-Connected Microgrid with Hybrid Renewable Generation and Storage. In Proceedings of the IEEE 24th International Symposium on Industrial Electronics (ISIE), Rio de Janeiro, Brazil, 3–5 June 2015. [Google Scholar] [CrossRef]
- Santis, E.D.; Rizzi, A.; Sadeghian, A. Hierarchical Genetic Optimization of a Fuzzy Logic System for Energy Flows Management in Microgrids. Appl. Soft Comput. 2017, 60, 135–149. [Google Scholar] [CrossRef]
- Battula, A.R.; Vuddanti, S.; Salkuti, S.R. Review of Energy Management System Approaches in Microgrids. Energies 2021, 14, 5459. [Google Scholar] [CrossRef]
- Jirdehi, M.A.; Tabar, V.S.; Ghassemzadeh, S.; Tohidi, S. Different Aspects of Microgrid Management: A Comprehensive Review. J. Energy Storage 2020, 30, 101457. [Google Scholar] [CrossRef]
- Alavi, S.A.; Ahmadian, A.; Aliakbar-Golkar, M. Optimal Probabilistic Energy Management in a Typical Micro-Grid Based-on Robust Optimization and Point Estimate Method. Energy Convers. Manag. 2015, 95, 314–325. [Google Scholar] [CrossRef]
- Xiao, F.; Ai, Q. New Modeling Framework Considering Economy, Uncertainty, and Security for Estimating the Dynamic Interchange Capability of Multi-Microgrids. Electr. Power Syst. Res. 2017, 152, 237–248. [Google Scholar] [CrossRef]
- Soares, J.; Ghazvini, M.A.; Vale, Z.; Oliveira, P.B.d.M. A Multi-Objective Model for the Day-Ahead Energy Resource Scheduling of a Smart Grid with High Penetration of Sensitive Loads. Appl. Energy 2016, 162, 1074–1088. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Gao, L. Stochastic Energy Scheduling in Microgrids Considering the Uncertainties in Both Supply and Demand. IEEE Syst. J. 2018, 12, 2589–2600. [Google Scholar] [CrossRef]
- Karimi, H.; Jadid, S. Optimal Energy Management for Multi-Microgrid Considering Demand Response Programs: A Stochastic Multi-Objective Framework. Energy 2020, 195, 116992. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids With High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Pippia, T.; Schutter, B.D.; Dotoli, M. Robust Optimal Control for Demand Side Management of Multi-Carrier Microgrids. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1338–1351. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, H. Two-Stage Stochastic Programming Based Model Predictive Control Strategy for Microgrid Energy Management under Uncertainties. In Proceedings of the International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, Z. Comparison of Scenario-Based and Interval Optimization Approaches to Stochastic SCUC. IEEE Trans. Power Syst. 2012, 27, 913–921. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, Z.; Liu, X. Security Constrained Unit Commitment with Extreme Wind Scenarios. J. Mod. Power Syst. Clean Energy 2020, 8, 464–472. [Google Scholar] [CrossRef]
- Luo, L.; Abdulkareem, S.; Rezvani, A.; RezaMiveh, M.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal Scheduling of a Renewable Based Microgrid Considering Photovoltaic System and Battery Energy Storage under Uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.Y.; Ma, J. Robust Operation of Microgrids via Two-Stage Coordinated Energy Storage and Direct Load Control. IEEE Trans. Power Syst. 2017, 32, 2858–2868. [Google Scholar] [CrossRef]
- Duan, Q.; Sheng, W.; Wang, H.; Zhao, C.; Ma, C. A Two-Stage Robust Optimization Method Based on the Expected Scenario for Islanded Microgrid Energy Management. Discret. Dyn. Nat. Soc. 2021, 2021, 7079296. [Google Scholar] [CrossRef]
- Liu, J.; Chen, H.; Zhang, W.; Yurkovich, B.; Rizzoni, G. Energy Management Problems Under Uncertainties for Grid-Connected Microgrids: A Chance Constrained Programming Approach. IEEE Trans. Smart Grid 2017, 8, 2585–2596. [Google Scholar] [CrossRef]
- Prodan, I.; Zio, E. A Model Predictive Control Framework for Reliable Microgrid Energy Management. Int. J. Electr. Power Energy Syst. 2014, 61, 399–409. [Google Scholar] [CrossRef]
- Bordons, C.; Teno, G.; Marquez, J.J.; Ridao, M.A. Effect of the Integration of Disturbances Prediction in Energy Management Systems for Microgrids. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model Predictive Control of Microgrids—An Overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Raveendran Nair, U.; Costa-Castelló, R. A Model Predictive Control-Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Patiño, J.; Márquez, A.; Espinosa, J. An Economic MPC Approach for a Microgrid Energy Management System. In Proceedings of the IEEE PES Transmission & Distribution Conference and Exposition-Latin America (PES T&D-LA), Medellin, Colombia, 10–13 September 2014. [Google Scholar] [CrossRef]
- Pereira, M.; Limon, D.; Peña, D.M.; de la Valverde, L.; Alamo, T. Periodic Economic Control of a Nonisolated Microgrid. IEEE Trans. Ind. Electron. 2015, 62, 5247–5255. [Google Scholar] [CrossRef]
- Mechleri, E.; Dorneanu, B.; Arellano-Garcia, H. A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids. Energies 2022, 3, 100–115. [Google Scholar] [CrossRef]
- Incremona, G.P.; Cucuzzella, M.; Magni, L.; Ferrara, A. MPC with Sliding Mode Control for the Energy Management System of Microgrids. IFAC Pap. 2017, 50, 7397–7402. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Wang, R.; Liu, Y.; Guo, B. Optimal Operation of a Smart Residential Microgrid Based on Model Predictive Control by Considering Uncertainties and Storage Impacts. Sol. Energy 2015, 122, 1052–1065. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Tan, R. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control. Syst. Technol. 2017, 26, 1028–1039. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; Muñoz de la Peña, D.; Liu, J. Distributed Model Predictive Control: A Tutorial Review and Future Research Directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. A Distributed Control Algorithm for Waterfilling of Networked Control Systems via Consensus. IEEE Control. Syst. Lett. 2017, 1, 334–339. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized Charging Control of Large Populations of Plug-in Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2013, 21, 67–78. [Google Scholar] [CrossRef]
- Cominesi, S.R.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A Two-Layer Stochastic Model Predictive Control Scheme for Microgrids. IEEE Trans. Control. Syst. Technol. 2017, 26, 1–13. [Google Scholar] [CrossRef]
- Hu, M.C.; Lu, S.Y.; Chen, Y.H. Stochastic Programming and Market Equilibrium Analysis of Microgrids Energy Management Systems. Energy 2016, 113, 662–670. [Google Scholar] [CrossRef]
- Elkazaz, M.; Sumner, M.; Thomas, D. Energy Management System for Hybrid PV-Wind-Battery Microgrid Using Convex Programming, Model Predictive and Rolling Horizon Predictive Control with Experimental Validation. Int. J. Electr. Power Energy Syst. 2020, 115, 105483. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Ruiz, C.; Li, Y.-F.; Zio, E. Analysis of Robust Optimization for Decentralized Microgrid Energy Management under Uncertainty. Int. J. Electr. Power Energy Syst. 2015, 64, 815–832. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Xie, X. Robust Optimization for Dynamic Economic Dispatch Under Wind Power Uncertainty With Different Levels of Uncertainty Budget. IEEE Access 2016, 4, 7633–7644. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust Optimization of Microgrid Based on Renewable Distributed Power Generation and Load Demand Uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Trigkas, D.; Gravanis, G.; Diamantaras, K.; Voutetakis, S.; Papadopoulou, S. Energy Management in Microgrids Using Model Predictive Control Empowered with Artificial Intelligence. Chem. Eng. Trans. 2022, 94, 961–966. [Google Scholar] [CrossRef]
- Feng, C.; Cui, M.; Hodge, B.-M.; Zhang, J. A Data-Driven Multi-Model Methodology with Deep Feature Selection for Short-Term Wind Forecasting. Appl. Energy 2017, 190, 1245–1257. [Google Scholar] [CrossRef]


| Features | Advantages | Disadvantages | |
|---|---|---|---|
| Centralized control | Centralized control has complete knowledge of the entire system and is in charge of ensuring its optimal operation. | It provides wide control over the entire system. Established control approach. Simple architecture. Easy to implement and maintain. It ensures optimal decision. | It requires a high performance computing unit and communication network. The failure of central control could cause the entire system to fail. Computational complexity is high. Low flexibility. |
| Decentralized control | Functions provided by centralized control are realized in a decentralized way. Local decisions contribute to achieving the goal. | It does not require a high performance computing unit and a high-level connectivity. Easy realization of plug-and-play functionality. | It requires an effective method to ensure corporation among local controllers. Low performance compared to centralized control due to low response time and incomplete information about the total microgrid system installation. High implementation complexity. |
| Hierarchical control Based methods | Each level provides supervisory control over lower-level systems. Three layers: tertiary, secondary, and primary control layers. The bandwidths of different control levels are separated. | Combining the centralized and decentralized controllers. Higher levels attempt to optimize the microgrid operation. Local controls regulate the voltage and current. It simplifies modelling and analysis of microgrid systems. | Proper coordination of all three layers is required. |
| Techniques | Advantages | Disadvantages |
|---|---|---|
| Mixed integer linear and non-linear programming methods | Availability of efficient software packages. Most flexible modelling. Optimal solution. | Computational complexity. |
| Generic algorithm | Possibility to use complex formulation. It can handle many objectives and constraints. Widely used in many fields. | GA is unable to ensure mathematical optimality in its output. |
| Particle swarm optimization (PSO) | It has fast convergence time. Commonly used in the sizing of distributed generators. It can handle a wide range of problems while achieving a set of goals. | PSO is unable to ensure mathematical optimality in its output. |
| Rule-based methods | The approach allows for a significant reduction in computational complexity. The method is easy to execute on various storage types once the essential rules have been established. | Solution could be a sub-optimal solution. |
| Fuzzy logic control methods | Gain more flexibility. It can be easily incorporated with other methods. | Solution could be a sub-optimal solution. High-quality processing unit is required. |
| Proposed Approach | Modelling Uncertainty | Uncertainty Handling | Scalability Handling Possibility |
|---|---|---|---|
| Optimal probabilistic energy management in a typical microgrid based on robust optimization and point estimate method [37] | Uncertainties of wind, solar, and load are used. | PEM and RO are used. The data determined from PEM are used in the PSO-based energy management algorithm. RO generates and transfers the load demand scenarios to the PSO algorithm. | The proposed algorithm is used in order to perform an optimal operation on a low voltage (LV) MG, including renewables and conventional DGs, as well as a battery bank. |
| Two-stage stochastic programming based MPC strategy for microgrid energy management under uncertainties [45] | Load, PV, and wind uncertainties are used. | Two stage scheduling strategy is used. The first stage makes a decision before the actual reality of the uncertainty becomes available, and the second stage makes a correction decision to compensate for infeasibilities from the first stage. | The proposed method combines the advantages of both two-stage SP and MPC. |
| A two-stage robust optimization method based on the expected scenario for islanded microgrid energy management [50] | Uncertainties of wind, solar, and load are considered. | Two stage scheduling strategy is used. Prescheduling stage and rescheduling stage are applied to reduce the impact of uncertain factors. | To manage various constraints during the optimization process and ensure the feasibility of individuals in the evolving population, a constraint-handling technique is developed. |
| Optimal operation of a smart residential microgrid based on model predictive control by considering uncertainties and storage impacts [59] | Uncertainties from solar, wind, load, and electricity price are used. | The MILP problem is incorporated into a MPC framework for compensating the potential disturbances. | Stochastic and distributed model predictive control techniques can be used to optimize large-scale microgrid systems. |
| Distributed MPC for grid-connected microgrid power management [60] | Uncertainty related to the availability wind and load are considered. | The MPC-based EMS is implemented under a distributed framework. Receding horizon methods are used to mitigate uncertainties. | The optimization problem is decomposed into several small-scale nonlinear continuous optimization problems and several integer programming problems. |
| A two-layer stochastic MPC scheme for microgrids [64] | Uncertainties from wind and PV are considered. | Shrinking-horizon MPC is implemented. A stochastic MPC runs at a higher frequency at the lower layer to compensate for uncertainties and maintain the energy exchange as close as to the desired value over each sampling period. | Stochastic MPC is used with high-level off-line economic optimization. |
| Stochastic programming and market equilibrium analysis of microgrid energy management systems [65] | Load, PV, and wind uncertainties are used. | Two-stage stochastic programming model is used. In the first stage, the decision for investment in microgrid devices is deter-mined, and energy management strategies are determined in the second stage. | A general algebraic modeling system is designed for solving large-scale, complex optimization problems. |
| Energy management system for hybrid PV-wind-battery microgrid using convex programming, model predictive and rolling horizon predictive control with experimental validation [66] | Uncertainties from solar, wind, load and electricity price are used. | A rolling horizon predictive controller with a MPC at the lower control layer with a one-minute sampling time reduces the impact of prediction and model uncertainties. | A rolling-horizon predictive controller does not require a complex optimization process. |
| Analysis of robust optimization for decentralized microgrid energy management under uncertainty [67] | Uncertainty related to the availability wind and load are considered. Prediction intervals are used. | The impact of different levels of uncertainty is evaluated. | Agent-based modelling (ABM) is used to describe the system, with each stakeholder modeled by an individual agent. |
| Robust optimization for dynamic economic dispatch under wind power uncertainty with different levels of uncertainty budget [68] | Wind uncertainties is used. | A robust optimization method with an adjustable uncertainty budget with different levels is proposed. | Constraint handling technique is also proposed to handle various constraints and ensure the feasibility of individuals in the evolutionary population. |
| Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty [69] | Uncertainties of wind, solar, and load are considered. | A two stage scheduling strategy is used. Robust adjustment parameters are optimized to make the microgrid have a reasonable robustness. | The robustness of grid operation is guaranteed by the proposed solution, which is more in line with technical realities and has better practical value. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinothine, S.; Widanagama Arachchige, L.N.; Rajapakse, A.D.; Kaluthanthrige, R. Microgrid Energy Management and Methods for Managing Forecast Uncertainties. Energies 2022, 15, 8525. https://doi.org/10.3390/en15228525
Vinothine S, Widanagama Arachchige LN, Rajapakse AD, Kaluthanthrige R. Microgrid Energy Management and Methods for Managing Forecast Uncertainties. Energies. 2022; 15(22):8525. https://doi.org/10.3390/en15228525
Chicago/Turabian StyleVinothine, Shanmugarajah, Lidula N. Widanagama Arachchige, Athula D. Rajapakse, and Roshani Kaluthanthrige. 2022. "Microgrid Energy Management and Methods for Managing Forecast Uncertainties" Energies 15, no. 22: 8525. https://doi.org/10.3390/en15228525
APA StyleVinothine, S., Widanagama Arachchige, L. N., Rajapakse, A. D., & Kaluthanthrige, R. (2022). Microgrid Energy Management and Methods for Managing Forecast Uncertainties. Energies, 15(22), 8525. https://doi.org/10.3390/en15228525








