Three Terminal Perovskite/Silicon Solar Cell with Bipolar Transistor Architecture
Abstract
1. Introduction
2. Structure and Operating Principle of the PVK/Si 3T-HBT Tandem
3. Methods
3.1. Device under Study
3.2. Simulation Approach and Material Models
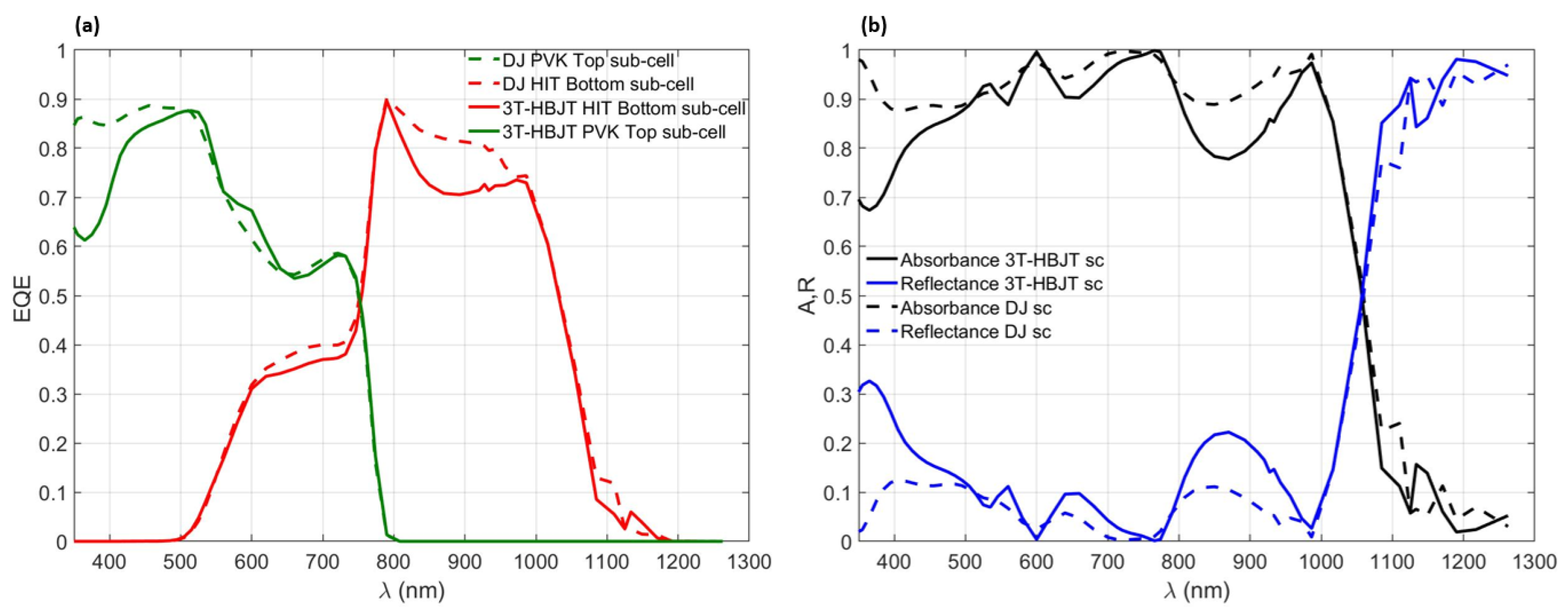
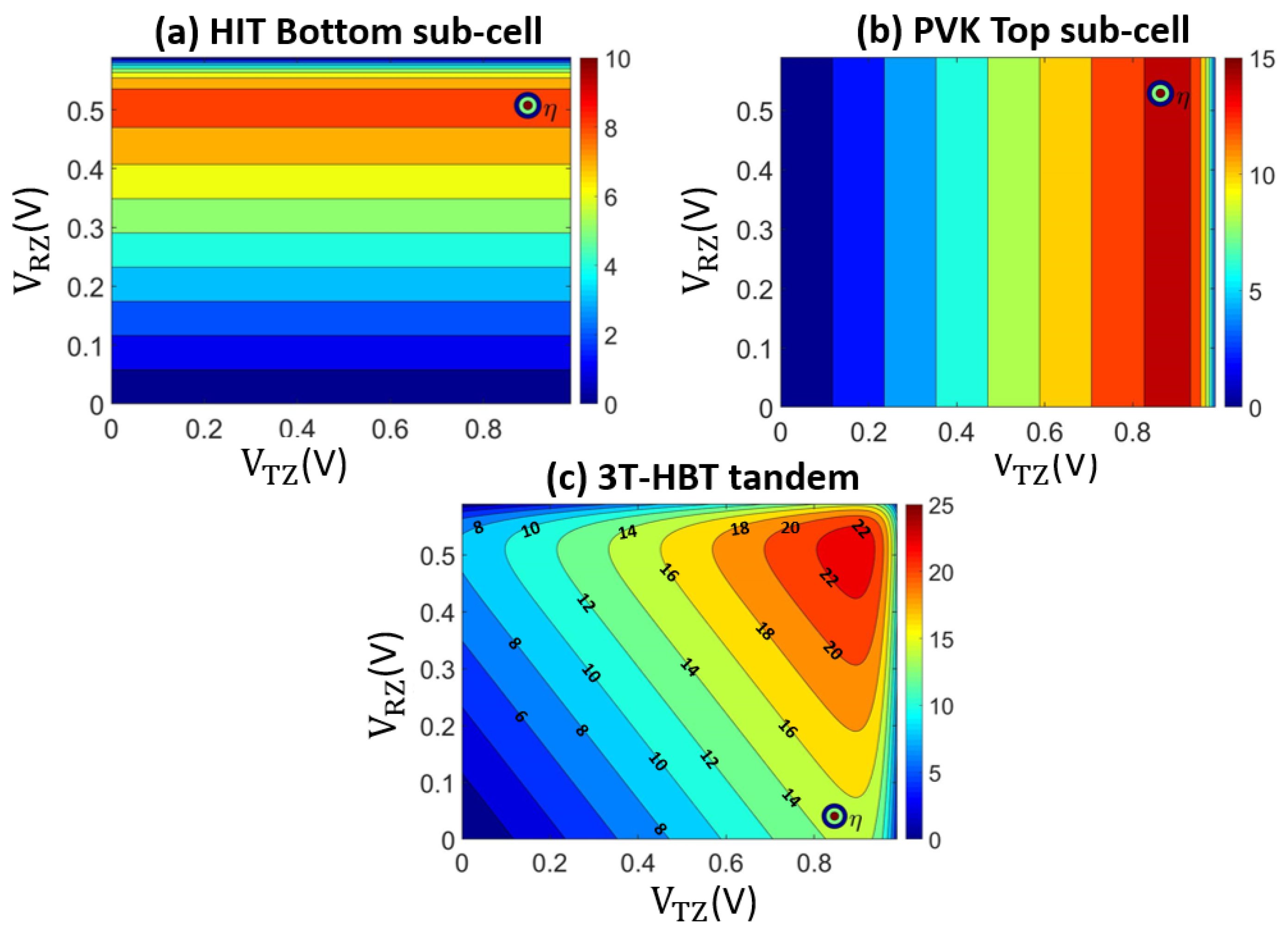
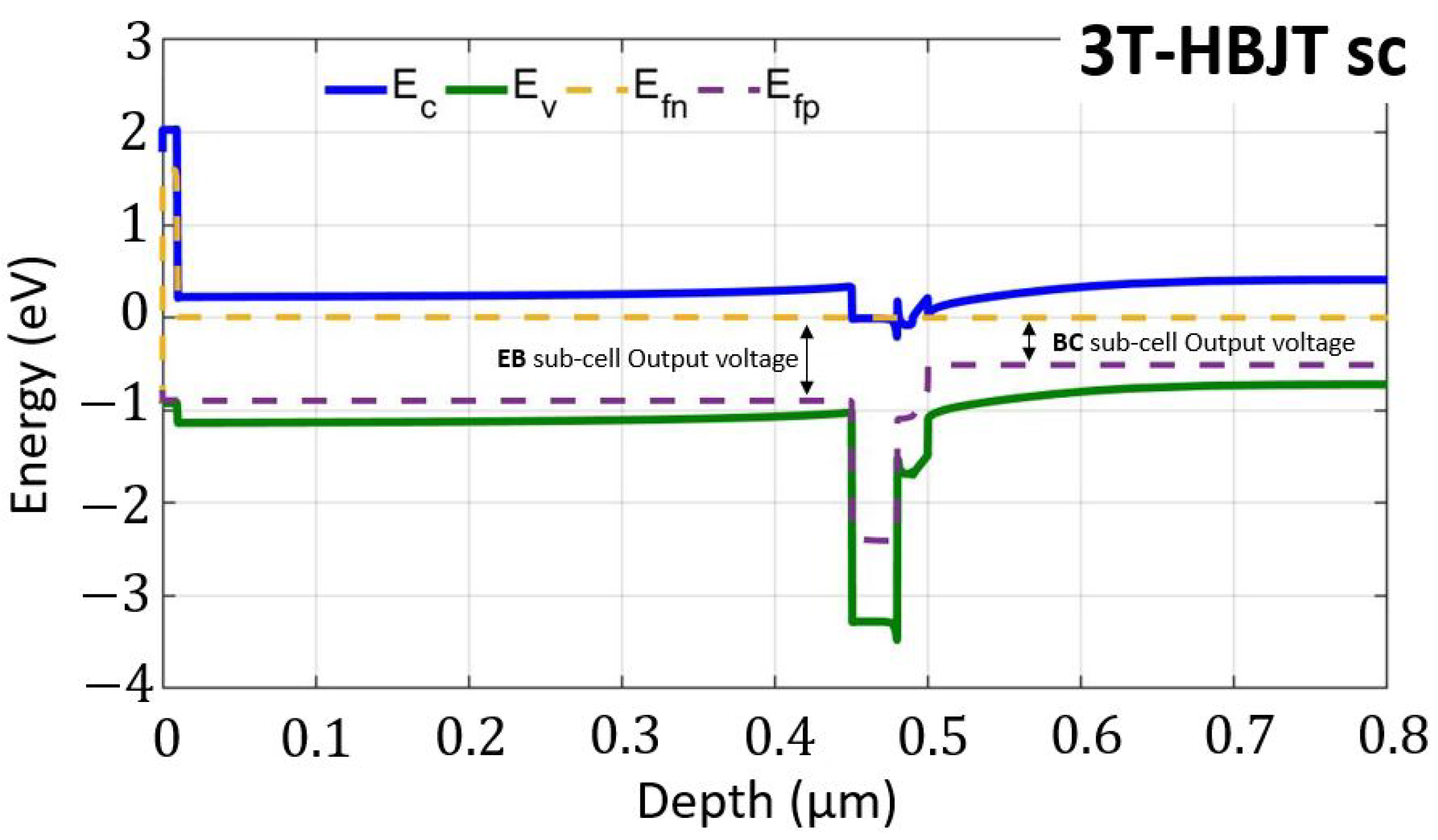
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Technology Roadmap for Photovoltaic (ITRPV), 11th ed.; 2020; Available online: https://resources.solarbusinesshub.com/solar-industry-reports/item/international-technology-roadmap-for-photovoltaic-itrpv-2019 (accessed on 1 September 2022).
- Green, M.; Dunlop, E.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. 3 Solar cell efficiency tables (version 57). Prog. Photovolt. Res. Appl. 2021, 29, 3–15. [Google Scholar] [CrossRef]
- De Vos, A. Detailed balance limit of the efficiency of tandem solar cells. J. Phys. D Appl. Phys. 1980, 13, 839. [Google Scholar] [CrossRef]
- Lal, N.N.; Dkhissi, Y.; Li, W.; Hou, Q.; Cheng, Y.B.; Bach, U. Perovskite Tandem Solar Cells. Adv. Energy Mater. 2017, 7, 1602761. [Google Scholar] [CrossRef]
- Fu, F.; Li, J.; Yang, T.C.J.; Liang, H.; Faes, A.; Jeangros, Q.; Ballif, C.; Hou, Y. Monolithic Perovskite-Silicon Tandem Solar Cells: From the Lab to Fab? Adv. Mater. 2022, 34, 2106540. [Google Scholar] [CrossRef] [PubMed]
- NREL. Best Research-Cell Efficiencies: Emerging Photovoltaics. 2022. Available online: https://www.nrel.gov/pv/assets/pdfs/cell-pv-eff-emergingpv-rev220630.pdf (accessed on 1 September 2022).
- Lee, D.K.; Park, N.G. Materials and Methods for High-Efficiency Perovskite Solar Modules. Sol. RRL 2022, 6, 2100455. [Google Scholar] [CrossRef]
- Reddy, S.H.; Di Giacomo, F.; Di Carlo, A. Low-Temperature-Processed Stable Perovskite Solar Cells and Modules: A Comprehensive Review. Adv. Energy Mater. 2022, 12, 2103534. [Google Scholar] [CrossRef]
- Huang, J.; He, S.; Zhang, W.; Saparbaev, A.; Wang, Y.; Gao, Y.; Shang, L.; Dong, G.; Nurumbetova, L.; Yue, G.; et al. Efficient and Stable All-Inorganic CsPbIBr2 Perovskite Solar Cells Enabled by Dynamic Vacuum-Assisted Low-Temperature Engineering. Sol. RRL 2022, 6, 2100839. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Kong, W.; Qiao, L.; Peng, B.; Shen, Z.; Han, Q.; Chen, H.; Yuan, Z.; Zheng, R.; et al. Transporting holes stably under iodide invasion in efficient perovskite solar cells. Science 2022, 377, 1227–1232. [Google Scholar] [CrossRef]
- Futscher, M.H.; Ehrler, B. Efficiency Limit of Perovskite/Si Tandem Solar Cells. ACS Energy Lett. 2016, 1, 863–868. [Google Scholar] [CrossRef]
- Leijtens, T.; Bush, K.A.; Prasanna, R.; McGehee, M.D. Opportunities and challenges for tandem solar cells using metal halide perovskite semiconductors. Nat. Energy 2018, 3, 828–838. [Google Scholar] [CrossRef]
- Messmer, C.; Goraya, B.S.; Nold, S.; Schulze, P.S.; Sittinger, V.; Schön, J.; Goldschmidt, J.C.; Bivour, M.; Glunz, S.W.; Hermle, M. The race for the best silicon bottom cell: Efficiency and cost evaluation of perovskite–silicon tandem solar cells. Prog. Photovolt. Res. Appl. 2021, 29, 744–759. [Google Scholar] [CrossRef]
- Sahli, F.; Kamino, B.A.; Werner, J.; Bräuninger, M.; Paviet-Salomon, B.; Barraud, L.; Monnard, R.; Seif, J.P.; Tomasi, A.; Jeangros, Q.; et al. Improved Optics in Monolithic Perovskite/Silicon Tandem Solar Cells with a Nanocrystalline Silicon Recombination Junction. Adv. Energy Mater. 2018, 8, 1701609. [Google Scholar] [CrossRef]
- Warren, E.L.; Deceglie, M.G.; Rienäcker, M.; Peibst, R.; Tamboli, A.C.; Stradins, P. Maximizing tandem solar cell power extraction using a three-terminal design. Sustain. Energy Fuels 2018, 2, 1141–1147. [Google Scholar] [CrossRef]
- Park, I.J.; Park, J.H.; Ji, S.G.; Park, M.A.; Jang, J.H.; Kim, J.Y. A three-terminal monolithic perovskite/Si tandem solar cell characterization platform. Joule 2019, 3, 807–818. [Google Scholar] [CrossRef]
- Gota, F.; Langenhorst, M.; Schmager, R.; Lehr, J.; Paetzold, U.W. Energy yield advantages of three-terminal perovskite-silicon tandem photovoltaics. Joule 2020, 4, 2387–2403. [Google Scholar] [CrossRef]
- Schulte-Huxel, H.; Friedman, D.J.; Tamboli, A.C. String-level modeling of two, three, and four terminal Si-based tandem modules. IEEE J. Photovolt. 2018, 8, 1370–1375. [Google Scholar] [CrossRef]
- Filipič, M.; Löper, P.; Niesen, B.; Wolf, S.D.; Krč, J.; Ballif, C.; Topič, M. CH3NH3PbI3 perovskite / silicon tandem solar cells: Characterization based optical simulations. Opt. Express 2015, 23, A263–A278. [Google Scholar] [CrossRef]
- Santbergen, R.; Uzu, H.; Yamamoto, K.; Zeman, M. Optimization of Three-Terminal Perovskite/Silicon Tandem Solar Cells. IEEE J. Photovolt. 2019, 9, 446–451. [Google Scholar] [CrossRef]
- Akhil, S.; Akash, S.; Pasha, A.; Kulkarni, B.; Jalalah, M.; Alsaiari, M.A.; Harraz, F.A.; Balakrishna, R.G. Review on perovskite silicon tandem solar cells: Status and prospects 2T, 3T and 4T for real world conditions. Mater. Des. 2021, 211, 110138. [Google Scholar] [CrossRef]
- Tockhorn, P.; Wagner, P.; Kegelmann, L.; Stang, J.C.; Mews, M.; Albrecht, S.; Korte, L. Three-terminal perovskite/silicon tandem solar cells with top and interdigitated rear contacts. ACS Appl. Energy Mater. 2020, 3, 1381–1392. [Google Scholar] [CrossRef]
- Martí, A.; Luque, A. Three-terminal heterojunction bipolar transistor solar cell for high-efficiency photovoltaic conversion. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Sze, S.M.; Ng, K.K. Bipolar Transistors. In Physics of Semiconductor Devices; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 241–292. [Google Scholar] [CrossRef]
- Zehender, M.H.; García, I.; Svatek, S.A.; Steiner, M.A.; García-Linares, P.; Warren, E.; Tamboli, A.; Martí, A.; Antolín, E. Demonstrating the GaInP/GaAs Three-Terminal Heterojunction Bipolar Transistor Solar Cell. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 35–40. [Google Scholar] [CrossRef]
- Antolín, E.; Zehender, M.H.; Svatek, S.A.; García-Linares, P.; Martí, A. III-V-on-silicon triple-junction based on the heterojunction bipolar transistor solar cell concept. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–1 August 2020; pp. 1226–1231. [Google Scholar] [CrossRef]
- Sahli, F.; Werner, J.; Kamino, B.A.; Bräuninger, M.; Monnard, R.; Paviet-Salomon, B.; Barraud, L.; Ding, L.; Diaz Leon, J.J.; Sacchetto, D.; et al. Fully textured monolithic perovskite/silicon tandem solar cells with 25.2% power conversion efficiency. Nat. Mater. 2018, 17, 820–826. [Google Scholar] [CrossRef] [PubMed]
- Rombach, F.M.; Haque, S.A.; Macdonald, T.J. Lessons learned from spiro-OMeTAD and PTAA in perovskite solar cells. Energy Environ. Sci. 2021, 14, 5161–5190. [Google Scholar] [CrossRef]
- Giliberti, G.; Cappelluti, F. Physical simulation of perovskite/silicon three-terminal tandems based on bipolar transistor structure. In Physics, Simulation, and Photonic Engineering of Photovoltaic Devices XI, Proceedings of the International Society for Optics and Photonics, SPIE, San Francisco, CA, USA, 22 January–28 February 2022; Freundlich, A., Collin, S., Hinzer, K., Eds.; SPIE OPTO: San Francisco, CA, USA, 2022; Volume 11996, p. 1199602. [Google Scholar] [CrossRef]
- Warren, E.L.; McMahon, W.E.; Rienäcker, M.; VanSant, K.T.; Whitehead, R.C.; Peibst, R.; Tamboli, A.C. A Taxonomy for Three-Terminal Tandem Solar Cells. ACS Energy Lett. 2020, 5, 1233–1242. [Google Scholar] [CrossRef]
- Antolín, E.; Zehender, M.H.; Svatek, S.A.; Steiner, M.A.; Martínez, M.; García, I.; García-Linares, P.; Warren, E.L.; Tamboli, A.C.; Martí, A. Progress in three-terminal heterojunction bipolar transistor solar cells. Prog. Photovolt. Res. Appl. 2022, 30, 843–850. [Google Scholar] [CrossRef]
- Giliberti, G.; Bonani, F.; Martí, A.; Cappelluti, F. Modeling of three-terminal heterojunction bipolar transistor solar cells. In Proceedings of the 2020 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Turin, Italy, 14–25 September 2020; pp. 43–44. [Google Scholar] [CrossRef]
- Olyaeefar, B.; Ahmadi-Kandjani, S.; Asgari, A. Bulk and interface recombination in planar lead halide perovskite solar cells: A Drift-Diffusion study. Phys. E-Low-Dimens. Syst. Nanostruct. 2017, 94, 118–122. [Google Scholar] [CrossRef]
- Imran, H.; Durrani, I.; Kamran, M.; Abdolkader, T.M.; Faryad, M.; Butt, N.Z. High-Performance Bifacial Perovskite/Silicon Double-Tandem Solar Cell. IEEE J. Photovolt. 2018, 8, 1222–1229. [Google Scholar] [CrossRef]
- Jošt, M.; Kegelmann, L.; Korte, L.; Albrecht, S. Monolithic Perovskite Tandem Solar Cells: A Review of the Present Status and Advanced Characterization Methods Toward 30% Efficiency. Adv. Energy Mater. 2020, 10, 1904102. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, Q.; Zhang, L.; Han, C.; Gao, H.; Zhang, Y.; Yan, H. SnO2-based electron transporting layer materials for perovskite solar cells: A review of recent progress. J. Energy Chem. 2019, 35, 144–167. [Google Scholar] [CrossRef]
- Min, H.; Lee, D.Y.; Kim, J.; Kim, G.; Lee, K.S.; Kim, J.; Paik, M.J.; Kim, Y.K.; Kim, K.S.; Kim, M.G.; et al. Perovskite solar cells with atomically coherent interlayers on SnO2 electrodes. Nature 2021, 598, 444–450. [Google Scholar] [CrossRef]
- Du, G.; Yang, L.; Zhang, C.; Zhang, X.; Rolston, N.; Luo, Z.; Zhang, J. Evaporated Undoped Spiro-OMeTAD Enables Stable Perovskite Solar Cells Exceeding 20% Efficiency. Adv. Energy Mater. 2022, 12, 2103966. [Google Scholar] [CrossRef]
- Kam, M.; Zhang, Q.; Zhang, D.; Fan, Z. Room-temperature sputtered SnO2 as robust electron transport layer for air-stable and efficient perovskite solar cells on rigid and flexible substrates. Sci. Rep. 2019, 9, 6963. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Yun, Y.J.; Kim, T.; Lee, C.; Ko, Y.; Jun, Y. Hydrolysis-Regulated Chemical Bath Deposition of Tin-Oxide-Based Electron Transport Layers for Efficient Perovskite Solar Cells with a Reduced Potential Loss. Chem. Mater. 2021, 33, 8194–8204. [Google Scholar] [CrossRef]
- Liu, A.; Nagel, S. Nonlinear dynamics: Jamming is not just cool any more. Nature 1998, 396, 21–22. [Google Scholar] [CrossRef]
- Bett, A.J.; Winkler, K.M.; Bivour, M.; Cojocaru, L.; Kabakli, O.S.; Schulze, P.S.; Siefer, G.; Tutsch, L.; Hermle, M.; Glunz, S.W.; et al. Semi-transparent perovskite solar cells with ITO directly sputtered on Spiro-OMeTAD for tandem applications. ACS Appl. Mater. Interfaces 2019, 11, 45796–45804. [Google Scholar] [CrossRef] [PubMed]
- Sentaurus Device Simulator, Synopsys Inc. 2017. Available online: https://www.synopsys.com/silicon/tcad/device-simulation/sentaurus-device.html (accessed on 1 September 2022).
- Miyano, K.; Tripathi, N.; Yanagida, M.; Shirai, Y. Lead Halide Perovskite Photovoltaic as a Model p–i–n Diode. Acc. Chem. Res. 2016, 49, 303–310. [Google Scholar] [CrossRef]
- Alnuaimi, A.; Almansouri, I.; Nayfeh, A. Effect of mobility and band structure of hole transport layer in planar heterojunction perovskite solar cells using 2D TCAD simulation. J. Comput. Electron. 2016, 15, 1110–1118. [Google Scholar] [CrossRef]
- Tao, S.; Schmidt, I.; Brocks, G.; Jiang, J.; Tranca, I.; Meerholz, K.; Olthof, S. Absolute energy level positions in tin- and lead-based halide perovskites. Nat. Commun. 2019, 10, 2560. [Google Scholar] [CrossRef]
- Giliberti, G.; Cappelluti, F. Database of Optical Parameters for the Simulation of Perovskite/Silicon Solar Cells. 2022. Available online: https://zenodo.org/record/7116993#.Y2B55eRBxPY (accessed on 27 September 2022).
- Kirchartz, T.; Staub, F.; Rau, U. Impact of Photon Recycling on the Open-Circuit Voltage of Metal Halide Perovskite Solar Cells. ACS Energy Lett. 2016, 1, 731–739. [Google Scholar] [CrossRef]
- Altazin, S.; Stepanova, L.; Werner, J.; Niesen, B.; Ballif, C.; Ruhstaller, B. Design of perovskite/crystalline-silicon monolithic tandem solar cells. Opt. Express 2018, 26, A579–A590. [Google Scholar] [CrossRef]
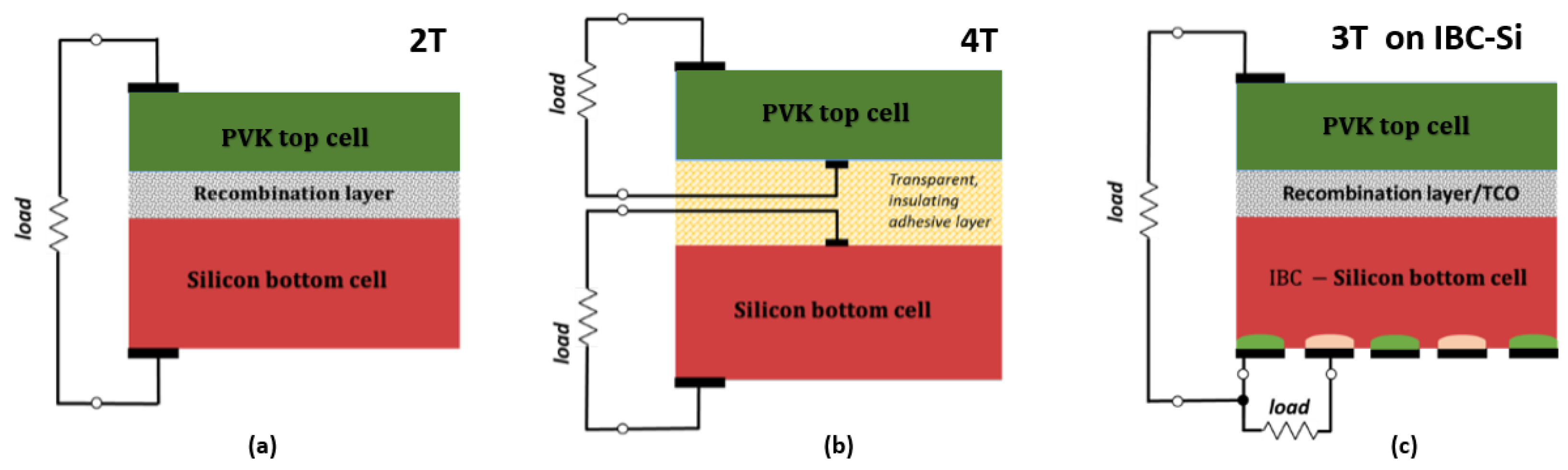

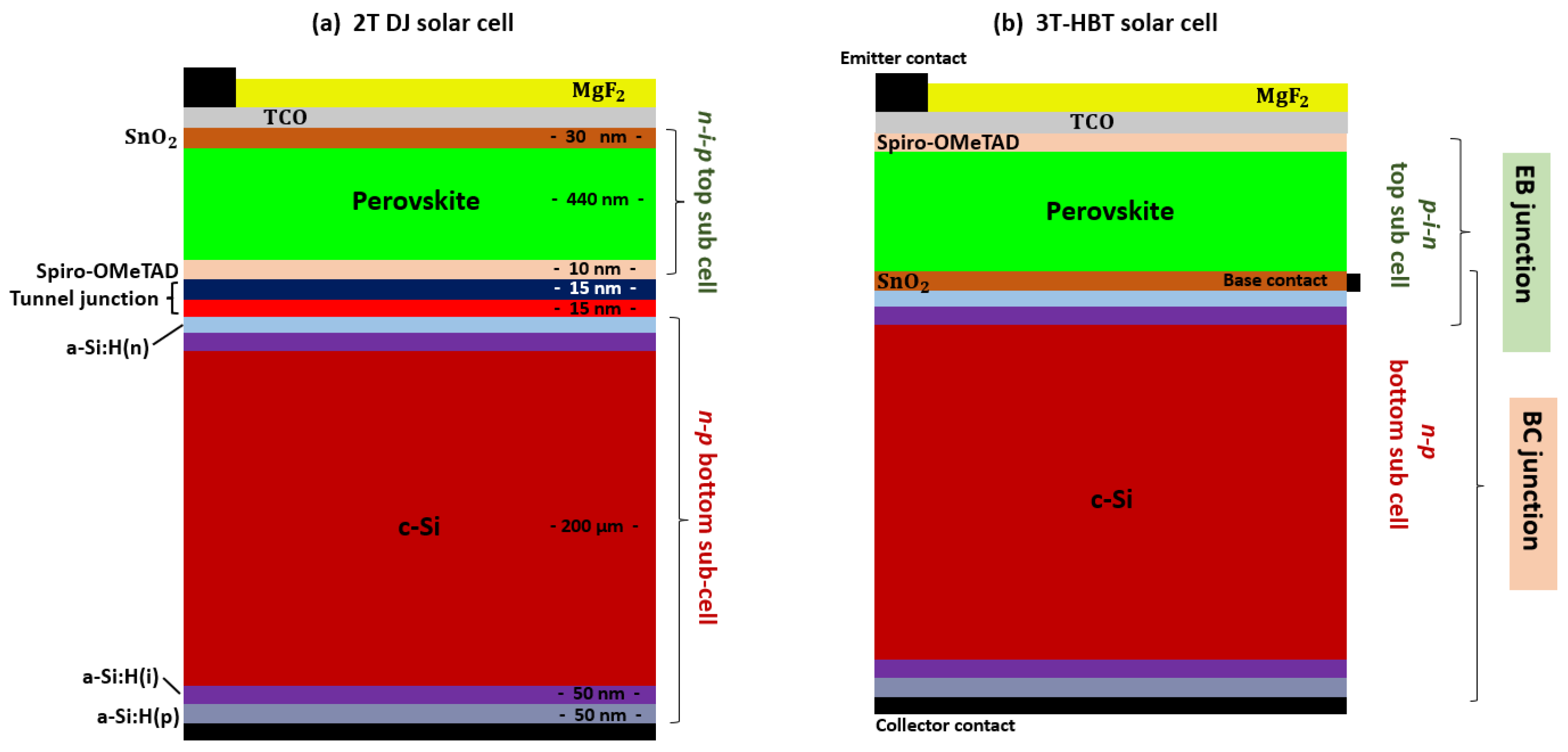
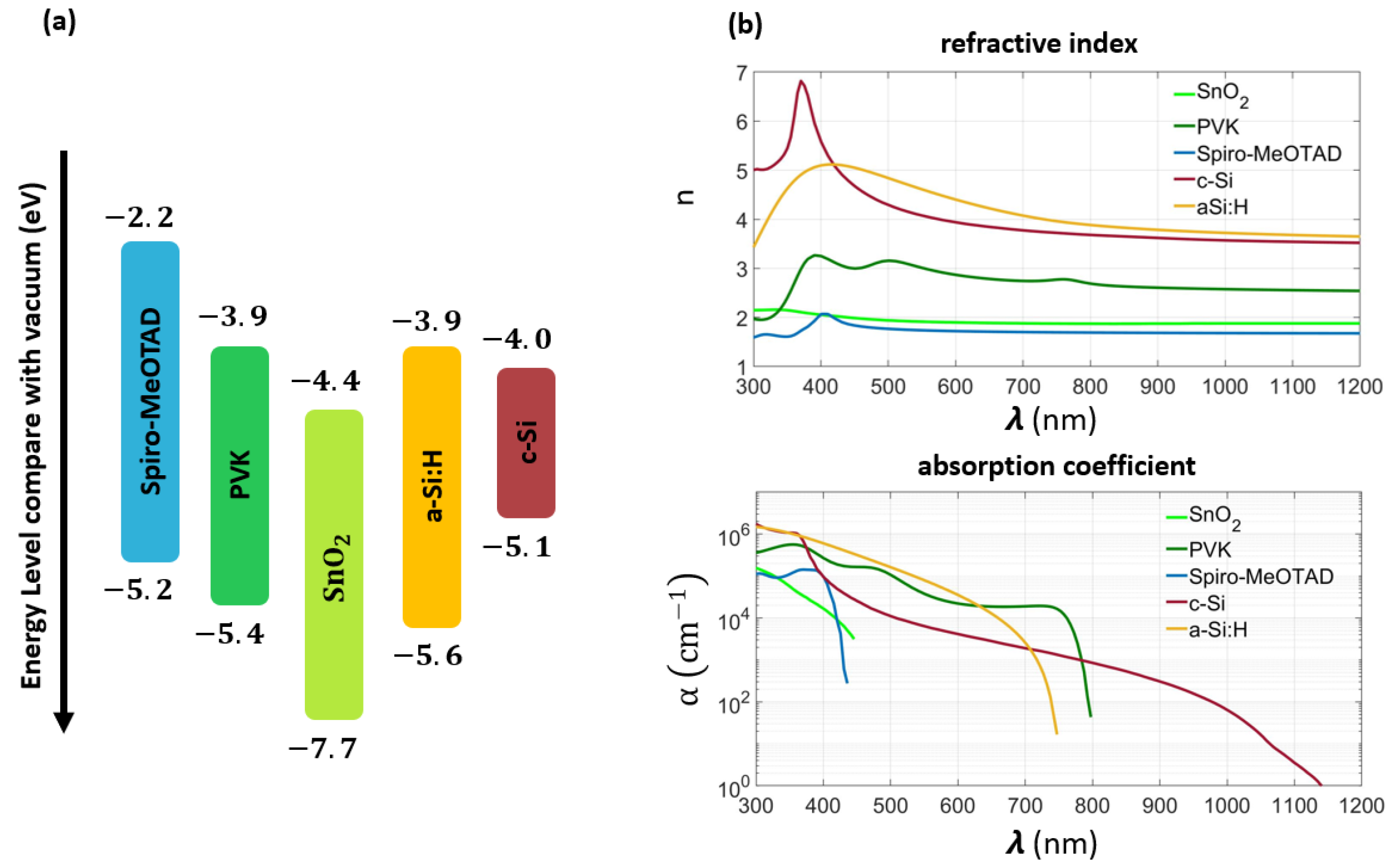
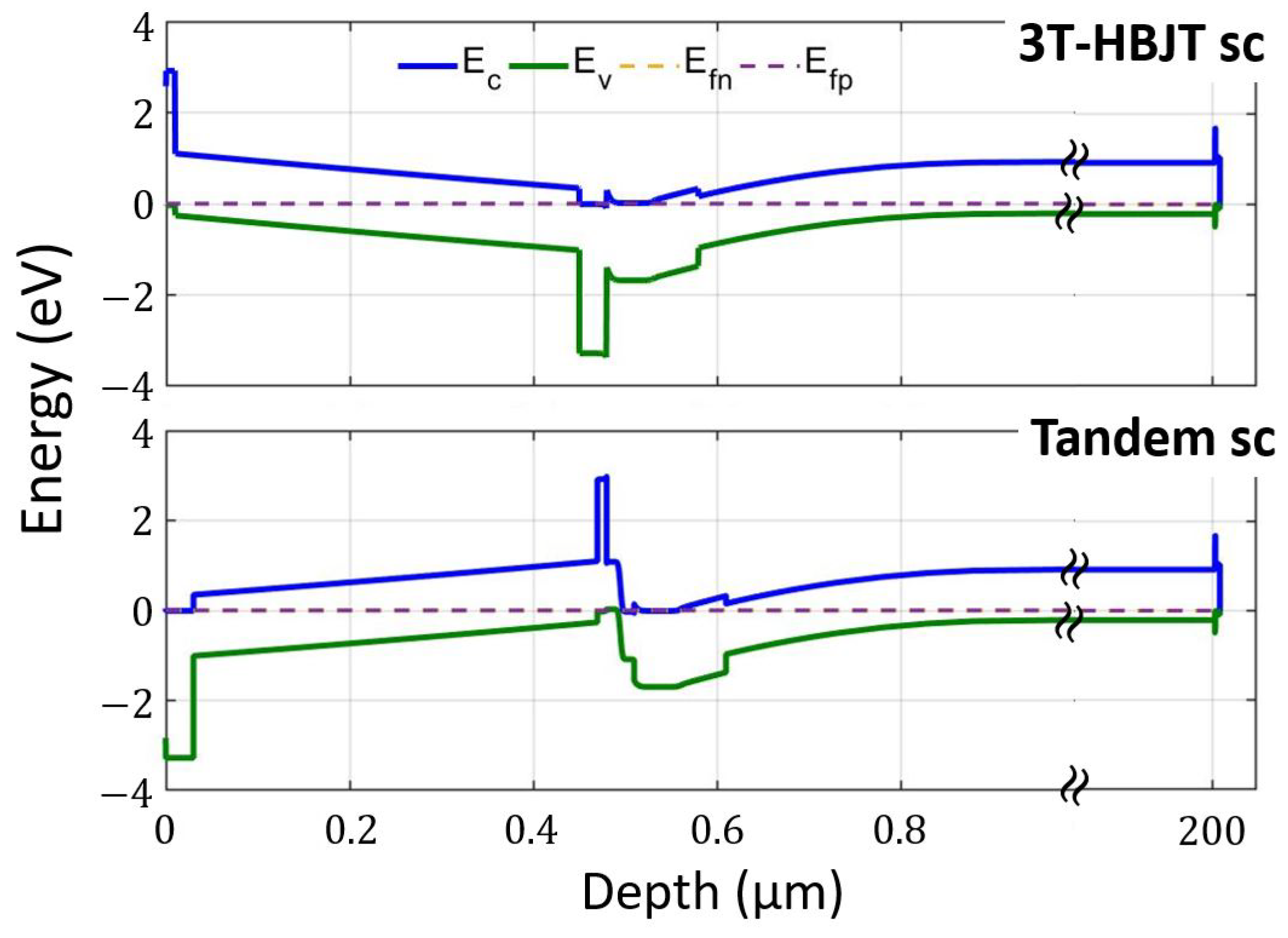
| PVK Top Cell | HIT Bottom Cell | ||||
|---|---|---|---|---|---|
| Spiro-OMeTAD | Perovskite | SnO | a-Si:H [34] | c-Si [43] | |
| (eV) | 2.95 [35] | 1.5 [35] | 3.28 [35] | 1.7 | 1.1 |
| (eV) | 2.18 | 3.93 | 4.35 | 3.9 | 4.05 |
| 3 | 6.5 [34] | 9.6 | 11.9 | 11.9 | |
| () | 2.2 × | 2 × | 4.1 × | 2.8 × | 2.8 × |
| () | 1.8 × | 2 × | 4.1 × | 1.0 × | 2.6 × |
| () | 0.0002 [33] | 11.8 [33] | 240 [36] | 20 5 | 1177 424 |
| N () | |||||
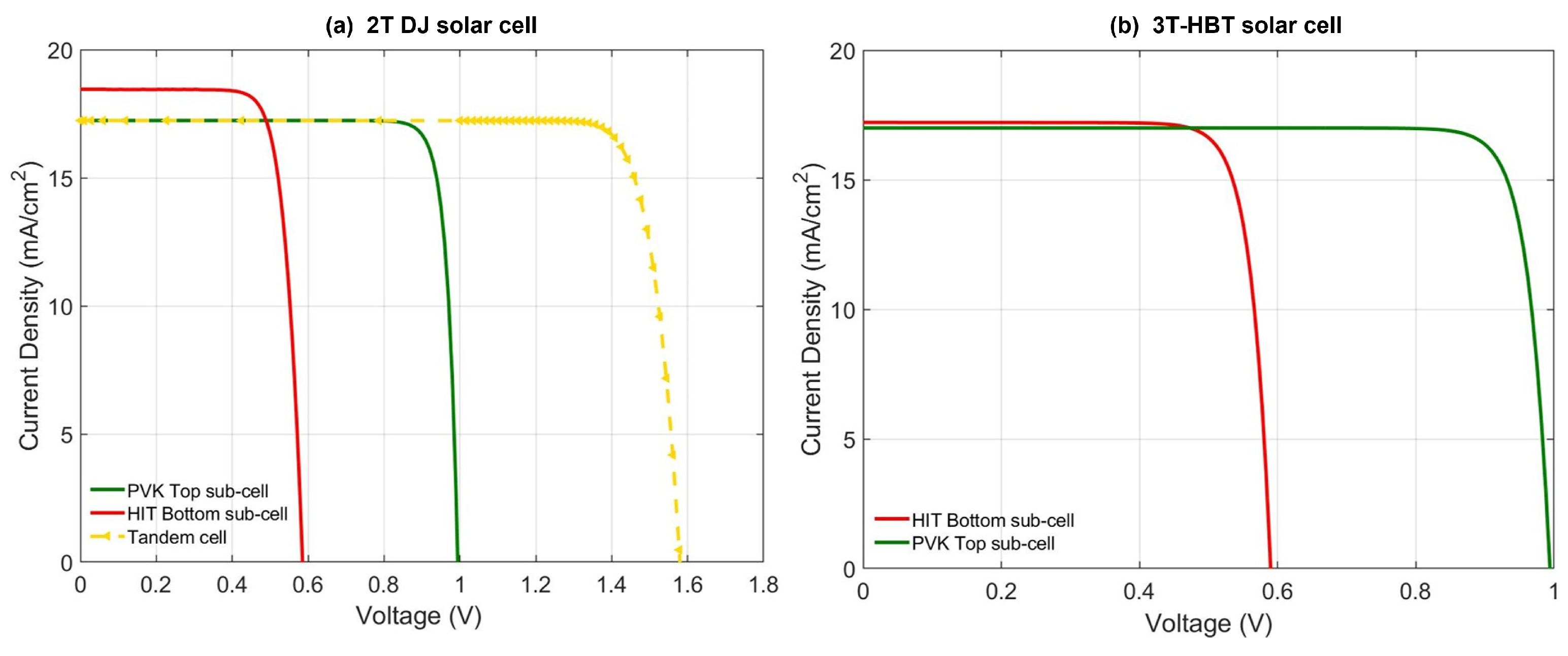
| Voc | Jsc | Vmpp | Jmpp | FF | eff | ||
|---|---|---|---|---|---|---|---|
| [V] | [mA/cm] | [V] | [mA/cm] | [%] | [%] | ||
| 3T-HBT sc | PVK Top sub-cell | 0.99 | 17 | 0.89 | 16.42 | 87.21 | 14.73 |
| HIT Bottom sub-cell | 0.59 | 17.2 | 0.51 | 16.3 | 82.16 | 8.33 | |
| Tandem Cell | - | - | - | - | - | 23.06 | |
| DJ sc | PVK Top sub-cell | 0.99 | 17.2 | 0.9 | 16.68 | 87.65 | 15.01 |
| HIT Bottom sub-cell | 0.58 | 18.44 | 0.48 | 17.37 | 78.18 | 8.44 | |
| Tandem Cell | 1.57 | 17.2 | 1.39 | 16.8 | 85.88 | 23.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giliberti, G.; Di Giacomo, F.; Cappelluti, F. Three Terminal Perovskite/Silicon Solar Cell with Bipolar Transistor Architecture. Energies 2022, 15, 8146. https://doi.org/10.3390/en15218146
Giliberti G, Di Giacomo F, Cappelluti F. Three Terminal Perovskite/Silicon Solar Cell with Bipolar Transistor Architecture. Energies. 2022; 15(21):8146. https://doi.org/10.3390/en15218146
Chicago/Turabian StyleGiliberti, Gemma, Francesco Di Giacomo, and Federica Cappelluti. 2022. "Three Terminal Perovskite/Silicon Solar Cell with Bipolar Transistor Architecture" Energies 15, no. 21: 8146. https://doi.org/10.3390/en15218146
APA StyleGiliberti, G., Di Giacomo, F., & Cappelluti, F. (2022). Three Terminal Perovskite/Silicon Solar Cell with Bipolar Transistor Architecture. Energies, 15(21), 8146. https://doi.org/10.3390/en15218146







