Thermo-Economic Performance Analysis of a Novel Organic Flash Rankine Cycle Using R600/R245fa Mixtures
Abstract
1. Introduction
2. System Description
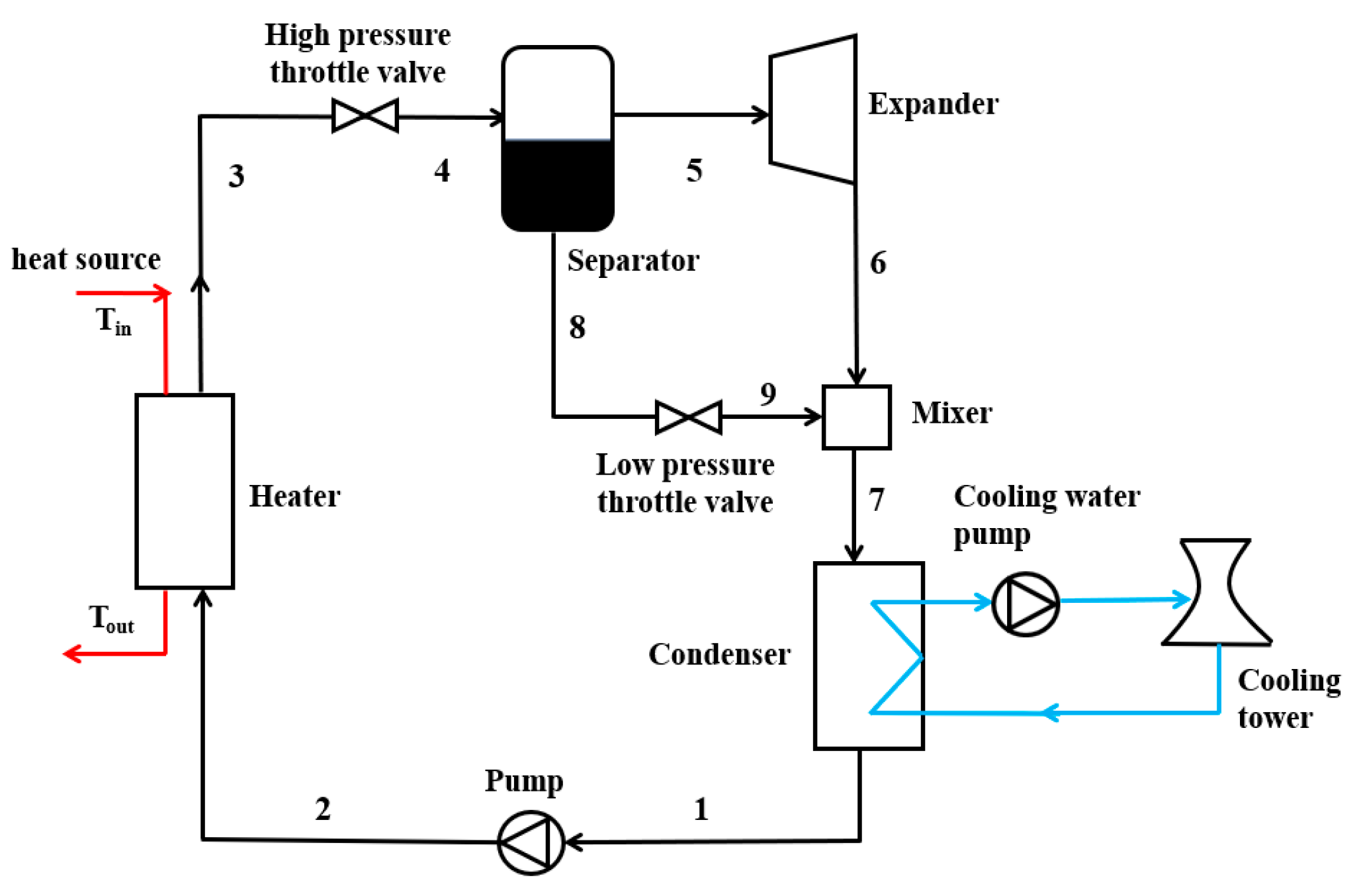
2.1. OFC System Description
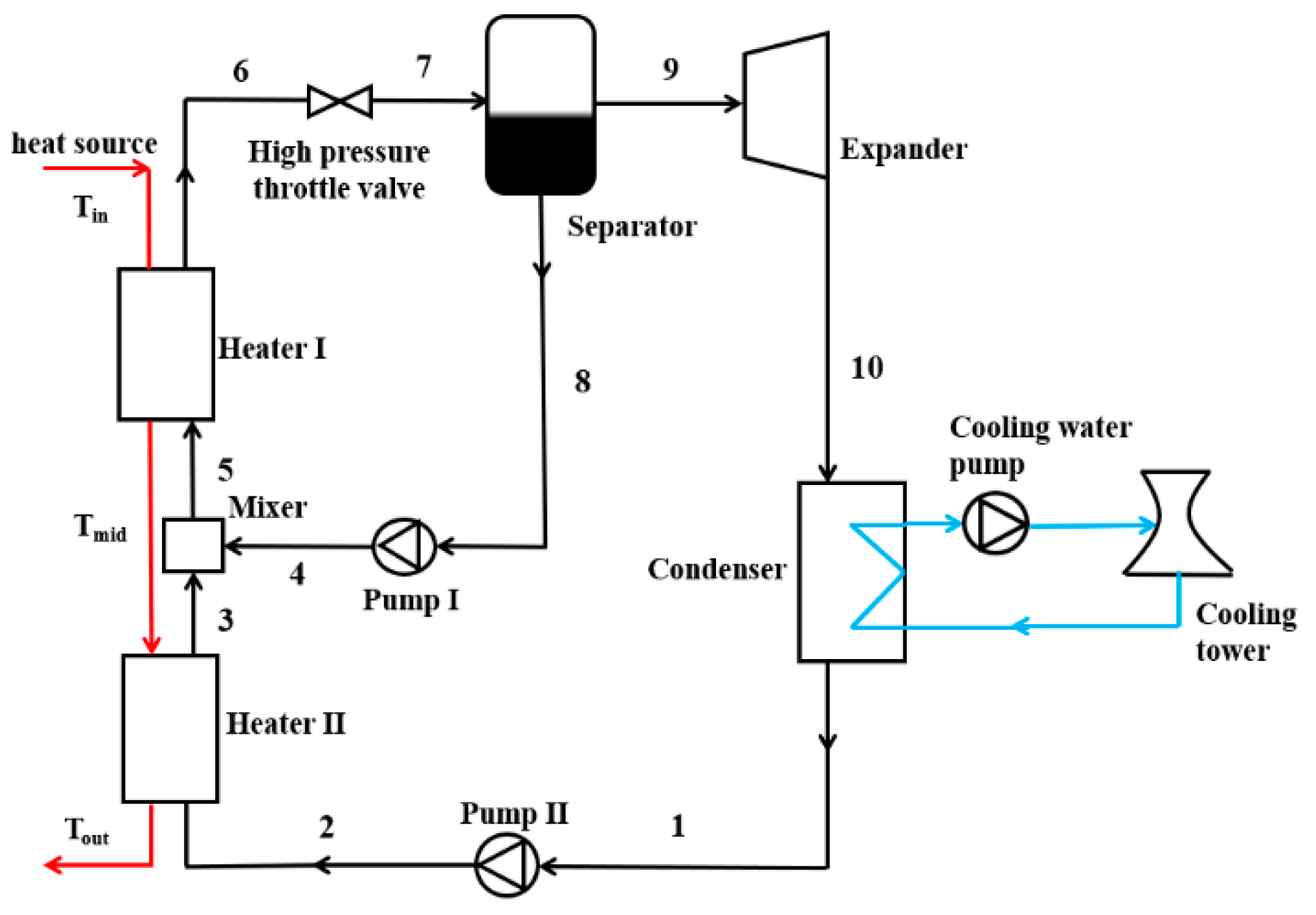
2.2. OFRC System Description
- (1)
- The OFRC system is in steady operation.
- (2)
- Each component and each connecting pipeline do not encounter heat dissipation and pressure loss.
- (3)
- The isentropic efficiency of the working fluid pump and turbine is constant.
- (4)
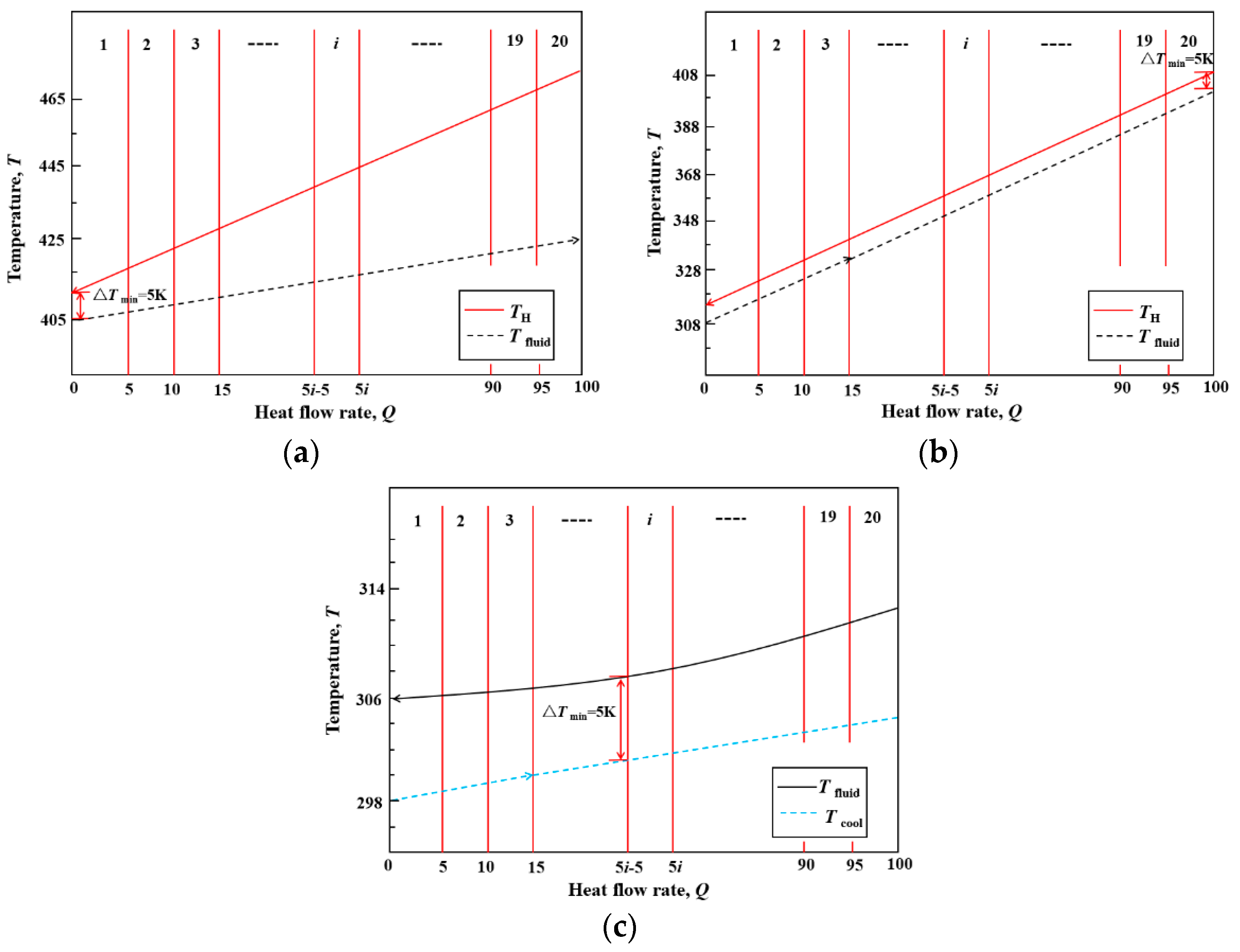
- The pinch point temperature is different between the heater and condenser.
- (5)
- The geothermal fluid and cooling water in this paper are approximately pure water.
3. Working Fluid Selection
4. Mathematical Model
4.1. Thermodynamic Analysis
4.2. Economic Analysis
5. Model Validation
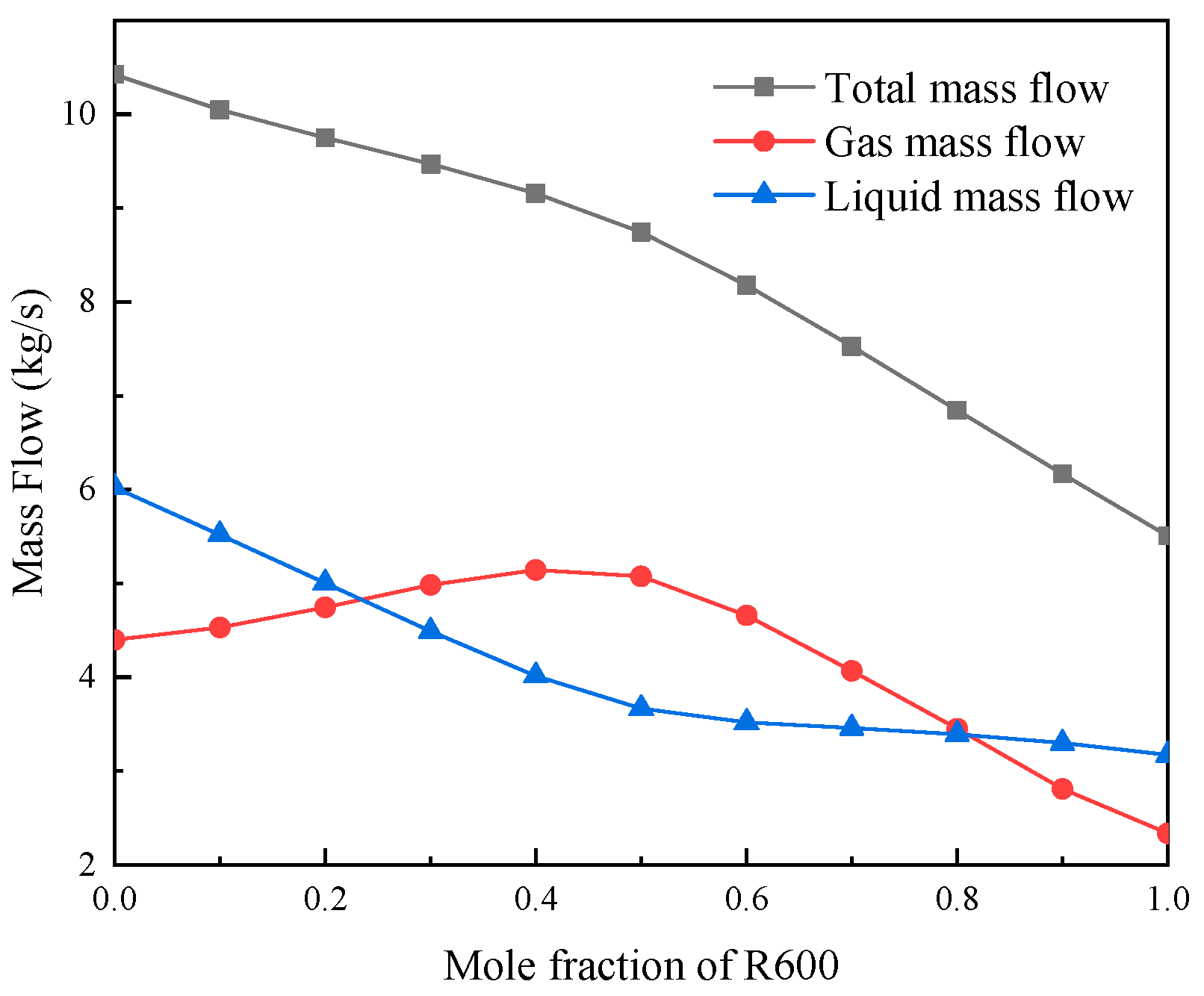
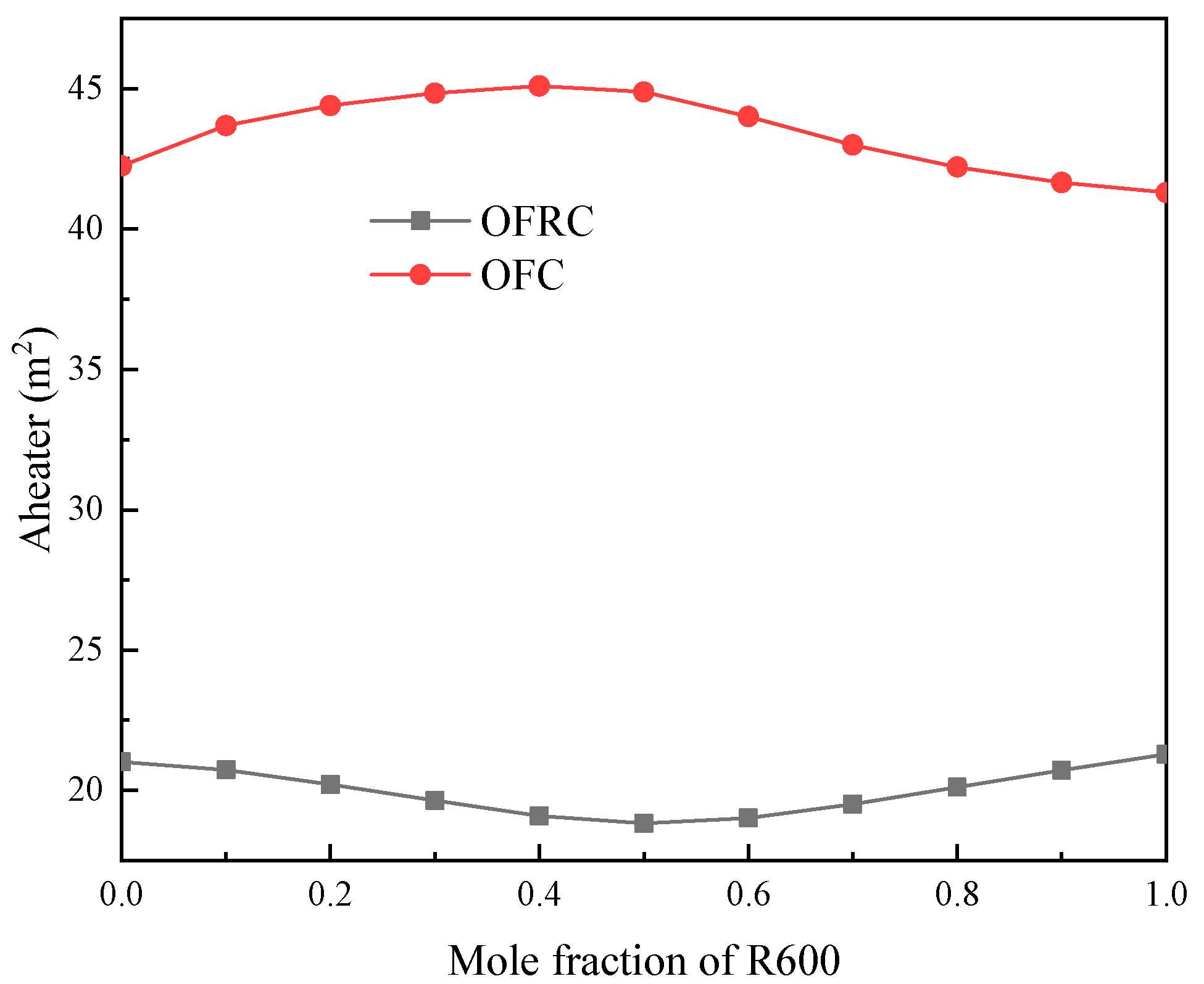
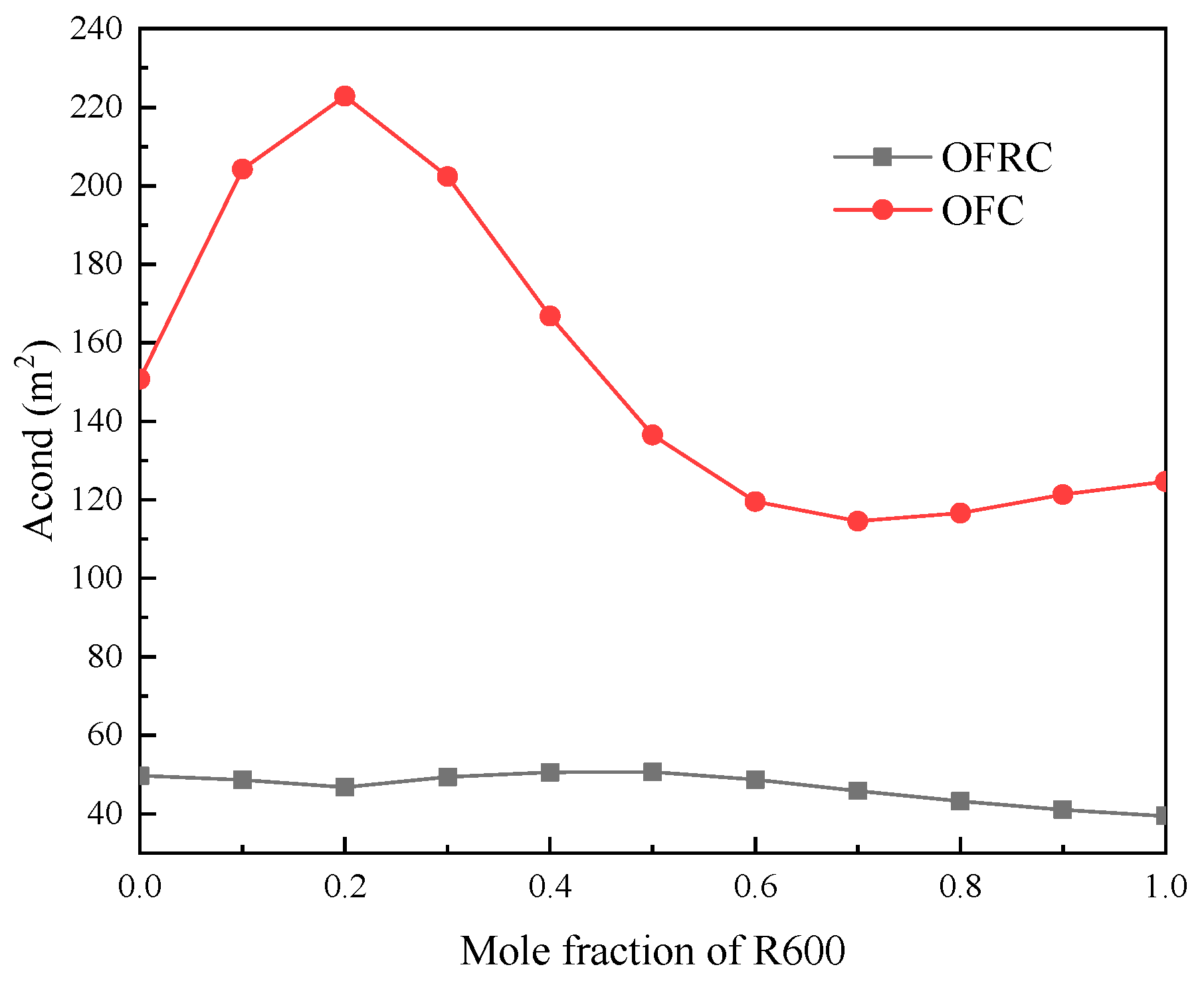
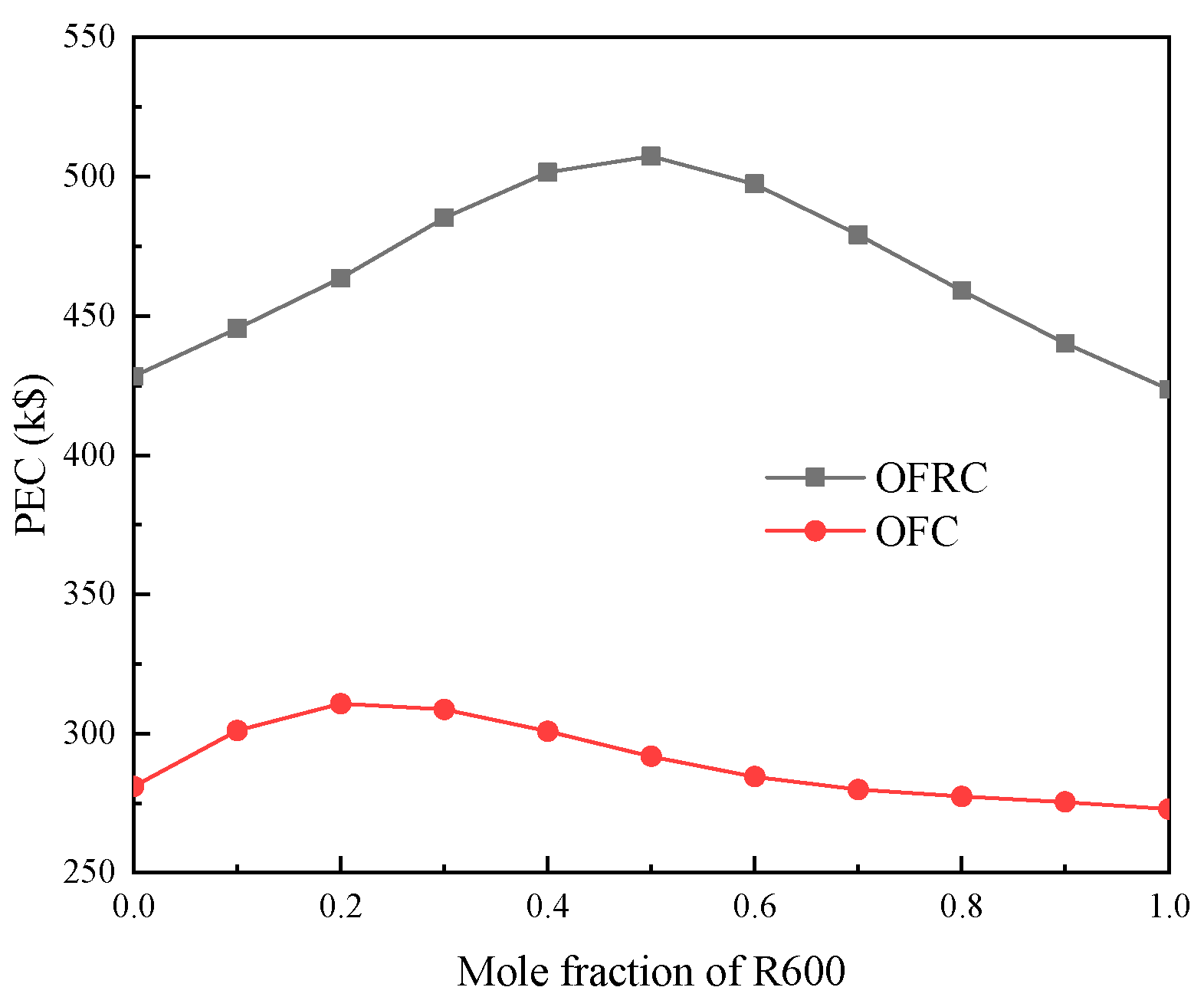
6. Results and Discussion
7. Conclusions
- (1)
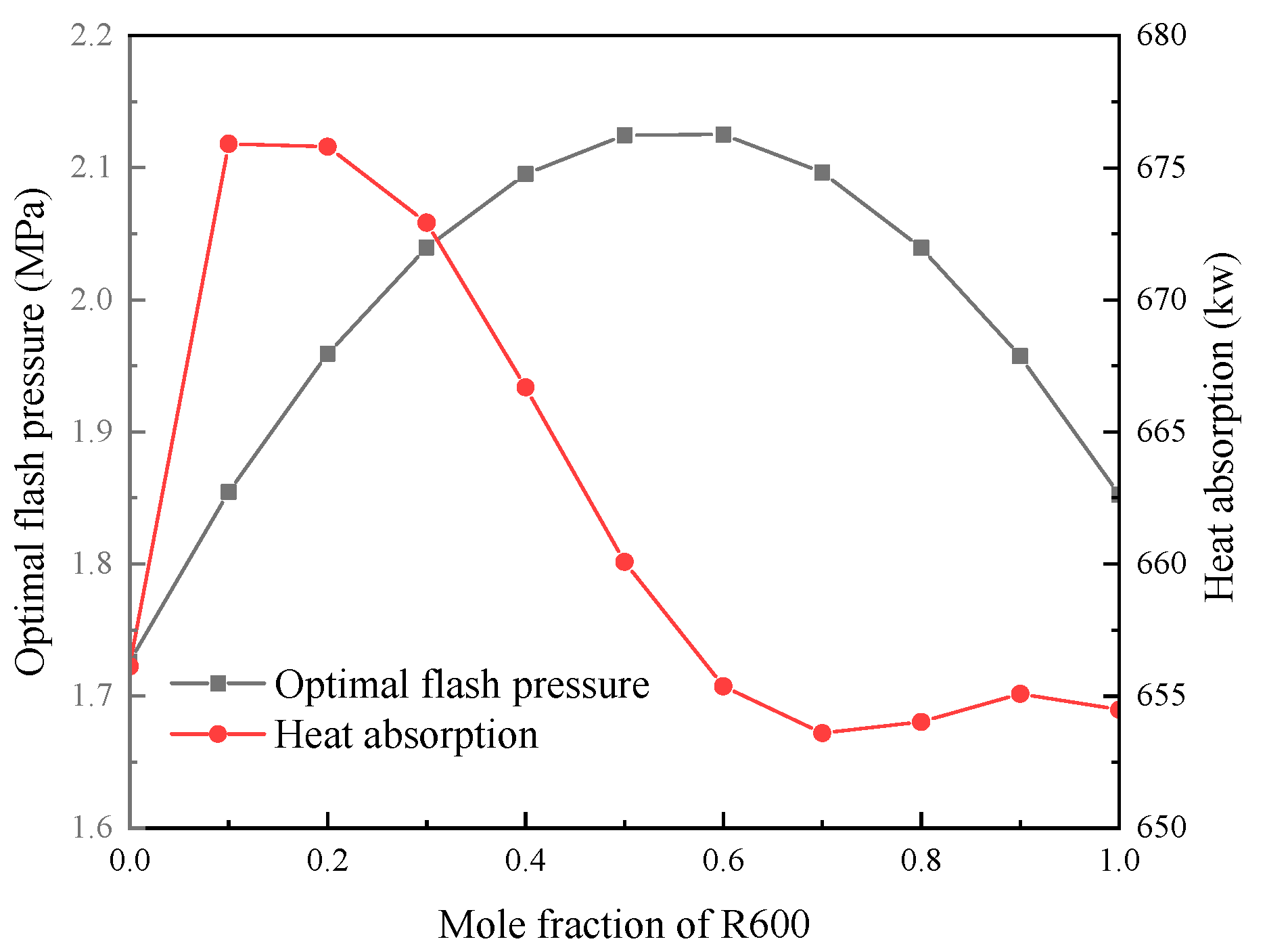
- When the R600 mole composition is between 0 and 1, the maximum net output power, thermal efficiency, and exergy efficiency of the OFRC system are all larger than those of the OFC system. When the R600 mole component is 0.5, the maximum net output power is 146.39 kW, the thermal efficiency is 21.51%, and the exergy efficiency is 80.94% in the OFRC system. By contrast, when the R600 mole component is 0.4, the maximum net output power is 48.91 kW, the thermal efficiency is 7.12%, and the exergy efficiency is 27.05% in the OFC system.
- (2)
- Dual heaters can effectively reduce exergy destruction in the endothermic process. When the R600 mole component is 0.5, the exergy loss of the heater in the OFRC system is only 7.42% of the total exergetic loss. Among the circulating components, the exergy loss of the condenser accounts for the largest proportion. When the R600 mole component is 0.6, the exergy loss of the condenser in the OFRC system accounts for 44.19%.
- (3)
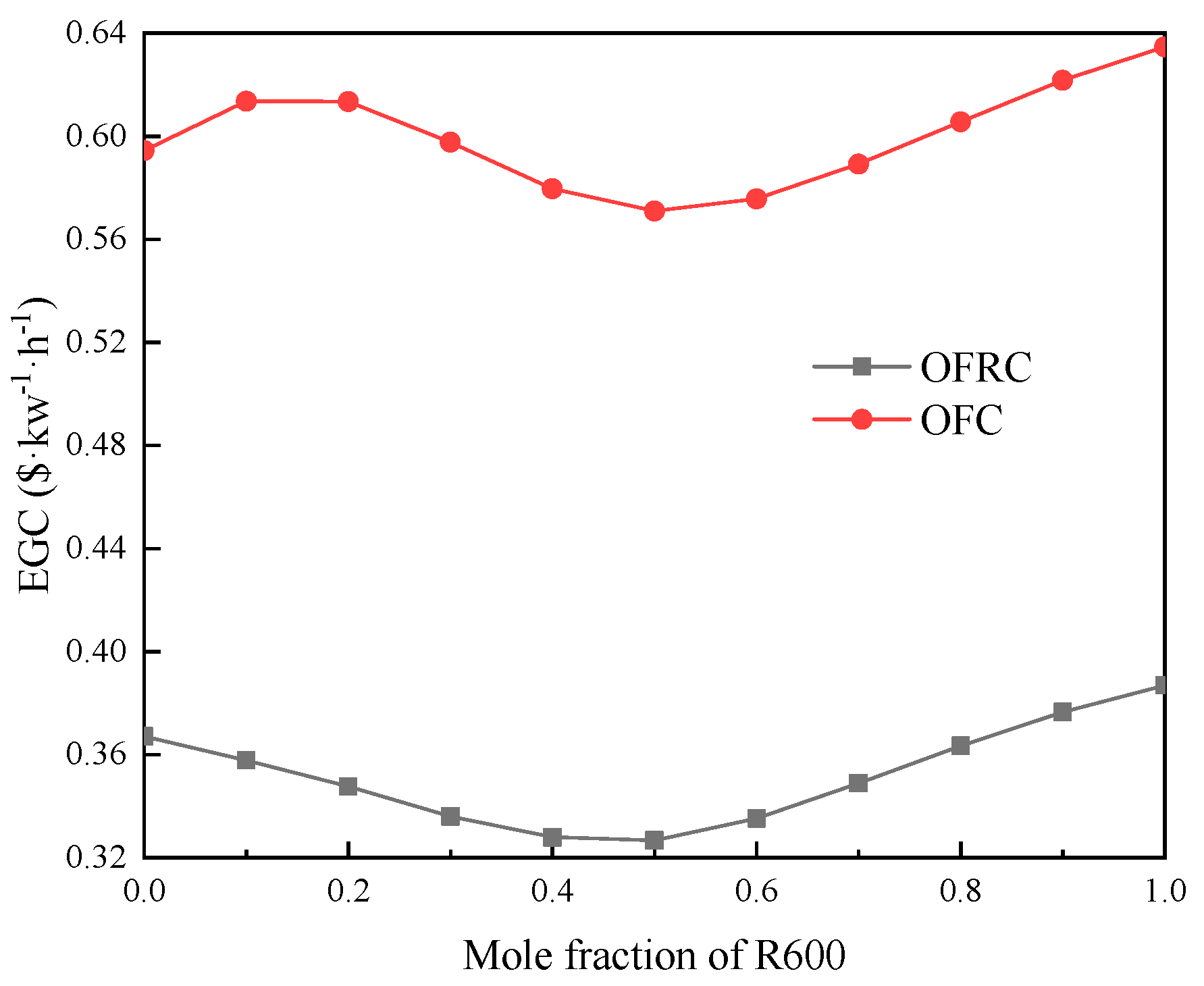
- The OFRC system has a slightly larger PEC than the OFC system owing to its larger mass flow of working fluid. Furthermore, the electricity generation cost of the OFRC system is much lower than that of the OFC system. When the R600 mole composition is 0.5, the EGCs of the OFRC and OFC systems are the smallest at 0.3267 and 0.5709 $·kW−1·h−1, respectively.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| E | Exergy loss, kW |
| g | Gravitational acceleration, 9.8 m·s−2 |
| H | Cooling water pump head, m |
| h | Specific enthalpy, kJ·kg−1 |
| m | Mass Flow, kg·s−1 |
| P | Pressure, MPa |
| Q | Heat absorption, kW |
| s | Specific entropy, kJ/(kg·K)−1 |
| T | Temperature, °C |
| ΔT | Temperature difference, °C |
| W | Power, kW |
| x | Steam dryness |
| η | Efficiency, % |
| A | Area, m2 |
| subscripts | |
| c | Condenser |
| cool | Cooling water |
| ex | Exergy |
| f | Working fluid |
| H | Heater |
| HPTV | High-pressure throttle valve |
| mid | Middle |
| in | Import |
| out | Export |
| g | Gas-phase components |
| l | Liquid components |
| net | Net output power |
| tot | Total value |
| P | Working fluid pump |
| T | Expander |
| mix | Mixer |
| sys | System |
| 0–10 | Status point |
References
- Helen, T. The geopolitics of fossil fuels and renewables reshape the world. Nature 2022, 603, 364. [Google Scholar]
- Ge, Z.; Wang, H.; Wang, H.T.; Wang, J.J.; Li, M.; Wu, F.Z.; Zhang, S.Y. Main parameters optimization of regenerative organic Rankine cycle driven by low-temperature flue gas waste heat. Energy 2015, 93, 1886–1895. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Batueva, D.E.; Buldysko, A.D.; Gil, B.; Starshaia, V.V. Fossil Energy in the Framework of Sustainable Development: Analysis of Prospects and Development of Forecast Scenarios. Energies 2021, 14, 5268. [Google Scholar] [CrossRef]
- Yan, J.; Yang, X. Thermal energy storage: An overview of papers published in Applied Energy 2009–2018. Appl. Energy 2021, 285, 116397. [Google Scholar] [CrossRef]
- Kuamr, A. The brief review on the various thermodynamic cycles. ACADEMICIA Int. Multidiscip. Res. J. 2021, 11, 2228–2233. [Google Scholar]
- Wang, Y.; Qin, G.; Zhang, Y.; Yang, S.; Liu, C.; Jia, C.; Cui, Q. Conventional and advanced exergy analyses of an organic Rankine cycle by using the thermodynamic cycle approach. Energy Sci. Eng. 2021, 9, 2474–2492. [Google Scholar] [CrossRef]
- Daniarta, S.; Kolasiński, P.; Imre, A.R. Thermodynamic efficiency of trilateral flash cycle, organic Rankine cycle and partially evaporated organic Rankine cycle. Energy Convers. Manag. 2021, 249, 114731. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, W.; Li, D.; Wang, J.; He, Z. Thermodynamic analysis and optimization of four organic flash cycle systems for waste heat recovery. Energy Convers. Manag. 2020, 221, 113171. [Google Scholar] [CrossRef]
- Kim, K.H.; Ko, H.J.; Han, C.H. Exergy Analysis of Kalina and Kalina Flash Cycles Driven by Renewable Energy. Appl. Sci. 2020, 10, 1813. [Google Scholar] [CrossRef]
- Mondal, S.; De, S. Waste heat recovery through organic flash cycle (OFC) using R245fa–R600 mixture as the working fluid. Clean Technol. Environ. Policy 2019, 21, 1575–1586. [Google Scholar] [CrossRef]
- Ho, T.; Mao, S.S.; Greif, R. Comparison of the Organic Flash Cycle (OFC) to other advanced vapor cycles for intermediate and high temperature waste heat reclamation and solar thermal energy. Energy 2012, 42, 213–223. [Google Scholar] [CrossRef]
- Varma, G.V.P.; Srinivas, T. Power Generation from Low Temperature Heat Recovery. Renew. Sustain. Energy Rev. 2016, 75, 402–412. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Bu, X.; Wang, L.; Xie, N.; Zeng, J. Performance characteristics and working fluid selection for low-temperature binary-flashing cycle. Appl. Therm. Eng. 2018, 141, 51–60. [Google Scholar] [CrossRef]
- Xu, W.; Zhao, R.; Deng, S.; Mao, S.S.; Zhao, L. Understanding the 3D construction method of thermodynamic cycle: Insights from limiting performance of pure working fluid. Energy Convers. Manag. 2020, 224, 113364. [Google Scholar] [CrossRef]
- Györke, G.; Deiters, U.K.; Groniewsky, A.; Lassu, I.; Imre, A.R. Novel classification of pure working fluids for Organic Rankine Cycle. Energy 2018, 145, 288–300. [Google Scholar] [CrossRef]
- Herath, H.M.D.P.; Wijewardane, M.A.; Ranasinghe, R.A.C.P.; Jayasekera, J.G.A.S. Working fluid selection of Organic Rankine Cycles. Energy Rep. 2020, 6, 680–686. [Google Scholar] [CrossRef]
- Abadi, G.B.; Kim, K.C. Investigation of organic Rankine cycles with zeotropic mixtures as a working fluid: Advantages and issues. Renew. Sustain. Energy Rev. 2017, 73, 1000–1013. [Google Scholar] [CrossRef]
- Andreasen, J.G.; Kærn, M.R.; Pierobon, L.; Larsen, U.; Haglind, F. Multi-Objective Optimization of Organic Rankine Cycle Power Plants Using Pure and Mixed Working Fluids. Energies 2016, 9, 322. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in Organic Rankine Cycles for low-enthalpy geothermal resources. Renew. Energy 2011, 37, 364–370. [Google Scholar] [CrossRef]
- Ge, Z.; Li, J.; Liu, Q.; Duan, Y.; Yang, Z. Thermodynamic analysis of dual-loop organic Rankine cycle using zeotropic mixtures for internal combustion engine waste heat recovery. Energy Convers. Manag. 2018, 166, 201–214. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, S.; Ge, Z.; Xie, Z.; Yuan, Z.; Tang, C.; Xie, J.; Xu, J. Thermal performance analysis of organic flash cycle using r600a/r601a mixtures with internal heat exchanger. Therm. Sci. 2021, 25, 767–779. [Google Scholar] [CrossRef]
- de Campos, G.B.; Bringhenti, C.; Traverso, A.; Tomita, J.T. Thermoeconomic comparison between the organic flash cycle and the novel organic Rankine flash cycle (ORFC). Energy Convers. Manag. 2020, 215, 112926. [Google Scholar] [CrossRef]
- Li, J.; Ge, Z.; Duan, Y.; Yang, Z. Effects of heat source temperature and mixture composition on the combined superiority of dual-pressure evaporation organic Rankine cycle and zeotropic mixtures. Energy 2019, 174, 436–449. [Google Scholar] [CrossRef]
- Kim, K.H. Thermodynamic Performance and Optimization Analysis of a Modified Organic Flash Cycle for the Recovery of Low-Grade Heat. Energies 2019, 12, 442. [Google Scholar] [CrossRef]
- Guidong, H.; Yongyuan, Z.; Zhong, G.; Zhiyong, X.; Huajiang, X.; Yinlian, Y.; Zhipeng, Y. Thermal performance study based on organic flash cycle of internal heat exchanger. Chin. J. Chem. Ind. 2020, 71, 3080–3090. [Google Scholar]
- Mondal, S.; Alam, S.; De, S. Performance assessment of a lowgrade waste heat driven organic flash cycle (OFC) with ejector. Energy 2018, 163, 849–862. [Google Scholar] [CrossRef]
- Das, D.; Kazim, M.; Sadr, R.; Pate, M. Optimal hydrocarbon based working fluid selection for a simple supercritical Organic Rankine Cycle. Energy Convers. Manag. 2021, 243, 114424. [Google Scholar] [CrossRef]
- Yang, J.; Gao, L.; Ye, Z.; Hwang, Y.; Chen, J. Binary-objective optimization of latest low-GWP alternatives to R245fa for organic Rankine cycle application. Energy 2021, 217, 119336. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Duan, Y.; Yang, Z. Performance analysis of organic Rankine cycles using R600/R601a mixtures with liquid-separated condensation. Applied Energy 2017, 190, 376–389. [Google Scholar] [CrossRef]
- Meng, D.; Liu, Q.; Ji, Z. Performance analyses of regenerative organic flash cycles for geothermal power generation. Energy Convers. Manag. 2020, 224, 113396. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Hu, S.; Duan, Y. Influences of fluid corrosivity and heat exchanger materials on design and thermo-economic performance of organic Rankine cycle systems. Energy 2021, 228, 120589. [Google Scholar] [CrossRef]
- Hadelu, L.M.; Boyaghchi, F.A. Exergoeconomic and exergoenvironmental analyses and optimization of different ejector based two stage expander-organic flash cycles fuelled by solar energy. Energy Convers. Manag. 2020, 216, 112943. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; Mclinden, M.O. NIST Reference Fluid Thermodynamic and Transports Properties-REFPROP, Version 9.0; National Institute of Technology, Standard Reference Date Program: Gaithersburg, MD, USA, 2013.





| Working Fluid | Type of Working Fluid | Critical Temperature (K) | Critical Pressure (MPa) | Normal Boiling Point (K) | Latent Heat of Vaporization (kJ/kg) | Security | Ozone Depletion Potential | Global Warming Potential |
|---|---|---|---|---|---|---|---|---|
| R600 | HCs | 425.13 | 3.7960 | 272.66 | 177.08 | A3 | 0 | 20 |
| R245fa | HFCs | 427.16 | 6.6511 | 288.29 | 336.82 | B1 | 0 | 1030 |
| Component | Y | K1 | K2 | K3 | FBM | B1 | B2 | FM | p/MPa | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heater/Condenser | Area (m2) | 4.3247 | −0.303 | 0.1634 | - | 1.63 | 1.66 | 1.35 | <0.6 | 0 | 0 | 0 |
| 0.6–14.1 | −0.00164 | −0.00627 | 0.0123 | |||||||||
| Expander | Power (kW) | 2.7051 | 1.4398 | −0.1776 | 3.5 | - | - | - | - | - | - | - |
| Pump | Power (kW) | 3.3892 | 0.0536 | 0.1538 | - | 1.89 | 1.35 | 1.55 | <1.1 | 0 | 0 | 0 |
| 1.1–10.1 | 0.3935 | 0.3957 | −0.00226 |
| Heat Source Temperature/(K) | Thermal Efficiency/(%) | Exergy Efficiency/(%) | ||||
|---|---|---|---|---|---|---|
| Present Study | Reference [22] | Relative Error | Present Study | Reference [22] | Relative Error | |
| 423.15 | 15.49 | 15.60 | 0.71 | 57.98 | 58.76 | 1.32 |
| 448.15 | 17.15 | 17.30 | 0.86 | 59.93 | 60.52 | 1.14 |
| 473.15 | 18.97 | 19.20 | 1.19 | 59.29 | 60.04 | 1.24 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| heat source temperature/K | 473.15 | working fluid pump isentropic efficiency/% | 75 |
| thermal fluid flow/(kg/s) | 1 | cooling pump efficiency/% | 85 |
| heat source fluid pressure/MPa | 1.6 | cooling water temperature/K | 298.15 |
| evaporator pinch temperature difference/K | 5 | cooling water temperature rise/K | 5 |
| condenser pinch point temperature difference/K | 5 | cooling water pump head/m | 10 |
| expander isentropic efficiency/% | 85 | ambient temperature/K | 293.15 |
| ambient atmospheric pressure/KPa | 101 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, G.; Zhang, S.; Ge, Z.; Li, J.; Xu, J.; Xie, J.; Xie, Z.; Yao, D.; Zhao, T.; Wang, Z.; et al. Thermo-Economic Performance Analysis of a Novel Organic Flash Rankine Cycle Using R600/R245fa Mixtures. Energies 2022, 15, 8055. https://doi.org/10.3390/en15218055
Fu G, Zhang S, Ge Z, Li J, Xu J, Xie J, Xie Z, Yao D, Zhao T, Wang Z, et al. Thermo-Economic Performance Analysis of a Novel Organic Flash Rankine Cycle Using R600/R245fa Mixtures. Energies. 2022; 15(21):8055. https://doi.org/10.3390/en15218055
Chicago/Turabian StyleFu, Guangbiao, Songyuan Zhang, Zhong Ge, Jian Li, Jian Xu, Jianbin Xie, Zhiyong Xie, Dong Yao, Tao Zhao, Zhijie Wang, and et al. 2022. "Thermo-Economic Performance Analysis of a Novel Organic Flash Rankine Cycle Using R600/R245fa Mixtures" Energies 15, no. 21: 8055. https://doi.org/10.3390/en15218055
APA StyleFu, G., Zhang, S., Ge, Z., Li, J., Xu, J., Xie, J., Xie, Z., Yao, D., Zhao, T., Wang, Z., Yue, S., Zhao, S., Liu, F., & Jiang, Q. (2022). Thermo-Economic Performance Analysis of a Novel Organic Flash Rankine Cycle Using R600/R245fa Mixtures. Energies, 15(21), 8055. https://doi.org/10.3390/en15218055







