1. Introduction
Model reduction of wind farms has been a subject of interest since the early 1990’s [
1]. Recent studies shows an ongoing demand for sound aggregated wind farm models [
2]. The need for a verification method for aggregation techniques for passive electrical systems for offshore wind farms (OWF) is evident. There is also a need for an indication of the validity of the aggregation. This paper presents a novel modal aggregation technique that serves both purposes. The proposed modal aggregation technique is, however, only looking into the collector system of offshore wind farm power systems. The aggregation of the collector system might also be relevant for active distribution networks (ADN), as these also consider wind farms equivalents [
3].
Much research has been conducted looking into full-aggregation of doubly-fed induction generator-based (DFIG) OWFs. The DFIG has been a popular wind turbine (WT) as it was the most frequently installed WT type from 2001 to 2004 world wide (Data is available from 1995 to 2004.) [
4]. A dynamic model equivalent has been developed by the swing equation in [
5,
6]. A similar dynamic model is developed in [
7] but by utilizing the flux linkage of the machine. The wind profile is furthermore included in [
8].
A German trend analysis of installed WT per type each year shows that the type-4 WT gained interest and accounts for at least 50 % of the installed WTs since 2010 (Data is available from 1998 to 2018.) [
9]. In [
10], a wind profile-based full-aggregated dynamic model equivalent is developed for the type-4 WT. It is however reported that full-aggregation methods neglect the internal oscillatory behavior and dynamics [
11]. Furthermore, it is claimed that the nonlinear power production and inertial response are neglected due to wake effects [
12], and the non-uniform wind speed distribution across the OWF [
13]. However, the semi-aggregation accommodates some non-uniformity in the model reduction either by the WT model aggregation [
14] or by representing the OWF by a multi-machine aggregated model [
15,
16,
17].
The multi-machine representation supports modal analysis, coherency analysis, and various clustering methods. An argument against these aggregation techniques is that they might ignore the electrical distance, i.e., a coherency analysis could find a common mode for two WTs in different strings [
11].
Aggregation of wind farms tends to neglect the system harmonics. Ref. [
18] investigates several methods to aggregate harmonic current emissions from WTs for prediction of power system harmonics by coupling the DC-link voltage and the PLL. This aggregation requires insight of the WT model itself, however.
Designing OWFs often involves collaboration with WT suppliers, who deliver black-boxed WT models. Thus, there is a distinction between a certain parameter-based model aggregation of white-boxed models and identified parameter-based model aggregation of black-boxed models. Parameters can be identified by optimization algorithms like particle swarm optimization [
19]. Another approach would be to perform vector fitting to the entire wind farm dynamics, as proposed in [
18]. An option is to develop a grey-box model that allows a dynamic equivalent model order reduction by parameter estimation in ADNs [
3,
20].
As a draw-back, grey-boxing loses some of the traceability of the system parameters and dynamics. This is the motivation for investigating the aggregation techniques of the passive system alone, i.e., the collector system (CS) of the OWF, as it is independent of the wind turbine type and the level of model transparency.
In [
21,
22,
23], a voltage drop-based analysis of the equivalent string impedance in the collector system is considered. In [
24,
25,
26,
27,
28], a similar approach is noted, but the individual impedance is weighted with respect to a consideration of power losses. Ref. [
29] proposes the short-circuit impedance given by the short-circuit level (SCL) of the OWF as the equivalent impedance of the entire system. Because the latter aggregation technique is based on doubly-fed induction machines (DFIGs), it will not be benchmarked as the aggregation technique bases on a specific type of WT.
The paper is organized in the following manner:
Section 2 presents the theory of the proposed modal aggregation technique.
Section 4 defines the benchmarked aggregation techniques and the immediate differences.
Section 3 outlines the case studies in terms of tests, dimensions of the OWF, and the model setup. Diverse wind farm layouts are discussed in [
30,
31,
32] but none of the aggregation techniques covers how branches in the individual strings are handled. The paper will thus benchmark the performance with respect to the existence of branches in the strings.
Section 5 shows and elaborates the results of the time-domain simulations.
Section 6 discusses the validity of aggregation for studies for higher frequencies, for larger impedance, and asymmetric strings.
Section 7 concludes on the most accurate aggregation technique, the potential of the dominant contribution factor ratio (DCFR) as a validity parameter of the aggregation, and suggests a validity threshold to the DCFR.
2. Modal Aggregation Technique
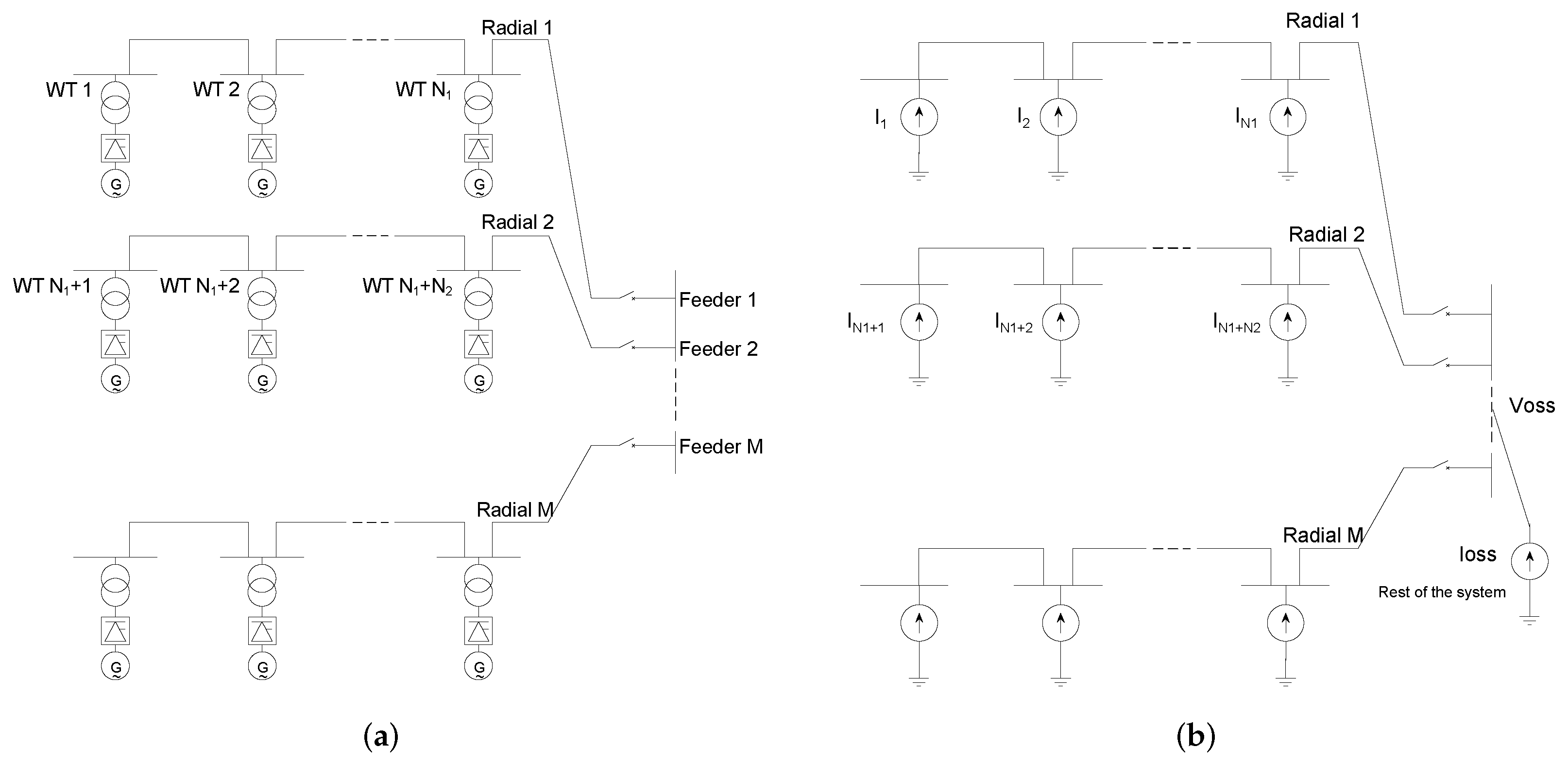
Offshore wind farms are an assembly of WTs connected in radial feeders to the offshore substation, which constitutes the collector system. As these array cable systems are in the 33–66 kV range and extend from 2–30 km, many dynamics take place in the collector system [
33]. It is desired to preserve the special dynamic response of the system after aggregation, motivated by speeding up the computation of grid interaction studies. In
Figure 1a, a high-level OWF model shows the conceptual layout of the WTs in feeders. In
Figure 1b, the conceptual equivalent-ready model is illustrated by the assumption of WTs as current sources.
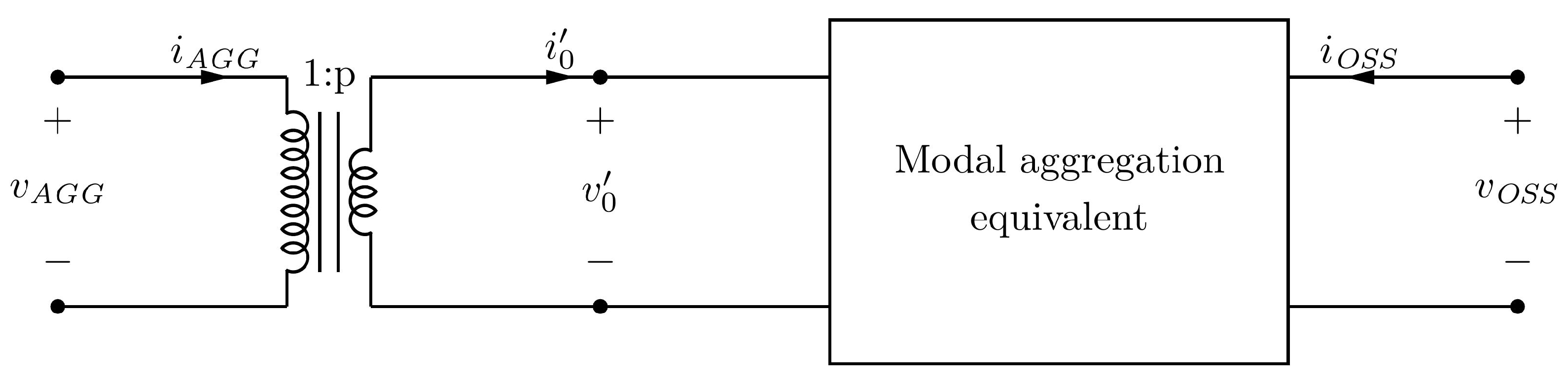
The aggregation represents the collector system and the power generation from WTs as a single WT representation of the system behind an equivalent RLC component connected to the offshore substation (OSS), as seen in
Figure 2:
The aggregation can be done by circuit analysis and assumptions on power generation (as it is shown in
Section 3). However, the equivalent impedance of the OWF collector system can also be aggregated by eigenvalues and eigenvectors of the system. Recalling relevant theory, it is noted that an eigenvalue
of a matrix
is associated with the right eigenvector
[
34], so that:
In matrix format, eigenvalues and eigenvectors are given:
Matrix notation allows similar expression as in (
1):
where
is the matrix of the right eigenvectors.
Application
For any CS associated with an OSS, there is
cable sections with respect to
N WTs in the cluster(s) (assuming no loops in the array system). The voltages at each node in the investigated system can be given in matrix format:
where
is the voltages at each node.
is the impedance matrix of the investigated system.
is the current injections at each node, all at the fundamental frequency. The matrix can be partitioned for better interpretation as follows:
where
is the voltage at the WT nodes.
is the OSS voltage.
is the partition of the impedance matrix of the system, representing the CS.
is the mutual impedance of the CS and the OSS.
is the partition of the impedance matrix of the investigated system, which could be associated with the grid.
is the current injections of the WTs.
is the current injection at the OSS. The system matrix
can be expressed in terms of (
3):
The partitioned voltages are thus rewritten:
Modal currents and voltages are defined as:
which leads to (
9) by substituting (
8) in (
7):
The impact of the modal currents on the OSS voltage from the current injection from the WTs are given by contribution factors (CF)
:
It is assumed for the sake of simplicity, that the current of the individual WT is considered to be identical and at nominal generation, i.e.,
per-unit (in
Section 6.1 it is shown that unequal current in phase and magnitude does not change the conclusion of this method):
It can be shown that in most cases, only one modal current is important, and the other modal currents are much smaller, i.e.,
. Therefore, (
9) can be approximated by only one model current and one modal voltage. Let 0 denote the index of the dominant contribution factor and let
be sorted in descending order with respect to magnitude:
The investigated system can thus be aggregated into two nodes, namely the OSS and a fictitious node representing the dominant modal voltage and current.
Since the modal currents and voltages are not identical to real currents and voltages, an ideal transformer is introduced to transform the voltage level to the same as before but scale the current up (as expected in an aggregated wind turbine), as seen in
Figure 3:
The turn ratio is given by
p and defined as:
where
. The transformer model enables the construction of the two port aggregated system (AS) by transforming back from modal to real domain:
The impedance matrix of the AS is asymmetric and nonreciprocal [
35,
36], i.e., the current and voltage of one port does not translate into the other port by means of passive electrical components and vice versa. In perspective, phase-shifting transformers are also asymmetric when the phase is different from 0,
[
37].
3. Case Study
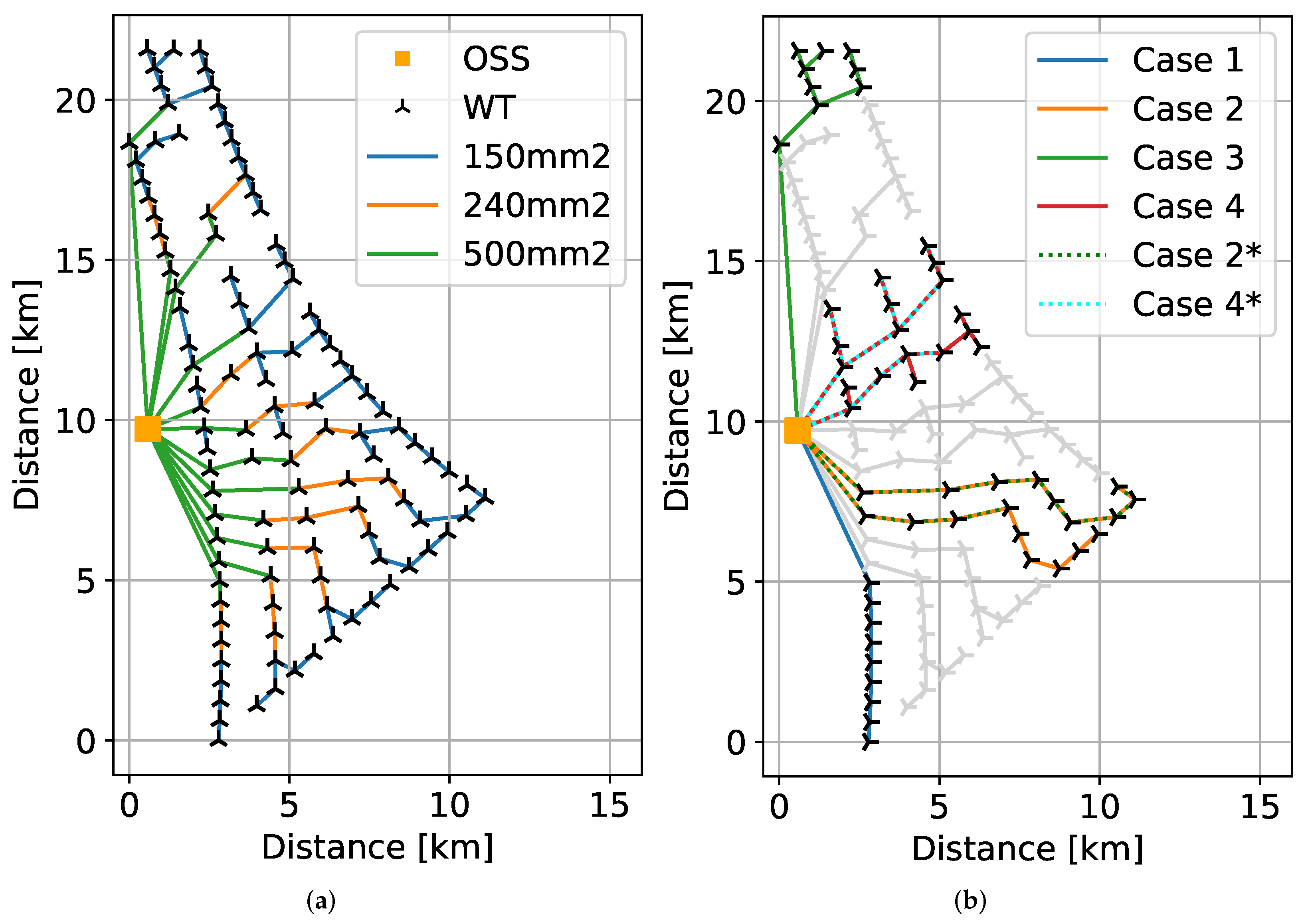
This paper intends to benchmark aggregation techniques against the modal aggregation technique based on different collector system layouts. Therefore, the paper is inspired by the Anholt Wind Farm (400 MW, with 111 WTs of 3.6 MW capacity distributed equally in 12 strings) located in Denmark [
38]. The layout of the wind farm is found in [
33] and shown in
Figure 4. The cable data is taken from [
39] and noted in
Table 1. Four base study cases are considered for model aggregation to study the behavior. Study case 2 and 4 are also investigated with an unequal number of WTs in each feeder to show the challenges with asymmetry. Layout properties are given in
Table 2. The wind farm layout and study cases are shown in
Figure 4:
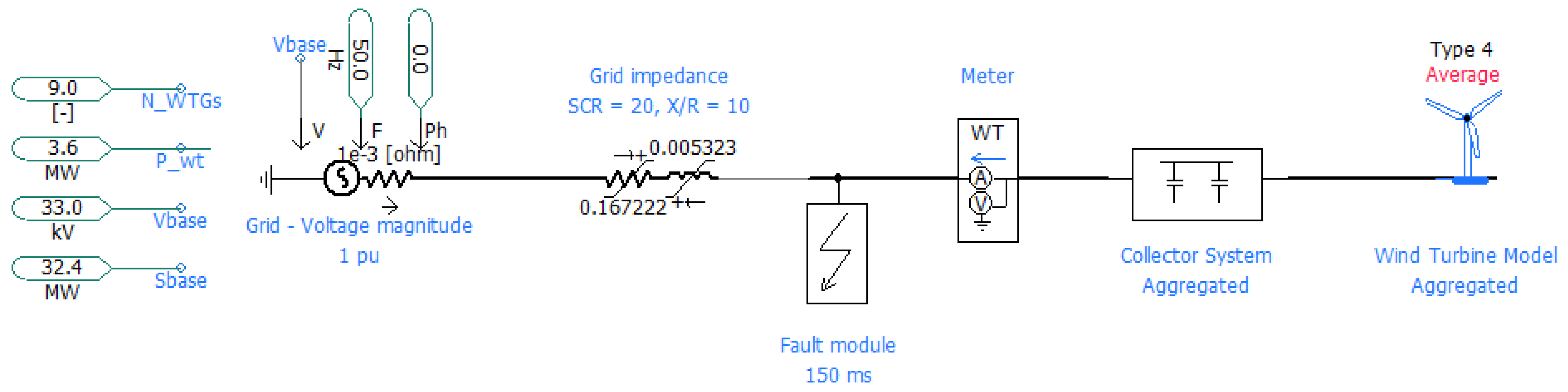
The model of the detailed and aggregated study cases are built in PSCAD 4.6.3. The WT model is a type-4B (includes aerodynamic and mechanical parts [
40]) and is publicly available in PSCAD examples [
41]. The model used is an averaged model, which disregards switching ripples. The WT model includes fault-ride-through (FRT) capabilities. The grid (OSS node) is modeled by a voltage source behind a grid impedance (
,
). All cables are modelled as PI-sections.
To compare the aggregation accuracy and precision, the dynamic behavior of the system is investigated in time-domain by applying a 3-phased bolted fault to ground at the OSS. The aggregated model implemented in PSCAD is shown in
Figure 5:
4. Aggregation Techniques
4.1. Benchmarked Aggregation Techniques
The voltage drop [
21,
22,
23], the power loss #1 [
42], and the power loss #2 [
22,
24,
28] aggregation techniques use weighting of the individual impedance with respect to the amount of current injected that it carries (per unit) (The IDs added for the power loss methods is our notation.). In
Figure 1a, an OWF is represented by
M feeders, with corresponding
WTs of the individual feeder,
m. In
Figure 1b, it is shown that the WT itself is simplified with a current source connected to the grid bus with the voltage
and an associated current source, representing current injections from the grid,
.
The aggregation of feeder
m is denoted as
and the aggregation of all feeders are denoted as
. The graph model of the system considers a weighting of each cable section as shown in
Figure 6 for an offshore substation (OSS) with two strings. In one of the strings, there are branches, and a basic array of WTs in the other. The example shows an asymmetry in number of WTs per string.
The mentioned aggregation techniques are shown in
Table 3. It is seen that the equivalent impedance of each feeder
is based on the weighting of each cable section (exemplified in
Figure 6). The weighting term for the voltage drop method is based on the relation
. The power loss method is based on the relation
in contrast.
The equivalent impedance of the feeders is common in the voltage drop and the power loss #1 technique, as they consider the equivalent impedance being the impedance in parallel considered from general electro-technics:
. The power loss #2 method suggests in contrast that the impedance of each string should be weighted with the number of WTs in the string and then normalized with the total number of WTs of strings aggregated (
20).
The equivalent capacitance of the cables are common for all the mentioned methods and considered to be parallel and thus summed up.
4.2. Developing a -Equivalent from the Modal Aggregation Technique
For benchmarking purposes of the impedance accuracy of the aggregation techniques mentioned in
Section 4.1, the equivalent grid impedance is considered as the receiving port of the AS impedance by the modal aggregation technique:
The admittance matrix is the inverse of
:
Because of the asymmetric properties of
, it is proposed to develop a
-equivalent by averaging the respective reciprocal element of
:
By disregarding the asymmetric properties of the modal aggregated impedance, it is obvious that some information of the internal dynamics of the collector system is disregarded as well. It, however, allows benchmarking the modal aggregation technique against the other aggregation techniques by time-domain simulations in an immediate manner.
5. Results
The two-norm of the error matrix of the modal aggregation technique and the associated
-equivalent for each of the aggregation techniques are compared. The results are found in
Table 4 and scaled in milliSiemens:
It is observed that the PL2 aggregation technique is by far the most precise aggregation technique with respect to the two-norm, deviating in average by 1.53 mS.
The equivalent impedances are calculated with respect to (
26) and (
15)–(
23) for each case study presented in
Section 3. A comparison of the impedances is given in
Figure 7 where the modal impedance is given by (
24).
The voltage drop technique differs from the modal aggregation technique in all cases. The power loss techniques match the modal aggregation technique in all cases except for power loss #1 in case 2* and 4*. The discrepancy is due to the asymmetric number of wind turbines in the individual aggregated string. It is thus clear that the power loss #2 technique is the only technique that matches with the modal aggregation technique in all test systems regardless of branches, multi-string aggregation, or asymmetric string properties.
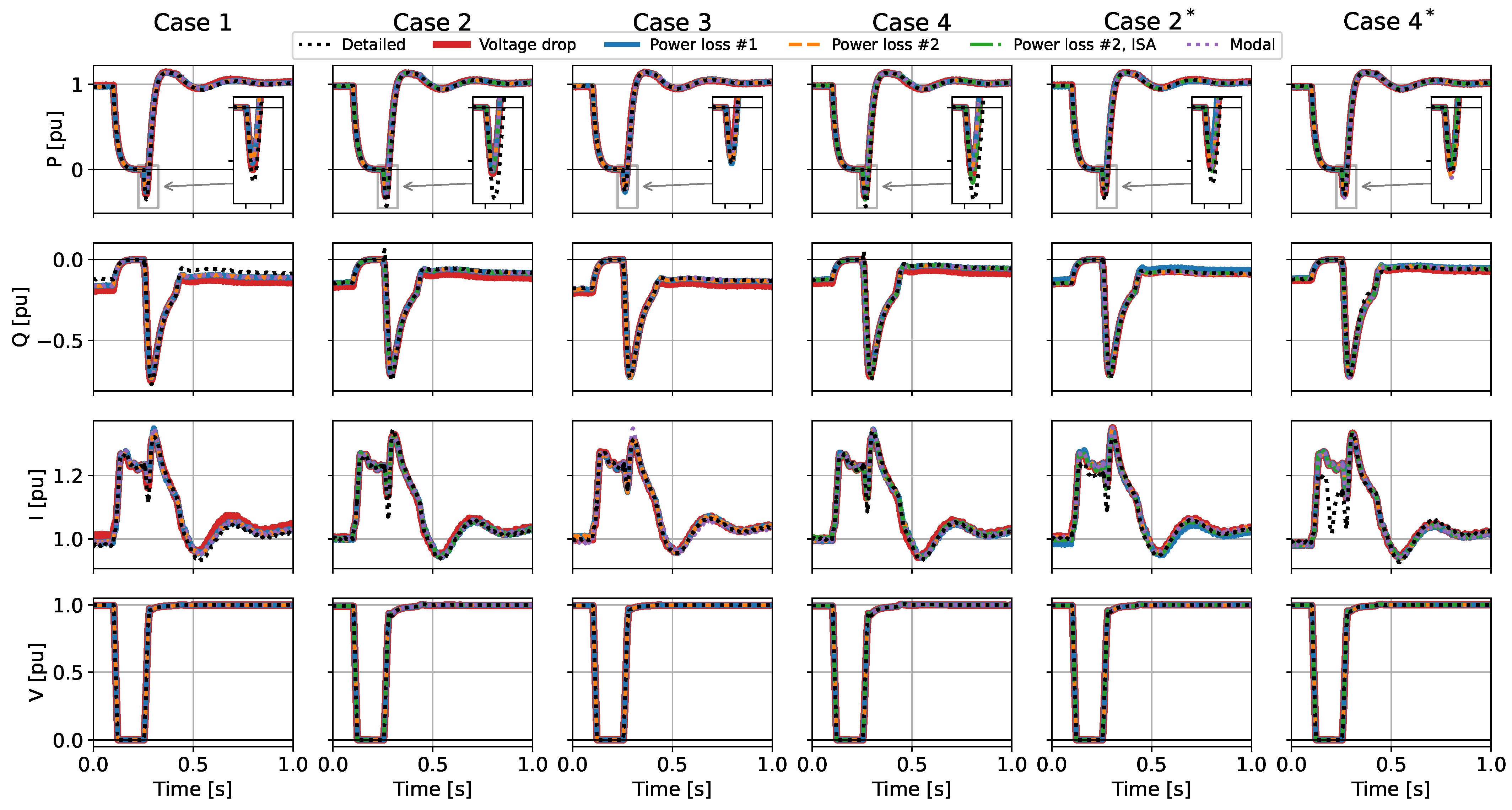
The equivalent impedance of the respective collector systems and aggregation technique allows a study of the accuracy of time-domain simulations against the detailed model.
Figure 8 shows two selected cases (the rest can be found in
Appendix A). For test systems, where the number of strings is greater than one, i.e.,
, results from an aggregated model with individual string aggregation (ISA) are plotted additionally.
All aggregation techniques match the active power response quite well in general. Only during the power reversal post-fault in the beginning of the recovery period, a difference is noted. Except for the VD, there is in general a reasonable match in reactive power. However, the asymmetric case test 4* shows some noticeable deviation. In general, the currents show a larger discrepancy. Case 1 (single string with radial configuration) shows a relatively large post fault deviation where all the other tests show a fair match. In most cases, the transients when recovering from the fault show deviations in peak values. During the fault, only a remarkable mismatch in asymmetric string configurations (test 2* and 4*) has been identified. Voltage similarity is satisfying.
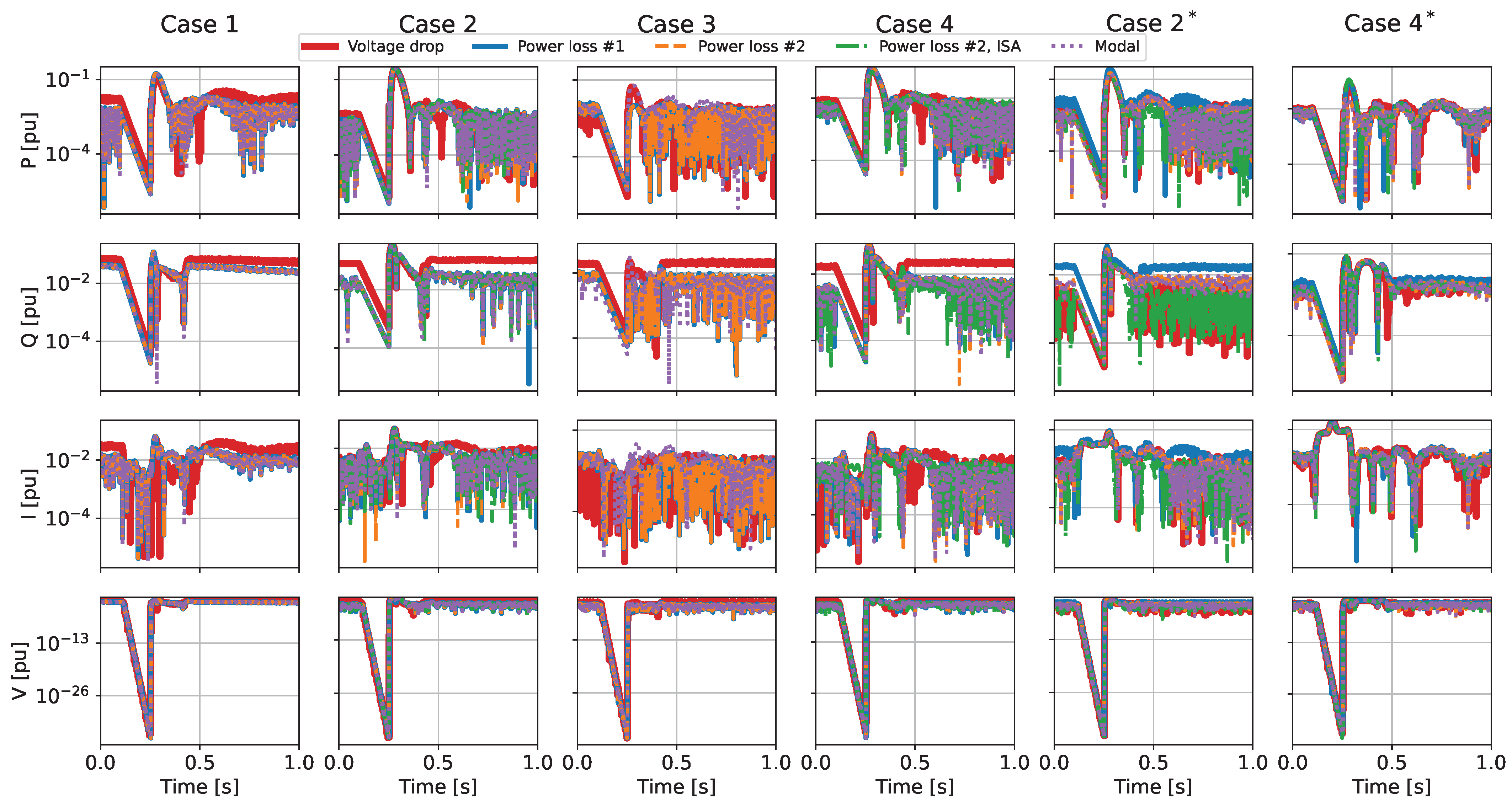
The error,
, of the aggregation techniques are plotted and can be found in the
Appendix B. To investigate the performance of the aggregation techniques further, the error is quantified by an RMS of the error:
The RMS errors are found in the
Table 5, where the best performing aggregation technique for active power, reactive power, current, and voltage for the respective tests is noted.
The power loss aggregation technique is best in general. It is also seen that there is no effective difference in PL1 and PL2, except for cases of asymmetric strings. In such cases, PL2 matches the best. In cases of more strings than 1, , it is generally seen that it is best to aggregate each string individually. However, ISA does not have any major effect in test 2 (two symmetric strings, no branches). In contrast, ISA has a remarkable effect in test 4 (two symmetric strings, branches). ISA has mixed results when it comes to asymmetric strings; PL2 is best in test 2* but underperforms a bit in test 4*.
The -equivalent model by the modal aggregation technique is in general performing well in comparison as it reaches an average matching ISA and beats VD and PL1, even though the ISA neglects some dynamic behavior stored in the eigenvalues by averaging the transfer admittance.
6. Discussion
The power loss aggregation technique is proven to be the best aggregation technique, and ISA is the optimal approach in most cases. The basis of the assumptions for the modal aggregation technique are discussed in this section. In
Section 6.1, the assumption of equal current injection is discussed and how non-equal current injections impact the DCFR. In
Section 6.2, the DCFR is investigated with respect to higher frequencies to demarcate the validity of the aggregation. In
Section 6.3, the sensitivity of DCFR is elaborated with respect to the impedance magnitude.
6.1. Equal Current Injection–Monte Carlo Simulation
The assumptions of the equal current distribution from (
11) can be argued to be naive. Monte Carlo simulation (MCS) can be a numerical support and justification of the assumptions of equally distributed currents.
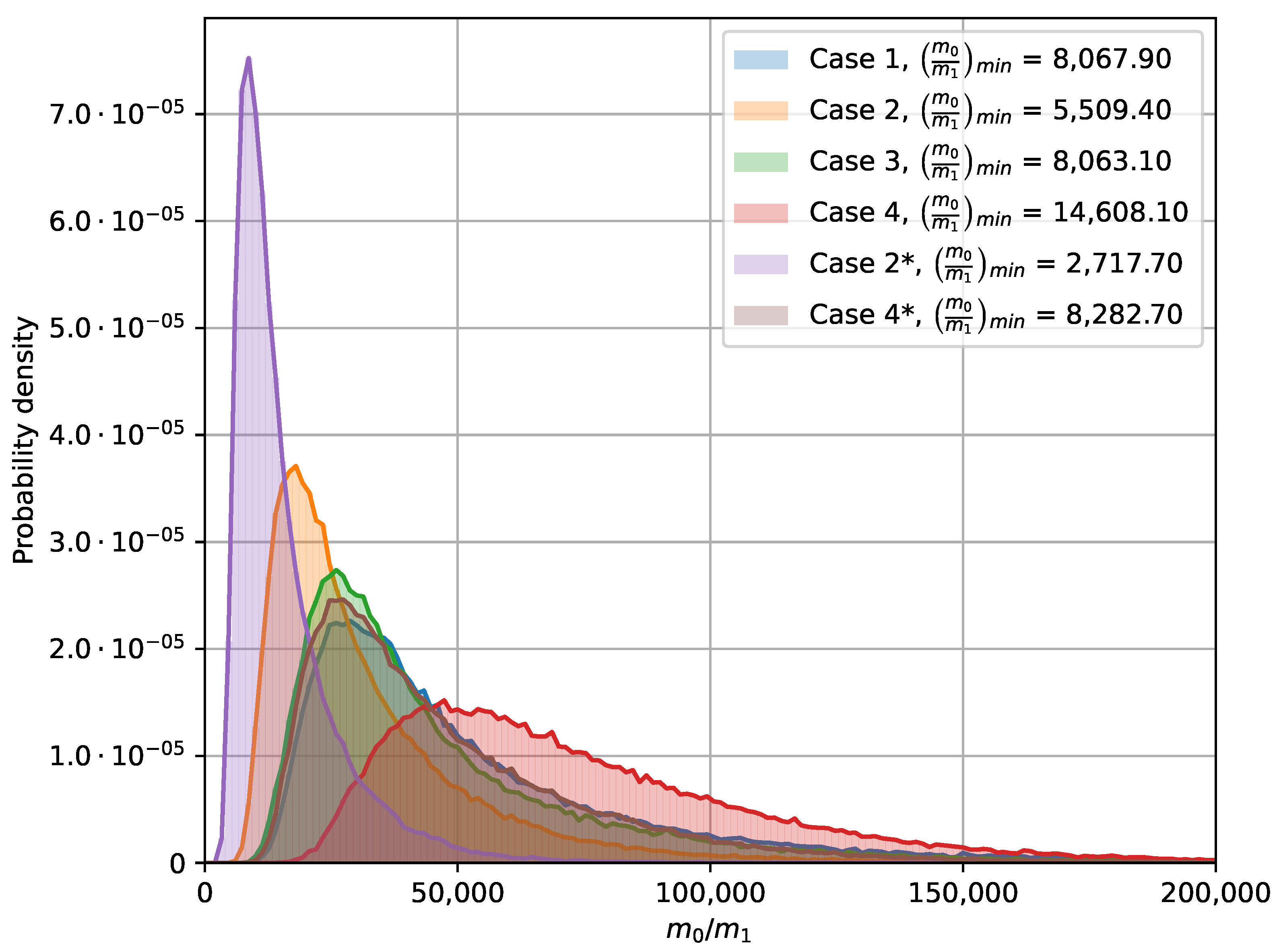
In the MCS presented, the dominant contribution factor ratio (DCFR) is considered from 100,000 samples, while randomizing the current magnitude uniformly distributed in [0.1, 1.0] and phase angle uniformly distributed in [−60
, 60
]. The dominant contribution factor ratio is defined as:
The DCFR is shown in
Figure 9. It is seen that the case studies have a great impact on the distribution of DCFR, but the DCFR is in either case very large and the impact of non-equal current injections are thus negligible. The lowest DCFR observed is 2665.5 for case 2*. It is noticed that asymmetric variants of the corresponding case study has a negative impact on the DCFR distribution, meaning that the aggregation would be more challenging.
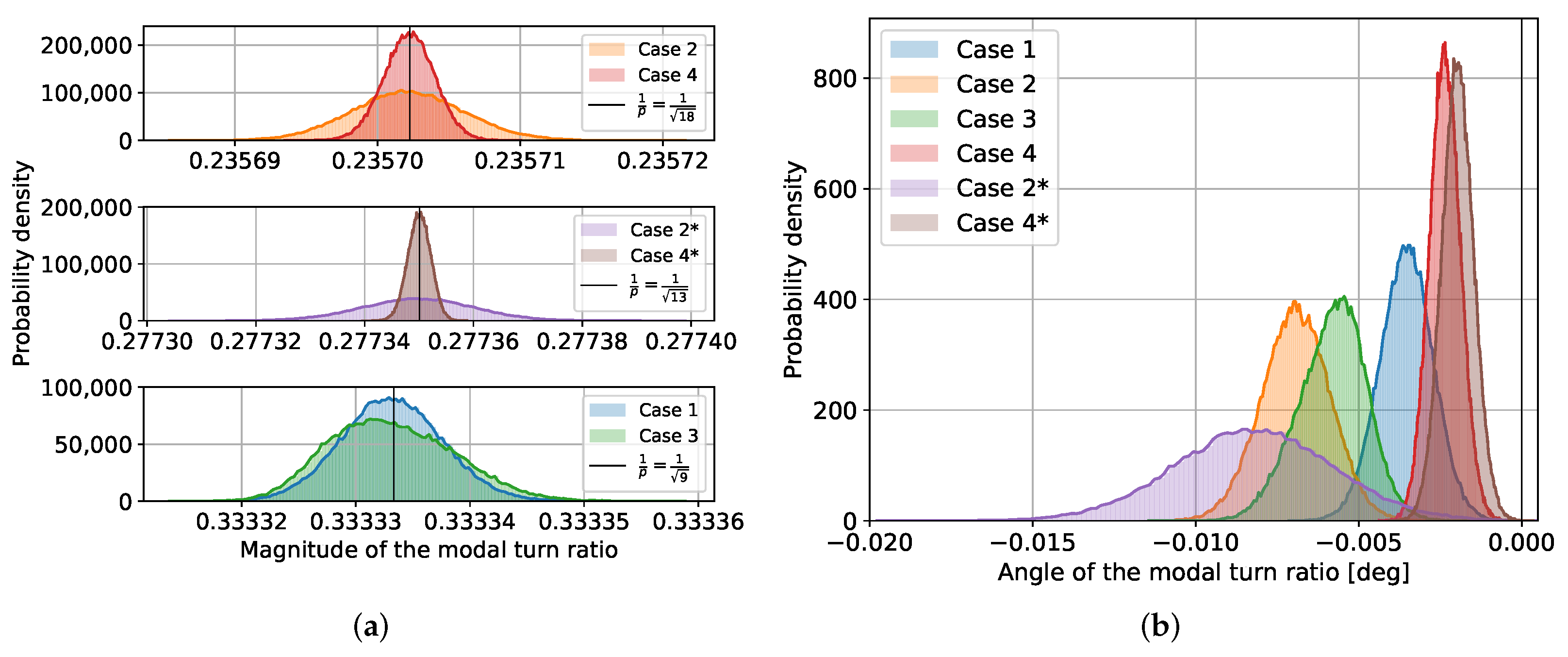
The impact on the modal turn ratio
p of non-equal current injections is considered by MCS. In
Figure 10a,b, the magnitude and phase angle of the modal turn ratio is considered, respectively. The magnitude of the modal turn ratio follows by high accuracy the rule,
, and seems to equal the mean of the distribution (except for case 3, which is slightly right-skewed). The phase angles do not differ much in most cases and are considered negligible. There is no clear pattern of impact of asymmetric strings, nor aggregating more strings than 1.
Non-equal current injections are thus considered not to have a devastating impact on the DCFR, and the modal aggregation technique thus holds as a verification model, as the contribution factors of the passive collector system do not depend on load flow conditions.
6.2. DCFR and Higher Frequencies
The harmonic impedance is of great importance when performing detailed studies. The DCFR is studied with respect to higher frequencies and plotted in
Figure 11.
Figure 11a, ranging 50–400 Hz, is a zoomed version of
Figure 11b, ranging 50–2500 Hz. In
Figure 11a, it is observed that the intersection of the DCFR and the tentative DCFR limit varies with respect to the case study. It is in general observed that the case studies with multiple strings are more impacted by higher frequencies. This fact supports the ISA approach.
It was investigated whether another DCFR would show itself for higher frequencies. This is, however, rejected by the plot in
Figure 11b as no other DCFR reaches over the tentative DCFR limit.
It is thus clear that studies of harmonic emissions from converter switching frequencies of around 1500 Hz or fast transients like switching impulses with a front time of 20 kHz [
43] are incompatible with an aggregated model. Using detailed models should thus be used for studies for high frequencies.
In an aggregation perspective, modelling higher frequencies would require a higher order of the RLC equivalent component to be realized.
6.3. Impedance Magnitude Distance (Mode Ratio)
Anholt Wind Farm was commissioned in 2013 and WTs have grown in size and capacity since then. This development increases the distance between the individual turbines for a better energy yield. As 66 kV is currently a new standard voltage for collector systems, new cable data will dictate the impedance characteristics of the collector system. However, the DCFR is studied by multiplying the length of all cable sections with a distance factor. The results are shown in
Figure 12.
The DCFR decreases as the network impedance increases by the distance factor. Case studies with multiple strings tend to decrease more rapidly in DCFR in contrast to the single string systems. For instance,
Figure 12 shows that Case 2 is not accurate when the distance factor is bigger than 8 (based on a tentative threshold for DCFR = 100). It is also noticed that the situation is even worse for asymmetrical cases, i.e., cases 2* and 4*.
In
Figure 13, the time-domain simulation of case 2 with a distance factor of 15 is plotted to emphasize the validity of aggregation fails, as the DCFR is very low (
) and the second-largest mode is no more negligible.
The detailed model has a little oscillation in active power post fault as it recovers. The modal and the power loss techniques are plotted on top of each other and fail to replicate this behavior. The voltage drop technique fails to stabilize before the detailed model.
7. Conclusions and Future Works
Aggregation of the collector system of an OWF is beneficial as it is not dependent on the type of the wind turbine. It is not dependent on the detailed model of the wind turbine either, i.e., the aggregation does not change whether it is a black-box, white-box, or a grey-box model.
Case studies of different collector system layouts were derived from the Anholt Wind Farm and aggregated with the voltage drop, power loss, and modal aggregation techniques. The results from a dynamic simulation of a 3-phase to ground fault showed that the power loss technique is the most accurate aggregation technique for collector systems.
The impact of unequal currents from the wind turbines is shown to be negligible and, therefore, the same aggregation can be used for different operating conditions (e.g., different wind speeds).
Aggregation is a model order reduction as the entire array cable system is simplified into one cable section. Therefore, the aggregated model is expected not to be able to represent certain dynamics. It is shown that the frequency and length of array cables have a big impact on the validity of the aggregation in contrast.
Future work will thus look into: (1) impact of the aggregation on the stability and reliability of power systems, (2) defining a DCFR-based validity threshold, (3) developing an aggregation model based on the exact modal aggregation technique (e.g., a higher order RLC component model or an active impedance equivalent), (4) developing multi-port aggregated models based on the dominant contribution factors or nodes of interest, (5) the impact on the mix of cable types in the aggregated string and impact of the string layout, i.e., branching; (6) quantifying the impact on the grid voltage from, (7) benchmark performance of aggregation techniques for meshed networks or wind farms with loops against a modal aggregation technique-derived model.