Hf Incorporation in (Ti,Zr)NiSn Half Heusler Solid Solutions via Mechanical Alloying
Abstract
1. Introduction
2. Materials and Methods
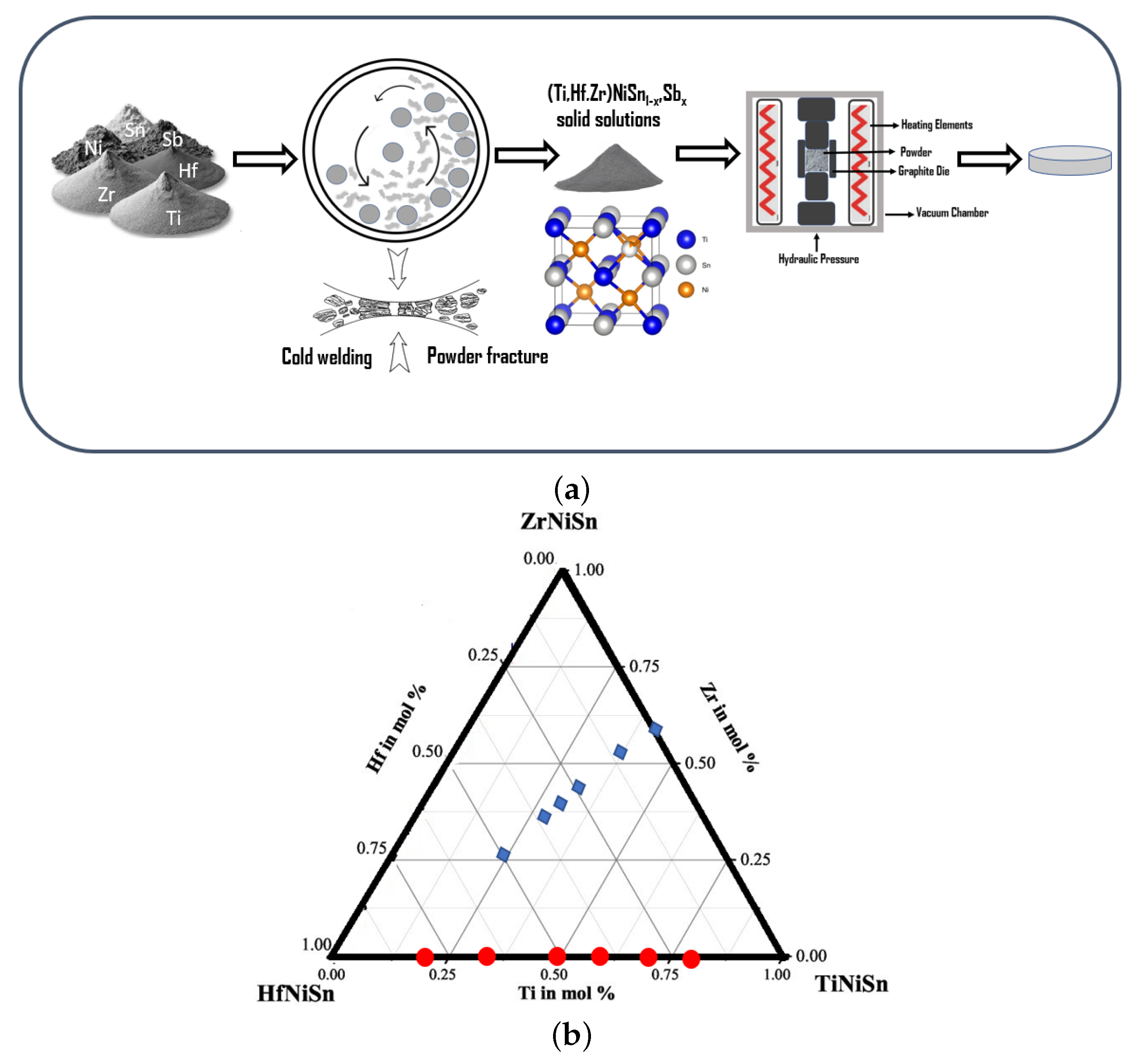
2.1. Fabrication of Half Heusler Materials
2.2. Microstructural Characterization
2.3. Thermoelectric Characterization
2.4. Mechanical Characterization
3. Results and Discussion
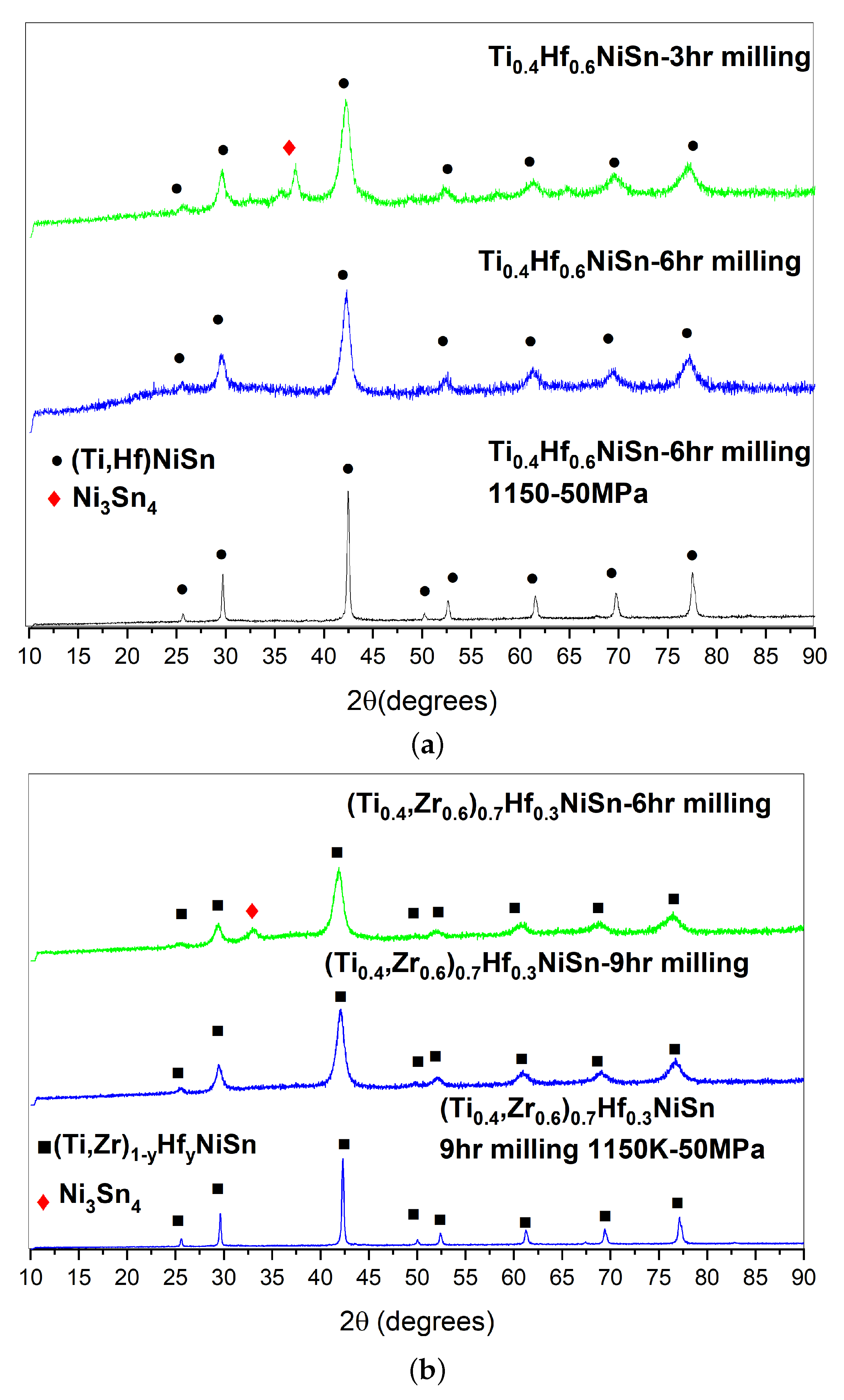
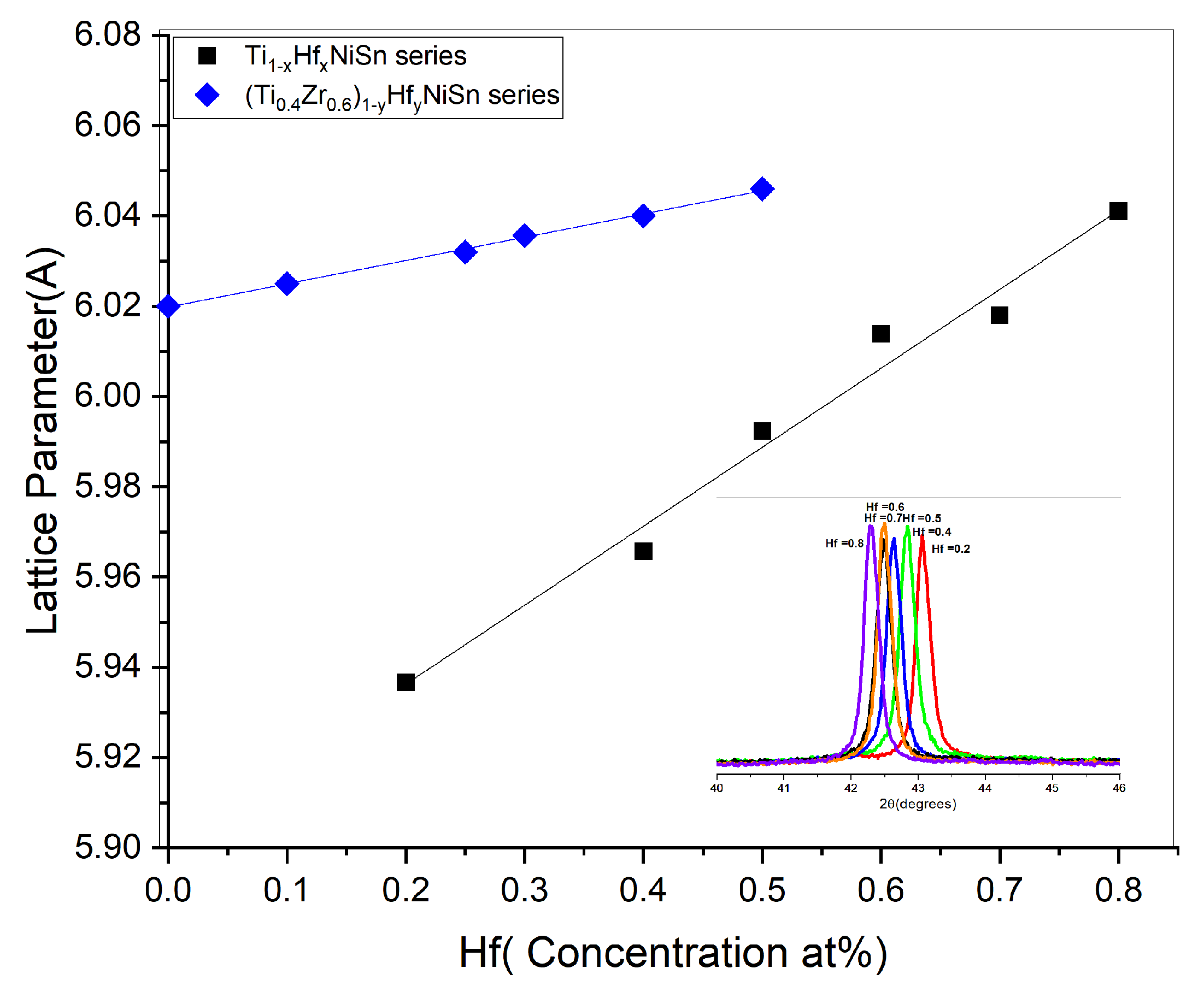
3.1. Synthesis of Ti-Hf and Ti-Hf-Zr Solid Solutions
3.2. Thermoelectric Properties of Ti-Hf and Ti-Hf-Zr Solid Solutions
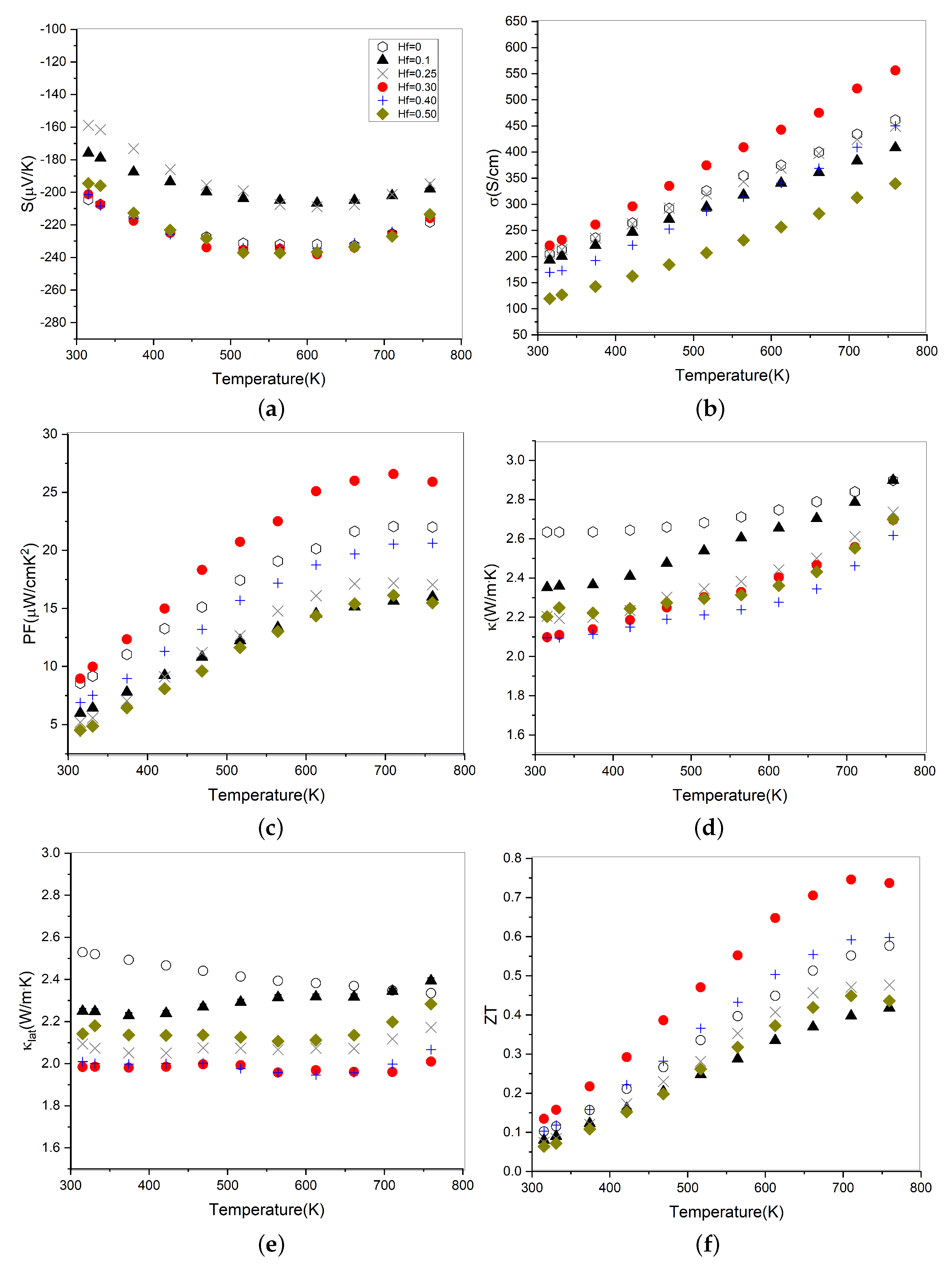
3.2.1. Thermoelectric Properties of the Ti1−xHfxNiSn Series
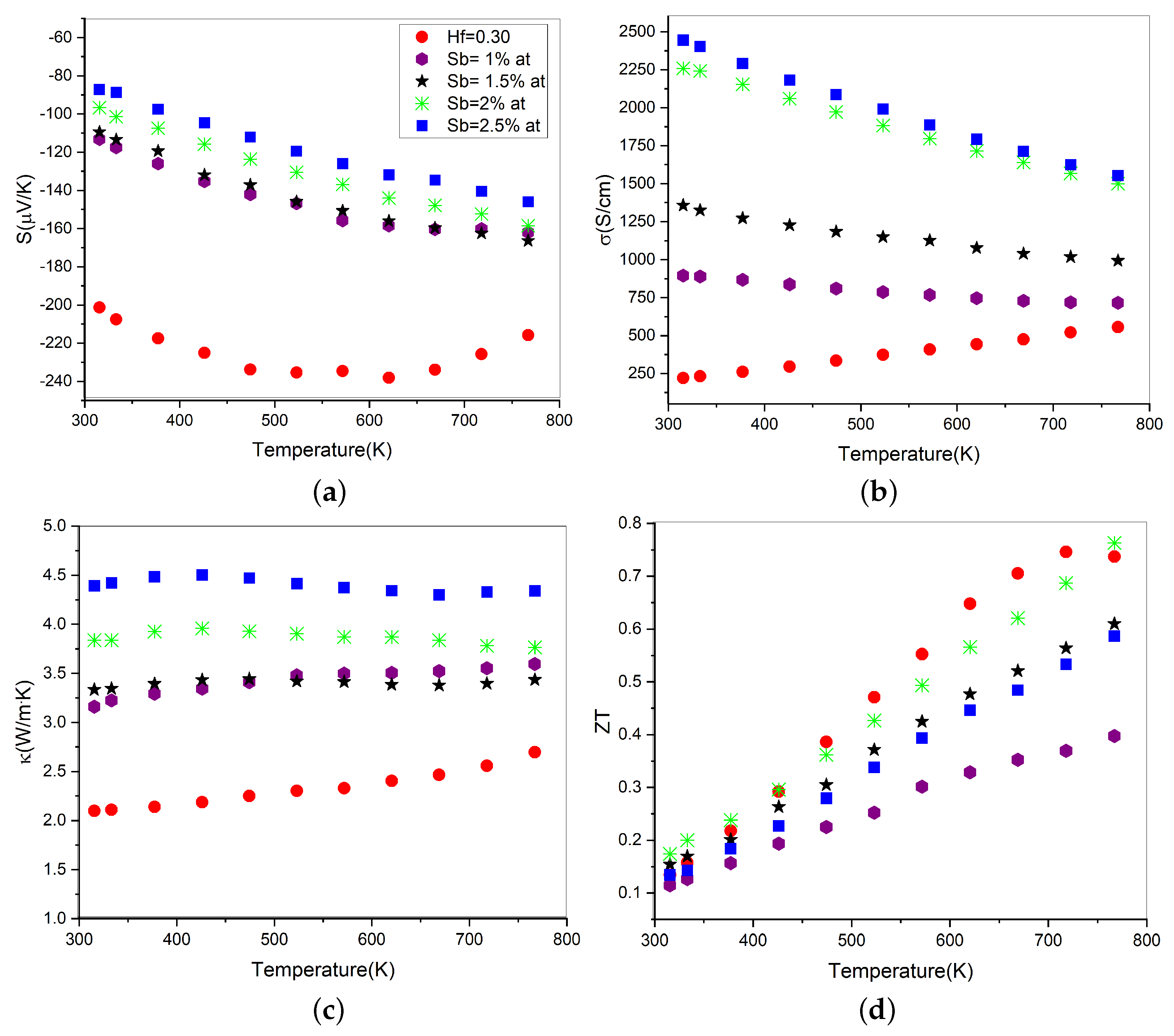
3.2.2. Thermoelectric Properties of Sb-Doped Ti0.4Hf0.6NiSn
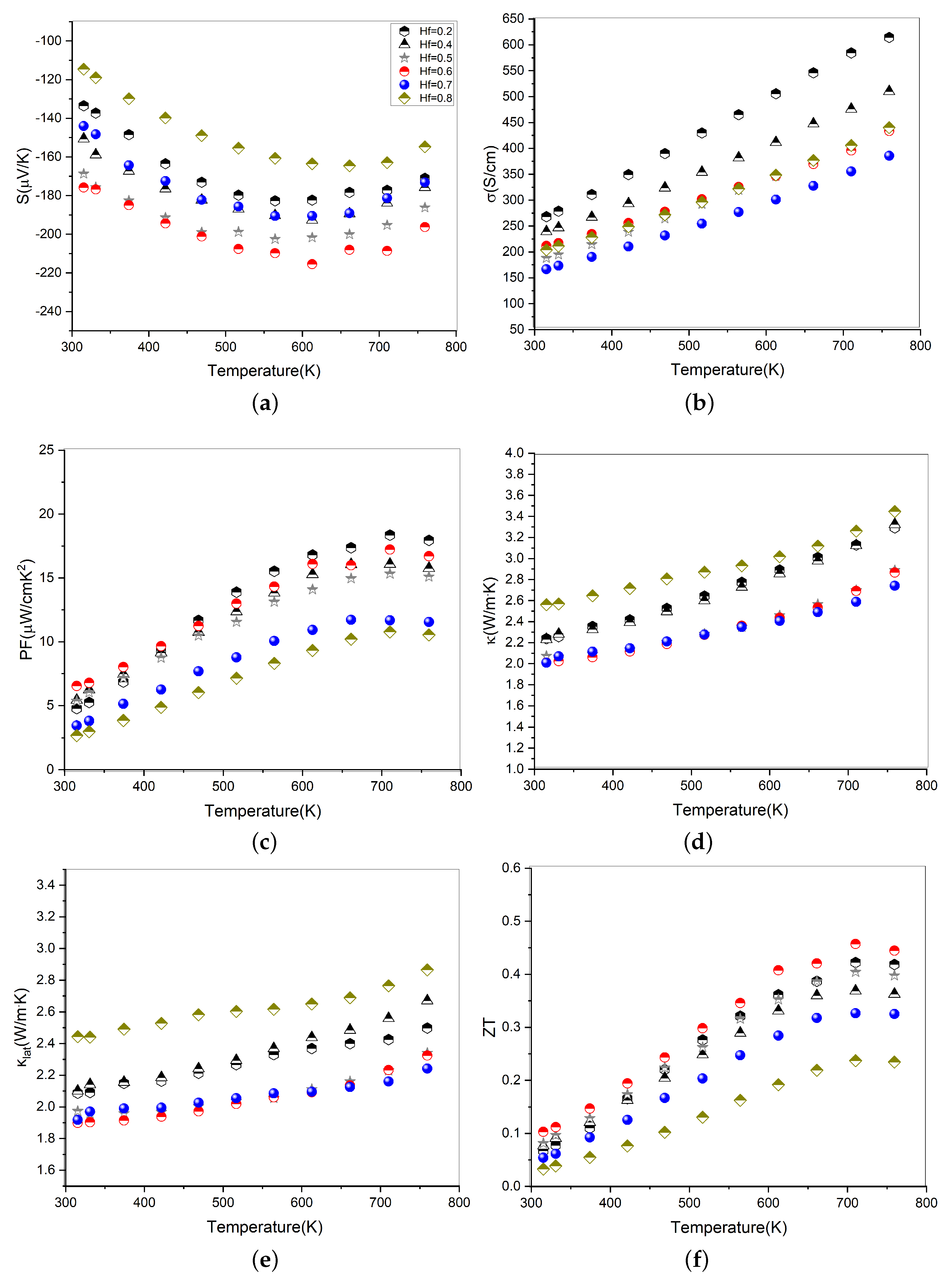
3.2.3. Thermoelectric Properties of the (Ti0.4Zr0.6)1−yHfyNiSn Series
3.2.4. Thermoelectric Properties of Sb-Doped (Ti0.4 Zr0.6)0.7Hf0.3NiSn
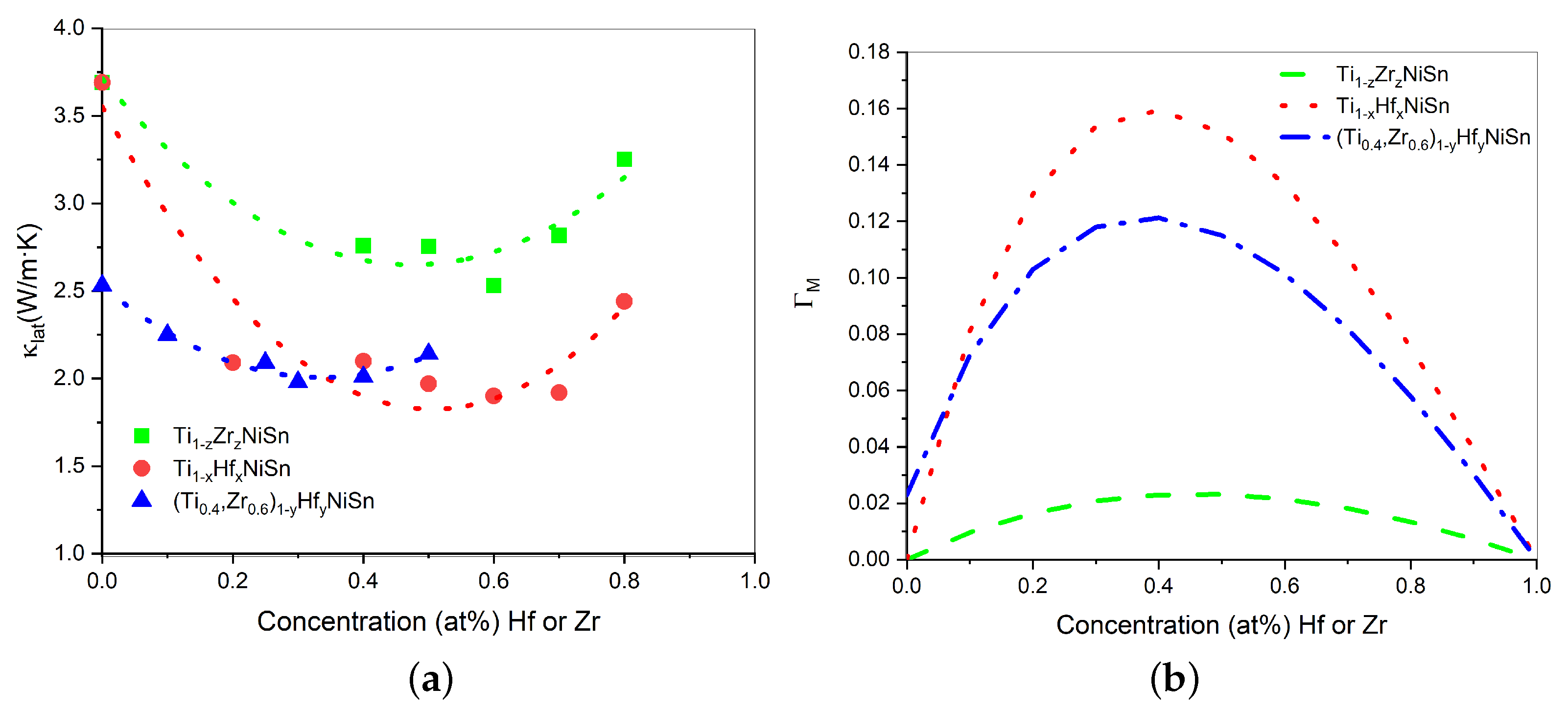
3.2.5. Thermal Conductivity of MA (Ti,Zr,Hf)NiSn Solid Solutions
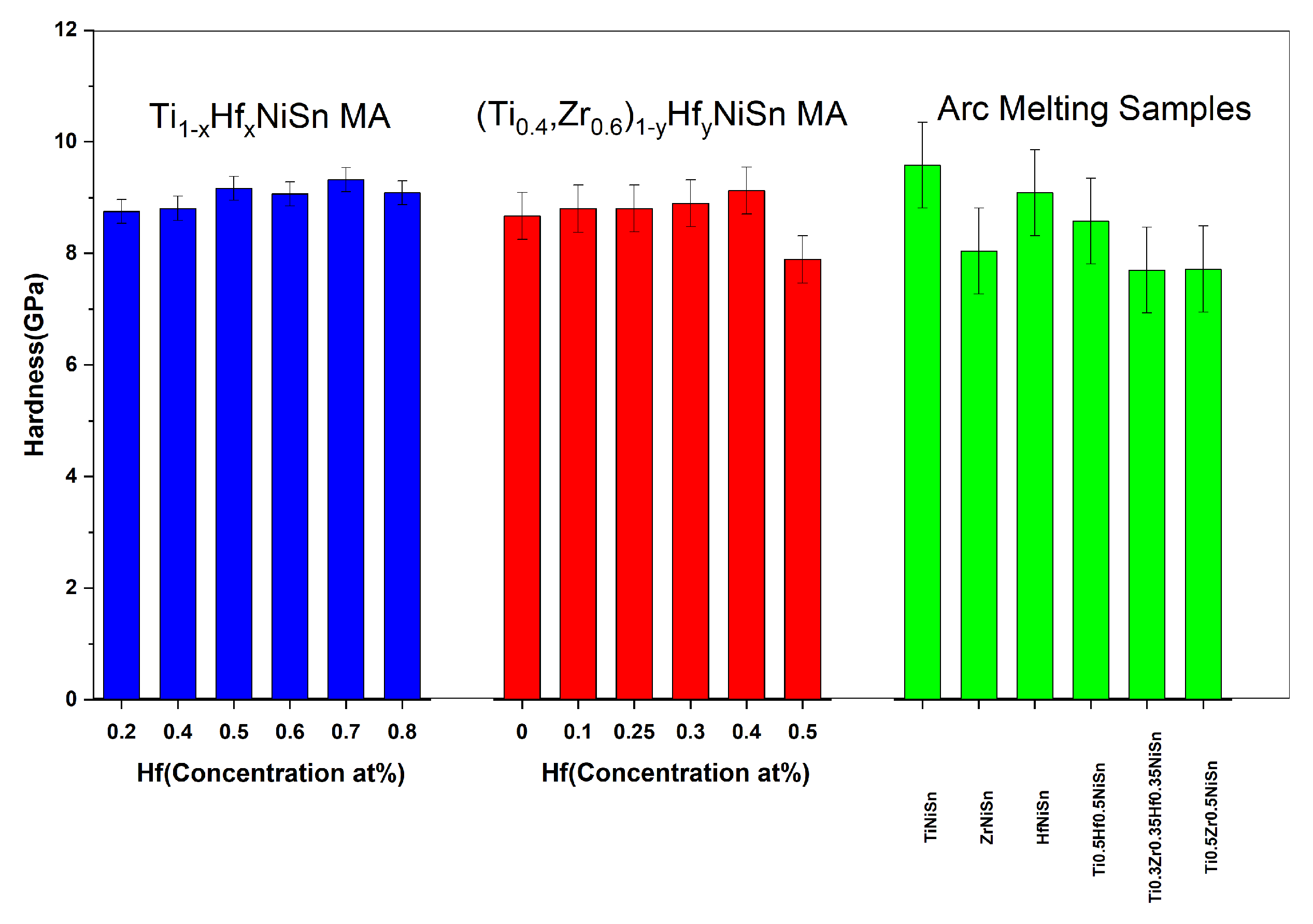
3.3. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Snyder, G.; Toberer, E. Complex Thermoelectric Materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Yang, L.; Ma, Z.; Song, P.; Zhang, M.; Ma, J.; Yang, F.; Wang, X. Review of current high-ZT thermoelectric materials. J. Mater. Sci. 2020, 55, 12642–12704. [Google Scholar] [CrossRef]
- Shi, X.L.; Zou, J.; Chen, Z.G. Advanced Thermoelectric Design: From Materials and Structures to Devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef] [PubMed]
- Rull-Bravo, M.; Moure, A.; Fernández, J.F.; Martín-González, M. Skutterudites as thermoelectric materials: Revisited. RSC Adv. 2015, 5, 41653–41667. [Google Scholar] [CrossRef]
- Rogl, G.; Ghosh, S.; Renk, O.; Yubuta, K.; Grytsiv, A.; Schafler, E.; Zehetbauer, M.; Mallik, R.C.; Bauer, E.; Rogl, P. Influence of shear strain on HPT-processed n-type skutterudites yielding ZT = 2.1. J. Alloys Compd. 2021, 855, 157409. [Google Scholar] [CrossRef]
- Schierning, G.; Chavez, R.; Schmechel, R.; Balke, B.; Rogl, G.; Rogl, P. Concepts for medium-high to high temperature thermoelectric heat-to-electricity conversion: A review of selected materials and basic considerations of module design. Transl. Mater. Res. 2015, 2, 025001. [Google Scholar] [CrossRef]
- Sankhla, A.; Kamila, H.; Kelm, K.; Mueller, E.; de Boor, J. Analyzing thermoelectric transport in n-type Mg2Si0.4Sn0.6 and correlation with microstructural effects: An insight on the role of Mg. Acta Mater. 2020, 199, 85–95. [Google Scholar] [CrossRef]
- Mesaritis, G.; Symeou, E.; Delimitis, A.; Constantinou, M.; Constantinides, G.; Jeagle, M.; Tarantik, K.; Kyratsi, T. Synthesis, characterization and thermoelectric performance of Mg2(Si,Sn,Ge) materials using Si-kerf waste from photovoltaic technology. J. Alloys Compd. 2020, 826, 153933. [Google Scholar] [CrossRef]
- Mesaritis, G.; Symeou, E.; Delimitis, A.; Oikonomidis, S.; Jaegle, M.; Tarantik, K.; Nicolaou, C.; Kyratsi, T. Recycling Si-kerf from photovoltaics: A very promising route to thermoelectrics. J. Alloys Compd. 2019, 775, 1036–1043. [Google Scholar] [CrossRef]
- Xie, W.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T.M. Recent Advances in Nanostructured Thermoelectric Half-Heusler Compounds. Nanomaterials 2012, 2, 379–412. [Google Scholar] [CrossRef]
- Zhu, T.; Fu, C.; Xie, H.; Liu, Y.; Zhao, X. High Efficiency Half-Heusler Thermoelectric Materials for Energy Harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Zeier, W.; Schmitt, J.; Hautier, G.; Aydemir, U.; Gibbs, Z.; Felser, C.; Snyder, G. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 2016, 1, 16032. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Skove, M.J.; Russell, M.; Tritt, T.M.; Xia, Y.; Ponnambalam, V.; Poon, S.J.; Thadhani, N. Effect of boundary scattering on the thermal conductivity of TiNiSn-based half-Heusler alloys. Phys. Rev. B 2008, 77, 184203. [Google Scholar] [CrossRef]
- Geng, H.; Meng, X.; Zhang, H.; Zhang, J. Lattice thermal conductivity of nanograined half-Heusler solid solutions. Appl. Phys. Lett. 2014, 104, 202104. [Google Scholar] [CrossRef]
- Schrade, M.; Berland, K.; Eliassen, S.; Guzik, M.; Echevarria-Bonet, C.; Sørby, M.; Jenus, P.; Hauback, B.; Tofan, R.; Gunnæs, A.; et al. The role of grain boundary scattering in reducing the thermal conductivity of polycrystalline XNiSn (X = Hf, Zr, Ti) half-Heusler alloys. Sci. Rep. 2017, 7, 13760. [Google Scholar] [CrossRef]
- Katayama, T.; Kim, S.; Kimura, Y.; Mishima, Y. The effects of quaternary additions on thermoelectric properties of TiNiSn-based half-Heusler alloys. J. Electron. Mater. 2003, 32, 1160–1165. [Google Scholar] [CrossRef]
- Hohl, H.; Ramirez, A.P.; Goldmann, C.; Ernst, G.; Wölfing, B.; Bucher, E. Efficient dopants for ZrNiSn-based thermoelectric materials. J. Phys. Condens. Matter 1999, 11, 1697–1709. [Google Scholar] [CrossRef]
- Joshi, G.; Dahal, T.; Chen, S.; Wang, H.; Shiomi, J.; Chen, G.; Ren, Z. Enhancement of thermoelectric figure-of-merit at low temperatures by titanium substitution for hafnium in n-type half-Heuslers Hf0.75−xTixZr0.25NiSn0.99Sb0.01. Nano Energy 2013, 2, 82–87. [Google Scholar] [CrossRef]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.P.; Uher, C. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 2001, 79, 4165–4167. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr,Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 2005, 86, 082105. [Google Scholar] [CrossRef]
- Zhu, H.; He, R.; Mao, J.; Zhu, Q.; Li, C.; Sun, J.; Ren, W.; Wang, Y.; Liu, Z.; Tang, Z.; et al. Discovery of ZrCoBi based half Heuslers with high thermoelectric conversion efficiency. Nat. Commun. 2018, 9, 2497. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Bai, S.; Liu, Y.; Tang, Y.; Chen, L.; Zhao, X.; Zhu, T. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 8144. [Google Scholar] [CrossRef] [PubMed]
- Young, J.; Reddy, R. Processing and Thermoelectric Properties of TiNiSn Materials: A Review. J. Mater. Eng. Perform. 2019, 28, 5917–5930. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Zou, B.; Xu, P.; Song, Y.; Xu, B.; Wang, Y.; Tang, G.; Yang, S. Significant enhancement in thermoelectric properties of half-Heusler compound TiNiSn by grain boundary engineering. J. Alloys Compd. 2022, 901, 163686. [Google Scholar] [CrossRef]
- Zou, M.; Li, J.F.; Du, B.; Liu, D.; Kita, T. Fabrication and thermoelectric properties of fine-grained TiNiSn compounds. J. Solid State Chem. 2009, 182, 3138–3142. [Google Scholar] [CrossRef]
- Tillard, M.; Berche, A.; Jund, P. Synthesis of Pure NiTiSn by Mechanical Alloying: An Investigation of the Optimal Experimental Conditions Supported by First Principles Calculations. Metals 2018, 8, 835. [Google Scholar] [CrossRef]
- Ioannou, I.; Ioannou, P.S.; Delimitis, A.; Gelbstein, Y.; Giapintzakis, I.J.; Kyratsi, T. High thermoelectric performance of p-type half-Heusler (Hf,Ti)Co(Sb,Sn) solid solutions fabricated by mechanical alloying. J. Alloys Compd. 2021, 858, 158330. [Google Scholar] [CrossRef]
- Ioannou, I.; Delimitis, A.; Gelbstein, Y.; Kyratsi, T. Reduction of Hf via Hf/Zr Substitution in Mechanically Alloyed (Hf,Ti)CoSb Half-Heusler Solid Solutions. Inorganics 2022, 10, 51. [Google Scholar] [CrossRef]
- Mesaritis, G.; Ioannou, I.; Delimitis, A.; Hatzikraniotis, E.; Gelbstein, Y.; Kyratsi, T. n-type (Zr,Ti)NiSn half Heusler materials via mechanical alloying: Structure, Sb-doping and thermoelectric properties. J. Phys. Chem. Solids 2022, 167, 110735. [Google Scholar] [CrossRef]
- Altomare, A.; Cuocci, C.; Giacovazzo, C.; Moliterni, A.; Rizzi, R.; Corriero, N.; Falcicchio, A. EXPO2013: A kit of tools for phasing crystal structures from powder data. J. Appl. Crystallogr. 2013, 46, 1231–1235. [Google Scholar] [CrossRef]
- Schwall, M.; Balke, B. On the Phase Separation in n-Type Thermoelectric Half-Heusler Materials. Materials 2018, 11, 649. [Google Scholar] [CrossRef]
- Page, A.; Van der Ven, A.; Poudeu, P.F.P.; Uher, C. Origins of phase separation in thermoelectric (Ti, Zr, Hf)NiSn half-Heusler alloys from first principles. J. Mater. Chem. A 2016, 4, 13949–13956. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Kim, K.; Kim, Y.; Mun, H.; Kim, J.; Park, J.; Borisevich, A.; Lee, K.; Kim, S. Direct Observation of Inherent Atomic-Scale Defect Disorders responsible for High-Performance Ti1−xHfxNiSn1−ySby Half-Heusler Thermoelectric Alloys. Adv. Mater. 2017, 29, 1702091. [Google Scholar] [CrossRef]
- Qiu, P.; Yang, J.; Huang, X.; Chen, X.; Chen, L. Effect of antisite defects on band structure and thermoelectric performance of ZrNiSn half-Heusler alloys. Appl. Phys. Lett. 2010, 96, 152105. [Google Scholar] [CrossRef]
- May, A.F.; Snyder, G.J. Introduction to Modeling Thermoelectric Transport at High Temperatures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Bhattacharya, S.; Pope, A.; Littleton, R.; Tritt, T.; Ponnambalam, V.; Xia, Y.; Poon, S. Effect of Sb doping on the thermoelectric properties of Ti-based half-Heusler compounds, TiNiSn1−xSbx. Appl. Phys. Lett. 2000, 77, 2476–2478. [Google Scholar] [CrossRef]
- Gong, B.; Liu, F.; Zhu, J.; Wang, X.; Ao, W.; Zhang, C.; Li, Y.; Li, J.; Xie, H. Effects of Sc, Ti, Hf, V, Nb and Ta doping on the properties of ZrNiSn alloys. J. Mater. Sci. 2019, 54, 10325–10334. [Google Scholar] [CrossRef]
- Yang, J.; Meisner, G.; Chen, L. Strain Field Fluctuation Effects on Lattice Thermal Conductivity of ZrNiSn-Based Thermoelectric Compounds. Appl. Phys. Lett. 2004, 85, 1140–1142. [Google Scholar] [CrossRef]
- He, R.; Gahlawat, S.; Guo, C.; Chen, S.; Dahal, T.; Zhang, H.; Liu, W.; Zhang, Q.; Chere, E.; White, K.; et al. Studies on mechanical properties of thermoelectric materials by nanoindentation. Phys. Status Solidi (a) 2015, 212, 2191–2195. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Gürth, M.; Tavassoli, A.; Ebner, C.; Wünschek, A.; Puchegger, S.; Soprunyuk, V.; Schranz, W.; Bauer, E.; et al. Mechanical properties of half-Heusler alloys. Acta Mater. 2016, 107, 178–195. [Google Scholar] [CrossRef]
- Kawaharada, Y.; Kurosaki, K.; Muta, H.; Uno, M.; Yamanaka, S. Thermophysical properties of NiZrSn1−xSbx half-Heusler compounds. J. Alloys Compd. 2004, 381, 9–11. [Google Scholar] [CrossRef]
- Hermet, P.; Ayral, R.; Theron, E.; Yot, P.; Salles, F.; Tillard, M.; Jund, P. Thermal Expansion of Ni–Ti–Sn Heusler and Half-Heusler Materials from First-Principles Calculations and Experiments. J. Phys. Chem. C 2014, 118, 22405. [Google Scholar] [CrossRef][Green Version]



| Samples | Ti | Hf | Ni | Sn + Sb |
|---|---|---|---|---|
| Nominal composition | ||||
| Ti0.4Hf0.6NiSn | 0.39 | 0.52 | 1.12 | 0.97 |
| Ti0.4Hf0.6NiSn0.99Sb0.01 | 0.39 | 0.51 | 1.13 | 0.97 |
| Ti0.4Hf0.6NiSn0.985Sb0.015 | 0.40 | 0.52 | 1.13 | 0.95 |
| Ti0.4Hf0.6NiSn0.98Sb0.02 | 0.41 | 0.53 | 1.13 | 0.93 |
| Samples | Ti | Zr | Hf | Ni | Sn + Sb |
|---|---|---|---|---|---|
| Nominal composition | |||||
| (Ti0.4Zr0.6)0.7Hf0.3NiSn | 0.31 | 0.46 | 0.29 | 0.99 | 0.96 |
| (Ti0.4Zr0.6)0.7Hf0.3NiSn0.99Sb0.01 | 0.29 | 0.44 | 0.29 | 0.99 | 0.99 |
| (Ti0.4Zr0.6)0.7Hf0.3NiSn0.985Sb0.015 | 0.29 | 0.45 | 0.29 | 0.99 | 0.92 |
| (Ti0.4Zr0.6)0.7Hf0.3NiSn0.98Sb0.02 | 0.28 | 0.45 | 0.30 | 0.98 | 0.93 |
| (Ti0.4Zr0.6)0.7Hf0.3NiSn0.975Sb0.025 | 0.30 | 0.45 | 0.29 | 0.98 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesaritis, G.; Kyratsi, T. Hf Incorporation in (Ti,Zr)NiSn Half Heusler Solid Solutions via Mechanical Alloying. Energies 2022, 15, 7885. https://doi.org/10.3390/en15217885
Mesaritis G, Kyratsi T. Hf Incorporation in (Ti,Zr)NiSn Half Heusler Solid Solutions via Mechanical Alloying. Energies. 2022; 15(21):7885. https://doi.org/10.3390/en15217885
Chicago/Turabian StyleMesaritis, Georgios, and Theodora Kyratsi. 2022. "Hf Incorporation in (Ti,Zr)NiSn Half Heusler Solid Solutions via Mechanical Alloying" Energies 15, no. 21: 7885. https://doi.org/10.3390/en15217885
APA StyleMesaritis, G., & Kyratsi, T. (2022). Hf Incorporation in (Ti,Zr)NiSn Half Heusler Solid Solutions via Mechanical Alloying. Energies, 15(21), 7885. https://doi.org/10.3390/en15217885







