Periodic Open Cellular Structures (POCS) as Catalyst Supports—A Review

Abstract

Periodic open cellular structures (POCS) are becoming increasingly popular as catalyst carriers due to favorable properties: mixing flow, intense heat/mass transfer and low flow resistance. Their design and manufacturing are relatively easy and cheap. The presented paper focuses on the characterization of POCS in relation to their definition, types, classification and properties. Next, the design and manufacturing methods are described. Finally, the literature review dealing with the application of POCS in catalytic processes are presented.

1. Introduction

Structured catalytic reactors became popular in different industrial processes many years ago as an alternative for conventional packed fixed-bed reactors. Their most beneficial feature is the ease of equipment optimization to overcome the current limitations of tubular reactors, such as low thermal conductivity, local overheating (resulting in increased formation of undesirable byproducts and faster catalyst deactivation) and high pressure drop (thus high cost of pumping media through the reactor) [1,2]. Process intensification can be obtained applying honeycomb monoliths, short-channel structures, wire gauzes and open-cell solid foams manufactured with conductive materials (metals).

Monolithic reactors are well-known as catalytic converters that reduce HC/CO emissions in exhaust gas treatment of vehicles [3,4,5]. Their main advantage is very low flow resistance and the ease of catalyst deposition onto its surface as a thin layer. However, they suffer from external mass transfer limitations due to channel length, in which the fully developed laminar flow exists. For this reason, the heat and mass transfer is weak. Short-channel structures (short monoliths) have been proposed by Kołodziej et al. [6] to obtain more intense heat and mass transfer. Shortening the long monolithic channels ensures the development of laminar flow in the majority of channels, hence heat and mass transfer coefficients are higher than in long monoliths. It has been proven that it is possible to easily control the transport flow characteristics by changing the ratio of the length of the channel to its diameter. More et al. [7] suggested to apply the short monoliths in front of the turbocharger to improve the overall performance of afterburning.

Wire meshes are another promising carrier applied in a number of catalytic processes which require great heat and mass transfer [8,9,10,11]. Other features are: a large contact area between the gas–solid phases, moderate flow resistance and low manufacturing cost. The possibility of producing meshes from various materials makes them more resistant to various unfavorable conditions of the process, e.g., contact with chemical agents or high temperatures. A huge number of available patterns derived from manufacturing processes (woven, knitted, expanded) and geometric flexibility (wire diameter, grid size) create a wide number of opportunities to adapt to the process requirements. However, wire meshes suffer from problems with the catalytic layer deposition with a uniform thickness over the wire surface and with the uniform gas flow distribution through the catalyst [10].

Recently, open-cell solid foams have attracted attention due to their high porosity (up to 97%), low weight in comparison to solid material, high specific surface area (up to 8000 m²/m³), high thermal conductivity (up to 27 W/mK) and good mechanical properties [12,13,14,15,16]. Considering their features, solid foams have the potential to achieve significant benefits in terms of enhancing heat/mass transfer, mixing and chemical reactions. For chemical engineering applications, solid foams are an alternative support in fixed-bed reactors for catalytic processes, such as combustion of methane, oxidation of hydrocarbons, selective catalytic reduction of NO_x by NH₃, carbon dioxide reforming and Fischer–Tropsch synthesis [13,14,17,18]. They offer clear advantages over conventional, randomly packed bed reactors, such as remarkably low pressure drop due to their high porosity, high geometric specific surface area available for the catalyst layer deposition and enhanced heat and mass transfer. Moreover, when comparing solid foams with honeycomb monoliths, it is noticeable that they ensure more intense heat/mass transfer than monoliths with acceptable flow resistance [12,18].

Although open-cell solid foams are widely employed in many industrial processes, e.g., metallurgy, aviation, automotive [19], they exhibit scattered properties because of their randomness and the narrow group of parameters that can be varied during the production process. The most commonly used characteristic of open-cell foams is the PPI (pores per inch), which can be obtained by counting the pores in a linear inch. However, the PPI characteristic does not define anything regarding foam properties and is generally provided by the manufacturer [20,21]. Investigations dealing with flow resistance and heat transfer in non-ideal foams, based on simple geometric parameters such as cell and strut size, were presented in a huge number of papers. However, correlations describing hydraulic and transport properties suffer from the irregularities of the foam matrix, which is an inevitable consequence of the manufacturing process and the type of material. Cell size and strut diameter vary over the whole foam structure, while studies over the heat transfer and fluid flow require accurate data such as the actual foam density sample and strut diameter [20,21,22].

In order to successfully design reactors and control the transport and fluid dynamics phenomena in them, a comprehensive knowledge of the geometric and morphological properties of catalyst carriers is the primary prerequisite. The recent emergence of the potential application of foams in new technologies induces the development of tools for the characterization of foam matrices. The available literature shows that pressure drop in solid foams is most affected by porosity and cell density, while the thermal convective coefficient is strongly dependent on surface area [22,23,24]. It should be emphasized that morphological parameters are directly related to strut shape.

The approach to pursue a complete characterization of open-cell solid foams assumes the use of periodic open cellular structures (POCS). Due to the lack of a comprehensive review focused only on POCS, basic knowledge necessary to characterize POCS in terms of their use as catalyst carriers has been gathered in this work. The following sections in this paper describe the POCS (definition, classification, types and properties) and their design and manufacturing. Finally, the literature review dealing with the application of POCS in catalytic processes is presented.

2. POCS Characterization

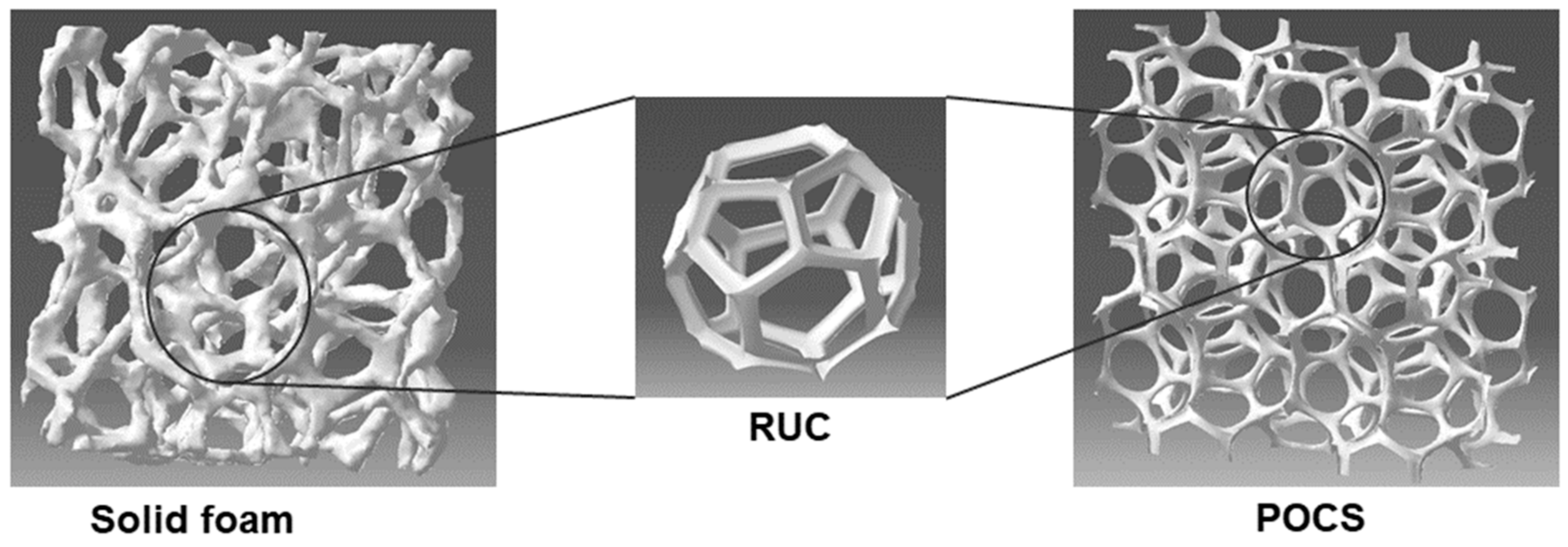
2.1. Definition

The concept of cellular structure (including foams and honeycombs) was originally proposed by Gibson and Ashby [25]. However, periodic open cellular structures are another type of cellular material. The difference between POCS, foams and honeycombs mainly lies in the unit cell topology and properties. In general, periodic open cellular structures are three-dimensional lattice structures with unit cell dimensions from 0.1 to 10 mm; thus, they are also called mesostructures [26,27,28,29]. Unlike solid foams (open- and closed-cell), POCS are categorized as non-stochastic cellular solids with a regular strut and node arrangement and controlled organization of their unit cells (see Figure 1). According to the crystal structure, POCS can also be specified as diamond-like lattices [30].

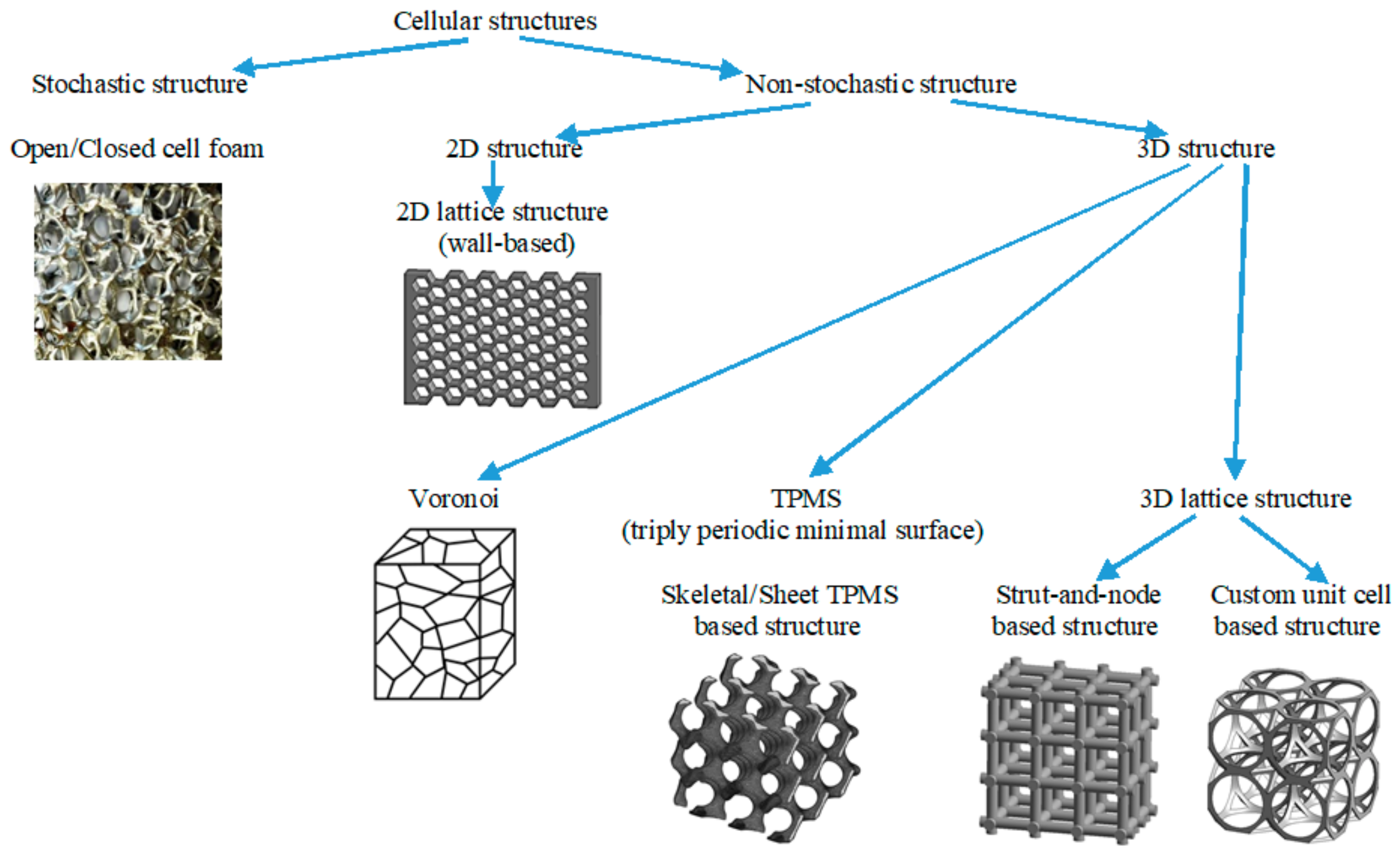
2.2. Classification

Of the many existing three-dimensional geometric figures, only some can create a complex three-dimensional structure that completely fills the space by folding and adding individual figures. However, the design process also requires knowledge of deformation mechanisms. Therefore, POCS can be classified as either stretching-dominated or bending-dominated (Figure 2). The difference between these two deformation modes is in their stiffness and strength, which scales in different ways with the relative density: linearly, in a stretching-dominated, and quadratically, in a bending-dominated [25,31,32]. The stretching-dominated structures are stronger than the bending-dominated ones, due to uniformly distributed axial stress at cross-sections, while bending stress is non-uniformly distributed. In other words, stretching-dominated structures are stiff and used as lightweight constructions, while bending-dominated are soft and used to absorb energy. The two types of structures can be converted to each other by changing their structural topology [33]. Foams are the bending-dominated structures, while monoliths are the stretching-dominated ones [25,34].

The deformation mechanism can be detected according to the Maxwell criterion, M [26,31,33]:

$$M=b-3j+6 \left\{\begin{array}{c} M<0 -the structure is bending-dominated\\ M=0-the structure is stretching-dominated\\ M>0-the structure is over-constrained\end{array}\right.$$

(1)

where b is the number of struts and j is the number of nodes.

2.3. Types

The principal idea of POCS appeared as an auxiliary tool for describing foam morphology. Open-cell solid foams are three-dimensional open-space structures (Figure 3), composed of cells that are formed by struts; strut-to-strut connectivity is called a node, and the neighboring cells are connected together by the openings called windows [16]. However, the dimensions of all these elements of geometry vary in the whole foam matrix; thus, the difficulties with their characterization appear. Therefore, the idea assumes to replace the foam pore by a representative unit cell (RUC) with a regular shape, and then create a structure by duplicating the RUC in all directions in space (see Figure 4) [35]. The morphological parameters (dimension and size of struts and cells) of the resulting structure (POCS) are easily determined.

The first subsection deals with models used to characterize the spatial structure of solid foams, which, to better reflect the real foam structures, are supplemented with various modifications taking into account, for example, the shape of struts or nodes. The authors emphasize, however, that this is a significant simplification, because foam is an anisotropic body and its individual elements are not identical: cells and windows are of different sizes, and struts are of different lengths and shapes. The second subsection provides other examples of POCS that can be considered as catalyst supports due to their geometry.

2.3.1. POCS for Solid Foam Characterization

(a)

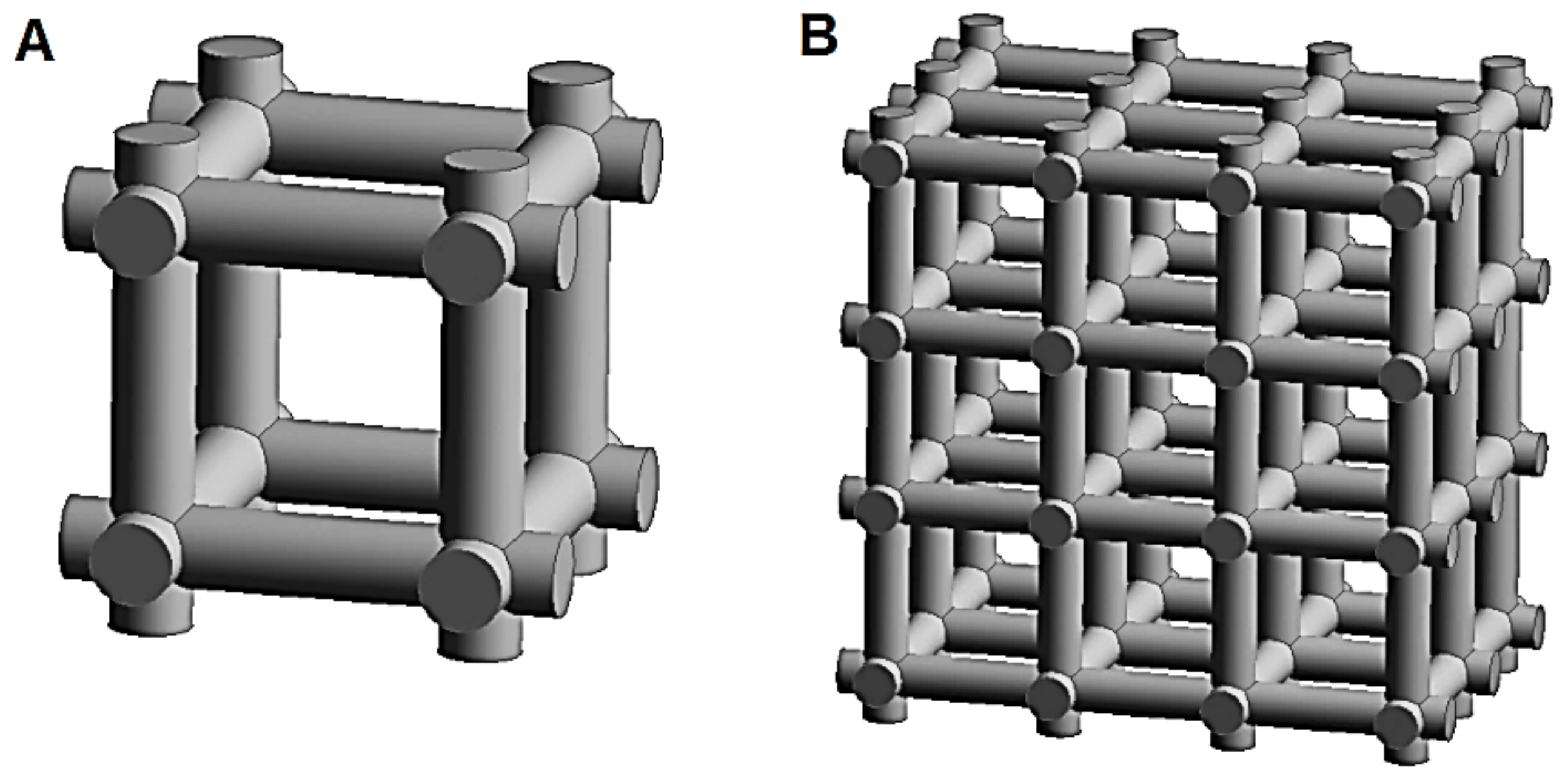
Cubic cell

The cubic cell is the simplest geometric model of POCS that can approximate the solid foam structure (Figure 5). Comparison of the modeling results of aluminum foams with a density of 10, 20 and 40 PPI with the manufacturer’s data shows that the use of a cylinder as a strut cross-section shape gives satisfactory results. However, the cell size in foam is not actually constant. On the other hand, the shape, which can approximate the cross-section of the strut, should be modeled as a square or a triangle, as they better reflect its actual cross-section [36].

The advantage of this model, in addition to its simplicity and an acceptable level of accuracy, is that it can be easily modified to consider a cuboid instead of a cube. This is important due to the anisotropy of foams, in which the pore sizes may vary depending on the considered cross-section: longitudinal or transverse [37].

The cubic cell was used to determine the relationship between the strut diameter and the spherical particle diameter for solid foams and beds with the same porosity and surface area. A new pressure drop model was developed, which is applicable with different PPI, foam porosities and foams made of different materials using standard Ergun parameters [38].

POCS with ideal cubic cell geometry were also applied to develop the model for the calculation of the specific surface area, which is based on strut diameter and cell length. Additionally, the correlation allowing the prediction of the pressure drop was proposed based on Ergun’s equation [39].

(b)

Kelvin cell

The works [20,40] present a model in which the foam cell is described by a 14-face consisting of eight regular hexagons, six squares and 36 edges (truncated octahedron or tetrakaidecahedron—TTKD—or Kelvin cell), shown in Figure 6. In this model, the struts have a triangular cross-section. The results of modeling the geometric surface of ceramic foams determined on the basis of the TTKD model were compared with the formula for the geometric surface of the porous bed and a geometric surface used in quantitative metallography. The obtained data for all three models are similar. However, as stated in [37], the foam and the grain structures differ diametrically; therefore, the analogy between these two types of support does not seem to be fully justified. The proposed model [20,40] is acceptable for ceramic foams with porosity in the range of 0.75 ÷ 0.8, but it is not recommended for foams with higher porosity, e.g., metal foams.

Real foams (ceramic—SiC—and metallic—Cu and Al) differing in porosity (0.827 ÷ 0.955) with equivalent Kelvin-cell lattices were compared applying CFD analysis to their geometrical, momentum and mass transfer characteristics. Small discrepancies in transport properties between the real and the modelled structures were found; however, a more favorable mass transfer to pressure drop trade off was achieved for Kelvin-cell lattices [41].

The TTKD model was also applied to describe the morphological parameters of the Al₂O₃-SiC-based ceramic foam [42]. In order to determine geometric surfaces, it was assumed, as in [39], that the edges have the shape of a prism with a triangular base, and, taking into account only the lateral surface area, they proposed the equation for the geometric surface.

The influence of the shape of the strut cross-section, considering the cylindrical and triangular concave (based on Steiner deltoid) shapes, on the geometric surface was determined using the TTKD model [23,43]. The selection of the appropriate strut shape can be made based on the actual shapes of the struts obtained; for example, as a result of the analysis of SEM images or based on their porosity, the cross-section of the struts varies, depending on the porosity of the solid foam, from round to triangular, according to the diagram shown in Figure 7B.

Such a relationship was previously observed by Bhattacharya et al. [21] (Figure 7A), who, compared to the works of Inayat et al. [23,43], introduced an additional cross-section between the triangular and circular, which corresponds to the cross-section of the struts of ceramic foams (triangular with rounded corners, called a triangular convex based on the Reuleaux triangle).

POCS with cubic and tetrakaidecahedral cells differing in strut cross-sectional shape—circular, square and triangular, as well as solid distribution along the strut—were investigated numerically [32]. It was found that the best heat transfer performance was obtained for POCS with a constant strut cross-section. It was also claimed that there is no remarkable effect of the strut shape on the effective thermal conductivity when comparing at the same solid distribution along the strut.

The impact of porosity (in the range of 60–95%) and strut shape (circular, square, rotated square, triangular, diamond, hexagon, rotated hexagon, star) on the thermal conductivity and pressure drop of foams was investigated based on Kelvin cells [15,44,45,46,47]. A database of effective thermal conductivity of Kelvin cells for various solid-to-fluid conductivity ratios (10–30,000) was generated. It was shown that the cell size and shape, as well as the strut shape, have a negligible impact on modeled predictions in the case of isotropic structures. The relevant features to determine the effective thermal conductivity are morphological parameters, effective solid-phase tortuosity and intrinsic solid-phase thermal conductivity. The impact of various strut shapes on hydraulic properties, as well as on the regime’s transition and pressure drop prediction, was also studied. It was claimed that the effect of strut shape and porosity is observed in transition and inertia flow regimes. However, it was confirmed that it is possible to predict accurately the pressure drop and effective thermal conductivity for different metallic and ceramic foams based on CFD modelling of POCS. The correlations between geometrical parameters and micro-scale flow properties were derived with good agreement for whole range of porosity and shapes.

(c)

Dodecahedron cell

The best approximation to the structure of the SiC foam can be obtained using a dodecahedron-based model consisting of 12 regular pentagons, 20 vertices and 30 edges (Figure 8) [38].

(d)

Weaire–Phelanc cell

After combining two dodecahedrons and six tetrahedrons, the structure proposed by Weaire and Phelan (Figure 9) can be obtained. This model can better represent the irregular structure of the foams. The struts are treated as cylinders with a hole inside. Moreover, it was suggested to take under consideration the material thickening at the strut joints, the so-called knots [48].

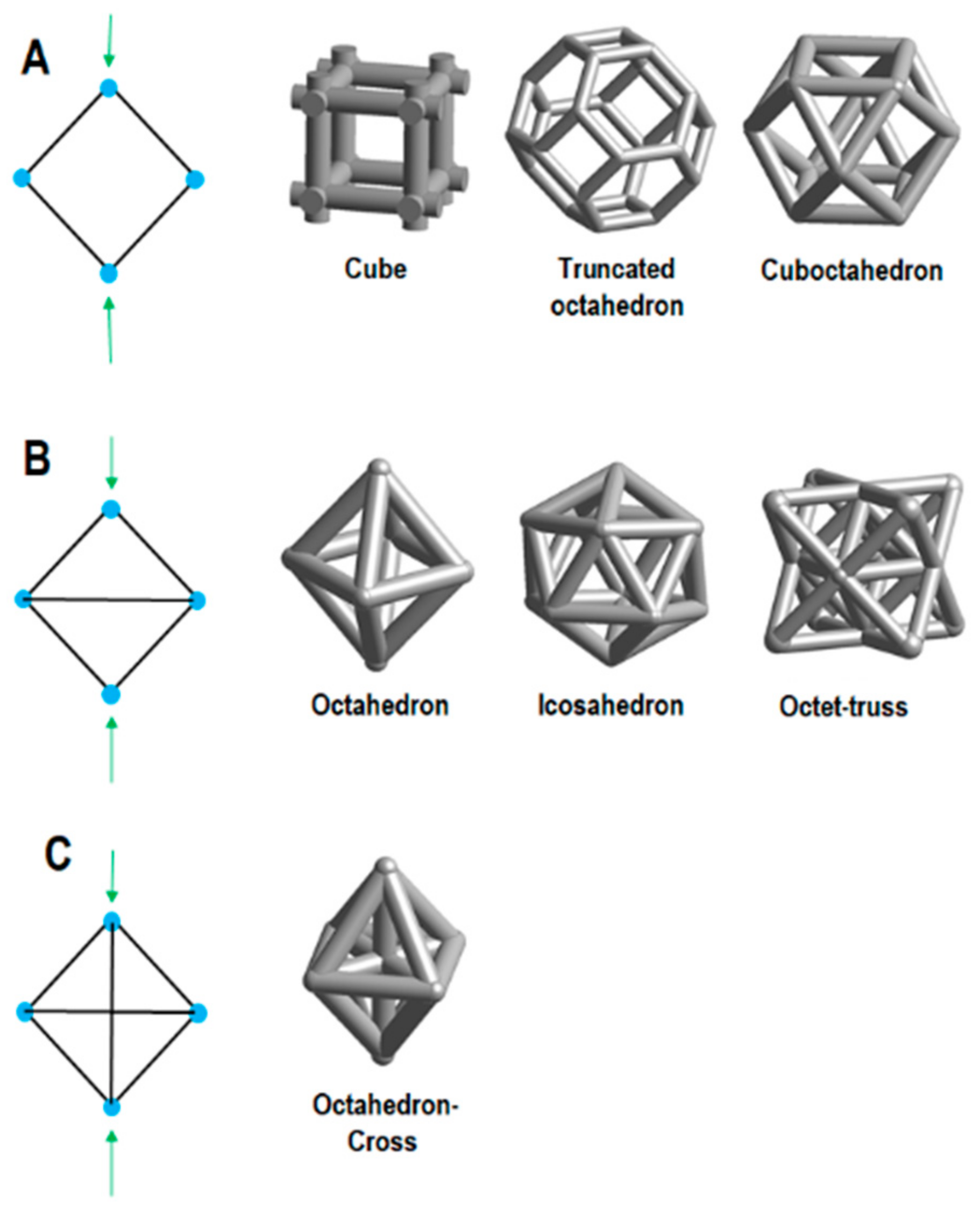
2.3.2. Other POCS Geometries

Figure 10 presents other examples of RUC geometries, which can be assembled into 3D array patterns to enclose completely the internal space to form a POCS matrix (Figure 11).

2.4. Properties

The choice of POCS design plays a big role in determining its physical, mechanical and thermal properties. The shape and structure of the unit cell influence on many desired features, such as a high strength-to-weight ratio, large surface area, excellent energy absorption, low heat conductivity, substantial acoustic and thermal insulation properties and minimized material requirements [26,28,51,52]. The geometry of POCS is, in some senses, a combination of a monolith structure and a solid foam matrix. Therefore, it is expected that they can combine the advantages of both packings: low pressure drop, high heat and mass transfer intensity and a cross-mixed flow pattern [36,53]. Some of the literature [54,55,56,57] revealed that POCS can display better performance than monoliths.

The effective thermal conductivity in the solid matrix of cubic, Kelvin, diamond and face-centered cubic (FCC) structures with a circular strut shape and wide range of porosities (0.65–0.97) was analyzed numerically [17,58]. It was confirmed that porosity is the only relevant parameter for the determination of thermal conductivity. Other features, such as the cell size and shape, have no significant influence on thermal conductivity. Therefore, the effective thermal conductivity of various cell shapes can be described using a single correlation. It was also found that the ratio between the node and strut diameters has a strong influence on the heat conduction performance; when this ratio is close to one, the effective heat conductivity is enhanced up to 30% in comparison with conventional open-cell foams.

Random foam was compared with regular lattices (Kelvin, cubic, octet-modified) within a porosity range of 75–90% using numerical simulations [59]. They received lower pressure drop for cubic and Kelvin cells with a porosity of 90%, while the greatest heat transfer coefficients were obtained for Kelvin and octet lattices in the whole studied range of porosity.

The heat and fluid flow characteristics of octet truss lattice geometries were studied numerically [60]. The authors considered octet truss units to be a potential application for multifunctional heat exchangers or heat sinks. The effective thermal conductivity, permeability, inertial coefficient, friction factor and Nusselt number for octet truss lattices were compared against stochastic metal foam empirical data. It was found that the permeability of octet truss units is 20–80% higher than stochastic foam for a given porosity, while the inertial coefficient is 50% lower that the foam data for a fixed porosity.

The thermo-hydraulic performance of stochastic metal foam and structure based on a rhombic dodecahedron unit cell was investigated [61]. Using computational simulations, it was proven that the heat transfer performances and the heat transfer rate through the finning surface are larger for the regular lattice components than for traditionally manufactured foam. As it was suggested, the reason might be related to the absence of a thermal interface material and the more favorable rhombic window geometries in the developed heat transfer model.

The heat transfer of periodic sintered geometry, which is the negative pattern of tetrahedral overlapping spheres, was tested experimentally and compared with commercial metal foam [62]. It was demonstrated that the comparatively thick, triangular-shaped ligaments combined with the high specific surface area led to significantly improved heat transfer.

The cubic-cell iso-reticulated POCS printed from Al-Si10-Mg alloy using DMLS was analyzed [63]. Samples of cylindrical shape with a 100 mm length and 25.4 mm diameter, differing in strut thickness (0.3–1 mm), cell diameter (1–2 mm) and angular orientation in two dimensions, were examined in relation to their pressure drop and heat transfer properties. The results show that the structures tested have a high surface area per unit volume, while presenting a very small pressure drop. Moreover, the heat transfer is improved by direct connection of the POCS geometry with skin and depends on the porosity and interfacial area between the sample surface and flowing gas.

The pressure drop of cubic, Kelvin and diamond lattices, varying in porosities (0.85–0.95), was studied numerically [64]. It was shown that the friction factor of diamond cells is the most dependent on the Reynolds number, whereas it is the least dependent on cell size. Additionally, the distribution of velocity and frequency was analyzed, and the best results were achieved for the diamond structure.

The hydrodynamic behavior of various POCS—Kelvin diamond and hybrid DiaKel (a combination of both)—was investigated experimentally to identify unit cells with high potential for achieving a homogeneous liquid distribution over the entire reactor cross-section [65,66]. It was revealed that hybrid DiaKel shows better performance than other unit cells.

3. POCS Design and Manufacturing

Review reports dealing with design and manufacturing of cellular structures can be found elsewhere. Generally, the reviews deal with all types of cellular structures, e.g., Feng et al. [49] described the design methods for lightweight structures, porous scaffolds and other structures with complex topology. Other works [26,51] focused mainly on POCS (called as mesoscale lattice structures, MSLS) design; Tamburino et al. [26] described the phases of the POCS design process that could be critical for the manufacturing constraints, while Nguyen et al. [50] focused on size, shape and topology optimization techniques.

As it was stated in [27,28], unit cells can be designed by a primitive-based method, implicit surface-based method and topology optimization method. These works also summarized additive manufacturing (AM) technologies in relation to their advantages and drawbacks.

Pan et al. [52] described the design and optimization methods of uniform and non-uniform lattice structures. The unit cell design based on geometric wireframes, mathematical algorithms and topology optimization is proposed for uniform lattice structures, while a design based on functional gradient design and structural optimization is suggested for non-uniform ones.

Manufacturing technologies were described in detail in [52,67,68]. Material type, unit cell type, printing size, application performance, advantages and disadvantages are taken into consideration.

Contrary to solid foams, periodic open cellular structures can be easily designed applying CAD software and fabricated using additive manufacturing (AM). A general procedure for optimizing POCS for specified applications can be summarized as shown in Figure 12 [35,62].

For any process, the starting point is the design of the unit cell with a known morphology using the CAD software tool. Next, computational simulations are performed on RUC to investigate its transport and flow properties. The combination of CAD and CFD modeling enables the optimization of POCS geometry to intensify heat/mass transfer and reduce pressure drop. The most beneficial RUC is then repeated in each spatial direction to create a POCS with desired volume. CAD geometry of POCS is converted to a file, e.g., STL, which is required for additive manufacturing techniques. After 3D printing, the structure is tested experimentally regarding its morphology, transport and flow properties to verify the numerical results. Finally, POCS are implemented in the assumed process.

3.1. CAD + CFD Modeling

CAD (Computer-Aided Design) and CFD (Computational Fluid Dynamics) tools provide a quick and cheap method to characterize reactors’ performance for their planned application. Available commercial packages offered by ANSYS [69], Dassault Systems [70], Materialise [71], Volume Graphics [72] and SimScale [73] can be used for POCS design and optimization. Brakke [74,75,76] developed a free program, Surface Evolver [77], to generate Kelvin or Weaire–Phelan cells, which was then implemented by researchers [78,79,80].

The simplest way to design a POCS is by creating firstly a RUC and then repeating it in three principal axes [27,29,34,49,50]. However, it should be emphasized that any geometry can be created as a virtual model, but not all can be printed. Therefore, design for manufacturing (DFM) is the most important thing about POCS design. This term means design and optimization of the structure to eliminate manufacturing difficulties and minimize costs [27,51].

Tamburino et al. [26] summarized the following aspects to be taken into consideration during the design of RUC:

(1)

Selection of RUC in terms of the number of struts b and nodes j on the basis of desired mechanical behavior (stretching- or bending-dominated);

(2)

Tuning the relative density of RUC by changing b and/or strut diameter ds (if the strut length ls is constant);

(3)

Tuning the strut and node arrangement taking under consideration the load direction;

(4)

Tuning the RUC geometry changing the amplitude of angles between the struts in relation to the load direction and its intensity.

As the authors stated [26], during AM constraints, the following aspects should be considered:

(1)

Minimum and maximum length of the struts;

(2)

Minimum and maximum thickness of the struts;

(3)

The sloping angle of the struts.

Bhate [81] provided a state-of-the-art solution that can help to select appropriate cellular material design:

(1)

The optimum unit cell can be selected based on the following classification:

• Tessellation (periodic, stochastic, hierarchical)—the division of space into smaller, repeating entities;
• Elements (beam, surface)—the material constituents of the space;
• Connectivity (edge, face, vertex)—the ways in which the constituents are connected;

(2)

the size of the cells and their distribution—the lower bound of the cell size is defined by manufacturing constraints (e.g. resolution) and the need for powder removal, while the upper bound may be defined by the maximum overhang distance; the distribution means gradients; however, most commercial design tools leave these problems to the user and perform optimization at the level of the cell parameters;

(3)

the optimal cell parameters—the dimensions (geometric parameters, e.g., length, thickness, junction) and material composition of the cell;

(4)

the cell integration with the larger form—a uniform infill may be used that assumes the replacement of the larger component by the cellular material with no remnant skin or the cell trimming by a skin.

The combination of CAD and CFD modelling is a helpful tool for performing preliminary studies of POCS. Numerical analysis provides thermal and hydraulic characteristics, so it provides the answer to which geometries could be implemented as a packing in the reactor. Meanwhile, CAD design enables the optimization of the geometry. This approach saves time and money, because lots of virtual geometries are drawn, but only the most promising one is chosen for the manufacturing process. CFD analysis is also helpful when some physical mechanism that is not observable during experimental studies occurs and needs to be understandood. Therefore, the creation of a database of heat/mass transfer and flow resistance using CAD and CFD tools for diverse POCS with various porosities and strut shapes is indispensable to understand and modify transport and hydraulic properties.

3.2. Additive Manufacturing

In recent years, additive manufacturing (AM) techniques offer the possibility to manufacture highly reproducible periodic open cellular structures (POCS) with a well-defined and ordered geometry and with the desired dimensions directly from CAD model [14,48,49,50,62]. AM methods are based on stacking layer upon layer of thin 2D cross-sectional slices of materials to produce complex shapes. Of the many AM methods available, only metal powder bed fusion allows the final metal mesostructure to be printed. The energy sources used to melt the metallic powders are lasers for selective laser melting (SLM) and electron beams for selective electron beam melting (SEBM) [27,52,62,82]. Compared to conventional manufacturing processes, AM methods have many advantages. For example, the ability to manufacture complex forms and shapes, which gives a whole new freedom for designers. Additive manufacturing saves time and energy, as well as reducing costs, because it is capable of directly producing technical components [29,49,62,83]. Additive manufacturing enables the use of, e.g., stainless steel, titanium, cobalt chromium, alloys and aluminum alloys [26,27,28,51]. Although some issues that should be resolved appear, e.g., differences in morphology and surface roughness of CAD-modelled and 3D-printed structures, limitations of strut dimensions that cand be printed and manufacturing processes that are still being developed and improved [28,29,50,52,83]. Therefore, POCS of various design with controlled morphological and geometrical parameters can be easily fabricated by 3D printing.

4. POCS Applications in Processes

The beneficial properties of POCS have resulted in the research project dealing with their application for high-temperature processes, e.g., in methane oxidation at ~1400 °C, as an active cooler in space vehicles entering planets’ atmospheres and as a catalytic support in biogas autothermal reforming in heat exchangers [84]. Another potential thermal application of POCS concerns the field of catalytic convertors, due to the great design flexibility of lattice structures and the high heat conduction with respect to traditional foams [52]. A summary of the applications of POCS in processes are gathered in

Table 1. A summary of POCS applications in processes.

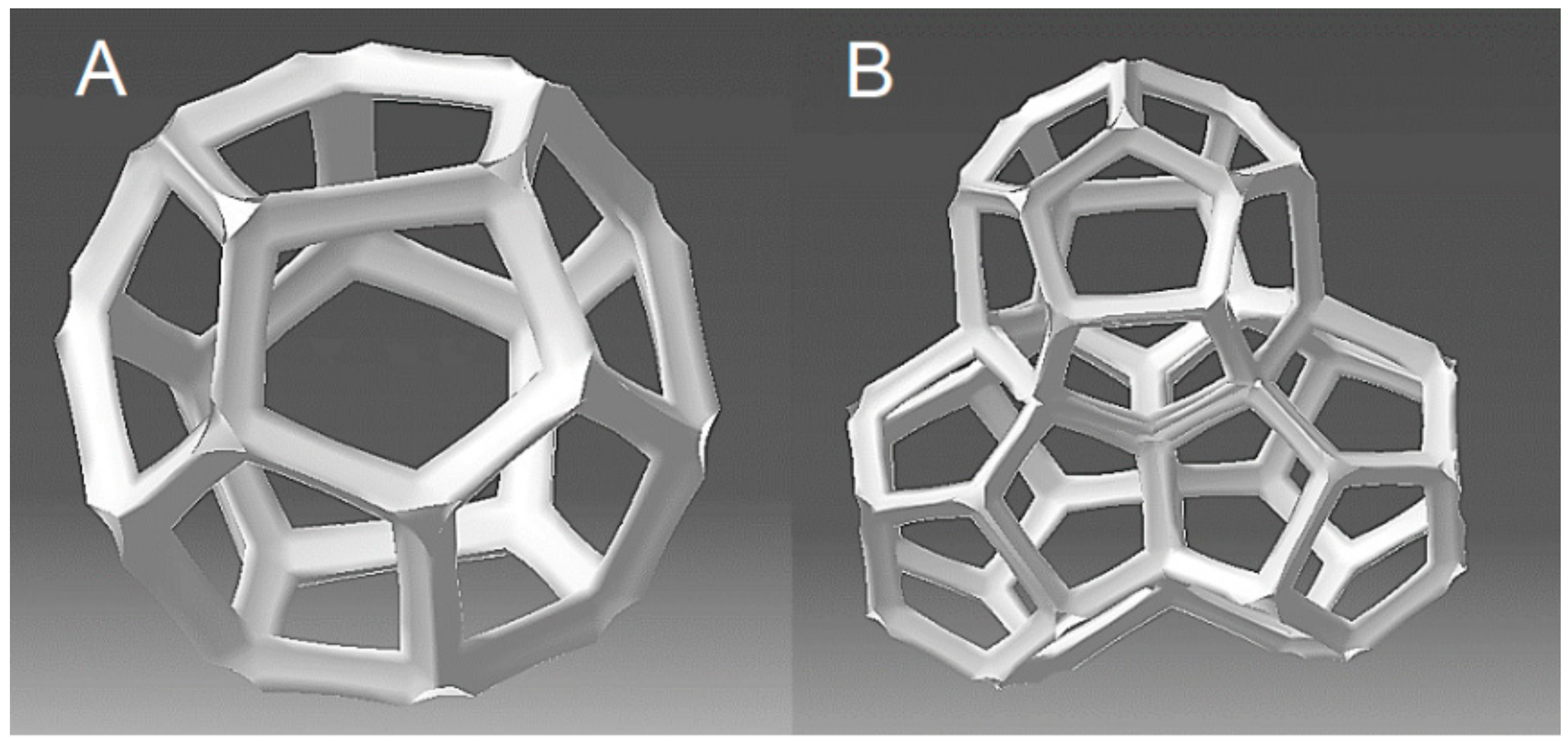
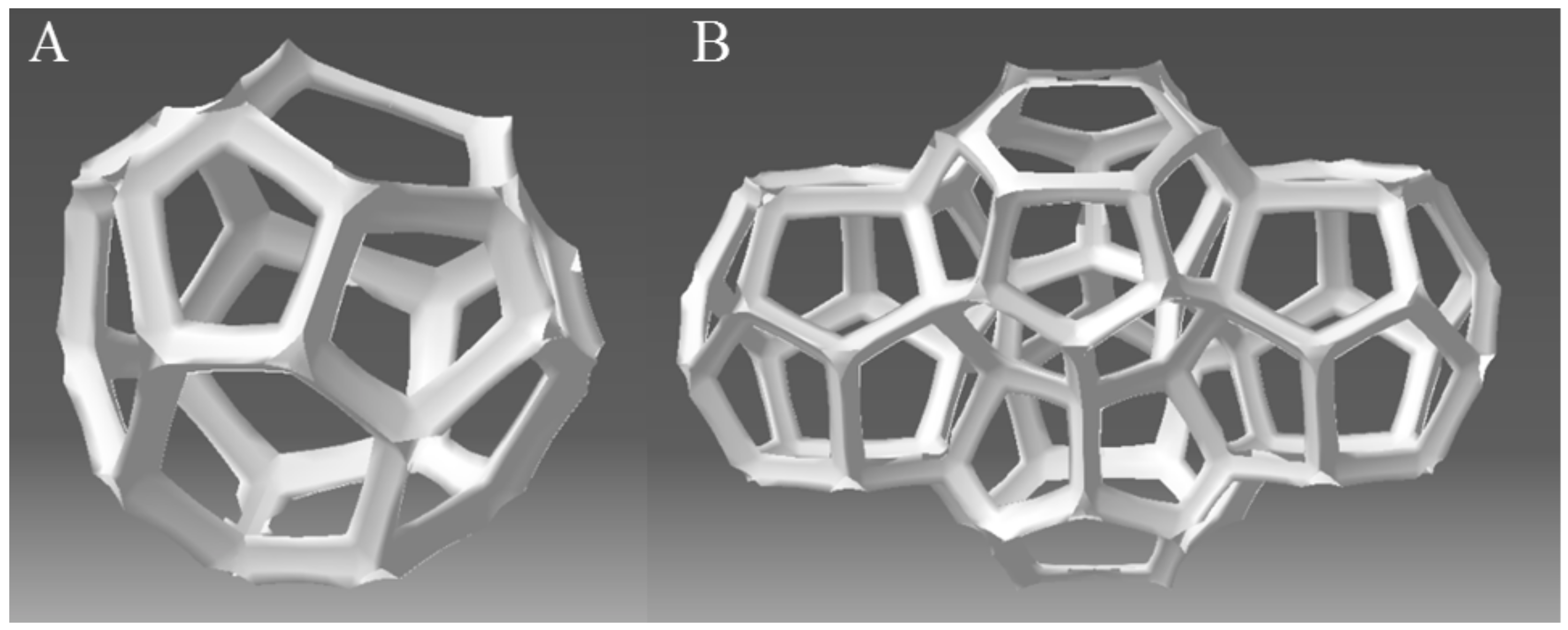
Unit Cell of POCS	Process	Research	Reference
Cubic Cubic rotated by 45° Kelvin	CH4 oxidation	CFD	[41,55]
Cubic	CO oxidation CH4 oxidation HC oxidation	CFD EXP	[56]
Cubic Diamond Kelvin	Sabatier reaction	EXP	[85,86]
Cubic	CO oxidation	EXP	[87]
Diamond	C2H6 hydrogenation	EXP	[88]

.

The computational simulation of mass transfer and pressure drop in Kelvin-cell structures and monoliths imposing methane oxidation was performed [41]. The results show higher momentum and mass transfer properties for Kelvin structures than for monoliths at moderate to high flow rates. A lower catalytic surface is required by the Kelvin-cell structure to achieve the same conversion as in the monolith. Various types of catalyst supports—cubic, cubic rotated by 45°, Kelvin, octet and honeycomb—differing in porosities (0.8–0.95) were investigated, also numerically, in relation to their flow and transport properties [55]. It was proved that all POCS indicate a better performance than monoliths. Octet and Kelvin cells have a higher performance index than cubic ones, while the cubic cell rotated by 45° seems to be the most promising catalyst substrate.

The 3D-printed cubic cell-based structure was tested both experimentally and numerically as a catalyst carrier in CO, methane and non-methane hydrocarbons oxidation in the aftertreatment system of a dual-fuel heavy-duty diesel engine [56]. It was shown that the additively manufactured catalytic converter provided better performance than the commercial monolith over most working conditions, although less catalyst was loaded onto the printed surface and the monolith had a higher channel per square inch density. It was suggested that the reason is internal turbulence generated by the 3D-printed substrate at moderate and high inlet temperatures, where internal and external mass transfer limit the reaction rate.

The use of Ti-6Al-4V and Al-Si10-Mg lattices (cubic, diamond and tetrakaidekahedron unit cells) as intensifiers of the catalytic processes was investigated [85]. It was proven that POCS filled with conventional industrial catalyst pellets are able of enhance the transfer heat rate of tubular reactors without their downsizing, against to packed foams. A computational fluid dynamics study was also performed [86] to prove the relation between strut diameter and cell porosity with heat and mass transfer properties.

The aluminum POCS with a cubic-cell geometry differing in cell size (1.5, 1.75 and 2.25 mm) with a constant strut thickness of 0.5 mm were tested [87]. Samples were of a cylindrical shape with a 9 mm diameter and 4–25 mm length. Pd/CeO₂ catalyst was deposited on the POCS surface by slurry-coating techniques and examined under mass transfer-limited conditions in CO oxidation. The results show a low volumetric mass transfer rate was obtained for POCS with a strut thickness of 0.5 mm in comparison with commercial monoliths. However, a smaller strut size (0.2 mm) can enhance the mass transfer rate of POCS to the same range and even higher than the monolith.

Ti-6Al-4V substrates based on a diamond lattice with tetrahedron-like nodes, with a pore and strut diameter of 1.8 and 0.5 mm, respectively, were studied [88]. Samples were produced by SEBM process and are cylinders with a diameter and length of 8.5 and 20 mm, respectively. Structures were coated with SiC and Pt using a combined chemical vapor deposition and carbide-derived carbon approach. The hydrogenation of ethane was the test reaction. A much higher activity was achieved for the SEBM catalyst in comparison with a commercial platinum on activated carbon catalyst. So far, researchers have considered cubic or Kelvin cells with a circular or triangular strut shape in order to describe the morphology, pressure drop and heat/mass transfer in non-ideal foams. Other POCS geometries and struts shapes are in the minority. Nevertheless, literature reports referring to experimental studies for POCS, manufactured by 3D printing, are in the minority and deal with ideal cubic cell geometry with circular or square struts [35,36,55,63]. In this regard, the use of POCS as a catalyst support is a relatively new and very promising concept because of their favorable properties (low pressure drop, high surface area, enhanced heat transfer, good fluid distribution). With the development of additive manufacturing techniques, it is possible to transform the virtual geometry of POCS into metal-based physical objects.

5. Conclusions

Random open-cell foams have been widely studied for a long time in regard to their application as structured packings in reactors. Due to their novelty, particularly their structure, and texture variability related to the different manufacturing processes, the geometrical parameters of solid foams, thus the transport properties, are still in scarce. The experimental data reported by independent scientists do not give close resemblances because they are valid for a given small set of foam samples (usually displaying very high porosity. Accurate understand the physical mechanisms behind the transport phenomena and the impact of individual geometrical parameters on them could be reached by the generation of a database of transport flow properties. Therefore, the development of geometric models and correlations providing the accurate prediction of solid foam properties, significant for the design of reactors and heat exchangers etc., filled with with foams is substantial.

Controlling the unit-cell topology of lattice structures such as periodic open cellular structures (POCS) can enable the customization of effective anisotropic material properties. The range of POCS geometries, as well as their dimensions, is wide and is limited only by the designer’s imagination. The resulting structure is easy to design and modify, and, most importantly, it is easy to determine its geometric dimensions. The POCS as catalyst support is a promising design that can similarly influence the development of catalytic reactors. In spite of their beneficial characteristics, the determination of optimal open cell architecture for a given set of constraints is difficult. Therefore, research is focused now on using CAD and CFD tools, because they allow for the systematic analysis of the relationship between the geometry (or morphology) and transport phenomena, e.g., in regard to heat/mass transfer and flow resistance. Therefore, the most promising structures can be quickly produced with good precision and from different materials.