Abstract
A digital twin (DT) for nuclear reactor monitoring can be implemented using either a differential equations-based physics model or a data-driven machine learning model. The challenge of a physics-model-based DT consists of achieving sufficient model fidelity to represent a complex experimental system, whereas the challenge of a data-driven DT consists of extensive training requirements and a potential lack of predictive ability. We investigate the performance of a hybrid approach, which is based on physics-informed neural networks (PINNs) that encode fundamental physical laws into the loss function of the neural network. We develop a PINN model to solve the point kinetic equations (PKEs), which are time-dependent, stiff, nonlinear, ordinary differential equations that constitute a nuclear reactor reduced-order model under the approximation of ignoring spatial dependence of the neutron flux. The PINN model solution of PKEs is developed to monitor the start-up transient of Purdue University Reactor Number One (PUR-1) using experimental parameters for the reactivity feedback schedule and the neutron source. The results demonstrate strong agreement between the PINN solution and finite difference numerical solution of PKEs. We investigate PINNs performance in both data interpolation and extrapolation. For the test cases considered, the extrapolation errors are comparable to those of interpolation predictions. Extrapolation accuracy decreases with increasing time interval.
1. Introduction
1.1. Digital Twin for Nuclear Reactor Monitoring
Advances in nuclear reactor performance efficiency can be accomplished using state-of-the-art monitoring capabilities. The concept of a Digital Twin (DT) has been proposed recently for process monitoring, including nuclear reactor monitoring [1]. The DT consists of a computational model that tracks the history, and continuously adjusts the model to detect anomalies, such as degradation and insipient signs of failure of components, materials, and sensors. Proposed approaches for the implementation of a DT involve either a physics-based differential equations model or on data-driven machine learning (ML) model. The challenges of using a model-based DT for nuclear reactor monitoring consist of accounting for a-priori unknown loss terms in the complex experimental system to achieve sufficiently close agreement between the model and observations. The data-driven ML model captures the information about the reactor system from the experimental data used for model training. However, unlike the model-based DT, which contains equations describing time evolution of the system, the ML-based DT has limited extrapolation capability and, in principle, requires an arbitrarily large amount of training data [2,3]. Indeed, ML models follow an empirical, data-driven approach in making predictions based on large collections of historical data in order to achieve high performance. Although ML models are computationally fast in making predictions and robust with respect to noisy data, they are frequently difficult to both interpret and to develop from data [2]. Furthermore, the data commonly need to be accompanied by labels that are not easily available. In addition, though ML models can be versatile, to a varying extent, in the resolution of input data, their usual requirement of large volumes of training data hinders model development. On the other hand, physics-based models can alleviate the constraint of the big data [4], as the DT training no longer relies solely on the behavior of input–output examples. Moreover, DTs may have to be constructed for the system where there is scarce data availability. There exist methods, such as few-shot learning [3], which offer the potential of learning from small datasets. However, in few-short learning, the lack of information content in short temporal space is usually compensated with another dimension of the data (e.g., the number of sensors). This imposes additional requirements on data collection.
Recently, a hybrid approach has emerged, consisting of physics-informed neural networks (PINN) designed to solve differential equations. The PINNs address the need for integrating governing physical equations of the process into ML models, which establishes theoretical constraints and biases to supplement measurement data. The integration of governing physical equations into ML models provides a solution to several limitations of purely data-driven machine learning (ML) models. First, in the case of data scarcity, most ML approaches are unable to effectively work, because there is a minimal required data volume to train the model. In the case of PINNs, the model can be trained without big data availability. Second, in the case of big data availability, ML approaches face severe challenges to extract interpretable knowledge. Furthermore, using purely data-driven models can lead to overfitting of the observations. As a result, this may introduce physically inconsistent predictions due to extrapolation or biases, and eventually result in low predictability. PINN performance is not directly related to the volume of data, rather the physics underlying the behavior of the system.
The governing equations for modeling a nuclear reactor are Boltzmann neutron transport and Bateman partial differential equations (PDEs). The numerical solution of these PDEs for a typical reactor geometry requires extensive computational resources. A reduced-order model consisting of a system of point kinetic equations (PKEs) has been developed for the case when the spatial dependence of the neutron flux can be ignored, which is typically valid for small reactors. In this paper, we investigate the application of PINNs to the numerical solution of PKEs, which models the Purdue University Reactor Number One (PUR-1) small research reactor. We develop the PINN solution of PKEs using the experimental parameters of PUR-1, such as values of the reactivity schedule and neutron source. The PKE case investigated in this paper involves time-dependent stiff nonlinear ODEs, where the range of values is approximately eight orders of magnitude, during a time interval of several hundred seconds. The results of this paper demonstrate strong agreement between the PINN solution and the numerical solution of PKEs using the finite difference solver.
1.2. Review of Prior Work on PINNs
The original idea of PINNs was introduced by Lagaris et al. [5] in 1998 and later established by Raissi et al. [6,7] in 2017 for solving two main classes of problems: the data-driven solution and data-driven discovery of differential equations. The formulation of PINNs was performed to tackle problems involving PDEs [8]. In the existing literature, there are many studies of PINN implementation for the solution of differential equations arising in heat transfer [9], fluid mechanics [10], solid mechanics [11], and reactor kinetics problems [12]. In addition, recent interest in the development of PINNs has resulted in the development of various libraries, such as DeepXDE [13], DGM [14], and PyDEns [15], that are built on top of TensorFlow, as well as NeuroDiffEq [16], which is built on top of Pytorch. In addition, two more actively developed libraries are NeuralPDE [17] and ADCME [18], which are written in Julia instead of Python. Specific examples of applications of the PINNs framework include the solution of Navier–Stokes, Allen–Cahn, and Schrodinger equations [19,20]. Additionally, PINNs have been used for the solution of high-dimensional stochastic PDEs [21], which suggested that PINNs can be considered as a class of Reinforcement Learning [22].
PINNs have also been investigated for the solution of ordinary differential equations (ODEs), where stiffness of the ODE system was the main challenge. In [23], PINNs were applied in stiff chemical kinetics equations. A variation of PINN, called stiff-PINN, was proposed, which showed better results than regular PINNs. Stiff-PINNs managed to accurately predict the solutions during the entire computational domain in two different cases, the ROBER and POLLU problems. On the other hand, regular PINNs seemed unable to predict the solutions during most time intervals in the computational domain. This failure was related to the stiffness of the differential equations.
Prior application of PINNs to the solution of ODEs includes the solution of PKEs. In previous work on PINNs, most references considered simplified PKEs. There is no literature investigating the PINN solution for six-group delayed neutron density concentration with the temperature feedback and neutron source, which is necessary for actual reactor monitoring. A variation of PINN, named X-TFC, was proposed in [24] to solve the PKEs. Although some of the test cases include the six-group delayed neutron precursors, density concentration and the temperature feedback reactivity, a neutron source term was not included in the model. In addition, one more PINN implementation in the reactor kinetics problem was studied in [25], with PKEs that include one-group delayed neutron precursors density concentration, temperature reactivity feedback, and no neutron source. The results were promising, but the computational time was deemed to be excessive for use in real-time applications. Another investigation of PINNs performance was reported in [12], with parameters chosen according to the real microreactor. The preliminary results showed performance with relatively small prediction errors and relatively fast runtime.
This paper is organized as follows. Section 2 describes the theory of PINNs. Section 3 introduces the nuclear reactor mathematical modelling framework, starting from the Boltzmann Neutron Transport Equation and Bateman Equation, followed by the PKEs reduced order model. Section 4 describes PUR-1 and discusses the details of experimental data acquisition. Section 5 provides a solution to the PKEs model of PUR-1 startup transient using the methodology of PINNs, whereas conclusions are discussed in Section 6.
2. Theory of Physics-Informed Neural Network (PINN)
PINNs are a new class of deep learning (DL) networks that are capable of encoding differential equations (DE) that govern a data set [26]. The difference between PINNs and traditional DE solvers [27] is that the former computes differential operators using automatic differentiation [28]. PINNs can be applied to both supervised and unsupervised learning tasks [29]. The PINN training procedure requires substantially less data than most DL methods, and the data do not need to be labeled. The challenges of PINN training consist of satisfying competing objectives: learning the DE solution within the domain, and satisfying the initial and boundary conditions (IC and BC). This leads to unbalanced gradients during the network training via gradient-based methods, and often causes PINNs to have difficulties with accurately approximating the DE solution [30]. This is a known challenge for gradient-based methods, which get stuck in limit cycles if several competing goals are present.
PINNs take as input a point in the computational domain (collocation point), and minimize a residual function (training step). The output is an approximate solution of the differential equations. The key advancement of PINN is the integration of a residual network that contains the governing equations. This network, given the output of a DL network (surrogate), calculates a residual value (loss function). Figure 1 shows a schematic of PINN, where the surrogate model consists of a fully connected neural network with time and space coordinates (t, x) as inputs, and is used to construct , which is an approximation to the numerical solution, . The residuals are calculated next to obtain the loss, , which is used for optimization of the approximation. The residual loss comprises the differential equation’s residual , the initial condition’s residual , and the boundary condition’s residual . The loss functions are defined in Equations (4)–(7) in Section 2.4.
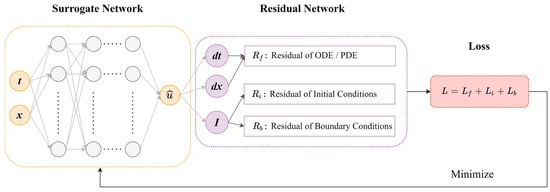
Figure 1.
Schematic of a physics-informed neural network (PINN). A fully connected neural network with time and space inputs is constructed to approximate the solutions of , which is then used to calculate the residual loss, . The residual loss comprises the differential equation’s residual , the initial condition’s residual , and the boundary condition’s residual . The derivatives of are computed by automatic differentiation. The parameters of the fully connected network are trained using gradient-descent methods based on the back-propagation process.
2.1. Surrogate Network Implementation with Fully Connected Neural Networks (FNNs)
In this work, we implement the surrogate network of the PINN using fully connected neural networks (FNNs). In general, a wide variety of neural networks have been developed, including the feed-forward neural network (FNN), the convolutional neural network (CNN), and the recurrent neural network (RNN). In this paper, we chose to use FNN, because it has been shown in the literature [13,26] to be efficient for the solution of PDE problems. Additionally, due to the architecture simplicity, FNN is easier to train compared to deep networks.
An FNN is composed of at least two layers. By convention, all networks that have at least two layers () are called deep. In general, FNN is a -layer neural network, with hidden layers. An FNN is denoted by , where and are the dimensions of the input and output, respectively. The number of neurons in the -th layer is denoted by. The number of neurons in the input and the output layers are denoted by and , respectively.
We define a weight matrix, ; a bias, ; and an activation function, , in each layer, . The weights of this network are trainable. The weights and biases are the neural network parameters, . The activation function can be chosen among other choices as the logistic sigmoid, the hyperbolic tangent (tanh), or the rectified linear unit (ReLU). An -layer DNN is defined as:
The FNN architecture for the implementation of the PINN surrogate model is depicted in Figure 2, which is an expanded version of the panel displaying the surrogate network in Figure 1. The FNN output is the predicted approximation of the DE solution, .
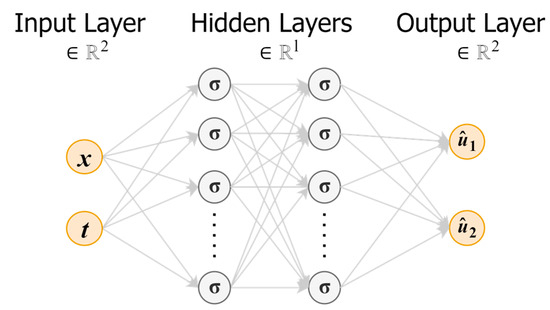
Figure 2.
FNN architecture for the implementation of the PINN surrogate model. The FNN consists of the input layer, the hidden layers (composed of weights, ; biases, ; and activation function, ), and an output layer.
2.2. Automatic Differentiation for Residual Network
PINN training involves the implementation of a framework for computing derivatives. Usually, the derivatives are written in the form of Jacobians or Hessian matrices. In general, computation methods include numerical differentiation, symbolic differentiation, and automatic differentiation (AD; also called algorithmic differentiation). Numerical finite difference and symbolic differentiation could result in reduced accuracy for complex functions [31]. AD automatically computes derivatives using the chain rule for the accumulation of values, instead of relying on derivative expressions. Given that neural networks represent a compositional function, AD applies the chain rule repeatedly to compute the derivatives. In addition, AD uses the technique of backpropagation, which aids in the fine tuning of a neural network’s weights, using the error obtained in the previous iteration. Choosing appropriate weights results in reduced errors, and increases the generalization of the model. The derivative of the objective function with respect to any weight or bias, which is backpropagated in the network, provides detailed insights into how the changes of weights and biases affect the overall behavior of the network. AD evaluates the derivatives in two steps. First, the forward pass calculates the values of all variables. Second, the backward pass computes the derivatives. Therefore, AD needs only one forward pass and one backward pass to compute all the derivatives, regardless of the input’s dimension. On the other hand, using finite differences requires at least forward passes to compute all the derivatives. Hence, AD performance is more efficient for problems with high-dimensional input.
2.3. Enforcement of Initial and Boundary Conditions
There are two steps involved in encoding the ICs and BCs into a PINN. First, each IC and/or BC can be treated independently, with each appearing one in the loss function as a separate term. This type of enforcement is known as soft constraint, where the goal is to minimize each term in the loss function at the same time. PINNs use the formulation . This method is considered simpler to implement, and it is suitable for high-dimensional differential equations and complex geometries.
Second, it is possible to transform the network output to some function, such that the IC and/or BC are satisfied by the design of the neural network. For instance, PINNs can use to always satisfy the IC . As a result, the total loss function includes only the losses due to the DEs. This method of enforcement is known as hard constraint, which ensures that the IC or BC are exactly satisfied. This reduces the complexity of the PINN training.
2.4. Loss Function and Metrics for Evaluation
Loss function measures the discrepancy between the neural network, , and the constraints imposed by the DEs and their respective IC and/or BC. We define the loss function as the weighted summation of the norm of residuals for the DE and IC/BC, in the form of a Mean Squared Error (MSE), as:
where , , and are the scalar weights for the DE, IC, and BC, respectively. The scalar weights are specified before training, and they are used to rank the importance of each loss term. The variables , , and are the training points inside the domain, at the IC and on the boundary. These sets of points are usually referred to as the sets of residual points. The terms , , and are the MSE of the residuals for the DE, IC, and BC, respectively. These are computed as:
The derivatives in the loss function terms are calculated with automatic differentiation.
To measure the initial and final performances of the trained model, two metrics are used. The first metric is the value of the loss function in Equation (4). The second metric is the relative error, , with respect to a reference solution, . The reference solution, , is usually obtained from a high-fidelity numerical solution of the DE. The relative error is defined as:
where denotes the standard norm. It is important to note that the error in the loss function, , measures the degree to which the governing equation is satisfied, not the error of the solution, , with respect to the reference solution, .
2.5. Activation Function
Activation function is used to map an input, x, to an output, y. In general, different activation functions may be used in different parts of the FNN. The activation function in the hidden layer controls how well the network model learns the training dataset, whereas the activation function in the output layer defines the type of predictions the model can make. Some of the most popular activation functions used in ML are the sigmoid, the hyperbolic tangent (tanh), and the Rectified Linear Unit (ReLU).
The ReLU activation function, defined as , has the advantage of computational speed, as compared to those of sigmoid or tanh units. ReLU is less susceptible to vanishing gradients that affect deep model training. Besides the accelerated training process, ReLU avoids saturation with large positive numbers [32]. In addition, the nonlinearity allows to conserve and learn patterns in the data. However, for regression applications, the ReLU function suffers from diminishing accuracy for second and higher-order derivatives.
Sigmoid activation function, also called the logistic sigmoid, takes any real value as the input, and produces output values in the range of 0 to 1. The sigmoid activation function is defined as and has an S-shaped graph. The larger the input, the closer the output value will be to 1, whereas the smaller the input, the closer the output will be to 0. Additionally, in contrast to the ReLU activation function, the sigmoid activation function can overcome the diminishing higher-order derivatives problem.
Hyperbolic tangent (tanh) activation function is very similar to the sigmoid activation function. The tanh activation function is defined as and has an S-shaped graph. Tanh takes any real value as the input, and produces output values in the range of −1 to 1. Similar to sigmoid activation function, tanh can overcome the problems related to diminishing higher-order derivatives. In general, both sigmoid and tanh activation functions are commonly used for classification problems due to their sensitivity around a central point, and their ability to categorize elements into different classes.
2.6. Optimization
An optimization algorithm accelerates the training procedure by using an algorithm to incrementally change the network weights to minimize a loss function. This is usually accomplished by using gradient-based optimizers, which compute the gradients of the loss functions with respect to all weights and biases. The gradients are computed in the direction from the output to the input, by applying the chain rule layer-by-layer. The backward flow of the gradients is the reason for naming the process as backward pass or backpropagation. In general, there are two optimizers that are used most frequently, the Adam optimizer and the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) optimizer.
The Adam (acronym of “adaptive moment estimation”) optimization algorithm is an extension to the stochastic gradient descent. The Adam algorithm updates the network weights iteratively during training by performing two operations. The first, called the momentum, calculates the exponentially weighed average of the gradients [33]. The second, called root mean square propagation (RMSP), calculates the exponential moving average. By using averages, the algorithm converges faster towards the minima. This is accomplished through minimizing oscillations when approaching the global minimum, while taking large enough steps to escape from the local minima.
The L-BFGS optimization algorithm is a quasi-Newton method that approximates the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm using less computer memory. L-BFGS uses an estimate of the inverse Hessian matrix, , to steer its search through parameter space, and stores only a few vectors that represent the approximation implicitly. Because of linear memory scaling, the L-BFGS method is particularly well suited for optimization problems with many variables.
2.7. Initialization
Optimization algorithms require a starting set of weight values with which to begin the optimization process. The selection of initial values could impact convergence of the optimization algorithm, with incorrect selection possibly resulting in complete convergence failure [34,35]. DNNs without proper weight initialization may suffer from vanishing or exploding gradients, which happens when the signal transmitted from layer-to-layer stops flowing or becomes saturated. To prevent the occurrence of such problems, the variance of the outputs of each layer should be equal to the variance of its inputs. Accordingly, the variance of the gradients should be equal before and after flowing through a layer during backpropagation. Two of most frequently used initialization techniques are the Glorot (also known as Xavier) initialization and the Kaiming (also known as He) initialization.
The initialization scheme named after Xavier Glorot initializes the weights of the neural network such that the variance of the activation functions is the same across each layer. As a result, constant variance leads to smooth gradient updates and overcomes the problem of exploding or vanishing gradients. Biases are initialized to zero, whereas the weights are initialized randomly at each layer as: , where is a uniform probability distribution, and is the size of the previous layer.
The Kaiming He initialization scheme is similar to Glorot initialization. In this method, the weights in each layer are initialized considering the values of the previous layer, thus achieving a global minimum of the cost function faster and more efficiently. The weights are random, but differ in range depending on the values of the previous layer of neurons. Biases are initialized to zero, whereas the weights are initialized randomly at each layer as: , where is a Gaussian probability distribution and, is the size of the previous layer. He Normal initialization is commonly used in conjunction with the ReLU activation function.
3. Point Kinetics Equations (PKEs)
The PKEs and delayed neutron precursor concentrations are reduced-order models of the Neutron Transport Equation and the Bateman equation, respectively. The point kinetics are derived under the approximation that the shape of the neutron flux and the neutron density distribution are ignored, thus assuming that the reactor acts as a point. The delayed neutron precursor concentrations are described by a set of differential equations that arise from simplifications of the Bateman equation. PKEs are a system of coupled nonlinear differential equations, which describe the kinetics of reactor variables, such as neutron density concentration, the delayed neutron precursor density concentration, and reactivity. Reactivity defined as the deviation of an effective multiplication factor, , from unity, is a measure of the state of the reactor relative to the critical state [35]. When , the reactor is subcritical; when , the reactor is critical; and when the reactor is supercritical. Reactivity is a dimensionless number, but it is commonly expressed in per cent mile or pcm units.
Changing the reactivity provides the means to control the reactor power. The solution of PKEs provides information on the nuclear reactor power level and the power fluctuation during the reactivity transient. The PKEs for several groups of delayed neutrons are given as [36]:
where represents the neutron density concentration; is the delayed neutron precursor density concentration for the group, i; is the reactivity feedback, which is a function of temperature; is the delayed neutron fraction for each group; is the sum of the delayed neutron fractions. In addition, is the mean neutron lifetime in the reactor core; is the mean neutron precursor lifetime for each group, i; and is the time-independent neutron source. At time t = 0, the reactor is in steady state, and we use the following initial conditions [36]:
where the values of , , and are suggested by the experimental data. In most systems, , and, therefore, under steady state conditions, we obtain [36]. Because of the stiffness of the ODE system, the numerical solution of the PKEs requires using relatively small time steps in the computational domain to achieve an accurate solution.
4. Purdue University Reactor Number One (PUR-1)
In this work, we develop a PINN model to monitor the start-up transient of Purdue University Reactor Number One. PUR-1 is an all-digital 10 kWth material test reactor (MTR)—pool type, with flat-plate-type fuel by BWXT Technologies [37,38]. The fuel material consists of high-essay, low-enriched uranium (19.75% 235U) in the form of U3Si2—Al. There are 16 total assemblies, where each standard assembly has up to 14 fuel elements. The core is submerged into a 5.2 m deep water pool, where water is used for both neutron moderation and fuel heat removal. The average thermal neutron flux in the fuel region is n/cm2·s, with the maximum thermal flux reaching the value of n/cm2·s. The reactor power is controlled with three control rods. Two of them are borated stainless steel shim safety rods (SS1 and SS2), and the third one is a 304 stainless steel regulating rod (RR). A schematic drawing of PUR-1 is shown in Figure 3. An inset panel in Figure 3 shows the relative locations of the fuel elements and control rods.
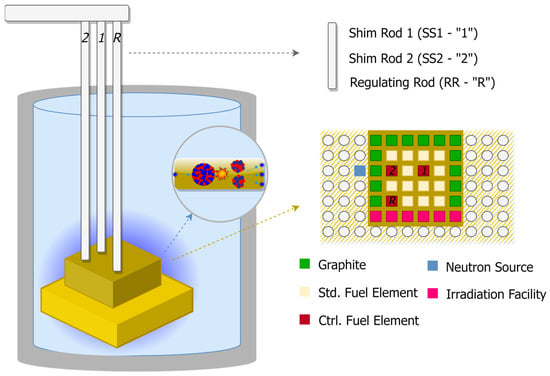
Figure 3.
Schematics of PUR-1.
To obtain the solution of PKEs, one has to have an auxiliary equation describing the evolution of reactivity in time. In PUR-1 operation, reactivity is changed by the movement of control rods. In principle, only one control rod (SS1 or SS2) is sufficient to shut down the reactor completely. When the reactor is shut down, the control rods are inserted into the reactor core, and the reactivity has a large negative value. During PUR-1 startup, control rods are slowly withdrawn from the core, which gradually increases reactivity until the reactor becomes critical. The operating speed of SS1 and SS2 is 11 cm/min, whereas the speed of RR is 45 cm/min. The typical startup time for PUR-1 is approximately 4 min. In general, reactivity is a function of temperature. However, because the temperature of the PUR-1 pool remains close to room temperature value during startup and normal operation, the dependence of reactivity on temperature is negligible.
From PUR-1 benchmarks, s and n/cm2∙s. The values of PUR-1 parameters and for six groups are listed in Table 1. We chose the value of n/cm2∙s.

Table 1.
Parameters of PUR-1.
An experiment was performed to obtain time-dependent values of reactivity during the start-up process of PUR-1. We used the SS2 control rod only because of its location near the edge of the core, as compared to location of SS1. At the start of the experiment, the SS1 and RR control rods were fully withdrawn, whereas the SS2 was fully inserted into the reactor core. Then, the SS2 control rod was withdrawn until criticality was reached. We list the data acquired from the experiment along with reactivity estimations in Table 2.

Table 2.
Reactivity values during the start-up of PUR-1 by withdrawing the SS2 control rod.
The first column of Table 2 lists the location of SS2 relative to the core measured at selected points. When the SS2 control rod is withdrawn 40 cm out of the core, the reactor is critical. The second column lists the estimated reactivity values, which are calculated using PUR-1 benchmarks for the Inhour equation. The third column of Table 2 lists the uncertainty values of the reactivity. The time needed to complete the start-up of PUR-1 was measured to be 3 min and 37 s or 217 s. This is consistent with the SS2 movement speed of 11 cm/min or 4.4 in/min. It should be noted that the reactivity insertion of 10 pcm is considered a very small value in practice, whereas the reactivity insertion of the order of 1 pcm is practically unrealizable in commercial light water reactors (LWRs). The mean reactivity uncertainty for all five reactivity insertion steps is 83.8 pcm. This can be considered a relatively small number when compared to the first three cases of reactivity insertion, which were measured with an uncertainty lower than 10%. The last two reactivity insertion steps, at locations 30 cm and 40 cm, were measured with larger reactivity uncertainty values, which could hinder the validity of the reactivity model. However, the calculated results are in close agreement with PUR-1 validation data, which include the reactor period and reactor power schedules. Therefore, it is safe to conclude that the reactivity uncertainty values can be neglected without affecting the reactivity model accuracy.
The solution of PKEs requires a continuous function of reactivity transient [39]. To obtain , we fitted a polynomial curve to the experimental points in Table 2. The graphs of the interpolated or S-curve (blue) and the polynomial fit (orange) are shown in Figure 4. The best fit was obtained using the 4th-order polynomial with the correlation:
where is the reactivity, and is the distance of the SS2 control rod withdrawal from the core of the reactor.
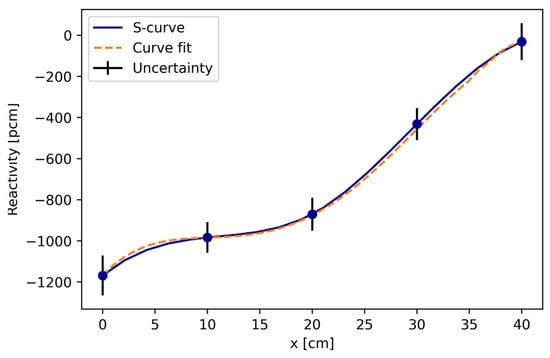
Figure 4.
S curve of the SS2 control rod (cm) with respect to the reactivity (pcm) is depicted by the blue-colored line. Curve fitting of the obtained S curve is depicted by the orange-colored dotted line. The error bar due to uncertainty is depicted by the black-colored line.
The operating speed of the SS2 is . Therefore, to obtain , we substitute in Equation (13) to arrive at the following equation:
where is the time measured in seconds. The reactivity transient in the time interval is plotted in Figure 5.
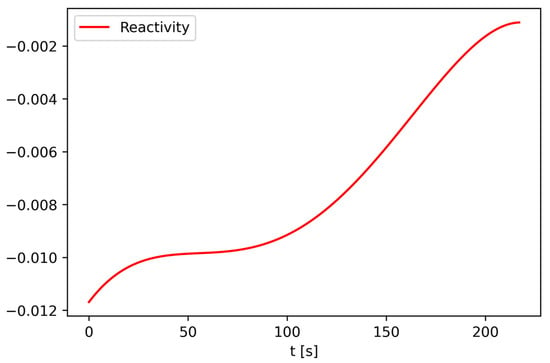
Figure 5.
Reactivity insertion at each second in the time interval of until steady state is reached.
To find the reference solution of all seven differential equations in the system of PKEs, we used the finite difference solver “solve_ivp” (from SciPy Python library) that integrates a system of ordinary differential equations given an initial value. The “LSODA” integration method was used, which is an Adams/BDF method with automatic stiffness detection and switching, based on the Fortran solver from ODEPACK.
5. PINN Solution of the PKE Model of PUR-1
5.1. PINN Model Development and Training
A PINN model was developed for the solution of PKEs with six groups of neutron precursor density concentrations, using the neutron source value and startup reactivity transient of PUR-1. Besides the PKEs, the problem contains ICs, which are treated as a special type of BCs. The loss comprises only the first two terms of Equation (4). The ICs were encoded into PINN as soft constraints. We compared the performance of PINN using soft and hard constraints, and no significant difference was found. The loss function involves 14 different terms, seven of them related to the ODEs, and the other seven related to their respective ICs.
Figure 6 displays the architecture of the PINN, which consists of two interconnected networks. The surrogate network takes as input time, t; and provides an approximation of the PKE solution, the state vector . The weights of the surrogate network are trainable. The residual network takes the approximate solution from the surrogate network, and calculates the residual that is used as a loss function to optimize the surrogate network. The residual network includes the governing PKE equations and the ICs.
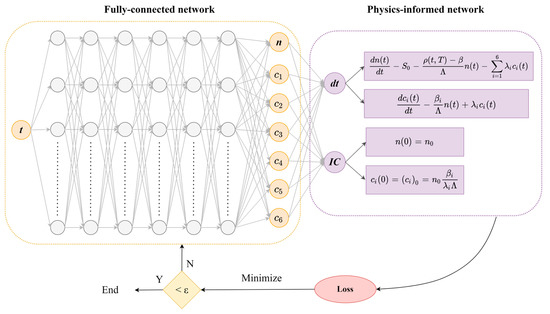
Figure 6.
Schematic of PINN for solving the PKEs with ICs. The input to surrogate network is time, t, and the output is the solution vector . The residual network tests if the solution vector satisfies the PKE governing equations and the ICs.
For fully connected PINN implementation, a six-layer FNN with the ReLU activation function was developed for the surrogate network. The FNN input layer consists of a single input, which is a point in the time domain. Every hidden layer consists of 64 neurons. The output layer consists of seven outputs, which are the neutron density concentration, , and the delayed neutron precursor’s density concentration, , for six groups. The Kaiming He method is used to initialize the weights of the FNN, which is the most common initialization method when using ReLU as the activation function [40]. The surrogate network calculates the approximate solution to the problem. Then, the residual network encodes the governing equations (PKEs) and ICs, and calculates the loss function (MSE of the residual), which must be minimized to optimize the surrogate network.
In our implementation of PINN, the loss function is minimized by using the Adam optimizer for 65,000 iterations, with a learning rate of λ = 0.001. The training data set consists of 42 collocation points. Specifically, 30 points were distributed inside the solution domain, and 12 training points were used for the ICs. The distribution of the collocation points is drawn from the Sobol sequence. The computational domain for evaluation of the residuals is the time domain, , which is the start-up period for PUR-1 to reach criticality. The implementation is performed in the Python environment using the Python library, DeepXDE [10]. The workflow for solving the PKEs using PINNs in the DeepXDE framework is shown in Table 3.

Table 3.
Workflow for solving PKEs using PINNs in DeepXDE framework.
Figure 7a shows the loss history of PINN after 65,000 iterations. The training took approximately 62 s, on a Windows PC with AMD Ryzen 7 5800H with Radeon Graphics, 8-core processor, and 32 GB of RAM. The loss is presented as the summed-up MSE of all terms for both training (blue) and testing (orange).
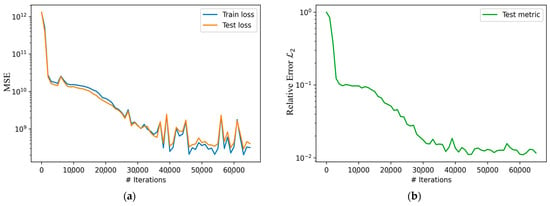
Figure 7.
History of the loss function of PINN after 65,000 iterations for interpolation. (a) The training (blue) and testing (orange) loss is the summed-up MSE loss of all terms in the PKEs. (b) The test metric is the relative error for the first ODE term.
The MSE of training starts at the value of and decreases to . It should be noted that the large absolute value of the loss is not indicative of the ability of PINN to make correct predictions. The fact that MSE decreased by a factor of indicates good performance of the PINN. To verify this, a numerical test was performed by reducing the value of the source term in Equation (9) from the actual value of n/cm2∙s to a hypothetical smaller value of n/cm2∙s. With the smaller source term, the magnitudes of the MSE values for every ODE term were in the range to at the conclusion of training, showing the same decrease, by a factor of , as in the case of the larger source term. Therefore, it can be concluded that the scaling of the source term does not affect the PINN model relative performance. In addition, by observing the pattern of the loss curve, it can be qualitatively determined that there is no overfitting of the network. Furthermore, the relative error was calculated to evaluate the performance of the PINN. The error metric for the neutron density concentration is shown in Figure 7b. The error starts at the value of and decreases to after 65,000 iterations. This indicates good accuracy in predictions with PINN.
5.2. PINN Solution of PKEs
Using PINN formalism, we solve the system of seven stiff nonlinear ODEs comprising the PKEs. The results are shown in Figure 8. The left panels, Figure 8a,c,e,g,i,k,m, display PINN predictions along with reference solutions for the neutron density concentration, and six groups of delayed neutron precursor density concentrations, respectively. As can be seen from the figures, PINN predictions closely approach the reference solution for the entire computational domain, . The stiffness of the PKE system does not prevent the PINN from capturing the basic dynamics of the system.
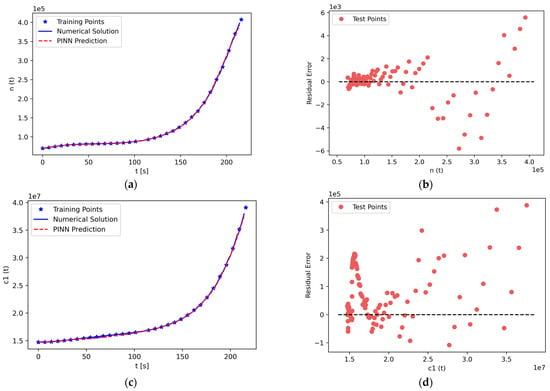
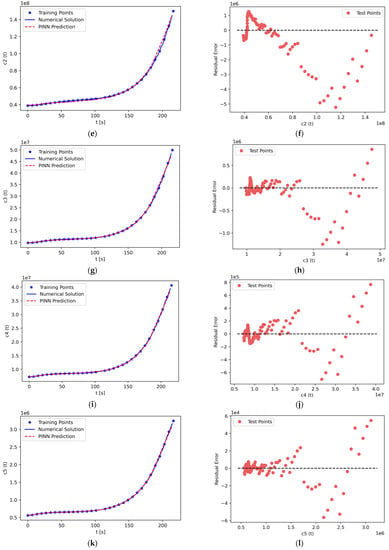
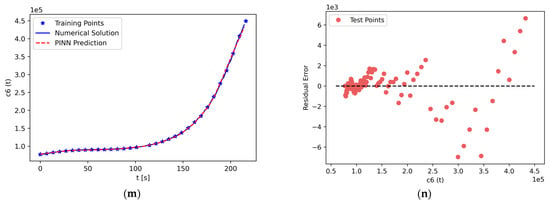
Figure 8.
(a) Solution of neutron density concentration, , in the time interval , along with PINN prediction. (b) Residual error plot of , which shows the error margin of the predictions. (c,e,g,i,k,m) Solutions of delayed neutron precursor density concentration of , , , , , and , respectively, in the time interval , along with PINN prediction. (d,f,h,j,l,n) Residual error plot of , , , , , and , respectively.
The right panels, Figure 8b,d,f,h,j,l,n, display the residual errors of neutron density concentration and delayed neutron precursor density concentrations for six groups, respectively. In most cases, the residual error is almost zero, especially in the time interval . This phenomenon is attributed to the weak change of the gradient during that time period, as compared to the significant change in the gradient occurring in the time interval . The error is the largest during the time interval . However, even for this time period, the residual errors remain small relative to the absolute values. For instance, for the neutron density concentration n(t) in Figure 8a,b, the largest value of the residual error is 6000, or 2.18% of the reference solution value of 275,000 n/cm2∙s. In the graphs of all panels in Figure 8, for each test point, one can observe a difference of at least two orders of magnitude between the residual error and the reference solution.
Though the PINN model has shown good performance in interpolation of the data, a more difficult challenge for all ML models is the extrapolation of the data. Therefore, as part of this investigation, the extrapolation capability of PINNs was explored by examining three different cases. In the first case, the model is trained in the time interval , and the extrapolation is performed in a five-seconds interval, . In the second case, the model is trained in the time interval of , and the extrapolation is performed in a 10 s time interval, . In the third case, the model is trained in the time interval , and the extrapolation is performed in a 15 s time interval, . The results of the second case are displayed in Figure 9 and Figure 10, whereas the percentage error findings for the first, second, and third case are presented in Table 4, Table 5, and Table 6 respectively.
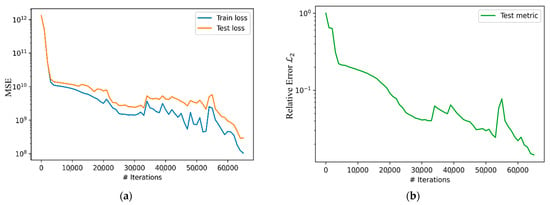
Figure 9.
History of the loss function of PINN after 65,000 iterations for extrapolation. (a) The training (blue) and testing (orange) loss is the summed-up MSE loss of all terms in the PKEs. (b) The test metric is the relative error for the first ODE term.
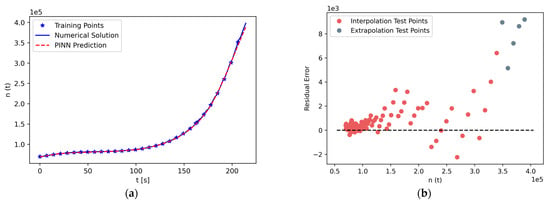
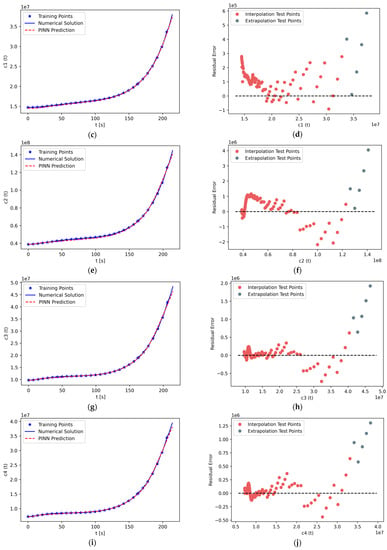
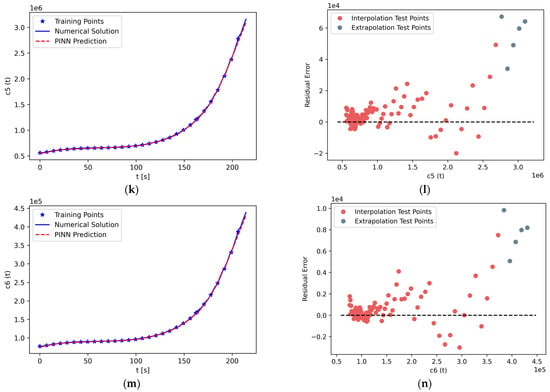
Figure 10.
(a) Solution of neutron density concentration, , in the time interval , along with PINN prediction. (b) Residual error plot of , which shows the error margin of the predictions. (c,e,g,i,k,m) Solutions of delayed neutron precursor density concentration of , , , , , and , respectively, in the time interval , along with PINN prediction. (d,f,h,j,l,n) Residual error plot of , , , , , and , respectively. The training data for interpolation are in the time interval , whereas the training data for extrapolation are in the time interval .

Table 4.
Case 1. Percentage error of extrapolation of the training data in time interval using five testing points in time interval .

Table 5.
Case 2. Percentage error of extrapolation of the training data in time interval using five testing points in time interval .

Table 6.
Case 3. Percentage error of extrapolation of the training data in time interval using five testing points in time interval .
The model’s architecture remains as described earlier in this Section, having a six-layer FNN with the ReLU activation function for the surrogate network. The FNN input layer consists of a single input, whereas the output layer consists of seven outputs. Every hidden layer consists of 64 neurons. In each case, the loss function is minimized by using the Adam optimizer for 65,000 iterations, with a learning rate of . The number of training data inside the domain consists of 30 collocation points, whereas the distribution of the collocation points is drawn from the Sobol sequence. The number of testing data inside the domain consists of 120 points, and they are randomly distributed. The implementation is performed in the Python environment using the Python library DeepXDE [10]. In the following, the results of the second case are presented, whereas the error rate percentage of all three cases are displayed later in different tables.
Figure 9a shows the MSE loss history of PINN after 65,000 iterations. The MSE of training starts at the value of and decreases to . Similarly, the fact that MSE decreased by a factor of indicates good performance of the PINN. In addition, the relative error was calculated to evaluate the performance of the PINN. The error metric for the neutron density concentration is shown in Figure 9b. The error starts at the value of and decreases to after 65,000 iterations. This indicates good accuracy in predictions with PINN.
The results of the solution of the PKEs are shown in Figure 10. The left panels, Figure 10a,c,e,g,i,k,m, display PINN predictions along with reference solutions for neutron density concentration, and six groups of delayed neutron precursor density concentrations, respectively. As can be seen from the figures, PINN predictions closely approach the reference solution for both the computational domain of interpolation, , and extrapolation, . More specifically, in the time interval of , the predictions seem to experience their lowest accuracy in the final second of the solution, whereas they maintain high accuracy in the rest time interval, even comparable to the interpolation case. Similar to before, the stiffness of the PKE system does not prevent the PINN from capturing the basic dynamics of the system.
The right panels, Figure 10b,d,f,h,j,l,n, display the residual errors of neutron density concentration and delayed neutron precursor density concentrations for six groups, respectively. The testing points used for interpolation are shown in red, and the testing points used for extrapolation are shown in gray. In every case, the largest error in extrapolation is greater than the largest error in interpolation. However, in most cases, the errors in extrapolation are comparable to errors in interpolation. Therefore, based on cases considered in the study, the PINN’s capacity to perform extrapolation is reasonably good compared to the interpolation capability.
The percentage error of extrapolation predictions for the first, second, and third cases are presented in Table 4, Table 5, and Table 6, respectively. Case 1 has the lowest prediction errors. This is to be expected because the extrapolation time interval is the shortest. The model achieved a percentage error varying from 0.037% to 2.404%. It has to be noted that the error did not exceed the 0.75% threshold for 8 out of 35 tests. The error remained in the 1–2% range for 27 out of 35 tests, and exceeded the 2% threshold only for 5 out of 35 tests.
Case 2 errors were in the range of 0.032% to 4.138%. The errors are distributed as: less than 1% threshold for 4 out of 35 tests, between 1% to 2% for 16 out of 35 tests, between 2–3% for 12 out of 35 tests, and above 3% threshold for 3 out of 35 tests.
Case 3 errors were in the range of 0.256% to 7.963%. The errors are distributed as: less than 1% threshold for 5 out of 35 tests, between 1% to 2% for 5 out of 35 tests, between 2–3% for 6 out of 35 tests, between 3–4% for 5 out of 35 tests, between 4–5% for 4 out of 35 tests, between 5–6% for 3 out of 35 tests, and above 6% threshold for 7 out of 35 tests.
The extrapolation errors for all three cases are comparable to interpolation errors. The findings imply that the PINN model extrapolation ability is directly correlated with the computational interval size. The smaller the size of the forecasting interval, the better the extrapolation accuracy.
6. Conclusions
This paper presents a new approach for developing a nuclear reactor digital twin (DT) based on physics-informed neural network (PINN), which uses machine learning methods to solve governing differential equations. Using PINN is a hybrid approach that provides alternatives to a purely physics-model-based DT, which has challenges in modelling complex experimental systems, and a purely data driven machine-learning-based DT, which relies on training data and has challenges with extrapolation.
In this work, we develop a PINN model for the solution of point kinetic equations (PKEs), which represent a reduced order model of a nuclear reactor. PKEs consist of a system of coupled nonlinear stiff ordinary differential equations. The surrogate model of a PINN is implemented with a feed-forward fully connected network. In training the PINN model, collocation points are selected from the Sobol Sequence distribution. All differential operators are implemented using automatic differentiation, which offers a mesh-free and time-efficient solution. The approximate solutions satisfying both the differential operator and the initial conditions are obtained via tuning the deep neural network hyperparameters. This is accomplished during training by minimizing the residuals’ loss function over the entire computational domain. In particular, the initial conditions are satisfied as soft constraints by adding a term for each to the loss function. The resulting loss function is used as the objective for minimization.
The effectiveness of the PINN method has been demonstrated by solving the PKEs that model the start-up transient of the PUR-1 water pool-type research reactor. The reactor power in PUR-1 is controlled through the insertion or withdrawal of control rods from the core. PUR-1 time-dependent reactivity was obtained from measurements during the reactor start-up transient. The PINN solution was obtained for PKEs with six groups of neutron precursor density concentrations, using the neutron source value and experimental startup reactivity transient of PUR-1. The results obtained with PINNs are in close agreement with solution of PKEs obtained with a conventional numerical integration approach.
As part of this work, we investigated the extrapolation capability of PINNs by considering several cases of a progressively increasing forecasting time interval. In general, for the intervals considered, the forecasting error in extrapolation was relatively small, as compared to interpolation errors. The findings indicate that the PINN model extrapolation ability is correlated with the computational interval size. The extrapolation accuracy is higher for the shorter forecasting time interval.
The main advantages of PINNs over the standard numerical methods are that PINNs do not require the time-consuming construction of elaborate grids, and offer low computational time, and can, therefore, be applied more efficiently to the solution in irregular and high-dimensional domains. Fast computations with PINN are particularly beneficial for real-time reactor operation monitoring. As shown in this work, given a reactivity schedule and initial values, PINNs execute rapidly on a regular PC, without resorting to high-performance computing hardware. Future work will consider using PINNs for monitoring different transients of PUR-1, including real-time monitoring and the detection of reactor operational anomalies. Whereas this paper serves as an investigation of PINN performance in solving ODEs, in the future, we will investigate the development of a PINN for the solution of auxiliary PDEs for structural health monitoring (heat transfer, Allen–Cahn, etc.) for a comprehensive reactor digital twin.
Author Contributions
Conceptualization, K.P. and A.H.; methodology, K.P. and A.H.; software, K.P.; validation, K.P.; formal analysis, K.P. and A.H.; investigation, K.P. and A.H.; resources, L.H.T. and A.H.; data curation, K.P.; writing—original draft preparation, K.P.; writing—review and editing, A.H.; visualization, K.P.; supervision, A.H. and L.H.T.; project administration, A.H.; funding acquisition, A.H. and L.H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the U.S. Department of Energy, Advanced Research Projects Agency-Energy (ARPA-E) under contract DE-AC02-06CH11357, and by a donation to AI Systems Lab (AISL) at Purdue University by Goldman Sachs Gives.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge PUR-1 management and staff, including Seungjin Kim, Stylianos Chatzidakis, and True Miller.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kochunas, B.; Huan, X. Digital Twin Concepts with Uncertainty for Nuclear Power Applications. Energies 2021, 14, 4235. [Google Scholar] [CrossRef]
- Kim, C.; Dinh, M.-C.; Sung, H.-J.; Kim, K.-H.; Choi, J.-H.; Graber, L.; Yu, I.-K.; Park, M. Design, Implementation, and Evaluation of an Output Prediction Model of the 10 MW Floating Offshore Wind Turbine for a Digital Twin. Energies 2022, 15, 6329. [Google Scholar] [CrossRef]
- Li, Y.; Yang, J. Meta-Learning Baselines and Database for Few-Shot Classification in Agriculture. Comput. Electron. Agric. 2021, 182, 106055. [Google Scholar] [CrossRef]
- Pylianidis, C.; Snow, V.; Overweg, H.; Osinga, S.; Kean, J.; Athanasiadis, I.N. Simulation-Assisted Machine Learning for Operational Digital Twins. Environ. Model. Softw. 2022, 148, 105274. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial Neural Networks for Solving Ordinary and Partial Differential Equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10566. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-Informed Machine Learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks for Heat Transfer Problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Fluid Mechanics: A Review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A Physics-Informed Deep Learning Framework for Inversion and Surrogate Modeling in Solid Mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Prantikos, K.; Tsoukalas, L.H.; Heifetz, A. Physics-Informed Neural Network Solution of Point Kinetics Equations for Development of Small Modular Reactor Digital Twin. In Proceedings of the 2022 American Nuclear Society Annual Meeting, Anaheim, CA, USA, 12–16 June 2022. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A Deep Learning Algorithm for Solving Partial Differential Equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Koryagin, A.; Khudorozkov, R.; Tsimfer, S. PyDEns: A python framework for solving differential equations with neural networks. arXiv 2019, arXiv:1909.11544. [Google Scholar]
- Chen, F.; Sondak, D.; Protopapas, P.; Mattheakis, M.; Liu, S.; Agarwal, D.; Di Giovanni, M. NeuroDiffEq: A Python Package for Solving Differential Equations with Neural Networks. JOSS 2020, 5, 1931. [Google Scholar] [CrossRef]
- Zubov, K.; McCarthy, Z.; Ma, Y.; Calisto, F.; Pagliarino, V.; Azeglio, S.; Bottero, L.; Luján, E.; Sulzer, V.; Bharambe, A.; et al. NeuralPDE: Automating Physics-Informed Neural Networks (PINNs) with Error Approximations. arXiv 2021, arXiv:2107.09443. [Google Scholar]
- Xu, K.; Darve, E. ADCME: Learning Spatially-Varying Physical Fields Using Deep Neural Networks. arXiv 2020, arXiv:2011.11955. [Google Scholar]
- Rudy, S.; Alla, A.; Brunton, S.L.; Kutz, J.N. Data-Driven Identification of Parametric Partial Differential Equations. SIAM J. Appl. Dyn. Syst. 2019, 18, 643–660. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.; Weinan, E. Solving High-Dimensional Partial Differential Equations Using Deep Learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef]
- Wiering, M.; van Otterlo, M. (Eds.) Reinforcement Learning. In Adaptation, Learning, and Optimization; Springer: Berlin/Heidelberg, Germany, 2012; Volume 12, ISBN 9783642276446. [Google Scholar]
- Ji, W.; Qiu, W.; Shi, Z.; Pan, S.; Deng, S. Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics. J. Phys. Chem. A 2021, 125, 8098–8106. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; De Florio, M.; Ganapol, B.D.; Picca, P.; Furfaro, R. Physics-Informed Neural Networks for the Point Kinetics Equations for Nuclear Reactor Dynamics. Ann. Nucl. Energy 2022, 167, 108833. [Google Scholar] [CrossRef]
- Akins, A.; Wu, X. Using Physics-Informed Neural Networks to solve a System of Coupled Nonlinear ODEs for a Reactivity Insertion Accident. In Proceedings of the 2022 Physics of Reactors, Pittsburgh, PA, USA, 15–20 May 2022. [Google Scholar]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Heifetz, A.; Ritter, L.R.; Olmstead, W.E.; Volpert, V.A. A numerical analysis of initiation of polymerization waves. Math. Comput. Model. 2005, 41, 271–285. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic Differentiation in Machine Learning: A Survey. arXiv 2015, arXiv:1502.05767. [Google Scholar]
- Lagari, P.L.; Tsoukalas, L.H.; Safarkhani, S.; Lagaris, I.E. Systematic Construction of Neural Forms for Solving Partial Differential Equations Inside Rectangular Domains, Subject to Initial, Boundary and Interface Conditions. Int. J. Artif. Intell. Tools 2020, 29, 2050009. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and Mitigating Gradient Flow Pathologies in Physics-Informed Neural Networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Margossian, C.C. A Review of Automatic Differentiation and Its Efficient Implementation. WIREs Data Min. Knowl. Discov. 2019, 9, e1305. [Google Scholar] [CrossRef]
- Eckle, K.; Schmidt-Hieber, J. A Comparison of Deep Networks with ReLU Activation Function and Linear Spline-Type Methods. Neural Netw. 2019, 110, 232–242. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Blum, A.; Hopcroft, J.E.; Kannan, R. Foundations of Data Science, 1st ed.; Cambridge University Press: New York, NY, USA, 2020; ISBN 9781108755528. [Google Scholar]
- Tsoukalas, L.H.; Uhrig, R.E. Fuzzy and Neural Approaches in Engineering. In Adaptive and Learning Systems for Signal Processing, Communications, and Control; Wiley: New York, NY, USA, 1997; ISBN 9780471160038. [Google Scholar]
- Lewis, E.E. Fundamentals of Nuclear Reactor Physics; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2008; ISBN 9780123706317. [Google Scholar]
- Townsend, C.H. License Power Capacity of the PUR-1 Research Reactor. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2018. [Google Scholar]
- Pantopoulou, S. Cybersecurity in the PUR-1 Nuclear Reactor. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2021. [Google Scholar]
- Baudron, A.-M.; Lautard, J.-J.; Maday, Y.; Riahi, M.K.; Salomon, J. Parareal in Time 3D Numerical Solver for the LWR Benchmark Neutron Diffusion Transient Model. J. Comput. Phys. 2014, 279, 67–79. [Google Scholar] [CrossRef][Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Washington, DC, USA, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).