Abstract
Random forest (RF) is one of the most popular machine learning (ML) models used for both classification and regression problems. As an ensemble model, it demonstrates high predictive accuracy and low variance, while being easy to learn and optimize. In this study, we use RF for short-term load forecasting (STLF), focusing on data representation and training modes. We consider seven methods of defining input patterns and three training modes: local, global and extended global. We also investigate key RF hyperparameters to learn about their optimal settings. The experimental part of the work demonstrates on four STLF problems that our model, in its optimal variant, can outperform both statistical and ML models, providing the most accurate forecasts.
1. Introduction
Electricity demand forecasting is extremely important for energy providers to ensure the secure, effective and economic operation of the power system. Short-term load forecasting (STLF) covers a forecast horizon of a few hours to a few days. STLF is necessary for generation resource planning to meet electricity demands and optimize the power flow on the transmission grid to avoid overloads. As electricity demand is a major driver of electricity prices, load forecasting plays a key role in competitive energy markets. The STLF accuracy directly affects the financial performance of energy market participants.
The importance of accurate electricity demand forecasts for the safe, reliable and effective operation of power systems is behind the great interest of researchers in this area. STLF problems are complex because electricity demand time series express a nonlinear trend, multiple seasonality, variable variance, significant random disruptions and changing daily profile. These challenging factors place high demands on STLF models.
1.1. Related Work
Roughly, STLF methods can be divided into statistical and ML methods. The most popular representatives of the first group are: auto-regressive integrated moving average (ARIMA) [1], exponential smoothing (ETS) [2], linear regression [3], and Kalman filtering [4]. The main drawbacks of the statistical methods are their linear character, limited adaptability, limited ability to deal with complex seasonal patterns, and problems with capturing long-term dependencies in time series and introducing exogenous variables into the model [5].
ML models provide more flexibility in modeling nonlinear functions. Unlike statistical methods, they do not require strong assumptions about the mapping function, and they learn relationships between predictors and targets directly from historical data. Among ML methods for forecasting, neural networks (NNs) have gained the most popularity in recent years [6]. The multitude of architectural solutions and mechanisms to improve performance encourage the use of NNs to solve complex forecasting problems such as STLF. Classical NNs were investigated for suitability for STLF in [7]. To deal with triple seasonality in time series, patterns of the daily profiles were introduced, which filter out the trend and the weekly and yearly seasonality (a similar approach was used in this study, where different definitions of patterns are examined). Among the considered NN architectures, which included Multilayer Perceptron (MLP), Radial Basis Function NN, General Regression NN (GRNN), Fuzzy Counterpropagation NN, and Self-Organizing Maps, GRNN and MLP stand out as performing with the highest accuracy.
In recent years, a development in the NN field has been the move towards deep and, especially useful in forecasting, recurrent architectures [6]. Deep NNs (DNNs) are especially beneficial in learning the most useful data representation for modeling a given target function, while Recurrent NNs (RNNs) are beneficial in modeling complex, short- and long-term temporal relationships in data. New mechanisms and procedures introduced to RNNs such as delayed connections, attention, hybrid architecture, dynamic training sets, residual connections and flexible loss functions improve their learning capabilities and expressive power to solve forecasting problems [5]. Some examples of using DNNs and RNNs for STLF are [8], where Convolutional NNs (CNNs) are utilized to extract load and temperature features, which are fed as inputs into the bidirectional propagating RNN to perform hourly electrical load forecasting [9], where a recurrent inception CNN is proposed for STLF that combines RNN and 1-dimensional CNN [10], where RNN with attention significantly reduced forecasting errors as compared to the current state-of-the-art results; and [11], where deep residual networks integrate domain knowledge and researchers’ understanding of the problem and enables probabilistic load forecasting using Monte Carlo dropout.
An effective way to increase the forecast accuracy and robustness of both statistical and ML models is ensembling. This combines multiple models for a common response to improve both the accuracy and stability of the final solution compared to a single model [12]. The theoretical properties of forecast combination investigated in [13] answer the question why a simple average of forecasts often outperforms forecasts from single models. They also prove that simple averages in many cases perform better than more complicated weighting schemes. The beneficial effects of the forecast aggregation on STLF accuracy are shown in many papers: in [14], several ML methods are aggregated in ensembles for one-day-ahead wind power forecasting; in [15], to forecast an interval-valued load, ensemble of RNNs is applied, which learns on the components of the bivariate empirical mode decomposition; in [5], ensembling of a hybrid model, which combines ETS and RNN, leads to a significant reduction in the forecast error; in [16], an ensemble of randomized DNN combined with a walk-forward decomposition is proposed; in [17], a stacking ensemble approach is used to combine DNNs, and in [18], several methods of aggregating base models (MLPs) are considered. Stacking, used in the last two papers, is a way of combining base models via meta-learning, i.e., a meta-model is trained on the predictions of the base models.
Alternatives to stacking are boosting and bagging. Popular representatives of these are gradient-boosted trees and random forest (RF), respectively. Both, used as forecasting models, are based on regression trees. It was shown in [19] that RF can compete with both classical models and NNs in STLF. It can deal with complex time series using appropriate data preprocessing, which produces normalized patterns of the daily profiles. Based on this research, in this study, to improve RF performance, we extend pattern definitions and introduce additional predictors. To enrich input information, in [20], the input patterns are extracted from electrical, meteorological and calendar data by temporal CNN. Fed with these patterns, a Light Gradient Boosting Machine, a type of gradient-boosted trees algorithm, was able to forecast very volatile industrial customer loads. A novel tree-based ensemble method called Warm-start Gradient Tree Boosting (WGTB) was proposed in [21]. It combines four different inference models and aggregates their outputs by a warm-start, bagging and boosting, which at the same time reduces bias and variance. The result proves the efficiency of the proposed strategy and shows an improvement in STLF accuracy over baseline models. Another type of tree-based ensemble, eXtreme Gradient Boosting (XGBoost), was used in [22] for forecasting electricity consumption by industrial customers. To deal with multiple seasonality, the time series were first decomposed using variational mode decomposition. Then, a linear regression model was applied for the trend series and a XGBoost regression model was applied for each fluctuation sub-series.
To close this section, we note that, according to some studies, tree-based ensembles are not inferior to NNs in terms of forecast accuracy. In [23], the authors have examined and reproduced a number of state-of-the-art DNNs for time series forecasting. DNNs were compared on different datasets to a Gradient Boosting Regression Tree (GBRT). The experimental results show that a conceptually simpler model such as GBRT can compete and sometimes outperform modern DNNs by efficiently feature-engineering the input and output structures of GBRT.
1.2. Motivation and Contribution
Tree-based methods are widely used as prediction models as they have very attractive properties such as a capacity for flexible nonlinear regression, which can capture complex interactions between variables and effectively handle multiple predictors (including exogenous ones) of various types (numeric, binary, and categorical). Moreover, they are robust against over-fitting of the training data, they are relatively simple to tune, and they are easy to implement with the available software. Their effectiveness has been confirmed in many forecasting competitions, for example those carried out on the Kaggle platform [24].
The excellent performance of tree-based approaches was demonstrated in the 2020 M5 forecasting competition. The top places in this competition, in terms of both accuracy and uncertainty, were dominated by entries that used tree-based ML methods such as gradient-boosted trees [25]. Four out of the five winning models used a variant of the tree-based method and most of the other top 50 best-performing models adopted similar approaches to the winning submission by training recursive and non-recursive tree-based models [26]. Thus, tree-based forecasting models appear to be strong competitors to NNs, which in the form of deep learning-based models dominate the recent literature on forecasting methods [6].
In this study, motivated by the excellent results of tree-based models in forecasting competitions, we apply RF to the challenging problem of STLF. RF gives similar results to boosting, but is easier to train and tune [27]. The main contribution of this work is to examine RF models using a variety of time series preprocessing methods and training modes. In the local mode, RF learns on samples similar to the query sample, which enables the model to focus on the local features of the target function around the query pattern and improve accuracy in this region. In the global mode, to achieve the same goal, i.e., focusing on the proper region of the target function, we introduce additional calendar variables. By examining different methods of time series preprocessing, we find the most useful data representation for achieving the highest accuracy of the model. We empirically demonstrate that the proposed approach outperforms in terms of accuracy both standard statistical models as well as more sophisticated ML approaches.
The novelty of this work in relation to our previous work [19] is twofold. First, we extend pattern definition by introducing seven types of patterns based on the historical data. They incorporate daily and/or weekly seasonality, while in [19], the patterns captured only daily seasonality. Second, we introduce a global mode of training with additional predictors representing calendar data. In [19], only a local training was considered without calendar inputs.
The rest of the paper is organized as follows. In Section 2, we propose several data prereprocessing methods for electricity demand times series. Section 3 defines the forecasting problem and RF training modes. Section 4 describes the RF algorithm in application to STLF. The experimental framework used to evaluate the performance of the proposed model and compare it with baseline models is described in Section 5. Finally, Section 6 concludes the work.
2. Data Preprocessing
The power system load or electricity demand time series express a trend, triple seasonality (annual, weekly and daily) and random fluctuations. These components are dependent on the system size, size of the economy served, customer structure, as well as weather and climatic conditions. The daily load profiles that we focus on in STLF vary throughout the year and depend on the day of the week [5].
To forecast future demand with the least possible error, the forecasting model should be fed by the most relevant predictors. In our univariate STLF model, which produces forecasts for the next day, the predictors are selected from recent history and are preprocessed accordingly. The forecasting model based on RF is fed by input patterns and produces encoded forecasts for hour t of day i, (MISO model).
Let be an electricity demand time series with hourly resolution and vector represents its 24-h-long sequence for day i. To capture the characteristic properties of the series, remove the trend and unify data, we define the input patterns as follows:
- r1
- The input patterns are defined based on the weekly sequence which precedes forecasted day i:where is the input pattern, is the demand sequence of the week preceding the forecasted day i and is the mean of this sequence.Input vectors (1), which for successive i represent overlapping weekly sequences shifted by one day, are normalized versions of centered vectors . They all have zero mean, the same variance and the same unity length. However, they differ in shape. Thus, we assume that the weekly shape carries the information about the forecasted demand of the day following this week.
- r2
- The input patterns are defined based on the daily sequence which precedes the forecasted day i. The encoding equation is (1), where and is the demand sequence of the day preceding the forecasted day i. In case of r2, a carrier of the information about the forecasted value is the shape of the preceding day.
- r3
- The input patterns are defined based on the sequence composed of the demands at hour t of seven consecutive days preceding the forecasted day i. In (1), and , where t is the forecasted hour of day i.
- r4
- The input patterns are defined based on the sequence composed of the demands at hour t of 21 consecutive days preceding the forecasted day i. In (1), and , where t is the forecasted hour of day i.
- r5
- The input patterns are defined based on the sequence composed of the demands at hour t of seven days preceding forecasted day i and representing the same day of the week as the forecasted day. For example, when the model predicts demand at hour t on Monday, the input pattern is composed of the demands at hour t of seven preceding Mondays. In (1), and , where t is the forecasted hour of day i.
- r6
- Cross-pattern combining r2 and r3—the input patterns are defined based on both: the daily sequence and the sequence composed of the demands at hour t of seven consecutive days preceding the forecasted day i. In (1), and , where t is the forecasted hour of day i.
- r7
- Cross-pattern combining r2 and r4—the input patterns are defined based on both: the daily sequence and the sequence composed of the demands at hour t of 21 consecutive days preceding the forecasted day i. In (1), and , where t is the forecasted hour of day i.
Figure 1 shows the sequences which are used for x-patterns construction and Figure 2 shows data used for construction patterns r6 and r7. Depending on the definition, x-patterns introduce different input information to the model. Pattern r1 introduces detailed information about the weekly sequence which precedes the forecasted day. Note that r1 expresses both daily and weekly seasonality unlike r2, which carries information only about the daily seasonality. To deal with weekly seasonality when r2-patterns are used, the model can be trained in the local mode, i.e., on the subset of x-patterns corresponding to the forecasting task (see Section 3).
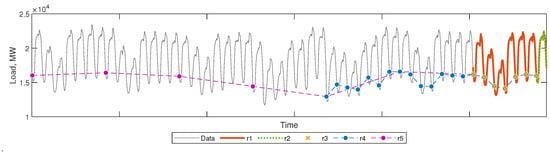
Figure 1.
Load time series points used for input patterns construction.
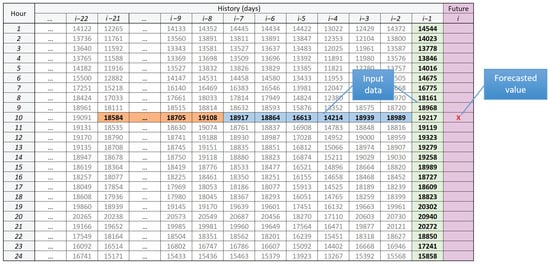
Figure 2.
Cross-patterns: r6 (green + blue) and r7 (green + orange + blue).
Pattern r3 introduces information on the demand in the previous seven days at the same hour as the forecasted one. It expresses only weekly seasonality. Information about the daily seasonality is not included, so the local mode of training, i.e., training on the selected r3-patterns corresponding to the forecasting task (see Section 3), can help with dealing with daily seasonality. Similar information as in r3 is contained in pattern r4 but from a longer 3-week period. Pattern r5 shows neither daily nor weekly seasonality. It carries information about the demand at the same hours as forecasted in previous days of the same type as the forecasted day.
Cross-patterns r6 and r7 express both daily and weekly seasonalities as r1, but in a more sparing form, using respectively 30 or 44 instead of 168 components. In [28], we showed that STLF based on both daily and weekly patterns gives better results than forecasting based on separate daily or weekly patterns. In [28], we aggregated forecasts generated by two neural models: a daily pattern-based model and a weekly pattern-based model, while in this study, we combine daily and weekly patterns into one pattern and use only one model.
Examples of input patterns r1–r7 are depicted in Figure 3. Note different shapes of patterns, carrying different input information.
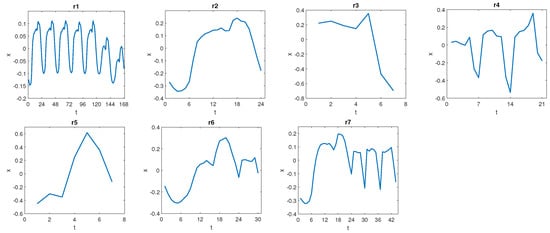
Figure 3.
Examples of input patterns r1–r7.
The output data, i.e., the electricity demand at hour t of day i, is encoded as follows:
where is the demand sequence preceding forecasted day i, defined depending on the x-pattern type r1–r7 (this is the same sequence based on which pattern was defined) and is the mean of this sequence.
The output data are encoded similarly to the input data, using the same coding variables: and . Thus, Equation (2) like Equation (1) filters the data by removing the local trend () and unifying the variance (this is a function of the denominator of these equations, which can be thought of as a measure of diversity of the input sequence). Such filtered and unified data are predicted by the forecasting model (RF). Then, the real forecast is determined from transformed Equation (2):
where is the model prediction and is the real forecast.
Note that (3) brings back the local current properties of the time series (level and dispersion), which were removed by (1) and (2) to simplify the relationships between input and output data. We have successfully used this kind of preprocessing of input and output data in our previous load forecasting models to deal with multiple seasonality, simplify the model and speed up training, see, e.g., [7,19,28,29,30,31,32].
3. Forecasting Problem and Training Modes
The forecasting task is defined as follows: predict electricity demand for hour (1, …, 24) of day based on historical data. Day represents day of the week (Monday, …, Sunday). To maximize the forecasting performance and to make the most of all available training data up to day (forecasted day), the forecasting model is trained individually for each forecasting task and it performs only one prediction: . Note that the “global” generalization property of the model is not important because it is built to make only one prediction. What is important is the “local” performance in the neighborhood of pattern . To increase this property, we use two approaches. In the first one, we train the model in the local mode and in the second one, we extend input patterns with calendar variables when we use global learning. For comparison we also train the model in the standard global mode.
The full training set determined on the historical data is , where i = 1, …, , t = 1, …, 24 and pair includes the input pattern and target defined according to r1–r7. The three training modes are as follows:
- Local
- The model is trained on the subset of containing pairs which correspond to the forecasting task, i.e., the pairs which include targets representing the same day type as forecasted, , and the same hour as forecasted, .
- Global
- The model is trained on full training set .
- Global extended
- The input data are extended with calendar information:
- season of the year encoded as follows [29]:where is the number of day i in the year,
- day of the week, (categorical variable), and
- hour of the day, (categorical variable).
The training set in the global extended mode is of the form: , , .
In the local training mode, the model solves the forecasting task by learning on the samples expressing similar properties and relationships between input and output data as those expressed by input pattern and forecasted value . That is, the training input patterns are limited to those that are similar in shape to pattern (further limitations in this regard can be made by selecting training data from the same period of the year as day or by selecting training data based on similarity to pattern [7], but we have not employed these approaches in this study). The relationships between input and output data expressed in the local training set are limited to those corresponding to day type and hour , so we expect the model to more accurately approximate the relationship between and than in case of global training on the full training set expressing the relationship for all day types and hours.
In the global training mode with extended inputs, the model has additional input information to more accurately solve the forecasting task, i.e., the calendar variables. Although the model is global, we expect that the calendar data will help to increase its local accuracy around pattern . A regression tree as a base forecasting model can more appropriately divide the input space using the calendar variables than without these variables, and therefore approximate locally the target function with greater accuracy. Although this will lead to a more complex model than in the other two training modes.
4. Random Forest for STLF
RF is a ensemble learning algorithm based on decision trees (CART [33]) as the base models [34]. It is suitable for either regression or classification problems. In this study, for forecasting problems, we focus on the regression RF based on regression trees.
RF is devoid of the well-known drawbacks of single trees such as unstable splits and a lack of smoothness [27]. It combines bagging [35] with a random subspace method [36]. The key idea in bagging is to average multiple noisy but approximately unbiased base models and thus reduce the variance. Trees as noisy and low biased models if they have grown sufficiently deep, are great candidates for bagging. The main goal of the random subspace method is to increase diversity between trees by restricting them to work on different random subsets of the full predictor space (more specifically, at each node of the tree, a random predictor subset is selected). Each tree in the forest is built from a bootstrap sample of the original dataset, which is an additional source of diversity. Random predictors selected in the nodes of bagged trees help to decorrelate the trees and improve prediction accuracy as well as reduce the model variance.
The RF algorithm draws a bootstrap sample of size N from training set for each of K trees, k = 1, …, K. For each bootstrapped sample, a tree T is grown by recursive partitioning the input space in each node until a minimum leaf size is reached. At each node, data splits based on p out of n predictors chosen at random are considered. The best split is determined by maximizing the reduction in mean squared error (MSE) over all splitting candidates and cutpoints. After all K trees are grown in this fashion, the RF predictor is [27]:
where is the input pattern and characterizes the k-th tree in terms of split predictors, cutpoints, and terminal-node values.
RF has the following hyperparameters:
- number of trees K. Intuitively, the number of trees should be as large as possible because the model variance reduces with K. Usually, the forecast error stabilizes with the number of trees, and the most reasonable RF size is selected.
- minimum leaf size m. As deeper trees have low bias and large variance, they are strongly recommended as RF members. Thus, the minimum leaf size should be small. The inventors of the algorithm recommend for regression forest.
- number of predictors to select at random for each split p. As p decreases, the correlation between trees reduces, and hence the variance of the average reduces. Typically, a value for p for regression RF is , as the inventors recommend.
In practice the best values for the hyperparameters are dependent on the problem, and they should be treated as tuning parameters.
The standard method of selecting split predictors [33] has two drawbacks. Firstly, it tends to miss important interactions between pairs of predictors and the response. Secondly, it tends to select continuous predictors that have many levels, which masks more important predictors that have fewer levels, such as categorical predictors. To mitigate selection bias and increase detection of important interactions, curvature or interaction tests can be applied [37,38]. Therefore, in this study we consider three methods of selecting the split predictors:
- s1
- Standard CART method. This selects the split predictor that maximizes the split-criterion gain over all possible splits of all predictors.
- s2
- Curvature test. This selects the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response.
- s3
- Interaction test. This performs the curvature test extended by the minimization of the p-value of a chi-square test of independence between each pair of predictors and the response.
The algorithm of RF construction for STLF is shown in Algorithm 1. It produces a set of K trees, . Based on them, to make a prediction for new point , we use (5). Then, the real forecast is calculated from (3). Note that training set is prepared for the selected training mode and input pattern type.
| Algorithm 1 Random forest construction for STLF |
|
In the experimental study (Section 5), we use RF specified in Algorithm 1 in several variants depending on the data preprocessing method (r1–r7) and training modes, i.e., local, global and global extended. In the global extended mode, the predictor vector is composed of . In the other training modes, the predictor vector is the same as input pattern (1).
5. Simulation Study
In this section, we investigate RF variants with different data preprocessing methods and training modes. We compare RF performance with that of other models based on classical statistical methods and ML methods.
STLF for four countries is performed: Poland (PL), Great Britain (GB), France (FR) and Germany (DE). The real-world data was collected from ENTSO-E repository (www.entsoe.eu/data/power-stats; accessed on 6 April 2016). It details the hourly power system load in the period from 2012 to 2015. The last year of the data (2015) is treated as a test period. We predict the daily load profiles for each day of this period, excluding atypical days such as public holidays (between 10 and 20 days a year). RF models were optimized on the data from 2012 to 2014, with validation data composed of 100 patterns selected randomly from 2014 and training data preceding the validation pattern.
5.1. Results for Different Preprocessing Methods and Training Modes
Table 1 and Table 2 show mean absolute percentage error (MAPE) and root mean square error (RMSE), respectively, for input patterns r1–r7 and different training modes. Figure 4, Figure 5 and Figure 6 show the boxplots of MAPE. The results can be summarised as follows:
- It is evident from these tables and figures that the global extended mode yields the lowest errors, when combined with patterns r4 (for PL, FR and DE) or r6 (for GB).
- The local training mode brings lower errors than the global one when patterns r1, r2, r6 and r7 are used, i.e., patterns which are composed of the daily curves. The local mode is usually better than the global extended one when patterns r1 and r2 are used, but it is worse than the global extended mode when cross-patterns are used, which also reflect a weekly seasonality.
- The highest errors for the global mode were observed when patterns r1 and r2 were used. In these cases, the errors were up to nine times greater than in the alternative training modes. Pattern r4 is recommended for the global mode, which for all countries provided the lowest errors. Modifying the global mode by extending the input patterns with calendar variables has always resulted in a reduction of errors.
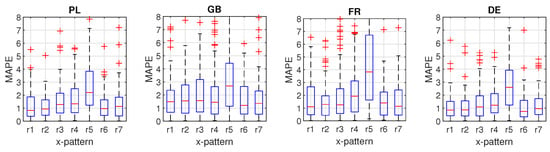
Figure 4.
Local training mode: Boxplots of validation MAPE for different input patterns r1–r7.
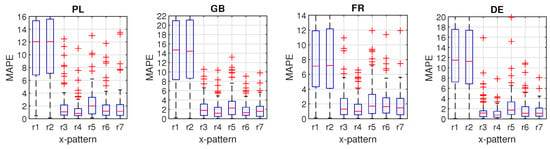
Figure 5.
Global training mode: Boxplots of validation MAPE for different input patterns r1–r7.
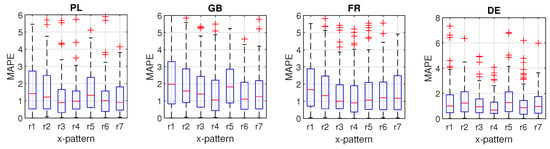
Figure 6.
Global extended training mode: Boxplots of validation MAPE for different input patterns r1–r7.

Table 1.
Validation MAPE for different input patterns r1–r7 and training modes (lowest errors in bold, second lowest errors in italics).
Table 1.
Validation MAPE for different input patterns r1–r7 and training modes (lowest errors in bold, second lowest errors in italics).
| Data | Training Mode | r1 | r2 | r3 | r4 | r5 | r6 | r7 |
|---|---|---|---|---|---|---|---|---|
| PL | Local | 1.54 | 1.55 | 1.89 | 2.17 | 3.66 | 1.45 | 1.63 |
| Global | 11.55 | 11.61 | 2.11 | 1.30 | 2.94 | 1.82 | 1.82 | |
| Global ext. | 1.92 | 1.79 | 1.40 | 1.24 | 1.96 | 1.50 | 1.55 | |
| GB | Local | 1.92 | 1.91 | 2.29 | 2.21 | 3.68 | 1.76 | 1.75 |
| Global | 14.88 | 15.01 | 2.21 | 1.75 | 2.92 | 1.84 | 1.83 | |
| Global ext. | 2.22 | 2.09 | 1.79 | 1.59 | 2.12 | 1.47 | 1.52 | |
| FR | Local | 1.88 | 1.77 | 2.12 | 2.43 | 5.10 | 1.74 | 1.86 |
| Global | 8.50 | 8.54 | 2.09 | 1.53 | 2.90 | 2.11 | 1.92 | |
| Global ext. | 1.98 | 1.71 | 1.59 | 1.37 | 1.71 | 1.63 | 1.64 | |
| DE | Local | 1.34 | 1.31 | 1.67 | 1.93 | 3.47 | 1.21 | 1.45 |
| Global | 12.33 | 12.34 | 1.62 | 1.07 | 2.61 | 1.79 | 1.54 | |
| Global ext. | 1.55 | 1.57 | 1.17 | 0.99 | 1.65 | 1.17 | 1.19 |

Table 2.
Validation RMSE for different input patterns r1–r7 and training modes (lowest errors in bold, second lowest errors in italics).
Table 2.
Validation RMSE for different input patterns r1–r7 and training modes (lowest errors in bold, second lowest errors in italics).
| Data | Training Mode | r1 | r2 | r3 | r4 | r5 | r6 | r7 |
|---|---|---|---|---|---|---|---|---|
| PL | Local | 436 | 522 | 489 | 540 | 1014 | 412 | 473 |
| Global | 2420 | 2427 | 577 | 347 | 741 | 454 | 458 | |
| Global ext. | 468 | 448 | 364 | 337 | 509 | 406 | 410 | |
| GB | Local | 918 | 825 | 1100 | 1118 | 1816 | 811 | 841 |
| Global | 6309 | 6358 | 1035 | 860 | 1445 | 811 | 824 | |
| Global ext. | 925 | 937 | 784 | 757 | 985 | 669 | 690 | |
| FR | Local | 1630 | 1576 | 1851 | 1939 | 3893 | 1406 | 1626 |
| Global | 5602 | 5635 | 1714 | 1144 | 2697 | 1538 | 1437 | |
| Global ext. | 1414 | 1280 | 1287 | 1048 | 1450 | 1232 | 1272 | |
| DE | Local | 1590 | 1190 | 1748 | 2099 | 3046 | 1168 | 1641 |
| Global | 8927 | 8926 | 1410 | 878 | 2094 | 1411 | 1131 | |
| Global ext. | 1224 | 1229 | 833 | 713 | 1261 | 915 | 883 |
Based on the results, the recommended training mode is global extended with r4 patterns for PL, FR and DE, and r6 patterns for GB. These variants of RF were used in the experiments described in the next sections.
5.2. Tuning Hyperparameters
In this experiment, we change the selected hyperparameter in the range shown in Figure 7, keeping the remaining hyperparameters at their constant values as follows: number of trees in the forest—K = 100, minimum number of leaf node observations—, and number of predictors to select at random for each decision split—.
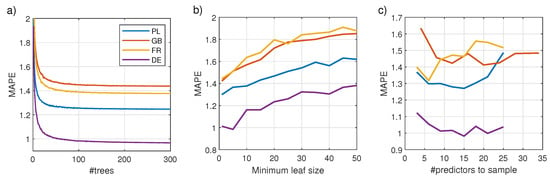
Figure 7.
Validation MAPE depending on hyperparameters: number of trees in the forest (a), minimum number of leaf node observations (b) and number of predictors to select at random for each decision split (c).
Figure 7 shows the impact of hyperparameters on the forecasting error (MAPE). As expected, the error decreases with the number of trees in the forest. The reduction in MAPE when the RF size changes from 1 do 300 trees was from 38.7% for PL to 50.0% for DE. At the same time, a significant reduction in the forecast variance was also observed from 63.8% for PL to 82.5% for DE. It can be seen from Figure 7b that an increase in the minimum leaf size leads to a deterioration in the results. Small values of m, close to 1, are preferred. This means that trees as deep as possible are the most beneficial in RF. The optimal number of predictors selected in the nodes to perform a split varies from country to country (see Figure 7c). For PL and DE it is 15, for GB it is 20, and for FR it is 6. These values differ from the recommended , which are 8 for PL, FR and DE, and 11 for GB.
Using optimal values of the hyperparameters for each country, we investigate the methods of split predictor selection s1–s3. Table 3 shows the results, validation MAPE and RMSE. Both accuracy measures show similar results for all methods of split predictor selection. Therefore, s1 is recommended as a simple, standard method, which does not cause any additional computational burden.

Table 3.
Validation MAPE and RMSE for different methods of split predictor selection (training mode: global extended, #trees: 300, minimum leaf size: 1; lowest errors in bold).
Figure 8 shows the “importance” or “predictive strength” of the predictors estimated on the out-of-bag data (this is discussed further in Section 5.4). As can be seen from this figure, when r4 extended pattern is used (PL, FR and DE), the most important predictor is the last component of the r-pattern, i.e., the predictor expressing electricity demand at forecasted hour t of the day preceding the forecasted day, . The importance of this predictor reaches 3.5 for FR and over 5 for PL and DE, while the importance of other demand predictors is usually below 2. Among the calendar predictors, the most important for r4 extended pattern are those coding the season of the year, especially for DE. For cross-pattern r6 (GB), the most important predictors are the calendar ones: day of the week and season of the year (). The next positions are occupied by predictors coding the demand for the last four hours of the day before the forecasted day ( is clearly the most important of these) and predictor coding demand at forecasted hour t week ago, . Note the low importance of the other predictors representing demand at hour t of the preceding days, –.
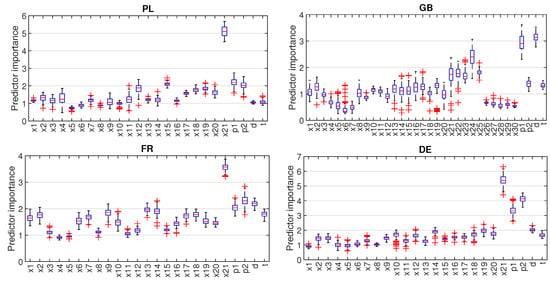
Figure 8.
Importance of the predictors (—predictors expressing demand pattern r4 or r6, and —components of vector expressing season of the year, d—day of the week, and t—hour of the day).
Table 4 shows the forecasting results for the test set when using RF with the optimal values of hyperparameters. As performance metrics we use: MAPE, MdAPE (median of absolute percentage error), IqrAPE (interquartile range of APE), RMSE, MPE (mean percentage error), and StdPE (standard deviation of PE). MdAPE measures the mean error without the influence of outliers, while RMSE, as a square error, is especially sensitive to outliers.

Table 4.
Results for test data (training mode: global extended, #trees: 300, minimum leaf size: 1, split predictor selection method: s1).
The MAPE and MdAPE values in Table 4 indicate that the most accurate forecasts were obtained for PL and DE, while the least accurate were for GB. MPE allows us to assess the forecast bias. Positive values of MPE indicate underprediction, while its negative values indicate overprediction. Note that for PL and DE the forecast bias was significantly smaller than for GB and FR. The same can be said about the forecasts dispersion measured by IqrAPE and StdPE.
5.3. Results Comparison with Other Models
We compare the performances of RF with other models including statistical models and ML models. The comparative models are outlined below (see [30,39] for further description). Their hyperparameters were selected on the data from 2012–2014 in grid search procedures using a variant of cross-validation or selected by experimentation (this applies to models with a large number of hyperparameters, which are difficult to optimize using standard methods due to the huge search space).
- Naive—naive model: ;
- ARIMA—Auto-Regressive Integrated Moving Average model;
- ETS—Exponential Smoothing model;
- Prophet—a modular additive regression model with nonlinear trend and seasonal components;
- MLP—perceptron with a single hidden layer and sigmoid nonlinearities;
- SVM—linear epsilon insensitive Support Vector Machine (-SVM);
- ANFIS—Adaptive Neuro-Fuzzy Inference System;
- LSTM—Long Short-Term Memory;
- FNM—Fuzzy Neighborhood Model;
- N-WE—Nadaraya–Watson Estimator;
- GRNN—General Regression NN;
- RandNN—ensemble of 100 Randomized NNs;
- MTGNN—Graph NN for multivariate time series forecasting;
- ES-adRNNe—ensemble of five hybrid and hierarchical models combining ETS and dilated RNN with attention mechanism.
We also compare our model with competitive tree-based ensembles: XGBoost [40] and LightGBM [41]. Their predictors include both calendar data (hour of the day, day of the week, quarter, month, year, day of the year, day of the month and week of the year) and historical demands (demands at hour t of 21 consecutive days preceding the forecasted day).
Table 5 compares MAPE for RF and the baseline models. From this table, you can clearly see the better performance of RF compared to the other models. RF outperformed all other models in terms of accuracy for PL, GB and DE. For FR it took third place after RandNN and SVM. To confirm the results, a pairwise one-sided Giacomini-White test was performed (GM test) [42]. Its results, p-values, are shown in Figure 9 (we used GW test implementation from [43]). Small p-values, below 0.05 (green color), indicate that the model on the X-axis significantly outperforms in terms of accuracy the model on the Y-axis.

Table 5.
MAPE comparison between RF and baseline models (lowest errors in bold).
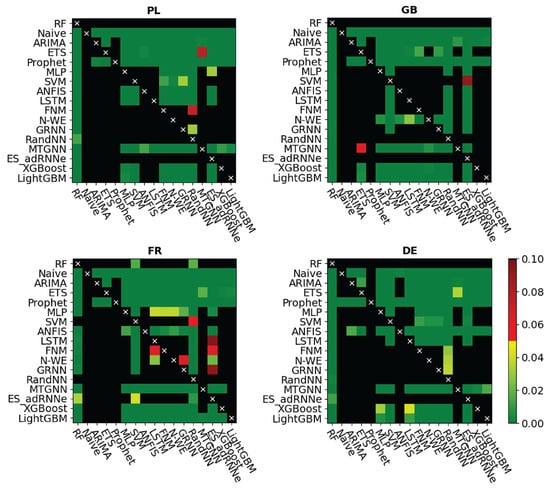
Figure 9.
Results of the Giacomini-White test for the proposed and baseline models (black color is for p-values larger than 0.10).
5.4. Discussion
In our previous work [19], we used a local training mode with input patterns r2, which express daily profiles. Our current research revealed that input patterns incorporating weekly seasonality (r4) or both daily and weekly seasonality (r6) combined with global training with extended inputs improve the results (note that in Table 1 and Table 2, patterns r4 and r6 provide lower errors than r2 for all countries). Calendar data used as additional input in the global extended training helps the trees to properly partition the input space and thus approximate the target function with greater accuracy. It does not take place without costs: the complexity of the model increases due to learning on all data, not just the selected data as in local training.
Table 5 and Figure 9 show that the proposed RF outperforms classical statistical models (ARIMA and ETS), modern statistical model (Prophet), classical ML models (MLP, SVM, ANFIS, GRNN), modern ML models (LSTM, RandNN), similarity-based models (FNM, N-WE) as well as state-of-the-art ML models (MTGNN, ES-adRNNe) and boosted regression trees (XGBoost, LightGBM). The last two models, as well as the proposed RF model, also used calendar variables, even in larger numbers. However, in contrast to these models, our model uses specific time series preprocessing, which may be a decisive advantage. Our model also outperforms ES-adRNNe, which is a very sophisticated and complex model developed especially for STLF [39]. To increase its predictive power, it is equipped with a new type of RNN cell with delayed connections and inherent attention, it processes time series adaptively, learning their representation and it learns in the cross-learning mode (i.e., it learns from many time series in the same time). It reveals its strength with a large amount of data, numerous and long time series. In our case, this condition was not met—there were only four, relatively short series available for training the models. In this case, the proposed RF model, which learns from individual series, generated more accurate forecasts than ES-adRNNe.
It is worth noting that RF has few hyperparameters to tune, which makes it easy to optimize (compare with DNNs with many hyperparameters). The results of our experiments confirmed that the number of trees in the forest should be as large as possible and the mimimum leaf size can be set to one. Therefore, the key hyperparameter remains the number of predictors to sample in the nodes. Its optimal values significantly differed from the recommended default values. Our attempt to increase the performance of the RF model through alternative methods of selecting predictors for split failed. Neither the curvature test nor the interaction test, which take into account the relationship between predictors and response when splitting data in nodes, improves the results significantly over the default CART method.
In our study, we used both continuous and categorical predictors. Such a mix causes many difficulties for other models such as ARIMA, ETS, NNs, SVM, LSTM and others. Categorical variables cannot be processed by these models directly. Such predictors must be converted into numerical data, so as to maintain the relationship between their values. The method of this conversion can be treated as an additional hyperparameter. RF has no problems with categorical variables, which is its big advantage. Moreover, RF can deal easily with any number of additional exogenous predictors and does not need to unify predictor ranges, which is often necessary for other models. RF can even deal with raw data because the predictors are not processed by the tree in any way, just selected in nodes, to construct a specific decision model (flowchart-like structure).
Regression tree provides fast one-pass training which does not need to repeatedly refer to the data. In contrast, NNs, which use a variant of the gradient descent optimization algorithm with multiple scanning of a dataset, are more time-consuming to train. Additionally due to the number of hyperparameters, they are also much more expensive to optimize in terms of time than RF. The training of a tree does not provide an optimal result because decisions about data split are made in nodes using a local rather than a global criterion, i.e., the split made may not be optimal from the point of view of the final result. However, the NN learning process also does not lead to optimal results due to sensitivity to the starting point and tendency to fall into the traps of the local minimum. Note that non-optimality of the trees is mitigated by their aggregation in the forest. Aggregation also smoothes out functions modeled by individual trees and reduces their variance. The learning process of RF can be easily paralleled because the individual trees learn independently.
One useful feature of RF is that it enables the generalization error to be estimated using out-of-bag (OOB) patterns, i.e., training patterns not selected for the bootstrap sample (approximately one third of the training patterns are left out in each bootstrap sample). Therefore, the time-consuming cross-validation that is widely used in other models for estimating the generalization error is not needed. Using OOB patterns, the generalization error can be estimated during one training session, along the way. Although for forecasting problems, where training patterns should precede validation to prevent data leakage, the OOB approach as well as standard cross-validation may be questionable. For this reason, we did not use the OOB approach in this study. Instead, we applied a different strategy. We chose a set of 100 validation patterns from 2014 and for each of them we trained RF on training patterns preceding the validation pattern.
A valuable feature of RF is its built-in mechanism for predictor selection. In each node, the predictor which improves the split-criterion the most is selected. The splitting criterion favors informative predictors over noisy ones, and can completely disregard irrelevant ones. Thus, in RFs an additional feature selection procedure is unnecessary. Based on the internal mechanism for selecting predictors, the predictor importance or strength can be estimated. The importance measure attributed to the splitting predictor is the accumulated improvement this predictor gives to the split-criterion at each split in each tree. RF also offers another method of estimating the predictor importance based on the OOB patterns [27]. When the tree is grown, the OOB patterns are passed down the tree, and the prediction error is recorded. Then the values for the given predictor are randomly permuted across the OOB samples, and the error is computed again. The importance measure is defined as the increase in error. This measure is computed for every tree, then averaged over the entire forest and divided by the standard deviation over the entire forest. Such a measure is presented in Figure 8. Note that information about the predictor importance is a key factor, which helps to improve the interpretability of the model and can be used for feature selection for other models.
Model interpretability is an emerging area in ML that aims to make the model more transparent and strengthen confidence in its results. This topic is also explored in electricity demand forecasting literature [44]. In [45], it was shown that the predictor importance is related to the model sensitivity to inputs and also to the method of importance estimation. An LSTM-based model, which is proposed in [45], is equipped with a built-in mechanism based on a mixture attention technique for temporal importance estimation of predictors. In the experimental study, this model demonstrated higher sensitivity to inputs than tree-based models (RF and XGBoost) which showed very low sensitivity on the predictors except one, which strongly dominated (the authors used built-in functions of scikit-learn to calculate the predictor importance for tree-based models). In our study, the predictor importance is more diverse (see Figure 8), which may result from the fact that our trees are very deep and thus involve a great number of predictors. Note that tree-based models enhance interpretability not only through built-in mechanisms of predictor importance estimation, which show predictive power of individual predictors, but also through their flowchart-like tree structure. They can be interpreted simply by plotting a tree and observing how the splits are made and what is the arrangement of the leaves. It should be noted, however, that while following the path that a single tree takes to make a decision is trivial and self-explanatory, following the paths of hundreds of trees in the ensemble is much more difficult. To facilitate this, in [46], model compression methods were proposed that transform a tree ensemble into a single tree that approximates the same decision function.
In this study we use a standard RF formulation which is a MISO model producing point forecasts. Thus for prediction of 24 values of the daily curve of electricity demand, we need to train 24 RF models. In [32], we proposed a multivariate regression tree for STLF, which produces a vector as an output, representing the 24 predicted values. Using such MIMO trees as ensemble members simplifies and speeds up the forecasting process. A promising extension of the RF in the direction of probabilistic forecasting can be achieved using a quantile regression forest, which can infer the full conditional distribution of the response variable for high-dimensional predictor variables [47].
6. Conclusions
ML ensemble models are state-of-the-art for forecasting problems. They dominate the most recent literature on forecasting. Among them, tree-based ensembles have a solid theoretical basis and have been thoroughly researched in a huge number of papers. Their predictive power has been confirmed in numerous forecasting competitions [24].
In this study, we propose a RF model for a challenging STLF problem with multiple seasonality, nonlinear trend, and varying variance in time series. Unlike DNNs, RF is simple and transparent, it does not require a complex, deep architecture, equipped with additional sophisticated mechanisms to deal with complex time series. The greatest advantages of RF as a forecasting model are: small number of tuning hyperparameters (we show that only one is key), fast training and optimization, ability to deal with multiple exogenous predictors of different types, and built-in mechanism for selecting predictors and estimating their importance.
As with any predictive model, the performance of RF depends significantly on data preprocessing and proper organization of the training process. In the simulation study, we show how the results of RF depend on the training method, definition of input variables and hyperparameters. Based on the results, we recommend the best method of predictor definition (r4 and r6) and training mode (global extended) for STLF. Comparing the performances of RF and baseline models including statistical and ML ones, we showed that RF can successfully compete with them, providing the most accurate forecasts.
In our future work, we plan to extend RF with random data projection (to further smooth the estimator and provide an additional source of diversity) and use RF for probabilistic forecasting. A quantile regression forest [47] is a promising tool for the latter task.
Funding
This research received no external funding.
Data Availability Statement
We use real-world data collected from www.entsoe.eu (accessed on 6 April 2016).
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| APE | Absolute Percentage Error |
| ARIMA | Auto-Regressive Integrated Moving Average |
| CART | Classification And Regression Trees |
| CNN | Convolutional Neural Network |
| DE | Germany |
| DNN | Deep Neural Network |
| ES-adRNNe | ensemble of five hybrid and hierarchical models combining ES |
| and dilated RNN with attention mechanism | |
| ETS | Exponential Smoothing |
| FR | France |
| FNM | Fuzzy Neighborhood Model |
| GB | Great Britain |
| GBRT | Gradient Boosting Regression Tree |
| GRNN | General Regression Neural Network |
| IqrAPE | Interquartile Range of Absolute Percentage Error |
| LightGBM | Light Gradient Boosting Machine |
| LSTM | Long Short Term Memory Neural Network |
| MAPE | Mean Absolute Percentage Error |
| MdAPE | Median of Absolute Percentage Error |
| MIMO | Multiple Input Multiple Output |
| MISO | Multiple Input Single Output |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MPE | Mean Percentage Error |
| MTGNN | Graph Neural Network for Multivariate Time series forecasting |
| N-WE | Nadaraya–Watson Estimator |
| NN | Neural Network |
| PE | Percentage Error |
| PL | Poland |
| RandNN | Randomized Neural Network |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| StdPE | Standard Deviation of Percentage Error |
| SVM | Support Vector Machine |
| STLF | Short-Term Load Forecasting |
| WGTB | Warm-start Gradient Tree Boosting |
| XGBoost | eXtreme Gradient Boosting |
References
- Arora, A.; Taylor, J.W. Rule-based autoregressive moving average models for forecasting load on special days: A case study for France. Eur. J. Oper. Res. 2018, 266, 259–268. [Google Scholar] [CrossRef]
- Taylor, J.W. Short-term load forecasting with exponentially weighted methods. IEEE Trans. Power Syst. 2012, 27, 458–464. [Google Scholar] [CrossRef]
- Charlton, N.; Singleton, C. A refined parametric model for short term load forecasting. Int. J. Forecast. 2014, 30, 364–368. [Google Scholar] [CrossRef]
- Takeda, H.; Tamura, Y.; Sato, S. Using the ensemble Kalman filter for electricity load forecasting and analysis. Energy 2016, 104, 184–198. [Google Scholar] [CrossRef]
- Smyl, S.; Dudek, G.; Pełka, P. ES-dRNN: A hybrid exponential smoothing and dilated recurrent neural network model for short-term load forecasting. arXiv 2021, arXiv:2112.02663. [Google Scholar]
- Benidis, K.; Rangapuram, S.S.; Flunkert, V.; Wang, Y.; Maddix, D.; Turkmen, C.; Gasthaus, J.; Bohlke-Schneider, M.; Salinas, D.; Stella, L.; et al. Deep Learning for Time Series Forecasting: Tutorial and Literature Survey. ACM Comput. Surv. 2022. accepted. [Google Scholar] [CrossRef]
- Dudek, G. Neural networks for pattern-based short-term load forecasting: A comparative study. Neurocomputing 2016, 205, 64–74. [Google Scholar] [CrossRef]
- Eskandari, H.; Imani, M.; Moghaddam, M.P. Convolutional and recurrent neural network based model for short-term load forecasting. Electr. Power Syst. Res. 2021, 195, 107173. [Google Scholar] [CrossRef]
- Kim, J.; Moon, J.; Hwang, E.; Kang, P. Recurrent inception convolution neural network for multi short-term load forecasting. Energy Build. 2019, 194, 328–341. [Google Scholar] [CrossRef]
- Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust short-term electrical load forecasting framework for commercial buildings using deep recurrent neural networks. Appl. Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-term load forecasting with deep residual networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef]
- Reeve, H.W.J.; Brown, G. Diversity and degrees of freedom in regression ensembles. Neurocomputing 2018, 298, 55–68. [Google Scholar] [CrossRef]
- Chan, F.; Pauwels, L.L. Some theoretical results on forecast combinations. Int. J. Forecast. 2018, 34, 64–74. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczyński, D.; Kopyt, M.; Gulczyński, T. Advanced ensemble methods using machine learning and deep learning for one-day-ahead forecasts of electric energy production in wind farms. Energies 2022, 15, 1252. [Google Scholar] [CrossRef]
- Yang, D.; Guo, J.; Sun, S.; Han, J.; Wang, S. An interval decomposition-ensemble approach with data-characteristic-driven reconstruction for short-term load forecasting. Appl. Energy 2022, 306A, 117992. [Google Scholar] [CrossRef]
- Gao, R.; Du, L.; Suganthan, P.N.; Zhou, Q.; Yuen, K.F. Random vector functional link neural network based ensemble deep learning for short-term load forecasting. Expert Syst. Appl. 2022, 206, 117784. [Google Scholar] [CrossRef]
- Moon, J.; Jung, S.; Rew, J.; Rho, S.; Hwang, E. Combination of short-term load forecasting models based on a stacking ensemble approach. Energy Build. 2020, 216, 109921. [Google Scholar] [CrossRef]
- Ribeiro, G.T.; Mariani, V.C.; Coelho, L.S. Enhanced ensemble structures using wavelet neural networks applied to short-term load forecasting. Eng. Appl. Artif. Intell. 2019, 82, 272–281. [Google Scholar] [CrossRef]
- Dudek, G. Short-term load forecasting using random forests. In Intelligent Systems’2014, Advances in Intelligent Systems and Computing; Filev, D., Jabłkowski, J., Kacprzyk, J., Krawczak, M., Popchev, I., Rutkowski, L., Sgurev, V., Sotirova, E., Szynkarczyk, P., Zadrożny, S., Eds.; Springer: Cham, Switzerland, 2015; Volume 323, pp. 821–828. [Google Scholar]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Short-term load forecasting based on hybrid strategy using warm-start gradient tree boosting. J. Renew. Sustain. Energy 2020, 12, 066102. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Chen, X.; Zeng, X.; Kong, Y.; Chen, J.; Guo, Y.; Wang, T. Short-term load forecasting of industrial customers based on SVMD and XGBoost. Int. J. Electr. Power Energy Syst. 2021, 129, 106830. [Google Scholar] [CrossRef]
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do we really need deep learning models for time series forecasting? arXiv 2021, arXiv:2101.02118. [Google Scholar]
- Bojer, C.S.; Meldgaard, J.P. Kaggle forecasting competitions: An overlooked learning opportunity. Int. J. Forecast. 2021, 37, 587–603. [Google Scholar] [CrossRef]
- Januschowski, T.; Wang, Y.; Torkkola, K.; Erkkilä, T.; Hasson, H.; Gasthaus, J. Forecasting with trees. Int. J. Forecast. 2021, 38, 1473–1481. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 accuracy competition: Results, findings, and conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Dudek, G. Short-term load cross-forecasting using pattern-based neural models. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering, EPE 2015, Kouty nad Desnou, Czech Republic, 20–22 May 2015; pp. 179–183. [Google Scholar]
- Dudek, G. Multilayer perceptron for short-term load forecasting: From global to local approach. Neural Comput. Appl. 2019, 32, 3695–3707. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P. Pattern similarity-based machine learning methods for mid-term load forecasting: A comparative study. Appl. Soft Comput. 2021, 104, 107223. [Google Scholar] [CrossRef]
- Pełka, P.; Dudek, G. Pattern-based long short-term memory for mid-term electrical load forecasting. In Proceedings of the 2020 International Joint Conference on Neural Networks, IJCNN 2020, Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Dudek, G. Multivariate regression tree for pattern-based forecasting time series with multiple seasonal cycles. In Information Systems Architecture and Technology, Proceedings of the 38th International Conference on Information Systems Architecture and Technology, ISAT 2017, Szklarska Poręba, Poland, 17–19 September 2017; Świątek, J., Borzemski, L., Wilimowska, Z., Eds.; Springer: Cham, Switzerland, 2018; Volume 655, pp. 85–94. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall: London, UK, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Loh, W.Y. Regression trees with unbiased variable selection and interaction detection. Stat. Sin. 2002, 12, 361–386. [Google Scholar]
- Smyl, S.; Dudek, G.; Pełka, P. ES-dRNN with dynamic attention for short-term load forecasting. In Proceedings of the 2022 International Joint Conference on Neural Networks IJCNN 2022, Padova, Italy, 18–23 July 2022. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining, ACM SIGKDD 2016, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the Conference on Advances in Neural Information Processing Systems 30, NIPS 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Giacomini, R.; White, H. Tests of conditional predictive ability. Econometrica 2006, 74, 1545–1578. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 116983. [Google Scholar] [CrossRef]
- Xu, C.; Liao, Z.; Li, C.; Zhou, X.; Xie, R. Review on interpretable machine learning in smart grid. Energies 2022, 15, 4427. [Google Scholar] [CrossRef]
- Li, C.; Dong, Z.; Ding, L.; Petersen, H.; Qiu, Z.; Chen, G.; Prasad, D. Interpretable memristive LSTM network design for probabilistic residential load forecasting. IEEE Trans. Circuits Syst. I 2022, 69, 2297–2310. [Google Scholar] [CrossRef]
- Sagi, O.; Lior, R. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).