Abstract
Currently, AC motors are a key element of industrial and commercial drive systems. During normal operation, the machines may become damaged, which may pose a threat to the users. Therefore, it is important to develop a fault detection method that allows for the detection of a fault at an early stage. Among the currently used diagnostic systems, applications based on deep neural structures are dynamically developed. Despite many examples of applications of deep learning methods, there are no formal rules for selecting the network structure and parameters of the training process. Such methods would make it possible to shorten the implementation process of deep networks in diagnostic systems of AC machines. The article presents a detailed analysis of the influence of deep convolutional network hyperparameters and training procedures on the precision of the interturn short-circuits detection system. The studies take into account the direct analysis of phase currents through the convolutional network for induction motors and permanent magnet synchronous motors. The research results presented in the article are an extension of the authors’ previous research.
1. Introduction
In recent years, there has been growing interest in diagnostics and prognostics of AC motor drives, as they are used in many industrial applications, including safety-critical devices. Among other things, it is related to the global drive to reduce carbon dioxide emissions and replace systems that use hydraulic and pneumatic power, as well as combustion engines with electric drives. This applies not only to areas such as industrial automation and robotics but also to transport and wind power generation. Therefore, diagnostics of electric drives, in particular those using induction motors (IMs) and permanent magnet synchronous motors (PMSMs), have been intensively developed in the last two decades [1,2,3,4,5,6,7,8,9]. Diagnostic systems use various methods to process electrical, mechanical, and acoustic signals, often assisted by artificial intelligence methods. In particular, neural networks (NNs) are used to detect, locate, and classify faults based on preprocessing the above-mentioned signals from the drive system. In recent years, researchers have focused more and more on the use of deep learning neural networks (DNNs), which, under the appropriate training process, are able to perform fault diagnosis tasks based on raw signals, i.e., without preprocessing the signals measured on the object.
Among the DNNs structures, convolutional neural networks (CNNs) [10,11] and autoencoders (AEs) [12,13] are currently the most frequently used. In addition, there are also known applications in the diagnostic technique of Deep Belief Neural Networks (DBFs) [14], Generative Adversarial Neural Networks (GANs) [15,16,17] and Long Short-Term Memory (LSTM) [18,19,20]. Among the above-mentioned DNN structures, diagnostic processes of electrical machines are mainly associated with CNNs. Convolutional networks make it possible to extract higher-order features from the input information, using the mathematical convolution operation for this purpose.
A characteristic feature of CNNs is its extensive structure and the lack of formal rules for designing and selecting training parameters. The number of convolutional layers is closely related to the type of signal characteristics sought. The overwhelming number of software implementations of CNNs refers to the use of multiple convolutional layers connected in a cascade [21,22] which results from the necessity to perform the splice operation several times to reveal the symptoms of damage. In the case of using CNNs in diagnostic processes, in most cases, the amount of information ensuring a high level of network efficiency is achieved by using three [23,24,25,26], in special cases, more convolutional layers [10,24,27,28]. In most cases, such a solution ensures high efficiency, and, at the same time, it is easy to analyze the individual layers of the network. Nevertheless, the literature describes the applications of CNNs working both in hierarchical structures [24,26,29] as well as parallel [30,31].
Despite the overarching role of the convolution operation, CNN structures contain many layers to aid the extraction of features (pooling layers, activation functions) as well as classifying layers (normalizing layers, dropout layers [32,33], and fully connected layers). However, the selection of individual structure parameters is still an unrecognized scientific issue. The currently proposed attempts to select structures in the literature are a combination of various computational techniques, such as the use of Sequential Model-Based Optimization (SMBO) proposed in [34] to optimize CNN hyperparameters. Despite the possibilities of optimizing the CNN structure described in this paper, no correlation between its parameters and the precision of the network was demonstrated. Another popular approach is the use of Genetic Algorithms (GAs) in DNN optimization tasks [35,36,37,38]. As in the case of [34], the GA-based approach proposed in [36] has not been discussed in terms of the influence of parameters on the classifier precision. Therefore, it is impossible to define the exact dependencies between the network parameters and the effectiveness of performing the tasks assigned to them. Furthermore, the use of the evolutionary algorithm to determine the optimal configuration of the AlexNET network does not ensure finding the global minimum due to the randomness of parameters [39]. Moreover, the classical methods of searching for the optimal structure: gradient search [40], random search [41], and Bayesian optimization-based method [38,42,43,44], are not presently analyzed for diagnostic applications. Currently, in machine learning techniques, Bayesian optimization is often used only in the case of AI applications, which show good performance. This method consists in optimizing a black box object with a noisy objective function that preserves the surrogate model learned using previously assessed solutions. The Gaussian [42] process is usually adopted as a proxy model, which easily copes with the uncertainty and noise of the objective function.
Apart from the necessity to select the parameters of the convolutional layer defining the features of the input matrices, the parameters of the pooling layers are also important in terms of network efficiency. The most commonly used type of CNN pooling layer is the maximum function [43,45], which results from the computational simplicity of this method. However, the following applications are common: mixed pooling [44], stochastic pooling [46], spectra pooling [47], average pooling [48], and ordinal pooling [49]. It should be clearly emphasized that the structure of CNN is very complex in terms of the number of neural connections and types of layers. Changes in CNN hyperparameters are reflected both in the final precision of the network and in the learning process.
The aforementioned CNN training process is carried out in an overwhelming number of cases following the Stochastic Gradient Descent (SGD) algorithm. The most important parameter of the SGD algorithm is the learning rate. This value is most often selected empirically on the basis of the analysis of learning curves. Unfortunately, this approach does not optimize the process because too high a value of the learning rate will cause rapid oscillation of the learning curve, while too low a value results in an extended training time. In addition, the SGD method is difficult to tune, which may result in loss of stability. Due to the key importance of the learning rate for the effectiveness of the training process, its optimization is the subject of many studies in the field of Artificial Intelligence (AI). Currently, the most common techniques for selecting this parameter are grid search, random search [41], Bayesian optimization [50], and the Gaussian regression process [51,52]. The most commonly used grid search technique consists of selecting a certain range of parameter values and then training the network for each hyperparameter value, which is dynamically updated during the computation. The disadvantage of this method is the complexity of the calculation and the very long process of determining the final value of the parameter. However, it is worth noting that with appropriately selected parameters, SGD is irreplaceable in the case of large classifications, which results in the popularity of this algorithm in both the adapting processes of CNN, RNN, and DBN weights [53]. However, despite its ease of implementation and convergence, SGD is a relatively slow algorithm. This limitation manifests itself, especially in the case of high curvature or many coherent gradients with small values. The improvement of the SGD algorithm can be obtained with its extension by the momentum parameter (SGDM) [54,55]. Due to its simplicity, this method is currently the most popular [55]. Furthermore, the constant necessity to select parameters forced the emergence of many methods of adaptive learning speed selection, such as AdaGrad [56], AdaDelta [57], RMSProp [58], and Adam [59,60,61].
As in the case of DNN structure hyperparameters, there are currently no rules determining which of the DNN training algorithms is the best. RMSProp, which is a modification of the AdaGrad method, is characterized by the lack of limitations found in AdaGrad in the form of premature and dynamic decreases in the learning rate, which makes it a more frequently used adaptive method. Moreover, the superiority of RMSProp is due to the low efficiency of the AdaGrad algorithm in the case of nonconvex functions. The process of adapting the weights according to AdaDelta is analogous to RMSProp and also consists in limiting the number of past analyzed gradients. The combination of the simplicity of the SGDM algorithm and the convergence of RMSProp has been used in the Adam algorithm. The use of two ideas provides both first- and second-order corrections so that the Adam algorithm does not require a precise selection of hyperparameters [60].
The adaptive algorithms currently used do not differ significantly from the well-tuned SGDM method based on a mini-batch of training data. The size of the mini-batch can be selected empirically or calculated based on information about the size of the available database [24]. As shown in [28], the use of a smaller mini-batch size of the training data results in higher NN efficiency. It should be noted that in each of the cases presented by the authors [28], the quotient of the size of the training database and the size of the mini-batch was an integer, which is consistent with the technique to select this parameter presented in [24]. The literature analysis shows that, in the case of well-known training data, it is recommended to use the SGDM method in the basic version or with Nesterov’s momentum coefficient. If, on the other hand, it is impossible to determine the approximate parameters of the training process, adaptive methods are the best approach.
Based on the review of CNN structure optimization methods presented above, it has been noticed that currently, no guidelines are known to facilitate the design of DNN-based systems. The overwhelming number of optimization methods require a very large computational effort and are individually adapted to a given task performed by the network. Currently, there are no methods to determine the basic structure and parameters of DNN training used in the field of technical diagnostics. Most of the cases analyzed in the literature concern AI applications in the recognition or analysis of images. Therefore, the research results presented in the further part of this article constitute a reliable source of information necessary for the design of diagnostic systems for AC machines based on DNN.
The article is divided into six sections. After the introduction, Section 2 presents the theoretical basis of the CNN structure used in the analysis as well as the training process on DNN. Section 3 is dedicated to a discussion on the methodology of conducted research. The laboratory setup is also presented in Section 3. Section 4 and Section 5 are the main part of the article. The analysis of the impact of the structure hyperparameters on the precision of IM and PMSM diagnostic applications is presented in the Section 4, while Section 5 contains the analysis of the influence of the training process hyperparameters on the accuracy of detection of the AC motors stator winding fault. The article is finished with Section 6, which contains conclusions resulting from the obtained results. All of the research results presented in the article are experimentally verified on the laboratory stands with IM and PMSM.
2. Deep Convolutional Neural Networks
2.1. Structure of the Convolutional Neural Network
Deep neural structures, apart from high requirements regarding the number of data, and stochastic training methods, are characterized by great freedom in developing the information replenishment method (network structure). A special feature of convolutional neural networks is the automatic search for the features of the input matrix (or vector) that enable the determination of belonging to a known state, e.g., a damage category. For this purpose, a mathematical convolution operation is used based on filters (windows of the convolution layer), which contain information about the relationships between the input elements (symptoms). Concerning diagnostic systems, thanks to the training process, the network automatically performs the symptom extraction process for subsequent classification (Figure 1). It should be noted that with the increasing difficulty in recognizing individual classes, the need for multiple plexus operations increases. Therefore, the search for higher-order features in the input matrix results in the presence of many convolutional layers in the CNN structure (as presented in Figure 1). In the following parts of the article, the structures of the CNNs are described in detail in relation to the stator winding diagnosis for PMSM and IM. More details on such diagnostic systems can be found for PMSMs in [62,63] and for IMs in [64,65,66], respectively.
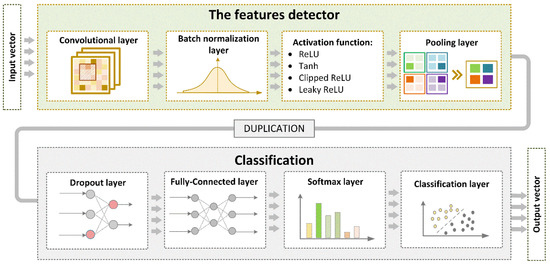
Figure 1.
Structure of the CNNs used in the research.
As can be observed in Figure 1, the four layers included in the detector set are the convolutional layer, batch normalization layer, activation function (ReLU), and pooling layer. Definition of the fault category based on the detected features of input matrices is possible thanks to the use of the set consisting of dropout, fully connected, softmax, and classification layers.
The convolutional layer (CONV) performs the function of a feature detector using the convolutional operation consisting of combining two data sets. The convolutional layers characterized parameters are mostly trained using a simple gradient (filters, activation maps) and configuration settings invariable during the network training process (filter size, input data depth, step, padding). According to the different range of elements of convolutional filters, to increase the dynamic of the training process and ensure the stability of the NN training, batch normalization layers (BNL) are used. The influence of the use of BNL is described in detail in [67]. The determination of non-linear relationships between the information stored in the layers of the feature detector is possible thanks to the activation function. Due to the low computational complexity of CNN structures, the rectified linear unit (ReLU) is the most frequently used.
In connection with the feature extraction task by convolutional layers, a very large number of parameters are stored in their filters. To finally classify the input matrix into the category to which it belongs, it is necessary to limit the number of symptoms only to those that are of the greatest importance in relation to the task of the entire neural structure. For this purpose, a pooling layer (PL) is used that calculates the constant function of the input batch.
The connection between detected symptoms (last PL output) and the classifier input (fully connected layer, FL) is characterized by large numbers of neural connections, which may result in partial loss of generalization ability. In order to avoid this situation, the dropout layer (DL) is often used. This layer ensures the random and periodic rejection of neurons (reduces neural connections). During the selection of the CNN structure, the probability of statistical rejection of the neuron is determined. Due to the use of the DL, the neural connection between the feature detector and the classification part is independent of each other. It should be noted that the DL reduces only the input and/or hidden layer neurons of the FL, and the number output layer constitutes the number of categories recognized by the CNN. Information from the FL is subsequently given to the softmax function and classification layers, which specifies the CNN response based on the cross-entropy of losses calculation.
2.2. Training of the Convolutional Network
As mentioned in the Introduction, many deep learning algorithms are used in the literature. However, the literature and the authors’ own experience show that the SGDM algorithm is currently the most commonly used because of its simplicity and efficiency. The initial stages of the research also showed that the SGDM algorithm works best for the CNN used in the studies (Figure 2). Therefore, it was decided to limit the research to the description of the results obtained with this CNN learning method. The following figures present examples of the CNN learning process with different well-known learning algorithms used in the diagnostic system of the stator windings of the IM drive.
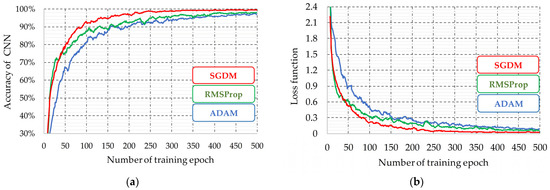
Figure 2.
Analysis of the CNN training algorithm—learning curves: (a) accuracy of the CNNs for testing data; (b) loss function.
As observed in Figure 2, the use of the Adam adaptive learning algorithm results in reduced dynamics of the process. Moreover, the system precision achieved, calculated for the test data, is lower than in the case of using the RMSProp algorithm (difference of about 0.5%). The use of the RMSProp algorithm was characterized by the high dynamics of the training process in the first stages of learning, comparable to the application of the SGDM method. However, the final value of the loss function was noticeably higher than in the case of SGDM, which corresponded to the lower precision of the system. During the analysis of the influence of the learning method on the CNN effectiveness, the same network structures, training, and testing data sets were used.
In order to compare the dynamics of learning processes, research was carried out involving the use of three basic algorithms for a different number of training epochs. The results of the training process times obtained are presented in Figure 3.
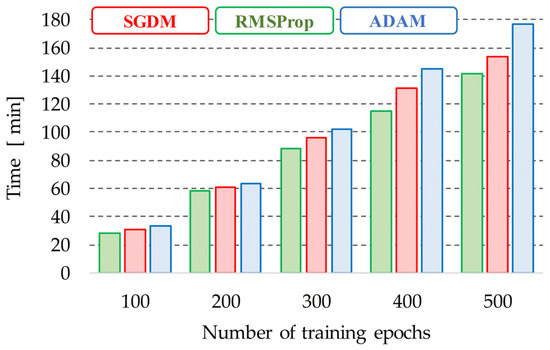
Figure 3.
Influence of the CNN learning method algorithm on the time of training process.
The use of the SGDM algorithm in the developed systems based on CNNs was a compromise between the high precision of the training process and the short learning time. As can be seen in Figure 3, with the increase in the number of learning epochs, the difference in learning time between particular algorithms increases.
3. Methodology of Diagnostics of AC Motor Drives Using CNNs
3.1. Description of the Main Goal of the Invstigation—Research Scenarios
In experimental studies on the use of CNNs in the diagnostic process, particular attention was paid to the influence of the network structure and parameters of the training process on the precision of the developed detection system. The analysis of the literature allows us to notice that, currently, there is a lack of formal rules regarding the selection of hyperparameters of the training process as well as the appropriate adjustment of the CNN structure to the task performed. The research results presented later in this article included CNN in the process of detecting and assessing the degree of damage to induction motors and synchronous motors with permanent magnets. Damages to electric circuits of AC motors, interturn short-circuits (ITSC), are characterized by high dynamics of the defect propagation, which has been repeatedly emphasized in the works [9,62,63]. Due to the short time between the onset of a defect and the complete failure of the windings, the issue of early detection is of particular importance. In addition, it is extremely important to correctly assess the level of damage to take into account the time needed to shut down a damaged machine. Therefore, the diagnostic system should be characterized by high efficiency of damage detection at an early stage in the shortest possible time.
The diagnostic systems proposed by the authors previously [62,63,64] carried out the direct analysis of phase current signals using CNN. To fully demonstrate the effectiveness of the developed diagnostic applications, stator failures in the form of ITSCs were taken into account. A full description of the process of designing diagnostic systems with the use of a CNN was presented, as well as their experimental verification. As presented in the works of the authors [62,63,64,65,66], the idea of designing the stator fault detection systems of the IM and PMSM based on the CNN does not differ significantly from each other. This fact results from a similar structure of the stator in the analyzed machines, as well as the influence of ITSCs on the signals of phase currents and voltages, which was shown in [65]. However, experimental studies have shown a significant influence of permanent magnets on phase currents in the case of a small load torque, which makes the process of PMSM stator damage detection much more difficult than in the case of IM [62].
In the experimental studies presented in the following sections of this article, the ITSC detection systems for the IM and PMSM are considered. The CNN structure, the basis of the respective diagnostic systems, was selected with the assumption of the possibility of detection and assessment of the degree and location of ITSCs. Therefore, CNNs adapted to the IM and PMSM stator diagnostics system are characterized by the different numbers of neural connections and, consequently, different features in the context of diagnostic ability. Detailed parameters of the CNN structures constituting the main element of the IM and PMSM diagnostic systems are summarized in Table 1. The optimal structure of CNN meeting the criterion of the stator fault detection efficiency was the reference point in the further study of the influence of the parameters of the training process and the CNN structure.

Table 1.
Influence of the number of convolutional layers on the precision of a CNN-based diagnostic system: BNL for ε = 0.001.
The previous works of the authors were carried out in several stages. The first stage of the research consisted in measuring selected diagnostic values on stands with AC motors (Section 3.2), where it was possible to model the stator winding failures physically. The next stage of research work included the development of training, validation, and testing data packages for the developed CNN structures using direct analysis of measured current signals (raw data). Based on the network input data, a training process and a preliminary assessment of the effectiveness of CNN were carried out. The third stage of the research included experimental verification of the proposed diagnostic systems based on CNNs during the continuous operation of the tested electric motor. Moreover, an analysis of the influence of machine operating conditions [63,64] and the applied diagnostic signal on the precision of the system [62] was carried out. These studies were the basis for the analysis of the impact of structure parameters and the CNN training process, which were the basis of this article.
The studies are divided into two parts, respectively: (1) the impact of CNN structure parameters (number of convolutional layers, number of convolutional filters, number of fully interconnected layers, number of FC layer neurons, activation functions used, application of the rejection layer and the type of collecting layers); and (2) training process (number of training epochs, initial learning rate, periodic rejection, momentum factor, mini data packet size).
In addition to the effectiveness of the damage severity assessment, the network training process was analyzed by assessing CNN learning curves. The training process of each structure was carried out under the SGDM algorithm detailed in Section 2.2.
3.2. Presentation of the Experimental Setups
Experimental tests of an IM and PMSM with physically introduced failures of the stator windings were carried out with the use of two laboratory stands. Below is a view of the test stand (Figure 4) and the method of conducting experimental tests depending on the type of machine under consideration.
The experimental tests, including the analysis of the impact of damage to the stator windings of the IM, were carried out on the stand shown in Figure 4. The considered drive system included two machines: the tested IM (INDUKTA Sg 100L—4B) with a power of 3 kW and the PMSM (Lenze MCS14H32) with a power of 4.7 kW generating a load torque. The motors were powered by industrial frequency converters operating with a switching frequency of 10 kHz (IM) and 8 kHz (PMSM), respectively. The NI PXIe—8840 real-time controller was responsible for the coordination of the entire control structure of the frequency converters. The developed control system used the measurement of phase currents and rotational speed through LEM transducers and an incremental encoder. Encoder pulses were counted by FPGA-based programmable logic (NI PXI—7851R), which was one of National Instruments rapid prototyping modules.
Tests were performed for the IM operating in a closed-loop structure of the direct rotor flux-oriented control (DRFOC). Measurements of diagnostic quantities were performed with a sampling frequency of 10 kHz. Data acquisition and visualization were performed using VeriStand and LabVIEW software.
Modeling of the ITSC in the stator windings of the IM was possible thanks to specially prepared leads from the windings in each of the three phases of the motor. Leads from the stator windings made it possible to make a short circuit in the range from 0–30 turns. In the research, special attention was paid to metallic short circuits (Rsh ≈ 0) due to their destructive course.
The tested drive system with PMSM motor, shown in the RHS of the lower part of Figure 4, consisted of two mechanically coupled machines with a power of 2.5 kW (tested motor—Lenze MCS14H15) and 4.7 kW (loading machine—Lenze MCS14H32) powered by industrial frequency converters by Lenze. The control of the tested motor, as well as the regulation of the load torque values, was performed with the use of the VeriStand and Lenze Studio environments. Acquisition of the measurement data was carried out using the NI PXI 8186 industrial computer equipped with a DAQ NI PXI—24472 measurement card with high resolution.
Due to the technical limitations of the laboratory stand, during the tests, it was possible to physically model failures only in one phase of the PMSM stator winding (up to 12 turns of the B phase). Measurements of phase currents were carried out during the failure of up to three shorted coils of the B phase with the sampling frequency of 8192 Hz. Phase current and voltage signals were measured with LEM transducers. Monitoring of diagnostic signals was performed with the use of a virtual measurement system developed in the LabVIEW environment. Measurements of diagnostic signals were carried out for changes in the frequency of the supply voltage in the range fs = 50–100 Hz and the load torque adjustment in the range TL = 0–TLN.
The design of the diagnostic system for faults in the IM and PMSM was carried out using LabVIEW (by National Instruments, Austin, TX, USA; ver. 2018) and Matlab (by MathWorks, Natick, MA, USA; ver. 2019a) environments. The use of Matlab in neural calculations ensured the stability of the program and a significant reduction in computation time. The acquisition of measurement data that constitute the CNN input vector was performed in the LabVIEW environment. The entire diagnostic system required the possibility of transferring information between LabVIEW and Matlab software.
4. Analysis of the Influence of CNN Structure on the Effectiveness of IM and PMSM Diagnostic Systems
In order to identify the influence of the CNN structure on the precision of the diagnostic system, the following studies were carried out:
- analysis of the impact of changes in the number of CONV and FC layers on the effectiveness of CNN;
- analysis of the impact of the number of CONV filters on the precision of the CNN network;
- assessment of the impact of the number of neurons in the FC layer and the declared probability of neuron rejection on the precision of the CNN;
- influence of the activation function used: ReLU, clipped ReLU function, leaky ReLU, hyperbolic tangent;
- assessment of the influence of the rejection and pooling layers on the precision of CNN.
The analyses conducted included CNNs that were responsible for assessing the degree of damage to the stator winding of the IM and PMSM. In view of the function of the CONV layers, namely the search for the features of the input matrix, the first stage of the research concerned the influence of the number of convolutional sets on the effectiveness of the diagnostic system. The list of parameters of the structures used for the induction motor and PMSM, respectively, is presented in Table 1.
In the use of CNN in the diagnostic process, the number of convolutional layers of the network is indirectly forced by the number of features in the set, allowing for an unequivocal determination of the belonging of the input matrix to one of the considered classes. The structures considered in Table 1 operated on the information contained in the phase current signals. As can be seen with the increase in the number of CONV layers, and thus with the increase in the share of higher-order features in the final assessment of the category, there is a clear increase in the precision of the network. Nevertheless, after exceeding the four layers, further increase in the network efficiency is stopped, which is observable in the applications for the two considered types of machines. The growth of the CNN structure by successive sets of CONV layers affects both the final precision of the system and the course of the training process (Figure 5). Due to the similar course of the learning curves in the early stages of the training process and during the convergence of the learning process, the figures also show zooms of characteristic points of the training process. Due to this, a detailed analysis of the dependence between network parameters and the dynamics of the training process and its final convergence can be done. A similar way of presenting the characteristic points of the shown waveforms was used in the following figures in the article.
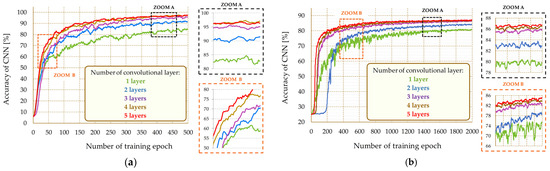
Figure 5.
Influence of the number of convolutional layers on the precision of the diagnostic system—learning curves: (a) induction motor; (b) PMSM.
The increased number of network layers results in an increase in the number of neural connections, which, in turn, translates into an extended training process. However, as can be seen in Figure 5, the ultimate precision of the lattice increases to a certain level with each successive convolutional layer. Additionally, faster stabilization of the training process is noticeable, both in the case of the IM winding damage diagnostic system (Figure 5a) and PMSM (Figure 5b).
The waveforms of the average network efficiency value for randomly assigned elements of the testing package shown in Figure 5 show that the use of more than four convolutional layers does not significantly affect the precision of the network. This is confirmed by the network efficiency values, calculated on the basis of responses to the testing data, presented in Table 1. It is also worth noting that the analysis of the influence of the convolution layer required the use of additional pooling layers, activation, and normalization functions. However, these layers are not subject to training; therefore, their impact on network performance is considered negligible. The attachment of successive convolutional layers is related to the necessity of extracting symptoms of higher order to facilitate the classification process. On the contrary, the size of the set of considered features is related to the declared number of filters, in particular, CONV. In order to analyze the effect of the number of filters, research was carried out on the CNN network with three CONV layers while increasing the number of filters (Table 2).

Table 2.
Effect of the number of CONV filters on CNN precision.
The analysis of the precision of the network response to the testing data, presented in Table 2 and Figure 6, shows a clear increase in CNN effectiveness while increasing the number of filters in each network layer. The biggest change is observed in the case of the IM damage detection system. The difference in precision between CNN structures with the highest and lowest scoring efficiency is about 12%. Much smaller changes in precision due to the increase in the number of filters are noticeable for the PMSM diagnostic system. In this case, the difference in the determined efficiencies is approximately 3%. To show the influence of the number of convolutional filters on the adaptation process of net weights, Figure 7 presents selected training curves recorded during the CNN training process.
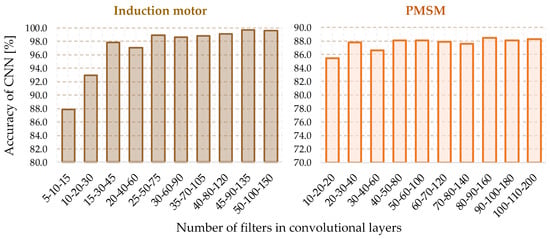
Figure 6.
Influence of the number of CONV filters on CNN precision.
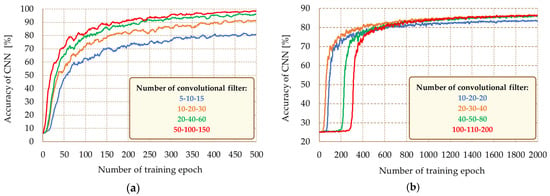
Figure 7.
Influence of the number of convolutional filters on the precision of the diagnostic system—learning curves: (a) induction motor; (b) PMSM.
As can be seen in Figure 7, the increase in the number of filters in the CONV layers results in the stabilization of the learning curves with a gradually higher level of precision for the IM and PMSM diagnostic systems. Furthermore, in the case of networks that perform the PMSM stator failure classification task (Figure 7b), a much longer tuning of the training process (initial slight change in the precision level) is noticeable than for the induction motor. This phenomenon results from the incompatibility of the training process parameters with the gradually increasing CNN structures. The assignment of the grid input matrix to one of the known categories on the basis of information about the features from the convolutional sets is possible thanks to the use of fully interconnected layers. Therefore, the next stage of research on the influence of the CNN structure on the precision of the diagnostic system involved changing the number of these layers. The research was carried out on the basis of a network with three convolution sets for both IM and PMSM. The test results are summarized in Table 3.

Table 3.
Effect of the number of fully connected layers on CNN precision.
Analysis of the summary of the approximate precision of the diagnostic system (Table 3) and the shape of the learning curves (Figure 8) showed that increasing the number of FC layers does not result in a significant increase in the CNN precision. Moreover, the determination of the contribution of particular features of the input matrix to the assessment of belonging to a given category can be successfully performed with the use of up to two fully connected layers. As shown in Figure 8, during the course of the training process, the learning curves coincide, while the stabilized level of precision of the network for all the cases analyzed is very similar. Nevertheless, limiting the number of layers to two avoids the situation where the response of the network depends mainly on the classifier set. Therefore, when selecting the number of FC layers, attention should be paid to the number of parameters in convolutional and classifying sets while taking into account the essential role of feature extraction.
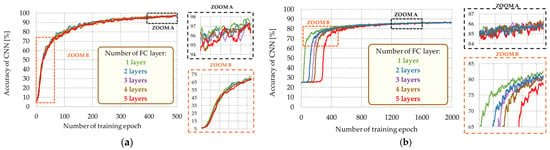
Figure 8.
Influence of the number of fully connected layers on the precision of the CNN network—learning curves: (a) induction motor; (b) PMSM.
As shown in Table 3, networks with two hidden layers were characterized by the highest level of precision, especially in the case of IM. In the case of PMSM, the differences were not as clear, but the use of two FC layers limits the expansion of the network structure, and increasing the number of these layers does not significantly improve the accuracy of the network response. Therefore, for both considered diagnostic systems, only the effect of the number of neurons in the first fully connected layer was analyzed since the number of neurons in the output layer is predetermined by the number of categories analyzed by the network (Figure 8a). Furthermore, due to the direct connection between the DROP and FC layer, the influence of the declared probability of neuron rejection on the operation of the developed diagnostic systems was checked (Figure 9b).
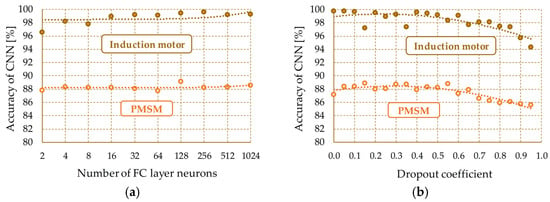
Figure 9.
Analysis of the effectiveness of the CNN network—learning curves: (a) the effect of the number of neurons in the FC layer; (b) the effect of the dropout factor.
The analysis of the results presented in Figure 10a showed that increasing the number of neurons in the FC layer did not change the precision value of the neural network. A noticeable lack of changes in efficiency for the entire range of the number of neurons used is observed in diagnostic systems for both types of electric motors. The results of the research on the effect of the probability of rejection of neurons presented in Figure 10b show that for a certain range of this parameter, the precision of the network increases. The highest level of precision is achieved with a rejection rate value of approximately p ≤ 0.5. An excessive number of rejected neurons (p ≥ 0.75) adversely affects the operation of the network. However, it is worth noting that the main task of the DROP layer is to eliminate the situation in which the state of one neuron of the network is strongly dependent on the state of another neuron. Random deactivation of neurons in the transition between the feature detector (convolution set) and the classifier ensures a faster course of the training process, which is presented in Figure 10.
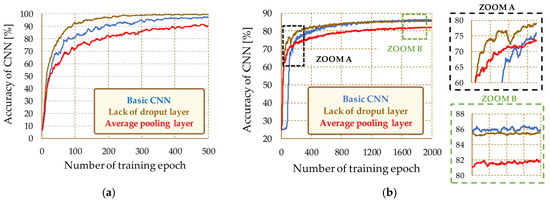
Figure 10.
Influence of the PL and DROP layers on the precision of the CNN network—learning curves: (a) IM; (b) PMSM.
The basic structure described in Figure 10 was adopted as a three-layer convolutional network with an implemented rejection layer (p = 0.5) and a pooling layer based on the ‘maximum’ function (pooling max). The observations of the learning curves shown in Figure 10 show that the use of the DROP layer reduces the dynamics of the training process. However, the results obtained for the PMSM (Figure 10b) indicate the advantage of the network with the rejecting layer. In this case, the network efficiency determined based on the responses to the test data (with the dropout layer applied) was greater by less than 2%. The use of a pooling layer based on the mean value of a given window results in a much lower level of precision of the diagnostic system. The summary of the values determined for the effectiveness of the evaluation of the technical condition of the stator winding of the IM and PMSM based on the CNN response to the testing data is presented in Table 4.

Table 4.
Influence of CNN structure parameters on the precision of responses to test data.
The last stage of the research on the impact of the network structure involved changing the activation function. For this purpose, the operation of the network using the activation functions in the form of a rectified linear function (ReLU), clipped ReLU, leaky ReLU, and the hyperbolic tangent (Tanh) function was analyzed. The course of the CNN network training process with different activation functions is presented in Figure 11.
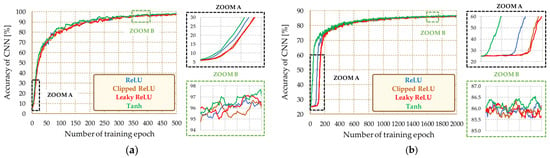
Figure 11.
Influence of the CNN activation function on the precision of the diagnostic system—learning curves: (a) induction motor; (b) PMSM.
As shown in Figure 11, the activation function used does not significantly affect the course of the neural network training process. The effectiveness of diagnostic systems is similar for all cases analyzed, which is additionally confirmed by the list in Table 4. However, the use of the activation function in the form of a hyperbolic tangent is characterized by greater dynamics of the learning process. It should be noted, however, that the application of this function is more complex in terms of computation; therefore, the update of the weighting factors is slower than when using the ReLU function or its variants.
In the next step, the influence of the training process parameters on the effectiveness of the diagnostic system implemented on CNN networks was analyzed. Research was carried out for networks containing three sets of convolutional layers with activation functions of the ReLU type. The classifying part of the analyzed structures, however, contained two fully connected layers and a rejection layer with a declared rejection probability of 0.5. According to the analysis of the literature presented in the Introduction, in the case of well-known training data, it is recommended to use the SGDM method. For this reason, the research was limited to the stochastic gradient with a momentum algorithm.
5. Analysis of the Impact of Training Process Parameters of CNN to the Effectiveness of IM and PMSM Diagnostic Systems
In order to estimate the impact of the parameters of the CNN training process using the CNN (using SGDM algorithm) on the precision of the diagnostic system, the following studies were carried out:
- the impact of changes in the number of training epochs on the precision of the diagnostic system of the stator windings of an IM and PMSM;
- analysis of the impact of the initial learning rate and the drop period on the course of the convolutional network training process;
- study of the influence of the momentum factor on the training process and the precision of the CNN;
- the impact of the data mini-batch size on the performance of a CNN-based diagnostic system.
The first stage of the research included an analysis of the impact of changes in the number of learning epochs on the final precision of the diagnostic system. For this purpose, the network training process was carried out 30 times for a different number of training periods declared. Then, for each of the CNNs, the effectiveness of the category score based on the response to the test packet was calculated. The results of the analyses for the diagnostic systems for IM and PMSM are presented in Figure 12.
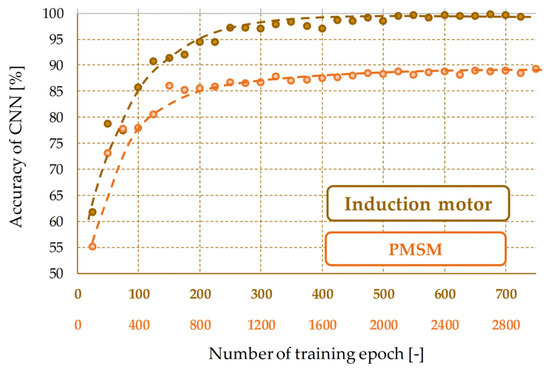
Figure 12.
Influence of the number of learning epochs on the precision of a diagnostic system.
The courses of dependence of the precision of diagnostic systems on the number of training epochs presented in Figure 12 show that after reaching 400 and 1600 epochs, respectively, for CNN-IM (CNN-based diagnostic system for IM) and CNN-PMSM (CNN-based diagnostic system for PMSM), a clear stabilization of the precision level occurs. An excessive increase in the number of learning epochs does not disturb the operation of the network. Moreover, due to the use of the techniques of normalization, rejection, and training based on a randomly created mini-batch of data, the risk of overmatching with the training data is minimized. However, during the practical implementation of CNN, in addition to analyzing the effectiveness of the network for training, validation, and final testing data, it is advisable to observe changes in the course of the loss function in each training epoch. Such an approach will make it possible to interrupt the learning process after achieving the assumed precision or, more importantly, during a sudden increase in the value of the loss function for validation data.
A particularly important parameter of the CNN training process, which ensures the appropriate dynamics of the learning process and its convergence, is the initial value of the learning constant (Figure 13a). Due to the inability to accurately determine the value of this constant, the drop period technique is often used before starting the training process. The study used a 5% decrease in the value of the learning constant for a variable period (Figure 13c). In order to determine the impact of the learning constant and the period of its decrease, both the change in the level of precision of the CNN (Figure 13a,c) and the impact on the course of the training process (Figure 13b,d) were analyzed.
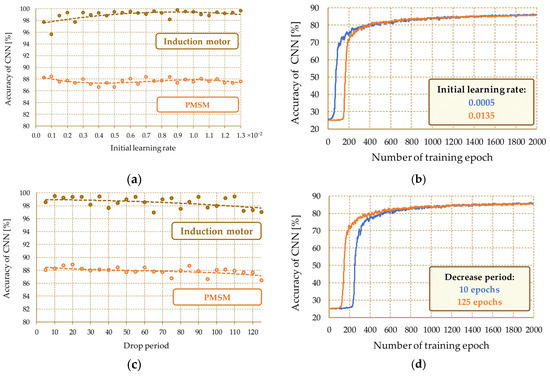
Figure 13.
Influence of CNN training process parameters on the precision of the diagnostic system: (a) change of the initial value of the learning constant; (b) the course of learning curves during changes of the learning constant—PMSM motor; (c) changing the period of decline of the learning constant; (d) the course of learning curves during changes of the learning constant decrease period—PMSM.
The research presented in Figure 13 shows that an initial value too high for the learning constant results in a slight improvement in the effectiveness of the network in the first epochs of the training process (Figure 13b). As the learning process progresses, the effectiveness of the network improves significantly. The test results presented for 27 cases (Figure 13a) show no significant influence of the initial value of the learning constant on the final value of the precision of the neural network. This fact results from the application of the drop of the learning rate technique (Figure 13c).
The analysis of the waveforms shown in Figure 13 shows that an increase in the frequency (decrease in the number of epochs) of the weakening of the constant results in an increase in the effectiveness of the system both when applied to IM and PMSM (Figure 13c). However, as the step is reduced, the reduced dynamics of the training process are noticeable, as shown by the flat sections of the learning curve in Figure 13d. The analysis of the results presented in Figure 13 shows that the optimal solution to the problem of the initial learning constant is to determine its overestimated value with the simultaneous application of a small weakening period.
The SGDM algorithm, thanks to the application of the momentum factor, enables the damping of the oscillation of the learning curves, as well as significantly accelerates the convention. Moreover, the momentum factor allows one to determine the participation of earlier gradients in the process of minimizing the assumed loss function.
Figure 14 shows the influence of the value of the momentum coefficient on CNN precision and the influence on the training process. The research results presented in Figure 14 clearly show the dependence of the convolutional precision of the neural network on the declared momentum coefficient. The highest level of precision of the network was obtained for the coefficient value equal to 0.95 (Figure 14a). Furthermore, the waveforms of the learning curves in Figure 14b show the stabilization of the training process at a much higher level of precision.
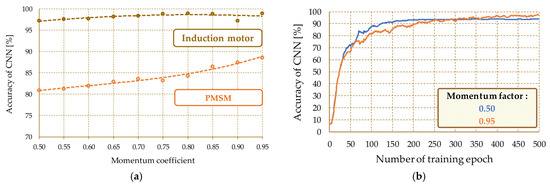
Figure 14.
Impact of changes in the momentum factor on the precision of the diagnostic system: (a) precision of the response to the elements of the testing package; (b) learning curves, induction motor.
The lower precision level observed in Figure 14b for the momentum coefficient of 0.5 is most likely due to being stuck at a local minimum. Increasing this parameter to 0.95 enables us to go through the local minimum and further search for the global minimum of the objective function. Taking into account the results of the research, as well as the examples described in [64], when selecting the parameters of the training process, it is recommended to determine the value of the momentum coefficient in the range of 0.5–0.95 and to observe changes in the value of the loss function (convergence of the training process).
The idea of the CNN training process in accordance with the SGDM algorithm is based on the determination of the approximate value of the gradient based on the average of the gradients for samples from the mini-data packet. The elements of the mini-batch are randomly selected with the same number of cases for each of the considered classes. On the contrary, the number of samples, which is the size of a mini data packet, is generally a few percent of the size of the training data packet. Note that the size of the mini-data packet also determines the number of iterations in each training epoch. Therefore, increasing the size results in a decrease in the number of iterations due to the need to present the network of all training packet samples in each epoch. So as to assess the impact of the parameter discussed, the effectiveness of CNN structures developed during changes in the size of the minibatch was analyzed within the range of 10–250 (Figure 15).
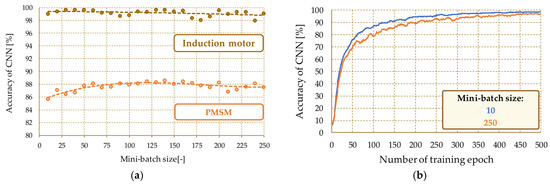
Figure 15.
Influence of CNN training process parameters on the precision of the diagnostic system: (a) response precision to the elements of the testing package; (b) learning curves—induction motor.
Based on the results of the research presented in Figure 15, it can be concluded that too large a mini-batch of data results in a decrease in the level of precision of the system (Figure 15a), as well as a reduction in the dynamics of the training process (Figure 15b). Although the small packet size requires an increased number of iterations, the process is computationally easier, and convergence is achieved faster. The analyses show that the developed structures were characterized by the highest level of effectiveness for mini-batch sizes equal to 30 and 140 for IM and PMSM, respectively. Taking into account the sizes of the training packages (1600 for the IM and 7200 for the PMSM), the sizes of minibatch used accounted for approximately 2% of the training data. In practice, it is recommended to use a size no greater than 5% of the dimension of the training data packet.
6. Conclusions
Based on the presented research on the impact of the CNN structure and parameters and its training process on the fault diagnosis task of AC motor drives, the following conclusions can be formulated:
- -
- Despite many similarities in the construction of the stator windings IM and PMSM motors, diagnostic systems based on CNN have different levels of precision. This phenomenon is observable during the analysis of the learning curves of the CNN training process. This fact results from the influence of the permanent magnets of the PMSM rotor, especially when working with low load torque. The influence of permanent magnets significantly limits the possibilities of direct processing of phase current signals by CNN. Therefore, when designing CNN-based detection systems, applications for IM and PMSM should be considered separately as systems with different properties.
- -
- The gradual increase in the number of convolutional layers results in an increase in the network precision index, which results from the increasing share of higher-order features in the final evaluation. However, the nature of these changes is true only for a certain range of the number of convolutional layers where the higher-order features contain useful diagnostic information.
- -
- Excessive expansion of the network structure significantly extends the training process while not improving its effectiveness; as the number of filters increases, the precision of the convection network is clearly improved, which is the result of the increased number of characteristic features for individual categories. However, as with the declaration of the number of convolutional layers, the improvement in the degree of precision due to the increase in the number of filters only takes place up to a certain level.
- -
- Increasing the number of fully interconnected layers, as well as the number of neurons in individual layers, does not significantly affect the precision of the convolutional structure. As has been shown in the research conducted, the use of only two layers ensures a high level of precision in determining the belonging of the input matrix to one of the considered classes.
- -
- The use of a rejection layer ensures that the generalization properties of the neural network are maintained, which results in an increase in the precision of the system for unknown samples. Moreover, the rejection layer should be located primarily in the places of the structure with the highest number of neural connections (at the transition between the convolution and the classification set). However, the declared probability of rejection should ensure the convergence of the training process. In most of the CNN implementation examples described, this value is 0.5.
- -
- The activation functions of the CNN network do not play a key role in the ultimate precision of the system. In the overwhelming majority of cases, deep networks use activation functions of the ReLU type or its variants. In addition, the use of sigmoidal functions makes it possible to achieve high precision in diagnostic systems. However, attention should be paid to the fact that the use of linear functions instead of sigmoid ones is aimed at simplifying the computational process of a significantly extended neural structure.
- -
- The selection of the number of learning epochs should take into account the number of iterations that ensure stabilization of the value of the loss function determined for the learning and testing data. Note that with each teaching epoch, the waveforms of the loss functions calculated for the teaching and testing data should have a similar shape. At the moment of the emergence of gradually larger differences in the waveforms (bifurcation of waveforms) or the complete lack of changes in the value of the loss function, the process should be stopped, and its parameters should be improved.
- -
- The use of the technique of periodic weakening of the learning constant eliminates to some extent the problem of precise adjustment of the initial learning constant. The cyclical reduction of the constant makes it possible to adjust the constant during the training process, which is noticeable in the form of flat fragments of the loss function. Proper selection of the number of epochs followed by the reduction of the constant (most often, the new value is 80–95% of the value before the update) enables a significant reduction of the tuning time of the learning constant. The research carried out has shown that the application of the SGDM algorithm with the declared value of the angular momentum coefficient in the range of 0.80–0.95 results in an increase in the precision of the convolutional network. Moreover, increasing the degree of participation of previous clients in the process of searching for the minimum of the objective function reduces the risk of stalling the training process resulting in a lack of a decrease in the value of the loss function; the selection of the size of the training data mini-batch should take into account the number of all cases included in the training packet. The research showed that despite the different sizes of the training packets for IM and PMSM, the highest level of precision was achieved for the minibatch size, which was about 2% of the size of the training packet.
Author Contributions
All the authors contributed equally to the concept of the paper, and proposed the methodology; M.S., C.T.K. and T.O.-K.; investigation and formal analyses, M.S.; software and data curation, M.S.; measurements, M.S.; software, M.S.; writing—original draft preparation, M.S., T.O.-K. and C.T.K.; writing—review and editing, M.S. and T.O.-K.; supervision, project administration and funding acquisition, M.S. and T.O-K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Science Centre Poland under projects 2017/27/B/ST7/00816 and 2021/41/N/ST7/01673.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Induction motor parameters.
Table A1.
Induction motor parameters.
| Name of the Parameter | Symbol | Value | Units |
|---|---|---|---|
| Power | PN | 3000 | [W] |
| Torque | TN | 19.83 | [Nm] |
| Speed | NN | 1445 | [r/min] |
| Stator phase voltage | UsN | 230 | [V] |
| Stator current | IsN | 6.8 | [A] |
| Frequency | fsN | 50 | [Hz] |
| Pole pairs number | pp | 2 | [-] |

Table A2.
PMSM parameters.
Table A2.
PMSM parameters.
| Name of the Parameter | Symbol | Value | Units |
|---|---|---|---|
| Power | PN | 2500 | [W] |
| Torque | TN | 16 | [Nm] |
| Speed | nN | 1500 | [r/min] |
| Stator phase voltage | UsN | 325 | [V] |
| Stator current | IsN | 6.6 | [A] |
| Frequency | fsN | 100 | [Hz] |
| Pole pairs number | pp | 4 | [-] |
| Number of stator winding turns | Ns | 2 × 125 | [-] |
References
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors—A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G.-A. Advances in diagnostic techniques for induction machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.A.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca, R.; Estima, J.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in Fault Diagnosis for Electrical Machines: A Review of Diagnostic Techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Capolino, G.A.; Antonino-Daviu, J.A.; Riera-Guasp, M. Modern diagnostics techniques for electrical machines, power electronics, and drives. IEEE Trans. Ind. Electron. 2015, 62, 1738–1745. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Capolino, G.A. Advances in electrical machine, power electronic and drive condition monitoring and fault detection: State of the art. IEEE Trans. Ind. Electron. 2015, 62, 1746–1759. [Google Scholar] [CrossRef]
- Choi, S.; Haque, M.S.; Tarek, M.T.B.; Mulpuri, V.; Duan, Y.; Das, S.; Toliyat, H.A. Fault diagnosis techniques for permanent magnet AC machine and drives—A review of current state of the art. IEEE Trans. Transp. Electrif. 2018, 4, 444–463. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, S.; Li, W.; Liang, H.; Wang, C. Faults and diagnosis methods of permanent magnet synchronous motors: A review. Appl. Sci. 2019, 9, 2116. [Google Scholar] [CrossRef]
- Frosini, L. Novel Diagnostic Techniques for Rotating Electrical Machines—A Review. Energies 2020, 13, 5066. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives–State of the Art and Future Challenges. IEEE Access 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Shen, W.; Huang, C. Online Fault Diagnosis Method based on Transfer Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2020, 69, 509–520. [Google Scholar] [CrossRef]
- Li, C.; Zhang, W.; Peng, G.; Liu, S. Bearing Fault Diagnosis Using Fully-Connected Winner-Take-All Autoencoder. IEEE Access 2018, 6, 6103–6115. [Google Scholar] [CrossRef]
- Principi, E.; Rossetti, D.; Squartini, S.; Piazza, F. Unsupervised electric motor fault detection by using deep autoencoders. IEEE/CAA J. Autom. Sin. 2019, 6, 441–451. [Google Scholar] [CrossRef]
- Shao, S.; Sun, W.; Wang, P.; Gao, R.X.; Yan, R. Learning features from vibration signals for induction motor fault diagnosis. In Proceedings of the International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016. [Google Scholar]
- Chattopadhyay, P.; Saha, N.; Delpha, C.; Sil, J. Deep Learning in Fault Diagnosis of Induction Motor Drives. In Proceedings of the Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018. [Google Scholar]
- Lee, Y.O.; Jo, J.; Hwang, J. Application of deep neural network and generative adversarial network to industrial maintenance: A case study of induction motor fault detection. In Proceedings of the IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017. [Google Scholar]
- Suh, S.; Lee, H.; Jo, J.; Łukowicz, P.; Lee, Y. Imbalanced Data on Bearing Fault Detection and Diagnosis. Appl. Sci. 2019, 9, 746. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Guo, L.; Lin, J.; Xing, S. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Khan, T.; Alekhya, P.; Seshadrinath, J. Incipient Inter-turn Fault Diagnosis fin Induction motors using CNN and LSTM based Methods. In Proceedings of the IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018. [Google Scholar]
- Luo, Y.; Qiu, J.; Shi, C. Fault Detection of Permanent Magnet Synchronous Motor based on Deep Learning Method. In Proceedings of the 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018. [Google Scholar]
- Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Wu, J.; Xie, Y.; Zhang, Y. Motor Fault Diagnosis based on Short-time Fourier Transform and Convolutional Neural Network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Ding, X.; He, Q. Energy-Fluctuated Multiscale Feature Learning with Deep ConvNet for Intelligent Spindle Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 1926–1935. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, H.; Li, Y.; Xu, M.; Chen, Y. A fault diagnosis scheme for rotating machinery using hierarchical symbolic analysis and convolutional neural network. ISA Trans. 2019, 91, 235–252. [Google Scholar] [CrossRef]
- Pan, J.; Zi, Y.; Chen, J.; Zhou, Z.; Wang, B. LiftingNet: A Novel Deep Learning Network with Layerwise Feature Learning from Noisy Mechanical Data for Fault Classification. IEEE Trans. Ind. Electron. 2018, 65, 4973–4982. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Liu, R.; Wang, F.; Yang, B.; Qin, S.J. Multi-scale Kernel based Residual Convolutional Neural Network for Motor Fault Diagnosis Under Non-stationary Conditions. IEEE Trans. Ind. Inform. 2019, 16, 3797–3806. [Google Scholar] [CrossRef]
- Shao, S.; Yan, R.; Lu, Y.; Wang, P.; Gao, R. DCNN-based Multi-signal Induction Motor Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 69, 2658–2669. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Talathi, S.S. Hyper-parameter optimization of deep convolutional networks for object recognition. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015. [Google Scholar]
- Sedki, A.; Ouazar, D.; El Mazoudi, E. Evolving neural network using real coded genetic algorithm for daily rainfall–runoff forecasting. Expert Syst. Appl. 2009, 36, 4523–4527. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, A.; Wang, C.; Niu, Z. Evolving neural network using real coded genetic algorithm (GA) for multispectral image classification. Future Gener. Comput. Syst. 2004, 20, 1119–1129. [Google Scholar] [CrossRef]
- Suganuma, M.; Shirakawa, S.; Nagao, T. A genetic programming approach to designing convolutional neural network architectures. In Proceedings of the ACM Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; pp. 497–504. [Google Scholar]
- Cui, H.; Bai, J. A new hyperparameters optimization method for convolutional neural networks. Pattern Recognit. Lett. 2019, 125, 828–834. [Google Scholar] [CrossRef]
- Yamasaki, T.; Honma, T.; Aizawa, K. Efficient optimization of convolutional neural networks using particle swarm optimization. In Proceedings of the IEEE Third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017. [Google Scholar]
- Bengio, Y. Gradient-based optimization of hyperparameters. Neural Comput. 2000, 12, 1889–1900. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS ’12), Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Pierre, S.; Soumith, C.; Yann, L. Convolutional Neural Networks Applied to House Numbers Digit Classification. arXiv 2012, arXiv:1204.3968. [Google Scholar] [CrossRef]
- Ngiam, J.; Chen, Z.; Chia, D.; Koh, P.W.; Le, Q.V.; Ng, A.Y. Tiled convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 6–11 December 2010. [Google Scholar]
- Scherer, D.; Muller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International Conference on Artificial Neural Networks, Thessaloniki, Greece, 15–18 September 2010. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Rippel, O.; Snoek, J.; Adams, R.P. Spectral representations for convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradientbased learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Deliège, A.; Istasse, M.; Kumar, A. Ordinal Pooling. In Proceedings of the 30th British Machine Vision Conference, Cardiff, UK, 9–12 September 2019. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Zhang, G.; Wang, P.; Chen, H.; Zhang, L. Wireless indoor localization using convolutional neural network and gaussian process regression. Sensors 2019, 19, 2508. [Google Scholar] [CrossRef]
- Zhang, M.; Li, H.; Lyu, J.; Ling, S.H.; Su, S. Multi-level cnn for lung nodule classification with gaussian process assisted hyperparameter optimization. arXiv 2019, arXiv:1901.00276. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. RMSProp: Divide the Gradient by a Running Average of Its Recent Magnitude. Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Dubey, S.R.; Chakraborty, S.; Roy, S.K.; Mukherjee, S.; Singh, S.K.; Chaudhuri, B.B. DiffGrad: An Optimization Method for Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4500–4511. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, L.J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of Adam and beyond. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Skowron, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Application of simplified convolutional neural networks for initial stator winding fault detection of the PMSM drive using different raw signal data. IET Electr. Power Appl. 2021, 15, 932–946. [Google Scholar] [CrossRef]
- Skowron, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Detection of permanent magnet damage of PMSM drive based on direct analysis of the stator phase currents using convolutional neural network. IEEE Trans. Ind. Electron. 2022, 69, 13665–13675. [Google Scholar] [CrossRef]
- Skowron, M.; Orlowska-Kowalska, T.; Wolkiewicz, M.; Kowalski, C.T. Convolutional Neural Network-Based Stator Current Data-Driven Incipient Stator Fault Diagnosis of Inverter-Fed Induction Motor. Energies 2020, 13, 1475. [Google Scholar] [CrossRef]
- Skowron, M. Application of deep learning neural networks for the diagnosis of electrical damage to the induction motor using the axial flux. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1039–1048. [Google Scholar]
- Skowron, M.; Wolkiewicz, M.; Tarchała, G. Stator winding fault diagnosis of induction motor operating under the field-oriented control with convolutional neural networks. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1031–1038. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
