2.1. Availability
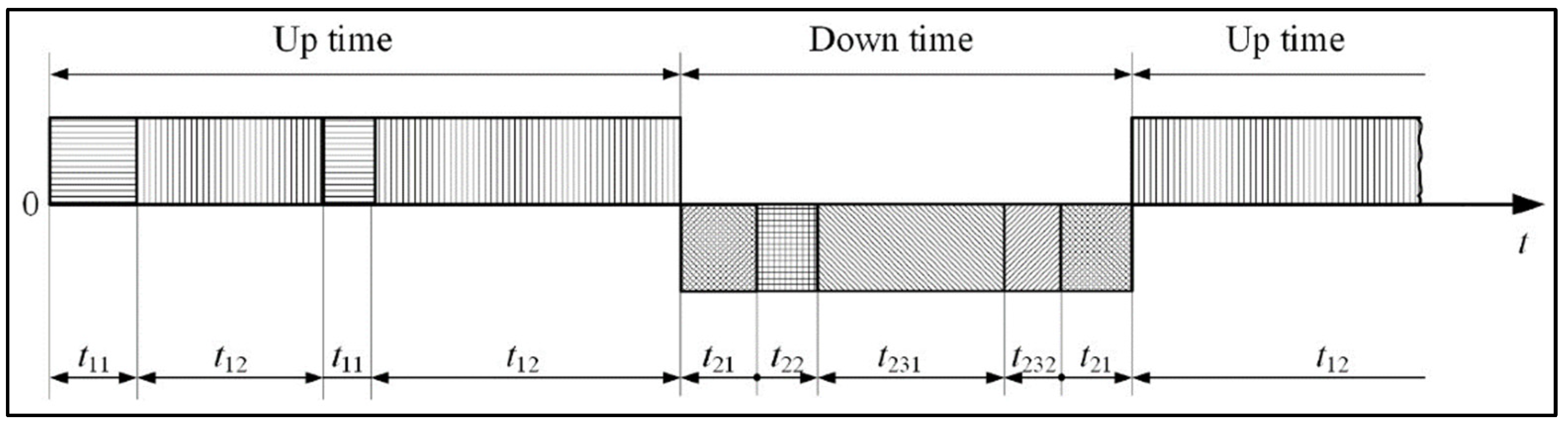
The availability is calculated on the basis of a time state picture, in which the times when the system is up alternate with the times when the system is down. The time picture of the state can be shown in
Figure 5. The time when the system is in a correct state can be divided into an inactive time, that is, the time when the system is standby (
) and the time when the system is in operation (
). The time when the system is in failure is divided into organizational time (
), logistic time (
), and active repair time (
), which can be time for corrective repairs (
) and time for preventive repairs (
) [
1,
19].
Availability is determined as the quotient of the total time during which the system is in a correct state and the total time that makes up the time in the correct state and time in failure (operational availability) [
1,
4].
The availability is a comprehensive concept that covers the entire lifetime of an engineering system [
12]. Additional definitions of availability can be found in the references [
9].
The operation of continuous systems at the open pits is characterized by changing the working environment conditions, changeable meteorological conditions, and a number of different technological phases and procedures. This is the reason why, for a sufficiently accurate determination of system parameters, including availability, its condition must be monitored over a longer period of time. It is common for the minimum monitoring period to be one year (in all seasons, through the technological phases of operation, current, and preventive maintenance). The availability based on formula (1) therefore requires the historical monitoring of operation and this formula can only be used after determining the uptime and downtime in a certain time interval.
On the basis of form (1), it can be stated that, broadly speaking, the constituent elements of availability are: correctness at a given moment as well as the satisfactory technical condition of the machine as a predictive category; design predetermination; and level of supportability for service and corrective maintenance.
2.2. Development of a Fuzzy Expert Model for the Availability Assessment
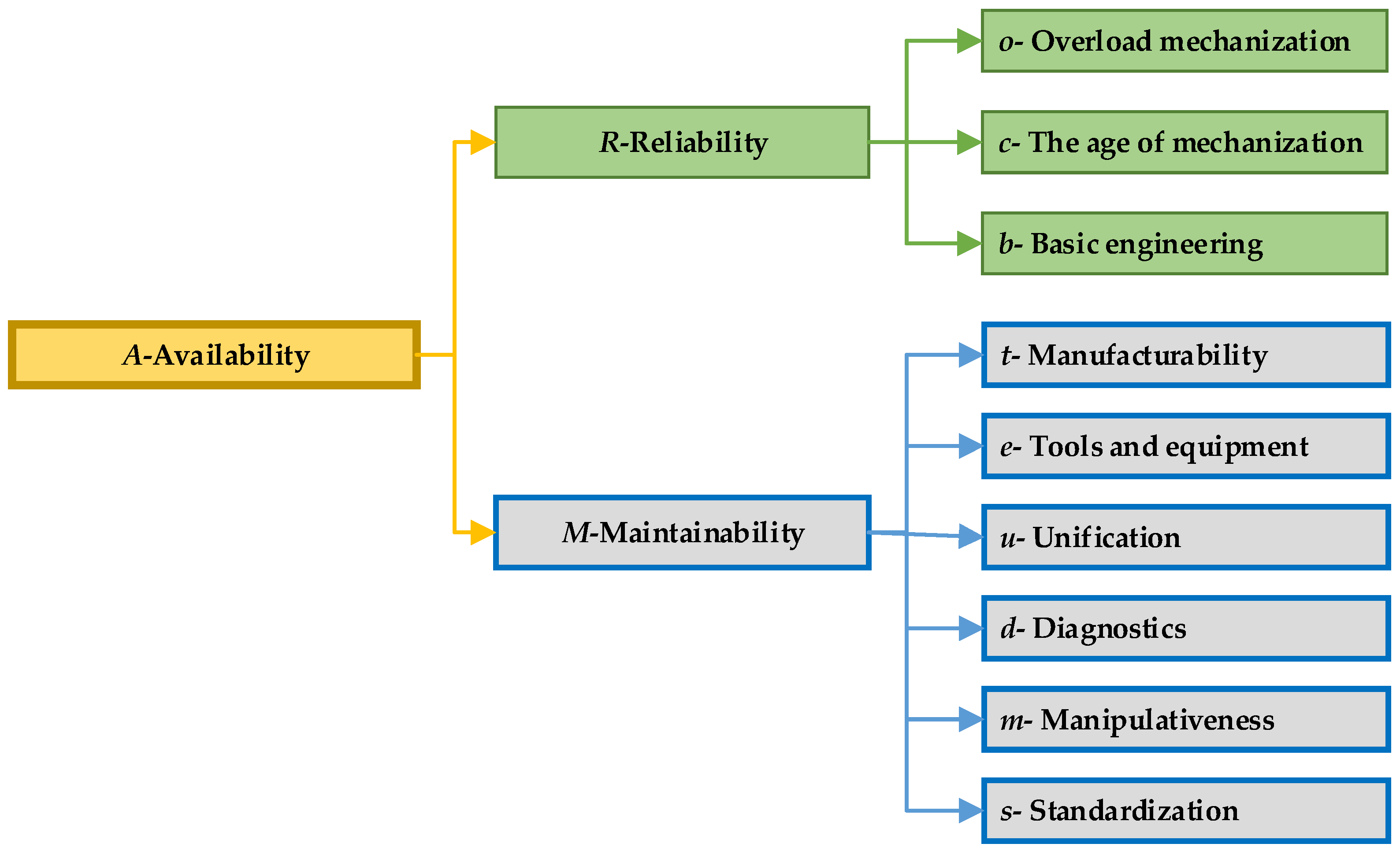
The availability as a measure of safety the system is in a function of appropriate factors, which in the literature are most often divided into two groups—partial indicators: reliability and ease of maintenance. These partial indicators, further, are a function of a number of independent parameters that are also considered as variables.
The first step in creating a fuzzy model is defining the linguistic variables that relate to the factors of partial indicators of availability, as follows:
Reliability represents the probability, at a certain level of confidence, that the system (machine) will successfully perform the function for which it is intended, without failure and within the specified performance limits, taking into account the previous time of the system use, during the specified duration of the task, when it is used in the prescribed manner and for the purpose for which it is intended, under the specified load levels [
2,
20].
Failure is a phenomenon in which the parameters of an element or system as a whole are outside the established limits. The reasons for failures include, among others, design, manufacturing, inadequate testing, human error, age, inadequate maintenance, or lack of overload protection.
Maintainability, as a set of structural characteristics that affect the time to eliminate failures or the time of performing other maintenance procedures, is an internal property of the observed technical system: therefore, it is called the structural ease of maintenance or repairability. The constructive maintainability is influenced by the following parameters:
—technology,
—tools and equipment,
—unification,
—diagnostics,
—manipulativeness,
—standardization [
21].
The technology of the maintenance technical system represents the accessibility of the maintenance places, and it also represents the complexity degree of disassembly or assembly operations. Tools and equipment are important parameters of the maintenance quality. A high degree of standardization and unification increases availability. Shortening the duration of maintenance activities is achieved through adequate diagnostics—identification and location of the resulting failure. Manipulability refers to the constructional characteristics of the technical system that enable its transportation and transfer from the place of work to the place of maintenance.
Figure 6 shows presentation of the partial availability indicators.
Regarding the number of linguistic variables, it can be concluded that seven is the maximum number of rationally recognizable variables that a person (expert) can simultaneously consider (identify) [
22].
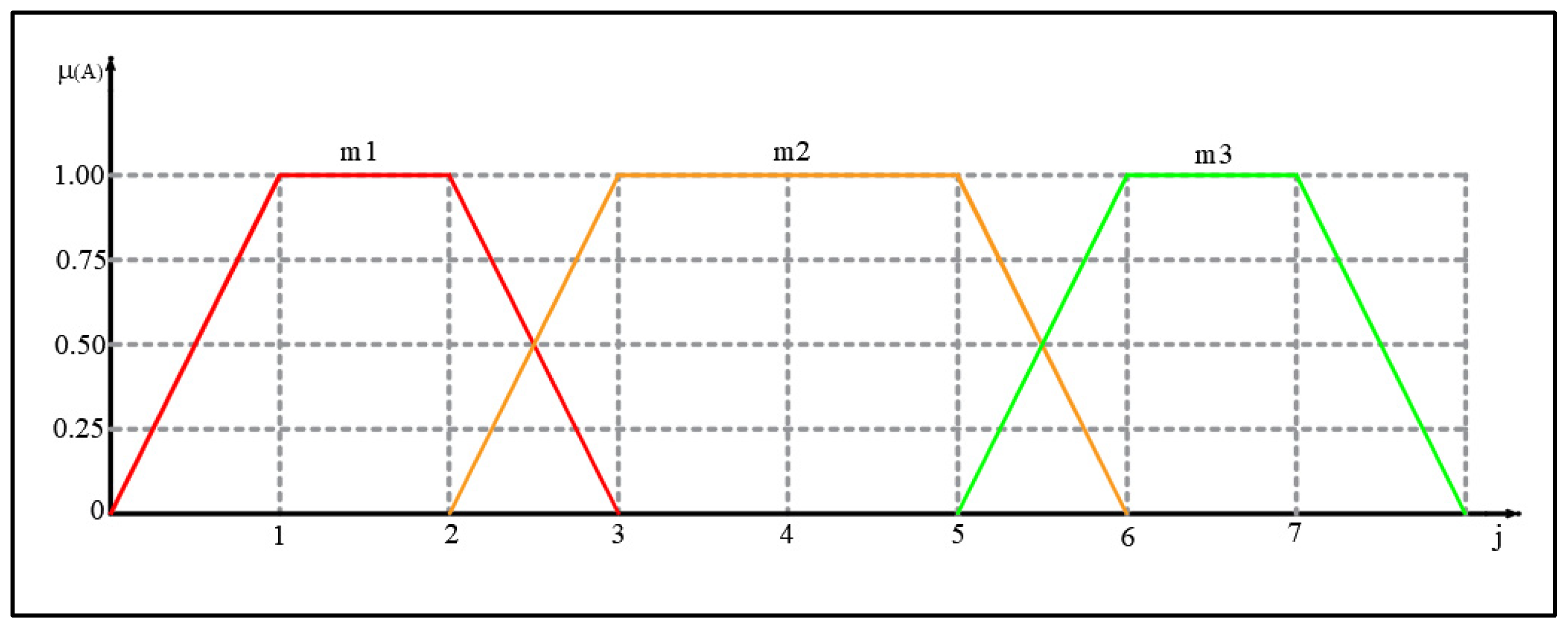
Accordingly, in this paper, four types of evaluations were considered in this work. Each of them is listed below.
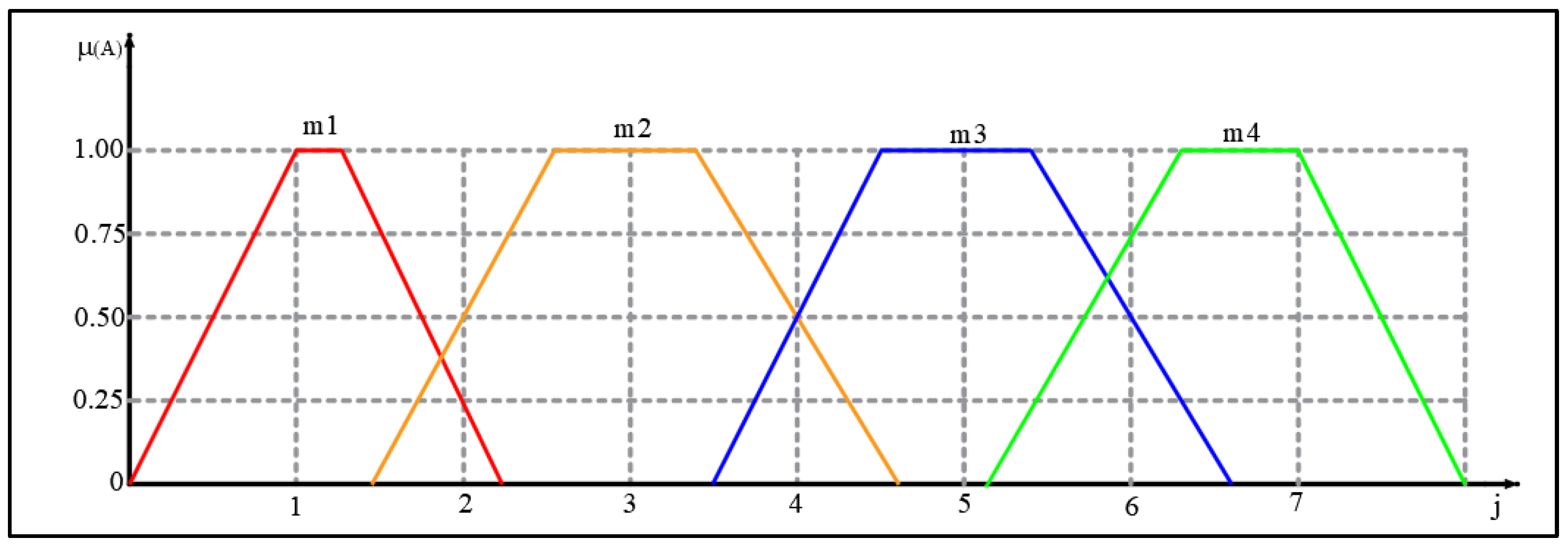
The first type of assessment that is used for the parameters of reliability, maintainability, overload, and availability
/
contains four linguistic variables defined as follows. The conditions of the working environment are such that unreliable/poor maintenance convenience/the engaged equipment is mostly not fulfilled/unavailable (mark m1). Low reliability/low convenience of maintenance/the technical characteristics of the equipment are mostly corresponding to the conditions of the working environment/low availability (mark m2); medium reliability/medium convenience of maintenance/the technical characteristics correspond to the conditions of the working environment/medium availability (mark m3); and high reliability/high convenience of maintenance/the technical characteristics of the equipment significantly exceed the requirements of the working environment/high availability (mark m4). Linguistic variables (ratings) are presented in
Figure 7.
The corresponding phase numbers of the mentioned linguistic variables are defined by (according to
Figure 7):
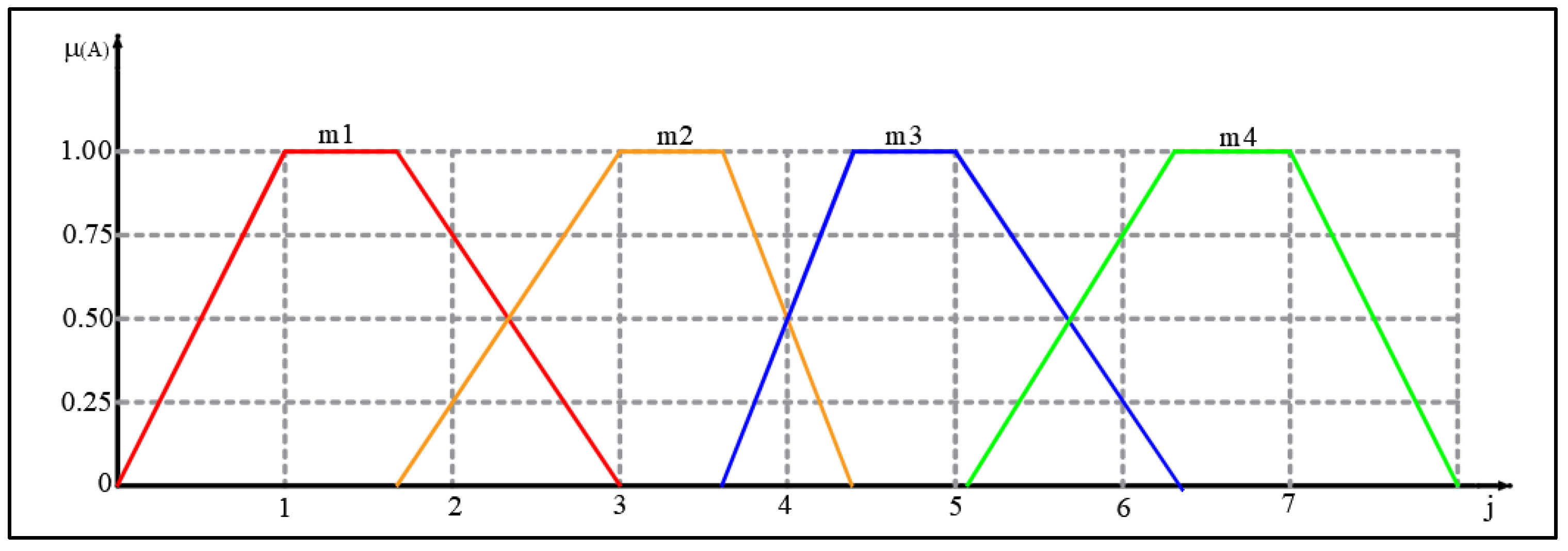
The second type of assessment that is used for the parameters // (technological/manipulative/standardization), contains four linguistic variables, defined as follows:
Technology and manipulativeness—poor (mark m1), sufficient (mark m2), good (mark m3), excellent (mark m4);
Standardization—no standardization (mark m1), partially present standardization (mark m2), present standardization (mark m3), complete standardization (mark m4). Linguistic variables (ratings) are presented in
Figure 8.
The corresponding fuzzy numbers of the mentioned linguistic variables are defined by (according to
Figure 8):
The third type of assessment, which is used for the parameters / (diagnostics, unification), contains four linguistic variables, defined as follows:
Diagnostics—no diagnostics (mark m1), limited diagnostics (mark m2), well-developed diagnostics (mark m3), excellently developed diagnostics (mark m4);
Unification—no unification (mark m1), little unification present (mark m2), mostly present unification (mark m3), complete unification (mark m4). Linguistic variables (ratings) are presented in
Figure 9.
The corresponding fuzzy numbers of the mentioned linguistic variables are defined by (according to
Figure 9):
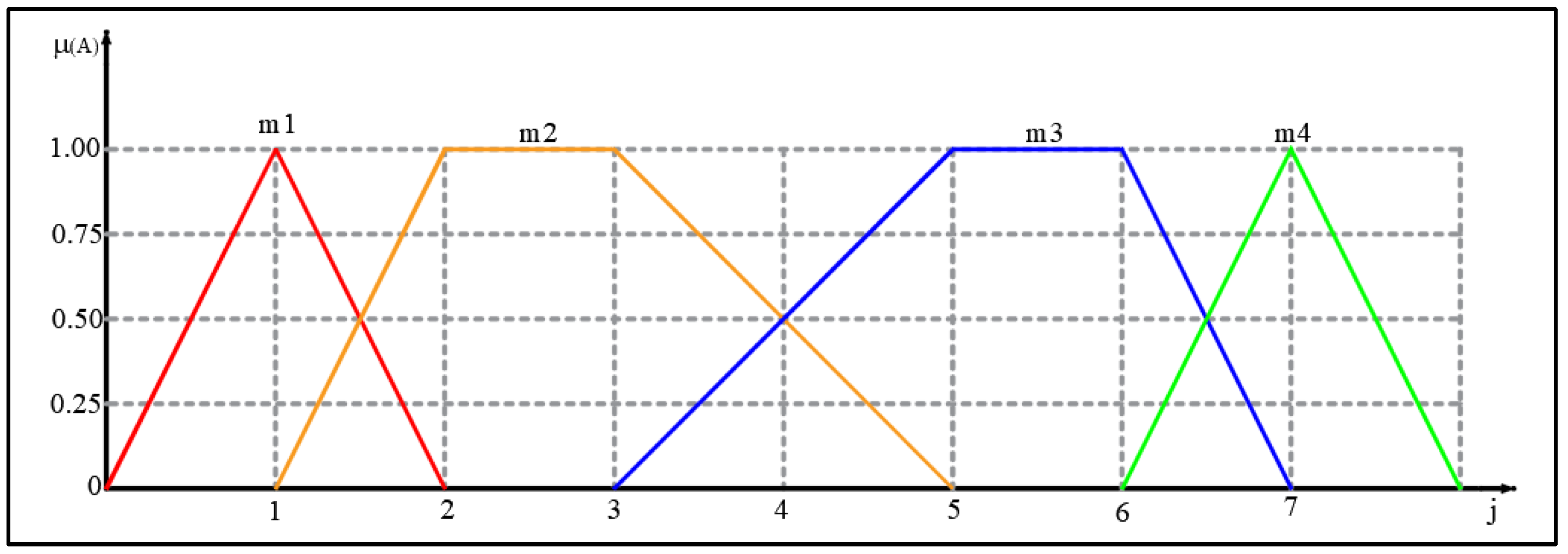
The fourth type of assessment that is used for the parameter
(tools and equipment), partial indicator
(age of machinery), and
-basic engineering contains three linguistic variables defined as follows: undeveloped equipment/machine at the end of its life/undeveloped basic engineering (mark m1), medium equipment/machine in the exploitation phase/medium basic engineering (mark m2), and good equipment/new machine (mechanization)/good basic engineering (mark m3). Linguistic variables (ratings) are presented in
Figure 10.
The corresponding fuzzy numbers of the mentioned linguistic variables are defined by (according to
Figure 10):
Trapezoid fuzzy sets were used for phenomena that are not clearly defined (e.g., medium basic engineering) and which are linguistically more uncertain, while triangular fuzzy sets were used for clearly defined phenomena (e.g., no unification).
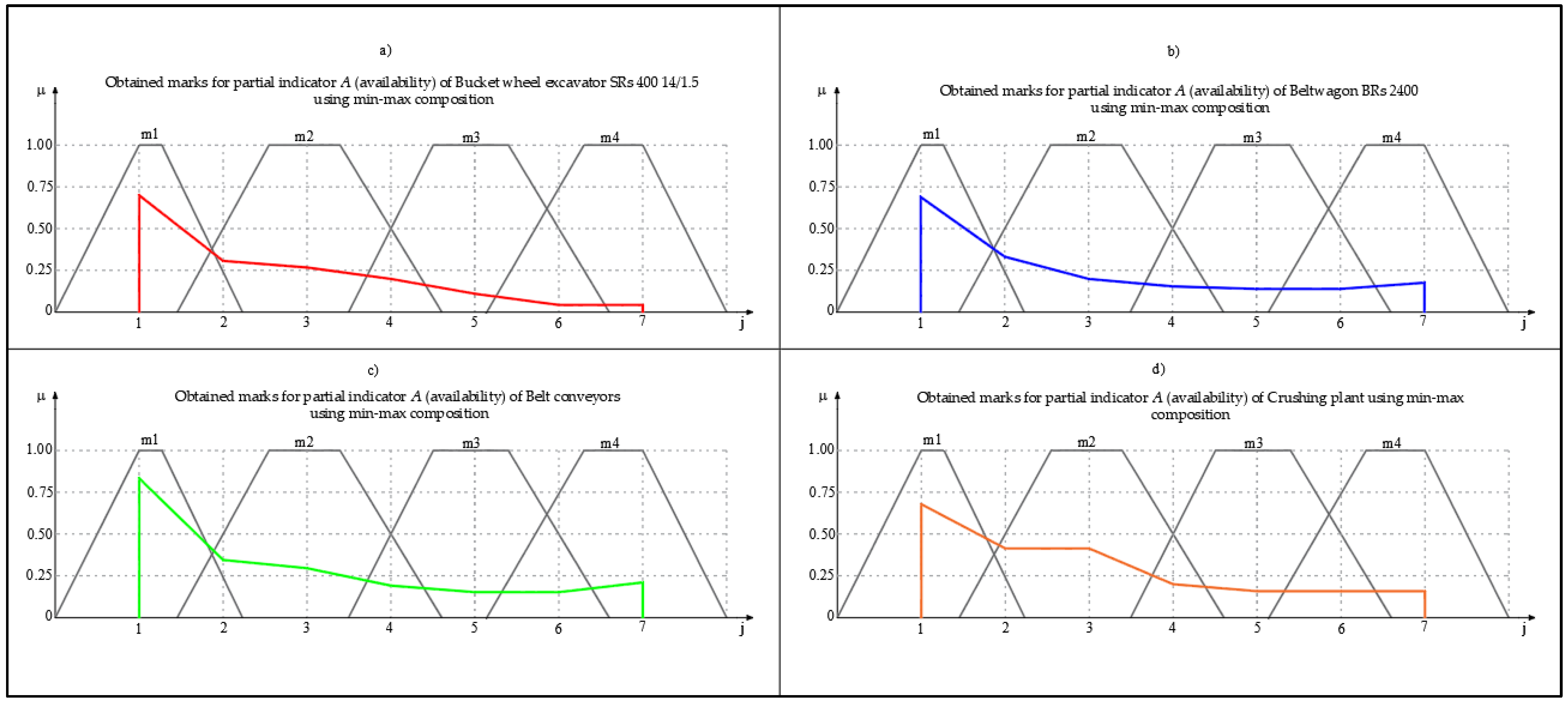
The partial indicators , , and more closely determine the partial indicator —reliability, while the partial indicators , , , , , and more closely determine the partial indicator —convenience of maintenance. The following shows how availability is determined based on the reliability indicators and maintenance convenience .
The idea of this work was to obtain a more accurate assessment of the availability of continuous systems at the open pit Drmno. Let the partial indicators
,
be shown in the form of the following fuzzy numbers:
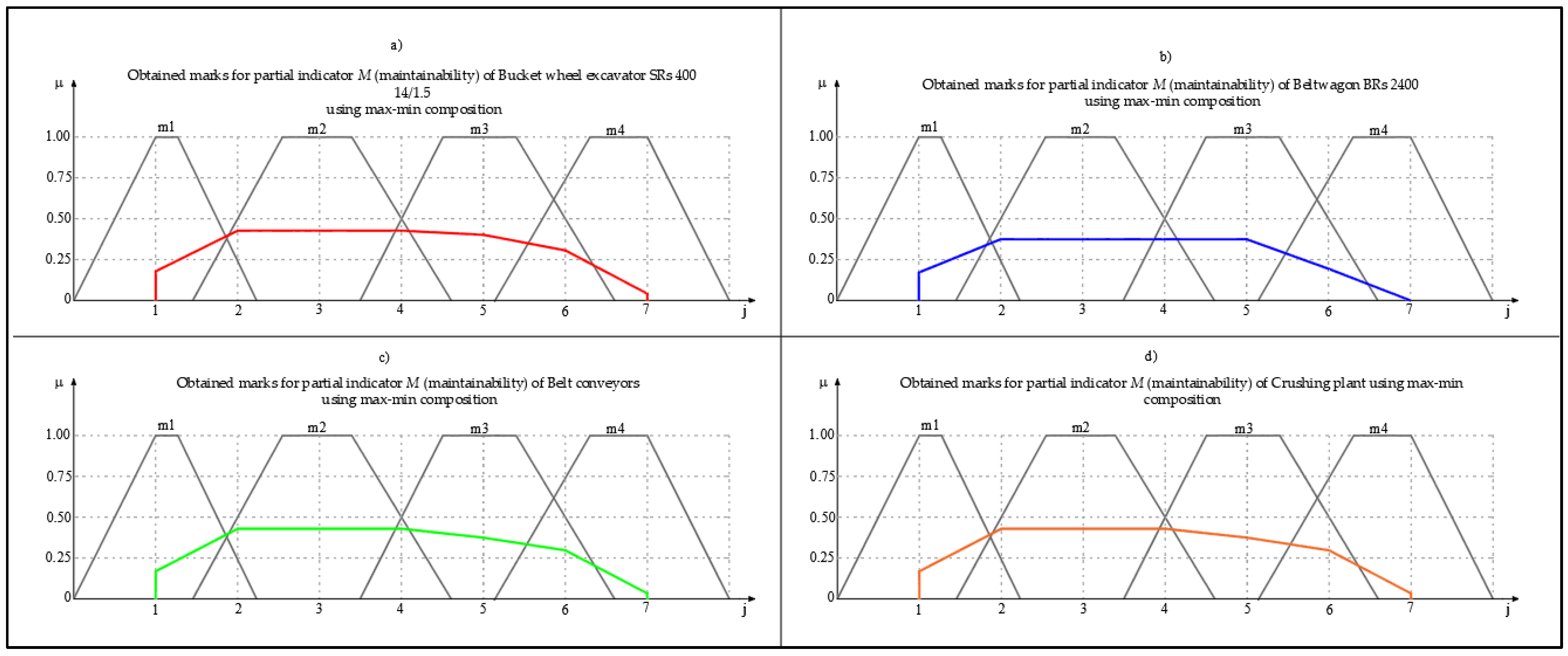
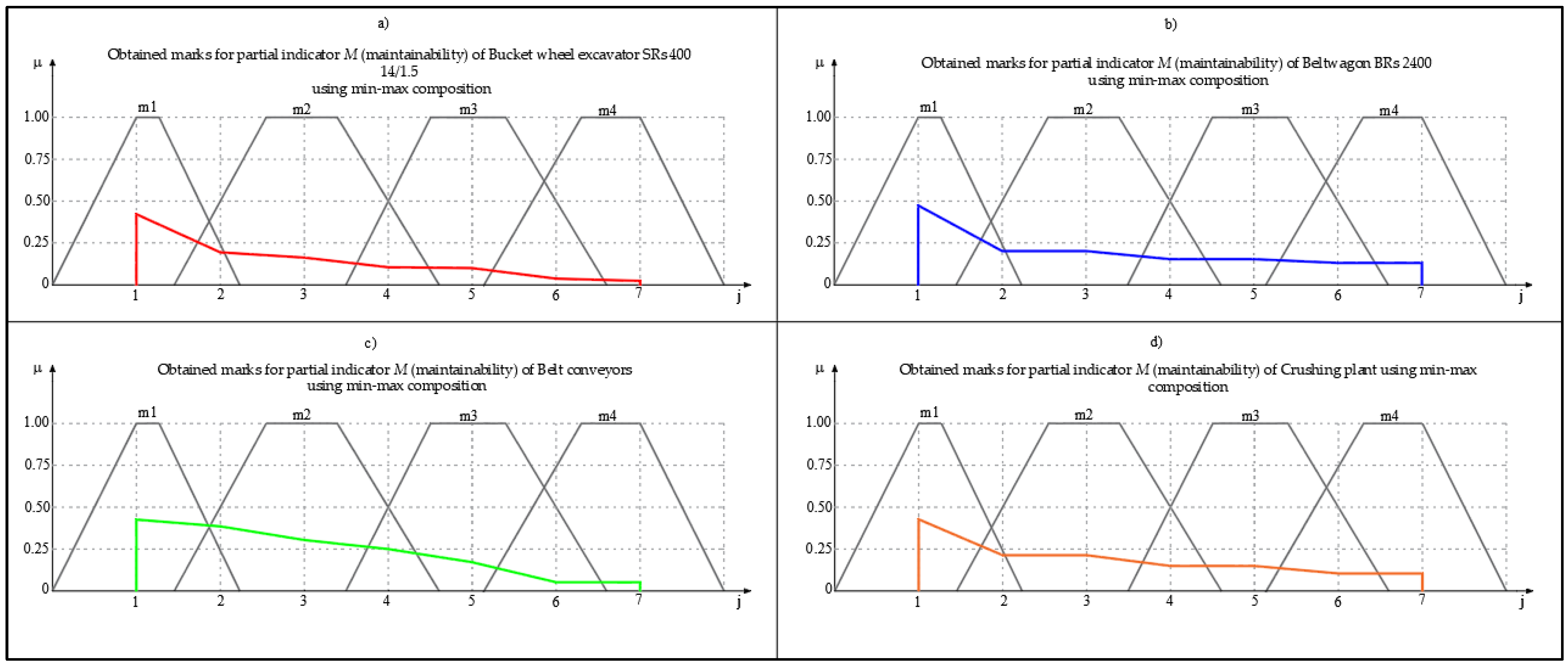
In the next step, the max–min and min–max compositions were performed on them. The max–min composition is also called the pessimistic composition, and is often used in the algebra phase as a synthesis model (for more information see [
22,
23,
24]) while the min–max composition is also called the optimistic composition.
If the partial indicators
,
are observed, it is possible to make
combinations of the appropriate membership functions, which will be further denoted by:
Each of these combinations represents one possible estimate of availability, and the following two values can be associated with it:
and,
It is clear that
takes values from the set {1,2,3,4,5,6,7}, and each of the mentioned values can be associated with the number
which represents the maximum value
of all those combinations for which
is equal to l, for
l ∈ {1,2,3,4,5,6,7}, that is:
In this way, the rating is obtained for the
availability:
Using the best fit method (for more information see [
16]) to transform the obtained rating into belonging to the fuzzy set, determined by (2), the distance is used that is defined by:
For
. Small values of
indicate proximity to the linguistic variable
. Accordingly, let
be the minimum value of the obtained distances
, then the normalized reciprocal values of relative distances can be associated to each of them, determined by:
and present belonging to the appropriate rating:
In the end, the corresponding linguistic rating is obtained as follows:
In a similar way, from the linguistic variables , , , , , , a rating for convenience of maintenance was obtained from the linguistic variables , , , , , which were later used to determine the availability of .
Figure 11 shows the fuzzy model algorithm for the availability assessment. In the first step in
Figure 11, the experts were given a questionnaire, based on which they had to give an expert opinion on different types of indicators. The next step involves the statistical processing of the obtained grades, as a necessary step that precedes the process of fuzzification. The fuzzy proposal represents the first segment of artificial intelligence (AI) in which each indicator is assigned a corresponding fuzzy number. In the next step, using fuzzy compositions (max–min and min–max), fuzzy numbers were defined for those indicators that were included in the final model and which depend on the indicators submitted in the questionnaire. After obtaining the grades, using adequate methods (best fit method), the obtained grade was identified.