1. Introduction
The first appearance of the Jiles–Atherton hysteresis loop model (J–A model) was in 1984 [
1], when the two researchers (D.C. Jiles and D.L. Atherton) introduced a physically based mathematical model that would accurately represent the hysteresis loop of magnetic material. The goal was to establish a general form of the hysteresis loop model, which would describe ferromagnetic material behavior with simple set of equations with a low number of parameters. The model equations are derived based on physical background of domain magnetization, domain-wall movements and rigid domain rotations. Later on, in [
2] (1986), the same authors improved the model by introducing flexible domain wall movement and, consequently, reversible and irreversible magnetization. This modified model was extensively described in the texts [
3,
4] and further improved on in [
5] by involving frequency-dependent hysteresis loops describing the electric conductivity of ferromagnetic materials.
The developed hysteresis loop model in [
2] is computationally inexpensive, due to its low number of variables and use of only one trigonometric function. On the other hand, obtaining the optimal values of the variables is not a straightforward task. Jiles, back in 1989 [
6] and 1992 [
4], wrote down instructions and advice to obtain the values of variables from the measured hysteresis loops. In the last two decades, different optimization techniques (i.e., generic algorithm, particle swarm optimization, etc.) were used to obtain model variable values more accurately [
7,
8,
9,
10,
11].
Further, with software technology improvement and expansion of the computational hardware resources, the use of the J–A model has been extended into real-time applications [
12,
13]. More accurate magnetic state predictions in real-time applications within electromagnetic models is one of the largest reasons why the number of research works based on the Jiles–Atherton model has significantly increased in last period.
Knowing the behavior of magnetic fields inside nonlinear ferromagnetic structures, such as, for example, electric machines and transformers, is very important for their performance calculation and iron loss assessment. The involvement of finite element-based design of electromagnetic structures gives us the possibility to predict their characteristics accordingly to the accurately described electromagnetic hysteresis states in nonlinear ferromagnetic material. Expertise on the nonlinear hysteretic behavior of magnetic fields can be further used in real-time models or in very fast non-real time applications (i.e., hardware in the loop), providing a large benefit in comparison to models describing only non-hysteresis nonlinear material presentation in the form of a magnetizing B–H curve. The values of hysteresis losses and, further on, overall iron losses (including eddy current and excessive losses) obtained by the hysteresis loop model are one of the most important results when developing and optimizing electromagnetic structures.
It was quite soon discovered that the basic Jiles–Atherton model [
2] with its variables having constant values is not accurate enough to cover all possible states of ferromagnetic material (i.e., minor loops, different amplitudes of external magnetic field strength excitation, etc.) with only one set of variables values. In addition, by using the basic hysteresis loop model [
2] and constant values of variables, the possibilities of an unphysical response of magnetic flux density
B over magnetic field strength
H in minor loops are highly common. The most widely known unphysical behavior is the response of magnetic flux density
B at the turning point of magnetic field strength
H (when
H is starting to decrease,
B is trending to unphysically increase), as well as the unclosed minor loops.
A number of research works introduce and apply different approaches to the basic Jiles–Atherton model to overcome the model’s unphysical behavior or to increase the accuracy of the model.
One of the first works to solve the model’s non-physical hysteresis loop response was made by Carpenter [
14]. The work describes how to use the major hysteresis loop solution to calculate the response for minor loops (i.e., loops that turn before reaching their saturation point). Carpenter introduced a scaling factor, making the saturation value of the minor loop the same as in the major hysteresis loop. The factor value is calculated at each loop’s turning point. The references of this work point to [
1,
2].
In the work by D. Lederer [
15], the authors try to overcome the model’s unphysical behavior by having non-closed minor loops. The approach is similar to Carpenter’s (using the scaling process of the magnetization), but with an additional predefined array of scaling factors as a function of the applied magnetic field strength amplitude value. Such an array improves the unphysical behavior of the model and provides that the minor loops are closed. The references used in this work are the basic Jiles–Atherton works [
2,
4].
The work [
16] represents the accuracy increase in the modeled minor loops by introducing a variable pinning parameter depending on the amplitude of the temporarily minor loop magnetization level. This work also refers to [
2,
4].
In [
8], a domain flexing function was introduced to increase the J–A model accuracy towards B–H loops measurements. The biggest drawback is that the introduced function depends on a predefined maximum level of applied magnetic field strength. The references in this work are [
3,
4], which are also the subject of this research work.
Further on, the authors in [
17] developed an anhysteretic magnetization equation based on the Cauchy–Lorentz distribution that better represents the energy states of magnetic moments in soft magnetic composite materials (SMC). In this work, [
2,
3] are referenced and represent the basics of the Jiles–Atherton hysteresis loop modeling approach.
The minimization of the non-closed minor loops problem was reviewed again by the Leite et al. [
18], who introduced a new variable associated with the reversible component of magnetization that limits the high-variation rate of the irreversible magnetization. The closing of the minor hysteresis loop is not mathematically provable, but is rather a tendency of the solution gained by the hysteresis model differential equation. The work also refers to the basic J–A hysteresis model [
2].
In the [
19], the energy balance equation of the basic Jiles–Atherton model was reconsidered. The main difference is in the description of the energy equation. Jiles and Atherton said that energy input into the loss sample is equal to the energy stored in the lossless sample and the losses in the same sample. On the other hand, in [
19], the energy delivered into the loss sample is equal to the energy stored in the loss sample and the losses in this sample. References in [
19] also include the works [
1,
2,
3,
4].
As can be seen from the short literature overview, one or more works [
1,
2,
3,
4] are always the origin of upgrades to the Jiles–Atherton model. Later in this work, we show that, without modifications of the latest mentioned works, these models don not provide a unique solution. Therefore, the works [
8,
14,
15,
16,
17,
18,
19] may not be directly comparable between themselves. As a result of this paper, a harmonized model will be proposed and the resulting J–A hysteresis model equations will be shown for better comparison between the works done worldwide.
At the beginning of this study, the set of equations forming the basic hysteresis loop model [
2] was used in the optimization procedure with the goal of calculating the values of model variables that would correctly describe the measured DC hysteresis loop. These hysteresis loops were further compared with the DC hysteresis loop model from Jiles’ later work [
5]. It was found out that both models [
2,
5] did not provide the same results, even though [
5] directly references [
2]. In addition, different notation in [
5] in comparison to [
2] was noticed while describing the same physical properties. Founded on these discrepancies, the study was extended to the Jiles’ articles [
2,
3,
4,
5,
7], which include explanations regarding the hysteresis model derivation and description of the model variables’ physical meaning. Furthermore, the work from author Ruoyang [
7] was included in the research by addressing his claim that less assumptions are made in comparison to the Jiles–Atherton model [
2,
3,
4,
5,
7] equations (i.e., model variable
c is not set to zero in the middle of the model derivation; this fact will be explained more in-depth in the following sections of the paper).
One of the conclusions of this study are findings about differences of the results as outcomes of [
2,
3,
4,
5,
7]. Knowing that all of the J–A model research, whether modified or used in applications, originate from [
2,
3,
4,
5,
7] (directly or indirectly), the comparison of these different works may not give us the desired view of the quality work done worldwide by J–A model researchers.
Within this paper, the derivation steps for models [
2,
3,
4,
5] are presented and a comparison between different solutions is made by graphical presentations of hysteresis loops and by the value of the corresponding hysteresis loss density as joules per unit volume. The models’ derivations are presented in detail and their comparisons are the base for the harmonization of the Jiles–Atherton models developed within [
2,
3,
4,
5,
7]. All these steps are lead to one goal: that all newly works can have a common J–A model and the common one and the new ones will become more comparable.
Based on the measured data and particle swarm optimization procedure, the variables values of the harmonized J–A model were calculated and presented. The measured data in the form of DC (static) hysteresis loops were obtained by magnetic measurement equipment (Remagraph RE3) [
20].
2. The Basic Model
As the starting point, the basic J–A model [
2] was taken into account. Within this section, the explanation of basic physical processes based on domain theory will be given and presented in the form of equations. The following description is a short summary of [
2] and it goes to a level such that the reader can understand the model’s concept. The reader can find more in depth theoretical explanations in [
2,
3].
The J–A model development is based on the energy balance equation and for that purpose, the energy per unit volume
E of a typical magnetic domain with magnetic moment
m per unit volume is applied in (1) [
2]. The coupling between the domains in ferromagnetic material is represented by the non-dimensional parameter
α (mean field parameter representing inter-domain coupling [
2]) linked with the bulk magnetization
M. The effective magnetic field strength (
He) is then expressed in (2) and is analogous to the Weiss mean field experienced by the individual magnetic moment within a ferromagnetic domain [
2]. The energy per unit volume of the domain with magnetic moment
m is now affected by the effective magnetic field strength (3).
Effective magnetic flux density
Be is defined as:
The anhysteretic magnetization
Man as a function of effective magnetic field strength
He is introduced by Equation (5) and is in the form of a Langevin function, where saturation magnetization is presented by
Ms, and
a is the variable with dimensions of magnetic field strength that form the shape of anhysteretic magnetization in an acceptable way [
2]:
If the ferromagnetic material were = ideal (e.g., lossless), the magnetization energy added to the material would be the same as the energy of the anhysteretic magnetization [
2].
Further on, the authors introduce the fact that irreversible changes in magnetization are present during domain-wall displacement and are described with the pinning process. By applying statistical method and energy management approach it was established that pinning energy
Epin can be written as:
where
k represents the pinning factor variable.
The hysteresis losses are defined as a consequence of the pinning sites and they are presented in energy balance Equation (7). The left hand-side of Equation (7) describes the magnetization energy supplied to the material, the first element on the right hand-side of (7) represents anhysteretic magnetization energy (e.g., the energy which would be obtained in the lossless case), and the second element on right side of Equation (7) denotes the hysteresis losses.
Differentiating Equation (7) with respect to
Be gives the solution (8) describing the magnetization processes. The variable
δ was introduced [
2] to guarantee that the pinning sites face the changes in magnetization
M, meaning that variable
δ has the value +1 when
H increases (
dH/dt > 0) and has the value −1 when
H decreases (
dH/dt < 0).
The hysteresis loop can be represented with
B as a function of
H (9):
or with
M against
H [
2] where the dependence of
M over
H is represented in differential form (10), with the aim that both relationships contain the same information.
Jiles and Atherton used an additional assumption [
2] that the domain wall should be flexible and as such, the wall between two pinning sites can be bent without being completely unattached. This means that if external magnetic field strength is at certain moment removed, the bent wall is relaxed and, therefore, the energy process is reversible (the process without losses). In that case, the amount of magnetization energy added to the sample is the same as energy of the anhysteretic magnetization:
According to the flexible domain wall movement, the total magnetization
M of the material sample was separated into the sum of reversible
Mrev and irreversible
Mirr magnetization (12).
As for the pinning energy, the physics background was introduced and described for reversible magnetization in [
2], where the domain-wall bending is represented with the geometric form of an arc. Using the energy balance among the magneto-static energy and the energy based on pressure change between domain walls, we obtain the change of the volume of the domain. Further on, this change is shown via a change in the reversible magnetization
Mrev:
where
c is the coefficient of proportionality [
2].
The irreversible component of magnetization
Mirr is given by the solution of (10):
Based on Equations (12) and (13), the Equations (15) and (16) are derived:
By summing the Equations (14)–(16), the final form of the J–A hysteresis model was proposed in [
2] as:
All the fundamental Equations (2), (5), (8), (12), (13) and the final differential Equation (17) of the J–A hysteresis model [
2] are gathered together in
Table 1. This will facilitate further comparison between equations representing the basic hysteresis models referenced to the [
2] and used by both different [
7] and the same [
3,
4,
5] authors.
3. Differences in the Articles
In the
Section 3, the model equations from the works [
3,
4,
5,
7] are extracted exactly as they were presented in articles. This was mainly done to further simplify the comparison between models derived in [
3,
4,
5,
7]. It has to be pointed out that the articles [
3,
4,
5,
7] all originate from the first article derived by Jiles and Atherton [
2].
In all articles, Equations (2), (5) and (12) (
Table 1) are equal; meanwhile for the other Equations (8), (13) and (17) (
Table 1), separate tables (
Table 2,
Table 3 and
Table 4) were prepared for better presentation of their differences.
All the hysteresis loop models from the analyzed literature [
2,
3,
4,
5,
7] presented in
Table 4 were programed using the MATLAB environment. The values of the variables used for the J–A model in [
2], described in
Section 2, were selected from the example presented in [
2]; they are shown in
Table 5, column Case 1. The same model variable values were applied to all other studied models [
3,
4,
5,
7] and the results in form of hysteresis loops are shown in
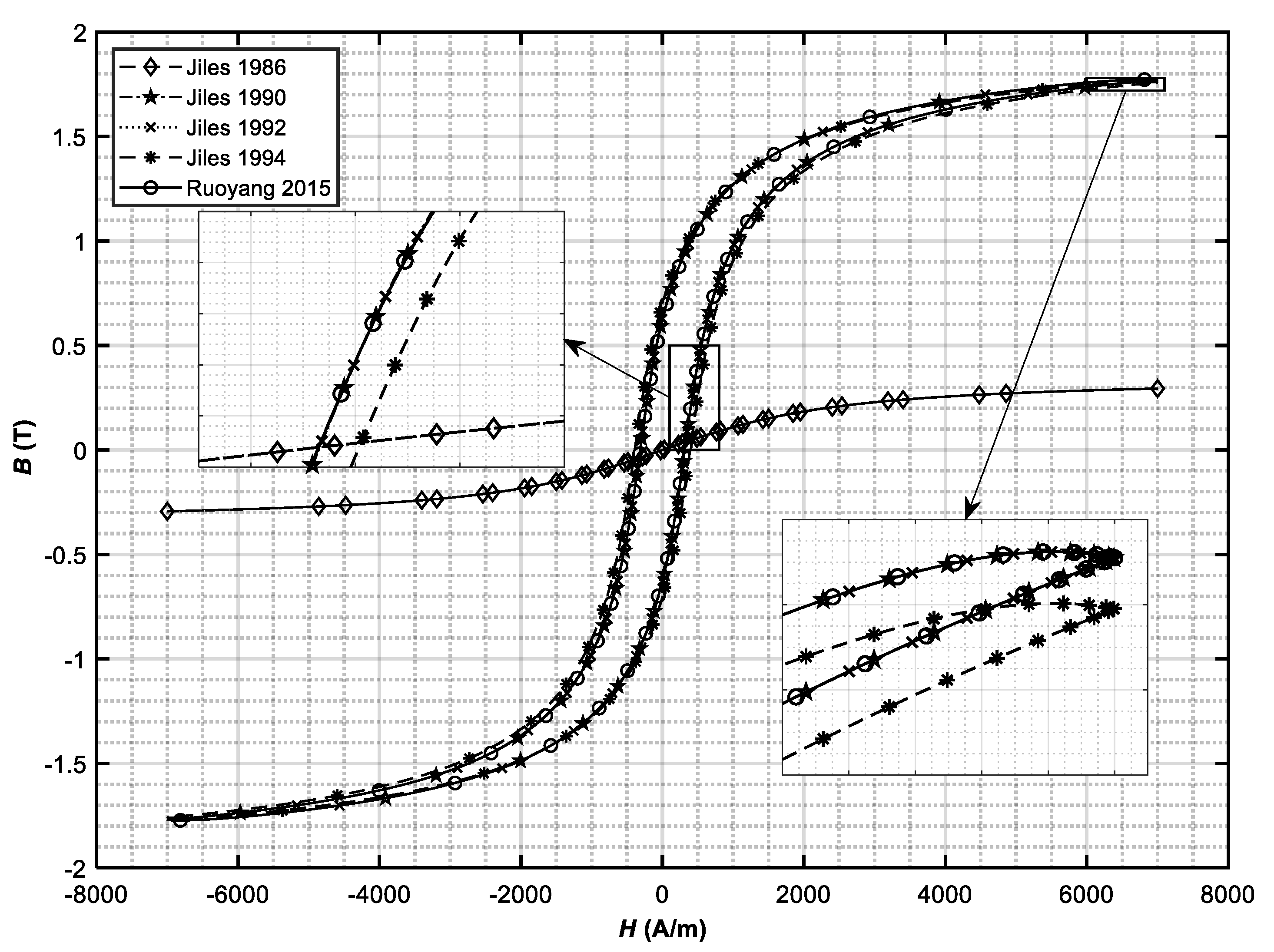
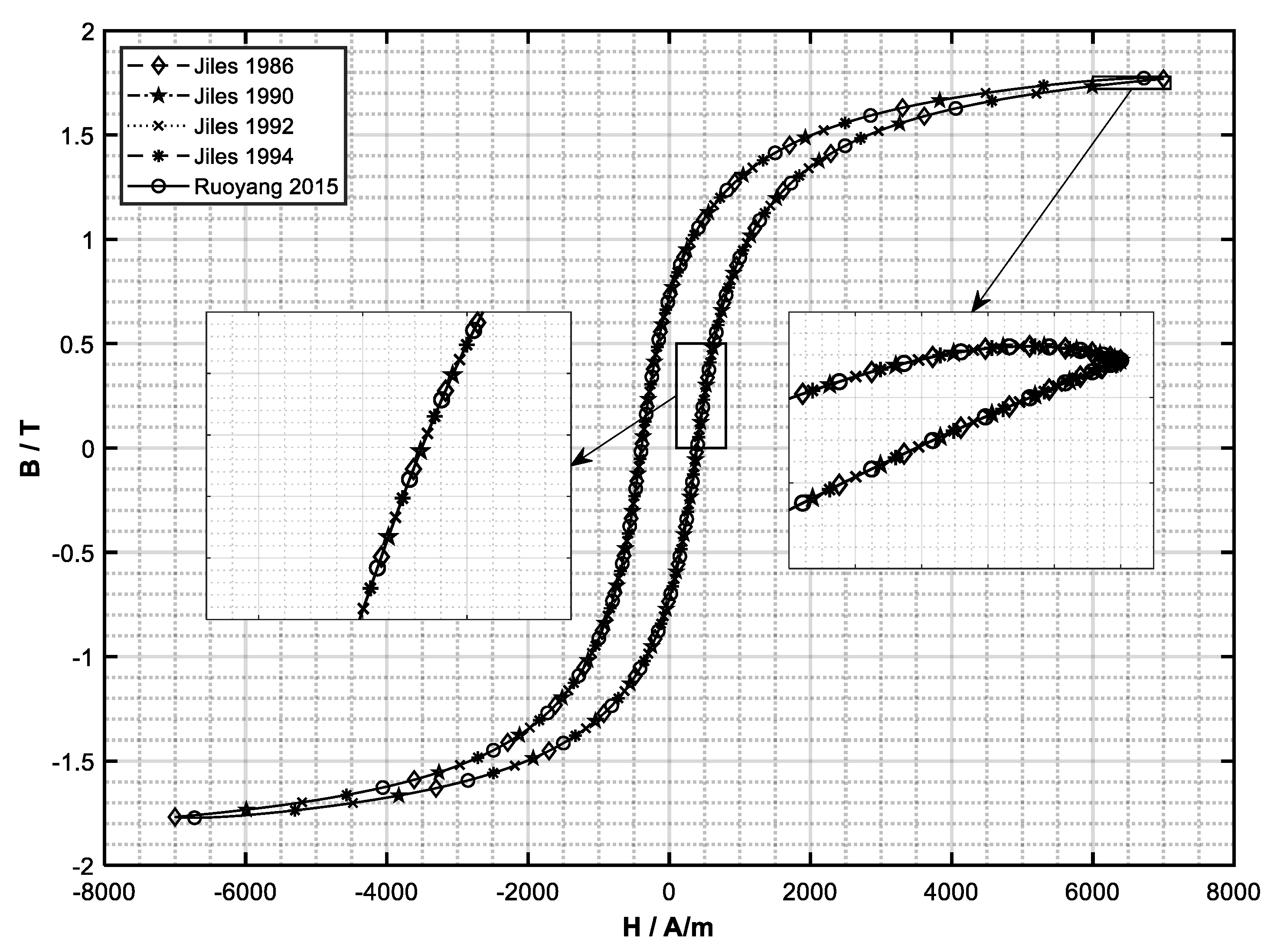
Figure 1. The difference between the J–A model from [
2] and all other works is obvious. According to the hysteresis loop presented in [
2] (Figure 12 in [
2]) and calculated by using the corresponding values of model variables (
Table 5, column Case 1), either there is a typo or the equation of pinning energy (6) was changed, in the same way as was done in [
3] and here is presented with Equation (26):
To make the J–A model from [
2] more comparable with other analyzed models [
3,
4,
5,
7], the original variable
k in [
2] was multiplied by the permeability of vacuum (
) and as such (27) is used in the corresponding J–A model [
2]. A new parameter
knew is introduced (27) and further used in the modified form of the J–A model (28) to keep the same equation topology (17) as in the original article [
2]. The new forms of hysteresis loops (
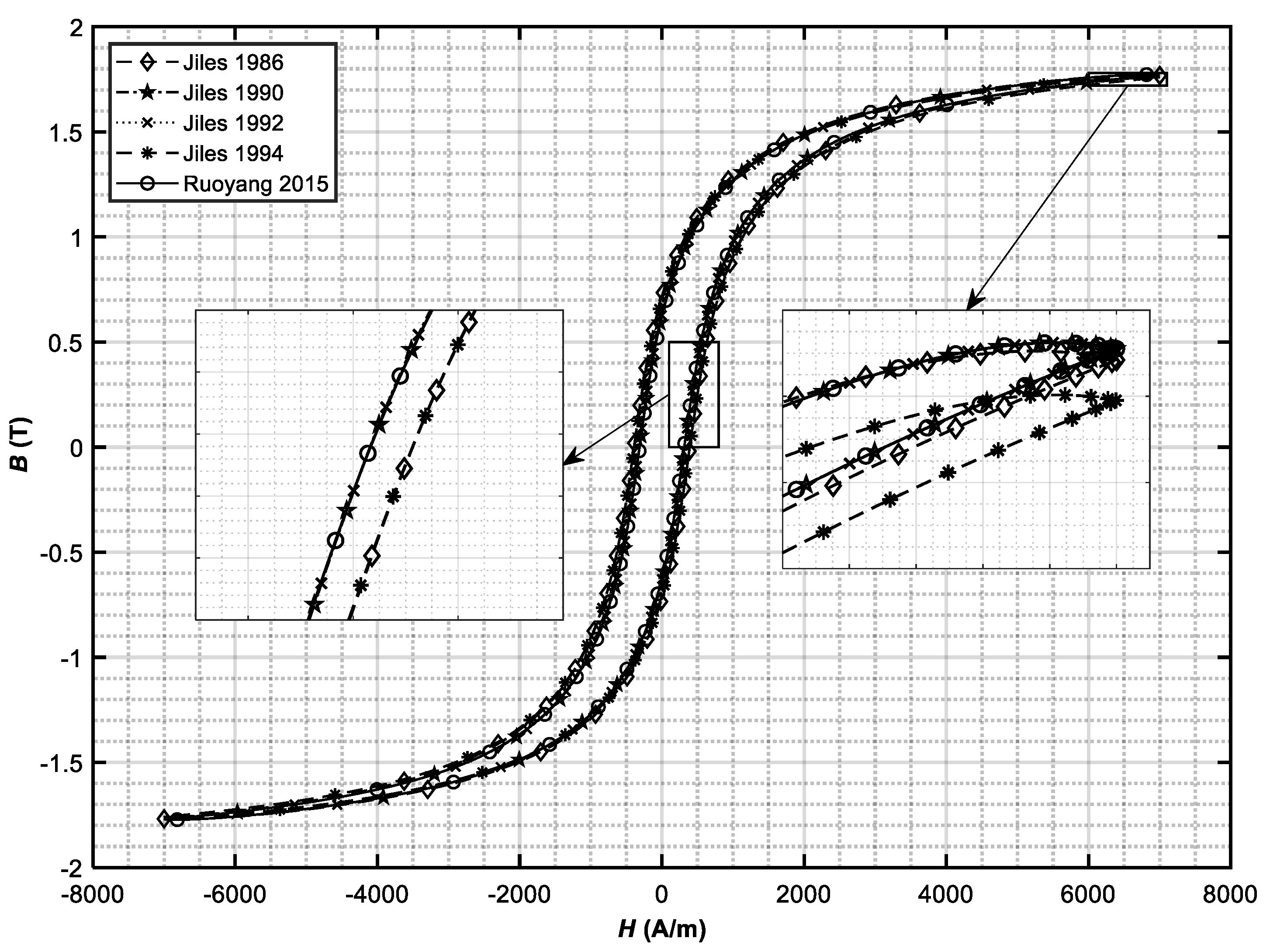
Figure 2) were calculated after application of the latest change (28).
From the
Table 2, it can be deduced that the equations describing the magnetization process are the most managed by the corresponding authors when forming hysteresis loop models. Consequently, the equations in
Table 4 representing the final form of hysteresis loop equations are different. We can observe that the variable
c has the significant influence (with its value and in creation of difference in hysteresis loops between models) (
Table 4) on the formation of the final hysteresis loop.
To expand the analysis, the second case (Case 2,
Table 5) was added beside the Case 1 presented in
Table 5 (values are the same as in [
2]). The values of parameters for both cases are shown in
Table 5. It must be pointed out that the changes to model variable
k (into
knew) for [
2] are already included in (27) and (28). The results are shown in
Figure 2 for Case 1 and in
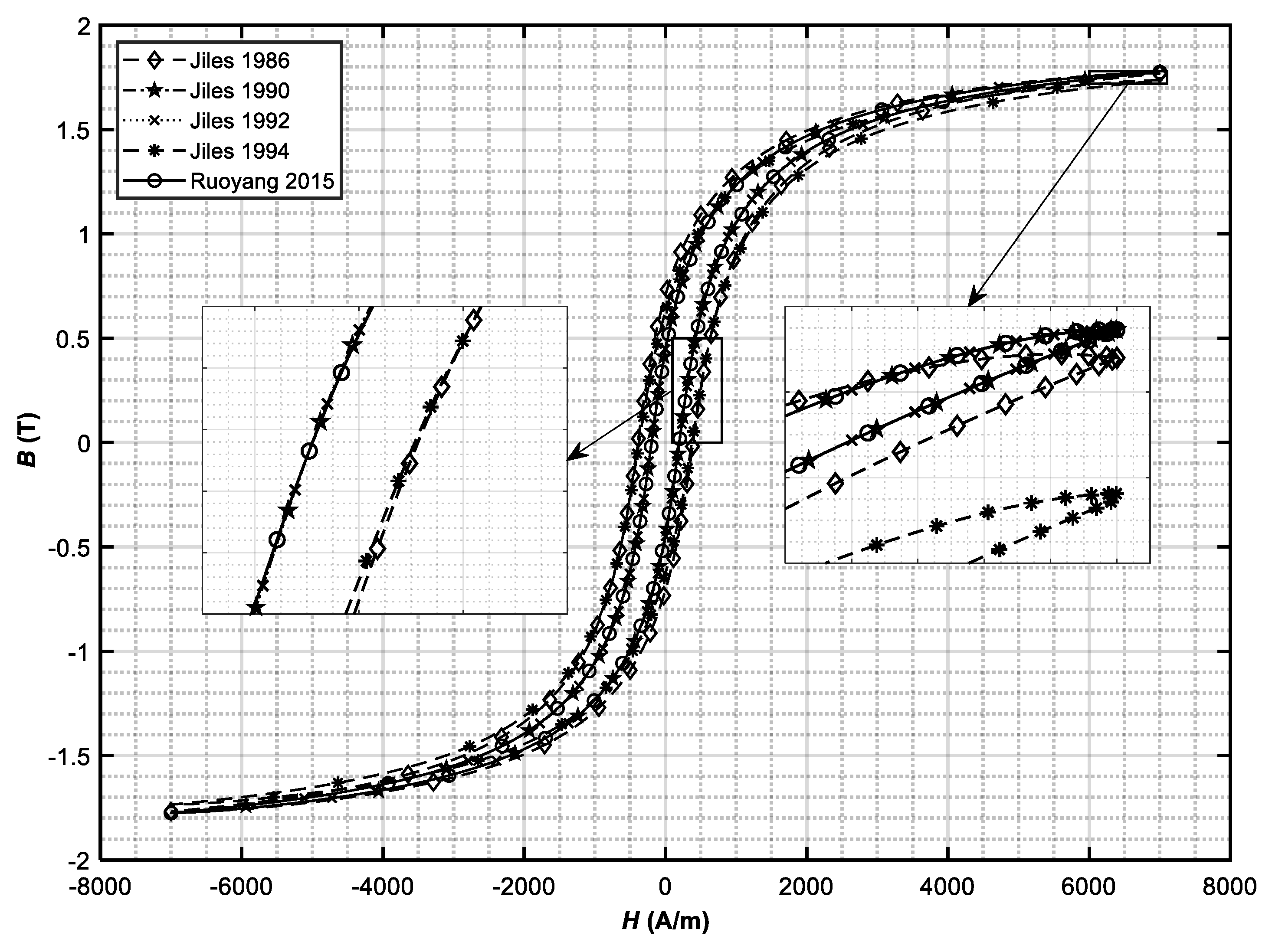
Figure 3 for Case 2.
From
Figure 2 and
Figure 3, it can be concluded that, although each reference directly cites the previously published one (from [
5] backwards to [
2]) and that all of them use “the same” J–A hysteresis model, the results are quite different between the applied models. Ref. [
7] is the only analyzed work where differences should occur, as it was already claimed by the author. The reason why the differences between hysteresis loops (
Figure 2 and
Figure 3) exist will be described further on in
Section 5. Besides the figures, the numerical representation of hysteresis losses will be introduced for additional assessment of the model differences.
4. Hysteresis Losses
One of the most important quantities from the J–A hysteresis model application point of view are hysteresis losses. Firstly, the energy loss equation needs to be derived for all analyzed models. The energy balance equation is introduced in [
2] and here rewritten again as (7). The second term of the right-hand side of Equation (7) is described as the energy loss due to the hysteresis loop. In this section, a common labeling for the hysteresis energy density is assigned as
whyst (29):
When all integrals in (7) are differentiated by
dBe, we obtain (30), which describes the magnetization process as already presented in the previous section (8).
In the analyzed scientific works [
2,
3,
4,
5,
7], the hysteresis loss energy density is not presented in a unique equation form. The hysteresis loss energy is described as the difference between the magnetization energy supplied to the sample and the energy that would be obtained in ideal or lossless cases. Both energies (magnetization energy and the energy in the lossless case) used in all references [
2,
3,
4,
5,
7] are described by (31) and (32), respectively. The subtraction of these two energies represents the hysteresis loss energy density (33) and will be used in the study of all models.
If Equation (33) is further differentiated over
dBe with the use of Equation (4), the differential of hysteresis loss energy density as a function of effective magnetic field strength
He can be introduced (34).
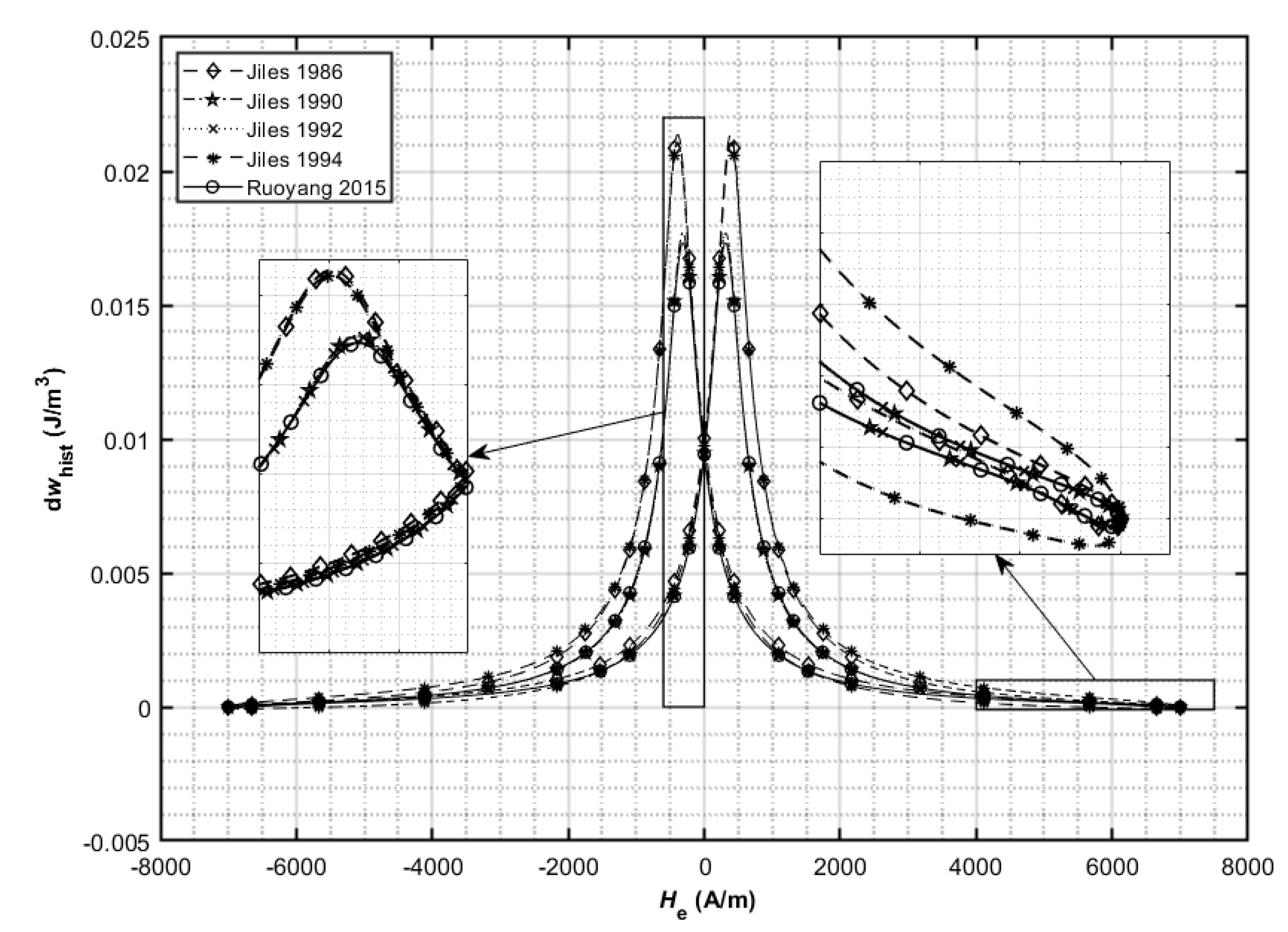
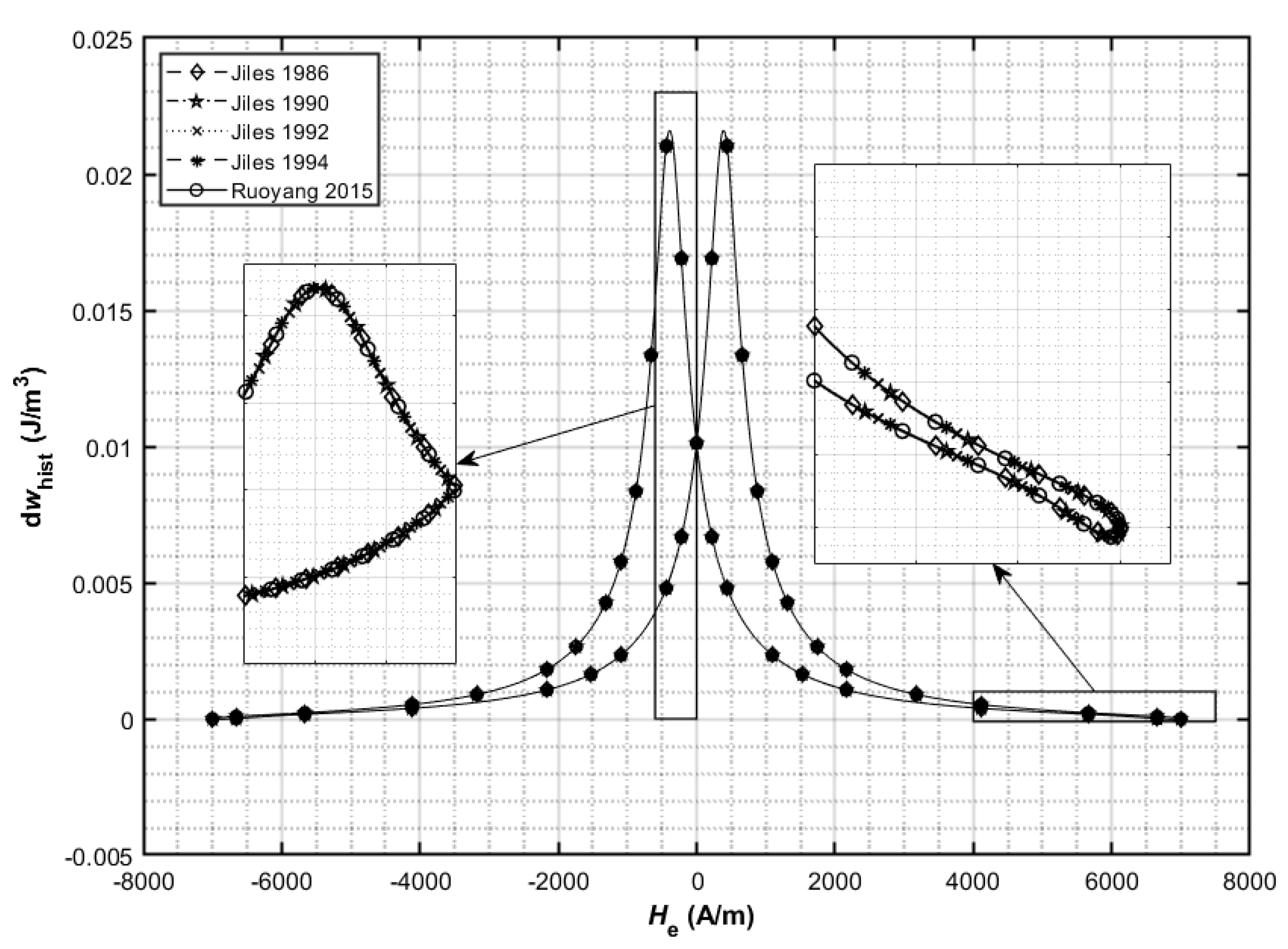
The differential hysteresis loss energy density (34) for both cases (
Table 5) as a function of applied magnetic field strength
He is shown in
Figure 4 and
Figure 5, respectively. The hysteresis losses over one magnetizing period of applied magnetic field strength
He are presented in
Table 6 in the form of value.
The results in
Table 6 additionally confirm that the studied hysteresis models [
2,
3,
4,
5,
7] gives different results, even though the authors claim that all the models are equal [
2,
3,
4,
5] (or, in [
7], the authors claim different model derivation approach, but the final results of hysteresis loop are equal as in [
3,
4]). To clarify why the differences between models occur and what should be adopted in the models to harmonize analyzed J–A hysteresis models, an additional explanation will be given in
Section 5.
6. Harmonization of J–A Hysteresis Loop Models
In the sub-sections above (
Section 5.1,
Section 5.2,
Section 5.3,
Section 5.4 and
Section 5.5), the core equations of different hysteresis models are presented. However, the reader is still not able to select the equations to calculate the J–A hysteresis loop that would give usable results and allow its upgrading, as well as model improvement. When selecting the five basic equations to be treated as the equations of the harmonized model, the equations must physically describe the magnetic happenings in the ferromagnetic material. From the
Table 2, it can be seen that the equations describing the magnetizing process are different. The models in [
2,
3] are the basic ones and originate from the physical representation of the material hysteresis behavior, where during model derivation, the result of irreversible magnetization was obtained with the assumption that variable
c is zero (i.e., there is no reversible magnetization). Even applying this fact, in further hysteresis modeling steps, the existence of reversible magnetization was used anyway. Following this assumption (
c = 0), the description of irreversible magnetization was obtained and further applied in the formation of the final differential Equation (17) for hysteresis loop calculation. On the other hand, in the models in [
4,
5] and, consequently, [
7], the introduced equation describing the magnetization process is different (setting the value of
c to zero). This originates from the results in [
2,
3], where the assumption that “
c is zero” has already been applied once. Following this fact, the models in [
4,
5,
7] cannot be treated as the basic ones or as usable for future J–A model upgrading and development.
By removing typos in [
2], (27) and (38), the only difference between [
2,
3] remains in the equations describing the reversible magnetization process (39) in [
2] and (40) in [
3]. Therefore, we introduce the new variable
with the goal of changing the range of the original variable
c in [
2] (originally between 0 and inf.) with new boundary limits (0 <
cnew < 1), thereby bringing it closer to the concept of the variable
c (0 <
c < 1) as it is used in [
3] (40). Following this, the variable
cnew becomes more representable in terms of defining the amount of reversible magnetization. This is further reason why the model in [
3] is selected as the base for harmonization of all studied hysteresis models.
The changes that need to be applied for the models in [
2,
5] to obtain the results as in [
3] are gathered together in
Table 7 and are marked with bold. For [
4,
7], there is no need for change because the equation form is the same as in [
3] by addressing the assumption that
c is zero in the equation describing the magnetization process. To briefly describe the harmonization process, firstly, the errors in articles [
2,
5] were revised not to confuse the readers. Secondly, the harmonization of the analyzed models forming the harmonized J–A hysteresis model was conducted, aiming to obtain the same results from all of the analyzed models. Consolidated results were expected because all models originate from the same model [
2].
However, according to the differences between the equations describing the magnetization process gathered in
Table 2, some discrepancies between hysteresis loops have appeared and been successfully overcome. On the other hand, Ruoyang [
7] claims that he made a different model by addressing the variable
c differently by not setting its value to zero during the model development, as in models before [
2,
3,
4,
5]. Nevertheless, the results show the opposite—that this model in [
6] is the same as the other ones [
2,
3,
4,
5]. By applying all presented modifications gathered and shown in
Table 7, all the models become equal. The assumption
c is equal to zero was first introduced in [
2] and [
3], and those results were further directly implemented into the description of the magnetization process [
4,
5,
7].
Following the previous discussions, the modified and finally harmonized J–A models are presented in
Table 7 (double lined cells).
Regarding the content of
Table 7, Equation (17) must be changed into (51) for the harmonization of the model in [
2].
where
knew and
cnew are formed based on the original variables in [
2]; they are (52) and (53):
As for the content of
Table 7, the Equation (24) must be changed into (48) for harmonization of the model in [
3].
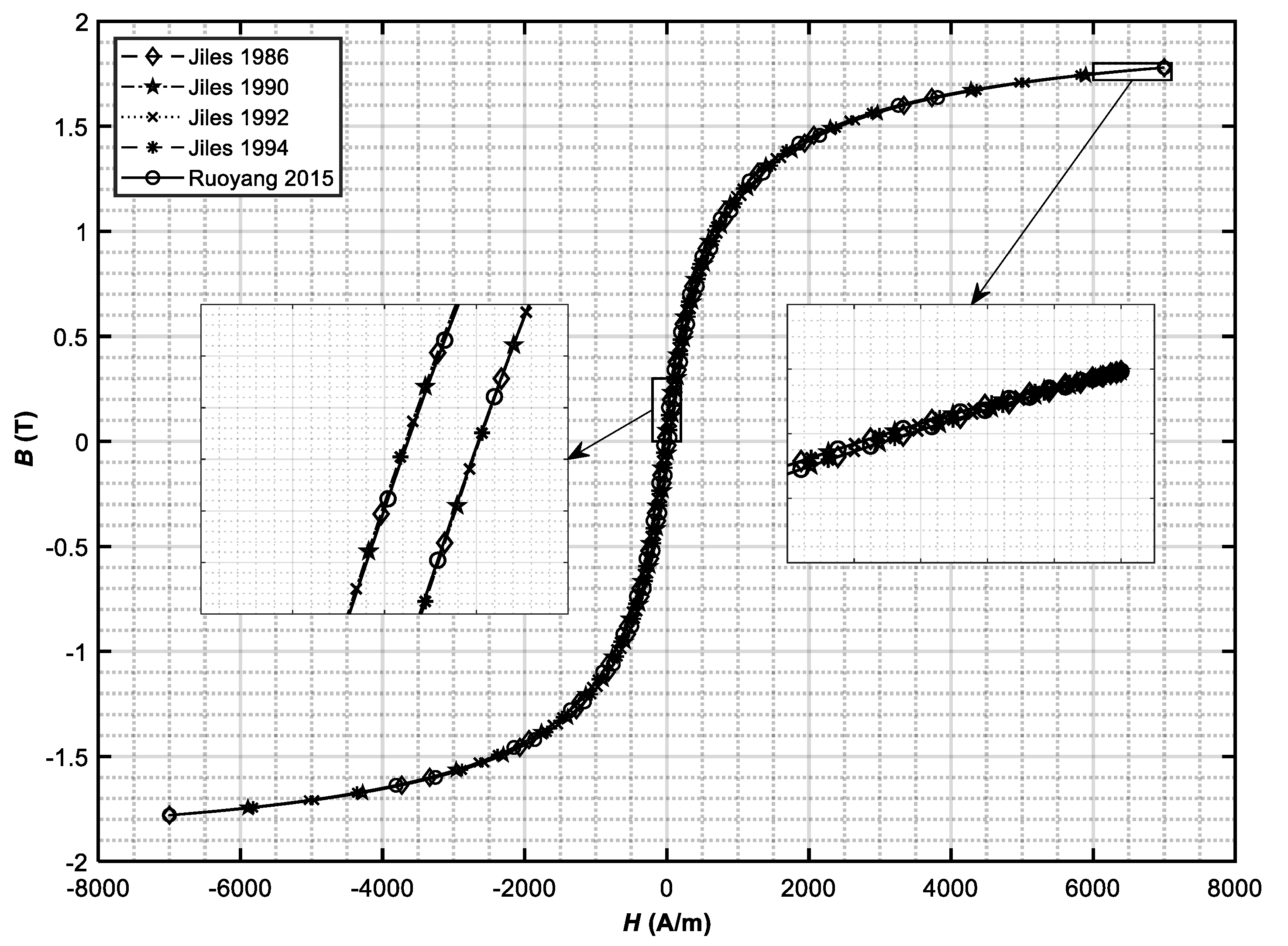
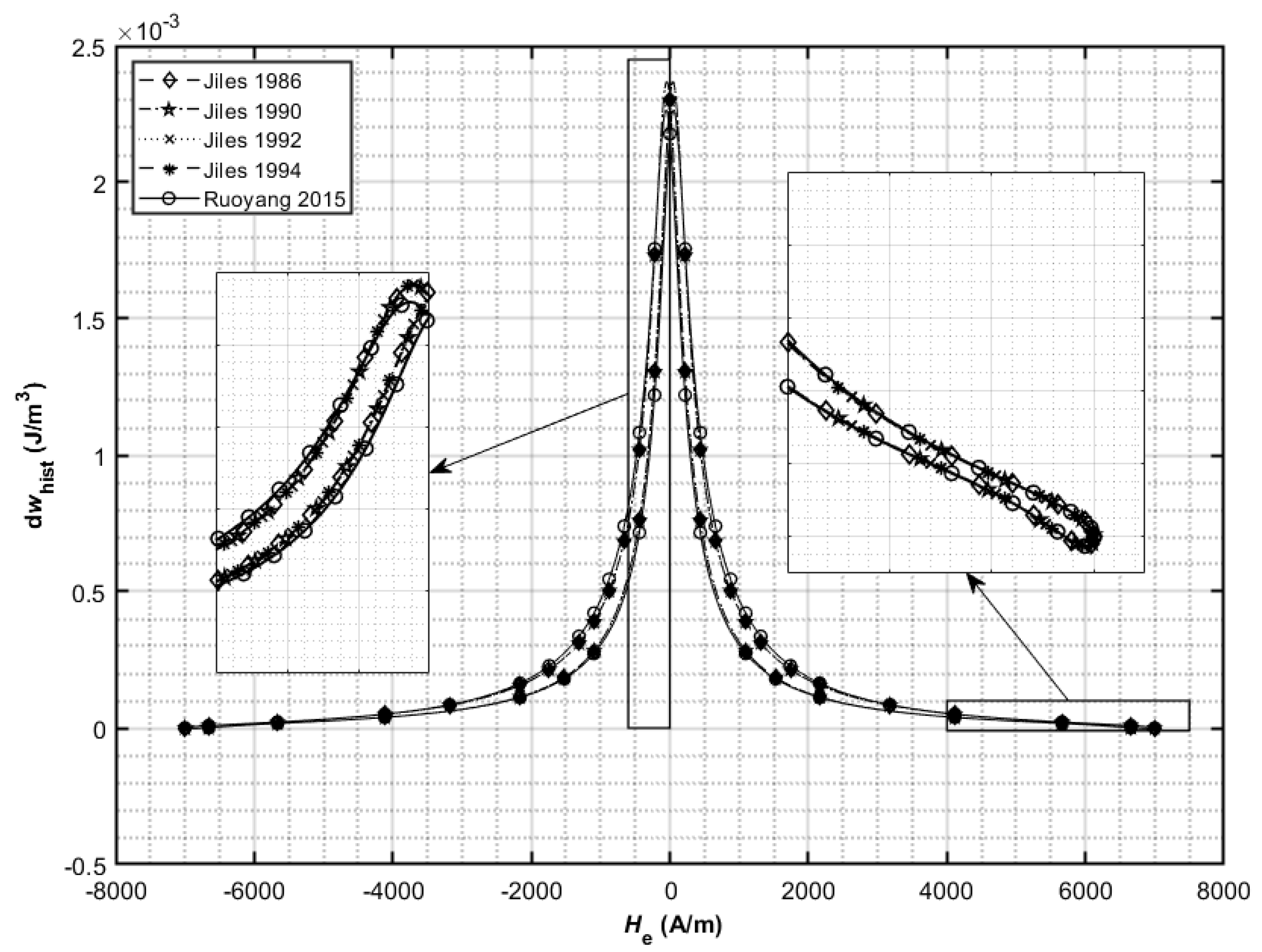
The behavior of the modified and harmonized J–A hysteresis models (right column of the
Table 7) with model variable values defined in
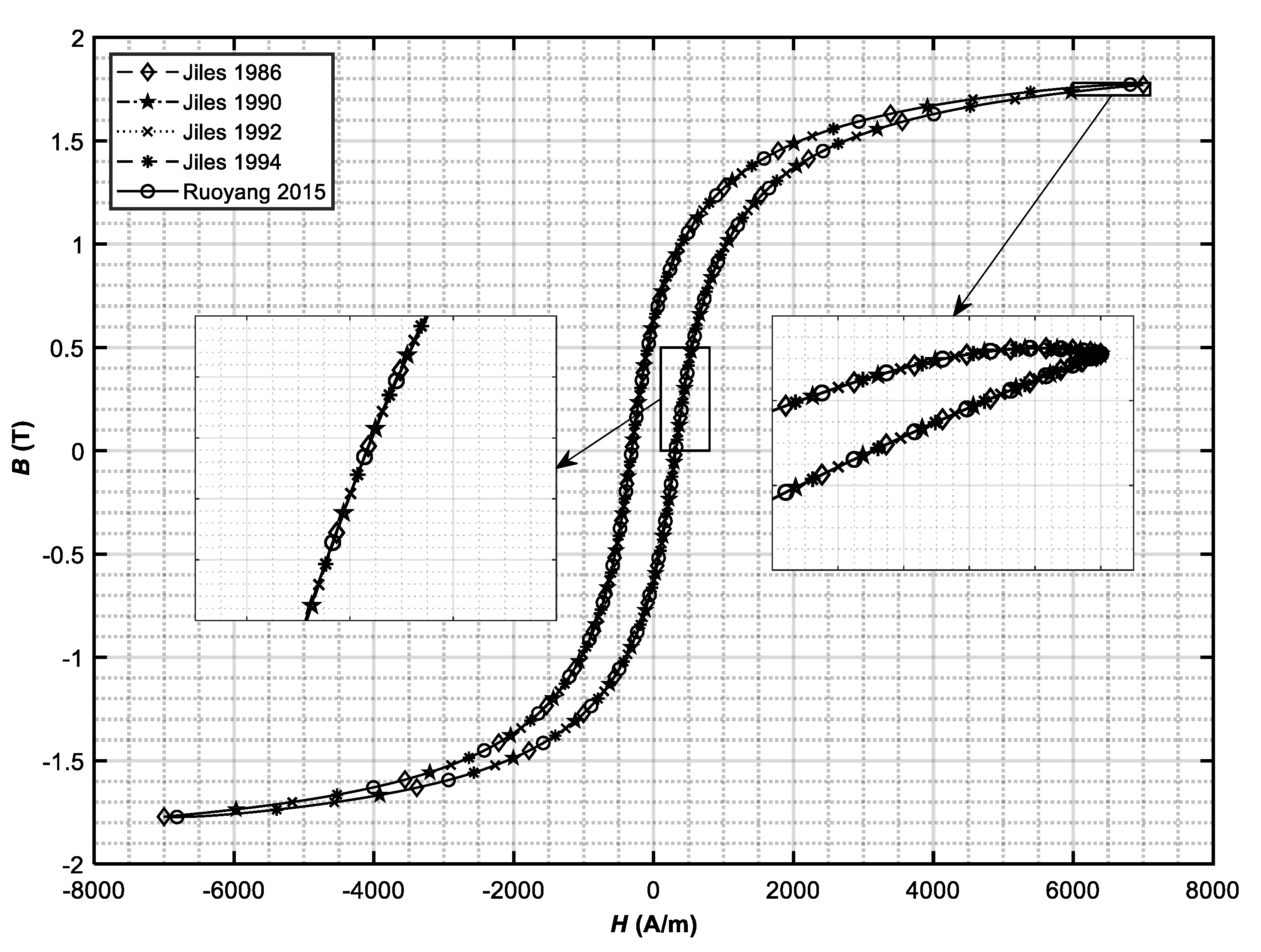
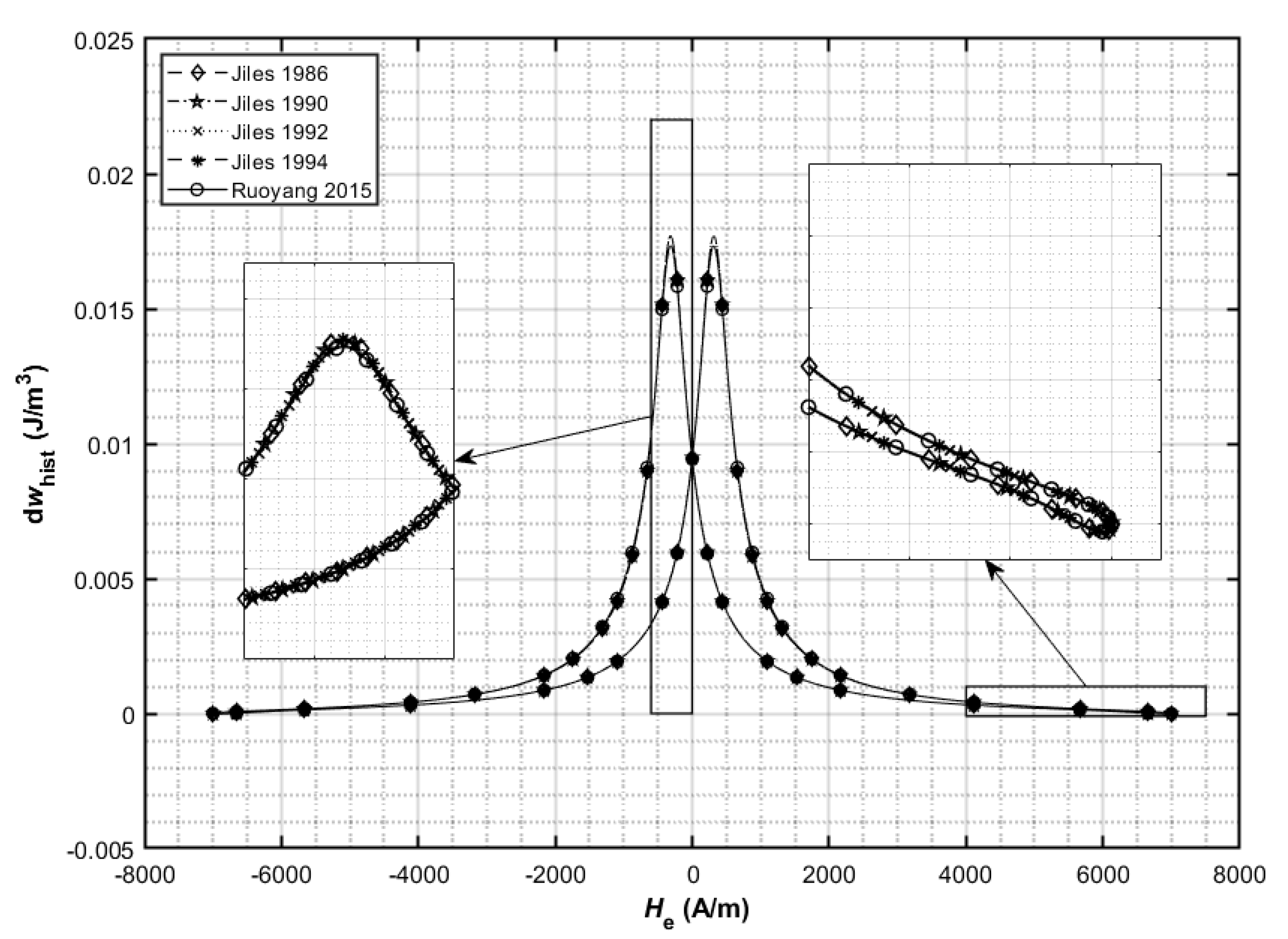
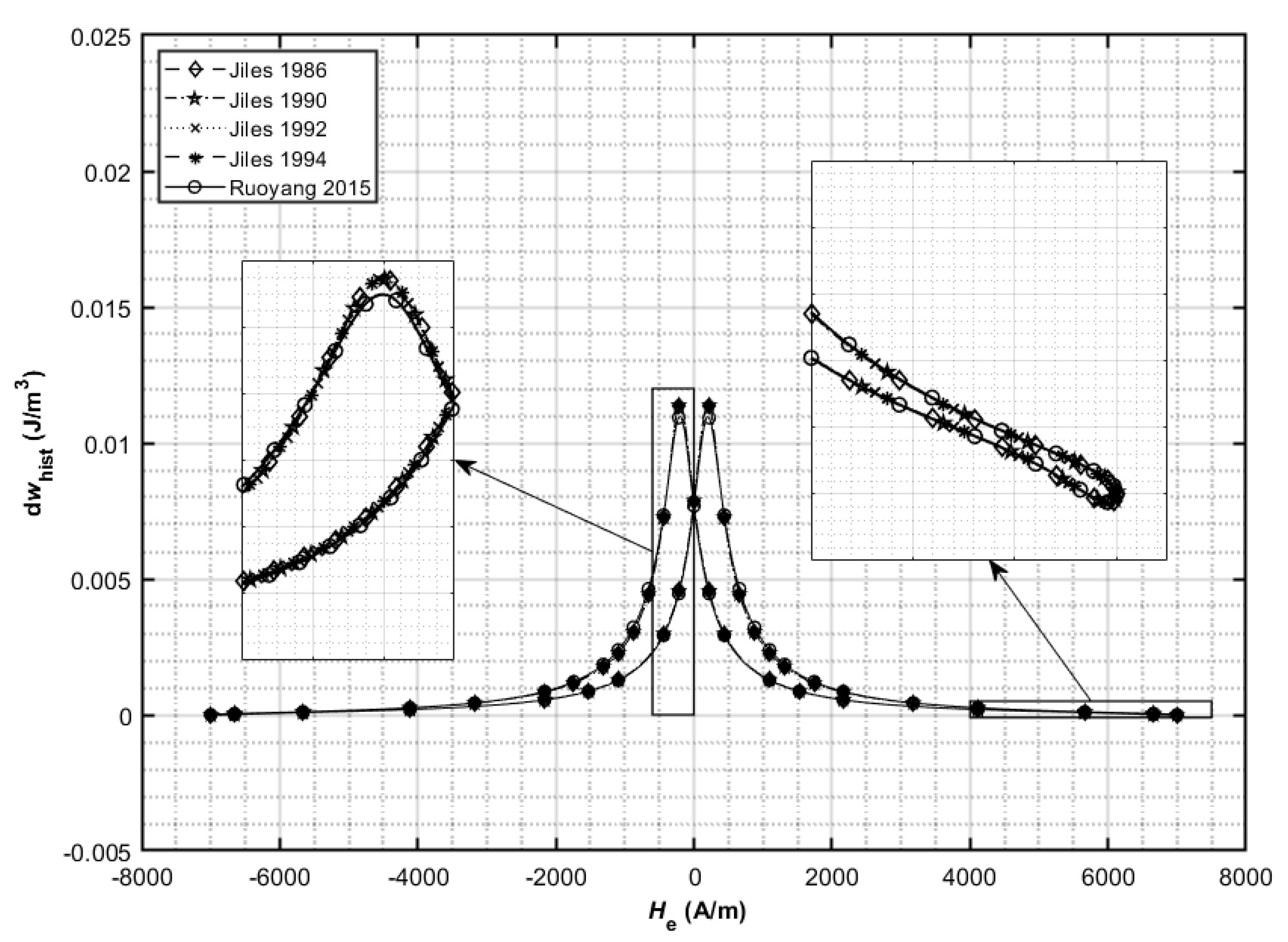
Table 5 (Case 1 and Case 2) was studied. The hysteresis loops and the variation of hysteresis loss energy density are shown for Case 1 in
Figure 6 and
Figure 7 and for Case 2 in
Figure 8 and
Figure 9, respectively. The results of hysteresis loss energy density over one period for different harmonized J–A hysteresis models are presented in
Table 8. The identical behavior of all modified and harmonized hysteresis models can be seen (the curves lie one on the other). A slight difference still exists in the model in [
6], originating from numerical calculation of differential Equation (25). The difference decreases an increasing number of calculating points (input variable
He).
In addition, the behavior of the harmonized models at extreme values of variable
c (43), with the values 0 and 0.9, was also analyzed. The new values of variables for Case 3 and Case 4 are shown in
Table 9. The results in the form of B–H curves and the variation of hysteresis energy loss density are demonstrated for Case 3 in
Figure 10 and
Figure 11 and for Case 4 in
Figure 12 and
Figure 13, respectively. The numerical values of hysteresis loss energy density for both cases are presented in
Table 10.
From the results in
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 showing hysteresis loops and from
Table 8 and
Table 10 presenting hysteresis losses, it can be concluded that after the model harmonization and by knowing the indirect assumptions made in the models, their results in the form of hysteresis loops and hysteresis losses became equalized. The harmonized model (i.e., a common base for all further J–A model development work) is presented in
Table 11. Basically, this is the set of equations forming the model from [
3]. The models [
2,
4,
5,
7] can be used as well, but must include the corrections from
Table 7 (for [
2,
5]) and with the awareness that the magnetization process equation in [
4,
5,
7] already includes the setting of variable
c to zero (meaning the reversible magnetization
Mrev does not exist).
After unification of all differently used nomenclatures in the studied models’ equations and discussions regarding the use of variable
c and setting its value to zero, finally, we must give some remarks regarding the introduction of this variable into the models. The equation of the magnetization process (8) based on the energy balance Equation (7) introduced in [
2] and re-used in the same form in [
3] is uniquely solvable. Further on, by splitting total magnetization into reversible and irreversible magnetization, the new variable (
c) is introduced by Equation (13). By doing so, larger nonlinearities can be achieved and, consequently, better fitting with measurement can be obtained, even for the family of hysteresis loops with different applied magnetic field strength amplitudes for the same material. However, at the same time, the energy balance equation is changed. From (10) and (14), it follows that
M is equal to
Mirr and, further, from (12), that
Mrev is zero, meaning that variable
because
M cannot be equal to
Man (if
it means there are no hysteresis losses). According to these facts, the irreversible magnetization is:
By applying (12), (13) and (54), the total magnetization is:
Finally, the corresponding energy balance equation follows:
As the reader can observe, Equation (56) differs from the basic energy balance equation (7) as it was proposed in [
2]. In further research work, the energy balance should be reconsidered (as, for example, in [
19]), as well as the involvement of pinning losses and flexible domain bending (reversible energy); thus, [
2] should be implemented by applying a different approach.
7. Measurements
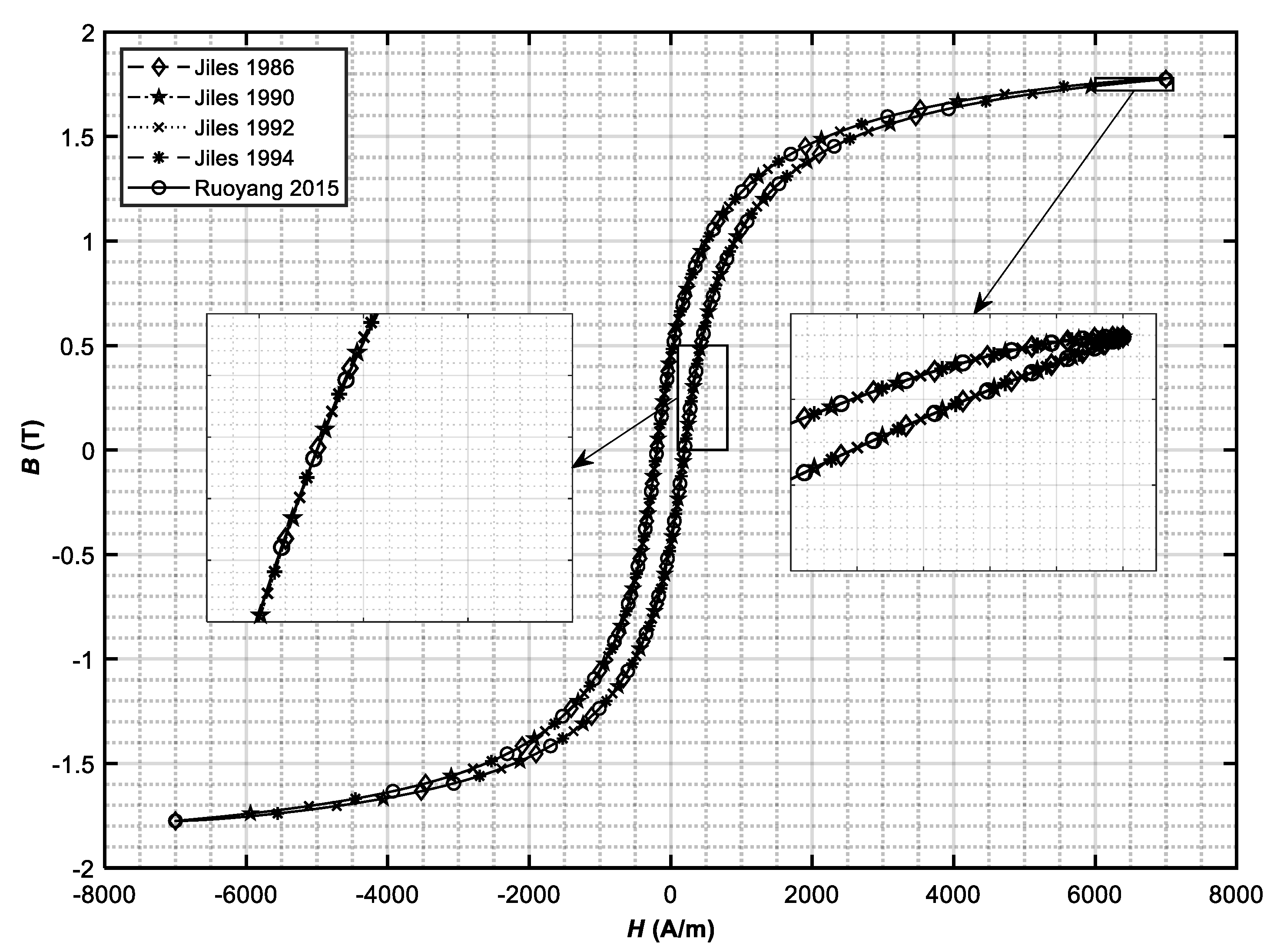
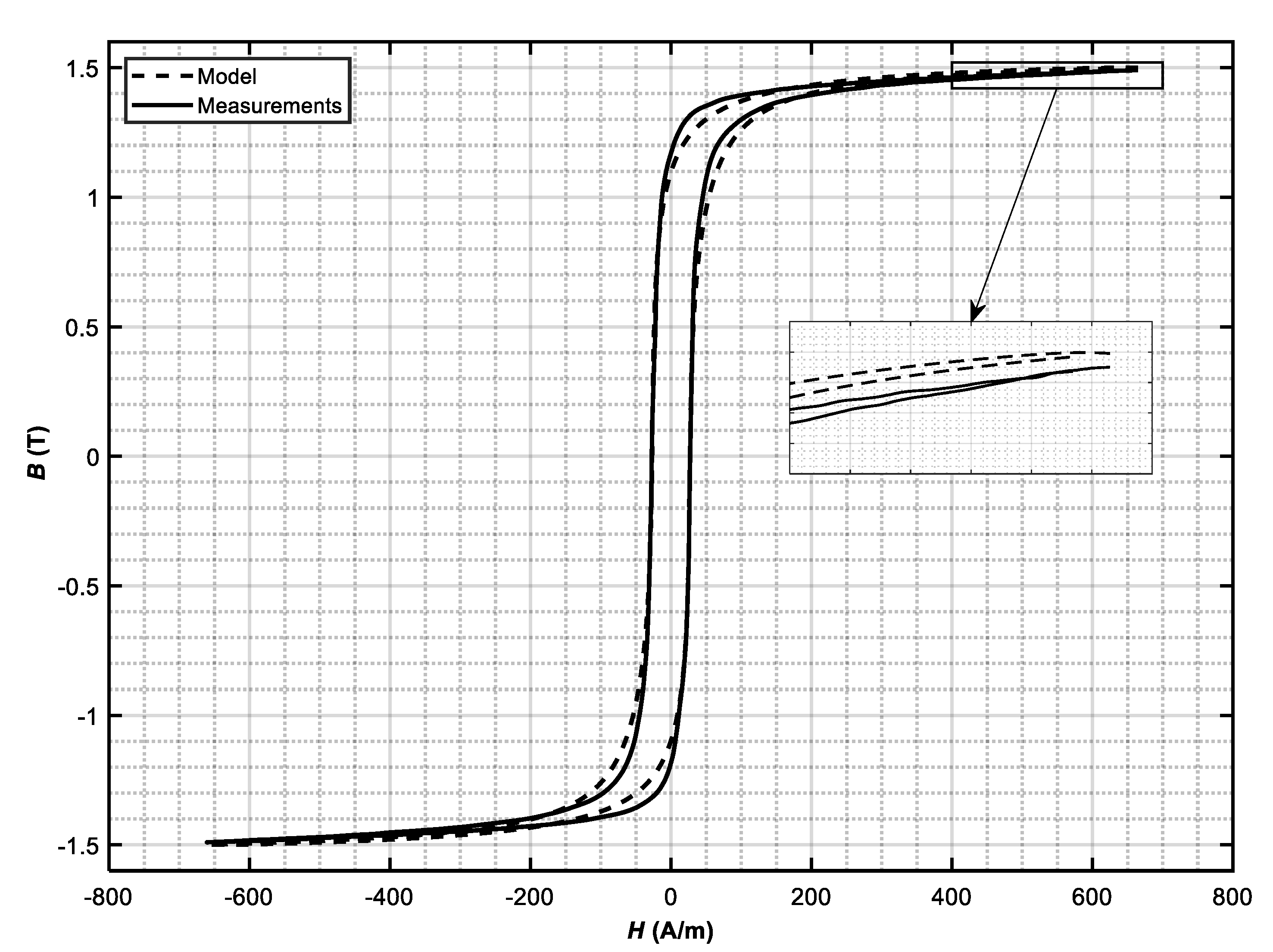
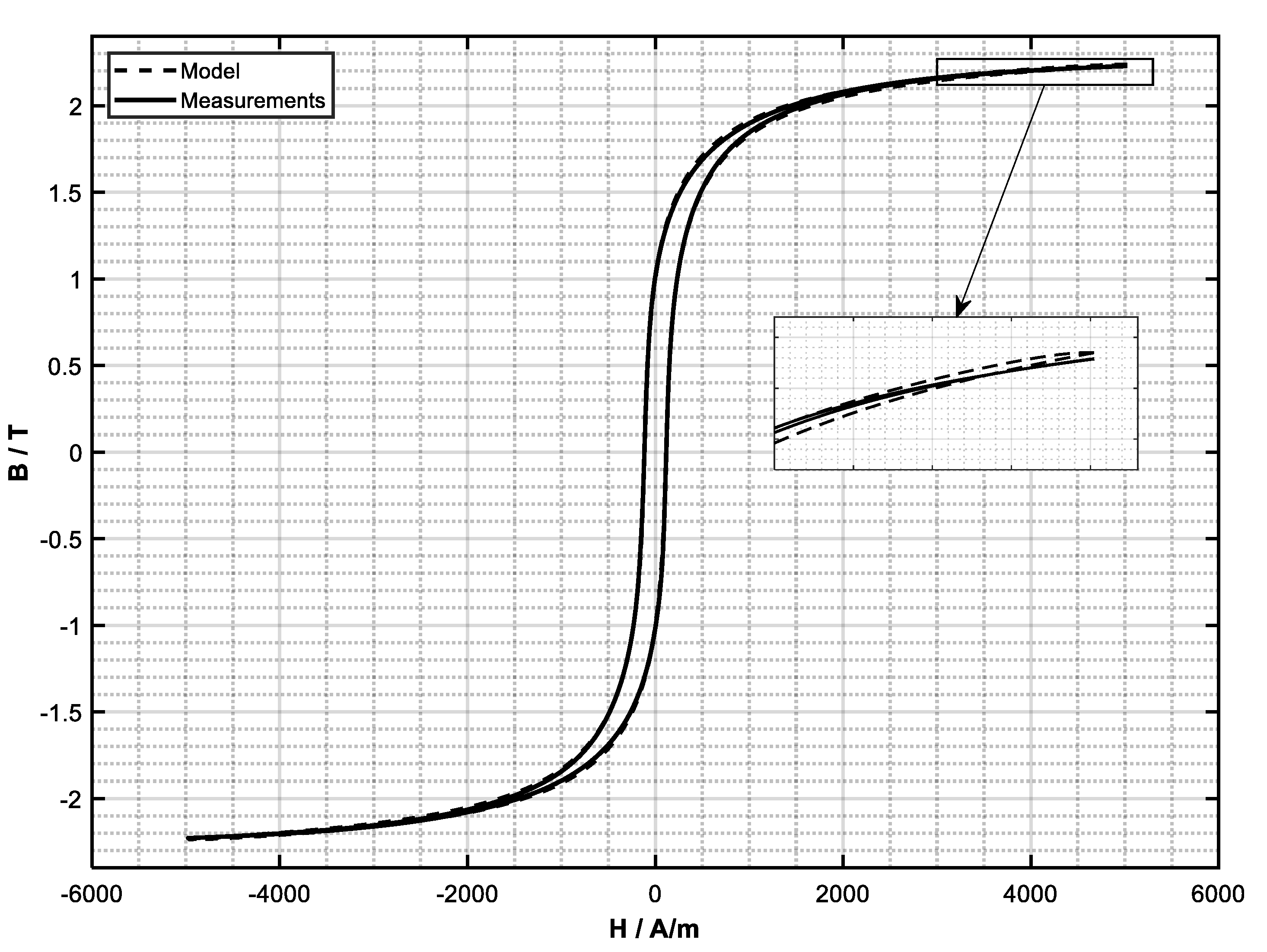
The harmonized J–A hysteresis model was tested on the two measured samples. First is standard M270-35A electric steel, which is mostly used in electric motors; the second is an iron–cobalt alloy, which has the potential to be used in electric motors, because of high relative permeability and high magnetic field saturation point. The measurements of the DC hysteresis loops were made with a Remagraph RE3 [
7] on a 40 × 100 mm sample for M270-35A and on a 100 mm long cylinder with diameter of 10 mm for the iron–cobalt alloy. Particle swarm optimization with equations of the harmonized model (
Table 11) was applied by using both measured hysteresis loops. The particle swarm optimization method needs the value limits for all included model variables. Limits for the searching range of variables
α (from 10
−7 to 10
−2) and
a (from 10
−1 to 10
4) were acquired from [
7]. The explanation of the variable
c range (0 to 1) has already been described above. Its actual searching area was set between 10
−4 and 0.999 to prevent numerical calculation error. According to Jiles’ work [
4], the value of the pinning parameter
k is near the value of the coercive magnetic field strength. The input bounds were set to 1 and 350 following the applicability for both materials. The value of the parameter
Ms was estimated using (9), where
B was replaced with the saturation value of magnetic flux density (
Bs), and in (9) the magnetic field strength was neglected due to its small value in comparison to the saturation magnetization. According to the measured data for the M270-35A, the saturation point is more than 1.5 T (
Ms > 1.19 × 10
6 A/m), and 2.2 T (
Ms > 1.75 × 10
6 A/m) for the FeCo alloy. The actual input limits for variable
Ms were then set from 1.1 × 10
6 to 2.2 × 10
6 A/m. The optimized values of the model’s variables are shown in
Table 12. The measured B–H loops and the loops obtained with the harmonized J–A model are presented in
Figure 14 for the M270-35A and for the iron–cobalt alloy in
Figure 15. Calculated hysteresis loss energy densities in one magnetizing period for all adopted models are shown in
Table 13. The modeling results of the harmonized J–A model using variable values for iron–cobalt alloy (
Figure 15) show higher accuracy in comparison to the modeled hysteresis loop for M270-35A (
Figure 14). The same alternation (mainly at the hysteresis loop knee point) has also been observed before (
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10 in [
4]). The error at the knee point can be minimized with various optimization settings (for example, using different fitting constraint functions in PSO), but then higher deviation may occur at the end points and/or in the coercivity area.
8. Conclusions
Equivalent results from all studied J–A models should be expected, because all the models originate from the same model [
2], but accordingly to the differences between equations describing the magnetization process (
Table 2), some discrepancies between hysteresis loops have appeared. Firstly, the errors in articles [
2,
3] were revised not to confuse the readers. Secondly, harmonization (
Table 7) of the analyzed models into s consistent J–A hysteresis model (
Table 11) was achieved. The modeled results from all of the analyzed models are now confidently expected to be equivalent.
With the consistent J–A hysteresis model (
Table 11), we now have a fundamental platform for further analyses and comparison between already developed models, as well as a method of performing quality checks on newly modified ones or newly developed hysteresis models.
Finally, some conclusive remarks regarding the variable
c and its setting to zero were given. This means that we should rethink the usage and the basic role of this variable in the models. The energy balance equation and, consequently, the magnetization process introduced in [
2] and re-used in the same form in [
3] is uniquely solvable. By introducing a new variable (
c) through Equation (13), a nonlinearity is introduced into the model, allowing the further increase of the model fitting capability to meet the measured data. At the same time, the energy balance equation is reformed into (56) and differs from the root energy balance Equation (7). In further research work, the involvement of pinning losses and flexible domain bending should be reconsidered by implementing a different approach. However, unquestionably, the reversible magnetization exists; it is described in [
2] and in even greater depth in [
3].