Abstract
Buildings are responsible for around 30 to 40% of the energy demand and greenhouse gas (GHG) emissions in European countries. Building stock energy models (BSEMs) are an established method to assess the energy demand and environmental impact of building stocks. Spatial analysis of building stock energy demand has so far been limited to cases where detailed, building specific data is available. This paper introduces two approaches of using synthetic building stock energy modelling (SBSEM) to model spatially distributed synthetic building stocks based on aggregate data. The two approaches build on different types of data that are implemented and validated for two separate case studies in Ireland and Austria. The results demonstrate the feasibility of both approaches to accurately reproduce the spatial distribution of the building stocks of the two cases. Furthermore, the results demonstrate that by using a SBSEM approach, a spatial analysis for building stock energy demand can be carried out for cases where no building level data is available and how these results may be used in energy planning.
1. Introduction
Buildings are responsible for around 30 to 40% of the energy demand and greenhouse gas (GHG) emissions in European countries [1]. Reducing the energy demand of buildings requires the implementation of targeted energy efficiency and emission reduction measures. The implementation of measures often falls to local municipalities and cities, which have to develop plans and strategies for clean energy transitioning to transform their local buildings stock. This challenging task is impeded by the complexity behind the process of planning for energy efficiency at scale as well as the implementation of renewable energy infrastructure, which is further made difficult by the lack of data for the analysis of spatial energy demand.
Building stock energy models (BSEMs) have long been used to assess the energy demand and environmental impact of building stocks [2,3], where they have been used for policy assessment [4,5,6], analysis of renovation strategies [7,8], and urban energy planning [9] among other applications. In recent years, the field of urban building energy modelling (UBEM) especially has become more and more popular, focusing on modelling the spatial distribution of building energy demand through building-specific BSEMs that model each building in a city or region individually [9,10]. This development has been possible through an increase in computational power as well as the widening availability of building-specific data on building stocks such as 3D city models, building registries and/or energy performance certificate data, which enable a spatially differentiated description of building stocks and their energy demand [11]. However, availability to the required datasets is also a limiting factor to the widespread use of spatial BSEMs, as access is often restricted, or certain data is missing completely [9]. Moreover, the underlying datasets are often faulty, incomplete and fractured, and therefore extensive data processing and cleaning is required in order to make use of them in building stock energy analysis [12]. This makes the application of spatial BSEMs a complex and time-consuming task preventing their wider application especially in smaller regions where resources for energy demand assessment are limited.
In this article, we address these issues by further developing the previously established methodology for synthetic building stock energy modelling (SBSEM) [13] to enable the modelling of spatially distributed synthetic building stocks. In the absence of detailed microdata, SBSEM synthetically generates disaggregated data of individual buildings in building stocks based on aggregate data [13]. It builds upon methodologies for the generation of disaggregated synthetic populations of individuals and households which have widespread use in microsimulations and agent-/individual-based models [14]. It has so far been applied for the modelling of national building stocks, describing the aggregate distribution in the stock based on synthetically generated buildings [13,15]. This article expands on this methodology by introducing two approaches for the generation of spatially distributed synthetic building stocks depending on different levels of data availability with focus on building energy demand. The aim of the article is therefore to:
- Develop and describe data-adapted approaches for generating spatially distributed synthetic building stocks that can be used in building stock modelling in data-scarce circumstances.
- Demonstrate the applications of the developed approaches for spatial synthetic building stock modelling based on two cases: Dublin (Ireland) and Waidhofen an der Thaya (Austria).
- Analyse the spatial distribution of energy demand of the building stock of the two cases based on the application of the approaches.
The following section outlines the approaches for generating spatially distributed synthetic building stock (Section 2.1), the building stock energy model used to evaluate the generated stocks (Section 2.2), and the adaptation to the two approaches to the respective cases (Section 2.3). The results of the generated building stocks and their validation are presented in Section 3 and discussed in Section 4. In Section 5, we present our conclusions and give an outlook on future work.
2. Materials and Methods
The methodology for synthetic spatial building stock modelling can be broken down into two steps similar to the methodology for synthetic building stock modelling as proposed by [13]: (1) building stock dataset generation and (2) building stock energy demand assessment (see Figure 1). The synthetic building stock generation is based on different data sources that include (aggregated) data on the structure and spatial distribution of the building stock (e.g., from building registries or census data), data on the distribution of building characteristics in the stock (e.g., from building typology, building standards and survey studies) and data on usage-relevant parameters of the building (e.g., from building standards and survey studies). This data is the basis for the synthetic building stock data generation process that generates a spatially distributed synthetic building stock dataset. The generated synthetic building stock is then fed into a building stock energy model (see Section 2.2), which is used to model the energy demand of the individual synthetically generated buildings. The model simulation result can then be aggregated and analysed according to its spatial distribution and distribution within the stock. All data processing and modelling steps in this paper are implemented in python using public libraries such as numpy, pandas, scipy, geopandas and shapely.
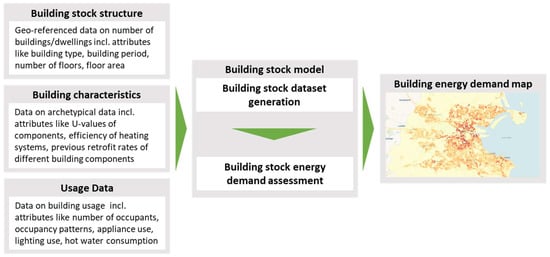
Figure 1.
Synthetic spatial building stock modelling for spatial energy demand analysis.
2.1. Building Stock Dataset Generation
The building stock dataset generation process can be adjusted depending on the data availability (see Figure 2). In the common building-specific BSEM approach, building-specific microdata (e.g., from building registries, Energy Performance Certificates (EPC) databases and/or 3D city models) is the basis of the modelling approach, which relies on merging, cleaning and processing the different datasets as well as further characterizing the individual buildings based on generic or archetypical data to generate the complete building stock dataset. If this building-specific data is either missing or only available for a sample dataset that may or may not be spatially distributed, the two proposed SBSEM approaches can be used to generate the complete building stock dataset: (1) Sample-based SBSEM or (2) Sample-free SBSEM. Both the terminology and methodology used for these two approaches are based on the respective methods to generate synthetic populations of individuals and households [16]. As the name suggests, the sample-based approach (see Section 2.1.1) relies on the use of a sample dataset of individual buildings. This sample data is used as a basis for the stock generation and is spatially distributed based on aggregate datasets describing the spatial distribution of the stock, for example using methods such as iterative proportional updating [17]. In contrast, the sample-free SBSEM approach (see Section 2.1.2) does not rely on a sample micro-dataset but instead uses data describing the distribution (and correlation between) of different attributes in the building stock to synthetically reconstruct the building stock. The adaptation of these methodologies from spatially distributed populations to building stocks as proposed in this paper follow the same methodological steps as the method for synthetic building stock modelling defined by [13] (see Figure 2):
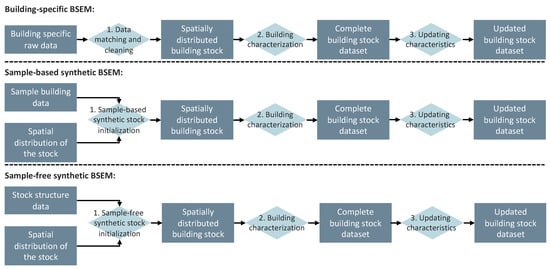
Figure 2.
Overview over different approaches for a spatial synthetic building stock dataset generation compared to the common building-specific approach.
- Building stock initialization: The first step initializes the synthetic building stock resulting in a dataset of individual building records that are spatially distributed. The generated datasets resemble the real building stock both in its structure (e.g., building type, size and age) and spatial distribution. The spatial resolution is determined by the available data and maybe be down to grid-cells or statistical areas;
- Building characterization: The second step further characterizes the individual buildings in the synthetic building stock and enriches the dataset by adding different attributes required for building stock energy modelling. These may include estimating the building geometry, assigning heating and ventilation systems and energy-relevant parameters (e.g., U-values). This may include stochastically assigning attributes based on distributions or assigning data based on archetype data;
- Updating building characteristics: The third step updates individual building characteristics to better represent the current state of the stock (e.g., in terms of current U -values) to account for past retrofits and other alterations. This step may be unnecessary in case the data used for step 2 is up to date.
Steps 2 and 3 work the same between the different methodologies as they are concerned with further characterizing and updating the building characteristics needed for building stock energy modelling of the individual buildings in the initialized synthetic building stock. The extent to which these two steps are necessary depends on the datasets used for step 1. It may be, for example, that in case of a sample-based approach, the sample data is complete enough to cover all or most of the building characteristics required, in which case both steps 2 and 3 can be omitted or be replaced by a simple data formatting step that converts the sample data structure into the data structure of the BSEM used to assess the building stock energy demand. As the different approaches do not differ in steps 2 and 3 of the methodology and these steps are described in detail in [13], the following two subchapters are limited to the description of step 1 of the two approaches.
2.1.1. Sample-Based SBSEM
The sample-based SBSEM approach is based on the Iterative Proportional Updating (IPU) approach to generate synthetic populations developed by Ye et al. [17]. Other sample-based approaches exist but following the example of [16], we used the approach developed by Ye et al. as a basis as in contrast to other approaches it can match the aggregated distribution of both individuals and households simultaneously [16], a feature that is also useful for synthetic building stocks when trying to match distributions on both the building and dwelling level. This approach synthetically reconstructs a population based on a sample of individuals that are grouped into households and data describing the aggregated spatial distribution of households and individuals [16]. The method then spatially distributes the individuals and households in the sample based on the aggregate data, matching the distribution of both individuals and households simultaneously [16]. The same approach can be applied for buildings to spatially distribute the building sample and match the spatial distribution of buildings and building usages (e.g., dwellings) and thereby synthetically reconstruct the spatially distributed building stock.
The IPU methodology requires two different input datasets: (1) a microdata sample of individual building records and (2) an aggregated dataset describing the spatial distribution of the building stock. The sample data should describe both the building and the corresponding building usage, such as dwellings or non-residential usages, in individual tables linked through a common identifier (e.g., a unique building id), which identifies which building usage corresponds to which building. The dataset describing the spatial distribution should include aggregated distributions of attributes of either the building and/or the building usages (e.g., number of buildings per building type, construction period, etc.). The spatial resolution of the data can range from different municipalities or climate regions to grid cells or statistical areas depending on the scope and scale of the building stock to be generated.
These datasets are used as an input to the IPU algorithm, which generates the spatially distributed building stock by first adjusting the weights for both buildings and building usages in the sample for each area in the aggregated dataset using a standard Iterative Proportional Fitting (IPF) procedure [17]. The IPF procedure adapts the weights in the sample until the marginal totals along different dimensions (e.g., building type, construction period, etc.) are equal or approach the aggregate distribution per area [18]. The procedure then generates the synthetic building stock by randomly sampling from the sample based on the adjusted weights. The whole process is repeated for each of the different areas in the aggregate data to complete the initialization of the synthetic building stock. This initialization can be repeated multiple times, choosing the dataset with the best fit with the aggregate data in order to improve the fit of the synthetically created building stock. However, depending on the size and spatial resolution of the synthetic building stock as well as the computational power of the computer used, this may take a long time to compute, hence there is a trade-off between improving the fit of the resulting synthetic building stock dataset and the computational time required. The resulting dataset of spatially distributed buildings can then be further characterized based on steps 2 and 3 of the methodology (see Section 2.1).
2.1.2. Sample-Free SBSEM
The sample-free SBSEM approach is based on the methodology for the generation of synthetic populations developed by [19]. As the name suggests, this approach does not rely on a microdata set but instead uses more aggregated data describing the structure and composition of the stock. This approach synthetically reconstructs a population based on aggregate data describing the structure and spatial distribution of households and individuals in the population. This is achieved by iteratively generating the population dataset household by household based on the probabilities and constraints in the composition of households given in the aggregate data. The adaptation of the approach for spatial building stock modelling follows a similar methodology to the approach outlined in [13] for the generation of national synthetic building stocks. However, the spatial distribution of the stock is given as an additional constraint and attributed to the initialization of the stock.
The sample-free approach for the SBSEM requires two different input datasets: (1) aggregate dataset(s) describing the structure of the building stock, and (2) aggregate dataset(s) describing the spatial distribution of the building stock. The structural data should describe the distribution of both the buildings and the building usages (e.g., dwellings, workplaces) in the stock according to different attributes (building type, construction type, etc.) and, more importantly, how these attributes correlate with each other (e.g., number of buildings per building type and construction period). This data is used to generate tables defining the conditional probability of different building attributes (e.g., probability of construction period based on building type, etc.). The dataset describing the spatial distribution can look much the same as in the sample-based approach and here serves as constraints to the generation of the synthetic building stock. It may also be the case that attributes on the spatial resolution of the stock are included in the aggregated structural data, for example when using a coarser spatial resolution such as municipalities or larger statistical areas. In this case, this additional dataset can be omitted and the information in the structural data used directly.
Based on this data, the synthetic building stock can be initialized one by one. This is done by first iteratively assigning different building characteristics and defining the corresponding building usages and attributes to the building by random sampling characteristics from the aggregate data. After each defined building characteristic, it is checked if a building corresponding to that attribute is allowed based on the constraints for that area. If so, the building is assigned to that area and the process moves on to assigning the corresponding building usage(s) (e.g., one or more dwellings) in a similar manner by sampling from aggregate data and checking if the building usage characteristic exists in the constraints. If the building is completed successfully with all characteristics fulfilling the constraining data, then the weights in the constraints and the aggregate data are updated based on the defined building (i.e., by reducing the weights corresponding to the defined building attributes) and the next building is generated. However, if after adding a characteristic the constraints are not met (e.g., no building of a certain size exists in this area), then the process is stopped and a new attempt to define the building is started. This iteration is continued until either the building is completed successfully, or a fixed limit of iterations is reached, at which point the constraint in question is disregarded and the last value is kept, or a default option is assigned (e.g., the most common value for a certain characteristic). This might especially be the case when defining the last buildings in a certain area or for the whole building stock, therefore, are buildings assigned one at a time for each area rather than completing an entire area and then moving on to the next. This also ensures that potential errors in assigning buildings might be spread over the entire area and are not depending on the order in which they are assigned.
2.2. Building Stock Energy Demand Assessment
The building stock energy demand assessment is done based on a previously developed and applied BSEM [8,13,20]. The BSEM has an integrated energy and impact assessment model, which is used to model the energy demand of each building in the generated dataset. The energy calculation is based on a hierarchical structure, calculating the energy demand according to different system boundaries (useful energy, final energy, delivered final energy, primary energy and GHG emissions) and differentiates the calculated energy demand and GHG emissions for different energy services (i.e., space heating, hot water, ventilation, appliances, lighting and auxiliary building services (e.g., pumps, etc.)). The useful energy demand for space heating is based on a monthly steady-state energy balance based on the norm ISO EN 52016-1 [21]. In this study we focused on the analysis of the heat demand (both space heating and hot water) of the generated building stocks and did not assess the energy demand for other energy services.
2.3. Validation
In order to validate the generated synthetic building stocks and estimate the fitting accuracy, we used the measure of Proportion of Good Prediction (PGP), a standard measure for validating the accuracy of synthetically generated datasets [16] (see Equation (1)). The PGP estimates the proportion of good predictions between the observed (O) and estimated (E) distribution in the building stock (or subset of the building stock). O and E describe the distribution of the number of buildings or dwellings in a given subset of the building stock across different dimensions (e.g., building type, construction period, size, etc.). The PGP is calculated based on building the ratio of the number of misclassified buildings over the total number of buildings in the subset. In Equation (1), the ratio is multiplied by 0.5 in order to avoid counting each misclassified building twice. The closer the PGP is to one, the better the generated building stock matches the observed distribution of attributes in the input data for a given region.
2.4. Cases
The two approaches to SBSEM were each applied in a respective case study in order to synthetically reconstruct the building stock and model and assess the spatial distribution of the building stock energy demand; the sample-based approach to model the residential building stocks of Dublin (Ireland) and the sample-free approach to model the complete building stock of Waidhofen an der Thaya (Austria). The data and specific processes applied in these cases are further explained in the following subsections.
2.4.1. Dublin (Ireland)
The Dublin Region, the capital city of Ireland, has a total population of 1.3 million and encompasses four local authority areas; Dublin City, Dún Laoghaire-Rathdown, Fingal and South Dublin, which together span an area of 92,200 hectares. The Dublin Region is projected to grow to a population of over 1.6 million by 2036 [22]. In [23], the existing building stock in Dublin is an inefficient and aging stock, this means that the majority of existing buildings in the Dublin Region will need to undergo energy efficiency upgrades or retrofits. Ireland’s Long Term Renovation Strategy suggests that, by 2050, it is expected that more than 1.5 million buildings in Ireland will need to be retrofitted [24]. Ireland has committed to radically decarbonising its energy system by 2050 and to making substantial progress within the next decade. Ireland’s heating sector faces huge challenges in terms of decarbonization—the main sources of energy in the Dublin Region can be attributed to natural gas and electricity, with the key use being for space and water heating.
The sample-based SBSEM approach was applied to model the residential building stock of the Dublin Region. The approach builds upon the data from the national census [25], which gives the spatial distribution of the building stock according to statistical areas (called small area) and the national EPC database BER [26], which serves as a sample for this approach, see Table 1. As both data sources were on the level of individual dwellings and did not give an indication on which dwellings were in the same building, each dwelling was modelled as its own building. This simplification was feasible as most dwellings were in single-dwelling buildings (about 85% of the stock).

Table 1.
Overview input data for Dublin.
Building Stock Initialization
Before the building stock can be initialized, the different input data first had to be cleaned and pre-processed. For the BER data, in some cases key data such as the U-values of components are missing, in which case these incomplete records were removed from the sample, reducing the total number of records from 270,439 to 239,231. The BER data and the census data use slightly different classifications for building types (e.g., the BER data includes different types of row houses, while the census data does not). These two classifications, therefore, needed to be aligned as well as the construction year in the BER data matched to the construction period classification in the Census data for the IPU algorithm to work.
Once the data was preprepared it was fed into the IPU algorithm to generate the spatially distributed building stock for the residential building stock of Dublin, by spatially distributing the sample BER data to the small area level based on the attributes, building type, building age and main energy carrier contained in the census data [25]. We used an existing implementation of the IPU algorithm based on [27], which was adapted to work with buildings instead of households and people. The BER data contains information on which postcode in Dublin the building is located in, therefore the generation was carried out for each postcode individually using the respective records in the BER data as a sample. The generation was repeated 100 times and each iteration was evaluated based on the PGP (see Equation (1)). Based on this, the version with the best fit was taken for each area. The aim of the repletion was to reduce the errors due to the stochastic nature of the method applied and a repletion of 100 times was found to yield stable results (i.e., no significant deviations in the PGP of the resulting synthetic building stock).
Building Stock Characterization
The building characterization step largely consists of converting the BER data into the data structure of the applied SBSEM [13], as most of the necessary building attributes such as the building geometry, component U-values, heating and ventilation systems are contained in the BER data. Missing data mainly consists of the building usage related data such as indoor temperature, number of occupants or hot water usage. These attributes were estimated based on standard user data contained in the BSEM [13,15]. The BER data was assumed to be up to date, which is why no additional building updating step was performed.
2.4.2. Waidhofen an der Thaya (Austria)
The region Thayaland comprises 15 municipalities of the Waidhofen an der Thaya district and is located in the north-west of Lower Austria. The cadastral area is 66,910 hectares with 43,433 hectares of agricultural area and 19,694 ha of forest. Contrary to the trend in Lower Austria, the population of the area of Thayaland is declining down from 28,607 in 1991 to around 25,682 in 2020. The rural structure in the region shows high biomass potential, which is already partially used in numerous heating systems. The proportion of biomass used in the region to cover the heating demand is around 45%, which is almost equivalent to the oil and gas share with 21% and 25% respectively. The remaining share is covered by electricity (8%) and others (coal, solar). Moreover, there are already numerous district heating systems in the region that use regionally available resources. Particularly noteworthy are 20 biomass heating plants for supplying entire towns or districts as well as 6 biogas plants producing between 100 and 500 kWel [28,29].
The sample-free SBSEM approach was applied to model the residential building stock of Waidhofen an der Thaya (Austria). The approach builds upon the data from the national building and dwelling registry [30], which gives the spatial distribution of the building stock and data from the national census [31] beside data on the structure and composition of the stock (see Table 2). The data is complemented with data from survey data of sample buildings as well as regional data sources in the area [28], which serve as a basis for the building characterization step. The sample dataset from the survey is, however, not comprehensive enough to be able to be used in a sample-based approach.

Table 2.
Overview input data for Waidhofen.
Building Stock Initialization
As in the Dublin case, here the different input data first also had to be cleaned and pre-processed. Even though both the spatial data as well as the census data came from the same data provider, each of them have slightly different classifications for certain attributes such as the building size or construction period categories, which needed to be aligned by aggregating them to a common classification. The original categorization in the census data was kept, however, as this was used to characterize the buildings and dwellings. The aggregated common classification was purely used to spatially distribute the buildings.
Once the data was pre-processed, the building stock was initialized building by building based on the approach described in Section 2.1.2 defining one building for each area in the spatial distribution at a time. Each building was described firstly by defining the building level characteristics (building type, construction period, number of dwellings and building size class) based on the probability defined in the aggregated data. Each new attribute was assigned based on the conditional probability of the previously assigned attributes. Each of the interval class attributes (e.g., the construction period, such as 1920–1944) were interpolated to obtain a numerical value. For open-ended class intervals (e.g., 10+ dwellings), which are not delimited on both sides, an exponential distribution was assumed.
Based on this data, the synthetic building stock can be initialized one by one. This is done by iteratively assigning first different building characteristics and defining the corresponding building usages (both for residential and non-residential usages) and attributes to the building by random sampling characteristics from the aggregate data. After each defined building characteristic, it is checked if a building corresponding to that attribute is allowed based on the constraints for that area. If so, the building is assigned to that area and the process moves on to assigning the corresponding building usage(s) (e.g., one or more dwellings) similarly by sampling from aggregate data and checking if the building usage characteristic exists in the constraints. In the case of non-residential buildings, the building usage is assumed to correspond to the respective building type (e.g., hotel usage in hotel buildings, etc.). If the building is completed successfully with all characteristics fulfilling the constraining data, then the weights in the constraints and the aggregate data are updated based on the defined building (i.e., by reducing the weights corresponding to the defined building attributes) and the next building is generated. However, if after adding a characteristic the constraints are not met (e.g., no dwellings of a certain size in this area), then the process is stopped and a new attempt to define the building is started. This iteration is continued until either the building is completed successfully, or a fixed limit of iterations is reached, at which point the constraint in question is disregarded and the last value is kept, or a default option is assigned (e.g., the most common value for a certain characteristic). This might especially be the case when defining the last buildings in a certain area or for the whole building stock, therefore, are buildings assigned one at a time for each area rather than completing an entire area and then moving on to the next. This also ensures that potential errors in assigning buildings might be spread over the entire area and not be clustered in individual areas. Similar to the sample-based approach, the generation was repeated 100 times from which the stock with the best fit was according to the highest PGP (see Equation (1)) in order to reduce the error due to the stochastic nature of the methodology.
Building Stock Characterization
The building characterization step fills in the remaining building attributes not included in the building and dwelling registry. This includes the building geometry, component U-values, heating and ventilation systems as well as the building usage related data such as indoor temperature, number of occupants or hot water usage. The building geometry is estimated by first estimating the area of the building footprint by dividing the total floor area by the number of floors. The building geometry can then be estimated based on calculated footprint, the number of floors and generic data such as the window to all ratio, aspect ratio and the floor height, which are estimated based on the building type and construction year of the building from data contained in the BSEM [13,15] as well as from [28]. A detailed description of the process can be found in [13]. The U-values of the different components are then estimated based on construction year and building type based on the data from [28]. The building usage-related data such as indoor temperature, number of occupants or hot water usage are estimated based on standard user data [13,15]. Lastly, each building is randomly assigned a heating system based on distribution in the stock based on the building type and location according to data from [28]. The system efficiency of the assigned heating system is then estimated from the generic data contained in the BSEM [13,15]. The data from [28] was assumed to be up to date, which is why no additional building updating step was performed.
3. Results
3.1. Validation
Figure 3 shows the spatial distribution of the achieved PGP (see Equation (1)) across the two case study areas. The PGP for each area in each case is calculated by comparing the observed and predicted distribution across different attributes. Due to different structure and content of the data used in the two cases, the PGP is calculated using the distributions across different attributes. In the case of Dublin, the PGP is calculated by comparing the distribution across the attributes building type, construction period and main energy carrier. In the case of the building stock of Waidhofen an der Thaya, the comparison is made across the attributes on both the building (building type, construction period, building size, number of dwellings) and building usage level (number of rooms and dwelling size). In both cases, the generated synthetic building stock matched the reference data well as highlighted by the high PGP overall. Figure 4 shows the distribution of PGP for each area, which shows the overall good fit for both cases.
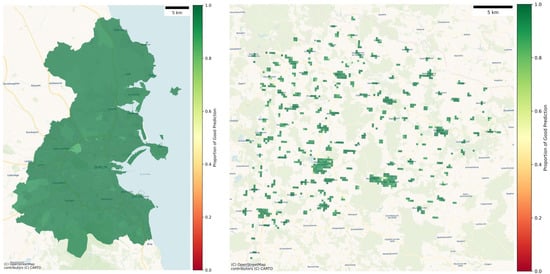
Figure 3.
Spatial distribution of the PGP for Dublin (left) and Waidhofen an der Thaya (right).
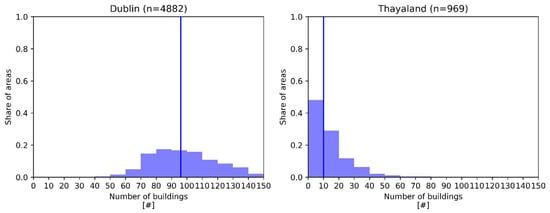
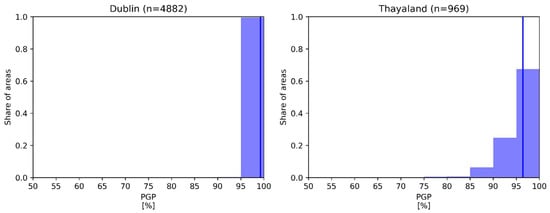
Figure 4.
Distribution of the number of buildings per area (top) and the PGP score per area (bottom) for both cases. The vertical line indicates the median value. An area constitutes the spatial unit used to generate the spatial building stock (Small area in the case of Dublin, grid cell in the case of Thayaland).
However, Figure 4 indicates a significantly larger share of areas with a lower PGP and also a lower median value for the Waidhofen case study compared to the Dublin case. This may be due to the larger number of reference data points for calculating the PGP as well as the significantly lower number of buildings per area in Waidhofen compared to the Dublin case. Both of these aspects make the generation of the synthetic building stock more complex and therefore harder to match the distribution in the reference data.
3.2. Distribution of Energy Demand
3.2.1. Dublin
Figure 5 provides an overview of the spatial distribution of the heat demand of the Dublin building stock as well as an overview of the energy carrier distribution. At the city core, the overview shows an area with low density, which corresponds to a commercially dominated area with very little residential usage. This core is surrounded by areas with relatively higher heat demand densities around the centre and lower densities in the surrounding areas.
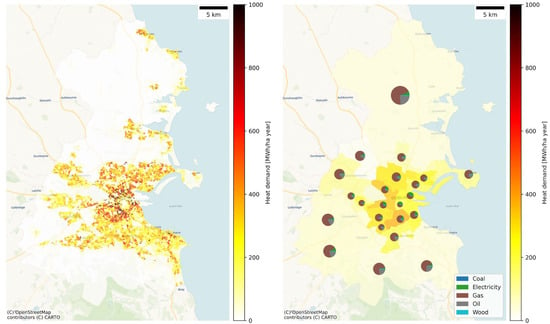
Figure 5.
Spatial distribution of the heat demand density per small area (left) and energy carrier distribution related to the required heat demand per postcode (right) in Dublin.
Overall, the heat demand in Dublin is gas dominated with 74% of the overall demand being covered by natural gas, followed by oil and electricity. The areas with higher heat demand density in the city centre are all gas-dominated as can be seen in Figure 5, while the surrounding areas show larger share of oil and electric heating, particularly in the northern areas. The higher energy demand densities in the gas-dominated areas would make them feasible for the development of district heating solutions as part of a decarbonization strategy, as there is a larger cluster of areas with a heat demand density of more than 500 MWh/ha, which makes them suitable for the development of such networks. This cluster might be even larger if the non-residential stock were included. Figure 6 shows that 34% of the areas fall into this category, which corresponds to about 21% of the floor area in Dublin. The remaining 66% of areas most likely will require other solutions for renewable heating such as heat pumps or an increase in wood-based heating systems, which might be more suitable.
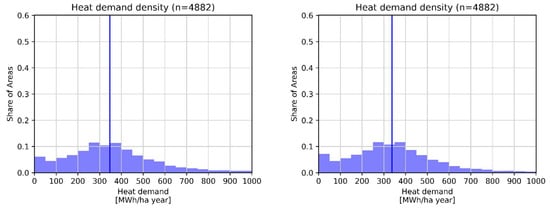
Figure 6.
Frequency of small areas according to their heat demand density in Dublin weighted based on the number of areas (left) or the total floor area of the respective area (right). The vertical line indicates the median value.
3.2.2. Waidhofen
Figure 7 gives an overview of the spatial distribution of the heat demand of the building stock in Waidhofen an der Thaya as well as an overview of the distribution of energy carriers used to cover the heat demand in the different municipalities in the area. Compared to the Dublin area, this is a rural-dominated region, which is seen by the comparatively lower heat demand densities in this region as well as large empty space in the spatial distribution of the heat demand shown in Figure 7. That said, some areas with higher heat demand densities exist, which constitute the larger population centres in the region. However, none of the areas exceeds a density of 500 MWh/ha (see also Figure 8).
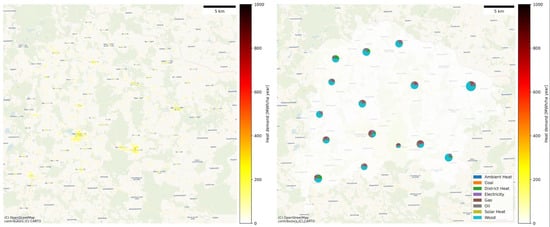
Figure 7.
Spatial distribution of the heat demand density per grid cell (left) and energy carrier distribution related to the required heat demand per municipality (right) in Waidhofen.
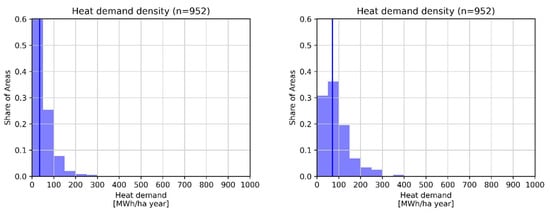
Figure 8.
Frequency of grid cells according to their heat demand density in Waidhofen weighted based on the number of areas (left) or the total floor area of the respective area (right). The vertical line indicates the median value.
Overall, the heat demand in Waidhofen is dominated by wood (and other biomass) making up about 49% of the heat demand, followed by oil and natural gas, each making up about 15% and 17%. Despite the relatively low heat demand densities, several small-scale district heating networks exist in the region [28] totalling about 9% of the modelled heat demand. However, Figure 8 shows that the majority of areas fall in areas with a heat demand density of well below 300 MWh/ha, making district heating not a viable option in the vast majority of the region. In these regions, continued use of wood and other biomass and expansion of other solutions for renewable heating such as heat pumps in combination with solar collectors or solar cells might be more suitable to replace the remaining fossil-fuel-based heating systems in the region.
4. Discussion
In this article, two approaches for the synthetic generation of spatially distributed building stocks were presented and implemented in two different countries and contexts (city and region) with different available datasets. The described approaches improved the existing building stock modelling approaches by enabling a detailed analysis of the spatial distribution of building stocks and their energy demand even in cases where building-level data was unavailable or incomplete. In comparison with a building-specific BSEM approach, the SBSEM approach did not rely on a complete building-specific dataset to function but worked also in cases where only a sample or no building-specific data was available. Therefore, an SBSEM approach is more flexible in its application as it mainly builds upon aggregate data that is ubiquitously available. Moreover, the approach gives more flexibility in what kind of data can be used as different datasets and data sources can be combined.
Because SBSEM approaches use a more simplified representation of a building that is at least partially synthetically reconstructed, the synthetic data is often cleaner and more uniform compared to building-specific BSEMs. This makes it easier to handle compared to more complex building-level data, which is often incomplete or faulty and therefore requires extensive data cleaning and processing before it can be used in a BSEM. Because of that process, certain buildings may have to be filtered out due to a lack of information (e.g., not all buildings have an energy performance certificate that forms the basis of the analysis) or faulty data, which affects the completeness of the output. This is not the case in the synthetic approaches presented in this paper as they work based on the aggregated stock data, which can be assumed to encompass the complete building stock and hence the output can be assumed to represent the complete building stock as well.
As SBSEM approaches build upon data that is publicly available, they may be more quickly deployed in a new region compared to a building-specific approach as no sensitive data is used that may need to be specially sourced or may otherwise be restricted in its use (e.g., limitations on what data can be published). This is especially true if an SBSEM has already been developed for a region with a similar data structure, e.g., a region in the same country. This makes these approaches especially suitable for more rural areas, such as the Waidhofen case described in this paper, where both the resources and data for spatial energy demand analysis are often more scarce compared to urban centres.
The quality of the generated synthetic building stock, and with it the obtained results from an SBSEM, still heavily depend on the quality of the input data. While additional data can be added through the building characterization step, the representativeness of the spatial distribution is limited to what is available in the base dataset. Hence, if data on the spatial distribution of key attributes is missing, this data cannot be replaced with more aggregate data, while at the same time still giving a reliable output on the spatial distribution of the energy demand. For example, if data on the spatial distribution of installed heating systems is missing, an analysis of the spatial distribution of the energy demand according to different energy carriers is not feasible. Therefore, the level of detail in the spatial analysis is limited to the spatial aggregation of the input data (e.g., statistical areas or grid cells). Moreover, in contrast to building-specific BSEMs, the finest level of detail in spatial aggregation (i.e., the building scale) is missing in SBSEMs as buildings are not referenced to a specific location but rather to a specific area (e.g., grid cell).
Moreover, both approaches for the SBSEM presented in this paper make use of stochastic methods to spatially distribute and characterize buildings. Hence, some errors and deviations in the composition and spatial distribution of the synthetic building stock compared to the input data may occur as shown in the validation of the case study results. However, this error can be minimized by repeating the stock generation multiple times and choosing the best fitting result as was done in this study.
The validation of the generated building stocks for the two cases shows, that both approaches can adequately reproduce the spatial distribution and structure of the original building stock reflected in the high PGP in both cases. The primary difference stems from the structure of the data used as a basis for the stock generation (i.e., the use of a sample or not). This inherent difference between the two approaches also comes with some differences in the applicability and characteristics of the generated stock.
The use of a sample has the advantage of using “real” building data as a basis of the analysis, which increases the reliability of the modelled results on the building level. However, the generated synthetic building stock is also limited through that sample. Especially, in cases where only a sample of a limited number of buildings is available, the generated building stock might not cover the full heterogeneity of buildings in the stock and rare cases of buildings might be missing in the sample. This might also impact the stock generation process using the IPU algorithm as the distribution of the sample depends on having access to a representative sample of buildings.
In contrast, the sample-free approach is not bound by these limitations and can also cover special cases, which may not be covered in a sample. This might make it easier for the sample-free approach to match the boundary conditions more closely, especially in areas with only a few buildings. However, as buildings are generated by randomly combining different building characteristics, the approach might also yield unrealistic combinations of building attributes in some cases, especially if reliable data on the combination of building characteristics is unavailable [13].
5. Conclusions
This paper presented two alternative approaches for spatial building stock energy demand analysis for cases where building-specific geo-referenced data is not available or not complete enough to model individual buildings. The two approaches were differentiated based on two common situations of data availability of building stock energy data: (1) where a sample of building-level data is available, and (2) where no sample is available. Both methods synthetically generate a spatially distributed building stock that can be used to analyse the spatial distribution of the energy demand of building stocks. The proposed approaches were applied to two different cases, Dublin and Waidhofen an der Thaya, and validated based on their ability to reconstruct the spatial distribution of the building stock for these cases. Both showed a good ability in reconstructing the spatial distribution of the stock and the choice of which approach to take, which therefore primarily depended on the data availability of the case in question.
The results of the two case studies demonstrated how by using a synthetic building stock modelling approach, a spatial analysis for building stock energy demand could be carried out for cases where no building level data is available. The case studies showed how the obtained results could be used for energy planning. As a next step, the estimated spatial distribution of heat demand should be matched with an assessment of renewable energy sources such as heat sources for local district heating as well as assess the feasibility of other renewable heating systems such as heat pumps and/or wood-based heating.
The spatial analysis of building stock energy demand using synthetic building stocks comes with many challenges, as outlined in this paper, and lays the groundwork for future work. A possible next step could be to combine the synthetic building stock with a synthetic population to improve the assessment of occupant behaviour on energy demand as well as enable assessments of the socio-economic impact of energy demand and potential measures to reduce energy demand or climate impact. For that purpose, the static model presented in this paper could be expanded with a dynamic model of the development of the spatial energy demand. Here, agent-based methodologies as presented in [15] could be a possible way forward. Lastly, although the method was designed to be applied in cases where data availability is poor, it can be used for a quick assessment of the demand distribution. The quality of the generated synthetic building stock depends on the quality of the input data and, if data on the spatial distribution of key attributes is missing, then the differences in the distribution of these attributes can also not be reconstructed in the generated synthetic stock. Hence, data on the spatial distribution of building attributes as well as the distribution of the combination of building attributes would help to improve the quality of synthetic spatial building stocks.
Author Contributions
Conceptualization, C.N.; Data curation, C.N., R.C. and S.S.; methodology, C.N.; validation, C.N.; formal analysis, C.N.; writing—original draft preparation, C.N.; writing—review and editing, C.N., L.T., H.W., R.C. and A.H.; visualization, C.N.; supervision, L.T. and H.W.; project administration, H.W. and L.T.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union’s Horizon 2020 research and innovation program (grant number agreement 775970), the Swedish Energy Agency (project number 47839-1), the Sustainable Energy Authority of Ireland (SEAI) (project number 19/RDD/581), and the Austrian Research Promotion Agency (FFG) (project number 872290).
Acknowledgments
This research work was accomplished within the project REDAP, an ERA-Net-SES initiative project which was funded by partners of the ERA-Net SES 2018 joint call RegSys (www.eranet-smartenergysystems.eu)—a network of 30 national and regional RTD funding agencies of 23 European countries. As such, this project received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 775970. The authors would also thank the Swedish Energy Agency (project number, 47839-1), the Sustainable Energy Authority of Ireland (SEAI) (project number 19/RDD/581) and the Austrian Research Promotion Agency (FFG) (project number 872290) for their financial support. Further the authors wish to express their gratitude to the project-need owners: City of Gothenburg Council, Codema, and eKUT (former Energy Agency of the Regions).
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Commission Factsheet: The Energy Performance of Buildings Directive. 2017. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/buildings_performance_factsheet.pdf (accessed on 13 September 2020).
- Kavgic, M.; Mumovic, D.; Summerfield, A.; Stevanovic, Z.; Ecim-djuric, O. Uncertainty and Modeling Energy Consumption: Sensitivity Analysis for a City-Scale Domestic Energy Model. Energy Build. 2013, 60, 1–11. [Google Scholar] [CrossRef]
- Langevin, J.; Reyna, J.L.; Ebrahimigharehbaghi, S.; Sandberg, N.; Fennell, P.; Nägeli, C.; Laverge, J.; Delghust, M.; Mata, É.; Van Hove, M.; et al. Developing a Common Approach for Classifying Building Stock Energy Models. Renew. Sustain. Energy Rev. 2020, 133, 110276. [Google Scholar] [CrossRef]
- Nägeli, C.; Jakob, M.; Catenazzi, G.; Ostermeyer, Y. Policies to Decarbonize the Swiss Residential Building Stock: An Agent-Based Building Stock Modeling Assessment. Energy Policy 2020, 146, 111814. [Google Scholar] [CrossRef]
- Sandberg, N.H.; Næss, J.S.; Brattebø, H.; Andresen, I.; Gustavsen, A. Large Potentials for Energy Saving and Greenhouse Gas Emission Reductions from Large-Scale Deployment of Zero Emission Building Technologies in a National Building Stock. Energy Policy 2021, 152, 112114. [Google Scholar] [CrossRef]
- Kranzl, L.; Hummel, M.; Müller, A.; Steinbach, J. Renewable Heating: Perspectives and the Impact of Policy Instruments. Energy Policy 2013, 59, 44–58. [Google Scholar] [CrossRef]
- Fonseca, J.A.; Nguyen, T.; Schlueter, A.; Marechal, F. City Energy Analyst (CEA): Integrated Framework for Analysis and Optimization of Building Energy Systems in Neighborhoods and City Districts. Energy Build. 2016, 113, 202–226. [Google Scholar] [CrossRef]
- Österbring, M.; Nägeli, C.; Camarasa, C.; Thuvander, L.; Wallbaum, H. Prioritizing Deep Renovation for Housing Portfolios. Energy Build. 2019, 202, 109361. [Google Scholar] [CrossRef]
- Reinhart, C.F.; Cerezo Davila, C. Urban Building Energy Modeling—A Review of a Nascent Field. Build. Environ. 2016, 97, 196–202. [Google Scholar] [CrossRef]
- Mastrucci, A.; Marvuglia, A.; Leopold, U.; Benetto, E. Life Cycle Assessment of Building Stocks from Urban to Transnational Scales: A Review. Renew. Sustain. Energy Rev. 2017, 74, 316–332. [Google Scholar] [CrossRef]
- Österbring, M.; Mata, É.; Thuvander, L.; Mangold, M.; Johnsson, F.; Wallbaum, H. A Differentiated Description of Building-Stocks for a Georeferenced Urban Bottom-up Building-Stock Model. Energy Build. 2016, 120, 78–84. [Google Scholar] [CrossRef] [Green Version]
- Mangold, M.; Österbring, M.; Wallbaum, H. Handling Data Uncertainties When Using Swedish Energy Performance Certificate Data to Describe Energy Usage in the Building Stock. Energy Build. 2015, 102, 328–336. [Google Scholar] [CrossRef]
- Nägeli, C.; Camarasa, C.; Jakob, M.; Catenazzi, G.; Ostermeyer, Y. Synthetic Building Stocks as a Way to Assess the Energy Demand and Greenhouse Gas Emissions of National Building Stocks. Energy Build. 2018, 173, 443–460. [Google Scholar] [CrossRef]
- Beckman, R.J.; Baggerly, K.A.; McKay, M.D. Creating Synthetic Baseline Populations. Transp. Res. Part A Policy Pract. 1996, 30, 415–429. [Google Scholar] [CrossRef]
- Nägeli, C.; Jakob, M.; Catenazzi, G.; Ostermeyer, Y. Towards Agent-Based Building Stock Modeling: Bottom-up Modeling of Long-Term Stock Dynamics Affecting the Energy and Climate Impact of Building Stocks. Energy Build. 2020, 211, 109763. [Google Scholar] [CrossRef]
- Lenormand, M.; Deffuant, G. Generating a Synthetic Population of Individuals in Households: Sample-Free vs. Sample-Based Methods. J. Artifical Soc. Soc. Simul. 2013, 16, 1–10. [Google Scholar] [CrossRef]
- Ye, X.; Konduri, K.; Pendyala, R.M.; Sana, B.; Waddel, P. A Methodology To Match Distributions of Both Household and Person Attributes in the Generation of Synthetic Populations. 88th Annu. Meet. Transp. Res. Board 2011, 9600, 1–25. [Google Scholar]
- Moeckel, R.; Spiekermann, K.; Wegener, M. Creating a Synthetic Population. In Proceedings of the 8th International Conference on Computers in Urban Planning and Urban Management (CUPUM), Sendai, Japan, 27 May 2003; pp. 1–18. [Google Scholar]
- Gargiulo, F.; Ternes, S.; Huet, S.; Deffuant, G. An Iterative Approach for Generating Statistically Realistic Populations of Households. PLoS ONE 2010, 5, e8828. [Google Scholar] [CrossRef] [PubMed]
- Nägeli, C.; Farahani, A.; Österbring, M.; Dalenbäck, J.O.; Wallbaum, H. A Service-Life Cycle Approach to Maintenance and Energy Retrofit Planning for Building Portfolios. Build. Environ. 2019, 160, 106212. [Google Scholar] [CrossRef]
- ISO 52016-1; Energy Performance of Buildings—Energy Needs for Heating and Cooling, Internal Temperatures and Sensible and Latent Heat Loads—Part 1: Calculation Procedures 2017. ISO: Geneva, Switzerland, 2017.
- CSO Regional Population Projections. Available online: https://www.cso.ie/en/statistics/population/regionalpopulationprojections/ (accessed on 25 January 2022).
- European Parliament Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings (Recast). Off. J. Eur. Union 2010, 53, 13–35. [CrossRef]
- Goverment of Ireland. Ireland’s Long-Term Renovation Strategy 2020; Goverment of Ireland: Dublin, Ireland, 2020.
- CSO Census 2016 Reports. Available online: https://www.cso.ie/en/census/census2016reports/ (accessed on 12 November 2020).
- SEAI BER Public Search. Available online: https://ndber.seai.ie/BERResearchTool/Register/Register.aspx (accessed on 12 November 2020).
- UDST UDST/Synthpop: Synthetic Populations from Census Data. Available online: https://github.com/UDST/synthpop (accessed on 1 November 2021).
- eKUT. Regional Energy Demand Analysis Portal: Thermal Energy Consumption in Thayaland Region; eKUT: Waidhofen/Thaya, Austria, 2021. [Google Scholar]
- KEM Energiezukunft Thayaland: Klima-Und Energie-Modellregionen. Available online: https://www.klimaundenergiemodellregionen.at/modellregionen/liste-der-regionen/getregion/32 (accessed on 25 January 2022).
- Statistics Austria. Regional Statsitics-Package Buildings and Dwellings Register; Statistics Austria: Vienna, Austria, 2020. [Google Scholar]
- Statistics Austria. Package Census 2011-Workplace/Local Units of Employment; Statistics Austria: Vienna, Austria, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).