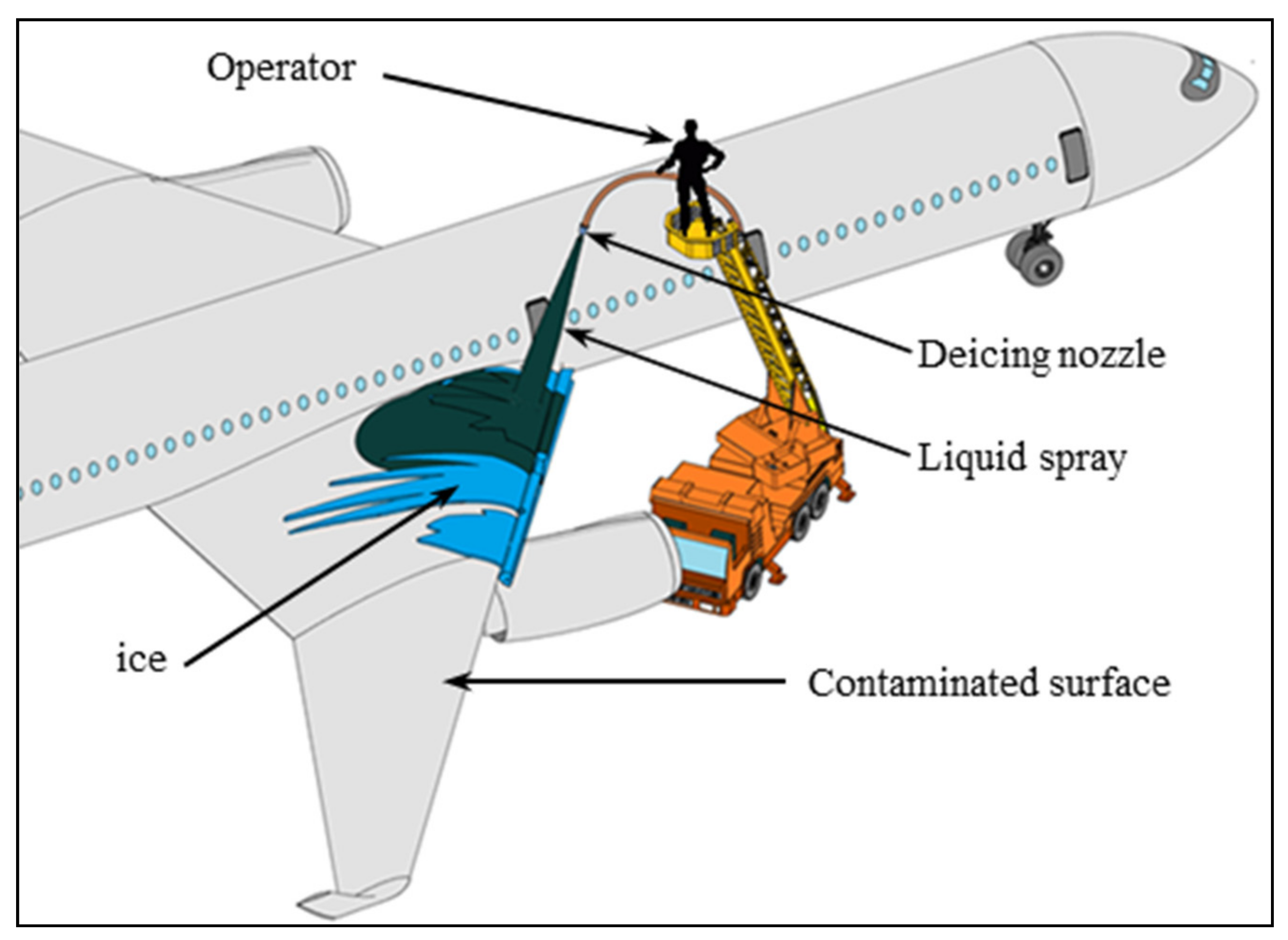
A Multi-Region CFD Model for Aircraft Ground Deicing by Dispersed Liquid Spray
Abstract
:1. Introduction
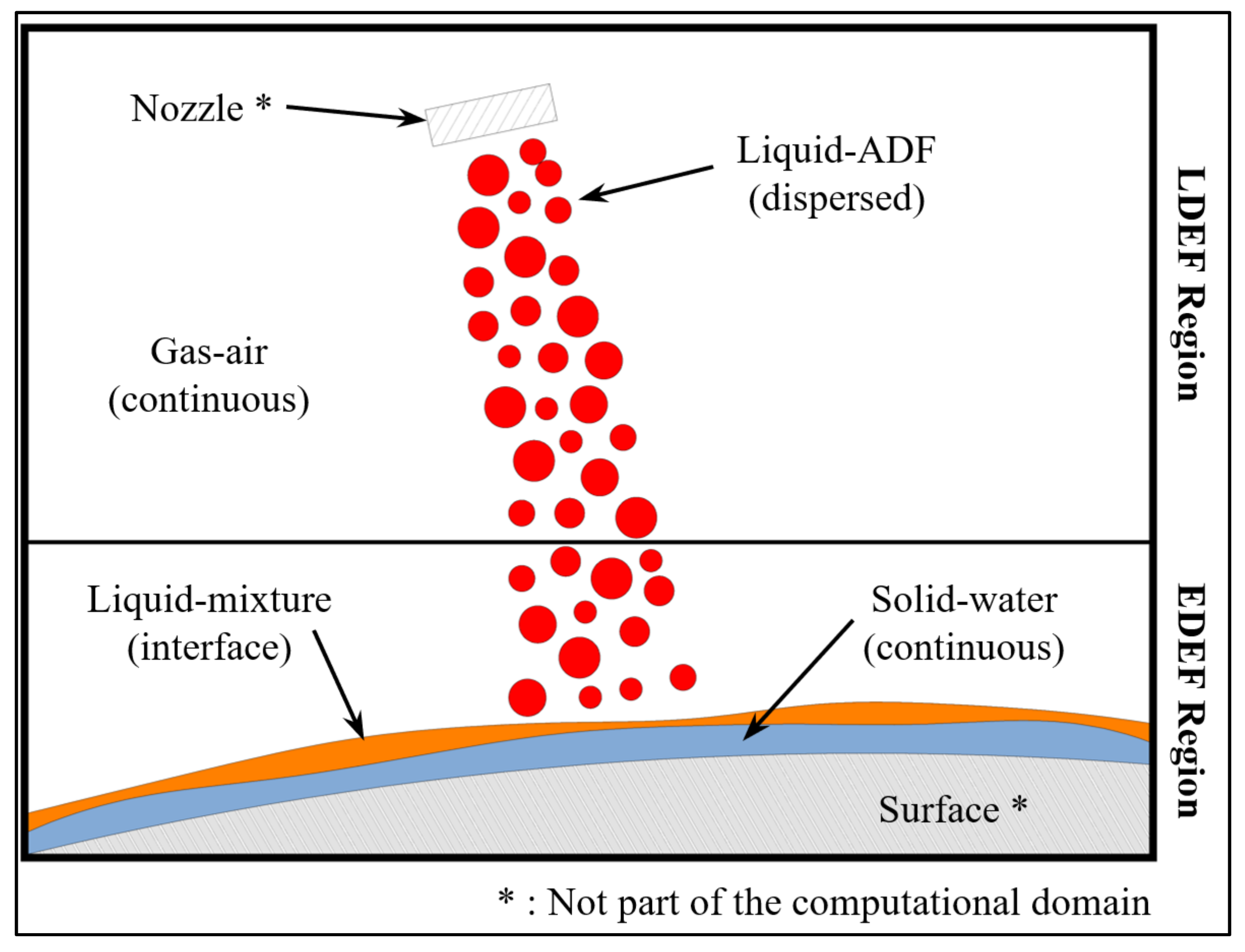
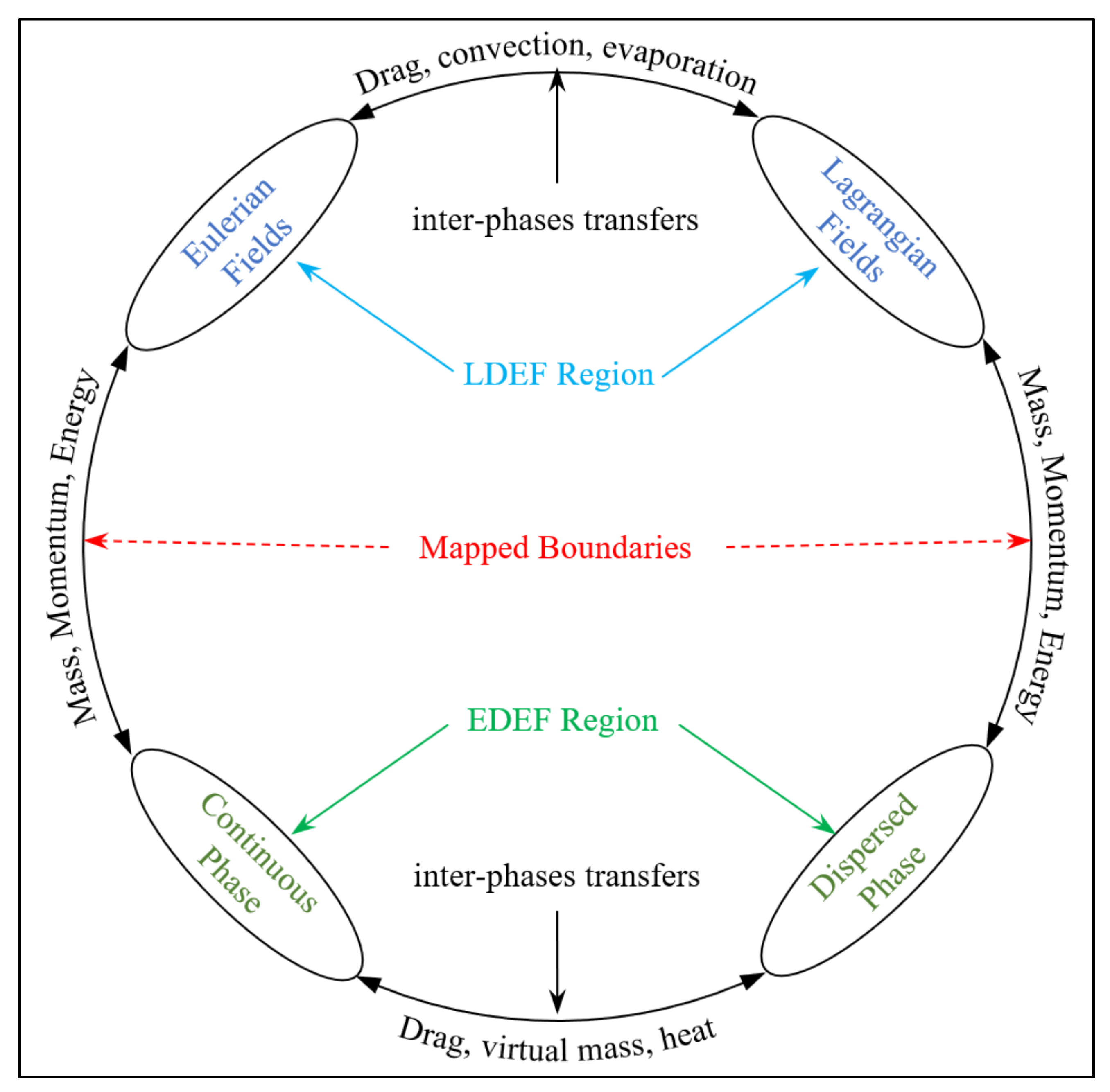
2. Mathematical Model
3. Numerical Method
- i.
- ii.
- Creating a source file to map the data between the two regions using Equations (1)–(3).
4. Verifications and Calibration
- i.
- Verify the grid- and the parcel-rate-induced errors for the Lagrangian model. This verification serves to set an adequate mesh and parcel rate for the LDEF region and to generate reference data to assess momentum conservation for the multi-region approach.
- ii.
- Verify the STP predicted using the multi-region approach compared with the STP predicted using the Lagrangian approach. This test aims to verify the momentum transfer between the two regions.
- iii.
- Calibrate the permeability coefficient of the extended enthalpy–porosity technique according to the methodology suggested in [19].
4.1. Spray Tip Penetration (STP) Test Case
4.1.1. Injection Parameters
4.1.2. Computational Domain and Mesh
4.1.3. Thermophysical Model
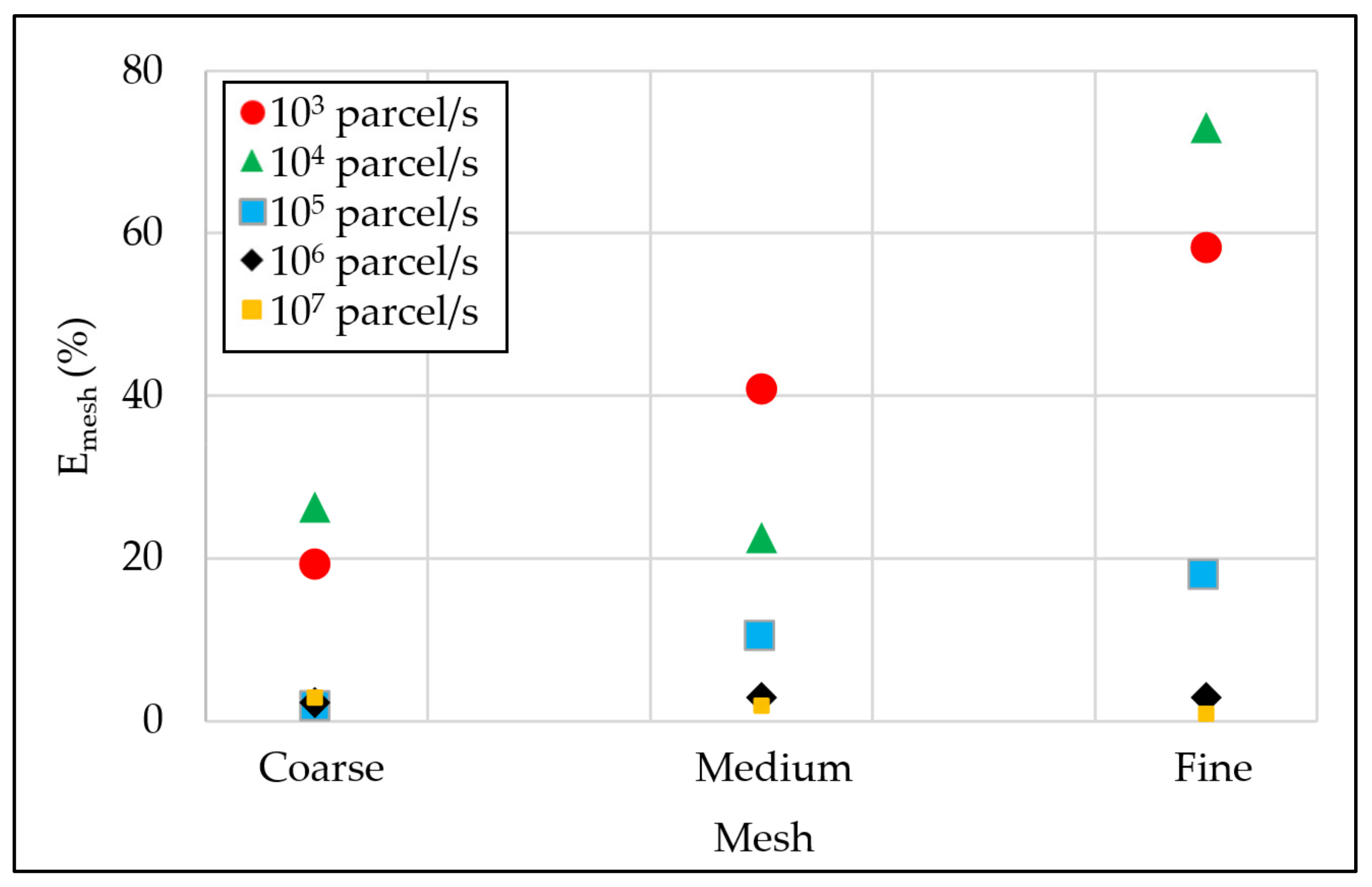
4.1.4. Parcel Rate Sensitivity
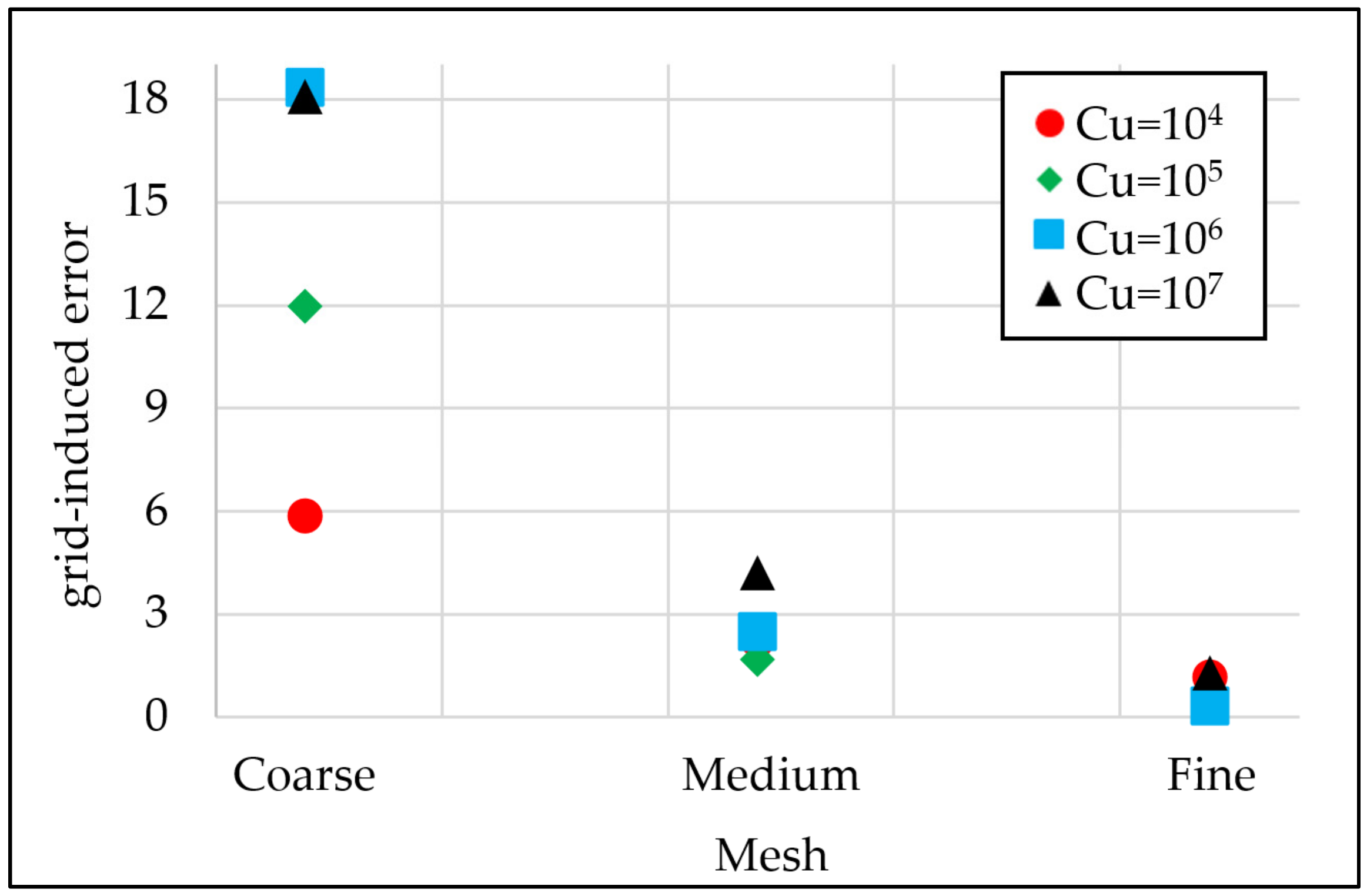
4.1.5. Grid Sensitivity
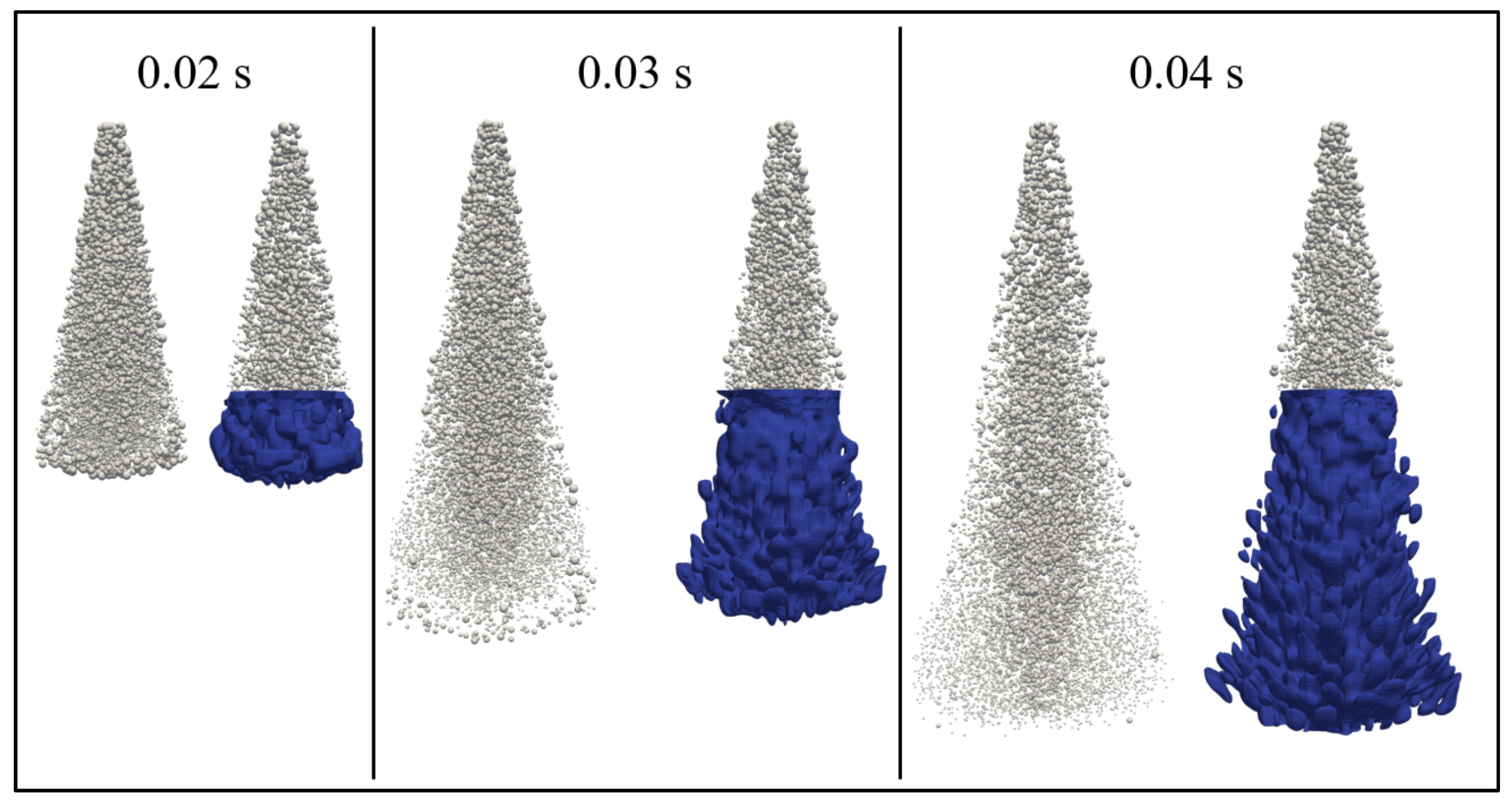
4.1.6. Multi-Region Validation
4.2. Permeability Coefficient Calibration
4.2.1. Test Case Setup and Meshes
4.2.2. Results and Analysis
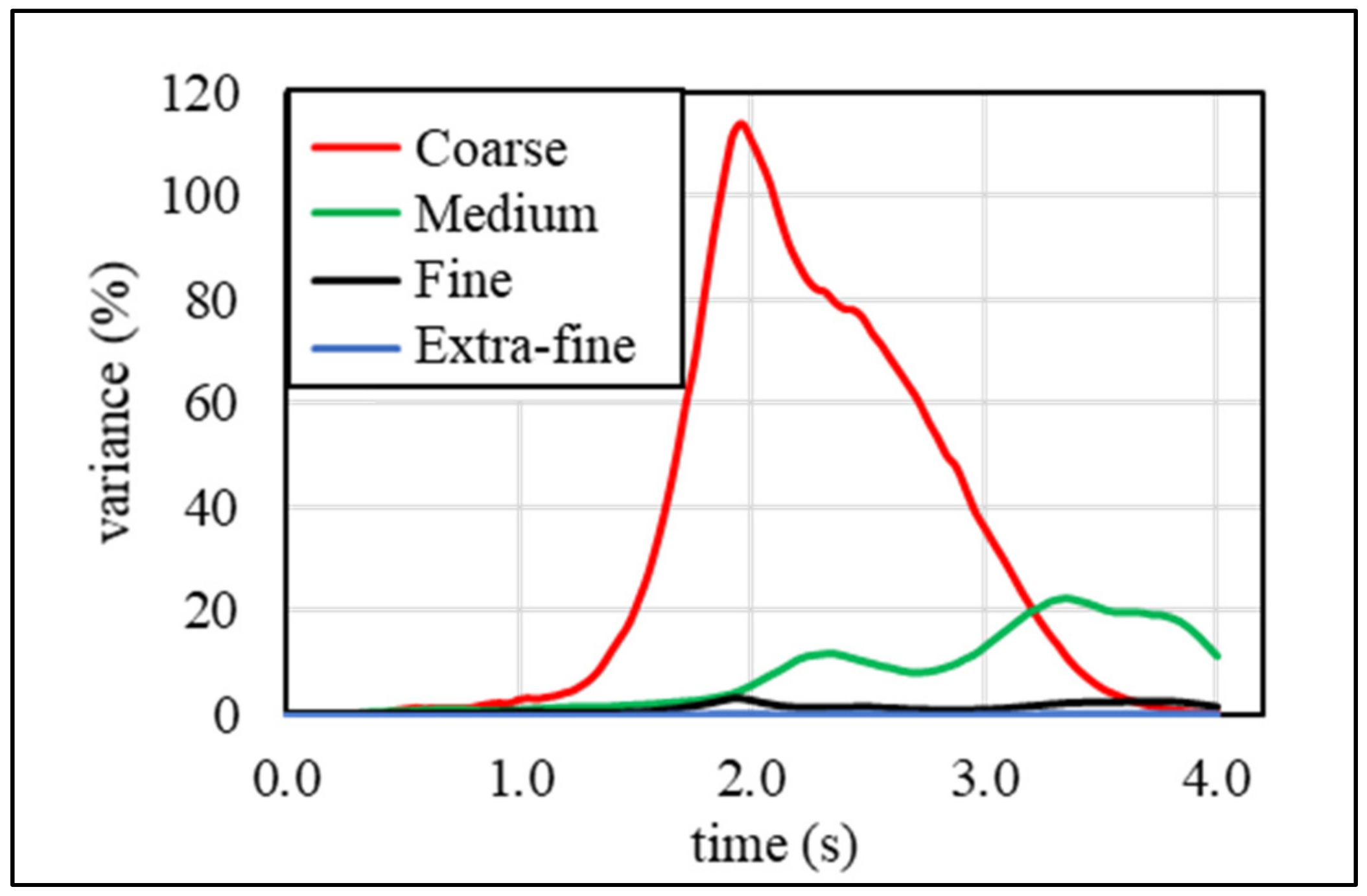
4.2.3. Grid Sensitivity
4.2.4. Permeability Coefficient Sensitivity
5. Conclusions
- Using a PR superior to brings the computations to independency from the mesh density in the Lagrangian region.
- Computations in the Eulerian region are more sensitive to the mesh density. The grid is acceptable for a mesh eight times finer than the medium mesh.
- A permeability coefficient of gives a good prediction (2%) using a medium mesh. For enhanced accuracy, it is advised to multiply the number of mesh elements by eight to reach results that are almost insensitive to the permeability coefficient.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Designation (unit) |
| Specific heat capacity | |
| Permeability coefficient | |
| Distance to the mean value (dimensionless) | |
| Parcel rate induced error | |
| Grid induced error | |
| Molar weight | |
| Mass | |
| Number of particles | |
| Parcel rate | |
| Pressure field | |
| Fluid constant | |
| Spray tip penetration | |
| Temperature | |
| Velocity | |
| Volume | |
| Species mass fraction (dimensionless) | |
| Volume fraction | |
| Solid volume fraction (dimensionless) | |
| Dynamic viscosity | |
| Phase density | |
| Variance of the normalized ice volume (dimensionless) |
Appendix A
Appendix A.1. LDEF Region Governing Equations
Appendix A.2. EDEF Region Governing Equations
References
- ICAO. International Standards and Recommended Practices: Annex 6—Operation of Aircraft—Part 1—International Commercial Air Transport—Aeroplanes: Paragraph 4.3.5.4; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- ACRP Fact Sheets, ‘De/Anti-Icing Optimization’, Transportation Research Board of the National Academies, sponsored by the FAA. 2016. Available online: http://onlinepubs.trb.org/onlinepubs/acrp/acrp_rpt_045factsheets.pdf (accessed on 28 June 2022).
- ICAO. Manual of Aircraft Ground De-Icing/Anti-Icing Operations; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- Chen, B.; Wang, L.; Gong, R.; Wang, S. Numerical simulation and experimental validation of aircraft ground deicing model. Adv. Mech. Eng. 2016, 8, 1687814016646976. [Google Scholar] [CrossRef]
- Chen, B.; Yang, Y.; Liu, J. Performance optimization of aircraft deicing equipment based on genetic algorithm. Sci. Prog. 2020, 103, 0036850419877735. [Google Scholar] [CrossRef] [PubMed]
- Yakhya, S.; Ernez, S.; Morency, F. Computational Fluid Dynamics Investigation of Transient Effects of Aircraft Ground Deicing Jets. J. Thermophys. Heat Transf. 2019, 33, 117–127. [Google Scholar] [CrossRef]
- Ernez, S.; Morency, F. Eulerian-Lagrangian CFD Model for Prediction of Heat Transfer Between Aircraft Deicing Liquid Sprays and a Surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2450–2475. [Google Scholar]
- Ernez, S.; Morency, F. CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows. Fluids 2021, 6, 210. [Google Scholar] [CrossRef]
- Durst, F.; Milojevic, D.; Schönung, B. Eulerian and Lagrangian predictions of particulate two- phase flows: A numerical study. Appl. Math. Model. 1984, 8, 101–115. [Google Scholar] [CrossRef]
- Gouesbet, G.; Berlemont, A. Eulerian and Lagrangian approaches for predicting the behaviour of discrete particles in turbulent flows. Prog. Energy Combust. Sci. 1999, 25, 133–159. [Google Scholar] [CrossRef]
- Nijdam, J.J.; Guo, B.; Fletcher, D.F.; Langrish, T.A.G. Lagrangian and Eulerian models for simulating turbulent dispersion and coalescence of droplets within a spray. Appl. Math. Model. 2006, 30, 1196–1211. [Google Scholar] [CrossRef]
- Subramaniam, S. Lagrangian–Eulerian methods for multiphase flows. Prog. Energy Combust. Sci. 2013, 39, 215–245. [Google Scholar] [CrossRef]
- Saidi, M.S.; Rismanian, M.; Monjezi, M.; Zendehbad, M.; Fatehiboroujeni, S. Comparison between Lagrangian and Eulerian approaches in predicting motion of micron-sized particles in laminar flows. Atmos. Environ. 2014, 89, 199–206. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Z.; Qu, H. Comparison between Lagrangian and Eulerian approaches for prediction of particle deposition in turbulent flows. Powder Technol. 2020, 360, 141–150. [Google Scholar] [CrossRef]
- Li, Y. Implementation of Multiple Time Steps for the Multi-Physics Solver Based on chtMultiRegionFoam. In CFD with OpenSource Software; Nilsson, H., Ed.; 2017; Available online: http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2016/YuzhuPearlLi/final_report_Jan2017.pdf (accessed on 28 June 2022).
- Nasr, G.G.; Yule, A.J.; Bendig, L. Industrial Sprays and Atomization; Springer: London, UK, 2002. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2016. [Google Scholar]
- Nobile, M. Improvement of Lagrangian Approach for Multiphase Flow. Göteborg, Sweden. 2015. Available online: http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2014/Matteo%20Nobile/RevisedReport_MatteoNobile.pdf (accessed on 28 June 2022).
- Ebrahimi, A.; Kleijn, C.R.; Richardson, I.M. Sensitivity of numerical predictions to the permeability coefficient in simulations of melting and solidification using the enthalpy-porosity method. Energies 2019, 12, 4360. [Google Scholar] [CrossRef]
- Mitroglou, N.; Nouri, J.M.; Gavaises, M.; Arcoumanis, C. Spray characteristics of a multi-hole injector for direct-injection gasoline engines. Int. J. Engine Res. 2006, 7, 255–270. [Google Scholar] [CrossRef]
- SAE. Aircraft Ground Deicing/Anti-Icing Processes AS6285D. Aerospace Standard. 2021. Available online: https://saemobilus.sae.org/content/as6285d (accessed on 28 June 2022).
- FAA. Standardized International Aircraft Ground Deice Program (SIAGDP); FAA: Washington, DC, USA, 2010. [Google Scholar]
- Task Force Tips Manual: Ice-Control Anti-Icing & Deicing Nozzles. Valparaiso, IN, USA. 2010. Available online: https://legacy.tft.com/literature/library/files/LIB-205_rev08.pdf (accessed on 28 June 2022).
- Ponziani, F.A.; Tinaburri, A. Water jet streams modeling for firefighting activities with the aid of CDF. Saf. Secur. Eng. VI 2015, 1, 323–334. [Google Scholar]
- NIST. JANAF Thermochemical Tables. NIST Standard Reference Database 13; 1998. Available online: https://janaf.nist.gov/ (accessed on 28 June 2022).
- Prakash, C.; Voller, V. On the Numerical Solution of Continuum Mixture Model Equations Describing Binary Solid-Liquid Phase Change. Numer. Heat Transf. Part B Fundam. Int. J. Comput. Methodol. 1989, 15, 171–189. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Gewerbestrasse: Cham, Switzerland; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College of Science, Technology & Medicine, London, UK, 2002. [Google Scholar]
- Kolev, N.I. Multiphase Flow Dynamics 2, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Marschall, H. Towards the Numerical Simulation of Multi-Scale Two-Phase Flows. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2011. [Google Scholar]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]


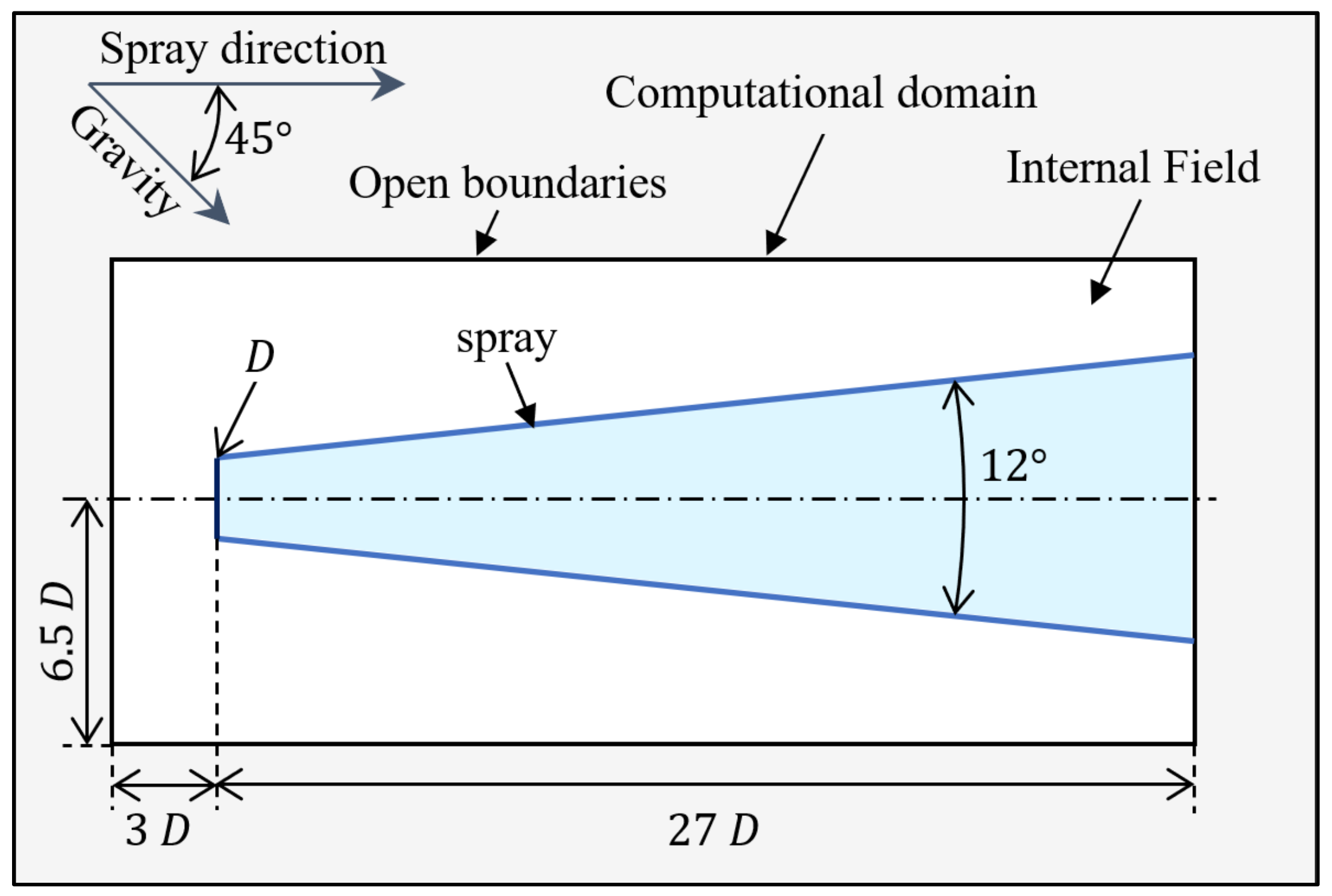








| Parameters | Fuel Sprays [20] | ADF Sprays |
|---|---|---|
| Injection pressure | 120–200 bar | 6 bar |
| Chamber pressure | 1–12 bar | 1 bar |
| Droplet mean diameter | 15–25 μm | 1–2 mm |
| Fluid viscosity | 0.78 cSt | 1 cSt |
| Fluid density | 692 kg/m3 | 1113 kg/m3 |
| Surface tension | 0.0188 N/m | 0.05 N/m |
| Spray Parameters | Values |
|---|---|
| Nozzle diameter | 38.1 mm |
| Injection pressure | 600 kPa |
| Flow rate | 200 L/min |
| Mean droplet diameter | 2.0 mm |
| Spray pattern | 12° |
| Temperature | 333.15 K |
| Meshes | Number of Cells | ||||
|---|---|---|---|---|---|
| Mesh1 | Coarse | 13 | 16 | 60 | 12,480 |
| Mesh2 | Medium | 20 | 24 | 90 | 43,200 |
| Mesh3 | Fine | 30 | 36 | 135 | 145,800 |
| Mesh4 | Extra-Fine | 45 | 60 | 200 | 540,000 |
| Mesh Id. | Number of Refinements | Number of Cells |
|---|---|---|
| Mesh 1 | 0 (medium mesh) | 43,200 |
| Mesh 2 | 1 | 184,320 |
| Mesh 3 | 2 | 1,316,640 |
| Coarse | 12.68 | 3.23 | 5.73 | 29.69 |
| Medium | 5.27 | 0.10 | 1.52 | 7.60 |
| Fine | 0.40 | 0.14 | 0.41 | 1.13 |
| Extra-fine | 0.08 | 0.11 | 0.40 | 0.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ernez, S.; Morency, F. A Multi-Region CFD Model for Aircraft Ground Deicing by Dispersed Liquid Spray. Energies 2022, 15, 6220. https://doi.org/10.3390/en15176220
Ernez S, Morency F. A Multi-Region CFD Model for Aircraft Ground Deicing by Dispersed Liquid Spray. Energies. 2022; 15(17):6220. https://doi.org/10.3390/en15176220
Chicago/Turabian StyleErnez, Sami, and François Morency. 2022. "A Multi-Region CFD Model for Aircraft Ground Deicing by Dispersed Liquid Spray" Energies 15, no. 17: 6220. https://doi.org/10.3390/en15176220
APA StyleErnez, S., & Morency, F. (2022). A Multi-Region CFD Model for Aircraft Ground Deicing by Dispersed Liquid Spray. Energies, 15(17), 6220. https://doi.org/10.3390/en15176220






