Capability for Hydrogeochemical Modelling within Discrete Fracture Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Equations for Solute Transport within DFNs
- [Pa] the residual pressure: (where g is the acceleration due to gravity, is the elevation above sea level, is the total pressure and is a reference density);
- [-] the mass fraction of solutes in the fracture;
- [-] the mass fraction of solutes in the matrix;
- [m] the effective hydraulic aperture in the fracture;
- [m] the transport aperture in the fracture;
- [kg m−3] and [kg m−1 s−1] the fluid density and viscosity, respectively. These can be calculated using an empirical expression [16];
- [m2 s−1] the volume of water flowing per second, per unit width of the fracture;
- [s] the time;
- the two-dimensional gradient operator within the fracture;
- [m2 s−1] the dispersion tensor within the mobile water in the fracture; this includes contributions from diffusion and from hydrodynamic dispersion; the latter has components parallel and perpendicular to the flow;
- [m2 s−1] the intrinsic diffusion coefficient for diffusion into the rock matrix;
- [m] the perpendicular distance from the fracture plane into the rock matrix;
- [-] the capacity factor (when there is no sorption, this is the same as the porosity of the matrix).
2.2. DFNs in ConnectFlow
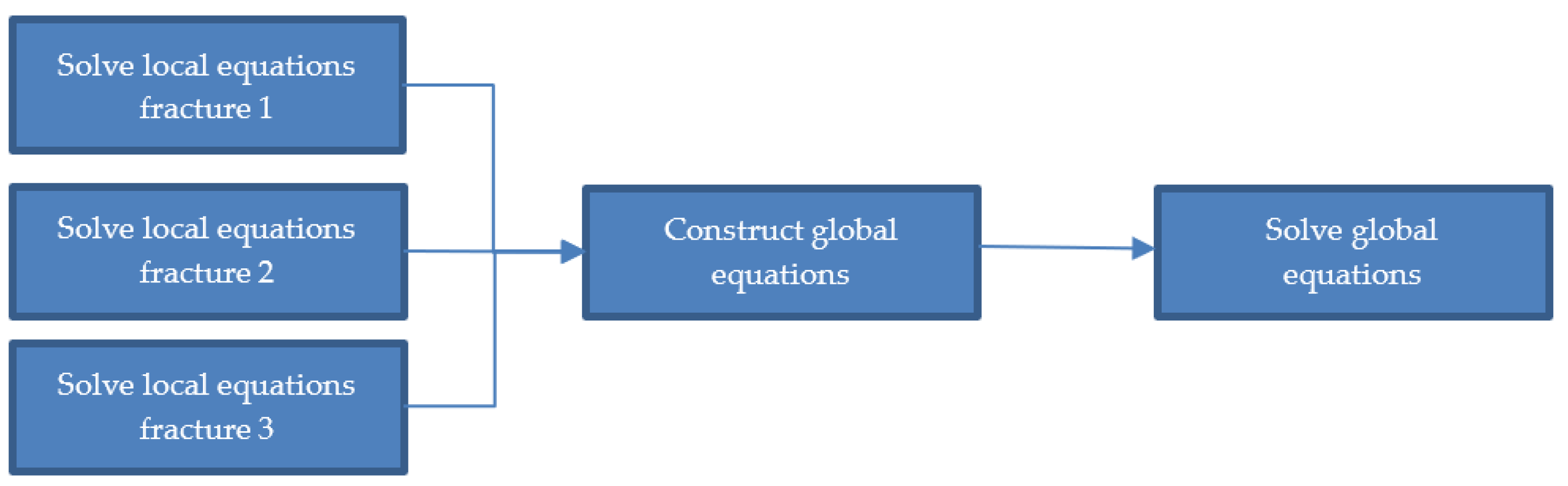
- The groundwater pressures are continuous between two intersecting fractures.
- Groundwater fluxes are conserved at an intersection between fractures.
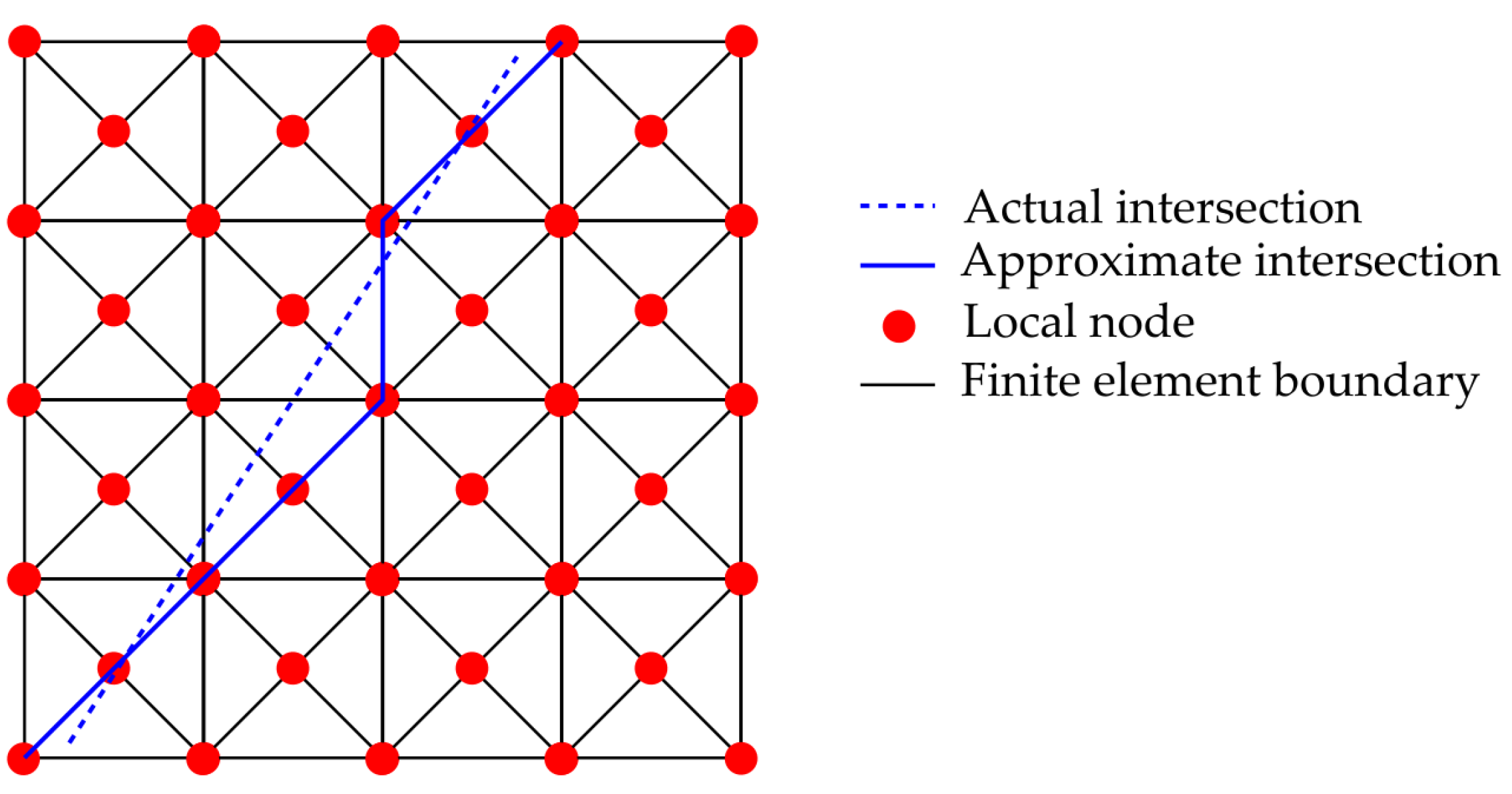
- A regular mesh of triangular elements is used to discretise individual fractures, as shown in Figure 2. The pressure and concentration are approximated on each element as a linear combination of basis functions. For each element, there is an associated node. For example, the pressure is given bywhere is the pressure at node i, and the basis function associated with node i, takes the value 1 at the node and 0 at all the other nodes. These nodes are referred to as “local nodes” in ConnectFlow.Each triangular finite element on the fracture can have a different hydraulic aperture, with values typically sampled from a probability distribution function.
- For the overall fracture network, the pressure and concentration are defined by their values at “global nodes” that exist on the intersections between fractures. The intersections are approximated using the lines formed by the boundaries of the triangular elements on the fracture (see Figure 2). The global nodes coincide with local nodes on the approximated intersection. The global problem does not have a separate mesh but rather relies on the underlying mesh on each fracture.Each global node I has a corresponding global basis function. This global basis function is approximated by the finite-element solution for the steady-state groundwater flow equations on the fracture in the case in which the residual pressure is specified to be at global node and at all the other global nodes on the fracture. The global flow and transport calculations can either be steady state or fully transient.
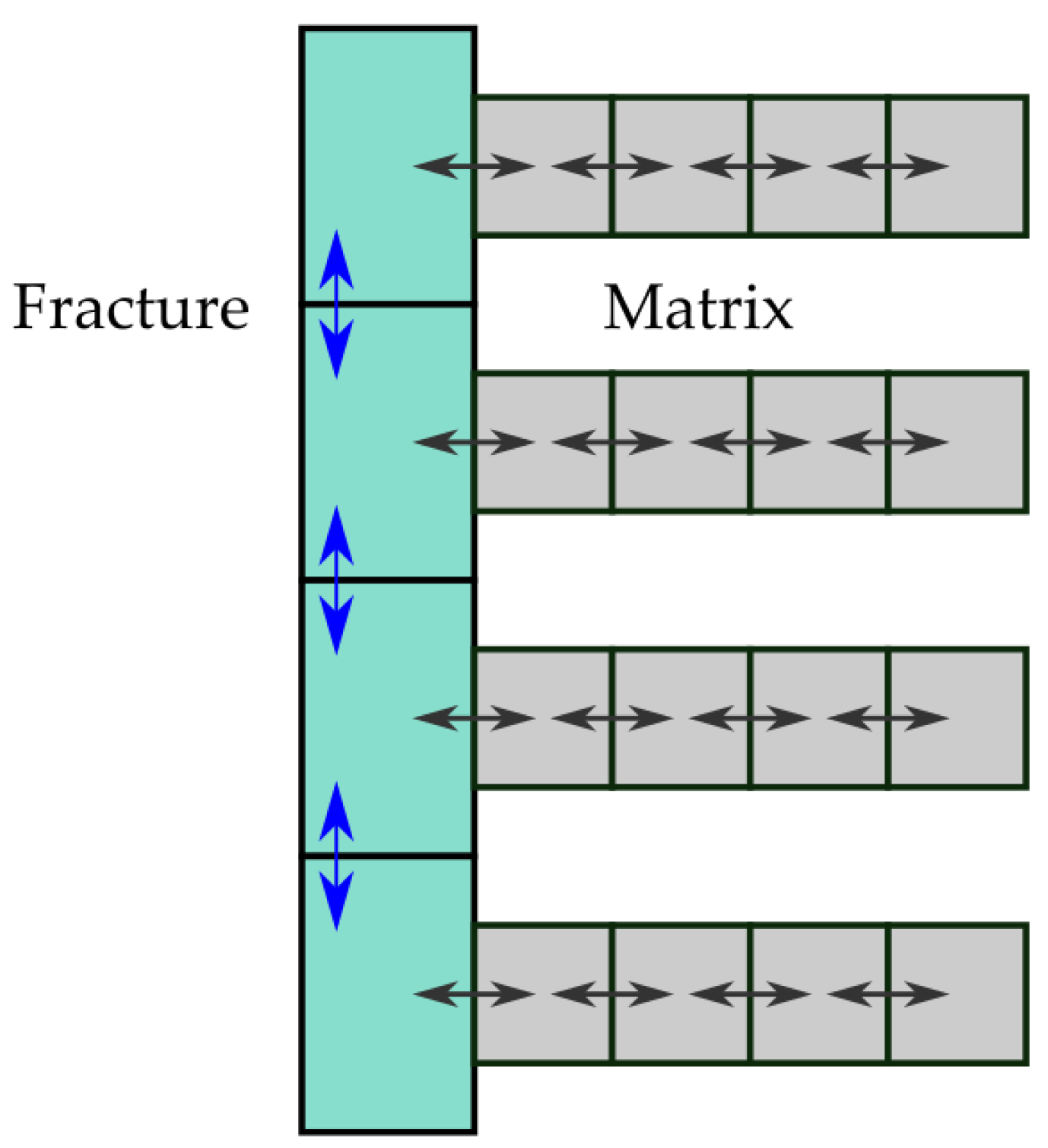
2.3. Rock Matrix Diffusion
- The total diffusion length into the matrix ;
- The number of finite volume cells per global node, ;
- The intrinsic diffusion coefficient, [m2/s];
- The porosity of the matrix or capacity factor, [-].
2.4. Representation of Solute Concentrations
- As a mass fraction, c, of a solute species, i, calculated from the mass of each species, Mi, divided by the sum of the masses of water, Mwat, and the solute species, Mj.
- 2.
- Using reference waters, which are waters (solutions) with defined (and fixed) solute compositions. In this case, n reference waters are specified, each of these has a specified composition of m solutes (fixed for the duration of the calculation). Given a mixture of reference waters, the mass fraction of a solute species i, is calculated by multiplying the fraction of each reference water Fw, by the mass fraction of species i contained within that reference water ci,w.ConnectFlow determines the proportion of each reference water with the assumption that the sum of all reference water fractions is one.
2.5. Reactive Transport
3. Results
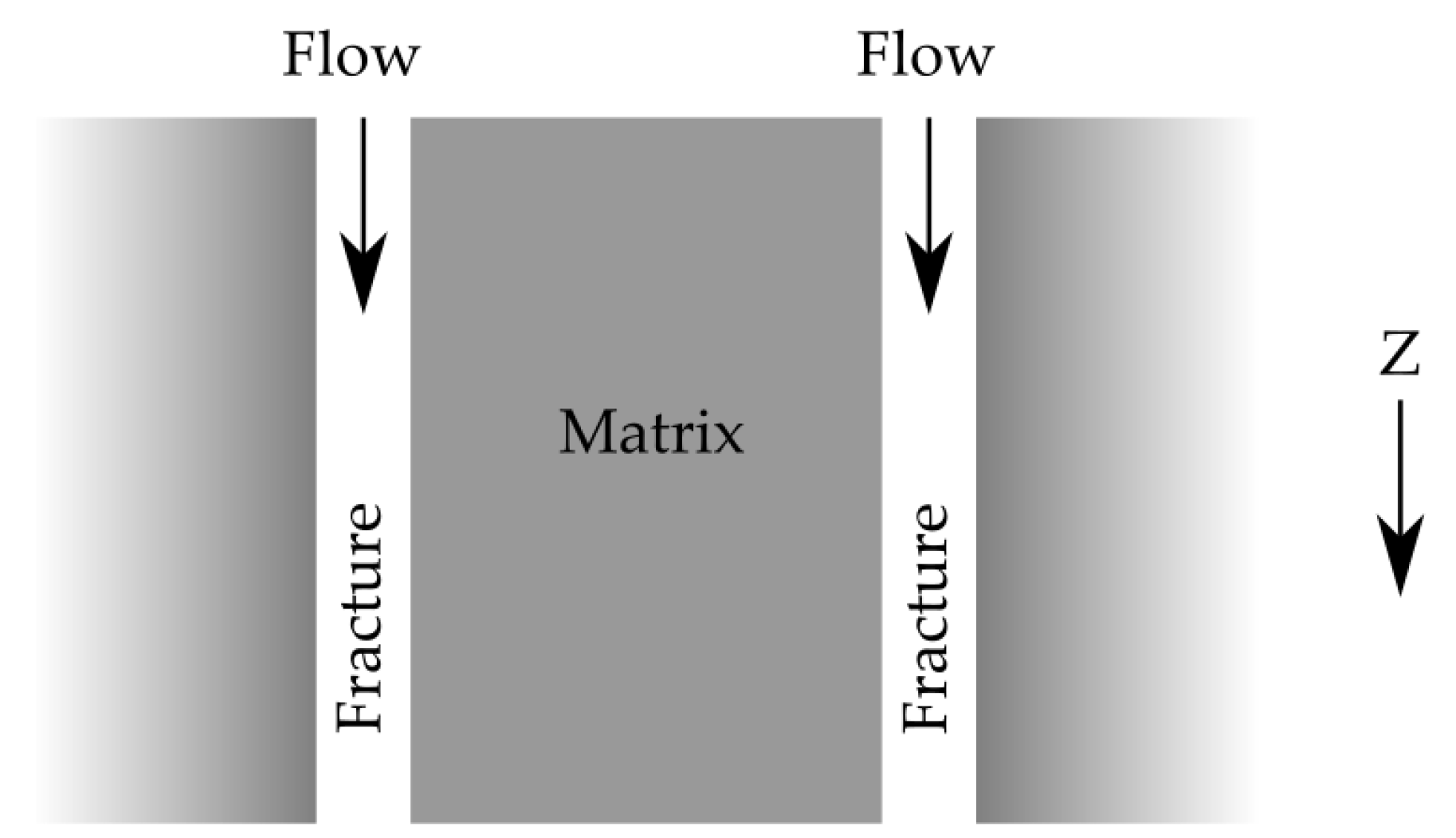
3.1. Analytical Solution for Transport within an Idealised Two Fracture System Including RMD
3.2. Single Fracture Calculations
3.3. Random Fracture Case
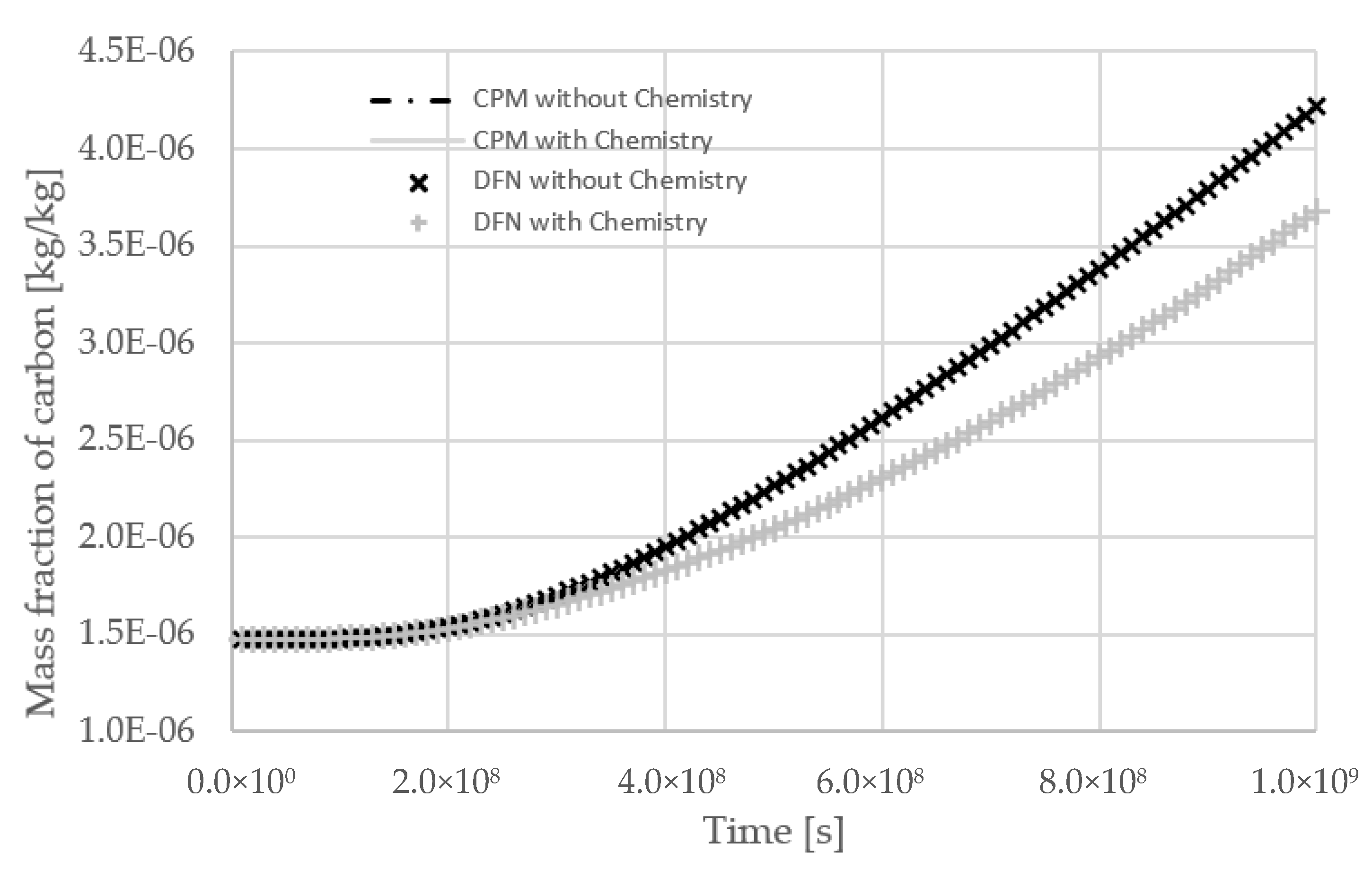
3.4. Verification for Reactive Transport in DFN Models
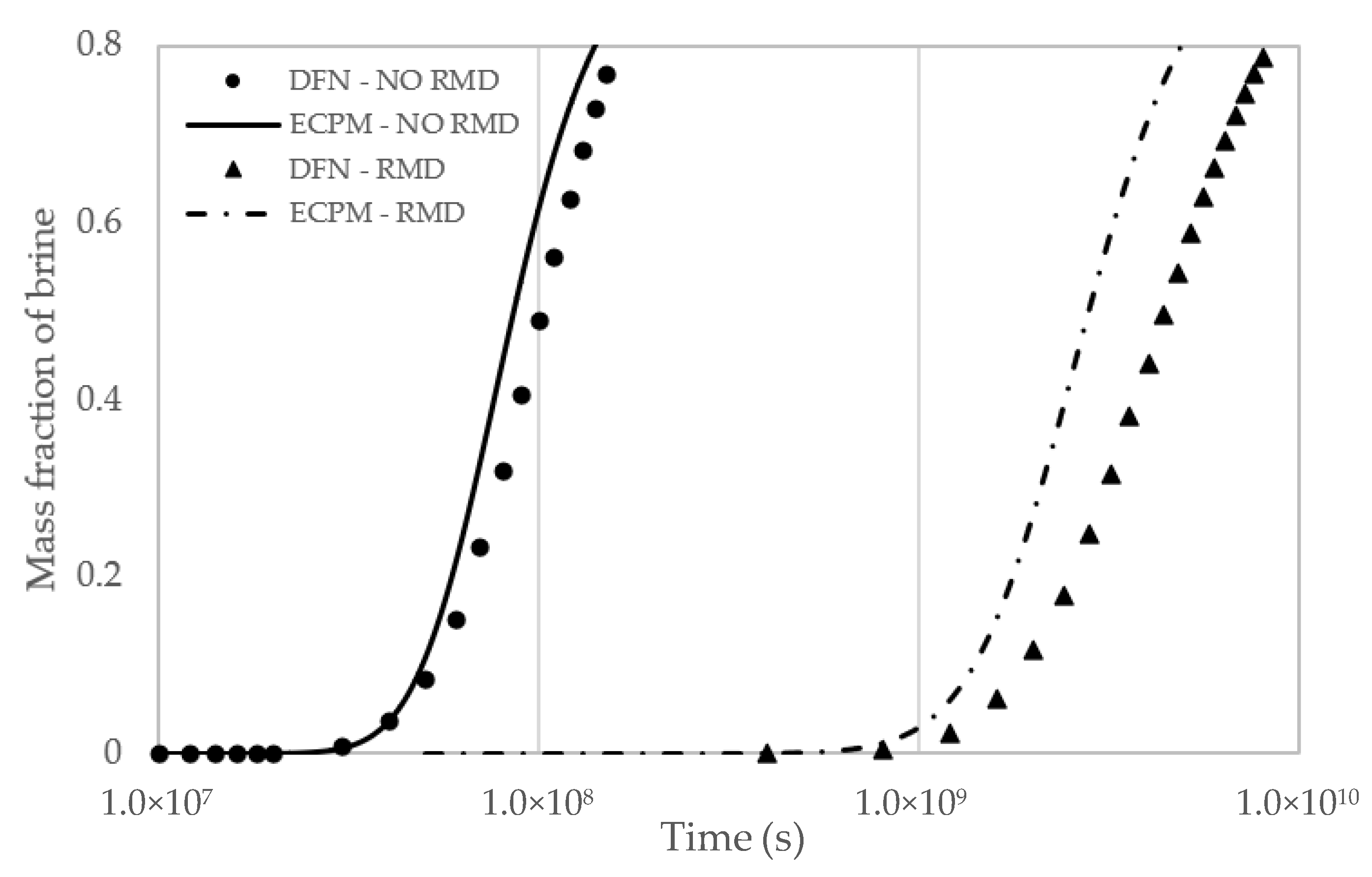
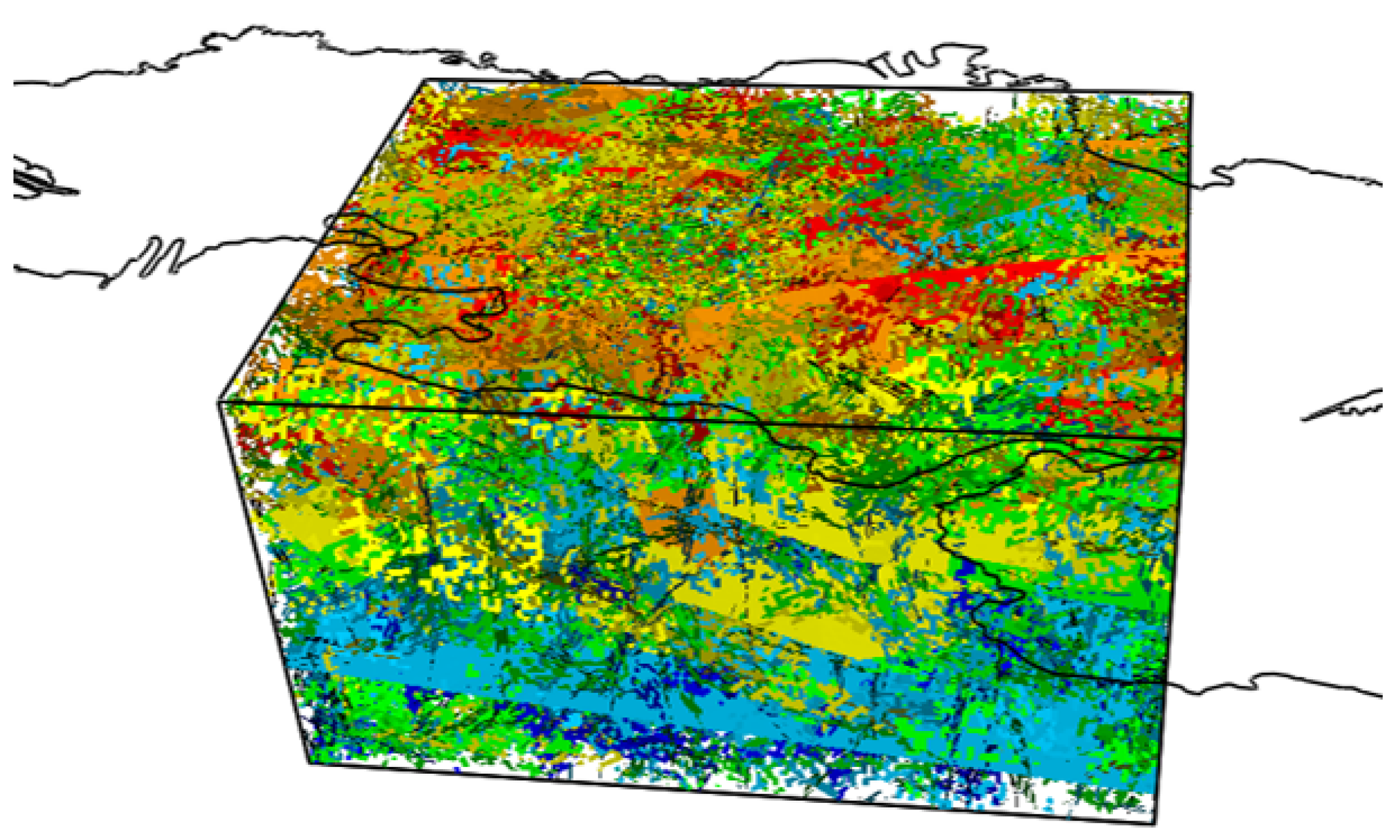
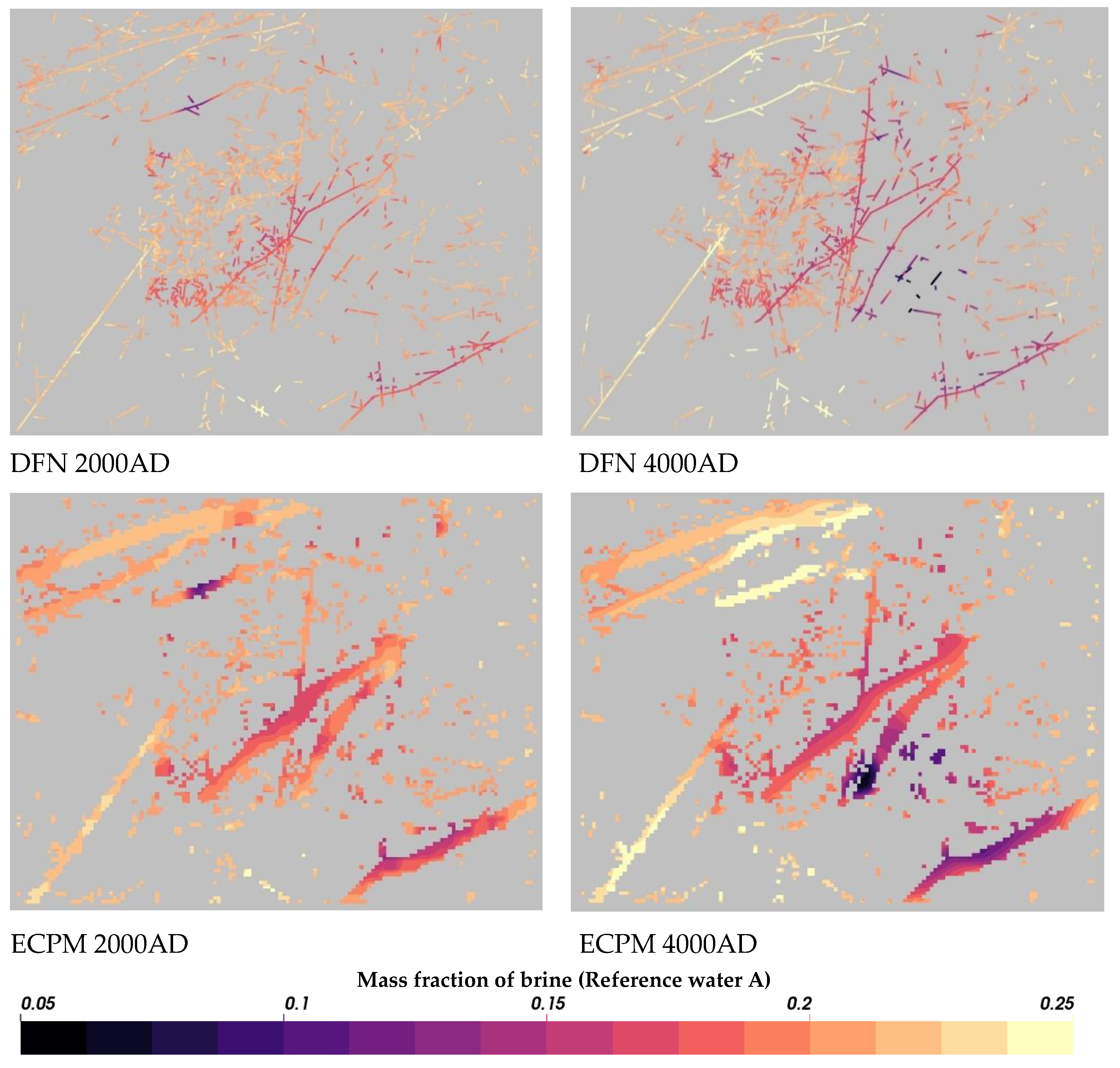
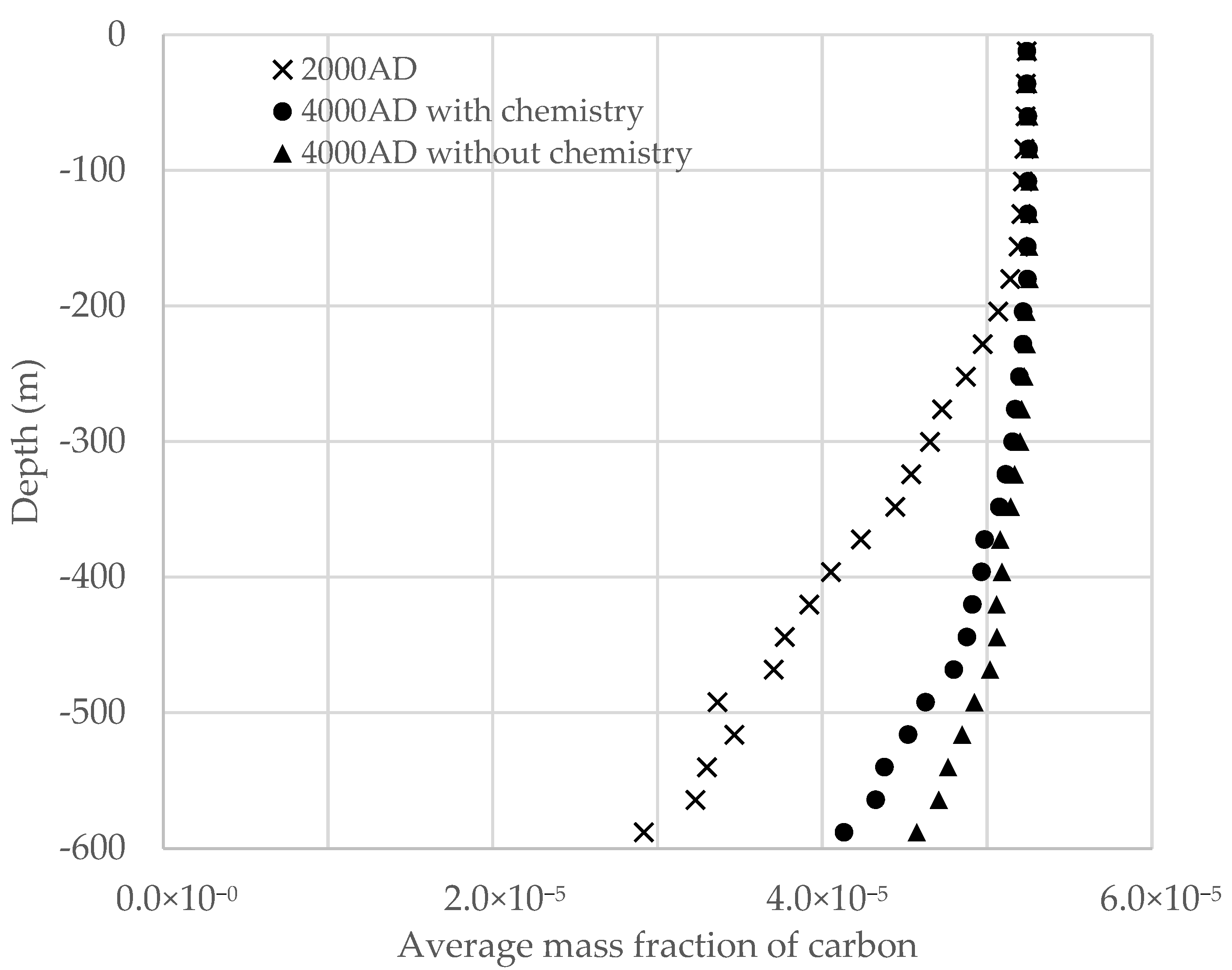
3.5. Meteoric Water Penetration at Olkiluoto Island
3.6. Laxemar Repository-Scale Model
4. Conclusions
- Transporting multiple solute species, coupled with the flow equation via the density and viscosity.
- An algorithm for calculating solute diffusion into the rock matrix (RMD) around each fracture.
- An interface with the iPhreeqc library to model chemical reactions involving solutes, rock minerals, and minerals on fracture/pore surfaces.
- The performance of ConnectFlow’s DFN module has also been significantly improved via parallelisation.
- Site-scale simulations of dilute water penetration at Olkiluoto including rock matrix diffusion.
- Repository scale calculations of dilute water penetration at Laxemar including calcite reactions and RMD. Over the 2000-year period simulated, freshwater ingress and calcite precipitation are both observed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- SKB. Long-Term Safety for the Final Repository for Spent Nuclear Fuel at Forsmark; SKB Report TR-11-01; SKB: Solna, Sweden, 2011. [Google Scholar]
- Salas, J.; José Gimeno, M.; Auqué, L.; Molinero, J.; Gómez, J.; Juárez, I. SR-Site—Hydrogeochemical Evolution of the Forsmark Site; SKB Report TR-10-58; SKB: Solna, Sweden, 2010. [Google Scholar]
- Trinchero, P.; Román-Ross, G.; Maia, F.; Molinero, J. Posiva Safety Case Hydrogeochemical Evolution of the Olkiluoto Site; Posiva Working Report 2014-09; Posiva Oy: Eurajoki, Finland, 2014. [Google Scholar]
- Joyce, S.; Applegate, D.; Appleyard, P.; Gordon, A.; Heath, T.; Hunter, F.; Hoek, J.; Jackson, P.; Swan, D.; Woollard, H. Groundwater Flow and Reactive Transport Modelling in ConnectFlow; SKB Report R-14-19; SKB: Solna, Sweden, 2014. [Google Scholar]
- Joyce, S.; Simpson, T.; Hartley, L.; Applegate, D.; Hoek, J.; Jackson, P.; Roberts, D.; Swan, D. Groundwater Flow Modelling of Periods with Temperate Climate Conditions—Laxemar; SKB Report R-09-24; SKB: Solna, Sweden, 2010. [Google Scholar]
- Gylling, B.; Trinchero, P.; Molinero, J.; Deissmann, G.; Svensson, U.; Ebrahimi, H.; Hammond, G.E.; Bosbach, D.; Puigdomenech, I. A DFN-based High Performance Computing approach to the simulation of radionuclide transport in mineralogically heterogeneous fractured rocks. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Pekala, M.; Wersin, P.; Pastina, B.; Lamminmäki, R.; Vuorio, M.; Jenni, A. Potential impact of cementitious leachates on the buffer porewater chemistry in the Finnish repository for spent nuclear fuel—A reactive transport modelling assessment. Appl. Geochem. 2021, 131, 105045. [Google Scholar] [CrossRef]
- Repina, M.; Bouyer, F.; Lagneau, V. Reactive transport modeling of glass alteration in a fractured vitrified nuclear glass canister: From upscaling to experimental validation. J. Nucl. Mater. 2020, 528, 151869. [Google Scholar] [CrossRef]
- Svensson, U.; Voutilainen, M.; Muuri, E.; Ferry, M.; Gylling, B. Modelling transport of reactive tracers in a heterogeneous crystalline rock matrix. J. Contam. Hydrol. 2019, 227, 103552. [Google Scholar] [CrossRef] [PubMed]
- Khafagy, M.M.; Abd-Elmegeed, M.A.; Hassah, A.E. Simulation of reactive transport in fractured geologic media using ran-dom-walk particle tracking method. Arab. J. Geosci. 2020, 13, 34. [Google Scholar] [CrossRef]
- Trinchero, P.; Puigdomenech, I.; Molinero, J.; Ebrahimi, H.; Gylling, B.; Svensson, U.; Bosbach, D.; Deissmann, G. Continu-um-based DFN-consistent simulations of oxygen ingress in fractured crystalline rocks. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. Abstract #H13N-02. [Google Scholar]
- Hoek, J.; Hartley, L.; Baxter, S. Hydrogeological Modelling for the Olkiluoto KBS 3H Safety Case; Posiva Working Report WR-2016-21; Posiva Oy: Eurajoki, Finland, 2016. [Google Scholar]
- Sherman, T.; Sole-Mari, G.; Hyman, J.; Sweeney, M.R.; Vassallo, D.; Bolster, D. Characterizing Reactive Transport Behavior in a Three-Dimensional Discrete Fracture Network. Transp. Porous Media 2021. [Google Scholar] [CrossRef]
- Vu, P.T.; Ni, C.-F.; Li, W.-C.; Lee, I.-H.; Lin, C.-P. Particle-Based Workflow for Modeling Uncertainty of Reactive Transport in 3D Discrete Fracture Networks. Water 2019, 11, 2502. [Google Scholar] [CrossRef]
- Sudicky, E.A.; Frind, E.O. Contaminant Transport in Fractured Porous Media: Analytical Solutions for a System of Parallel Fractures. Water Resour. Res. 1982, 18, 1634–1642. [Google Scholar] [CrossRef]
- Kestin, J.; Khalifa, E.; Correia, R. Tables of the dynamic and kinematic viscosity of aqueous NaCl solutions in the temperature range 20–150 °C and the pressure range 0.1–35 MPa. J. Phys. Chem. Ref. Data 1981, 10, 71. [Google Scholar] [CrossRef]
- ConnectFlow Website. Available online: https://www.connectflow.com/resources/docs/conflow_technical.pdf (accessed on 28 February 2022).
- Galerkin, B.G. Rods and Plates, Series Occurring in Various Questions Concerning the Elastic Equilibrium of Rods and Plates. Vestnik Inzhenerov i Tekhnikov 1915, 19, 897–908. English Translation: 63-18925, Clearinghouse Fed. Sci. Tech. Info.1963. (In Russian) [Google Scholar]
- Cordes, C.; Kinzelbach, W. Continuous Groundwater Velocity Fields and Path Lines in Linear, Bilinear, and Trilinear Finite Elements. Water Resour. Res. 1992, 28, 2903–2911. [Google Scholar] [CrossRef]
- Neretnieks, I. Diffusion in the rock matrix: An important factor in radionuclide retardation? J. Geophys. Res. 1980, 85, 4379–4397. [Google Scholar] [CrossRef] [Green Version]
- Charlton, S.R.; Parkhurst, D.L. Modules Based on the Geochemical Model PHREEQC for Use in Scripting and Pro-gramming Languages. Comput. Geosci. 2011, 11, 1653–1663. [Google Scholar] [CrossRef]
- Applegate, D.; Appleyard, P.; Joyce, S. Modelling Solute Transport and Water-Rock Interactions in Discrete Fracture Networks; Posiva Working Report WR-2020-01; Posiva Oy: Eurajoki, Finland, 2020. [Google Scholar]
- Hartley, L.; Appleyard, P.; Baxter, S.; Hoek, J.; Roberts, D.; Swan, D. Development of a Hydrogeological Discrete Fracture Network Model of Olkiluoto; Site Descriptive Model 2011; Posiva Working Report WR-2012-32; Posiva Oy: Eurajoki, Finland, 2012. [Google Scholar]
- Smellie, J.; Pitkänen, P.; Koskinen, L.; Aaltonen, I.; Eichinger, F.; Waber, F.; Sahlstedt, E.; Siitari-Kauppi, M.; Karhu, J.; Löfman, J.; et al. Evolution of the Olkiluoto Site: Palaeohydrogeochemical Considerations; Posiva Working Report WR-2014-27; Posiva Oy: Eurajoki, Finland, 2014. [Google Scholar]
- Posiva. Nuclear Waste Management at Olkiluoto and Loviisa Power Plants: Review of Current Status and Future Plans for 2013–2015; Posiva Report YJH-2012; Posiva Oy: Eurajoki, Finland, 2012. [Google Scholar]
- Posiva. Modelling Hydrogeochemical Evolution for the Olkiluoto KBS-3H Safety Case; Posiva Report 2016-11; Posiva Oy: Eurajoki, Finland, 2017. [Google Scholar]
- SKB. Summary of Discrete Fracture Network Modelling as Applied to Hydrogeology of the Forsmark and Laxemar Sites; SKB Report SKB R-12-04; SKB: Solna, Sweden, 2013. [Google Scholar]
- SKB. SFL—Groundwater Flow and Reactive Transport Modelling of Temperate Conditions; SKB Report SKB R-19-02; SKB: Solna, Sweden, 2019. [Google Scholar]
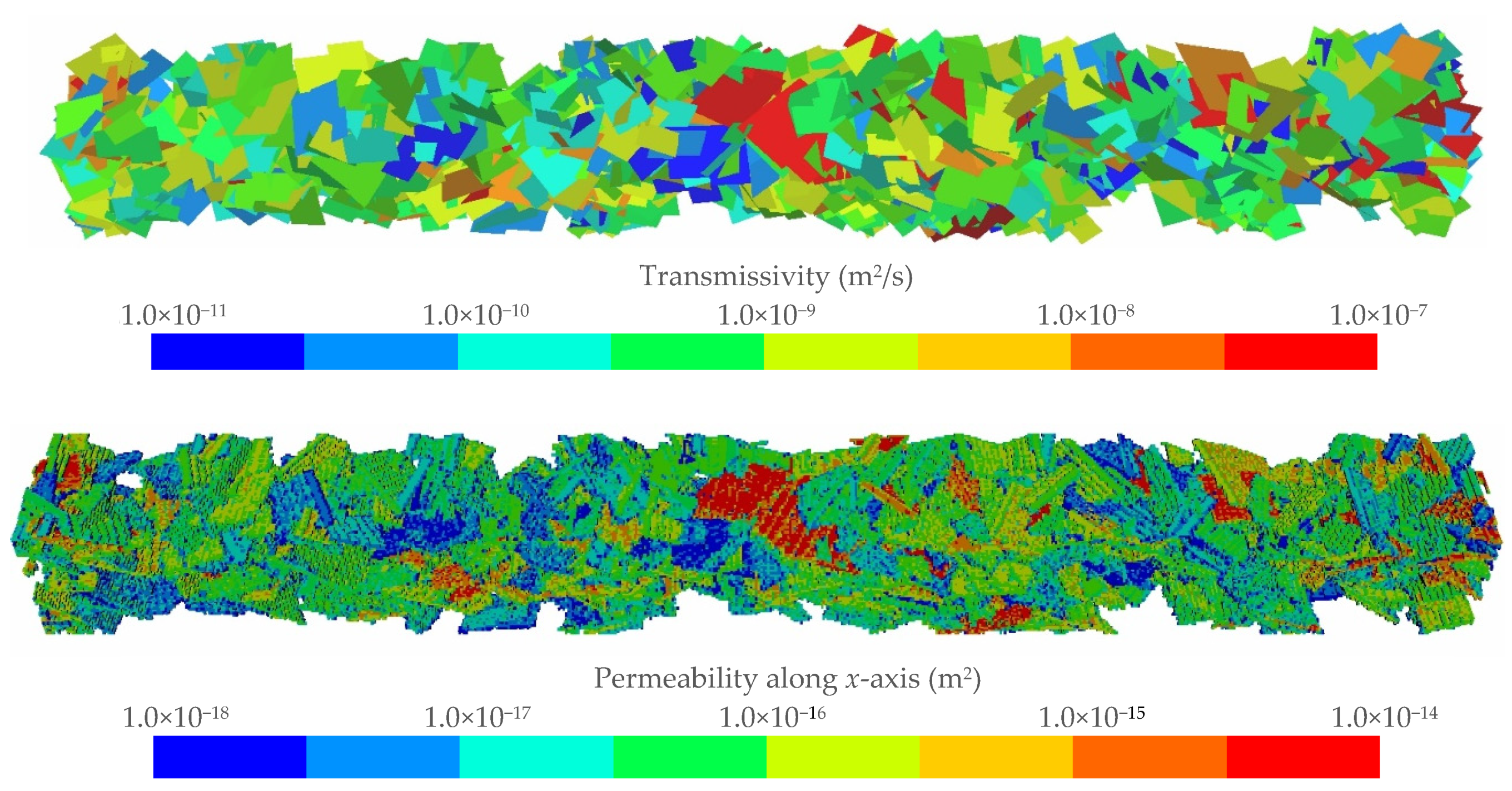

| Parameter | Symbol | Value |
|---|---|---|
| Dispersion length (longitudinal and transverse) | 100 m, 10 m | |
| Transmissivity | 9.77 × 10−5 m2/s | |
| Transport aperture | 0.02 m |
| Diffusion Length (m) | Matrix Diffusion Coeff. (m2 s−1) | Matrix Porosity | Retardation (Calculated) | Retardation 5 Finite Vols. | Retardation 500 Finite Vols. |
|---|---|---|---|---|---|
| 0.495 | 3.0 × 10−12 | 0.3 | 9.1 | 5.5 | 8.9 |
| 0.495 | 1.0 × 10−11 | 0.3 | 22.8 | 20.5 | 22.4 |
| 0.495 | 5.0 × 10−11 | 0.3 | 29 | 28.4 | 28.8 |
| 0.495 | 2.0 × 10−10 | 0.3 | 30 | 29.8 | 29.9 |
| 0.495 | 5.0 × 10−11 | 0.1 | 10.3 | 10.1 | 10.3 |
| 0.495 | 5.0 × 10−11 | 0.6 | 57 | 55.9 | 56.6 |
| 0.1 | 5.0 × 10−11 | 0.3 | 6.6 | 6.8 | 6.8 |
| 0.9 | 5.0 × 10−11 | 0.3 | 49.9 | 48.6 | 49.4 |
| Parameter | Symbol | Value |
|---|---|---|
| Dispersion length (longitudinal and transverse) | 7 m, 1.4 m | |
| Matrix porosity | 10−4 | |
| Intrinsic diffusion coefficient | 5 × 10−12 m2/s | |
| Fracture area per unit volume (whole model) | 0.481 m2/m3 | |
| Matrix diffusion length | 2.08 m |
| Result | Value |
|---|---|
| DFN travel time without RMD | 1.02 × 108 s |
| ECPM travel time without RMD | 8.55 × 107 s |
| DFN travel time with RMD | 4.08 × 109 s |
| ECPM travel time with RMD | 2.78 × 109 s |
| Retardation for ECPM | 32.6 |
| Retardation for DFN | 40.1 |
| Analytical retardation | 39.6 |
| Parameter | Symbol | Value |
|---|---|---|
| Dispersion length (longitudinal and transverse) | 100 m, 10 m | |
| Kinematic porosity (CPM) | 0.01 | |
| Transport aperture (DFN) | 0.01 m | |
| Density of fresh and saline water | 998.2 kg/m3, 1026 kg/m3 | |
| Matrix porosity | 0.3 | |
| Matrix diffusion coefficient | 5 × 10−11 m2/s | |
| Matrix diffusion length | 0.495 m |
| Component | Seawater | Dilute Water |
|---|---|---|
| C [kg/kg] | 2.01 × 10−5 | 1.47 × 10−6 |
| Ca [kg/kg] | 6.69 × 10−5 | 4.92 × 10−6 |
| Cl [kg/kg] | 4.06 × 10−3 | 3.54 × 10−8 |
| Na [kg/kg] | 2.59 × 10−3 | 2.30 × 10−8 |
| H [kg/kg] | 1.62 × 10−6 | 1.68 × 10−7 |
| O [kg/kg] | 7.97 × 10−5 | 7.22 × 10−6 |
| E [-] | −1.52 × 10−16 | −2.03 × 10−19 |
| pH [-] | 7.98 | 9.91 |
| pe [-] | −4.45 | −6.58 |
| Property | Value | Units |
|---|---|---|
| Number of fractures | 29,012 | |
| Number of sub-fractures | 461,687 | |
| Total fracture area per unit volume (P32) | 2.02 × 10−2 | m−1 |
| P32 for Hydrozone (averaged over model) | 2.56 × 10−3 | m−1 |
| Tessellation length | 20 | m |
| Description | Saline Concentration (kg/m3) * | Density (kg/m3) * | Viscosity (Pa.s) * | Salinity (g/kg) | |
|---|---|---|---|---|---|
| Ref. water A | Brine | 77.50 | 1051.4 | 1.128 × 10−3 | 73.71 |
| Ref. water B | Meteoric | 2.42 | 999.9 | 1.005 × 10−3 | 2.420 |
| Property | Symbol | Value |
|---|---|---|
| Porosity of matrix | 0.005 | |
| Intrinsic diffusion coefficient | 6 × 10−14 m2/s | |
| Flow wetted surface (ECPM) | 3.238 m2/m3 (0 to −50 m depth) 0.692 m2/m3 (−50 m to −150 m) 0.698 m2/m3 (−150 m to −400 m) 0.372 m2/m3 (below −400 m) | |
| Matrix diffusion length | (Random fractures) | |
| Number of RMD finite volumes | 5 | |
| Finite volume lengths |
| Surface | Concentration | Pressure |
|---|---|---|
| Top | Initial value | Initial value |
| Sides | Initial value | Zero flow |
| Bottom | Initial value | Zero flow |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Applegate, D.; Appleyard, P. Capability for Hydrogeochemical Modelling within Discrete Fracture Networks. Energies 2022, 15, 6199. https://doi.org/10.3390/en15176199
Applegate D, Appleyard P. Capability for Hydrogeochemical Modelling within Discrete Fracture Networks. Energies. 2022; 15(17):6199. https://doi.org/10.3390/en15176199
Chicago/Turabian StyleApplegate, David, and Pete Appleyard. 2022. "Capability for Hydrogeochemical Modelling within Discrete Fracture Networks" Energies 15, no. 17: 6199. https://doi.org/10.3390/en15176199
APA StyleApplegate, D., & Appleyard, P. (2022). Capability for Hydrogeochemical Modelling within Discrete Fracture Networks. Energies, 15(17), 6199. https://doi.org/10.3390/en15176199






