Abstract
In the era of aiming toward reaching a sustainable ecosystem, the primary focus is to curb the emissions generated by non-conventional resources. One way to achieve this goal is to find an alternative to traditional power plants (TPP) by integrating various distributed energy resources (DERs) via a Virtual Power Plant (VPP) in modern power systems. Apart from reducing emissions, a VPP enhances the monetary benefits to all its participants, including the DER owners, participants, and utility personnel. In this paper, the multi-objective optimal scheduling of the VPP problem considering multiple renewable energy resources has been solved using the multi-objective black widow optimization (MOBWO) algorithm. Renewable resources consist of solar PV modules, wind turbines, fuel cells, electric loads, heat-only units, and CHP units. The weighting factor method was adopted to handle the multi-objective optimal scheduling (MOOS) problem by simultaneously maximizing profit and minimizing emission while satisfying the related constraints. In this research, a peak valley power pricing strategy is introduced and the optimal scheduling of the VPP is attained by performing a multi-objective scheduling strategy (MOSS), which is day-ahead (on an hourly basis) and 15-min based (for a one-day profile), to observe the behavior of the anticipated system with a better constraint handling method. This algorithm is capable of dealing with a complex problem in a reduced computational time, ensuring the attainment of the considered objective functions. The numerical results obtained by the MOBWO algorithm after 100 independent trials were compared with the latest published work showing the effectiveness and suitability of the developed system.
1. Introduction
A virtual power plant (VPP) is an assembly of energy resources that are owned by a private entity and can be interconnected for combined operation. The essence of a VPP is that it is owned and operated independently, it can be controlled centrally and monitored with the help of advanced software. This helps the distributed resources which are coming from disparate locations to respond quickly to the energy supply and demand Refs. [1,2,3,4]. The goal of the VPP is to handle the energy demand of consumers communally and to resolve the future failure of networks. A VPP consists of remote software that helps to standardize specific energy use by linking, organizing, and controlling decentralized and controlled charging generators.
A VPP acts as an energy hub and is capable of becoming the future of power systems. It offers variable generation at reduced inertia levels and at the same time provides ancillary services, including controlling the voltage imbalances, frequency regulation, and congestion management and helps in the black start. The VPP also resolves some of the most prominent grid-related issues, viz., improved forecasting, real-time mitigation of power quality-related concerns, and proper balancing of the demand and supply gap. Apart from offering technical services, a virtual power plant offers commercial services by participating in wholesale and energy reserve markets. By enhancing the visibility of small, distributed energy resources (DERs), they are capable of offering pecuniary services by managing spot pricing (SP) and time of use (TOU) pricing schemes. The simple characterization of DER is any energy resource that is connected to the grid at the distribution level, viz., fuel cells, captive power plants, natural gas turbines, electric vehicles (EVs), and energy storage (ES).
Virtual power plants can certainly be a supporting system for implementing 5-min bidding and can respond to various rapid and fast-moving markets through various DERs. Some of the diverse challenges which can be answered by a VPP are listed below.
- (a)
- A VPP diminishes the need for the conventional generation to provide the provision of dynamic ancillary services.
- (b)
- It controls a cluster of heterogeneous renewable energy resources (RERs).
- (c)
- The intermittency and uncertainty caused by renewables such as solar and wind power, which are highly weather dependent, can be reduced to a certain extent.
- (d)
- It maintains favorable grid conditions for real-time management and supervision in emergencies.
There are various other requirements to make the operation of VPPs more robust, including ensuring cyber security which is a very important concern due to the involvement of highly advanced software. Information and communication technologies (ICTs) are also a prerequisite for reliable communication. Integrated resource planning (IRP), peer-to-peer (P2P) transactions, net-metering policy (NM), and behind the meter (BTM) technology are some of the regulatory mechanisms which play a key role in deciding the future of this technology.
A case study was carried out by P. Pal et al., Ref. [5] in which a PV panel, fuel cell, wind turbine, micro-turbine, and battery-connected energy storage system were connected to analyze the optimal scheduling of a VPP. The setup was made in such a way that three kinds of scenarios were considered using a beetle search antenna algorithm for optimal dispatching. The authors compared the performance of this method with algorithms such as particle swarm optimization (PSO) and genetic algorithm (GA). Some of the important parameters such as load analysis on an hourly basis and dynamic pricing of the grid were utilized and implemented for the day-ahead market strategy. S. Han et al., Ref. [6] highlighted the benefits of a VPP considering incentive prices and load data on an annual basis to assess the revenue generated. The profit evaluation of a VPP involves load filling as well as load shaving. A VPP requires the lowest investment cost to achieve the same load shaving effect when compared to gas power, coal power, pumped storage, and energy storage as well. The operating cost for the demand response (DR) is very low compared to an old-style power plant. The overall feasibility of the development of VPPs is verified by conducting simulation studies from the perspective of the power grid. P. Lombardi et al., Ref. [7] presented an article in which a synchronized measurement was implemented in the state estimation algorithm which could turn out to be a solution of equations strictly related to state estimation. They selected a CHP, photovoltaic plant, and wind park to supply energy and therefore can be called energy suppliers. An external boiler was also included in the analysis to manage the surplus electricity. A CHP unit was included in the study as it is a useful source by which the power load can be managed efficiently. To ensure the optimal operation of the VPP, forecasting errors that arise due to the intermittent nature of RERs and unpredictable weather need to be reduced as much as possible. S. M. M. Saabit et al., Ref. [8] explored why the concept of Vehicle-to-Home (V2H) has been given more emphasis instead of V2G and G2V. Three approaches were well-thought-out and include the grid-connected PV with battery storage system (BSS), grid-connected battery storage systems without PV, and just a battery storage system. The intention was to highlight the capabilities of batteries when they are installed at retail sites and eventually set up a VPP. Two types of load profiles were analyzed: are flat consumption and varying load profile. The Perturb and Observe technique was employed to track the maximum power point. The settlement period of the proposed system was estimated to be 9 years to overcome the installation cost. A hybrid energy generation system was used to resolve the problem of optimal scheduling which consisted of battery-connected solar PV modules, wind farms, and thermal generators in S. S. Reddy et al., Ref. [9]. A two-point estimation system and genetic algorithm were used to test the efficacy of their proposed strategy. Based on the simulation studies carried out, it could be observed that there was a marginal enhancement in the generation scheduling of the day-ahead strategy. In Ref. [10], Y. Zhang et al., attempted to propose the scheduling strategies of a VPP that can accommodate various development phases in the electricity market. A bi-directional context was proposed in the paper so the VPP participates in the electricity markets and acts only as a price-taker. Apart from raising the overall revenue, it also focused on the objective of social welfare which can be achieved by the effective allocation of resources.
To solve the unbalancing problem, T. Zhang et al., Ref. [11] proposed a VPP optimal scheduling model. They studied the energy cost model of the VPP and developed an optimal dispatch strategy in which the uncertainty of the energy prices and variable output of RESs were included. The VPP structure comprised small-scale wind power plants, solar PV systems, and gas turbine power plants along with energy storage systems. Few types of VPPs, when participating in the electricity market, are briefly discussed, namely the Joint-Venture model, Bi-lateral Transaction model, and medium-long term contract model. They considered the overall power balance without any network constraints. A small-scale VPP model was comprised of two DG sources and two controllable loads, and the same was verified in MATLAB/ Simulink by Naina et al., Ref. [12]. An algorithm of an energy management system that acts as a centralized controller operates in three modes, i.e., grid import (operated in an off-peak hour), grid export (operated in peak hours), and no power exchange mode (power exchange does not take place between the grid and VPP). Three different models were included in this analysis, the main grid, dynamic load, and distribution generation model. In this study, consecutive energy management (CEM) is proposed to make the regular energy management system more economic by satisfying the electric constraints of the power system. The control objective was to develop a framework so that the VPP can contribute to the energy market and at the same time cater to ancillary services.
A. Zahedmanesh et al., Ref. [13] discussed two hierarchies; i.e., the first involves a daily scheduling approach while the second is reactive power compensation which is a very crucial requirement of a power system. As per the claim, both voltage quality and energy cost were improved by employing CEM in the analysis without violating any electric constraints. The power of the conventional generators relies on the quantity of energy produced by renewable energy sources. The storage facility plays a prominent role in case the load shaving factor increases. The optimal design of the storage facility is highly recommended by Lombardi P. et al., Ref. [14] so that the system can balance the intermittent generation. The total demand for analysis is taken as 1 MW which is fulfilled by conventional generators and partially by renewable energy resources such as solar and wind. It was observed that the shaving factor has a very minimal impact on the optimum storage capacity only if the quantity of energy generated by the RERs is high.
S. Mishra et al., Ref. [15] offered an innovative business model in which consumers could be given full control over how much power they require, giving them the liberty to utilize power per their requirements and needs, and is known as energy-as-a-service (EAAS). This model is empowered by peer-to-peer (P2P) energy exchange especially designed for the local power markets. They also proposed a novel computation strategy in which a comparison was made between profit-based ordering and random selection to conclude the most preferred strategies for an energy-related transaction. A design that is termed a smart contract was discussed which allows a particular system to be independent and reliable for handling exchanges when multiple sectors are involved. This study aims at a multi-stage PSO method to improve energy penetration along with small-scale signal stability by T. K. Renuka et al., Ref. [16].
The proposed technique was tested on the IEEE 14-bus system and the results were validated. This bus system contained three synchronous generators and turbine governors. Real-time coordination, as well as a controller for the active supervision of real and reactive power in all the grids, are necessary for addressing the intermittency issues and increased penetration of renewable energy. It has been emphasized that realistic control strategies can be obtained by optimization studies to perform an integrated operation. O. H. Mohammed et al., Ref. [17] defined an economic problem that consists of the optimal sizing of the system, state of charge (SOC) of the battery, and high reliability of the system. The characteristics and advantages of the PSO are highlighted over various conventional algorithms. The objective function consists of the total net present cost with the sole intention to optimize the generated power of a hybridized renewable energy system comprised of PV modules, batteries, tidal, and wind turbines. The important aspects of the batteries such as the floating charge voltage and their maintenance are considered to achieve the desired optimization. The problem that is being explored in this study is more economical and converted into a multi-objective problem in which the purpose is to minimize the cost of energy and the total net present cost (TNPC) of the system without compromising the flexibility and versatility of the hybrid energy system.
Pio Lombardi Ref. [18] optimized a multi-criterion-based VPP that was autonomous. This study involved three main criteria, i.e., service reliability, the cost associated with the system, and the quantity of pollution. In the desired load management program, the VPP comprised a wind farm, PV plant, and CHP in which the prime movers were a gas turbine, active consumers, and a battery switch station. In addition, the authors performed a sensitivity analysis to verify that the optimal solution is robust. The autonomous VPP is economically competitive as the total cost generation is less than that compared to traditional power systems. M. F. Dehghanniri et al., Ref. [19] examined the involvement of a VPP in the real-time market, day-ahead market, and reserves. The sources considered were wind turbines, combined heat and power, diesel generators, and electric vehicles, with electrical and thermal as their two storages. To maximize the profit, two-stage planning was used. In the first stage, optimization of DA and reserves was accomplished, followed by optimizing the real-time market. The simulation was carried out on an IEEE 21 bus network to assess the performance evaluation of the VPP. They emphasized two important parameters, namely, the inclusion of EVs and the price sensitivity of the load. An artificial neural network was used for forecasting the data and planning the required number of EVs required for day-ahead scheduling.
M. Khandelwal et al., Ref. [20] dealt with the impact of locational marginal prices on a VPP in terms of resource allocation by satisfying the constraints related to network flow within the limits. To enhance the profit by a considerable margin, technical and market aspects were discussed. The problem formulation of profit was created in such a way that it was the difference between the cost of energy and revenue from market trading. To analyze the impact of aggregation, 24-h scheduling was considered. M. Gough et al., Ref. [21] focused on the technical and grid-related constraints. They developed a VPP that dealt with technical details rather than commercial or financial outcomes. The impact of voltage profile, power losses, and network congestion was analyzed along with the thermal relief of the consumers. The obtained profit was split into two parts, namely, revenue from the electricity sold to commercial clients and the cost of functioning the technical VPP in consideration of both economic and technical constraints. S. Hadayeghparast et al., Ref. [22] projected a typical model for optimizing a VPP’s day-ahead scheduling, consisting of power dispatching and unit commitment (UC). The multi-objective approach deals with capitalizing on the day-ahead net daily turnover of the VPP and curtailing the pollutants and daily emissions. In this study, the VPP was assumed to control all resources in the local network, including loads and DERs. The scenario-based approach was used for modeling the uncertainty of the market price, solar radiation, and electrical load.
Based on the critical review carried out in the literature survey, it was found that the problem statement requires an advanced meta-heuristic technique that can handle the objective function in a simpler yet efficient way by reducing the complexities which are unavoidable due to the non-linear nature of the problem when solved by established techniques such as PSO, GA, etc. The below-mentioned points are anticipated as research gaps that were not given the attention they require in the explored literature.
- To ensure efficient management of the grid, sources such as fuel cells and CHP can be considered for optimal scheduling to reduce the cost of power generation along with emissions in a VPP system.
- To handle a non-convex problem such as VPP efficiently, advanced, and recently developed soft computing (SC) techniques can be implemented or modified by choosing related constraints.
- To incentivize the participants, peak-valley pricing mechanisms with the incorporation of (15 min) interval scheduling is introduced and compared with day-ahead scheduling.
In Table 1, various control methods, mostly used in the work reported in the literature, to carry out optimization are listed. MOBWO is the only technique, to the best of our knowledge, that is not being employed to carry out the intended VPP problem. The control method is mentioned for the existing studies along with its characteristics and the nature of the problem. The limitations of the existing work and advantages of the anticipated MOBWO algorithm, along with the improvements, are highlighted over other techniques.

Table 1.
Control methods employed for optimal scheduling purposes.
Virtual power plants are gaining interest very rapidly in the new era of energy management to have better management of the associated resources in modern electrical systems. Even though a lot of researchers are showing interest in exploring the domain of VPPs to know their feasibility and economic viability, all the studies related to optimal scheduling, which were carried out previously, were only day-ahead types, and emission was not given the kind of attention it requires, especially in today’s scenario in which a considerable reduction in emissions is needed to contribute towards sustainable living. This study deals specifically with the optimal scheduling of a VPP considering both day-ahead scheduling and 15 min scheduling which shows close resemblance to the real-time scenario.
In this article, an attempt has been made to carry out multi-objective optimal scheduling and the key features of this research work are highlighted below:
- One centrally controlled VPP system comprised of multiple resources including solar PV modules, WT, fuel cells, electric loads, heat-only units, and CHP units has been attempted to solve the multi-objective optimal scheduling problem.
- The multi-objective optimal scheduling of the VPP considering renewable resources has been solved using the weighting factor method to simultaneously maximize profit and minimize emissions.
- Peak valley’s power pricing strategy is introduced in the multi-objective optimal scheduling of the VPP problem.
- The new price-based multi-objective black widow optimization (MOBWO) is presented and implemented by considering constraint handling.
- Statistical analysis was performed for both single and multi-objective optimal scheduling of the VPP problems and quality solution sets were obtained from the MOBWO algorithm after 100 different independent trials.
- Pareto optimal solutions were obtained specifically for multi-objective optimal scheduling of the VPP problem for the maximization of profit along with simultaneously minimizing the emissions for both scenarios I and II, respectively.
- Results obtained by the proposed MOBWO algorithm were also compared with the latest published works.
The organization of this research article is as follows:
Section 2 deals with the basic concepts, challenges, and framework of VPP. Section 3 presents problem formulation which comprises the objective function, followed by the constraint handling. The optimization algorithm-related explanation is then discussed in Section 4. The implementation part of the case studies along with simulation outcomes is presented in Section 5, and, lastly, concluding notes followed by future work highlights are given in Section 6.
2. VPP Concept
A VPP facilitates the synchronization of power generation and uses more efficiently. It provides a sustainable supply and demand adjustment mechanism with a high level of precision and encourages the storage of electricity that generates the capacity for the usage of renewable energy in the power division. As a result, there is a significant potential for the VPP to link operating technologies with communications infrastructure and external data properties, thus collecting the forecasting data from scattered entities. In addition, the VPP can provide deep insights into the results by offering smoother and quicker decision-making and taking real-time action to enhance performance. The framework of the VPP followed is depicted in Figure 1.
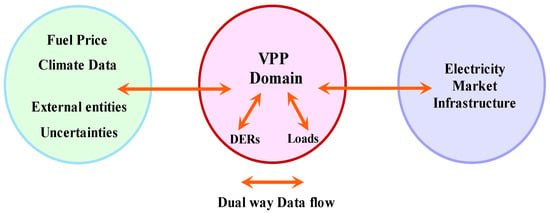
Figure 1.
The Framework of a VPP.
Several challenges involved when considering a VPP can be categorized in terms of technical, commercial, and regulatory restrictions, followed by environmental concerns which are often ignored and not given the importance that it deserves. In Figure 2 some of the most prominent challenges of the VPP are highlighted.
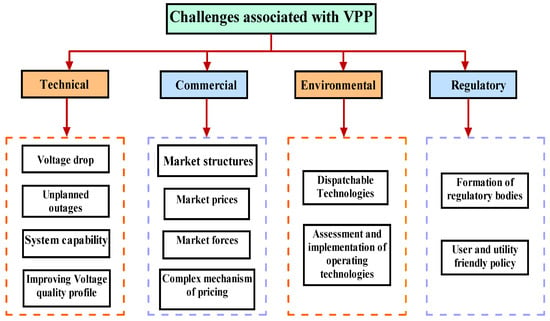
Figure 2.
Different aspects of VPP.
The crux of a VPP is that it is not restricted geographically, unlike a Microgrid. A VPP is more concerned with flexible resources and indulges in power trading in the energy market and their mode of interconnection is always grid-connected Ref. [36].
Methodology
The process flow followed is demonstrated in Figure 3 in which the detailed organization is sequenced to make it easy for the readers looking for optimum operation and scheduling of a virtual power plant considering multi-objective profit maximization and emission minimization. The optimization is carried out with respect to the constraints handling which also includes the technical constraints of the associated resources. The methodology starts with the selection of resources, i.e., solar PV, wind, and combined heat and power, which comprise heat-only units, followed by the fuel cell. The next step after selecting appropriate resources for the optimal scheduling of the virtual power plant is the collection of data in which raw data are obtained for renewable sources such as wind and solar power and a few secondary data taken from the literature. The next step is to set up the computational framework in which a suitable selection of an advanced meta-heuristic technique is performed, keeping the requirements into consideration. In the next stage, a scheduling strategy is adopted in which two scenarios are considered.
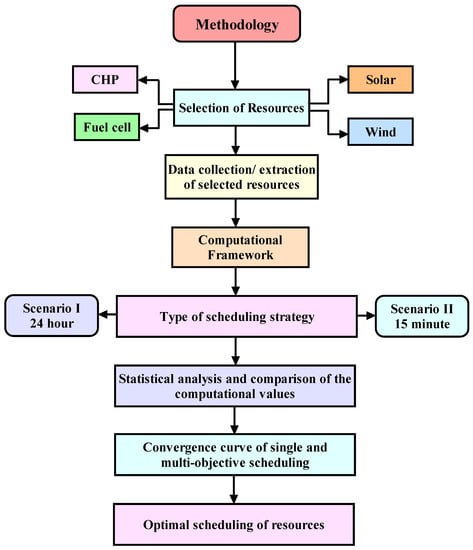
Figure 3.
Methodology and process flow of the proposed strategy.
In scenario I, day-ahead scheduling, i.e., 24 h, is performed followed by a 15-min interval which is scenario II. The multi-objective case is performed for both scenarios I and II. Based on the optimization algorithm, a detailed statistical analysis has been accomplished and highlighted in tabular form and the same is compared with another optimization technique. The superiority and effectiveness of the same are evident in the form of numerical results. The convergence characteristics are displayed for all three cases, respectively, and the two scenarios are followed by the Pareto graph which helps the VPP operator in deciding the best available trade-off in terms of monetary advantages as well as emission considerations that helps in achieving the sustainable development goals which is one of the sole purposes of a VPP.
In Figure 4, a pictorial representation of the envisioned system under study is represented in which renewables and co-generation units are considered. The resources associated with the current VPP system under study are solar photovoltaics (PV), wind turbine (WT), fuel cell (FC), combined heat and power (CHP), and electric load (EL), followed by connecting the energy market (EM) and electricity price (peak valley) to the VPP operator. These resources are used to supply the electricity to the consumers of VPP based on the transactions between the energy market and the VPP operator. The energy market, which is indeed an integral feature of the VPP, is also associated to make the delivery of peak valley electricity pricing when applicable.
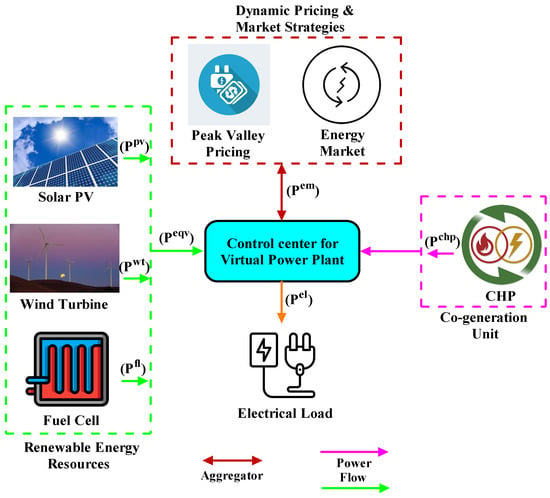
Figure 4.
The proposed VPP system under study.
3. Problem Formulation
3.1. Objective Function
The objective function is segmented into two categories. The first deals with the maximization of the net profit and is followed by the minimization of total emissions generated by the associated resources, specifically with CHP and heat-only units.
3.1.1. Net Profit
The running costs of the system consists of power acquisition costs from the main grid, power selling costs to the main grid, and costs associated with wind generators, solar power, and fuel cells. The installation cost of the wind turbine and the photovoltaic array is not considered. The objective function is categorized into two segments, i.e., the main objective function deals with the maximization of net profit followed by the other objective function which is emission minimization.
Net Profit =
where:
- p and s are set of plants and scenarios, t is time ranges from 1 to 24 in Day-ahead scheduling, followed by 1 to 96 in 15-min scheduling.
- cph and cse are the tariffs for purchasing and selling power from the grid system.
- πs is the probability of scenarios.
- pem is the energy market price; cens is the cost of energy not served.
- cchp and chou are the cost function of CHP and heat-only units.
- phou is the price of heat-only units.
3.1.2. Emission
Along with the main objective function of net profit represented in the above Equation (1), the emission is also considered as a supportive objective function in which minimization of the day-ahead emission is carried out to see the effect of the statistical analysis performed in Section 5.
where:
- echp and ehou are the emissions by CHP and heat-only units, respectively.
- eph and ese are the emissions by the grid system.
The total emissions by CHP and heat-only units, and the purchase and selling power coming from the main grid system can be evaluated by the below-mentioned Equations (3)–(5).
In the aforementioned Equation (5), the measure of emissions related to the grid system is considered only when the electricity is purchased from the power market.
3.1.3. Multi-Objective Framework
The objective function of the multi-objective optimal scheduling of the VPP problem is to handle objectives, namely, the maximization of profit and simultaneous minimization of the emission in such a way as to obtain the best compromise solution. Multi-objective optimal scheduling of the VPP problem is solved by using the weighting factor method and the mathematical expression is given by:
where:
- w is considered as 0.5 for giving equal weightage to both objectives.
3.2. Constraints Handling
3.2.1. Power Balancing
The electrical power balance is represented in Equation (7) in which depicts the equivalent electrical output power of each plant.
where:
- is equivalent to power scenario s, time t, and plant p.
- is the exchanging power between the main grid and the CHP system at interval i (MW).
- is the power of the fuel cell at interval i (MW).
- is the power of the wind turbine at interval i (MW).
- is the power of the solar photovoltaic at interval i (MW).
- is the electrical load at interval i (MW).
3.2.2. Heat Balancing
Constrictions related to the heat balancing equation must satisfy the waste heat and gas boiler.
where:
- is the ratio of heat to the electricity of the fuel cell at interval i (MW).
- is the efficiency of the heat rate boiler (MW).
- is the power of a gas boiler at interval i (MW).
- is thermal power balance at interval i (MW).
3.3. Power Switching between Main Grid and CHP Units
The operational constraints between the CHP and main grid are expressed in the following equation. The switching power which takings place between these two is within the permitted limits.
where:
- is the minimum exchange of power between the main grid and the CHP system.
- is the maximum exchange of power between the main grid and the CHP system.
3.4. Constraints of Waste Heat and Gas Boiler
The waste heat and gas boiler are able to generate power in their precise electrical capacity.
where:
- is the minimum limit of the waste heat boiler.
- is the maximum limit of the waste heat boiler.
- is the minimum limit of the gas boiler.
- is the maximum limit of the gas boiler.
3.5. Fuel Cells
The efficacy of fuel cells can be expressed in the part-load ratio (PLR). The modeling is adapted from Ref. [37]. The mathematical formulations associated with the function of PLR are defined in Equations (12)–(14). The fuel cell units are capable of supplying part of the demand load in the form of electrical energy.
When PLR_i < 0.05
When PLR_i ≥ 0.05
where:
- is the fuel cell efficiency at interval i (p.u.) and
- is the ratio of heat to the electricity of the fuel cell at interval i (MW).
Ramp Rate Limit of Fuel Cell
The power generated by the unit is not allowed to exceed the power generated in the previous interval by more than a specific amount.
where:
- T is the up-ramp limit and is the down-ramp limit of the fuel cell.
- is the power generated by the fuel cell at interval i (kW).
- is the power generated by the fuel cell at the previous interval (kW).
3.6. CHP Units
To achieve optimal scheduling, two categories of CHP units having diverse feasible regions of operation (FOR) have been considered Ref. [38]. Equations (16) and (17) represent the maximum electric and thermal output power constrictions of the CHP unit.
where:
- is the electrical output power of the CHP and
- is the commitment status of the CHP.
The feasible regions of operation (FOR) are shown in Figure 5. In the Type 1 CHP unit, FOR is a convex type which is followed by a non-convex FOR as shown in Type 2.
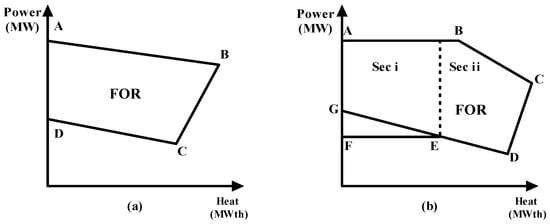
Figure 5.
Feasible operating region (a) Type 1, (b) Type 2.
3.7. Solar PV Modules
The output of the photovoltaic modules is affected largely by solar radiation, characteristic of the module, followed by the ambient temperature of the specific location Ref. [39]. The availability of solar power is plentiful in the daytime, which can be seen in Figure 6, in which the peak ranges from 11 a.m. to 3 p.m. Usually, it follows the beta probability distribution function (PDF).
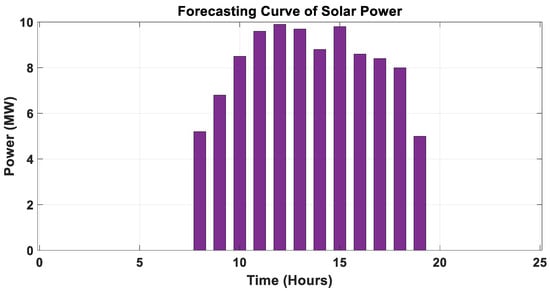
Figure 6.
Forecasting curve of solar PV modules.
Certain parameters influence the output power of PV modules. The fill factor (FF) is the measure of the efficiency of a photovoltaic module. The ideal FF of a solar cell is around 0.7. It is defined as the maximum power obtainable from the solar module to the actual power obtained and it is expressed in Equation (18).
The characteristics of the module are represented below:
where:
- is output power, is the number of PV modules, and is the solar radiation (KW/).
- is the open-circuit voltage and is the short circuit current.
- is the current temperature and is the voltage temperature coefficient.
- is the solar cell temperature and FF denotes the Fill Factor of the PV module.
3.8. Wind Turbine
Wind power follows the Weibull PDF due to its ability to represent the variation in wind speeds. The forecasting curve of wind power generation with respect to time is shown in Figure 7. The primary problem with wind power is the rapid fluctuation due to varying climate conditions.
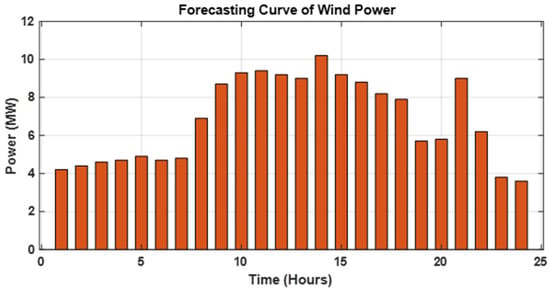
Figure 7.
The forecasting curve of wind power generation.
The power from the wind turbine is calculated from Equations (22)–(25). The modeling of the wind turbine is referred to from Ref. [40].
where:
- is the output power of the wind turbine (MW).
- is the nominal power of the wind turbine (MW).
- is the number of wind turbines.
The crucial parameters considered to evaluate the intended objective function are listed in Table 2, Table 3, Table 4, Table 5 and Table 6 and referred from [22,40,41,42,43].

Table 2.
Emission factors related to SO2, NOX, and CO2.

Table 3.
Parameters for the wind turbine.

Table 4.
Parameters for solar PV.

Table 5.
Parameters for heat-only units.

Table 6.
Parameters of the CHP unit.
The complete procedure adopted for solving the optimization problem is mentioned in Figure 8. All the mathematical equations involved in this study are highlighted in the flowchart.
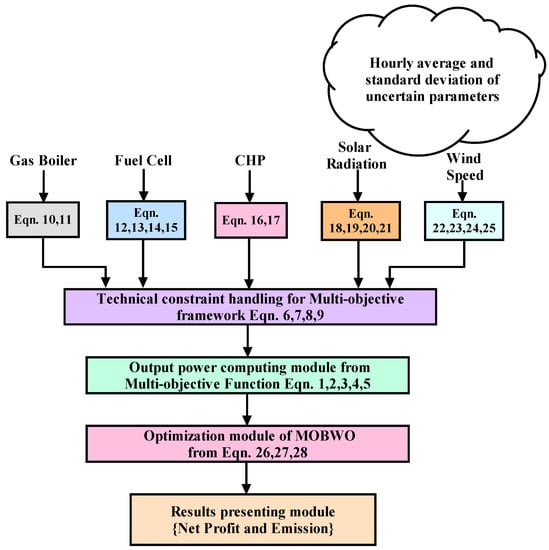
Figure 8.
Process flow for the adopted methodology.
There are uncertain factors that affect the stability of the VPP system due to the uncertain nature of renewable energy generation, fluctuation in market prices, and varying load demand. These three aspects are crucial in overcoming the barrier caused by these uncertainties and can be managed by incorporating methods, viz., the Monte Carlo simulation (MCS), robust optimization (RO), and auto-regressive integrated moving average (ARIMA) probabilistic and possibilistic methods to name a few Ref. [44]. The focus on carrying out the uncertainty aspect is out of scope for the current work, and it is left for future work.
4. Optimization Algorithm
The nature-inspired algorithms are the best way to solve the selected non-convex type problems that come with lesser mathematical complexities and an efficient way to ensure the reachability of a global optimum value. To carry out the intended optimization, the MOBWO was selected over other algorithms due to its unique ability to overcome the local optima trap. It offers numerous search agents to estimate the global optimum, which is remarkable in this recently developed highly advanced optimization technique. The two most important aspects of every optimization are exploration and exploitation. Producing numerous offspring enhances the exploration of search space, followed by omitting the unfeasible solutions to move toward the best possible solution. The resulting early convergence is certainly a trait of selected optimization which is missing in most of the well-established nature-inspired techniques such as PSO and GA.
The system is initialized with a population of random spiders and searches for global optima by updating the population. The BWO algorithm attempts to solve an objective function by generating a mutation population (mute pop) and mutation variables (mute vars) Ref. [45]. The BWO concept consists of terminologies in which the search agents in the form of the widow are assumed to solve any specific problem in the same way that the crossover and mutation operator does in GA, followed by the population of particles in PSO.
4.1. Population Initialization
The array of the search agent is and the dimensional value is in the optimization problem expressed in Equation (26).
where:
- are the floating numbers in the form of variables.
A fitness search agent in the form of the widow is determined using the fitness function expressed in Equation (27).
4.2. Procreation, Cannibalism, Mutation
The BWO algorithm starts with selecting the parents which is known as the procreate stage. This step is very much necessary to start the exploration in the search area to avoid the local optima trap. To reproduce in BWO algorithms, the array referred to is created and consists of random numbers which contain the offspring produced by Equation (28) in which denote parents and refer to the offspring.
where:
are the offspring.
are the parents.
is the array matrix.
The process is repeated for MVar two times, in which duplication should be avoided to enhance the accuracy of the fitness value among the pairs. The next step is the cannibalism rate which ensures better performance for the exploitation and guarantees faster convergence at the same time for BWO. Every operator corresponds to a contender solution to the given problem. The mutation stage is considered to bring the balance between both exploration and exploitation.
The performance of a BWO depends on its parameters such as reproduction rate (RP), cannibalism rate (CR), mutation rate (MR), and, of course, the lower bound (LB) and upper bound (UB). Appropriate selection of the controlling parameter, which is the cannibalism operator, may ensure superior performance of the exploitation stage by disregarding the unfitting individuals from the population, resulting in a lesser number of iterations to reach the optimum solution. The flowchart of the proposed MOBWO algorithm is shown in Figure 9 and an effort has been made to simplify the process of obtaining the optimum value by minimizing the complications associated with this algorithm. The MOBWO is carefully chosen to carry out the numerical analysis in this research as it is a recently developed meta-heuristic technique with a unique ability to handle the multi-objective problem with reduced complications, improved convergence characteristics, and better computational efficiency. Every possible effort has been made while developing the code to avoid local entrapment to reach the global optimum reasonably.
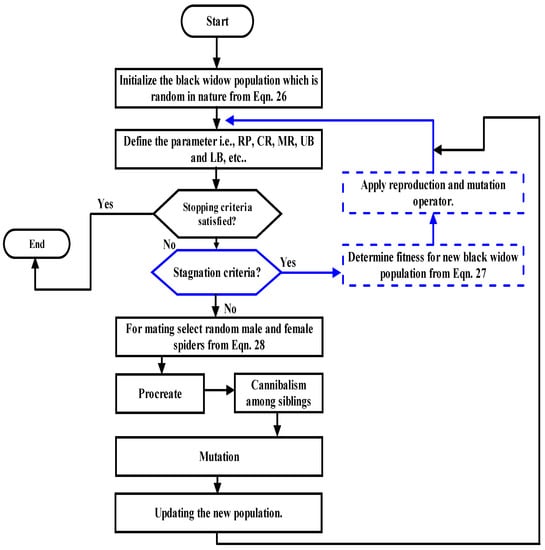
Figure 9.
Flowchart of the proposed MOBWO algorithm.
5. Results
During the off-peak periods, the VPP obtains power from the energy market as a purchaser when electricity prices are on the lower side; when prices are high, the VPP trades electricity to the energy market. When electricity costs are cheaper, buying energy from the wholesale market is more profitable than making electricity which is also an attractive feature of CHP units. By enabling these units, the demand and supply gap can be balanced with great ease, especially when the power from solar and wind units cannot be extracted at night-time.
In this study, three cases have been considered to evaluate the feasibility of the virtual power plant.
- Case I: Single-objective scheduling for profit maximization.
- Case II: Single-objective scheduling for emission minimization.
- Case III: Multi-objective scheduling for profit/emission, i.e., maximization followed by minimization.
To ensure security and continuity of power supply, the balance between load and power generation must be synchronized. The large presence of renewables, especially intermittent and highly volatile sources, i.e., solar and wind energy, makes this more complex. The surplus power in the network can be utilized in peak times when the electricity price is higher. This excess power can be stored in energy storage systems (ESSs), viz., battery storage or electric vehicles, and can be made available as and when needed through the VPP operator at a higher price that opens the option of attaining a higher economic benefit, which is beneficial to all the participants involved in the VPP system.
In the case of day-ahead scheduling, the electrical power balance for both Cases I and II are presented on an hourly basis and shown in Figure 10 and Figure 11. Power is represented on the primary Y-axis which is on the left-hand side expressed in MW. To reduce the complexity, the electricity price is plotted on the secondary Y-axis which is on the right-hand side and is expressed in ($/MWhr).
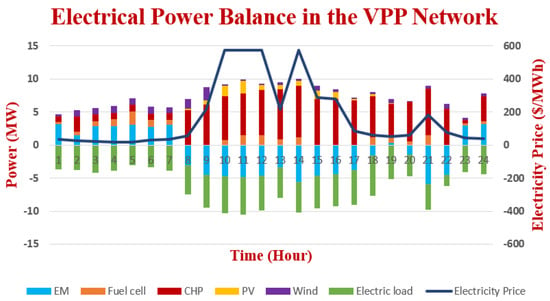
Figure 10.
Case I Electrical power balance in the VPP network for 24 h.
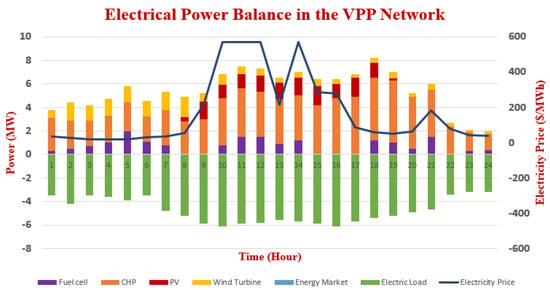
Figure 11.
Case II Electrical power balance in the VPP network for 24 h.
When the prices of electricity are low, the CHP units can be changed to a not committed (NC) status as the acquisition of electricity from the electricity market is considered more cost-effective and the VPP buys the electricity from the trading market. On the other hand, when the electricity prices are high, it is not economical to purchase the power from the wholesale market and in those instances, the VPP similarly trades power similar to any other conventional power plant.
5.1. Scenario Generation
Two scenarios have been considered to examine the performance of the projected technique. Scenario I is considered for day-ahead scheduling, followed by scenario II which is 15-min scheduling. All the results obtained in Scenario I are based on hourly scheduling and the performance is quite satisfactory and improved when compared with the other different techniques.
The numerical studies were carried out by using the multi-objective black widow optimization (MOBWO) algorithm with a code developed with utmost care and keeping in mind that the computation time should be as low as possible. In the BWO algorithm, the number of search agents and iterations is assumed to be 100 and 200, respectively. The behavior of the algorithm seems to be quite satisfactory, and it is capable of avoiding any premature convergence as well as local entrapment which is one of the most unfortunate traits of any nature-inspired algorithm. Along with BWO, other popular techniques, i.e., artificial bee colony (ABC) and ant colony optimization (ACO), are also selected to see their performance and the obtained results are discussed in the subsequent section. The case studies and scenario generation are executed and carried out in MATLAB software on a DELL laptop with a processor having an Intel(R) Core (TM) i7-6600U CPU @ 2.60 GHz.
5.1.1. Scenario I (Day-ahead Scheduling)
For demonstration purposes, the program was developed for day-ahead scheduling (DA), i.e., a 24-h period. The obtained results of the convergence for profit and emission by the proposed method are discussed and displayed in Case I and Case II, respectively, and compared with published results. In this paper, two scenarios are considered, i.e., day-ahead (hourly-based scheduling), followed by a 15 min-based scheduling. All the numerical results obtained from the proposed MOBWO algorithm in scenario I are compared with the existing published results in which the MOPSO technique is used. For the selected problem statement of the proposed system, only one relevant paper is reported in the literature, i.e., Ref. [22], to the best of our knowledge. Another comparison has been made, i.e., Ref. [46], and the obtained value of net profit from the proposed technique was higher. Similarly, the emission value was compared with Ref. [47] and found that the obtained values of both net profit and emission in a single objective, as well as multi-objective optimal day-ahead scheduling, are better in addition to the reduced computational time of the proposed MOBWO algorithm over all the other control methods as evident in Table 7 and Table 8 for each case, respectively.

Table 7.
Comparison of net profit with different techniques for Case I.

Table 8.
Comparison of emissions with different techniques for Case II.
Case I: The statistical results obtained after 100 independent runs from MOBWO converge to an optimum value of 27,785.6723 $ which outperforms the existing value of 23,302.8271 $ obtained from multi-objective particle swarm optimization (MOPSO) Ref. [22]. Additionally, the numerical results for other techniques are mentioned in Table 7.
In Case I, the computational time for the proposed MOBWO of 123.0548 (for 100 runs) is less when compared with the multi-objective particle swarm optimization (MOPSO) of 148.0945 (for 20 runs). The convergence curve of the proposed algorithm for Case I is presented in Figure 12 and it is evident that the proposed technique produces the optimum value.
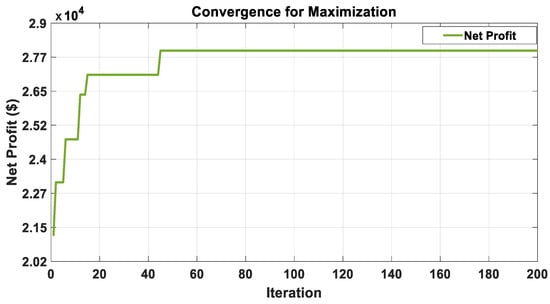
Figure 12.
Convergence curve of MOBWO algorithm for Case I.
Case II: On the other hand, in Case II, the purpose is to reduce emissions and the level of emission is reduced significantly by a considerable margin. The unit of the emission is in Kg and it is the combination of three emission factors, namely, . The statistical results obtained after 100 independent runs from MOBWO are shown in Table 8 as converging to an optimum value of 57,532.2738 Kg which outperforms the existing value of 64,432.3217 Kg obtained from MOPSO Ref. [22]. In Case II, the computational time for the proposed MOBWO is 81.3745 (for 100 runs), much less when compared with 171.4826 (for 20 runs) from MOPSO. In addition, the convergence characteristics of the proposed algorithm for Case II are shown in Figure 13.
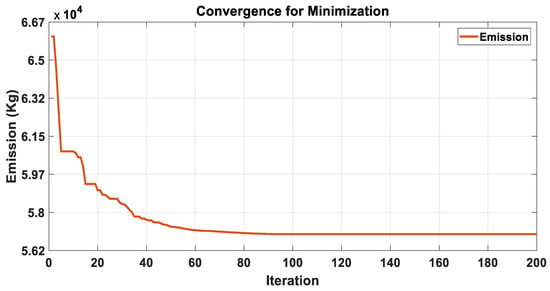
Figure 13.
Convergence characteristics of the MOBWO algorithm for Case II.
Computation time plays a significant role in selecting a suitable optimization technique which is usually problem specific. Cumulative factors are involved in solving real-world problems, i.e., selection of parameters, constraints handling, computation time, etc. Based on any particular optimization technique, these factors vary to some extent and the best trade-off is selected for the chosen technique. The nature-inspired algorithms are the best way to solve these non-convex type problems and come with lesser mathematical complexities and an efficient way to reach a global optimum value. Black widow optimization (BWO) is selected to carry out the numerical analysis in this research as it is a recently developed meta-heuristic technique and it has a unique ability to handle the multi-objective problem with reduced complications, improved convergence characteristics, and better computational efficiency. The cases which have been considered for single, as well as multi-objective, are compared with PSO and the resulting computation time is better with BWO.
Case III: The multi-objective optimal scheduling is carried out and the convergence of both objectives is displayed together in Figure 14, followed by Figure 15 and Figure 16 with other techniques. It is worth mentioning that including emission as an objective function has an immense effect on the overall working of the system since the CHP unit is considered one of the resources. Here, the peak valley electricity pricing is considered which is very essential in the peak load shifting to enhance the economic benefit. For every time period, the sale and purchase prices are given in Table 9. The effect of this pricing scheme on the operating costs has been given proper consideration in this paper.
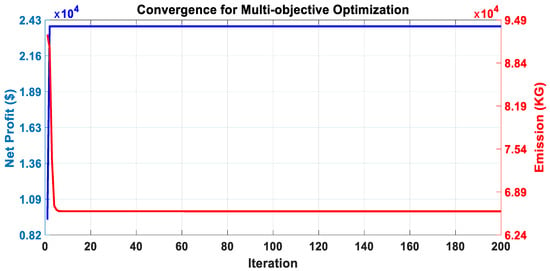
Figure 14.
Convergence characteristics of the ABC algorithm for Case III.
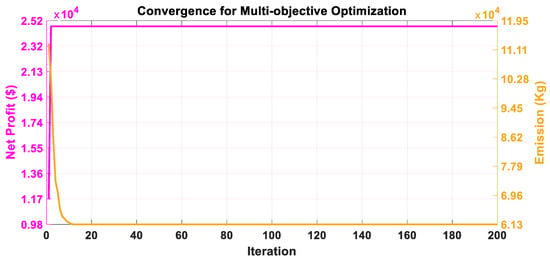
Figure 15.
Convergence characteristics of the ACO algorithm for Case III.
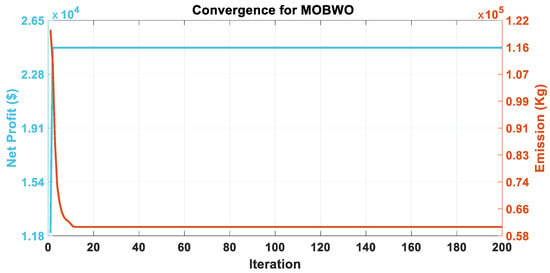
Figure 16.
Convergence characteristics of the MOBWO algorithm for Case III.

Table 9.
Comparison of emissions with different techniques.
A comparison of the statistical analysis is also presented in Table 10 and obtained after 100 independent runs. It can be observed that by adopting the peak valley power pricing concept in this paper, better compromise solutions are given which show enhancement in the performance and behavior of the price-based-MOBWO algorithm.

Table 10.
Comparison of multi-objective with published and proposed techniques.
The main purpose of obtaining the Pareto graph is to provide the VPP operator a chance to select a trade-off solution that is in line with the environmental restrictions and satisfies the economic constraints at the same time. To this end, Case III has been implemented with multi-objective scheduling and obtaining the Pareto optimal solutions, respectively, as shown in Figure 17.
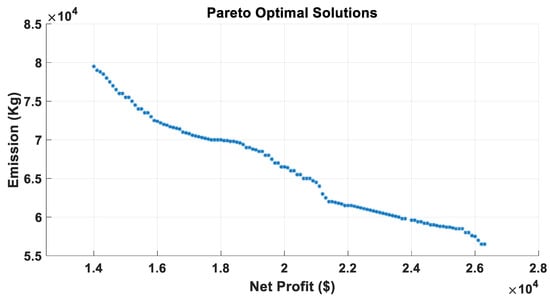
Figure 17.
Pareto optimal solutions for Case III of Scenario I (proposed MOBWO technique).
In the existing program, a pricing strategy was also incorporated to see the behavior of the convergence obtained from the proposed MOBWO. The code was developed very carefully, and the program was run for multiple trials. All the displayed results were obtained after running the program for 100 trials to ensure the precision of the algorithm.
5.1.2. Scenario II (15-min Interval Scheduling)
For further analysis, scenario II is presented in which the type of scheduling is transformed to a 15-min basis and the available data are extrapolated for carrying out the real-time analysis. The overall power balance in the case of a 15 min schedule for a one-day profile, is represented in Figure 18 and Figure 19, and the unit of time is taken in hours. All the associated resources are represented in a vertical bar and the electricity price is projected on the right-hand side of the secondary Y-axis.
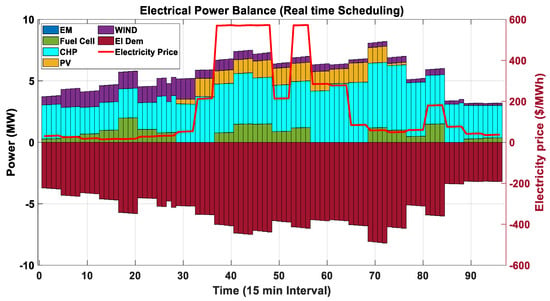
Figure 18.
Case I power balance (electrical) in the VPP system for 15-min.
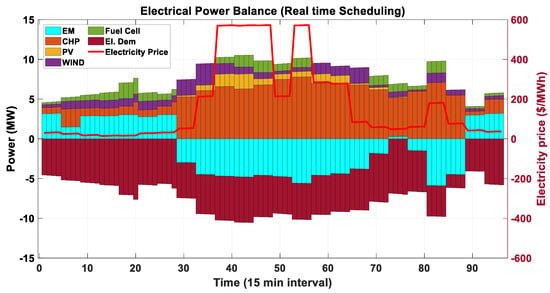
Figure 19.
Case II power balance (electrical) in the VPP network for 15-min.
Likewise, in scenario II, i.e., 15-min scheduling, the proposed scenario has no comparison available in the existing literature. The pay-off table is mentioned below, and it can be observed that the results are quite reasonable in real-time scheduling, especially in terms of profit as compared to the day-ahead scheduling which can be seen in Table 11, followed by Figure 20, Figure 21 and Figure 22 obtained by ABC, ACO, and MOBWO after 100 independent trials.

Table 11.
The pay-off table for the proposed MOBWO (15-min scheduling).
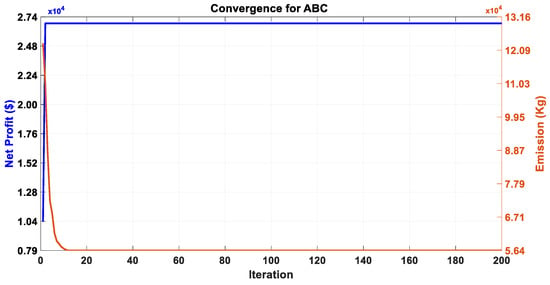
Figure 20.
Convergence curve of the ABC algorithm.
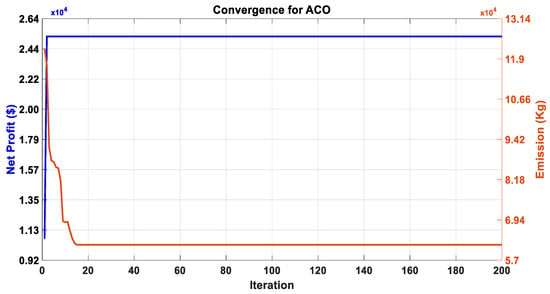
Figure 21.
Convergence curve of the ACO algorithm.
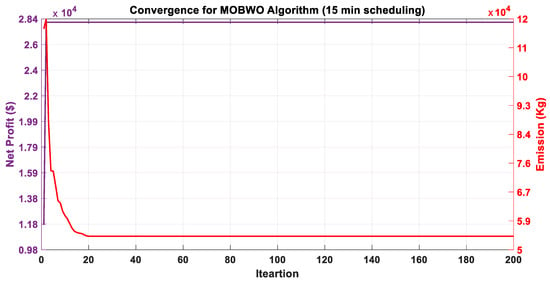
Figure 22.
Convergence curve of the proposed MOBWO algorithm.
Figure 23 shows the Pareto graph for scenario II, the 15-min scheduling. In generating the graph, the operator of the VPP can select an appropriate solution that deals with the possibilities of both technical constraints as well as the related economical limitations.
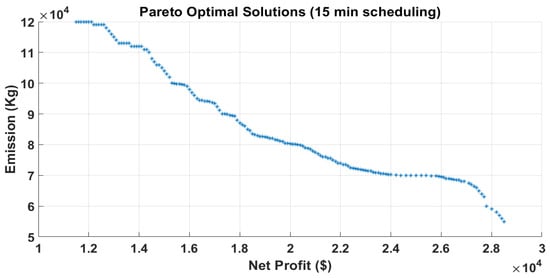
Figure 23.
Pareto optimal solutions for Case III of Scenario II (proposed MOBWO technique).
Marcos Tostado-Veliz et al. Ref. [48] proposed a MILP optimization framework that is segmented into two parts, i.e., based on historical consumption, the most suitable tariff is determined followed by the optimal hours which are referred to as ‘Happy hours’ tariff plans. Three different tariffs are discussed, viz., the fixed tariff, time-variable tariff, and happy hours tariff. The Spanish retail market is considered for the developed framework case study in which the price of selling electricity is set to zero during the happy hours time to avert any unrealistic transactions among the home and utility grid. In a deregulated electricity market, a framework for the decision for tariff selection is presented along with some useful results in which the Happy hours, i.e., 7:00–8:00 a.m., are stressed.
To balance the price volatility, scheduling strategies play a vital role. They are categorized as day-ahead scheduling, for a 24 h profile, and 15 min schedule. Merits of day-ahead scheduling are highlighted:
- (a)
- Buying and selling of electricity one day before the following day.
- (b)
- The VPP acts as a price taker in the day-ahead market.
- (c)
- Ease of unit commitment and power dispatching.
The advantages of the 15-minute scheduling are mentioned below:
- (a)
- This scheduling helps to determine the imbalance in settlement prices.
- (b)
- Offers the purchase and selling of electricity during the functioning day.
- (c)
- Real-time scheduling stabilizes the differences between day-ahead and real-time demand and production of electricity.
- (d)
- Operating systems that work in real-time can execute quickly without any delay, resulting in a nearly immediate output.
For a practical case, real-time scheduling (a few seconds to 5-min intervals) is preferable due to its inherent characteristics of reliability and performance-orientation, and the requirement of only minimal, latest, and most relevant data followed by a rapid response for given circumstances.
The proposed approach is more suitable for advancing the existing system by adding a few more resources that can act as a spinning reserve, i.e., an energy storage system, and ensure the continuity of electricity supply in case of any power deficit. The capacity of the power supply system considered in the current VPP system is 10.48 MW. Since the main concept of a VPP is that it is not restricted by any geographical location, it is always connected to the grid which is not the case when discussing a Microgrid that can be islanded and constrained in a confined region of operation. The selected VPP system under study is assumed to be a national power system.
The multi-objective optimal scheduling of VPP considering various renewable resources has been solved using the weighting factor method to simultaneously maximize profit and minimize emission. Peak valley’s power pricing (PVPP) strategy is introduced in the multi-objective optimal scheduling of the VPP problem. Moreover, a new price based MOBWO is presented and implemented, satisfying all the related constraints. For both scenarios I and II, Pareto optimal solutions are obtained specifically for the multi-objective optimal scheduling of the VPP problem for maximization of profit along with minimization of emissions. The statistical results for all three cases show the effectiveness and suitability of the proposed approach and are compared with various other techniques along with the published results.
6. Conclusions
The optimal scheduling of a VPP consisting of various resources is carried out and the performance of the BWO algorithm shows superiority in terms of the numerical results obtained. It can be inferred that taking emission as an objective function leads to a considerable reduction in the amount of day-ahead emission. In scenario I, the net profit for hourly-based scheduling leads to 26,167.7823 ($), followed by the daily emission which is 116,400.8473 (Kg). Although, when the same process is followed for scenario II, which is a 15-min interval, the numerical results are reasonably better, i.e., net profit leads to 28,415.3525 ($). However, in the case of emission, there is no significant improvement as the obtained value is 119,843.4532 (Kg). The single objective scheduling is performed for both net profits along with emission as an objective function, followed by multi-objective scheduling; Pareto optimal solutions are presented for both scenarios. Statistical analysis was performed for both single and multi-objective scheduling of the VPP problem. Optimal scheduling of the selected VPP problem was performed with three different techniques, i.e., ABC, ACO, and MOBWO, and it was observed that the developed MOBWO algorithm performance was superior in terms of reduction in computation time as well as the ability to escape from local entrapment by reaching a global optimum.
In the future, more resources such as hydro, thermal, or a combination of hydro-thermal will be incorporated into the VPP system. It will be very interesting to see how the performance of the system and the aspect of the reliability index will be explored. Similarly, adding some specific pricing and bidding strategies along with exploring the impact of market constraints on effective analysis is anticipated in a forthcoming study.
Author Contributions
Conceptualization, A.K.P. and V.K.J.; methodology, A.K.P. and V.K.J.; software, A.K.P. and V.K.J.; validation, A.K.P., V.K.J. and J.N.S.; formal analysis, A.K.P.; investigation, A.K.P., V.K.J. and J.N.S.; resources, A.K.P. and V.K.J.; data curation, A.K.P.; writing—original draft preparation, A.K.P.; writing—review and editing, V.K.J. and J.N.S.; visualization, A.K.P., V.K.J. and J.N.S.; supervision, V.K.J. and J.N.S.; project administration, V.K.J. and J.N.S.; and funding acquisition, A.K.P., V.K.J. and J.N.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by DST sponsored INSPIRE Fellowship, Govt. of India, fellowship number [INSPIRE Code: IF 190938] and “The APC is funded by MANIPAL ACADEMY OF HIGHER EDUCATION (MAHE) MANIPAL”.
Institutional Review Board Statement
Not applicable.
Informed Con sent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The first author positively acknowledges the funding organization: DST sponsored INSPIRE Fellowship, Govt. of India, [INSPIRE Code: IF 190938] in carrying out the research work with their incessant funding. The authors also acknowledge gratefulness to the host University Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, Karnataka, India for providing a conducive research atmosphere to carry out the envisioned research work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
All the abbreviations used in the manuscript are listed:
| TPP | Traditional power plant |
| DERs | Distributed energy resources |
| VPP | Virtual power plant |
| MOBWO | Multi-objective black widow optimization |
| MOOS | Multi-objective optimal scheduling |
| MOSS | Multi-objective scheduling strategy |
| SP | Spot pricing |
| TOU | Time of use |
| EVs | Electric vehicles |
| ES | Energy storage |
| RERs | Renewable energy resources |
| ICT | Information communication technology |
| IRP | Integrated resource planning |
| P2P | Peer to peer |
| NM | Net metering |
| BTM | Behind the meter |
| PSO | Particle swarm optimization |
| GA | Genetic algorithm |
| DR | Demand response |
| V2H | Vehicle to home |
| BSS | Battery storage system |
| CEM | Consecutive energy management |
| SOC | State of charge |
| TNPC | Total net present cost |
| UC | Unit commitment |
| SC | Soft computing |
| PV | Photovoltaics |
| WT | Wind turbine |
| FC | Fuel cells |
| CHP | Combined heat and power |
| EL | Electric load |
| EM | Energy market |
| PLR | Part load ratios |
| FOR | Feasible regions of operation |
| Probability distribution function | |
| FF | Fill factor |
| ACO | Ant colony optimization |
| ABC | Artificial bee colony |
| ANN | Artificial neural network |
| CR | Cannibalism rate |
| MR | Mutation rate |
| RP | Reproduction rate |
| PVPP | Peak valley power pricing |
References
- Saswat, S.S.; Patra, S.; Mishra, D.P.; Salkuti, S.R.; Senapati, R.N. Harnessing wind and solar PV system to build hybrid power system. Int. J. Power Electron. Drive Syst. 2021, 12, 2160. [Google Scholar] [CrossRef]
- Salkuti, S.R. Short-term optimal hydro-thermal scheduling using clustered adaptive teaching learning based optimization. Int. J. Electr. Comput. Eng. 2019, 9, 3359. [Google Scholar] [CrossRef]
- Reddy, S.S. Multi-objective based adaptive immune algorithm for solving the economic and environmental dispatch problem. Int. J. Appl. Eng. Res. 2017, 12, 1043–1048. [Google Scholar]
- Sravanthi, P.; Vuddanti, S. Solving realistic reactive power market clearing problem of wind-thermal power system with system security. Int. J. Emerg. Electr. Power Syst. 2022, 23, 125–144. [Google Scholar]
- Pal, P.; Krishnamoorthy, P.A.; Rukmani, D.K.; Antony, S.J.; Ocheme, S.; Subramanian, U.; Elavarasan, R.M.; Das, N.; Hasanien, H.M. Optimal Dispatch Strategy of Virtual Power Plant for Day-Ahead Market Framework. Appl. Sci. 2021, 11, 3814. [Google Scholar] [CrossRef]
- Han, S.; Mao, T.; Guo, X.; Wu, W.; Sun, L.; Wang, T.; Zhou, B.; Zhao, W. Profit Evaluation for Virtual Power Plant in Power Load Response: From the Perspective of Power Grid. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2874–2878. [Google Scholar]
- Lombardi, P.; Powalko, M.; Rudion, K. Optimal operation of a virtual power plant. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2019; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Saabit, S.M.; Hasan, S.; Chowdhury, N.A. Virtual Power Plant Implementation and Cost Minimization for Retail Industry. In Proceedings of the 2021 2nd International Conference for Emerging Technology (INCET), Belagavi, India, 21–23 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Reddy, S.S. Optimal scheduling of thermal-wind-solar power system with storage. Renew. Energy 2017, 101, 1357–1368. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, K.; Zheng, B.; Zhu, G.; Wang, D.; Li, S.; Xu, K.; Tu, T. Optimal Scheduling Strategies of the Virtual Power Plant Considering Different Development Stages of the Electricity Market. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1010–1016. [Google Scholar]
- Zhang, T.; Qin, Y.; Wu, W.; Zheng, M.; Huang, W.; Wang, L.; Xu, S.; Yan, X.; Ma, J.; Shao, Z. Research on Optimal Scheduling in Market Transaction for the Participation of Virtual Power Plants. In Proceedings of the 2019 6th International Conference on Information Science and Control Engineering (ICISCE), Shanghai, China, 20–22 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 841–845. [Google Scholar]
- Naina, P.M.; Rajamani, H.; Swarup, K.S. Modeling and simulation of virtual power plant in energy management system applications. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 392–397. [Google Scholar]
- Zahedmanesh, A.; Muttaqi, K.M.; Sutanto, D. A consecutive energy management approach for a VPP comprising commercial loads and electric vehicle parking lots integrated with solar PV units and energy storage systems. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 21–15 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 242–247. [Google Scholar]
- Lombardi, P.; Sokolnikova, T.; Styczynski, Z.; Voropai, N. Virtual power plant management considering energy storage systems. IFAC Proc. Vol. 2012, 45, 132–137. [Google Scholar]
- Mishra, S.; Crasta, C.J.; Bordin, C.; Mateo-Fornés, J. Smart contract formation enabling energy-as-a-service in a virtual power plant. Int. J. Energy Res. 2022, 46, 3272–3294. [Google Scholar] [CrossRef]
- Renuka, T.K.; Reji, P.; Sreedharan, S. An enhanced particle swarm optimization algorithm for improving the renewable energy penetration and small signal stability in power system. Renew. Wind Water Sol. 2018, 5, 6. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M. Particle swarm optimization of a hybrid wind/tidal/PV/battery energy system. Application to a remote area in Bretagne, France. Energy Procedia 2019, 162, 87–96. [Google Scholar] [CrossRef]
- Lombardi, P. Multi criteria Optimization of an autonomous virtual power plant with high degree of renewable energy sources. In Proceedings of the 17th PSCC, Stockholm, Sweden, 22–26 August 2011; pp. 22–26. [Google Scholar]
- Dehghanniri, M.F.; Golkar, M.A.; Jahangir, H. Virtual power plant performance strategy in the DA and RT market under uncertainties. In Proceedings of the 2021 11th Smart Grid Conference (SGC), Tabriz, Iran, 7–9 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Khandelwal, M.; Mathuria, P.; Bhakar, R. Profit based self-scheduling of virtual power plant under multiple locational marginal prices. In Proceedings of the 2018 20th National Power Systems Conference (NPSC), Tiruchirappalli, India, 14–16 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Gough, M.; Santos, S.F.; Lotfi, M.; Javadi, M.S.; Osorio, G.J.; Ashraf, P.; Castro, R.; Catalao, J.P.S. Operation of a Technical Virtual Power Plant Considering Diverse Distributed Energy Resources. IEEE Trans. Ind. Appl. 2022, 58, 2547–2558. [Google Scholar] [CrossRef]
- Hadayeghparast, S.; Farsangi, A.S.; Shayanfar, H. Day-ahead stochastic multi-objective economic/ emission operational scheduling of a large scale virtual power plant. Energy 2019, 172, 630–646. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Erdinc, O.; Uzunoglu, M.; Karakas, A. An adaptive load dispatching and forecasting strategy for a virtual power plant including renewable energy conversion units. Appl. Energy 2014, 119, 445–453. [Google Scholar] [CrossRef]
- Zhang, C.; Ouyang, D.; Ning, J. An artificial bee colony approach for clustering. Expert Syst. Appl. 2010, 37, 4761–4767. [Google Scholar] [CrossRef]
- Aydin, D.; Özyön, S.; Yaşar, C.; Liao, T. Artificial bee colony algorithm with dynamic population size to combined economic and emission dispatch problem. Int. J. Electr. Power Energy Syst. 2014, 54, 144–153. [Google Scholar] [CrossRef]
- Narkhede, M.S.; Chatterji, S.; Ghosh, S. Multi objective optimal dispatch in a virtual power plant using genetic algorithm. In Proceedings of the 2013 International Conference on Renewable Energy and Sustainable Energy (ICRESE), Coimbatore, India, 5–6 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 238–242. [Google Scholar]
- Eiben, Á.E.; Hinterding, R.; Michalewicz, Z. Parameter control in evolutionary algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
- Kumar, S.; Pal, N.S. Ant colony optimization for less power consumption and fast charging of battery in solar grid system. In Proceedings of the 2017 4th IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics (UPCON), Mathura, India, 26–28 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 244–249. [Google Scholar]
- Rekik, M.; Chtourou, Z.; Mitton, N.; Atieh, A. Geographic routing protocol for the deployment of virtual power plant within the smart grid. Sustain. Cities Soc. 2016, 25, 39–48. [Google Scholar] [CrossRef]
- Biswas, M.A.R.; Robinson, M.D.; Fumo, N. Prediction of residential building energy consumption: A neural network approach. Energy 2016, 117, 84–92. [Google Scholar] [CrossRef]
- You, S. Developing Virtual Power Plant for Optimized Distributed Energy Resources Operation and Integration. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2010. [Google Scholar]
- Simoes, M.; Bose, B.K.; Spiegel, R.J. Design and performance evaluation of a fuzzy-logic-based variable-speed wind generation system. IEEE Trans. Ind. Appl. 1997, 33, 956–965. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Narimani, M.R. An efficient scenario-based stochastic programming framework for multi-objective optimal micro-grid operation. Appl. Energy 2012, 99, 455–470. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory. IEEE Trans. Smart Grid 2015, 7, 510–519. [Google Scholar] [CrossRef]
- Dabbagh, S.R.; Sheikh-El-Eslami, M.K. Risk-based profit allocation to DERs integrated with a virtual power plant using cooperative Game theory. Electr. Power Syst. Res. 2015, 121, 368–378. [Google Scholar] [CrossRef]
- Pandey, A.K.; Jadoun, V.K.; Jayalakshmi, N.S. Virtual Power Plants: A New Era of Energy Management in Modern Power Systems. In Proceedings of the 2021 8th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 26–27 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 538–543. [Google Scholar]
- Wu, Z.; Gu, W.; Wang, R.; Yuan, X.; Liu, W. Economic optimal schedule of CHP microgrid system using chance constrained programming and particle swarm optimization. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–11. [Google Scholar]
- Nazari-Heris, M.; Abapour, S.; Mohammadi-Ivatloo, B. Optimal economic dispatch of FC-CHP based heat and power micro-grids. Appl. Therm. Eng. 2017, 114, 756–769. [Google Scholar] [CrossRef]
- Zamani, A.G.; Zakariazadeh, A.; Jadid, S.; Kazemi, A. Stochastic operational scheduling of distributed energy resources in a large scale virtual power plant. Int. J. Electr. Power Energy Syst. 2016, 82, 608–620. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Application of fuel cell and electrolyzer as hydrogen energy storage system in energy management of electricity energy retailer in the presence of the renewable energy sources and plug-in electric vehicles. Energy Convers. Manag. 2017, 136, 404–417. [Google Scholar] [CrossRef]
- Ali, E.S.; El-Sehiemy, R.A.; El-Ela, A.A.A.; Tostado-Véliz, M.; Kamel, S. A proposed uncertainty reduction criterion of renewable energy sources for optimal operation of distribution systems. Appl. Sci. 2022, 12, 623. [Google Scholar] [CrossRef]
- Available online: https://www.meteoblue.com/en/weather/archive/export/basel_switzerland_2661604 (accessed on 7 March 2022).
- Available online: https://niwe.res.in/department_r&d,rdaf_time_series_data.php (accessed on 7 March 2022).
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Devi, M.R.; Jeya, I.J.S. Black Widow Optimization Algorithm and Similarity Index Based Adaptive Scheduled Partitioning Technique for Reliable Emergency Message Broadcasting in VANET. Mapp. Intimacies 2021. [Google Scholar] [CrossRef]
- Zamani, A.G.; Zakariazadeh, A.; Jadid, S. Day-ahead resource scheduling of a renewable energy based virtual power plant. Appl. Energy 2016, 169, 324–340. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Stochastic multi-objective operational planning of smart distribution systems considering demand response programs. Electr. Power Syst. Res. 2014, 111, 156–168. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Mouassa, S.; Jurado, F. A MILP framework for electricity tariff-choosing decision process in smart homes considering ‘Happy Hours’ tariffs. Int. J. Electr. Power Energy Syst. 2021, 131, 107139. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).