1. Introduction
The increasing number of offshore wind farms commissioned, under construction, or under development in Europe brings many independent electricity transmission systems to the seas to dispatch their renewable power [
1,
2]. To implement an optimal system, new topologies and control techniques have been developed to meet the current need.
According to current state-of-the-art technology, voltage source converters (VSC-HVDC) transmission systems have been demonstrated to be the most appropriate technology for offshore applications; at least 200 HVDC converter stations will be installed offshore with their respective platforms [
2]. It is possible to assume a 500 MW average AC/DC conversion capacity if the scenario is considered [
3].
Among all HVDC converters, the modular multilevel converter (MMC) is the most widely used in offshore wind power transmission applications. However, the MMC-HVDC scheme has significant disadvantages: high installation cost, the enormous offshore platform required, and high loss due to high switching frequency. As the transmission capacity continues to increase, the size and weight of the offshore station will increase [
4].
Using diode semiconductors, a 10% loss reduction can be expected. Diode-based rectifier (DR) stations to connect offshore wind farm power plants to HVDC links can contribute to a significant reduction in capital expenditure (CAPEX) and operational expenditure (OPEX) by increasing the efficiency and robustness of the overall system [
4,
5,
6,
7,
8]. Conversion savings = VSC − Diodes = 99 M€/year [
2,
3].
The proposed DR solution is a reality and is already being implemented as an alternative, using different topologies to convert the power from the offshore AC line into a DC line [
9,
10,
11,
12].
One difficulty in using a DR station is the fact that it cannot establish a stable AC voltage for an offshore wind farm such as the MMC; this duty AC control part will be taken up by the wind turbines (WT). In the state-of-the-art [
11,
12,
13], different forms for the AC line control are proposed, using the WT as an active part of the control and being necessary to modify the existing control. There are three types of this control: centralized control [
14], phase-locked loop (PLL) distributed control [
15], and decentralized control [
5,
16]. The current proposal is to perform complete control dynamics without modifying the WT firmware using a PPC and proving the real and optimized communication strategy on the test bench.
All the controls proposed for the WTs connected to the DR-based HVDC system used the principal WT active current, active power, to regulate its output voltage amplitude. In contrast, the reactive current of WT controls the offshore frequency. The difference between them is how to obtain the references and communication mode, but all the controllers proposed to modify the firmware of commercial wind turbines. The solution proposed in this article does not have to modify any aspect of the commercial wind turbine.
The centralized control has good performance in islanded and grid-connected modes. It obtains measurements at the point of common connection, which leads to the need for a high-speed communication grid. In the PLL distributed control, the main grid-forming scheme is based on the PLL equipment, which synchronizes directly to the WTs, dismissing the need for communication. Furthermore, the decentralized control uses the references of the external control, obtains the measurements, and communicates directly with the WT; with appropriate system communication, this control can operate stably and is experimentally proven in this work.
One of the main gaps to investigate is how to initialize the isolated offshore grid since there is no external power supply with the DR system. The WT connected to the DR system has an additional purpose of implementing grid formation control.
In the current literature, some ways to solve the black start are presented, as in [
17,
18], which proposes different topologies and controls, always with external elements or significant control variations in the converters. Moreover, [
19,
20,
21] offer several forms of control that act in part of the OWF system; these proposed controls have satisfactory theoretical results, but also with a great variation of the control of the WTs.
In [
22,
23], the aim is to initialize the system with external elements, using batteries and converters only for initialization. It is also a way to do it, but it dictates that these elements are always present for a reboot, increasing the total cost and size of the solution.
Another way would be to use mixed rectifier, diode, and VSC topologies, as proposed in [
6,
24], but we would have complex control dynamics and would increase the total costs of the solution.
This article proposes a new way to initialize the system more simply and practically, using the WTs as a current source to generate the offshore grid, proving in experimental results the effectiveness of the control.
This paper proposes an initialization, synchronization, and frequency regulation stabilization control of offshore wind farms (OWFs) connected to an HVDC system based on a diode rectifier, proven in the proposed test bench.
Compared with the state-of-the-art, the main contributions of this paper are summarized as follows. A new solution for the black start system that uses the same converters, operating to start the AC line to connect the wind farm, is proposed; the application of the novel integrated control to the wind turbine in centralized management using the PPC, allows the use of any commercial wind turbine without modifying its control; a smooth transition is proposed to switch from the synthetic grid to the real grid; this work achieves a real scalable test bench to apply the experimental validation not seen in the state-of-the-art.
This paper is organized as follows:
Section 2 defines the method and scope.
Section 3 shows the test bench materials.
Section 4 shows the results and demonstrates the effectiveness of the topology and the control.
Section 5 and
Section 6 make the discussions and conclusions, respectively.
2. Method and Scope
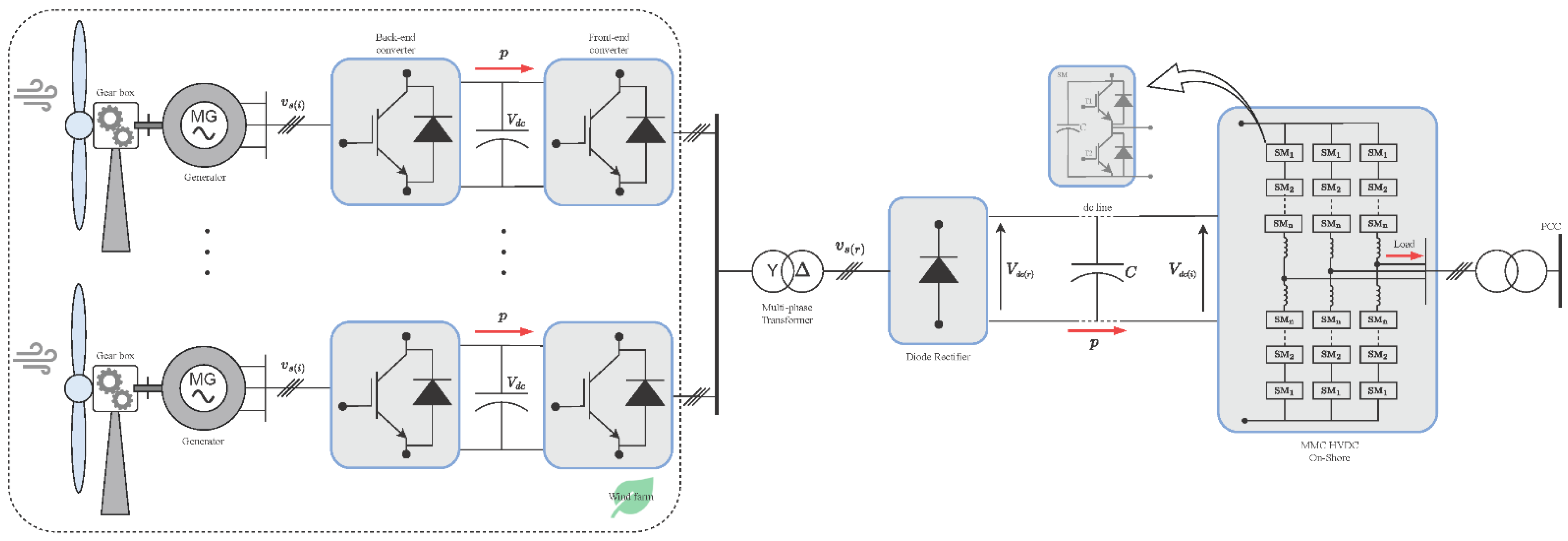
The first milestone to be reached is how to generate a stable grid in amplitude and controlled frequency. This grid corresponds to the offshore AC link of the wind farm, as seen in
Figure 1.
The 12-pulse diode rectifier station is connected to the offshore AC grid by a star-star and a star-delta connected transformer. A filter bank regulates the harmonics and provides dynamics to the reactive power compensation for the diode rectifier. The onshore MMC regulates the DC voltage of the HVDC link.
As the new topology no longer contemplates a controlled off-shore HVDC rectifier, since its initial role would be to generate the grid, it becomes necessary to create and control the offshore AC grid.
With the proposed new topology, the diode rectifier can no longer generate this grid, since, for the system, the rectifier is a passive element of connection to the HVDC link.
The type of WT considered for the OWF used the full conversion converter topology, B2B. The fully controlled converter leads to the complete decoupling of the wind turbine behavior from the grid generator. The WT DC voltage is controlled by the back-end converter (the converter connected to the wind power generator) for the WT generation system. In this way, the active and reactive power in the front-end converter (the converter connected to the offshore grid) can be freely used to regulate the voltage and frequency of the offshore AC grid. As a result, this system has the capacity to control the grid, actively contributing to the limitation of the effect of grid failure and the restoration to regular operation after a fault on the grid.
2.1. Modelling the System Analytically
To demonstrate the control strategy and the performance of the entire system, we highlight the fundamental concept of the method, which is the relationship between the reactive power and the frequency. Droop control is the basic scheme to achieve active and reactive power sharing based on the type of system impedance [
25].
Table 1 shows the droop control under the impedance characteristics of the proposed topology.
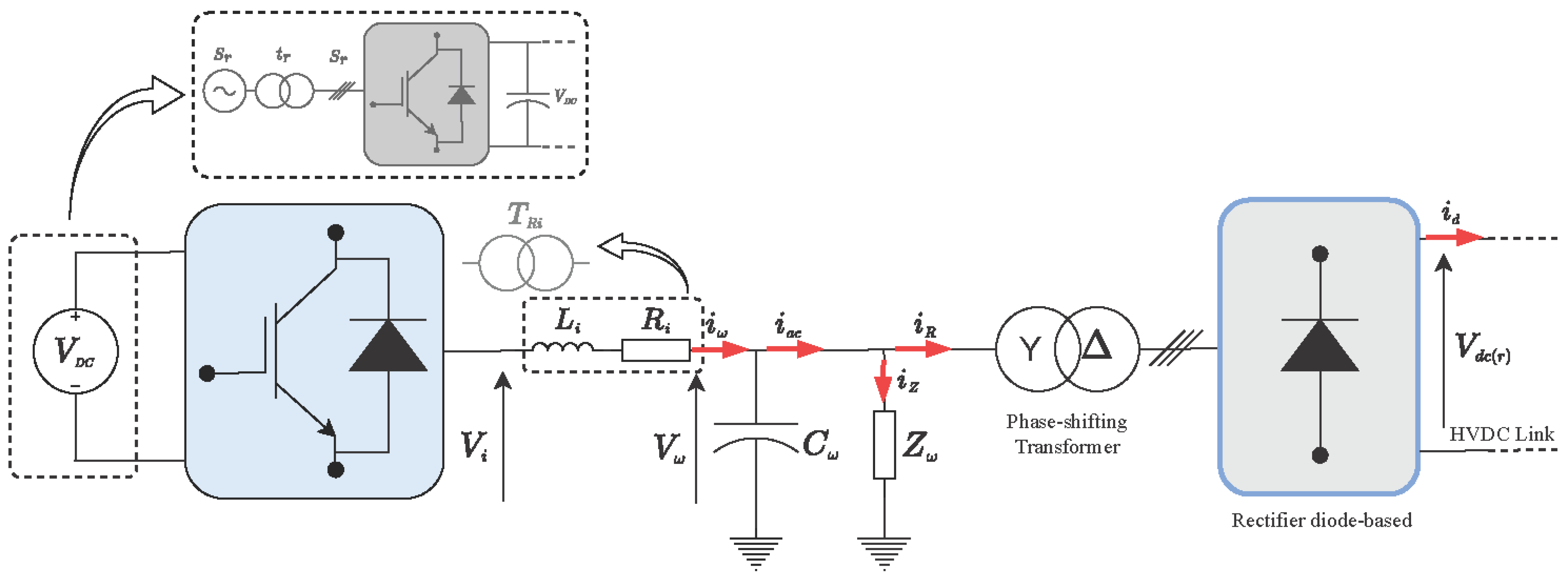
Figure 2 shows the modeled system of the offshore AC grid. The dynamics of the AC grid of the simplified model can be expressed in a synchronous frame oriented on
, i.e.,
[
4,
7].
The capacitive effect of the mathematical analysis is considered within the inverter filter and is not taken into account in the following analysis. As a consequence,
and
are obtained:
and the corresponding derivatives of
and
would be:
Since
remains constant in steady state:
and the corresponding derivatives of
and
would be:
A change of coordinates towards the output voltage
can be chosen. Therefore the
. In the new axes, the current component
would also become zero since both phasors are in phase, considering the
of the rectifier is approximately equal to 1.
From this model in dynamic axes DQ, the expressions for active and reactive power can be calculated:
is the amplitude of the current
and is calculated as:
The reactive power that comes out of the inverter is consumed in the reactive power absorbed by the inductance and the one absorbed by the transformer. In this expression, the reactive power absorbed by the rectifier due to harmonics has not been considered, since all sinusoidal variables have been considered.
The reactive power due to the rectifier harmonics can be calculated from the definition of power factor:
is the amplitude of the first harmonic of the input voltage to the rectifier.
With this expression, it is possible to obtain the relation between the reactive and active power in the diode rectifier.
The currents can be used to control the offshore AC grid. The
can be used to control the voltage and
can be used as a control action for the frequency of the offshore grid [
19]. The features of the offshore AC grid are largely determined by the reactance of transformer leakage and the capacitance of the combined filters [
14,
26]. To control the AC offshore grid, it presents a way to control external reference powers by using centralized control, PPC, which communicates with the wind farm in the next session.
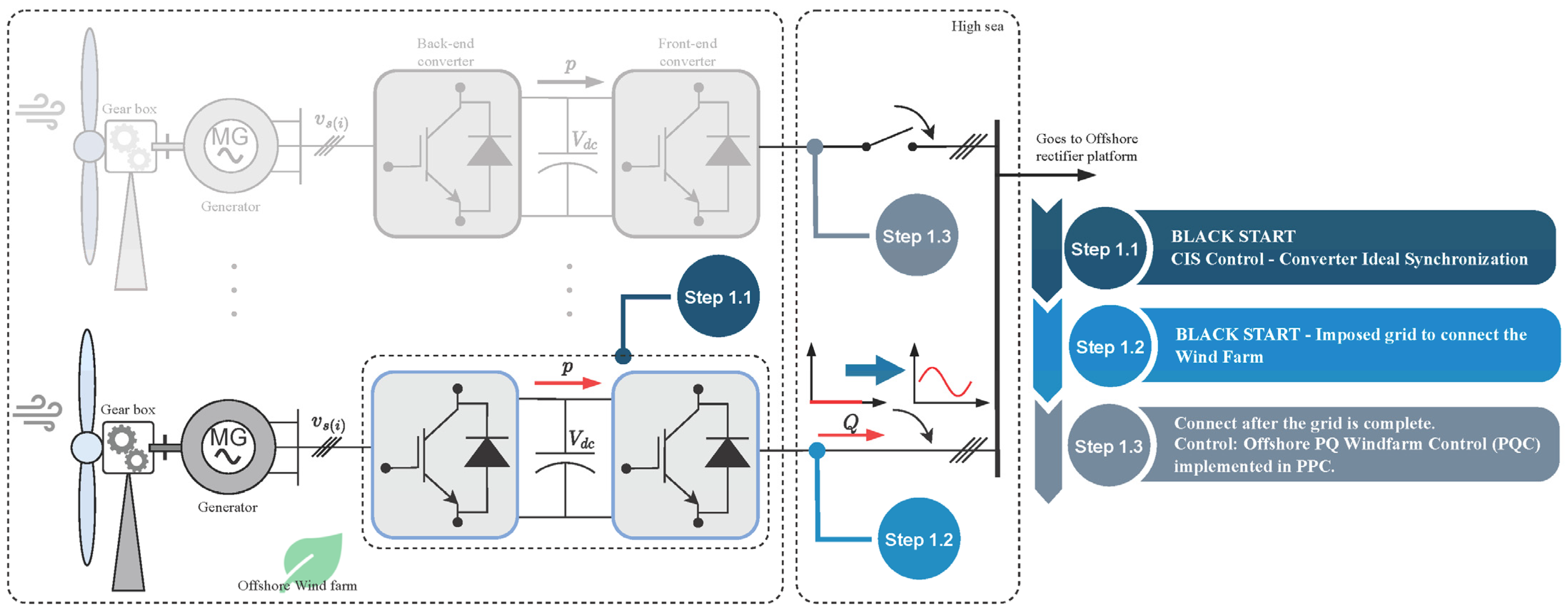
2.2. Propose Controls Steps
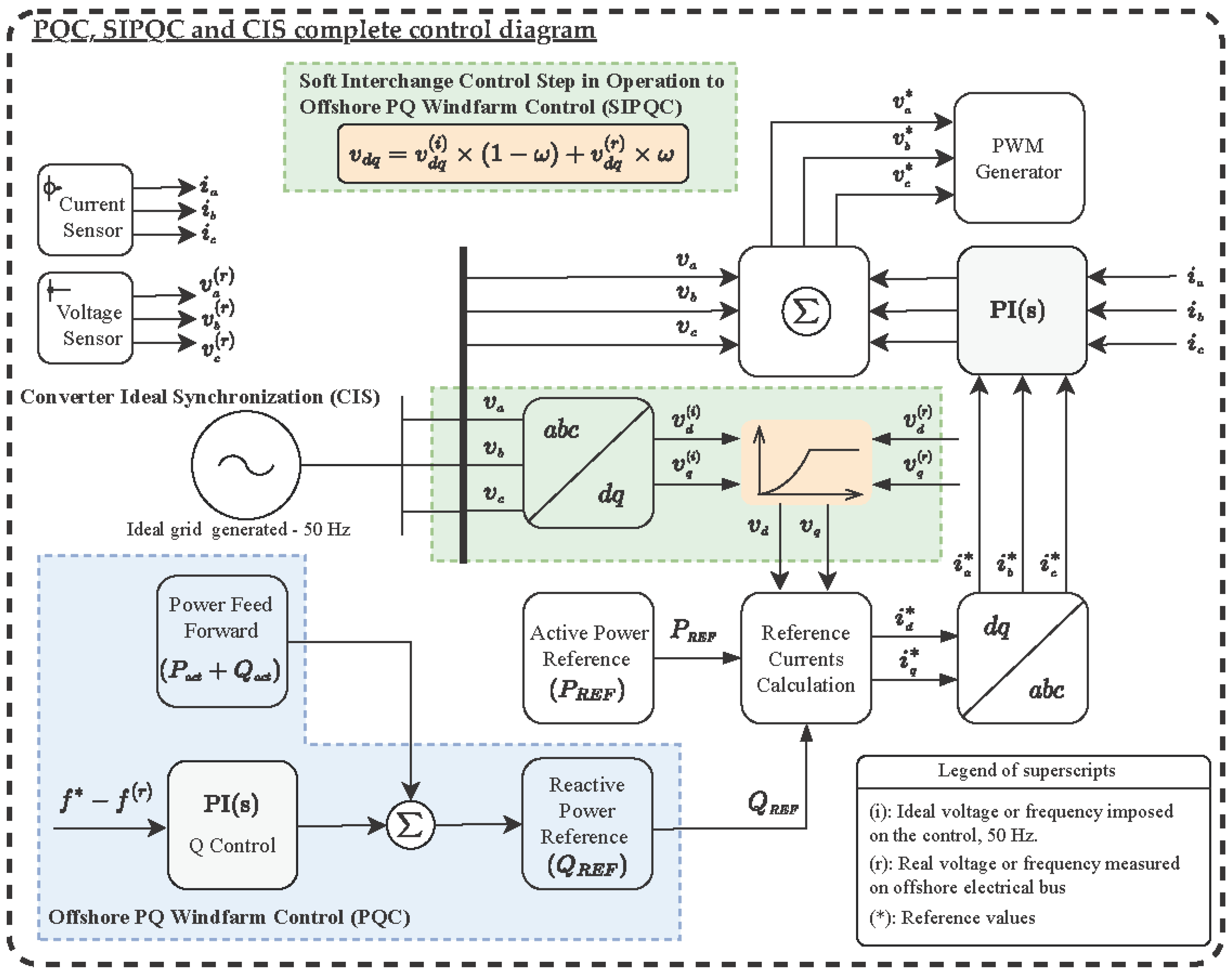
The dynamics for starting the OWF are done in three steps of different controls. It is important to note that we initialized the local grid, solving the existing black start problem. The complete control flow chart can be seen in
Figure 3 and
Figure 4.
The three proposed control steps are: Black Start Non-Linear Control Proposed—Converter Ideal Synchronization Control (CIS), Soft Interchange Control Step in Operation to Offshore PQ Windfarm Control (SIPQC), and Offshore PQ Windfarm Control (PQC).
2.2.1. Black Start Non-Linear Control Proposed—Step 1
Taking into account the characteristics of the topology, when a three-phase sinusoidal current is injected into the diode bridge if it has a stable DC voltage at its output [
27], a pulsed sine wave voltage is generated whose voltage value is bounded by the DC voltage of the rectifier.
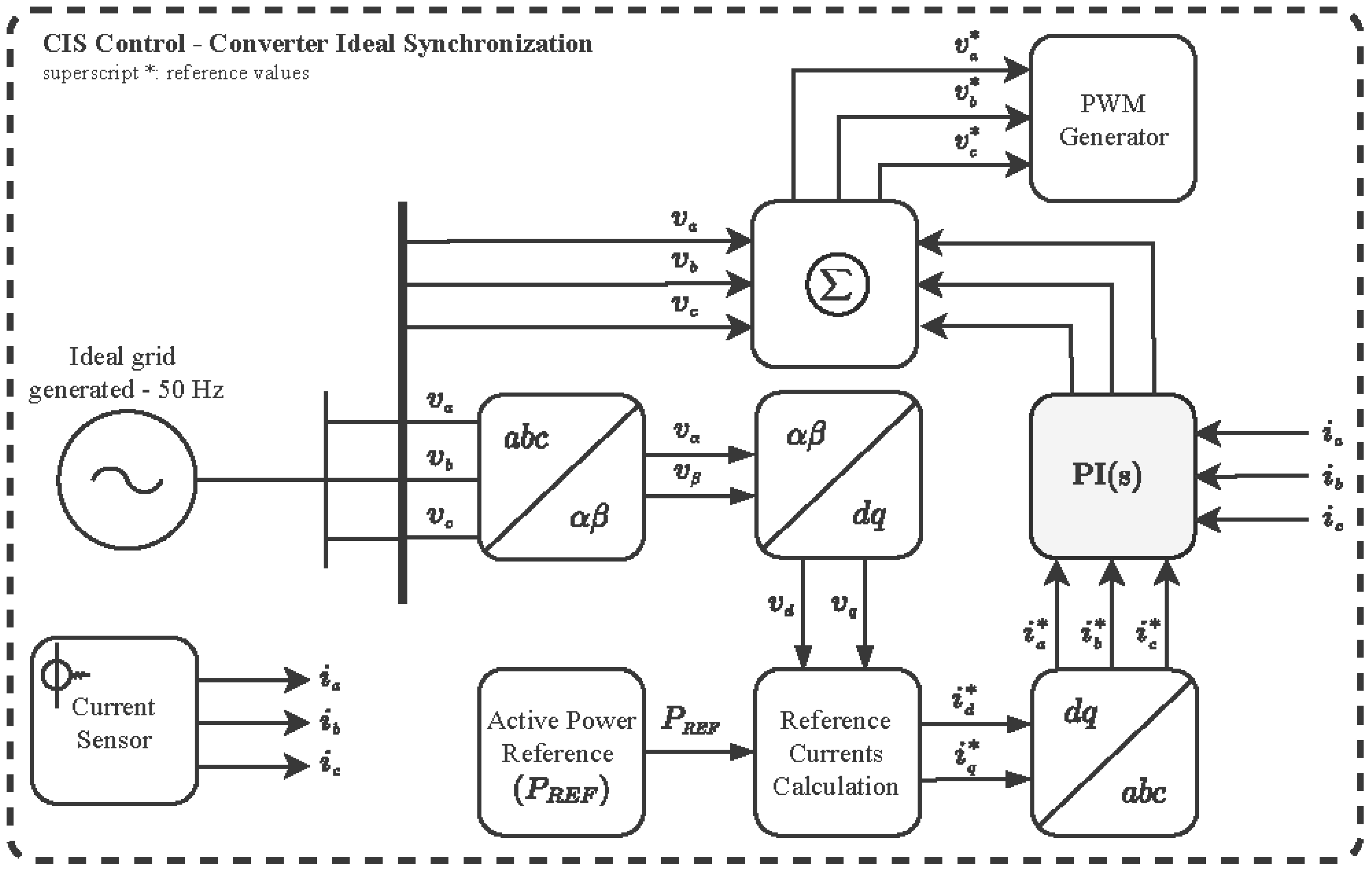
Taking advantage of this fact, a novel black start method is proposed to establish the local AC grid voltage system of the wind farm. An algorithm has been proposed for the Black Start Non-Linear in the B2B converter capable of operating in the current mode without initially having a balanced three-phase grid to synchronize. The algorithm, called “CIS (Converter Ideal Synchronization)”, can be seen in
Figure 5.
It is important to note that the wind turbine does not have its firmware modified. Therefore, the way to start the WT is to impose an ideal synthesized voltage on its voltage measurements.
Creating a grid following the control of a WT works to generate the initial grid of the system.
In this way, P and Q are imposed on the wind turbine using the PPC, and the generated current is controlled, producing a constant voltage on the busbar with an equal frequency and in phase with the current injected naturally, as detailed in the mathematical model.
Three sine waves of known amplitude are generated at a frequency of 50 Hz and offset by 120°. What is being done is to generate a balanced three-phase voltage system mathematically.
Once the ideal three-phase voltage has been generated, it is possible to pass the voltages to DQ synchronous axes.
At this point, current references can be calculated based on the desired power set points. Being synchronized with the ideal voltage that has been generated, the converter can produce an accurate sinewave current that is poured into the rectifier, thus producing a controlled power recirculation.
Thus, the other WTs can connect to the system and also initialize the PPC control system. In this way, dynamic PQ steady-state control is actively entered.
However, the offshore AC line control is still conditioned to the WT used to the black start, as the ideal voltages impose the frequency.
With the WTs connected and already activated to react with the reactive energy for frequency control, step 2 of the system begins. The first connected WT has to pass its control from the synthetic grid to the real grid. For this purpose, a new control step is developed in the following section.
2.2.2. Soft Interchange Control Step to Offshore PQ Windfarm Control (SIPQC)—Synthetic Grid to the Real Grid—Step 2
To change the synthetic voltage imposed to the real voltage, it is not possible to do its voltages abruptly, since it is observed that the rectifier induces a lag between the ideal grid and the real grid, thus avoiding a sudden transient.
Therefore, it is proposed to move from one magnitude to another in a soft and weighted way, so it is necessary to calculate the real voltages in DQ using a PLL block that calculates the frequency at which the grid rotates.
Due to the distortion of the voltage wave with the characteristics of a 12-pulse rectifier, it is necessary to filter the voltages in αβ by means of a second-order filter. The solution to this problem is based on the following equation:
Being: ω: weights are given to each magnitude.
The parameter ω can take values between 0 and 1. The idea is to vary these weights from 0 to 1 on the ramp. Thus, only the ideal voltages are considered at the beginning, and at the end, only the real voltages will be considered.
In addition to the voltage, it is also necessary that the current is generated with the angle of the real grid and not with the ideal grid angle. Both the angle of the real grid and the angle of the ideal grid are known, so it is proposed to make a smooth transition from one to another by applying the same weighting concept as with the voltages.
Thus, at the end of the transition, the current in phase with the grid is read directly. This new interpolated angle must also be used to transform the reference voltages.
The proposed algorithm is based on the fact that the frequency of the grid is proportional to the reactive that is injected. Therefore, the grid’s frequency can be controlled by correctly controlling the reactive power.
This is only possible if all previous steps and controls are correctly synchronized. It can be verified that, when making the weighted transition between ideal grid and real grid, the frequency suffers deviations making the system unstable if it is not acted upon. To solve this problem, an external PI controller is designed based on the frequency error responsible for providing the reactive power reference necessary to maintain the grid frequency at the desired value.
This control is a transition to the final control proposed, but it has been observed that the frequency control has to enter this intermediate step to keep the system stable.
Figure 6 shows the proposed control frequency.
is the initial value for reactive power.
This controller starts to act at the moment when the transition begins. It must be fast enough to prevent the frequency from suffering serious deviations.
This algorithm was implemented in simulation and later implemented on the test bench.
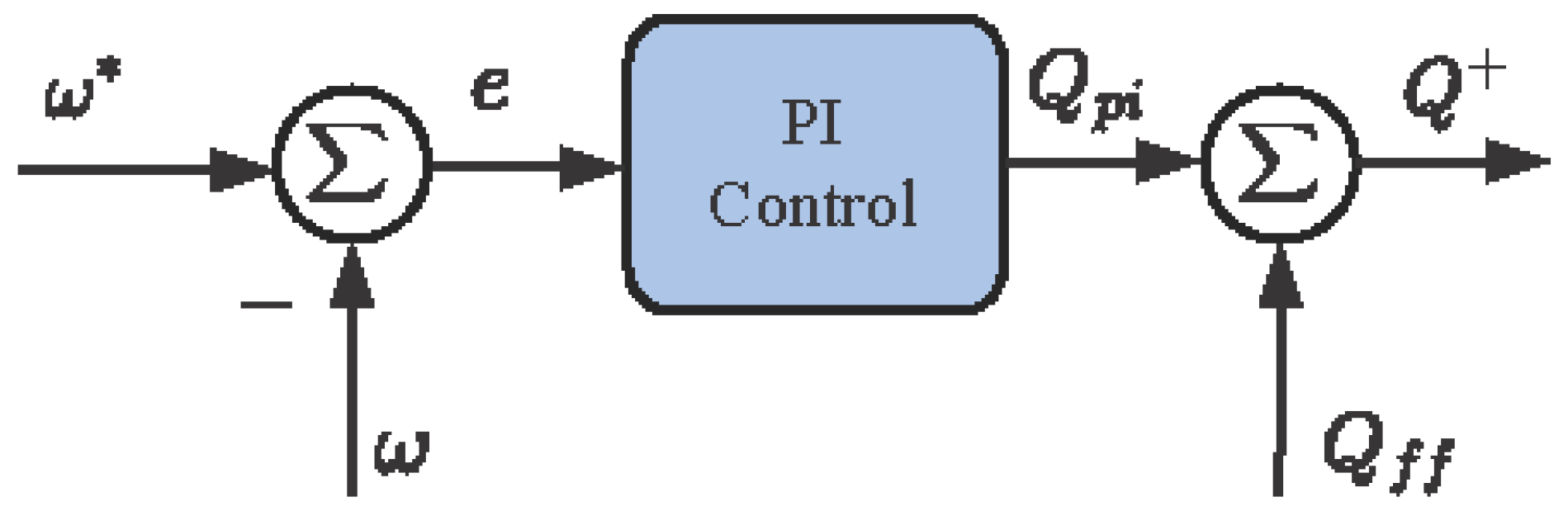
2.2.3. Offshore PQ Windfarm Control (PQC)—Step 3—Permanent Regime
The complete control in the block diagram is shown in
Figure 7.
The diagram represents the different parts of the control system. In blue, the PQC is shown, responsible for controlling the frequency and generating the reactive power reference. The PQC control is inside the PPC.
In green, the system initialization process is shown using the CIS technique and the SIPQC control exchange process, where the voltage used by the control algorithm changes from the synthetic voltage to the real voltage.
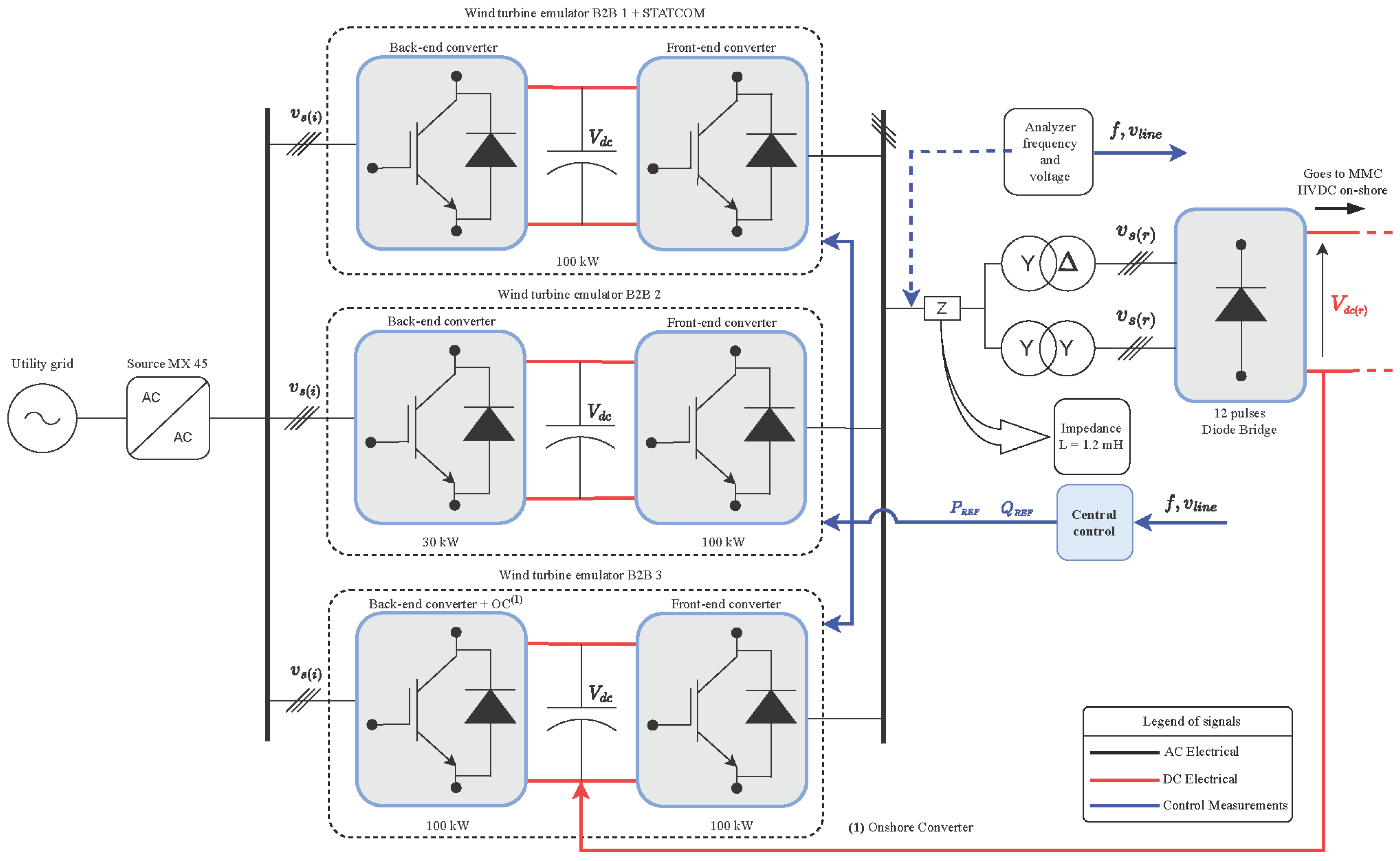
3. Test Bench Materials
The test bench is modeled using three aggregated wind converters of different rated powers (back-to-back converter (B2B) 1: 100 kW, B2B 2: 30 kW back-end converter and 100 kW front-end converter, and B2B 3: 100 kW front-end and back-end converter) as shown in
Figure 8. The B2B 3, the front-end converter, connects the HVDC link and recirculates the power. The active and reactive power added together for the bench have a total rated capacity of 100 kVA.
The topology and method were tested on a 100 kVA power test bench laboratory.
Figure 9 shows part of the converters, B2B 1: 100 kW and B2B 2: 30 kW back-end converter and 100 kW front-end converter. The B2B 3 comprises two 100 kW converters, the same model as the B2B 2 front-end converter.
Figure 10a shows the 12th pulse diode-based rectifier, and
Figure 10b shows the most important component, the whole B2B 1 converter, used to manage the controls steps, black start, interchange control (SIPQC), and PQC. The B2Bs 2 and 3 are only connected directly using the final control step Offshore PQ Windfarm Control (PQC).
Table 2 shows the main characteristics of the test bench.
Regarding the test bench, all converters were connected to a laboratory source, which emulates a 400 V and 50 Hz grid. The source was a California Instruments MX45, whose protections were configured to open a circuit if the system failed. The source’s primary purpose is to isolate the system from the external grid connection. The outer grid connection only supplies energy from the loss of power recirculation.
A Fluke 434 grid analyzer was used to measure the off-shore AC link of the wind farm. All B2B converters have input and output sensors, protections for all elements, and SCADA software for their correct control.
The converter control hardware was distributed among a central control unit and three local control units (one on each B2B). The main control unit consists of a PPC that runs the offshore PQ Windfarm Control. The local control hardware system was composed of DSP and FPGA, which can correctly process signals to control each B2B. The B2Bs 2 and 3 implement the Offshore PQ Windfarm Control. The B2B 1 managed all the control steps and started the offshore AC link.
4. Results
The newly proposed concept of external control for offshore wind farms has been validated using a scalable test bench used to demonstrate the technical controllers and MATLAB® simulations to compare the results. Several steps and scenarios have been considered to ensure that, under any extreme working conditions, the control can keep the main variables, voltage, and frequency, between the normal operating limits. Some examples of the analysis performed include black start critical steps, transformer/rectifier system behavior together with the wind farm and its interactions, power generation variations, and transient situations. The main results to validate the external control are depicted in this article.
The results are organized according to the previous sections and proposed:
Black Start Nonlinear Control Proposed—CIS—Converter Ideal Synchronization Control result.
Soft Interchange Control Step in Operation to Offshore PQ Windfarm Control (SIPQC) result.
Offshore AC grid voltage and frequency control using the external control result.
P and Q relationship result.
4.1. The Black Start Nonlinear Control Results
The novel part of this control is its application for this type of offshore AC grid, and imposes the ideal grid on the same, as commented before.
For the correct application, many adaptations had to be made to the B2B converter and the control to a bench-level application.
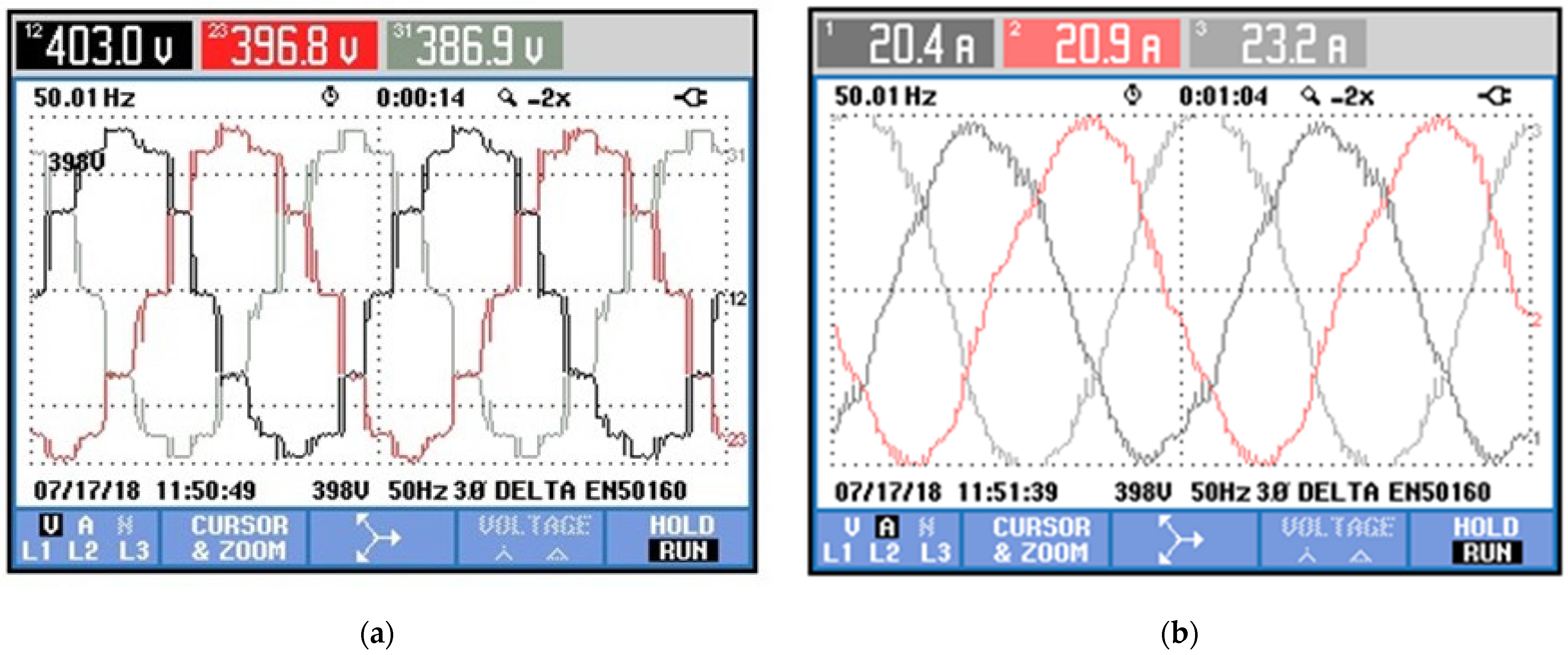
The results are presented in
Figure 11,
Figure 12 and
Figure 13. The results presented were taken with a FLUKE model 434 Power Quality Analyzer.
Figure 11a presents the results of the grid generated on the offshore AC link. This generated grid is the main objective of this first part of the control. It is possible to clearly observe the characteristics of the 12-pulse rectifier and the stability of the generated grid.
As expected, the results of the THD have the characteristics of a 12-pulse rectifier, with values below those expected for the topology. In
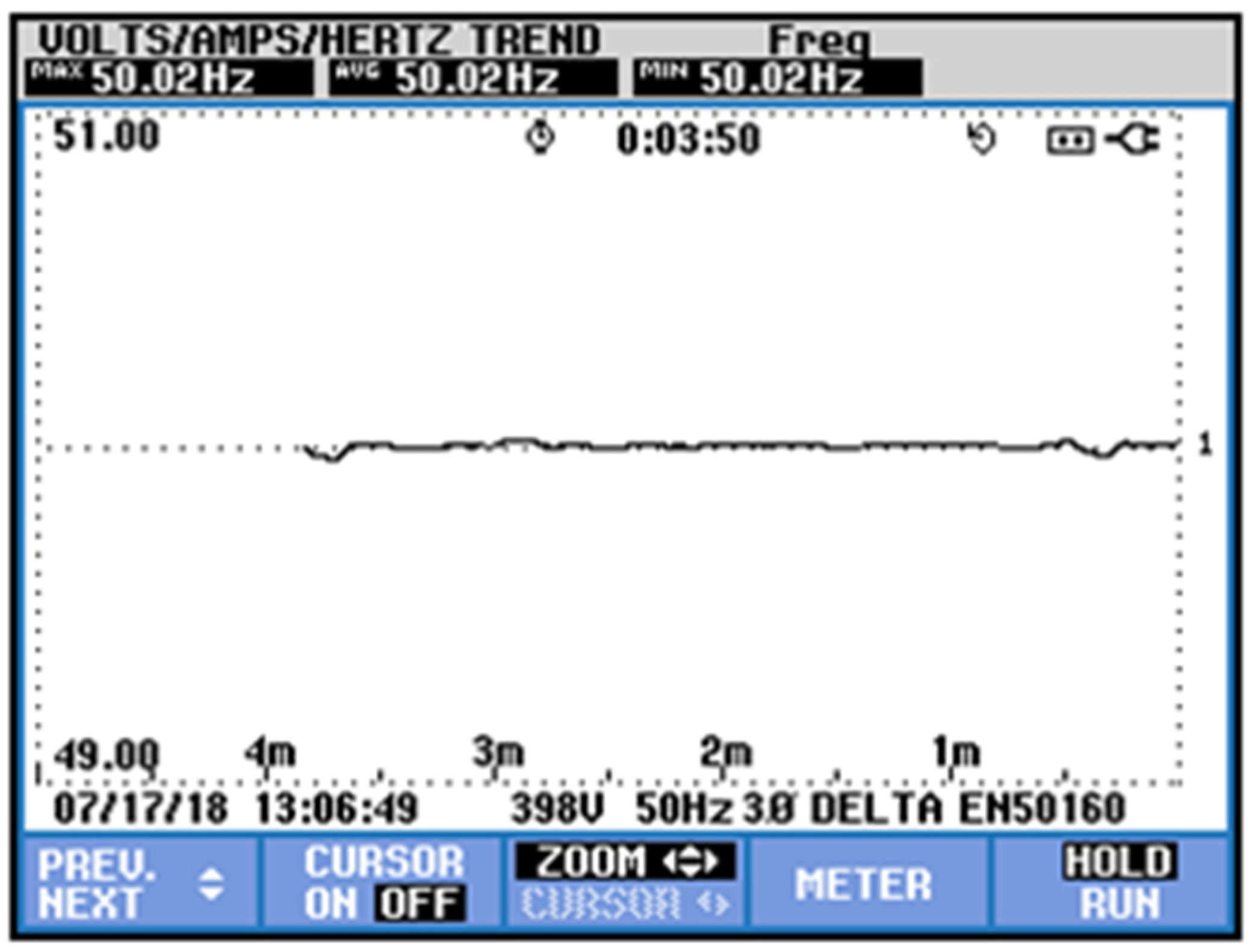
Figure 12, the correct control of the frequency imposed by the generated grid can be observed.
4.2. Soft-Interchange Control at Transient Results
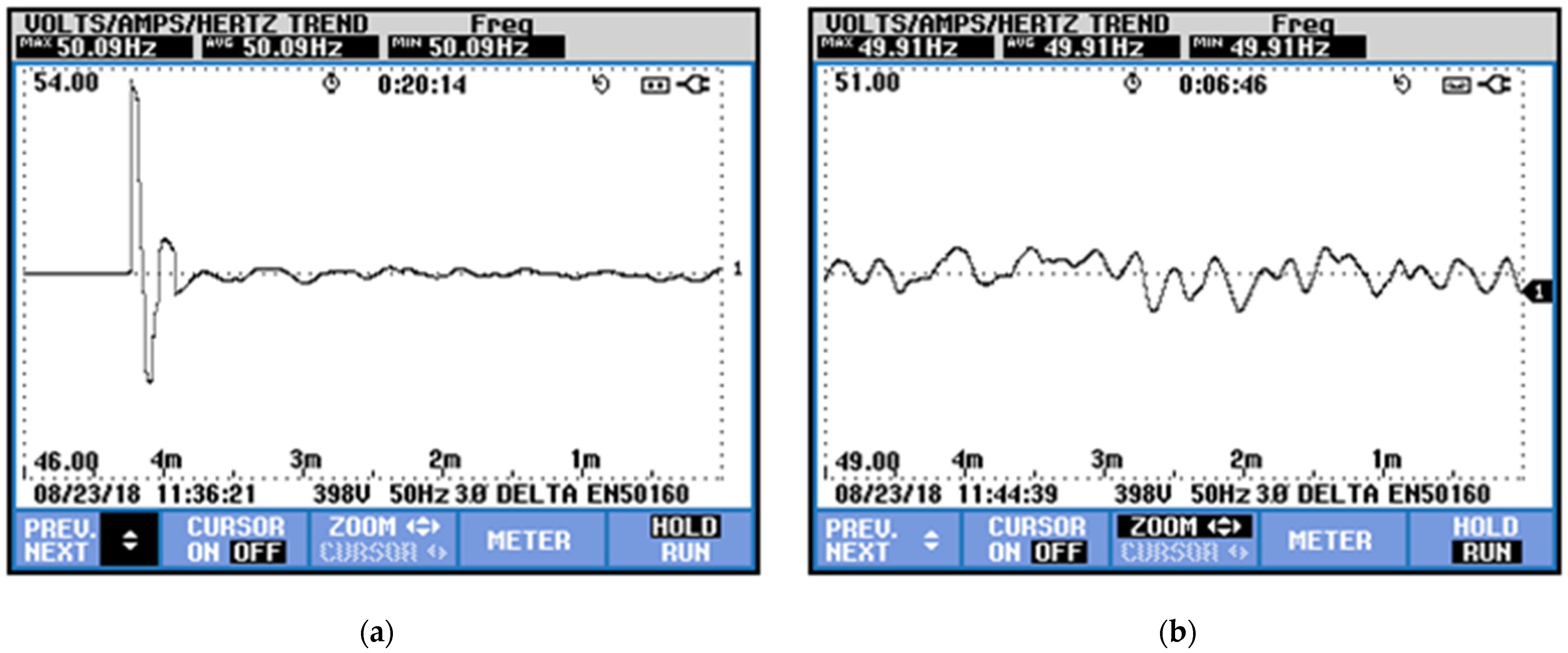
The results obtained are presented in
Figure 14a,b. Since this control is in the transition phase and occurs at the moment, Fluke helps to record the exact transition moments.
The exact moment of the control change can be observed in
Figure 14a,b; a transitory change in frequency is observed. Now, as the frequency is controlled, a more significant variation in frequency is also observed. This variation is less than 0.2 Hz.
Transient Frequency in Load and Variation in Soft-Interchange
It is important to note that the AC grid voltage remains stable and without variation in the transient, and the HVDC link remains stable and without sudden variation due to the transition of the control.
4.3. Advanced PQ Control System for the Local Grid in Permanent Regime
In the proposed absolute control, it is intended that with changes in active power generated by the wind, the frequency control will act, and a response will be made in reactive power to keep the frequency stable.
In this section, several active power changes are shown to verify the correct frequency control. In addition, the control is tested at different frequencies, which generally is 50 Hz, but this offshore busbar does not have frequency dependence.
Finally, the results were obtained to find the dependency equation between active and reactive power for this proposed test bench.
4.3.1. Frequency Variation and Reactive Power Response
As can be seen in
Figure 15, the proposed control has a rapid response to changes with very precise transients. These frequency changes during test bench operation are an outstanding achievement.
4.3.2. Active Power Variation and Its Reactive Power Response
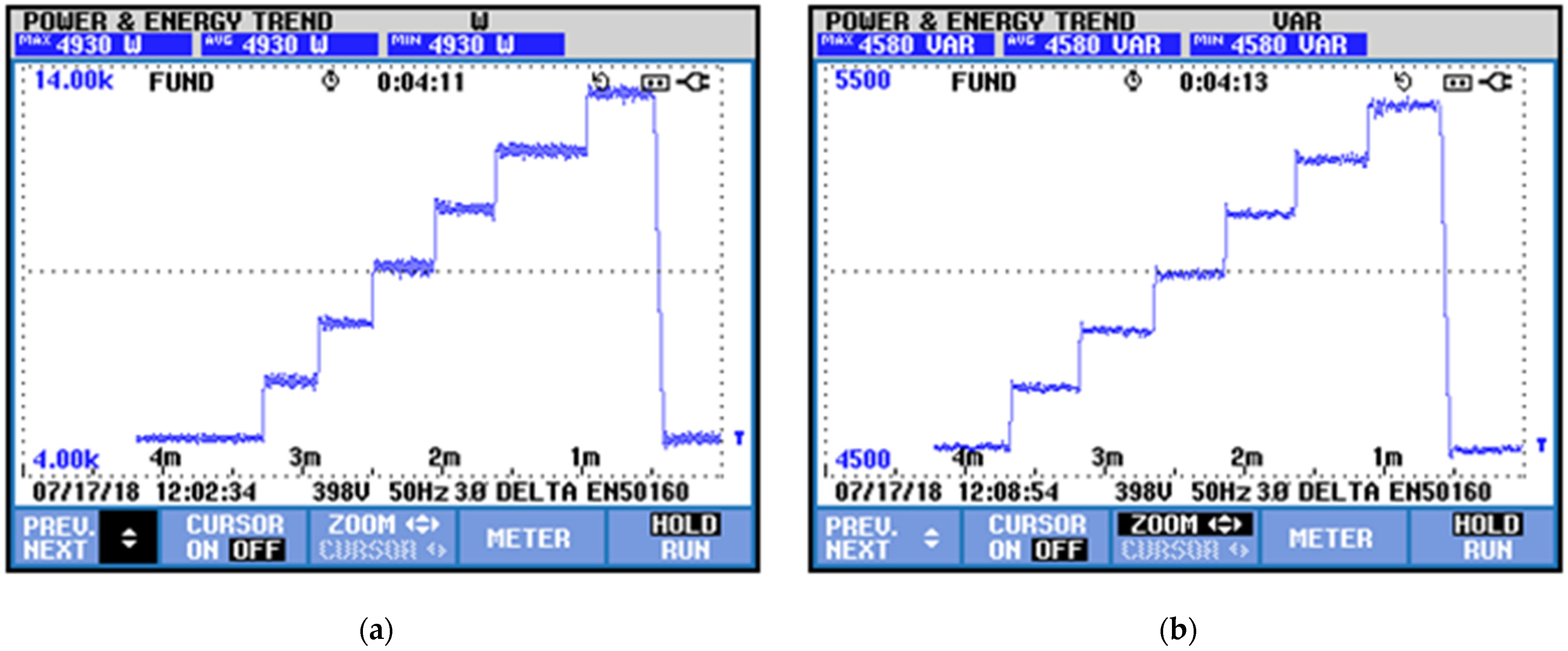
For this test, active power variations of 2, 4, 6, 8, 10, 12, and 14 kW, respectively, are proposed, and the results of equivalent reactive energy are sought to maintain the grid at 50 Hz, as can be seen in
Figure 16.
At the end of the test, an abrupt power change is made to check the robustness of the proposed control. Even with great variations in active power in frequency, no transient variation is observed.
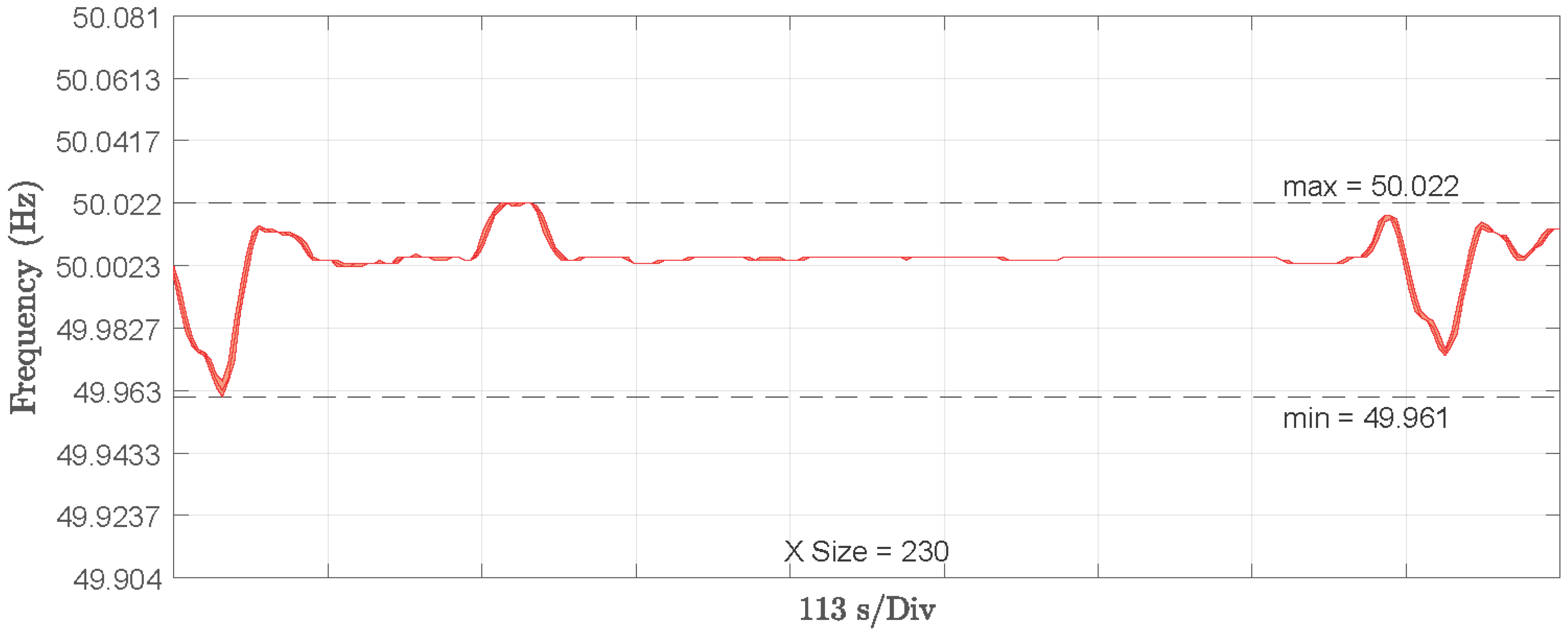
4.3.3. AC Busbar Frequency Variation with Stimulated Power Variation (Winds Gusts)
It can be observed in
Figure 17 that, when abrupt variations in active power were forced, the maximum variation seen in the frequency was 50.022 Hz and the minimum 49.961 Hz. This verifies the correct performance of the proposed control.
It can be seen that the control imposed on the reactive energy works in a precise way. It is impossible to observe significant variations to reach the desired value, and the transients are minimal.
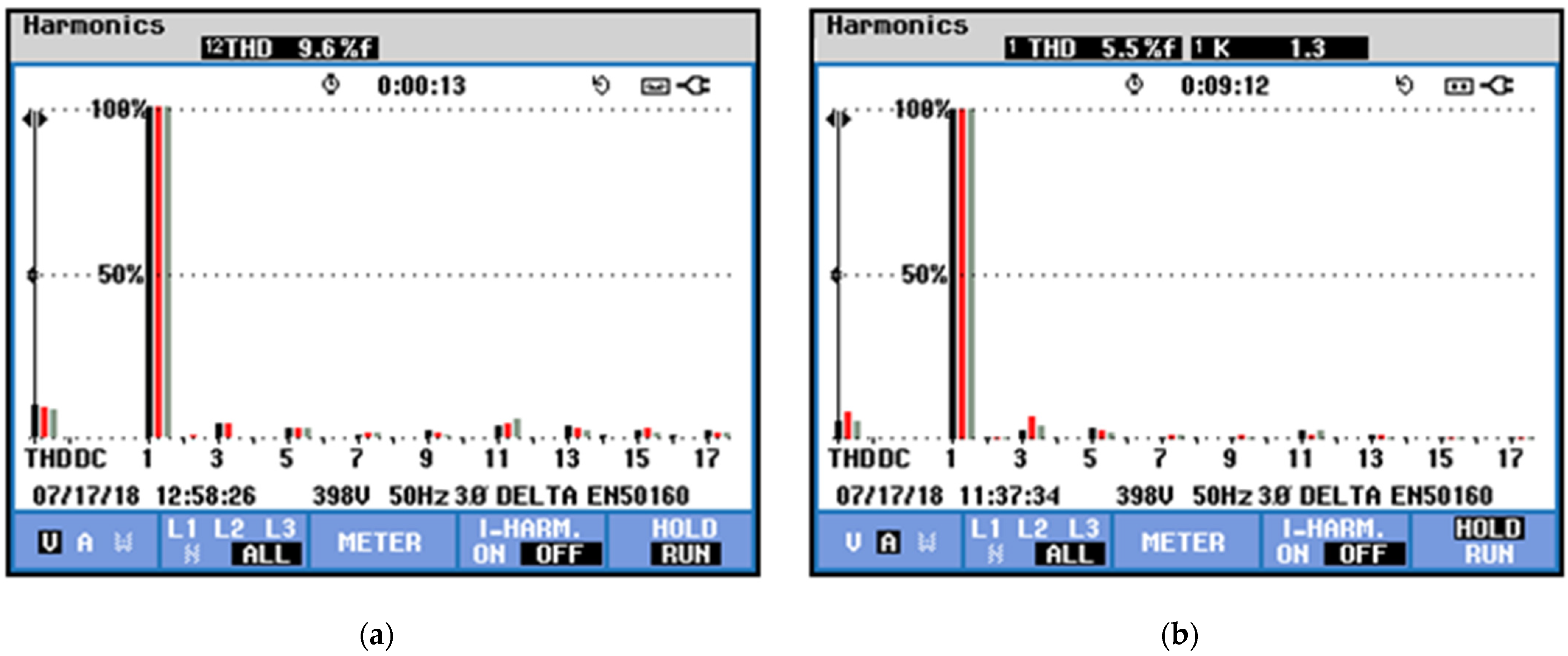
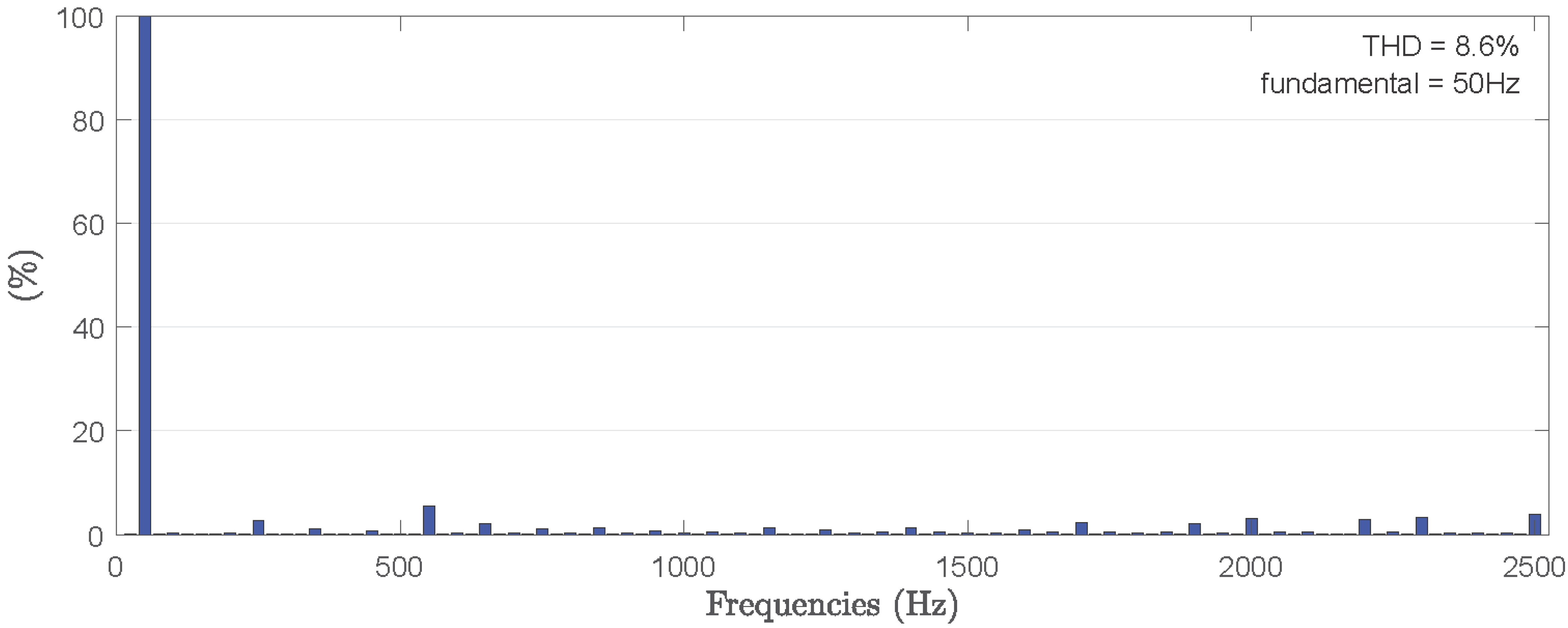
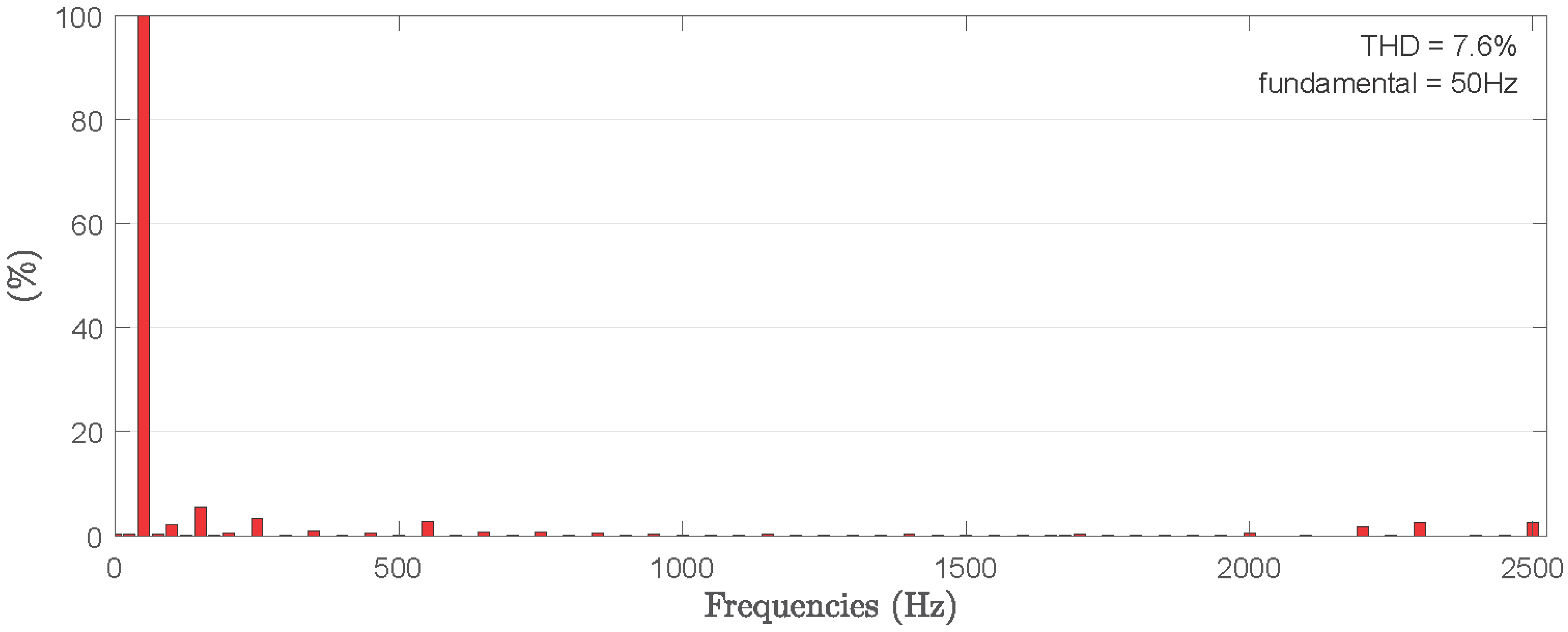
4.3.4. Quality AC Busbar for 50—THD
Figure 18 and
Figure 19 show the voltage and the current harmonics spectrums at the offshore AC bus bar connected to the 12-pulse rectifier. The harmonics 5º, 7º, 17º, 19º, 29º, 31º, etc., have been canceled by interacting with the two rectifiers of six pulses, whose voltages have a phase shift of 30°.
4.3.5. Active Power and Reactive Power Relationship Result
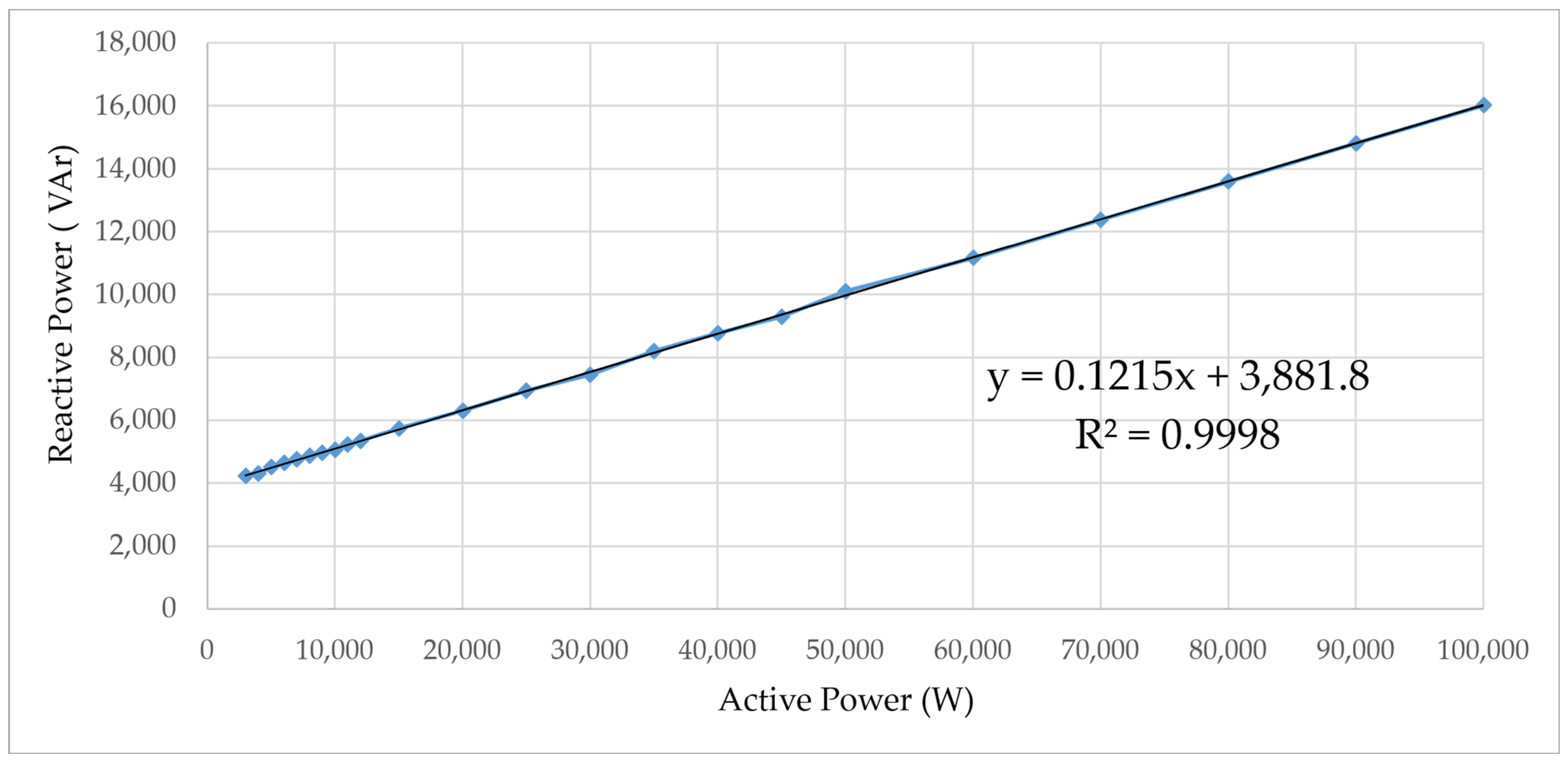
Table 3 shows the relationship between active power and reactive power. It can be observed from the results between the ratio of active and reactive power that there is an initial offset of approximately 3.8 kVAr.
In
Figure 20, the equation of the relation between the active and reactive powers is obtained.
where k can be obtained from Equation (21):
and
can be obtained from Equation (18):
The offset is due to the transformer magnetizing impedance which absorbs a constant reactive power because the rectifier voltage is constant, as is considered before an Equation (18). Using those equations, this magnetizing reactive can be calculated as 3881.8 VAr, with = 100 mH, and .
Additionally, the slope k, can be calculated as 0.1215, with the
, measured in
Figure 18 and
which confirms that
current component it is close to zero.
4.3.6. Centralized and Decentralized Control for the Wind Farm—Time Delay Concepts
Table 4 shows the results obtained with the proposed decentralized control. The most challenging part of this control is the fast communication system when the force-time delay can observe the increment frequency variation. The goal is to know the different results of the time delays and evaluate the optimal communication link with the external control. One of the concerns would be the delay in communications between the PPC of the WF and each WT. With this section, it was possible to verify that the control is effective even with some delays in the communications. To prove the frequency variation with time delays, the dynamics of the power variation in
Figure 16 was considered.
5. Discussion
An offshore wind farm DR HVDC topology was detailed, along with developing a new algorithm based on frequency regulation to generate an AC voltage grid on the wind farm side.
A test bench is used to obtain real results from topology concepts. A similar test bench has not been found in the state-of-the-art. The system initialization and synchronization with the proposed algorithm have been challenging, and the experiments have confirmed the value of this test bench to demonstrate that it is possible to start and operate a real DR HVDC link.
The main articles in the literature that propose the DR solution [
9,
10,
11,
12,
13,
14,
15,
16] always seek to modify the controller firmware inside the wind turbines, which, despite being effective controls, enter the problem of changing the WT certification, as it is a complex procedure. Therefore, in this work, the Advanced Control System algorithm of the offshore local area network is performed through a centralized PPC, thus maintaining the commercial WTs without changing the firmware. Moreover, this proposed algorithm can be used in WTs that are in operation.
The main challenges of this algorithm were proven with bench performance, using a real PLC to implement the PPC, and replicating the real communication carried out for a WF.
It should also be noted that several communication time delays were tested to verify the limitations and needs of centralized control (PPC).
The relationship between active and reactive power for the test bench has been obtained and confirmed analytically, and this relationship facilitates the design and development of DR HVDC link technology. It has been proved that the reactive required for effectively controlling the frequency increases when the AC grid voltage THD is higher. By choosing a suitable non-controlled diode rectifier topology with a higher pulse level, it is possible to use a lower THD voltage and thus reduce the reactive power required to control the frequency of the AC voltage grid [
6,
24].
The entire process developed to initialize the DR HVDC topology is new; in all cases in the current literature, they analyze ways of acting, constantly modifying or placing some external element [
17,
18,
20,
21,
22,
23]. The proposed control can be easily implemented without changing the WT firmware.
This work tests a 50 Hz frequency reference control on the AC voltage line, and the results are shown. The operation of a 60 Hz frequency reference control was also verified. It is important to emphasize that, as the AC line is isolated, it is possible to vary the frequency and test new passive filters and different control strategies. This important topic has been studied in the literature.
This work facilitates future research in this field by including mathematical modeling of the problem. It would be an excellent opportunity to develop new controllers, such as the predictive one, thus improving the results and reducing the frequency variation.
6. Conclusions
This paper presents a new frequency control algorithm for the AC voltage line of an offshore wind farm connected to a DR HVDC link. In the state-of-the-art, some references analyze this problem, and the solution proposed in the literature requires significant changes in the internal WT control algorithm. The proposed control is implemented in the PPC of the wind farm using commercial WTs, and no firmware changes are required. A new DQ reference frame model has been implemented considering the step-up transformer magnetizing impedance. The reactive power consumed by the DR has been obtained from the DQ model, resulting in a well-known expression for this electrical system.
The experimental results have been verified on a real test bench, confirming the validity of the proposed approach.
Experiments have demonstrated that the AC voltage line of the DR HVDC link can start from zero (black start). The proposed control has been implemented on the test bench using a PLC with a communication protocol and delays time similar to those used in a real WF. Experiments demonstrated that it is possible to use this PPC acting as a frequency control proposed in this application.
Using the proposed external control, the results in this article show neglectable frequency and voltage variation, resulting in a very stable system with great benefits for wind park operation.
The newly proposed topology and its external control allowed energy transmission in the HVDC link based on diode bridge rectifiers. Consequently, a remarkable reduction in the total weight of the offshore rectifier platform is obtained. Another important benefit is the significant cost reduction of construction and engineering activities.
Finally, as an additional value, the proposed solution allows commercial wind turbines to be easily integrated since it does not demand modifications in the internal controller’s structure. Furthermore, the outcomes of the proposed topology demonstrate the feasibility of using n-pulse transformers, leading to viable, robust, reduced cost, and therefore a competitive solution for integrating commercial wind turbines.