MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts
Abstract
:1. Introduction
- (i)
- Level-1, AC voltage at 120/240 V with a maximum current of 15 A and a maximum power of 3.3 kW;
- (ii)
- Level-2, AC voltage at 240 V with a maximum current of 60 A and a maximum power of 14.4 kW; and
- (iii)
- Level-3, through a charging station, DC voltage directly to the battery via a DC connector, with a maximum power of 240 kW.
- (i)
- Using different sizes of batteries; and/or
- (ii)
- Connecting to the grid and importing power when solar power is inadequate.
- (1)
- Scheduling strategy for an off-grid solar PV charging station based on 24-h day-ahead solar forecast and probability of vehicle arrival for charging.
- (2)
- Emphasizing and illustrating the dependency of a solar PV-based charging station on the size of the BESS, and subsequently indicating that the net profit is dependent on the size of the BESS.
- (3)
- Offering an optimization technique to realize maximum profit from an off-grid solar PV charging station.
- (4)
- Highlighting the shortfalls of an off-grid solar PV charging station.
- (5)
- Demonstrating an application of the MILP method in determining the solution for such optimization problem.
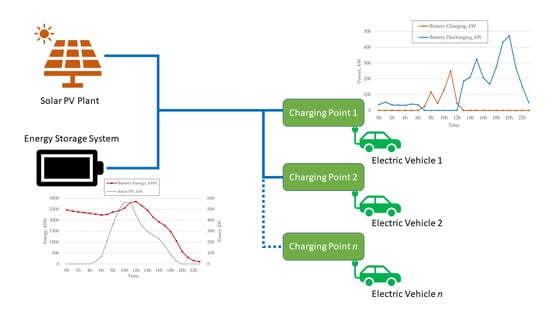
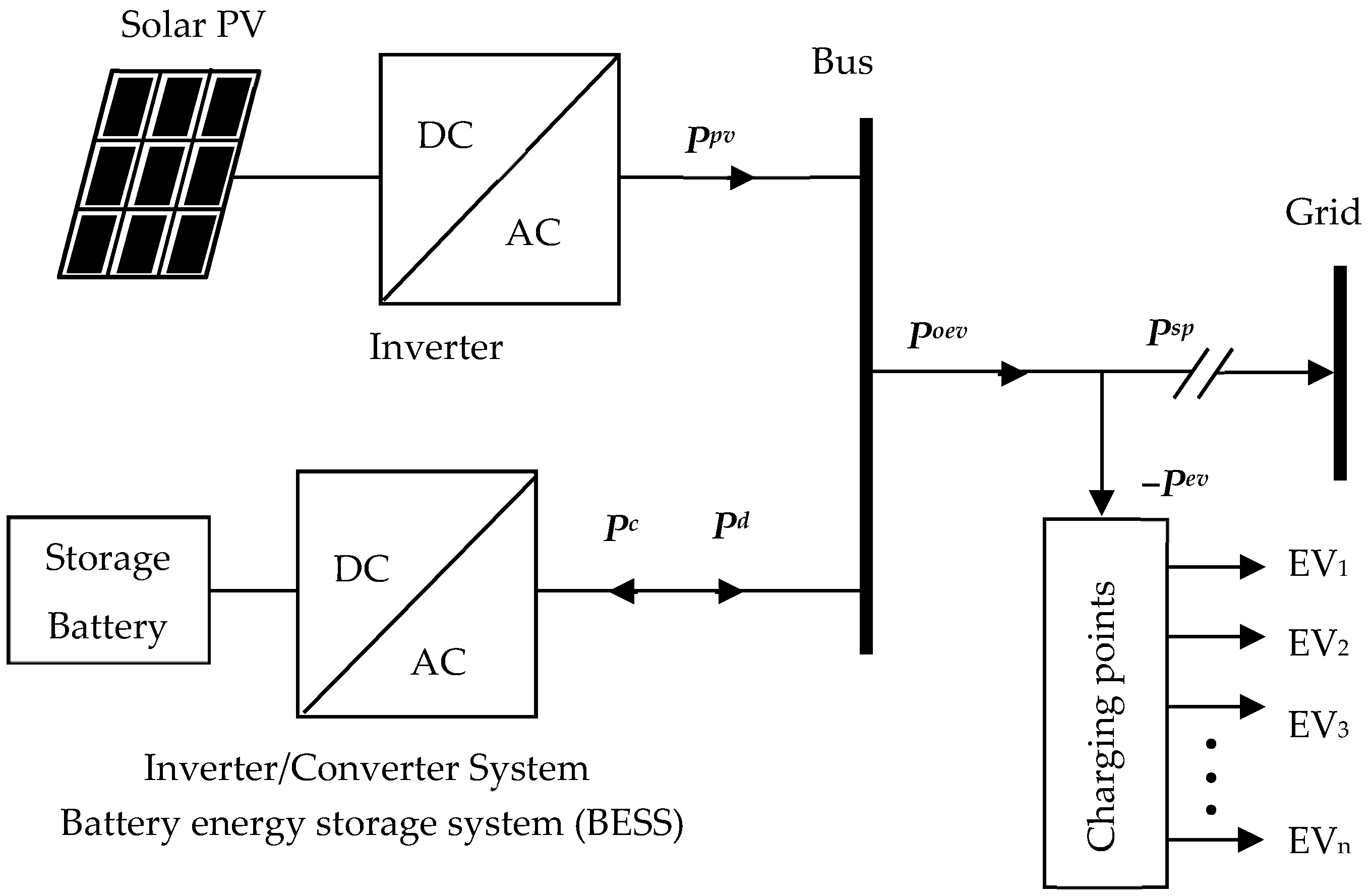
2. Solar PV Charging System Model and Formulation
2.1. EV Charging Modality, Grid, and Revenue
2.2. Solar PV Economic Model
2.3. EV-Load Model
2.4. BESS Model
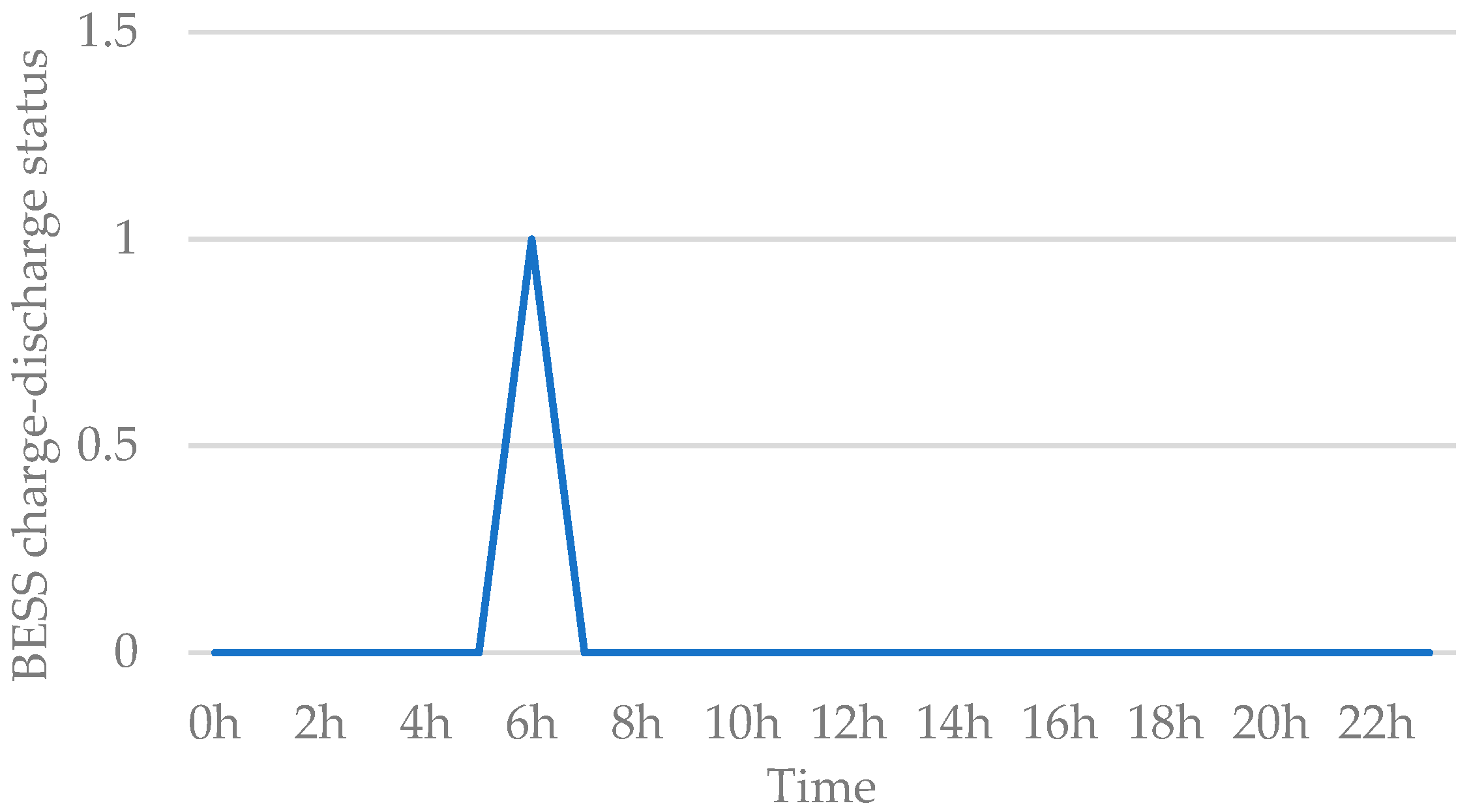
2.4.1. Limitation While Getting Charged at the tth Hour
2.4.2. Limitation While Getting Discharged at the tth Hour
2.4.3. Minimizing Costs Related to Charge–Discharge Cycle
2.4.4. Limits on the Total Amount of Battery Energy Et
2.5. Profit and the Overall System Output
3. Results and Analysis
3.1. Data
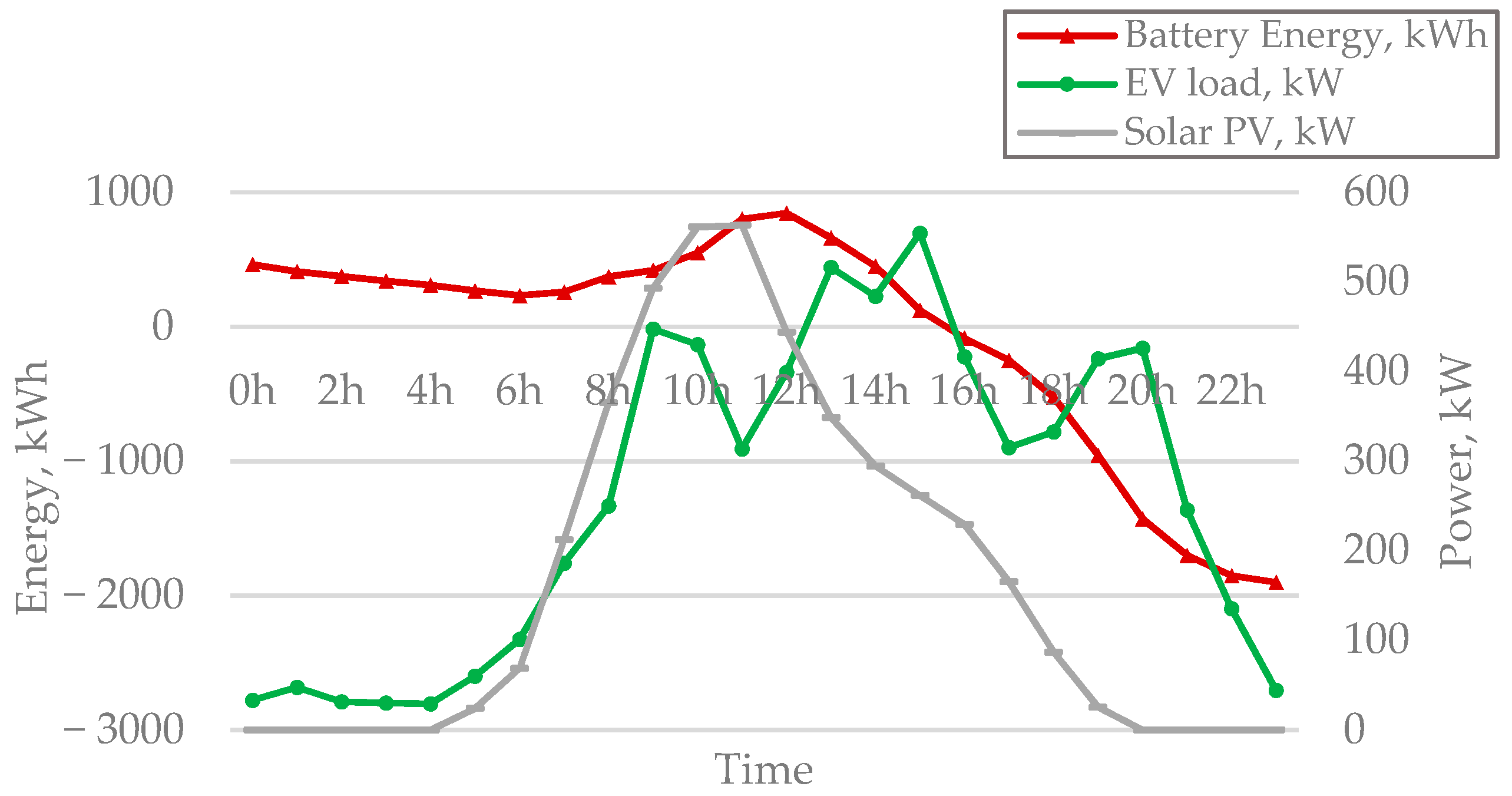
3.1.1. Solar PV and BESS
3.1.2. EV Arrival and Tariff
3.2. Analysis
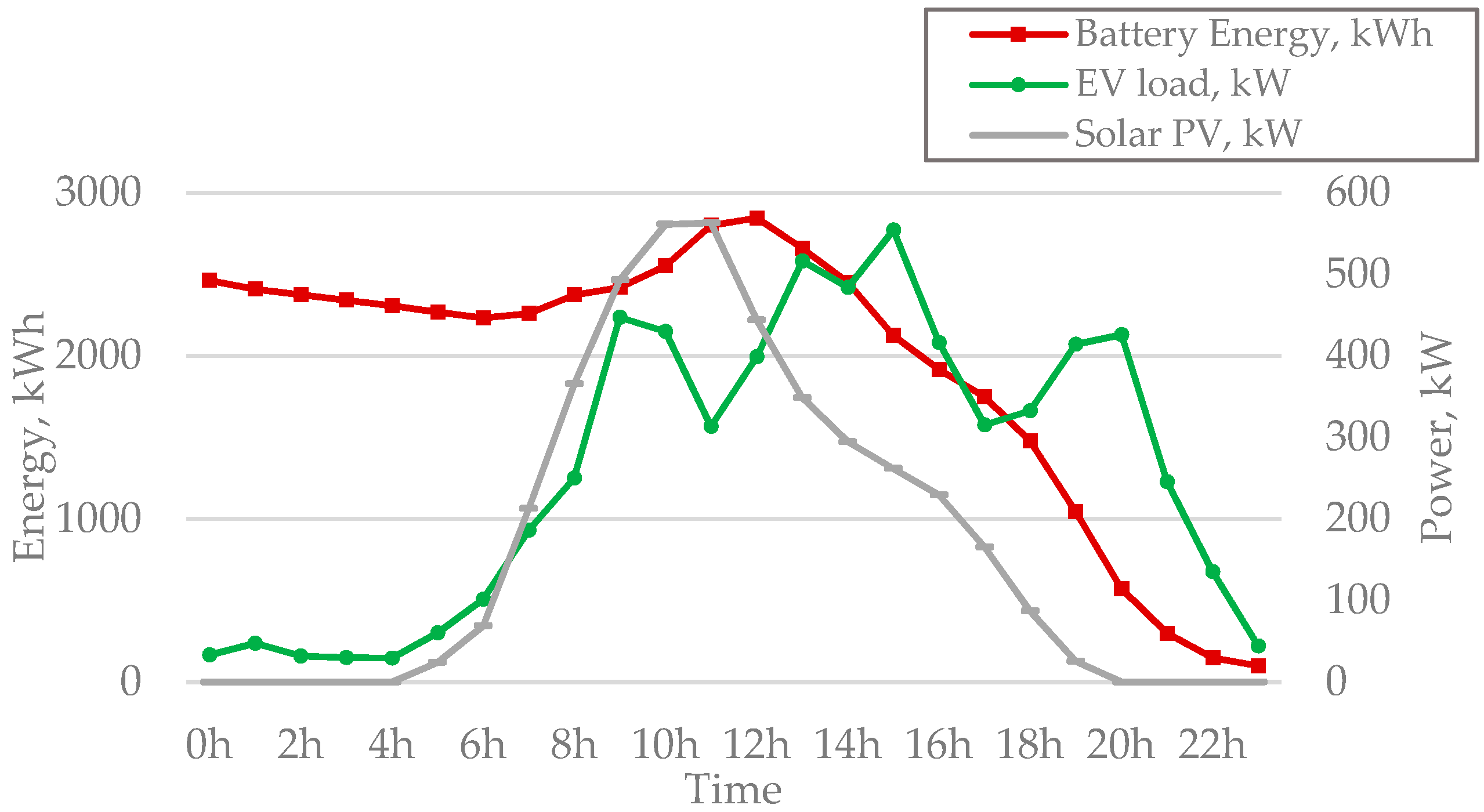
3.2.1. Battery Size, = 1000 kWh, E(0) = 500 kWh
- (i)
- Buy additional power from the grid at the prevailing price of the hour and resell to the EV; or
- (ii)
- Use a larger-sized battery to meet the load demand, in which case, the fixed and linearly varying costs of the BESS will increase.
3.2.2. Optimal Battery Size, = ,
- -
- = 2746 kWh; and
- -
- = 2400 kWh
- -
- = 3000 kWh;
- -
- E(0) = 2500 kWh; and
- -
- Revised fixed and linearly varying costs of the BESS.
3.2.3. Optimal Solution with and without the Formulation
- (i)
- Case A: solution without BESS and optimization;
- (ii)
- Case B: solution with BESS, but without optimization; and
- (iii)
- Case C: solution with the proposed formulation.
4. Conclusions
- (i)
- Increasing the size of battery; or
- (ii)
- Importing additional power from the grid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Piekut, M. The consumption of renewable Energy Sources (RES) by the European Union Households between 2004 and 2019. Energies 2021, 14, 5560. [Google Scholar] [CrossRef]
- Victoria, M.; Haegel, N.; Peters, I.M.; Sinton, R.; Jäger-Waldau, A.; del Cañizo, C.; Breyer, C.; Stocks, M.; Blakers, A.; Kaizuka, I.; et al. Solar Photovoltaics Is Ready to Power a Sustainable Future. Joule 2021, 5, 1041–1056. [Google Scholar] [CrossRef]
- Solar Energy. Available online: https://www.irena.org/solar (accessed on 1 June 2022).
- Wassiliadis, N.; Schneider, J.; Frank, A.; Wildfeuer, L.; Lin, X.; Jossen, A.; Lienkamp, M. Review of Fast Charging Strategies for Lithium-Ion Battery Systems and Their Applicability for Battery Electric Vehicles. J. Energy Storage 2021, 44, 103306. [Google Scholar] [CrossRef]
- Fitt, H.M.; Espiner, N.T. Looking beyond Limitations: Electric Vehicle Use in New Zealand Holidays; Lincoln University|Te Whare Wānaka o Aoraki. LEaP: Lincoln, New Zealand, 2021. [Google Scholar]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation-A Case Study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Z.; Wen, F.; Wong, K.P. Traffic-Constrained Multiobjective Planning of Electric-Vehicle Charging Stations. IEEE Trans. Power Deliv. 2013, 28, 2363–2372. [Google Scholar] [CrossRef]
- Mukherjee, J.C.; Gupta, A. A Review of Charge Scheduling of Electric Vehicles in Smart Grid. IEEE Syst. J. 2015, 9, 1541–1553. [Google Scholar] [CrossRef]
- Khan, W.; Ahmad, A.; Ahmad, F.; Saad Alam, M. A Comprehensive Review of Fast Charging Infrastructure for Electric Vehicles. Smart Sci. 2018, 6, 256–270. [Google Scholar] [CrossRef]
- Tian, H.; Tzelepis, D.; Papadopoulos, P.N. Electric Vehicle Charger Static and Dynamic Modelling for Power System Studies. Energies 2021, 14, 1801. [Google Scholar] [CrossRef]
- Falvo, M.; Sbordone, D.; Bayram, I.S.; Devetsikiotis, M. EV Charging Stations and Modes: International Standards. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2014, Ischia, Italy, 1 June 2014; pp. 1134–1139. [Google Scholar]
- Bryden, T.S.; Hilton, G.; Cruden, A.; Holton, T. Electric Vehicle Fast Charging Station Usage and Power Requirements. Energy 2018, 152, 322–332. [Google Scholar] [CrossRef]
- Quiros-Tortos, J.; Ochoa, L.; Butler, T. How Electric Vehicles and the Grid Work Together: Lessons Learned from One of the Largest Electric Vehicle Trials in the World. IEEE Power Energy Mag. 2018, 16, 64–76. [Google Scholar] [CrossRef]
- Lee, J.H.; Chakraborty, D.; Hardman, S.J.; Tal, G. Exploring Electric Vehicle Charging Patterns: Mixed Usage of Charging Infrastructure. Transp. Res. Part D Transport. Environ. 2020, 79, 102249. [Google Scholar] [CrossRef]
- Alghamdi, T.G.; Said, D.; Mouftah, H.T. Profit Maximization for EVSEs-Based Solar Energy in Smart Cities. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June 2021–2 July 2021; IEEE: Harbin, China, 28 June 2021; pp. 1575–1580. [Google Scholar]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized Operational Cost Reduction for an EV Charging Station Integrated with Battery Energy Storage and PV Generation. IEEE Trans. Smart Grid 2019, 10, 2096–2106. [Google Scholar] [CrossRef]
- Wang, S.; Bi, S.; Zhang, Y.-J.A.; Huang, J. Electrical Vehicle Charging Station Profit Maximization: Admission, Pricing, and Online Scheduling. IEEE Trans. Sustain. Energy 2018, 9, 1722–1731. [Google Scholar] [CrossRef] [Green Version]
- Bagherzadeh, E.; Ghiasian, A.; Rabiee, A. Long-Term Profit for Electric Vehicle Charging Stations: A Stochastic Optimization Approach. Sustain. Energy Grids Netw. 2020, 24, 100391. [Google Scholar] [CrossRef]
- Baik, S.; Jin, Y.; Yoon, Y. Determining Equipment Capacity of Electric Vehicle Charging Station Operator for Profit Maximization. Energies 2018, 11, 2301. [Google Scholar] [CrossRef] [Green Version]
- Carli, R.; Dotoli, M. A Distributed Control Algorithm for Optimal Charging of Electric Vehicle Fleets with Congestion Management. IFAC-PapersOnLine 2008, 51, 373–378. [Google Scholar] [CrossRef]
- Stüdli, S.; Crisostomi, E.; Middleton, R.; Shorten, R. A flexible distributed framework for realising electric and plug-in hybrid vehicle charging policies. Int. J. Control. 2012, 85, 1130–1145. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized Charging Control of Large Populations of Plug-in Electric Vehicles. IEEE Trans. Contr. Syst. Technol. 2013, 21, 67–78. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. A Distributed Control Algorithm for Waterfilling of Networked Control Systems via Consensus. IEEE Control. Syst. Lett. 2017, 1, 334–339. [Google Scholar] [CrossRef]
- Lv, Y.; Guan, L.; Tang, Z.; Zhao, Q. A Probability Model of PV for the Middle-Term to Long-Term Power System Analysis and Its Application. Energy Procedia 2016, 103, 28–33. [Google Scholar] [CrossRef]
- Singla, A.; Singh, K.; Kumar Yadav, V. Optimization of Distributed Solar Photovoltaic Power Generation in Day-Ahead Electricity Market Incorporating Irradiance Uncertainty. J. Mod. Power Syst. Clean Energy 2021, 9, 545–560. [Google Scholar] [CrossRef]
- Khatod, D.K.; Pant, V.; Sharma, J. Evolutionary Programming Based Optimal Placement of Renewable Distributed Generators. IEEE Trans. Power Syst. 2013, 28, 683–695. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.J.; Hernández, J.C.; Jurado, F. Probabilistic Load Flow for Radial Distribution Networks with Photovoltaic Generators. IET Renew. Power Gener. 2012, 6, 110. [Google Scholar] [CrossRef]
- Dukpa, A.; Duggal, I.; Venkatesh, B.; Chang, L. Optimal Participation and Risk Mitigation of Wind Generators in an Electricity Market. IET Renew. Power Gener. 2010, 4, 165. [Google Scholar] [CrossRef]
- Lugo-Laguna, D.; Arcos-Vargas, A.; Nuñez-Hernandez, F. A European Assessment of the Solar Energy Cost: Key Factors and Optimal Technology. Sustainability 2021, 13, 3238. [Google Scholar] [CrossRef]
- Development of Rapid Ultra Rapid Charging UK. Available online: https://uk.mer.eco/news/the-development-of-rapid-ultra-rapid-charging-in-the-uk/ (accessed on 6 June 2022).
- Nait-Sidi-Moh, A.; Ruzmetov, A.; Bakhouya, M.; Naitmalek, Y.; Gaber, J. A Prediction Model of Electric Vehicle Charging Requests. Procedia Comput. Sci. 2018, 141, 127–134. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal Scheduling for Charging and Discharging of Electric Vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Xydas, E.S.; Marmaras, C.E.; Cipcigan, L.M.; Hassan, A.S.; Jenkins, N. Forecasting Electric Vehicle Charging Demand Using Support Vector Machines. In Proceedings of the 48th International Universities’ Power Engineering Conference (UPEC 2013), Dublin, Ireland, 2–5 September 2013; IEEE: Dublin, Ireland, September 2013; pp. 1–6. [Google Scholar]
- Renewables.ninja. Available online: https://www.renewables.ninja/ (accessed on 9 June 2022).
- Mongird, K.; Viswanathan, V.; Balducci, P.; Alam, J.; Fotedar, V.; Koritarov, V.; Hadjerioua, B. An Evaluation of Energy Storage Cost and Performance Characteristics. Energies 2020, 13, 3307. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; van der Sluis, L. Stochastic Modeling of Power Demand Due to EVs Using Copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Zhang, M. Short-Term Load Forecasting for Electric Vehicle Charging Station Based on Niche Immunity Lion Algorithm and Convolutional Neural Network. Energies 2018, 11, 1253. [Google Scholar] [CrossRef] [Green Version]
- Twój Partner, W.; Zakresie Elektromobilności, W. Europie Środkowo-Wschodniej-GreenWay. Available online: https://greenwaypolska.pl/uslugi-ladowania (accessed on 8 June 2022).



| Solar PV: Apv ($) | 1.267 | Fixed cost of solar PV system for fixed plate that includes installation costs, soft costs, and hardware costs [34] |
| Solar PV: Bpv ($/kWh) | 0.000017 | Variable cost (operation and maintenance) of solar PV system [34] |
| Battery: Ac ($/kWh) | 0.0011 | Fixed cost of charging Li-ion battery [35] |
| Battery: Bc ($/kWh) | 0.0011 | Variable cost of charging Li-ion battery [35] |
| Battery: Ad ($/kWh) | 0.0011 | Fixed cost of charging Li-ion battery [35] |
| Battery: Bd ($/kWh) | 0.0011 | Variable cost of charging Li-ion battery [35] |
| Battery: ($/Cycle) | 0.134 | Cost-per-cycle of Li-ion battery [35] with 3500 cycles at 80% DoD |
| Battery: Efficiency, (%) | 90 | Efficiency of Li-ion battery; Li-ion batteries have one of the highest efficiencies |
| Depth of Discharge: DOD (%) | 80 | Battery allowed to discharge to 80% |
| Battery Size: (kWh) | 1000 | Size of the battery |
| Time | EV Arrival Data from [37] (kW) | EV Probability (%) |
|---|---|---|
| 0 h | 282 | 4.2 |
| 1 h | 402 | 6.0 |
| 2 h | 269 | 4.0 |
| 3 h | 251 | 3.8 |
| 4 h | 246 | 3.7 |
| 5 h | 503 | 7.6 |
| 6 h | 850 | 12.8 |
| 7 h | 1560 | 23.5 |
| 8 h | 2100 | 31.6 |
| 9 h | 3757 | 56.5 |
| 10 h | 3612 | 54.3 |
| 11 h | 2635 | 39.6 |
| 12 h | 3354 | 50.4 |
| 13 h | 4335 | 65.2 |
| 14 h | 4063 | 61.1 |
| 15 h | 4654 | 70.0 |
| 16 h | 3498 | 52.6 |
| 17 h | 2647 | 39.8 |
| 18 h | 2795 | 42.0 |
| 19 h | 3479 | 52.3 |
| 20 h | 3577 | 53.8 |
| 21 h | 2059 | 31.0 |
| 22 h | 1135 | 17.1 |
| 23 h | 374 | 5.6 |
| Case A | Case B | Case C | |
|---|---|---|---|
| Profit ($) | 1462.8 | 2612.1 | 2674.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dukpa, A.; Butrylo, B. MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts. Energies 2022, 15, 5760. https://doi.org/10.3390/en15155760
Dukpa A, Butrylo B. MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts. Energies. 2022; 15(15):5760. https://doi.org/10.3390/en15155760
Chicago/Turabian StyleDukpa, Andu, and Boguslaw Butrylo. 2022. "MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts" Energies 15, no. 15: 5760. https://doi.org/10.3390/en15155760
APA StyleDukpa, A., & Butrylo, B. (2022). MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts. Energies, 15(15), 5760. https://doi.org/10.3390/en15155760