Analysis of Energy Loss on a Tunable Check Valve through the Numerical Simulation
Abstract
1. Introduction
2. Working Principle of a Tunable Check Valve
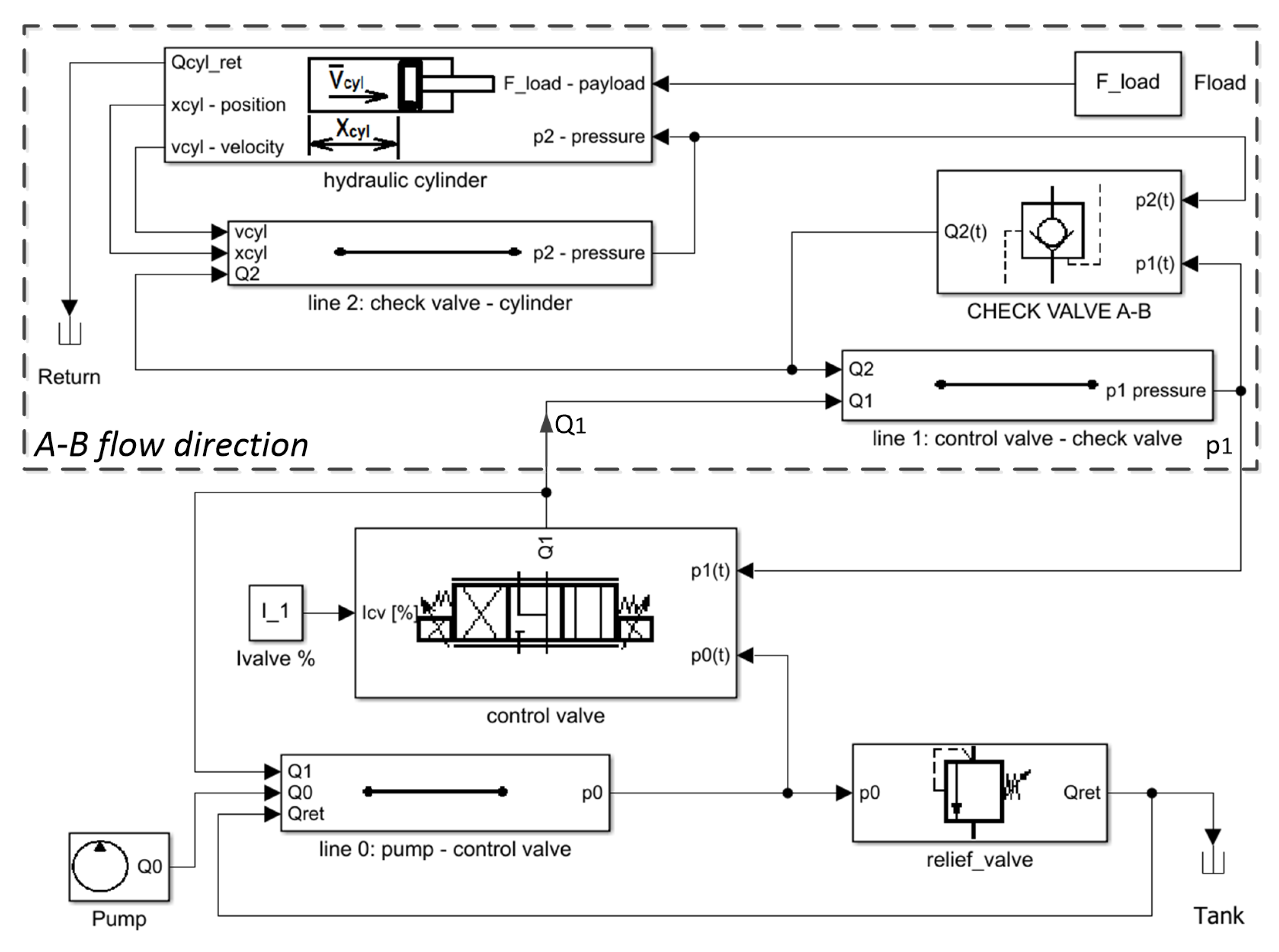
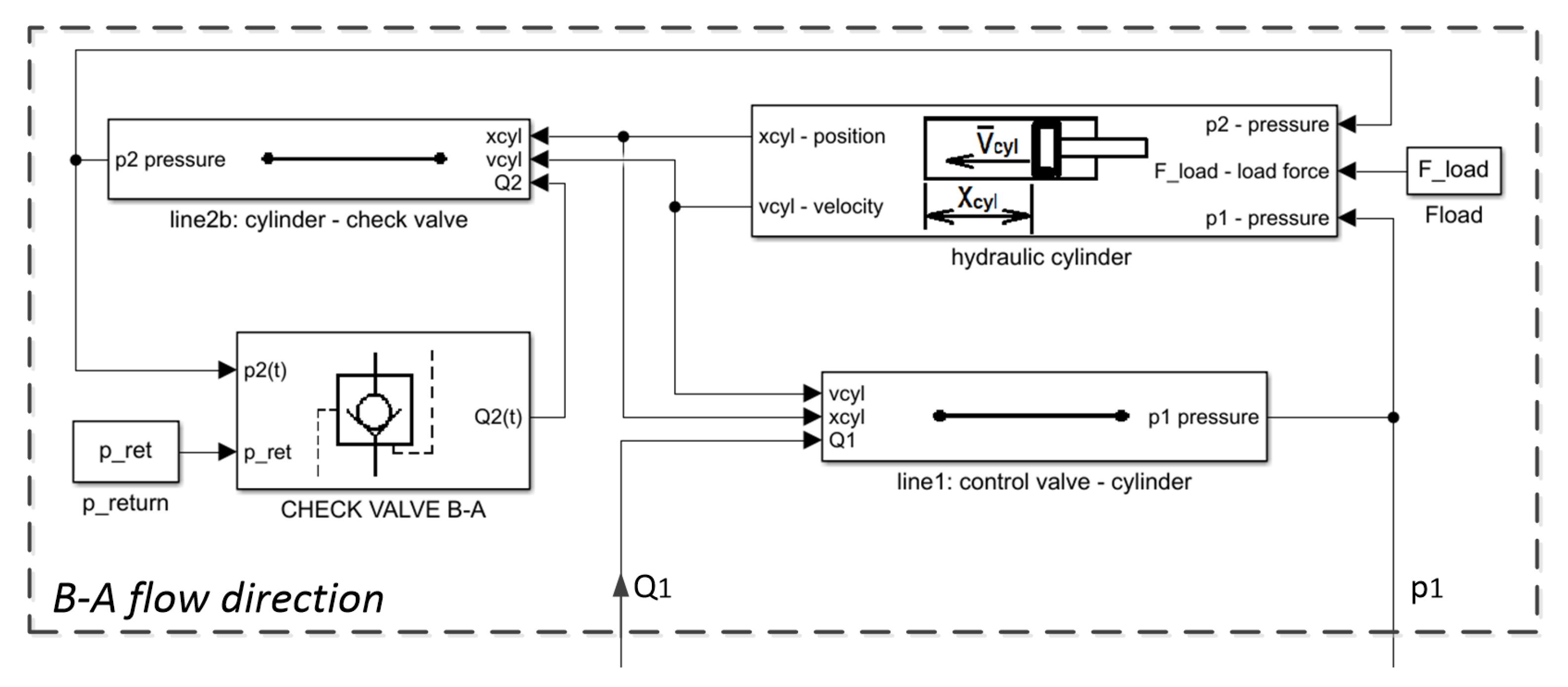
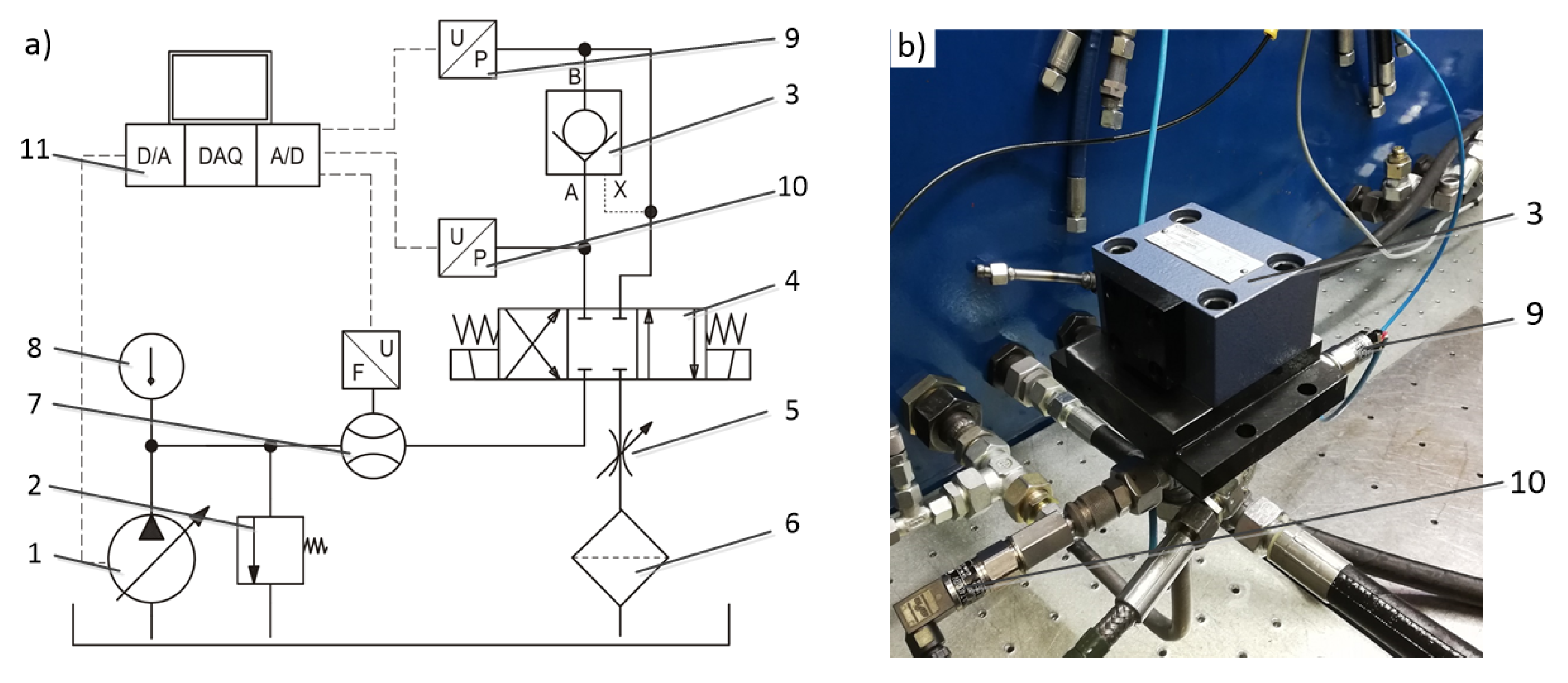
3. Mathematical Model of the System
4. Check Valve Discrete Model and CFD Analysis
4.1. Boundary Conditions and Turbulence Model
4.2. Meshing and Assessing Mesh Quality
4.3. CFD Simulation Results
5. Simulations in Matlab/Simulink Environment
5.1. Determining the Valve Gap Width and Actuator Piston Displacement
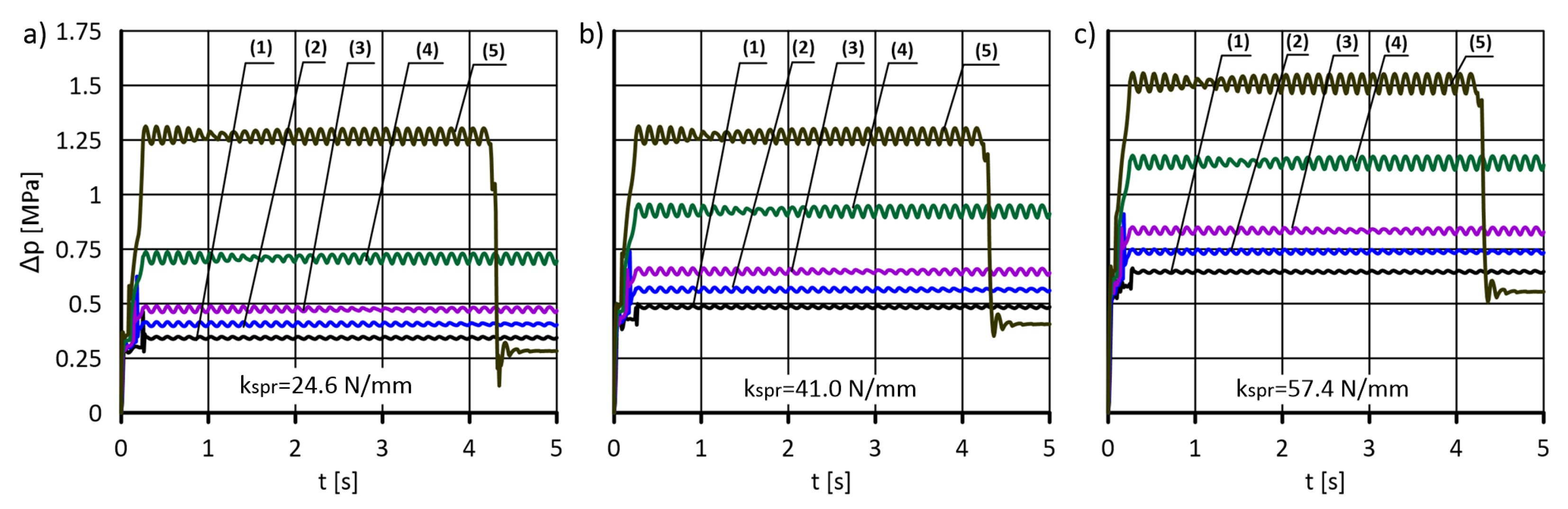
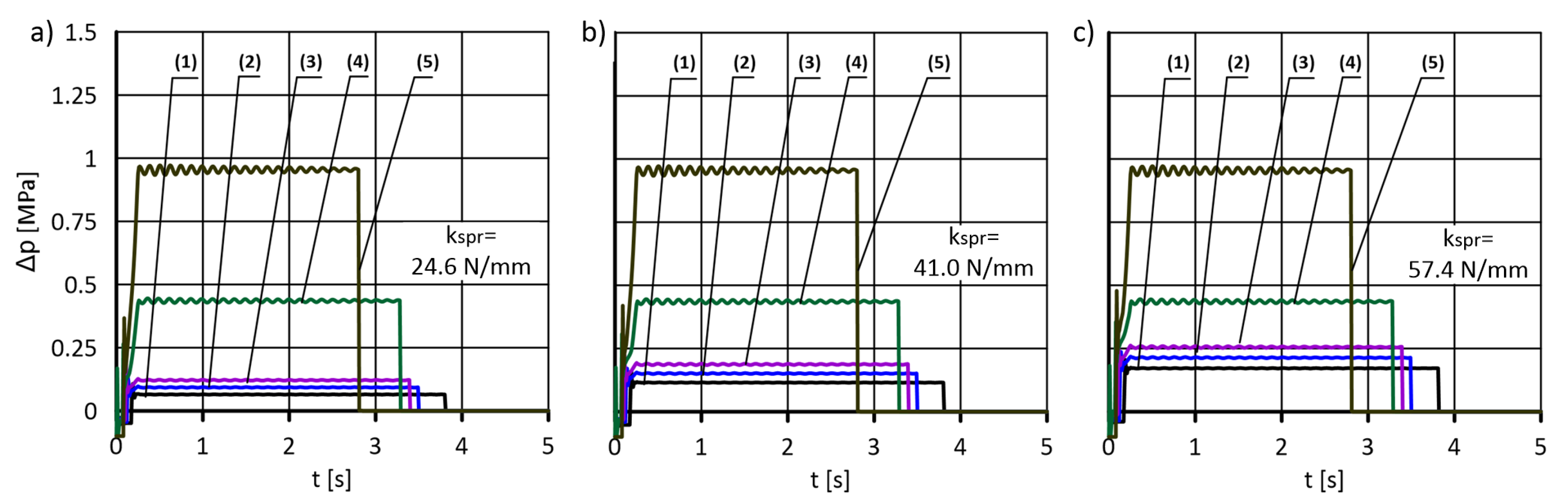
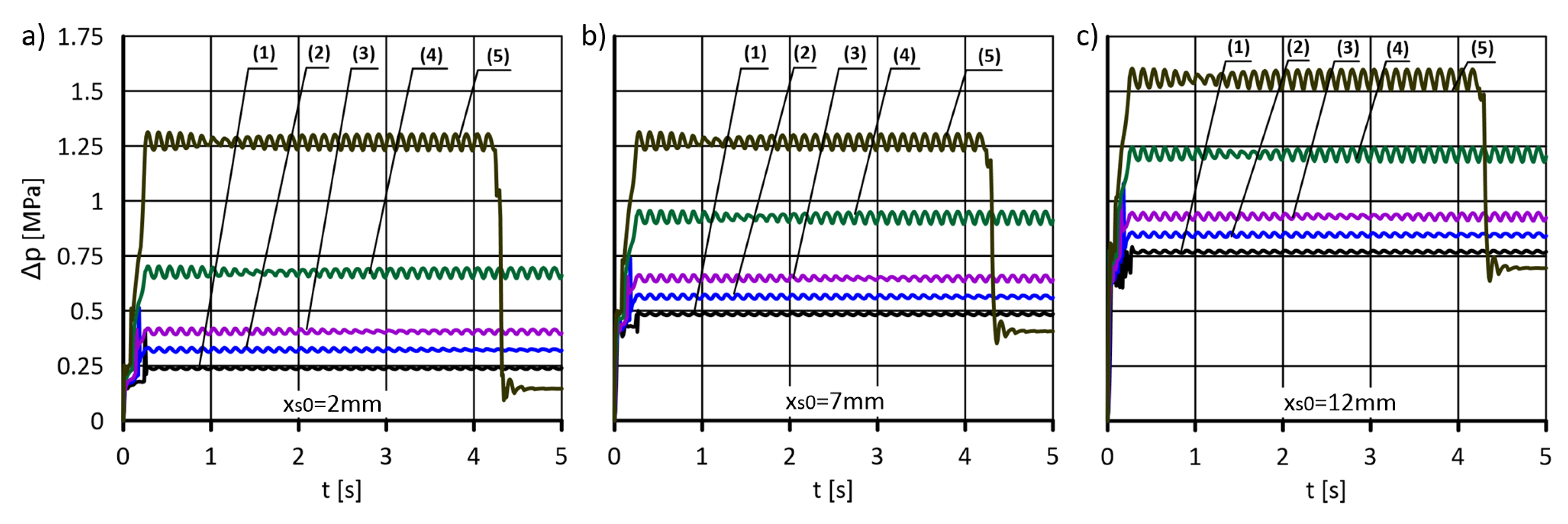
5.2. Determination of the Pressure Drop across the Valve
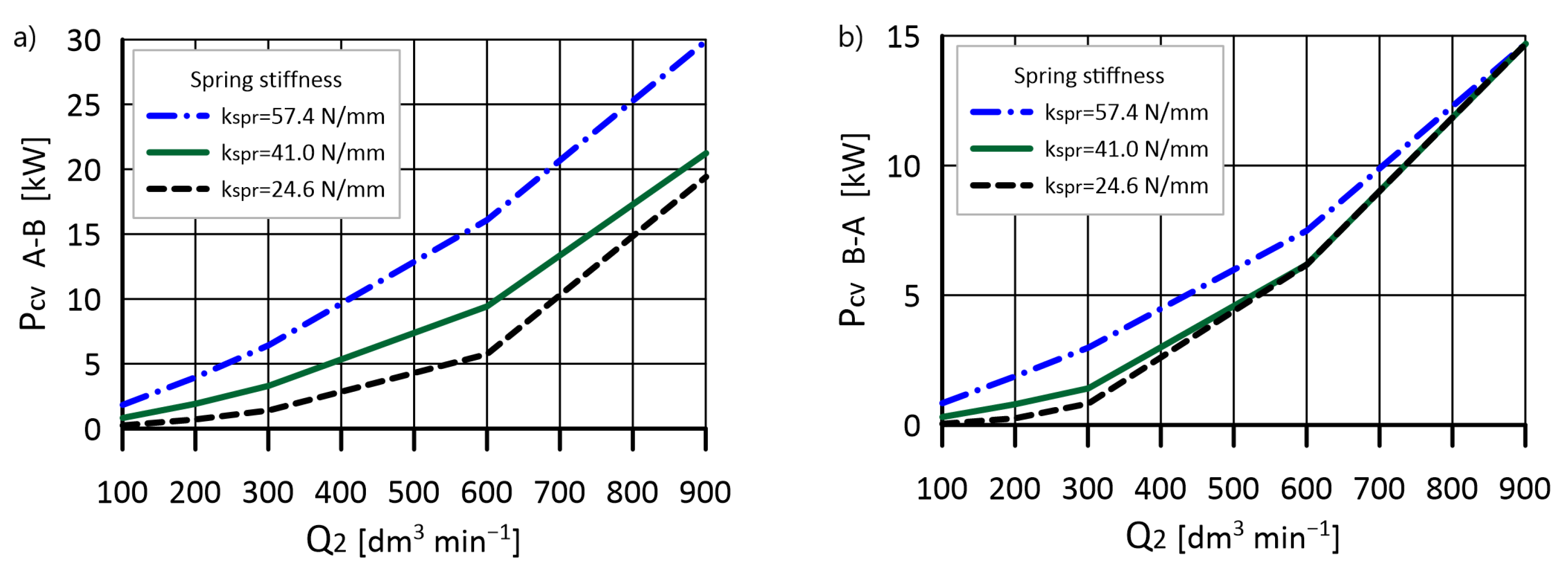
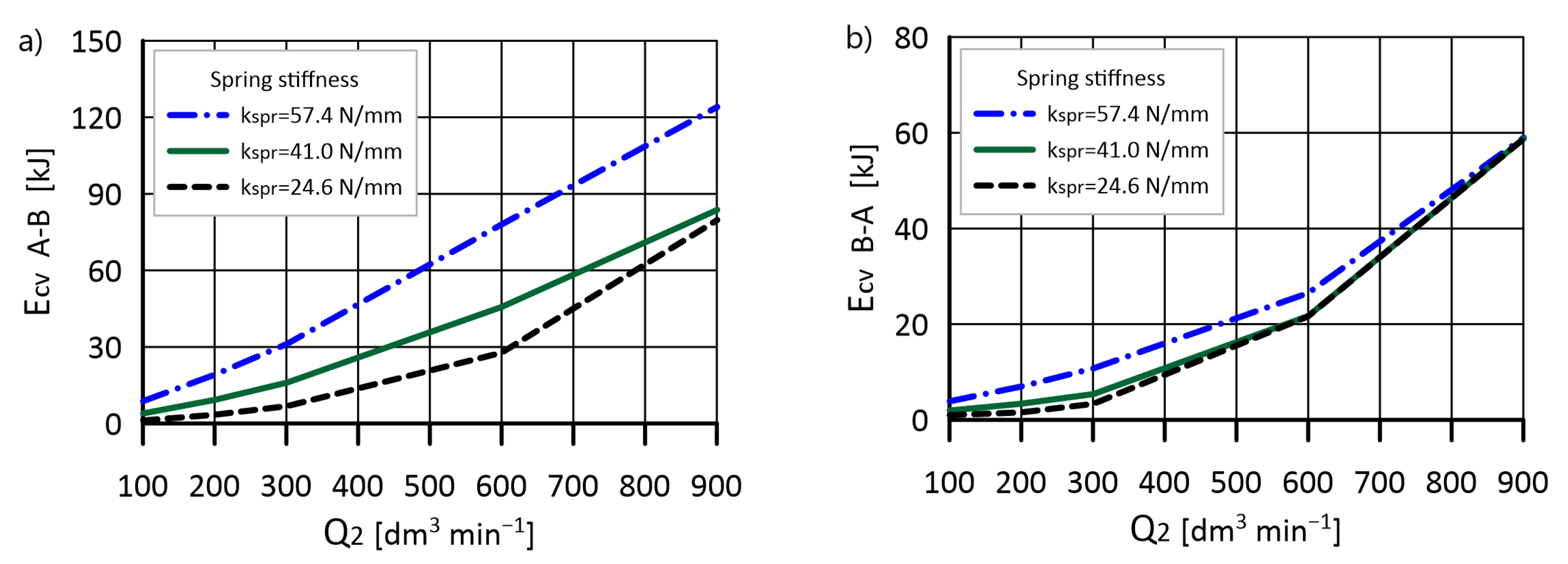
5.3. Estimation of the Check Valve Energy Efficiency
6. Comparison of Results with Laboratory Experiments
7. Summary and Conclusions
- The energy losses across the valve vary substantially depending on flow direction. Although the same connection diameters are used, the flow direction significantly impacts the amount of loss.
- The spring stiffness and the initial tension, which is necessary to maintain tightness, are of significant importance for the level of energy loss, especially at lower flows. On the other hand, energy losses at the flow that guarantees full valve opening no longer depend on the spring parameters.
- With the flow rate not exceeding the nominal value dm3 min−1, the determined energy losses are at the maximum level of 2–4% of the total system demand. However, the results show that the valve is not fully open. On the one hand, this makes the spring parameters more affecting the pressure drop, while on the other, it encourages research on expanding the flow rate range.
- Doubled nominal flow dm3 min−1 causes the valve to open fully in the B-A direction and almost entirely in the A-B when using a softer spring. The share of energy losses, in this case, was 2.5% (B-A) and 4.1% (A-B), which can be considered acceptable values, as they are close to those obtained by a valve with a standard spring at nominal flow.
- The maximum flow rate dm3 min−1 resulted in full opening in both directions. Depending on the flow direction, energy losses were estimated at 5.2–8.2%. These are not disqualifying values; however, taking into account the additional losses on the other components of the system, they should be included in the overall energy balance of the system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices | |
| flow line | |
| check valve | |
| hydraulic cylinder | |
| p | poppet of the check valve |
| return line | |
| Parameters | |
| cylinder piston area, piston area on the rod side (m2) | |
| valve poppet left/right sectional area (m2) | |
| valve pilot sectional area (m2) | |
| fluid bulk modulus (Pa) | |
| turbulence model constants (-) | |
| total energy consumption per operating cycle (kJ) | |
| external force exerted on the hydraulic cylinder (N) | |
| force: hydrostatic, hydrodynamic, spring, friction (N) | |
| turbulence model factors: intensity, length scale (-, m) | |
| nominal flow rate (dm3 min−1) | |
| flow rate: pump, line 1, 2, return (dm3 min−1) | |
| U | control valve control signal (percentage) (%) |
| volume: supply line, line 1,2 (m3) | |
| poppet dimensions: diameter, length, clearance, eccentricity (m) | |
| valve spring stiffness (N m−1) | |
| mass: valve poppet, valve pilot, cylinder piston with rod (kg) | |
| pressure: supply line, 1, 2, return line (MPa) | |
| pressure drop (MPa) | |
| pump piston stroke rate per revolution (m3/rev) | |
| turbulence model constants (-) | |
| time, start-up time (s) | |
| velocity: poppet, cylinder piston, fluid (average) (m s−1) | |
| position: valve poppet, hydraulic cylinder piston (m) | |
| initial valve spring deflection (m) | |
| z | number of pistons (pump) (-) |
| poppet head opening angle (°) | |
| fluid dynamic viscosity (Pa s) | |
| check valve jet angle coefficient (-) | |
| fluid kinematic viscosity (m2 s−1) | |
| turbulent viscosity (m2 s−1) | |
| fluid density (kg m−3) | |
| damping coefficient (N s m−1) | |
| valve poppet friction force geometrical factor (m) | |
| pump rotational speed, pump nominal speed (rev/s) |
References
- Ye, J.; Zhao, Z.; Zheng, J.; Salem, S.; Yu, J.; Cui, J.; Jiao, X. Transient Flow Characteristic of High-Pressure Hydrogen Gas in Check Valve during the Opening Process. Energies 2020, 13, 4222. [Google Scholar] [CrossRef]
- Ye, J.; Zhao, Z.; Cui, J.; Hua, Z.; Peng, W.; Jiang, P. Transient flow behaviors of the check valve with different spool-head angle in high-pressure hydrogen storage systems. J. Energy Storage 2022, 46, 103761. [Google Scholar] [CrossRef]
- Kim, N.S.; Jeong, Y.H. An investigation of pressure build-up effects due to check valve’s closing characteristics using dynamic mesh techniques of CFD. Ann. Nucl. Energy 2021, 152, 107996. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, Y.; Chen, Z.; Wang, W. Numerical simulation and experimental validation of flow characteristics for a butterfly check valve in small modular reactor. Nucl. Eng. Des. 2022, 391, 111732. [Google Scholar] [CrossRef]
- Lai, Z.; Karney, B.; Yang, S.; Wu, D.; Zhang, F. Transient performance of a dual disc check valve during the opening period. Ann. Nucl. Energy 2017, 101, 15–22. [Google Scholar] [CrossRef]
- Gomez, I.; Gonzalez-Mancera, A.; Newell, B.; Garcia-Bravo, J. Analysis of the Design of a Poppet Valve by Transitory Simulation. Energies 2019, 12, 889. [Google Scholar] [CrossRef]
- Deng, H.; Liu, Y.; Li, P.; Ma, Y.; Zhang, S. Integrated probabilistic modeling method for transient opening height prediction of check valves in oil-gas multiphase pumps. Adv. Eng. Softw. 2018, 118, 18–26. [Google Scholar] [CrossRef]
- Ling, M.; He, X.; Wu, M.; Cao, L. Dynamic Design of a Novel High-Speed Piezoelectric Flow Control Valve Based on Compliant Mechanism. IEEE/ASME Trans. Mechatron. 2022, 1–9. [Google Scholar] [CrossRef]
- Shin, S.M.; Kim, D.S.; Kang, H.G. Power-operated check valve in abnormal situations. Nucl. Eng. Des. 2018, 330, 28–35. [Google Scholar] [CrossRef]
- Morgan, S.C.; Hendricks, A.D.; Seto, M.L.; Sieben, V.J. A Magnetically Tunable Check Valve Applied to a Lab-on-Chip Nitrite Sensor. Sensors 2019, 19, 4619. [Google Scholar] [CrossRef]
- Gao, Z.x.; Liu, P.; Yue, Y.; Li, J.y.; Wu, H. Comparison of Swing and Tilting Check Valves Flowing Compressible Fluids. Micromachines 2020, 11, 758. [Google Scholar] [CrossRef] [PubMed]
- Baluyev, D.; Gusev, D.; Meshkov, S.; Nikanorov, O.; Osipov, S.; Rogozhkin, S.; Rukhlin, S.; Shepelev, S. Study of functional characteristics for safety system check valve using scaled model. Nucl. Energy Technol. 2015, 1, 99–102. [Google Scholar] [CrossRef][Green Version]
- Yang, L.J.; Waikhom, R.; Wang, W.C.; Jabaraj Joseph, V.; Esakki, B.; Kumar Unnam, N.; Li, X.H.; Lee, C.Y. Check-Valve Design in Enhancing Aerodynamic Performance of Flapping Wings. Appl. Sci. 2021, 11, 3416. [Google Scholar] [CrossRef]
- Schickhofer, L.; Wimmer, J. Fluid–structure interaction and dynamic stability of shock absorber check valves. J. Fluids Struct. 2022, 110, 103536. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Pressure Loss Reduction in an Innovative Directional Poppet Control Valve. Energies 2020, 13, 3149. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Design and Flow Analysis of an Adjustable Check Valve by Means of CFD Method. Energies 2021, 14, 2237. [Google Scholar] [CrossRef]
- Novak, P.; Guinot, V.; Jeffrey, A.; Reeve, D.E. Hydraulic Modelling—An Introduction: Principles, Methods and Applications; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lisowski, E.; Filo, G. CFD analysis of the characteristics of a proportional flow control valve with an innovative opening shape. Energy Convers. Manag. 2016, 123, 15–28. [Google Scholar] [CrossRef]
- Valdés, J.R.; Miana, M.J.; Núñez, J.L.; Pütz, T. Reduced order model for estimation of fluid flow and flow forces in hydraulic proportional valves. Energy Convers. Manag. 2008, 49, 1517–1529. [Google Scholar] [CrossRef]
- Posa, A.; Oresta, P.; Lippolis, A. Analysis of a directional hydraulic valve by a Direct Numerical Simulation using an immersed-boundary method. Energy Convers. Manag. 2013, 65, 497–506. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Pressure compensation using flow forces in a multi-section proportional directional control valve. Energy Convers. Manag. 2015, 103, 1052–1064. [Google Scholar] [CrossRef]
- Anh, P.N.; Bae, J.S.; Hwang, J.H. Computational Fluid Dynamic Analysis of Flow Rate Performance of a Small Piezoelectric-Hydraulic Pump. Appl. Sci. 2021, 11, 4888. [Google Scholar] [CrossRef]
- Woldemariam, E.T.; Lemu, H.G.; Wang, G.G. CFD-Driven Valve Shape Optimization for Performance Improvement of a Micro Cross-Flow Turbine. Energies 2018, 11, 248. [Google Scholar] [CrossRef]
- Chen, F.; Qian, J.; Chen, M.; Zhang, M.; Chen, L.; Jin, Z. Turbulent compressible flow analysis on multi-stage high pressure reducing valve. Flow Meas. Instrum. 2018, 61, 26–37. [Google Scholar] [CrossRef]
- Jin-yuan, Q.; Lin, W.; Zhi-jiang, J.; Jian-kai, W.; Han, Z.; An-le, L. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve. Energy Convers. Manag. 2014, 87, 220–226. [Google Scholar] [CrossRef]
- Scuro, N.; Angelo, E.; Angelo, G.; Andrade, D. A CFD analysis of the flow dynamics of a directly-operated safety relief valve. Nucl. Eng. Des. 2018, 328, 321–332. [Google Scholar] [CrossRef]
- ANSYS Fluent Tutorial Guide, 18.0 ed.; ANSYS Inc.: Canonsburg, PA, USA, 2017; Available online: http://www.ansys.com (accessed on 6 June 2022).
- ISO:4411:2019; Hydraulic Fluid Power—Valves—Determination of Differential Pressure/Flow Rate Characteristics. ISO: Geneva, Switzerland, 2019.
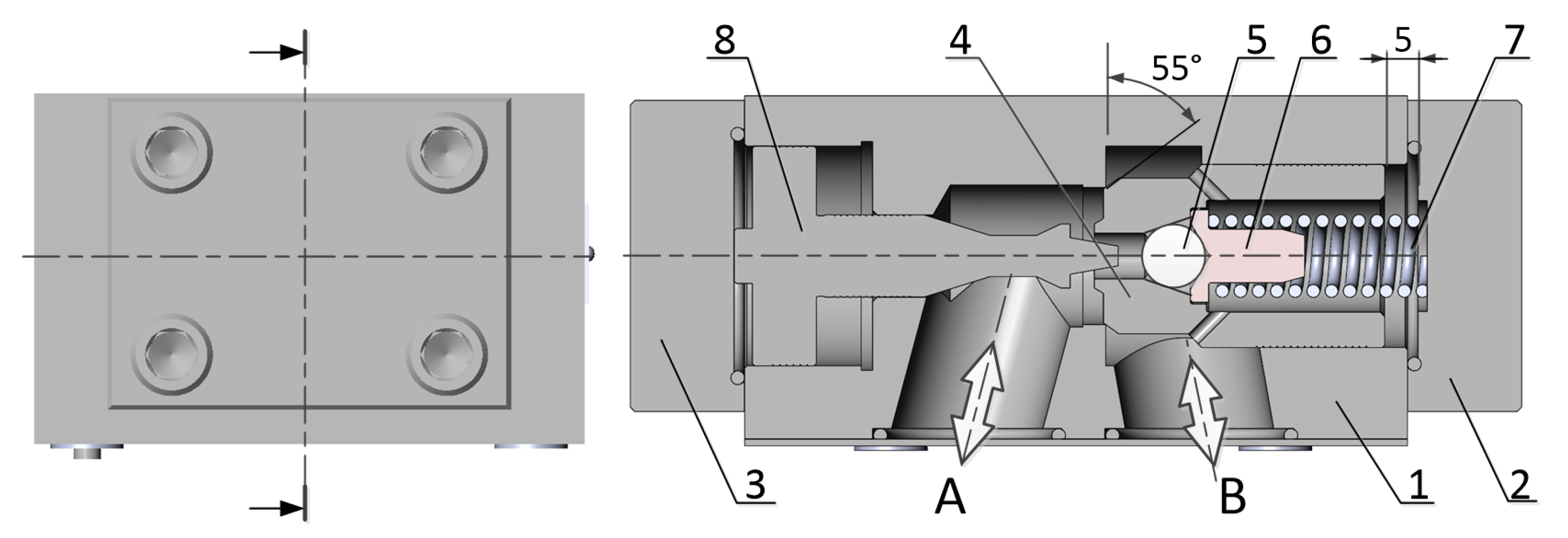
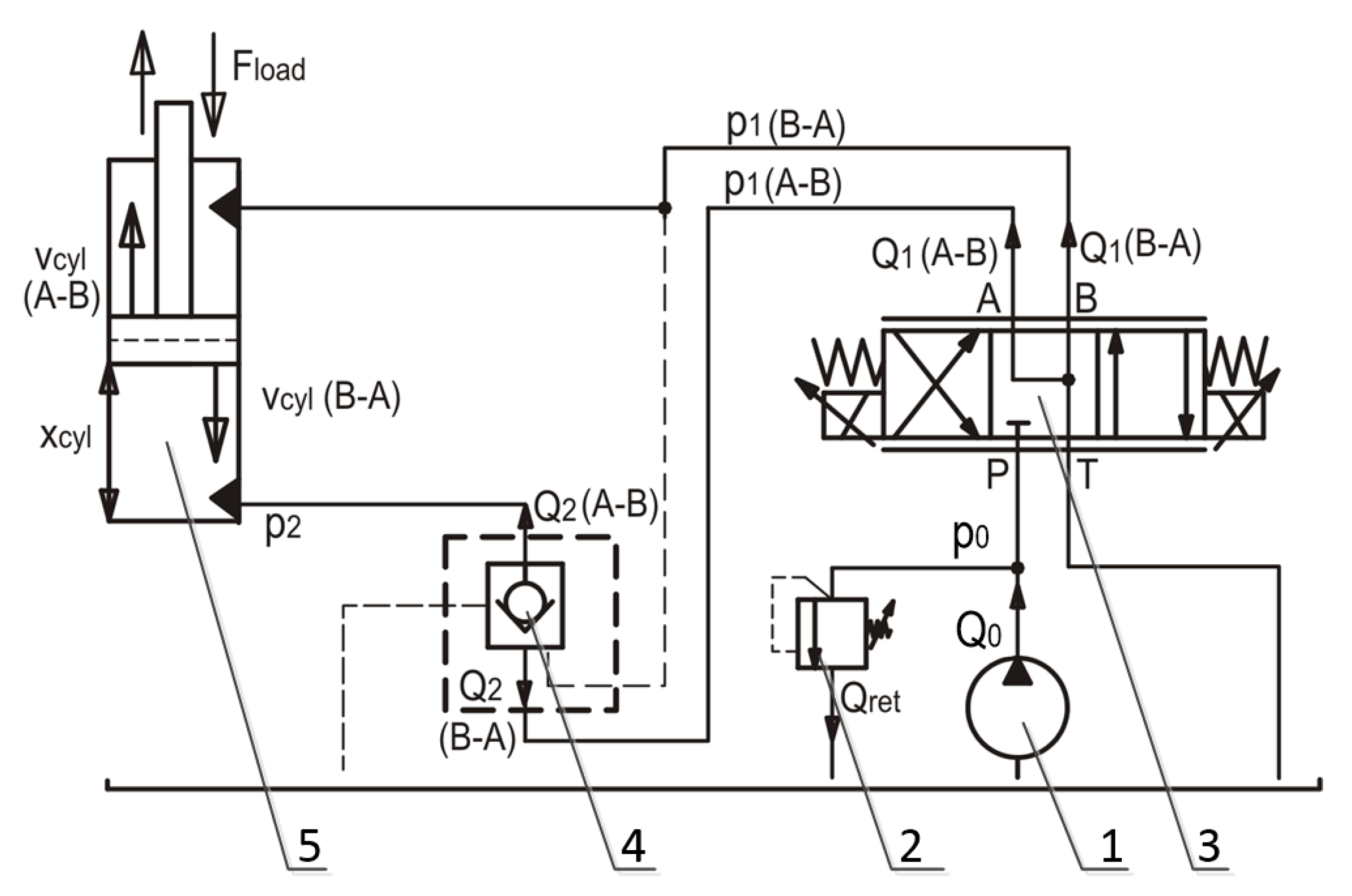
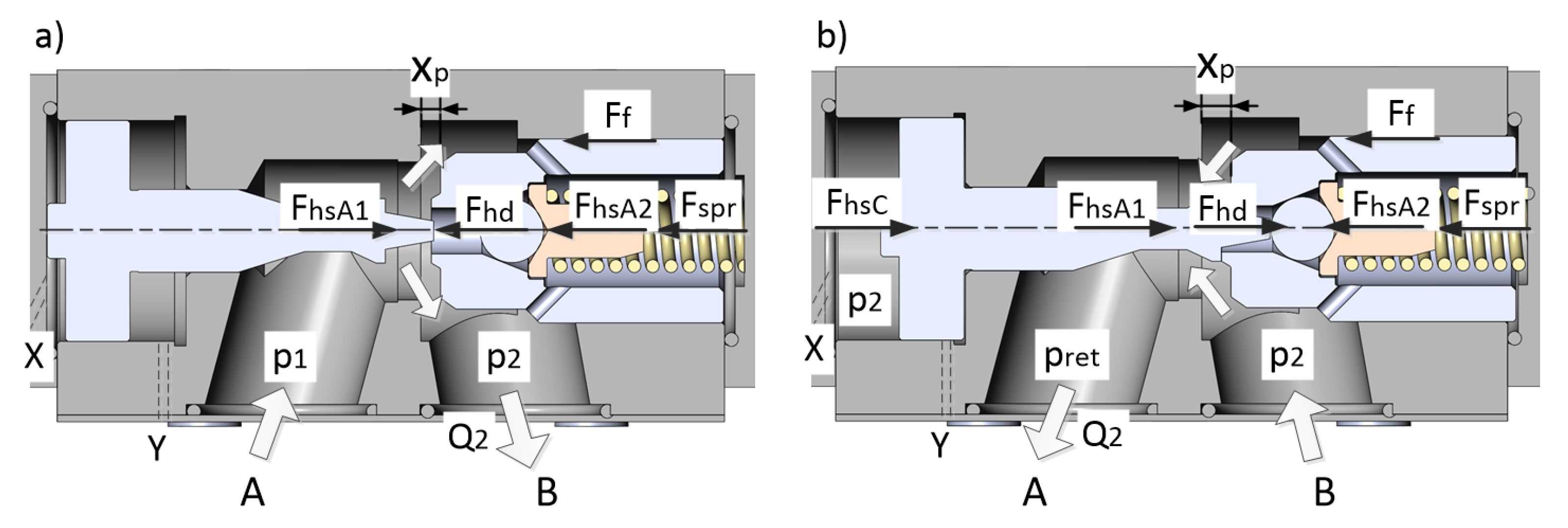

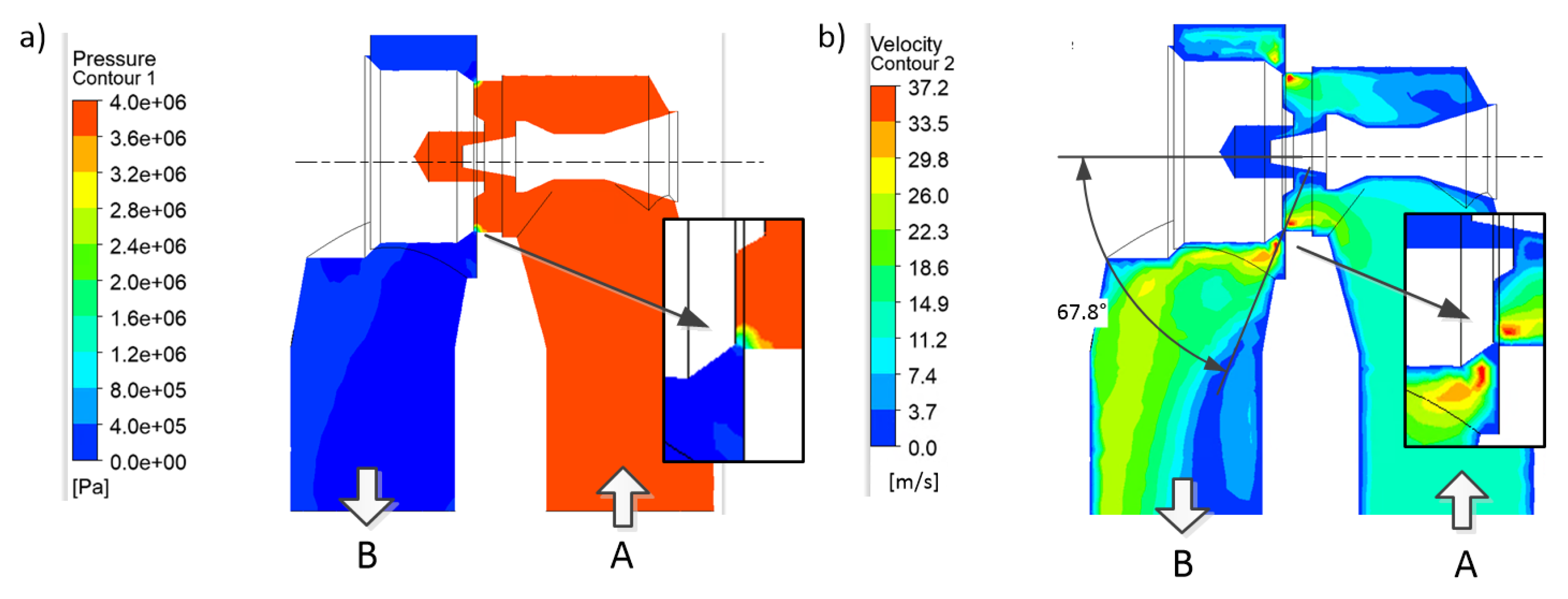
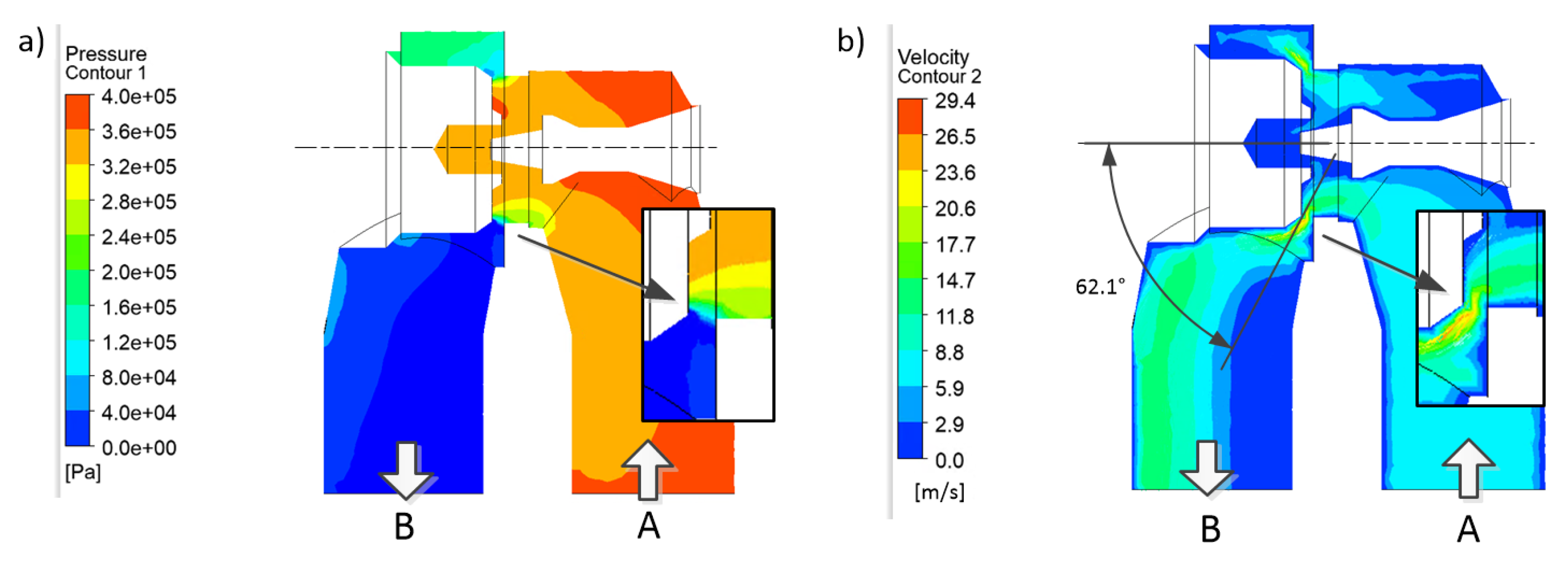
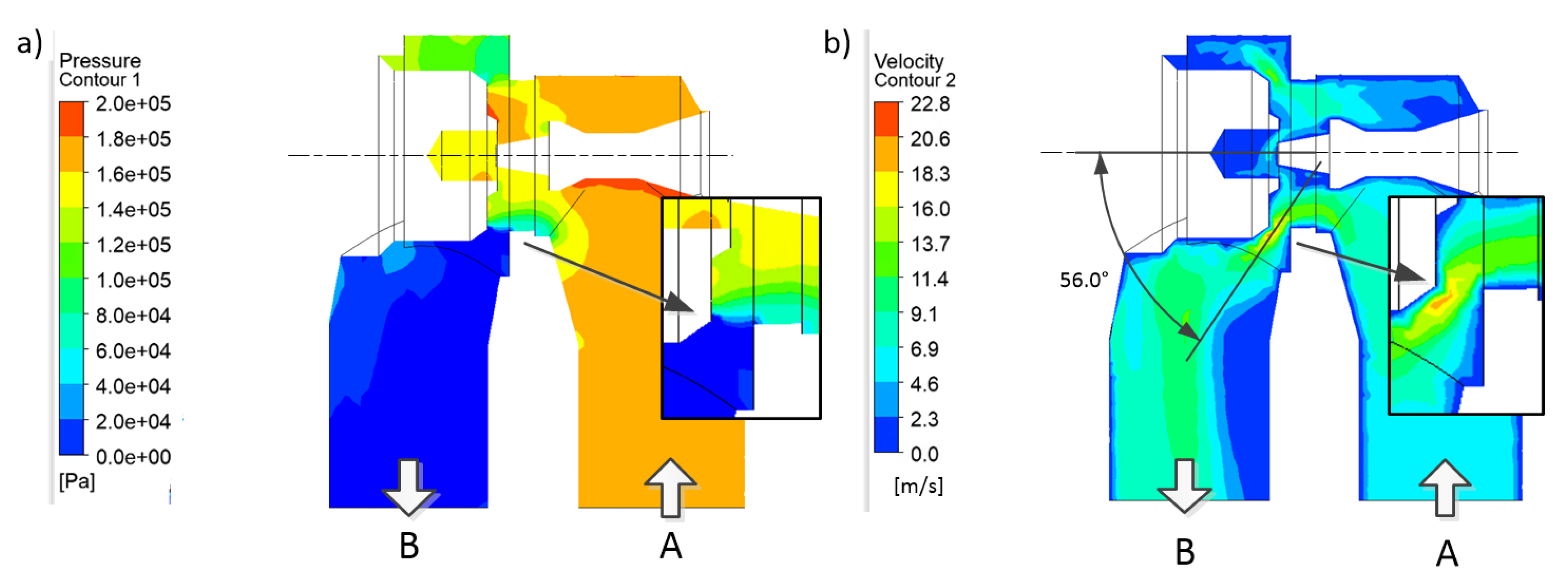
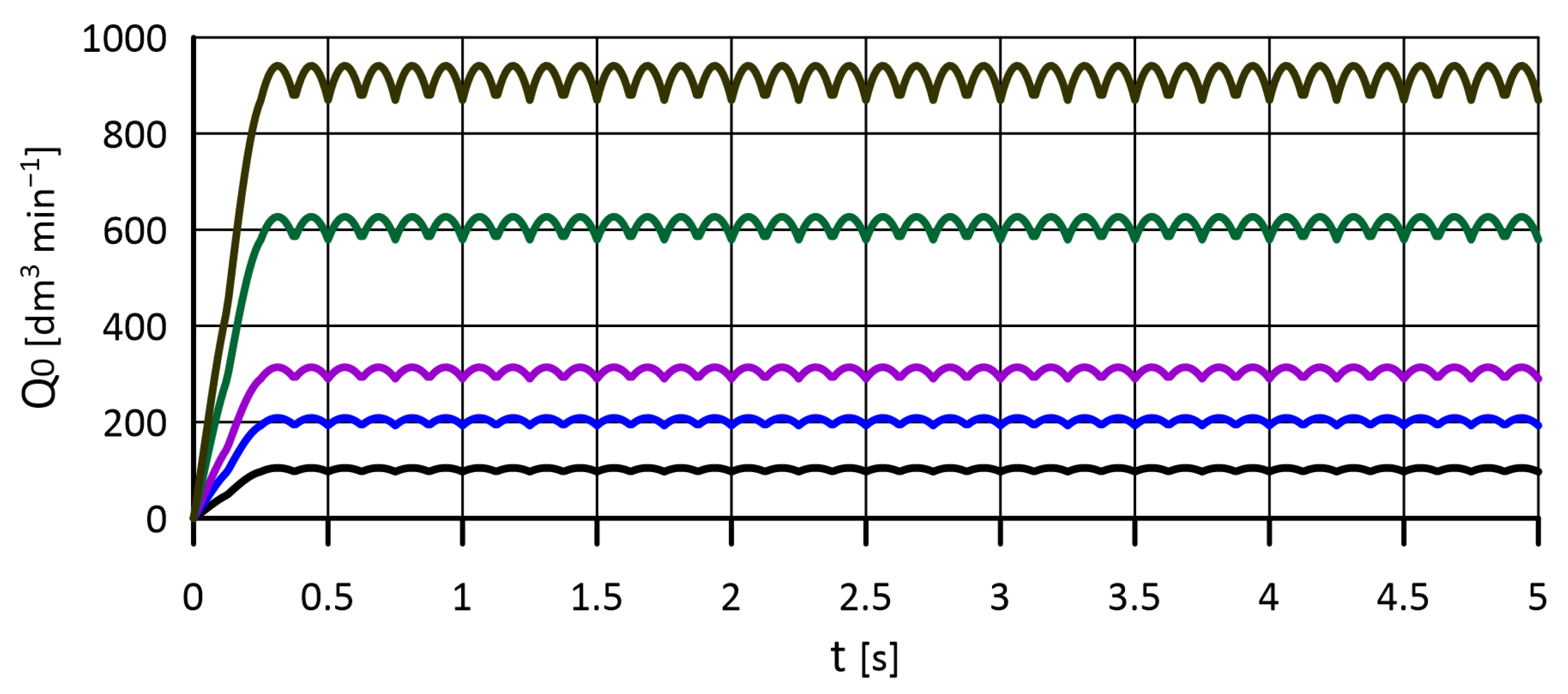
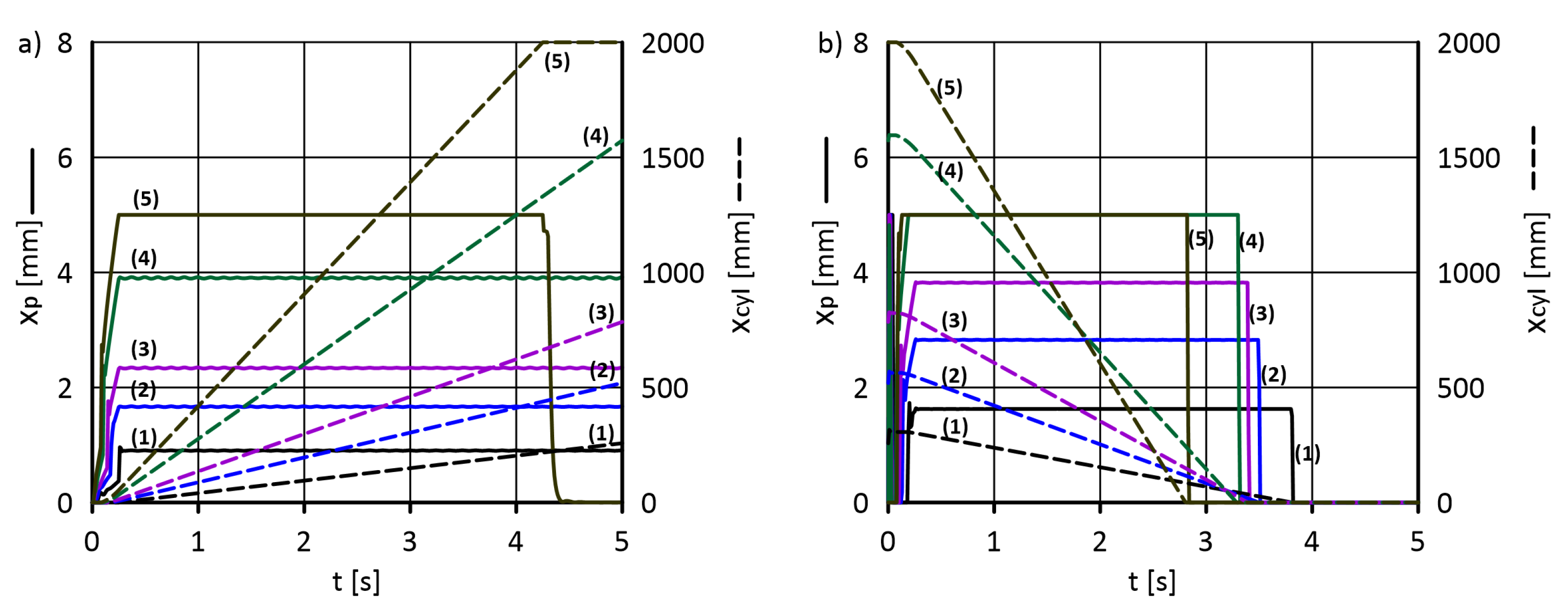
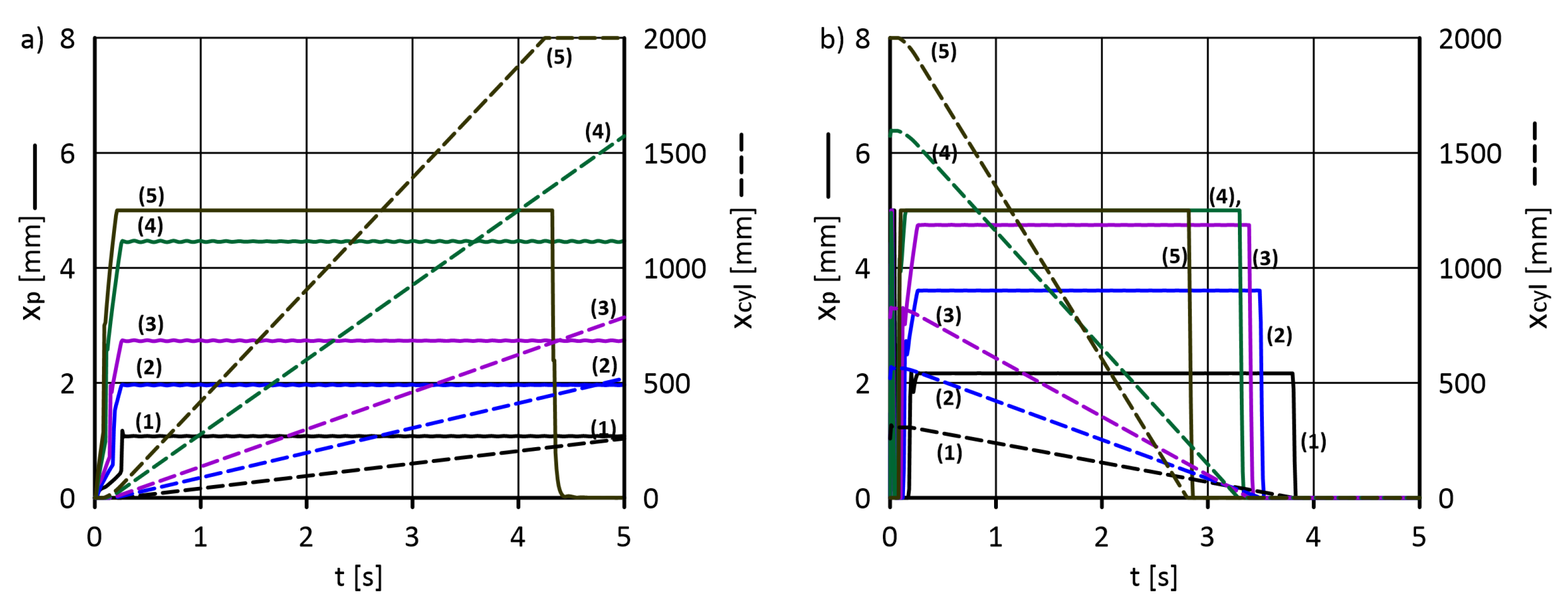
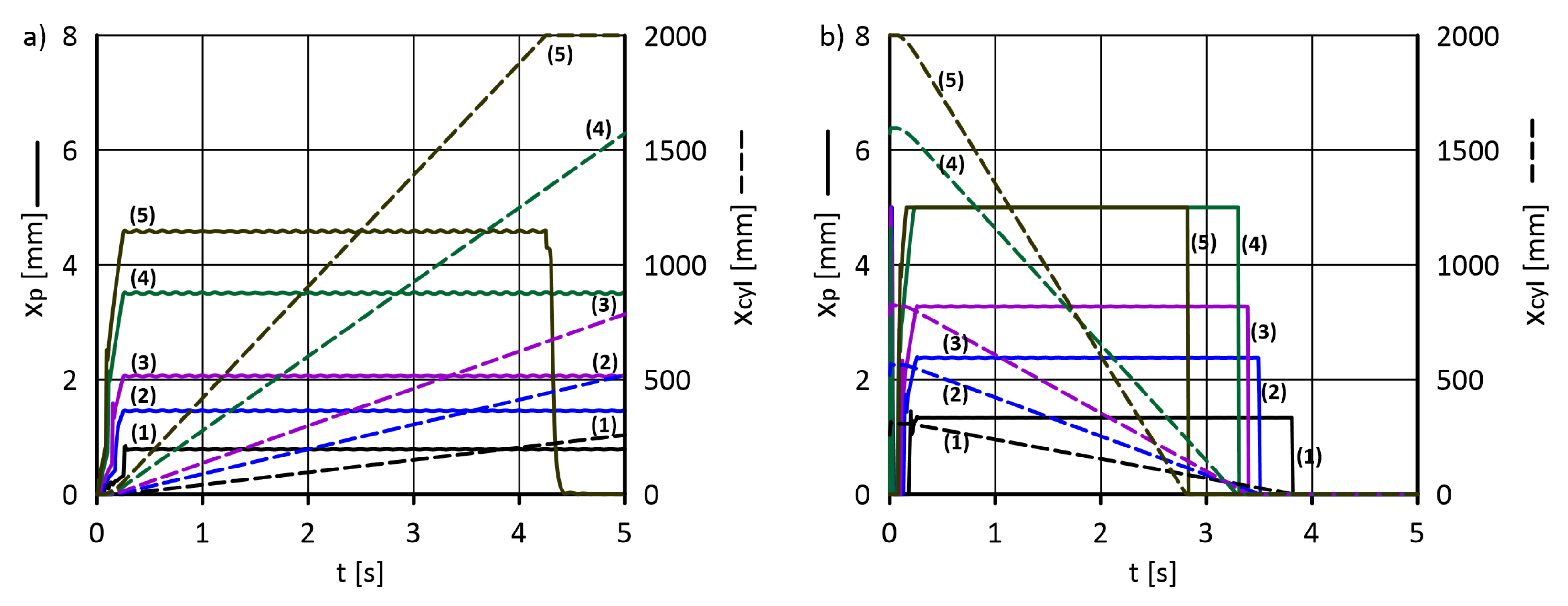


| Kinematic Viscosity | Density | Temperature | Min Inlet FLOW Rate | Max Inlet Flow Rate | Outlet Pressure |
|---|---|---|---|---|---|
| T | |||||
| 870 | 50.0 | 100 | 900 | 0.1 | |
| m2 s−1 | kg m−3 | °C | dm3 min−1 | dm3 min−1 | MPa |
| Kinetic Energy Constant | Kinetic Energy Dissipation Constants | Turbulent Viscosity Constant | Turbulence Intensity | Length Scale | ||
|---|---|---|---|---|---|---|
| I | ℓ | |||||
| 1.0 | 1.3 | 1.44 | 1.92 | 0.09 | 4.5–5.9 | 1.53 |
| - | - | - | - | - | % | mm |
| Mesh Case | No. of Nodes | No. of Elements | Comput. Time | Pressure Drop | Difference from Laboratory Result |
|---|---|---|---|---|---|
| Initial (I) | 30 min | MPa | % | ||
| Dense, refined (II) | 240 min | MPa | % | ||
| Double dense, refined (III) | 1660 min | MPa | % |
| Input | Q (dm3 min−1) | 300 | ||||
| (mm) | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | |
| Output | () | 67.8 | 65.0 | 62.1 | 58.9 | 56.0 |
mm | Q dm3 min−1 | N/mm | N/mm | N/mm | |||
|---|---|---|---|---|---|---|---|
| A-B | B-A | A-B | B-A | A-B | B-A | ||
| 7.0 | 100 | 0.34 | 0.06 | 0.48 | 0.12 | 0.65 | 0.17 |
| 200 | 0.41 | 0.10 | 0.56 | 0.15 | 0.74 | 0.21 | |
| 300 | 0.47 | 0.15 | 0.65 | 0.19 | 0.83 | 0.25 | |
| 600 | 0.70 | 0.39 | 0.92 | 0.42 | 1.15 | 0.43 | |
| 900 | 1.26 | 0.89 | 1.37 | 0.92 | 1.51 | 0.92 | |
N/mm | Q dm3 min−1 | mm | mm | mm | |||
|---|---|---|---|---|---|---|---|
| A-B | B-A | A-B | B-A | A-B | B-A | ||
| 41.0 | 100 | 0.24 | 0.05 | 0.48 | 0.12 | 0.77 | 0.21 |
| 200 | 0.32 | 0.08 | 0.56 | 0.15 | 0.85 | 0.24 | |
| 300 | 0.41 | 0.11 | 0.65 | 0.19 | 0.93 | 0.26 | |
| 600 | 0.67 | 0.39 | 0.92 | 0.42 | 1.21 | 0.43 | |
| 900 | 1.26 | 0.90 | 1.37 | 0.92 | 1.56 | 0.92 | |
| Direction | Q dm3 min−1 | N/mm | N/mm | N/mm | |||
|---|---|---|---|---|---|---|---|
| A-B | 100 | 2.1 | 95.4 | 2.9 | 94.6 | 3.8 | 93.7 |
| 200 | 2.4 | 95.1 | 3.4 | 94.2 | 4.3 | 93.2 | |
| 300 | 2.8 | 94.3 | 3.8 | 93.3 | 4.9 | 92.3 | |
| 600 | 4.1 | 91.5 | 5.2 | 90.4 | 6.4 | 89.3 | |
| 900 | 7.0 | 88.3 | 7.0 | 86.7 | 8.2 | 85.6 | |
| B-A | 100 | 0.9 | 98.1 | 1.2 | 97.9 | 1.6 | 97.7 |
| 200 | 0.8 | 98.0 | 1.2 | 97.7 | 1.5 | 97.5 | |
| 300 | 0.9 | 97.6 | 1.3 | 97.3 | 1.7 | 97.1 | |
| 600 | 2.5 | 95.5 | 2.5 | 95.5 | 2.6 | 95.4 | |
| 900 | 5.2 | 91.5 | 5.2 | 91.5 | 5.2 | 91.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisowski, E.; Filo, G.; Rajda, J. Analysis of Energy Loss on a Tunable Check Valve through the Numerical Simulation. Energies 2022, 15, 5740. https://doi.org/10.3390/en15155740
Lisowski E, Filo G, Rajda J. Analysis of Energy Loss on a Tunable Check Valve through the Numerical Simulation. Energies. 2022; 15(15):5740. https://doi.org/10.3390/en15155740
Chicago/Turabian StyleLisowski, Edward, Grzegorz Filo, and Janusz Rajda. 2022. "Analysis of Energy Loss on a Tunable Check Valve through the Numerical Simulation" Energies 15, no. 15: 5740. https://doi.org/10.3390/en15155740
APA StyleLisowski, E., Filo, G., & Rajda, J. (2022). Analysis of Energy Loss on a Tunable Check Valve through the Numerical Simulation. Energies, 15(15), 5740. https://doi.org/10.3390/en15155740







