A Comparative Study on Wind Energy Assessment Distribution Models: A Case Study on Weibull Distribution

Abstract

Wind power generation highly depends on the determination of wind power potential, which drives the design and feasibility of the wind energy production investment. This gives an important role to wind power estimation, which creates the need for an accurate wind data analysis and wind energy potential assessments for a given location. Such assessments require the implementation of an accurate and suitable wind distribution model. Therefore, in the quest for a well-fitted model, eight methods for estimating the Weibull parameters are investigated in this paper. The methods were then investigated by employing statistical tools, and their performances have been discussed in terms of various error indicators such as root mean squared error (RMSE), regression error (R2), chi-square (X2), and mean absolute error (MAE). Meteorological data for diverse terrain from 14 provinces with 30 sites scattered across Iran were employed to examine the performance of the investigated methods. The results demonstrated that the empirical method has superiority over the investigated technique in terms of errors.

1. Introduction

Fossil fuels have been relied upon for energy production in many countries. They are nearly always readily available, but an excessive amount of the exploitation of fossil fuels has impacted the environment on an outsized scale. Energy, partnered with the environment, constitutes a major crisis in today’s world. Global CO₂ emissions have already reached a historical peak in 2021, which makes it urgent to take steps toward sustainable fuels [1]. On the other hand, the energy demand is increasing at a rapid pace, creating an environmental concern. Moreover, it is anticipated that fossil fuel reserves will be depleted in the near future.

There is a significant increase in the interest of using sustainable, environmental, and cost-effective sources of energy in both developed and developing countries. By conducting thorough research, top engineers developed renewable energy sources to supplement fossil fuels. Renewable energy sources can be in the form of wind, geothermal, hydroelectric, and solar energy. All the forms of renewable energy mentioned have potentials depending on the geographical locations in which they function. It can be seen that wind energy has a higher interest compared to others and that it is the fastest-growing source in terms of the yearly growth of installed capacities [2]. As an alternative energy source, the wind does not pollute the lower layer of the atmosphere compared to fossil fuels.

Wind energy provides sustainable income to the landowners upon whose land a wind farm is established. The parameters to be determined in any wind harvesting activity are the wind speed and characteristics of the given location. For this purpose, required systematic examination starts with data collection using various sensors, such as pressure, temperature, humidity, anemometers, etc. The collected data are processed to find the wind potential. The measured wind speed data form the wind distribution. This distribution is used to calculate the wind power potential. Weibull and Rayleigh are the two most used distribution functions in the literature [3,4,5,6,7,8,9]. The Weibull distribution function is defined by a dimensionless parameter k and a scale parameter c in (m/s). The Weibull distribution can be described by the probability density functions (PDFs) f(v) and cumulative distribution functions (CDFs) F(v). Detailed definitions are given in the following section.

Some research has been conducted to compare the various Weibull distribution models for different regions [3,4,5,6] where the methods were ranked using statistical tools. Besides those studies, Carrillo et.al. (2014) performed research based on Weibull probability density function (PDF) to find the best-fit wind speed distributions for Galicia/Spain while testing the performance of four fitting methods [7]. They found that the moment method performed better for the fit for the given region. Bingol (2020) performed a study for Izmir/Turkey using five fitting methods [8] and concluded that if wind shows a diverse characteristic, using the Maximum Likelihood Method (MLM) gives better correlations. Patidar et.al. (2022) performed a similar study for the Gulf of Khambhat/India using six models [9], where they found that MLM is more favorable for wind potential estimations.

In the literature, 3 to 6 Weibull models are compared; however, a study of eight Weibull models with more sites has not yet been performed. In this paper, the Weibull distribution model is used to analyze wind speed and power density distributions using eight Weibull methods. The wind speed characteristics of 30 sites in Iran are investigated using the Weibull probability distribution function (PDF). The Weibull (PDF) provided good approximations of the observed wind speeds for the areas under study. The investigated Weibull methods are the energy pattern factor method (EPF), empirical method (EM), moment iteration method (MIM), method of moments (MOM), empirical method of Mabchour (EMM), power density method (PDM), maximum likelihood method (MLM), and modified maximum likelihood method (MMLM).

2. Materials and Methods

2.1. Wind Speed Data

The data were collected by “Renewable Energy and Energy Efficiency Organization (SATBA)” in Iran and available for open access [10]. The considered sites in this paper are 14 provinces across Iran consisting of 30 sites where one-year wind speed data were collected.

Table 1. Location of the investigated sites.

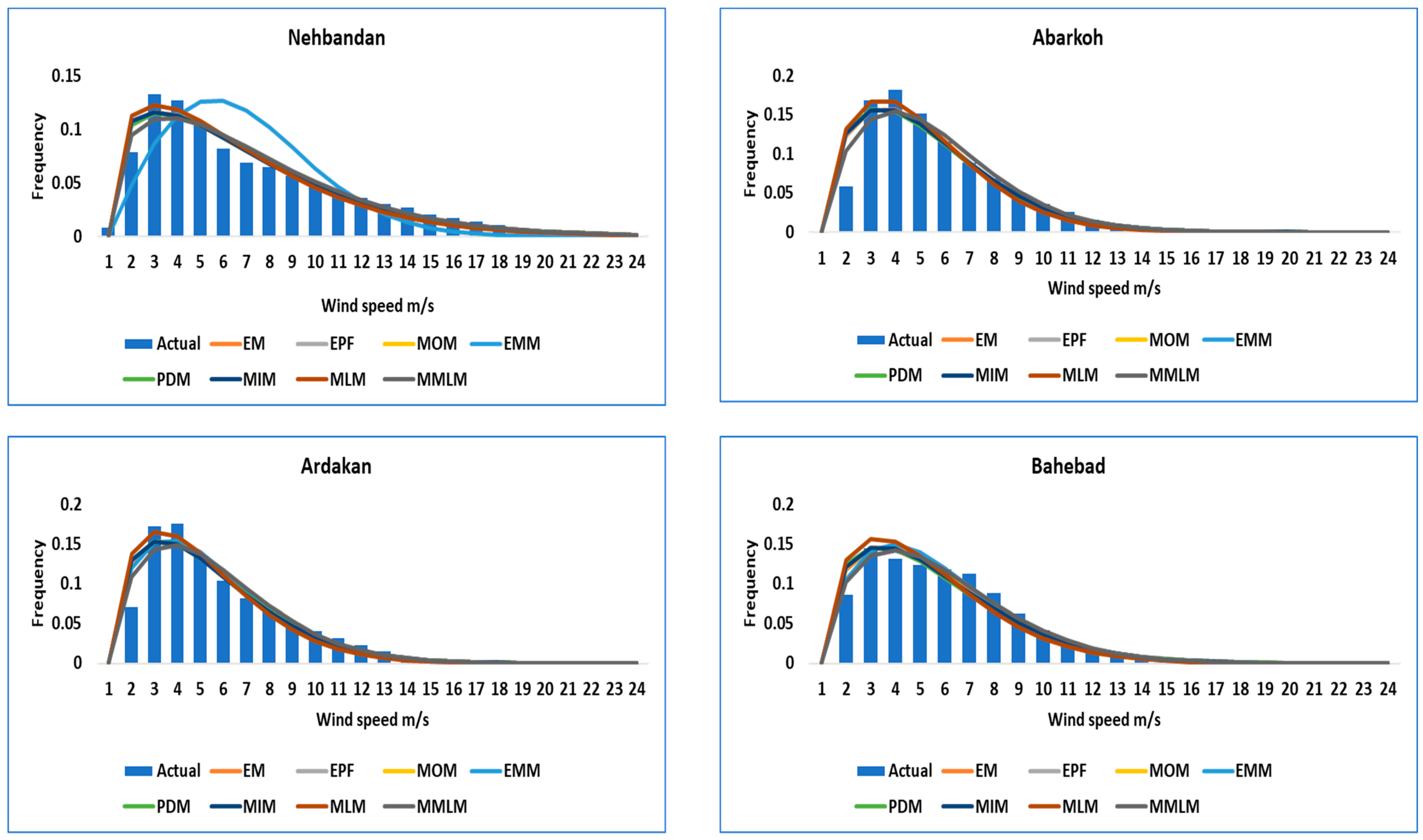
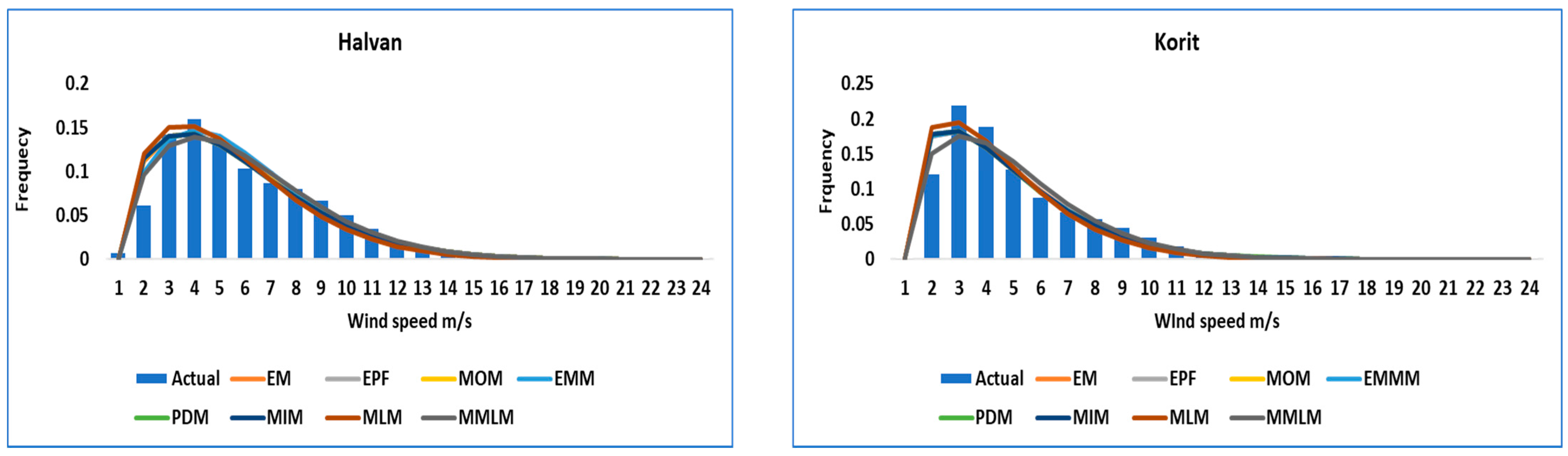
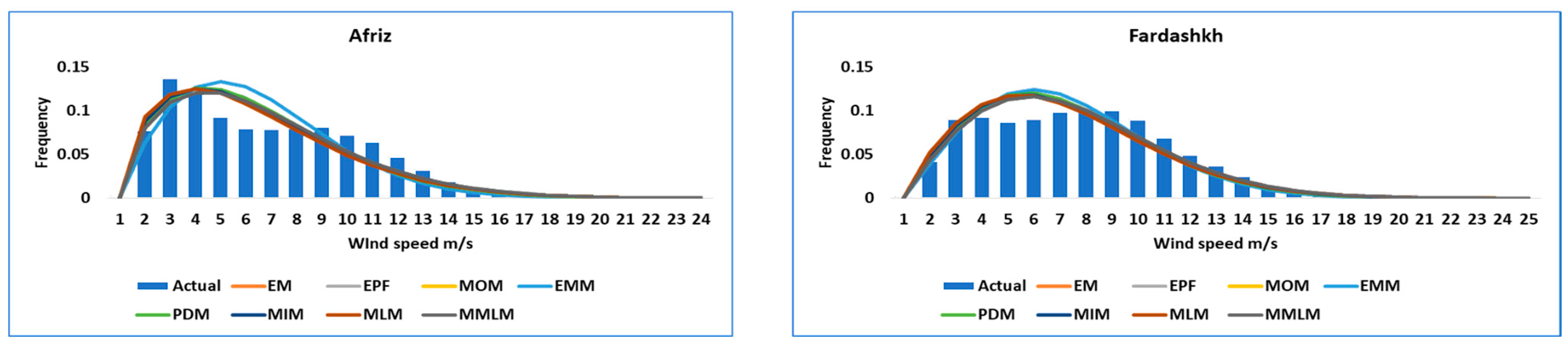
Province	Site	E	N	Province	Site	E	N
Fars	Shiraz	52.52	29.61	Kerman	Rafsanjani	56.22	30.32
Gilan	Langrod	50.15	37.20	Kermanshah	Songhor	47.60	34.78
Hormoz Gan	Kish	54.25	26.68	Alborz	Teleghat	50.77	36.18
Semnan	Hadadeh	31.96	35.93	Qazvin	Kohin	49.71	36.34
	Moaleman	54.57	34.87		Nekoieh	49.90	36.29
Bushehr	Bordkhon	51.49	27.98	North Khorasan	Bonjord	57.32	37.47
	Delvar	51.05	28.84		Sarafayen	57.47	37.07
Sistan and Baluchistan	Lotak	61.39	30.73	South Khorasan	Afriz	58.96	33.45
	Mil Nader	61.16	31.09		Fardashkh	58.17	34.02
	Shandol	61.66	31.15		Nehbandan	60.05	31.57
Razavi Khorasan	Bardaskan	57.97	35.26	Yazd	Abarkoh	53.31	31.10
	Davarzan	56.81	36.27		Ardakan	54.27	32.59
	Ghamdamghah	59.01	36.06		Bahebad	56.02	31.87
	Jangal	59.21	34.70		Halvan	56.28	33.95
	Roodab	57.31	36.02		Korit	56.96	33.44

shows the site’s latitudes and longitudes. The wind speed data collected were at a height of 40 m for all the sites. They are listed as reported in

Table 2. Annual Wind speed.

Province	Site	Mean Wind Speed (m/s)	Province	Site	Mean Wind Speed (m/s)
Fars	Shiraz	3.28	Kerman	Rafsanjan	5.56
Gilan	Langrod	3.71	Kermanshah	Songhor	4.77
Hormozgan	Kish	5.34	Alborz	Teleghat	3.28
Semnan	Hadadeh	5.84	Qazvin	Kohin	7.23
	Moaleman	6.17		Nekoieh	7.29
Bushehr	Bordkhon	5.83	North Khorasan	Bonjord	5.82
	Delvar	4.25		Sarafayen	4.37
Sistan and Baluchistan	Lotak	6.48	South Khorasan	Afriz	5.42
	Mil Nader	7.14		Fardashkh	6.16
	Shandol	6.64		Nehbandan	5.85
Razavi Khorasan	Bardaskan	4.72	Yazd	Abarkoh	4.27
	Davarzan	4.19		Ardakan	4.36
	Ghamdamghah	5.25		Bahebad	4.58
	Jangal	4.79		Halvan	4.69
	Roodab	6.05		Korit	3.62

.

The sites under study are represented in the map demonstrated in Figure 1. The areas that are studied are marked in red dots.

2.2. Methods

Statistical methods were implemented to estimate the wind energy potential of the locations whereby there are two methods to evaluate wind power. The first method, which is the most accurate, comprise calculating wind power potentials based on the measured values recorded at the sites. The second method comprise using probability distribution functions with the most common one being the Weibull distribution, which has higher accuracy and simplicity [11,12]. Some of the other methods are Poisson, Beta, Rayleigh, Gamma, Normal, Gaussian, and lognormal distribution. The statistical analysis is presented based on wind data collected at a height of 40 m. The Weibull probability density function is defined as follows [13,14,15]:

$$f_{\left(v\right)}=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}exp \left[-{\left(\frac{v}{c}\right)}^k\right]$$

(1)

where f(v) is the probability of observed wind speeds (v), k is the dimensionless Weibull parameter, and c is the Weibull scale parameter (m/s), which can be related to the mean wind speed $\underset{\_}{v}$ through the shape factor. The shape factor determines the consistency of wind speeds at a given location. The cumulative distribution F(v) is an integral part of the probability density function and is expressed as follows [16].

$$F_{\left(v\right)}={{\displaystyle \int }}_0^v{f}_{\left(v\right)}dv=1-e^{-{\left(\frac{v}{c}\right)}^k}$$

(2)

As mentioned earlier, the Weibull distribution function is easier to use and, therefore, was implemented to quickly and easily determine the average annual production of a given wind turbine. For effective applications of the Weibull distribution, the parameters’ mean and standard deviation are calculated by using the following equation:

$$\underset{\_}{v}=\frac{1}{n}{\displaystyle \sum }_{i=1}^v{v}_i$$

(3)

$$\sigma ={\left[\frac{1}{n-1} {\displaystyle \sum }_{i=1}^v{\left(v_i-\underset{\_}{v} \right)}^2\right]}^{0.5}$$

(4)

where n is the number of bins, $\sigma$ is the standard deviation, and $v_i$ is the ith wind speed. The above equations can be derived in terms of Weibull parameters as [17]:

$$\underset{\_}{v}=c\Gamma \left(1+\frac{1}{k}\right)$$

(5)

$$\sigma =\sqrt{c^2\left[\Gamma \left(1+\frac{2}{k}\right)-{\left[\Gamma \left(1+\frac{1}{k}\right)\right]}^2\right]}$$

(6)

where $\Gamma$ is the Gamma function.

Since wind is an unpredictable occurrence, it is important to use statistical methods that express wind data by a probability distribution function to determine the wind energy potential of a site.

The methods for estimation of Weibull parameters used in the literature are provided below.

2.2.1. Energy Pattern Factor Method (EPF)

The energy pattern method does not require higher computational efforts to estimate the available wind power density and wind speed variation to account for the energy power density of an area throughout a given period. The energy pattern factor is connected to the average data of wind speed and can be defined as the ratio of mean cubic wind speed to the cube of mean wind speed. The energy pattern factor (EPF) can be expressed as [18]:

$$\mathrm{EPF}=\frac{1}{\left({\underset{\_}{v}}^3\right)}\left({\displaystyle \sum }_{i=1}^n\frac{v_i^3}{N}\right)=\frac{\Gamma \left(1+\frac{3}{k}\right)}{{\Gamma }^3\left(1+\frac{1}{k}\right)}$$

(7)

where $v_i$ is the wind speed in m/s for ith observation, N is the total number of wind speed observations, and $\underset{\_}{v}$ is the mean wind speed. After calculating EPF, the Weibull parameters are estimated using the following formulas.

$$k=1+\frac{3.69}{{\left(\mathrm{EPF}\right)}^2}$$

(8)

$$c=\frac{\underset{\_}{v}}{\Gamma \left(1+\frac{1}{k}\right)}$$

(9)

2.2.2. Mean Standard Deviation Method

It is a method whereby only two parameters, such as mean wind speed and standard deviations, are available. The method is famously known as the empirical method and may be considered a unique case of the method of moments. The Weibull parameters characterize the wind potential of the region and can be computed as follows [19,20,21,22,23].

$$k={\left(\frac{\sigma }{\underset{\_}{v}}\right)}^{-1.806}$$

(10)

$$c=\frac{\underset{\_}{v}}{\Gamma \left(1+\frac{1}{k}\right)}$$

(11)

2.2.3. Moment Iteration Method (MIM)

Having calculated the mean and standard deviation from Equations (5) and (6) of the wind speed data, we divide the square of Equations (5) by (6) to obtain the following.

$$\frac{{\underset{\_}{v}}^2}{{\sigma }^2}=\frac{\left\{\Gamma \left(1+\frac{1}{k}\right)\right\}}{\Gamma \left(1+\frac{2}{k}\right)-{\Gamma }^2\left(1+\frac{1}{k}\right)}$$

(12)

Therefore, from Equation (10), the numerical iteration method is applied to calculate the value of k, and c is calculated using Equation (9).

2.2.4. Method of Moments (MOM)

It is one of the imperative techniques used universally in Weibull parameters evaluation. The method is also known as the standard deviation method. MOM is executed by the application of standard deviation and the mean of the data being analyzed using Weibull distributions. The equation below shows the relationship between the mean wind speed and the standard deviation of the wind speed [24].

$$\frac{{\underset{\_}{v}}^2}{{\sigma }^2}=\frac{\left\{\Gamma \left(1+\frac{1}{k}\right)\right\}}{\Gamma \left(1+\frac{2}{k}\right)-{\Gamma }^2\left(1+\frac{1}{k}\right)}$$

(13)

$${\left(\frac{\sigma }{\underset{\_}{v}}\right)}^2=\frac{\Gamma \left(1+\frac{2}{k}\right)}{{\left[\Gamma \left(1+\frac{1}{k}\right)\right]}^2}-1$$

(14)

The dimensionless Weibull parameters k and c are calculated as follows.

$$k={\left(\frac{0.9874}{\frac{\sigma }{\underset{\_}{v}}}\right)}^{1.0983}$$

(15)

$$c=\frac{\underset{\_}{v}}{\Gamma \left(1+\frac{1}{k}\right)}$$

(16)

2.2.5. Empirical Method of Mabchour (EMM)

This was first introduced by Mabchour in 1999 [24] when he used it in the assessment of wind potential energy in Morocco. The scale parameter for this method is calculated with the same method shown in Equation (9). The Weibull k and c parameters are found by the following.

$$k=1+{\langle 0.483 * \left(v-2\right)\rangle }^{0.51}$$

(17)

$$c=\frac{\underset{\_}{v}}{\Gamma \left(1+\frac{1}{k}\right)}$$

(18)

2.2.6. Power Density Method (PDM)

The PDM is related to the energy pattern factor method and is proposed in [18] and is recommended as an estimation method for its high accuracy and fewer computations. It can be expressed as follows.

$$\mathrm{EPF}=\frac{1}{\left({\underset{\_}{v}}^3\right)}\left({\displaystyle \sum }_{i=1}^n\frac{v_i^3}{N}\right)=\frac{\Gamma \left(1+\frac{3}{k}\right)}{{\Gamma }^3\left(1+\frac{1}{k}\right)}$$

(19)

2.2.7. Maximum Likelihood Method (MLM)

The MLM method is a mathematical expression of the wind speed data in time series format. The Weibull parameters are estimated using the Equations that follow:

$$k={\left[\frac{{{\displaystyle \sum }}_{i=1}^n{v}_i^{k}lnln \left(v_i\right) }{{{\displaystyle \sum }}_{i=1}^n{v}_i^k}-\frac{{{\displaystyle \sum }}_{i=1}^{n}lnln (v_i) }{n}\right]}^{-1}$$

(20)

$$c={\left(\frac{1}{n}{\displaystyle \sum }_{i=1}^n{v}_i^k\right)}^{\frac{1}{k}}$$

(21)

where $v_i$ is the wind speed in timestep, and $i$and $n$ are the non-zero wind speed data points. To solve Equation (17), the use of numerical iteration is implemented, and then Equation (18) can be solved.

2.2.8. Modified Maximum Likelihood Method (MMLM)

This method is only used for wind speed data available in the Weibull distribution format. Similarly, to the MLM, it is also solved numerically to determine the following parameters.

$$k={\left[\frac{{{\displaystyle \sum }}_{i=1}^n{v}_i^k\left(v_i\right) \left(v_i\right) }{{{\displaystyle \sum }}_{i=1}^n{v}_i^k\left(v_i\right) }-\frac{{{\displaystyle \sum }}_{i=1}^{n}lnln (v_i)\left(v_i\right) }{f\left(v\ge 0\right)}\right]}^{-1}$$

(22)

$$c={\left[\frac{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{v}_i^k\left(v_i\right) }{f\left(v\ge 0\right)}\right]}^{-1}$$

(23)

2.3. Statistical Accuracy Analysis

The data must be exact. Accurate data are more reliable because it helps in analysis and in making logical conclusions. The best analysis method was found by using several previously used statistical tools to analyze the efficiency of the above-mentioned methods. There were 6 methods used in this research: root mean square error (RMSE), coefficient of determination $\left(R^2\right)$, chi-square error $(X^2)$, relative percentage error (RPE), mean bias error (MBE), and mean absolute error (MAE).

2.3.1. Root Mean Square Error (RMSE)

This method’s accuracy is dependent on how close to zero the error is. RMSE tells you how concentrated the data are around the line of best fit. It is also the standard deviation of the residuals (prediction errors), which shows the distance of the data points from the regression line; therefore, RMSE is a measure of how to spread out these residuals. It is given by [18]:

$$\mathrm{RMSE}={\left[\frac{1}{N}{\displaystyle \sum }_{i=1}^n{(y_{i,m}-x_{i,w})}^2\right]}^{0.5}$$

(24)

where N is the number of wind speed observations or the number of intervals, $x_{i,w}$ is the frequency of Weibull or ith calculated value from Weibull distribution, and $y_{i,m}$ is the frequency of observed wind data or the ith calculated value from measured data.

2.3.2. Coefficient of Determination $\left(R^2\right)$

The method is used to determine the linear relationship between the calculated values and the Weibull distribution and measured data. The ideal value of the coefficient is equal to one. The coefficient of determination $\left(R^2\right)$ is computed as [5]:

$$R^2=\frac{{{\displaystyle \sum }}_{i=1}^n{(y_{i,m}-z_{i,\underset{\_}{v}})}^2-{{\displaystyle \sum }}_{i=1}^n{(y_{i,m}-x_{i,w})}^2 }{{{\displaystyle \sum }}_{i=1}^n{(y_{i,m}-z_{i,\underset{\_}{v}})}^2}$$

(25)

where $y_{i,m}$, $x_{i,w}$, and $z_{i,w}$ are the observed and Weibull frequencies and mean wind speed, respectively, and N is the number of observations.

2.3.3. Chi-Square Error $\left(X^2\right)$

The method is a special case of a gamma distribution, which is one of the most widely used probability distributions in inferential distributions. The error formula is expressed as follows [25].

$$X^2={\displaystyle \sum }_{i=1}^n\frac{{(y_{i,m}-x_{i,w})}^2}{x_{i,w}}$$

(26)

2.3.4. Mean Absolute Error (MAE)

Mean error captures the average bias error in the predicted values and the calculated values, whereas the mean absolute error denotes the ratio of the 1 norm of the error vector to the number of samples [26]:

$$\mathrm{MAE}=\frac{1}{N}{\displaystyle \sum }_{i=1}^n\left|y_{i,m}-x_{i,w}\right|$$

(27)

where $y_{i,m}$ and $x_{i,w}$ are the observed and Weibull frequencies, respectively, and N is the number of observations.

2.4. Wind Power Density (WPD)

Wind power density can be considered as a value that represents the energy potential of a selected region under investigation. It may be defined as the mean annual power per square meter of the swept area of a turbine, and it is calculated at different heights above the ground. Wind power is mainly dictated by the air density and velocity of the wind. From the relation, we can see that the wind power density is calculated as:

$$\mathrm{WPD}=\frac{P}{A}=\frac{1}{2}\rho {\underset{\_}{v}}^3$$

(28)

where ${\underset{\_}{v}}^3$ is the wind speed cubed in m/s, $\rho$ is the standard air density at sea level $\left(\rho =1.225\frac{\mathrm{kg}}{{\mathrm{m}}^3}\right)$, and P is power watts and A is the swept area in ${\mathrm{m}}^2$. Wind power density is demonstrated in Watt per square meter $\left(\frac{\mathrm{W}}{{\mathrm{m}}^2}\right)$ and is considered to be a better indicator of the available wind energy source. Therefore, the average wind power density is expressed as:

$$\left(\frac{P}{A}\right)=\frac{1}{2n}{\displaystyle \sum }_{i=1}^n\rho \left({\underset{\_}{v}}^3\right)$$

(29)

where (i) is the measured wind speed over time intervals of 10 min, and n is the number of bins. The Weibull distribution analysis may be used to develop the calculation of the wind power density (WPD), which is based on the wind speed that is provided by field measurements at the different locations using the expression below [27].

$$\frac{P}{A}=\frac{1}{2}\rho c^3\Gamma \left(\frac{k+3}{k}\right)$$

(30)

3. Results and Discussion

Weibull parameters k and c were estimated using each approach with observed wind data to compare the accuracy of the methods in this study. Figure 2 shows the Weibull PDF versus the mean wind speed for the measured daily wind speed data in one year for each site. It can be observed from the figures that the curves representing the Weibull PDF for all methods in the analysis match the histograms of the actual data.

Then, the methods were ranked based on their performance when examined with statistical tests.

Table 3. Best-performing Weibull methods.

	Method	k	c	Measured (WPD)	WPD	R2	X2	RMSE	MAE
SHIRAZ	MOM	1.308	3.552	614.42	641.44	0.9799	0.00251	0.00420	0.00014
	EM	1.322	3.563		630.99	0.9792	0.00258	0.00021	0.00013
LANGROD	EM	1.879	4.177	580.13	557.28	0.9476	0.00621	0.00034	0.00003
	EMM	1.421	4.077		808.10	0.7992	0.02465	0.00428	0.00068
KISH	EMM	1.823	6.011	1854.30	1724.47	0.9749	0.00168	0.00436	0.00026
	EM	1.727	5.995		1839.06	0.9665	0.00213	0.00020	0.00002
HADADEH	EM	1.722	6.557	2336.25	2412.62	0.8666	0.00736	0.00039	0.00002
	MIM	1.698	6.546		2454.61	0.8685	0.08577	0.00455	0.00205
MOALEMAN	EM	1.804	6.940	2652.43	2685.11	0.9407	0.00309	0.00024	0.00001
	MOM	1.791	6.932		2707.12	0.9407	0.00307	0.00435	0.00001
BORDKHON	EM	1.848	6.568	2263.93	2211.88	0.9377	0.00371	0.00026	0.00001
	EMM	1.944	6.579		2094.06	0.9561	0.00267	0.00435	0.00034
DELVAR	EM	1.743	4.776	932.96	917.83	0.9633	0.00328	0.00025	0.00003
	EMM	1.723	4.772		1065.48	0.9214	0.00687	0.00430	0.00037
LOTAK	EM	1.608	7.232	3601.38	3594.59	0.9352	0.00294	0.00024	0.00002
	EPF	1.604	7.225		3601.97	0.9348	0.00296	0.00434	0.00002
MIL NADER	EM	1.516	7.924	5229.34	5232.99	0.9246	0.00281	0.00023	0.00003
	EPF	1.514	7.916		5233.68	0.9244	0.00281	0.00434	0.00003
SHANDOL	EM	1.665	7.435	3705.97	3697.52	0.9572	0.00185	0.00019	0.00002
	EPF	1.662	7.428		3702.37	0.9569	0.00186	0.00435	0.00002
BARDASKAN	EM	1.502	5.233	1510.36	1531.82	0.9622	0.00283	0.00023	0.00005
	EMM	1.670	5.282		1321.92	0.9686	0.00281	0.00433	0.00034
DAVARZAN	EM	1.287	4.534	1408.55	1387.62	0.8812	0.01178	0.00046	0.00010
	MIM	1.270	4.519		1416.81	0.8775	0.10712	0.00424	0.00177
GHADAMGHAH	EM	1.353	5.729	2398.96	2489.97	0.9221	0.00479	0.00030	0.00007
	MOM	1.339	5.714		2529.01	0.9222	0.00479	0.00428	0.00007
JANGAL	EM	2.007	5.404	1132.07	1119.43	0.9671	0.00276	0.00023	0.00001
	EPF	1.996	5.400		1125.54	0.9658	0.00285	0.00435	0.00001
ROODAB	EM	1.656	6.768	2769.81	2811.13	0.9449	0.00278	0.00023	0.00002
	MOM	1.643	6.758		2839.30	0.9447	0.00277	0.00436	0.00002
RAFSANJAN	EM	1.999	6.282	1850.39	1766.38	0.9693	0.00222	0.00020	0.00001
	MLM	1.995	6.281		1772.09	0.9687	0.09969	0.00435	0.00189
SONGHOR	MOM	1.390	5.230	1741.22	1784.46	0.9677	0.00222	0.00429	0.00007
	EM	1.404	5.243		1759.18	0.9674	0.00224	0.00020	0.00006
TELEGHAT	MLM	1.417	3.848	614.42	683.14	0.9834	0.13458	0.00420	0.00176
	EM	1.322	3.562		630.99	0.9792	0.00258	0.00021	0.00013
KOHIN	EM	1.750	8.124	4442.72	4486.09	0.9603	0.00157	0.00018	0.00001
	EPF	1.757	8.120		4461.83	0.9610	0.00156	0.00447	0.00001
NEKOIEH	EM	1.759	8.193	4589.46	4568.76	0.9720	0.00106	0.00014	0.00001
	EPF	1.756	8.186		4575.63	0.9715	0.00108	0.00441	0.00001
BONJORD	EPF	1.851	6.555	2205.91	2195.58	0.9572	0.00268	0.00435	0.00001
	EM	1.814	6.555		2246.46	0.9553	0.00268	0.00023	0.00001
SARAFAYEN	EM	1.534	4.861	1184.37	1181.62	0.9454	0.00449	0.00029	0.00005
	EMM	1.585	4.873		1127.87	0.9503	0.00410	0.00432	0.00035
AFRIZ	EM	1.588	6.046	2075.13	2143.63	0.9172	0.00486	0.00030	0.00003
	MOM	1.574	6.036		2167.18	0.9183	0.00478	0.00432	0.00003
FARDASHKH	EM	1.888	6.940	2498.95	2537.69	0.9335	0.00362	0.00026	0.00001
	MOM	1.876	6.934		2556.09	0.9331	0.00362	0.00435	0.00001
NEHBANDAN	PDM	1.330	6.366	3550.90	3550.88	0.9632	0.07997	0.00446	0.00198
	MOM	1.507	5.072		1388.42	0.9647	0.00265	0.00453	0.00006
ABARKOH	EM	1.577	4.766	1105.48	1061.39	0.9403	0.00537	0.00033	0.00005
	MOM	1.564	4.757		1073.22	0.9372	0.00565	0.00453	0.00005
ARDAKAN	EM	1.509	4.835	1216.57	1199.11	0.9432	0.00475	0.00031	0.00006
	EMM	1.581	4.856		1120.07	0.9525	0.00396	0.00455	0.00035
BAHEBAD	EM	1.521	5.082	1442.29	1371.87	0.9670	0.00247	0.00023	0.00005
	EMM	1.635	5.114		1239.50	0.9784	0.00171	0.00455	0.00026
HALVAN	EM	1.538	5.214	1481.74	1452.58	0.9497	0.00368	0.00028	0.00005
	EMM	1.663	5.248		1304.82	0.9644	0.00269	0.00455	0.00033
KORIT	EM	1.401	3.972	790.81	769.04	0.9463	0.00590	0.00034	0.00010
	EMM	1.398	3.968		769.85	0.9458	0.00596	0.00447	0.00038

illustrates the best-performing methods for all sites in this study.

The eight methods mentioned are found to be effective in the evaluation of the Weibull distribution for the available data. This is corroborated by the RMSE, Chi-square, R², and MAE values, which are all extremely similar to each other for the eight Weibull PDF methods based on data gathered in all the sites. The best parameter estimations will show the lowest values of RMSE and Chi-square and the highest values of R².

The PDM method showed satisfactory results when the wind power density was considered. It produced results close to the exact values when compared with the measured data. However, when the method was assessed using the error methods, it came last in the ranking.

Table 4. Weibull parameters, wind power density, and errors using PDM.

	k	c	Measured (WPD)	WPD	R2	X2	RMSE	MAE
SHIRAZ	1.340	3.569	614.42	614.45	0.9778	0.14239	0.00421	0.00177
LANGROD	1.813	4.170	580.13	580.13	0.9337	0.14139	0.00434	0.00188
KISH	1.715	5.991	1854.30	1854.29	0.9649	0.09561	0.00435	0.00189
HADADEH	1.768	6.563	2336.25	2336.29	0.8613	0.08761	0.00455	0.00206
MOALEMAN	1.823	6.938	2652.43	2652.39	0.9399	0.08515	0.00435	0.00188
BORDKHON	1.811	6.562	2263.93	2263.88	0.9287	0.08956	0.00435	0.00188
DELVAR	1.720	4.771	932.96	932.98	0.9594	0.12044	0.00433	0.00187
LOTAK	1.604	7.225	3601.38	3601.35	0.9348	0.07624	0.00434	0.00187
MIL NADER	1.515	7.917	5229.34	5229.36	0.9245	0.06766	0.00434	0.00188
SHANDOL	1.661	7.428	3705.97	3706.04	0.9568	0.07564	0.00435	0.00189
BARDASKAN	1.515	5.234	1510.36	1510.34	0.9634	0.10295	0.00431	0.00185
DAVARZAN	1.274	4.522	1408.55	1408.56	0.8784	0.10718	0.00424	0.00177
GHAMDAMGHAH	1.381	5.745	2398.96	2399.00	0.9211	0.08940	0.00429	0.00183
JANGAL	1.985	5.399	1132.07	1132.09	0.9647	0.11561	0.00435	0.00189
ROODAB	1.674	6.768	2769.81	2769.83	0.9444	0.08327	0.00437	0.00190
RAFSANJAN	1.911	6.272	1850.39	1850.38	0.9542	0.09717	0.00435	0.00189
SONGHOR	1.412	5.243	1741.22	1741.20	0.9670	0.09955	0.00429	0.00184
TELEGHAT	1.340	3.569	614.42	614.44	0.9778	0.14239	0.00421	0.00177
KOHIN	1.753	8.118	4442.72	4475.50	0.9604	0.07128	0.00447	0.00200
NEKOIEH	1.752	8.185	4589.46	4589.56	0.9708	0.07070	0.00441	0.00194
BONJORD	1.843	6.554	2205.91	2205.94	0.9568	0.09077	0.00435	0.00189
SARAFAYEN	1.531	4.856	1184.37	1184.38	0.9448	0.11110	0.00431	0.00185
AFRIZ	1.625	6.054	2075.13	2075.11	0.9127	0.09146	0.00433	0.00187
FARDASHKH	1.916	6.939	2498.95	2498.92	0.9332	0.08750	0.00435	0.00189
NEHBANDAN	1.330	6.366	3550.90	3550.88	0.9632	0.07997	0.00446	0.00198
ABARKOH	1.531	4.747	1105.48	1105.48	0.9298	0.11337	0.00453	0.00204
ARDAKAN	1.493	4.825	1216.57	1216.59	0.9404	0.11031	0.00453	0.00204
BAHEBAD	1.469	5.056	1442.29	1442.27	0.9579	0.10507	0.00452	0.00204
HALVAN	1.516	5.202	1481.74	1481.72	0.9453	0.10330	0.00453	0.00205
KORIT	1.376	3.958	790.81	790.81	0.9418	0.12900	0.00446	0.00198

shows the Weibull parameters c and k, wind power density, and the errors calculated from the Power Density Method (PDM). The wind power density is then compared to the measured data. From the data analyzed, it can be seen that the best method to use is the EM for all sites, followed by MOM, and the third in rank is EPF. Moreover, it can be seen that the best method is MMLM followed by EM, and MLM is ranked third. For the regression error, it can be seen that the best method is EM followed by MOM, and PDM is third in rank.

4. Conclusions

The performance analysis of the eight Weibull methods for the estimation of the wind speed distributions in 30 sites from 14 provinces in Iran at the height of 40 m was the subject of this paper. The main aim was to select the most accurate and efficient methods to observe how close the measured data are to the two-parameter Weibull PDF. It was concluded that the aforementioned Weibull methods are effective in evaluating the parameters of the Weibull distribution for the available data since the values of the RMSE, Chi-square, R², and MAE are very close to each other. As a result of the findings, it is strongly recommended that the EM method be used wherever possible as a more accurate estimation of the Weibull parameters to eliminate errors in wind energy production computation. The MOM and the EPF methods can also be used as alternatives. The PDM method produced WPD values close to the exact values, but when it was compared to the other methods, it came in last and is, therefore, not recommended.