FTCN: A Reservoir Parameter Prediction Method Based on a Fusional Temporal Convolutional Network
Abstract
:1. Introduction
- (1)
- Our method can predict reservoir porosity, permeability and water saturation effectively. It is beneficial for logging interpreters to analyze rock strata and identify oil and gas resources;
- (2)
- A new reservoir parameter prediction method named FTCN is proposed. We introduce a fusion module based on TCN to utilize the information from different network layers adequately, which improves the effect of curve prediction;
- (3)
- We have conducted various experiments on the real logging dataset to illustrate the effectiveness of this method. FTCN can predict well where the log curve changes abruptly and is effective when the properties of underground strata change greatly.
2. Previous Work
3. Methodology
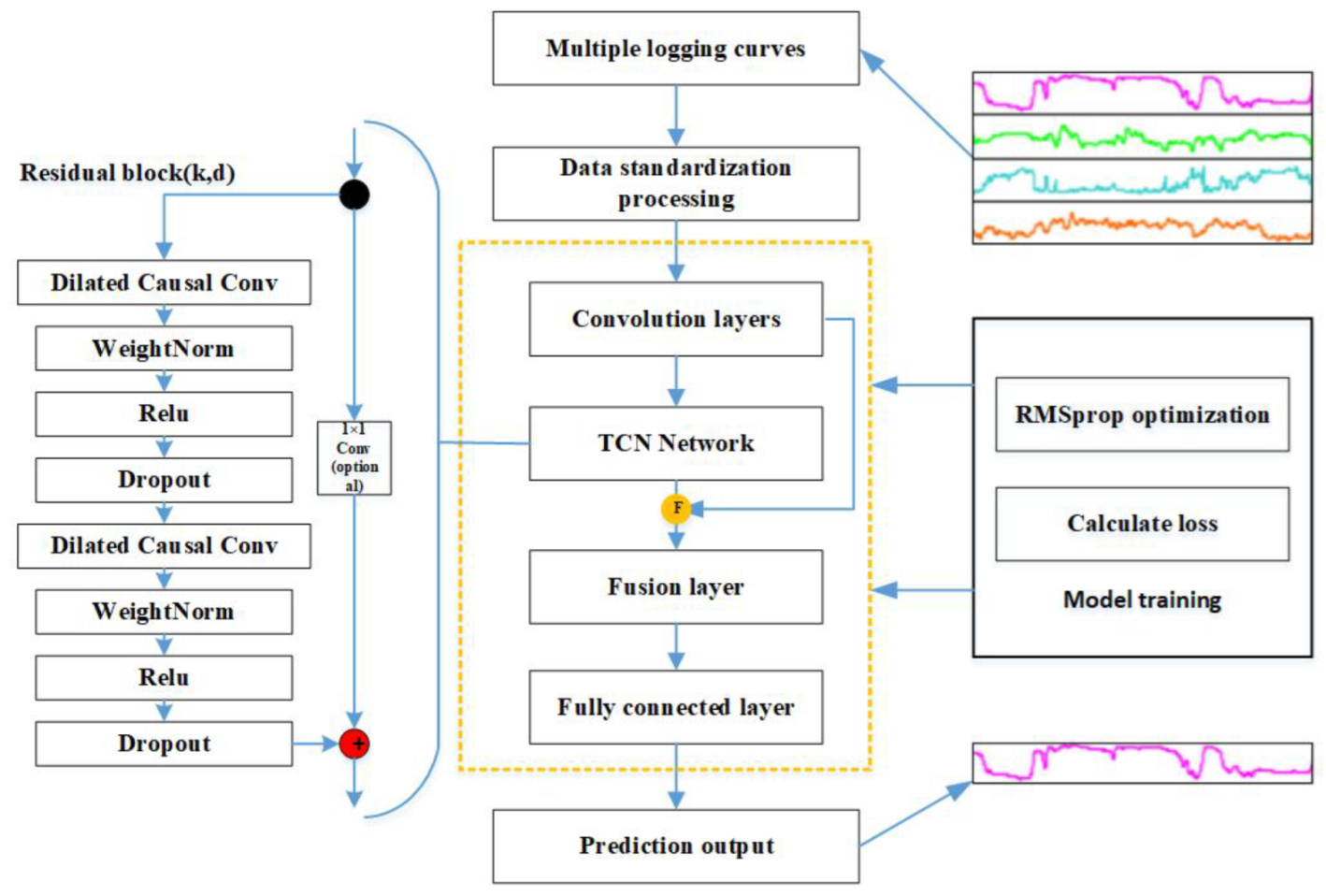
3.1. FTCN Network Model
3.2. Fusional Module
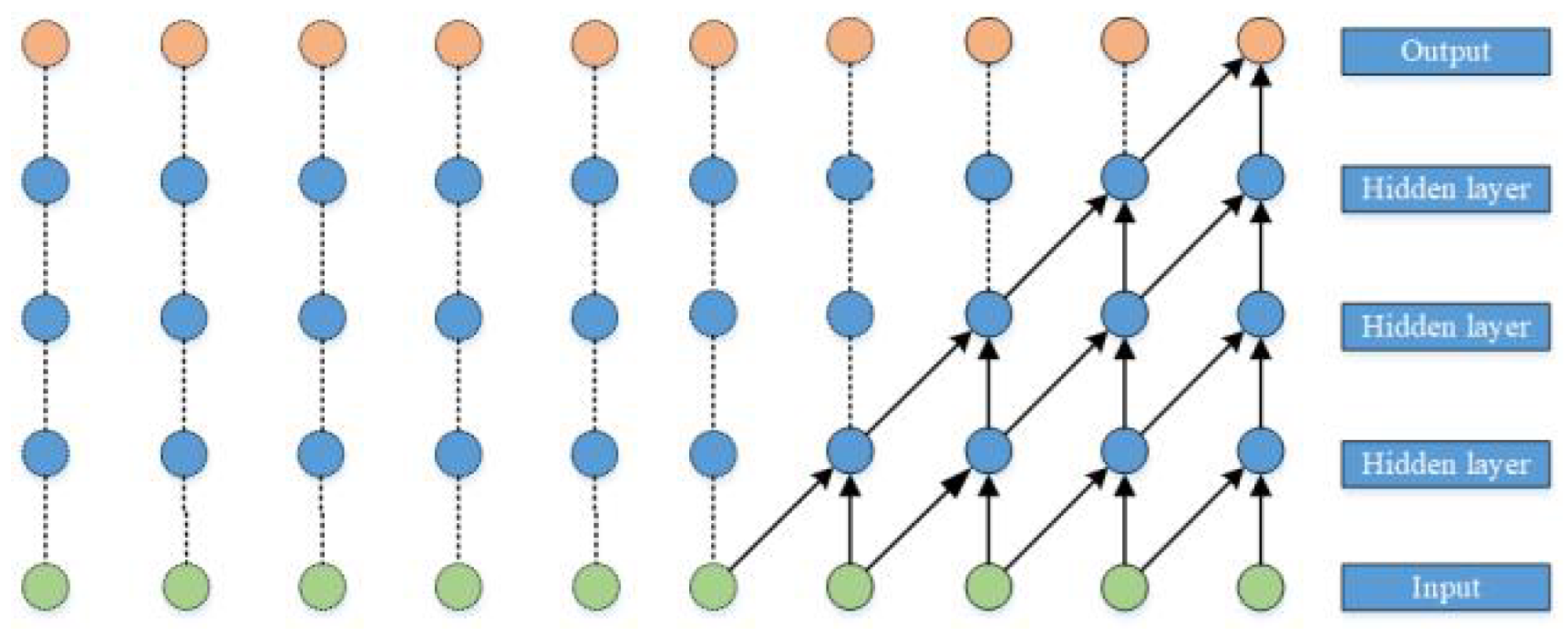
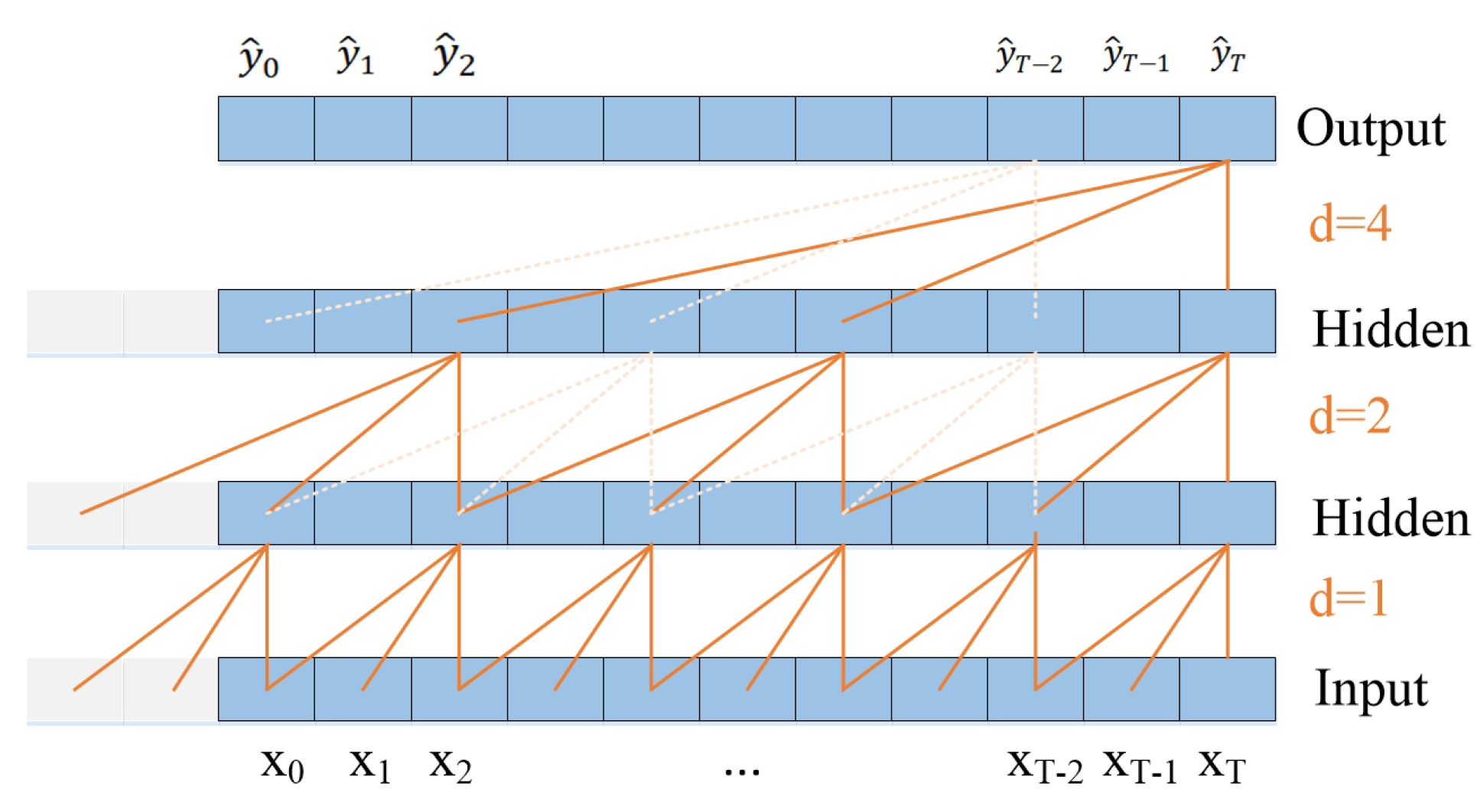
3.3. TCN Network
3.4. FTCN Network Flow
| Algorithm 1: FTCN RP = FTCN(LCS). |
 |
4. Results and Discussion
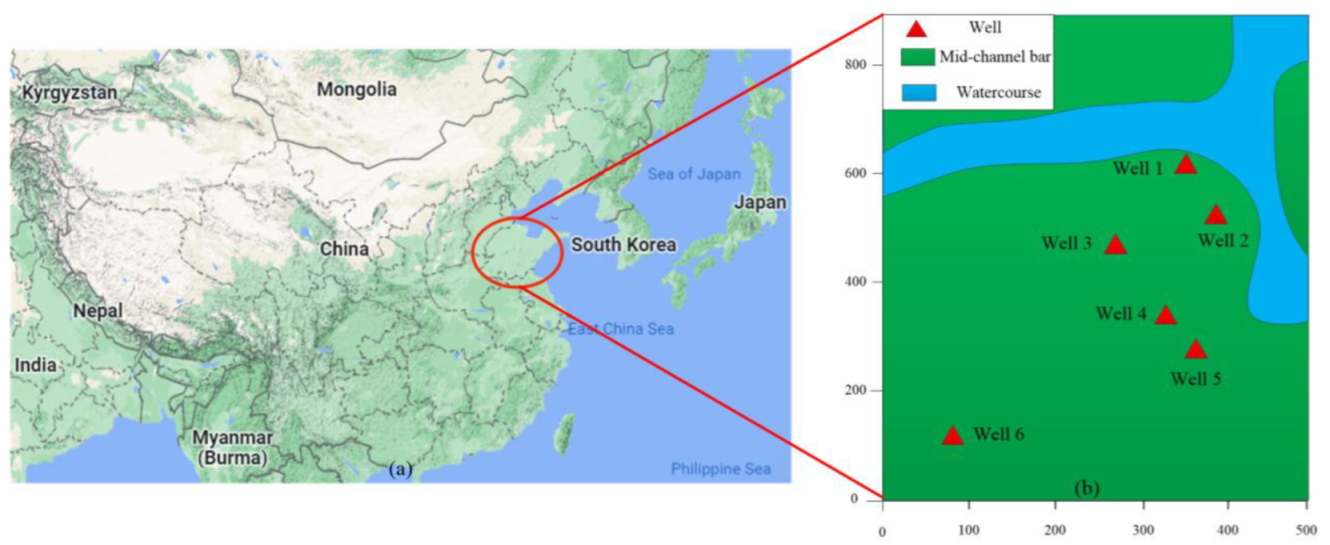
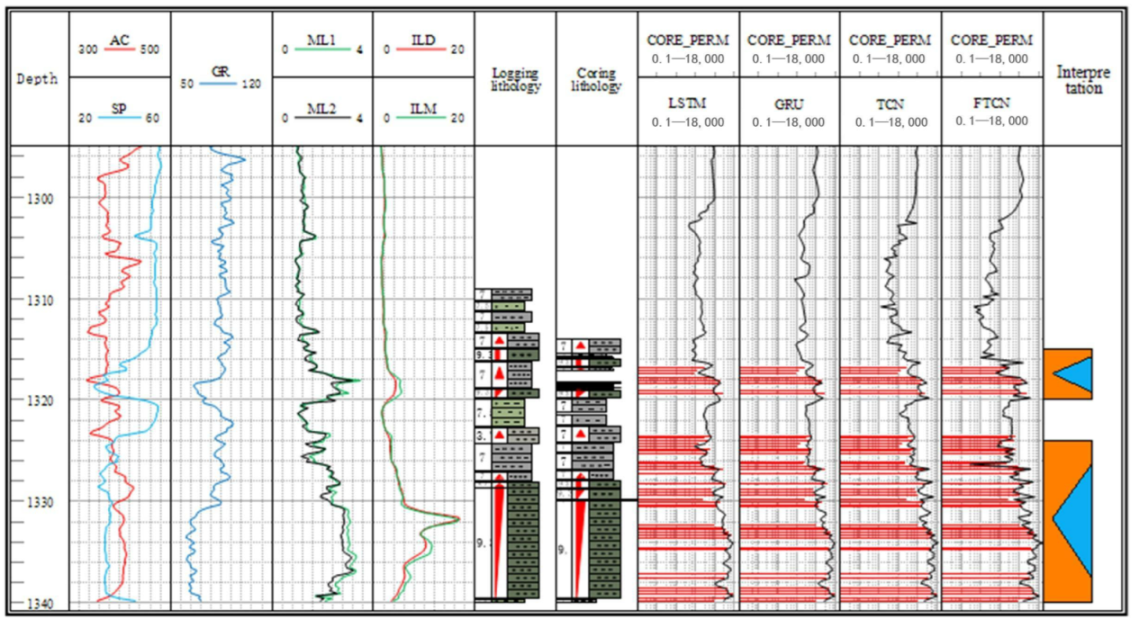
4.1. Geological Setting and Data Source
4.2. Evaluation Metrics
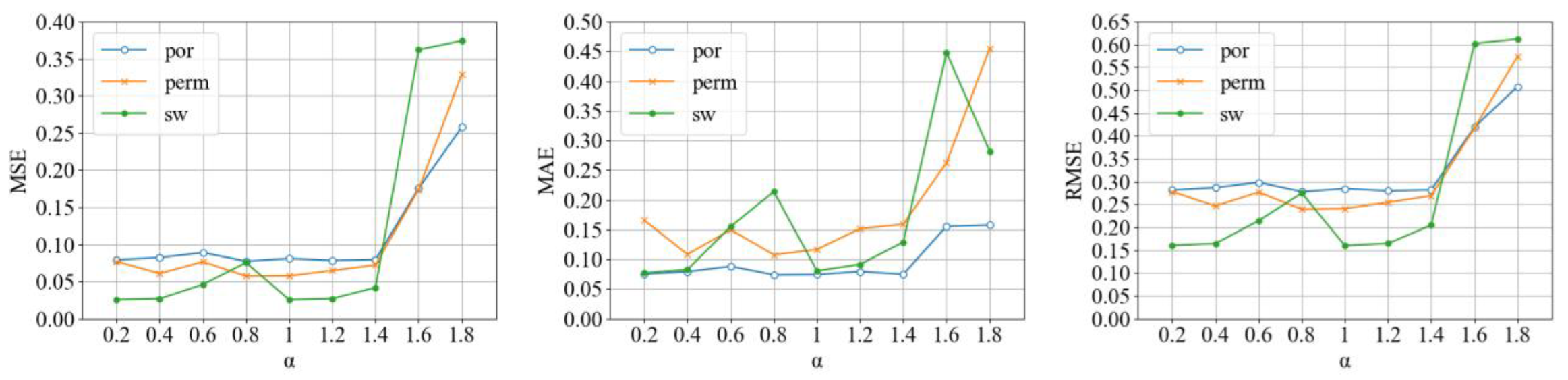
4.3. FTCN Parameter Setting
4.3.1. Setting
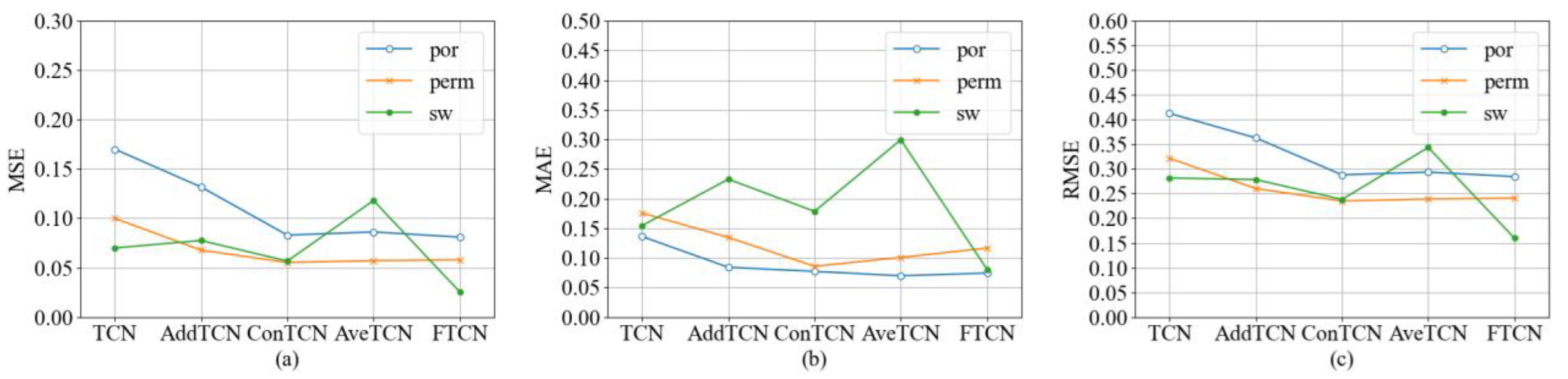
4.3.2. Verification of Fusional Module
- (1)
- AddTCN refers to the method of the add operation, which is to carry out a sum operation on the output of the merged layer to fuse the information;
- (2)
- ConTCN refers to the method of the concat operation, which splices the output of the layer to be merged along the last dimension and then fuses the information;
- (3)
- AveTCN refers to the method of the average operation, which fuses the output of the layer to be merged by the element mean.
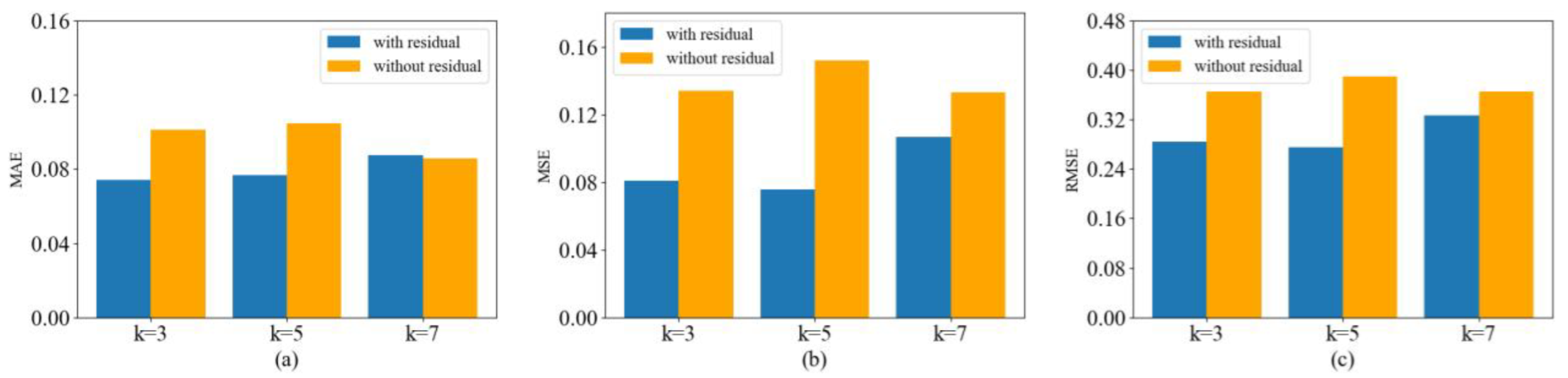
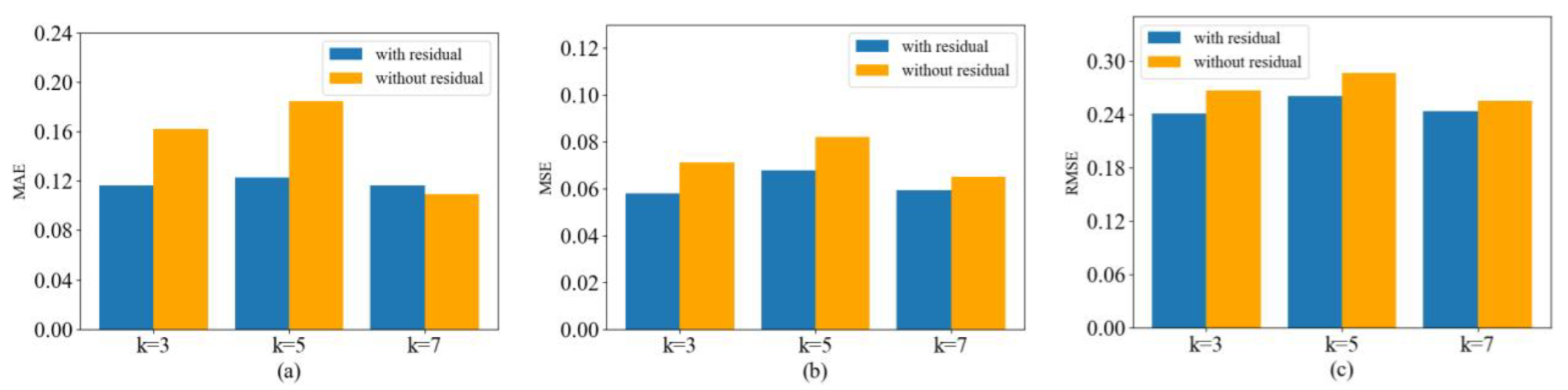
4.3.3. Influence of Filter Size k and Residual Block
4.4. Influence of Input Logging Curves
- (1)
- Curve_Set1 contains the acoustic travel time, density, compensated neutron logging, natural gamma ray, and spontaneous potential, which are closely related to porosity.
- (2)
- Curve_Set2 adds micro potential resistivity, micro-gradient resistivity, deep and medium investigation induction log, and high-definition induction logging curve M2R10, which are closely related to permeability calculation to the Curve_Set1.
- (3)
- Curve_Set3 contains all the input logs used for permeability prediction in this paper.
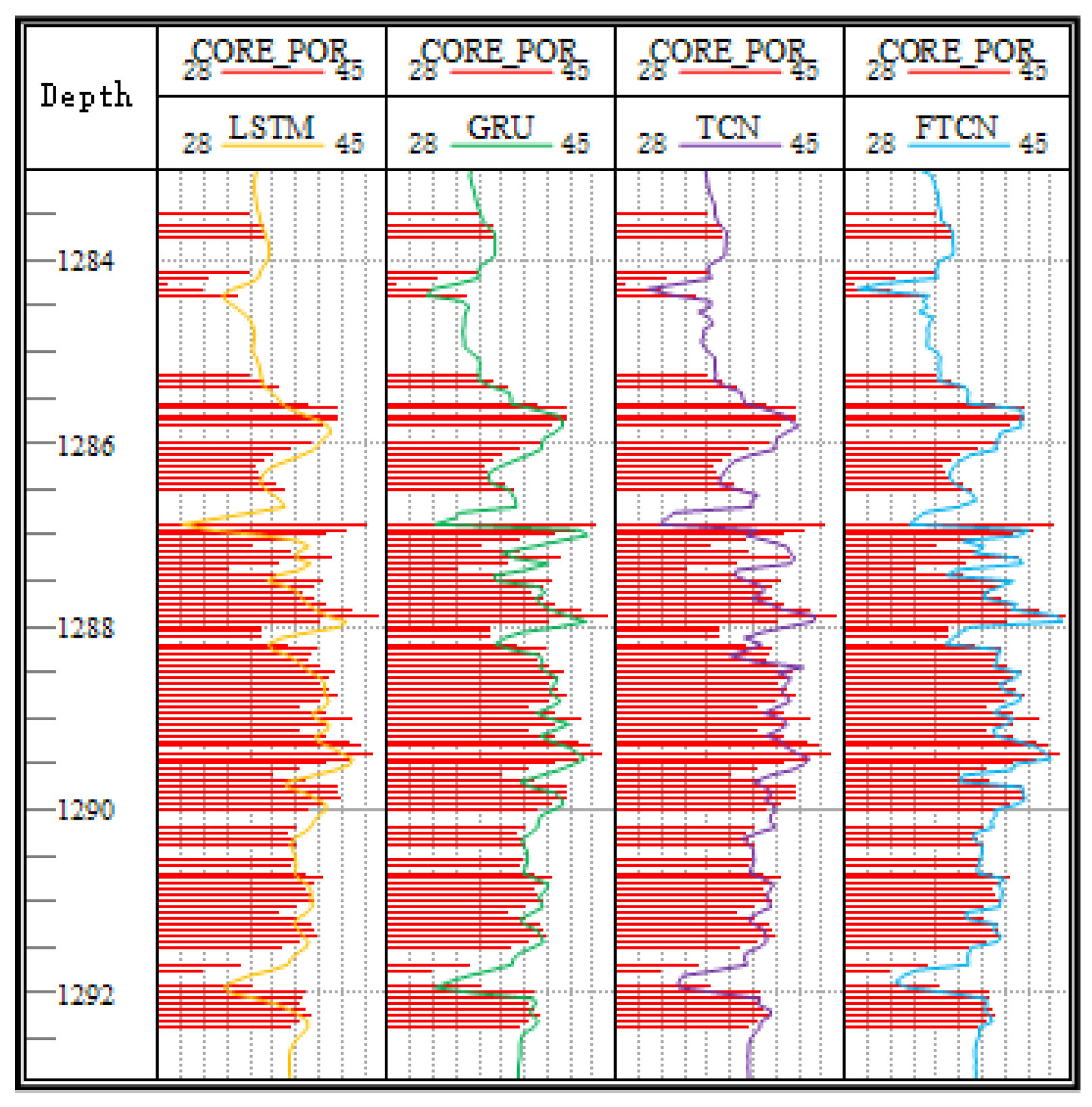
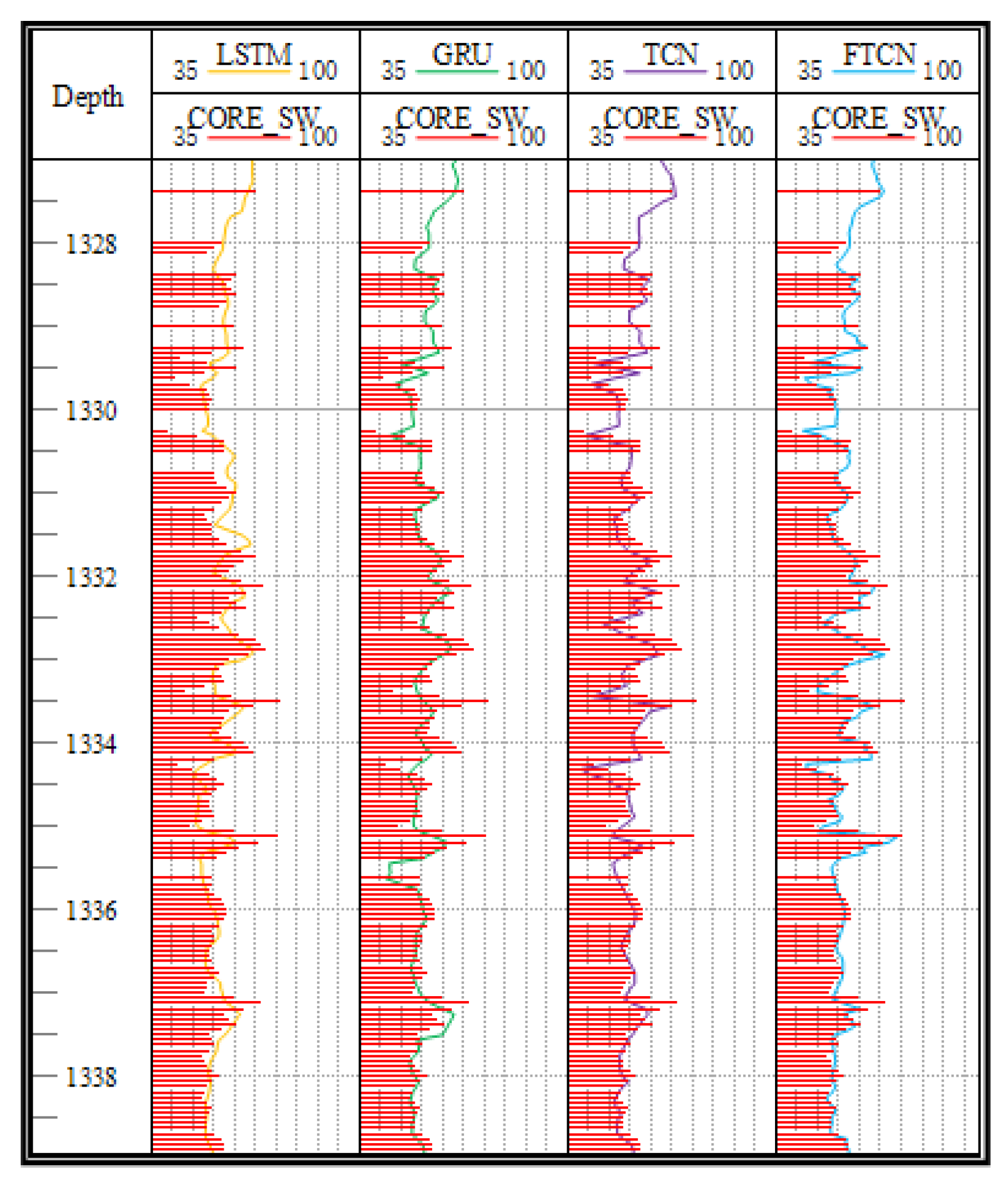
4.5. Comparison of Methods
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, B.; Wu, H.; Feng, Z.; Li, Y.; Wang, K.; Liu, P. Application status and prospects of artificial intelligence in well logging and formation evaluation. Acta Pet. Sin. 2021, 42, 508–522. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- dos Santos, D.T.; Roisenberg, M.; dos Santos Nascimento, M. Deep Recurrent Neural Networks Approach to Sedimentary Facies Classification Using Well Logs. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Al-Shabandar, R.; Jaddoa, A.; Liatsis, P.; Hussain, A.J. A deep gated recurrent neural network for petroleum production forecasting. Mach. Learn. Appl. 2021, 3, 100013. [Google Scholar] [CrossRef]
- Heghedus, C.; Shchipanov, A.; Rong, C. Advancing deep learning to improve upstream petroleum monitoring. IEEE Access 2019, 7, 106248–106259. [Google Scholar] [CrossRef]
- Kuanzhi, Z.; Zhang, L.; Zheng, D.; Chonghao, S.; Qingning, D. A reserve calculation method for fracture-cavity carbonate reservoirs in Tarim Basin, NW China. Pet. Explor. Dev. 2015, 42, 277–282. [Google Scholar]
- Al-Jawad, S.N.; Saleh, A.H.; Al-Dabaj, A.A.A.; Al-Rawi, Y.T. Reservoir flow unit identification of the Mishrif formation in North Rumaila Field. Arab. J. Geosci. 2014, 7, 2711–2728. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, C.; Gu, X.; Li, J. A novel deep learning-based method for damage identification of smart building structures. Struct. Health Monit. 2019, 18, 143–163. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Rashidi, M.; Samali, B.; Mohammadi, M.; Nguyen, T.N.; Zhou, X. Crack detection of concrete structures using deep convolutional neural networks optimized by enhanced chicken swarm algorithm. Struct. Health Monit. 2022, 14759217211053546. [Google Scholar] [CrossRef]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Choubey, S.; Karmakar, G. Artificial intelligence techniques and their application in oil and gas industry. Artif. Intell. Rev. 2021, 54, 3665–3683. [Google Scholar] [CrossRef]
- Janjuhah, H.T.; Kontakiotis, G.; Wahid, A.; Khan, D.M.; Zarkogiannis, S.D.; Antonarakou, A. Integrated Porosity Classification and Quantification Scheme for Enhanced Carbonate Reservoir Quality: Implications from the Miocene Malaysian Carbonates. J. Mar. Sci. Eng. 2021, 9, 1410. [Google Scholar] [CrossRef]
- Adeniran, A.A.; Adebayo, A.R.; Salami, H.O.; Yahaya, M.O.; Abdulraheem, A. A competitive ensemble model for permeability prediction in heterogeneous oil and gas reservoirs. Appl. Comput. Geosci. 2019, 1, 100004. [Google Scholar] [CrossRef]
- Liu, J.J.; Liu, J.C. An intelligent approach for reservoir quality evaluation in tight sandstone reservoir using gradient boosting decision tree algorithm-A case study of the Yanchang Formation, mid-eastern Ordos Basin, China. Mar. Pet. Geol. 2021, 126, 104939. [Google Scholar] [CrossRef]
- Yong Hong, W.; Zhengnan, Z.; Shufa, Z. Estimation of porosity using seismic and logging data. Oil Geophys. Prospect. 1990, 25, 572–577. [Google Scholar]
- Jinzhong, Z. An Empirical Formula for Estimating Permeability Based on Well Logging Data and Its Physuical Background Analysis. J. Xi’an Shiyou Univ. 1991, 6, 16–20. [Google Scholar]
- Xie, J.; Chen, W.; Zhang, D.; Zu, S. Application of principal component analysis in weighted stacking of seismic data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1213–1217. [Google Scholar] [CrossRef]
- Inyang, N.J.; Agbasi, O.E.; Akpabio, G.T. Integrated analysis of well logs for productivity prediction in sand-shale sequence reservoirs of the Niger Delta—A case study. Arab. J. Geosci. 2021, 14, 1–9. [Google Scholar] [CrossRef]
- Kuang, L.; He, L.; Yili, R.; Kai, L.; Mingyu, S.; Jian, S.; Xin, L. Application and development trend of artificial intelligence in petroleum exploration and development. Pet. Explor. Dev. 2021, 48, 1–14. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Zhu, P.; Lin, C.; Wu, P.; Fan, R.; Zhang, H.; Pu, W. Permeability prediction of tight sandstone reservoirs using improved BP neural network. Open Pet. Eng. J. 2015, 8, 288–292. [Google Scholar] [CrossRef] [Green Version]
- Mahdaviara, M.; Rostami, A.; Keivanimehr, F.; Shahbazi, K. Accurate determination of permeability in carbonate reservoirs using Gaussian Process Regression. J. Pet. Sci. Eng. 2021, 196, 107807. [Google Scholar] [CrossRef]
- Gholami, R.; Shahraki, A.; Paghaleh, M.J. Prediction of Hydrocarbon Reservoirs Permeability Using Support Vector Machine. Math. Probl. Eng. 2012, 2012, 670723. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Zhou, G.; Yang, Y.; Li, F.; Jiao, Z. A novel prediction method for favorable reservoir of oil field based on grey wolf optimizer and twin support vector machine. J. Pet. Sci. Eng. 2020, 189, 106952. [Google Scholar] [CrossRef]
- Akande, K.O.; Owolabi, T.O.; Olatunji, S.O.; AbdulRaheem, A. A hybrid pARTICLE swarm optimization and support vector regression model for modelling permeability prediction of hydrocarbon reservoir. J. Pet. Sci. Eng. 2017, 150, 43–53. [Google Scholar] [CrossRef]
- Okon, A.N.; Adewole, S.E.; Uguma, E.M. Artificial neural network model for reservoir petrophysical properties: Porosity, permeability and water saturation prediction. Model. Earth Syst. Environ. 2021, 7, 2373–2390. [Google Scholar] [CrossRef]
- Hamidi, H.; Rafati, R. Prediction of oil reservoir porosity based on BP-ANN. In Proceedings of the 2012 International Conference on Innovation Management and Technology Research, Malacca, Malaysia, 21–22 May 2012; pp. 241–246. [Google Scholar]
- Xiang, Y.F.; Kang, Z.H.; Hao, W.J.; Fu, K.N.; Wang, F.S. A Composite Method of Reservoir Parameter Prediction Based on Linear Regression and Neural Network. Sci. Technol. Eng. 2017, 17, 46–52. [Google Scholar]
- Nasir, I.M.; Bibi, A.; Shah, J.H.; Khan, M.A.; Sharif, M.; Iqbal, K.; Nam, Y.; Kadry, S. Deep learning-based classification of fruit diseases: An application for precision agriculture. CMC-Comput. Mater. Contin. 2021, 66, 1949–1962. [Google Scholar] [CrossRef]
- Ouahabi, A.; Taleb-Ahmed, A. Deep learning for real-time semantic segmentation: Application in ultrasound imaging. Pattern Recognit. Lett. 2021, 144, 27–34. [Google Scholar] [CrossRef]
- Muhammad, A.N.; Aseere, A.M.; Chiroma, H.; Shah, H.; Gital, A.Y.; Hashem, I.A.T. Deep learning application in smart cities: Recent development, taxonomy, challenges and research prospects. Neural Comput. Appl. 2021, 33, 2973–3009. [Google Scholar] [CrossRef]
- Yuyang, L.; Xinhua, M.; Xiaowei, Z.; Wei, G.; Lixia, K.; Rongze, Y.; Yuping, S. Shale gas well flowback rate prediction for Weiyuan field based on a deep learning algorithm. J. Pet. Sci. Eng. 2021, 203, 108637. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, F.; Cai, J. 3D tight sandstone digital rock reconstruction with deep learning. J. Pet. Sci. Eng. 2021, 207, 109020. [Google Scholar] [CrossRef]
- An, P.; Cao, D.P.; Zhao, B.Y.; Yang, X.L.; Zhang, M. Reservoir physical parameters prediction based on LSTM recurrent neural network. Prog. Geophys. 2019, 34, 1849–1858. [Google Scholar]
- Chen, W.; Yang, L.; Zha, B.; Zhang, M.; Chen, Y. Deep learning reservoir porosity prediction based on multilayer long short-term memory network. Geophysics 2020, 85, WA213–WA225. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Wang, P.; Dimitri, R. On a Deep Learning Method of Estimating Reservoir Porosity. Math. Probl. Eng. 2021, 2021, 6641678. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Gehring, J.; Auli, M.; Grangier, D.; Yarats, D.; Dauphin, Y.N. Convolutional sequence to sequence learning. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1243–1252. [Google Scholar]
- Tieleman, T.; Hinton, G. Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 6, 26–31. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]






| POR | PERM | SW | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| LSTM | 0.23 | 0.26 | 0.51 | 0.28 | 0.23 | 0.48 | 0.22 | 0.17 | 0.41 |
| GRU | 0.17 | 0.22 | 0.47 | 0.25 | 0.19 | 0.44 | 0.20 | 0.13 | 0.36 |
| TCN | 0.13 | 0.17 | 0.41 | 0.17 | 0.10 | 0.32 | 0.15 | 0.07 | 0.28 |
| FTCN | 0.07 | 0.08 | 0.28 | 0.12 | 0.06 | 0.24 | 0.08 | 0.03 | 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Fu, K.; Lv, Z.; Wang, Z.; Shi, J.; Yu, H.; Ge, X. FTCN: A Reservoir Parameter Prediction Method Based on a Fusional Temporal Convolutional Network. Energies 2022, 15, 5680. https://doi.org/10.3390/en15155680
Zhang H, Fu K, Lv Z, Wang Z, Shi J, Yu H, Ge X. FTCN: A Reservoir Parameter Prediction Method Based on a Fusional Temporal Convolutional Network. Energies. 2022; 15(15):5680. https://doi.org/10.3390/en15155680
Chicago/Turabian StyleZhang, Hongxia, Kaijie Fu, Zhihao Lv, Zhe Wang, Jiqiang Shi, Huawei Yu, and Xinmin Ge. 2022. "FTCN: A Reservoir Parameter Prediction Method Based on a Fusional Temporal Convolutional Network" Energies 15, no. 15: 5680. https://doi.org/10.3390/en15155680
APA StyleZhang, H., Fu, K., Lv, Z., Wang, Z., Shi, J., Yu, H., & Ge, X. (2022). FTCN: A Reservoir Parameter Prediction Method Based on a Fusional Temporal Convolutional Network. Energies, 15(15), 5680. https://doi.org/10.3390/en15155680





