Propagation Characteristics and Identification of High-Order Harmonics of a Traction Power Supply System

Abstract

High-order harmonics in the traction power supply show negative effects on the safe and stable operation of the railway transportation system. There is a fixed resonant frequency in the traction network. When the harmonic current frequency produced by the locomotive matches the resonant frequency of the traction network, it will cause high-frequency resonant overvoltage. The propagation path of the high-order harmonics of the traction load is analyzed based on a V/v wiring traction transformer. The propagation characteristics of high-order harmonics on self-used equipment at 380 V low-voltage side and 27.5 kV high-voltage side are expounded. A simulation model for the low-voltage self-consumption power system is established and the singular value decomposition algorithm is proposed to identify the harmonic impedance. The simulation results show that the proposed method can reduce the error to within 0.1%. Under realistic conditions, the overvoltage caused by high-order harmonics is difficult to identify. To solve this problem, an overvoltage identification algorithm for Electric Multiple Units based on a convolutional neural network is proposed. The ShuffleNet neural network model is then used to identify high-order harmonics overvoltage and other types of overvoltage. The overall accuracy of the proposed classification model can be improved from 97.12% to 98.44%. Better recognition and classification performances can also be achieved.

1. Introduction

In recent years, with the rapid development of the railway electrification system, the railway has become an important transportation tool for people’s daily travel and freight transportation. High-order harmonics resonance in the traction power supply system has become a hot research topic in the railway electrification system.

Much research has been done on the propagation characteristics of high-order harmonics in the traction power supply system [1,2,3,4]. For better analysis, circuit mathematical models [5,6] and simulation models [7] of locomotives and traction networks have been built. The basis of mathematical and simulation models, the harmonic emission and propagation characteristics of locomotive currents are studied by combining the modal analysis method and the spectrum analysis method [8]. To evaluate the degree of resonance, so that more resonance-related problems can be solved effectively, the double Fourier series is applied to describe the PWM waveform in [9,10], an online identification method of the resonance frequency is proposed in [11], and the resonance suppression method is studied in [12,13,14,15]. However, the above literature is limited to the study of the propagation characteristics of high-order harmonics in traction power supply systems (27.5 kV). The influence of high-order harmonics on three-phase public grids (110 kV or 220 kV) and power consumption systems (low-voltage three-phase systems) are not considered. Reference [16] focuses on the transmission characteristics of high-order harmonics to low-voltage power systems. The accuracy of the model is verified by some experimental data, and the permeability of high-order harmonics in a low-voltage 380 V system is analyzed.

High-order harmonics not only propagate laterally to the high-voltage system but also permeate into the low-voltage system. High harmonic resonance overvoltage will occur when the condition is serious. During overvoltage identification, the data is decomposed by combining the time domain and frequency domains [17]. The wavelet transform method [18], singular entropy spectrum [19], and principal component analysis [20] are used to extract features, fuzzy mathematics, and genetic algorithms [21] for classification. Overvoltage characteristic information is extracted by wavelet analysis. Although high accuracy can be achieved via the abovementioned methods, the manual extraction of overvoltage characteristic information is required. The obtained results are susceptible to overvoltage duration, overvoltage peaks, harmonic frequency, etc. The complexity of identification is also increased, and the generalization ability of the model is poor.

In this paper, the mechanism by which high-order harmonics are generated is analyzed, and the transverse transmission characteristic and longitudinal permeability characteristic of harmonic waves are deduced. Based on the mechanism of harmonic coupling, a layout scheme for higher harmonic measuring points is proposed. The singular value decomposition (SVD) algorithm is used to identify the harmonic impedance parameters of self-consumption electrical loads via simulation models of the traction power supply and low-voltage power distribution systems. A modified method for evaluating and identifying high-frequency resonance overvoltage of Electric Multiple Units (EMUs) is then proposed using the ShuffleNet lightweight convolutional neural network (CNN), including the innovative use of lightweight CNN as a training model. Texture fingerprint features (of overvoltages data) are transferred into the proposed model for training. Different parameters, such as optimal learning rate, sample size, network complexity, and the number of textures, are derived through model training to achieve a high accuracy rate with small sample datasets. Compared with traditional machine learning, this method can avoid the complexity of manual feature extraction and improve the generalization ability of the model.

The harmonic transfer characteristics of this study are briefly introduced in Section 2. Impedance identification based on the SVD algorithm is presented in Section 3. In Section 4, an overvoltage identification method based on the ShuffleNet neural network is proposed. The effects of four parameters on the model performance are investigated. Section 5 summarizes the work of this paper.

2. Transmission Characteristics of High-Order Harmonics in a Traction Power Supply System

Since the V/v wiring mode is generally applied in current traction transformers, the content of this section analyzes the transmission path of high-order harmonics of the traction load based on the V/v wiring.

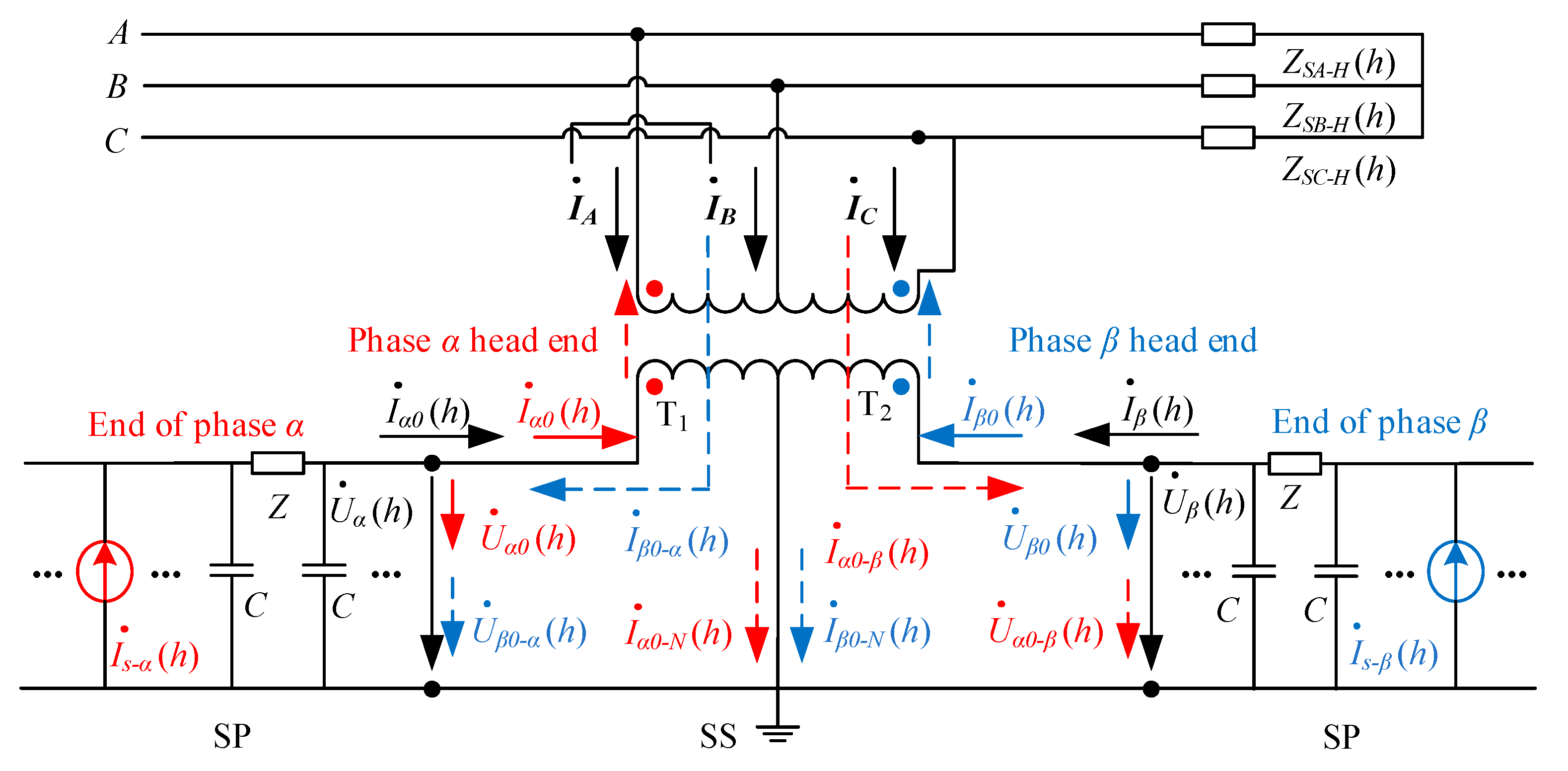
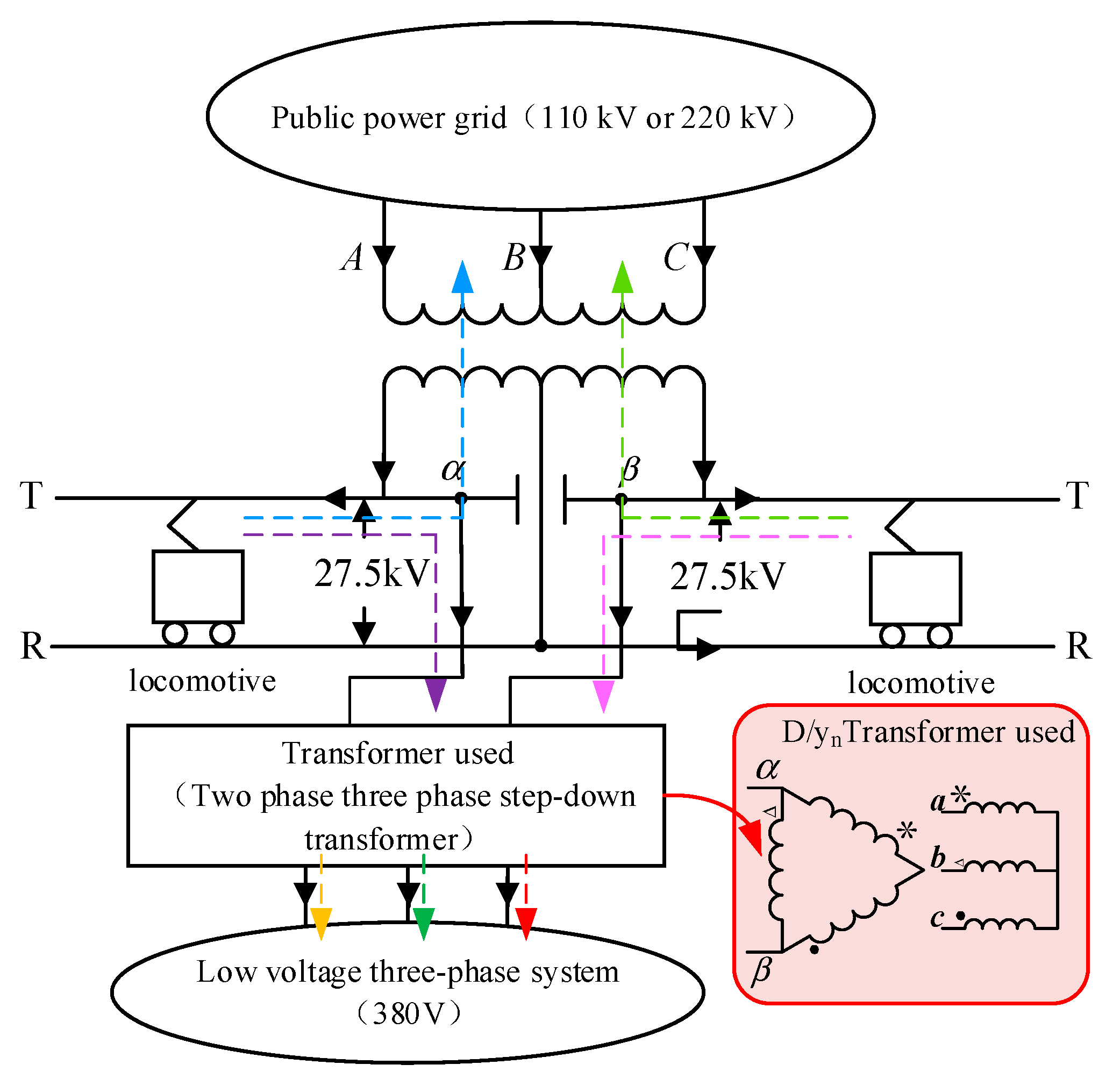
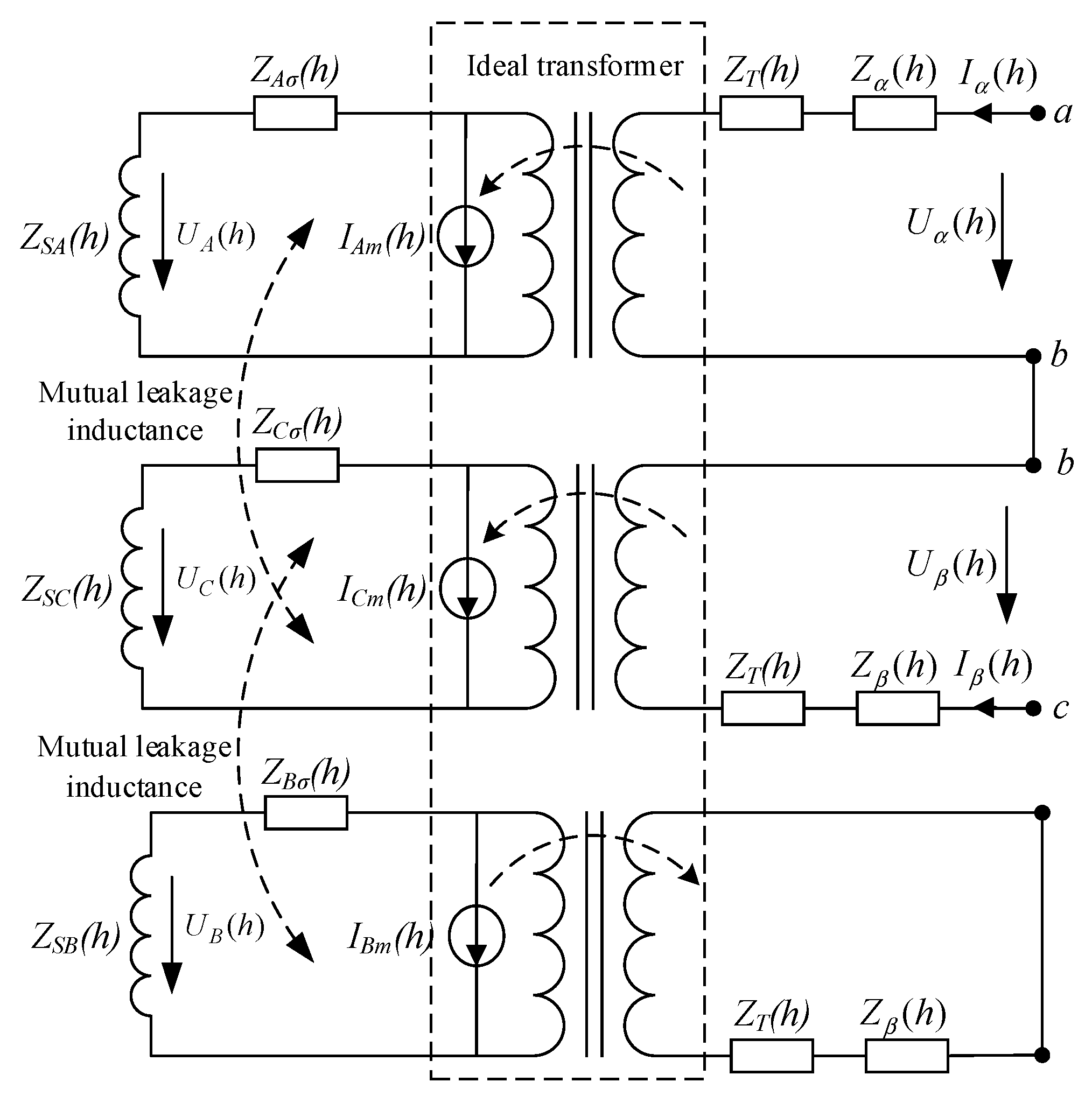
2.1. V/v Wiring Traction Substation Model

The electrified railway is composed of a primary power supply system and a traction power supply system. Traction substations, traction networks, and AC electric locomotives are included in the traction power supply system. Common transformer wiring types in traction power supply systems include V/v, V/x, YNd11, Scott, etc. Generally, V/v wiring is used in electrified railways. Therefore, the transmission path of high-order harmonic waves for the traction load under a V/v wiring traction transformer is analyzed in this paper. Figure 1 shows the internal wiring schematic diagram and phasor diagram of a V/v wiring traction transformer.

A V/v wiring traction transformer can be regarded as the series connection of the high-voltage side windings of two single-phase dual-winding transformers with an equal or unequal capacity. The high-voltage side winding ratios, denoted as w_AB and w_CB, are set to be the same, i.e., w_AB = w_CB = w₁. The common connection point o accesses phase B in the three-phase power system, and the other two terminals are connected to phase A and phase C, respectively. Traction side windings are connected in series, and the traction side winding ratios satisfy the relationship w_α = w_β = w₂. The common connection point b is connected to the rail. Terminal a, terminal c, and common connection point b constitute the α port and the β port. The traction side bus voltages are $\dot{U}$_α and $\dot{U}$_β, and the phase difference is π/3. According to the wiring diagram of a V/v wiring traction transformer, the current and voltage on the high-voltage side can be calculated as:

$$\left[\begin{array}{c}\dot{I_A}\\ \dot{I_B}\\ \dot{I_C}\end{array}\right]=\frac{1}{k_T}\left[\begin{array}{cc}1& 0\\ -1& -1\\ 0& 1\end{array}\right]\left[\begin{array}{c}\dot{I_{\alpha }}\\ \dot{I_{\beta }}\end{array}\right]$$

(1)

$$\left[\begin{array}{c}\dot{U_{\alpha }}\\ \dot{U_{\beta }}\end{array}\right]=\frac{1}{k_T}\left[\begin{array}{ccc}1& -1& 0\\ 0& -1& 1\end{array}\right]\left[\begin{array}{c}\dot{U_A}\\ \dot{U_B}\\ \dot{U_C}\end{array}\right]-\left[\begin{array}{cc}{Z}_{T_1}& 0\\ 0& Z_{T_2}\end{array}\right]\left[\begin{array}{c}\dot{I_{\alpha }}\\ \dot{I_{\beta }}\end{array}\right]$$

(2)

where $\dot{I}$_A, $\dot{I}$_B, and $\dot{I}$_C are the three-phase currents, k_T is the ratio of the primary and secondary windings calculated as k_T = w₁/w₂, and Z_T1 and Z_T2 are referred to as the impedances on the low-voltage side.

When the system impedance is taken into account, the traction side voltage is calculated as:

$$\left[\begin{array}{c}\dot{U_{\alpha }}\\ \dot{U_{\beta }}\end{array}\right]=\frac{1}{k_T}\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& -1\end{array}\right]\left[\begin{array}{c}\dot{U_A}\\ \dot{U_B}\\ \dot{U_C}\end{array}\right]-\left[\begin{array}{cc}2Z_S{}^{(2)}+Z_{T_1}& Z_S{}^{(2)}\\ Z_S{}^{(2)}& 2Z_S{}^{(2)}+Z_{T_2}\end{array}\right]\left[\begin{array}{c}\dot{I_{\alpha }}\\ \dot{I_{\beta }}\end{array}\right]$$

(3)

where Z_s⁽²⁾ refers to the impedance on the low-voltage side. Equations (1)–(3) reflect the primary side-to-side transformation relationship of a traction transformer with a V/v connection under the fundamental wave and embody the electrical coupling relationship of the fundamental wave between phase and phase or side and side.

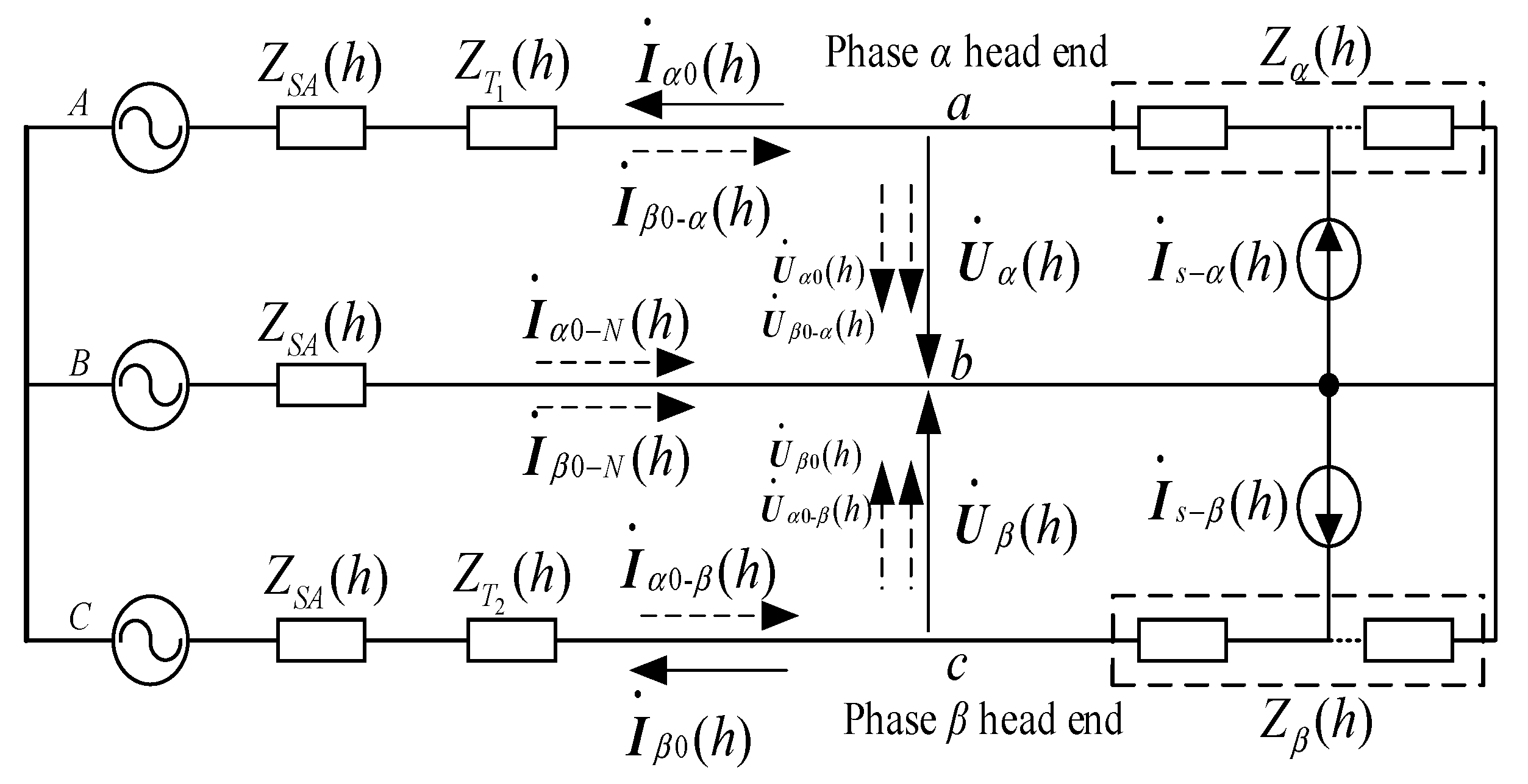
2.2. Analysis of Transverse Propagation Characteristics of High-Order Harmonics in Traction Load

The transverse propagation path of high-order harmonics based on impedance is shown in Figure 2. Z_SA-H(h), Z_SB-H(h), and Z_SC-H(h) are the equivalent system harmonic impedances of the three-phase power system. $\dot{I}$_s-α(h) and $\dot{I}$_s-β(h) are the equivalent harmonic current sources. When the phase α locomotive is running at the end of the power supply arm, its equivalent harmonic current $\dot{I}$_s-α(h) goes through the line equivalent impedance Z and the line equivalent capacitance C to the ground and arrives at the head of the phase α power supply arm to form the total feeder harmonic current $\dot{I}$_α0(h). $\dot{U}$_α0-β(h) is the harmonic voltage caused by the harmonic current $\dot{I}$_α0-β(h) from $\dot{I}$_α0(h) to phase β, which shows the harmonic transverse propagation process from phase α to phase β. The voltage distortions of the high-voltage side on phases A and B are caused by the electric coupling between the primary pair of the transformer and the traction transformer T₁. The distorted voltage drop is coupled to the traction side of 27.5 kV via the traction transformer T₂.

According to its propagation path and principle, the equivalent circuit of harmonic transversal propagation in the V/v wiring traction transformer can be established, as shown in Figure 3. In the traction power supply system, the high-order harmonics in the three-phase power system are generally small. Therefore, the influence of the harmonics from the power grid can be ignored when establishing the equivalent circuit of the transverse propagation of harmonics. The inrush current of the transformer can also be ignored.

In the equivalent circuit, Z_SA(h), Z_SB(h), and Z_SC(h) are the short-circuit impedances of the three-phase system on phases A, B, and C, respectively, referring to 27.5 kV. Z_α(h) and Z_β(h) are the equivalent line impedances of power supply arms on phase α and phase β. Z_T1(h) and Z_T2(h) are the short-circuit impedances of traction transformers T₁ and T₂ to 27.5 kV, respectively. The symmetry of the three-phase power system and the wiring structure of the traction transformer can be known, Z_SA(h) = Z_SB(h) = Z_SC(h) = Z_S(h), Z_T1(h) = Z_T2(h) = Z_T1(h) = Z_T(h), and $\dot{U}$_α(h), and $\dot{U}$_β(h) are the harmonic voltages of the α port and β port, respectively.

According to the equivalent circuit in the diagram, the circuit model can be established as:

$$\{\begin{array}{c}{\dot{I}}_{\alpha }\left(h\right)={\dot{I}}_{\alpha 0-N}\left(h\right)+{\dot{I}}_{\alpha 0-\beta }\left(h\right)\\ {\dot{I}}_{\beta }\left(h\right)={\dot{I}}_{\beta 0-N}\left(h\right)+{\dot{I}}_{\beta 0-\alpha }\left(h\right)\end{array}$$

(4)

Based on the shunting theorem under the action of impedance mechanism, when the locomotive on phase α is running alone, the harmonic current $\dot{I}$_α0-β(h) represents the propagation from phase α to phase β. When the locomotive on phase β is running alone, the harmonic current $\dot{I}$_β0-α(h) represents the propagation from phase β to phase α. The relationship can be written as:

$$\{\begin{array}{c}{\dot{I}}_{\alpha 0-\beta }\left(h\right)=\frac{Z_s\left(h\right)\times {\dot{I}}_{\alpha 0}\left(h\right)}{Z_{\beta }\left(h\right)+2Z_s\left(h\right)+Z_T\left(h\right)}\\ {\dot{I}}_{\beta 0-\alpha }\left(h\right)=\frac{Z_s\left(h\right)\times {\dot{I}}_{\beta 0}\left(h\right)}{Z_{\alpha }\left(h\right)+2Z_s\left(h\right)+Z_T\left(h\right)}\end{array}$$

(5)

Using the superposition theorem, we find that when the locomotives on both phases are running, the total feeder current of the phase α port is denoted as $\dot{I}$_α(h), and the total harmonic voltage is denoted as $\dot{U}$_α(h). Similarly, the total feeder current of the phase β port is denoted as $\dot{I}$_β(h), and the total harmonic voltage is denoted as $\dot{U}$_β(h), expressed as:

$$\{\begin{array}{c}{\dot{I}}_{\alpha }\left(h\right)={\dot{I}}_{\alpha 0}\left(h\right)-{\dot{I}}_{\beta 0-\alpha }\left(h\right)\\ {\dot{I}}_{\beta }\left(h\right)={\dot{I}}_{\beta 0}\left(h\right)-{\dot{I}}_{\alpha 0-\beta }\left(h\right)\end{array}$$

(6)

$$\{\begin{array}{c}{\dot{U}}_{\alpha }\left(h\right)={\dot{U}}_{\alpha 0}\left(h\right)+{\dot{U}}_{\beta 0-\alpha }\left(h\right)=\left[Z_s\left(h\right)+Z_T\left(h\right)\right]\times {\dot{I}}_{\alpha 0}\left(h\right)+\frac{Z_s\left(h\right)\left[Z_s\left(h\right)+Z_T\left(h\right)+Z_{\beta }\left(h\right)\right]}{Z_{\beta }\left(h\right)+2Z_s\left(h\right)+Z_T\left(h\right)}\\ {\dot{U}}_{\beta }\left(h\right)={\dot{U}}_{\beta 0}\left(h\right)+{\dot{U}}_{\alpha 0-\beta }\left(h\right)=\left[Z_s\left(h\right)+Z_T\left(h\right)\right]\times {\dot{I}}_{\beta 0}\left(h\right)+\frac{Z_s\left(h\right)\left[Z_s\left(h\right)+Z_T\left(h\right)+Z_{\beta }\left(h\right)\right]}{Z_{\alpha }\left(h\right)+2Z_s\left(h\right)+Z_T\left(h\right)}\end{array}$$

(7)

2.3. Analysis of Longitudinal Propagation Characteristics of High-Order Harmonics in Traction Load

Figure 4 shows a schematic of the direct power supply mode in the traction power supply system. There are direct or indirect coupling relationships between the locomotive, traction network, public power network (high-voltage three-phase system), and the power system used (low-voltage three-phase system). The penetration path of the high-order harmonics to the high-voltage side and the distribution side is shown by the dotted arrow.

When the high-order harmonics are propagating in the longitudinal path, the harmonic current and harmonic voltage relationships between the high and low-voltage levels can be rewritten as:

$$\left[\begin{array}{c}{\dot{I}}_A\left(h\right)\\ {\dot{I}}_B\left(h\right)\\ {\dot{I}}_C\left(h\right)\end{array}\right]=\frac{1}{k_T}\left[\begin{array}{cc}1& 0\\ -1& -1\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\dot{I}}_{\alpha }\left(h\right)\\ {\dot{I}}_{\beta }\left(h\right)\end{array}\right]$$

(8)

$$\left[\begin{array}{c}\dot{U_{\alpha }}\left(h\right)\\ \dot{U_{\beta }\left(h\right)}\end{array}\right]=\frac{1}{k_T}\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& -1\end{array}\right]\left[\begin{array}{c}\dot{U_A\left(h\right)}\\ \dot{U_B\left(h\right)}\\ \dot{U_C\left(h\right)}\end{array}\right]-\left[\begin{array}{cc}2Z_S{}^{(2)}+Z_{T_1}& Z_S{}^{(2)}\\ Z_S{}^{(2)}& 2Z_S{}^{(2)}+Z_{T_2}\end{array}\right]\left[\begin{array}{c}\dot{I_{\alpha }\left(h\right)}\\ \dot{I_{\beta }\left(h\right)}\end{array}\right]$$

(9)

The harmonic propagation path of the high-voltage side of the V/v wiring traction transformer is shown in Figure 5. The harmonic current generated on the 27.5 kV side penetrates the windings of the traction transformer and penetrates the high-voltage three-phase power system through the coupling effect of the original auxiliary side magnetism. The harmonic voltage U_x(h) (x = A, B, C) is the voltage across the equivalent leakage reactance Z_σ,_x(h) and short circuit impedance Z_S,x(h) on the high-voltage side. Since Z_σ,_x(h) is insignificant, U_x(h) can be regarded as the voltage across the leakage reactance. The dotted arrow represents the path of the high-order harmonics from the traction side to the high-voltage side.

The low-voltage distribution system of the traction substation is supplied by the 27.5 kV traction network. The D/y_n transformer wiring structure and phasor diagram are shown in Figure 6. $\dot{U}$_a, $\dot{U}$_b, and $\dot{U}$_c are the three-phase voltages for the distribution system, and the phase difference is π/3. $\dot{U}$_vw is the phase α port voltage of the traction side, $\dot{U}$_uw is the phase β port voltage of the traction side, and the phase difference is 2π/3. The number of turns of the winding on the traction side is denoted as w_α = w_β = w₁. The number of turns of the winding on the low-voltage distribution side is denoted as w_a = w_b = w_c = w₂, and the ratio is defined as k_t = w₁/w₂.

The electrical coupling relationships of the primary and secondary sides are expressed as:

$$\left[\begin{array}{c}\dot{I_{\alpha }}(h)\\ \dot{I_{\beta }}(h)\end{array}\right]=\frac{1}{k_t}\left[\begin{array}{ccc}1& -1& 0\\ 0& 1& -1\end{array}\right]\left[\begin{array}{c}\dot{I_a}(h)\\ \dot{I_b}(h)\\ \dot{I_c}(h)\end{array}\right]$$

(10)

$$\left[\begin{array}{c}{\dot{U}}_a(h)\\ {\dot{U}}_b(h)\\ {\dot{U}}_c(h)\end{array}\right]=\frac{1}{k_t}\left[\begin{array}{cc}1& 0\\ -1& 1\\ 0& -1\end{array}\right]\left[\begin{array}{c}{\dot{U}}_{\alpha }(h)\\ {\dot{U}}_{\beta }(h)\end{array}\right]-\left[\begin{array}{ccc}2Z_s{}^{(2)}+Z_{aN-vw}& Z_s{}^{(2)}& Z_s{}^{(2)}\\ Z_s{}^{(2)}& 2Z_s{}^{(2)}+Z_{bN-uv}& Z_s{}^{(2)}\\ Z_s{}^{(2)}& Z_s{}^{(2)}& 2Z_s{}^{(2)}+Z_{cN-uw}\end{array}\right]\left[\begin{array}{c}\dot{I_a}(h)\\ \dot{I_b}(h)\\ \dot{I_c}(h)\end{array}\right]$$

(11)

where Z_xN-vw, (x = a, b, c) is the short-circuit impedance referring to the low-voltage side between the traction side winding and the low-voltage side winding.

3. Impedance Identification Based on the SVD Algorithm

In the traction power supply system, high-order harmonics show harmful effects on high-voltage side electrical equipment and electric locomotives. Most current studies are limited to the traction side (27.5 kV) and public grid side (110 or 220 kV). The effect of high-order harmonics on the low-voltage 380 V side is not considered. At present, there are few methods for dealing with the high-order harmonics in the low-voltage self-service power system and for identifying the parameters of harmonic impedance. In this section, a simulation model of a traction power supply system based on V/v wiring is established in MATLAB/Simulink. The influence of high-order harmonics on low-voltage power supply systems is analyzed. A parameter identification method based on SVD for harmonic impedance with a self-service load is proposed.

3.1. Influence and Key Factor Analysis Based on Simulation Data

A simulation model of a low-voltage self-consumption power system was built using MATLAB/Simulink. Key factors, such as transformer capacity, line length, and locomotive positions, affect the low-voltage system and are discussed in this section. Based on the simulation model, the results of the 31st, 33rd, 35th, 37th, 39th, and 41st harmonics of the 27.5 kV side on the low-voltage self-consumption power system are studied.

Figure 7a presents the effects of high harmonics on low-voltage self-powered systems under different capacities of a transformer of the D/yn type. With the increase in capacity of the transformer, the main harmonic content of the three-phase voltage increases. However, with the increase in capacity, the harmonic content increases slowly and gradually moves towards saturation. When the selected capacity of the transformer is smaller than 200 kVA, the high-order harmonic content of the three-phase voltage from the 27.5 kV traction side to the low-voltage self-service power system is greatly affected by the selected capacity of the transformer. When the transformer capacity is larger than 200 kVA, the influence of the harmonic is small.

Figure 7b shows the relationship between the harmonic voltages and line length which can be used to study the influence of high harmonics on a low-voltage self-powered system when the locomotive is located at the end of the line under different line lengths. The V/v wiring traction transformer capacity is set to 100 kVA. It can be seen that the harmonic voltages show different peak values for different orders. The largest peak value is observed in the 35th harmonic voltages located at 40 km of line length, equal to 426 V. The peak values of the 35th, 37th, 39th, and 41st harmonic voltages appear at 35 km. The peak values of the 31st and 33rd harmonic voltages appear at 45 km. Compared with the 35th harmonic voltages, the other harmonic voltages have less influence on the three-phase voltage.

Figure 7c shows the analysis of the impact on the low-voltage self-powered system when the locomotive is in different positions. The length of the power supply arms on both sides of the traction transformer was fixed at 40 km, all other parameters were kept constant. The position of the locomotive at the head of the line (traction substation) was changed to study the influence of high harmonics on the low-voltage self-powered system when the locomotive is at different positions on the line. In Figure 7c, harmonic voltage peaks all appear in the 35th harmonic, and their value increases with the location, with the maximum value of 410 V at 40 km, and the minimum value of 150 V at 0 km.

Therefore, the influence of key factors can be summarized as:

(1)

The size of high-order harmonics in the low-voltage three-phase system will be affected by the capacity of the transformer used. When the capacity is small, the impact is greater, but when the capacity is large, there is no significant impact;

(2)

The magnitude of the higher harmonics in the low-voltage three-phase system is greatly affected by the length of the line and the location of the locomotive.

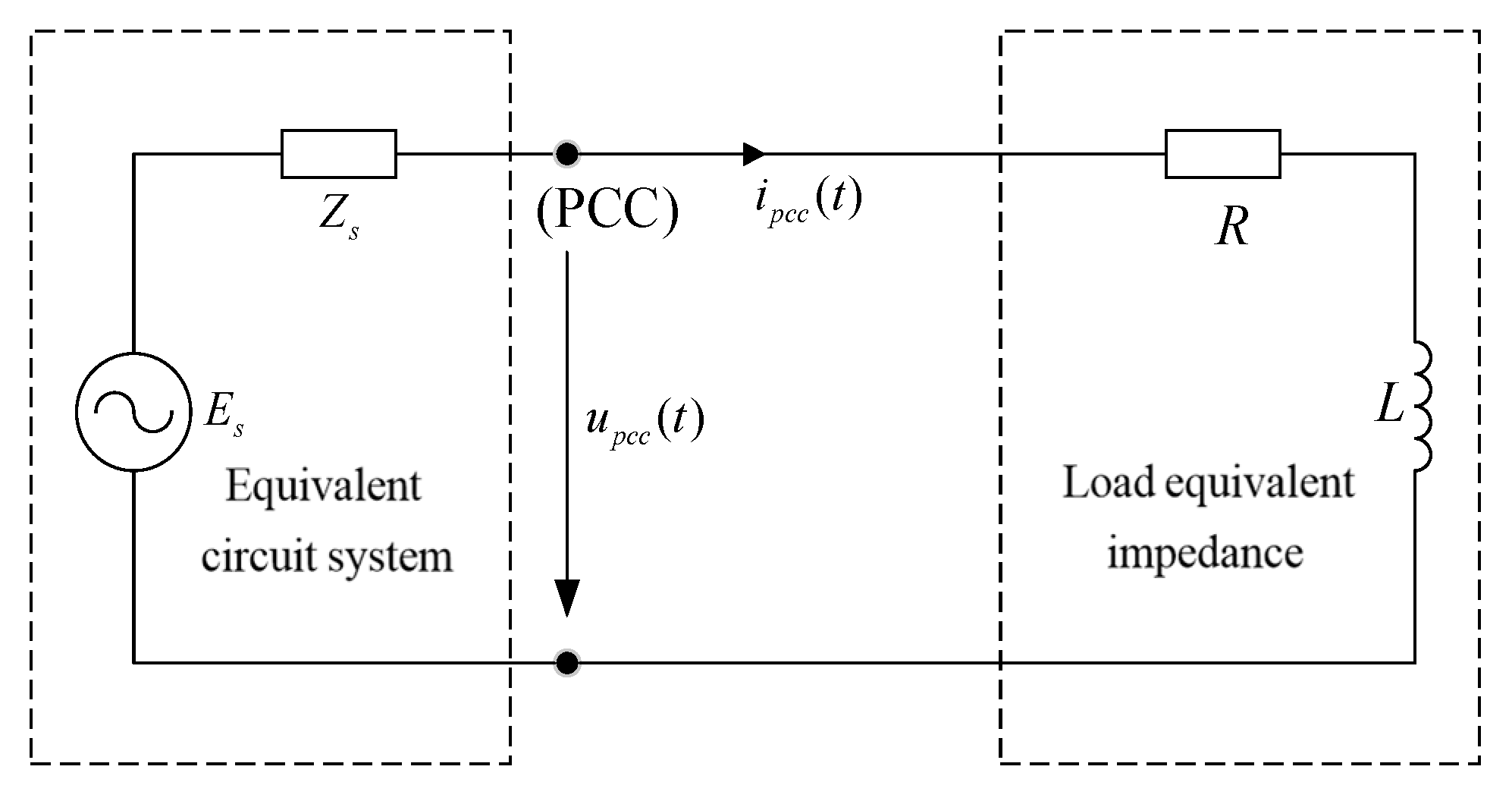
3.2. Mathematical Model and Circuit Model of a Low-Voltage Self-Use Power System

Taking the unknown circuit as the black box, the port voltage u_pcc and current i_pcc are regarded as the output and input variables, respectively, as shown in Figure 8. In the low-voltage power distribution system, the inductive load can be considered the majority part. Therefore, the load model can be equivalent to the impedance representation of the resistance and the inductance in series. This load can be equivalent to an inductive RL load. When the inductance L is negative, the load is capacitive.

The dynamic model of the port voltage can be described as:

$$u_{PCC}(t)=R(t)i_{PCC}(t)+L(t)\frac{\mathrm{d}{i}_{PCC}(t)}{\mathrm{d}t}$$

(12)

Compared with the grid frequency, the sampling frequency is very high. Therefore, the load parameters can be regarded as constant, which can be calculated as:

$$\left[\begin{array}{c}R(t)\\ L(t)\end{array}\right]={\left[\begin{array}{cc}{i}_{PCC}(t_1)& i^{\prime }{}_{PCC}(t_1)\\ i_{PCC}(t_2)& i^{\prime }{}_{PCC}(t_2)\end{array}\right]}^{-1}\left[\begin{array}{c}{u}_{PCC}(t_1)\\ u_{PCC}(t_2)\end{array}\right]$$

(13)

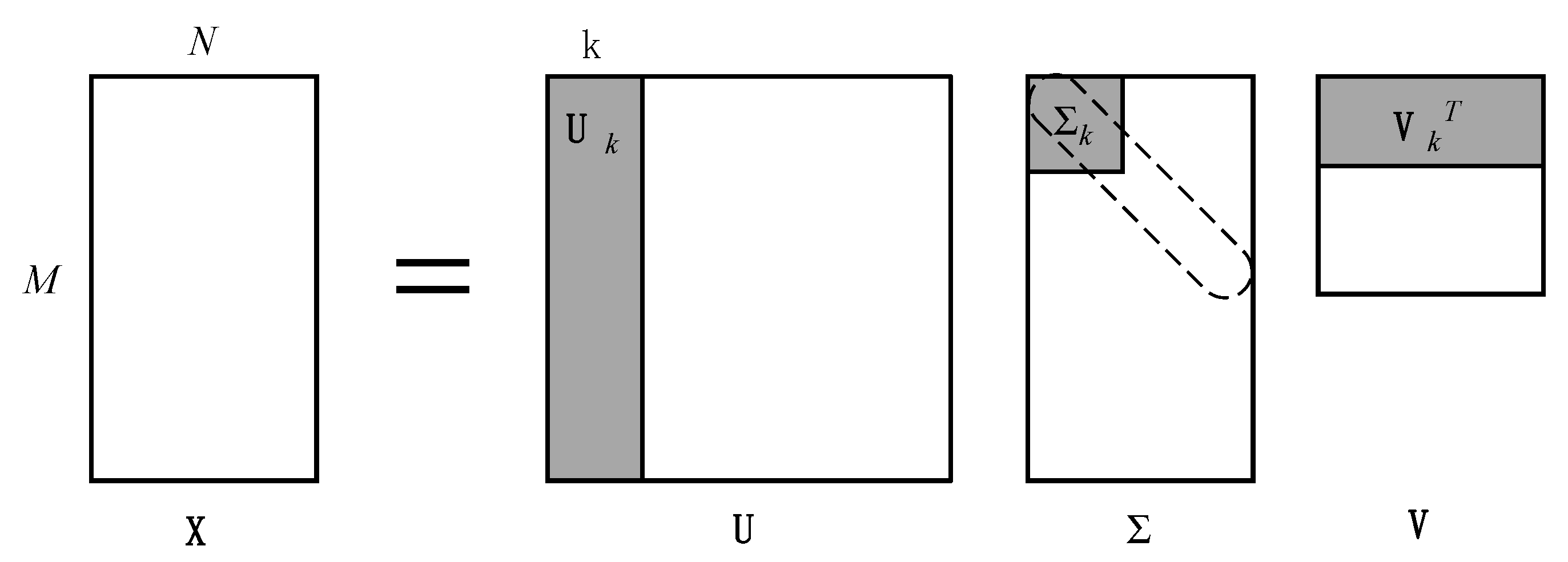
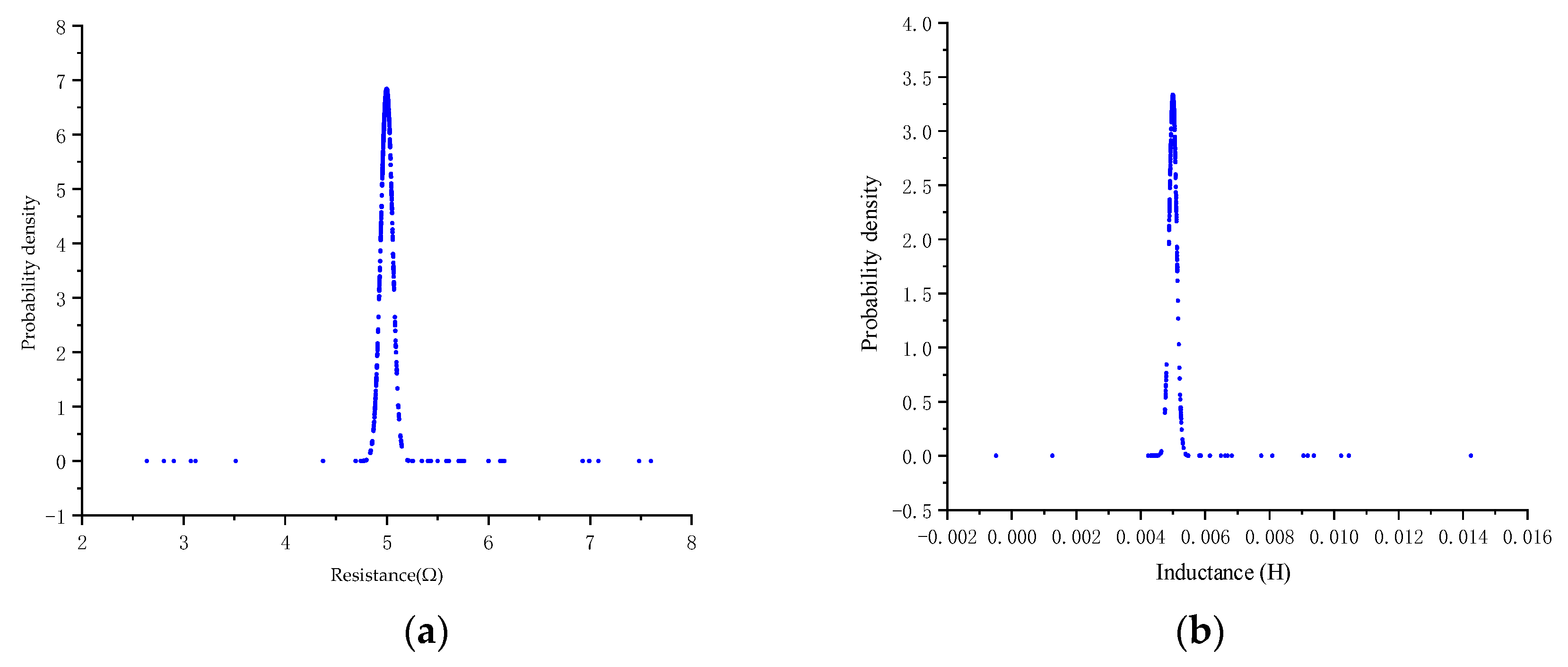
3.3. Parameter Identification Method Based on Singular Value Decomposition

The SVD transformation is essentially a method of orthogonal transformation of a matrix. By multiplying an orthogonal matrix on the left and an orthogonal matrix on the right, the square matrix can be transformed into a diagonal matrix. The rank of the matrix is equal to the number of non-zero singular values. Let X be a matrix of order M × N with rank r, then there is an M-order orthogonal matrix U, whose columns consist of the eigenvectors of XX^T, and an orthogonal matrix V of order N, and its rows consist of the eigenvectors of X^TX:

$$U^{\mathrm{T}}XV=DX=UD{V}^{\mathrm{T}}$$

(14)

$$D=\left[\begin{array}{cc}{\sum }_r& 0\\ 0& 0\end{array}\right],{\sum }_r=diag\left({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_r\right)$$

(15)

σ_i =$\sqrt{{\lambda }_i}$(i = 1,2,…,r), λ₁ ≥ λ₂ ≥ … ≥ λ_r > 0. Call σ_i the singular value of X, and λ_i is the non-zero eigenvalues of the matrix X^TX.

$$X=UD{V}^{\mathrm{T}}$$

(16)

Figure 9 shows a schematic of the SVD algorithm. U = (U_k, U_l), U_k is a matrix of the m × k order. U_k is composed of the orthogonal vector sets of the first k columns in U. V = (V_k, V_l), V_k is a matrix of the n × k order. V_k is composed of the orthogonal vector sets of the first k columns in V. If the generalized inverse of the matrix X is defined as:

$$X^{-1}=V_k{\sum }^{-1}{U}_k{}^{\mathrm{T}}$$

(17)

then the system of linear equations solution Xz = B can be expressed as:

$$z=X^{-1}B=V_k{\sum }^{-1}{U}_k{}^{\mathrm{T}}B$$

(18)

Singular value decomposition is a decomposition method that can be applied to any matrix. It can solve the matrix ill-condition problem caused by an improper sampling frequency. Moreover, the matrix ill-condition can be measured. A unique least norm solution in the least square solution can be obtained, which makes the identification result more accurate.

Case I: No background harmonic

The load is set to be a three-phase inductive load, where R = 5 Ω and L = 5 mH. By using the SVD algorithm, the equivalent parameters of the model are identified, as shown in Figure 10. The average value of resistance value identification is 4.9994 Ω, and the average value of inductor identification is 5 mH. The load parameters identified by the SVD algorithm are similar to the parameter values in the simulation model.

Case II: Background harmonic included

The 3rd, 5th, 9th, 28th–31st, and 35th–44th harmonics are added to the simulation model, and the load simulation parameters are set to R = 5 Ω, L = 5 mH. The parameters of resistance and inductance will fluctuate due to the influence of the background harmonic. Figure 11 shows the probability density curve of the identified resistance value versus the inductance value, resistance R~N (4.9996, 0.0583²), and inductance L~N (0.0049979, 0.0001197²).

4. Overvoltage Identification Based on Deep Learning

There are various types of overvoltages in the traction power supply system. Based on deep learning, the identification method of high-frequency resonance overvoltage in the high-voltage electrical system of EMUs is studied. The ShuffleNet CNN is used to identify and classify high-frequency resonant overvoltage and other overvoltages.

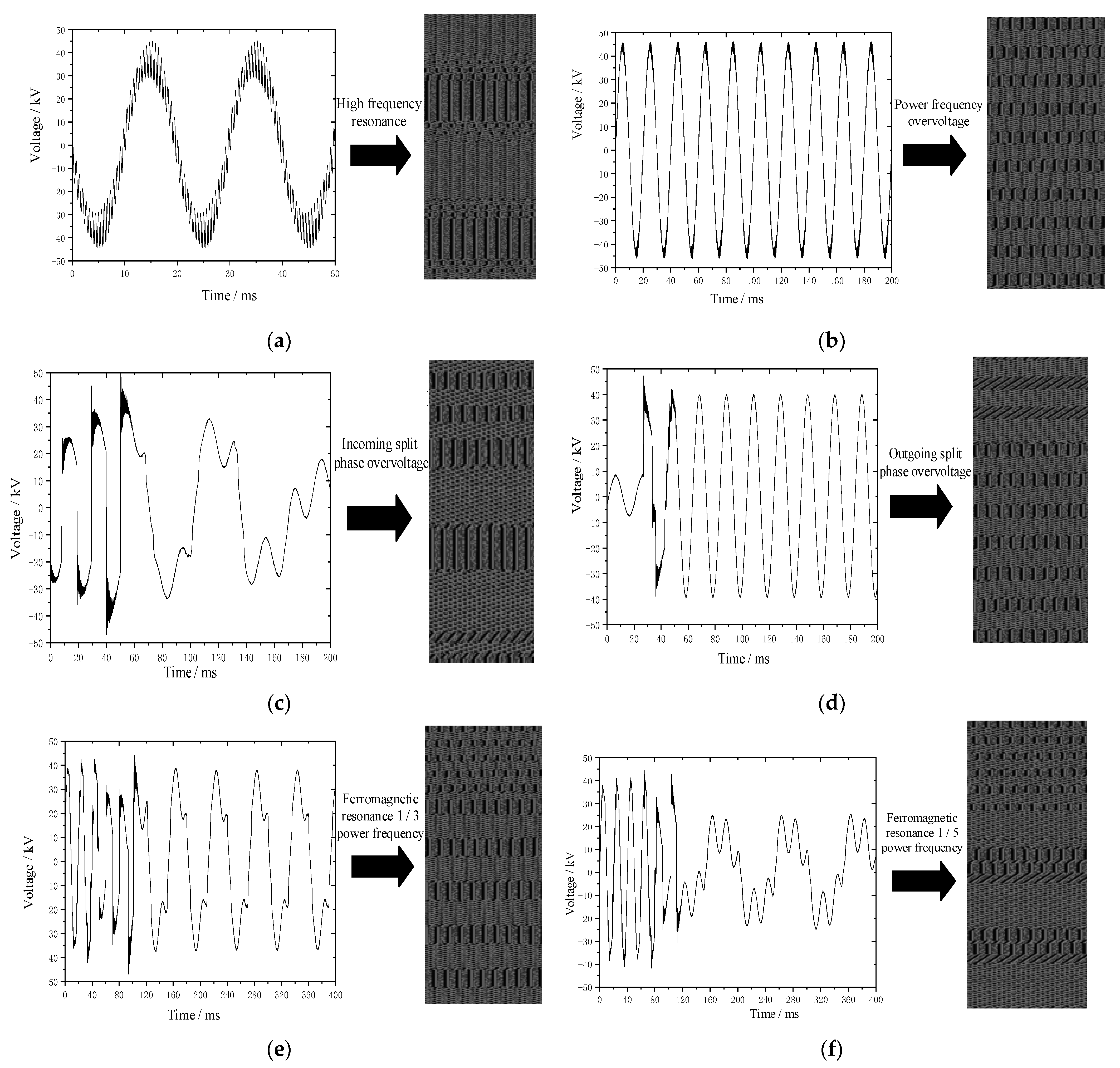
4.1. Overvoltage Grayscale Image Mapping Algorithm

The grayscale image mapping algorithm is used to convert the overvoltage raw data into a grayscale image. Figure 12 shows different types of overvoltage and their corresponding grayscale images. It can be seen that the images of various overvoltages are different, which provides a basis for identifying overvoltage.

4.2. Overvoltage Identification Based on ShuffleNet

ShuffleNet network architecture is a computing method with high computational accuracy and low computational cost. Based on the measured data of China Railways High-speed 5 (CRH5) EMUs in Shenyang EMUs, 271 overvoltage samples were sent into the model for identification: 190 samples were selected randomly for training, and the remaining were used for further testing. The learning rate was set to be 0.0004, the batch size was 50, the texture number was 4000, and the iteration number was 250. The model identification results are shown in

Table 1. The results of model classification.

Type	Actual Value	Predictive Value	Correct Rate
High-frequency resonance overvoltage	10	10	100%
Power frequency overvoltage	24	24	100%
Entering neutral section overvoltage	11	9	82%
Out neutral section overvoltage	20	20	100%
Ferroresonant overvoltage (1/3 power frequency)	19	19	100%
Ferroresonant overvoltage (1/5 power frequency)	27	27	100%

.

There are 11 entering neutral section overvoltages in the model. The number of correct identifications is nine, leading to an accuracy rate equal to 82%. By analyzing the incorrectly identified entering neutral section overvoltages, it was found that this type of test data has no obvious characteristics in the time domain, and the high-frequency content of the data classifies it as a type of high-frequency resonant overvoltage. The remaining five types of overvoltage can reach an accuracy rate of 100%.

In addition, the classification index and classification performance of the model are analyzed according to the confusion matrix. The confusion matrix usually has four indexes: precision, recall, specificity, and accuracy. The precision is the proportion of model predictions that are correct among all outcomes whose predicted values are in the category. The recall is the proportion of model predictions that are correct among all outcomes whose true values are in the category. The specificity is the proportion of model predictions that are correct among all outcomes whose true values are not in the category. The accuracy is for the whole model and refers to the proportion of all correctly judged outcomes of the classification model compared to the total number of observations.

Table 2. Confusion matrix classification index.

Type	Precision Rate	Recall Rate	Specificity	Accuracy Rate
High-frequency resonance overvoltage	100%	100%	10%	98.44%
Power frequency overvoltage	100%	100%	4%
Entering neutral section overvoltage	82%	100%	0%
Out neutral section overvoltage	100%	100%	0%
Ferroresonant overvoltage (1/3 power frequency)	100%	100%	0%
Ferroresonant overvoltage (1/5 power frequency)	100%	93%	0%

shows the results of the confusion matrix classification index. For each overvoltage category, the accuracy rate is 100%. except for the entering neutral section overvoltages, the recall rate is 100% except for the ferroresonant overvoltage (1/5 power frequency), the specificity is at a low level, up to 10%, and the overall accuracy of the overvoltage classification model reaches 98. 44%.

To verify the classification performance of this model, results obtained from six machine learning models were compared with the proposed method, including decision tree, Naive Bayes, random forest, support vector machine, logistic regression, and K nearest neighbor. The comparative results are shown in Figure 13. The recognition accuracy of the model in this paper is higher than that of the other six methods when the number of textures changes, with an average accuracy of 94%.

Table 3. The results of different classification models.

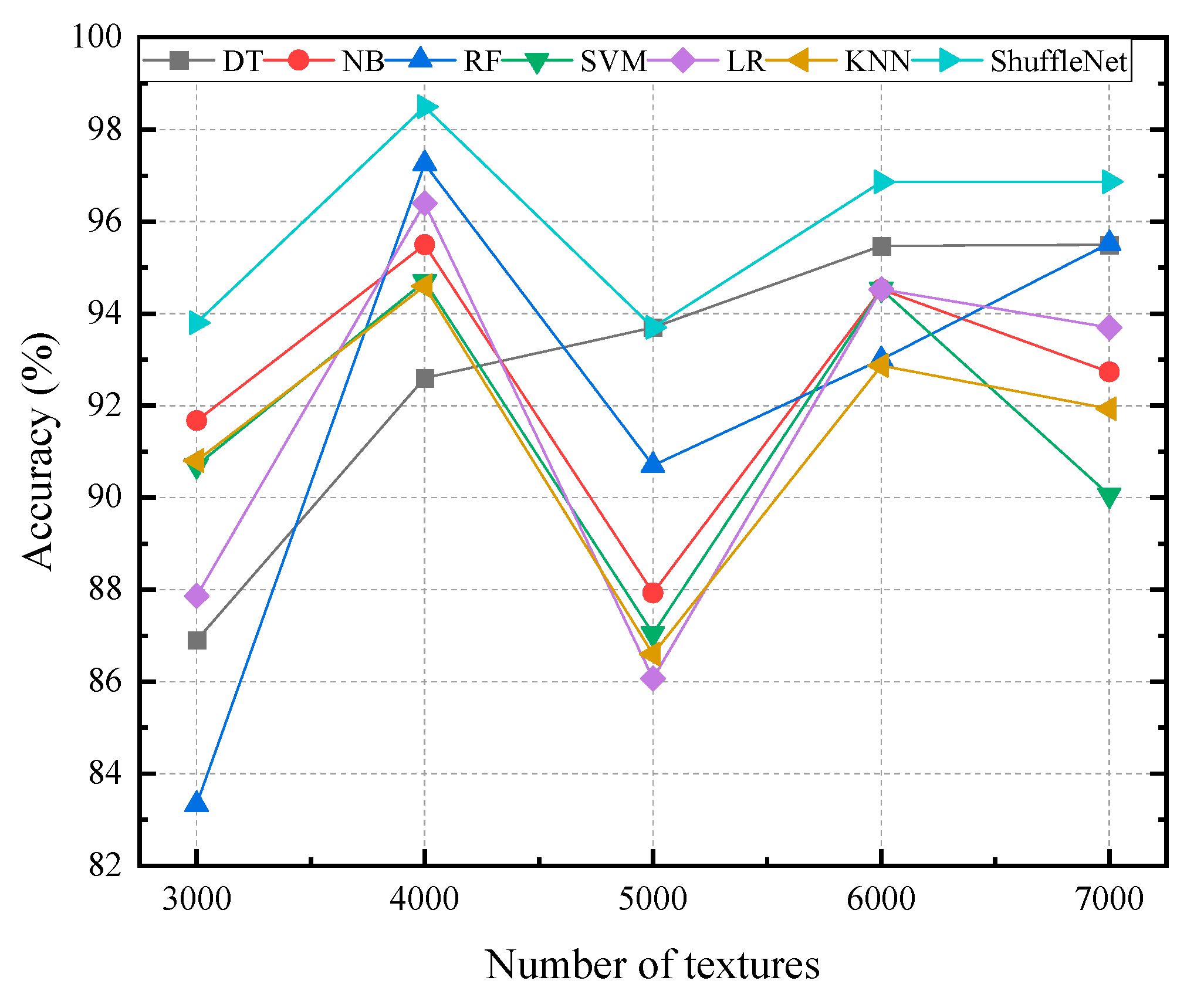
Textures Number	Decision Tree (DT)	Naive Bayes (NB)	Random Forest (RF)	Support Vector Machine (SVM)	Logistic Regression (LR)	K Nearest Neighbor (KNN)	ShuffleNet (Proposed)
3000	92.59	83.33	91.67	90.74	87.86	90.74	93.75
4000	95.50	95.50	97.3	94.77	96.40	94.77	98.44
5000	87.04	89.76	90.74	87.04	86.11	86.59	93.75
6000	95.50	94.59	93.69	94.59	94.59	92.79	96.88
7000	93.69	92.70	95.50	90.10	93.69	91.89	96.88

shows the results of the different classification models. The accuracy can be improved to 98.44% when the number of textures is 4000. Therefore, the method proposed in this paper has a superior recognition ability.

In this paper, six common types of overvoltage in the high-voltage electrical system of electric locomotives are selected. Based on the measured waveform data, a method of overvoltage identification is proposed. Using the B2G algorithm, the measured overvoltage waveform data is converted into a grey-scale image with a grey-scale value of 0–255 for each pixel point, and the features are selected and downscaled. The ShuffleNet lightweight CNN-based overvoltage recognition method is proposed. This method considers the effect of different model parameters on classification performance. It can identify the overvoltage type quickly and accurately with a small data set. The method proposed can also be applied to the identification of many other overvoltage types.

5. Conclusions

The propagation path and the transmission mechanism of the high-order harmonics of the traction load are analyzed in this paper, and an arrangement plan for the measurement points of high-order harmonics is proposed. The key factors affecting the low-voltage self-consumption power system by high-order harmonics are quantitatively analyzed, and an equivalent circuit model of the low-voltage load is established. The method of singular value decomposition is used to identify the harmonic impedance parameters of the low-voltage self-consumption power load.

Six common overvoltage types in the high-voltage electrical system of an electric locomotive are selected to analyze the generation mechanism of overvoltage and its time-frequency domain characteristics. An overvoltage identification method based on ShuffleNet lightweight CNN is proposed, which comprehensively considers the influence of different model parameters on classification performance. The results show that the proposed method can identify overvoltage types in small data sets quickly and accurately. The method proposed in this paper can be applied to the identification and classification of other overvoltage types. Simultaneously, the complexity of extracting feature information manually can be avoided with this method.