Principles of Magnetohydrodynamical Control of Internal and External Supersonic Flows

Abstract

This paper demonstrates the possibility of active magnetohydrodynamic (MHD) control of supersonic flows containing shock waves. The shock wave configurations that occur at the inlet to a supersonic diffuser and in front of a streamlined semicylindrical model are used for the purpose of investigation. The impact is carried out by organizing local gas discharge regions when applying a magnetic field transverse to gas discharge currents. It has been shown that by changing the local region of application, the intensity and the direction of the gas discharge currents, it is possible to change the intensity and direction of the ponderomotive force acting on the gas flow during MHD interaction. The ponderomotive force control allows for acting locally on the shape and position of shock waves, the speed and direction of the flow, and the increase or reduction of pressure near the surface of the streamlined body. The experiments were carried out on a gas dynamic setup based on a shock tube in a gas dynamic path, capable of creating supersonic flows in a wide range of Mach numbers at M = 4–7. There was a possibility of organizing the electric and pulsed magnetic fields with an intensity of up to 1.5 T. The given experimental Schlieren flow patterns and the analysis of the obtained data demonstrate the MHD effect on: the change in the angle of inclination of the attached shocks, both into increase and decrease; the bow shock wave approaching the body or the removal from it; and the change in the aerodynamic drag and lift force of the streamlined bodies.

1. Introduction

Magnetic gas dynamics is one of the promising areas of modern science, and interest in this area of physics is constantly growing. Most of the experimental work in the field of magnetic gas dynamics is aimed at studying the magnetohydrodynamic (MHD) interaction in a continuous flow. This paper considers the MHD effect on a supersonic flow containing shock waves. This is a new line of research in magnetic gas dynamics, caused by the need to control the shock wave configurations in supersonic diffusers and the bow shock wave that occurs during supersonic flow around bodies.

One of the most important problems is the regulation of the position of the attached shock waves that occur at the inlet to the air intake of supersonic aircraft. When the altitude and flight speed of the aircraft change, the position of the shocks changes, while the total pressure in the air intake and the oxygen consumption during fuel combustion change. The system exits the design mode and it becomes necessary to return the shock waves to their original position. The rapid adjustment of inlet devices at supersonic flight speeds by mechanical means becomes ineffective, and alternative control systems are required.

The task of controlling the position of the bow shock wave is also of relevance. This occurs in supersonic flight at the nose of the aircraft as well as at the wing, thereby increasing the size of the device and, consequently, the aerodynamic drag. Rapid control of the position and size of the head wave will also allow for changing the aerodynamic drag. Therefore, it is necessary to develop non-mechanical methods for controlling supersonic flow. In this paper, the control of a weak ionized supersonic flow containing shock waves using the MHD method is considered.

The main problem for experimental gas dynamic studies is the creation of supersonic flows with large Mach numbers. In addition, an experimental study of the possibility of using magnetohydrodynamics for flow control implies the availability of electromagnetic equipment for creating powerful magnetic fields with a magnetic induction of more than 1 T, as well as powerful electric fields. This reduces the range of experimental work and leads to the predominance of computational work in this area. The theoretical foundations for the application of the magnetohydrodynamic method for changing the parameters of a supersonic flow were proposed in [1,2,3,4]. The works were mainly devoted to the MHD effect on the flow parameters around blunt bodies, due to the magnetically induced EMF that occurs when an ionized flow moves in a transverse magnetic field. The theoretical development of this method was continued in works [5,6,7], including on the flow around a cylinder [8]. The theoretical concept of a plasma probe to magnetically influence or control weakly ionized free-stream plasma flows is presented in [9].

Initial quantitative measurements of the change in the bow shock standoff distance upon application of the magnetic field were made in [10]. Experimentally, the possibility of MHD control of the flow around a semicylindrical body with artificial generation of gas discharge currents was shown in [11]. The results of an experimental study on the MHD control of the bow shock wave in the case of a supersonic flow of a weakly ionized gas around a blunt body are given in [12]. Works on the study of the MHD effect on a supersonic flow were carried out in [13], in order to increase the aerodynamic drag of bodies entering the dense layers of the atmosphere. The idea of implementing an MHD parachute was used, theoretically developed in [14,15,16] and further continued in [17], where the position of the bow shock wave in the MHD interaction was theoretically calculated. An unsuccessful attempt to experimentally measure the magnetohydrodynamic force capable of changing the aerodynamic drag was made in [18]. In paper [19], the main applications of plasma and MHD in hyper/supersonic inlet and dynamics models were introduced. The review paper [20] summarizes and discusses the developments on MHD flow control technology based on high temperature real gas effect, including the experimental technique, numerical method, and the influence rules and dynamics mechanism of MHD flow control. Its development trend is also discussed and prospected in the paper.

The main goal of this work is to study the possibility of controlling the position of shock waves under the influence of external electric and magnetic fields. The objects of the study are a shock wave configuration in the form of two attached shocks that occur at the entrance to a supersonic diffuser, and a bow shock wave that occurs in a supersonic flow around a blunt semi-cylindrical aerodynamic model. The main task of the experiment is to reveal the main patterns of the impact of external fields on the position of shocks, and to find a way to most effectively apply these impacts. The use of the MHD method to control supersonic flows is based on the force action from the ponderomotive force F_L = j × B. Vector j has the value of density of the electric current that has arisen spontaneously during the MHD interaction (magnetically induced) or was created from an external source. This vector has the direction of the current and is perpendicular to the magnetic induction vector B. The ponderomotive force acts on the gas flow, and arises as a result of the redistribution of the Lorentz force. It is acting on moving charged particles in a transverse magnetic field during the exchange of energies in collision processes. The direction of the vector F_L is perpendicular to both vectors j and B. The flow in the action area must be ionized.

An inert gas xenon is used for the study which, compared to air, has a relatively slow recombination rate [21]. This makes it possible to preserve the previously created ionization, and to have a conductivity sufficient for MHD experiments in the impact zone. This approach makes it possible to simulate aerodynamics for internal and external supersonic flow according to the main similarity criteria: the Mach number, the MHD interaction parameter, the thermal effect parameter, and the Hall parameter using an inert gas.

The main advantage of magnetohydrodynamic (MHD) action in comparison with mechanical methods of flow control is speed. In addition, with a special organization of gas discharge currents, the MHD effect (in contrast to the mechanical one) does not depend on either the flow velocity or the angle of attack of the oncoming flow, and can have a wider range of applications at supersonic flows control.

2. Experiment Arrangement

2.1. Experimental Setup Parameters

Figure 1 shows a diagram of an experimental setup based on a shock tube. This consists of a high-pressure chamber 1, a low-pressure chamber 2 and a specially designed vacuum working chamber 7. A flat supersonic nozzle 4 with an inclination angle of 11⁰ and an aerodynamic model: supersonic diffuser 6 is used to study flow control in internal flow, while a semi-cylindrical model is used to study external flow. The shock-compressed gas in the shock tube is decelerated at the end of tube 3, thermally ionized, and then entered in the nozzle through the inlet slot and then to the model, where the impact is carried out and studied. The magnetic field in the direction transverse to the flow is created in the entire volume of the working chamber, with the help of special Heimholtz coils located on its sides. The diameter and distance between the coils were chosen so as to create a uniform magnetic field in the entire region of the studied flow. The maximum possible value of the magnetic induction is 1.3 T. The duration of the stationary stage of the magnetic field, when the magnetic induction can be considered constant, corresponds to the duration of the ionized flow around the body. This is about 600 μs and determines the time of the investigation in one experiment. To close the magnetically induced current and to create gas discharge currents of various configurations, specially mounted electrodes are used, with the possibility of applying an external voltage to them.

Figure 1 shows the main dimensions of the installation, as well as the calculated deceleration parameters. These are the initial parameters at the entrance to the nozzle, and the parameters at the nozzle exit before entering the diffuser. The xenon used as a working gas makes it possible to maintain a high conductivity at the nozzle outlet. The flow at the nozzle outlet remains ionized with a conductivity of 600 S/m.

2.2. Visualization of the Flow Structure

In order to visualize the structure of the flow, a Schlieren installation for visualizing high-speed flows is used, the scheme of which is shown in Figure 2.

The operation of the installation is based on the deviation of the transmission radiation from the laser on the density gradients of the object under study [22]. The entrance slit is illuminated by laser radiation from a CW laser with a wavelength of 532 nm. The objective L₂ with a diameter D₁ = 110 mm, located at a focal length F₁ = 900 mm from the slit, forms a parallel beam of light passing through the object under study O. Exactly the same lens L₃ (F₂ = 900 mm, D₂ = 110 mm) collects the radiation that has passed through the observation area in its focal plane, in which the knife K is placed, covering half of the image of the entrance slit. The recording system is a high-speed intensified CCD camera PCO hsfc pro, which allows for obtaining up to six Schlieren patterns during the experiment with different duty cycles and exposures. To combine the recording system of the high-speed camera with the Schlieren system, an additional lens L₄ and distances from the object under study to the lens L₂ were chosen. This is so that a clear image of the region under study, with a size corresponding to the size of the recording matrix could be selected, while not blocking the illuminating laser radiation. When the process under study proceeds in the observation area, the illuminating laser radiation is refracted by density gradients, deviates from the propagation axis, and is overlapped by a knife, thereby visualizing gas density discontinuities, including shock waves.

3. MHD Interaction in a Supersonic Diffuser

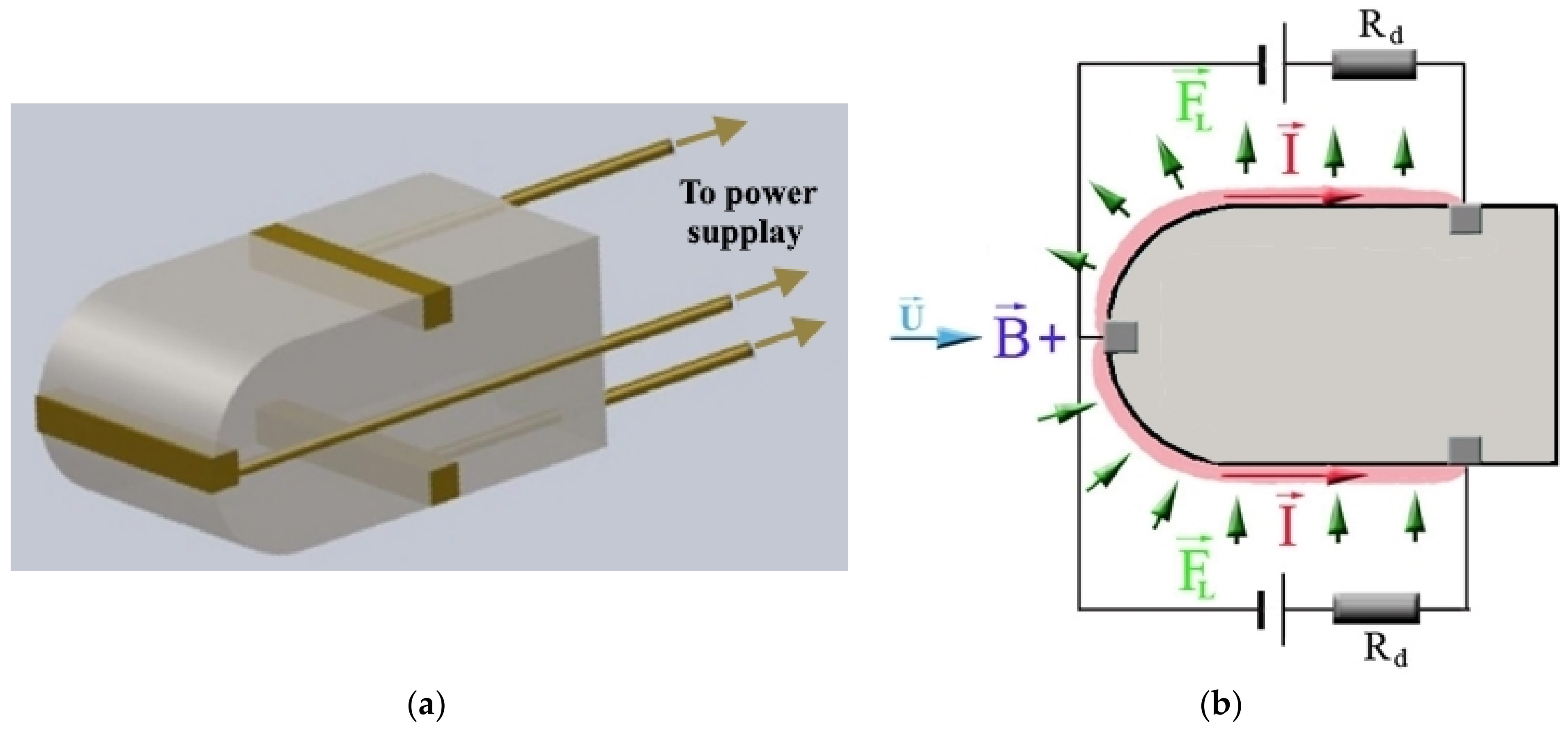
3.1. Model Description

Figure 3 shows the diagram of the nozzle and the location of the diffuser in more detail. The shock wave configuration under study is the two attached shocks that appear at the diffuser inlet. Brass electrodes are mounted in the walls of the nozzle and the diffuser over the entire width of the flow.

When the ionized gas moves in the channel in a transverse magnetic field, an electromotive force (EMF) ε = uBh arises (where u is the flow velocity, B is the magnetic induction vector, and h is the distance between the electrodes), separating charges in opposite directions. When a magnetically induced current or a current from an external source is closed through the electrodes, the ponderomotive force F_L will act on the flow. The speed of the oncoming flow will change, while the position of the attached shocks will also change.

The obtained Schlieren pattern of the flow in the absence of external influences is shown in Figure 4a. This is the initial position of the attached shocks. Figure 4b shows the layout of the shocks and the parameters that were used to characterize the degree of change in their position. This is the distance X_c from the entrance to the diffuser to the point of intersection of the shocks, the angle α at which the shocks meet, and the angle of inclination of the shock to the diffuser wall φ. Here the initial experimental values of these parameters are shown, 2α = 42°, X_c = 42 mm, φ = 15.5°. The main experimental problem for MHD flow control in this case is to change the angle of inclination of the attached shocks, both into increase and decrease.

3.2. Organization of MHD Impact

A preliminary study of the current-voltage characteristics showed that due to the large near-electrode and near-wall layers in this configuration of the diffuser, it is impossible to close the magnetically induced current. Therefore, studies are carried out both with the imposition of external magnetic and external electric fields. This approach has some advantages, since it provides wider opportunities for research. In particular, there is the opportunity to investigate not only the braking, but also the accelerating effect of the pondermotive force. This is not possible when only the magnetically induced current is closed, or when the ponderomotive force works only for braking.

An external electric field is created by applying an external voltage to the electrodes from specially created LC circuits. The current is closed through a circuit consisting of an interelectrode plasma gap with resistance R_eff and a load resistance R_L. The current configuration can be changed by connecting different pairs of electrodes. The gas discharge current closes without keys at the moment when ionized gas enters the interelectrode gap. The external voltage connection diagram and the direction of action of the ponderomotive force in the case of a transverse circuit of the current, when the upper electrode is the cathode, are shown in Figure 5a. With such a circuit, the current from the external voltage coincides in direction with the magnetically induced current, and the ponderomotive force acts to decelerate the flow. If the current is directed in the opposite direction, as shown in the following Figure 5b, the ponderomotive force works to accelerate the flow. Similarly, it is possible to connect any number of electrodes in different areas of the diffuser. It is possible to circuit both the transverse and longitudinal current. The numbering of electrodes adopted in the work is also indicated in the figures.

The equivalent circuit for connecting magnetically induced EMF ε and external voltage V for such a circuit is shown in Figure 5c. Here the LC circuit is represented as an external source of EMF, supplying a voltage V to the electrode circuit. It is connected in series with an MHD generator with ε = uBh and internal resistance R_eff, which is the sum of the volume resistance of the plasma gap between the electrodes. The total value of the EMF and the applied voltage is partly applied to the load resistance R_L, and partly to the internal resistance of the interelectrode gap R_eff. Ohm’s law in this case is:

uBh ± V = V_pl + V_R,

(1)

where the voltage drops across the internal resistance:

$$V_{pl}=I{R}_{eff}=\hspace{0.17em}(1\hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}k)(uBh\hspace{0.17em}\hspace{0.17em}\pm \hspace{0.17em}\hspace{0.17em}V),$$

(2)

voltage drop across the load:

$$V_R=I{R}_L=\hspace{0.17em}k(uBh\hspace{0.17em}\hspace{0.17em}\pm \hspace{0.17em}\hspace{0.17em}{V}_{}),$$

(3)

k is the load factor:

$$k\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\frac{R_L}{R_L\hspace{0.17em}+\hspace{0.17em}{R}_{eff}},$$

(4)

The “+” sign before V means the MHD brake, the “−” sign means the MHD accelerator. The main factors affecting the flow structure under the action of external fields are the work of the ponderomotive force, which either slows down or accelerates the supersonic flow depending on the direction of the current; Joule heating of the gas in the external and magnetically induced electric fields, which always leads to deceleration of the supersonic flow; and the influence of the near-wall layer. The Stewart parameter is chosen as a parameter characterizing the force effect. It is the ratio of the work of the ponderomotive force over the length of the interaction zone L, to the doubled kinetic energy of the flow at the inlet (j is the current density, ρ₀ and u₀ are the initial density and velocity of the gas):

$$St=\frac{jBL}{{\rho }_0{u}_0^2}.$$

(5)

The ratio of the Joule heat released during the interaction to the doubled kinetic energy of the flow was taken as the thermal parameter of the impact:

$$N=j(1-k)(uB+\frac{V}{h})\cdot \frac{L}{u}\cdot \frac{1}{{\rho }_0{u}_0^2},$$

(6)

These parameters are used in evaluating the effectiveness of external influences. In this case, the gas dynamic parameters are taken from the calculation, and the main electro-physical parameters are determined in the experiment; for this, the current-voltage characteristics of the discharge were taken. The potential difference between the electrodes V_AC was measured, as well as voltage on the load resistance to determine the current in the circuit. The most effective action is considered to be the one that, at the lowest force parameter St and thermal parameter N, leads to a stronger change in the position of the attached shocks.

3.3. Characteristics of the Ionized Gas in the Impact Area

The current-voltage characteristic for the input pair of electrodes, obtained in the absence of a magnetic field by varying the external voltage, is shown in Figure 6a (blue squares). The near-electrode drop is about ΔV = 50 V. The current-voltage characteristic when a magnetic field of 1.3 T is applied is shown here by red circles. It turns out that the addition of magnetically induced EMF does not lead to an increase in current.

To determine the conductivity of the gas in the core of the flow, the potential distribution in the interelectrode gap was measured. Point electrodes were mounted in the side walls of the diffuser in the region of the inlet pair of electrodes. The change in the potential distribution, when currents of different magnitudes flow through the plasma, is shown in Figure 6b. The break in the distribution shows near-electrode potential drops. As can be seen, for different values of the applied external voltage, the experimental distribution of the potential in the core of the flow is described by almost parallel straight lines. From this it is clear that when the current in the circuit changes, the voltage drop in the core of the flow practically does not change, which indicates an increase in the conductivity of the core of the flux as the electric current increases. The magnitude of the near-electrode voltage drop ΔV is the sum of the voltage drop at the cathode ΔV_C. The voltage drops at the anode ΔV_A is about 50–60 V, which is comparable to the magnitude of the magnetically induced EMF. All distributions are characterized by the dependence ΔV_A ≤ ΔV_C, and there is a clear tendency to reduce the total near-electrode drop ΔV = ΔV_A + ΔV_C with an increasing current. When a magnetic field is applied, the near-electrode voltage drops increase.

The graph in Figure 7a compares the effective plasma conductivity (squares). It shows the averaged conductivity over the entire interelectrode gap, with the conductivity in the flow core without near-electrode regions (circles) in the absence of a magnetic field (blue color) and during MHD interaction (red color). It can be seen that the conductivity increases with an increasing current due to the development of nonequilibrium ionization. The conductivity in the core of the flow is higher than the effective one. The imposition of a magnetic field reduces both the effective conductivity and the conductivity of the flux core. This is due to the imperfection of the electrodes and the Hall effect, as well as due to the increase in the near-wall boundary layer during MHD interaction.

Electron temperature and density were also measured in the experiment. To do this, a series of spectral measurements were carried out using an Ocean Optics 2000 spectrograph made by Ocean Optics Company in USA. The temperature was measured from the decay of continuous radiation in the ultraviolet region of the spectrum. Due to the peculiarities of the location of the energy levels of inert gases, the intensity of continuous luminescence in the ultraviolet region can be described by the exponential formula:

$$I_{\nu }=C\frac{n_e{}^2}{\sqrt{T_e}}{e}^{-\frac{h_P\nu }{k_B{T}_e}},$$

(7)

where n_e and T_e are the electron density and temperature, C is some constant, ν is the radiation frequency, and h_P and k_B are the Planck and Boltzmann constants, respectively. If we take the logarithm of this expression, we see that the ratio logarithm of the intensities at two frequencies, ν1 and ν2 in the ultraviolet region will characterize the electron temperature:

$$T_e=\frac{h_P}{k_B}\frac{\nu 2-\nu 1}{\ln \left(\frac{I_{\nu 1}}{I_{\nu 2}}\right)}$$

(8)

In this case, the electron concentration will be determined by the expression:

$$n_e=\frac{1}{C}{\left(I_{\lambda 1}\right)}^{\frac{1}{2}}{\left(T_e\right)}^{\frac{1}{4}}{e}^{\frac{h_{P}c}{2\lambda 1k_B{T}_e}}.$$

(9)

As a luminosity standard for determining the spectral sensitivity of the spectrograph and the absolute values of the intensity, we used the luminescence of a plug of shock-compressed gas in a shock tube under known and well-studied flow regimes. The experimentally measured values of temperature and electron density are shown in Figure 7b. It can be seen that the temperature and electron density increase with the increasing current due to the selective heating of electrons. This increases the conductivity of the gas and, consequently, the intensity of the MHD effect on the flow.

3.4. Characteristics of the Ionized Gas in the Impact Area

The first series of experiments was carried out to study the influence of the magnetic field on the change in the shock wave configuration. Figure 8 shows the Schlieren flow patterns when the transverse current in the braking mode was closed through all pairs of electrodes located in the diffuser. The length of the impact zone L is marked in the figure. When a small magnetic field is applied a shift of the shocks is visible, due to a decrease in the Mach number of the flow. Compared with the picture in the absence of fields, the angle of inclination of the shocks relative to the wall of diffuser has increased. The point of intersection of the shocks has shifted from X_c = 42 mm to 35 mm. Qualitatively, this picture can be called a weak MHD interaction. The position of the shocks has changed, but their reflection from each other remains regular.

When a magnetic field of 1.3 T is applied, the flow pattern changes significantly. The regular reflection of the shocks becomes Mach reflection; we see the formation of a direct shock of MHD deceleration, which transforms the supersonic flow into the subsonic one. This is a typical case of strong MHD interaction. However, the picture is complicated by the development of the near-wall layer; its thickness increased in comparison with the weak MHD interaction. Figure 8b plots the distance to the point of intersection with the jumps, depending on the magnitude of the magnetic induction. In analyzing the shock wave configuration, depending on the degree of MHD interaction, three types of MHD interaction can be distinguished: weak, when the distance X_c decreases but the reflection remains regular; strong, when in the flow core at a distance X_sh the shock of MHD deceleration is formed; and the detected unstable MHD interaction, when the position of the shock crossing point is unstable, apparently due to the formation of local subsonic zones. Neither a strong nor an unstable type of MHD interaction is suitable for the problem of controlling the position of attached shocks; therefore, we carried out subsequent studies for regimes where the reflection of shocks remains regular.

3.5. Local Impact Zones in Case of Transversal Current Short Circuit

To determine the most effective area of influence on the position of the jumps, a series of experiments was carried out with the localization of the current in certain areas of the diffuser. Figure 9a shows the flow structure when the transverse current in the braking mode was closed in the entire diffuser, with the exception of the input pair of electrodes No. 3. Despite the fact that the length of the interaction zone in this case is quite large (L ≈ 70 mm), the force and heat contribution to the flow is large. When applying only an electric field at B = 0, and during MHD interaction at B = 1.3 T, there is no noticeable displacement of the jumps. X_c remains equal to approximately 41 mm, only their slight curvature and growth of the near-wall layer are visible, and its growth begins from the region where the current begins to flow.

In contrast to this case, when the transverse current in the braking mode is applied only to the input pair of electrodes No. 3, even when the current is closed without applying a magnetic field, and due to only Joule heating, a clear increase in the slope angles of the attached shocks is observed. The intersection point approaches the channel entrance and X_c decreases to 37 mm. This is despite the much smaller interaction zone L ≈ 20 mm as can be seen from Figure 9b. An increase in the near-wall layer is also noticeable, starting from the very entrance to the diffuser. During MHD interaction, the distance decreases even more, and wide near-wall layers are clearly visible.

Table 1. Parameters of impact in the case of the transverse current.

Interaction Zone	St	N	Xc, mm
without an inlet	0.18	0.22	41
in the inlet	0.04	0.06	32

compares the power and thermal parameters for these two current faults. As can be seen, when the current is closed in the diffuser without the inlet part, despite the greater power and thermal contribution to the flow, the MHD interaction has a weaker effect on the position of the attached shocks than when the current is connected only in the inlet part of the diffuser. Thus, in order for the local effect on the flow to be effective, this effect should be applied in the inlet part of the diffuser.

3.6. MHD Control of Attached Shocks in the Inlet Part of the Diffuser

It is natural to continue studying the action of magnetic and electric fields when them are localized in the short inlet part of the diffuser. The intention is to try not only to slow down the flow, but also to speed it up in order to reduce the slope angles of the shocks, thereby demonstrating the possibility of controlling their position. Figure 10 shows examples of Schlieren pictures obtained at the same current I₃ = 500 A (j₃ = 3.8 × 10⁵ A/m²).

The first picture (Figure 10a) was obtained in the absence of a magnetic field. One can see a decrease in X_c, and an increase in the angles φ and α due to the deceleration of the flow as a result of the Joule heating of the gas. Next, the flow pattern during MHD interaction in the MHD brake mode is shown in the Figure 10b, where one can see even stronger deceleration and an even greater change in the position of the shocks to angles increasing. The last Schlieren picture (Figure 10c) demonstrates the shock wave structure formed during MHD interaction in the MHD acceleration mode. It is evident that in comparison with the picture in the absence of external fields, no acceleration has occurred, since the deceleration as a result of the Joule heating turned out to be stronger than the acceleration due to the ponderomotive force. However, if we compare this picture with the picture of the flow when only an electric field is applied, it can be seen that the ponderomotive force has weakened the effect of the Joule heating and has led to an acceleration of the flow.

The presented graph in Figure 10d demonstrates the accelerating action of the ponderomotive force. Here, the angle α is marked depending on the magnetic induction for the above three modes. It is assumed that if the ponderomotive force is directed to deceleration, the magnetic induction is negative if the acceleration is positive. The horizontal line is the angle in the absence of a magnetic field. Relative to this value, the angle has increased during braking and decreased during acceleration.

3.7. Areas of Dominance of the Ponderomotive Force and Joule Heating

To study how the position of the attached shocks reacts to the action of electric and magnetic fields in the inlet part of the diffuser, the following series of experiments was conducted. At the same value of the magnetic induction B = 1.3 T and ε = 65 V, a voltage from an external source of different values and polarity was applied to the third pair of electrodes. Thus, the studies were carried out both in braking and accelerating modes. The results of these experiments are presented in Figure 11. Here, the dependence of the current and the half-angle (under which the attached shocks α occur is shown) on the value of the external voltage V, is divided to the magnetically induced EMF, i.e., from V/ε.

The experimentally obtained current-voltage characteristic (CVC), that is the dependence I(V/ε) presented in Figure 11 is clearly non-linear, and the current values in almost all experiments are significantly less than the theoretically expected values. This testifies to the important role of near-electrode processes in the current flow. Moreover, it turns out that this role is not the same for V > 0 and V < 0. An analysis of the CVC makes it possible to estimate the magnitude of the near-electrode potential drop ΔV at low currents. It is determined by the initial section of the CVC up to the values of V, at which there is a sharp decrease in the dependence gradient I(V/ε). Therefore, for V > 0 (braking mode) ΔV/ε ≈ 1.1, i.e., the magnitude of the near-electrode potential drop in this case is close in its value to the magnetically induced EMF. This is also evidenced by the fact that at V=0, when only the EMF acts on the plasma, there is practically no current through the interelectrode gap. This is probably due to the fact that non-compensated space charge regions have formed near the electrodes, since cold non-emitting electrodes are used in the experiment. In addition, the current flow is hindered by cold gas dynamic boundary layers and possible separation of the flow.

It is interesting to note that when the sign of the external stress changes, the nature of the dependence I(V/ε) changes. At |V/ε|> 1, in the region of negative values of V, the increase in current occurs more sharply than in the region of positive values of V. The plasma resistance, determined from the CVC in the region V/ε < −1, turned out to be approximately 0.25 Ω, while in the region V/ε > 1 it is noticeably larger and equal to 0.43 Ω. Thus, the behavior of the current-voltage characteristics indicates that the role of near-wall effects in the braking regime is greater than in the accelerating regime.

The vertical lines in Figure 11 mark the boundary values of V/ε separating the areas with different dominant impacts. Four regions can be distinguished: according to the direction of the gas discharge current and the action of the ponderomotive force, these regions are divided into regions of flow deceleration—I, II at a positive current, and regions of its acceleration—III, IV at a negative current. Region I, determined by the condition V/ε > 1.3, corresponds to such relationships between the applied voltage and EMF, at which the deceleration of the flow due to Joule heating in an external electric field is stronger than the deceleration due to the MHD interaction. In region II, −1.0 < V/ε < 1.15, the ponderomotive force dominates in flow deceleration. Region III, which is in a narrow range of values −1.15 < V/ε < −1.0, determines the relationship between the external voltage and the magnetically induced EMF, under which the acceleration of the flow under the action of the ponderomotive force is possible. In region IV, V/ε < −1.15, deceleration due to Joule heating in an external electric field prevails over the accelerating action of the magnetic field.

With positive values of V (V > 0) in region II, the angle α changes slightly. This is due to the fact that because of near-electrode processes, the current strength in this region is insufficient to significantly slow down the flow. A stronger increase in the angle α occurs in region I, where the current has noticeably increased and the flow deceleration has increased. This is due to the combined action of gas heating in an external electric field and the ponderomotive force. In the region of negative values V (V < 0) of region II, in contrast to the values at V > 0, already at a current of 40 A, the angle α increased noticeably. Despite the negative voltage value, the current in the circuit remains positive, while the ponderomotive force continues to slow down the flow and increase the angle of jumps. It is possible that the observed difference in near-electrode drops at positive and negative voltage values also has an effect. At V < 0, the voltage drop at the electrodes is smaller, which leads to the fact that most of the external voltage is used to heat the core of the flow and additional braking. In area III the current has changed direction, but the effect showing the acceleration of the flow, i.e., the decrease in the angle α compared to its initial value at V = 0 did not occur. However, it should be noted that compared with the previous situation in region II at negative voltage values, a decrease in the angle α is noticeable. Consequently, there is a relative increase in the flow velocity due to the action of the ponderomotive force on its acceleration. In region IV the angle α increases again, which indicates that the flow is decelerating in this region, since the effect of heating the gas in an external field dominates over the accelerating effect of the ponderomotive force.

Thus, under the conditions of this experiment, the most noticeable effect on the flow is exerted by Joule heating in an electric field, both in deceleration and accelerating modes. This creates favorable conditions for increasing the angle of inclination of shock waves. In order to produce a noticeable MHD acceleration of the flow and a decrease in the angle of inclination of the shocks, it is necessary to increase the magnetic field or a noticeable increase in the conductivity of the flow to reduce Joule heating, while maintaining the current density required for the MHD effect.

3.8. MHD Action at Longitudinal Short Circuit

The next series of experiments investigates the effect of external fields in the case of a local longitudinal current closure. Figure 12a shows the organization of the MHD effect on the pattern of supersonic flow in the diffuser. The longitudinal current from an external source is organized in the near-wall region, behind the attached shocks between the 3rd and 4th electrodes located near the upper and lower walls of the diffuser. The arrows show the direction of the current and the action of the ponderomotive force.

In the Schlieren patterns of the steady flow, Figure 12b shows the asymmetric arrangement of the shocks. The explanatory diagram shows the position of shocks in the absence of fields shows by solid lines, and their displacement under the action of the ponderomotive force is shown by dashed lines. At B = 0 and V = 0, the shocks are located symmetrically about the axis, and the angle of inclination of the shocks to the diffuser walls is φ = 15°. When the magnetic field is turned on and a longitudinal current is passed in the local region 3-4, the shock slope at the upper wall decreased and became equal to 13°, i.e., the jump moved deeper into the diffuser. At the lower wall, the shock slope increased to 17⁰ and the shock approached the diffuser inlet. This behavior of the attached shocks is due to the fact that, as a result of the directed action of the ponderomotive force, the gas pressure decreased near the upper wall and the shock pressed against the wall. At the lower wall, the force from the magnetic field acts in the opposite direction and leads to an increase in pressure, which pushes the shock away from the wall.

This experiment shows that in order to control the position of the shocks, it is sufficient to have a limited region with a gas discharge current near the diffuser wall and a transverse magnetic field. Depending on the direction of the current, due to the action of the ponderomotive force, the attached shock can change its angle of inclination in one direction or another. It should be noted that such a connection slightly perturbs the core of the flow.

A stronger effect of the ponderomotive force on the position of the jumps is seen when the longitudinal current flows in the entire volume of the diffuser. To do this, voltage from an external source is applied between the second electrodes in the nozzle and the fifth electrodes in the diffuser on the upper and lower walls. In this case, the second electrodes on the lower and upper walls of the diffuser were cathodes, and the fifth electrodes were anodes. Figure 13a shows the diagram of the electrode connection in the diffuser and the calculated picture of the current flow distribution, made on the assumption that the electrodes are point ones. The direction of action of the ponderomotive force is also shown. The average value of the circuit currents of the upper and lower electrodes was 600 A.

The flow patterns obtained by applying only an electric field is shown in Figure 13b, and the combined action of electric and magnetic fields is shown in Figure 13c. The diagrams for deciphering the main gas dynamic discontinuities are also given here: “a” refers to attached shocks, “b” refers to shocks resulting from the interaction of attached shocks, and “f” refers to shocks reflected from the walls. In addition to these main gas dynamic discontinuities, oblique shocks (“r”) appeared in the channel, which formed near the nozzle electrodes as a result of the heating of the near-wall layer. This was due to a higher current density near the electrodes. In the absence of a magnetic field, the flow picture is symmetrical. When an external magnetic field is applied, the picture becomes asymmetric. In this current configuration, there is an increase in gas pressure at the bottom wall of the diffuser. As a result, the attached shock increases its angle of inclination. At the lower wall the pressure decreases, so the attached shock approaches the wall. In all likelihood, the change in the direction of the velocity vector towards the lower wall under the influence of the ponderomotive force also has an effect, which leads to a decrease in the angle of attack near the upper wedge and an increase near the lower one.

Thus, in order to control the attached shocks in a weakly ionized flow, it is sufficient to have a transverse magnetic field and a transverse current in the inlet part of the diffuser, or a longitudinal current in a narrow near-wall region. Depending on the direction of the current, the angle of inclination of the shock will either decrease or increase.

4. MHD Control of Supersonic Flow around a Body

4.1. Organization of MHD Impact

The next series of experiments studied the magnetohydrodynamic effect on the position and shape of the bow shock wave that occurs in a supersonic flow around a semicylindrical body with a rounded part radius of 2 cm. It is located on the axis of a flat supersonic nozzle at a distance of 20 cm from the inlet. The calculated parameters of the flow incident on the body in this case are as follows: M = 7, T_h = 587 K, ρ = 0.033 kg/m³. The scheme of the body position in the nozzle is shown in Figure 14.

MHD action is carried out in a narrow area between the body and the shock wave by organizing a gas discharge current near the surface of the nose of the body in a magnetic field transverse to the current. The shape of the streamlined body is shown in more detail in Figure 15a. Three electrodes are mounted in the body: one central and two lateral. This makes it possible to create various gas discharge configurations near the body’s surface by applying voltage from special LC chains. Possible options for closing the current are shown in Figure 14 according to the two-electrode circuit, and in Figure 15b according to the three-electrode circuit. The discharge simultaneously ionizes the gas and accelerates the charged ions. In a transverse magnetic field with the magnetic induction vector B, this leads to the emergence of the Lorentz force acting on the charged particles in the direction perpendicular to the motion of the particles. Due to the rapid energy exchange in the collision of ions with neutral gas atoms, a ponderomotive force F_L = j × B arises, acting in the same direction directly on the gas, and, consequently, on the flow parameters.

Figure 16a shows the gas conductivity measured in the gas discharge gap during the organization of a surface discharge in the region between the body and the shock wave, depending on the magnitude of the gas discharge current. A significant increase in conductivity with an increasing current is seen. Figure 16b shows the pressure values obtained at the surface of the body P_v during the discharge, divided to the pressure P₀ without discharge in the absence of a magnetic field. A significant increase in pressure was found near the surface of the body with an increasing current. The pressure was measured during the discharge near the entire leading edge of the body, when the pressure on the upper and lower sensors was approximately the same.

4.2. MHD Interaction in the Near Surface Region of the Body

Figure 17 demonstrates the MHD effect on the head shock wave when the gas discharge current is organized according to a two-electrode scheme, excluding the central electrode from the scheme (Figure 14). The gas discharge current covers the leading edge of the body along a semicircular trajectory, which is demonstrated by the glow pattern in Figure 17a. Figure 17b shows the Schlieren pattern of the flow and the position of the shock wave during the organization of such a discharge, but in the absence of a magnetic field. Figure 17c shows the flow pattern during MHD exposure, when the current flows from the upper electrode to the lower one and the ponderomotive force is directed towards the body, as in Figure 14. Here, the MHD increase in pressure in the region between the shock wave and the body leads to the departure of the shock wave. The distance between the shock wave and the body has increased significantly. In Figure 17d, the action of the ponderomotive force is in the opposite direction; in this case, the gas discharge current is directed from the lower electrode to the upper one, and the gas is moved away from the body. As a result, the wave approaches the body. Compared to the position of the wave in the absence of a magnetic field (Figure 17b), the distance between the shock wave and the body has significantly decreased due to the MHD pressure decrease.

Figure 18 shows the flow patterns around the body when the current is organized according to the three-electrode circuit (Figure 15b). The glow of the gas discharge plasma is clearly seen in Figure 18a. The gas discharge current covers the upper and lower surfaces between the central electrode and the electrodes located on the upper and lower surfaces. The Schlieren picture of the flow with the current at absent of a magnetic field is shown in Figure 18b. When the current is directed from the central electrode to the side ones, the ion current is generated at the upper and lower edges of the body in the direction coinciding with the direction of the gas flow. This additionally contributes to an increase in the velocity of the charged ions. Figure 18c shows the Schlieren pattern of such a flow at B = 1.3 T. One can see a strong distortion of the bow shock wave, as it becomes asymmetric. With such a closure of the current, the ponderomotive force contributes to the moving away of gas from the body and a decrease in pressure in the upper half of the flow, and to the approaching of the gas to the body and an increase in pressure in the lower one. As a result, the shock wave approached the body in the upper part of the flow, and moved away from the body in the lower part. If the direction of the gas discharge current is reversed from the side electrodes to the central one, the ponderomotive action in the upper and lower parts of the flow also changes to the opposite, and the shape of the shock wave also changes (as shown in Figure 18d). Here, the reverse picture is visible: now the shock wave is pressed against the body in the lower part of the flow; the pressure has decreased here, and is removed from the body in the upper part due to the MHD increase in pressure.

It should be noted that a change in the shape of the bow shock wave also leads to a change in the aerodynamic drag. The closer the shock wave is to the body, the lower the aerodynamic drag and vice versa. In addition, the MHD action near the surface of the streamlined body leads to a change in pressure. By creating different pressures at the lower and upper surfaces of the streamlined body using the MHD method, it is also possible to change the lifting force. This significantly expands the possibilities of the MHD method for controlling supersonic flows.

5. Conclusions

This paper shows the possibility of controlling supersonic flows and shock wave configurations using the magnetohydrodynamic method. The control was carried out by the organization of the ponderomotive force acting on the gas. Depending on the task at hand, the ponderomotive force can be applied locally by creating local gas discharge regions in a transverse magnetic field. By changing the direction, magnitude and place of application of the gas discharge current, it is possible to control the action of the ponderomotive force, change the shock wave configuration, increase or decrease the aerodynamic drag, and also change the lifting force.

This study has shown that:

• The presence of a magnetic field transverse to the flow, and a transverse current in the inlet part of the diffuser or a longitudinal current in a narrow near-wall region, is sufficient to control the attached shocks that occur at the entrance to a supersonic diffuser in a weakly ionized flow. Depending on the direction of the gas discharge current, the angle of inclination of the jump will either decrease or increase. When organizing a transverse current in a magnetic field before entering the diffuser, it is possible to change the angle of attack of the oncoming flow.
• A significant role in the MHD action on the supersonic flow is played by the Joule heating of the gas in an electric field. An optimal balance between the work of the ponderomotive force and the effect of Joule heat is necessary for effective flow control. To accelerate the flow, the Stewart parameter must prevail over the thermal parameter.
• To control the position of the head shock wave that occurs in the supersonic flow around aerodynamic bodies, it is sufficient to organize a gas discharge in a narrow near-wall region between the shock wave and the body and a transverse magnetic field. Depending on the direction of the current, the MHD action can move the wave away from the body or bring it closer, thereby increasing or decreasing the aerodynamic drag.
• The organization of a discharge at the lower and upper walls of a streamlined body in a transverse magnetic field, depending on the chosen current direction, will contribute to an increase or decrease in pressure near the lower and upper surfaces of the body. By creating the desired pressure difference, one can change the lifting force.