Developing a Grey Forecasting Model for the Air Flowing across the Parallel Plate Duct

Abstract

The focus of this work is on developing a nonlinear grey model for the laminar flow regime of carrier fluid across the flat plate collector. The trust region reflective algorithm was used to solve the nonlinear laminar flow problem and handle the sparse matrix. The stream function, dimensionless velocity, gradients of velocity components, carrier fluid temperature, and the absorber plate temperature were estimated for a flat plate collector operated with and without a circular chimney. Similarly, the same technique was adopted to determine a model for heat transfer across the absorber plate. The numerically obtained solution was also compared with the parameters obtained through the instrumental measurement. The relative tolerance was kept at 10⁻⁵ for the white and grey box solutions. The developed model was noticed to have a smaller deviation than the conventional analytical model to predict the experimental values. The slip condition was observed for the proposed scheme. The uncertainty in the temperature measurement through the proposed model varies from ±0.53 to ±1.47 K. The minimum absolute percentage error (MAPE) lies in the domain of 0.52–1.67% for the nonlinear grey model, whereas the linear grey model for measuring absorber plate temperature has a percentage error of 0.0011–0.02%.

1. Introduction

Awareness related to green energy has increased among the masses as they have realised the negative consequences of excessive release of greenhouse gases (GHGs) into the atmosphere. In a 2018 report, a group of scientists and government bodies unanimously concluded that the upper threshold of the global temperature rise should not be higher than 1.5 °C to steer clear of the detrimental impact of GHGs and maintain a liveable ecosystem. However, the current scenario speaks volumes about the adverse effects of CO₂ emissions on global temperature. It was estimated that the global temperature would increase by 4.4 °C by the end of the century [1]. Society cannot bank on conventional sources to fulfil its objectives. The future demands an alternative way to address the upcoming energy crisis. To avoid a chaotic situation, green energy must be brought into the mainstream and its contribution should be increased multi-fold. One such application is drying technology, where a dryer utilises solar energy to carry out the drying of different types of perishable food items. The basic backdrop of the drying process can be understood by the way of providing thermal energy to the agricultural product. It could be either performed by laying the food on open ground or keeping it in a cabinet for a direct gain of thermal energy. The merit of direct gain over the traditional way of drying is the protection against dust and pests, and the process becomes rather fast and can be controlled at a pilot scale. Some advancements achieved in the past century include the use of a blower for the forced circulation of air, but the main issue with the unit was the erratic change in the temperature profile of the food item. The underlying issue was later resolved by using an indirect type of active device that was also used in this study. Converting a short wave into heat and releasing it to the incoming air through an absorber plate is the basic modus operandi of the active device. The detailed literature reviews and shortcomings are discussed in the subsequent paragraphs.

The recent developments in the context of drying technology can be studied in the literature. According to material selection criteria, a corrugate aluminium (Al) alloy plate was examined for free and forced convection of air across a parallel duct. It was observed that the increase in the mass flow rate by 33% would also improve the thermal efficiency of the unit by 27% [2]. However, the study focused on the statistical methodology rather than on the intrinsic factors of the system.

In another work, a textile-based solar air collector (TB-SAC) was compared with the flat plate collector (FPC) and it was seen that the available energy of the system was relatively augmented by 32% as compared to the FPC. Nevertheless, the pressure drop was significantly increased and it was omitted in the work. As compared to the Al alloy plate, instantaneous collector efficiency was also increased with a rise in the mass flow rate for TB-SAC [3].

A thermal boundary effect on the temperature and velocity distribution of air was explained for the basic FPC system, but it was a one-dimensional aspect of thermal science. The dynamics of air on the smooth collector surface were avoided in the work [4].

The effect of air orientation on the PV surface was also examined using the Pohlhausen method so that the best orientation of PV modules can be estimated. The derived solution for the different PV models was promising, but the approach was confined to a quadratic approximation of dimensionless velocity [5].

A different arrangement of two-pass solar collectors (with fins and phase change material (PCM), with fins alone, with PCM only, and without fins and PCM) was used to examine the effect on the energy distribution of carrier fluid at the output end. It was concluded that a solar collector equipped with fins and PCM would have a significant influence on the exergy and energy of the system. It was reported that the highest efficiency attained by the collector would be 66.5%. However, the study was based on the quantitative aspect of the discussed design of the solar air collector. The objective of the work was to compare different materials without discussing thermodynamic state variables [6].

In different study, the exergy and effectiveness were calculated for each component used for manufacturing a solar collector, and it was reported that the exergy of the unit would vary from 28.39% to 33% [7]. A transpired solar air collector with PCM was examined and it was found that the overall efficiency of the system was increased by 10.6%, whereas the temperature difference between outlet and ambient was elevated by 8.8 °C. The operating hour is also significantly improved for the proposed collector [8].

A promising and financially effective model was proposed for the transient state of the solar thermal collector for drying purposes. A common tool, SIMULINK, was adopted to simulate the behaviour of the solar thermal collector. The double transparent walls and storage rocks were used to improve the efficiency of the solar collector. However, no experimental evidence was provided to determine whether the proposed model is reliable or not [9].

In another case, metal wool was used to manufacture the absorber plate since the porous matrix can enhance sensible heat. The period of the charging/discharging depends on the degree of stratification, and therefore, an appropriate selection of material based on its cost, availability and effectiveness is needed. In the case of porous material, the thermal gradient remains positive throughout operational time, whereas a negative gradient is often noticed during discharging of energy [10]. The level of stratification and its effectiveness can be determined by energy analysis. The porous material of one particular kind is not enough; therefore, a combination of different materials (spherical-shaped rock, cast iron and copper) was used. It was noticed that thermal storage and level of stratification were enhanced by 85% and 135%, respectively [11].

Porous media with different porosities were also considered to enhance the overall heat transfer between the air and porous media. They used a two-pass solar collector and it was estimated that the thermal efficiency could vary from 60% to 70% with the application of porous material [12].

In another similar work, it was stated that the collector efficiency was augmented by 20–70% higher than the collector operated without porous media [13]. However, the proposed mathematical model exhibited deviation that was too high to predict temperature difference and thermal efficiency of the collector [12,13].

Another case study of porous material reported that the solar air heater was increased by 10% [14]. There is a notable discrepancy in the performance of the solar collector with the use of different types of porous media.

The proposed unsteady model was not robust to provide a better convergence near the true data. The different modelling tools such as Engineering Equation solver (EES), WATSUN, Polysun and TRNSYS were used along with porous media to simulate a similar environment for the solar thermal system [15,16]. However, the application of different software may have little or no effect on the stability of a given model unless the proposed algorithm is robust in itself to tackle the given problem. The overall focus of the past research work is either based on the material design or some partial differential equation that can be easily derived and solved by using the graphic user interface. However, some research related to simulation and modelling has been performed, but the calculation is confined to temperature and energy distribution [2,3,9]. None of them are related to the interaction of air with the surface of the absorber plate.

In this work, the focus is mainly on the dynamic behaviour of air and on developing a nonlinear model that could simulate the instrumental data with the least residual error. The grey model for the heat transfer is based on the numerical technique used to discretise the Euclidean plane, and the scheme is based on the linear grey box model. The novelty of this work is to determine a substitute model for the hydrodynamic flow of air inside the solar collector. This can also be generalized to fluids other than air, which makes it flexible and robust.

2. Materials and Methods

Mathematical Model

The dynamics of carrier fluid (air) were solved using a continuous-time grey model system. The ordinary differential equation (ODE)/partial differential equation for the air flow was mapped to a continuous-time state–space model structure (input vector) (Equation (1)).

$$\dot{u}=\mathrm{A} u\left(t\right)+\mathrm{B}z\left(t\right)+\mathrm{C}p\left(t\right)$$

(1)

where A and B are the matrices that are parameterised by the given parameters of the differential equation. The matrix C is a noise matrix. However, matrix C is an additional matrix that can be estimated by the given model. The call function in the script does not parametrise this quantity. To derive the output matrix, the following equation (Equation (2)) is programmed.

Similarly, the output vector can be defined in the same fashion:

$$I \left(t\right)=D u\left(t\right)+E z\left(t\right)+F p\left(t\right)$$

(2)

where D and E are matrices related to the states and inputs of the models, whereas F denotes the noise matrix.

Equations (1) and (2) are in the time domain. To define them as a state–space model, replace t with the node.

The grey model can be linearly as well as nonlinearly programmed by using the same coding except for some syntactic changes in the script. Additionally, the input, output and the number of state equations were defined by the order $N=\left\{N_I, N_z, N_u\right\}$ of the nonlinear grey model. In other words, a set of differential equations is required to carry out nonlinear programming of the given fluid dynamics problem. The time domain is based on the sampling frequency of the experimental work. Theoretically speaking, the adopted approach acquires physiological information from the analytical model and combines it with the data to form a new model that correlates the differential equation with the experimental data set. However, it is translucent in characteristics.

The Prandtl differential equation was solved for the laminar boundary flow near the surface of the copper plate using Verner’s 7th and 8th Order embedded Runge–Kutta method. Similarly, non-steady and one-dimensional heat conduction was solved using the spatial discretisation of the parabolic equation. For the same, the programming script was written down. The interface used for the mathematical calculation is MATLAB 2015a (Math Works, CA, USA). The pictorial representation of the laminar flow is shown in Figure 1. The modelling data used for numerical analysis are provided in

Table 1. The miscellaneous parameters used for the modelling.

Parameters	With Chimney	Without Chimney
hfp [17]	2.49 W·m−2·K−1	0.70 W·m−2·K−1
hr [17]	5.57 W·m−2·K−1	5.62 W·m−2·K−1
Tair	299.4 K
Cp [18]	0.39 kJ·kg−1·K−1
k [18]	385 W·m−1·K−1
Cf [19]	1.01 kJ·kg−1·K−1
ρ [18]	8960 kg·m−3
ρa [19]	1.10 kg·m−3
ν [19]	1.77 × 10−5 m2·s−1	1.78 × 10−5 m2·s−1

. The pressure gradient along the Y-axis was assumed to be negligibly small. Similarly, the shear rate along the length of the plate was considered to be marginally low. In this way, the following momentum equation can be considered.

$$u\frac{\partial u}{\partial x}+\mathrm{v}\frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial y^2}+\frac{1}{\rho }\frac{dp}{dx}$$

(3)

Likewise, the momentum equation along the Y-axis can be written as

$$u\frac{\partial \mathrm{v}}{\partial x}+\mathrm{v}\frac{\partial \mathrm{v}}{\partial x}=\nu \frac{{\partial }^2\mathrm{v}}{\partial y^2}$$

(4)

In the case of invariant fluid properties and zero pressure gradient, i.e., $\left(\frac{dp}{dx}=0\right)$, the Equation (1) can be written as

$$u\frac{\partial u}{\partial x}+\mathrm{v}\frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial y^2}$$

(5)

A suitable scaling of explanatory and response variables might not affect the numerical solution if the boundary condition remains unaffected during the transformation. The velocity profile is geometrically identically along the collector surface, so it only varies along the transverse axis by a factor that is called the stretching factor. In simple words, the dimension ratio of velocity can be correlated with the dimensionless distance from the solid boundary φ $\left(\frac{y}{\delta }\right)$.

The relationship between the local Reynolds number (Re_x) and boundary layer thickness, δ, near the boundary layer can be expressed by Equation (6):

$$\frac{\delta }{x}=\frac{1}{\sqrt{R{e}_x}}$$

(6)

Thus,

$$\frac{u}{U}=\phi \left(\frac{y\sqrt{R{e}_x}}{x}\right)=\phi \left(\eta \right)$$

(7)

where $\eta =y\sqrt{\frac{U}{\nu x}}$ represents the stretching factor.

Differentiate Equation (7) with respect to x and y and substitute the values in Equation (3),

$$-\frac{U^2}{2x}\eta \frac{d^{3}f}{d{\eta }^3}+\frac{1}{2x}{U}^2\frac{d^{2}f}{d{\eta }^2}\left[\eta \frac{df}{d\eta }-f\right]=\frac{U^2}{2x}\frac{d^{3}f}{d{\eta }^3}$$

(8)

where $f\left(\eta \right)=\frac{\Psi }{\sqrt{U\nu x}}$ = ${{\displaystyle \int }}^{}\phi \left(\eta \right)d\eta +C_1$.

The initial conditions for Equation (8) are as follows:

At $\eta =0$, $f\left(0\right)=0$

Similarly, $\frac{df}{d\eta }=0$ at $\eta =0$

To determine the grey model for the given equation, a sparse matrix-based equation is chosen. For a state–space model, the spatial grid sizes (Δx and Δy) and orders $\left(\frac{x}{\Delta x}\right)$ and $\left(\frac{y}{\Delta y}\right)$ were chosen. The grid size is based on the dimension of the absorber plate and the number of nodes depends on the experimental observations for a given parameter. In this case, the temperature of the absorber plate is a measurand.

The right side of Equation (3) can be written using the following difference approximation:

$$\frac{{\partial }^{2}u}{\partial y^2}=\left(\frac{u\left(x,y+\Delta y\right)-2u\left(x,y\right)+u\left(x,y-\Delta y\right)}{\Delta y^2}\right)$$

Likewise, it can be written for the momentum equation along the Y-axis (Equation (4)).

After the selection of appropriate grid sizes, the state–space matrixes were derived.

For one-dimensional nonlinear heat transfer, a similar approach was adopted.

$$\frac{1}{\alpha }\frac{\partial T_p}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}+\frac{q}{k}+\frac{2\times h_e}{k}\left(T_p-T_{air}\right)$$

(9)

The equivalent heat transfer coefficient between the cover and absorber plates can be determined by the following expression:

$$h_e=h_{fp}+\left(\frac{h_r{h}_{fc}}{h_r+h_{fc}}\right)$$

(10)

An equivalent radiative heat transfer coefficient is defined as:

$$h_r=\frac{4\times \sigma \times T_{av}^3}{\left(\frac{1}{{\epsilon }_p}+\frac{1}{{\epsilon }_c}-1\right)}$$

(11)

where $T_{av}=\frac{\left(T_{pm}+T_{cm}\right)}{2}$

The circular duct was used to measure the velocity of air at the inlet of the flat plate solar collector. The stack at the exhaust end of the drying chamber was provided to improve the dynamic pressure inside the drying chamber.

The copper sheet of C110 grade was selectively painted matte black. The schematic diagram of the unit is provided in Figure 2. The geometrical details of the solar collector are provided in

Table 2. The geometrical detail of the solar collector.

Material	Dimension (L × W × H)	Component
Plexiglass	1160 × 460 × 4	Glazing cover
Poplar wood	1200 × 500 × 150	Collector main body
C110	1160 × 460 × 1.2	Absorber plate
Polystyrene	1160 × 460 × 80	Insulation sheet
PVC	200 × 45 × 3.17	Connecting duct

. The experimental data were gathered from 25 September 2019 to 30 September 2019. The uncertainty related to the experimental measurement is provided in

Table 3. Experimental uncertainties in the measurand.

Parameters	The System with the Chimney	Conventional System
Absorber plate temperature	±0.45 K	±0.52 K
Carrier fluid temperature at the inlet	±0.53 K	±1.23 K
The velocity of air at the inlet	±0.03 m·s−1	±0.288 m·s−1

. The duration of the experimental work was from 10:00 a.m. to 3:00 p.m. per day. Thermocouple type K (RISEPRO, Bengaluru, Karnataka, India) was used to measure temperature across the solar collector and drying chamber. The air velocity at the inlet of the collector was recorded by a digital anemometer (Eurochron EC-MR, Neue Str. 1 99846 Seebach, Germany) with an accuracy of ±0.3%. The inclined surface of the solar collector faced true south. The solar air heater was installed at the tilt angle of 45°. The data acquisition system used for measuring global radiation was ADAMS4018 (Advantech, Taipei, Taiwan). The chimney length for the given design is 2 m. The PVC material was used to make a circular chimney. The height of the stack used for the given system is 2 m. The circular duct diameter is 100 mm. The dimension height of the drying chamber is 1000 × 500 mm². The insulation material used for manufacturing the drying chamber was polystyrene. The airflow pattern was examined with/without the incorporation of the circular chimney. The pyranometer (CM-11, Kipp & Zonen, Delft, The Netherlands) was used to measure global irradiation. The orientation of the solar air heater was true south.

3. Results and Discussion

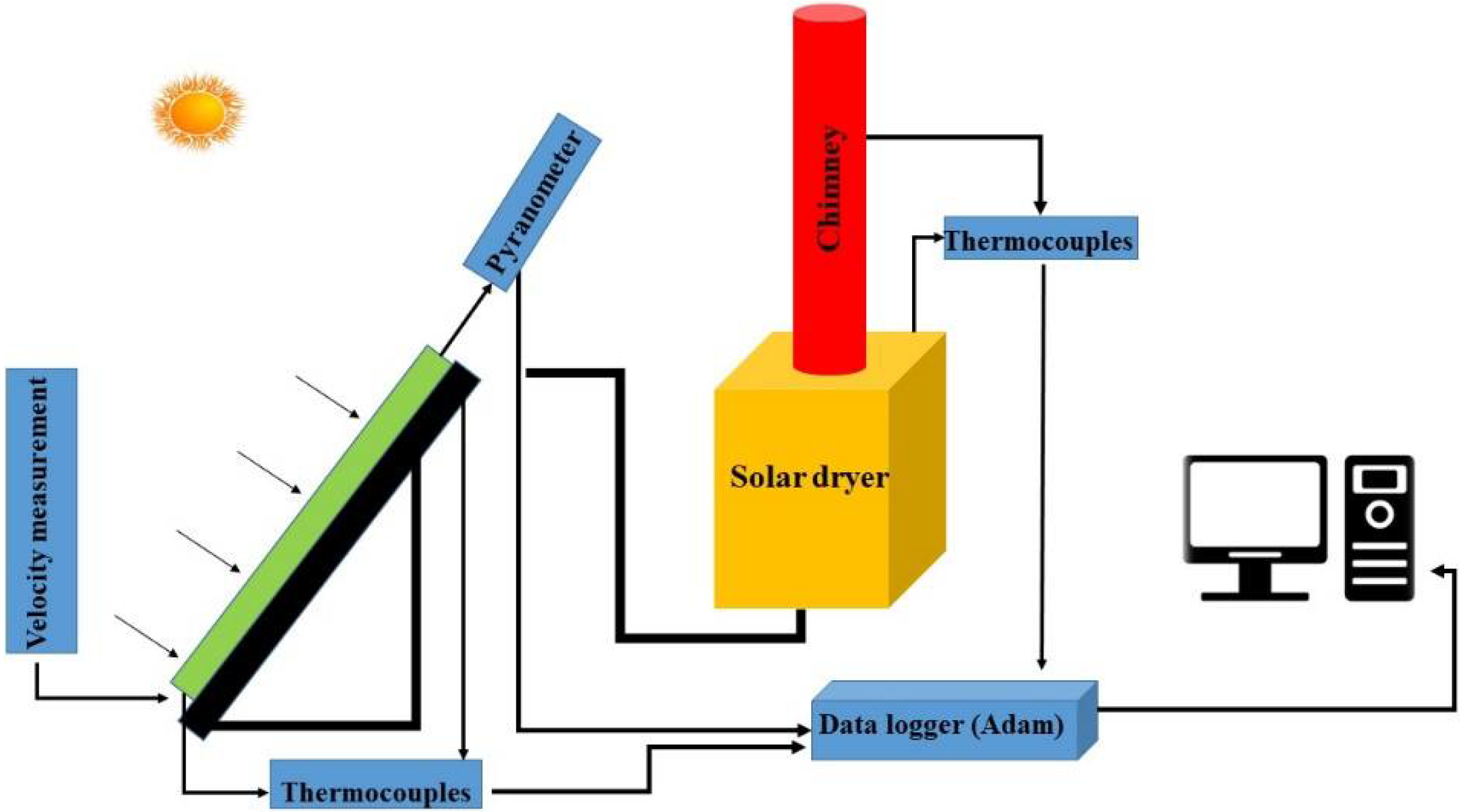
The computational and simulation work is divided into two parts: modelling of laminar flow and heat transfer analysis. The behaviour of air along the surface is predicted with the help of a nonlinear grey model for discreet sampling rate, whereas the heat transfer is based on a continuous-time state–space model.

3.1. Airflow Modelling

The variation in dimensionless velocity $\left(\frac{u}{U}\right)$ with the stretching factor (η) is shown in Figure 3. In the case of a solar collector equipped with a circular chimney, the analytical solution of the Blasius equation was compared with the grey model box proposed for a similar flow regime (Figure 3a). According to the physical interpretation, the ratio of local velocity (u) to the mainstream velocity (U) near the solid boundary of the absorber plate predicts the slip condition for the proposed grey model. As compared to the analytical solution, the gradient of the dimensionless velocity $\left(\frac{u}{U}\right)$ derived from the grey model was increased by 27.86% near the vicinity of the solid boundary. With the further increase in the stretching factor (η), the relative change in the gradient of the dimensionless velocity derived from the grey model dropped by 11.41%. This also implies that the nonlinear model has relatively poor approximation near the solid boundary if the system is operated by a circular chimney. Thus, the model is unable to distinguish whether it is continuum flow or slip flow. The Knudsen value would always be greater than 0.01 if the flow velocity is measured by the proposed scheme. The velocity at the boundary layer thickness (δ) was estimated to be lowered by 2% for the constant change in the stretching factor, η. The relative skewness in the distribution pattern of $\left(\frac{u}{U}\right)$ dropped by 18.76% for the grey model. Similarly, the kurtosis (Kr) in the grey model solution is 37.14% lower than that obtained through the analytical method. Relatively speaking, the solution derived from the grey model is more symmetric than the white box model. The likelihood of predicting the boundary condition through the white box model is relatively good as compared to the grey model. Despite the involvement of the viscous effect near the solid boundary, the grey model is relatively resilient to influencing the dimensionless velocity, $\left(\frac{u}{U}\right)$ at $\eta ~ 0$.

Likewise, to predict the solution for the conventional system (without a chimney), the change in the $\left(\frac{u}{U}\right)$ ratio is shown in Figure 3b. The slip condition was also predicted by the grey model solution for the conventional system. Relatively, a sharp rise in the gradient of dimensionless velocity by 174.57% was observed for the analytical solution (Blasius) in the vicinity of the solid boundary. The skewness in the distribution pattern of the dimensionless velocity fell by 96.90% in the solution of the grey model for the conventional system, which implies that the relative variation in the local velocity inside the boundary layer would be more symmetric or Gaussian in nature than that noticed in a system fitted with the circular chimney. Unlike the chimney system, the local velocity will approach the mainstream velocity with the increase in the stretching factor. The kurtosis of the dimensionless velocity distribution for the grey model was observed to drop by 40.38%. It is also clear that the analytical solution would have a better ability to determine the extreme values inside the boundary layer. It can be concluded the grey model would be much more reliable to predict the solution for the conventional system with the numerical uncertainty of ±0.06, which is 14.93% lower than that derived for the circular chimney.

The other solutions of the Blasius equation are also compared with the grey box model.

The change in the function value f (η) with the stretching factor (η) for a circular chimney is shown in Figure 4a. With the functional value of f (η), the stream function for the two-dimensional flow of air was computed. Unlike the derived solution of the Blasius equation, the functional value of f (η) derived through the nonlinear grey model dropped by 68.60% near the solid boundary of the absorber plate. This implies that the stream function value for the constant η would be relatively low for the grey model. However, an inflexion in the mathematical solution of the grey model was noticed at η = 1.3. Both the grey and the white box models exhibit the linearity of f (η) with the stretching factor, η.

The stream function will not be zero at the solid boundary for the grey model, which shows that the normal and tangential components of velocity along the boundary layer would exist at the solid boundary. Thus, there is an existence of yield stress, for the air if its flow is monitored with the grey model, whereas it does not exist for the analytical solution of the Blasius equation. The distribution function of f (η) derived for the grey model is positively skewed (0.047). Conversely, the analytical solution exhibits negative skewness (−0.367) to the normal distribution function. It can be concluded that the prediction of stream function value through the grey model would be high near the boundary layer thickness, δ. On the contrary, this is not the case for the analytical model, and the stream function may attain a higher value near the solid boundary of the absorber plate. Unlike Figure 3, the asymmetric behaviour would differ while estimating the stream function value through the grey model. The kurtosis of the distribution function of f (η) was estimated to decrease by 11.67% for the grey model. As it was seen in the derived solutions of the dimensionless velocity, the probability of predicting the extreme value of stream function determined by the analytical model would not be properly estimated. However, the most important thing when estimating the solution is the adaptability of a model to the actual environment.

Similarly, both models were also compared for the conventional system in Figure 4b. The characteristic of function f (η) for a conventional system is similar to the system equipped with the circular chimney, except there is no inflexion point observed. The stream function value proportionally dropped by 93.57% at the solid boundary for the conventional system. The distribution function of f (η) was also noticed to be positively skewed (0.0544), whereas the Blasius model for the conventional unit has a negative skewness of −0.0968. However, the kurtosis (Kr) of the solution derived through the grey model is marginally reduced by 0.74%. Relatively, to some extent, the forecasting ability of the grey model is akin to the Blasius model for the conventional system.

The second derivative of f (η) for a system equipped with a circular chimney is illustrated in Figure 5. The second derivative denotes the gradient of the dimensionless velocity discussed in Figure 1. In the case of the nonlinear grey model, the gradient $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ would remain constant in the vicinity of the absorber plate, whereas the recorded drop in the analytical solution of $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ was 58% for the same domain of η. Moving along the Y-axis, the phenomenal change in $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ derived by the nonlinear grey model was 43.60% higher than that obtained for the analytical solution in the domain of η $\in$(1.3, 1.95). In the given domain of stretching factor (η), the change in $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ was relatively gradual for the analytical solution (Blasius). Both the models have a positive skewness, but the degree of skewness in the nonlinear grey model increased by 36%. In the same fashion, kurtosis is elevated by 44% for the grey model, which implies that the likelihood of variability in the gradient would be rather high for the grey model than its counterpart, the white box model.

The variation in $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ with the stretching factor for the conventional system (without chimney) is shown in Figure 5b. At the solid boundary, as compared to the analytical solution (Blasius), the gradient value derived from the grey model is relatively decreased by 10.81% for the conventional system. However, the characteristic of the gradient curve derived from the grey model is the same for both the systems ((a) and (b)) near the surface of the absorber plate. The only difference is the gradual shift in the value of $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ with the stretching factor. Near the solid boundary, the gradient value for a system with a circular chimney would be 8.32% higher than that estimated for the conventional system by the same nonlinear grey model. It can be concluded that the boundary values, as well as the shape factor, will change with the change in the flow parameter of air at the inlet of the solar collector. A 2% drop in $\left(\frac{d\left(\frac{u}{U}\right)}{d\eta }\right)$ was observed at the solid boundary when the same system was investigated with the help of the Blasius solution. The distribution of the numerical solution obtained from the nonlinear grey model has negative skewness, whereas the Blasius solution is positively skewed about the mean position of the normal distribution function. The difference proves that the likelihood of the existence of a higher gradient is more near the surface of the absorber plate for the grey model, while this is not the case for the numerical solution estimated from the Blasius equation. Upon comparing the fourth central moment in the data distribution, the kurtosis in the grey model solution is 10.45% higher than that derived for the analytical solution. So, the variability would be noticeably higher in the conventional system if the flow pattern is estimated via the nonlinear grey model than the Blasius model. The sharp change in the gradient would occur at η = 1.245 for the Blasius model, whereas it happens at 1.761 if the same system is examined by a nonlinear grey model. The susceptibility of the model to being affected by the stretching factor is relatively low in the nonlinear grey model.

In Figure 6, the numerical solutions derived from the white and grey box models are compared with the instrumental value of mainstream velocity for a system with/without a circular chimney. The numerical solutions derived from the analytical and grey models were used to forecast the mainstream velocity of air calculated using the anemometer. From the statistical analysis, the experimental data obtained for the solar collector equipped with the circular chimney have a negative skewness, whereas the positive skewness is obtained for the conventional system. Similarly, the kurtosis derived for the circular chimney dropped by 57.10% compared with the conventional system. Thus, the characteristic of measured velocity for the circular chimney is binomial in nature, whereas the conventional system possesses the characteristic of a super-Gaussian or leptokurtic curve. Both the simulated curves derived from Blasius and the nonlinear grey model for the circular chimney are negatively skewed about the mean value of the normal distribution. Comparatively, the negative skewness in the numerical solution of the nonlinear grey model decreased by 5.66%, whereas it increased by 195% when it was compared with the experimental data set for a system with a circular chimney. Likewise, the kurtosis of the numerical solution obtained from the nonlinear is 6.66% lower than the corresponding value estimated for the Blasius model. Both models have a propensity to behave as a binomial curve if they are applied to forecast the mainstream velocity of air for a system with a circular chimney. In the case of the conventional system, grey and Blasius models are positively skewed. However, the skewness in the numerical solution of the grey model increased by 2.16% when it was equated with the skewness of the Blasius model, whereas the kurtosis of the grey model dropped by 1.69%. Both models share the characteristic of super-Gaussian distribution. Moreover, for the conventional system, the distribution characteristic resonates with the experimentally derived data.

The statistical behaviours of both the experimental data and the models share similar traits; therefore, the relative accuracy of the model can be predicted with the mean absolute error percentage that is provided for both the models in Figure 7.

To determine the accuracy of the proposed model, the mean absolute percentage error (MAPE%) was determined while computing the mainstream velocity of the air. The change in MAPE value with time is shown in Figure 7. From the statistical analyses of white and grey models, it was confirmed that the nonlinear grey box model would show affinity with the analytical model for the conventional system, and its effect was also felt while computing the mean absolute percentage error between the true and predicted values. The rate of convergence with time was noticed to be higher for the grey model than for the Blasius model. For a system with a circular chimney, the convergence of the solution estimated from the proposed model was 23.72% higher than the Blasius model for the same time interval. As compared to the analytical solution, the maximum error that can occur while forecasting velocity for a system with a circular chimney was reduced by 28.49% for the nonlinear grey model. However, the error % in the grey model becomes asymptotic for a system that operates for a prolonged period, which is not true for the Blasius solution. The analytical solution derived through the Blasius equation converges slowly and steadily with time and provides better forecasting if a given system runs for a long period.

Conversely, the nonlinear grey model seems to have better predictability for a unit without a circular chimney; however, it converges slower than its counterpart grey model for a system equipped with a circular chimney. According to the MAPE data, the rate of convergence dropped by 43% for the nonlinear grey model when it was deployed for the conventional system. However, in long run, the nonlinear grey model competes with the analytical model at a similar pace. While operating a conventional system for a prolonged duration, the convergence of the analytical solution relatively increased by 11% when it was compared with the nonlinear grey model. In the case of a system operated with the circular chimney, the average MAPE% for a grey model is reduced by 24.63%, while it was marginally increased by 6% for the conventional unit. So, the overall mean absolute percentage error remains lower for the nonlinear grey model if it is used to forecast the velocity distribution of air, which is not true for the conventional system.

The velocity gradient along the x and y directions with the shear stress is illustrated in Figure 8a–c. As compared to the analytical solution for the velocity gradient $\left(\frac{\partial u}{\partial x}\right)$, the maximum velocity gradient predicted by the grey model is reduced by 18.73% at the inlet of the collector. Similarly, the lowest possible value of $\left(\frac{\partial u}{\partial x}\right)$ obtained through the grey model was 1.95% higher than that estimated by the Blasius solution. Similarly, for the conventional system, the highest possible value derived for $\left(\frac{\partial u}{\partial x}\right)$ dropped by 29.36%, which is 56.75% lower than its counterpart grey model for a system equipped with a circular chimney. Unlike in the case of the circular chimney, the lowest derived value of $\left(\frac{\partial u}{\partial x}\right)$ is curtailed by 10% while equating it with the corresponding value of $\left(\frac{\partial u}{\partial x}\right)$ calculated through the Blasius model. In comparison to the corresponding average values of $\left(\frac{\partial u}{\partial x}\right)$ for the circular chimney, the average value of $\left(\frac{\partial u}{\partial x}\right)$ for the conventional system dropped by 88% for the grey model, whereas it decreased by 81.91% for the Blasius model.

According to the statistical perspective, both the models (grey and Blasius models) are positively skewed around the mean value of the normal distribution function for a system with a circular chimney. The skewness in the grey model dwindled by 17.34% as compared to the skewness in the Blasius solution. The kurtosis of the numerical solutions does not significantly differ for both models. A similar kind of variability would be noticed. Comparatively, the skewness in the numerical solution of the nonlinear grey model for the conventional unit dropped by 17.81%, which implies that the computational uncertainty in estimating $\left(\frac{\partial u}{\partial x}\right)$ would be rather low. The excessive kurtosis (Kr) (leptokurtic) in the numerical solutions was seen in both grey and Blasius models for the conventional system, which also implies that the concentration of the data points would be relatively higher around the mean value. The shear rate or velocity gradient along the air passage thickness (y) is illustrated in Figure 8b. The shear rate near the solid boundary dropped by 18.72% when it was estimated by the grey model. The lowest shear rate was obtained at y = 0.039 m from the surface of the absorber plate. Relatively, the shear rate derived from the grey model for a system with a circular chimney is 1.98% higher than its counterpart grey model designed for the conventional system. The shear rate would change its orientation in the interval of 0.028–0.032 m. This implies that the shear stress would act along the flow direction for the given air passage thickness. However, a similar event would occur much earlier for the conventional unit. For the conventional unit, the inflexion in the numerical solution of $\left(\frac{\partial u}{\partial y}\right)$ would lie in the domain of 0.0036–0.0072 m. This can also be explained through the distribution of shear stress in the transverse direction. The least shear rate for the conventional system is estimated to be −9.814 s⁻¹ by the nonlinear grey model, which is 9.63% higher than the corresponding value obtained at the same point by the Blasius model. The numerical solutions derived by grey and Blasius models have a positive skewness for non-conventional systems (with chimney). Comparatively, for grey models, the skewness in the numerical solution for a non-conventional system is 83.99% lower than the skewness in the derived solution for the conventional system. As compared to the non-conventional system, the kurtosis in the numerical solution of the grey model for the conventional system dropped by 58.67%. The average value of the shear rate $\left(\frac{\partial u}{\partial y}\right)$ obtained from the nonlinear grey model is 4.420 s⁻¹, which is 22.45% lower than the average value derived through the Blasius model. Similarly, for the conventional system, the estimated value of $\left(\frac{\partial u}{\partial y}\right)$ by the nonlinear grey model was reduced by 49.20% compared with the Blasius model.

The graphical plot of shear stress is shown in Figure 8c. The wall shear stress $\left(\mathsf{\nu }{\rho }_f{\left(\frac{\partial u}{\partial y}\right)}_{y=0}\right)$ computed by the grey model for the non-conventional and conventional systems is 7.04 × 10⁻⁴ N·m⁻² and 3.88 × 10⁻⁴ N·m⁻², respectively, and it varies from 5.49 × 10⁻⁴ N·m⁻² to 8.65 × 10⁻⁴ N·m⁻² for the Blasius model. The shear stress would be zero in the open interval of 0.0288–0.0324 m for the non-conventional system. In the case of the non-conventional model, the lowest shear stress would be obtained at a transverse distance of 0.0396 m from the solid boundary for both the models, whereas it would attain the lowest value at 0.018 m for the conventional system. With the increase in the transverse distance, the shear stress would change its orientation along the flow direction and support the flow of air inside the solar collector. However, this event would occur much earlier for the conventional system than for the non-conventional system. Therefore, it can be concluded that the involvement of natural draught with the solar collector would eventually increase the wall shear stress and hydrodynamic losses, but this will not happen with the conventional unit. However, it can also be seen that the shear rate would promote a healthy flow system inside the non-conventional unit, whereas the amplitude of the shear rate would not be that high for the conventional system.

3.2. Linear Grey Modelling of Thermal Energy

The modelling of heat flow and temperature distribution was examined using the linear grey model for the one-dimensional heat flow problem for the absorber plate. Similarly, the linear grey model of the Whillier equation [20] was also developed for the air stream. The change in the temperature of the absorber plate and air with time is shown in Figure 9. The average temperature of the absorber plate derived from the linear grey model was estimated to be 377.94 K for a non-conventional system, which is 0.17% higher than the average temperature of the absorber plate determined by the thermocouple. The instrumental uncertainty in the temperature measurement of the absorber plate was estimated to be ±0.45 K, whereas it was ±0.43 K for the numerical solution derived through the linear grey model. The negative skewness of −0.0158 was found in the proposed grey model. Conversely, the experimental data are positively skewed about the mean position of the normal distribution. The kurtosis of the numerical and experimental data exhibits characteristics of the binomial distribution. In the same way, the simulated temperature for the carrier fluid (air) has a skewness of −1.03, which is 2.5% higher than the corresponding skewness value for the instrumental data set. The uncertainty in the numerical solution of air temperature was ±0.53, whereas the thermocouple installed at the inlet of the solar air heater provided the instrumental uncertainty of ±0.54. The percentage fit of the linear grey model is 96% with the experimental data obtained for the air temperature at the inlet of the solar air collector.

In the case of the conventional unit (Figure 9b), the uncertainty in the experimental value is ±0.52 K, which is 0.19% higher than the corresponding uncertainty recorded in the simulated solution of the linear grey model for absorber plate temperature. The average experimental temperature of the absorber plate was estimated to be 493.75 K, which is insignificantly higher than the average value derived through the linear grey model. Both experimental and simulated data sets are negatively skewed around the mean value of the normal distribution function. The kurtosis of the simulated solution was relatively reduced by 0.57% as compared to the corresponding value of the kurtosis estimated for the experimental data. The distribution characteristic of both the simulated and experimental is equivalent to the super-Gaussian function. The average value of experimental air temperature at the inlet of the solar collector is 320.23 K for the conventional unit. The uncertainty in the air temperature measurement is ±1.23 K. As compared to the experimental data set, the average value derived from the numerical solution dropped by 0.37%. The uncertainty is ±1.47 for the linear grey model. The statistical investigation depicts that both the experimental and simulated data sets have a negative skewness to the normal distribution function.

Relatively, the kurtosis of the numerical solution is increased by 1.086%. The nature of the distribution pattern is leptokurtic. To investigate the model in more detail, the error analysis is performed to determine whether the solution estimated through the linear grey model is feasible or not. The mean absolute percentage error (MAPE(T)) estimated while predicting the temperature of the absorber plate and inlet temperature of the carrier is shown in Figure 10. The maximum MAPE(T) for the linear grey model was 0.037% while comparing the instrumental data of the absorber plate, whereas the lowest possible MAPE(T) was 3.46 × 10⁻⁴% during the time interval of 14,000–16,000 s. When the generated solutions were compared, the maximum value of MAPE(T) dropped by 85.18% for the numerical solution derived for the conventional system. The lowest possible MAPE(T) was also reduced by a margin of 51.64%.

Similarly, for the carrier fluid (air), the MAPE(T) has a maximum value of 9.97 × 10⁻³% for the non-conventional system, which is 39.72% lower than the MAPE(T) value evaluated for the conventional system. So, it could be seen that the linear grey model is suitable to predict the temperature distribution of air at the inlet of the solar air heater, whereas in the case of forecasting the absorber plate temperature, the proposed model provided a robust solution for the conventional solar air heater. The convergence of the nonlinear grey model is also better than the analytical model to forecast the velocity of air inside the collector, although it is susceptible to the duration of the experiment.

The complied average values of discussed parameters are provided in

Table 4. Parametric information about the grey and analytical models.

Parameters	Model Structure	With Chimney	Without Chimney
MAPE %	Grey model	0.52%	1.67%
	Blasius	0.69%	1.66%
	Absorber plate temperature	0.02%	0.0011%
	Carrier fluid temperature	0.0026%	0.0037%
Ψ (m2·s−1)	Grey model	7.60 × 10−3	0.95
	Blasius	7.80 × 10−3	0.96
u (m·s−1)	Grey model	0.26	4.60 × 10−2
	Blasius	0.31	4.80 × 10−2
v (m·s−1)	Grey model	−1.20 × 10−2	−0.90 × 10−3
	Blasius	−0.01	−0.85 × 10−3
$\frac{\partial u}{\partial x}$ (s−1)	Grey model	0.20	0.02
	Blasius	0.26	0.04
$\frac{\partial u}{\partial y}$ (s−1)	Grey model	4.42	0.52
	Blasius	5.70	1.04
$\frac{\partial v}{\partial x}$ (s−1)	Grey model	−3.60 × 10−3	5.80 × 10−3
	Blasius	−3.10 × 10−3	5.60 × 10−3
$\frac{\partial v}{\partial y}$ (s−1)	Grey model	−0.08	0.12
	Blasius	−0.07	0.12
U (m·s−1)	Grey model	0.41	0.05
	Blasius	0.40	0.05
	Experimental	0.43	0.09
τ (N·m−2)	Grey model	8.62 × 10−5	10.34 × 10−6
	Blasius	11.12 × 10−5	20.23 × 10−6

. The average value of stream function estimated through the nonlinear grey model dropped by 2.56% as compared to the Blasius solution. The vertical component of mainstream velocity (v) reduced by 9.90% while simulating it with the nonlinear grey model for a non-conventional system. In the case of the conventional system, the margin of percentage drop in the vertical component of velocity was reduced by 40.60%. The average shear stress experienced by the conventional unit was remarkably reduced by 88% while using the proposed nonlinear grey model, whereas it was estimated to be diminished by 81.80% when the same parameters were computed through the analytical model.

4. Conclusions

The analytical model, Blasius, was compared with the proposed nonlinear grey model to determine the flow parameters for the air flowing across the parallel plate duct. For determining the temperature measurement, a linear grey model was used to simulate the instrumental data set for the absorber plate and the carrier fluid (air).

Based on the observation, the following salient points are summarised below.

• The flow behaviour near the surface of the absorber plate was noticed to exhibit slip condition when the numerical solution was computed using the nonlinear grey model. However, no tendency for slip was observed while computing the dimensionless velocity through the Blasius model. This implies that the viscous effect of air near the surface was not affect the numerical solution derived by the nonlinear grey model. It also shows that some yield stress would be offered by the grey model that is not properly manifested by the numerical solution of the Blasius model.
• While estimating the stream function characteristic, it was found that the proposed grey model is congruent with the Blasius solution for the conventional system. However, statistical differences do exist between them. The kurtosis of the stream function computed through the grey model was reduced by 11.67% for the non-conventional system, whereas the difference between the fourth moments of the grey and analytical models were reduced by 0.74% for the conventional system. Through the convergence plot, it can be concluded that the grey model would forecast the experimental solution in a much more reliable way than that expected from the Blasius model for the conventional system.
• The uncertainty in the numerical solution of the conventional unit decreased by 14.93% when it was compared with the uncertainty computed for the non-conventional unit. In the context of the Blasius solution, the maximum error in the grey model dropped by 28.49% while forecasting the mainstream velocity, although the percentage % in the grey model would be asymptotic along the axis $U=0$. This implies that the convergence level remains constant irrespective of the duration provided for the experimental work.
• The shear stress calculated for the non-conventional system would be zero for the given interval of 0.0288–0.0324 m. In the case of the conventional unit, the interval decreased to 0.0036–0.0072 m. The maximum shear stress estimated through the grey and Blasius models is 3.88 × 10⁻⁰⁴ N·m⁻² and 5.49 × 10⁻⁰⁴ N·m⁻², respectively.
• The uncertainty in the numerical solution to predict the absorber plate temperature is ±0.43K for the non-conventional system. The variability in the numerical solution would be high at the onset of experimental work. The distribution behaviour of the numerical solution for absorber plate temperature will share the characteristic of the binomial distribution function. For the conventional system, the distribution characteristic of numerical solution for air temperature would be equivalent to a high-order Gaussian function. The percentage fit of the linear grey model is 96% with the experimental data sets of absorber plate and air temperature. In the case of the air temperature measurement for the nonconventional system, the numerical solution encountered uncertainty of ±0.53 K, whereas it was ±1.47 K while evaluating the air temperature for the conventional unit. While forecasting the absorber plate temperature for the nonconventional system, the maximum MAPE(T) in the numerical solution of the linear grey model was 0.037%, which further dropped by 85.18% for the conventional system.