Fault Diagnosis of Coal Mill Based on Kernel Extreme Learning Machine with Variational Model Feature Extraction
Abstract
:1. Introduction
2. Fault Diagnosis Model
2.1. Signal Decomposition and Feature Extraction
2.1.1. Signal Decomposition
- (1)
- Calculate the bandwidth of each intrinsic model function. For each model uk, the corresponding analytical signal is calculated by Hilbert transform to obtain a one-sided spectrum, and then an exponential term is added to adjust the respective center frequency, and the spectrum of each intrinsic model function is modulated to the baseband. Gaussian smoothing is applied to the demodulated signal to estimate the corresponding bandwidth, so the constrained variational model is constructed as Equation (1).where δ(t) is the unit shock function, t is time; {uk} is the model set, which can be expressed as {u1,⋯,uK}; {ωk} is the corresponding center frequency set, which can be expressed as {ω1,⋯,ωK}; The constraint is that the sum of the models is equal to the input signal f.
- (2)
- In order to make the problem into an unconstrained optimization problem, the quadratic penalty factor α and the Lagrange multiplier λ are introduced. Using Augmented Lagrangian to solve the unconstrained variational problem, the original minimization problem of Equation (1) is transformed into seeking the “saddle point” of Equation (2):where K is the number of intrinsic modal functions.
- (3)
- In order to solve the variational problem of Equation (2), the alternating direction multiplier method (ADMM) is used to update alternately. The problem is transformed to the frequency domain and solved using the Parseval/Plancherel Fourier equidistant in the L2 norm. Among them, i and n represent different parameters to obtain arbitrary values. The solution expressions are Equations (3) and (4), respectively:
- (4)
- Update ωkn + 1, λkn + 1, in the same way, see Equations (5)–(7).where τ is a variable; ωkn + 1 is the center frequency of the current spectrum. Stop updating when the accuracy satisfies Equation (7); ε is the convergence accuracy, ε > 0.
- (5)
- Finally, the inverse Fourier transform is used to convert to the time domain, and the k narrowband IMF components after the power sequence are decomposed are obtained, and the adaptive segmentation of the signal in the frequency domain is completed.
2.1.2. Feature Extraction
(1) The Sample Entropy
- (1)
- Matrix Q is obtained by the phase space reconstruction of the time series signal P(p(n), n = 1,2,…,N) based on Equation (8).where m is the model dimension; 1 ≤ i, j, k ≤ N − m + 1.
- (2)
- Calculate the maximum difference between vector Q(i) and the corresponding element in Q(j) based on Equation (9), and define its absolute value as the distance d(i,j) between them.where 0 ≤ k ≤ m − 1; 1 ≤ i, j ≤ N − m + 1, j ≠ i.
- (3)
- The number of d(i,j) less than the similar tolerance threshold r is recorded as . The ratio of it to the total number of vectors N−m is recorded as , and the average value of N − m + 1 is recorded as , according to Equations (10) and (11).
- (4)
- The dimension is increased to m + 1 to obtain a set of m + 1-dimensional vectors. The can be achieved by repeating steps (1)–(3).
- (5)
- Substitutions of Bm(r) and Bm + 1(r) into Equation (12) can solve the sample entropy.
(2) The Feature Energy
(3) Kernel Principal Component Analysis
2.2. GA-KELM Model and Verification
2.2.1. Principle of GA-KELM Model
2.2.2. Model Validation Based on Bearing Public Datasets
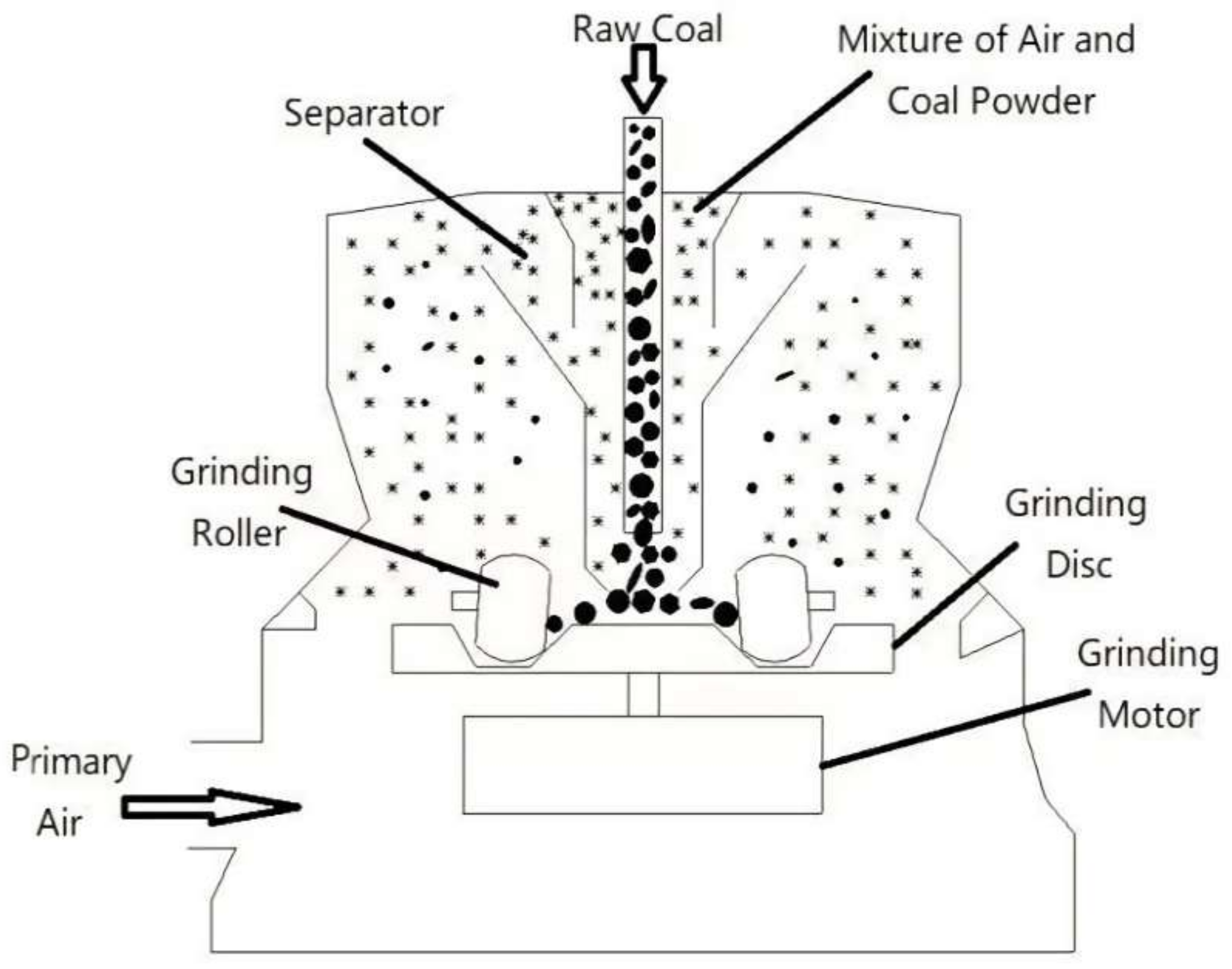
3. Establishment of Fault Diagnosis Model for Coal Mill
- (1)
- The vibration signals of a medium-speed coal mill under various working conditions are collected, and the abnormal values are processed; then, the bad points are removed to form the vibration signal sequence.
- (2)
- The VMD signal decomposition method described in 2.1.1 (Formulas 1–5) is used to decompose the vibration signal of the coal mill to obtain the distribution change of the intrinsic mode function.
- (3)
- The feature extraction method described in 2.1.2 is used to calculate the intrinsic mode functions obtained in (2), in which the sample entropy is calculated by Formulas 8–13; the characteristic energy is calculated by Formulas 14–15.
- (4)
- The kernel principal component analysis is carried out on the feature data set composed of sample entropy and feature energy by Formulas 16–24, and the CPV is used as an index to realize data dimension reduction.
- (5)
- The dimension-reduced fault label data are divided into a training set and a test set. The GA-KELM model described in 2.2 is used to train the training set, and then the test set is used to evaluate the diagnostic accuracy of the model.
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Hu, Y.; Ping, B.Y.; Zeng, D.L.; Niu, Y.G.; Gao, Y.K.; Zhang, D.M. Research on fault diagnosis of coal mill system based on the simulated typical fault samples. Measurement 2020, 161, 107864. [Google Scholar] [CrossRef]
- Gao, Y.; Zeng, D.; Liu, J.; Jian, Y. Optimization control of a pulverizing system on the basis of the estimation of the outlet coal powder flow of a coal mill. Control Eng. Pract. 2017, 63, 69–80. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, S.; Zhang, D.; Qiu, X.; Zhou, W. Coal mill fault diagnosis based on Gaussian process regression. IOP Conf. Ser. Earth Environ. Sci. 2019, 332, 042034. [Google Scholar] [CrossRef]
- Agrawal, V.; Panigrahi, B.K.; Subbarao, P. Intelligent Decision Support System for Detection and Root Cause Analysis of Faults in Coal Mills. IEEE Trans. Fuzzy Syst. 2017, 25, 934–944. [Google Scholar] [CrossRef]
- Fan, G.Q.; Rees, N.W. An intelligent expert system (KBOSS) for power plant coal mill supervision and control-ScienceDirect. Control Eng. Pract. 1997, 5, 101–108. [Google Scholar] [CrossRef]
- Wang, J.; Wei, J.; Shen, G. Condition Monitoring of Power Plant Milling Process Using Intelligent Optimisation and Model Based Techniques. Fault Detect. 2010, 19, 405–423. [Google Scholar]
- Wang, J.; Wei, J.; Zachariades, P.; Guo, S. On-line condition and safety monitoring of pulverised coal mills using a mode based pattern recognition technique. In Project B85A; The University of Birmingham, BCURA: Birmingham, UK, 2009. [Google Scholar]
- Guo, S.; Wang, J.; Wei, J.; Zachariades, P. A new model-based approach for power plant Tube-ball mill condition monitoring and fault detection. Energy Convers. Manag. 2014, 80, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.L.; Wang, J.; Wu, Q.H. Development of a Multisegment Coal Mill Model Using an Evolutionary Computation Technique. IEEE Trans. Energy Convers. 2007, 22, 718–727. [Google Scholar] [CrossRef]
- Su, Z.G.; Wang, P.H.; Yu, X.J.; Lv, Z.Z. Experimental investigation of vibration signal of an industrial tubular ball mill: Monitoring and diagnosing. Miner. Eng. 2008, 21, 699–710. [Google Scholar] [CrossRef]
- Kisic, E.; Petrovic, V.; Vujnovic, S.; Durovic, Z.; Ivezic, M. Analysis of the condition of coal grinding mills in thermal power plants based on the T multivariate control chart applied on acoustic measurements. Facta Univ.-Ser. Autom. Control Robot. 2012, 11, 141–151. [Google Scholar]
- Tao, X.U.; Wang, Q. Application of Multiscale Principal Component Analysis Based on Wavelet Packet in Sensor Fault Diagnosis. Proc. Csee 2007, 27, 28. [Google Scholar]
- Si, D.T. The Fourier Transform and Principles of Quantum Mechanics. Appl. Math. 2018, 9, 347–354. [Google Scholar] [CrossRef] [Green Version]
- Bagheri, A.; Fatemi, A.A.; Amiri, G.G. Simulation of earthquake records by means of empirical mode decomposition and Hilbert spectral analysis. J. Earthq. Tsunami 2014, 8, 1450002. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Processing 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, X.; He, Y.; Lin, X.; Gu, X. Energy efficiency analysis for ethylene plant based on PCA-DEA. Ciesc J. 2015, 66, 278–283. [Google Scholar]
- Bounoua, W.; Bakdi, A. Fault detection and diagnosis of nonlinear dynamical processes through correlation dimension and fractal analysis based dynamic kernel PCA. Chem. Eng. Sci. 2021, 229, 116099. [Google Scholar] [CrossRef]
- Amin, M.T.; Khan, F.; Ahmed, S.; Imtiaz, S. A data-driven Bayesian network learning method for process fault diagnosis. Process Saf. Environ. Prot. 2021, 150, 110–122. [Google Scholar] [CrossRef]
- Cao, W.; Wang, X.; Ming, Z.; Gao, J. A review on neural networks with random weights. Neurocomputing 2018, 275, 278–287. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, P. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme Learning Machines: A Survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Goel, T.; Murugan, R. Classifier for Face Recognition Based on Deep Convolutional-Optimized Kernel Extreme Learning Machine. Comput. Electr. Eng. 2020, 85, 159–164. [Google Scholar] [CrossRef]
- Khoshnami, A.; Sadeghkhani, I. Sample entropy-based fault detection for photovoltaic arrays. IET Renew. Power Gener. 2018, 12, 1966–1976. [Google Scholar] [CrossRef]
- Pahon, E.; Steiner, N.Y.; Jemei, S.; Hissel, D.; Pera, M.C.; Wang, K.; Mocoteguy, P. Solid oxide fuel cell fault diagnosis and ageing estimation based on wavelet transform approach. Int. J. Hydrog. Energy 2016, 41, 13678–13687. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Wen, H.; Fan, H.; Xie, W.; Pei, J. Hybrid Structure-Adaptive RBF-ELM Network Classifier. IEEE Access 2017, 5, 16539–16554. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2018, 135, 271–281. [Google Scholar] [CrossRef]
- Muhammad, A.R.; Yuan, X.; Ozgur, K.; Muhammad, A.; Asif, M. Stream Flow Forecasting of Poorly Gauged Mountainous Watershed by Least Square Support Vector Machine, Fuzzy Genetic Algorithm and M5 Model Tree Using Climatic Data from Nearby Station. Water Resour. Manag. 2018, 32, 4469–4486. [Google Scholar]
- Wan, J.; Li, S. Modeling and application of industrial process fault detection based on pruning vine copula. Chemom. Intell. Lab. Syst. 2019, 184, 1–13. [Google Scholar] [CrossRef]
- Ren, X.; Zhu, K.; Cai, T.; Li, S. Fault Detection and Diagnosis for Nonlinear and Non-Gaussian Processes Based on Copula Subspace Division. Ind. Eng. Chem. Res. 2017, 56, 11545–11564. [Google Scholar] [CrossRef]


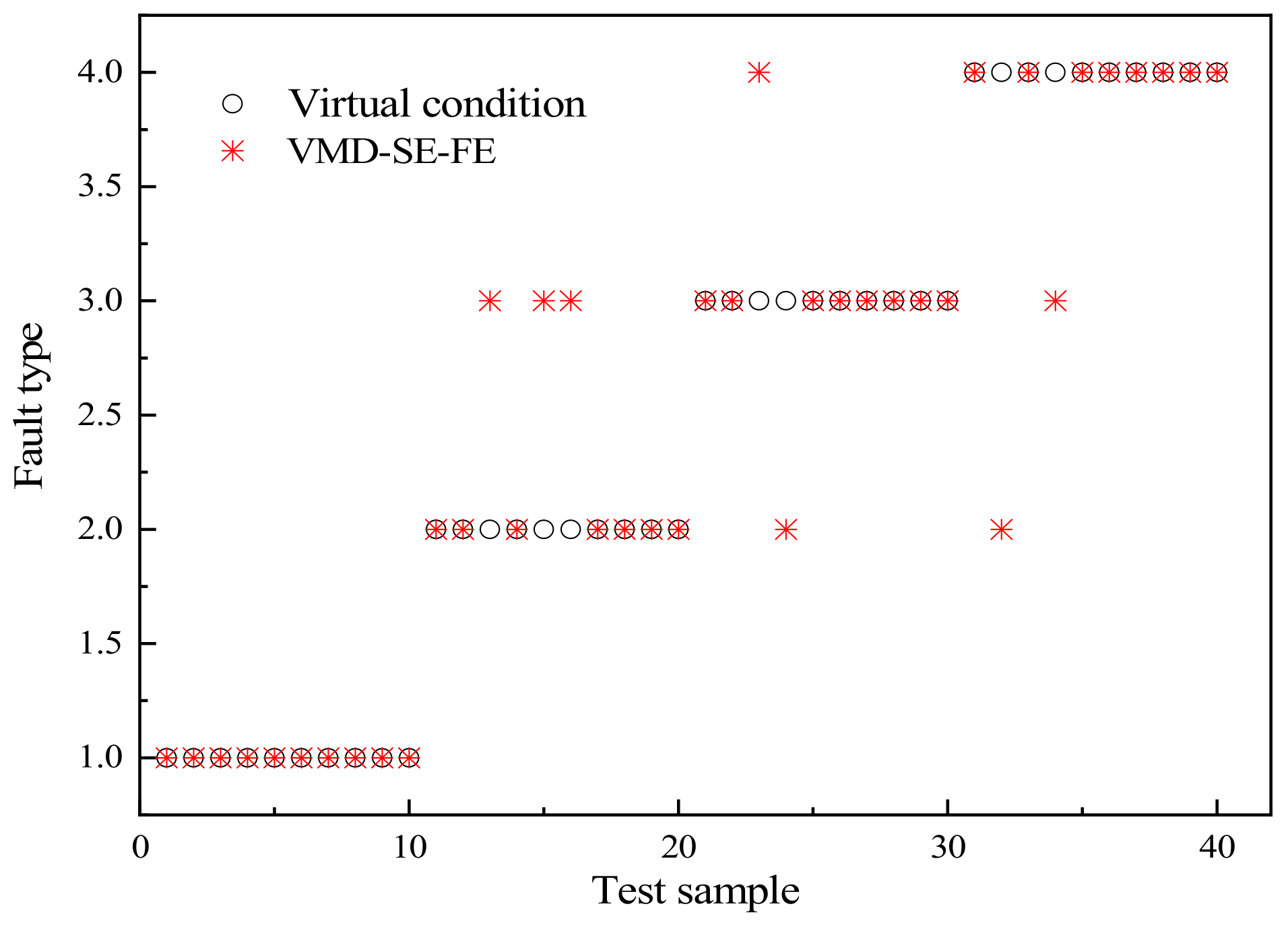
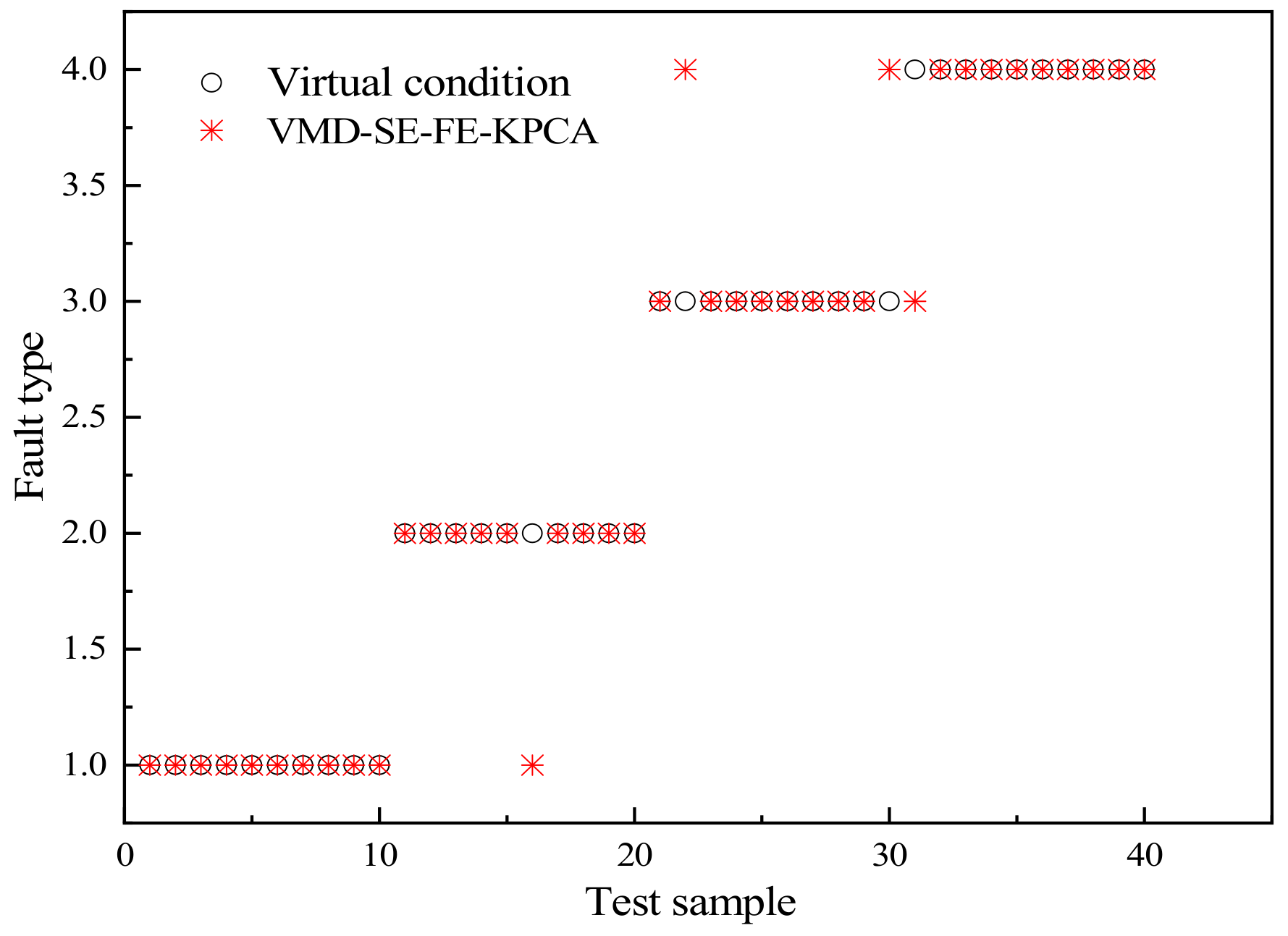
| Model | Training Accuracy (%) | Testing Accuracy (%) | Testing Time (s) |
|---|---|---|---|
| BP | 93.33 | 32.50 | 15.32 |
| SVM | 100 | 62.50 | 6101.44 |
| ELM | 100 | 45.00 | 147.65 |
| KELM | 96.67 | 72.50 | 95.28 |
| No. | Item | Unit | ZGM123G-III |
|---|---|---|---|
| 1 | Coal type | Fat coal, poor coal, some anthracite and black lignite | |
| 2 | Coal powder fineness | R90 = 10–40% | |
| 3 | Guaranteed output (R90 = 13.9%, HGI = 45, W = 11.9%) | t/h | 73.53 |
| 4 | Rate power of motor | kW | 900 |
| 5 | Voltage of motor | kV | 6.6 |
| 6 | Rated speed of the mill | r/min | 30.9 |
| 7 | Windage (Guaranteed output) | Pa | 7340 |
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | |
|---|---|---|---|---|---|---|---|---|
| Fault 1 | 0.0523 | 0.3394 | 0.5420 | 0.5384 | 0.4853 | 0.4084 | 0.2518 | 0.0500 |
| Fault 1 | 0.0560 | 0.2238 | 0.5133 | 0.6298 | 0.5637 | 0.3849 | 0.1747 | 0.0496 |
| Fault 2 | 0.0880 | 0.5982 | 1.3503 | 1.4385 | 1.3853 | 1.2403 | 0.6876 | 0.2654 |
| Fault 2 | 0.0845 | 0.5889 | 1.3017 | 1.4184 | 1.2870 | 1.1994 | 0.7982 | 0.3461 |
| Fault 3 | 0.1351 | 0.7370 | 1.3986 | 1.4055 | 1.3835 | 1.3403 | 1.0675 | 0.4099 |
| Fault 3 | 0.1061 | 0.8253 | 1.2439 | 1.4709 | 1.3817 | 1.2144 | 0.8679 | 0.3727 |
| Label | PC1 | PC2 | PC 3 | Label | PC1 | PC2 | PC3 |
|---|---|---|---|---|---|---|---|
| 1 | 0.687 | 1.994 | −1.998 | 2 | −4.046 | −0.433 | 0.435 |
| 1 | −0.060 | 2.237 | −1.020 | 3 | −3.383 | −1.699 | 0.464 |
| 2 | −4.046 | −0.433 | 0.435 | 3 | −3.090 | −1.760 | 0.355 |
| Model | Regularization Coefficient | Kernel Parameters |
|---|---|---|
| VMD-SE | 37.43 | 8.43 |
| VMD-FE | 46.26 | 1.21 |
| VMD-FE-SE | 68.52 | 0.83 |
| FE-SE-PCA | 78.16 | 2.21 |
| FE-SE-KPCA | 186.15 | 3.25 |
| Model | Training Accuracy (%) | Testing Accuracy (%) | Testing Time (s) |
|---|---|---|---|
| KELM | 89.2 | 67.5 | 9.36 |
| VMD-SE | 86.7 | 70 | 12.63 |
| VMD-FE | 89.2 | 77.5 | 13.92 |
| VMD-FE+SE | 96.6 | 82.50 | 25.27 |
| FE+SE+PCA | 95 | 80 | 18.49 |
| FE+SE+KPCA | 95.8 | 87.5 | 16.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Pan, C.; Wang, Y.; Xu, M.; Zhou, F.; Yang, X.; Zhu, L.; Zhao, C.; Song, Y.; Chen, H. Fault Diagnosis of Coal Mill Based on Kernel Extreme Learning Machine with Variational Model Feature Extraction. Energies 2022, 15, 5385. https://doi.org/10.3390/en15155385
Zhang H, Pan C, Wang Y, Xu M, Zhou F, Yang X, Zhu L, Zhao C, Song Y, Chen H. Fault Diagnosis of Coal Mill Based on Kernel Extreme Learning Machine with Variational Model Feature Extraction. Energies. 2022; 15(15):5385. https://doi.org/10.3390/en15155385
Chicago/Turabian StyleZhang, Hui, Cunhua Pan, Yuanxin Wang, Min Xu, Fu Zhou, Xin Yang, Lou Zhu, Chao Zhao, Yangfan Song, and Hongwei Chen. 2022. "Fault Diagnosis of Coal Mill Based on Kernel Extreme Learning Machine with Variational Model Feature Extraction" Energies 15, no. 15: 5385. https://doi.org/10.3390/en15155385
APA StyleZhang, H., Pan, C., Wang, Y., Xu, M., Zhou, F., Yang, X., Zhu, L., Zhao, C., Song, Y., & Chen, H. (2022). Fault Diagnosis of Coal Mill Based on Kernel Extreme Learning Machine with Variational Model Feature Extraction. Energies, 15(15), 5385. https://doi.org/10.3390/en15155385





