A Hybrid Three-Level ZVZCS Converter for Photovoltaic Power Connecting to MVDC Collection System

Abstract

Compared with the medium voltage ac (MVAC) collection system, the medium voltage dc (MVDC) one for renewable energy sources has many advantages. High-power dc/dc converters are one of the key stages of the MVDC collection system to boost the voltage generated by photovoltaic or wind turbine. A novel hybrid three-level dc/dc converter utilizing a blocking capacitor to realize zero-voltage zero-current-switching (ZVZCS) is proposed. A higher overall efficiency can be achieved by reducing conduction losses. Detailed experimental results on a scaled-down hardware prototype rated at 150 V/750 V/1 kW are demonstrated to verify the proposed converter performance.

1. Introduction

With the rapid development of photovoltaic cell technology, the photovoltaic power generation capacity has increased significantly [1,2]. Until 2021, the centralized photovoltaic power was about 198 GW, and the distributed photovoltaic power was 107 GW in China, and the distributed photovoltaic power is growing faster because it is closer to the load side and easier to be absorbed. At present, distributed photovoltaic power generation is basically connected to an ac distribution network [3,4], while the photovoltaic cells are dc output components. Therefore, if the photovoltaic is connected to the dc distribution network, then the dc/ac power conversion stage can be saved, and the dc distribution network has the advantages of low transmission losses, high power quality, a longer power supply radius, and no reactive power [5,6].

At present, some low- and medium-voltage dc power distribution networks have been implemented. The research work on the low-voltage dc power distribution network is mainly reflected in the low-voltage dc microgrid, e.g., the green building research plan proposed by Virginia University of technology [7,8] and the bipolar dc distribution network system designed by Osaka University [9]. For the medium voltage dc (MVDC) power distribution network, a 5 kV campus dc distribution project has been built in RWTH Aachen University in Germany [10]. Moreover, in China, more than five MVDC power distribution networks have been built in Guizhou, Hangzhou, Suzhou, Zhangbei, and Zhuhai [11].

A high-power, high-gain dc/dc converter is the key equipment to connect the distributed photovoltaic and MVDC network, such as the resonant switched capacitor converter [12] and classical full bridge converter. With the increase of photovoltaic cell voltage to 1.5 kV [13], higher voltage stress is required for the input voltage side of the dc/dc converter, and the classical full bridge structure may not be able to fit the new occasion. A multilevel converter is a good alternative to reduce the voltage stress of power switch; a good example is the widely used three-level (TL) converter, in which the voltage stress of power switch is only half of the input voltage. Soft switching technology is essential in high power applications in order to reduce the switching losses and, thus, to increase the switching frequency. Zero-voltage-switching (ZVS) TL converters are studied comprehensively to realize ZVS for the main switches [14,15,16]. It is well-known that the ZVS is suitable for MOSFETs, which have large parasitic capacitance, while their voltage/current ratings are relatively lower. For the high-power converter, the IGBTs are preferred. Due to the current tailing characteristic of IGBT, the zero-current-switching (ZCS) technology can reduce the turn-off losses of IGBT significantly. Several ZVZCS TL dc/dc converters have been proposed with excellent performance recently [17,18,19]. It also should be noted that some of the main IGBT switches can only realize ZVS, for which there are still relatively larger turn-off losses. In Reference [20], a hybrid ZVZCS TL converter was proposed for which all the four main IGBTs realize ZCS turn-off and two auxiliary IGBTs realize ZVZCS; thus, the turn-off losses can be further reduced. However, there still is a certain circulating current flowing in vain through the main/auxiliary IGBTs and auxiliary transformer, causing larger conduction losses, while there is no circulating current in the classical ZVZCS TL converter.

In this paper, an improved hybrid ZVZCS TL converter is proposed in which the circulating current is eliminated by modifying the rectifier circuit and introducing a blocking capacitor. This paper is organized as follows. The proposed circuit and basic operation principle are discussed in Section 2. The design procedure of the converter is presented in Section 3. The simulation and experimental results are provided and analyzed in Section 4 and Section 5. Finally, some brief conclusions are given in Section 6.

2. Circuit Configuration and Operation Principles

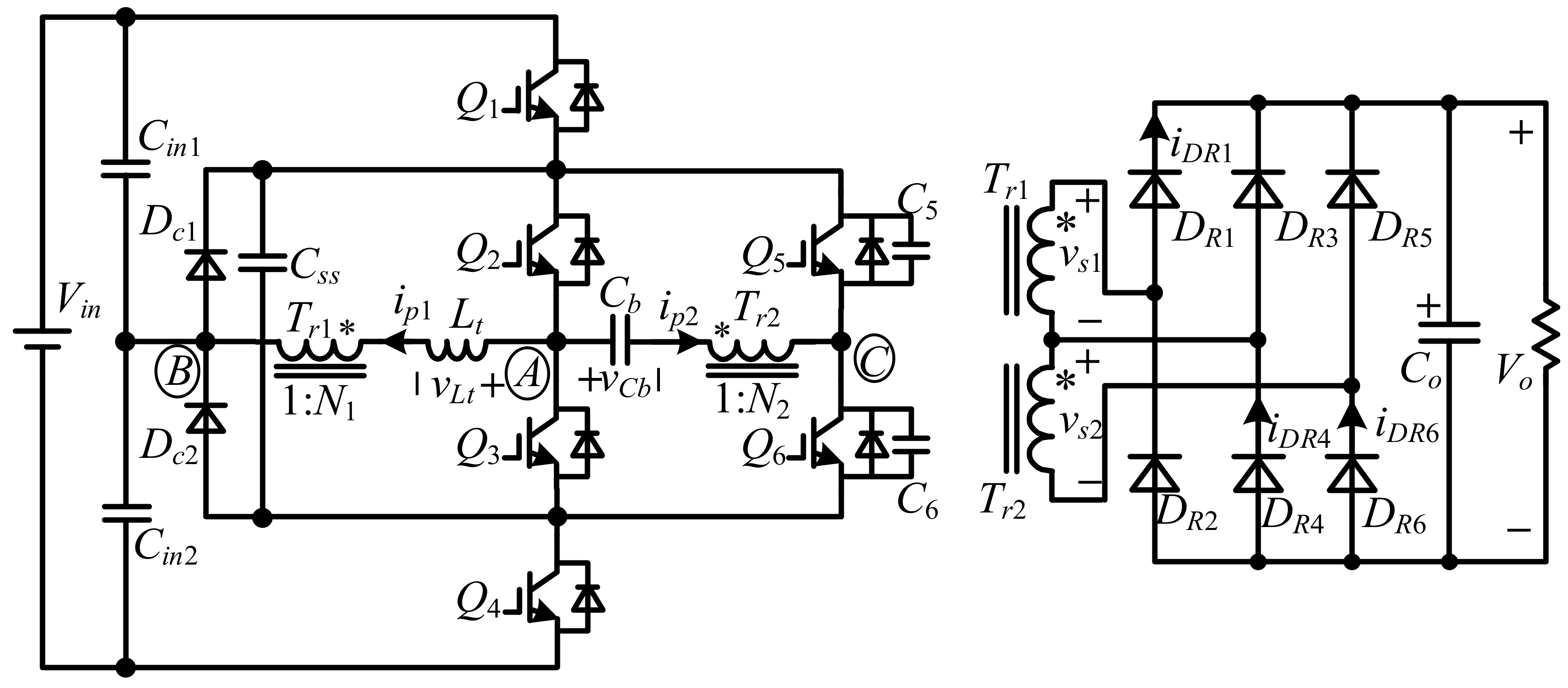
The proposed hybrid ZVZCS TL converter is shown in Figure 1. The conventional TL unit is composed of two input divided capacitors, C_in1 and C_in2; four main switches, Q₁~Q₄; two clamping diodes, D_c1 and D_c2; a flying capacitor, C_ss; a primary winding of main transformer, T_r1; and a transmission inductor, L_t. The auxiliary structure is composed of switches Q₅ and Q₆ (including two extra paralleled capacitors, C₅ and C₆), blocking capacitor C_b, and primary winding of auxiliary transformer T_r2. At the rectifier side, the secondary windings of T_r1 and T_r2 are connected in series, and six diodes, D_R1~D_R6, form two full-bridge rectifier cells, in which D_R1, D_R2, D_R5, and D_R6 form one rectifier cell and D_R1~D_R4 form another one. C_o is the output filter capacitor. N₁ is the turns ratio of T_r1, N₂ is the turns ratio of T_r2, and N₂ should be smaller than N₁ to make the converter work properly.

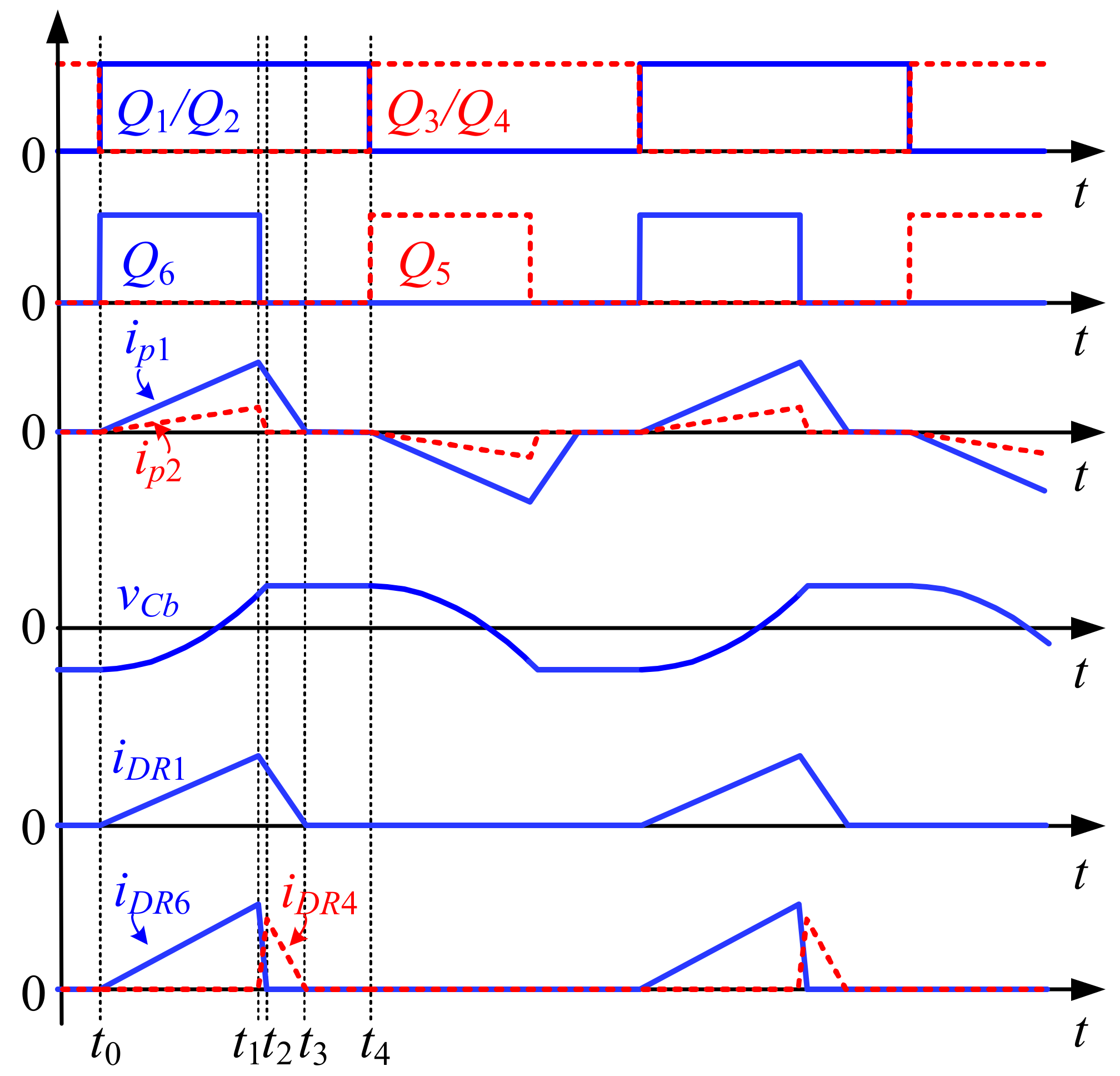
The key waveforms of the proposed converter are given in Figure 2. The switches Q₁/Q₂ and Q₃/Q₄ in the three-level unit are complementarily switched at a fixed 50% duty cycle with a dead time. Q₅ and Q₆ use PWM chopping control and have the same turn-on time as Q₃ and Q₁, respectively. The C_in1 and C_in2 are identical and large enough so that the input voltage, V_in, is considered constant at the steady state and identically divided by the two capacitors. Considering symmetry, a half-switching cycle over four modes was studied and is depicted in Figure 3.

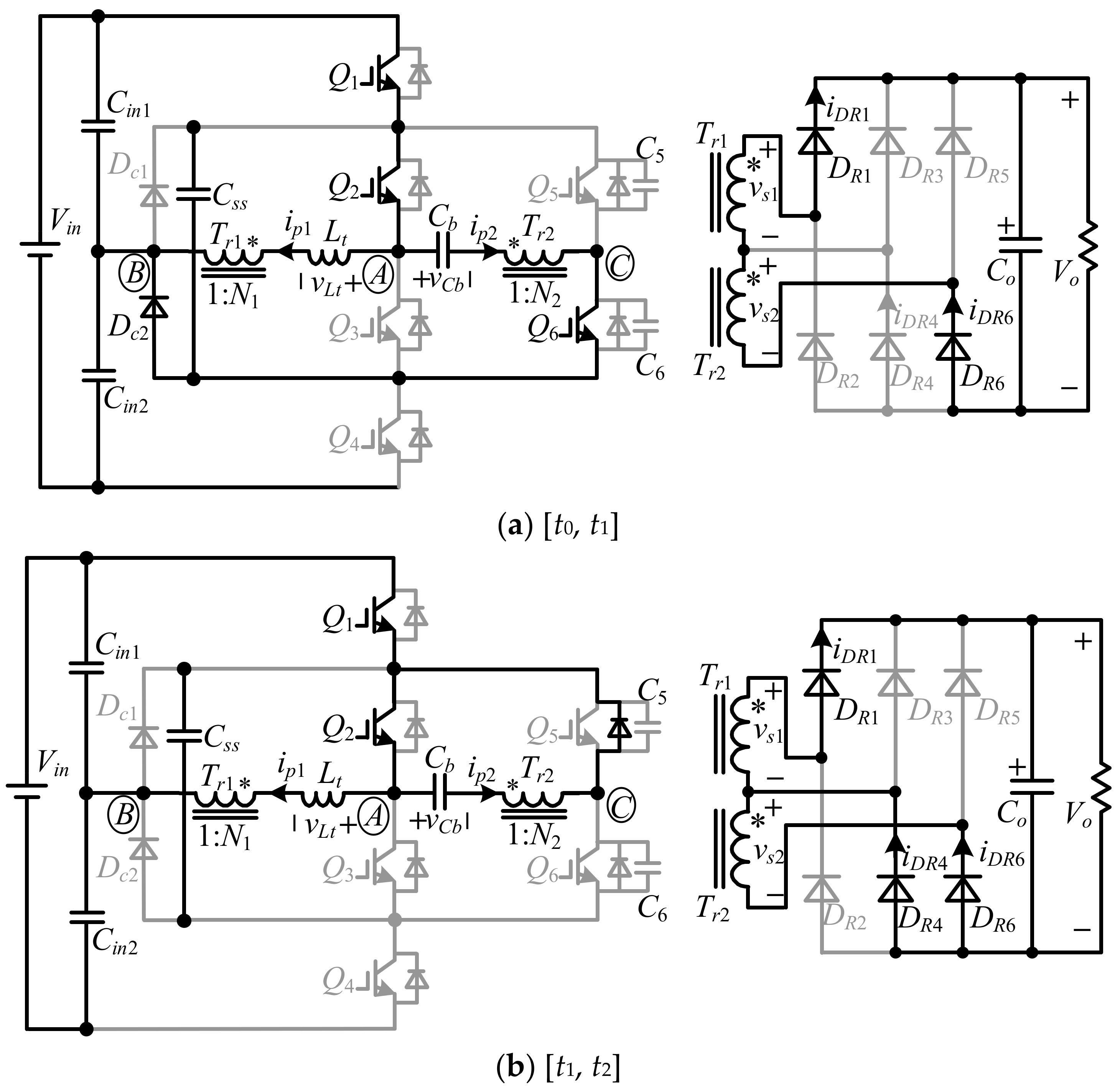
(1) Mode 1 [t₀, t₁]: At t₀, Q₃ and Q₄ are turned off, and Q₁, Q₂, and Q₆ are turned on. Due to the fact that there are no currents flowing through all switches before t₀, Q₁, Q₂, and Q₆ are turned on with the ZCS condition. As shown in Figure 3a, active power is transferred from source to load through two transformers. At the input side, the primary current (i_p1) of transformer T_r1 flows through Q₁, Q₂, primary winding of T_r1, L_t, and C_in1; the primary current (i_p2) of transformer T_r2 flows through Q₁, Q₂, C_b, primary winding of T_r2, Q₆, D_c2, and C_in1; and v_AB = v_AC = V_in/2. At the output side, the current flows through the secondary windings of T_r1 and T_r2, and through D_R1 and D_R6. The leakage inductance of T_r1 is involved in the transmission inductance, L_t, and the leakage inductance of T_r2 is represented as L_lk, which is not shown in Figure 1. The voltages across the L_t, C_b, and L_lk are represented as v_Lt, v_Cb, and v_Llk, respectively. Therefore, the voltages of the secondary windings of T_r1 and T_r2, and v_s1 and v_s2, respectively, can be derived as follows:

$$\left\{\begin{array}{c}{v}_{s1}\left(t\right)=N_1\left(V_{in}/2-v_{L_t}\left(t\right)\right)\\ v_{s2}\left(t\right)=N_2\left(V_{in}/2-v_{Cb}\left(t\right)-v_{L_{lk}}\left(t\right)\right)\end{array}\right.$$

(1)

The voltages v_Lt and v_Llk can be expressed as follows:

$$\left\{\begin{array}{c}{v}_{Lt }\left(t\right)=L_t\frac{d{i}_{p1}\left(t\right)}{dt}\\ v_{Llk}\left(t\right)=L_{lk}\frac{d{i}_{p2}\left(t\right)}{dt}\end{array}\right.$$

(2)

For the blocking capacitor, C_b, we have the following:

$$i_{p2}\left(t\right)=C_b\frac{d{v}_{Cb}\left(t\right)}{dt}$$

(3)

For the output side, we have the following:

$$i_{DR1}\left(t\right)=i_{DR6}\left(t\right)=\frac{i_{p1}\left(t\right)}{N_1}=\frac{i_{p2}\left(t\right)}{N_2}$$

(4)

$$v_{s1}\left(t\right)+v_{s2}\left(t\right)=V_o$$

(5)

where i_DR1 and i_DR6 are the currents flowing through D_R1 and D_R6, respectively.

Substitution of (1)~(4) into (5), and we can have the following:

$$\left(L_{lk}+\frac{N_1{}^2}{N_2{}^2}·L_t\right)C_b·\frac{d^2{v}_{Cb}\left(t\right)}{d{t}^2}+v_{Cb}\left(t\right)=\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}$$

(6)

At t₀, the value of v_Cb is v_Cb(t₀) and i_p2(t₀) = 0, and (7) can be obtained from (6):

$$\begin{gathered} {\left[v_{Cb}\left(t\right)-\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}\right]}^2+{\left[\frac{1}{N_2}\sqrt{\frac{N_1{}^2·L_t+N_2{}^2·L_{lk}}{C_b}}{i}_{p2}\left(t\right)\right]}^2 \\ ={\left[\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}-v_{Cb}\left(t_0\right)\right]}^2 \end{gathered}$$

(7)

According to the analysis, the equivalent circuit reflecting to the secondary sides of transformers is given in Figure 4, and we have the following:

$$v_{Cb}\left(t\right)=\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}+\left[v_{Cb}\left(t_0\right)-\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}\right]\cos \left({\omega }_r\left(t-t_0\right)\right)$$

(8)

$$i_{p2}\left(t\right)=-\left[\frac{2N_2{v}_{Cb}\left(t_0\right)-\left(N_1+N_2\right)V_{in}+2V_o}{2N_2}\right]{\omega }_{r}sin\left({\omega }_r\left(t-t_0\right)\right)$$

(9)

where we have the following:

$$\left\{\begin{array}{c}{\omega }_r=\frac{N_2}{\sqrt{\left(N_1{}^2·L_t+N_2{}^2·L_{lk}\right)·C_b}}\\ \\ Z_r=N_2\sqrt{\frac{N_1{}^2·L_t+N_2{}^2·L_{lk}}{C_b}}\end{array}\right.$$

(10)

(2) Mode 2 [t₁, t₂]: At t₁, Q₆ is turned off. Due to C₅ and C₆, the rise rate of the voltage across Q₆ is limited, and Q₆ achieves ZVS turn-off. When C₅ is charged to V_in/2 and C₆ is discharged to zero, the anti-parallel diode of Q₅ naturally conducts, and i_p2 flows through it. Then i_p2 flows through Q₂, the primary winding of T_r2, C_b, and the anti-parallel diode of Q₅, and it should be noted that v_Cb(t₁) is positive now and, thus, i_p2 will decay rapidly with the help of v_Cb. At the output side, the current flowing through the secondary winding of T_r2 also decays rapidly while the current is flowing through the secondary winding of T_r1 almost unchanged; thus, D_R4 conducts to compensate for the reduced current of T_r2. In other words, both D_R4 and D_R6 conduct in this mode. At t₂, both i_p2 and i_DR6 are decayed to zero; hence, the circulating currents are removed from Q₂, Q₅, and T_r2, and D_R6 is turned off with the ZCS condition. The voltage v_Cb is considered to be constant during the mode because the time interval [t₁, t₂] is very short:

$$v_{Cb}\left(t\right)=v_{Cb}\left(t_1\right)\approx v_{Cb}\left(t_2\right)$$

(11)

$$\left\{\begin{array}{c}{i}_{p1}\left(t\right)=i_{p1}\left(t_1\right)-\left(\frac{V_0}{N_1}-\frac{V_{in}}{2}\right)\frac{\left(t-t_1\right)}{L_t}\\ \\ i_{p2}\left(t\right)=i_{p2}\left(t_1\right)-v_{Cb}\left(t_1\right)\frac{\left(t-t_1\right)}{L_{lk}}\end{array}\right.$$

(12)

$$i_{DR4}\left(t\right)=i_{DR1}\left(t\right)-i_{DR6}\left(t\right)$$

(13)

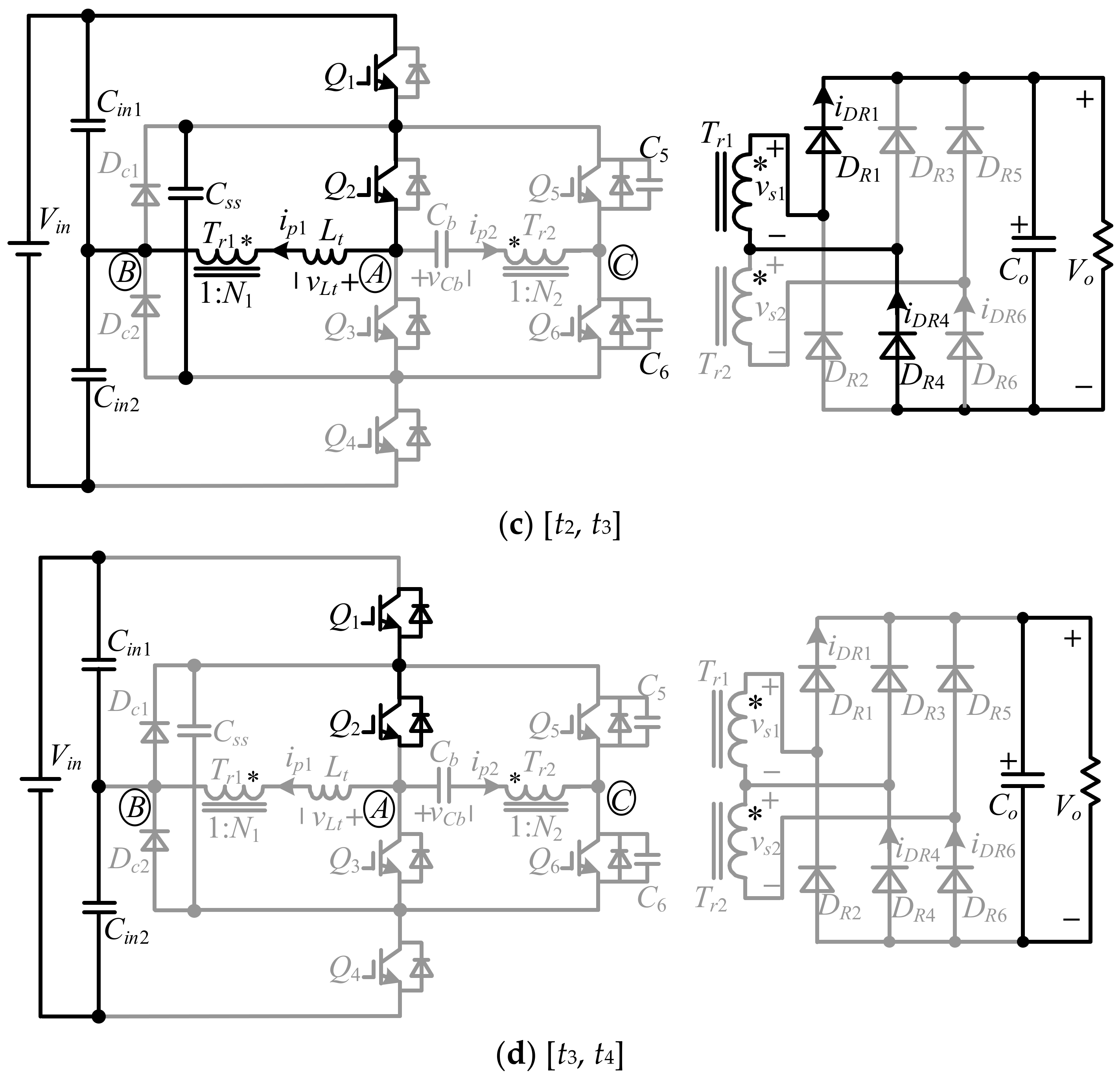
(3) Mode 3 [t₂, t₃]: As shown in Figure 3c, the current loop of i_p1 is still the same as that in Modes 1 and 2, while at the output side, the current flows through D_R4, the secondary winding of T_r1 and D_R1. Thus, the voltage across the secondary winding of T_r1 is clamped at V_o, and i_p1 has the same expression as (12), and it decreases to zero at t₃. Moreover, v_Cb stays constant in this mode:

$$i_{p1}\left(t\right)=i_{p1}\left(t_2\right)-\left(\frac{V_o}{N_1}-\frac{V_{in}}{2}\right)\frac{\left(t-t_2\right)}{L_t}$$

(14)

$$i_{DR1}\left(t\right)=i_{DR4}\left(t\right)=\frac{i_{p1}\left(t\right)}{N_1}$$

(15)

$$v_{Cb}\left(t\right)=v_{Cb}\left(t_2\right)=v_{Cb}\left(t_3\right)$$

(16)

For the proper operation of the converter, V_in/2 must be lower than V_o/N₁, as i_p1 decays linearly in this mode.

(4) Mode 4 [t₃, t₄]: As shown in Figure 3d, at t₃, i_p1, i_DR1, and i_DR4 decrease to zero, and D_R1 and D_R4 are turned off with ZCS. Although Q₁ and Q₂ are still ON, the voltage across the secondary winding of T_r1 is lower than V_o, and, thus, there is no current flowing through them, and v_Cb remains unchanged in this mode. The load is only supplied by C_o. At t₄, Q₁ and Q₂ are turned off with ZCS, while Q₂, Q₃, and Q₅ are turned on with the ZCS condition. Moreover, the voltage of Q₅ equals v_Cb(t₃) and is relatively lower than V_in in this mode, meaning that Q₅ is turned on with the approximate ZVZCS condition.

According to the above analysis, it can be seen that the four main IGBT switches, Q₁~Q₄, realize ZCS turn-on and turn-off; and the two auxiliary IGBT switches, Q₅ and Q₆, realize ZVZCS turn-on and ZVS turn-off. Due to the fact that the current flowing through the auxiliary IGBTs is relatively lower than that in the main IGBTs, the switching losses of the converter can be reduced significantly, and, moreover, the circulating current in the primary side of T_r2 is also eliminated and the conduction losses of Q₂, Q₃, Q₅, and Q₆ can be reduced further.

3. Converter Design Procedure

For the convenience of design and simulation, the given parameters are as follows: input voltage, V_in, is 1500 V; output voltage, V_o, is 15 kV; rated power, P_N, is 2 MW; and the switching frequency, f_s, is 1000 Hz.

3.1. Capacitance of C_b

The voltage rating of the blocking capacitor, v_Cb(t₀), is heavily dependent on the capacitance of C_b; in addition, it also determines the time interval of Mode 2 (t₁~t₂). It is well-known that, the larger the value of C_b, the lower the required voltage rating of C_b is; however, the longer time interval of (t₁~t₂) is, in other words, generating larger conduction losses in primary side switches.

According to the operation principle and Figure 2, we have the following:

$$-v_{Cb}\left(t_0\right)=v_{Cb}\left(t_2\right)\approx v_{Cb}\left(t_1\right)$$

(17)

Substitute (17) into (9), and we have the following:

$$v_{Cb}\left(t_0\right)=\frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_2}\frac{\cos \left({\omega }_r\left(t_1-t_0\right)\right)-1}{\cos \left({\omega }_r\left(t_1-t_0\right)\right)+1}$$

(18)

Normalize C_b to C_{b_nom} and v_Cb(t₀) to v_{Cb_nom}(t₀), and Equation (18) can be rewritten as follows:

$$v_{Cb\_nom}\left(t_0\right)=\frac{\left(\cos a+1\right)}{\left(\cos a-1\right)}\frac{\left[\cos \left(\frac{a}{\sqrt{C_{b\_nom}}}\right)-1\right]}{\left[\cos \left(\frac{a}{\sqrt{C_{b\_nom}}}\right)+1\right]}$$

(19)

where we have the following:

$$a=\frac{N_2}{\sqrt{\left(N_1{}^2·L_t+N_2{}^2·L_m\right)}}·\left(t_1-t_0\right)$$

(20)

Obviously, the time interval of mode 1 is smaller than the half resonance cycle, which should satisfy the following:

$$\left\{\begin{array}{c}0<a<\frac{\pi }{2}\\ 0<\frac{a}{\sqrt[ ]{C_{b\_nom}}}<\frac{\pi }{2}\end{array}\right.$$

(21)

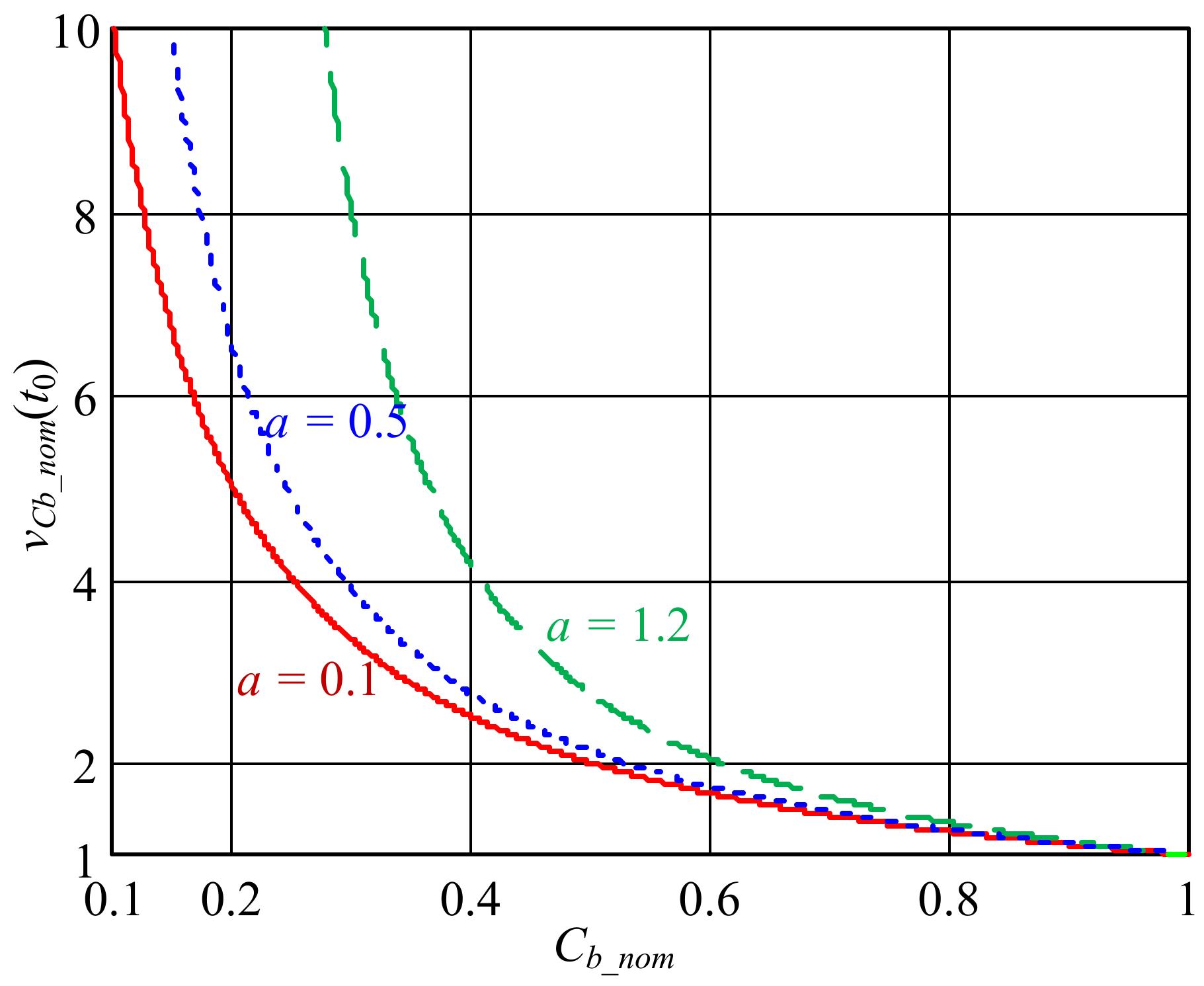
Without losing generality, three different values of a (0.1, 0.5 and 1.2) are selected, and v_{Cb_nom}(t₀) can be drawn versus C_{b_nom} with (19), as shown in Figure 5. It can be seen that v_{Cb_nom}(t₀) increases with the decrease of C_{b_nom}. Taking a = 0.5, for instance, when the C_{b_nom} is shrunk to 1/7, the v_{Cb_nom}(t₀) will increase 10 times. Therefore, the C_b should be set relatively larger to keep a smaller voltage rating.

From the analysis in Section 2, the role of C_b is to reset the primary current of T_r2 to zero during the freewheeling state (t₁, t₃), and, in general, the C_b is set to relatively larger to make the v_Cb smaller enough compared with the input voltage, V_in. Furthermore, due to the fact that the L_lk is smaller than L_t, and N₂ is smaller than N₁ for the proper operation of the converter, according to Figure 4, the currents of the secondary windings of T_r1 and T_r2 can be simplified as follows:

$$\frac{i_{p1}\left(t\right)}{N_1}=\frac{i_{p2}\left(t\right)}{N_2}\approx \frac{\left(N_1+N_2\right)V_{in}-2V_o}{2N_1{}^2{L}_t}\left(t-t_0\right)$$

(22)

From (12), we have the following:

$$i_{p2}\left(t_1\right)=v_{Cb}\left(t_1\right)\frac{\left(t_2-t_1\right)}{L_{lk}}$$

(23)

From (12) and (14), we have the following:

$$i_{p1}\left(t_1\right)=\left(\frac{V_0}{N_1}-\frac{V_{in}}{2}\right)\frac{\left(t_3-t_1\right)}{L_t}$$

(24)

Combining (23) and (24) yields, the following:

$$\frac{t_2-t_1}{t_3-t_1}=\frac{N_2{L}_{lk}\left(2V_o-V_{in}{N}_1\right)}{2N_1{}^2{L}_t{v}_{Cb}\left(t_1\right)}$$

(25)

C_b is always charged in Mode 1, and thus we have the following:

$$C_b\left(v_{Cb}\left(t_1\right)-v_{Cb}\left(t_0\right)\right)=\frac{\left(N_1+N_2\right)V_{in}-2V_o}{4N_1{}^2{L}_t}{N}_2{(t_1-t_0)}^2$$

(26)

Moreover, the value of C_b can be expressed by the following:

$$C_b=\frac{\left(N_1+N_2\right)V_{in}-2V_o}{8N_1{}^2{L}_t{v}_{Cb}\left(t_1\right)}{N}_2{(t_1-t_0)}^2$$

(27)

3.2. Turns Ratios N₁ and N₂

It was mentioned in Section 2 that most of the converter power should be delivered by T_r1 to reduce the switching losses through the proper design of N₁ and N₂, which is analyzed in this subsection. Only the power transmission during [t₀, t₄] is analyzed here due to the symmetry operation between two half cycles. Assuming 100% conversion efficiency of the converter and the transmission power, P_tot, during [t₀, t₄] can be expressed by the following:

$$P_{tot}=\frac{2}{T_s}{{\displaystyle \int }}_{t_0}^{t_4}{V}_o{i}_{DR1}dt=\frac{2V_o}{T_s}{{\displaystyle \int }}_{t_0}^{t_3}{i}_{DR1}dt$$

(28)

The power delivered by T_r1 and T_r2 is as follows:

$$P_{tr1}=\frac{2}{T_s}{{\displaystyle \int }}_{t_0}^{t_4}\frac{V_{in}}{2}{i}_{p1}dt=\frac{V_{in}}{T_s}{{\displaystyle \int }}_{t_0}^{t_3}{N}_1{i}_{DR1}dt=\frac{N_1{V}_{in}}{T_s}{{\displaystyle \int }}_{t_0}^{t_3}{i}_{DR1}dt$$

(29)

$$P_{tr2}=P_{tot}-P_{tr1}$$

(30)

By combining (28) and (29), we have the following:

$$\frac{P_{tr1}}{P_{tr2}}=\frac{P_{tr1}}{P_{tot}-P_{tr1}}=\frac{N_1{V}_{in}}{2V_o-N_1{V}_{in}}$$

(31)

It can be seen from (31) that P_tr1/P_tr2 is only determined by N₁ for the given V_o and V_in, and Figure 6 is illustrated with the given parameters. It can be seen that P_tr1/P_tr2 increases with the increase of N₁, and without losing generality, N₁ is set to 18, and P_tr1/P_tr2 = 9:1, as shown in Figure 6.

The converter should operate in the critical current continuous mode to reduce the peak current as far as possible under full load condition; in other words, there is no Mode 4:

$$t_3-t_0=0.5T_s$$

(32)

For L_t, the Equation (33) can be obtained by the volt–second balance rule.

$$\left[\left(N_1+N_2\right)\frac{V_{in}}{2}-V_o\right]\left(t_1-t_0\right)=\left(V_o-N_1\frac{V_{in}}{2}\right)\left(t_3-t_1\right)$$

(33)

Combining (32) and (33) yields the following:

$$V_o=\left(N_1+2D{N}_2\right)\frac{V_{in}}{2}$$

(34)

where D = (t₁ − t₀)/T_s is the duty cycle.

Obviously, D < 0.5, and we have the following:

$$N_2>\frac{2V_o}{V_{in}}-N_1$$

(35)

Then N₂ should be larger than 2 when N₁ = 18.

Under full load condition, P_tr1 can be expressed as follows:

$$P_{tr1}=V_{in}\frac{i_p{}_1\left(t_1\right)}{4}$$

(36)

By combining (31) and (36), we have the following:

$$i_p{}_1\left(t_1\right)=\frac{2N_1{P}_N}{V_o}$$

(37)

$$i_p{}_2\left(t_1\right)=\frac{2N_2{P}_N}{V_o}$$

(38)

From (38), it can be seen that, the smaller N₂ is, the lower i_p2(t₁) is, which also is the peak current and turn-off current of Q₅/Q₆. Therefore, to reduce the turn-off losses of Q₅/Q₆, N₂ should be as smaller as possible.

3.3. Transmission Inductance L_t and L_lk of T_r2

Under full load condition with (22), (34), and (38), we have the following:

$$L_t=\frac{V_o{T}_s\left(V_o-N_1{V}_{in}/2\right)\left[\left(N_1+N_2\right)V_{in}/2-V_o\right]}{2N_1{}^2{N}_2{V}_{in}{P}_N}$$

(39)

Figure 7 can be illustrated with (39) for the given parameters, and N₁ = 18. It can be seen that, the lower N₂ is, the smaller the L_t is required to be. However, L_t has a minimum inductance due to the existence of the leakage inductance of T_r1.

From (12), we can find that the time interval of Mode 2 [t₁, t₂] is determined by L_lk. Therefore, L_lk should be designed to be as small as possible to shrink the freewheeling state to reduce the conduction losses.

4. Simulation Verification

With the design parameters given in Section 3, we see that N₁ = 18, N₂ = 4, and L_t = 4.32 μH with (39), and without losing the generality, the L_lk is set to 2μH. Three different C_b values (200, 800, and 1400 μF) are selected to compare its influence and represented as Case−A, Case−B, and Case−C, respectively. The simulation results of i_p1, i_p2, v_Cb, i_DR1, i_DR4, and i_DR6 are given in Figure 8 and

Table 1. Comparison of simulation results of three cases.

Parameter	Case−A	Case−B	Case−C
|vCb(t0)| (V)	388.9	98.095	57.34
ip1(t1) (A)	4567.9	4594.9	4583.1
ip2(t1) (A)	1015.1	1021.1	1018.5
(t2-t1) (μs)	5.2	21.3	36.4
(t3-t1) (μs)	225.1	234.2	226.3

.

It can be seen that C_b almost has little effect on the i_p1(t₁), i_p2(t₁) and (t₃-t₁), which agrees well with the previous theoretical analysis. Case−A has the largest |v_Cb(t₀)| and also the shortest time interval of Mode 2 (t₂-t₁). Due to its smallest value of C_b, the currents of i_p1 and i_p2 show somewhat resonance in Figure 8a. For Case−C, it has the lowest |v_Cb(t₀)| and the longest commutation process of D_R6 to D_R4.

5. Experimental Results

The switching process and performance of the proposed converter are experimentally verified by a hardware prototype with 150–750 V, 1 kW. The turns ratios are N₁ = 9 and N₂ = 2, inductors are L_t = 8 μH and L_lk = 3 μH, blocking capacitor is C_b = 10 μF, flying capacitor is C_ss = 1 μF, Q₁~Q₆ are CRG60T60AK3HD, D_R1~D_R6 are RHRG30120, and switching frequency is f_s = 10 kHz. The prototype converter is shown in Figure 9.

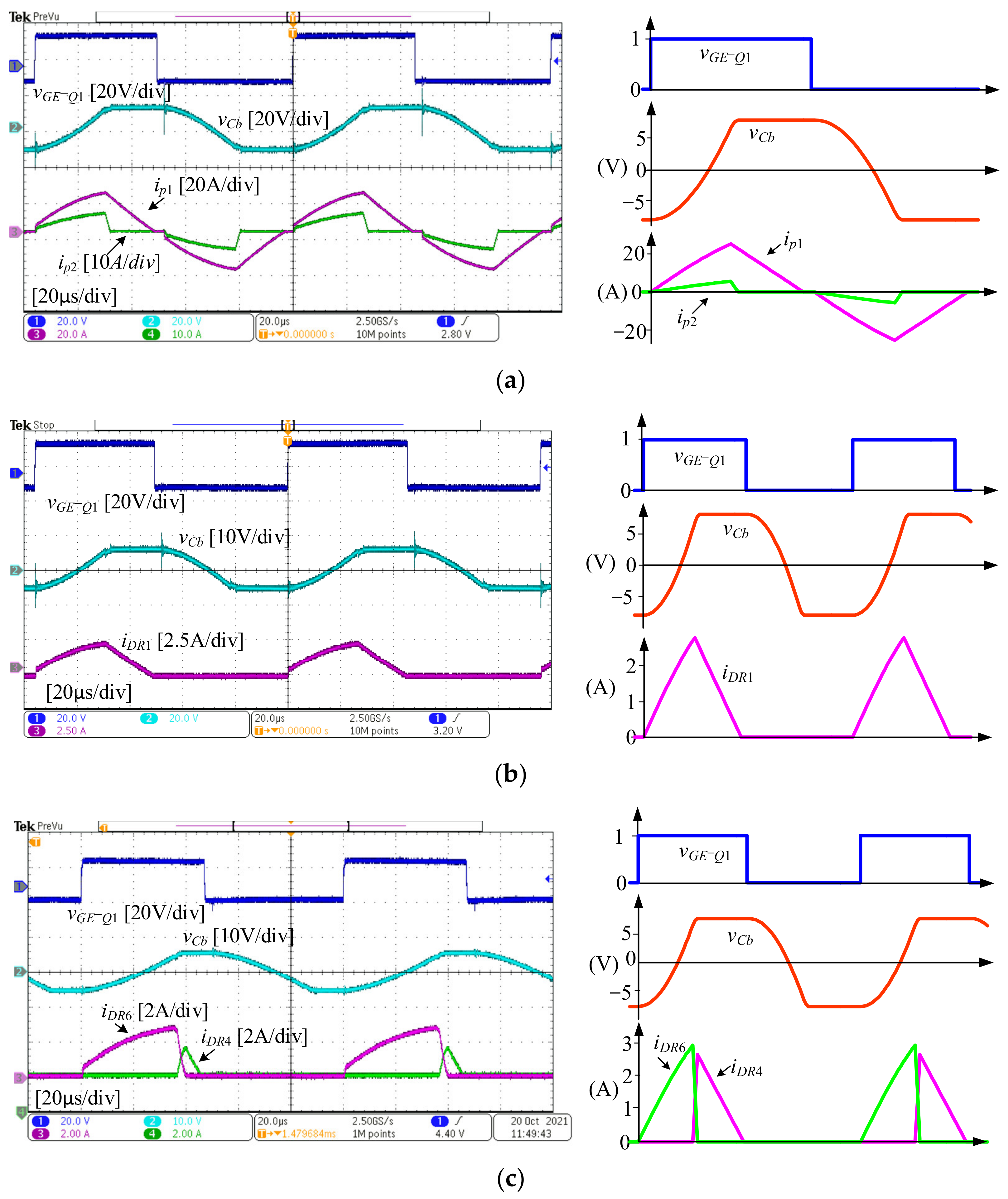
The main waveforms of the proposed three-level converter under rated power are shown in Figure 10 and Figure 11. For each experimental waveform, its corresponding simulation waveform is also given to verify the correction. As seen from Figure 10a, the current of i_p2 rapidly falls to zero, while the current i_p1 slowly decays to zero before the auxiliary switches are turned off. As seen from Figure 10b,c, all the currents flowing through the rectifier diodes linearly fall to zero without reverse recovery losses. The experimental waveforms match well with both the theoretical and simulation waveforms.

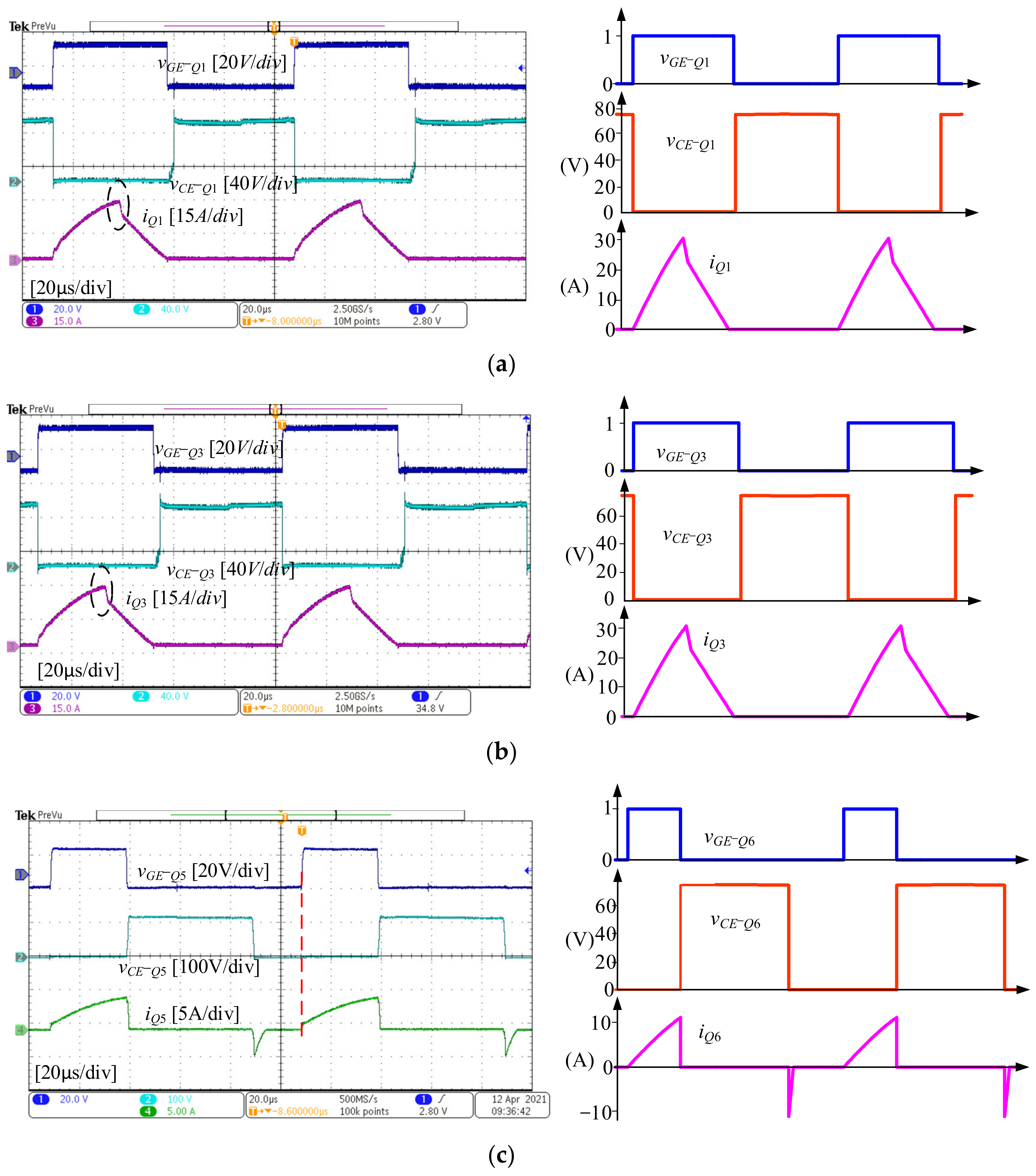
Figure 11 shows the gate–emitter voltage, ν_GE; the collector–emitter voltage, ν_CE; and the collector current of the switches, Q₁, Q₃, and Q₆. For the main switches, Q₁ and Q₃, they are turned on and off with ZCS condition, while for the auxiliary switch, Q₆, it is turned off with ZVS and turned on with ZVZCS condition. Since i_Q1 in Mode 1 is the sum of i_p1 and i_p2, and only i_p1 in Mode 2, there is a phenomenon of current drop, as shown in the dotted box in Figure 11a.

Compared to Reference [20], the remarkable feature of the proposed converter is that the primary side conduction losses of Q₂, Q₃, Q₅, Q₆, and T_r2 are decreased due to the rapid decline of i_p2, and if C_b, D_R3, and D_R4 are removed from the converter, the converter will have a similar operation principle to that in Reference [20].

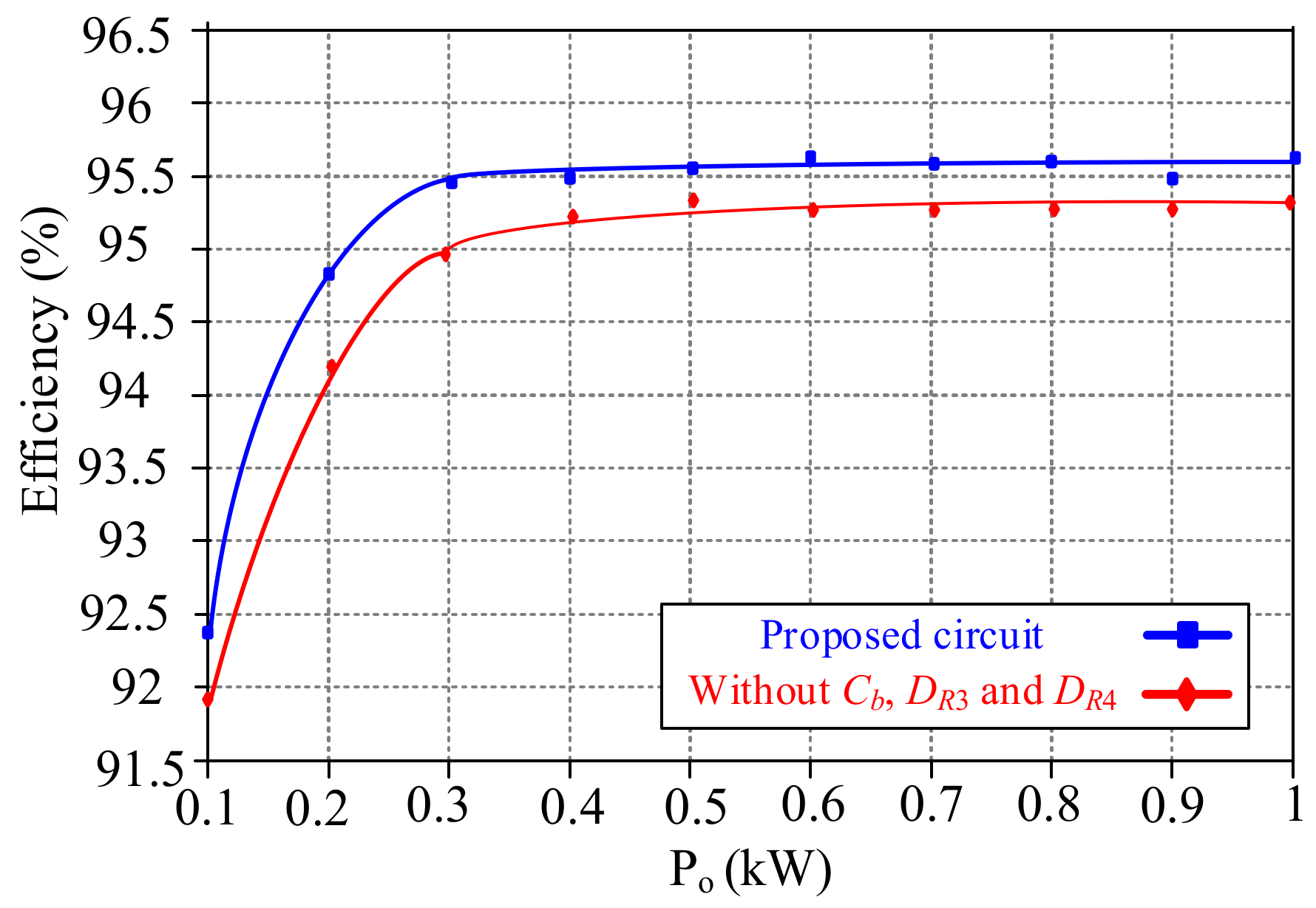
To show the advantages of the introduced blocking capacitor, Figure 12 shows the comparison between the efficiencies of the proposed converter and that, without C_b, D_R3, and D_R4, it is obvious that, due to the reduced conduction losses of Q₂, Q₃, Q₅, Q₆, and T_r2, the proposed converter has a higher efficiency.

6. Conclusions

A hybrid three-level ZVZCS converter was proposed and analyzed in this paper for photovoltaic power connecting to an MVDC collection system. The outstanding feature of the converter is that it allows four main switches to operate with ZCS turn-on and turn-off and two auxiliary switches to operate with ZVZCS turn-on and ZVS turn-off. Moreover, the proposed converter has an additional blocking capacitor, which is used to eliminate the useless circulating current in the primary side of auxiliary full bridge cell, leading to reduced conduction losses and 0.3% higher conversion efficiency. The operation principle of the proposed converter was analyzed in detail and verified by a 1 kW prototype.