Adaptive Second-Order Sliding Mode Control of Buck Converters with Multi-Disturbances
Abstract
:1. Introduction
- Without loss of generality, the possible parameter perturbations and external disturbances of the buck converters are all considered in modeling;
- The robust stability of the converter system is investigated;
- The adaptive mechanism of online zero-crossing detection is investigated;
- The control magnitude of the controller can vary to a minimal admissible level, and the steady error of the output voltage can converge to the expected value.
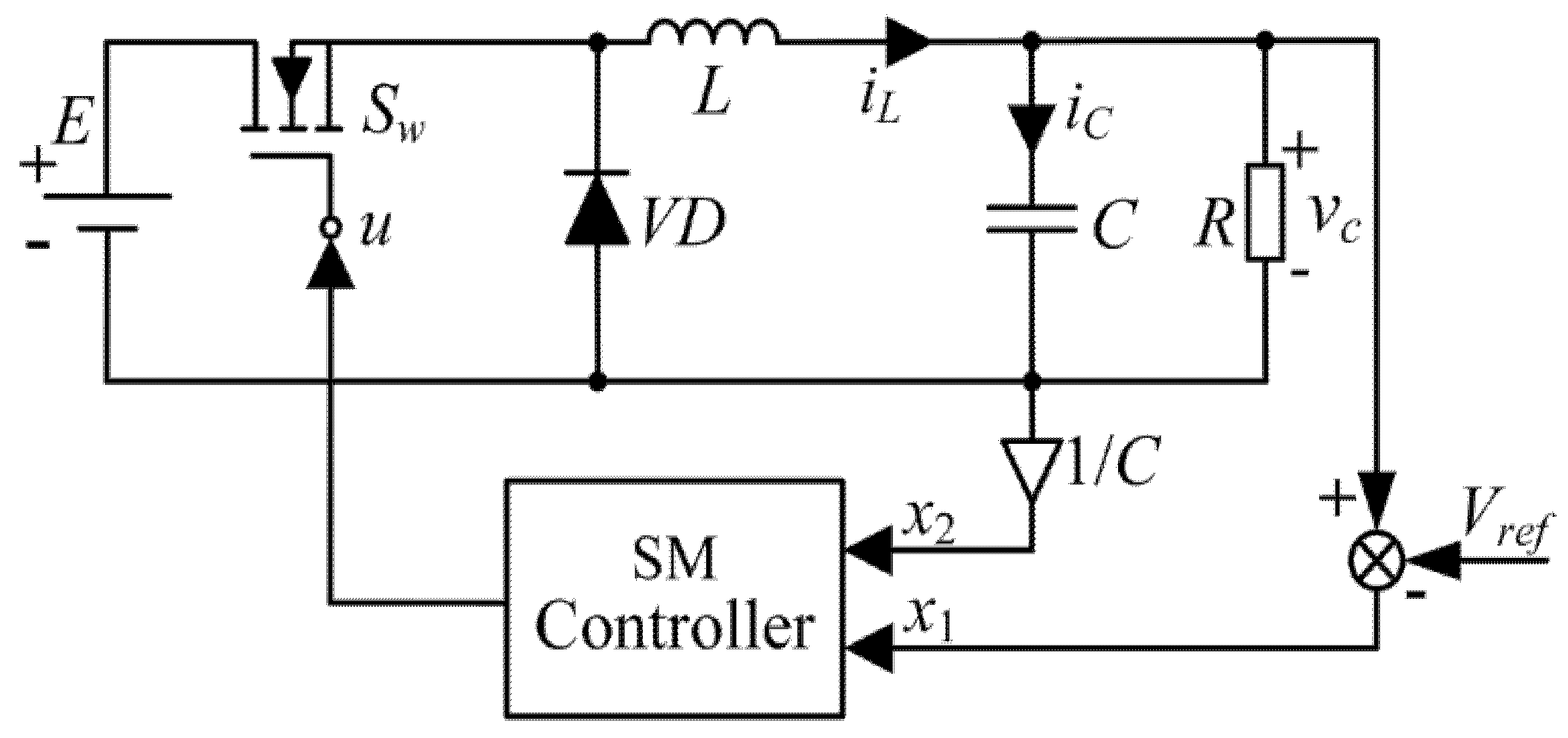
2. Model of Buck Converters with Multi-Disturbances
2.1. Modeling of Buck Converters with Multi-Disturbances
- Continuous conduction mode (CCM), i.e., the inductor current iL ≠ 0;
- DC input voltage 0 < E < Emax, where Emax is its maximum;
- MOSFET or IGBT act as the power switch Sw, the ON/OFF switching control of which is implemented by triggering its gate pole.
- The derivatives of the external disturbances d1(t) and d2(t) exist, and |d1(t)| ≤ ψd1, |d2(t)| ≤ ψd2, || ≤ ψd3, || ≤ ψd4, where ψd1, ψd2, ψd3 and ψd4 are constants;
- μβ1min ≤ |β1| < μβ1max, μβ2min ≤ |β2| < μβ2max, μβ3min ≤ β3 ≤ μβ3max and μβ4min ≤ |β4(t)| ≤ μβ4max, where μβ1 min, μβ1 max, μβ2min, μβ2max, μβ3 min, μβ3 max, μβ4min, μβ4 max are constants.
2.2. Implementation Steps of SM Controller
- Step 1: Design of sliding surface
- Step 2: Design of robust control law
3. Traditional 2-SM Controller with Fixed Control Gain
3.1. Controller Design of Twisting Algorithm
3.2. Stability Analysis
- Case 1: In the phase S12→S14 with . As observed from Figure 2, since in the left half-plane, the value of changes continuously from negative to positive. Attention should be paid to the fact that the increase of rates of in Region III and in Region IV are different. In Region III, there is from (8); while in Region IV, there is . Therefore, by combining (12) and (13), the stability condition of the system in (11) can be deduced.
- Case 2: In the phase S14→S22 with . Similarly, when the system moves in the right half-plane, the value of changes continuously from positive to negative. In Region II, the control law is , while in Region I, there is . By combining (12) and (13), the stability condition of the system should be satisfied with
4. Improved Adaptive 2-SM Controller
4.1. Design of Sliding Surface
4.2. Design of Control Law
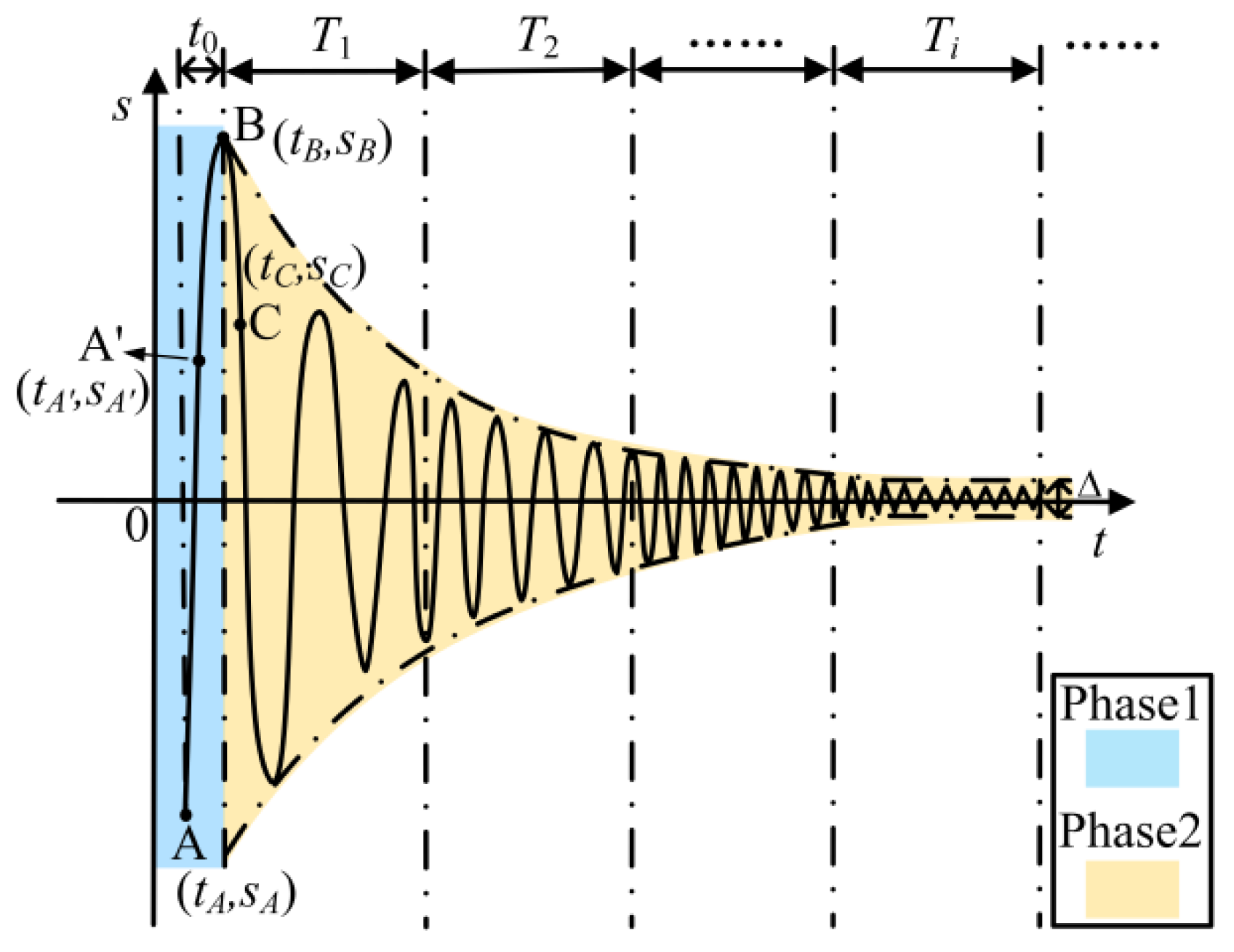
- Phase 1: Point A–Point B
- Phase 2: Convergence process after Point B
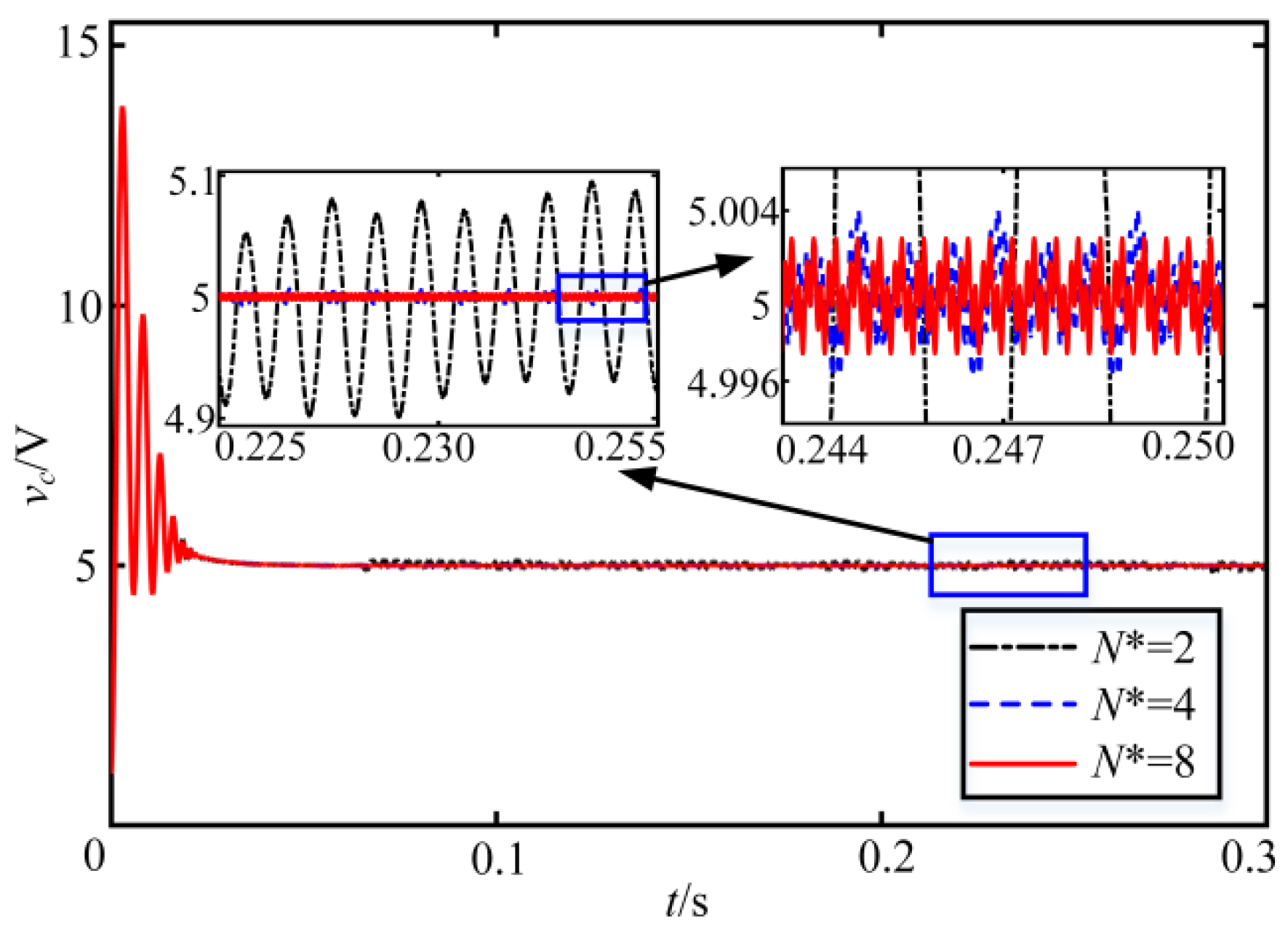
5. Simulations and Experiments
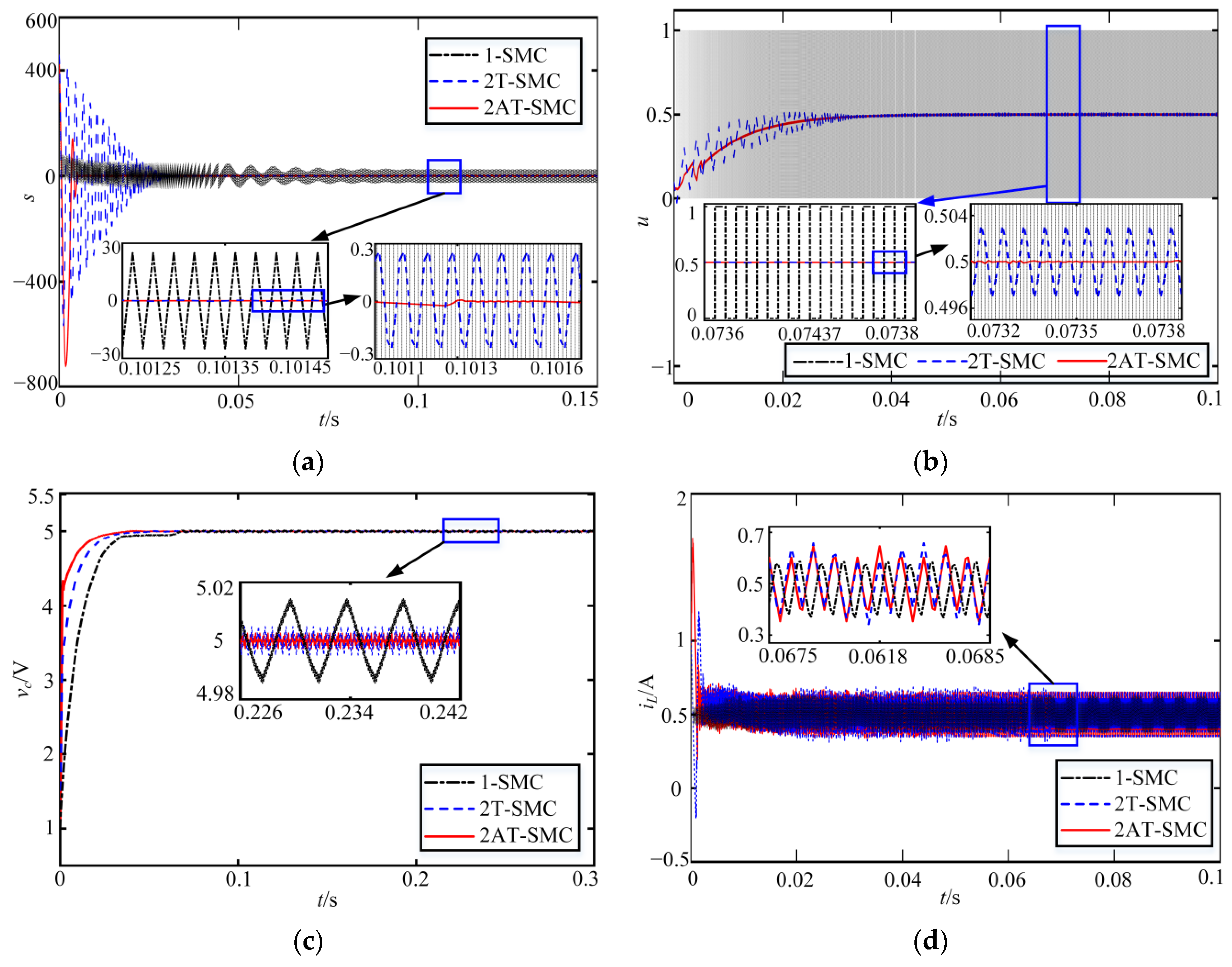
5.1. Simulation Results and Analysis
- SMC
- 2T-SMC
- 2AT-SMC
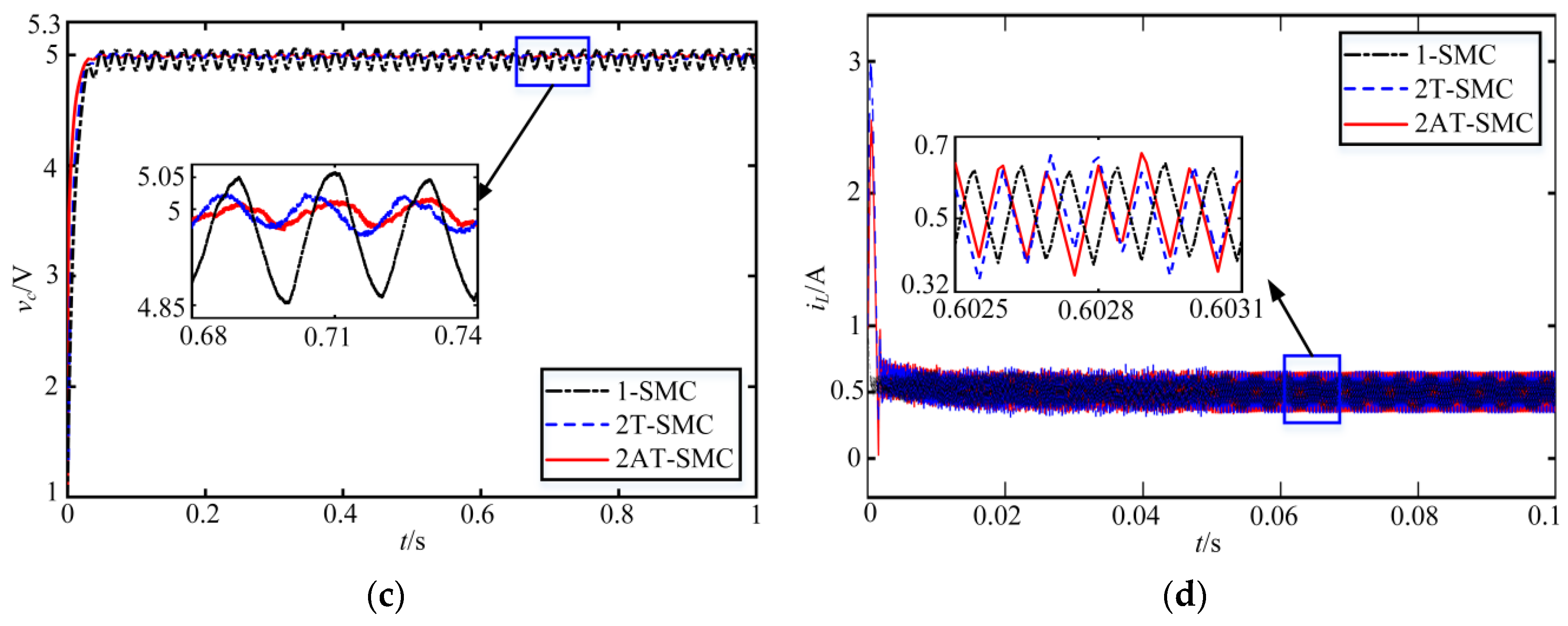
- Case 1: Rated working condition.
- Case 2: The working condition with multi-disturbances.
5.2. Experiment
- The input voltage E increased from 10 V to 11 V at t = 1 s, and then reduced to 10 V at t = 2 s, i.e., ∆E = 1 V;
- The reference voltage Vref increased from 5 V to 5.5 V at t = 3 s, and then reduced to 5 V at t = 4 s, i.e., ∆Vref = 0.5 V;
- The load resistor R increased from 10 Ω to 11 Ω at t = 5 s, and then reduced to 10Ω at t = 6 s, i.e., ∆R = 1 Ω.
- The above three disturbances existed simultaneously at t = 7 s, and then disappeared at t = 8 s.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Niu, Z.; Yang, M.; Sun, L.; Zhang, W. Stability of Sliding Mode Controlled Buck Converters with Unmodelled Dynamics of Circuit Elements and Hall Sensor. IET Power Electron. 2021, 14, 602–613. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, Y.; Zhang, P.; Duan, G. Unified Approach for Robust Stability Analysis of Buck Converters with Discrete-Time Sliding Mode Control. Math. Probl. Eng. 2021, 2021, 5527047. [Google Scholar] [CrossRef]
- Chen, C.H.; Cheng, P.G.; Xie, M.J. Current Sharing of Paralleled DC-DC Converters Using GA-based PID Controllers. Expert Syst. Appl. 2010, 14, 733–740. [Google Scholar] [CrossRef]
- Olm, J.M.; Biel, D. Linear Robust Output Regulation in a Class of Switched Power Converters. Math. Probl. Eng. 2010, 2010, 724531. [Google Scholar] [CrossRef]
- Chen, G.; Chen, L.; Deng, Y. Single Coupled-inductor Dual Output Soft-switching DC–DC Converters with Improvedcross-regulation and Reduced Components. IET Power Electron. 2017, 10, 1665–1678. [Google Scholar] [CrossRef] [Green Version]
- Cha, H.R.; Kim, Y.; Park, K.H.; Choi, Y.J. Modeling and Control of Double-Sided LCC Compensation Topology with Semi-Bridgeless Active Rectifier for Inductive Power Transfer System. Energies 2019, 12, 3921. [Google Scholar] [CrossRef] [Green Version]
- Tan, S.; Lai, C.D.; Cheung, K.H.; Tse, C.K. General Design Issues of Sliding-mode Controllers in DC–DC Converters. IEEE Trans. Power Electron. 2005, 20, 425–437. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ali, A. Active Disturbance Rejection Control of DC-DC Boost Converter: A Review with Modifications for Improved Performance. IET Power Electron. 2019, 12, 2095–2107. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A Sliding-Mode Duty-Ratio Controller for DC/DC Buck Converters With Constant Power Loads. IEEE Trans. Ind. Appl. 2014, 50, 1448–1458. [Google Scholar] [CrossRef] [Green Version]
- Gautam, A.R.; Gourav, K.; Guerrero, J.M.; Fulwani, D.M. Ripple Mitigation with Improved Line-Load Transients Response in a Two-Stage DC-DC-AC Converter: Adaptive SMC Approach. IEEE Trans. Ind. Electron. 2018, 65, 3125–3135. [Google Scholar] [CrossRef]
- Mattavelli, P.; Rossetto, L.; Spiazzi, G.; Tenti, P. General-purpose fuzzy controller for DC-DC converters. IEEE Trans. Power Electron. 1997, 12, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Babes, B.; Mekhilef, S.; Boutaghane, A.; Rahmani, L. Fuzzy Approximation-Based Fractional-Order Nonsingular Terminal Sliding Mode Controller for DC-DC Buck Converters. IEEE Trans. Power Electron. 2022, 37, 2749–2760. [Google Scholar] [CrossRef]
- Rubaai, A.; Ofoli, A.R.; Burge, L.; Garuba, M. Hardware Implementation of an Adaptive Network-based Fuzzy Controller for DC-DC Converters. IEEE Trans. Ind. Appl. 2005, 41, 1557–1565. [Google Scholar] [CrossRef]
- Rojas-Dueñas, G.; Riba, J.R.; Moreno-Eguilaz, M. Black-Box Modeling of DC-DC Converters Based on Wavelet Convolutional Neural Networks. IEEE Trans. Inst. Meas. 2021, 70, 2005609. [Google Scholar] [CrossRef]
- Bastos, R.F.; Aguiar, C.R.; Gonçalves, A.F.Q.; Machado, R.Q. An Intelligent Control System Used to Improve Energy Production from Alternative Sources With DC-DC Integration. IEEE Trans. Smart Grid. 2014, 5, 2486–2495. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M.; Farsizadeh, H.; Masoudian, A.; Boudjadar, J. A New Intelligent Hybrid Control Approach for DC-DC Converters in Zero-Emission Ferry Ships. IEEE Trans. Power Electron. 2020, 35, 5832–5841. [Google Scholar] [CrossRef]
- Chanjira, P.; Tunyasrirut, S. Intelligent Control Using Metaheuristic Optimization for Buck-Boost Converter. J. Eng. 2020, 2020, 5462871. [Google Scholar] [CrossRef]
- Fang, J.S.; Tsai, S.H.; Yan, J.J.; Chen, P.L.; Guo, S.M. Realization of DC-DC Buck Converter Based on Hybrid H2 Model Following Control. IEEE Trans. Ind. Electron. 2022, 69, 1782–1790. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, P.; Ji, S.; Dai, M. Improved Linear Sliding Mode Controller of Buck Converters through Adding Terminal Sliding Mode. In Proceedings of the 11th Asian Control Conference (ASCC), Gold Coast, Australia, 17–20 December 2017; pp. 682–686. [Google Scholar]
- Amin, M.S.; Babaei, E. Robust Nonlinear Controller Based on Control Lyapunov Function and Terminal Sliding Mode for Buck Converter. Int. J. Numer. Model. Electron. Netw. Device Fields 2016, 29, 1055–1069. [Google Scholar]
- Hasan, K. Non-singular Terminal Sliding-mode Control of DC-DC Buck Converters. Control Eng. Pract. 2013, 21, 321–332. [Google Scholar]
- Elnady, A. Newly Developed First-order Sliding Mode of Power and Voltage Control for the Diode-clamped Multilevel Inverter. Int. J. Power Energy Syst. 2017, 37, 150–163. [Google Scholar] [CrossRef]
- Xiong, X.G.; Chen, H.; Liu, Z.; Yamamoto, M.; Lou, Y. Implicit Discrete-Time Adaptive First-Order Sliding Mode Control with Predefined Convergence Time. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 68, 3562–3566. [Google Scholar] [CrossRef]
- Sivaramakrishnan, S.; Tangirala, A.K.; Chidambaram, M. Sliding Mode Controller for Unstable Systems. Chem. Biochem. Eng. Q. 2008, 22, 41–47. [Google Scholar]
- Boiko, I.; Fridman, L. Analysis of Chattering in Continuous Sliding-mode Controllers. IEEE Trans. Autom. Control 2005, 50, 1442–1446. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Liu, C. Sliding Mode Control of a New Chaotic System. Chin. Phys. B 2010, 10, 148–150. [Google Scholar]
- Ma, H.; Wu, J.; Xiong, Z. Active Chatter Control in Turning Processes with Input Constraint. Int. J. Adv. Manuf. Technol. 2020, 108, 3737–3751. [Google Scholar] [CrossRef]
- Hua, S.; Wang, X.; Zhu, Y. Sliding-mode Control for a Rolling-missile with Input Constraints. J. Syst. Eng. Electron. 2020, 31, 1041–1050. [Google Scholar]
- Zong, Q.; Zhao, Z.; Zhang, J. Higher Order Sliding Mode Control with Self-tuning Law Based on Integral Sliding Mode. IET Control Theory Appl. 2010, 4, 1282–1289. [Google Scholar] [CrossRef]
- Mahjoub, S.; Ayadi, M.; Derbel, N. Comparative Study of Smart Energy Management Control Strategies for Hybrid Renewable System Based Dual Input-single Output DC-DC Converter. J. Electr. Syst. 2020, 16, 218–234. [Google Scholar]
- Farhoud, A.; Erfanian, A. Fully Automatic Control of Paraplegic FES Pedaling Using Higher-Order Sliding Mode and Fuzzy Logic Control. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 533–542. [Google Scholar] [CrossRef]
- Djilali, L.; Badillo-Olvera, A.; Yuliana Rios, Y.; López-Beltrán, H.; Saihi, L. Neural High Order Sliding Mode Control for Doubly Fed Induction Generator based Wind Turbines. IEEE Latin Am. Trans. 2022, 20, 223–232. [Google Scholar] [CrossRef]
- Levant, A. Principles of 2-sliding Mode Design. Automatica 2007, 43, 576–586. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Wang, J.; Zheng, W. Second-Order Sliding Mode Control for Nonlinear Uncertain Systems Bounded by Positive Functions. IEEE Trans. Ind. Electron 2015, 62, 5899–5909. [Google Scholar] [CrossRef]
- Rakht Ala, S.M.; Yasoubi, M.; HosseinNia, H. Design of Second Order Sliding Mode and Sliding Mode Algorithms: A Practical Insight to DC-DC Buck Converter. IEEE-CAA J. Automatica Sin. 2017, 4, 483–497. [Google Scholar] [CrossRef] [Green Version]
- Lazar, M.; Heemels, W.P.M.H.; Roset, B.J.P.; van den Bosch, P.P.J. Input-to-state Stabilizing Sub-optimal NMPC with an Application to DC–DC Converters. Int. J. Robust Nonlinear Control 2008, 18, 890–904. [Google Scholar] [CrossRef]
- Rakhtala, S.M.; Casavola, A. Real-Time Voltage Control Based on a Cascaded Super Twisting Algorithm Structure for DC–DC Converters. IEEE Trans. Ind. Electron 2022, 69, 633–641. [Google Scholar] [CrossRef]
- Singh, S.; Srivastava, P.; Janardhanan, S. Adaptive Higher Order Sliding Mode Control for Nonlinear Uncertain Systems. In Proceedings of the 5th IFAC Conference on Advances in Control and Optimization of Dynamical Systems (ACODS), Hyderabad, India, 18–22 February 2018; pp. 341–346. [Google Scholar]
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive Second-order Sliding-Mode Observer for PMSM Sensorless Control Considering VSI Nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Thanh, H.L.N.; Hong, S.K. Quadcopter Robust Adaptive Second-Order Sliding Mode Control Based on PID Sliding Surface. IEEE Access 2018, 6, 66850–66860. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive Second-Order Fast Nonsingular Terminal Sliding Mode Tracking Control for Fully Actuated Autonomous Underwater Vehicles. IEEE J. Ocean Eng. 2019, 44, 363–385. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Alcaide, A.M.; Yin, Y.; Leon, J.I.; Sergio, V.; Franquelo, L.G. Adaptive Second-Order Sliding Mode Control for Grid-Connected NPC Converters with Enhanced Disturbance Rejection. IEEE Trans. Power Electron. 2022, 37, 206–220. [Google Scholar] [CrossRef]
- Mei, K.; Ding, S.; Zheng, W. Fuzzy Adaptive SOSM Based Control of a Type of Nonlinear System. IEEE Trans. Circuits Syst. II-Express Briefs 2022, 69, 1342–1346. [Google Scholar] [CrossRef]
- Li, S.; Fei, A.J. Adaptive Second-Order Sliding Mode Fuzzy Control Based on Linear Feedback Strategy for Three-Phase Active Power Filter. IEEE Access 2018, 6, 72992–73000. [Google Scholar] [CrossRef]
- Carolina, A.E.; Alessandro, P.; Paul, P.; Elio, U. Receding Horizon Adaptive Second-Order Sliding Mode Control for Doubly-Fed Induction Generator Based Wind Turbine. IEEE Trans. Control Syst. Technol. 2017, 25, 73–84. [Google Scholar]
- Wong, O.; Wong, H.; Tam, W.; Kok, C. Parasitic Capacitance Effect on the Performance of Two-phase Switched-capacitor DC–DC Converters. IET Power Electron. 2015, 8, 1195–1208. [Google Scholar] [CrossRef]
- Rudziński, A. Modelling of Battery-powered Boost DC-DC Power LED Driver with Parasitics by Multivariate Power Series Expansion. Int. J. Circuit Theory Appl. 2015, 43, 1197–1208. [Google Scholar] [CrossRef]






| Symbols | Parameters | Values |
|---|---|---|
| L | Inductance | 1 mH |
| C | Capacitance | 1000 μF |
| R | Load resistance | 10 Ω |
| Vref | the Reference voltage | 5 V |
| E | Input DC voltage | 10 V |
| SM Controller | Output Voltage vc | Inductor Current iL | ||
|---|---|---|---|---|
| Steady Error (mV) | Convergence Time (s) | Steady Error (A) | Convergence Time (s) | |
| 1-SMC | 15.13 | 0.055 | 0.098 | 0.057 |
| 2T-SMC | 6.09 | 0.042 | 0.113 | 0.043 |
| 2AT-SMC | 3.01 | 0.031 | 0.101 | 0.032 |
| Disturbance Source | Disturbance Modle |
|---|---|
| ∆L | 0.1sin(100πt) (mH) |
| ∆C | 100sin(100πt) (μF) |
| ∆R | sin(100πt) (Ω) |
| ∆E | sin(100πt) (V) |
| ∆Vref | 0.5sin(100πt) (V) |
| d1(t) | 0.04sin(4 × 107πt) (V) |
| d2(t) | 0.04sin(4 × 107πt) (V) |
| SMC Algorithm | Output Voltage vc | Inductor Current iL | ||
|---|---|---|---|---|
| Steady Error (mV) | Convergence Time (s) | Steady Error (A) | Convergence Time (s) | |
| 1-SMC | 155.13 | 0.069 | 0.121 | 0.071 |
| 2T-SMC | 51.26 | 0.050 | 0.233 | 0.057 |
| 2AT-SMC | 25.41 | 0.039 | 0.135 | 0.040 |
| Disturbance Source | SM Algorithms | |||||
|---|---|---|---|---|---|---|
| 1-SMC | 2T-SMC | 2AT-SMC | ||||
| vc (mV) | iL (A) | vc (mV) | iL (A) | vc (mV) | iL (A) | |
| - | 314.05 | 0.407 | 152.42 | 0.396 | 114.23 | 0.367 |
| ∆E(1 s–2 s) | 367.41 | 0.422 | 171.40 | 0.412 | 124.11 | 0.384 |
| ∆Vref (3 s–4 s) | 322.32 | 0.437 | 153.32 | 0.427 | 116.33 | 0.401 |
| ∆R(5 s–6 s) | 415.34 | 0.385 | 196.13 | 0.366 | 152.24 | 0.337 |
| [∆E + ∆Vref + ∆R](7 s–8 s) | 454.38 | 0.374 | 234.03 | 0.358 | 183.03 | 0.327 |
| Disturbance Source | SM Algorithms | |||||
|---|---|---|---|---|---|---|
| 1-SMC | 2T-SMC | 2AT-SMC | ||||
| t(vc) (s) | t(iL) (s) | t(vc) (s) | t(iL) (s) | t(vc) (s) | t(iL) (s) | |
| ∆E(1 s–2 s) | 0.115 | 0.117 | 0.094 | 0.102 | 0.082 | 0.089 |
| ∆Vref (3 s–4 s) | 0.099 | 0.104 | 0.085 | 0.093 | 0.078 | 0.085 |
| ∆R(5 s–6 s) | 0.118 | 0.121 | 0.102 | 0.109 | 0.087 | 0.099 |
| [∆E + ∆Vref + ∆R](7 s–8 s) | 0.132 | 0.135 | 0.112 | 0.118 | 0.089 | 0.105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, W.; Yang, Y.; Xue, C.; Yuan, S.; Zhang, H. Adaptive Second-Order Sliding Mode Control of Buck Converters with Multi-Disturbances. Energies 2022, 15, 5139. https://doi.org/10.3390/en15145139
Wang Y, Zhang W, Yang Y, Xue C, Yuan S, Zhang H. Adaptive Second-Order Sliding Mode Control of Buck Converters with Multi-Disturbances. Energies. 2022; 15(14):5139. https://doi.org/10.3390/en15145139
Chicago/Turabian StyleWang, Yanmin, Weiqi Zhang, Yalong Yang, Chen Xue, Shibo Yuan, and Hanqing Zhang. 2022. "Adaptive Second-Order Sliding Mode Control of Buck Converters with Multi-Disturbances" Energies 15, no. 14: 5139. https://doi.org/10.3390/en15145139
APA StyleWang, Y., Zhang, W., Yang, Y., Xue, C., Yuan, S., & Zhang, H. (2022). Adaptive Second-Order Sliding Mode Control of Buck Converters with Multi-Disturbances. Energies, 15(14), 5139. https://doi.org/10.3390/en15145139








