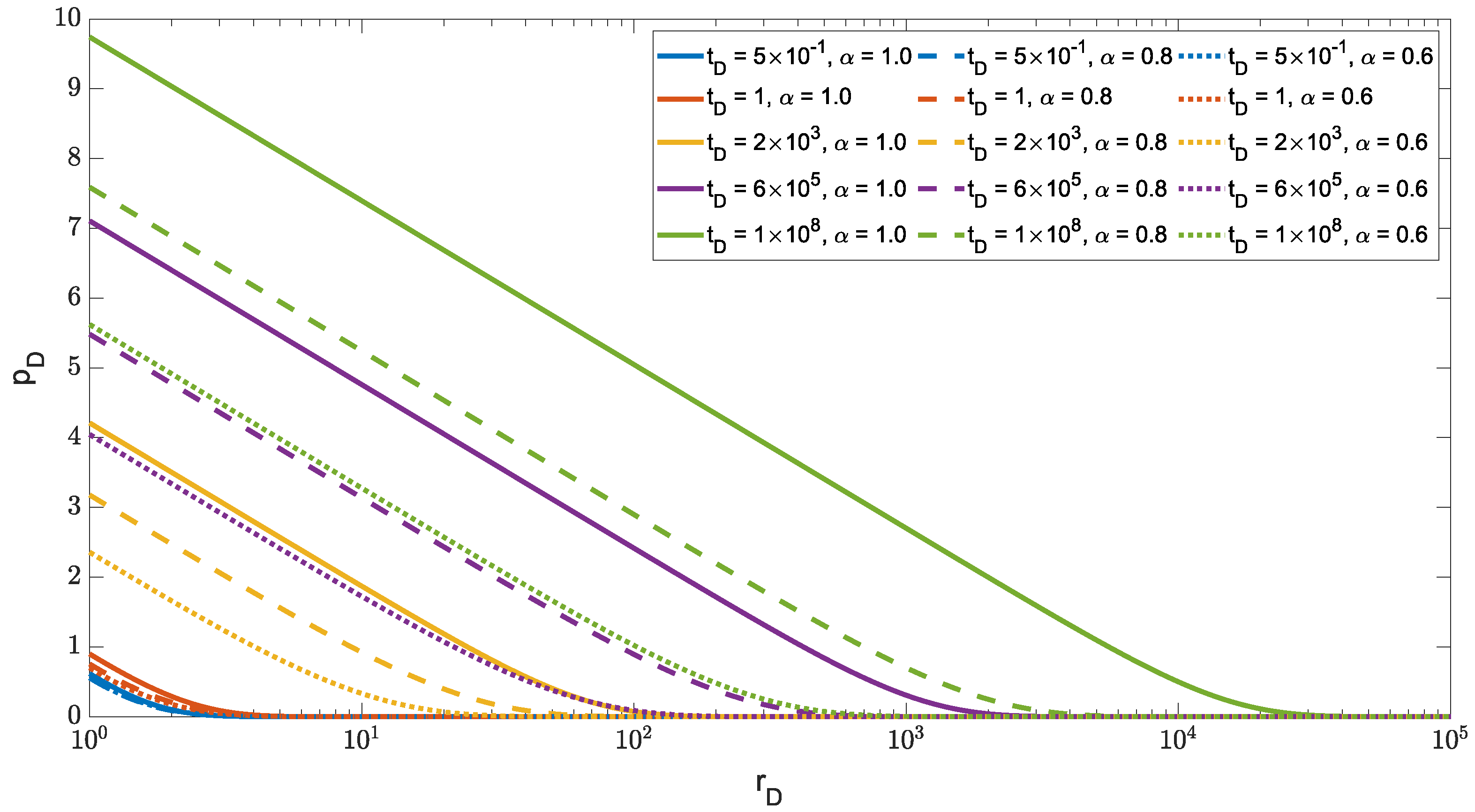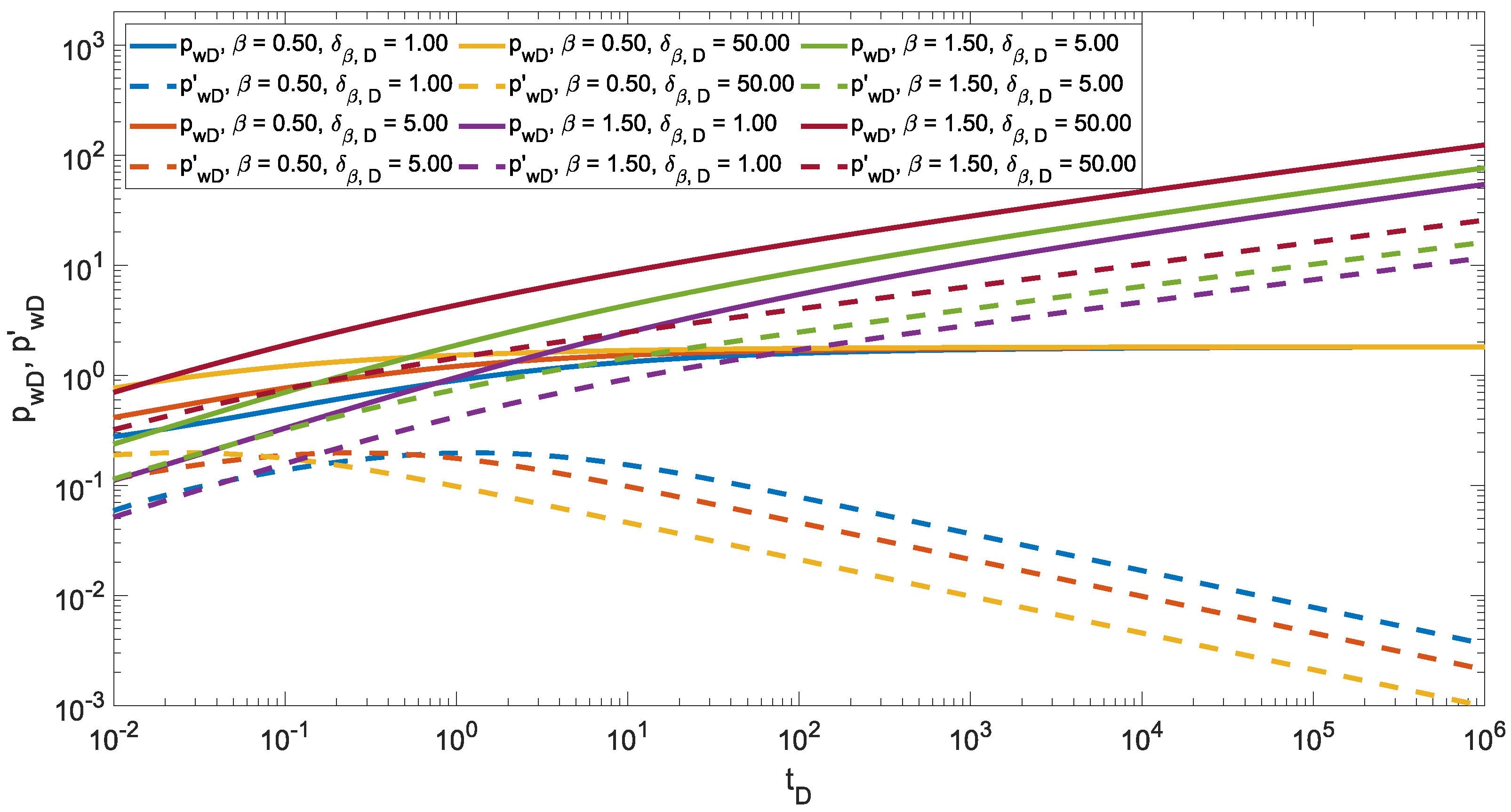Spatial Fractional Darcy’s Law on the Diffusion Equation with a Fractional Time Derivative in Single-Porosity Naturally Fractured Reservoirs

Abstract

Due to the complexity imposed by all the attributes of the fracture network of many naturally fractured reservoirs, it has been observed that fluid flow does not necessarily represent a normal diffusion, i.e., Darcy’s law. Thus, to capture the sub-diffusion process, various tools have been implemented, from fractal geometry to characterize the structure of the porous medium to fractional calculus to include the memory effect in the fluid flow. Considering infinite naturally fractured reservoirs (Type I system of Nelson), a spatial fractional Darcy’s law is proposed, where the spatial derivative is replaced by the Weyl fractional derivative, and the resulting flow model also considers Caputo’s fractional derivative in time. The proposed model maintains its dimensional balance and is solved numerically. The results of analyzing the effect of the spatial fractional Darcy’s law on the pressure drop and its Bourdet derivative are shown, proving that two definitions of fractional derivatives are compatible. Finally, the results of the proposed model are compared with models that consider fractal geometry showing a good agreement. It is shown that modified Darcy’s law, which considers the dependency of the fluid flow path, includes the intrinsic geometry of the porous medium, thus recovering the heterogeneity at the phenomenological level.

1. Introduction

The modeling of physical phenomena is always a complex task in which hypotheses and idealizations are used in order to implement already studied laws or similar models. In particular, modeling the transient pressure behavior in naturally fractured reservoirs is a task that has been studied and worked on by various researchers over decades, where the heterogeneity of the porous medium and anomalous fluid flow has been a challenge for which more complex models have been generated and implemented, obtaining results that constantly improve the understanding of the phenomenon.

Considering the complexity of the porous medium, Chang and Yortsos [1] are the pioneers that considered the porous medium as a fractal system, allowing them to describe reservoirs with spatial disorder and, therefore, a complex fluid flow path.

In recent years, fractional calculus has become a useful tool that, applied to diffusion-type problems, explains the behavior of anomalous flow (where the movement of the fluid does not have a Brownian-type behavior) by demonstrating that the fluid has memory [2].

The study of Metzler et al. [3] has become an important reference when studying the phenomenon of anomalous diffusion in a medium with a fractal structure, allowing endless researchers to explore the implications considering different approaches [4,5,6,7].

Although all these models have allowed a more precise understanding of the phenomenon in non-homogeneous reservoirs; the task of understanding this complex phenomenon has also included modifications to Darcy’s law. When considering non-Darcy flows, i.e., a sub-diffusive process, to include the memory effect, the fractional derivative approach is used.

To include the memory effect in Darcy’s law, Caputo’s fractional time derivative is used in Darcy’s law modeling, to account for the effect of a decrease in permeability with time [8]. Raghavan [9] shows that using the properties of the fractional derivative, one can translate the fractional time derivative into the continuity equation.

Several variants of the temporal fractional derivative have been applied to Darcy’s law. Chang et al. [10] replace the spatial derivative in Darcy’s law with the Riemann–Liouville fractional derivative to quantify the spatial path dependence of a fluid flow. El-Amin [11] constructs the fractional mass equation and combines it with variants of Darcy’s law that include adding the fractional time derivative and replacing the space derivative with Caputo’s fractional derivative. Chang and Sun [12] replace the time derivative with Caputo’s fractional time derivative to describe the heavy tail decay at long times and the space derivative with the Riemann–Liouville fractional time derivative to describe the dependence of non-local concentration change on a wide range of spatial areas.

Likewise, Caputo and Plastino [13], considering infinite media, add a term proportional to the spatial fractional derivative of the Caputo type to the classic Darcy’s law, which represents the effect of spatial memory, i.e., the pressure gradient investigated from the initial point to the measured point.

Obembe et al. [14], in their excellent review work, show a model of Darcy’s law, among others, where the temporal fractional derivative is applied to a complex combination of a spatial fractional derivative and complementary temporal fractional derivative; that reflects the presence of flow hindrances, while the spatial fractional derivatives consider flow buffers.

Finally, in order to consider the intrinsic geometry of the porous medium, Cloot and Botha [15] replace the spatial derivative in Darcy’s law with Weyl’s fractional derivative; they consider that the fluid flow at a given point is governed not only by the properties of the pressure field at a specific position but also depends on the global spatial distribution of that field.

Therefore, in order to model the transient pressure behavior in a naturally fractured reservoir, including spatial and temporal memory, a new model will be proposed that incorporates both the fractional time derivative in the Caputo sense, in the continuity equation, and the fractional Weyl derivative, in Darcy’s law. This work is organized as follows: Section 2 describes the essential mathematical tools used; Section 3 shows the development of the model, explaining the modified Darcy’s law used and the spatial fractional diffusion model developed; Section 4 shows the results of solving this model and the effect of every parameter of the model, Section 5 compares the proposed model with models that consider the porous medium as fractal; in the end, Section 6 describes the main conclusions reached.

2. Mathematical Background

This section presents the mathematical tools that will be applied throughout this work. For more details, see [16,17,18].

Definition 1.

Let $t_0<\infty$. The Riemann–Liouville fractional integral ${}^{RL}{I}_{t_0+}^{\alpha }y$ of order $\alpha \in \mathbb{R}$ is defined by

$$\left({}^{RL}{I}_{t_0+}^{\alpha }y\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_{t_0}^t{(t-\tau )}^{\alpha -1}y\left(\tau \right)d\tau ,t>t_0$$

(1)

where $\mathrm{\Gamma }(·)$ is Euler’s gamma function.

The Caputo fractional derivative, expressed from the fractional integral, is defined as follows:

Definition 2.

Let $t_0<\infty$. For $\alpha \in \mathbb{R}$, the Caputo fractional derivative, ${}^C{D}_{t_0+}^{\alpha }y$ is defined by

$$\left({}^C{D}_{t_0+}^{\alpha }y\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_{t_0}^t{(t-\tau )}^{n-\alpha -1}{y}^{\left(n\right)}\left(\tau \right)d\tau =\left({}^{RL}{I}_{t_0+}^{n-\alpha }{D}^{n}y\right)\left(t\right),t>t_0$$

(2)

where $D=d/dt$ and $n\in \mathbb{N}$ with $n-1<\alpha \le n$.

Proposition 1.

The Caputo fractional derivative provides an inverse operator to the Riemann–Liouvile fractional integral, that is

$$\begin{array}{ccc}\hfill \left({}^C{D}_{t_0+}^{\alpha }{}^{RL}{I}_{t_0+}^{\alpha }y\right)\left(t\right)& =& y\left(t\right);\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \left({}^{RL}{I}_{t_0+}^{\alpha }{}^C{D}_{t_0+}^{\alpha }y\right)\left(t\right)& =& y\left(t\right)-\sum _{k=0}^{n-1}\frac{y^{\left(k\right)}\left(t_0\right)}{k!}{\left(t-t_0\right)}^k.\hfill \end{array}$$

(4)

The above definitions consider $t_0<\infty$; however, similar definitions exist on the whole axis $\mathbb{R}$.

Definition 3.

The Weyl fractional integral of order $\beta \in \mathbb{R}$ is defined by

$$\left(W^{-\beta }y\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_t^{\infty }{(\tau -t)}^{\beta -1}y\left(\tau \right)d\tau ,t>0.$$

(5)

Indeed, the Weyl fractional integral is interesting; however, care should be taken when using this definition because it may not be applied to all functions.

Partcularly, if $y\left(t\right)$ is integrable on any finite subinterval of $J=[0,\infty )$, and, if $y\left(t\right)$ behaves like $t^{-\mu }$ for t large, then the Weyl fractional integral of y of order $\beta$ will exist if $0<\beta <\mu$.

Definition 4.

If $y\left(t\right)$ is a function for which $W^{-\beta }y\left(t\right)$ exists and has n continous derivatives; then, the Weyl fractional derivative of y of order $\nu \in \mathbb{R}$ is defined by

$$W^{\beta }y\left(t\right)={(-1)}^n{D}^n\left[W^{-(n-\beta )}y\left(t\right)\right]$$

(6)

where $D=d/dt$ and $n\in \mathbb{N}$ with $n-1<\beta \le n$.

Before finishing this long list of definitions, some interesting properties of fractional operators will be shown.

Proposition 2. 

Let $\mu ,\beta \in \mathbb{R}$ and $n\in \mathbb{N}$ with $n-1<\beta \le n$. Both, the fractional Weyl integral and the fractional Weyl derivative satisfy the following:

• $D^n\left[W^{-\beta }y\left(t\right)\right]=W^{-\beta }\left[D^{n}y\left(t\right)\right].$
• $W^{-\mu }\left[W^{-\beta }y\left(t\right)\right]=W^{-\beta }\left[W^{-\mu }y\left(t\right)\right]=W^{-(\mu +\beta )}y\left(t\right).$
• $W^{-\beta }\left[W^{\beta }y\left(t\right)\right]=y\left(t\right)=W^{\beta }\left[W^{-\beta }y\left(t\right)\right].$
• $W^{\mu }\left[W^{\beta }y\left(t\right)\right]=W^{\beta }\left[W^{\mu }y\left(t\right)\right]=W^{\mu +\beta }y\left(t\right).$

3. Model Development

In this section, the proposed Darcy’s law will be presented, which integrates the fractional derivative of Weyl, and the flow equation with spatial fractional Darcy flow will be constructed.

We consider a fully penetrated well in an infinite porous media with a single porosity system, i.e., a Type I fractured system of Nelson [19], constant initial pressure, permeability, density and viscosity. Furthermore, we consider that the fluid flow at a given point is governed not only by the properties of the pressure field at that specific position but also depends on the global spatial distribution of that field, and lastly, we consider that the radial symmetry is valid. The model in dimensionless variables with a fractional time derivative for the fluid transfer equation, resulting from the combination of the continuity equation and Darcy’s law, in radial coordinates and considering a Euclidean porous medium, is given by

$${\tau }_D^{\alpha -1}\frac{{\partial }^{\alpha }{p}_D}{\partial t_D^{\alpha }}=-\frac{1}{r_D}\frac{\partial }{\partial r_D}\left(r_D{\mathit{q}}_{\mathit{D}}\right),{\mathit{q}}_{\mathit{D}}=-\frac{\partial p_D}{\partial r_D};$$

(7)

whereas, when considering a fractal porous medium, that is, a fractal reservoir, the model is

$$\frac{{\partial }^{\alpha }{p}_D}{\partial t_D^{\alpha }}=-\frac{1}{r_D^{d_{mf}-1}}\frac{\partial }{\partial r_D}\left(r_D^{\gamma }{\mathit{q}}_{\mathit{D}}\right),{\mathit{q}}_{\mathit{D}}=-\frac{\partial p_D}{\partial r_D},$$

(8)

where $\gamma =d_{mf}-\theta -1$. Additionally, it is defined $\nu =\frac{1-\gamma }{\theta +2}$ [20].

In Equations (7) and (8), the fractional time derivative is the Caputo fractional derivative, $\frac{{\partial }^{\alpha }{p}_D}{\partial t_D^{\alpha }}\equiv {}^C{D}_{0+}^{\alpha }{p}_D$, with $0<\alpha \le 1$. For both models, the following initial and boundary conditions are considered.

• Initial condition

  $$p_D(r_D,t_D=0)=0.$$

  (9)
• Inner boundary condition

  $$\underset{r_D\to 1}{lim}{r}_D{\mathit{q}}_{\mathit{D}}(r_D,t_D)=-1.$$

  (10)
• Outer boundary condition

  $$\underset{r_D\to \infty }{lim}{p}_D(r_D,t_D)=0.$$

  (11)

The dimensionless variables are defined as follows:

$$\begin{array}{c}\hfill r_D=\frac{r}{r_w};p_D=\frac{2\pi h\kappa }{Q_0{B}_0\mu }\left(P_i-p\right);{\mathit{q}}_{\mathit{D}}=\frac{2\pi h{r}_w}{Q_0{B}_0}\mathit{q};\\ \hfill t_D=\frac{\kappa }{\varphi c{r}_w^2\mu }t;{\tau }_D=\frac{\kappa }{\varphi c{r}_w^2\mu }\tau ;\end{array}$$

where $\tau$ is a constant introduced for the purpose of maintaining dimensional balance.

The proposed model considers a slightly compressible liquid; that is, all the complexities due to the multiphase gas–oil interactions are not taken into consideration [21]. Furthermore, the model presented in this paper does not consider petrophysical properties dependent on the stress state, which even for a Nelson Type I reservoir, imposes a challenge [22].

3.1. Spatial Fractional Darcy’s Law

Figure 1 shows the solution of Equations (7) and (9)–(11), i.e., the behavior of the pressure drop, $p_D$, throughout space for different times and values of the fractional time derivative order, $\alpha$.

Figure 1 shows the decreasing behavior of the pressure drop in space and, therefore, shows that it is valid to apply the Weyl fractional derivative to $p_D$.

For that reason, it is proposed to modify Darcy’s law by substituting the spatial derivative for the Weyl fractional derivative, obtaining the following spatial fractional Darcy’s law:

$${\mathit{q}}_{\mathbf{\beta },\mathbf{D}}=-{\delta }_{\beta ,D}\frac{{\partial }^{\beta }}{\partial r_D^{\beta }}{p}_D,\mathrm{with}\frac{{\partial }^{\beta }}{\partial r_D^{\beta }}{p}_D-W^{\beta }{p}_D\mathrm{and}{\delta }_{\beta ,D}=r_w^{1-\beta }{\delta }^{\beta -1};$$

(12)

where $0<\beta <2$ and $\delta$ is a constant term included to maintain dimensional balance in the flow equation. Note that setting $\beta =1$, $\frac{{\partial }^{\beta }}{\partial r_D^{\beta }}{p}_D=\frac{\partial }{\partial r_D}{p}_D$ and, therefore, the classical Darcy’s law is recovered.

3.2. Spatial Fractional Diffusion Model

Given the continuity equation, the first equation in (7), the traditional Darcy’s law, ${\mathit{q}}_{\mathit{D}}$, is replaced by the spatial fractional Darcy’s law, Equation (12), where the spatial fractional diffusion model is obtained, namely

$${\tau }_D^{\alpha -1}\frac{{\partial }^{\alpha }{p}_D}{\partial t_D^{\alpha }}=\frac{1}{r_D}\frac{\partial }{\partial r_D}\left(r_D{\delta }_{\beta ,D}\frac{{\partial }^{\beta }}{\partial r_D^{\beta }}{p}_D\right).$$

(13)

As a consequence of the spatial fractional Darcy’s law, the inner boundary condition is also modified, namely

$$\underset{r_D\to 1}{lim}{r}_D{\mathit{q}}_{\mathbf{\beta },\mathbf{D}}(r_D,t_D)=-1.$$

(14)

Therefore, the spatial fractional diffusion model to be solved is the one constituted by Equations (9), (11), (13) and (14).

With these modifications, it is intended that the fluid flow at a given point in the porous medium be governed by the global spatial distribution of the pressure field and not only by the behavior in the direct neighborhood of the pressure around that point.

4. Results

In this section, the solution of the spatial fractional diffusion model will be shown, as well as its behavior when its parameters vary, and such behavior will be compared with the model that considers a fractal reservoir.

The spatial fractional diffusion model was solved using the finite difference method, considering an implicit scheme in time and Crank–Nicholson in space.

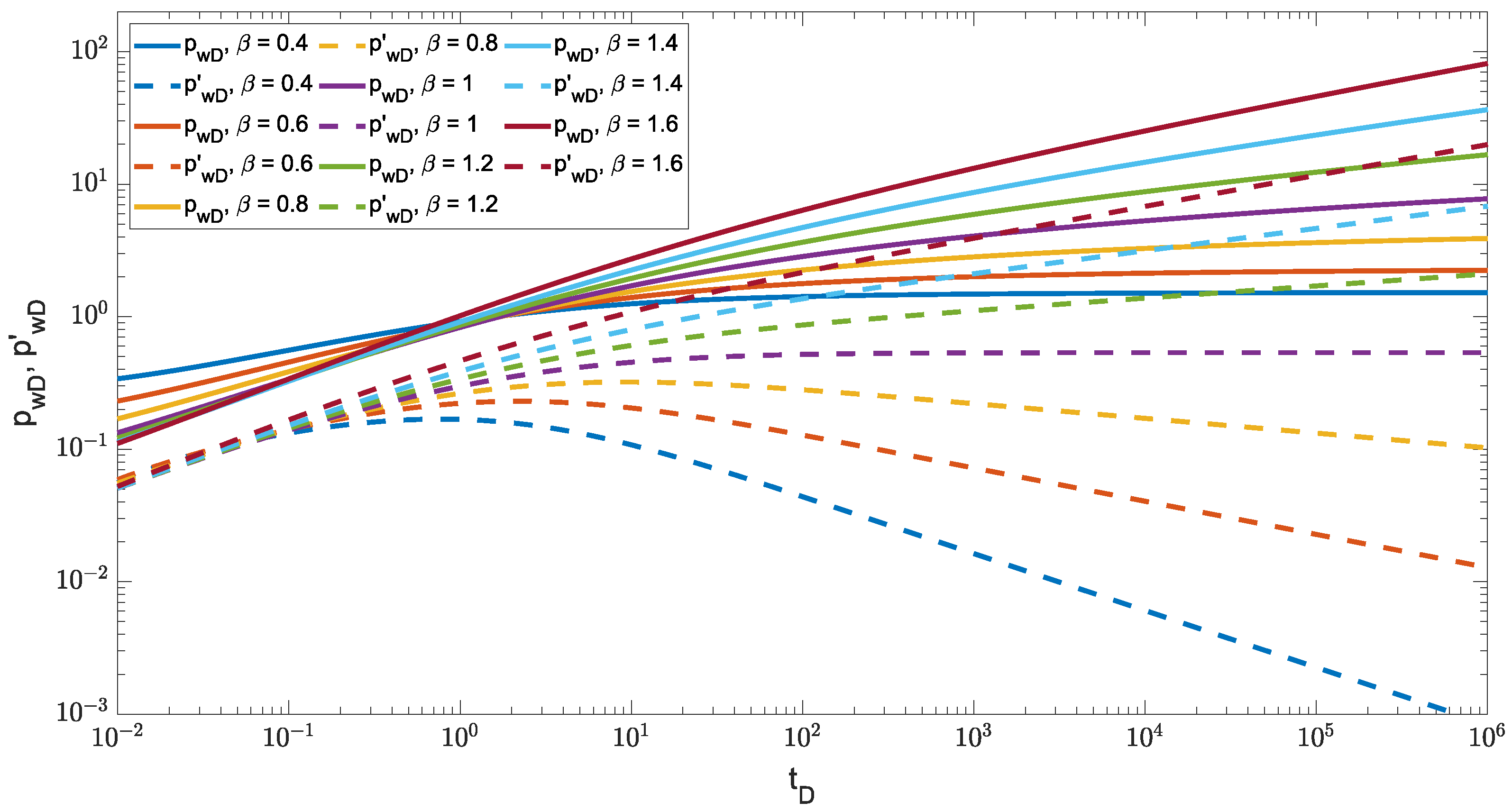
Figure 2 shows the numerical solution of solving the spatial fractional diffusion model considering the classical time derivative, $\alpha =1$, and varying the order in the fractional Darcy’s law, $\beta$. The solution in the well, $p_{wD}=p_D(r_D=1,t_D)$, and its Bourdet semi-logarithmic derivative, $p_{wD}^{\prime }$ [23], are shown.

In Figure 2, two important features can be described when modifying $\beta$ in the spatial fractional Darcy’s law.

At short times, the pressure drop is lower than the pressure drop of the classical case, $\beta =1$, which corresponds to a higher order in the spatial fractional Darcy’s law; while if $\beta$ is lower than one (i.e., classical case), a higher pressure drop will be obtained. However, in the Bourdet derivative, $\beta$ in the spatial fractional Darcy’s law does not seem to have a remarkable impact, except by keeping a power-law behavior with a slope of 0.5.

At long times, when $\beta <1$, the pressure drop is lower than that in the classic case and its respective Bourdet derivative shows a decrease following a power-law behaviour, showing a greater connectivity of pores that provide preferential flow paths; while for $\beta >1$, the pressure drop is greater than in the classic case following a power-law behaviour, and the same happens with the pressure derivative. Both power-law behaviors are parallel, evidencing the creation of flow buffers in the porous medium.

Figure 3 shows the combined effect of the fractional temporal derivative and the spatial fractional Darcy’s law, that is, for different values of $\beta$ in the space fractional Darcy’s law, on the pressure drop and its Bourdet derivative for different values of the order of the fractional time derivative, $\alpha$.

It is necessary to highlight that the results shown in Figure 3 demonstrate the compatibility of two different definitions of fractional derivative; that is, Caputo’s fractional derivative for the temporal derivative and Weyl’s fractional derivative for the spatial derivative in Darcy’s law, which allows better modeling of a complex phenomenon by making each fractional derivative capture different characteristics of this phenomenon.

Figure 3a shows for $\beta <1$ the effect of varying the order of the fractional time derivative, $\alpha$. In the case with the integer time derivative, $\alpha =1$, the effect of spatial fractional Darcy’s law creates a larger short-time pressure drop that quickly loses its effect, making the long-time pressure drop smaller the smaller $\alpha$ is; this is a consequence of a greater connectivity of pores that provide preferential flow paths. In the case of $\beta =0.5$, Figure 3a, we can observe that the influence of $\alpha$ is not as big as that observed in the pressure derivative, where we observe power-law behaviors at late times, which could be an indication of flow restrictions.

Figure 3b shows for $\beta >1$ the effect of varying the order of the fractional time derivative, $\alpha$, on the pressure deficit and its Bourdet derivative. For the case with an integer time derivative, $\alpha =1$; at short times, the spatial fractional Darcy’s law causes the fluid flow velocity to have a behavior similar to the case with the classical Darcy’s law, i.e., a linear flow behavior; however, the pressure drop is smaller. Subsequently, for long times, the pressure drop is lower than in the classical case, the lower $\alpha$ is; this is caused by the displacement of dead pores that creates preferential flow paths, which is reflected in the increase in flow velocity and, therefore, in the decrease of the pressure drop. By incorporating the memory effect of the fluid flow, the dependence of the previous pressure on the subsequent pressures is observed; that is, the flow of the fluid receives an increase in the phenomenon that is reflected in the decrease of the pressure drop and its Bourdet derivative.

It is important to point out that in all cases with $\beta =1.5$ and $\alpha$ less or equal to one, Figure 3b, at late times, there is parallel power-law behavior for both the pressure drop and semilog pressure derivative. This behavior is similar to the fractal behavior, and both cases are expressions of anomalous diffusion; in this case, there is a super-diffusion because of the memory effect, and in the fractal case, there is sub-diffusion.

Figure 4 shows the effect of ${\delta }_{\beta ,D}$, the dimensionless variable introduced in the spatial fractional Darcy’s law to maintain the dimensional balance in the fractional flow equation, for the cases $\beta <1$ and $\beta >1$ with $\alpha =1$.

The effect of ${\delta }_{\beta ,D}$ is remarkable throughout the whole phenomenon. For $\beta <1$ and in short times, it is observed that the greater the value of ${\delta }_{\beta ,D}$, the greater the value of $p_{wD}$, also affecting the transition phase, presenting itself at different times for each value of ${\delta }_{\beta ,D}$ and finally reaching the same value of $p_{wD}$ in the stability phase. Bourdet’s derivative shows that although in short times, the greater the value of ${\delta }_{\beta ,D}$ the greater $p_{wD}^{\prime }$ will be and the faster the decrement in $p_{wD}^{\prime }$ to such a degree that upon reaching the stability phase, it will be shown that the higher the value of ${\delta }_{\beta ,D}$, the lower the value of $p_{wD}^{\prime }$, also showing a parallel behavior for all the values of ${\delta }_{\beta ,D}$.

On the other hand, for $\beta >1$ at short times, it is observed that in the same way as in the previous case, the greater ${\delta }_{\beta ,D}$, the greater the value of $p_{wD}$, changing the growth rate in the transient phase and subsequently having a constant growth rate for each value of ${\delta }_{\beta ,D}$. This behavior is maintained in the Bourdet derivative, where, in short times, the higher the value for $p_{wD}^{\prime }$, the higher the ${\delta }_{\beta ,D}$, followed by a parallel growth for the different values of ${\delta }_{\beta ,D}$, changing the growth rate during the transient phase until reaching a constant and parallel growth for the different values of ${\delta }_{\beta ,D}$.

5. Discussion

In this section, the spatial fractional diffusion model, derived from the equation of continuity with a fractional time derivative and the proposed spatial fractional Darcy’s law, and the results from the fractal model are compared.

Figure 5 shows, on the one hand, the model of Razminia et al. [4], which considers a fractal reservoir, Equations (8)–(11); and on the other hand, the spatial fractional diffusion model, Equations (9), (11), (13) and (14).

The purpose is to compare, through the results shown, the approaches considered by both models. The spatial fractional diffusion model shows a great agreement with the data of the model that considers a fractal reservoir, both for the pressure drop and its Bourdet derivative; thereby, it can be considered that by including the spatial fractional Darcy’s law, the heterogeneity of the porous medium is recovered through the use of the fractional approach.

Furthermore, the above makes sense considering that the spatial fractional Darcy’s law takes into account the geometry of the porous medium in two ways; on the one hand, the geometry of the porous medium is implicitly included through the parameter in the Weyl fractional derivative, $\beta$; while, on the other hand, it is explicitly included through the $\delta$ parameter, which also helps with dimensional balance.

With the above, it is shown that the spatial fractional Darcy’s law, by including the dependence on the fluid flow path, i.e., spatial memory, also takes into account the intrinsic geometry of the porous medium.

The proposed model can be part of a robust deep learning model, such as the one suggested by [24], for the automated analysis of pressure tests.

6. Conclusions

Considering the hypotheses that the Type I naturally fractured reservoir of Nelson is embedded in an infinite porous medium, with a slightly compressible fluid and stress-independent petrophysical properties, we have the following conclusions:

1.

Fluid flow at a given point is governed not only by the properties of the pressure field at that specific position but also depends on the global spatial distribution of that field; it is proposed to modify Darcy’s law by replacing the spatial derivative with the Weyl fractional derivative.

2.

The proposed model, with the Caputo fractional time derivative and Weyl fractional derivative on the gradient, proves that two different definitions of the fractional derivative can be compatible.

3.

The results show that the spatial fractional Darcy’s law can, on the one hand, reflect the preferential flow paths, and on the other hand, the creation of flow buffers during the phenomenon, whereas the time-fractional derivative incorporates the memory effect of the fluid flow.

4.

The proposed model not only resembles the results obtained in models that incorporate fractal geometry, but it also incorporates the intrinsic geometry of the porous medium and, therefore, allows recovering the heterogeneity of the porous medium. This is important because it is confirmed for the first time that both the fractal and fractional approaches represent two possible ways of capturing anomalous diffusion.