Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter
Abstract
:1. Introduction
2. Modeling for the Control System
2.1. Modeling for Plant
- The disturbances (load currents) is finite energy signals.
- The DC link voltage is well controlled as an ideal DC source by other DC sources such as the battery.
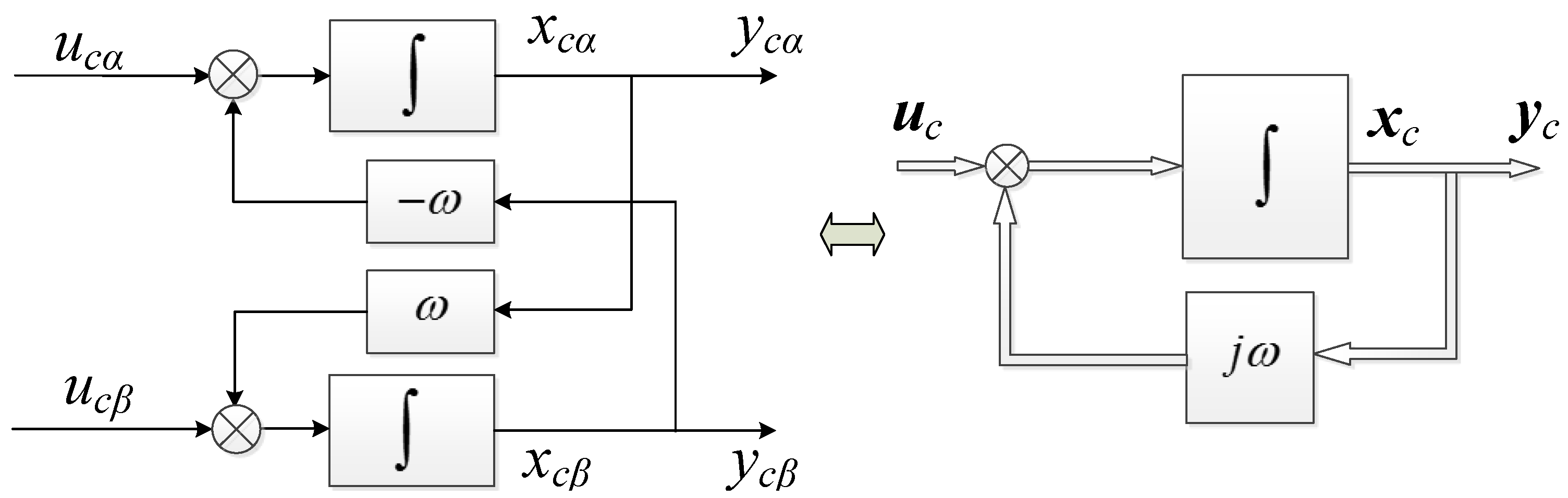
2.2. Complex Variable Resonant Controller
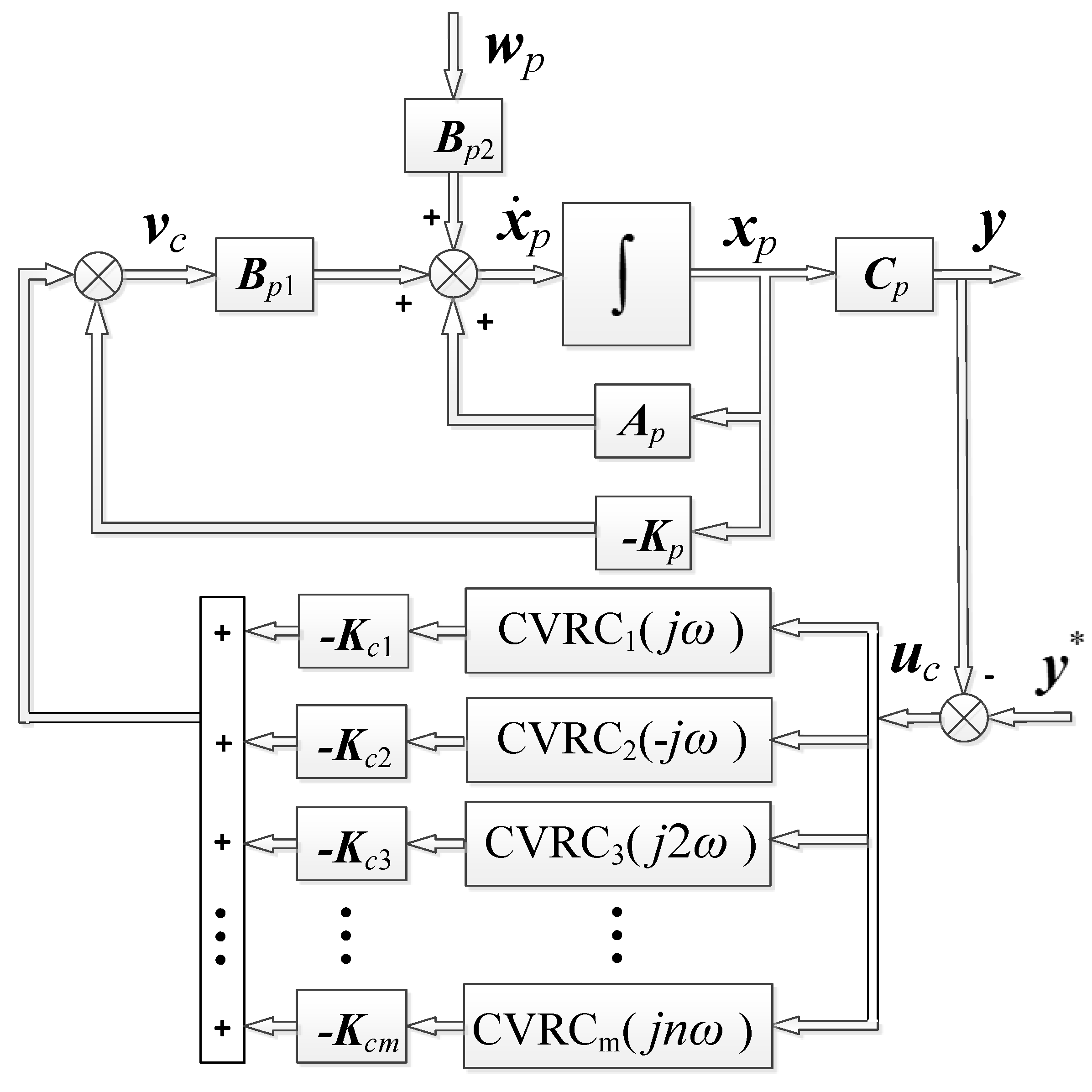
2.3. Augmented Modeling for the System
3. Control Parameter Design
3.1. Linear Quadratic (LQ) Control
- The closed-loop steady and
- The LQ index.
3.2. H∞ Norm Constraint
3.3. Poles Region Constraint
3.4. The Comprehensive Optimization
- Step (1)
- Build augmented system model (6).
- Step (2)
- Establish the LMI constraint (22) and (23) with the identity matrix R.
- Step (3)
- Establish the LMI constraint (29).
- Step (4)
- Establish the LMI constraint (31) with the selectable region
- Step (5)
- Based on the selected a and b, solve the optimization problem (33).
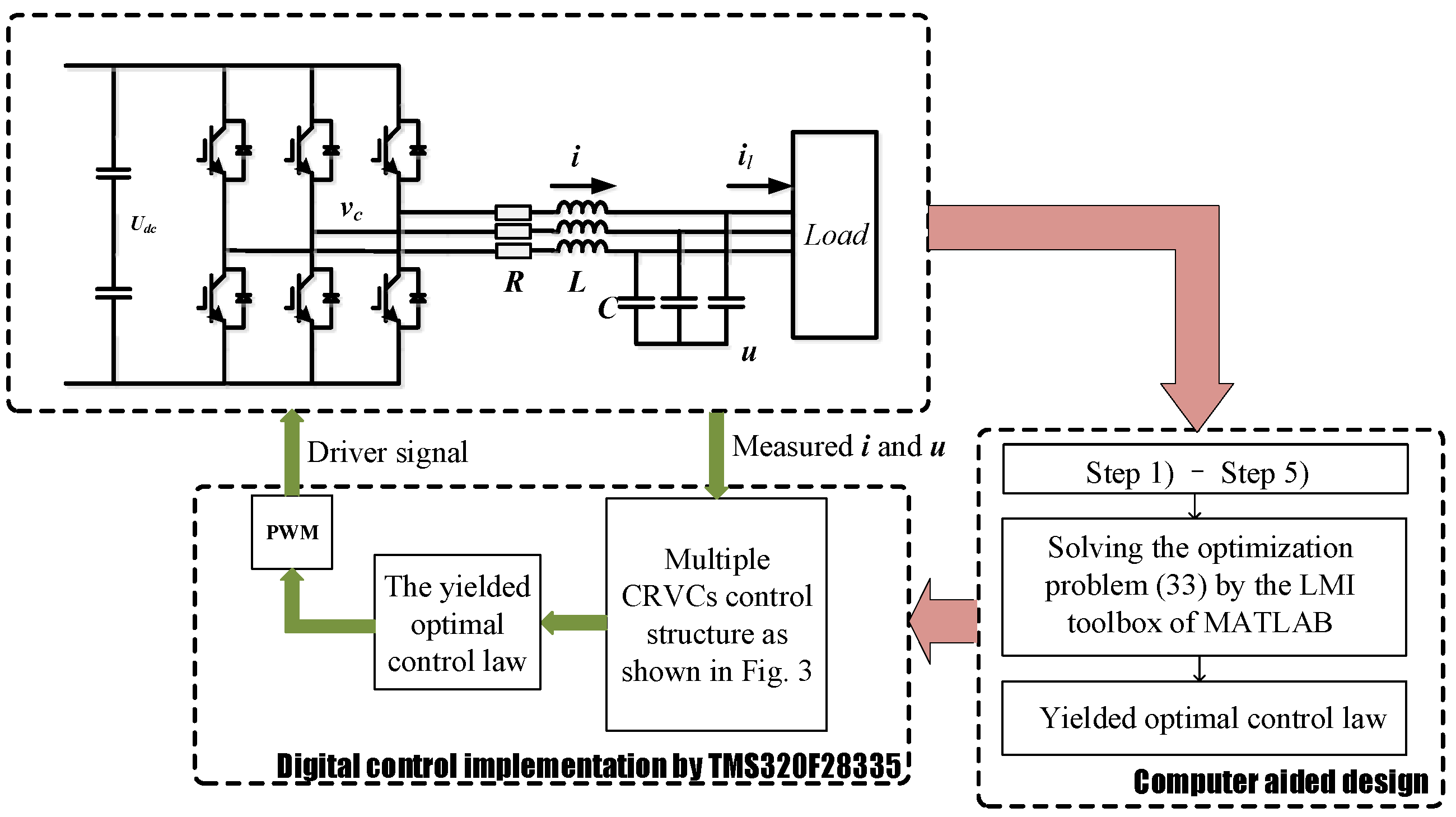
4. Application and Verification
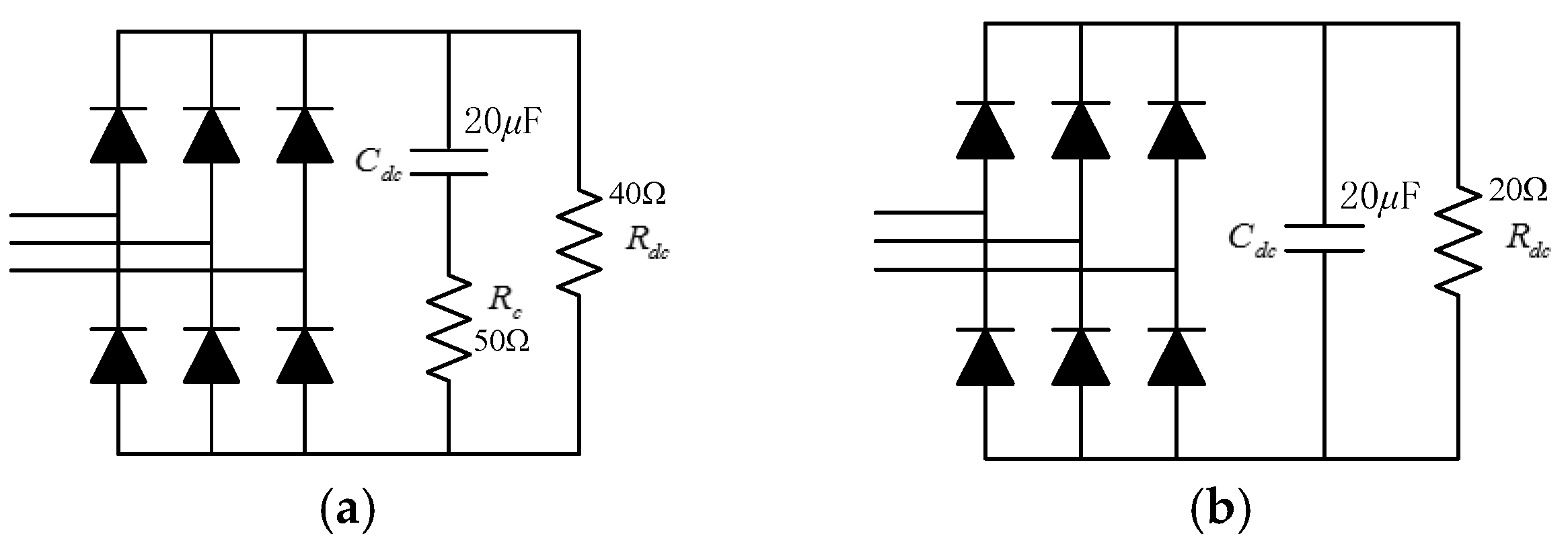
4.1. Case Study
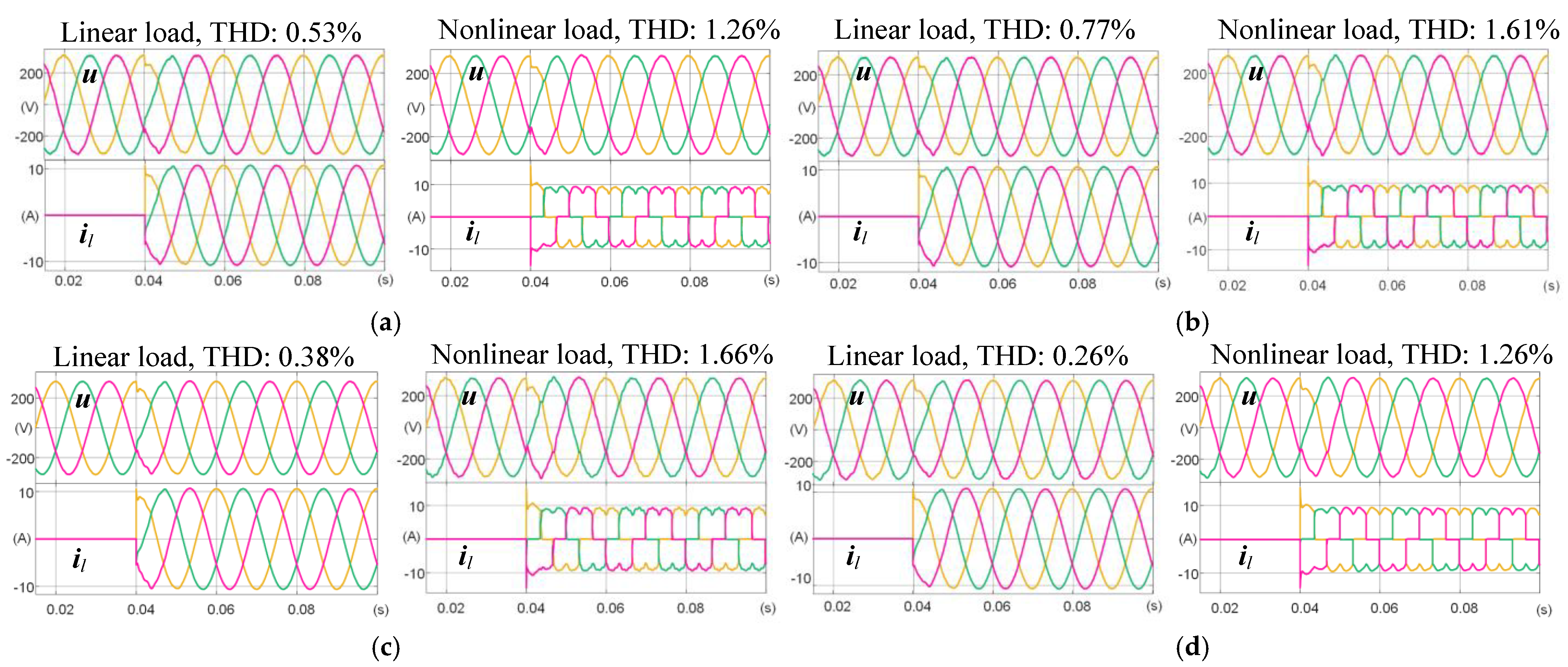
4.2. Simulation Verifications
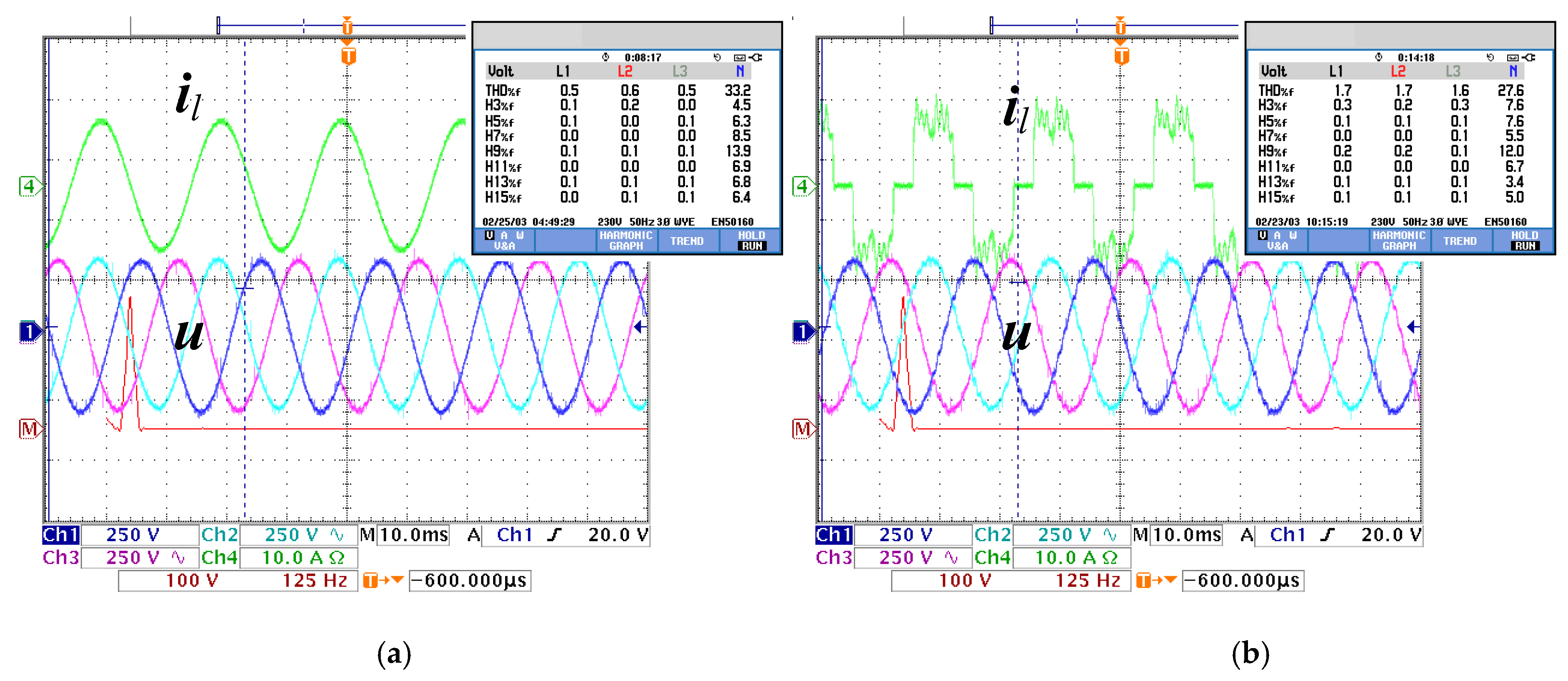
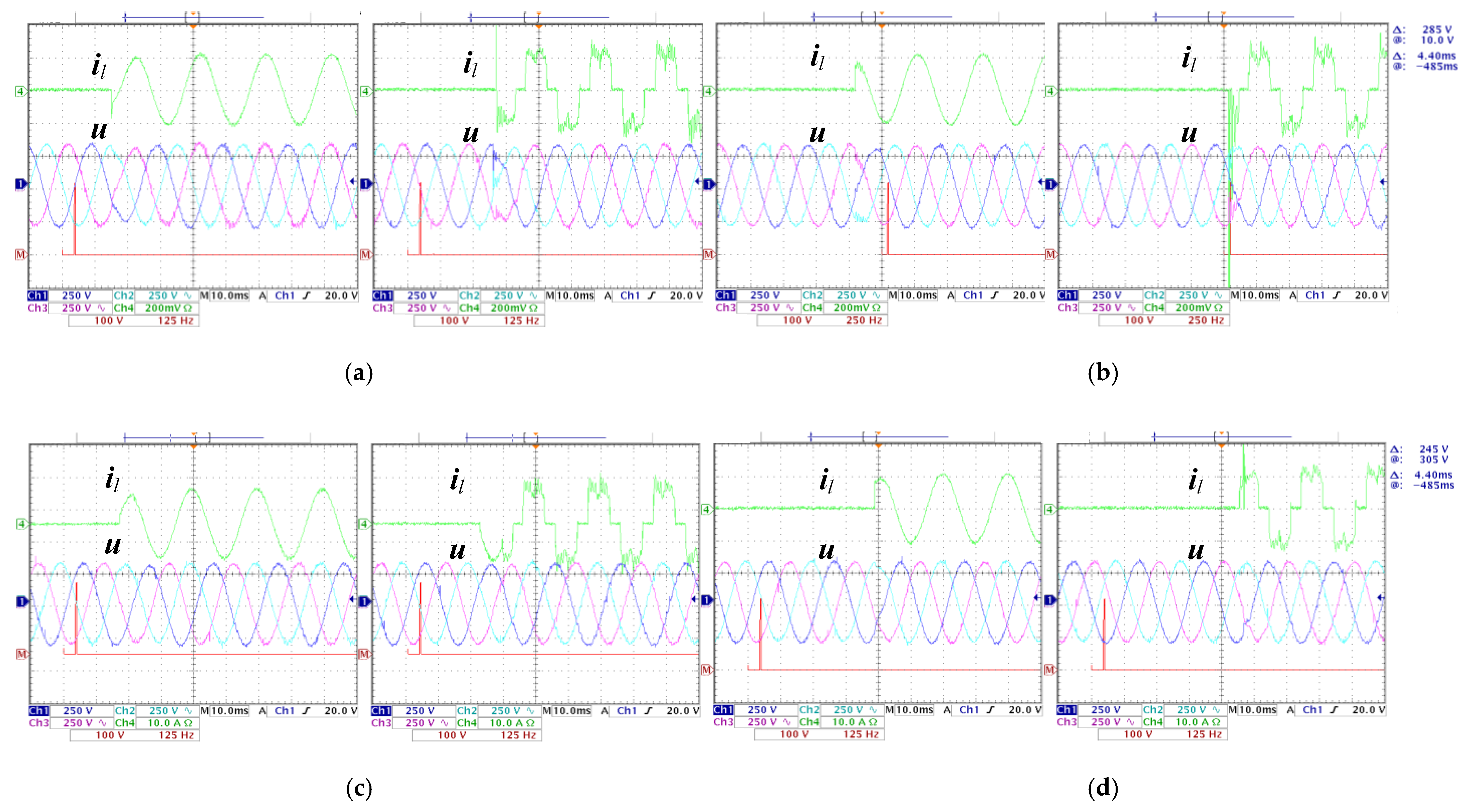
4.3. Experiment Verifications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, Z.; de Carne, G.; Buticchi, G.; Liserre, M. Smart Transformer-Fed Variable Frequency Distribution Grid. IEEE Trans. Ind. Electron. 2018, 65, 749–759. [Google Scholar] [CrossRef]
- Zou, Z.; Buticchi, G.; Liserre, M. Grid Identification and Adaptive Voltage Control in a Smart Transformer-Fed Grid. IEEE Trans. Power Electron. 2019, 34, 2327–2338. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Golshan, M.E.H.; Hatziargyriou, N.D. A Decentralized Functional Observer Based Optimal LFC Considering Unknown Inputs, Uncertainties, and Cyber-Attacks. IEEE Trans. Power Syst. 2019, 34, 4408–4417. [Google Scholar] [CrossRef]
- Haesalhelou, H.; Parthasarathy, H.; Nagpal, N.; Agarwal, V.; Nagpal, H.; Siano, P. Decentralised Stochastic Disturbance Observer-Based Optimal Frequency Control Method for Interconnected Power Systems with High Renewable Shares. IEEE Trans. Ind. Inform. 2021. [Google Scholar] [CrossRef]
- Quan, X.; Huang, A.Q.; Yu, H. A Novel Order Reduced Synchronous Power Control for Grid-Forming Inverters. IEEE Trans. Ind. Electron. 2020, 67, 10989–10995. [Google Scholar] [CrossRef]
- Quan, X.; Yu, R.; Zhao, X.; Lei, Y.; Chen, T.; Li, C.; Huang, A.Q. Photovoltaic Synchronous Generator: Architecture and Control Strategy for a Grid-Forming PV Energy System. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 936–948. [Google Scholar] [CrossRef]
- Loh, P.C.; Newman, M.J.; Zmood, D.N.; Holmes, D.G. A comparative analysis of multiloop voltage regulation strategies for single and three-phase UPS systems. IEEE Trans. Power Electron. 2003, 18, 1176–1185. [Google Scholar]
- Mohamed, Y.A.R.I.; Radwan, A. Hierarchical control system for robust microgrid operation and seamless mode transfer in active distribution systems. IEEE Trans. Smart Grid. 2011, 2, 352–362. [Google Scholar] [CrossRef]
- Deng, H.; Oruganti, R.; Srinivasan, D. A simple control method for high-performance UPS inverters through output-impedance reduction. IEEE Trans. Ind. Electron. 2008, 55, 888–898. [Google Scholar] [CrossRef]
- Kawabata, T.; Miyashita, T.; Yamamoto, Y. Dead beat control of three phase PWM inverter. IEEE Trans. Power Electron. 1990, 5, 21–28. [Google Scholar] [CrossRef]
- Mattavelli, P. An improved deadbeat control for UPS using disturbance observers. IEEE Trans. Ind. Electron. 2005, 52, 206–212. [Google Scholar] [CrossRef]
- Escobar, G.; Valdez, A.A.; Leyva-Ramos, J.; Mattavelli, P. Repetitive-based controller for a UPS inverter to compensate unbalance and harmonic distortion. IEEE Trans. Ind. Electron. 2007, 54, 504–510. [Google Scholar] [CrossRef]
- Jung, S.L.; Tzou, Y.Y. Discrete sliding-mode control of a PWM inverter for sinusoidal output waveform synthesis with optimal sliding curve. IEEE Trans. Power Electron. 1996, 11, 567–577. [Google Scholar] [CrossRef]
- Komurcugil, H. Rotating-sliding-line-based sliding-mode control for single-phase UPS inverters. IEEE Trans. Ind. Electron. 2012, 59, 3719–3726. [Google Scholar] [CrossRef]
- Cortés, P.; Ortiz, G.; Yuz, J.I.; Rodríguez, J.; Vazquez, S.; Franquelo, L.G. Model predictive control of an inverter with output LC filter for UPS applications. IEEE Trans. Ind. Electron. 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
- Yaramasu, V.; Rivera, M.R.; Narimani, M.; Wuet, B.; Rodriguez, J. Model Predictive Approach for a Simple and Effective Load Voltage Control of Four-Leg Inverter with an Output Filter. IEEE Trans. Ind. Electron. 2012, 61, 5259–5270. [Google Scholar] [CrossRef]
- Do, T.D.; Leu, V.Q.; Choi, Y.S.; Choiet, H.H.; Jung, J. An adaptive voltage control strategy of three-phase inverter for stand-alone distributed generation systems. IEEE Trans. Ind. Electron. 2013, 60, 5660–5672. [Google Scholar] [CrossRef]
- Jung, J.W.; Vu, N.T.T.; Dang, D.Q.; Doet, T.D.; Choi, Y.; Choi, H.H. A three-phase inverter for a standalone distributed generation system: Adaptive voltage control design and stability analysis. IEEE Trans. Energy Convers. 2014, 29, 46–56. [Google Scholar] [CrossRef]
- Kim, D.E.; Lee, D.C. Feedback linearization control of three-phase UPS inverter systems. IEEE Trans. Ind. Electron. 2010, 57, 963–968. [Google Scholar]
- Houari, A.; Renaudineau, H.; Martin, J.P.; Pierfederici, S.; Meibody-Tabar, F. Flatness-based control of three-phase inverter with output filter. IEEE Trans. Ind. Electron. 2012, 59, 2890–2897. [Google Scholar] [CrossRef]
- Komurcugil, H.; Altin, N.; Ozdemir, S.; Sefa, I. An Extended Lyapunov-Function-Based Control Strategy for Single-Phase UPS Inverters. IEEE Trans. Power Electron. 2015, 30, 3976–3983. [Google Scholar] [CrossRef]
- Razi, R.; Monfared, M. Simple control scheme for single-phase uninterruptible power supply inverters with Kalman filter-based estimation of the output voltage. IET Power Electron. 2015, 8, 1817–1824. [Google Scholar] [CrossRef] [Green Version]
- Willmann, G.; Coutinho, D.F.; Pereira, L.F.A.; Líbano, F.B. Multiple-loop H-infinity control design for uninterruptible power supplies. IEEE Trans. Ind. Electron. 2012, 54, 1591–1602. [Google Scholar] [CrossRef]
- Lim, J.S.; Lee, Y.I. Design of a robust controller for three-phase UPS systems using LMI approach. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20 June 2012. [Google Scholar]
- Lim, J.S.; Park, C.; Han, J.; Lee, Y.I. Robust Tracking Control of a Three-Phase DC–AC Inverter for UPS Applications. IEEE Trans. Ind. Electron. 2014, 61, 4142–4151. [Google Scholar] [CrossRef]
- Pereira, L.F.A.; Flores, J.V.; Bonan, G.; Gomes da Silva, J.M., Jr. Multiple resonant controllers for uninterruptible power supplies—A systematic robust control design approach. IEEE Trans. Ind. Electron. 2014, 61, 1528–1538. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. State feedback control of the PMSM servo-drive with sinusoidal voltage source inverter. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS2a. 6-1–DS2a. 6-6. [Google Scholar]
- Hasanzadeh, A.; Edrington, C.S.; Maghsoudlou, B.; Mokhtari, H. Optimal LQR-based multi-loop linear control strategy for UPS inverter applications using resonant controller. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 3080–3085. [Google Scholar]
- Hasanzadeh, A.; Edrington, C.S.; Maghsoudlou, B.; Fleming, F.; Mokhtari, H. Multi-loop linear resonant voltage source inverter controller design for distorted loads using the linear quadratic regulator method. IET. Power Electron. 2012, 5, 5841–5851. [Google Scholar] [CrossRef]
- Kaszewski, A.; Grzesiak, L.M.; Ufnalski, B. Multi-oscillatory LQR for a three-phase four-wire inverter with L 3n C output filter. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3449–3455. [Google Scholar]
- Quan, X. Improved Dynamic Response Design for Proportional Resonant Control Applied to Three-Phase Grid-Forming Inverter. IEEE Trans. Ind. Electron. 2021, 68, 9919–9930. [Google Scholar] [CrossRef]
- Quan, X.; Dou, X.; Wu, Z.; Hu, M.; Song, H.; Huang, A.Q. A Novel Dominant Dynamic Elimination Control for Voltage-Controlled Inverter. IEEE Trans. Ind. Electron. 2018, 65, 6800–6812. [Google Scholar] [CrossRef]
- Ufnalski, B.; Kaszewski, A.; Grzesiak, L.M. Particle Swarm Optimization of the Multioscillatory LQR for a Three-Phase Four-Wire Voltage-Source Inverter with an Output Filter. IEEE Trans. Ind. Electron. 2015, 62, 484–493. [Google Scholar] [CrossRef]
- Quan, X.; Dou, X.; Wu, Z.; Hu, M.; Yuan, J. Harmonic voltage resonant compensation control of a three-phase inverter for battery energy storage systems applied in isolated microgrid. Electr. Power Syst. Res. 2016, 131, 205–217. [Google Scholar] [CrossRef]
- Kim, E.K.; Mwasilu, F.; Choi, H.H.; Jung, J.W. An Observer-Based Optimal Voltage Control Scheme for Three-Phase UPS Systems. IEEE Trans. Ind. Electron. 2015, 62, 2073–2081. [Google Scholar] [CrossRef]
- Scherer, C. H∞ control by state feedback: An iterative algorithm and characterization of high-gain occurence. Syst. Control. Lett. 1989, 12, 383–391. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Leon, A.E.; Solsona, J.A. Current controller based on reduced order generalized integrators for distributed generation systems. IEEE Trans. Ind. Electron. 2012, 59, 2898–2909. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Scherer, C.; Weiland, S. Linear Matrix Inequalities in Control; Lecture Notes; Dutch Institute for Systems and Control: Delft, The Netherlands, 2000. [Google Scholar]
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control. 1996, 41, 358–367. [Google Scholar] [CrossRef]
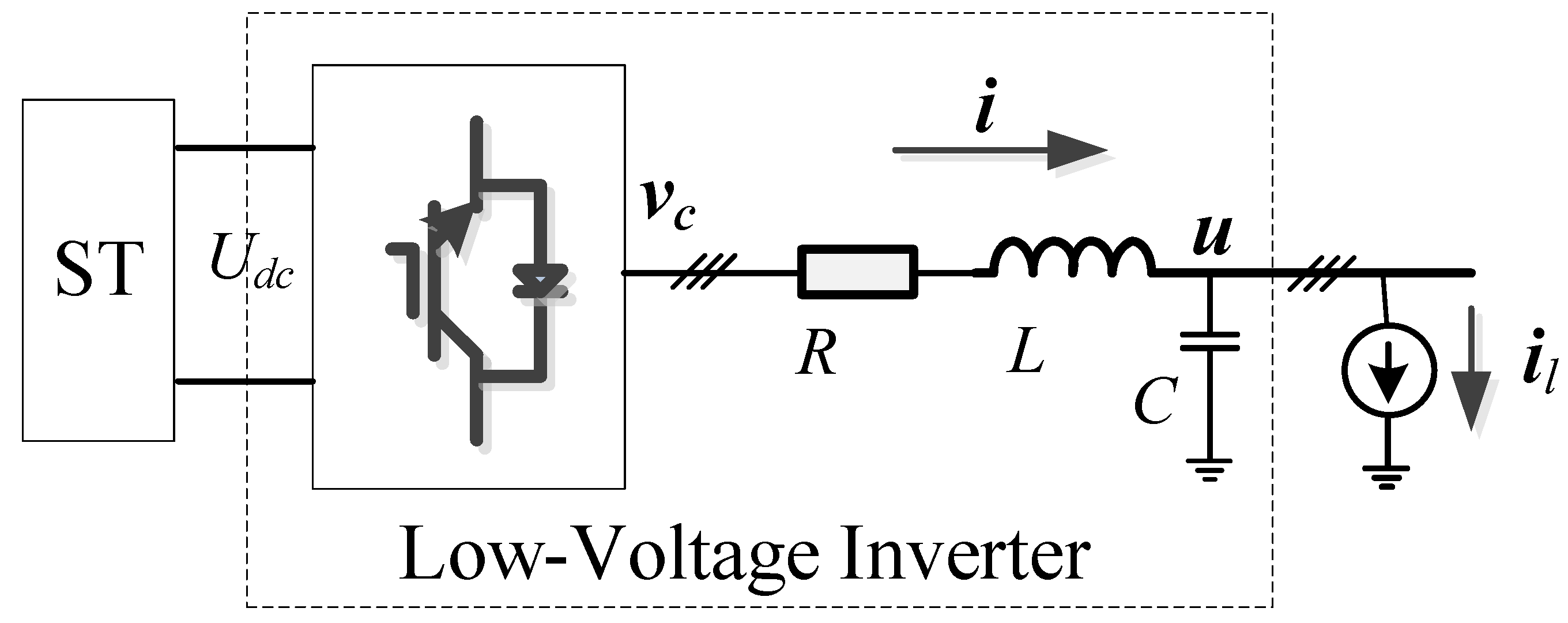



| Scheme | a | b | Significance |
|---|---|---|---|
| ① | 0 | 0 | no optimization |
| ② | 0 | 1 | optimal LQ index with regional closed-loop pole placement |
| ③ | 1 | 0 | optimal H∞ norm with regional closed-loop pole placement |
| ④ | 1 | 1 | optimal H∞ norm plus LQ index with regional closed-loop pole placement |
| Variable | Significance | Value |
|---|---|---|
| L | Inductance | 2 mH |
| C | Capacitance | 30 μF |
| R | Inductor resistance | 0.5 Ω |
| fs | Switch frequency | 12,800 Hz |
| Output voltage peak | 311 V | |
| DC link voltage | 650 V |
| Variable | Method in 26 | LQR | The Proposed Approach with a = 1, b = 1 |
|---|---|---|---|
| 15.8836306685511 − j0.236950325611173 | 4.97008210384462 | 6.1118757040980984 − j0.34847163443228379 | |
| 0.90564004136966 − j0.0795364207060859 | 0.328182730006515 − j0.0264301565213812 | 0.01969918364658270 − j0.1087245143573579 | |
| −224.980219438506 + j200.222952492662 | −98.8992557609345 + j14.7965269551116 | −187.17608886575 + j226.78327067540437 | |
| −318.59139186677 + j244.142045864815 | −98.8196531191056 + j15.3191434949775 | −312.155066799714 + j236.03740844488078 | |
| −337.457407096336 − j 193.141886574298 | −70.0566409645719 − j9.59515798520183 | −291.80188834927043 − j228.45515137729637 | |
| −285.046690109709 − j7.02975962859623 | −69.4806377962434 + j13.1316781649438 | −227.27849531760467 − j83.591874218641919 | |
| −257.199648231256 − j82.264392533777 | −64.8801674954042 − j28.1169675777419 | −186.70790924243212 + j44.445109123432452 | |
| −181.365786957522 + j228.403814890761 | −23.3264892093487 + j66.7523400426255 | −82.369151850982988 + j68.96189605286802 |
| 1 mH, 30 μF | 2 mH, 15 μF | 2 mH, 30 μF (Nominal) | 2 mH, 60 μF | |||||
|---|---|---|---|---|---|---|---|---|
| Linear Load | Nonlinear Load | Linear Load | Nonlinear Load | Linear Load | Nonlinear Load | Linear Load | Nonlinear Load | |
| The proposed approach | Inferior dynamic performance, THD: 2.1% RMS: 220.1 V | Inferior dynamic performance, THD: 1.9% RMS: 220.2 V | Inferior dynamic performance, THD: 0.6% RMS: 220.1 V | Good dynamic performance, THD: 1.8% RMS: 220.1 V | Excellent dynamic performance, THD: 0.5% RMS: 220 V | Excellent dynamic performance, THD: 1.7% RMS: 220.1 V | Good dynamic performance, THD: 0.3% RMS: 220 V | Good dynamic performance, THD:1.4% RMS: 220 V |
| The method in [26] | Can’t start up * | Can’t start up | Can’t start up | Can’t start up | Instability * | Instability | Inferior dynamic performance, THD: 0.7% RMS: 219.8 V | Inferior dynamic performance, THD: 2.0% RMS: 219.8 V |
| LQR | Can’t start up | Can’t start up | Instability * | Instability | Inferior dynamic performance, THD: 0.7% RMS: 220 V | Inferior dynamic performance, THD: 3.4% RMS: 220.2 V | Inferior dynamic performance, THD: 0.6% RMS: 219.9 V | Inferior dynamic performance, THD: 2.1% RMS: 220 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Shen, Y.; Yang, Z.; Min, H. Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter. Energies 2022, 15, 365. https://doi.org/10.3390/en15010365
Hu W, Shen Y, Yang Z, Min H. Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter. Energies. 2022; 15(1):365. https://doi.org/10.3390/en15010365
Chicago/Turabian StyleHu, Wei, Yu Shen, Zhichun Yang, and Huaidong Min. 2022. "Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter" Energies 15, no. 1: 365. https://doi.org/10.3390/en15010365
APA StyleHu, W., Shen, Y., Yang, Z., & Min, H. (2022). Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter. Energies, 15(1), 365. https://doi.org/10.3390/en15010365





