Abstract
Surprisingly, little is known whether the net present value (NPV) used as a financial metric in budgeting and investment planning to analyse a projects’ profitability is universal. Meanwhile, the epochal green energy revolution ensuring carbon neutrality through green innovations requires enormous investments, and projects realised must ensure energy security. Therefore, there is a need to reanalyse financial metrics used in financial planning, including NPV. We eliminate this research gap and, based on data from Poland, Romania, Hungary, Croatia, the USA, the United Kingdom, Japan, Israel, and Euro Zone, explain why one may not perceive the currently used NPV formula as a universal financial metric. We show that the variable discount rate influences the time value of money. Therefore, there is a need to redefine the NPV formula. This study makes two main contributions. First, it creates new ground by revisiting the NPV formula in the emerging market context compared to stable economies and contributes to developing business and management theory. Second, we propose and empirically verify the modified NPV formula as a financial metric that considers the situation of energy firms in emerging markets. Thus, this research helps the capital budgeting process, and the modified NPV formula can help provide optimal outcomes in firms, helping to reduce financial risks. Our study contributes to a further contextual diagnosis of business projects and can, in turn, be relevant for other energy sector analyses.
1. Introduction
No doubt, one of the critical industries in today’s economy is the energy industry, and there is a connection between energy consumption and economic growth, c.f. [1,2,3]. All projects in the energy sector must be well planned and implemented. It results from management rationality and the influence of the energy sector on other branches of the economy. Energy firms are obliged by law to ensure energy security, which we understand from Dobrowolski’s definition: “the state of the economy that allows covering the current and future fuel and energy supplies in a technically and economically justified manner while maintaining environmental protection requirements. Energy security can also be understood as the diversification of energy supply sources and ensuring the certainty of their supply at a price acceptable to society and the economy. It is also the optimal use of domestic energy resources, with the simultaneous use of new technology and active participation in international environmental and energy initiatives. In the local sense, energy safety can be understood as a process aiming to meet the energy needs of local communities.” [4,5,6]. The implemented green revolution, also known as the 5G revolution, aimed at carbon neutrality through green innovations, requires enormous financial outlays and excellent financial planning of investments. In addition, there is one more aspect, which is the obligation imposed by the States on energy companies in terms of ensuring energy security. We define green energy security as generating energy from environmentally neutral sources and ensuring the certainty of their supply at a price acceptable to society and the economy.
Mismanagement in the energy sector reduces the competitiveness of energy firms and other economic entities. Despite many studies, there is a research gap regarding whether the NPV metric is universal—whether one may use the NPV in different countries with different economic stability? Therefore, the research problem needs to be solved: Does the currently applicable NPV metric fit emerging markets? Our research aims to verify the following hypothesis: the variable discount rate influences the time value of money, requiring redefining the NPV formula as a financial metric.
This article presents a theory that explains why NPV cannot be perceived as a universal metric used in the budgeting decisions of firms worldwide. The rules governing the project selection process depend upon the economic environment, and therefore they may have many restrictions and detailed guidance. Our findings are rooted in corporate finance’s mainstream literature and the previous studies on NPV limitations, e.g., [7]. To prove our assumption, we develop a new NPV metric that considers the situation of firms in emerging markets. Next, we empirically verify this model.
Our findings are based on the capital budgeting literature, c.f. [7,8,9], and they have several implications for both researchers and firms. They help modify the NPV and reconcile the theory with actual firm capital budgeting practices from an academic standpoint. Our research shows that current NPV is an ineffective metric. However, in opposition to the previous studies mentioned above, we prove that NPV is not the universal metric because of information constraints between the firms’ headquarters and their branches. There is another more serious argument. The NPV is not considering the differences in firms’ situation resulting from their location in stable and emerging markets, and therefore it cannot be a universal metric.
We believe this research is related to the UN Sustainable Development Goals and European Green Deal. It is because we aim to reduce the investment risk through the improvement of the NPV formula. Ensuring in a better way the financial reality in energy investment reduces the risk of losing financial and other resources and helps achieve the planned goals wisely. In addition, transformations in the energy sector from traditional energy sources into green energy need the support of decision-makers. Any failures in this process can question efforts taken and create unnecessary uncertainty on financial markets.
To present our findings in the best way, we first discuss the NPV used contemporarily in the context of interest rates and business risk. Next, we provide evidence that the current NPV metric is not universal and formulate the new NPV formula. Finally, we formulate a conclusion and point out opportunities for further research.
2. Literature Review
Under uncertainty, the economic reliability of project financing requires solid economic metrics [10]. One of these metrics is the net present value (NPV), understood as the difference between the present values of cash inflows and cash outflows analysed over some time. This understanding of NPV is used in capital budgeting and investment planning, enabling analysis of a projected investment or project [11]. The application of NPV in capital budgeting and investments is widely presented in the literature, e.g., [7,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The researchers emphasise the importance of NPV for investment planning. Net Present Value enables the comparison between the money that must be paid to complete the planned investment with all the cash flows that the undertaking will generate in the future [7,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].
One may measure economic profitability with absolute metrics in capital asset projects, including the net present value. This metric expresses a value increase in monetary units. One may also use relative metrics, showing rates of return or profitability indices to identify a project’s financial efficiency. Many factors are influencing the preference for absolute metrics or relative metrics in practice. They may depend on the company’s policy, bank requirements, and shareholders’ requirements [7,27,28,29,30,31,32]. We do not develop the topic of factors that influence decision-makers choice between absolute and relative metrics. However, we notice ongoing discussion based on the literature presented above. We also notice discussion on factors influencing NPV [13,14,15,16,17,18,19,20,21,24,31,32,33]. Percoco and Borgonovo [34] and others [35,36,37,38] analyse the dependencies between the NPV and the internal rate of return (IRR). Finally, we notice that Magni and Marchioni proposed using NPV to project ranking [10]. However, based on the literature review, we note that little is known about using the NPV metric in an unstable market with unstable interest rates during the investment in energy security.
Based on the literature review [5,39,40,41,42,43,44,45,46,47,48,49], one may formulate a generalisation that energy security is a multifaceted issue, including but not limited to “reducing emissions, reducing dependence on fossil sources, diversifying energy supplies, securing energy routes, building liquefied gas tanks, modernising transmission lines” [5] together with reducing the energy consumption. In some countries, especially developing countries, energy security is also understood as access to energy services by the poorest, or it is understood as a mechanism that limits the dominance of a single energy system. Energy security fits sustainable development, including the energy supply chain [5]. It may ultimately be an essential component of human-environmental security and influence food production and the distribution and treatment of drinking water [5,40,41,47,48,49]. Energy security understood as constant energy availability can be required by law. It has to be underlined that the European Member States must comply with Directive 2005/89/EC of the European Parliament and of the Council of 18 January 2006 on measures to ensure the safety of electricity supply and infrastructure investments [5,50]. This Directive states that “the European Union Member States must require transmission system operators to maintain an adequate level of operational network safety, which is to be understood as the uninterrupted operation of the energy transmission network” [5]. One may generalise those energy companies operate in different legal conditions than other firms. They need to ensure energy security and realise the public task of being under government oversight. It constitutes that they are hybrid, linking business operations with public interest [6,51].
The influence of energy security on sustainability is evident. Researchers (e.g., Holmberg, Reed, and Harris) underline that the concept of sustainability includes three key aspects of development: social, economic, and environmental. One may generalise that an economic aspect means that the constant production of goods and services should not lead to unmanageable government and external debt levels. It also means the need to avoid extreme business cycle fluctuations. An environmental aspect means that economic and social development is based on renewable energy resources and ensures energy security. A social aspect means fairness in realising public tasks, and it is linked with accountability, transparency, and integrity. From an ecological perspective, any human activity must consider the natural environment [52,53,54,55]. This postulate may be achievable if green energy production, distribution, and consumption are well designed and realised. Furthermore, green energy will reduce the demand for nonrenewable resources.
We analyse energy availability through the prism of its production and delivery. It means that any investments in energy security must be well planned, including the capital budgeting point of view. This statement emphasises the role of financial planning of investments in energy firms, regardless of whether they are private or public entities. Any financial turbulence during the investment phase may affect future prices of energy production and delivery.
The payback period, or “payback method”, can be perceived as an alternative method to NPV, showing how long the investment will be repaid. Such information is crucial for any investor and critical stakeholders. However, this method fails to account for the time value of money, which is its drawback. Meanwhile, one must assume that one cannot compare the money used today with money used tomorrow, and it is not only due to inflation. The amount of money used today is worth more than the same amount of money in the future because of its potential profit through investment. This weakness of the payback method is noticeable the longer investments take place.
The “internal rate of return” (IRR) method is similar to NPV in general assumption. However, in the IRR method, the discount rate is stable in an assumed time. In reality, such a situation is rare, especially in unstable markets. Furthermore, although the IRR is helpful, it has some limitations. For example, in projects with unconventional net cash flows (e.g., in the mining industry, when negative net cash flows appear not only at the beginning of the investment but also in the final phase after depletion of deposits), one can obtain several values of internal rates of return, none of which does take into account actual farming conditions. As mentioned earlier, NPV uses discounted cash flows following the time value of money (TMV).
The NPV relies on assumptions and estimates. One assumption is that investment projects will be realised in a certain period. However, a project may require unforeseen expenditures to get off the ground or additional expenditures to finish it. Additionally, NPV may ignore future tax credits. There is also a need to account for inflation, which may be volatile. In addition, the correct calculation of depreciation must be used to calculate the cost correctly, which influences the revenue. Therefore, the NPV method should not be considered the only investment profitability assessment source. The decision to undertake or reject a given investment project should be based on more than one method. In this article, however, we investigate the NPV to show that the premise of the current NPV method is not universal.
3. Materials and Methods
We used literature studies, taking into account the methodology of systematic literature review, including bibliometric analysis. Based on this review, we revealed that little is known whether NPV as an economic metric can be used during investment planning related to energy security in any energy market. Next, we analysed information on changes in interest rates during a ten year period in randomly selected countries divided into two groups: first, in stable economies characterised by stable interest rates; second, in less stable economies where interest rate fluctuations have occurred. We used data about interest rates from central bank databases from Poland, Romania, Hungary, Croatia, the USA, the United Kingdom, Japan, Israel, and Euro Zone [56,57,58,59,60,61,62,63,64]. Comparative analysis allowed us to verify the following hypothesis: the variable discount rate influences the time value of money, requiring redefining the NPV formula.
When conducting literature studies, we shared the view of Nordqvist, Gardner, Short, and Payne’s view that it can inspire research and serve as a platform for comparing our findings with other results [65,66]. When planning the study, we recognised that management understood as an academic discipline develops in conjunction with practice, particularly in the Anglo–Saxon context. However, regardless of the level of formulated generalisations, the concepts created must be based on some commonly shared cognitive assumptions defined after Kuhn as a paradigm [67]. We also assumed that we use the classification of paradigms by Burrell and Morgan [68] for further considerations on the adopted paradigms, reflected in the researcher’s attitude and the methodology used. The analysis of epistemological assumptions leads to the next issue, which is strategy-making in our research. Following Babbie [69], one could distinguish between inductive and deductive strategies or mixed inductive–deductive strategies. It was also possible to analyse the strategy issue, considering the dominant or alternative paradigm theories division. We used the strategy of epistemological pluralism, allowing for the combination of approaches drawn from different paradigms. It means the possibility of using typically functionalist concepts, such as hypotheses, verification, falsification, and experiment, but also interpretative concepts, such as meaning and interpretation. Thus, we based our methodology on the assumption of complementarity, exemplified by the adopted methodological triangulation, which helps, as noted by Campbell, Fiske, Webb, et al., Greene et al. [70,71,72], in obtaining a broader context of the studied phenomenon and limiting measurement errors.
4. Results and Discussion
4.1. Current NPV as a Financial Metric and Interest Rates
The NPV as a financial metric, commonly used in capital budgeting, expresses the difference between current cash inflows and current cash outflows. Since money has a time value, cash flows must follow the same denominator to be compared. Owing to the NPV, it is possible to assess the cash flows related to the project (they require comparing the updated value of future revenues with the capital expenditures made today). In other words, the NPV metric is based on discounting future cash flows to their present values. Therefore, one may assume that NPV helps make the right decision from the shareholders and other decision-makers points of view.
NPV enables selecting an action option that is acceptable in terms of financial objectives [73]. Is it like that every time? Or are there situations where the current NPV metric fails? We think calculating an investment’s economic efficiency without applying the inflationary factors, and the exchange rate is a mistake because it considers inputs and outputs equally valuable. An increase or decrease in the time value of money is characteristic of all economies but more affected in unstable markets (e.g., eastern and central European countries). The time value of money is influenced by macroeconomic factors such as inflationary processes and changes in exchange rates [74,75,76,77,78]. Additionally, microeconomic factors need to be considered, including investor preference for the distribution of consumption over time, the risk of asset impairment, and the risk of lost profits. Without going into a broader description of the time value of money, it can be stated that the value of money is an essential issue from the standpoint of valuation of economic events and directly affects the objectivity and usefulness of the calculations obtained using the economic calculus. This issue concerns the financial analysis of investments because there is a long time horizon between incurring the outlay and the moment of obtaining subsequent effects from operating the investment. What does it mean for practitioners? It means that there is a need to draw attention to a discount technique to assess the efficiency of tangible investments. Determining the value of the parameter “r” (discount rate) allows choosing the value of expected future effects when incurring the expenditure. One may conclude that the constant discount rate used in the presented dynamic method of investment project appraisal does not consider its construction the actual management conditions because the discount rate may change. It is a severe problem in terms of the rationality of business decisions. Meanwhile, Simon revealed that the concept of bounded rationality might lead to serious business mistakes [79,80,81].
Much attention is devoted to capital structure theory, c.f. [82,83,84,85,86,87,88,89]. For example, Myers determines the capital structure to maximise its value [82]. Broadly cited, Rayan analyses financial leverage issues to increase the return on equity [88]. Others analyse how to estimate equity and debt value [89]. However, none of the presented concepts describing the investment process develop a dynamic approach to the cost of capital. Such an approach manifests itself in the constant discount rate assumption throughout the entire investment implementation period. It distorts the conditions of management that can be observed, for example, when considering the level of base interest rates over time. Because the volatility of base interest rates occurs both in the short term and in the long period, such a situation does not allow for an upbeat assessment of the usefulness of the NPV method recommended in the literature, assuming the constancy of interest rates. This issue is one of the main factors limiting the reliability of the investment’s economic calculus, particularly in unstable economic conditions.
This problem can be illustrated by presenting interest rates in central Europe (from January 2010 to December 2020) (Figure 1) in comparison to interest rates in the USA, Israel, United Kingdom, Japan, and Euro Zone (Figure 2).
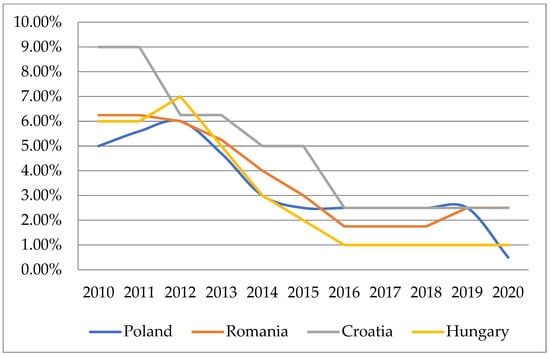
Figure 1.
Changes in the interest rate in emerging markets for the years 2010–2020 [56,57,58,59].
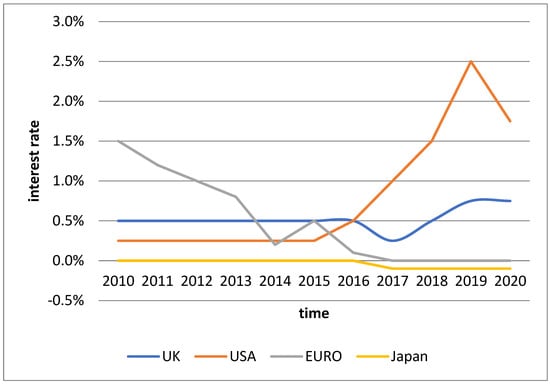
Figure 2.
Changes in the interest rate in stable markets for the years 2010–2020 [60,61,62,63,64].
The analysis of these data confirms the generalisations made earlier about interest rate fluctuations. In the Polish case, the interest rate (Lombard rate) fell from 5 percent to 0.5 percent in ten years. It means a difference of 4.5 percentage points. In the analysed period, the pawn shopper’s rate fluctuated in plus and minus. In May 2012, after a period of decline, the monetary authorities raised the Lombard rate (to 6.25 percent) and then lowered it again. It should be noted that the rediscount rates, together with the WIBOR (Warsaw Interbank Offer Rate), are the interest rates to which bank lending rates are indexed, which are the basis for calculating the cost of capital for investment. The situation is similar for interest rate levels in other central and eastern European countries: Romania, Croatia, and Hungary [56,57,58,59].
The use of economic calculation in making investment decisions should be treated as a manifestation of rationality [90]. However, this rationality is diminished by the fluctuation of the parameter “r” in the NPV model, which prevents companies from making decisions to achieve their action objectives (see Figure 2). Our findings follow Fleisher and Bensoussan [91], who aptly noted that all analytical techniques could be usefully applied provided the correct information is available. Otherwise, the analytical results obtained will be subjective assessments. Lind, Marchal, and Mason [92] also have a similar point of view.
We argue that changing in time parameter “r”, treated as constant in the NPV model, limits the management process rationality because changes seemingly common to all enterprises create different opportunities and determine individual threats. The fundamental question, however, is as follows for this problem: How can companies manage information in an environment of widespread volatility in many pricing parameters? In this case, it is essential to distinguish between short-term details and knowledge necessary to identify action options in the long term. The feature of short-term information is a short horizon of its influence on processes in a company. For long investment horizons, the effects of the use of information extend over many periods, which is the sine qua non for the firm’s survival and growth. Therefore, the subject of special attention is the precise determination of the size of the decision parameters.
The fundamental problem and reason for the existing concern about the rationality of financial decisions in the energy sector in central and eastern European countries is the dependence between interest rates and turbulent economic conditions. Similar to other researchers [93,94,95,96,97,98,99], we argue that interest rate volatility would be typical of post-socialist countries for a long time to come due to its use as an active monetary policy instrument. Such a situation creates completely different conditions for firms responsible for energy security than in stable economies.
Interest rates in countries with established market economies are not as unstable as in emerging markets [100,101,102,103,104,105]. It causes interest rates to be used to a greater extent by companies to evaluate investment directions. A stable interest rate contributes to the flat yield curve effect on which the concept of profitable valuation methods is based. The example of the UK can illustrate the level of interest rate volatility in established market economies. Between 2010 and 2020, the pattern of interest rate in the UK economy was in the range of 0.25 percentage points. The level of change in discount rates can be considered very small and insignificant in indexing bank interest rates. In the USA, United Kingdom, Euro Zone, and Japan, the interest rate changes did not exceed three percentage points in 2010–2020 [60,61,62,63,64].
The example of the UK can illustrate the level of interest rate changes in established market economies. Between 2010 and 2020, the interest rate in the UK economy changed about 0.25 percentage points. In the case of Japan, the difference between the interest rate level in 2010 and 2020 was 0.10 percentage points. In the USA, the base rate level was subject to fluctuations (2.25 percent). However, it is noticeable that the base rate level had persisted for extended periods (2010–2016) at the same level. During that period, the interest rate was 0.25 percent. Analysis of data in the Euro Zone indicates high stability of the interest rate over time. Changes in the interest rate level are symbolic, and they did not exceed 0.1 percentage points [60,61,62,63,64]. In such a stable financial environment, business planning in the energy sector is more reliable, and risk management of energy security may be effective.
A factor affecting the discount rate variability is the level of risk that accompanies implementing an investment project in its various phases. This problem can be considered from the lender’s perspective, which can increase the risk premium by monitoring the investor’s financial standing. It increases the level of the discount rate, which reduces the present value of the cash flows. We argue similarly to other researchers that the risk problem can be viewed from the perspective of an investment’s life cycle [106,107,108,109,110,111]. Different degrees of risk can be attributed to each phase of the investment cycle. The risk level is entirely different at starting the investment and at the end of the process. This assumption should also be taken into account in determining the level of the discount rate over time.
We argue that the assumption of a constant discount rate in the economic calculation should be revised. Correcting the economic calculus parameters is a tool to assess the risk and, thus, the investment’s safety. Methods for adjusting the discount rate are described in the literature, c.f. [107,108,112,113,114]. However, the proposed adjustments only consider adopting a higher discount rate level and checking the investment efficiency level. Discount rate adjustment methods draw attention to the limit of investment security (due to the increased discount rate). Still, they remain within the concept of a fixed discount rate. Thus, the problem of discount rate volatility remains. Additionally, using a higher discount rate in an economic calculation does not guarantee that the assumed level will be maximised in the long run. The problem is similar when using the average expected discount rate and its associated standard deviation. Determining the average usual discount rate is done by assessing the probability of a given level in the future. While this method could have some justification in the first year of investment operation, when specific trends in the economy may be preserved, the determination of probabilities for subsequent periods is already the result of subjective assessments (intuition). Therefore, these methods should also be regarded as unhelpful. These observations make it necessary to modify the algorithms containing the discount rate. The issue of rate variability through time can be illustrated using the NPV formula. In the classic NPV formula, the parameter “r” is fixed for each cash flow generation period:
where: r—appropriate market capitalization rate, i.e., opportunity cost of capital invested in risky projects; n—project effect lifetime in years; NCF—net cash flow; and I—investment outlays.
Assuming that the parameter “r” would be subject to change in each year, the algorithm should take the following form:
where: NPV—net present value; NCFn—cash flows generated in particular years of investment exploitation; n—investment duration; I—investment outlay; and r1, r2 … rn—discount rates for particular years of investment exploitation.
The assumption that the parameter “r” is always one year is also a significant simplification that does not consider actual business conditions. The algorithm to reflect actual market conditions follows:
where: r11 … r1m—annual interest rates from 1 to m in the first year of investment; t11 … t1m—validity period of annual interest rates in the first calculation year of the investment calculated in days (the sum of t11 to t1m equals 360 days); r21 … r2m—annual interest rates from 1 to m in the second year of the implemented investment; t21 … t2m—time of validity of annual interest rates in the second calculation year of the implemented investment calculated in days (the sum of t21 to t2m equals 360 days); rn1 … rnm—annual interest rates from 1 to m in the nth year of the implemented investment; and tn1 … tnm—duration of annual interest rates in the nth year of the investment calculation (the sum of tn1 to tnm equals 360).
The essence of using this algorithm amounts to determining the parameter “r” and its duration “t”. This formula eliminates the situation where the decision-maker conducts the economic calculus devoid of financial management tools in space–time.
4.2. Towards a Modified NPV as a Financial Metric
The traditional NPV model and its modified form allowed us to create a research model that shows how the NPV with a fixed interest rate is inadequate to reality.
Our model follows:
where: —the value of the deviation within the implemented investment; NPVf—at a constant discount rate; and NPVv—at a variable discount rate.
The magnitude of the difference () between the NPVf measure, assuming the discount rate to be constant, and the NPVv containing the actual (variable) discount rates from the period under analysis, allows us to show the former’s disadvantages. The model, assuming that the interest rate changes once a year, is presented as follows:
Assuming that NPV > 0 and where:
—deviation value; I—investment outlays; NCF1, NCF2 … NCFn—financial surpluses generated in the following years of investment’s exploitation; n—a consecutive year of the calculation period (investment’s lifetime); and r1, r2 … rn—discount rates for each year. If the discount rate is changed more than once a year, the present value multiplier for one year takes the following form:
where: r11 … r1m—annual interest rates in the first year of investment (from 1 to m); t11 … t1m—duration of annual interest rates in the first calculation year of the investment (in days, the sum of t11 to t1m equals 360); rn1 … rnm—annual interest rate in the nth year of calculating the investment realized; and tn1 … tnm—duration of annual interest rates in the nth year of the implemented investment (the sum of tn1 to tnm equals 360).
In addition to the arguments presented above, to prove the correctness of our approach, we use an experiment and present the investment activities of two hypothetical energy companies. One of them uses the traditional NPV as an economic measure. The second company uses our new, modified NPV economic metric in investment planning. We present the results of the comparative analysis below.
The investor spent EURO 10 million for investment. The duration of the investment is six years. The net cash flow (NCF) is assumed to vary from investment year to the following (Table 1).

Table 1.
Financial surplus over six years of investment (in EURO).
These changes are reflected in the calculations below (Table 2 and Table 3). The unfixed interest rate of the investment loan is an example (adopted for this experiment). It indicates a deviation from the assumed fixed interest rate. Over the assumed 6-year investment period, the interest rate fluctuated “in plus” and “in minus” (see Table 2). These changes are reflected in the calculations below (Table 3). Value of updated financial surplus (PV) assuming fixed and unfixed interest rate in EURO is presented in Table 4.

Table 2.
Level of fixed and unfixed interest rates.

Table 3.
PVIF values at fixed and unfixed discount rates.

Table 4.
Value of updated financial surplus (PV) assuming fixed and unfixed interest rate (in EURO).
These calculations help to illustrate the negative effect of changes in interest rates on the present value of the financial surpluses obtained. This can be seen by comparing the number of deviations in the first two years of the investment, where changes in interest rates were very small. Comparing this situation with subsequent years of the investment project under study, one can see the emergence of several times higher values of deviation (43,783 in the second year of the investment and 358,405 in the last year of the investment realised) (Table 4).
NPV(r fixed) = PV − I = EURO 10,992,179 − EURO 10,000,000 = EURO 992,179
NPV(r unfixed) = PV − I = EURO 12,181,421 − EURO 10,000,000 = EURO 2,181,421
Deviation (x) = NPV(r fixed) − NPV(r unfixed)
X = EURO 992,179 − EURO 2,181,421
X = EURO 1,189,242, which gives 119.86 percent difference to NPV (r fixed)
The difference in the results obtained is 119.86 percent. This value illustrates the magnitude of the error that occurs when a constant interest rate is assumed over 6 years.
The difference in the results obtained is EURO 1,189,242 for the investment in question. It means that compared to the planned NPV (at a fixed interest rate), the difference is as high as 119.86 percent. Thus, the difference obtained shows the scale of error that the company obtains when applying a fixed discount rate. The fact that there is such a difference in the calculations from the decision-making point of view proves that the assumption of a fixed discount rate is wrong (Figure 3).
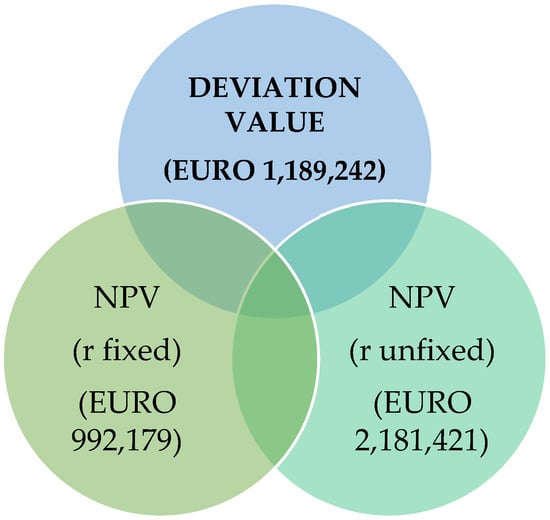
Figure 3.
Deviation of NPV based on fixed and unfixed interest rates.
5. Conclusions
We argue the same as other researchers, c.f. [115,116,117,118,119,120,121,122], that the energy sector is fast-growing, which drives investments. Energy efficiency, development of renewable energy resources, decarbonisation, and energy security are the key energy policy priorities in many countries, and it is essential to use the proper economic metrics during the planning and realising investments. Investments in the energy sector share three features: (1) these are usually capital-intensive projects that require significant financial resources; (2) investments in the energy sector require many years to implement, and a more extended investment period increases the risk of volatility in the investment environment; and (3) investments in the energy sector have enormous consequences for its business and political environment.
The use of NPV in the investment process is widely presented in the literature. The authors point to the possibility of using NPV to identify more and less profitable projects. Such financial analysis permits the strategic selection of an investment portfolio from among available sources. However, no one has so far given attention to the fact that the NPV concept is not universal and does not consider the situation in volatile markets characterised by fluctuations of interest rates. We prove that the current NPV model does not fit emerging markets, where the volatility of interest rates is commonplace. This original study and the all-new NPV model, created during this research, apply to all emerging markets globally, although we selected several European economies to prove our hypothesis.
We compared the volatility of interest rates in the United States, United Kingdom, Japan, Israel, Euro Zone, and emerging markets in central European countries: Poland, Hungary, Croatia, and Romania. Analysing the methodological side of the investment process, we drew attention to the incompatibility of corporate finance theory’s recommendations in evaluating long-term investment projects with the economy’s actual conditions (typical for the period of institutional changes). We showed that the dynamic methods of investment project evaluation recommended in the literature are based on a parameter’s constancy, a component of the present (updated) value multiplier. This methodology contradicts actual business conditions in emerging markets characterised by interest rate volatility. We assumed that the volatility of these parameters, especially the interest rate, leads to a situation where companies are already making decisions relying on data whose usefulness and reliability over longer time horizons are questionable. It is known that the parameters of investment projects are subject to change as a result of market conditions. However, their volatility must be reflected in the financial parameters. Otherwise, such a situation significantly hinders decision-making in the framework of ongoing green investments.
Our findings showed the need to determine the interest (discount) rate during a long-term period, including any changes, if any decision-maker does not want to reduce the reliability of evaluating the benefits and costs of activity and decrease the rationality of decisions. Modification of the classical NPV formula to a new form assuming different interest rates and variable time of their occurrence allows us to draw the following conclusions:
- When deciding to carry out a given investment based on the traditional NPV model, which assumes a fixed interest rate, the investor is exposed to the lack of credibility of the calculations obtained; usage of the traditional NPV model creates a possibility of rejecting investment projects that may become profitable in the case of favourable changes in the price of money in later periods. Such a situation may lead to loss of future profit or even to the reduction of future market position.
- There is a risk of choosing a wrong project, which may lead to the company’s bankruptcy.
- Frequent changes of interest rates shaped by monetary institutions make it difficult to estimate their level in the medium and long term, which significantly reduces the financial rationality of investments; investors’ financial problems may be exacerbated by the negative interaction between interest rates and the level of cash flows. Realising the method of expressing the difference between the current cash inflows and their current outflows will allow for a better assessment of the investment effectiveness in the event of the volatility of interest rates.
The finding helps the capital budgeting process by illustrating how modified NPV can provide optimal outcomes. The proposed modification of the NPV formula reduces the risk of financing the investment, making the economic environment of the investment more realistic. Nevertheless, even in investments financed from sources other than bank credit, the investor should assume the profitability of the investment by taking into account alternative concepts of investing capital.
Analysing research limitations may lead anyone to the question, whether the proposed modified NPV was verified in the investment process. Our answer to this question is the following statement. We proved that arguing that the NVP is a universal metric is premature. We showed that in some countries, the interest rates were not stable and that this situation needs to be reflected in the NPV formula. We provided the modified NPV formula, and then using data of two firms, we showed whether financial outcomes of both firms are the same if we use traditional and modified NPV formulas. Further research should provide evidence on how the investment processes are conducted using the new NPV formula. Furthermore, future research should also establish whether the internal rate of return or other methods of assessing the economic efficiency of a tangible investment are universal or should be modified in the case of markets characterised by a variable interest rate, such as in the NPV case.
This study can form a source for an inquiry process at any energy firm and country, thus contributing to a better contextual diagnosis of the stage where the firm builds its business future.
Author Contributions
Conceptualization: Z.D. and G.D.; research: Z.D. and G.D.; wrote and final editing: Z.D. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
Jagiellonian University: funding program no: FS.1.2.2021. Open access license of the publication was funded by the Priority Research Area Society of the Future under the program “Excellence Initiative—Research University” at the Jagiellonian University in Kraków.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Al-Mulali, U. GDP growth—Energy consumption relationship: Revisited. Int. J. Energy Sect. Manag. 2014, 8, 356–379. [Google Scholar] [CrossRef]
- Simionescu, M.; Bilan, Y.; Krajňáková, E.; Streimikiene, D.; Gȩdek, S. Renewable energy in the electricity sector and GDP per capita in the European Union. Energies 2019, 12, 2520. [Google Scholar] [CrossRef] [Green Version]
- Hannesson, R. Energy and GDP growth. Int. J. Energy Sect. Manag. 2009, 3, 157–170. [Google Scholar] [CrossRef]
- Dobrowolski, Z. Internet of Things and Other E-Solutions in Supply Chain Management May Generate Threats in the Energy Sector—The Quest for Preventive Measures. Energies 2021, 14, 5381. [Google Scholar] [CrossRef]
- Dobrowolski, Z. Energy and Local Safety: How the Administration Limits Energy Security. Energies 2021, 14, 4841. [Google Scholar] [CrossRef]
- Najwyższa Izba Kontroli. Lokalne Bezpieczeństwo Energetyczne. Warszawa. 2020. Available online: https://www.nik.gov.pl/kontrole/P/19/014/ (accessed on 17 May 2021).
- Berkovitch, E.; Israel, R. Why the NPV Criterion does not Maximize NPV. Rev. Financ. Stud. 2004, 17, 239–255. [Google Scholar] [CrossRef]
- Antle, R.; Eppen, G.D. Capital Rationing and Organizational Slack in Capital Budgeting. Manag. Sci. 1985, 31, 163–174. [Google Scholar] [CrossRef]
- Harris, M.; Raviv, A. The Capital Budgeting Process, Incentives and Information. J. Financ. 1996, 51, 1139–1174. [Google Scholar] [CrossRef]
- Magni, C.A.; Marchioni, A. Average rates of return, working capital, and NPV-consistency in project appraisal: A sensitivity analysis approach. Int. J. Prod. Econ. 2020, 229, 107769. [Google Scholar] [CrossRef]
- Investopedia. Net Present Value (NPV). Available online: https://www.investopedia.com/terms/n/npv.asp (accessed on 23 March 2021).
- Goldenberg, J.; Libai, B.; Moldovan, S.; Muller, E. The NPV of bad news. Int. J. Res. Mark. 2007, 24, 186–200. [Google Scholar] [CrossRef]
- Shank, J.K. Analysing technology investments—From NPV to Strategic Cost Management (SCM). Manag. Account. Res. 1996, 7, 185–197. [Google Scholar] [CrossRef]
- Osborne, M.J. A resolution to the NPV–IRR debate? Q. Rev. Econ. Financ. 2010, 50, 234–239. [Google Scholar] [CrossRef]
- Stein, J.C. Internal Capital Markets and the Competition for Corporate Resources. J. Financ. 1997, 52, 111–133. [Google Scholar] [CrossRef]
- Gardiner, P.D.; Stewart, K. Revisiting the golden triangle of cost, time and quality: The role of NPV in project control, success and failure. Int. J. Proj. Manag. 2000, 18, 251–256. [Google Scholar] [CrossRef]
- Ramezanalizadeh, T.; Monjezi, M.; Sayadi, A.R.; Mousavi, A. Development of a MIP model to maximize NPV and minimize adverse environmental impact—A heuristic approach. Env. Monit. Assess. 2020, 192, 605. [Google Scholar] [CrossRef]
- Cigola, M.; Peccati, L. On the comparison between the APV and the NPV computer via the WACC. Eur. J. Oper. Res. 2005, 161, 377–385. [Google Scholar] [CrossRef]
- Chiang, Y.; Cheng, E.; Lam, P. Employing the Net Present Value-Consistent IRR Methods for PFI Contracts. J. Constr. Eng. Manag. 2010, 136, 811–814. [Google Scholar] [CrossRef]
- Hajdasinski, M.M. NPV-compatibility, project ranking, and related issues. Eng. Econ. 1997, 42, 325–339. [Google Scholar] [CrossRef]
- Hartman, J.C. On the equivalence of net present value and market value added as measures of a project’s economic worth. Eng. Econ. 2000, 45, 158–165. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. Decision Making for Project Appraisal in Uncertain Environments: A Fuzzy-Possibilistic Approach of the Expanded NPV Method. Symmetry 2021, 13, 27. [Google Scholar] [CrossRef]
- Castagneto, G.; Zakeri, G.B.; Dodds, P.E.; Subkhankulova, D. Evaluating consumer investments in distributed energy technologies. Energy Policy 2021, 149, 112008. [Google Scholar] [CrossRef]
- Pfeiffer, T. Net Present Value-consistent investment criteria based on accruals: A generalisation of the residual income-identity. J. Bus. Financ. Account. 2004, 31, 905–926. [Google Scholar] [CrossRef]
- Quaranta, E.; Dorati, C.; Pistocchi, A. Water, energy and climate benefits of urban greening throughout Europe under different climatic scenarios. Sci. Rep. 2021, 11, 12163. [Google Scholar] [CrossRef]
- Wyrobek, J.; Popławski, Ł.; Dzikuć, M. Analysis of Financial Problems of Wind Farms in Poland. Energies 2021, 14, 1239. [Google Scholar] [CrossRef]
- Mukhtar, M.; Ameyaw, B.; Yimen, N.; Zhang, Q.; Bamisile, O.; Adun, H.; Dagbasi, M. Building Retrofit and Energy Conservation/Efficiency Review: A Techno-Environ-Economic Assessment of Heat Pump System Retrofit in Housing Stock. Sustainability 2021, 13, 983. [Google Scholar] [CrossRef]
- Pike, R.H.; Ooi, T.S. The impact of corporate investment objectives and constraints on capital budgeting practices. Br. Account. Rev. 1988, 20, 159–173. [Google Scholar] [CrossRef]
- Evans, D.A.; Forbes, S.M. Decision making and display methods: The case of prescription and practice in capital budgeting. Eng. Econ. 1993, 39, 87–92. [Google Scholar] [CrossRef]
- Graham, J.R.; Harvey, C.R. The theory and practice of corporate finance: Evidence from the field. J. Financ. Econ. 2001, 60, 187–243. [Google Scholar] [CrossRef]
- Lindblom, T.; Sjögren, S. Increasing goal congruence in project evaluation by introducing a strict market depreciation schedule. Int. J. Prod. Econ. 2009, 121, 519–532. [Google Scholar] [CrossRef]
- Sandahl, G.; Sjögren, S. Capital budgeting methods among Sweden’s largest groups of companies. The state of the art and a comparison with earlier studies. Int. J. Prod. Econ. 2003, 84, 51–69. [Google Scholar] [CrossRef]
- Pasqual, J.; Padilla, E.; Jadotte, E. Technical note: Equivalence of different profitability criteria with the net present value. Int. J. Prod. Econ. 2013, 142, 205–210. [Google Scholar] [CrossRef]
- Percoco, M.; Borgonovo, E. A note on the sensitivity analysis of the internal rate of return. Int. J. Prod. Econ. 2012, 135, 526–529. [Google Scholar] [CrossRef]
- Borgonovo, E.; Peccati, L. Sensitivity analysis in investment project evaluation. Int. J. Prod. Econ. 2004, 90, 17–25. [Google Scholar] [CrossRef]
- Borgonovo, E.; Peccati, L. Uncertainty and global sensitivity analysis in the evaluation of investment projects. Int. J. Prod. Econ. 2006, 104, 62–73. [Google Scholar] [CrossRef]
- Magni, C.A. Average Internal Rate of Return and investment decisions: A new perspective. Eng. Econ. 2010, 55, 150–180. [Google Scholar] [CrossRef]
- Marchioni, A.; Magni, C. AInvestment decisions and sensitivity analysis: NPV consistency of rates of return. Eur. J. Oper. Res. 2018, 268, 361–372. [Google Scholar] [CrossRef] [Green Version]
- Li, X. Diversification and localization of energy systems for sustainable development and energy security. Energy Policy 2005, 33, 2237–2243. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Mukherjee, I. Conceptualizing and measuring energy security: A synthesized approach. Energy 2011, 36, 5343–5355. [Google Scholar] [CrossRef]
- Hossain, Y.; Loring, P.A.; Marsik, T. Defining energy security in the rural North—Historical and contemporary perspectives from Alaska. Energy Res. Soc. Sci. 2016, 16, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Sovacool, B.K.; Brown, M.A. Competing dimensions of energy security: An international perspective. Annu. Rev. Environ. Resour. 2010, 35, 77–108. [Google Scholar] [CrossRef] [Green Version]
- Kruyt, B.; van Vuuren, D.P.; de Vries, H.J.M.; Groenenberg, H. Indicators for energy security. Energy Policy 2009, 37, 2166–2181. [Google Scholar] [CrossRef]
- Yergin, D. Ensuring Energy Security. Foreign Aff. 2006, 85, 69–82. [Google Scholar] [CrossRef]
- Unruh, G.C. Understanding carbon lock-in. Energy Policy 2000, 28, 817–830. [Google Scholar] [CrossRef]
- Bottomly, J.M. Energy assistance programs: Keeping older adults housed and warm. Top. Geriatr. Rehabil. 2001, 17, 71–81. [Google Scholar] [CrossRef]
- Kuik, O.J.; Lima, M.B.; Gupta, J. Energy security in a developing world. Wiley Interdiscip. Rev. 2011, 2, 627–634. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A. The environment–Energy security nexus: Critical analysis of an energy ‘love triangle’ in Southeast Asia. Third World Q. 2007, 28, 539–554. [Google Scholar] [CrossRef]
- Muller-Kraenner, S. Energy Security, 1st ed.; Routledge: London, UK, 2007. [Google Scholar]
- Vukadinovic, R.D. Directive 2005/89/EC of the European Parliament and of the Council of 18 January 2006 concerning measures to safeguard security supply and infrastructure investment. Rev. Eur. L. 2007, 9, 109. [Google Scholar]
- Dobrowolski, Z.; Sułkowski, Ł. Business Model Canvas and Energy Enterprises. Energies 2021, 14, 7198. [Google Scholar] [CrossRef]
- Harris, J.M. Sustainability and Sustainable Development, Internet Encyclopaedia of Ecological Economics, International Society for Ecological Economics. 2003. Available online: https://www.researchgate.net/publication/237398200_Sustainability_and_Sustainable_Development (accessed on 16 October 2019).
- Boyer, R.H.; Peterson, N.D.; Arora, P.; Caldwell, K. Five approaches to social sustainability and an integrated way forward. Sustainability 2016, 8, 878. [Google Scholar] [CrossRef] [Green Version]
- Chohaney, M.L.; Yeager, C.D.; Gatrell, J.D.; Nemeth, D.J. Poverty, Sustainability, & Metal Recycling: Geovisualizing the Case of Scrapping as a Sustainable Urban Industry in Detroit. In Urban Sustainability: Policy and Praxis; Gatrell, J.D., Jensen, R.R., Patterson, M.W., Hoalst-Pullen, N., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 99–133. [Google Scholar]
- Herremans, I.M.; Nazari, J.A.; Mahmoudian, F. Stakeholder relationships, engagement, and sustainability reporting. J. Bus. Ethics 2016, 138, 417–435. [Google Scholar] [CrossRef]
- Basic NBP Interest Rates in 1998–2020. NBP. Available online: https://www.nbp.pl (accessed on 23 February 2021).
- Monetary Policy and Standing Facilities Interest Rates. BNR. Available online: https://www.bnro.ro (accessed on 6 February 2021).
- Monetary Policy Implementation. HNB. Available online: https://www.hnb.hr (accessed on 3 February 2021).
- Monetary Policy. MNB. Available online: http://www.mnb.hu (accessed on 9 March 2021).
- Interest Rates and Bank Rate. Bank of England. Available online: https://www.bankofengland.co.uk (accessed on 4 March 2021).
- Monetary Policy. Bank of Japan. Available online: www.boj.or.jp (accessed on 12 March 2021).
- Monetary Policy. FOMC. Available online: www.federalreserve.gov (accessed on 10 March 2021).
- Monetary Policy. Bank of Israel. Available online: www.boi.org.il (accessed on 6 February 2021).
- Euro Area Interest Rate. 2021. Available online: www.tradingeconomics.com/euro-area/interest-rate (accessed on 11 August 2021).
- Nordqvist, M.; Gartner, W.B. Literature, fiction, and the family business. Fam. Bus. Rev. 2020, 33, 122–129. [Google Scholar] [CrossRef]
- Short, J.C.; Payne, G.T. In Their Own Words: A Call for Increased Use of Organizational Narratives in Family Business Research. Fam. Bus. Rev. 2020, 33, 342–350. [Google Scholar] [CrossRef]
- Kuhn, T. The Structure of Scientific Revolutions; 50th Anniversary Edition; The University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Burrell, G.; Morgan, G. Sociological Paradigms and Organisational Analysis. Elements of the Sociology of Corporate Life; Routledge: London, UK, 2017. [Google Scholar]
- Babbie, E. The Practice of Social Research, 15th ed.; Cengage: Boston, MA, USA, 2021. [Google Scholar]
- Campbell, D.T.; Fiske, D.W. Convergent and Discriminant Validation by the Multitrait-Multimethod Matrix. Psychol. Bull. 1959, 56, 81–105. [Google Scholar] [CrossRef] [Green Version]
- Webb, E.J.; Campbell, D.T.; Schwartz, R.D.; Sechrest, L. Unobtrustive Maeasures. Revised Edition; Sage Publications: Thousand Oaks, CA, USA, 2000. [Google Scholar]
- Greene, J.C.; Caracelli, V.J.; Graham, W.F. Toward a Conceptual Framework for Mixed Evaluation Design. Educ. Eval. Policy Anal. 1989, 11, 255–274. [Google Scholar] [CrossRef]
- Brealey, R.; Myers, S. Principles of Corporate Finance, 13th ed.; McGraw-Hill Education: New York, NY, USA, 2020. [Google Scholar]
- Cogley, T. A Simple Adaptive Measure of Core Inflation. J. Money Credit Bank 2002, 34, 94–113. [Google Scholar] [CrossRef]
- Marques, C.R.; Neves, P.D.; Sarmento, L.M. Evaluating Core Inflation Indicators. Econ. Model. 2003, 20, 765–775. [Google Scholar] [CrossRef] [Green Version]
- O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Datta, T.K.; Pal, A.K. Effects of inflation and time-value of money on an inventory model with linear time-dependent demand rate and shortages. Eur. J. Oper. Res. 1991, 52, 326–333. [Google Scholar] [CrossRef]
- Leclerc, F.; Schmitt, B.H.; Dubé, L. Waiting Time and Decision Making: Is Time like Money? J. Consum. Res. 1995, 22, 110–119. [Google Scholar] [CrossRef]
- Selten, R. Bounded Rationality. J. Inst. Theor. Econ. 1990, 146, 649–658. [Google Scholar]
- Jones, B.D. Bounded Rationality. Annu. Rev. Political Sci. 1999, 2, 297–321. [Google Scholar] [CrossRef]
- Simon, H.A. Bounded rationality in social science: Today and tomorrow. Mind Soc. 2000, 1, 25–39. [Google Scholar] [CrossRef]
- Myers, S.C. Capital structure. J. Econ. Perspect. 2001, 15, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Harris, M.; Raviv, A. The Theory of Capital Structure. J. Financ. 1991, 46, 297–355. [Google Scholar] [CrossRef]
- Baker, M.; Wurgler, M.J. Market Timing and Capital Structure. J. Financ. 2020, 57, 1–32. [Google Scholar] [CrossRef]
- Titman, S.; Wessels, R. The Determinants of Capital Structure Choice. J. Financ. 1988, 43, 1–19. [Google Scholar] [CrossRef]
- Faulkender, M.; Petersen, M.A. Does the Source of Capital Affect Capital Structure? Rev. Financ. Stud. 2006, 19, 45–79. [Google Scholar] [CrossRef] [Green Version]
- Scott, J.H., Jr. A Theory of Optimal Capital Structure. Bell J. Econ. 1976, 7, 33–54. [Google Scholar] [CrossRef]
- Rayan, K. Financial leverage and firm value. University of Pretoria, The South Africa. 2008. Available online: https://repository.up.ac.za/bitstream/handle/2263/23237/dissertation.pdf?sequence=1 (accessed on 6 February 2021).
- Campbell, T.C.; Galpin, N.; Johnson, S.A. Optimal inside debt compensation and the value of equity and debt. J. Financ. Econ. 2016, 119, 336–352. [Google Scholar] [CrossRef]
- Hill, C.W.L.; Jones, G.R. Strategic Management Theory: An Integrated Approach; Cengage: Boston, MA, USA, 2015. [Google Scholar]
- Fleisher, C.S.; Bensoussan, B. Strategic and Competitive Analysis: Methods and Techniques for Analyzing Business Competition; Prentice-Hall: New York, NY, USA, 2003. [Google Scholar]
- Lind, D.A.; Marchal, W.G.; Mason, R.D. Statistical Techniques in Business and Economics, 17th ed.; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- Carstensen, K.; Toubal, F. Foreign direct investment in Central and Eastern European countries: A dynamic panel analysis. J. Comp. Econ. 2004, 3, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Bevan, A.A.; Estrin, S. The determinants of foreign direct investment into European transition economies. J. Comp. Econ. 2004, 32, 775–787. [Google Scholar] [CrossRef]
- Janicki, H.P.; Wunnava, P.V. Determinants of foreign direct investment: Empirical evidence from EU accession candidates. Appl. Econ. 2004, 36, 505–509. [Google Scholar] [CrossRef]
- Égert, B.; Crespo-Cuaresma, J.; Reininger, T. Interest rate pass-through in central and Eastern Europe: Reborn from ashes merely to pass away? J. Policy Model. 2007, 29, 209–225. [Google Scholar] [CrossRef] [Green Version]
- Agapova, A.; McNulty, J.E. Interest rate spreads and banking system efficiency: General considerations with an application to the transition economies of Central and Eastern Europe. Int. Rev. Financ. Anal. 2016, 47, 154–165. [Google Scholar] [CrossRef]
- Niţoi, M.; Spulbar, C. An Examination of Banks’ Cost Efficiency in Central and Eastern Europe. Procedia Econ. Financ. 2015, 22, 544–551. [Google Scholar] [CrossRef] [Green Version]
- Moagăr-Poladian, S.; Clichici, D.; Stanciu, C.-V. The Comovement of Exchange Rates and Stock Markets in Central and Eastern Europe. Sustainability 2019, 11, 3985. [Google Scholar] [CrossRef] [Green Version]
- Kiani, K.M. Federal budget deficits and long-term interest rates in USA. Q. Rev. Econ. Financ. 2009, 49, 74–84. [Google Scholar] [CrossRef]
- Peiró, A. Stock prices, production and interest rates: Comparison of three European countries with the USA. Empir. Econ. 1996, 21, 221–234. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Reziti, I.; Spiliotis, A. Monetary and banking policy transmission through interest rates: An empirical application to the USA, Canada, the UK and the Eurozone. Int. Rev. Appl. Econ. 2010, 24, 119–136. [Google Scholar] [CrossRef]
- Yazgan, M.E.; Yilmazkuday, H. Monetary policy rules in practice: Evidence from Turkey and Israel. Appl. Financ. Econ. 2007, 17, 1–8. [Google Scholar] [CrossRef]
- Ólan, T.H. Regime switching in the relationship between equity returns and short-term interest rates in the UK. J. Bank. Financ. 2009, 33, 405–414. [Google Scholar]
- Apergis, N.; Cooray, A. Asymmetric interest rate pass-through in the U.S., the U.K. and Australia: New evidence from selected individual banks. J. Macroecon. 2015, 45, 155–172. [Google Scholar] [CrossRef]
- Dunning, J.H. The investment development cycle revisited. Weltwirtschaftliches Arch. 1986, 122, 667–676. [Google Scholar] [CrossRef]
- Culp, C.L. The Risk Management Process. Business Strategy and Tactics; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Aven, T.; Renn, O. Risk Management and Risk Governance. Concepts, Guidelines and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hoyt, R.E.; Liebenberg, A.P. The Value of Enterprise Risk Management. J. Risk Insur. 2011, 78, 795–822. [Google Scholar] [CrossRef]
- Dickinson, G. Enterprise Risk Management: Its Origins and Conceptual Foundation. Geneva Pap. Risk Insur. Issues Pract. 2001, 26, 360–366. [Google Scholar] [CrossRef]
- Froot, K.A.; Scharfstein, D.S.; Stein, J.C. Risk Management: Coordinating Corporate Investment and Financing Policies. J. Financ. 1993, 48, 1629–1658. [Google Scholar] [CrossRef] [Green Version]
- Baker, H.K.; Filberg, G. Investment Risk Management; Oxford University Press: Oxford, UK; New York, NY, USA, 2015. [Google Scholar]
- Tupa, J.; Simota, J.; Steiner, F. Aspects of risk management implementation for Industry 4.0. Procedia Manuf. 2017, 11, 1223–1230. [Google Scholar] [CrossRef]
- Shirley, R.; Kammen, D. Renewable energy sector development in the Caribbean: Current trends and lessons from history. Energy Policy 2013, 57, 244–252. [Google Scholar] [CrossRef]
- Papież, M.; Śmiech, S.; Frodyma, K. Effects of renewable energy sector development on electricity consumption–Growth nexus in the European Union. Renew. Sustain. Energy Rev. 2019, 113, 109276. [Google Scholar] [CrossRef]
- Pakulska, T. Green Energy in Central and Eastern European (CEE) Countries: New Challenges on the Path to Sustainable Development. Energies 2021, 14, 884. [Google Scholar] [CrossRef]
- Kat, B.; Paltsev, S.; Yuan, M. Turkish energy sector development and the Paris Agreement goals: A CGE model assessment. Energy Policy 2018, 122, 84–96. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Zhang, D.; Zhang, C.; Streimikiene, D. Sustainability assessment of energy sector development in China and European Union. Sustain. Dev. 2020, 28, 1063–1076. [Google Scholar] [CrossRef]
- Amstalden, R.W.; Kost, M.; Nathani, C.; Imboden, D.M. Economic potential of energy-efficient retrofitting in the Swiss residential building sector: The effects of policy instruments and energy price expectations. Energy Policy 2007, 35, 1819–1829. [Google Scholar] [CrossRef]
- Dziekański, P.; Prus, P.; Maitah, M.; Wrońska, M. Assessment of Spatial Diversity of the Potential of the Natural Environment in the Context of Sustainable Development of Counties in Poland. Energies 2021, 14, 6027. [Google Scholar] [CrossRef]
- Drozdowski, G. Economic Calculus Qua an Instrument to Support Sustainable Development under Increasing Risk. J. Risk Financ. Manag. 2021, 14, 15. [Google Scholar] [CrossRef]
- Dobrowolski, Z.; Drozdowski, G.; Dobrowolska, M.; Sobon, J.; Sobon, D. Economic Calculus and Weak Signals: Prevention Against Foggy Bottom. Eur. Res. Stud. J. 2021, 14, 165–174. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).