Abstract
Modern wind turbines depend on their blade pitch systems for start-ups, shutdowns, and power control. Pitch system failures have, therefore, a considerable impact on their operation and integrity. Hydraulic pitch systems are very common, due to their flexibility, maintainability, and cost; hence, the relevance of diagnostic algorithms specifically targeted at them. We propose one such algorithm based on sensor data available to the vast majority of turbine controllers, which we process to fit a model of the hydraulic pitch system to obtain significant indicators of the presence of the critical failure modes. This algorithm differs from state-of-the-art, model-based algorithms in that it does not numerically time-integrate the model equations in parallel with the physical turbine, which is demanding in terms of in situ computation (or, alternatively, data transmission) and is highly susceptible to drift. Our algorithm requires only a modest amount of local sensor data processing, which can be asynchronous and intermittent, to produce negligible quantities of data to be transmitted for remote storage and analysis. In order to validate our algorithm, we use synthetic data generated with state-of-the-art aeroelastic and hydraulic simulation software. The results suggest that a diagnosis of the critical wind turbine hydraulic pitch system failure modes based on our algorithm is viable.
1. Introduction
Wind turbine monitoring is a considerably popular topic, which elicits much research, especially regarding critical subsystems [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Wind turbine reliability databases are notoriously heterogeneous [16,17,18,19], and so are, as a result, conclusions reached from their analysis as to the fundamental relationships between turbine design details and their operational consequences. However, it seems clear that the blade pitch system, whether hydraulic or electric in nature, requires considerable attention of turbine operators. We are here interested specifically in hydraulic pitch systems, both because we are in the business of manufacturing them and because they are very common, due to their flexibility, maintainability, and cost [20].
Although the pitch system is quite critical to turbine operation, even to the point where unexpected changes in blade pitch angles can have catastrophic consequences [21], turbines are generally able to withstand, albeit via an emergency shutdown, the sudden loss of their ability to pitch one of their blades. This normally makes robustness enhancements based on redundancy, such as those typical of aircrafts [22,23,24], uneconomical, since the increased availability is insufficient to compensate for the added cost. However, it is vital to detect pitch system failures in a timely manner, in order to carry out the emergency shutdown on which turbine integrity is then contingent.
A common high-level approach to fault detection in a tracking system, which a pitch actuator is, since it tracks a reference with the cylinder position, is to simply compare what one would expect the system to do, possibly by processing the reference via a model, and what it actually does. For example, Le [25] patented such a method to detect malfunctioning aircraft pitch axes and disable them to avoid flutter. Many examples of this approach are available in the literature [26,27,28,29,30,31]. Wind turbine controllers typically do something very similar, and trigger an emergency shutdown when they consider the pitch angle reference and measurement to differ excessively.
It is however also interesting to detect subtler failures, where a pitch system component sees its functionality degraded in a way that may impact turbine operation in the longer term without necessarily prompting an immediate reaction from the safety system, i.e., the pitch system still tracks the reference cylinder position, but its operational envelope is reduced, so it cannot handle wind conditions well within its design specifications. The potential benefits of a system capable of such detection are evident, and they have long elicited ample research, as shown by the detailed and current review of the literature provided by Asmussen et al. [32], who point out that realistic methods able to cope with the stochastic nature of wind turbine behavior are yet to be developed (hence, this paper).
It is often straightforward to come up with a set of extra sensors that may conceivably allow a relatively simple algorithm to detect a specific failure. For example, Brandt [33] patented a system to detect leaks in a hydraulic system by estimating the fluid flow rate into the system from pump speed and pressure, while measuring the fluid flow rate out of the system via a flow rate meter. As long as the hydraulic system is not capable of any significant accumulation of hydraulic fluid, the detection algorithm is then based on the differential flow rate, i.e., if more goes in than comes out, there must be a leak. Similarly, Watanabe [34] patented a system to detect loss of pump performance by blocking the pump output and controlling the pressure via variation of the displacement. The steady-state ratio of displacement to output pressure is then an indicator of pump health. More recently, some methods have been proposed [35,36] to detect valve degradation by measuring the current drawn by their solenoids.
Things get more complicated when there are no simple relationships between a failure and a set of measurements, and so then do the detection algorithms. For example, Wu et al. [37] use the cylinder chamber pressures, the flow rates into said chambers, the cylinder position and the force at the rod to put together an adaptive actuator model from which they calculate internal and external leakage coefficients, as well as effective fluid compressibility; Yao et al. [38] use the cylinder position and velocity, as well as the chamber pressures to compute an internal cylinder leak indicator; Wu et al. [39] use the mean proportional valve spool position and cylinder chamber pressures during different simulations as the features of a classification algorithm to detect a leak between the cylinder chambers. However, one would rather keep the extra sensors to a minimum, for obvious economic and reliability-related reasons. This is why the more recent literature is rife with work in which only the typical pitch system sensors are utilized, which require a dynamic model to run in real time, the output of which is compared to sensor data to produce a residual.
Tutivén et al. [40] compute two residuals, one between the measured pitch acceleration and that they expect from processing the pitch reference, angle, and velocity with a second-order linear model of the healthy pitch system; the other between the parameters of said second-order linear model, and those of another, which they fit to the pitch reference, angle, velocity, and acceleration via a normalized gradient method. They then use these residuals as indicators of a pitch system failure. Zhao et al. [41] suggest a similar, residual-based method, as does Cho [42].
Wu and Liu [43] use the reference pitch angle and a second order linear model with a range of parameter values they deem representative of a healthy actuator to compute a range of pitch angles about said reference. They then consider the actuator to be faulty when the measured pitch angle is outside this range. Pujol-Vazquez et al. [44] do something very similar, only they use a range of input errors rather than one of parameter values. Another variation on this is used by Sun et al. [45], who combine different parameter ranges corresponding to different failures to compute residual thresholds in real time via a number of third order linear models. Yet another variation is used by Dalla Vedova et al. [46,47,48,49], who use a genetic algorithm to find the model parameters that minimize the residual, then use those parameters to identify several failures.
The issue of determining what model parameters correspond to a healthy actuator is often approached via some sort of system identification. For example, Vásquez et al. [50] introduce an excitation signal in the blade pitch angle reference, both during a configuration phase, i.e., at a time when they know the hydraulic system to be healthy, and sporadically during operation, in order to identify third-order linear models for the relationship between the pitch angle reference and the measured pitch angles. They then use variations in the natural frequency and damping of the high-frequency oscillation due to fluid compressibility to detect aeration, which reduces the natural frequency by increasing overall fluid compressibility, and friction, which increases damping due to its passive nature. The models used for this sort of identification may be of a variety of natures, such as neural networks [51,52], wavelet transform coefficients [53,54,55], spectral analysis failure maps [56], fuzzy systems [57], support vector machines [58], classification trees [59], or multi-scale permutation entropy feature vectors [60].
The problem with these schemes is that, when applied to real systems in realistic operational conditions, they require more detailed models for residual calculation. This naturally causes the model states to quickly exceed what one would be realistically willing to measure, which immediately suggests implementation of the models in the form of observers, in order to keep their states from drifting excessively. The literature is very prolific in such observers [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75], but the complexities of real hydraulic pitch systems and operating conditions, together with uncertainties regarding each individual pitch system component, have so far managed to stay ahead of any attempts to consistently identify subtle failures by comparing measurements to the output of one or more models or observers.
It may well be possible, one day, to put together such a perfect digital twin of a particular hydraulic pitch system that the residual-based approach becomes viable. We, however, seek a more mundane method to analyze the data available to the turbine controller during operation to figure out what, if anything, may be wrong with a hydraulic pitch system. This, crucially, we know to be possible for experienced technicians, who can often diagnose subtle failures by mere inspection of these data. The challenge is, therefore, to package that knowledge in the form of a data processing algorithm.
Let us begin by specifying what failures we wish to identify. Although there are more general standards one may use to study this [76], Liniger et al. [77,78,79] provide a more focused and thorough study of how hydraulic pitch system design features impact reliability. The most critical failure modes they come up with are oil and gas leaks, ruptures (i.e., large, sudden leaks), valve seizures, excessive friction and electrical signal degradation (i.e., sensor data loss or corruption). This paper is however not only about what we can do to mitigate the effects of failures, but about how we can detect them first. There is possibly a number of viable strategies to deal with hose ruptures and proportional valve seizures, but detecting them is trivial, since the corresponding actuators stop being functional entirely and immediately. Something similar may be said about external oil leaks, which are directly reflected by the descending reservoir level. Other valve seizures and electrical problems can, sometimes, have more subtle effects on pitch system behavior. However, it is relatively straightforward to come up with specific test procedures to detect them on startup. It is gas and internal oil leaks that can be very hard to detect without carefully monitoring operational variables. We, therefore, like so many before us, will focus here on piston seal leaks, excessive friction at the cylinders or pitch bearings, accumulator gas leaks, and internal pump leaks.
Liniger et al. [80] have perhaps been the closest to a viable accumulator gas leakage estimation algorithm. They have however encountered a drift problem which, we will argue in Section 2, is insurmountable. We propose a novel approach based on their basic idea of flow rate comparisons and also build leak estimation into it. We then add a comparison of proportional valve opening and cylinder velocity to also identify excessive friction.
Our contribution to the field of hydraulic pitch system fault detection and identification is a turbine controller data processing method to produce a set of parameters every few minutes, which cluster in a way that makes them useful for fault detection and identification. The method seems, as will be shown, viable, and is significantly simpler and less computationally burdensome than all other methods we were able to find in the literature.
2. Materials and Methods
2.1. The Basic Algorithm
Figure 1 shows the generic hydraulic system design considered here, which is consistent with common pitch systems [79]. One or more cylinders per blade extend to increase the pitch angle and retract to decrease it. Sensor S1 measures the cylinder position, which is made to track the reference given by the wind turbine controller by means of proportional valve PV1–PV2, while solenoid valves EV2, EV4, EV5, and EV6 are energized. This results in the pressurized fluid in accumulator A1 being channeled by the proportional valve to its port A for cylinder extension, B for retraction. The circuit is regenerative, i.e., cylinder extension results in fluid from the rod-side chamber flowing back to port P of the proportional valve via check-valve CV4, rather tan back to tank via CV3 and the proportional valve. The pressure at A1 is monitored via sensor S2 and topped up when necessary by energizing EV1. Finally, when all solenoids are de-energized, accumulator A1 forces fluid to flow to the piston-side chamber via EV4, O1, and CV5, while the rod-side chamber is allowed to discharge to tank via O2 and EV6. This is normally the case during emergency shutdowns.
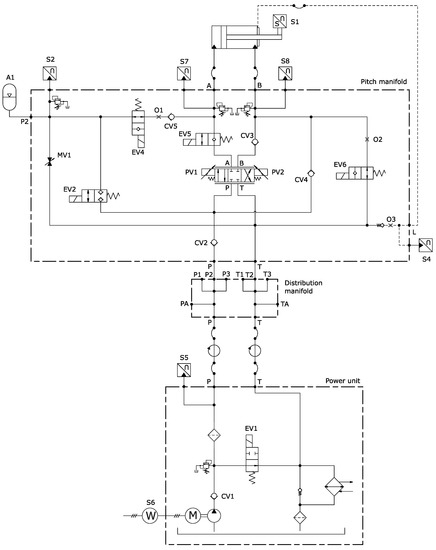
Figure 1.
Reference hydraulic diagram.
Sensors S1 and S2 are always present, since they are necessary to control the blade pitch angle and supply pressure, respectively. Other sensors, such as S4 or S5 may or may not be present in different designs. Finally, cylinder chamber pressure sensors S7 and S8 are rare, as are current or power measurements represented by watt meter S6. We therefore seek a failure identification method based only on S1 and S2, i.e., cylinder position and accumulator pressure. An intuitive approach to this is to consider that cylinder motion consumes fluid from the accumulator, at a rate roughly proportional to piston velocity, while the power unit provides fluid to the accumulator, roughly at its nominal rate. This allows a first estimation of the flow rate out of the accumulator, and we know there is a very definite relationship between that flow rate and accumulator pressure. Liniger et al. [80] give a very accurate formulation of this relationship, which they use to put together a gas volume, temperature, and mass observer. Crucially, said observer estimates the gas volume via integration of the estimated oil flow rate out of the accumulator, which results in a random walk. This can be slowed down via more and more accurate estimation or measurement of the flow rate, but it can never be stopped altogether, which limits the usability of this method. However, could we somehow do this without integrating the flow rate? This is the question we wish now to answer.
Consider the following equation of state [81]:
where P, V, and T are the pressure, volume, and temperature of the gas in an accumulator, respectively, while n, R and Z are the amount of substance (in mol), the ideal gas constant and the compressibility factor, respectively. The compressibility factor Z is 1 for ideal gases, while it can differ from 1 significantly for real ones, especially at low temperatures.
Solving (2) for yields
Consider also the internal energy of the gas,
where is the molar heat capacity at constant volume, which, for ideal gases, is
while f is the number of degrees of freedom of a gas molecule. In the case of nitrogen, a diatomic gas, [82].
Differentiation of (4) yields
while the energy balance dictates that
where is the differential of heat transmitted to the gas.
Dividing (8) by the time differential and adopting Newton’s notation for differentiation, yields:
which can be used as a second way to roughly estimate the oil flow rate out of the accumulator, which is precisely , by assuming constant values , and , where the latter is the ambient or accumulator surface temperature. Note that this means using an ideal gas model and, as mentioned above, considering the process adiabatic.
We therefore propose accumulator flow rate estimators
and
where and are the piston and rod diameters, respectively; is the nominal pump flow rate, which obviously depends on whether EV1 is energized; is the piston velocity, with corresponding to cylinder extension; is the accumulator volume and is the nominal gas pressure at temperature , i.e., the nominal pre-charge.
It goes without saying that, with such rough estimators, we can hope even less than others with more sophisticated ones to detect failures directly from residual . No consideration was made in (10) regarding chamber pressure variations, so we can expect q to be too small when they are growing and too large when they are diminishing. Similarly, no heat transfer was allowed in (11), so we can expect to be too small during and after expansion and too large during and after compression. Further, (11) is based on an ideal gas model, so we can expect a difference in scale between q and .
To deal with the inaccuracy caused in q by large, fast changes in cylinder chamber pressures, of which there must be one every time the actuator transitions from extension to retraction or vice versa, due to the regeneration imposing accumulator pressure on the rod side during extension—or in , by large, fast variations in gas temperature, of which there must be one every time the actuator transitions from pressurizing the accumulator to discharging it and vice versa, due to the accompanying reversion of heat flow—we can simply ignore data for a while after such transitions. Note that such cherry-picking of data points can be problematic in observer-based algorithms, but not here, since we are driving no observer or model with the data. From the rest of data, we expect a certain proportionality between q and , i.e.,
From experimental data reported in the literature [83], at about 293 K and 250 bar, , and , so we could expect .
Since a gas leak results in a smaller quantity of gas n in the accumulator, we expect, from (9) that it will result in a smaller proportionality constant . Intuitively, this means that looking at the accumulator pressure and assuming the nominal quantity of gas is present will result in a larger estimation of the flow rate into or out of it, while the estimation based on cylinder and pump activity will be unaffected.
Similarly, cylinder and pump leaks will change the actual flow rate at the accumulator and, as a consequence, , but will not affect q. However, the change in will not be proportional to q, since the leaks do not depend on cylinder motion. We instead expect to observe an offset between q and proportional to the leak flow rate.
Finally, friction will have no noticeable effect on either q or . However, it will require larger proportional valve opening values to get the cylinder to move as prescribed by the turbine controller.
2.2. Synthetic Data
In order to test the ideas of Section 2.1, we have put together the model shown by Figure 2 for the production of synthetic data. It uses the DTU 10 MW reference wind turbine model [84,85] for OpenFAST version 2.3 [86] compiled for Simulink and a turbine controller written by one of the authors [87,88]. The turbine controller produces, as usual [89], generator torque and blade pitch angle references based on the generator speed. The torque reference is passed directly to the turbine model, because generator dynamics are besides the scope of this work, but the blade pitch angle reference is passed to a pitch system model, which then tries to track it with the actual pitch angles that are passed to the turbine model. The blade root moments calculated by OpenFAST are fed into this pitch system model to calculate the cylinder rod forces. The yaw and brake are left unused.
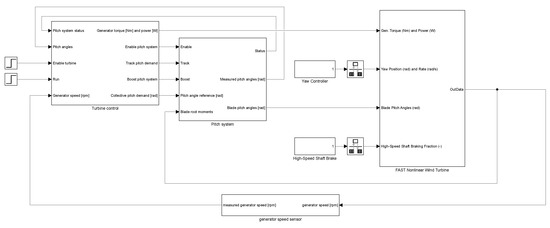
Figure 2.
Aeroelastic and hydraulic models, with turbine control.
Figure 3 shows the Simulink model corresponding to the pitch system sub-model on Figure 2. The pitch system control receives a blade pitch angle set-point and various other commands from the wind turbine controller, as well as sensor data from the hydraulic pitch system. It then reports its status and the blade pitch angles it calculates from cylinder position measurements back to the turbine controller, and sends commands to the pitch system valves to track the turbine controller’s set-point and maintain an acceptable pressure at the accumulators.

Figure 3.
Hydraulic pitch system model, with control.
The hydraulic system model itself is a power unit connected, via pipelines or hoses, to three identical pitch actuators. The power unit receives a valve command to be discussed below, and sends some sensor data back to the pitch controller. Similarly, each of the actuators receives valve commands from the pitch controller and sends back sensor data. It also receives the blade root moments to calculate the force opposing its cylinders, and outputs the true pitch angle to send to the turbine model.
The power unit model is shown by Figure 4. It consists of three gear pumps in parallel, each driven by an induction motor directly connected to a 50 Hz, 400 V source. Note the orifices for pump leak simulation. The pumps supply, via check-valves, a pressure line, which is drained by solenoid valve EV1 when not energized. Thus, when the controller decides to top up the accumulators, it energizes EV1 to force the fluid towards the actuators. Evidently, when EV1 is not energized, one may perhaps in practice switch the motors off to save some energy. This does however not influence any variable we are interested in here, so we have omitted it.
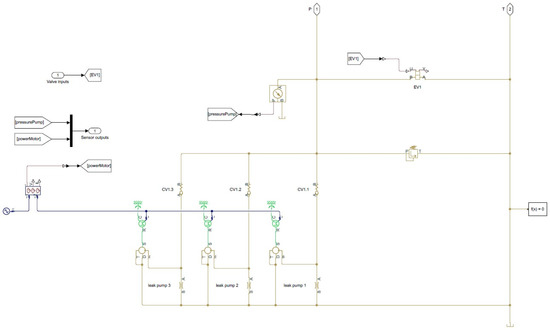
Figure 4.
Power unit model.
Each individual blade actuator model consists, as shown by Figure 5, of a hydraulic manifold, where all the valves and accumulators are mounted, a pitch mechanism, where the cylinders push or pull the hub and blade, and a pitch bearing, where the blade root moments are combined to calculate the pitching moment to oppose the actuator.
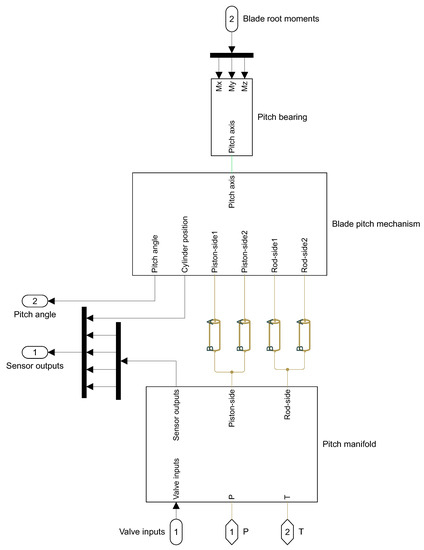
Figure 5.
Individual blade pitch system model.
The blade manifold model is shown by Figure 6. It is essentially the same hydraulic diagram of Figure 1, only implemented with Simscape.

Figure 6.
Individual blade manifold model.
The pitch mechanism model is shown by Figure 7. Note the two cylinders working in parallel between two joints, one on the hub and the other on the blade, which are represented by the reference and center of mass elements, respectively, the latter also determining the blade inertia about its pitching axis. The rectangular elements are rigid beams, which determine the relative position between the center of hub-blade rotation and each of the joints. Configurable leaks and friction are also present, for failure simulation. The position of the blade-side joint respective to the center of hub-blade rotation is measured and used to simulate the cylinder position sensor and the actual pitch angle to be sent to the turbine model. Also note that noise is added to the sensor signal. This, although not shown for the sake of brevity, is also done to every other sensor signal in the model. Figure 8 shows the noise levels we have used.

Figure 7.
Individual blade pitching mechanism model.

Figure 8.
Noise levels added to simulated signals.
Finally, the pitch bearing model is shown by Figure 9. The pitching moment calculated by the turbine model is passed to the pitch system model via a torque source, while the edgewise and flap-wise blade root moments are combined to calculate the magnitude of the friction force at the bearing, which is imposed on the pitch system model via a velocity-force look-up table implemented within the custom Simulink block.

Figure 9.
Pitch bearing model.
Although some of the components used in the Simscape model, such as the hydraulic reference, the pressure sensor or the torque source are provided by the foundation Simscape library, most components are Ikerlan’s proprietary implementations [90] which draw on the ample literature on the topic [81,91,92,93,94,95,96,97,98,99,100,101,102,103]. In particular, the accumulator models are, like Liniger et al.’s [80], based on the Benedict–Webb–Rubin equation of state for molecular nitrogen [104] with Otis and Pourmovahed’s heat transfer model [105] (the difference is, of course, that we only use this model to generate validation data, not as part of an observer). Further details regarding the model may be an interesting topic for a dedicated paper, but are besides our purpose here. Suffice it to say that the validation model is not only reasonably accurate and complex, but considerably more so than the model underlying the identification method we are proposing, which is very simple, as discussed in Section 2.1.
A total of 500 10-min simulations were carried out, 100 of which corresponded to nominal pitch system conditions, while another 100 corresponded to each of the failure modes considered here. The leaks were of approximately 6 L/min (in the case of the cylinder leak, this varies with load), which was less than 10% of the nominal flow rate supplied by the tree pumps together, i.e., 70 L/min. The accumulator gas leak was simulated by setting the nitrogen content of one of the accumulators to 50% of nominal. The extra friction was of 200 kN, which was about 25% of the force available per blade during normal operation.
The full-field turbulent wind speed input files were generated with TurbSim, with speeds ranging approximately between 10 and 20 m/s, with a different random seed for each individual simulation and TurbSim set to IEC class C turbulence, according to the normal turbulence model [106].
Figure 10 shows one simulation corresponding to each of the pitch system conditions. Note the turbulence mentioned above, as well as the effects of the failure modes on the measured variables. Although no differences are appreciable in the tracking of the cylinder position reference, each failure mode has a distinct effect on other variables. The cylinder leak at blade 1 results in the corresponding proportional valve opening being slightly below normal, while the corresponding accumulator is always the first to lose pressure; this is as expected, since the leak hinders cylinder retraction, aids cylinder extension and expends accumulator oil. The extra friction at blade 3 is apparent in that the corresponding proportional valve opening is larger than normal in absolute value, while nothing else changes; this is as expected, since the friction hinders both cylinder retraction and extension, but does not expend any extra oil. The loss of accumulator nitrogen at blade 1 results in the said accumulator always being the first to lose pressure, and forcing the accumulator pressure cycles to be shorter; this is as expected, because the accumulator has a steeper p-v curve in the operating range, so less oil suffices to cycle between the pressure limits. Finally, the pump leak is apparent in that the accumulators take longer to charge; this is as expected because the net flow rate into the accumulators is smaller.
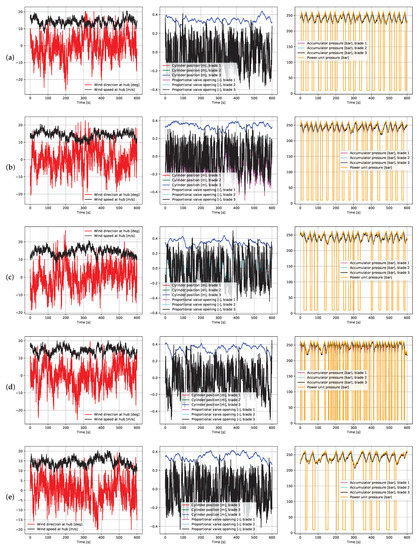
Figure 10.
Results of some 10 min simulations with (a) nominal conditions, (b) a piston seal leak at blade 1, (c) extra friction at blade 3, (d) 50% loss of nitrogen at blade 1 and (e) 6 L/min loss of pump flow.
2.3. Data Processing
The simulation data were processed with Algorithms 1 and 2, which automatically cherry-picked the data, as shown by Figure 11, to calculate eight different parameters per blade and simulation. The cherry-picking is simple: we only took data points when the cylinder was moving in the same direction and the pumps were in the same state (on or off) for a few seconds, while we discarded bits where short, slow movements happened, or just after the pumps turned on or off. This keeps the relations assumed on Section 2.1 relevant.
| Algorithm 1 Calculate , , , , and from a 10 min simulation. | |
| 1: for each blade do | |
| 2: | Calculate q via (10), with one-third of the nominal pump flow if the pumps are on, zero otherwise. |
| 3: | Calculate via (11). |
| 4: | Discard pairs corresponding to instants when the cylinders have not been moving in the same direction, at over 1 mm/s, for at least 3 s. ▷ This eliminates q values that are inaccurate due to large, fast variations in cylinder pressures. |
| 5: | Discard pairs corresponding to instants when the pumps have not been continuously on or off for at least 3 s. ▷ This eliminates values that are inaccurate due to large, fast variations in nitrogen temperature. |
| 6: | Discard pairs corresponding to instants in which the pumps are on and the accumulator pressures differ by more than 5 bar. ▷ This eliminates q values that are inaccurate due to the pump flow not being evenly distributed between blades. |
| 7: | Separate the remaining pairs into four groups, depending on whether the pumps are on or off and the cylinders are extending (x going ’up’) or retracting (x going ’down’). |
| 8: end for | |
| 9: do | |
| 10: | Fit a linear regression to each group of pairs, forcing the slopes of regressions corresponding to the same blade and the same pump state (on or off) to be mutually equal. |
| 11: | Discard pairs farther from their regression than 1.5 times the median of all pairs. |
| 12: while any pair was discarded | |
| 13: Take the regression parameters of each group as with and . | |
| Algorithm 2 Calculate and from a 10 min simulation. | |
| 1: for each blade do | |
| 2: | Take cylinder velocity and proportional valve opening u. |
| 3: | Discard pairs per steps 4–6 of Algorithm 1. |
| 4: | Fit a non-linear regression to the remaining pairs. |
| 5: | Use the fitted regression to predict cylinder velocity at () and (). |
| 6: end for | |
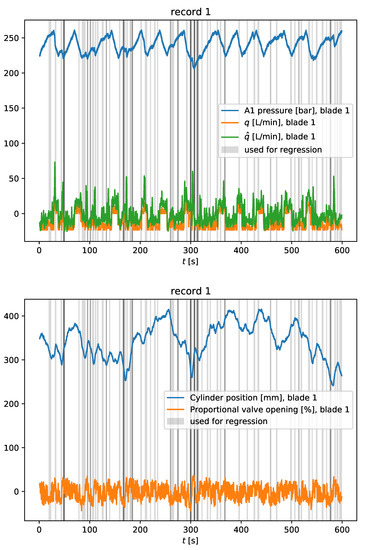
Figure 11.
Data selection from a 10 min simulation.
is the proportionality constant between and q, which are the flow rates out of the accumulator that we estimate from the variation of the accumulator pressure and the cylinder motion, respectively. If we are overestimating because there is less nitrogen in the accumulator than we thought, then is smaller than 0.75 (see Section 2.1). We allow to be different when the pumps are working and when they are not, because we estimate q by dividing the flow rate from the pumps equally between all blades, while an accumulator with less nitrogen draws less than the others in reality (and in the simulations). This means that, when the pumps are on, we estimate q with an error that is proportional to the pump flow rate minus the flow rate consumed by the cylinders, so we underestimate q for blades with less nitrogen in their accumulators and overestimate q for the rest of the blades, by a margin that gets smaller as the actual q grows. This results in the of other blades decreasing when the pumps are on due to lower nitrogen levels in one blade, while its own decreases less than when the pumps are off, and, in general, and can be expected to be different.
Moreover, our estimation of is based on the assumption that there is no heat transfer between the nitrogen and the ambient or oil. This is, of course, not true. When the pumps are on, the accumulator pressure grows, as does the temperature of the nitrogen. Neither, however, grows as it would adiabatically, so we are overestimating (underestimating its absolute value) by a more or less fixed amount, corresponding to the heat transfer. The opposite happens when the pumps are off, so we can expect an offset between the lines corresponding to the pumps being on and off. Moreover, because the pressure levels corresponding to cylinder extension and retraction are very different, due to the regenerative nature of the circuit, an offset in the estimation of q appears between the corresponding lines. We therefore expect , , and , the intercepts of the lines corresponding to each of the combinations of pumps being on or off and the cylinders extending or retracting, to be generally different. As we specify on Algorithms 1 and 2, we separate data points into four groups accordingly for regression.
3. Results
Figure 12 shows, in washed-out colors, the scatter plots of the pairs left after step 12 of Algorithm 1 (lines are used, rather than dots, to make the resulting pdf faster to render). Overlay, in solid colors, are the linear regressions fitted to said pairs on step 13 of Algorithm 1, with the legends indicating the regression parameters (the slope) and (the intercept). Each of the columns corresponds to one of the three blades, while each of the rows corresponds to a different pitch system condition. Note that remains near the expectable 0.75 in all cases except when a piston leak or a low pre-charge are present. The behavior of the intercepts is harder to interpret on this figure, and will be commented on below.
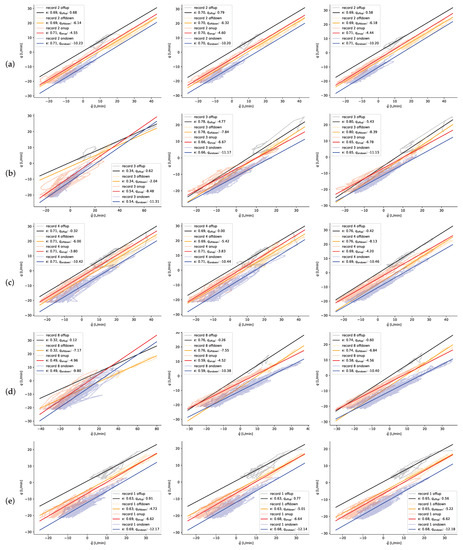
Figure 12.
Flow rate estimation comparison with some 10 min simulations and (a) nominal conditions, (b) a piston seal leak at blade 1, (c) extra friction at blade 3, (d) 50% loss of nitrogen at blade 1, and (e) 6 L/min loss of pump flow.
Figure 13 shows, in gray, the scatter plots of the pairs used in Algorithm 2. Overlay, in solid red, are the non-linear regressions fitted to said pairs, while the red shading indicates a confidence interval, which is naturally wider where less data points are present. Black dots indicate the cylinder velocity predictions corresponding to valve commands () and (). Said predictions are written on the legends. Again, each column is for each blade, each row for each condition.

Figure 13.
Cylinder velocity prediction with some 10 min simulations and (a) nominal conditions, (b) a piston seal leak at blade 1, (c) extra friction at blade 3, (d) 50% loss of nitrogen at blade 1, and (e) 6 L/min loss of pump flow.
Although Figure 12 and Figure 13 help illustrate the data processing algorithms, the parameter values they give can be hard to interpret due to their being affected by the stochastic nature of simulation inputs. It is therefore easier to discuss the results while also looking at the parameter distributions across a large set of simulations, shown by the histograms on Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21.

Figure 14.
Simulation parameter distribution, .

Figure 15.
Simulation parameter distribution, .

Figure 16.
Simulation parameter distribution, .
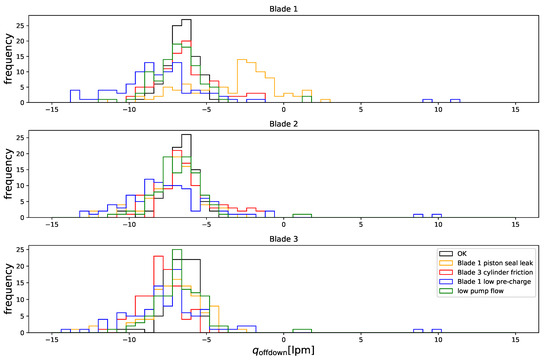
Figure 17.
Simulation parameter distribution, .

Figure 18.
Simulation parameter distribution, .

Figure 19.
Simulation parameter distribution, .
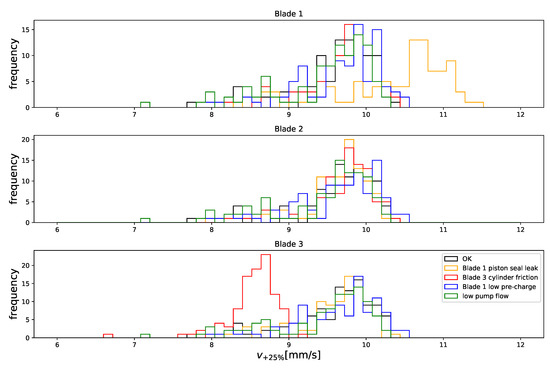
Figure 20.
Simulation parameter distribution, .
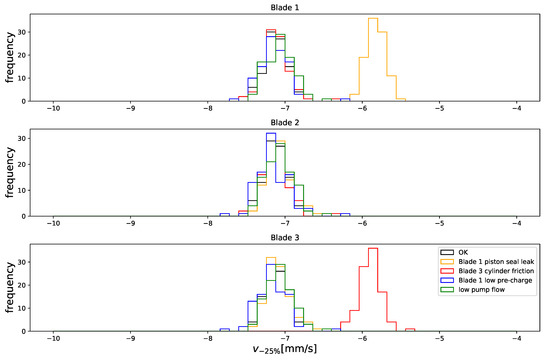
Figure 21.
Simulation parameter distribution, .
The distribution of is centered at about 0.75, as expected from our discussion in Section 2.1, except when the pre-charge is 50% lower than nominal, in which case it is centered at about half that. It is also affected by the cylinder leak, although the reason for this is not as intuitively obvious.
The distribution of is very similar to that of , with the notable difference that the shift due to low pre-charge (as well as the cylinder leak) is shared by the distributions corresponding to all three blades. This is due to our having assumed—when calculating q—that flow from the pumps is distributed equally between the accumulators, whereas, in fact, more goes to the accumulators with the higher pre-charge. The resulting effect on is quite apparent on Figure 12d.
Parameters and are practically unaffected by failures, except in the case of the cylinder leak, which shifts the latter by about 6 L/min, i.e., the magnitude of the leak. This is as expected, since the leak only consumes accumulator fluid during retraction, while none of the other failures ought to be noticeable as a constant oil deficiency when the pumps are off.
In the presence of low pump flow, parameters and shift by about 2 L/min on all the blades, i.e., the 6 L/min of pump flow deficit in aggregate. They also shift with the cylinder leak, although, as in the case of and , it is not intuitively obvious why.
Finally, parameters and shift by about 1 mm/s in the presence of the cylinder leak and the extra friction. Both these failures affect retraction equally, by slowing it down, while the leak speeds up extension instead of slowing it down (like friction). This is as observed in Section 2.2.
These results suggest that internal cylinder or pump leaks, friction, and loss of nitrogen, even if relatively small, to the point where they do not yet noticeably affect the performance of the pitch system, may be detectable by means of an algorithm such as that discussed here, given that the shifts that they cause in the distribution of algorithm outputs is large when compared to the dispersion of the latter, as clearly shown by Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. Furthermore, these shifts are not linearly dependent, so the failures may be identified as well as detected. This is better illustrated by the projections of parameter space shown by Figure 22, where a very decent grouping can be seen. Note that the projection on the plane shows orthogonal shifts for friction and pre-charge, while the projection on the plane shows the same for low pump flow and pre-charge. The low pump flow causes a shift on the parameters of all blades, because it affects all blades, while the friction only causes a shift on the parameters of the blade it affects. The low pre-charge and the cylinder leak cause larger shifts on the parameters of the blades at which they happen, but they also cause smaller shifts on the other two. Finally, although the right combination of low pre-charge and friction can result in the same parameter shift as a cylinder leak on the plane, it cannot do so on both the and simultaneously.

Figure 22.
Projections of parameter space.
4. Discussion
We suggested an algorithm to detect, identify, and quantify four hydraulic pitch system failure modes that are not trivial to detect because they have no direct impact on any one variable that is normally measured. We have then used the most accurate model available to us to carry out hundreds of simulations to process with our algorithm. The results show that even when still not noticeable in terms of turbine performance, the failure modes are identifiable from their effects on the relationships between measured variables.
Although the simulation data used here are of a very considerable realism, it is obvious that our next step will have to be to obtain test bench data and process them in a similar way, in order to check their consistency with our findings. Such work is already under way and its results will be communicated in the near future. After that, if the results are as encouraging as those shown here, it will be time for a long testing campaign on one or more wind turbines.
However, although it can be no surprise that component failures affect measurable variables, e.g., by consuming accumulator fluid faster than could be expected, and that said effects can be observed with data processing algorithms, such as those suggested here, their use in practice requires careful consideration. As already discussed, we do not wish to take the place of the monitoring algorithms, which immediately shut the turbine down when a threshold is passed, but interpret available data to estimate how far the turbine is from finding its pitch system insufficiently effective (which it arguably does not yet in our simulations, despite the considerable leaks, friction, and loss of pre-charge). It is relatively easy to conceive, although possibly very expensive to conduct, a set of tests in which different failures would be purposefully caused on the pitch system of an actual turbine. The result would be entirely realistic data on which to run detection algorithms. There would still be, of course, a fair deal of uncertainty regarding the condition of all the rest of of the pitch system and the turbine, and, crucially, we would still not know how far the failures (which in these hypothetical test we would already know as much as possible about, since we would be carefully staging them) put the turbine from being unable to withstand wind conditions, which we expect it to. The problem is akin to that of calculating the loads we expect a turbine to be subjected to: we cannot wait and measure, but must simulate and use short, limited tests to adjust or validate the simulation models. Similarly, in order to use pitch system condition monitoring algorithms (or, rather, their outputs) to inform turbine operation and maintenance, we cannot cause failures, wait and measure their effects on the turbine’s ability to face the winds it may encounter, but must simulate (repeatedly, with different failures and combinations thereof, to find the surface in failure space where we can no longer expect the pitch system to carry the turbine through) and use short, limited tests to adjust or validate the simulation models.
Author Contributions
Conceptualization, I.A. and I.E.; methodology, I.A. and I.E.; software, I.E. and H.M.-A.; validation, I.A., A.Z., I.E. and H.M.-A.; formal analysis, I.E.; investigation, I.E.; writing—original draft preparation, I.E.; writing—review and editing, I.E. and I.A.; supervision, I.A., A.P.-A. and C.C.; project administration, A.Z., A.P.-A. and C.C.; funding acquisition, I.A., I.E., A.P.-A. and C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Maritime and Fisheries Fund (EMFF) via 2018 Blue Economy project DOCC-OFF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ghoshal, A.; Sundaresan, M.J.; Schulz, M.J.; Frank Pai, P. Structural health monitoring techniques for wind turbine blades. J. Wind. Eng. Ind. Aerodyn. 2000, 85, 309–324. [Google Scholar] [CrossRef]
- Rumsey, M.A.; Paquette, J.A. Structural health monitoring of wind turbine blades. In Smart Sensor Phenomena, Technology, Networks, and Systems 2008; Ecke, W., Peters, K.J., Meyendorf, N.G., Eds.; International Society for Optics and Photonics: Washington, DC, USA, 2008; Volume 6933, pp. 104–118. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Wu, X.; Yang, Z. A review of recent advances in wind turbine condition monitoring and fault diagnosis. In Proceedings of the 2009 IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, W.; Tang, B.; Jiang, Y. Status and problems of wind turbine structural health monitoring techniques in China. Renew. Energy 2010, 35, 1414–1418. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D.; Yang, X. Wind Turbine Generator Condition-Monitoring Using Temperature Trend Analysis. IEEE Trans. Sustain. Energy 2012, 3, 124–133. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Qiu, Y.; Crabtree, C.J.; Long, H.; Tavner, P.J. Monitoring wind turbine gearboxes. Wind Energy 2013, 16, 728–740. [Google Scholar] [CrossRef]
- Yang, W.; Court, R.; Jiang, J. Wind turbine condition monitoring by the approach of SCADA data analysis. Renew. Energy 2013, 53, 365–376. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind turbine condition monitoring: Technical and commercial challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef] [Green Version]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef] [Green Version]
- Luo, N.; Vidal, Y.; Acho, L. Wind Turbine Control and Monitoring; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- de Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A review of wind turbine bearing condition monitoring: State of the art and challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Nguyen, T.C.; Huynh, T.C.; Yi, J.H.; Kim, J.T. Hybrid bolt-loosening detection in wind turbine tower structures by vibration and impedance responses. Wind. Struct. 2017, 24, 385–403. [Google Scholar] [CrossRef]
- Oliveira, G.; Magalhães, F.; Cunha, Á.; Caetano, E. Continuous dynamic monitoring of an onshore wind turbine. Eng. Struct. 2018, 164, 22–39. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Lebranchu, A.; Charbonnier, S.; Bérenguer, C.; Prévost, F. A combined mono- and multi-turbine approach for fault indicator synthesis and wind turbine monitoring using SCADA data. ISA Trans. 2019, 87, 272–281. [Google Scholar] [CrossRef]
- Carroll, J.; McDonald, A.; McMillan, D. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar] [CrossRef] [Green Version]
- Su, C.; Yang, Y.; Wang, X.; Hu, Z. Failures analysis of wind turbines: Case study of a Chinese wind farm. In Proceedings of the Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef] [Green Version]
- Liniger, J.; Soltani, M.N.; Pedersen, H.; Sepehri, N. Feasibility Study of a Simulation Driven Approach for Estimating Reliability of Wind Turbine Fluid Power Pitch Systems. In Safety and Reliability—Safe Societies in a Changing World, Proceedings of the European Safety and Reliability Conference 2018 (ESREL 2018), Trondheim, Norway, 17–18 June 2018, 1st ed.; Haugen, S., Barros, A., van Gulijk, C., Kongsvik, T., Vinnem, J., Eds.; CRC Press/Balkema: Boca Raton, FL, USA, 2018; pp. 2037–2044. [Google Scholar]
- Chen, W.; Wang, X.; Zhang, F.; Liu, H.; Lin, Y. Review of the application of hydraulic technology in wind turbine. Wind Energy 2020, 23, 1495–1522. [Google Scholar] [CrossRef]
- Lee, Y.B.; Lee, G.C.; Yang, J.D.; Park, J.W.; Baek, D.C. Failure analysis of a hydraulic power system in the wind turbine. Eng. Fail. Anal. 2020, 107, 104218. [Google Scholar] [CrossRef]
- Ryder, D.R. Redundant Actuator Development Study; Technical Report CR-114730; NASA, Ames Research Center: Moffet Field, CA, USA, 1973.
- Álvarez García, J.J. Flow Control Electro-Hydraulic Servovalve Assembly with In-Built Automatic Failure Detection and Compensation. In Proceedings of the 22nd International Congress of Aeronautical Sciences (ICAS), Harrogate, UK, 27 August 2000; p. 633. [Google Scholar]
- Andreev, M.; Kolesnikov, A.; Grätz, U.; Gundermann, J. Simulation-Based System Reliability Analysis of Electrohydraulic Actuator with Dual Modular Redundancy. In Proceedings of the 12th International Fluid Power Conference, Dresden, Germany, 9–11 March 2020; pp. 333–342. [Google Scholar] [CrossRef]
- Le, L.T. Oscillatory Failure Monitor. U.S. Patent US4826110A, 22 June 1987. [Google Scholar]
- Goupil, P. Method and Device for Detecting Oscillatory Failures in a Position Servocontrol Subsystem of an Aircraft Control Surface. U.S. Patent US20070124038A1, 20 November 2006. [Google Scholar]
- Cherepinsky, I.; Driscoll, J.T.; Kinkead, W.D.; Wengler, L.M.J. Control Surface Failure Detection for Fly-by-Wire Aircraft. U.S. Patent US20090012658A1, 29 November 2007. [Google Scholar]
- Fadiga, L.; Cazaurang, F.; Lavigne, L.; Goupil, P. Sequential probability ratio test using first Laplace distribution for oscillatory fault detection of an hydraulic actuator. IFAC Proc. Vol. 2011, 44, 4326–4331. [Google Scholar] [CrossRef]
- Schaeffer, J.M. Derived Rate Monitor for Detection of Degradation of Fuel Control Servo Valves. U.S. Patent US20130124016A1, 16 November 2011. [Google Scholar]
- Efimov, D.; Cieslak, J.; Zolghadri, A.; Henry, D. Actuator fault detection in aircraft systems: Oscillatory failure case study. Annu. Rev. Control 2013, 37, 180–190. [Google Scholar] [CrossRef]
- Márton, L.; Ossmann, D. Energetic Approach for Control Surface Disconnection Fault Detection in Hydraulic Aircraft Actuators. IFAC Proc. Vol. 2012, 45, 1149–1154. [Google Scholar] [CrossRef] [Green Version]
- Asmussen, M.F.; Liniger, J.; Pedersen, H.C. Fault Detection and Diagnosis Methods for Fluid Power Pitch System Components—A Review. Energies 2021, 14, 1305. [Google Scholar] [CrossRef]
- Brandt, C. Hydraulic Leak Detection System. U.S. Patent US5748077A, 13 May 1995. [Google Scholar]
- Watanabe, H.; Eiki, I. Failure Detection System for Hydraulic Pump. U.S. Patent US4489551A, 18 January 1984. [Google Scholar]
- Filho, J.; De Negri, V. Model-Based Fault Detection for Hydraulic Servoproportional Valves. In Proceedings of the 13th Scandinavian International Conference on Fluid Power, Linkoping, Sweden, 3–5 June 2013; pp. 389–398. [Google Scholar] [CrossRef] [Green Version]
- Liniger, J.; Stubkier, S.; Soltani, M.; Pedersen, H. Early Detection of Coil Failure in Solenoid Valves. IEEE/ASME Trans. Mechatron. 2020, 25, 683–693. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Li, F.; Yang, Z.; Teng, W. Adaptive Estimation-Based Leakage Detection for a Wind Turbine Hydraulic Pitching System. IEEE/ASME Trans. Mechatron. 2012, 17, 907–914. [Google Scholar] [CrossRef]
- Yao, J.; Yang, G.; Ma, D. Internal Leakage Fault Detection and Tolerant Control of Single-Rod Hydraulic Actuators. Math. Probl. Eng. 2014, 2014, 345345. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Su, R.; Lu, C.; Rui, X. Internal leakage detection for wind turbine hydraulic pitching system with computationally efficient adaptive asymmetric SVM. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 6126–6130. [Google Scholar] [CrossRef]
- Tutivén Gálvez, C.; Segui, Y.; Acho, L.; Rodellar, J. A fault detection method for pitch actuators faults in wind turbines. In Proceedings of the International Conference on Renewable Energy and Power Quality Journal (ICREPQ’15), La Coruña, Spain, 25–27 March 2015. [Google Scholar]
- Zhao, H.S.; Lian, S.S.; Shao, L. Fault Prediction of Pitch Actuator for Wind Turbines. In Vehicle, Mechanical and Electrical Engineering; Trans Tech Publications Ltd.: Durnten-Zurich, Switzerland, 2015; Volume 721, pp. 397–401. [Google Scholar] [CrossRef]
- Cho, S. Model-Based Fault Detection and Diagnosis of a Blade Pitch System in Floating Wind Turbines. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2020. [Google Scholar]
- Wu, D.; Liu, W. A new fault diagnosis approach for the pitch system of wind turbines. Adv. Mech. Eng. 2017, 9, 1687814017703350. [Google Scholar] [CrossRef] [Green Version]
- Pujol-Vazquez, G.; Acho, L.; Gibergans-Báguena, J. Fault Detection Algorithm for Wind Turbines’ Pitch Actuator Systems. Energies 2020, 13, 2861. [Google Scholar] [CrossRef]
- Sun, X.; Wang, X.; Lin, S. Multi-Fault Diagnosis Approach Based on Updated Interacting Multiple Model for Aviation Hydraulic Actuator. Information 2020, 11, 410. [Google Scholar] [CrossRef]
- Dalla Vedova, M.; Bonanno, G.; Maggiore, P. Electrohydraulic Servomechanisms Affected by Multiple Failures: A Model-Based Prognostic Method Using Genetic Algorithms. WSEAS Trans. Electron. 2016, 7, 85–91. [Google Scholar]
- Dalla Vedova, M.; Bonanno, G.; Maggiore, P. A new genetic algorithm model-based prognostic approach applied to onboard electrohydraulic servomechanisms. WSEAS Trans. Environ. Dev. 2017, 13, 431–440. [Google Scholar]
- Dalla Vedova, M.D.; Berri, P.C.; Bonanno, G.; Maggiore, P. Fault Detection and Identification Method Based on Genetic Algorithms to Monitor Degradation of Electrohydraulic Servomechanisms. In Proceedings of the 2019 4th International Conference on System Reliability and Safety (ICSRS), Rome, Italy, 20–22 November 2019; pp. 304–311. [Google Scholar] [CrossRef]
- Dalla Vedova, M.; Borghetto, M. Optimization algorithms for prognostics of electrohydraulic on-board servomechanisms. Int. J. Mech. 2019, 13, 21–30. [Google Scholar]
- Vásquez, S.; Kinnaert, M.; Pintelon, R. Active Fault Diagnosis on a Hydraulic Pitch System Based on Frequency-Domain Identification. IEEE Trans. Control Syst. Technol. 2019, 27, 663–678. [Google Scholar] [CrossRef]
- Linaric, D.; Koroman, V. Fault diagnosis of a hydraulic actuator using neural network. In Proceedings of the IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; Volume 1, pp. 108–111. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P. Innovative Actuator Fault Identification Based on Back Electromotive Force Reconstruction. Actuators 2020, 9, 50. [Google Scholar] [CrossRef]
- Yazdanpanah Goharrizi, A.; Sepehri, N. A Wavelet-Based Approach to Internal Seal Damage Diagnosis in Hydraulic Actuators. IEEE Trans. Ind. Electron. 2010, 57, 1755–1763. [Google Scholar] [CrossRef]
- Yao, Z.; Tang, J.; Rui, T.; Duan, J. A time–frequency analysis based internal leakage detection method for hydraulic actuators. Adv. Mech. Eng. 2017, 9, 1687814016685058. [Google Scholar] [CrossRef] [Green Version]
- Manyala, J.O.; Fritz, T.W. Signal-Based Actuators Fault Detection and Isolation for Gearbox Applications. SAE Int. J. Commer. Veh. 2014, 7, 315–323. [Google Scholar] [CrossRef]
- Pace, L.; Dalla Vedova, M.; Maggiore, P. Proposal of prognostic parametric method applied to an electrohydraulic servomechanism affected by multiple failures. WSEAS Trans. Environ. Dev. 2014, 10, 478. [Google Scholar]
- Simani, S.; Castani, P. Fault Diagnosis Techniques for a Wind Turbine System. In Fault Detection, Diagnosis and Prognosis; IntechOpen: Rijeka, Croatia, 2019; Chapter 4; pp. 1–20. [Google Scholar] [CrossRef] [Green Version]
- Berri, P.; Dalla Vedova, M.; Quattrocchi, G.; Maggiore, P. Model-based strategy and surrogate function for health condition assessment of actuation devices. In Proceedings of the 10th EASN International Conference, Salerno, Italy, 2–4 September 2020. [Google Scholar]
- Adams, S.; Beling, P.; Farinholt, K.; Brown, N.; Polter, S.; Dong, Q. Condition Based Monitoring for a Hydraulic Actuator. In Proceedings of the Annual Conference Of The Prognostics And Health Management Society, Denver, CO, USA, 3–6 October 2016. [Google Scholar]
- Huang, J.; Wang, X.; Wang, D.; Wang, Z.; Hua, X. Analysis of Weak Fault in Hydraulic System Based on Multi-scale Permutation Entropy of Fault-Sensitive Intrinsic Mode Function and Deep Belief Network. Entropy 2019, 21, 425. [Google Scholar] [CrossRef] [Green Version]
- Vos, D.W.; Motazed, B. Application of fault-tolerant controls to UAVs. In Navigation and Control Technologies for Unmanned Systems; Speigle, S.A., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 1996; Volume 2738, pp. 69–75. [Google Scholar] [CrossRef]
- Crepin, P.Y.; Kress, R. Model Based Fault Detection For An Aircraft actuator. In Proceedings of the International Council of the Aeronautical Sciences (ICAS), Harrogate, UK, 27 August–1 September 2000; p. 631. [Google Scholar]
- Batur, C.; Zhang, L. Sliding mode observer and controller design for a hydraulic motion control system. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 2, pp. 1721–1726. [Google Scholar] [CrossRef]
- Garimella, P.; Yao, B. Fault Detection of an Electro-Hydraulic Cylinder Using Adaptive Robust Observers. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004; Volume 11. [Google Scholar] [CrossRef] [Green Version]
- Garimella, P.; Yao, B. Model based fault detection of an electro-hydraulic cylinder. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 1, pp. 484–489. [Google Scholar] [CrossRef]
- Khan, H.; Abou, S.C.; Sepehri, N. Nonlinear observer-based fault detection technique for electro-hydraulic servo-positioning systems. Mechatronics 2005, 15, 1037–1059. [Google Scholar] [CrossRef]
- Werlefors, M.; Medvedev, A. Observer-based leakage detection in hydraulic systems with position and velocity feedback. In Proceedings of the 2008 IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008; pp. 948–953. [Google Scholar] [CrossRef]
- An, L.; Sepehri, N. Leakage fault detection in hydraulic actuators subject to unknown external loading. Int. J. Fluid Power 2008, 9, 15–25. [Google Scholar] [CrossRef]
- Márton, L.; Varga, A. Detection of overload generated faults in electro-hydrostatic actuators. In Proceedings of the 2011 19th Mediterranean Conference on Control Automation (MED), Corfu, Greece, 20–23 June 2011; pp. 767–772. [Google Scholar] [CrossRef] [Green Version]
- Gojny, M.; Carl, U.B.; Sachs, H. Device and Method for the Residual Analysis of a Residuum to Detect System Errors in the System Behaviour of a System of an Aircraft. U.S. Patent US9535419B2, 27 October 2011. [Google Scholar]
- Choux, M.; Tyapin, I.; Hovland, G. Leakage-detection in blade pitch control systems for wind turbines. In Proceedings of the 2012 Annual Reliability and Maintainability Symposium, Reno, NV, USA, 23–26 January 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Ossmann, D.; van der Linden, F.L.J. Advanced sensor fault detection and isolation for electro-mechanical flight actuators. In Proceedings of the 2015 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Montreal, QC, Canada, 15–18 June 2015; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Patton, R.J.; Lan, J. Fault-tolerant Individual Pitch Control using Adaptive Sliding Mode Observer. IFAC-Pap. 2018, 51, 1127–1132. [Google Scholar] [CrossRef]
- Asmussen, M.F.; Pedersen, H.C.; Lilleengen, L.; Larsen, A.; Farsakoglou, T. Investigating Fault Detection and Diagnosis in a Hydraulic Pitch System Using a State Augmented EKF-Approach. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019. [Google Scholar] [CrossRef]
- Sørensen, F.; von Benzon, M.; Klemmensen, S.; Schmidt, K.; Liniger, J. Estimation of prepressure in hydraulic piston accumulators for industrial wind turbines using multi-model adaptive estimation. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- IEC. Failure Modes and Effects Analysis (FMEA and FMECA): IEC 60812; International Electrotechnical Commission: Geneva, Switzerland, 2018. [Google Scholar]
- Liniger, J.; Soltani, M.; Pedersen, H.; Carroll, J.; Sepehri, N. Reliability Based Design of Fluid Power Pitch Systems for Wind Turbines. Wind Energy 2017, 20, 1097–1110. [Google Scholar] [CrossRef] [Green Version]
- Liniger, J.; Pedersen, H.C.; Soltani, M. Risk-based Comparative Study of Fluid Power Pitch Concepts. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power & Motion Control, Sarasota, FL, USA, 16–19 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Liniger, J. Design of Reliable Fluid Power Pitch Systems for Wind Turbines. Ph.D. Thesis, Aalborg Universitet, Aalborg, Denmark, 2018. [Google Scholar] [CrossRef]
- Liniger, J.; Pedersen, H.C.; Soltani, M. Model-based Estimation of Gas Leakage for Fluid Power Accumulators in Wind Turbines. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 16–19 October 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Properties of Gases and Liquids 5E; McGraw Hill Professional, McGraw-Hill Education: New York, NY, USA, 2000. [Google Scholar]
- Fitzpatrick, R. Thermodynamics and Statistical Mechanics: An Intermediate Level Course; Lulu: Tokyo, Japan, 2005. [Google Scholar]
- Canfield, F.B.; Leland, T.W.; Kobayashi, R. Compressibility Factors for Helium-Nitrogen Mixtures. J. Chem. Eng. Data 1965, 10, 92–96. [Google Scholar] [CrossRef]
- Bak, C.; Bitsche, R.; Yde, A.; Kim, T.; Hansen, M.; Zahle, F.; Gaunaa, M.; Blasques, J.; Døssing, M.; Heinen, J.J.; et al. Light rotor: The 10-MW Reference Wind Turbine. In Proceedings of the European Wind Energy Association (EWEA), Copenhagen, Denmark, 16–19 April 2012; Volume 1. [Google Scholar]
- Wind Energy. Available online: https://rwt.windenergy.dtu.dk/dtu10mw/dtu-10mw-rwt/-/tree/master/aeroelastic_models/fast/DTU10MWRWT_FAST_v1.00 (accessed on 17 August 2021).
- Github. Available online: https://github.com/OpenFAST/openfast/releases/tag/v2.3.0 (accessed on 12 July 2021).
- Elorza, I.; Calleja, C.; Pujana-Arrese, A. On Wind Turbine Power Delta Control. Energies 2019, 12, 2344. [Google Scholar] [CrossRef] [Green Version]
- Github. Available online: https://github.com/ielorza/OpenDiscon/tree/739288c3ff9a06d405d2cd8e3e2eb3c7a7439ec3 (accessed on 23 August 2021).
- Jenkins, N.; Burton, A.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Rodriguez-Guerra, J.; Calleja, C.; Elorza, I.; Macarulla, A.M.; Pujana, A.; Azurmendi, I. A Methodology for Real-Time HiL Validation of Hydraulic-Press Controllers Based on Novel Modeling Techniques. IEEE Access 2019, 7, 110541–110553. [Google Scholar] [CrossRef]
- Eryilmaz, B.; Wilson, B. Modeling the Internal Leakage of Hydraulic Servovalves. In Proceedings of the International Mechanical Engineering Congress and Exposition, (ASME), Orlando, FL, USA, 5–10 November 2000. [Google Scholar]
- Nahian, S.A.; Truong, D.Q.; Chowdhury, P.; Das, D.; Ahn, K.K. Modeling and fault tolerant control of an electro-hydraulic actuator. Int. J. Precis. Eng. Manuf. 2016, 17, 1285–1297. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.; Bachynski, E.E.; Nejad, A.R.; Gao, Z.; Moan, T. Numerical modeling of the hydraulic blade pitch actuator in a spar-type floating wind turbine considering fault conditions and their effects on global dynamic responses. Wind Energy 2020, 23, 370–390. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Berri, P.; Dalla Vedova, M.; Maggiore, P. Back-EMF Reconstruction for Electromechanical Actuators in Presence of Faults. In Proceedings of the 30th European Safety and Reliability Conference and the 15th Probabilistic Safety Assessment and Management Conference (ESREL2020/PSAM15), Venice, Italy, 1–5 November 2020. [Google Scholar] [CrossRef]
- Berri, P.; Dalla Vedova, M. A review of simplified servovalve models for digital twins of electrohydraulic actuators. J. Phys. Conf. Ser. 2020, 1603, 012016. [Google Scholar] [CrossRef]
- Dalla Vedova, M.; Berri, P.; Corsi, C.; Alimhillaj, P. New Synthetic Fluid Dynamic Model For Aerospace Four-Ways Servovalve. Int. J. Mech. Control 2019, 20, 105–112. [Google Scholar]
- Dalla Vedova, M.; Alimhillaj, P. Novel fluid dynamic nonlinear numerical models of servovalves for aerospace. Int. J. Mech. 2019, 13, 39–51. [Google Scholar]
- Dalla Vedova, M.; Maggiore, P.; Riva, G. A new CFD-Simulink based systems engineering approach applied to the modelling of a hydraulic safety relief valve. Int. J. Mech. 2017, 11, 43–50. [Google Scholar]
- Dalla Vedova, M.; Maggiore, P.; Scanavino, M. Numerical modelling of sinusoidal brushless motor for aerospace actuator systems. WSEAS Trans. Circuits Syst. 2017, 12. [Google Scholar]
- Pace, L.; Dalla Vedova, M.; Maggiore, P.; Facciotto, S. Numerical methods for the electromagnetic modelling of actuators for primary and secondary flight controls. In Proceedings of the 18th International Conference on Automatic Control, Modelling & Simulation (ACMOS ’16), Venice, Italy, 29–31 January 2016. [Google Scholar]
- Rakoto, L.; Schorsch, J.; Kinnaert, M. Modelling hydraulic pitch actuator for wind turbine simulation under healthy and faulty conditions. IFAC-Pap. 2015, 48, 577–582. [Google Scholar] [CrossRef]
- Narayanan, V.L.; Ramakrishnan, R. Design and implementation of an intelligent digital pitch controller for digital hydraulic pitch system hardware-in-the-loop simulator of wind turbine. Int. J. Green Energy 2021, 18, 17–36. [Google Scholar] [CrossRef]
- ISO. Hydraulic Fluid Power—Electrically Modulated Hydraulic Control Valves—Part 1: Test Methods for Four-Port Directional Flow-Control Valves; ISO 10770-1; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 7th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Otis, D.R.; Pourmovahed, A. An Algorithm for Computing Nonflow Gas Processes in Gas Springs and Hydropneumatic Accumulators. J. Dyn. Syst. Meas. Control 1985, 107, 93–96. [Google Scholar] [CrossRef]
- IEC. Wind Turbines—Part 1: Design Requirements; IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).