A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor
Abstract
1. Introduction
2. Model
2.1. Pore Scale Model
- (1)
- The matrix is considered as opaque and inert porous media.
- (2)
- The surface-to-surface radiation is taken into account and computed by DO model, solid surface scattering is ignored.
- (3)
- The heat loss by the outer surfaces to the surroundings is neglected.
- (4)
- The radiation at inlet and outlet is neglected because the local temperature is low.
- (5)
- There is a uniform distribution of channels.
2.2. Volume-Average Model
- (1)
- The mixture is assumed to be an ideal gas, ignoring radiation.
- (2)
- Porous media are noncatalytic, homogeneous, and optically thick. Solid radiation is considered using the Rosseland method.
- (3)
- There is thermal non-equilibrium between gas and solid.
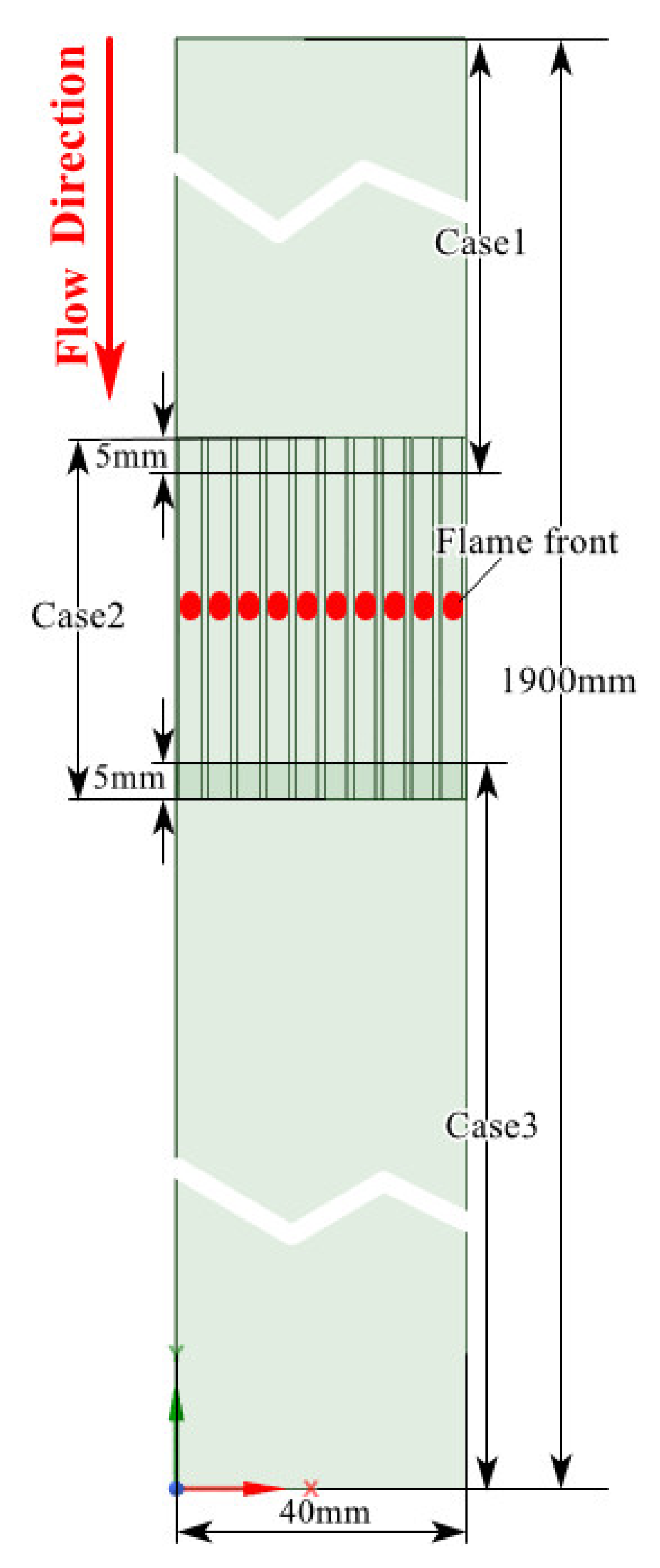
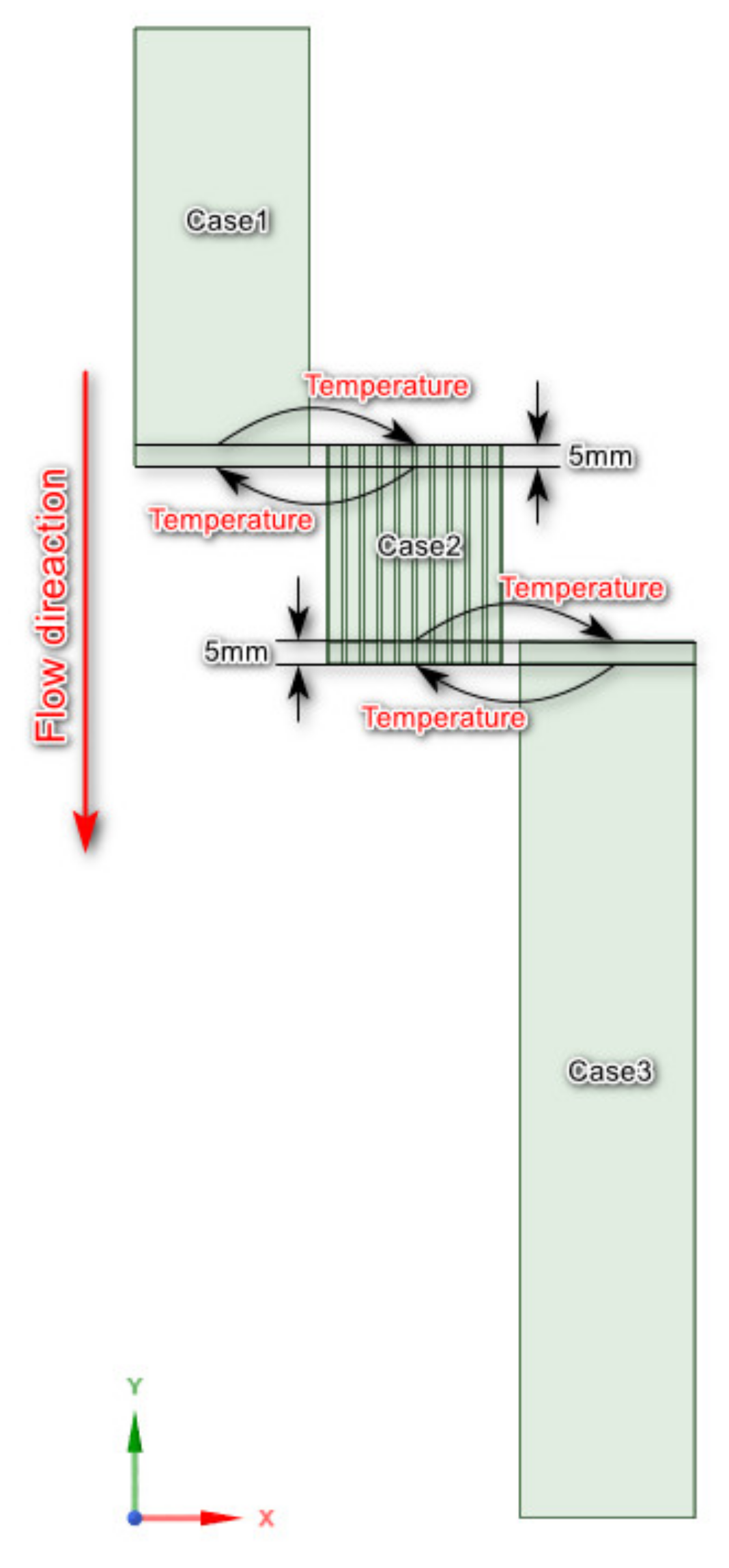
2.3. Mesh
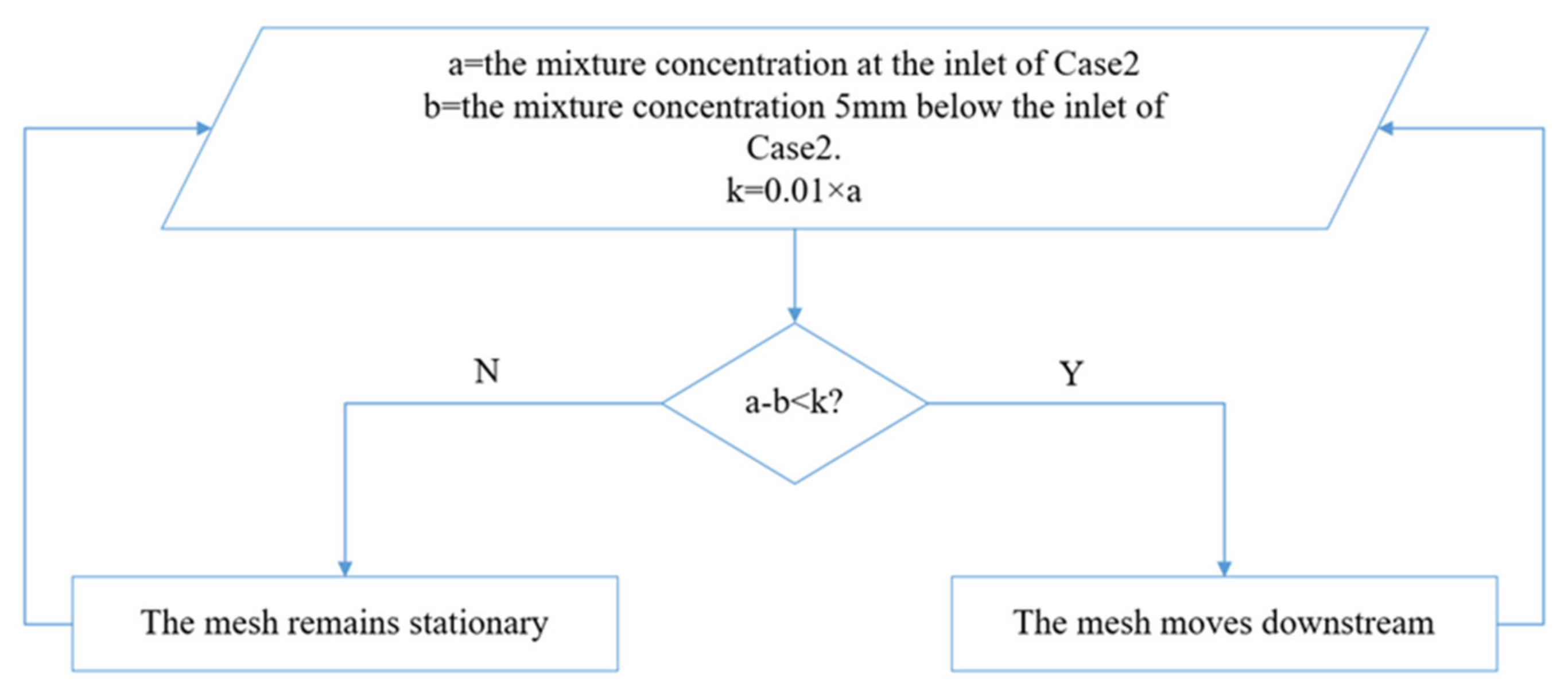
2.4. Setup
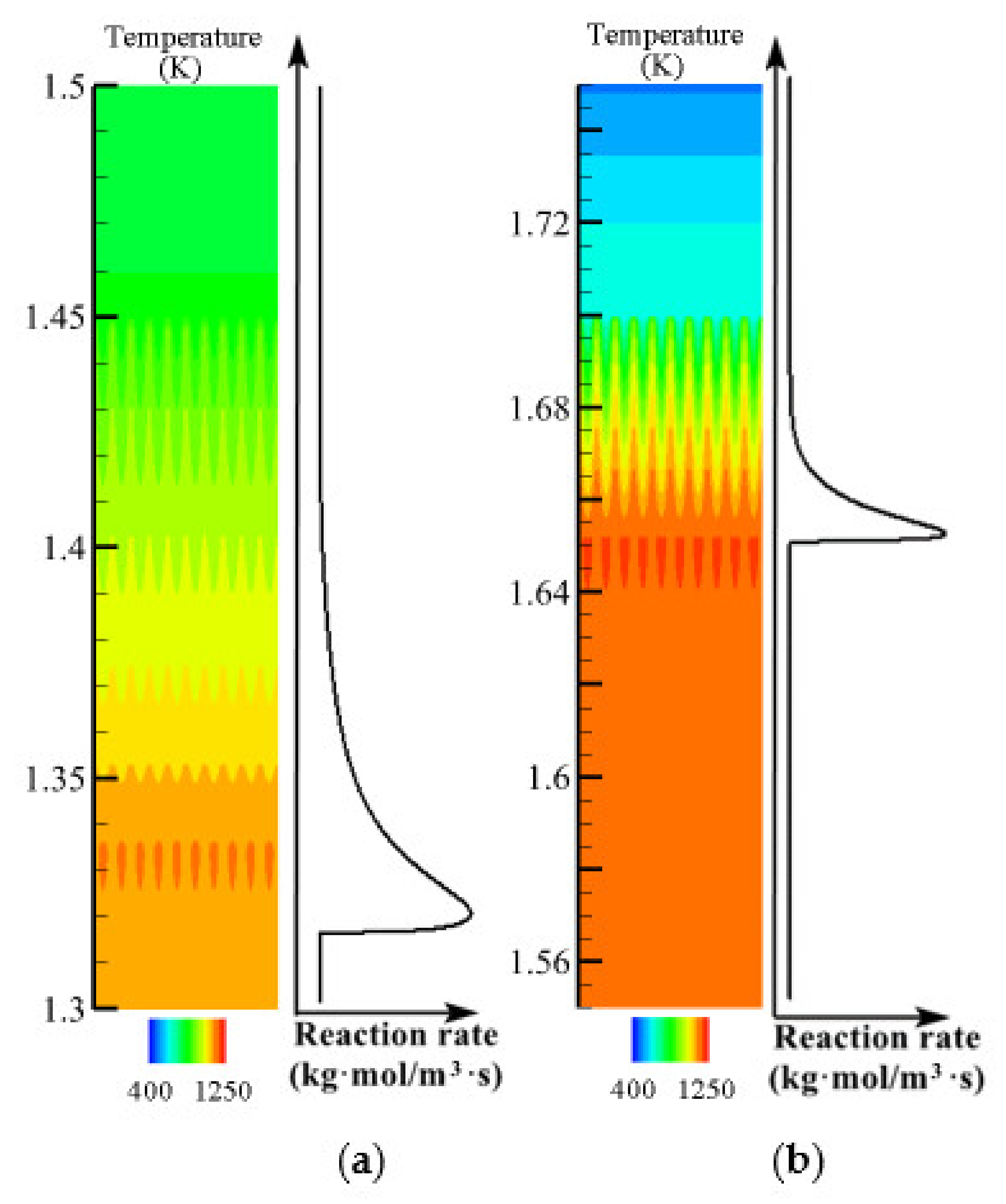
3. Results and Discussion
3.1. Model Validation
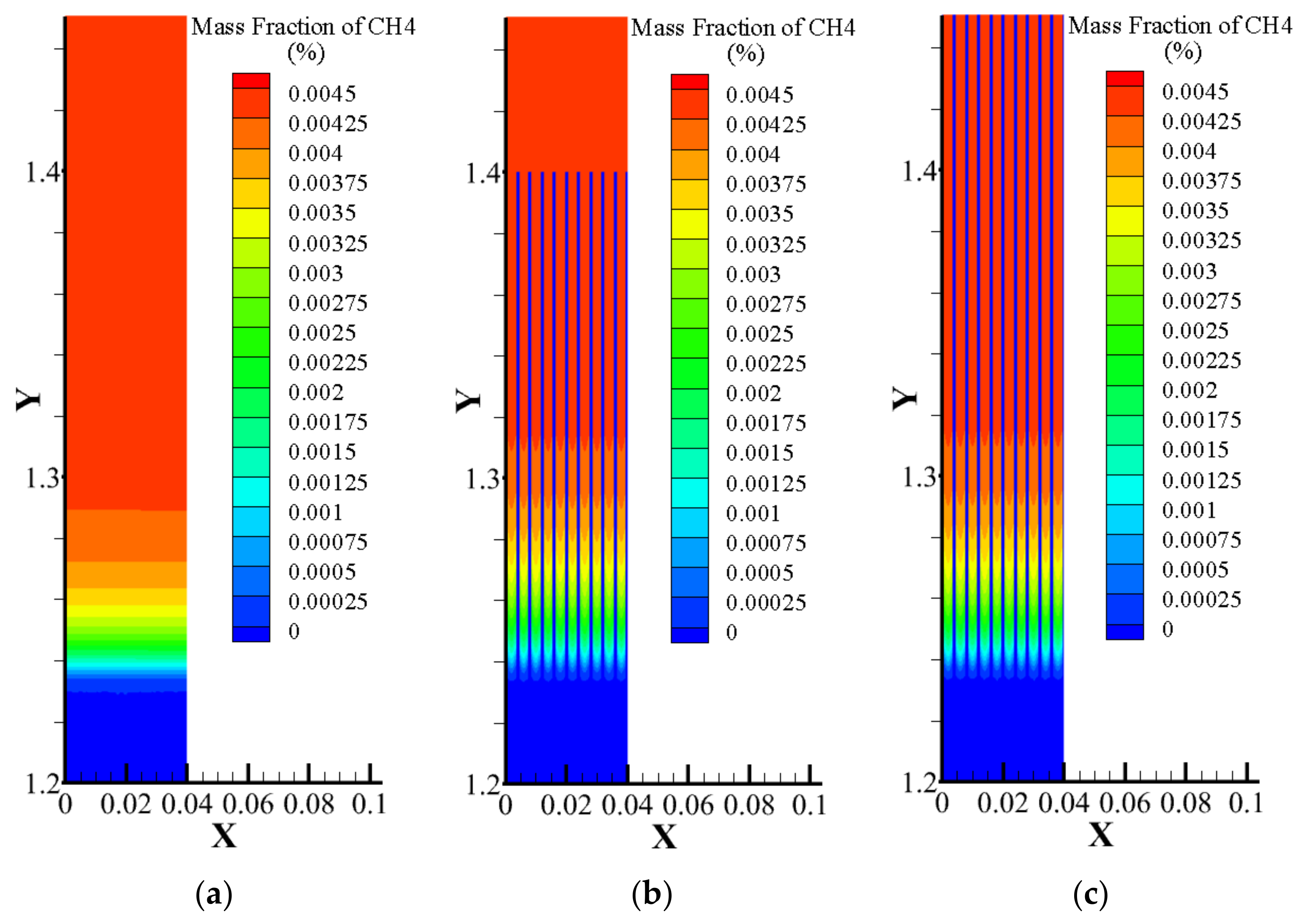
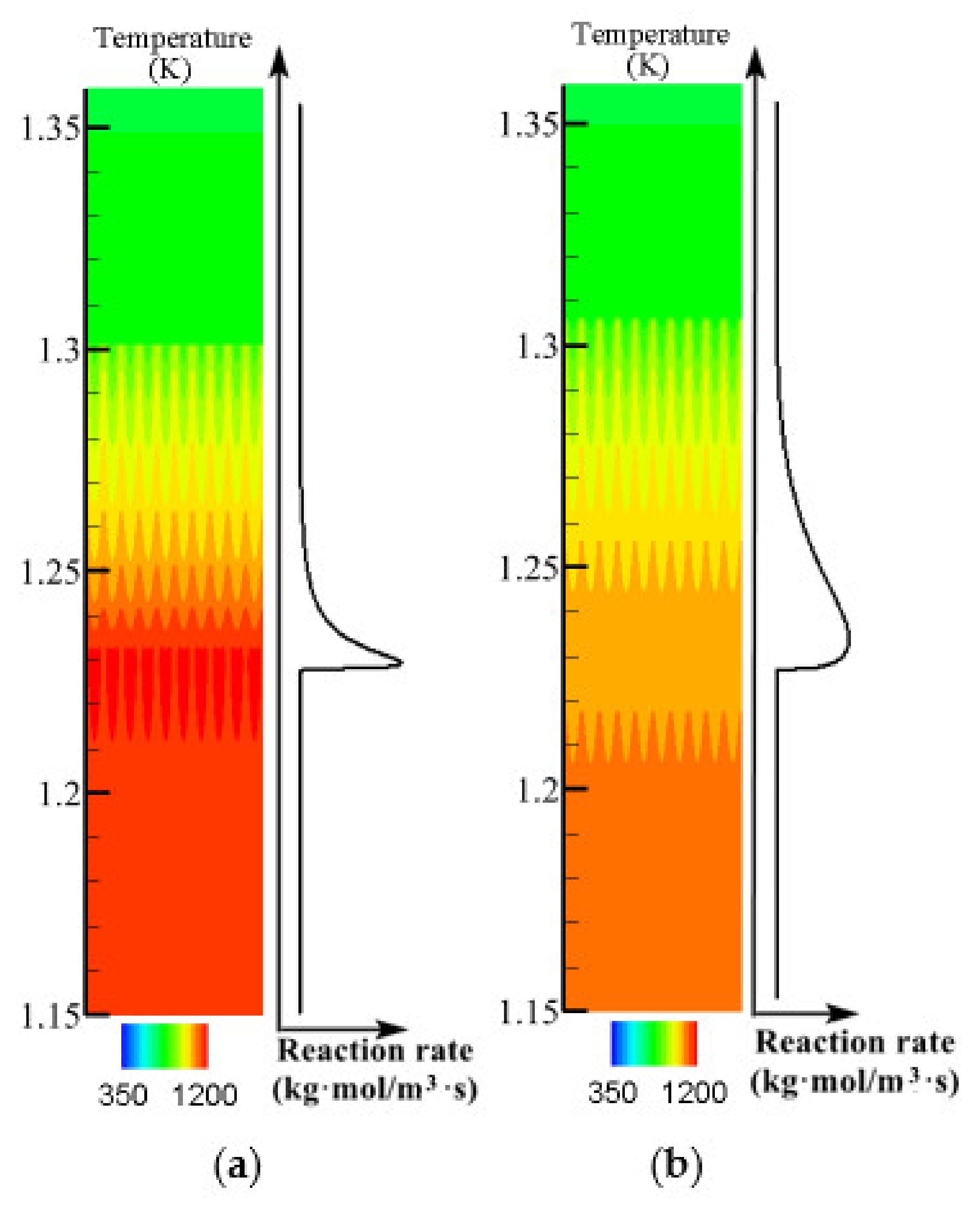
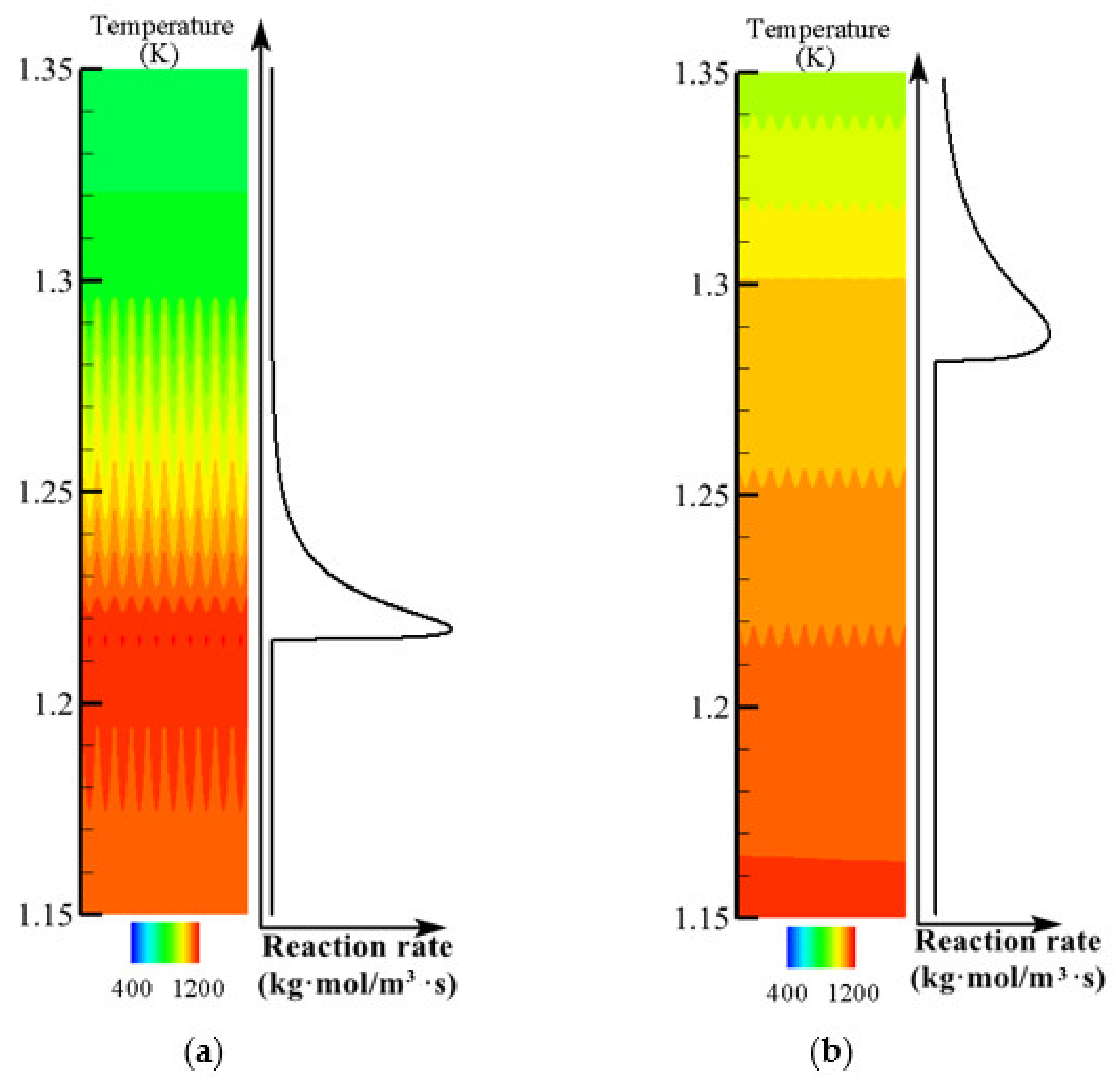
3.2. Comparison of Volume Average Model, Multi-Scale Model, and Pore-Scale Model
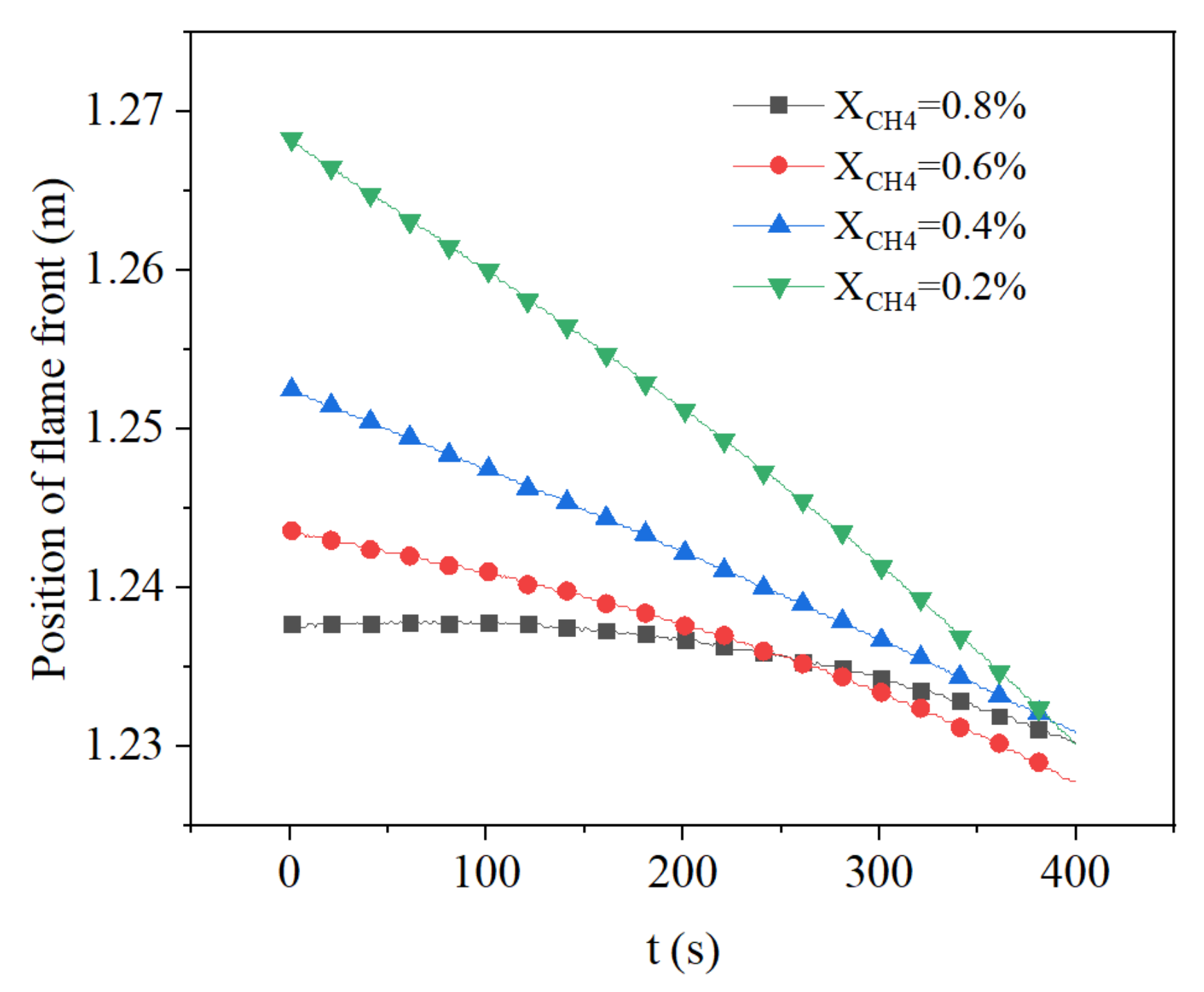
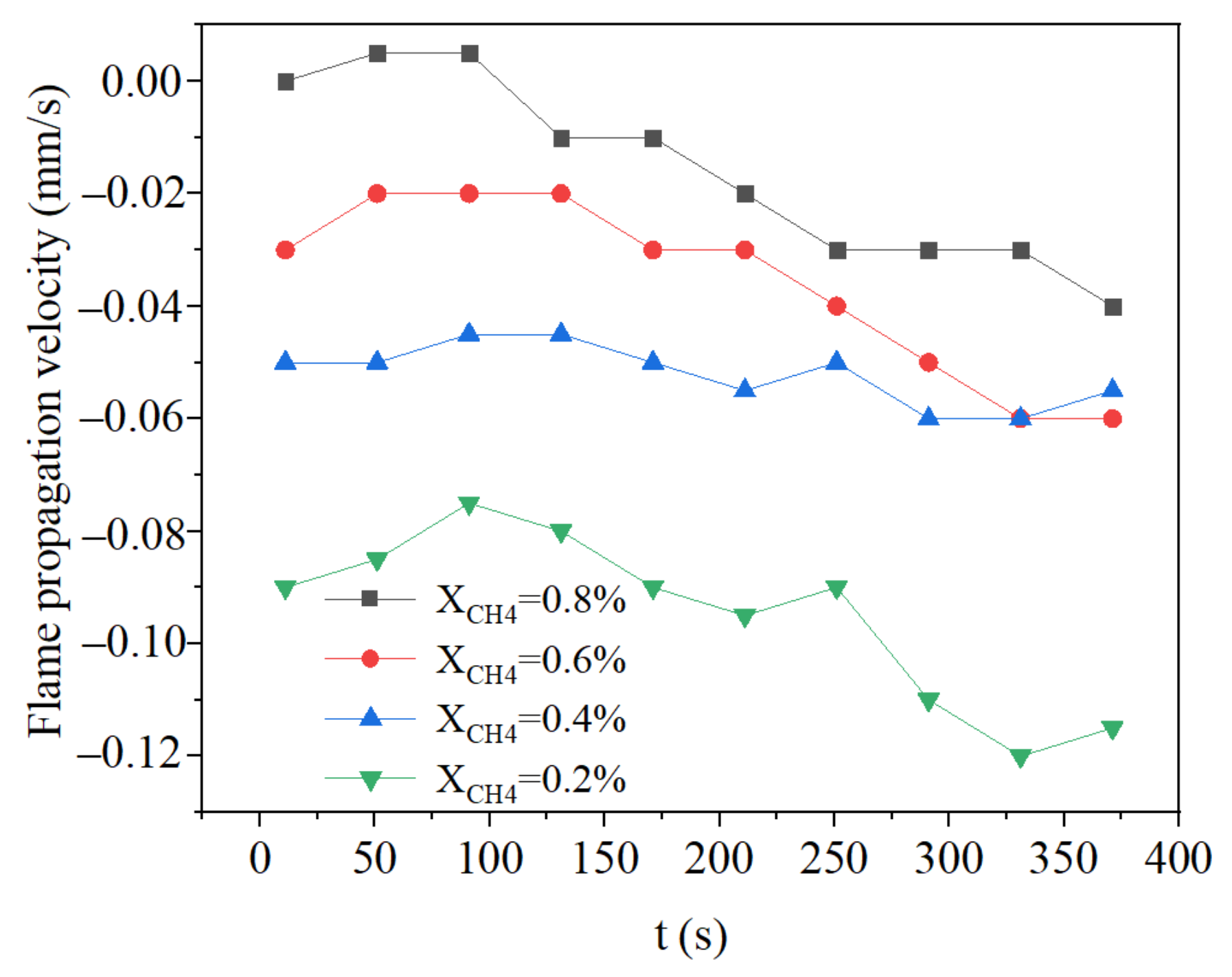
3.3. Effect of Methane Concentration on Flame Propagation and Thickness of the Flame
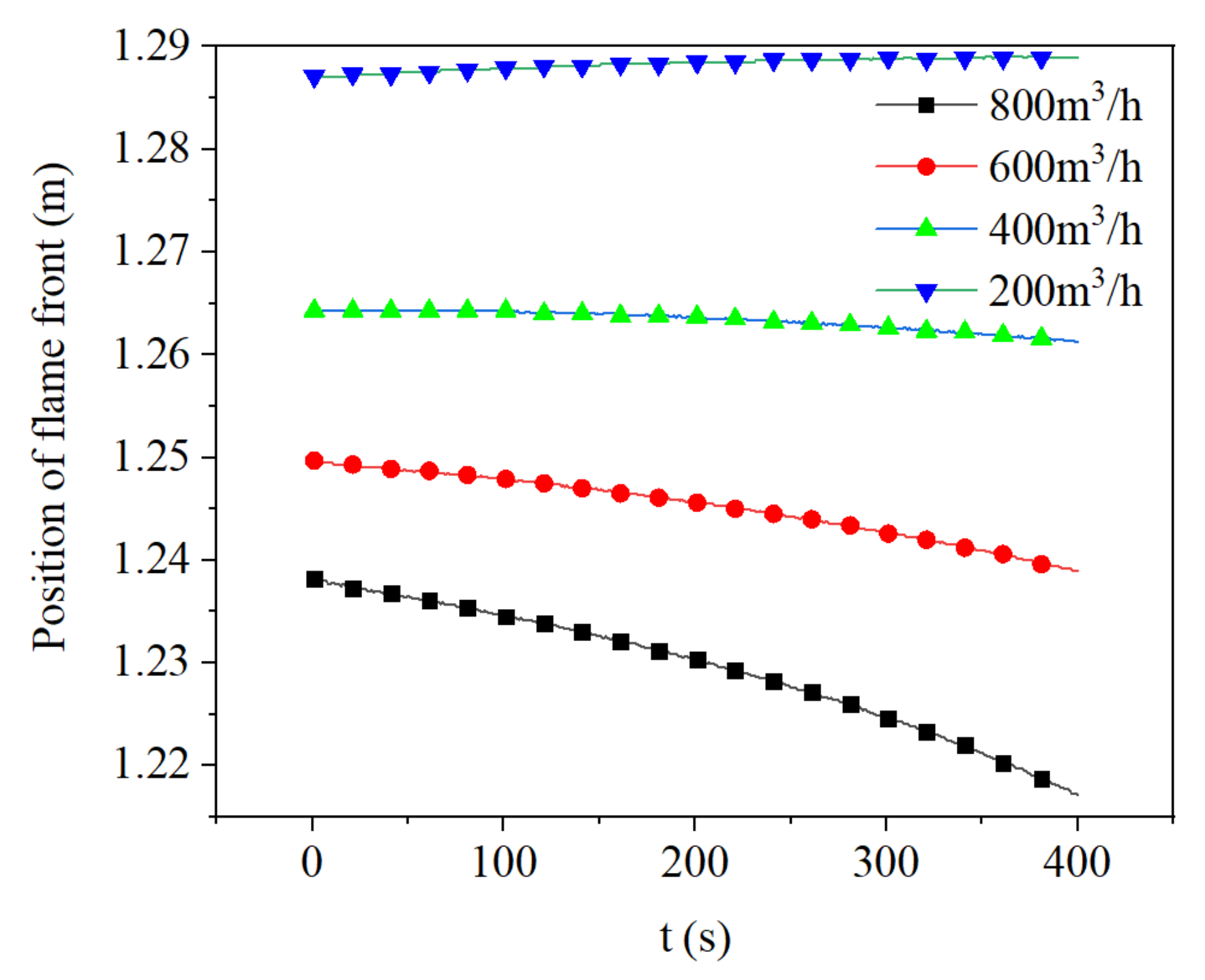
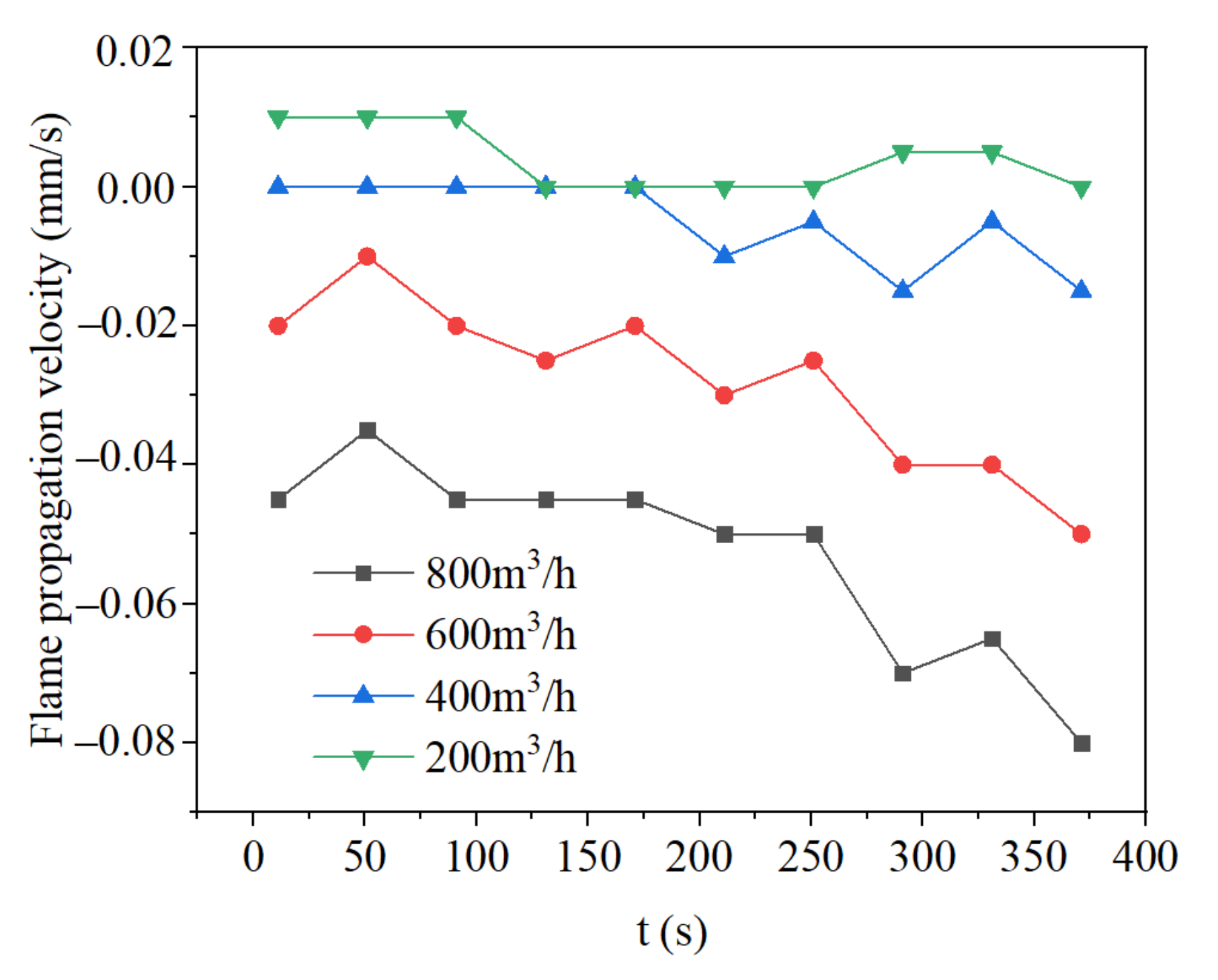
3.4. Effect of Flow Rate on Flame Propagation and Flame Thickness
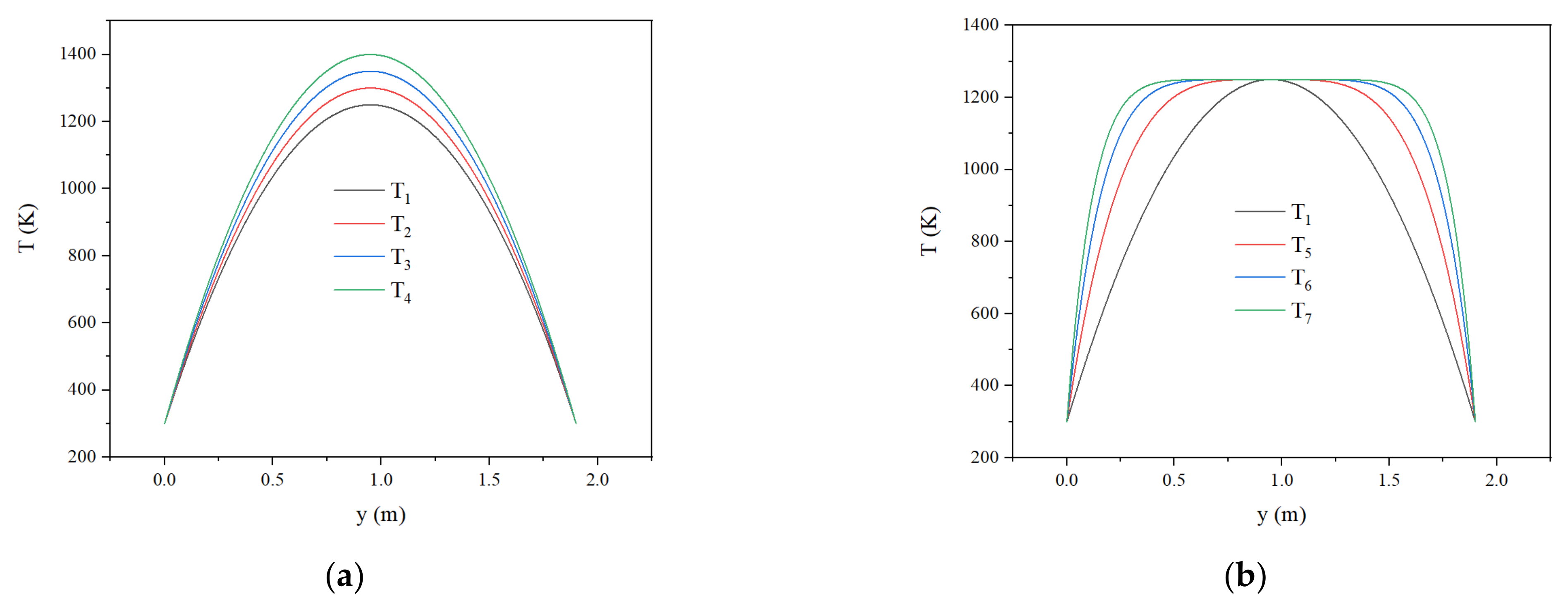
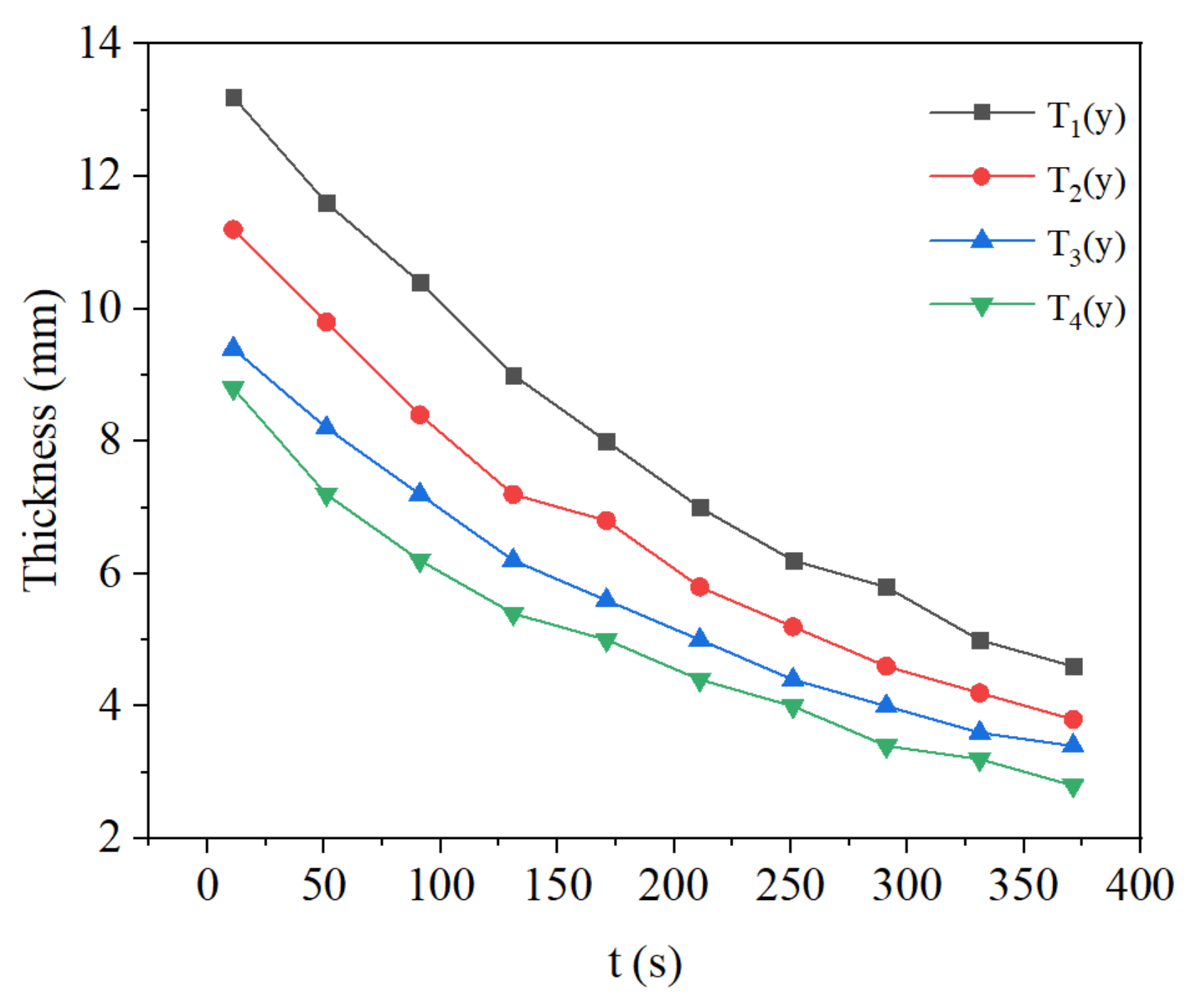
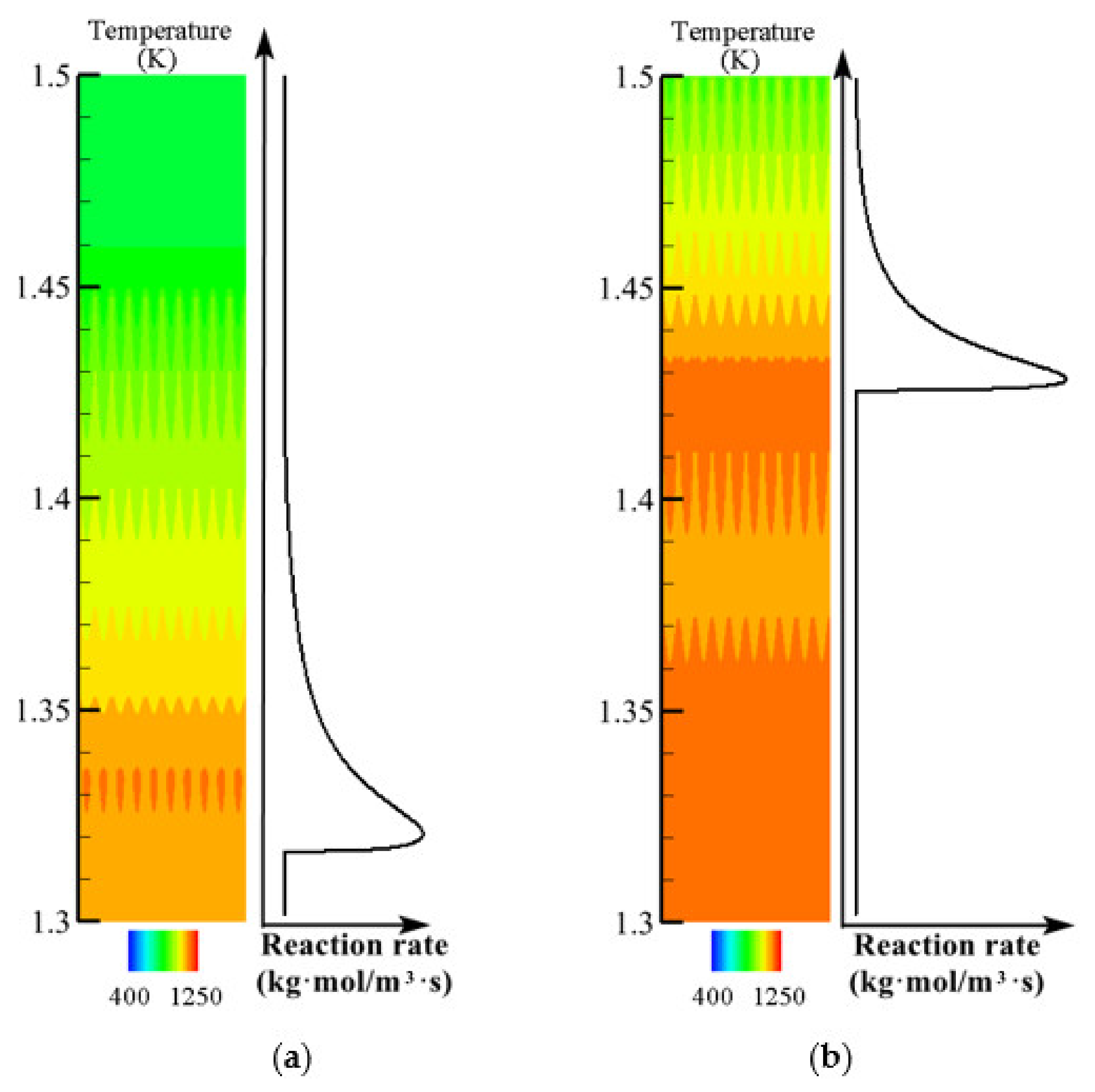
3.5. Effect of Initial Temperature Field on Flame Propagation and Flame Thickness
4. Conclusions
- (1)
- Compared with the VAM model, the temperature non-equilibrium between gas and solid can be shown more intuitively in the multi-scale model proposed in this paper. The multi-scale model can display the flame thickness and propagation more accurately. Compared with the pore-scale model, the multi-scale model saves computing resources. The results from the multi-scale model are in good agreement with the experimental results.
- (2)
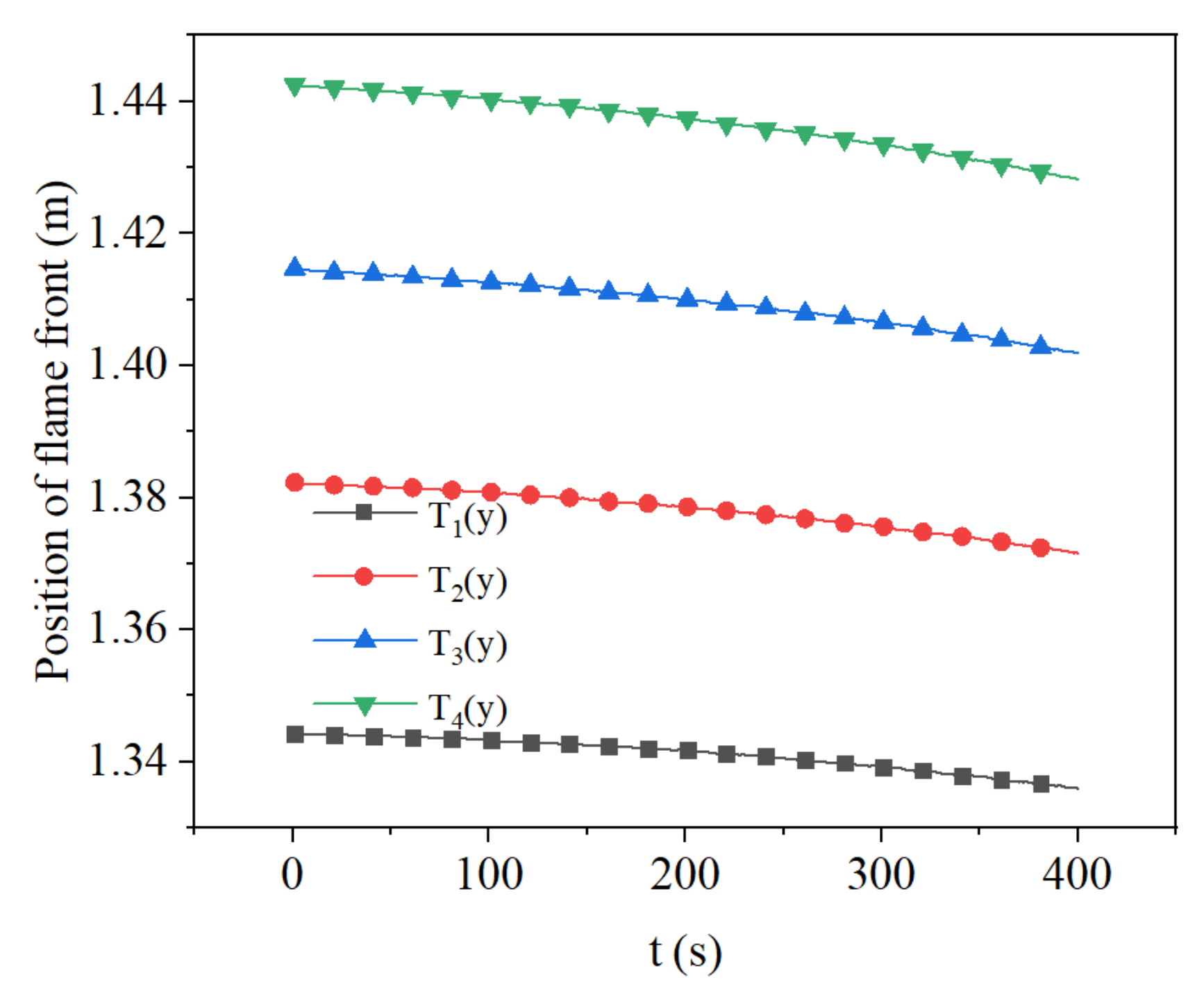
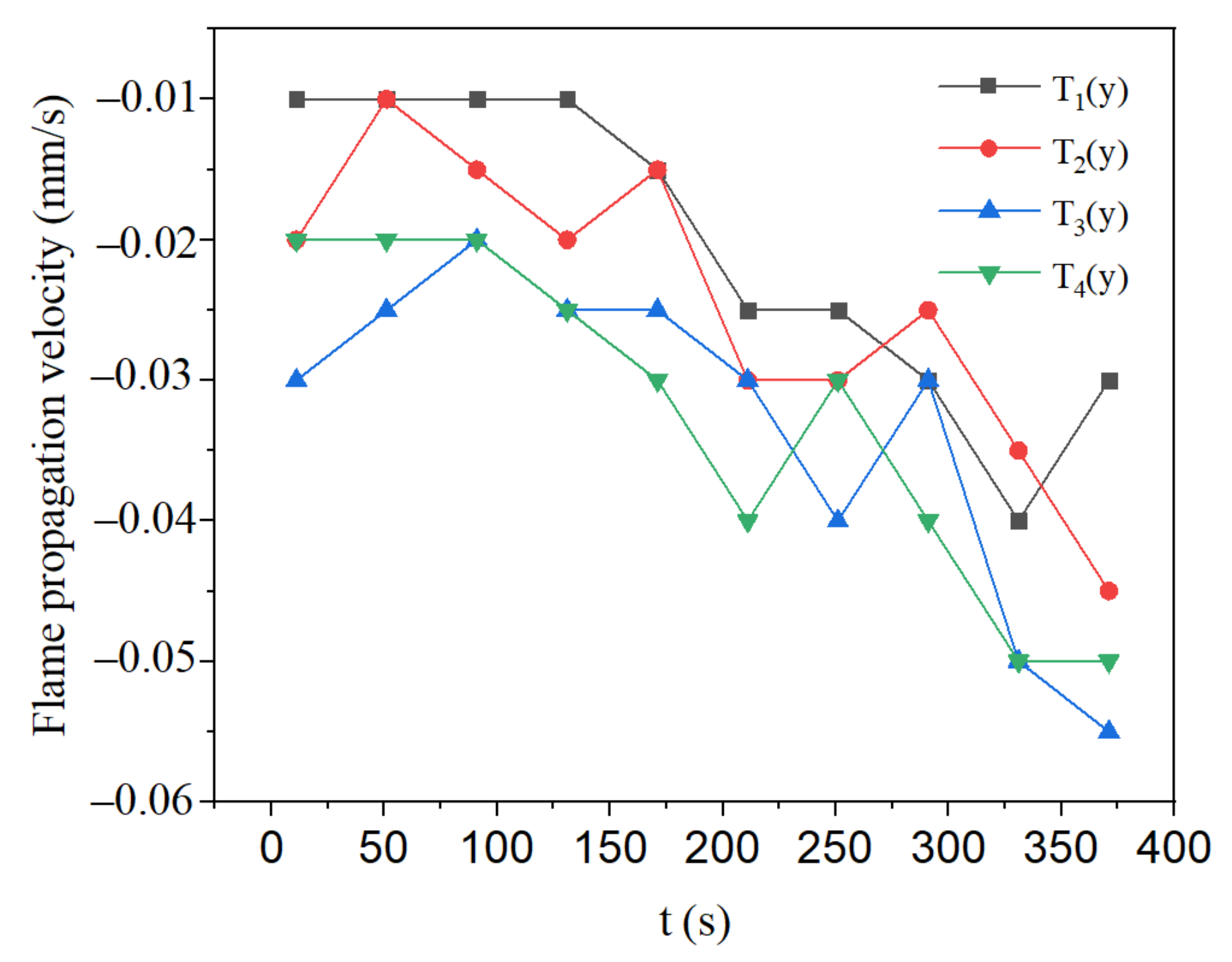
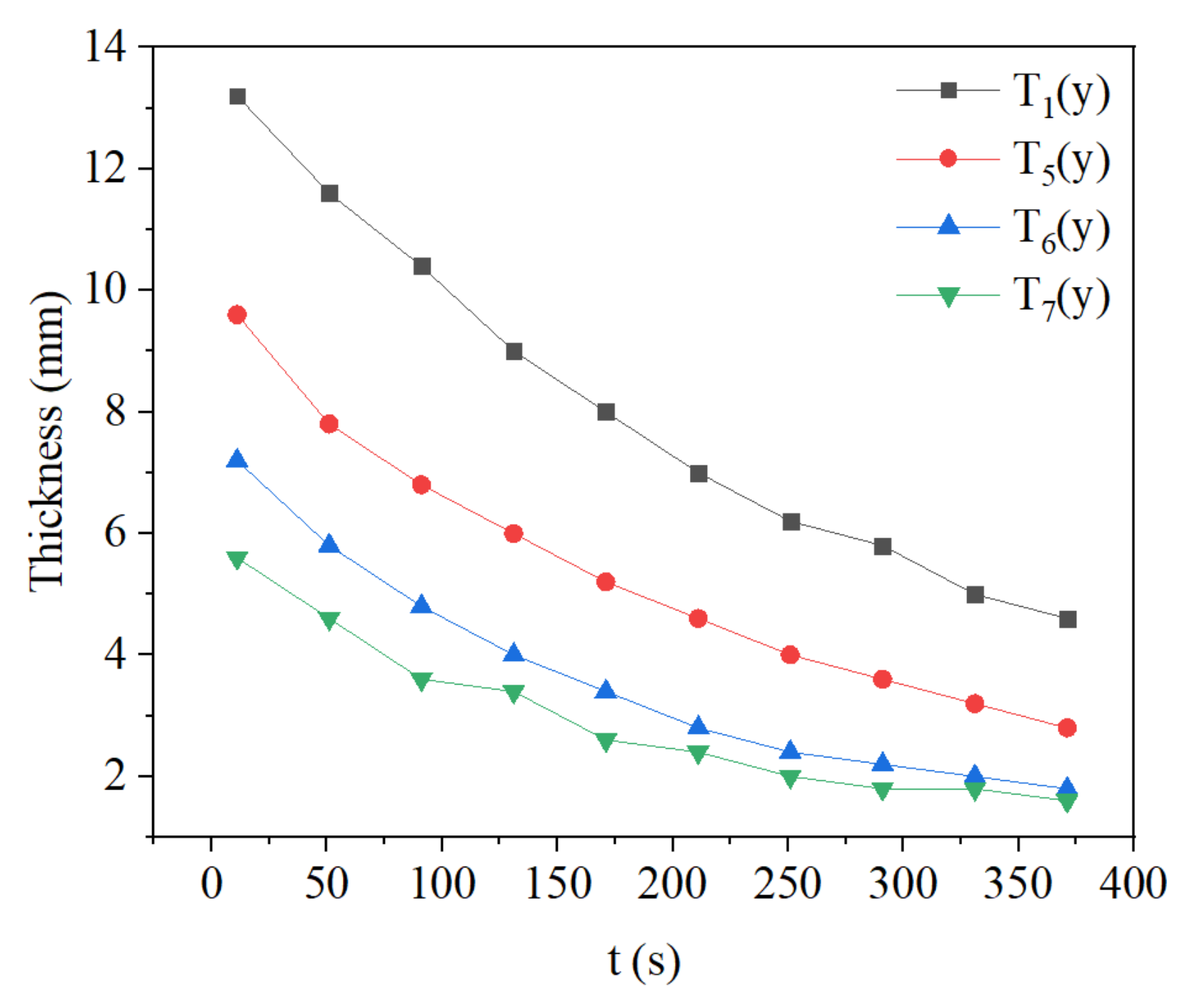
- During the flame downward propagation, the propagation velocity increases and the flame thickness gets smaller with time. This is because the heat generated by the reaction increases the temperature of the reaction zone.
- (3)
- The growth of intake concentration increases the reaction rate and temperature, leading to a decrease of flame propagation velocity and smaller flame thickness.
- (4)
- The increase of flow rate increases the average temperature of the reaction zone and the reaction rate, thus making the flame thickness smaller. When the inlet flow rate increases, the growth rate of the flow rate is greater than that of the reaction rate in the reaction zone. Then the flame propagation velocity accelerates.
- (5)
- The larger peak value and width of the high-temperature zone of the initial temperature field increase the average temperature of the reaction zone. The high average temperature speeds up the flame propagation and decreases the flame thickness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Somers, J.M.; Schultz, H.L. Coal mine ventilation air emissions: Project development planning and mitigation technologies. In Proceedings of the 13th United States/North American Mine Ventilation Symposium, Sudbury, ON, Canada, 13–16 June 2010; pp. 115–121. [Google Scholar]
- Boucher, O.; Folberth, G.A. New Directions: Atmospheric methane removal as a way to mitigate climate change. Atmos. Environ. 2010, 44, 3343–3345. [Google Scholar] [CrossRef]
- Uddin, N.; Blommerde, M.; Taplin, R.; Laurence, D. Sustainable development outcomes of coal mine methane clean development mechanism projects in China. Renew. Sustain. Energy Rev. 2015, 45, 1–9. [Google Scholar] [CrossRef]
- Zhou, F.; Xia, T.; Wang, X.; Zhang, Y.; Sun, Y.; Liu, J. Recent developments in coal mine methane extraction and utilization in China: A review. J. Nat. Gas Sci. Eng. 2016, 31, 437–458. [Google Scholar] [CrossRef]
- Su, S.; Beath, A.; Guo, H.; Mallett, C. An assessment of mine methane mitigation and utilization technologies. Prog. Energy Combust. Sci. 2005, 31, 123–170. [Google Scholar] [CrossRef]
- Shi, J.; Yu, C.; Li, B.; Xia, Y.; Xue, Z. Experimental and numerical studies on the flame instabilities in porous media. Fuel 2013, 106, 674–681. [Google Scholar] [CrossRef]
- Zheng, C.; Cheng, L.; Saveliev, A.; Luo, Z.; Cen, K. Numerical studies on flame inclination in porous media combustors. Int. J. Heat Mass Transf. 2011, 54, 3642–3649. [Google Scholar] [CrossRef]
- Chen, L.; Xia, Y.; Li, B.; Shi, J. Flame front inclination instability in the porous media combustion with inhomogeneous preheating temperature distribution. Appl. Therm. Eng. 2018, 128, 1520–1530. [Google Scholar] [CrossRef]
- Wang, G.; Tang, P.; Li, Y.; Xu, J.; Durst, F. Flame front stability of low calorific fuel gas combustion with preheated air in a porous burner. Energy 2019, 170, 1279–1288. [Google Scholar] [CrossRef]
- Shi, J.; Chen, Z.; Li, H.; Lv, J.; Mao, M. Pore-scale study of thermal nonequilibrium in a two-layer burner formed by staggered arrangement of particles. Appl. Therm. Eng. 2020, 176, 1359–4311. [Google Scholar] [CrossRef]
- Shi, J.; Mao, M.; Li, H.; Liu, Y.; Lv, J. A pore level study of syngas production in two-layer burner formed by staggered arrangement of particles. Int. J. Hydrog. Energy 2020, 45, 2331–2340. [Google Scholar] [CrossRef]
- Yue, M.; Xie, M.-Z.; Shi, J.-R.; Liu, H.-S.; Chen, Z.-S.; Chang, Y.-C. Numerical and Experimental Investigations on Combustion Characteristics of Premixed Lean Methane–Air in a Staggered Arrangement Burner with Discrete Cylinders. Energies 2020, 13, 6397. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Shi, J.; Xiao, R.; Li, H. Pore-level numerical simulation of methane-air combustion in a simplified two-layer porous burner. Chin. J. Chem. Eng. 2021, 34, 87–96. [Google Scholar] [CrossRef]
- Bharadwaj, V.S.; Pecha, M.B.; Bu, L.; Dagle, V.L.; Dagle, R.A.; Ciesielski, P.N. Multi-scale simulation of reaction, transport and deactivation in a SBA-16 supported catalyst for the conversion of ethanol to butadiene. Catal. Today 2019, 338, 141–151. [Google Scholar] [CrossRef]
- Tang, Y.; Valocchi, A.J.; Werth, C.J. A hybrid pore-scale and continuum-scale model for solute diffusion, reaction, and biofilm development in porous media. Water Resour. Res. 2015, 51, 1846–1859. [Google Scholar] [CrossRef]
- Xin, C.; Lu, L.; Shi, B.; Liu, Z. Numerical investigation of local thermal non-equilibrium effects in coal porous media with cryogenic nitrogen injection. Int. J. Therm. Sci. 2018, 133, 32–40. [Google Scholar] [CrossRef]
- Lu, L.; Du, X.; Xin, C. Modeling and Simulation of Local Thermal Non-equilibrium Effects in Porous Media with Small Thermal Conductivity. Transp. Porous Media 2018, 124, 553–575. [Google Scholar] [CrossRef]
- Kardaś, D.; Polesek-Karczewska, S.; Tiutiurski, P.; Wardach-Świȩcicka, I. Applying dynamic mesh to examine evolution of effective thermal conductivity in porous medium undergoing macrostructure change. Appl. Therm. Eng. 2021, 187, 116583. [Google Scholar] [CrossRef]
- Qin, C.; Guo, B.; Celia, M.; Wu, R. Dynamic pore-network modeling of air-water flow through thin porous layers. Chem. Eng. Sci. 2019, 202, 194–207. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Liu, H.; Jia, M.; Wang, Q.; Zhang, M.; Xu, Y. Modeling of the dynamic behaviors of heat transfer during the construction of roadway using moving mesh. Case Stud. Therm. Eng. 2021, 26, 100958. [Google Scholar] [CrossRef]
- Pitsch, H. A consistent level set formulation for large-eddy simulation of premixed turbulent combustion. Combust. Flame 2005, 143, 587–598. [Google Scholar] [CrossRef]
- Semlitsch, B.; Orchini, A.; Dowling, A.P.; Juniper, M.P. G-equation modelling of thermoacoustic oscillations of partially premixed flames. Int. J. Spray Combust. Dyn. 2017, 9, 260–276. [Google Scholar] [CrossRef]
- Mao, M.; Shi, J.; Liu, Y.; Gao, M.; Chen, Q. Experimental investigation on control of temperature asymmetry and nonuniformity in a pilot scale thermal flow reversal reactor. Appl. Therm. Eng. 2020, 175, 1359–4311. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D.; Leutcha, P.; Marsano, D. Strategies for the Numerical Modelling of Regenerative Pre-heating Systems for Recycled Glass Raw Material. Math. Model. Eng. Probl. 2019, 6, 324–332. [Google Scholar] [CrossRef][Green Version]
- Hayes, A.M.; Khan, J.A.; Shaaban, A.H.; Spearing, I.G. The thermal modeling of a matrix heat exchanger using a porous medium and the thermal non-equilibrium model. Int. J. Therm. Sci. 2008, 47, 1306–1315. [Google Scholar] [CrossRef]
- Azizi, S.; Hosseini, S.H.; Moraveji, M.; Ahmadi, G. CFD modeling of a spouted bed with a porous draft tube. Particuology 2010, 8, 415–424. [Google Scholar] [CrossRef]
- Mao, M.; Liu, Y.; Gao, Z.; Tang, S.; You, Y. Experimental study on flow uniformity in a hot countercurrent reaction. J. China Coal Soc. 2011, 36, 1349–1353. [Google Scholar]
- Li, Q.; Bai, F.; Yang, B.; Wang, Y.; Xu, L.; Chang, Z.; Wang, Z.; El Hefni, B.; Yang, Z.; Kubo, S.; et al. Dynamic simulations of a honeycomb ceramic thermal energy storage in a solar thermal power plant using air as the heat transfer fluid. Appl. Therm. Eng. 2018, 129, 636–645. [Google Scholar] [CrossRef]
- Fu, X.; Viskanta, R.; Gore, J.P. Measurement and correlation of volumetric heat transfer coefficients of cellular ceramics. Exp. Therm. Therm. Fluid Sci. 1998, 17, 285–293. [Google Scholar]
- Bubnovich, V.; Toledo, M. Analytical modelling of filtration combustion in inert porous media. Appl. Therm. Eng. 2007, 27, 1144–1149. [Google Scholar] [CrossRef]
- Huang, H.; Sun, T.; Zhang, G.; Li, D.; Wei, H. Evaluation of a developed SST k-ω turbulence model for the prediction of turbulent slot jet impingement heat transfer. Int. J. Heat Mass Transf. 2019, 139, 700–712. [Google Scholar] [CrossRef]
- Cademartori, S.; Cravero, C.; Marini, M.; Marsano, D. CFD Simulation of the Slot Jet Impingement Heat Transfer Process and Application to a Temperature Control System for Galvanizing Line of Metal Band. Appl. Sci. 2021, 11, 1149. [Google Scholar] [CrossRef]
- Wang, S.; Fan, A. Combustion regimes of syngas flame in a micro flow reactor with controlled temperature profile: A numerical study. Combust. Flame 2021, 230, 10–2180. [Google Scholar] [CrossRef]











| Nomenclature | |||
|---|---|---|---|
| C | specific heat, kJ/kg·K | Di | diffusion coefficient of species i, cm2/s |
| w | width of model | hi | molar enthalpy of species i, kj/Kg |
| a | mixture concentration at the inlet of Case2; coefficient | b | mixture concentration 5 mm below the inlet of Case2; coefficient |
| G | incident radiation, W/m2 | qR | radiation heat flux, W/m3 |
| p | pressure, Pa | T0 | ambient temperature, K |
| T | temperature, K | v | vertical velocity, m/s |
| u | horizontal velocity, m/s | Wi | molecular weight of species i, Kg/Kmol |
| gas velocity vector, m/s | X | molar fraction | |
| x | vertical coordinate, m | Y | mass fraction |
| y | horizontal coordinate, m | k | difference value |
| m | an experimental coefficient | t | time |
| ui | the i component of velocity vector | Q | heat content of the premixed mixture |
| R | general constant of the gas | C1 | permeability resistance |
| C2 | inertial resistance | ||
| Greek symbols | |||
| φ | equivalent ratio | λ | thermal conductivity, W/m·K |
| ρ | density, kg/m3 | ε | porosity |
| εr | solid surface emissivity | ωi | reaction rate of species i, Kmol/m3·s |
| σ | Stephan–Boltzmann constant, W/m2·K4 | μ | kinematic viscosity, Pa·s |
| α | gas absorption coefficient, 1/m | β | heat loss coefficient, W/m3·K |
| Subscripts | |||
| g | gas | s | solid |
| in | burner inlet | out | burner outlet |
| i | species in the gas mixture | ||
| Name | Grid Size of Case1 | Grid Size of Case2 | Grid Size of Case3 |
|---|---|---|---|
| Mesh1 | 0.2 mm | 0.1 mm | 0.2 mm |
| Mesh2 | 0.5 mm | 0.2 mm | 0.5 mm |
| Mesh3 | 1 mm | 0.5 mm | 1 mm |
| XCH4 | Inlet Flow Rate | T0 | Initial Temperature Field |
|---|---|---|---|
| 0.8% | 700 m3/h | 300 K | |
| 0.6% | 700 m3/h | 300 K | |
| 0.4% | 700 m3/h | 300 K | |
| 0.2% | 700 m3/h | 300 K |
| XCH4 | Inlet Flow Rate | T0 | Initial Temperature Field |
|---|---|---|---|
| 0.6% | 800 m3/h | 300 K | |
| 0.6% | 600 m3/h | 300 K | |
| 0.6% | 400 m3/h | 300 K | |
| 0.6% | 200 m3/h | 300 K |
| XCH4 | Inlet Flow Rate | T0 | Initial Temperature Field |
|---|---|---|---|
| 0.6% | 700 m3/h | 300 K | T1(y) |
| 0.6% | 700 m3/h | 300 K | T2(y) |
| 0.6% | 700 m3/h | 300 K | T3(y) |
| 0.6% | 700 m3/h | 300 K | T4(y) |
| 0.6% | 700 m3/h | 300 K | T5(y) |
| 0.6% | 700 m3/h | 300 K | T6(y) |
| 0.6% | 700 m3/h | 300 K | T7(y) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Mao, M.-M.; Gao, M.; Chen, Q.; Shi, J.-R.; Liu, Y.-Q. A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor. Energies 2022, 15, 318. https://doi.org/10.3390/en15010318
Li J, Mao M-M, Gao M, Chen Q, Shi J-R, Liu Y-Q. A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor. Energies. 2022; 15(1):318. https://doi.org/10.3390/en15010318
Chicago/Turabian StyleLi, Jia, Ming-Ming Mao, Min Gao, Qiang Chen, Jun-Rui Shi, and Yong-Qi Liu. 2022. "A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor" Energies 15, no. 1: 318. https://doi.org/10.3390/en15010318
APA StyleLi, J., Mao, M.-M., Gao, M., Chen, Q., Shi, J.-R., & Liu, Y.-Q. (2022). A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor. Energies, 15(1), 318. https://doi.org/10.3390/en15010318





