Abstract
In this article, we present a numerical analysis of the energy and mass transport behavior of microrotational flow via Riga plate, considering suction or injection and mixed convection. The thermal stratified parameters of nanofluid are captured using an interpretation of the well-known Keller box model, which helps us to determine the characteristic properties of the physical parameters. The formulated boundary layer equations (nonlinear partial differential equations) are transformed into coupled ODEs with nonlinearities for the stratified controlled regimes. The impact of embedded flow and all physical quantities of practical interest, such as velocity, temperature, and concentration profile, are inspected and presented through tables and graphs. We found that the heat transfer on the surface decreases for the temperature stratification factor as mass transfer increases. Additionally, the fluid velocity increases as the modified Hartmann number increases.
1. Introduction
A large number of examinations on non-Newtonian fluids with applications in many areas including materials science, fluid mechanics, chemistry, and biology have been carried out in recent years. Different studies aimed to identify the mixed convection effects on the squeezed flow of Sutter by fluid in the presence of double stratification. The double stratification of liquid occurs due to the concentration and temperature differences. Thermal stratification happens when two kinds of streams come in to contact with different temperatures. Their temperature distinction makes the colder and heavier water settle at the lower part of the liquid surface, while permitting the hotter and lighter liquid to drift over the cold liquid []. From a modern perspective, numerous applications use the idea of double stratification, for example, heat dismissal from climate nuclear power storing frameworks and sun-based energy as better stratification results in the higher energy execution. Numerous studies have been performed to explore the numerical analysis of double stratified convective flow [,,,]. Waqas et al. [] studied stratified Oldroyd-B nanofluid flow via the homotopy technique. Daniel et al. [] considered double stratification with additional slip effects for nanofluids. Recently, Eswaramoorthi et al. [] studied double-stratification impacts on Williamson liquid for Riga surface. Mutuku and Makinde [] conducted a numerical study of double-stratification effects for the Buongiorno model. Aaiza et al. [] examined energy transfer in a mixed convection MHD flow of nanofluid containing different shapes of nanoparticles. They considered the fluid a channel filled with saturated porous medium. In addition, Hayat et al. [] investigated nanoliquids over an extended surface by incorporating stratified impacts.
The poor temperature conductivity of traditional coolants such as water, crude oil, mineral oil, etc., has limited the cooling capabilities of heat transfer devices. Notably, metals have somewhat high thermal conductivity compared to liquids. Hence, dissipating nanometer-sized metallic particles in liquids is perhaps the best method to further develop heat movement. The concept of nanofluid was introduced by Choi and Eastman [] to address most problems of practical interest. Over the past few centuries, engineers and scientists have successfully investigated nanofluid convective heat transfer [,,,,]. Recently, Rafique et al. [] investigated micropolar nanofluid flow over a slanted surface and portrayed the inclination effect.
Nowadays, numerous issues in different fields of engineering and industry need to be addressed due to their significant applications in daily life, such controlling an engine’s temperature, machine speed, construction, and other scientific uses. The model of micropolar liquid might be used to develop models of the dust or smoke particles in gas or the environment. Unfortunately, these issues or models have some complicated nonlinear terms that are difficult to tackle logically. A few techniques can be utilized to address such problems: a notable technique is the Keller box technique. Rafique et al. [] studied the characteristics of the microrotational effect on heat and mass transport rates via the Keller box scheme. Recently, Koriko et al. [] investigated bioconvection flow by considering nanoparticles and gyrotactic micro-organisms. Mabood et al. [] examined micropolar fluid flow for a moving plate and drawn streamlines. In addition, micropolar fluid flow on a wavy slanted was plate discussed by Srinivasacharya and Ramana [].
In addition to all the key problems experienced with linear extending sheets, the available literature also describes the flow produced via an exponential extending surface as a significant factor in the vast field of engineering and processing. Initially, Magyari and Keller [] started the analysis of flow through an exponentially stretching surface. They studied the energy and mass exchange phenomenon of fluid flow over a surface that is stretched with an exponential velocity. Later, Elbashbeshy [] extended their work for heat transport with the addition of the suction/injection factor. Bidin and Nazar [] numerically investigated the exponential extending surface with the influence of radiation. Hayat et al. [] examined a stretching Riga plate by incorporating variable thickness effects. Shaw et al. [] investigated an extending Riga surface with variable effects. Nadeem et al. [] considered an exponential stretching Riga plate for the nanofluid regime. Moreover, Eid [] discussed the extending Riga surface with the impacts of radiation. Recently, Abbas et al. [] studied nanofluid flow for an exponentially extending Riga surface. The latest work on a stretching Riga plate was performed by Alotaibi and Rafique [] considering mixed convection impacts.
To the best of our knowledge, no previous studies of the micropolar nanofluid flow generated by exponentially stretching Riga plate for double stratification have been reported. The impact of stratification is a significant aspect in energy and mass exchange investigations. Double stratification occurs due to different densities, different temperatures, and different concentrations of liquids. In the phenomenon of energy and mass transport, it is important to analyze the impact of double stratification on flow. The study of mixed convection in a double-stratified medium is a research hotspot due to its significance in nuclear power, solar ponds, geophysical flows etc. []. In this study, we aimed to address such limitations and develop and provide theoretical support for and to further develop the study of non-Newtonian fluids with practical applications. The system of equations was numerically solved using the boundary value problem solver (Keller box), which is available in MATLAB. A direct comparison with the findings in the literature for specific conditions confirmed the accuracy of our current work. This study’s findings will be useful in chemical and biomedical applications, such as breast cancer tumors and human thermal plumes, and other engineering applications.
2. Materials and Methods
In this study, we adopted a 2D-steady micropolar nanofluid with an exponentially stretching sheet, considering double stratification and suction or injection. We assumed that the velocity of the stretching plate has an exponential form, i.e., . The velocities field along the x and y axis are u, and v, respectively. The flow is characterized by velocity, which is governed by a randomly expanding surface. The fluid elements in the micropolar nanofluid have a stronger ability to stay in place before colliding with another fluid molecule, resulting in gyration effects as these molecules spin in the fluid continuum []. The gyration vector in a micropolar nanofluid is an ideal replacement for exhibiting the conjugate effects of heat and mass transport. The Riga plate structure presented in Figure 1, while the physical model of current flow presented in Figure 2. The equations defining the computational domain are provided below.
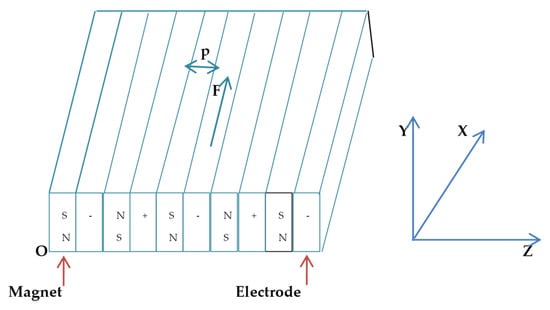
Figure 1.
Physical structure of Riga plate.
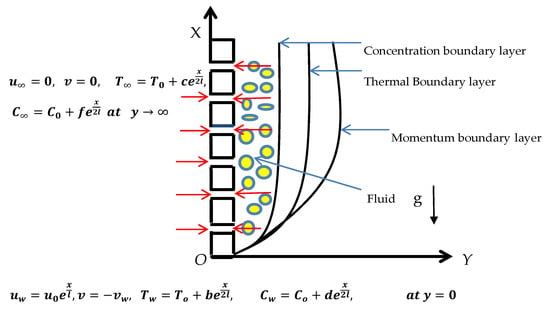
Figure 2.
Geometry of the physical configuration.
The basic equations were developed from []:
The suitable boundary conditions for this flow regime are given as
where
Applying
with the use of Equation (7), Equations (2)–(5) take the above form, and Equation (1) is identically satisfied.
In the previous dimensionless equations, the prime emphasizes differentiation with respect to , and is the fluid’s kinematic viscosity; denotes the modified Hartmann number; Pr is the Prandtl quantity; is the dimensionless parameter; Le is the Lewis quantity; K is the dimensionless vortex viscosity; denotes the local Grashof number denotes the modified Grashof number; , where denotes Brownian motion and deontes thermophoresis variable; and are stratification parameters.
The boundary conditions (6) are changed to:
We signify the following quantities associated with local Nusselt number, local Sherwood number, and skin friction;
The above relation can also be written in the form:
The local Reynolds number is .
3. Results
Numerical simulation was performed to obtain the energy and mass exchange characteristics of the flow field against different parameters. The current investigation incorporated physical parameters such as the Brownian motion parameter ; the thermophoresis parameter , the stratification coefficients , ; the suction parameter ; the Prandtl number ; the material parameter ; the modified Hartmann number and the Lewis number . For the approximate solution of ordinary differential equations that are nonlinear Equations (8)–(11) influenced by boundary conditions (13), we performed a numerical procedure using the Keller box method. Table 1 compares our results with those in the literature, whereas Table 2 presents the impacts of incorporating parameters of energy and mass exchange changes. In this study, w aimed to investigate the heat and mass exchange rates in the presence of double stratification and exponential velocity over a Riga plate. Figure 3 depicts the behavior of velocity field with respect to for numerous variations in the modified Hartmann number . An acceleration was produced in velocity as we increased the strength of . This concurs well with the physics of the problem, because helps the flow phenomenon during flow distribution. The pattern in this figure shows that with increasing strength of , the external electric field strengthened. As a result, the velocity profile increased. In such circumstances, as the magnetic strength increased, there was an equivalent increase in the electromagnetic field. Moreover, the Lorentz powers prompted by Riga plate, corresponding to the surface, produced more surface strain; accordingly, the liquid speed increased. Figure 4 presents the impact of suction/injection factor on the velocity field. We found that the boundary layer thickness decreased with the increase in while the opposite behavior was observed in the case of injection .

Table 1.
Comparison of our result with those previously published when .

Table 2.
Values of , , and .
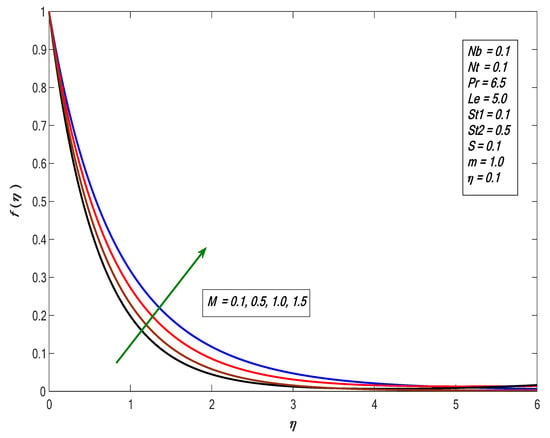
Figure 3.
Impact of the modified Hartmann number M on velocity profiles against .
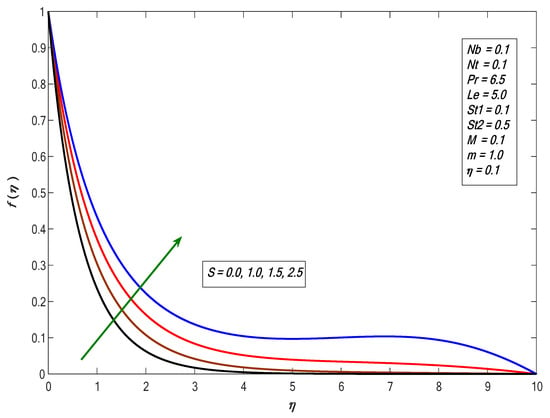
Figure 4.
Impact of suction/injection on velocity profiles against .
Figure 5 and Figure 6 show that the temperature profiles increased with increasing values of and respectively. As Brownian motion is the random movement of the fluid particles, in return, more heat was generated and temperature distribution was enhanced. If the particles had kinetic energy, this would lead to a collision of particles, because thermophoresis causes tiny particles to move away from hotspots to cold surfaces. Figure 7 depicts the effects of thermal stratification on the temperature profile, showing that the temperature profile decreased for increases in , since increases in decreased surface temperature and decreased the thickness of the thermal boundary layer. Figure 8 displays the behavior of , where the concentration profile declines as the value increases. Figure 9 shows the effect of : the concentration distribution increases and increase the value of . Figure 10 shows the result of the stratified parameter on the concentration profile, where the concentration profile decreases with the growth in . It is clear that increases in reduce the concentration difference between the liquid and sheet.
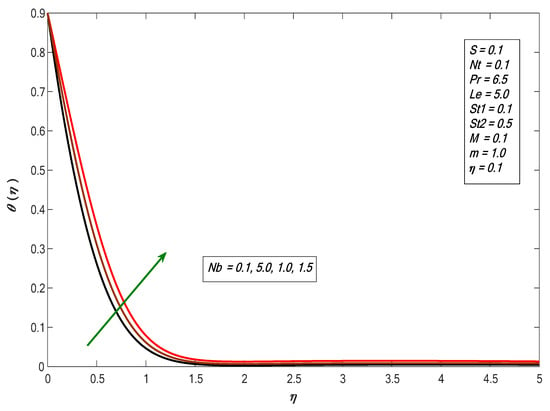
Figure 5.
Impact of Brownian motion on temperature profiles against .
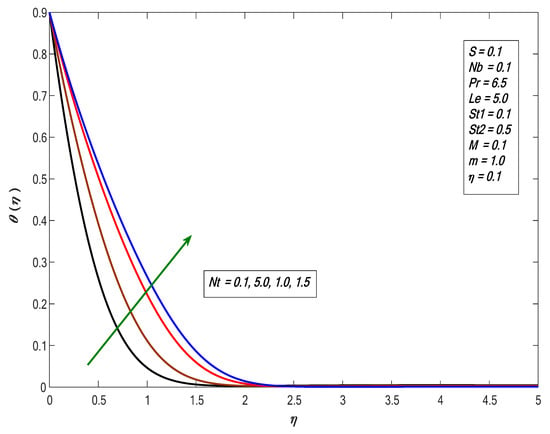
Figure 6.
Impact of the thermophoresis factor on temperature profiles against .
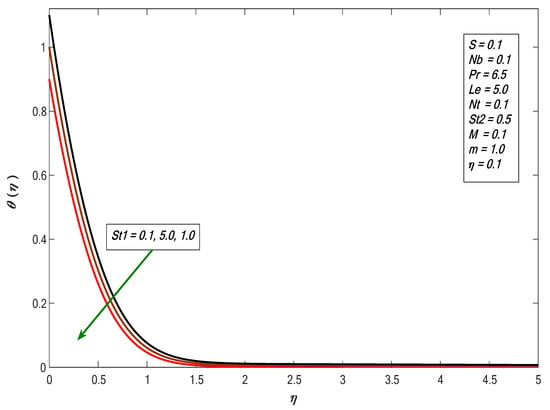
Figure 7.
Impact of stratification on temperature profiles against .
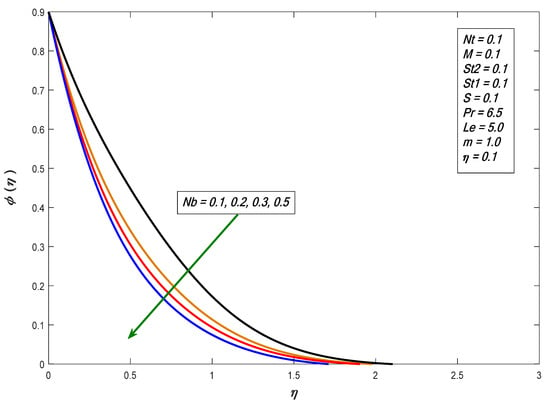
Figure 8.
Impact of Brownian motion on concentration profiles against .
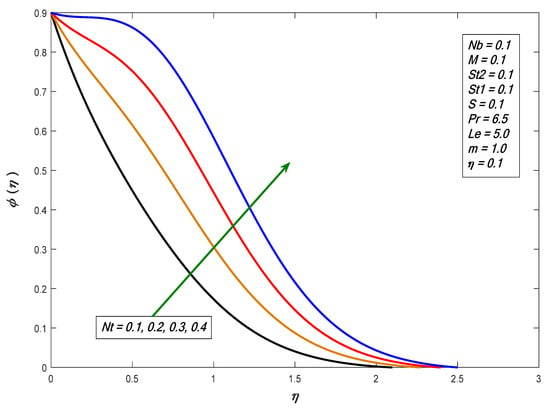
Figure 9.
Impact of the thermophoresis factor on concentration profiles against .
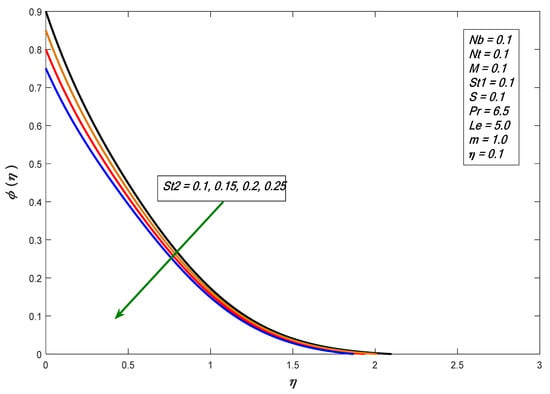
Figure 10.
Impact of stratification on concentration profiles against .
4. Conclusions
In this study, we addressed stratified micropolar nanofluid flow over an exponentially stretchable Riga surface. The Keller box scheme was applied to obtain the results of the modeled flow equations. From this analysis, our most important findings are summarized as:
- The thermal stratification factor decreases the energy exchange rate while the concentration stratification factor increases the mass exchange rate.
- Energy and mass transport rates are directly related to the local and modified Grashof numbers.
- The dimensionless factor () shows and inverse relationship with the energy and mass exchange rate.
- The temperature profile increases while the concentration profile decreases with increasing .
- As increases, both temperature and concentration increase.
Author Contributions
Formulation done by K.R. and H.A. Problem solved by N.I. Numerical computations and results discussion is done by I.K., K.R. and H.A. All authors contributed equally in writing manuscript. Revision done by K.R. and I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful of the Taif University research supporting project number (TURSP-2020/304), Taif University, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| fluid concentration | |
| Skin friction | |
| Specific heat at constant pressure | |
| Surface volume fraction | |
| Ambient nanoparticle volume fraction | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient | |
| Similarity function for velocity | |
| Gravitational acceleration | |
| Micro inertia per unit mass | |
| Material parameter | |
| Thermal conductivity | |
| Vertex viscosity | |
| Reference length | |
| Lewis number | |
| Modified Hartmann number | |
| Nondimensional angular velocity | |
| Brownian motion parameter | |
| Thermophoretic parameter | |
| Nusselt number | |
| Prandtl number | |
| Reynolds number | |
| Sherwood number | |
| Thermal stratification | |
| Concentration stratification | |
| Fluid temperature | |
| Wall temperature | |
| Velocity in the direction | |
| Wall Velocity | |
| Ambient velocity | |
| Velocity in the direction | |
| Cartesian coordinate | |
| Thermal diffusivity | |
| Concentration expansion coefficient | |
| Spin gradient viscosity | |
| Modified Grashof number | |
| Local Grashof number | |
| Similarity independent variable | |
| Wall velocity | |
| Dynamic viscosity | |
| Electric conductivity | |
| Dimensionless temperature | |
| Ambient condition | |
| Condition at the wall | |
| Differentiation with respect to |
References
- Sohn, H.; Yang, J.Y.; Lee, H.S.; Park, B.J. Sensing solutions for assessing and monitoring of nuclear power plants (NPPs). In Sensor Technologies for Civil Infrastructures; Woodhead Publishing: Sawston, UK, 2014; pp. 605–637. [Google Scholar]
- Khashi’Ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Dual Stratified Nanofluid Flow Past a Permeable Shrinking/Stretching Sheet Using a Non-Fourier Energy Model. Appl. Sci. 2019, 9, 2124. [Google Scholar] [CrossRef] [Green Version]
- Yasin, M.H.M.; Arifin, N.M.; Nazar, R.; Ismail, F.; Pop, I. Mixed Convection Boundary Layer Flow Embedded in a Thermally Stratified Porous Medium Saturated by a Nanofluid. Adv. Mech. Eng. 2013, 2013, 121943. [Google Scholar] [CrossRef] [Green Version]
- Hussain, T.; Hussain, S.; Hayat, T. Impact of double stratification and magnetic field in mixed convective radiative flow of Maxwell nanofluid. J. Mol. Liq. 2016, 220, 870–878. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. Eng. 2017, 71, 307–314. [Google Scholar] [CrossRef]
- Waqas, M.; Khan, M.I.; Hayat, T.; Alsaedi, A. Stratified flow of an Oldroyd-B nanoliquid with heat generation. Results Phys. 2017, 7, 2489–2496. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Bahar, A. Unsteady EMHD dual stratified flow of nanofluid with slips impacts. Alex. Eng. J. 2020, 59, 177–189. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Alessa, N.; Sangeethavaanee, M.; Namgyel, N. Numerical and Analytical Investigation for Darcy-Forchheimer Flow of a Williamson Fluid over a Riga Plate with Double Stratification and Cattaneo-Christov Dual Flux. Adv. Math. Phys. 2021, 2021, 1867824. [Google Scholar] [CrossRef]
- Mutuku, W.N.; Makinde, O.D. Double stratification effects on heat and mass transfer in unsteady MHD nanofluid flow over a flat surface. Asia Pac. J. Comput. Eng. 2017, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Aaiza, G.; Khan, I.; Shafie, S. Energy Transfer in Mixed Convection MHD Flow of Nanofluid Containing Different Shapes of Nanoparticles in a Channel Filled with Saturated Porous Medium. Nanoscale Res. Lett. 2015, 10, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Ullah, I.; Alsaedi, A.; Waqas, M. Double stratfied flow of nanofluid subject to temperature based thermal conductivity and heat source. Therm. Sci. 2020, 24, 1157–1171. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sheykholeslami, F.B.; Khoshhal, S.; Mola-Abasia, H.; Ganji, D.D.; Rokni, H.B. Effect of magnetic field on Cu–water nanofluid heat transfer using GMDH-type neural network. Neural Comput. Appl. 2014, 25, 171–178. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. Forced convection in a parallel-plate channel occupied by a nanofluid or a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2014, 70, 430–433. [Google Scholar] [CrossRef]
- Wang, R.-J.; Du, J.; Zhu, Z. Effects of wall slip and nanoparticles’ thermophoresis on the convective heat transfer enhancement of nanofluid in a microchannel. J. Therm. Sci. Technol. 2016, 11, JTST00017. [Google Scholar] [CrossRef] [Green Version]
- Rafique, K.; Alotaibi, H.; Nofal, T.A.; Anwar, M.I.; Misiran, M.; Khan, I. Numerical Solutions of Micropolar Nanofluid over an Inclined Surface Using Keller Box Analysis. J. Math. 2020, 2020, 6617652. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Asjad, M.I. Energy and mass transport of micropolar nanofluid flow over an inclined surface with Keller-Box simulation. Heat Transf. 2020, 49, 4592–4611. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1379. [Google Scholar] [CrossRef] [Green Version]
- Koriko, O.K.; Shah, N.A.; Saleem, S.; Chung, J.D.; Omowaye, A.J.; Oreyeni, T. Exploration of bioconvection flow of MHD thixotropic nanofluid past a vertical surface coexisting with both nanoparticles and gyrotactic microorganisms. Sci. Rep. 2021, 11, 16627. [Google Scholar] [CrossRef] [PubMed]
- Mabood, F.; Shamshuddin, M.D.; Mishra, S.R. Characteristics of thermophoresis and Brownian motion on radiative reactive micropolar fluid flow towards continuously moving flat plate: HAM solution. Math. Comput. Simul. 2022, 191, 187–202. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Sita Ramana, K. Mixed convection of a nanofluid past an inclined wavy surface in the presence of gyrotactic microorganisms. Heat Transf. 2021, 50, 8579–8597. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over an exponentially stretching continuous surface with suction. Arch. Mech. 2001, 53, 643–651. [Google Scholar]
- Bidin, B.; Nazar, R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur. J. Sci. Res. 2009, 33, 710–717. [Google Scholar]
- Hayat, T.; Abbas, T.; Ayub, M.; Farooq, M.; Alsaedi, A. Flow of nanofluid due to convectively heated Riga plate with variable thickness. J. Mol. Liq. 2016, 222, 854–862. [Google Scholar] [CrossRef]
- Shaw, S.; Nayak, M.K.; Makinde, O.D. Transient rotational flow of radiative nanofluids over an impermeable Riga plate with variable properties. In Defect and Diffusion Forum; Trans Tech Publications Ltd.: Freinbach, Switzerland, 2018; Volume 387, pp. 640–652. [Google Scholar]
- Nadeem, S.; Malik, M.Y.; Abbas, N. Heat transfer of three-dimensional micropolar fluid on a Riga plate. Can. J. Phys. 2020, 98, 32–38. [Google Scholar] [CrossRef]
- Eid, M.R. Thermal Characteristics of 3D Nanofluid Flow over a Convectively Heated Riga Surface in a Darcy–Forchheimer Porous Material with Linear Thermal Radiation: An Optimal Analysis. Arab. J. Sci. Eng. 2020, 45, 9803–9814. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Saleem, S.; Issakhov, A. Transportation of modified nanofluid flow with time dependent viscosity over a Riga plate: Exponentially stretching. Ain Shams Eng. J. 2021, 12, 3967–3973. [Google Scholar] [CrossRef]
- Alotaibi, H.; Rafique, K. Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate. Crystals 2021, 11, 1315. [Google Scholar] [CrossRef]
- Ibrahim, W.; Makinde, O.D. The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput. Fluids 2013, 86, 433–441. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).