Abstract
This comparative research investigates the influence of a flexible magnetic flux and a chemical change on the freely fluid motion of a (MHD) magneto hydrodynamic boundary layer incompressible nanofluid across an exponentially expanding sheet. Water and ethanol are used for this analysis. The temperature transmission improvement of fluids is described using the Buongiorno model, which includes Brownian movement and thermophoretic distribution. The nonlinear partial differential equalities governing the boundary layer were changed to a set of standard nonlinear differential equalities utilizing certain appropriate similarity transformations. The bvp4c algorithm is then used to tackle the transformed equations numerically. Fluid motion is slowed by the magnetic field, but it is sped up by thermal and mass buoyancy forces and thermophoretic distribution increases non-dimensional fluid temperature resulting in higher temperature and thicker boundary layers. Temperature and concentration, on the other hand, have the same trend in terms of the concentration exponent, Brownian motion constraint, and chemical reaction constraint. Furthermore, The occurrence of a magnetic field, which is aided by thermal and mass buoyancies, assists in the enhancement of heat transmission and wall shear stress, whereas a smaller concentration boundary layer is produced by a first-order chemical reaction and a lower Schmidt number.
1. Introduction
The learning of flow and temperature transmission across a stretched surface has piqued the interest of many investigators over the past few decades due to its various important engineering applications. Initially, Crane [] investigated the boundary layer flow overstretched surfaces theoretically. Das [] explained the slip movement of nanofluid above a porous enlarging surface. Later on, a slew of researchers [,,,,] has stepped up to contribute to various areas of movement and temperature transmission problems concerning stretched surfaces.
Fluids containing nanoparticles of 100 nanometers or smaller in size, like oxides and metals, as well as traditional base fluids including water, kerosene oil, are called nanofluid. Because nano-sized particles have a higher temperature transfer rate than base fluids. They are utilized as efficient coolants in electronics and nuclear plants, lubricants, etc. Choi [] made an ironic start by studying experimentally and revealing to the public the increase of temperature conductivity of liquids using nanoparticles. Hussain et al. [] discussed the nanofluid flow over the rotating cone. Makinde and Aziz [] utilized the convective surface settings to illustrate the frontier layer movement of a nanofluid across a stretched surface. The boundary-layer movement of nanofluids across stretched sheets was established by Khan and Pop []. Buongiorno [] later developed a heterogeneous symmetry model to represent the temperature transmission increase of nanofluid caused by Brownian movement and thermophoretic distribution of nanoparticles. Hussain et al. [] discussed the multi-based nanofluid flow over an embrittled cone. Nayak et al. [] have examined the 3D (three-dimensional) MHD movement of nanofluid across a porous linear expanding surface with free convection with the effect of heat radiation, taking into consideration realistic factors.
Many researchers [,,,,,] have investigated the nanofluid with MHD movement and temperature transmission possessions in different physical problems until now. This is owing to important uses in industrial processes, such as its wide variety of biological applications, including wound therapy and sterilization. The movement and temperature transmission features of magneto-nanofluid were addressed by Bahiraei and Hangi []. Hsiao [] elaborated the micro polar nanofluid flow with different effects towards a stretching sheet. Akber et al. [] developed a computational method for modeling MHD transportation of nanofluids via a perpendicular stretching sheet that took into account nonlinear temperature-dependent viscosity and buoyancy possessions. Through an exponential enlarging sheet, Nadeem et al. [] examined the thermo-physical characteristics of water-based nanofluids. Bahiraei [] stressed the need for studying nanoparticle dispersion concerning effective variables on particle movement and phenomenological coefficients using Lagrangian simulation.
The chemical reaction is crucial because, among other things, it influences the design of chemical processing facilities, food & beverages, chillers, fog production, and distribution. In light of the aforementioned uses, numerous researchers have researched and published their findings on the impact of chemical reactions on the movement of temperature and/or mass transmission through various faces. The stimulus of chemical processes on MHD immobility point movement of water-based in a permeable medium driven by heat radiation and viscid intemperance was studied by Mabood et al. []. They discovered that increasing the chemical reaction constraint improves the non-dimensional combination profiles of water-based nanofluids in their research. They also discovered that when the rate of chemical reactions rises, so does the rate of mass transfer. The MHD movement of a viscoelastic fluid across a permeable stretched sheet was described by Nayak []. Sheikholeslami & Sadoughi [] deliberated the Mesoscopic method for MHD nanofluid considering various shapes of nanoparticles. The rotational flow of nanofluid across a nonlinear extending surface was mathematically deliberated by Mushtaq et al. []. MHD immobility point movement was reported by Kahn et al. []. Bhatti and Rashidi [] investigated the thermal transmission and effects of heat radiation on non-Newtonian nanofluid. Sui et al. [] reported the Cattaneo–Christov distribution in viscoelastic nanofluid. The MHD movement of nanofluid across a radiative nonlinear enlarging sheet was presented by Imtiaz et al. []. Some of the preceding research’ applications can be viewed in this way via [,,]. Recently, Hussain et al. [] made an extra ordinary research for Two-Phase Nanofluid in Brittle Medium and heat transmission analysis. Sulochana et al. [] numerically investigated the thermophoresis and Brownian movement for MHD flow due to a rotational cone. Raju et al. [] explained the Jeffrey (MHD) nanofluid movement over a cone with chemical reaction. Makinde et al. [] described the stagnation point movement of MHD chemically reacting radiative heat.
According to the above-mentioned review of the literature, no one has investigated the stimulus of a flexible transversal magnetic strength and chemical reaction on unrestricted convection of a nano fluid movement via an exponentially enlarging surface using Brownian movement and thermophoretic distribution till now. As a result, the novelty of our research is to look comparatively for water and ethanol due to many industrial applications e.g., manufacturing of plastics, polishes, and cosmetics. Similarly ethanol is used in medicine as a topical anti-infective. The impact of a variable transversal magnetic strength and a chemical reaction in a free convective nanofluid flowing above an exponential extending surface is discussed for both fluids. The leading boundary layer equalities are numerically tackled using the bvp4c algorithm at Matlab. The effects of velocity streamlines, non-dimensional concentration, temperature and velocity profiles of nanoparticles, alongside the skin resistance, Nusselt and Sherwood numbers, are explored and illustrated in graphs, and tables.
2. Problem Formulation
Above an exponentially stretching surface, we examine a steady three dimensional (3D) incompressible boundary layer flow of electrically conducing magneto hydrodynamic nanofluid. Assume that an a variable magnetic field is applied parallel to the . It is expected that the persuaded magnetic and electric fields would be ignored. Owing to the existence of binary significant velocity-slip factors, such as Brownian movement and thermophoretic distribution of nanoparticles, the Buongiorno model [] is used in this work to explain the analogues increase of temperature transmission. There are the following main equations for mass, momentum, energy, and nanoparticle concentration:
The following are the corresponding frontier conditions for the current problem:
here and are velocity components alongside and -directions respectively. is kinematics viscosity, is gravitational acceleration, is thermal expansion (of volumetric concentration of), is mass expansion (of volumetric concentration). is the of surrounding temperature, is nanoparticle concentration at the free stream, the electrical conductiviness of fluid is . is a consistent magnetic field, is the density of the fluid, is the temperature distribution of fluid, is a proportion between effective heat capacitance of nanoparticle material and heat capability of fluid, is Brownian movement constant, is thermophoretic distribution constant, is chemical reaction constraint, are fixed velocities, is locus length, is the temperature at the surface and is nanoparticle concentration over the surface of the sheet.
To make the investigation easier, the boundary layer equalities are rendered to dimensionless form utilizing the following similarity transformation:
here are temperature and concentration exponents respectively. By using Equation (8) in Equations (1)–(5) we satisfying the continuity equation and gain the following transformed equations:
With transformed boundary conditions:
here
here are surface stretching velocity proportion constraint, Prandtl number, temperature and mass Grashof number, Schmidt number, Brownian movement, and thermophoresis constraints respectively. The Hartman coefficient and () which is defined as: and respectively. Temperature convective constraint along and is defined as: and respectively. The mass convective constraints in x-direction and y-direction is defined as: and respectively. The local Reynold number in is defined as: and respectively. Skin frictions in x-direction and y-direction are defined as:
here and are wall shear stresses in and directions respectively.
The non-dimensional forms of Equations (15) and (16) can be written as:
The Nusselt and Sherwood coefficients are articulated as:
here is wall heat flux and is mass flux from extending sheet respectively. The non-dimensional form of Equations (19) and (20) is written as:
3. Discussion and Graphical Results
The boundary conditions are specified in Equation (13) and the system of linked nonlinear differential Equations (9)–(12) is solved numerically using the bvp4c algorithm. This technique converts higher-order ordinary differential equations (ODEs) into first-order ODEs and is then tackled numerically at MATLAB.
The current work looked at the impact of a changing perpendicular magnetic strength and a chemical reaction on the free convective movement of fluids across an exponentially extending surface. Additionally, the Buongiorno model is utilized to examine the impact of Brownian movement and thermophoretic distribution. The bvp4c algorithm is employed to tackle the similarity transformed governing boundary layer equalities and related converted boundary conditions. In the tables below and graphs, the acquired results are presented. The configuration of the problem is presented in the following (see Figure 1).
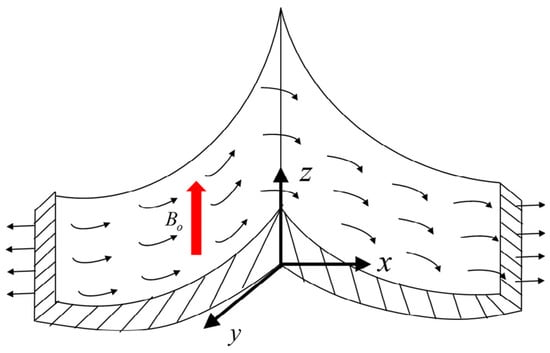
Figure 1.
Exponentially stretching surface MHD flow.
3.1. Velocity Profiles
The following figures show the effects of flow constraints on non-dimensional velocity, temperature, concentration profiles of nanoparticles. For varying intensity of the Hartman number , the fluctuation of velocity constituents alongside the and is shown in Figure 2a,b. It is clear that velocity constitutes and gain deceleration by increasing which results in a thinner boundary layer for both fluids. This is because the electromagnetic contact among the magnetic field strength and the electrically conducting fluid produces a resisting Lorentz force, which decelerates the fluid’s velocity across the boundary layer area. To put it another way, if magnetic field is not applied, there would be no contact between the electrically conducting fluid and the magnetic field, and therefore, there will be no velocity slow down and the velocity would remain constant. It is said to have arrived at the deduction that the existence of alters the fluid velocity significantly. The influence of temperature convective constraint is shown in Figure 3a,b. Basically, thermal convection is the transfer of heat related to conduction and motion of fluid over a given body. So, when thermal convective parameter increases, both velocities and accelerate. Convective mass transfer is the movement of material related to the motion of a fluid. Therefore, when the mass convective parameter increases the velocity of the fluid also increases. This behavior can be noted for mass convective parameter in Figure 4a,b. We concluded from this discussion that thermal convective constraint and mass convective constraint both have direct relation with fluid’s velocity constitutes and .
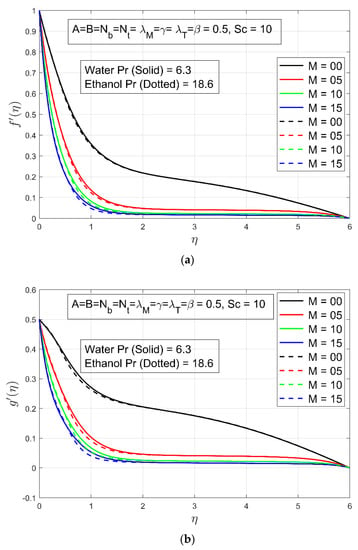
Figure 2.
(a) The effect of M on the velocity profile ; (b) The effect of on the velocity profile .
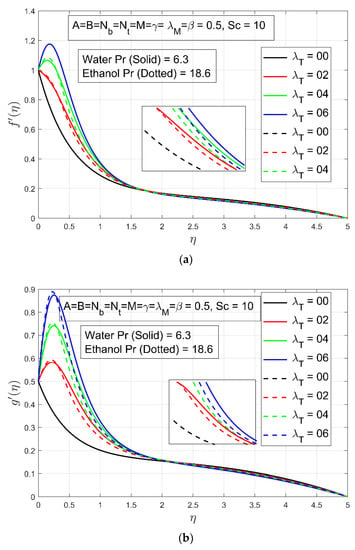
Figure 3.
(a) The effect of on velocity profile ; (b) The effect of on velocity profile .
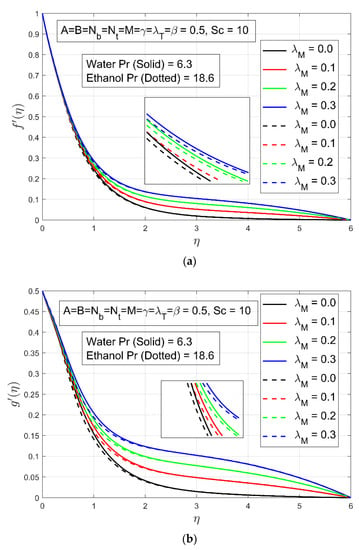
Figure 4.
(a) The effect of on velocity profile ; (b) The effect of on velocity profile .
3.2. Temperature Profile
The effect of Hartmann number or magnetic field constraint , temperature/heat exponent and thermophoresis constraint for temperature profile is presented in the following Figures. The essential conclusion that can be drawn from Figure 5a is that the temperature rises as the Hartmann number rises. The sole explanation about this phenomenon is because an increment in generates a rise in electromagnetic force, which restricts liquid motion, causing the temperature to rise and a denser thermal boundary layer to form. In reality, the fluid temperature in the flow field could not be increased if there was no magnetic field. So, magnetic field constraint and temperature profile have direct relation to each other. It’s worth noting that, just as the fluid temperature rises as rises, the temperature of the liquid rises as the thermophoresis constraint rises. This is because thermophoretic distribution tends to a rise in the non-dimensional fluid temperature, increasing the fluid’s thermal resistance (see Figure 5b). This phenomenon is caused by the temperature gradient. As the thermophoresis constraint increases, the particles of fluid move towards the high energy level leaving the colder region and the temperature profile rises. In this way thermophoresis constraint have direct relation with temperature profile. We also argue that in Figure 5c, the temperature exponent , when compared to and , exhibits the opposite tendency on temperature profiles. The temperature exponent decays the temperature profile decays as the value of increases. So we arrived at the conclusion that temperature exponent have inverse relation with temperature profile.
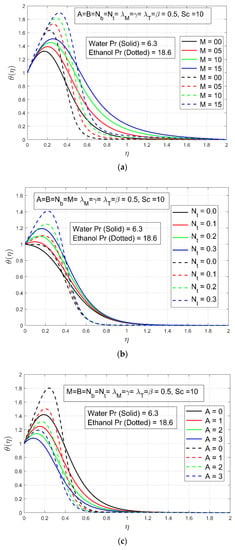
Figure 5.
(a) The effect of on temperature profile ; (b) The effect of on temperature profile ; (c) The effect of on temperature profile .
3.3. Concentration Profile
In terms of concentration profiles, the following Figures shows the variations in concentration constitute for dissimilar values of the thermophoresis constraint , the concentration exponent , and the chemical reaction constraint , as well as the variations in the thermal Brownian movement constraint , the convective constraint , and the Schmidt number . The effect of thermophoresis constraint and Brownian motion constraint can be seen in Figure 6a. The concentration constitute decreases with rising thermophoresis constraint and Brownian motion constraint . The frontier layer thickness expands in the case of the thermophoresis constraint as compared to Brownian motion constraint . We can to conclude that thermophoresis constraint and Brownian motion constraint have inverse relation with the concentration profile. The effect of concentration exponent and thermal convective parameter can be noted in Figure 6b. The concentration profile get deceleration by rising the concentration exponent and thermal convective parameter . So, concentration profile have inverse relation with concentration exponent and thermal convective parameter . The impact of Schmidt number and chemical reaction constraint is displayed in Figure 6c. It can be noted that enlarge change in shows a decay in the nano-particles concentration. The change in Schmidt number gets lower solutal transmission which notify a reduced nanofluid concentration. The concentration profile also decays as and chemical reaction parameter boots up. The reason behind this phenomenon is that when increases the particles take part in the chemical reaction and overall concentration profile decreases. So, chemical reaction parameter and Schmidt number have inverse relation with the concentration constitute.
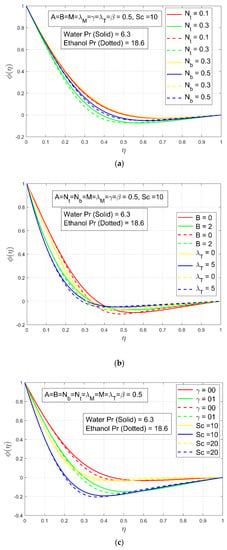
Figure 6.
(a) The effect of and on concentration profile ; (b) The effect of and on concentration profile ; (c) The effect of and on concentration profile .
3.4. Skin Friction
Table 1 and Table 2 show the manners of skin resistance for both fluids with the effect of , and in both . These tables show that in the absence and presence of the magnetic field. Skin friction and therefore wall shear pressure decrease as the ratio parameter increases. The step-size increment in velocity ratio and Hartman number has decreased the skin friction in x-direction for both water and ethanol case. The skin friction for both cases although has decreased but very minor gradual decline is observed with increment in both velocity ratio and temperature convective parameter (See Table 1). The skin friction in y-direction has been observed decreasing with an increment in ratio of surface velocity, Hartman number and temperature convective parameters (See Table 2). In both tables the skin friction decreases rapidly in case of water as compared to ethanol . The reason is that low number fluids behave like Newtonian fluids.

Table 1.
Skin friction for different values when .

Table 2.
Skin friction for different values when .
3.5. Nusselt and Sherwood Number
Table 3 and Table 4 shows the manners of Nusselt and Sherwood number under the effect of thermophoresis constraint , Schmidt number , temperature convective constraint , and mass convective constraint . As thermophoresis constraint rises, the Nusselt number decays in the existence of mass and thermal buoyancies within the thermal boundary layer. Increases in thermal buoyancy assist to decay temperature and increase in mass buoyancy resulting in a rise wall temperature gradient, as seen by the data in Table 3. It is noted low Prandtl liquids have low thermal distribution, high Prandtl liquid have high thermal distribution overstretched surface. It is noteworthy to point out that Nusselt numbers associated with various values are quite comparable to one another, since a change in results in a substantial change in thermal distribution in the thermal frontier layer. Similarly, as the Schmidt number upsurges, the Sherwood number increases in the existence of mass and thermal buoyancies within the thermal boundary layer. Increases in thermal and mass buoyancies both assist to rise the wall temperature gradient, as seen by the data in Table 4. It is worth noting that Nusselt number decreases rapidly in case of ethanol as compared to water and Sherwood number increases rapidly for water as compared to ethanol.

Table 3.
Nusselt number for both fluids with .

Table 4.
Sherwood number for both fluids with .
4. Conclusions
This article involves the comparative analysis for water and ethanol with different study parameters. Graphs and tables have been used to examine the impact of a changing magnetic strength and a chemical reaction on the free convection movement of an electrically conducting having constant density nano liquid above an exponential expandable surface. The Buongiorno model, which is related to Brownian movement and thermophoretic distribution, is used in this work to improve the heat transmission. The following are the key findings of the recent study:
- The fluid motion is decelerated by the increasing magnetic strength, while heat and mass buoyancy forces boost up the fluid movement, resulting in a larger momentum barrier layer.
- Because of the Prandtl number, magnetic field intensity, and thermophoretic distribution increase fluid temperature owing to a rise in thermal opposition, in the case of ethanol this behavior is noted highly when compared to water.
- In the existence of a magnetic strength, skin resistance reduces in the and directions as the magnitude of the thermal and mass convective parameters increases.
- Increases in the thermophoresis parameter cause concentration to increase.
- Concentration decreases as an upsurge in the concentration exponent, chemical reaction constraint, Brownian movement constraint, thermal convective constraint, and Schmidt number is noted.
- Consistent temperature transference rate observed for water as compared to ethanol.
Author Contributions
Conceptualization, M.A. and A.H. (Azad Hussain); methodology, A.H. (Ali Hassan); software, M.A.; validation, Q.H., A.A. and A.H.I.; formal analysis, M.S.A.; investigation, A.H.A.; resources, A.H. (Ali Hassan); data curation, Q.H.; writing—original draft preparation, M.A.; writing—review and editing, A.A.; visualization, A.H. (Azad Hussain); supervision, M.A. and A.H. (Azad Hussain); project administration, M.A. and A.H. (Ali Hassan); funding acquisition, A.H.I., M.S.A. and A.H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by Taif University researchers supporting project number TURSP-2020/252, Taif University, Taif, Saudi Arabia.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge financial support from the Taif University researchers supporting project number TURSP-2020/252, Taif University, Taif, Saudi Arabia. The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, for the materiel support to this research.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| u, v, w | Velocity constituents in x, y, z direction |
| Electrical conductivity | |
| Thermal and mass expansion coefficients respectively | |
| Thermal conductivity, density, kinematic viscidity and dynamic viscidity of fluid | |
| Thermophoretic diffusion, Brownian motion | |
| Wall shear stress along x and y-direction | |
| Thermal diffusivity | |
| Nusselt number, Sherwood number | |
| Gravational accerlation | |
| Stretching ratio parameter | |
| Temperature and concentration at surface and free stream | |
| Magnetic field | |
| Skin frictions along x and y axis | |
| ,T | Particle volume fraction, temperature of fluid |
| Heat capacitance of fluid and nanoparticles | |
| Prandtl number | |
| Temperature, concentration exponents and Hartmann number | |
| Chemical reaction constraint | |
| Similarity variable, Reynold number | |
| Solid, fluid, nanofluid, wall free stream |
References
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Das, K. Slip flow and convective heat transfer of nanofluids over a permeable stretching surface. Comput. Fluids 2012, 64, 34–42. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Alshehri, N.A. Heat Transmission of Engine-Oil-Based Rotating Nanofluids Flow with Influence of Partial Slip Condition: A Computational Model. Energies 2012, 14, 3859. [Google Scholar] [CrossRef]
- Hussain, A.; Elkotb, M.A.; Arshad, M.; Rehman, A.; Sooppy Nisar, K.; Hassan, A.; Saleel, C.A. Computational Investigation of the Combined Impact of Nonlinear Radiation and Magnetic Field on Three-Dimensional Rotational Nanofluid Flow across a Stretchy Surface. Processes 2021, 9, 1453. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Ahmad, H.; Ishan, A. Three-Dimensional Water-Based Magneto-Hydrodynamic Rotating Nanofluid Flow over a Linear Extending Sheet and Heat Transport Analysis: A Numerical Approach. Energies 2021, 14, 5133. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Unsteady three-dimensional MHD-boundary-layer flow due to the impulsive motion of a stretching surface. Acta Mech. 2001, 146, 59–71. [Google Scholar] [CrossRef]
- Nadeem, S.; Ur Rehman, A.; Mehmood, R.; Adil Sadiq, M. Partial Slip effects on a rotating flow of two phase nano fluid over a stretching surface. Curr. Nanosci. 2014, 10, 846–854. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Argonne, IL, USA, 1995. [Google Scholar]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud. Therm. Eng. 2021, 27, 101244. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Arshad, M.; Rehman, A.; Matoog, R.T.; Abdeljawad, T. Numerical simulation and thermal enhancement of multi-based nanofluid over an embrittled cone. Case Stud. Therm. Eng. 2021, 28, 101614. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Pandey, V.S.; Khan, Z.H.; Tripathi, D. 3D free convective MHD flow of nanofluid over permeable linear stretching sheet with thermal radiation. Powder Technol. 2017, 315, 205–215. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Arshad, M. Comsolic solution of an elliptic cylindrical compressible fluid flow. Sci. Rep. 2021, 11, 20030. [Google Scholar] [CrossRef]
- Zhou, C.J.; Abidi, A.; Shi, Q.H.; Khan, M.R.; Rehman, A.; Issakhov, A.; Galal, A.M. Unsteady radiative slip flow of MHD Casson fluid over a permeable stretched surface subject to a non-uniform heat source. Case Stud. Therm. Eng. 2021, 26, 101141. [Google Scholar] [CrossRef]
- Mustafa, M. MHD nanofluid flow over a rotating disk with partial slip effects: Buongiorno model. Int. J. Heat Mass Transf. 2017, 108, 1910–1916. [Google Scholar] [CrossRef]
- Bahiraei, M. Effect of particle migration on flow and heat transfer characteristics of magnetic nanoparticle suspensions. J. Mol. Liq. 2015, 209, 531–538. [Google Scholar] [CrossRef]
- Hussain, A.; Rehman, A.; Nadeem, S.; Khan, M.R.; Issakhov, A. A Computational Model for the Radiated Kinetic Molecular Postulate of Fluid-Originated Nanomaterial Liquid Flow in the Induced Magnetic Flux Regime. Math. Probl. Eng. 2021, 2021, 6690366. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H.; Nadeem, S. The combined effects of slip and convective boundary conditions on stagnation-point flow of CNT suspended nanofluid over a stretching sheet. J. Mol. Liq. 2014, 196, 21–25. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Bég, O.A. A numerical study of magnetohydrodynamic transport of nanofluids over a vertical stretching sheet with exponential temperature-dependent viscosity and buoyancy effects. Chem. Phys. Lett. 2016, 661, 20–30. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet. Alex. Eng. J. 2014, 53, 219–224. [Google Scholar] [CrossRef] [Green Version]
- Bahiraei, M. Studying nanoparticle distribution in nanofluids considering the effective factors on particle migration and determination of phenomenological constants by Eulerian–Lagrangian simulation. Adv. Powder Technol. 2015, 26, 802–810. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S.; Rashidi, M.M.; Momoniat, E.; Freidoonimehr, N.J.A.P.T. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 742–749. [Google Scholar] [CrossRef]
- Nayak, M.K. Chemical reaction effect on MHD viscoelastic fluid over a stretching sheet through porous medium. Meccanica 2016, 51, 1699–1711. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sadoughi, M. Mesoscopic method for MHD nanofluid flow inside a porous cavity considering various shapes of nanoparticles. Int. J. Heat Mass Transf. 2017, 113, 106–114. [Google Scholar] [CrossRef]
- Mushtaq, A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study for rotating flow of nanofluids caused by an exponentially stretching sheet. Adv. Powder Technol. 2016, 27, 2223–2231. [Google Scholar] [CrossRef]
- Khan, W.A.; Makinde, O.D.; Khan, Z.H. Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat. Int. J. Heat Mass Transf. 2016, 96, 525–534. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liq. 2016, 221, 567–573. [Google Scholar] [CrossRef]
- Sui, J.; Zheng, L.; Zhang, X. Boundary layer heat and mass transfer with Cattaneo–Christov double-diffusion in upper-convected Maxwell nanofluid past a stretching sheet with slip velocity. Int. J. Therm. Sci. 2016, 104, 461–468. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A. Flow of magneto nanofluid by a radiative exponentially stretching surface with dissipation effect. Adv. Powder Technol. 2016, 27, 2214–2222. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A. Electrothermal transport of nanofluids via peristaltic pumping in a finite micro-channel: Effects of Joule heating and Helmholtz-Smoluchowski velocity. Int. J. Heat Mass Transf. 2017, 111, 138–149. [Google Scholar] [CrossRef]
- Akbar, N.S.; Abid, S.A.; Tripathi, D.; Mir, N.A. Nanostructures study of CNT nanofluids transport with temperature-dependent variable viscosity in a muscular tube. Eur. Phys. J. Plus 2017, 132, 110. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Hussain, A.; Haider, Q.; Rehman, A.; Abdussattar, A.; Malik, M.Y. A New Heat Dissipation Model and Convective Two-Phase Nanofluid in Brittle Medium Flow over a Cone. Math. Probl. Eng. 2021, 2021, 6688747. [Google Scholar] [CrossRef]
- Sulochana, C.; Ashwinkumar, G.P.; Sandeep, N. Numerical investigation of chemically reacting MHD flow due to a rotating cone with thermophoresis and Brownian motion. Int. J. Adv. Sci. Technol. 2016, 86, 61–74. [Google Scholar] [CrossRef]
- Raju, C.S.; Jayachandra Babu, M.; Sandeep, N. Chemically reacting radiative MHD Jeffrey nanofluid flow over a cone in porous medium. In International Journal of Engineering Research in Africa; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2016; Volume 19, pp. 75–90. [Google Scholar]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Stagnation point flow of MHD chemically reacting nanofluid over a stretching convective surface with slip and radiative heat. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 695–703. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).