Abstract
In loop heat pipes (LHPs), wick materials and their structures are important in achieving continuous heat transfer with a favorable distribution of the working fluid. This article introduces the characteristics of loop heat pipes with different wicks: (i) sintered stainless steel and (ii) ceramic. The evaporator has a flat-rectangular assembly under gravity-assisted conditions. Water was used as a working fluid, and the performance of the LHP was analyzed in terms of temperatures at different locations of the LHP and thermal resistance. As to the results, a stable operation can be maintained in the range of 50 to 520 W for the LHP with the stainless-steel wick, matching the desired limited temperature for electronics of 85 °C at the heater surface at 350 W (129.6 kW·m−2). Results using the ceramic wick showed that a heater surface temperature of below 85 °C could be obtained when operating at 54 W (20 kW·m−2).
1. Introduction
Loop heat pipes use a passive two-phase heat transport device in which advantageous characteristics are offered, such as operation against the gravity through the capillary effect and flexible characteristics. They have been widely used in energy applications, spacecraft thermal control, electronic device cooling, and commercial radiators [1]. Zhou [2] fabricated a plate-type loop heat pipe (LHP) and investigated the effect on the heat transfer performance of the LHP with multilayer metal foams as a wick structure. Their flat evaporator’s experimental results show that multilayer copper foams have better performance than nickel foam because of higher thermal conductivity and smaller pore size. Siedel [3] presented a numerical simulation, comparing it with the experimental data of a flat disk-shaped evaporator. The results showed that the larger effective thermal conductivity of wick has an influence on the overall thermal performance of the LHP. However, other researchers, Maydanik [4] and Hoang [5], suggested the wick material, with its lower effective thermal conductivity, to handle the problem of heat leakage. In addition, the hydrophilic effect on the ceramic wick structure is higher than that of stainless steel [6]. Therefore, the performances of stainless-steel wicks and ceramic wicks in LHPs are compared in this study, of which the ceramic wick has much lower thermal conductivity and a higher hydrophilic effect [7,8]. In an LHP system, the porous wicks’ structure is essential because it provides the capillary force for working fluid circulations, a liquid flow path, and a place for phase change heat transfer. Moreover, the porosity effect of the wick materials inside the evaporator is necessarily considered for improving the overall performance of LHPs [9]. Therefore, the porosity, pore diameter, and thermal conductivity of the wicks were measured. The influence of the different wicks on the performance of LHPs is tested with the designed evaporator. Although this is a simple case study of an arrangement with different wicks, the appropriate engineering approach of the calculation procedure related to applying the designed evaporator is presented in this paper. It may improve the understanding of the problems that exist in the LHP evaporator and future LHP systems.
The LHP has some similar operation principles with conventional HPs. The phase changing process is happened in the LHP system and the capillary force is used as the motivation for the operation. Figure 1 demonstrates the scheme of the analytical LHP and an operation cycle diagram.
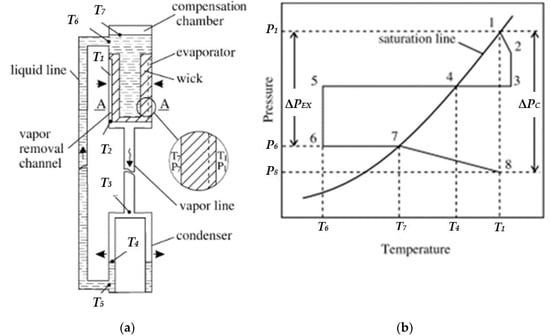
Figure 1.
Principles of LHP: (a) Scheme of analytical LHP. (b) LHP working cycle diagram. Reproduced from [1], Yu.F.Maydanik: 2005.
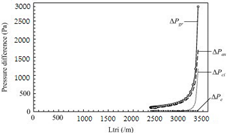
At first, the system is not supplied with heat load. In this case, the liquid stays at Level A–A as an assumption. The liquid found at the evaporator zone (Point 1) and the compensation chamber evaporates from the wick when heat is supplied to the evaporator. The vapor from the evaporator flows. Then, it approches to the heating wall. As a result, the vapor pressure reduces. Simultaneously, the temperature rises a little (Point 2) and is higher than the vapor located at the compensation chamber. In this situation, the wick behaves as a thermal barrier. The vapor which is superheated condition in the evaporator zone cannot pass the compensation chamber through the wick which is saturated due to the force of capillary that keeps the liquid inside. Then, the hydraulic lock is happened in the wick. Afterwards, the vapor continuously flow to the condenser’s inlet (Point 3). When vapor flows from Point 2 to Point 3, both temperature and pressure decrease. The de-superheat, condensation, and subcooled processes happen from Point 3 to Point 5. In this case, there is no pressure loss from Point 3 to Point 5 as an assumption. Because of the pressure loss and the hydrostatic resistance caused by friction, the pressure difference ∆P56 includes the pressure loss. Afterward, the liquid located at Stage 6 flows into the chamber for compensation. Moreover, some parts of the heat load are provided to the evaporator at the expense of the working fluid. This condition is heated to temperature T7. The progress from Point 7 and Point 8 are relative to the filtration of the liquid through the wick into the evaporation place. In this way, the liquid may prove to be superheated. However, its boiling-up does not happen because of its short duration in such a state. The state of the working fluid in the vicinity of the evaporating menisci is represented by Point 8. Pressure loss (dP1–8) corresponds to the total value of pressure losses in all the working-fluid circulation sections. From the above analysis, the function of the LHP is considered in three conditions. At first, the capillary condition is the condition for conventional HPs for an operation.
where
∆Pv is the working fluid’s pressure loss during the vapor state’s motion.
∆Pl is the working fluid’s pressure loss during the liquid state’s motion.
∆Pg is the pressure loss because of the hydrostatic of the liquid column.
∆Pc is the wick capillary pressure.
The second condition is just for the LHP. At the LHP’s startup, it ensures that the liquid is exhibited from the evaporating zone to the compensation chamber.
where
∂P/∂T is the derivative of the saturated line’s slope. Tv is the mean temperature between T1 and T7.
ΔPEX is the total pressure loss in all the sections of the working fluid’s circulation except the wick.
At the third condition, the liquid is prevented from steaming in the liquid line because of the ambient pressure loss and heating.
where
∂P/∂T is the derivative of the saturation line’s slope. Tv is the mean temperature between T4 and T5.
ΔP5–6 is the pressure loss in total from State 5 to State 6.
The working fluid should own a high value of dP/dT to minimize the temperature difference ΔP1–7 and ΔP4–6 from the second condition.
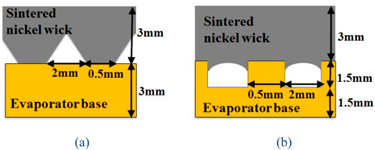
The purpose of the tested LHP in this study is the cooling of electronics such as processors located at Data Centers (DCs). Therefore, the evaporator surface which is heated needs to be flat to improve the evaporator and electronics’ contact quality. Moreover, it will make the heat flux q and distribution of temperature on the active surfaces uniform and eliminate the occurrence of mounting blocks at the evaporator. The investigated evaporator design belongs to the evaporator group with opposite replenishment (EOA). In this design, liquid flows from the top to the bottom surface of the wick structure, as shown in Figure 2a. Figure 2b shows the evaporator with longitudinal replenishment (ELR). The liquid from ELR is provided from the compensation chamber which is located behind the wick. Otherwise, the liquid flows perpendicular to the heat flow rate. The evaporator with opposite replenishment own a simple structure and the liquid absorption surface is large. However, the evaporator can become thicker because the compensation chamber is located above the capillary system. Moreover, the heat leak from the evaporator to the compensation chamber through the wick will be more severe because of the large cross-section of the wick.
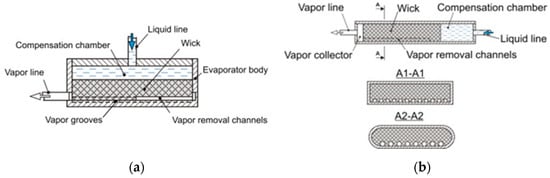
Figure 2.
LHP evaporators (a) Opposite replenishment, (b) Longitudinal replenishment. Reproduced from [10], Y.F.Maydanik: 2014.
The investigated evaporator has two parts: the vapor collector and the wick’s space and compensation chamber. The copper plate is used for the separation between two elements. The brazing method is used to fix them. Additionally, to install the thermocouples, a hole with a 1-mm diameter and 22.5 mm for the length was fabricated at the evaporator’s base. The heating block’s top surface and the evaporator’s bottom surface have the same area: 27 cm2 (45 × 60 mm). This dimension was considered based upon the specifications of some processors, as presented in Table 1. Different LHP technologies focussing on various designs of the LHP’s evaporator and other types of LHPs such as miniature LHPs, micro LHPs, evaporator with longitudinal replenishment (ELR) LHPs, and LHPs with parallel condensers are compared and summarized in Table 2.

Table 1.
Processor specifications.

Table 2.
Different LHP technologies from the literature.
2. Experimental Setups and Data Reduction
2.1. Description of Test LHP
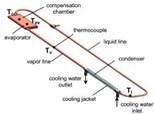
The elevation difference between the evaporator and condenser is 350 mm in this experiment. Cartridge heaters were used and inserted into the copper heating block at the evaporator base. The heat is rejected at the water-cooled condenser. The mass flow rate and inlet temperature of cooling water were around 7.5 × 10−3 kg s−1 and 27.5 °C, respectively. The power supplied to the evaporator was adjusted and measured by a volt slider and a digital power meter, respectively. The thermal contact resistance between the heating block and the evaporator is minimized by thermal grease, which was filled in the interface and fixed with screws. Pressure transducers and four thermocouples were inserted directly into the path of the working fluid at different positions of the LHP, such as at evaporator outlet Teo, condenser inlet Tci, condenser outlet Tco, and the inlet of compensation chamber Tcci. These temperature transducers detect the temperature distribution inside the LHP. Therefore, the characteristics of circulation, as well as phase distribution, can be evaluated. Pressure transducer Pe was installed at the outlet of the evaporator. Figure 3 and Figure 4 and Table 3 show the schematic diagram, photo of the real experimental setup, and the main specifications of the LHP.
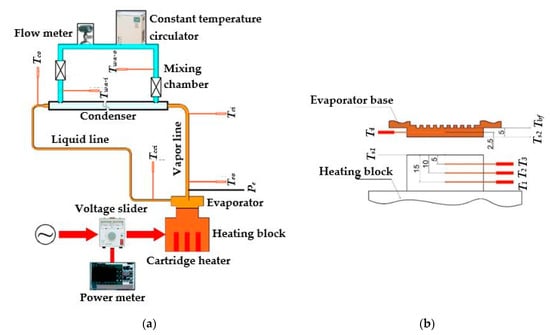
Figure 3.
Test LHP: (a) Schematic diagram of the LHP and temperature measurement points. (b) The locations of thermocouples on heating block and evaporator.
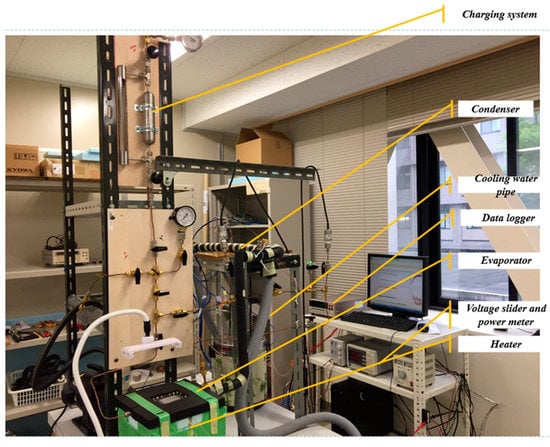
Figure 4.
Photograph of the real experimental setup under gravity-assisted conditions.

Table 3.
Main parameters of the LHP.
Thermocouples T1, T2, T3 were installed, as shown in Figure 3b, to consider the temperature gradient caused by the heat flux and the temperature on the top surface of heating block Ts1, and the correct values of heating power and heat flux supplied to the evaporator were accessed. In the evaporator base, thermocouple T4 was inserted to estimate the temperature at the evaporator’s bottom surface; Ts2 measures the temperature at the base of fin Tbf. The heat released from the condenser, Qc, is obtained from the temperature difference of cooling water Twa-i, Twa-o, and the mass flow rate of cooling water. All measured data were collected and recorded by the KEITHLEY 2701 data acquisition system. Moreover, the level of liquid inside the compensation chamber can be observed by the polycarbonate evaporator cover.
Table 4 describes the uncertainties of the mass flow meter and thermocouples (obtained from the calibration process in which a Pt100 thermometer (Chino Co. Model—R900-F25AT) was used as the standard source). Figure 5 and Figure 6 demonstrate the structure of the evaporator and the geometry of the evaporator’s inner surface.

Table 4.
Uncertainty values.
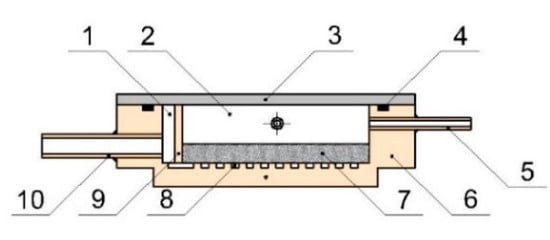
Figure 5.
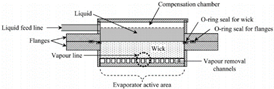
Schematic design of the evaporator. 1: vapor collector; 2: compensation chamber; 3: polycarbonate lid; 4: O-ring; 5: charging pipe; 6: copper evaporator body; 7: wick; 8: vapor grooves; 9: copperplate; 10: vapor pipe.

Figure 6.
The inner surface geometry of the evaporator (a) before and (b) after installing the wick.
Furthermore, the experimental uncertainty analysis of the computed heat transfer coefficients is given by the following equation (Equations (4)–(13)).
The experimental result R is assumed to be calculated from a set of measurements using a data interpretation program presented by [21].
R = R(X1, X2, X3, …, XN)
Each measurement uncertainty’s effect on the calculated result if only that one measurement were in error would be
The partial derivative of R with respect to Xi is the sensitivity coefficient for result R with respect to measurement Xi. The single terms are combined by a root-sum-square method when respective independent variables are used in function R.
Then, the parameter ΔT12 can be defined as,
The uncertainty for ΔT12 is shown in Equation (8).
where
ΔT12 is the temperature difference between T1 and T2 at the heating block.
The parameter ΔT23 can be defined as,
The uncertainty for ΔT23 is shown in Equation (10).
where
ΔT23 is the temperature difference between T2 and T3 at the heating block.
The parameter ΔT13 can be defined as,
The uncertainty for ΔT13 is shown in Equation (12).
where
ΔT13 is the temperature difference between T1 and T3 at the heating block.
The parameter q can be defined as,
The uncertainty for q is shown in Equation (14).
where
q is the heat flux; k is the thermal conductivity of copper.
δ1 is the distance between the heating block’s thermocouples.
The parameter Tbf can be defined as,
The uncertainty for Tbf is shown in Equation (16).
where
Tbf is the evaporator fin’ base temperature.
T4 is the evaporator’s base temperature.
The parameter he can be defined as,
The uncertainty for he is shown in Equation (18).
where
he is the heat transfer coefficient of the evaporator.
Teo is the evaporator outlet temperature.
The parameter hesat can be defined as,
The uncertainty for hesat is shown in Equation (20).
where
hesat is the heat transfer coefficient of the evaporator, calculated from the saturation temperature.
Tesat is the saturation temperature accessed from vapor pressure.
2.2. Description of the Wick’s Thermal Conductivity Measuring System
The wick materials’ thermal conductivity was measured by the transient hot-wire method. Figure 7 shows a schematic diagram of the thermal conductivity measuring device and sensor unit. It consists of a power supply device, a measuring device, a sensor unit, and a recording device (Personal Computer, PC). At the time of measurement, a constant current is applied from the power supply to the sensor. In addition, the voltage drop of the sensor unit is measured by a measuring device at regular intervals and recorded by a recording device.
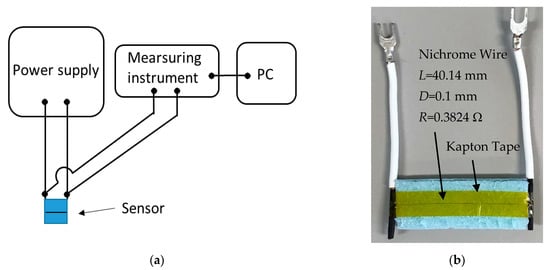
Figure 7.
Thermal conductivity measuring device (a) Schematic Diagram (b) Sensor Unit.
The basic equation for thermal conductivity measurement is expressed by the following equations (Equations (21)–(24)).
The thermal conductivity of the wicks (Equation (21)) [22],
where
λ2 is the thermal conductivity of the wick sample.
λ1 is the thermal conductivity of the insulator.
q* is the amount of heating per wire length.
t is the time taken.
ΔT is the temperature change from t = 0 s.
Resistance of thin wire at a certain temperature,
where
Ro is the initial electrical resistance.
α is the temperature coefficient of resistance.
From Equation (22) and Ohm’s Law,
where
V is the voltage drop on the thin wire.
I is the current.
By substituting ΔT into Equation (21),
Then, the wick materials’ thermal conductivity can be obtained from the slope of the relationship between the voltage drop of the thin wire and the logarithm of the heating time. The measured thermal conductivity of the tested wicks and the comparison with literature data [7,8] are presented in Table 5.

Table 5.
Thermal conductivity of wicks.
2.3. Description of Condenser
In this study, the condenser is a double-pipe heat exchanger with a counter flow arrangement. Cooling water from the constant temperature pump flows in the annular area while the vapor condenses inside the copper tube. The condenser structure is described in Figure 8 and Table 6.

Figure 8.
Photograph of the condenser.

Table 6.
Specification of the condenser.
Furthermore, the same copper smooth tube is used for the vapor pipe and liquid pipe of the LHP, whose OD/ID is 6.35/4.35 and 3.2/1.5 mm, respectively.
2.4. Data Reduction
From Figure 3b, the values of heat flux q, heat transfer coefficient he, and thermal resistances Re, Rc, and Rct can be estimated by the following equations (Equations (25)–(36)): A = 27 cm2, δ1 = 5 mm, δ2 = 2.5 mm.
Heat flux flowing from the heating block to the evaporator’s active area is calculated by Fourier’s Law of heat conduction as
where
is the heat transfer rate per unit heating block’s surface area.
k is the thermal conductivity of the copper heating block.
T1 to T3 is the heater temperature.
δ1 is the distance between the thermocouples inside the heating block.
Then, the mean of can be expressed by Equation (26).
Additionally, the temperature of the heating block’s top surface, Ts1, and the evaporator bottom’s temperature, Ts2, can be determined by Equations (28) and (29).
3. Results and Discussion
Figure 9 displays the values of temperature at various locations in the experiment. The results show that the stainless-steel wick exhibits higher heat flux when compared to the ceramic wick. During the heat load range of 50 to 520 W in Figure 9a and 53 to 155 W in Figure 9b, the values of Teo and Tci are almost similar, and Tco and Tcci are nearly equal. We affirm that the working fluid circulates stably inside the loop heat pipe. However, in the LHP with a ceramic wick, some fluctuations were found in the range of heat power, from 53 to 80 W, where the values of Tcci were higher than Tco. This phenomenon happened because there was the intermittent appearance of a vapor–liquid interface near the position of thermocouple Tcci in the liquid line. In the experiment of the LHP with a stainless steel wick, the supplying liquid for the compensation chamber was more stable than the LHP with the ceramic wick. Moreover, in this experimental research, temperature Ts1 on the heating block’s top surface can be viewed as the electronics temperature, which is normally recommended to be lower than 85 °C for reliable and effective operation [23]. Therefore, this present LHP, with stainless steel and ceramic wicks, can satisfy the recommendation until the heat load reaches 350 and 54 W, respectively. The measured values and frequency of pore distribution by the mercury injection method [24] are given in Table 7 and Figure 10.
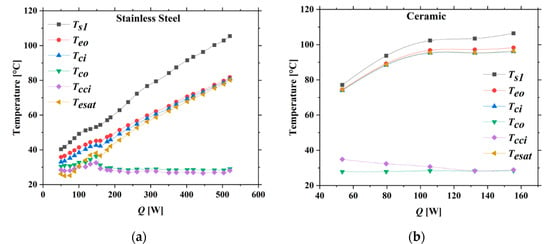
Figure 9.
LHP’s temperatures distribution at different heat loads when installed with (a) a stainless-steel wick and (b) a ceramic wick.

Table 7.
Test results of pore distribution measurement by the mercury injection method.
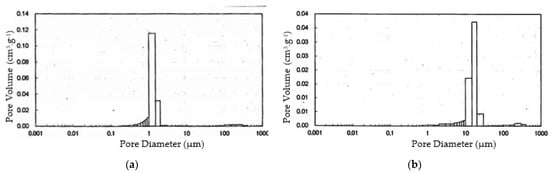
Figure 10.
Pore frequency distribution graphs (a) Ceramic wick (b) Stainless steel wick. Reproduced from [25], Saga Ceramics Research Laboratory: 2019.
3.1. Performance Evaluation
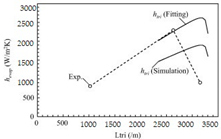
The thermal performance can be evaluated in terms of heat flux q, heat transfer coefficient he, and thermal resistances, which are evaporator Re, condenser Rc, and contact surface Rct, as shown in Figure 11 and Figure 12. In this study, the evaporator heat transfer coefficient was calculated from vapor temperature Teo at the outlet of the evaporator and saturation temperature Tesat, accessed from the vapor pressure measured at the outlet of the evaporator.

Figure 11.
SEM images (100 µm magnification) of (a) a stainless steel wick and (b) a ceramic wick. Reproduced from [25], Saga Ceramics Research Laboratory: 2019.
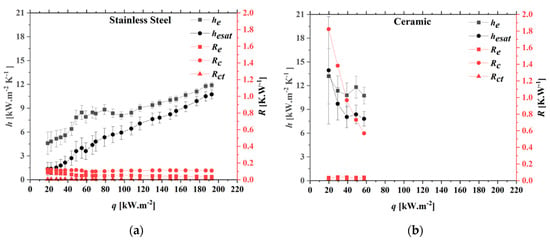
Figure 12.
he, R, vs. q of (a) a stainless steel wick and (b) a ceramic wick.
In both experiments of stainless steel and ceramic LHPs, the evaporator heat transfer coefficient obtained from Teo was higher than the values calculated from saturation temperature Tesat. Observing the difference in the results, the vapor might be superheated before leaving the evaporator. This superheating process could happen when vapor flows in the crossing grooves, and the heat of this process comes from the surrounding area of the fins and the grooves’ surface. The possible operating heat flux for the stainless-steel wick was higher than the ceramic wick. Comparing the evaporator heat transfer coefficient of the LHPs, the evaporator operating with the ceramic wick had the higher evaporator heat transfer coefficient when the heat transfer coefficient, he, linearly increased with the heat flux in the LHP with the stainless steel wick. However, the ceramic LHP did not operate better than the stainless steel one. The significant mass flow rate of vapor requires large pore sizes in the ceramic wick to reduce resistance. Otherwise, the performance of the condenser decreases. The numerical values obtained from the experimental uncertainty analysis of the computed heat transfer coefficients are presented in Table 8 and Table 9.

Table 8.
Uncertainty values of the computed heat transfer coefficients for LHPs with stainless steel wicks.

Table 9.
Uncertainty values of the computed heat transfer coefficients for LHPs with ceramic wicks.
Performance of Evaporator and Condenser
Figure 12a,b displays the evaporator and condenser thermal resistances, Re and Rc, of the stainless steel and ceramics LHPs. In the LHP with the stainless steel wick, the values of Re became smaller with the increase in heating power. However, thermal resistance Re for the ceramic one gradually increased in the same operating conditions, although the performance of the evaporator with the ceramic wick was more effective than the one with the stainless steel wick. For the thermal resistances of the condenser at the stainless steel LHP, it was reduced to the minimum value of 0.09 K.W−1, then raised up slightly, as shown in Figure 12a. The higher the heat power supplied to the evaporator, the less liquid exists inside the compensation chamber. As a result, with more liquid present in the condenser with the increasing heat load, the performance of the condenser was slightly reduced.
For the LHP with the ceramic wick, Rc’s values were significantly high, i.e., 1.8 K.W−1 at 53 W, due to the lower performance of the condenser. Additionally, particle differences between the stainless steel wick and ceramic wick are apparent in Figure 11a,b; the interfaces between the particles in Figure 11b are not as straightforward as those in Figure 11a. In the loop heat pipe with the stainless-steel wick, the working fluid was smoothly circulating inside the LHP because the flow resistance through the stainless-steel wick was lower than that of the ceramic wick. Therefore, the heat supplied made the working fluid evaporate, and the heat leak through the stainless-steel wick became small. In the ceramic wick’s case, the working fluid was not able to circulate correctly inside the LHP due to the high hydraulic resistance in the ceramic wick. As a result, heat flow, called a heat leak, became dominant in the evaporator with the ceramic wick.
4. Conclusions
The influence of two different wicks was tested in this study and used to describe the LHPs’ performance with a flat rectangular evaporator. The experimental results demonstrate that the LHP with the stainless-steel wick has better cooling performance than the LHP with the ceramic wick. The heater surface temperature of the LHP with the stainless steel wick increased from 40 to 105 °C in the range of a heat load from 50 to 520 W. In the ceramic wick LHP, this surface temperature reached 106 °C at a heat load of 155 W. Under gravity-assisted conditions, the LHP with the stainless steel wick could keep the temperature on the heater surface at 85 °C for a heat load of 350 W. However, the LHP with the ceramic wick could operate only at lower than 118 W for the same LHP, and the heater’s surface temperature approached 85 °C when the LHP was conducted at 54 W (20 kW·m−2). The ceramic wick cannot handle a high heat flux because of the conflict between vapor release and liquid suction. Large pore sizes are required to reduce resistance for the significant mass flow rate of vapor. It has been explained by Meléndez and Reyes [26].
where
mv is the vapor mass flow rate; ρv, σ, μv, and ε are vapor density, surface tension, viscosity, and porosity, respectively; δ is the wick thickness, and de is the effective pore diameter.
On the other hand, large capillary pressure is achieved by tiny pores for liquid suction, according to the Laplace-Young equation.
As a result, the vapor release and liquid suction of the ceramic wick require different pore sizes for better heat performance in LHPs.
Author Contributions
Conceptualization, A.M. and K.K.; methodology, A.M., K.K. and P.H.H.; software, P.H.H. and K.Z.H.; validation, P.H.H. and K.Z.H.; formal analysis, P.H.H. and K.Z.H.; investigation, P.H.H. and K.Z.H.; resources, A.M. and K.K.; data curation, P.H.H. and K.Z.H.; writing—original draft preparation, K.Z.H.; writing—review and editing, K.Z.H. and A.M.; visualization, P.H.H. and K.Z.H.; supervision, A.M.; project administration, A.M. and K.K.; funding acquisition, A.M. and K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Ts1 | temperature at heater surface (°C) | Tbf | fin base temperature (°C) |
| ID.OD | pipe inner.outer diameter (mm) | Tci | condenser inlet temperature (°C) |
| k | thermal conductivity of copper heating block [W·(m K)−1] | Tco | condenser outlet temperature (°C) |
| q | heat flux (kW·m−2) | Tcci | compensation chamber inlet temperature (°C) |
| Q | heat load (W) | Teo | evaporator outlet temperature (°C) |
| Re | thermal resistance of evaporator (K.W−1) | Ts2 | evaporator bottom surface temperature (°C) |
| Rc | thermal resistance of condenser (K.W−1) | Twa-i | cooling water temperature at inlet position (°C) |
| Rct | thermal contact resistance (K.W−1) | Twa-o | cooling water temperature at outlet position (°C) |
| T1 to T3 | heater temperature (°C) | δ1 | distance between the thermocouples inside heating block (m) |
| T4 | evaporator base temperature (°C) | δ2 | distance between the thermocouple T4 and the bottom surface of evaporator (m) |
| Qc | heat released from condenser (W) | CP | specific heat of cooling water [J.(kg K)−1] |
| mwa | mass flow rate of cooling water (kg·s−1) | Tesat | saturation temperature accessed from vapor pressure |
| he | heat transfer coefficient of evaporator(kW·m−2 K−1) | hesat | evaporator heat transfer coefficient calculated from saturation temperature (kW·m−2 K−1) |
| ΔT | temperature change from t = 0 (°C) | t | time (s) |
| q* | amount of heating per wire length (W·m−1) | To | initial temperature (°C) |
| Ro | initial electrical resistance (Ω) | α | temperature coefficient of resistance (°C−1) |
| V | voltage drop on thin wire (V) | L | thin wire length (mm) |
| A | area of heating block surface (m2) | λ2 | thermal conductivity of wick sample [W·(m K)−1] |
| I | electric current (I) | λ1 | thermal conductivity of insulator [W·(m K)−1] |
| heat transfer rate per unit heating block’s surface area (kW·m−2) |
References
- Maydanik, Y.F. Loop heat pipes. Appl. Therm. Eng. 2005, 25, 635–657. [Google Scholar] [CrossRef]
- Zhou, W.; Ling, W.; Duan, L.; Hui, K. Development and tests of loop heat pipe with multi-layer metal foams as wick structure. Appl. Therm. Eng. 2016, 94, 324–330. [Google Scholar] [CrossRef]
- Siedel, B.; Sartre, V.; Lefèvre, F. Numerical investigation of the thermo hydraulic behaviour of a complete loop heat pipe. Appl. Therm. Eng. 2013, 61, 541–553. [Google Scholar] [CrossRef]
- Maydanik, Y.; Fershtater, Y.G.; Pastukhov, V.G. Loop Heat Pipes: Development, Investigation and Elements of Engineering Calculations; Technical Report; Ural Division of the USSR Academy of Sciences: Moscow, Russia, 1989. [Google Scholar]
- Hoang, T.T.; O’Connell, T.A.; Ku, J.; Butler, C.D.; Swanson, T.D. Miniature loop heat pipes for electronic cooling. In Proceedings of the ASME 2003 International Electronic Packaging Technical Conference and Exhibition, Maui, HI, USA, 6–11 July 2003; pp. 517–525. [Google Scholar]
- Kondou, C.; Umemoto, S.; Koyama, S.; Mitooka, Y. Improving the heat dissipation performance of a looped thermosyphon using low-GWP volatile fluids R1234ze(Z) and R1234ze(E) with a super-hydrophilic boiling surface. Appl. Therm. Eng. 2017, 118, 147–158. [Google Scholar] [CrossRef]
- Santos, P.H.; Bazzo, E.; Becker, S.; Kulenovic, R.; Mertz, R. Development of LHPs with ceramic wick. Appl. Therm. Eng. 2010, 30, 1784–1789. [Google Scholar] [CrossRef]
- Canti, G.; Celata, G.P.; Cumo, M.; Furrer, M. Thermal hydraulic characterization of stainless steel wicks for heat pipe applications. Rev. Gén. Therm. 1998, 37, 5–16. [Google Scholar] [CrossRef]
- Ji, X.; Wang, Y.; Xu, J.; Huang, Y. Experimental study of heat transfer and start-up of loop heat pipe with multiscale porous wicks. Appl. Therm. Eng. 2017, 117, 782–798. [Google Scholar] [CrossRef]
- Maydanik, Y.; Chernysheva, M.; Pastukhov, V.G. Review: Loop heat pipes with flat evaporators. Appl. Therm. Eng. 2014, 67, 294–307. [Google Scholar] [CrossRef]
- Fukushima, K.; Nagano, H. International Journal of Heat and Mass Transfer New evaporator structure for micro loop heat pipes. Int. J. Heat Mass Transf. 2017, 106, 1327–1334. [Google Scholar] [CrossRef]
- Nishikawara, M.; Nagano, H. International Journal of Heat and Mass Transfer Optimization of wick shape in a loop heat pipe for high heat transfer. Int. J. Heat Mass Transf. 2017, 104, 1083–1089. [Google Scholar] [CrossRef]
- Xu, J.; Ji, X.; Yang, W.; Zhao, Z. Modulated porous wick evaporator for loop heat pipes: Experiment. Int. J. Heat Mass Transf. 2014, 72, 163–176. [Google Scholar] [CrossRef]
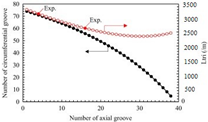
- Wu, S.; Wang, D.; Gao, J.; Huang, Z.; Chen, Y. Effect of the number of grooves on a wick’s surface on the heat transfer performance of loop heat pipe. Appl. Therm. Eng. 2014, 71, 371–377. [Google Scholar] [CrossRef]
- Choi, J.; Sung, B.; Kim, C.; Borca-Tasciuc, D.-A. Interface engineering to enhance thermal contact conductance of evaporators in miniature loop heat pipe systems. Appl. Therm. Eng. 2013, 60, 371–378. [Google Scholar] [CrossRef]
- Singh, R.; Akbarzadeh, A.; Mochizuki, M. Operational characteristics of a miniature loop heat pipe with flat evaporator. Int. J. Therm. Sci. 2008, 47, 1504–1515. [Google Scholar] [CrossRef]
- Chernysheva, M.; Yushakova, S.; Maydanik, Y. Copper–water loop heat pipes for energy-efficient cooling systems of supercomputers. Energy 2014, 69, 534–542. [Google Scholar] [CrossRef]
- Zhou, G.; Li, J.; Lv, L. An ultra-thin miniature loop heat pipe cooler for mobile electronics. Appl. Therm. Eng. 2016, 109, 514–523. [Google Scholar] [CrossRef]
- Shioga, T.; Mizuno, Y. Micro loop heat pipe for mobile electronics applications. In Proceedings of the 2015 31st Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 15–19 March 2015; pp. 50–55. [Google Scholar]
- Li, J.; Lin, F.; Wang, D.; Tian, W. A loop-heat-pipe heat sink with parallel condensers for high-power integrated LED chips. Appl. Therm. Eng. 2013, 56, 18–26. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Takekoshi, E.; Imura, S.; Hirasawa, Y.; Takenaka, T. Method for Measuring Thermal Conductivity of Solids by Transient Thin Wire heating Comparison Method (Edition. B); Japan Society of Mechanical Engineers: Tokyo, Japan, 1981; Volume 47, pp. 1307–1316. [Google Scholar] [CrossRef]
- Ebrahimi, K.; Jones, G.F.; Fleischer, A.S. A review of data center cooling technology, operating conditions and the corresponding low-grade waste heat recovery opportunities. Renew. Sustain. Energy Rev. 2014, 31, 622–638. [Google Scholar] [CrossRef]
- Nourzadeh, N.; Shadizadeh, S.R.; Manshad, A.K. Determination of pore size distribution profile along wellbore: Using repeat formation tester. J. Pet. Explor. Prod. Technol. 2017, 7, 621–626. [Google Scholar] [CrossRef]
- Saga Ceramics Research Laboratory. Available online: https://www.scrl.gr.jp/main/ (accessed on 28 November 2019).
- Meléndez, E.; Reyes, R. The pool boiling heat transfer enhancement from experiments with binary mixtures and porous heating covers. Exp. Therm. Fluid Sci. 2006, 30, 185–192. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).