Design and Experimental Validation of a Single-Stage PV String Inverter with Optimal Number of Interleaved Buck-Boost Cells

Abstract

Increasing converter power density is a problem of topical interest. This paper discusses an interleaved approach of the efficiency increase in the buck-boost stage of an inverter with unfolding circuit in terms of losses in semiconductors, output voltage ripples and power density. Main trends in the power converter development are reviewed. A losses model was designed and used for the proposed solution to find an optimal number of interleaved cells. It describes static and dynamic losses in semiconductor switches for buck and boost mode. The presented calculation results demonstrate the efficiency of the interleaved approach for photovoltaic system. 1 kW power converter prototype was designed with two parallel dc-dc cells for experimental verification of obtained theoretical results. The experimental results confirm theoretical statements.

1. Introduction

The Google Little Box Challenge (GLBC) has shown a close relation with the topic of high-power density inverters for Photovoltaic (PV) applications that have demonstrated extremely high-power density of power electronics converters achievable [1,2,3]. One of the GLBC project outcomes is the concept of a very high-power density converter. The finalists demonstrated a similar approach. It includes the basic full-bridge interleaved inverter, an active decoupling circuit and use of Wide Band-Gap (WBG) semiconductors.

WBGs market has an upward trend in today’s power electronics due to their high electron mobility and high voltage breakdown field [4,5,6]. As a result, fast switching high voltage semiconductor devices are already available on the power electronics market. The challenge is still the cost of those devices, which, however, is decreasing year by year.

At the same time, several configurations may be used in the PV systems [7,8]. Single PV panels are available for low power applications. They suffer from the voltage drop when the temperature is increasing. In the serial or string connection, one of the major drawbacks is a significant voltage drop at partial shadowing. Both connections lead to a wide range of input voltage variation during the energy utilization time. The GLBC solution is intended for narrow input voltage regulation, and it cannot provide a high and efficient PV energy conversion in heating or shadowing conditions. Neither can dual-back inverters [9,10] or boost inverters reported in [11,12] be considered as a solution at a wide range of regulation. Intermediate voltage boost dc-dc converters are used to overcome this drawback. At the same time, this solution is more complex and more expensive.

An alternative is to use single-stage buck-boost for a single input dc source. In this solution, inverters with an active boost cell are used [13,14,15,16]. They can provide very high boost of the input voltage but suffer from high current spikes in semiconductors and passive elements. The buck-boost solutions based on an active boost cell are rare in industrial applications.

New solutions are required to design an inverter with wide input voltage regulation along with high-power density and acceptable efficiency. For almost a decade, the impedance-source converters have attracted attention of the researchers [17,18,19,20,21,22]. But only a few attempts of industrial design can be found [23,24].

Several interesting single-stage buck-boost inverters are proposed in [25,26,27,28,29]. The solution based on the input boost and buck converter along with a line frequency unfolding circuit seems to be interesting for practical applications [29,30,31].

Another perspective method to decrease the size of passive components is using an interleaved approach [32,33,34,35,36,37,38]. In a general case, this method assumes use of two parallel circuits with the phase shift of control signals. The main advantage of such approach is reducing current through each single component, which allows reducing energy in the passive component and switch conduction losses that are proportional to the current and sizes.

Interleaved approach has been applied to different topologies, such as boost interleaved inverters with coupled inductors [33], two-phase interleaved inverters [35], three-phase grid-connected interleaved inverters [36], buck-boost interleaved inverters [37], and the three-level interleaved topology [38]. The advantages of the interleaved approach in terms of power density, cost and total converter efficiency have resulted in the improvement of the boost and buck stage in the power factor corrected rectifier system [39,40,41].

The main disadvantages of this topology are greater number of passive and active components, higher voltage drop on active components, and more complicated control technique.

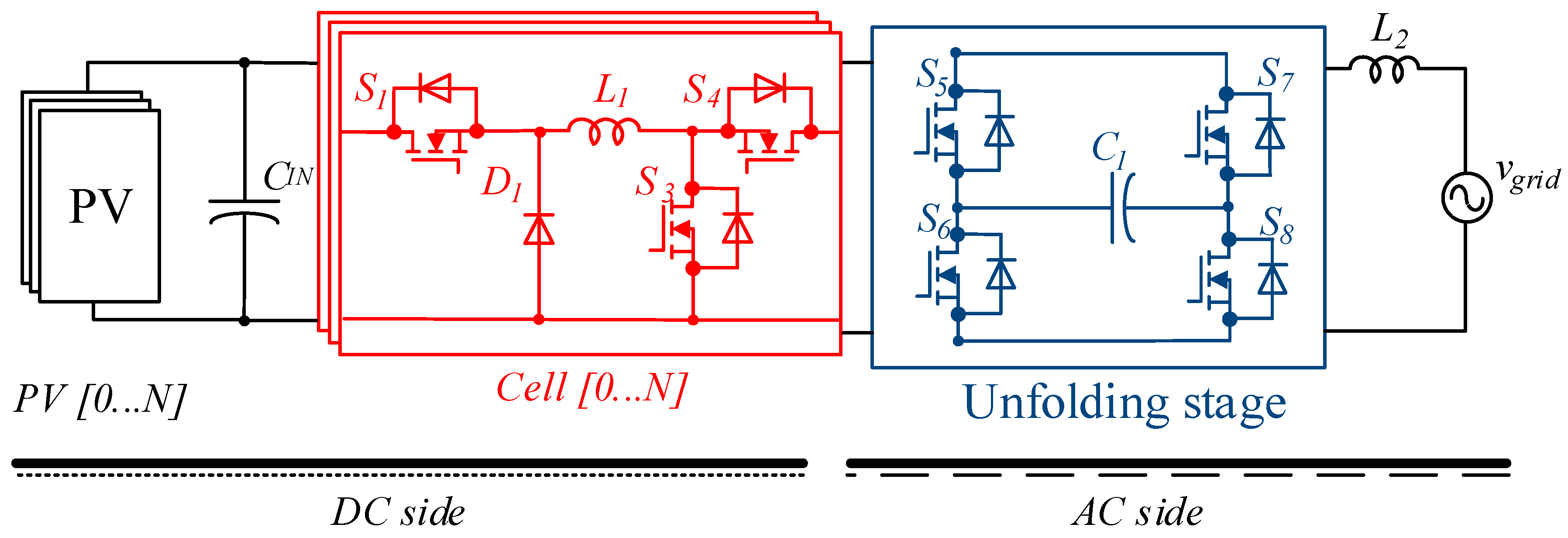
This paper focuses on further modifications of the buck-boost inverter with unfolding circuit using the interleaving approach. Figure 1 shows the inverter structure with the N-cell dc-dc stage. This approach allows for the reduction of losses in semiconductor components, in inductor energy and output voltage ripples. The main goal of this work is to find an optimal number of the interleaved cells.

2. Description of the Case Study System

First, the selected system is intended for PV application. Thus, the PV panel (PV string) is the input source for this topology. As a rule, a PV station has several solar panels, which can be reconfigured as parallel or serial connections to obtain the higher current or voltage, respectively. This section explains the characteristics of the real PV string applied along with brief topology features.

The set of HNS-SD140 solar panels was used as the PV string. Figure 2a shows the real PV string on the roof of the Chernihiv Polytechnic National University. The string consists of seven panels connected in series. The single panel generates around 140 W with a full panel lighting. The open circuit voltage equals 75 V with the single panel and 525 V with the PV string, while the short circuit current is 2.5 A. The total output power reaches up to 1 kW. The PV string parameters from the datasheet are listed in

Table 1. PV string parameters from the datasheet.

№	Parameter	Value
1	Input power, W	up to 1000
2	Open circuit voltage, V	525
3	Short circuit current, A	2.5
4	Maximum Power Voltage, V	413
5	Maximum Power Current, A	2.17

. Figure 2b demonstrates the real power characteristic of the PV string in the middle of the day.

Topology Description

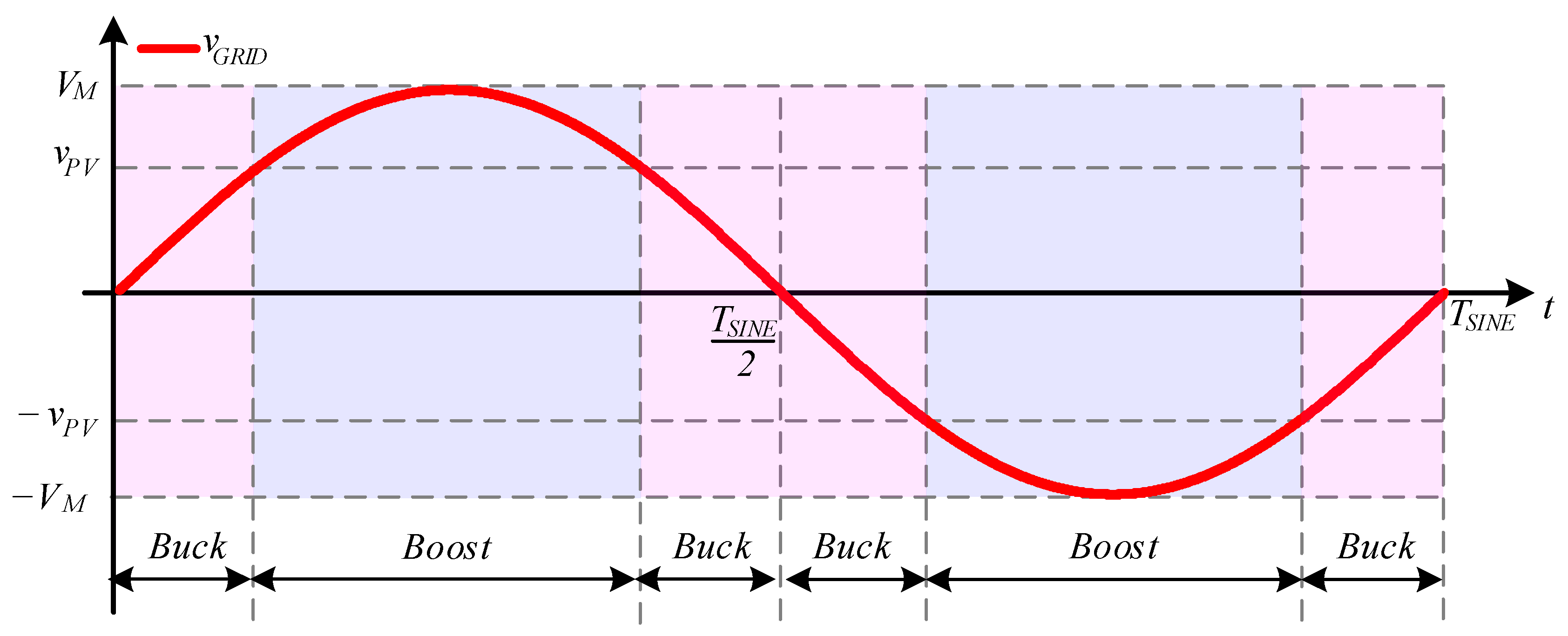
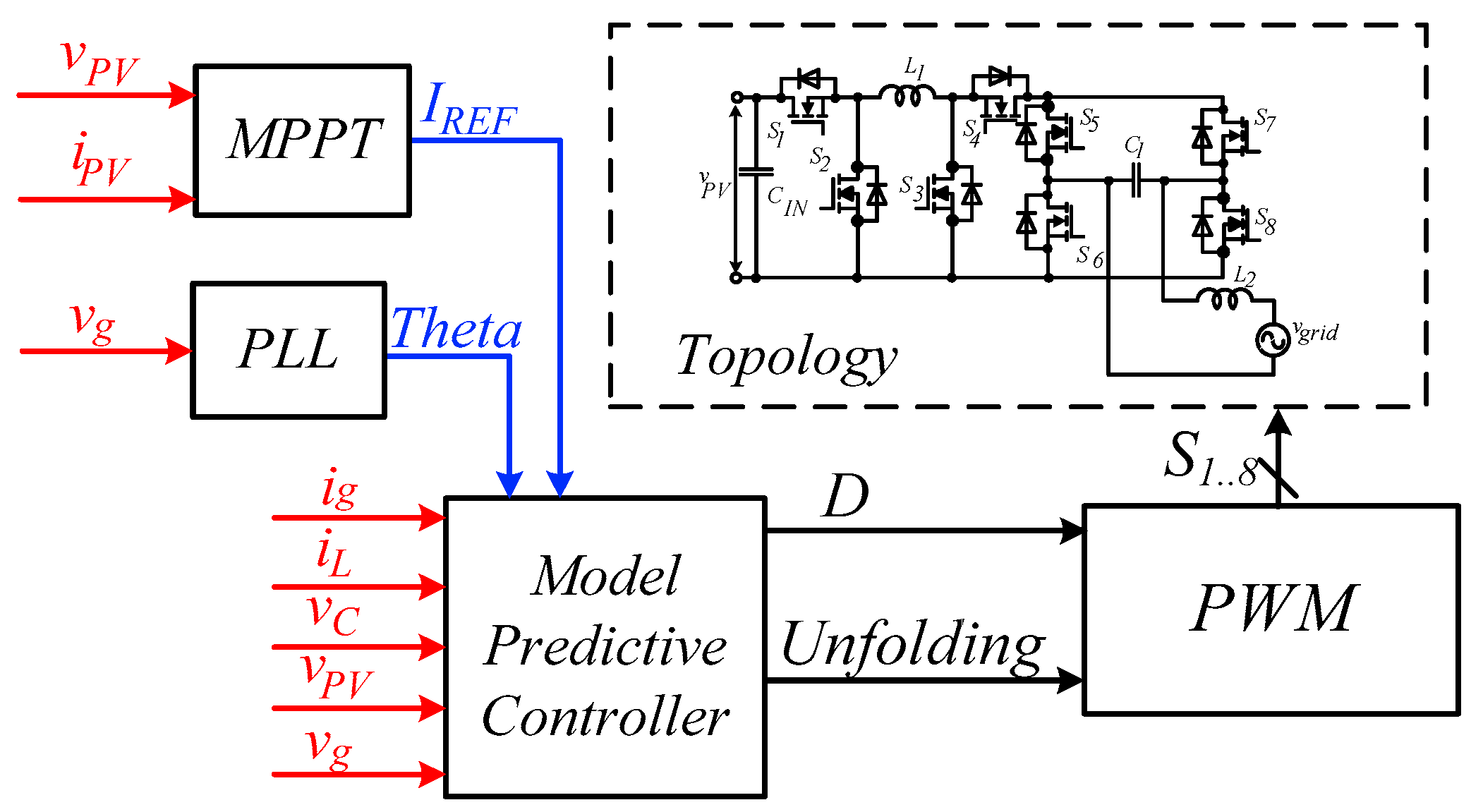
The aim of the inverter is to convert the PV string power into the ac power and to deliver it into the grid. The buck-boost inverter has two parts of circuits. The buck-boost part is the high-switching circuit that generates the unipolar sine shape at the output side using PWM. The unfolding circuit changes the sign of the output signal. The unfolding part is a low-switching part. Besides, the unfolding circuit commutes under zero voltage and zero current; thus, the dynamic losses equal zero. One of the advantages of the inverter is a wide range of the input voltage regulation. The input voltage can vary from 100 V to 500 V, while the peak of the output voltage is 320 V. Thus, the converter might be operating in a buck or in a boost mode. If the value of the grid voltage is less than the input voltage, the system operates in the buck mode, otherwise the boost mode is chosen. Figure 3 shows the principle of mode selection based on the grid voltage value.

Figure 4 shows the commutation principle of both modes for a single buck-boost cell. Only two switches are operating during the PWM period. The principle of the buck mode is to connect or disconnect the PV side from the inverter. The boost mode is operating with energy storage by the input inductor and is giving the storage energy instant to the grid.

If the buck-boost cell is not a single cell, the PWM channels are shifted between each other. The shifted phase is calculated as follows:

$${\phi }_i=\frac{{360}^{\circ }}{N}\cdot i$$

(1)

where N is the number of buck-boost cells, i is the current cell number.

3. Losses Model for the Buck-Boost Cell and Unfolding Circuit

It is known that the results of the calculations and those of the experiment cannot be absolutely the same because experimental parameters depend on different factors, such as the environment conditions, quality design, and other factors. Thus, the following calculation regards the power loss under ideal external conditions.

The designed model includes both types of the power losses: dynamic and static. The power signals were analyzed in detail during the model design. Figure 5 explains the high-frequency ripples of the semiconductor currents during the operation of the buck-boost case. Moreover, the buck and the boost modes require separate calculation of the power losses. Therefore, it is required to have correspondence of transistors with the modes:

$$\begin{gathered} S_1\equiv S_{BUCK}, S_2\equiv S_{NBUCK},S_3\equiv S_{BOOST}, S_4\equiv S_{NBOOST}, S_6\equiv S_7\equiv S_{UNFOLD}, \\ {S}_5\equiv S_8\equiv S_{NUNFOLD}. \end{gathered}$$

(2)

So, it is necessary to take into account dependences of the duty cycle for each mode. The expressions of the duty cycle are the same as in the case of a simple buck and boost dc-dc converter, but the output voltage is considered as a sine shape signal:

$$D_{BUCK}=\frac{\left|v_{GRID}\right|}{v_{PV}}, D_{BOOST}=\frac{\left|v_{GRID}\right|-v_{PV}}{\left|v_{GRID}\right|}, v_{GRID}=V_M\cdot \sin (\phi ),$$

(3)

where v_GRID is the grid voltage, v_PV is the PV voltage, V_M is an amplitude of the grid voltage, φ is the current phase of the grid voltage, v_C output capacitor voltage.

In the context of the steady state analysis, the currents depend on the input power and on the duty cycle. It is worth nothing that the inductor current is inversely proportional to the number of the buck-boost cells. The expressions are as follows:

$$i_{PV}=\frac{2\cdot P}{v_{PV}}\cdot {\sin }^2\left(\phi \right), i_{L\_BUCK}=\frac{i_{PV}}{N\cdot D_{BUCK}}, i_{L\_BOOST}=\frac{i_{PV}}{N},$$

(4)

where P is an average value of the input power, N is the number of buck-boost cells.

The steady state analysis allows obtaining the expression of the ripples in the passive elements. The pulsations of rising and falling states are considered the same. Figure 5g shows the high frequency ripple of the inductance current. The expressions of the inductor current ripples for the different modes are given below:

$$\Delta i_{L\_BUCK}=\frac{v_{PV}-\left|v_{GRID}\right|}{2\cdot f_{SW}\cdot L_1\cdot N}\cdot D_{BUCK}, \Delta i_{L\_BOOST}=\frac{v_{PV}}{2\cdot f_{SW}\cdot L_1\cdot N}\cdot D_{BOOST},$$

(5)

where f_SW is the switching frequency, L₁ is the value of the inductance.

Further calculations take into account each high-switching period. The dependences of the rising and falling of the inductor current are obtained using a canonical equation of the line. The inductor current depends on the time and on the current switching period. The expressions of the buck mode are as follows:

$$i_{L\_BUCK\_RISE}=i_{L\_BUCK}-\Delta i_{L\_BUCK}+2\cdot \Delta i_{L\_BUCK}\cdot \frac{t-i\cdot T_{SW}}{D_{BUCK}\cdot T_{SW}},$$

(6)

$$i_{L\_BUCK\_FALL}=i_{L\_BUCK}+\Delta i_{L\_BUCK}-2\cdot \Delta i_{L\_BUCK}\cdot \frac{t-\left(i+D_{BUCK}\right)\cdot T_{SW}}{\left(1-D_{BUCK}\right)\cdot T_{SW}},$$

(7)

where T_SW is the switching period, “i” is the current number of the high-switching period.

The same equations are used for the boost mode. Moreover, any power signal or other variables are presented as the function of the current switching period:

$$\begin{gathered} \phi \to \phi \left(i\right)={\omega }_0\cdot i\cdot T_{SW},i_{L\_BUCK\_RISE}\to i_{L\_BUCK\_RISE}\left(i\right), \\ {i}_{L\_BUCK\_FALL}\to i_{L\_BUCK\_FALL}\left(i\right), \end{gathered}$$

(8)

$$D_{BUCK}\to D_{BUCK}\left(i\right), D_{BOOST}\to D_{BOOST}\left(i\right).$$

(9)

However, the currents of the transistors are not continuous, so it is required to consider a different time span for each semiconductor.

3.1. Static Losses Model

The static model corresponds to the law of Joule-Lenz. Thus, the overall static losses are equal to the sum of each semiconductor power loss. The general static losses are derived with the next expression:

$$P_{CLOSS}={\displaystyle \sum _{i=1}^M\left(I_{i\_RMS}^2\cdot R_{DSON}\right)},$$

(10)

where M is the number of transistors, I_{i_RMS} is the RMS value of the transistor current, R_DSON equals the ON-state resistor declared in the document of the element.

On the other hand, the current ripples through the semiconductor element were taken into account during the RMS calculation. Certainly, each high-switching period is considered. So, the square RMS values of the semiconductor currents are expressed as:

$$I_{T\_BUCK\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[{\displaystyle \underset{i\cdot T_{SW}}{\overset{(i+D_{BUCK}\left(i\right))\cdot T_{SW}}{\int }}\left(i_{L\_BUCK\_RISE}^2\left(i\right)\cdot dt\right)}\right]},$$

(11)

$$I_{T\_NBUCK\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[{\displaystyle \underset{(i+D_{BUCK}\left(i\right))\cdot T_{SW}}{\overset{(i+1)\cdot T_{SW}}{\int }}\left(i_{L\_BUCK\_FALL}^2\left(i\right)\cdot dt\right)}\right]},$$

(12)

$$I_{T\_BOOST\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[{\displaystyle \underset{i\cdot T_{SW}}{\overset{(i+D_{BOOST}\left(i\right))\cdot T_{SW}}{\int }}\left(i_{L\_BOOST\_RISE}^2\left(i\right)\cdot dt\right)}\right]},$$

(13)

$$I_{T\_NBOOST\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[{\displaystyle \underset{(i+D_{BOOST}\left(i\right))\cdot T_{SW}}{\overset{(i+1)\cdot T_{SW}}{\int }}\left(i_{L\_BOOST\_FALL}^2\left(i\right)\cdot dt\right)}\right]},$$

(14)

$$I_{T\_UNFOLD\_BUCK\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[\begin{array}{l}{\displaystyle \underset{i\cdot T_{SW}}{\overset{(i+D_{BUCK}\left(i\right))\cdot T_{SW}}{\int }}\left(i_{L\_BUCK\_RISE}^2\left(i\right)\cdot dt\right)+}\\ +{\displaystyle \underset{(i+D_{BUCK}\left(i\right))\cdot T_{SW}}{\overset{(i+1)\cdot T_{SW}}{\int }}\left(i_{L\_BUCK\_FALL}^2\left(i\right)\cdot dt\right)}\end{array}\right]},$$

(15)

$$I_{T\_UNFOLD\_BOOST\_RMS}^2=\frac{1}{T_{SINE}}\cdot {\displaystyle \sum _{i=0}^Q\left[{\displaystyle \underset{(i+D_{BOOST}\left(i\right))\cdot T_{SW}}{\overset{(i+1)\cdot T_{SW}}{\int }}\left(i_{L\_BOOST\_FALL}^2\left(i\right)\cdot dt\right)}\right]},$$

(16)

where T_SINE is the sine period, Q is the amount of the high-switching periods per one sine period.

3.2. Dynamic Losses Model

The dynamic losses can be obtained using the same principle: consider each high-switching period. The next expression allows the calculation of the switching loss during the sine period:

$$P_{DLOSS}=\frac{1}{T_{SW}}\cdot \left(\frac{t_{dON}+t_r+t_{dOFF}+t_f}{2}\cdot I_{P\_AVG}\cdot V_{P\_AVG}+\frac{5}{4}\cdot Q_{rr}\cdot V_{P\_AVG}\right),$$

(17)

where t_dON is the turn on the delay time, t_r is the rise time of the transistor, t_dOFF is the turn-off delay time, t_f is the fall time, I_{P_AVG} equals an average value of transistor current spikes during the grid period, V_{P_AVG} is the average value of the transistor drain source stress during the sine period, Q_rr is the reverse recovery charge of the reverse diode.

The average current spikes during the grid period can be obtained from previous Equations (3)–(15) for each switch. As is known, they correspond to the maximum ripple of the inductor current at each moment of the transistor conduction (one high-switching period):

$$I_{T\_BUCK}^{}\left(i\right)=i_{L\_BUCK}\left(i\right), I_{T\_NBUCK}^{}\left(i\right)=i_{L\_BUCK}\left(i\right),$$

(18)

$$I_{T\_BOOST}^{}\left(i\right)=i_{L\_BOOST}\left(i\right), I_{T\_NBOOST}^{}\left(i\right)=i_{L\_BOOST}\left(i\right),$$

(19)

The average voltage spikes can be derived from a simple differential equation of equivalent circuits. The values of the peak of one high-switching period are as follows:

$$v_{DS\_BUCK}^{}\left(i\right)=v_{PV}\left(i\right), v_{DS\_NBUCK}^{}\left(i\right)=v_{PV}\left(i\right),$$

(20)

$$v_{DS\_BOOST}^{}\left(i\right)=v_{PV}\left(i\right), v_{DS\_NBOOST}^{}\left(i\right)=v_{PV}\left(i\right).$$

(21)

4. Study of the Optimal Number of the Buck-Boost Cells

An interleaved approach for the buck-boost stage of the inverter has some advantages and disadvantages. Parallel connection of dc-dc cells increases the number of semiconductor switches, and as a result, it increases the number of high-frequency commutations, and even may increase the total converter volume and the size. On the other hand, an interleaved feature allows the distribution of the input current between the cells, which leads to the reduction of conduction losses in the semiconductors. At the same time, the input inductances can be redesigned for lower current. This section is devoted to finding an optimal number of cells.

4.1. Conclusions from the Calculations

Section 3 described the calculation based on the real semiconductor parameters. The transistor UJC0650K was chosen for the buck-boost part, while IPP60R060P7 is embedded in the unfolding part. The parameters of the switches are listed in

Table 2. Parameters of the semiconductors.

Parameter	UJC0650K	IPP60R060P7
VDS, V	650	650
RDS_on, Ω	34	60
ID_max, A	36.5	38
td_on, ns	29	23
tr, ns	10	12
td_off,ns	70	79
tf, ns	15	4
Qrr, µC	0.95	2.9

.

Note that the semiconductor parameters from the datasheet are given under some conditions: constant drain current, environment temperature, case temperature and other conditions. Thus, it is impossible to acquire the same efficiency obtained in the experiment tests. Besides, the parasitic parameters of the board also influence the dynamic characteristics of the switches. Therefore, the calculation has some errors and expresses an approximate shape of efficiency as compared with that of a real case.

First, the static loss will be considered. Logically, to increase the number of cells, the static losses should be decreased because the current is evenly split between the cells. The last statement is an advantage. Figure 6 presents dependences for the static loss. The boost case causes significant differences in the static losses with different amounts of cells. However, a big difference can be seen with the higher input power, for example, from 1 kW, as shown in Figure 6a. On the other hand, the lower input power does not affect static losses considerably, even with a great boost ratio (Figure 6b).

Despite the static losses decreasing under greater number of cells, the dynamic losses are increasing. The reason is the number of commutations, because four semiconductors are added with each additional cell. However, the current distribution in the case of several buck-boost cells provides fewer dynamic losses for a single component, but the number of components is increasing. Figure 7 shows dependences of dynamic losses based on the PV voltage and the input power. The dynamic losses are rising linearly with a higher input power, while the PV voltage is constant, as shown in Figure 7a. The dynamic losses with three buck-boost cells are greater than with one or two cells during a wide range of the input power and voltages. Thus, when an engineer designs an interleaved approach, the weight of static advantages versus the weight of dynamic drawbacks must be estimated.

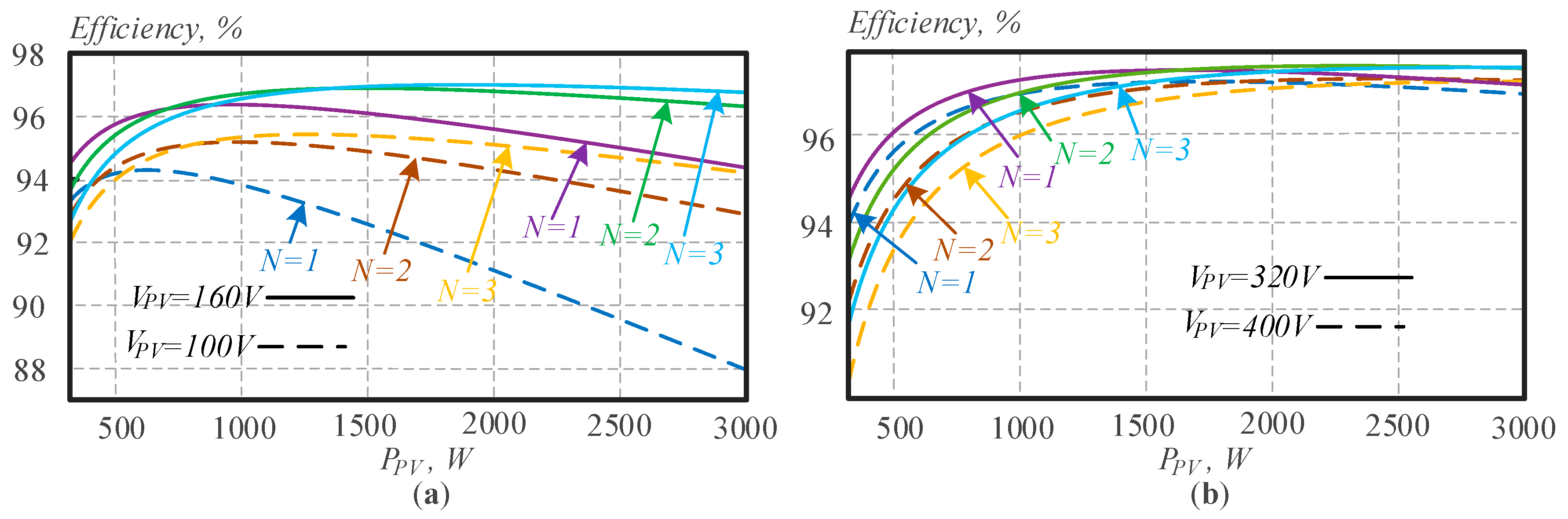
Finally, the dependences of the efficiency based on the input voltage and the input power were built. Figure 8 shows that the interleaved approach is more effective with higher input power. The inverter with two or three cells has better efficiency at the input power over 800 W in the case of boost (Figure 8a). The buck mode is more effective at the input power over 2 kW, as shown in Figure 8b. However, the results of the efficiency depend on the switches that were chosen, i.e., this efficiency dependence is in correspondence only for an inverter with selected transistors (Table 2).

Switch S₂ can be changed by diode. In Section 3 equations for transistor were presented. Comparative study of system with transistor and diode reviled small influence of this factor on efficiency in general. Transistor instead of diode allows for a more flexible control strategy. On the other hand, it should be mention that transistor in boost mode has bigger static losses then dynamic. And in buck mode dynamic losses prevail on static losses. Figure 9 demonstrate insignificant influence of component type on efficiency in buck-boost and buck mode for a different number of parallel cells. For these reasons, diode was chosen for experimental study.

4.2. Qualitative Assessment of the Interleaved Approach

Based on the results obtained, theoretical assumption about the efficiency of the interleaved approach for the buck-boost cell in terms of active component losses was verified. On the other hand, there are other parameters that should be taken into account during designing, such as size of the power converter because it requires a greater number of switches and more driver circuits; the cost of element base; the passive elements. This section presents the qualitative comparison between the single-, two- and tree cells by a square of the power board, overall energy of inductances, efficiency and cost of semiconductors.

The influence of the interleaved approach on the linear size of the converter was analyzed. This parameter establishes relationship between the number of active components, their control circuits and PCB size. The area for the one buck-boost cell S_{BB_cell} consists of the area of inductors S_L, the area of the active switch S_SW, which is multiplied on the number of active components and the area of the driver S_Driver for each semiconductor. The area for unfolding circuit was calculated by the same method for different types of switches and is presented as a constant parameter S_UNF. The overall area of the inverter can be obtained by the next expression:

$$S=N\cdot \left(S_L+4\cdot (S_{SW}+S_{Driver})\right)+4\cdot (S_{UNF}+S_{Driver}).$$

(22)

The second parameter compared is an overall inductance energy of the inverter. This parameter contains the sum of the energy of all inductances. The energy of the inductor allows indirect estimation of the size of the inductor because it depends on the inductor value and the maximum current. The overall energy of inductances is as follows:

$$E_L=N\cdot \frac{I_L^2\cdot L_1}{2}+\frac{I_{GRID}^2\cdot L_{GRID}}{2}.$$

(23)

The third parameter is the cost. With regard to the interleaved approach, it is necessary to consider the cost of all semiconductors C_{BB_SW}, C_{UNFOLD_SW} and their drivers C_Driver. Besides, the cost of the inverter depends on the board size C_PCB. The cost of the inverter based on the number of cells is obtained by the next expression:

$$C=4\cdot N\cdot \left(C_{BB\_SW}+C_{Driver}\right)+4\cdot \left(C_{UNFOLD\_SW}+C_{Driver}\right)+C_{PCB}.$$

(24)

The last parameter mentioned in Section 4.1 is the efficiency. All the parameters were normalized on the single cell, except for the efficiency. However, some aspects were missing. For example, with the number of parallel cells increasing, the control system complexity also increases. This trend leads to extremely expensive MCU or even FPGA for three and more parallel cells. But many chips contain a sufficient number of PWM channels that cover single-, two-, or three cells.

Figure 10 shows the diagrams that compare the buck-boost cells in relative units. The condition of the comparison was that the efficiency of several buck-boost cells is higher or the same with a single cell. The overall inductance energy is 2 times lower in the case of two buck-boost cells and 3 times lower in the case of three cells, respectively. However, the cost and the area are increasing linearly with the higher cells, as shown in Figure 10a. The efficiency of the inverter is the same for all sets of cells in the case of the buck mode. The boost mode is more effective for higher sets of cells (Figure 10b).

Finally, the optimal number of buck-boost cells can be obtained from the previous calculation and estimation. In the case of the current case study system, the optimal number is single-, or two- buck-boost cells because with the second cell, the efficiency is growing up in the boost mode, while it is the same during the buck mode. Further cell number increase will lead to a significant cost increase without a significant efficiency increase.

5. Control System Description

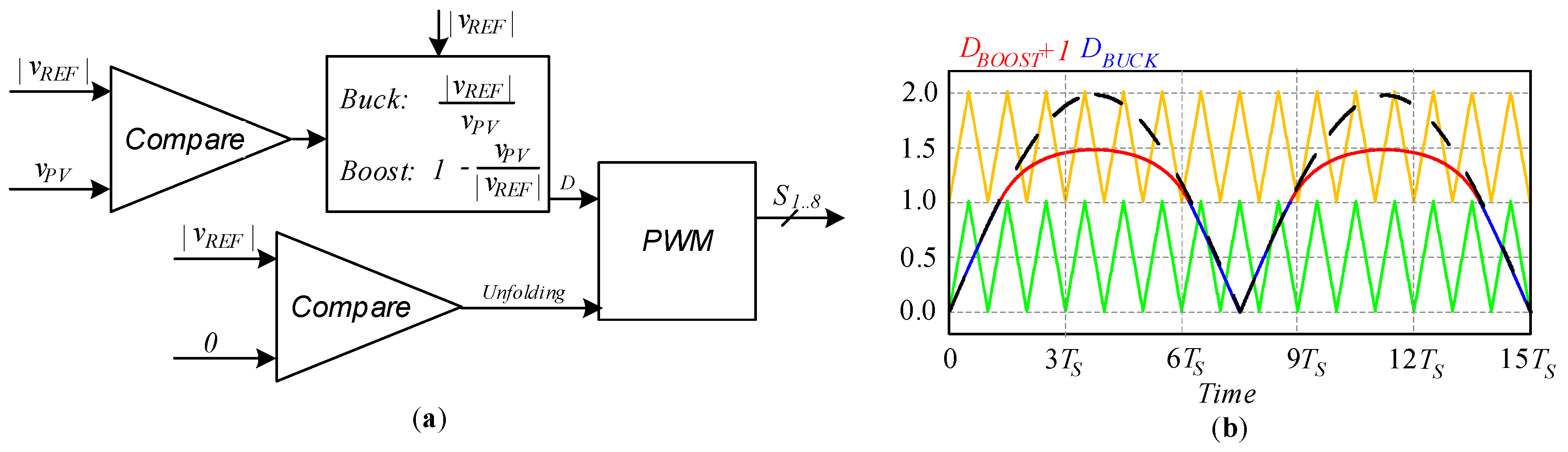
For the efficiency measurement, the open-loop system was chosen. Figure 11 shows the strategy of the modulator with Pulse Width Modulation (PWM). The principle is as follows: the sine signal is generated by the control unit; the reference signal is compared with the input voltage and with zero; the result of the comparison with the input voltage leads to choosing a suitable mode, while the comparison with zero changes unfolding circuit signals; all the results are going to PWM, as shown in Figure 11a. The principle of PWM is demonstrated in Figure 11b.

The closed-loop system provides stable operation with a grid connection. The control system consists of the next blocks: Phase-Locked-Loop block (PLL), Maximum Power Point Tracking (MPPT), Model Predictive control (MPC) and Modulator, as shown in Figure 12 [42].

There are three current and voltage sensors in the system. These sensors provide measurement of the input and the output voltages and currents. Measurements of the current in the inductances and the voltage of the capacitor are necessary to achieve the required accuracy.

The system is synchronized with the network voltage by using a PLL block. The MPPT calculates the amplitude of the PV output current to produce the reference signal. The system selects the operation mode and calculates the optimal value of the duty cycles for the converter based on the weather conditions, solar irradiation, and other parameters. The MPC block predicts the next values of the currents and voltages and selects the necessary duty cycle for the next high-switching period. MPC also defines the state of the unfolding circuit. Finally, the new duty cycle and the unfolding states are sent to PWM.

6. Experimental Verification

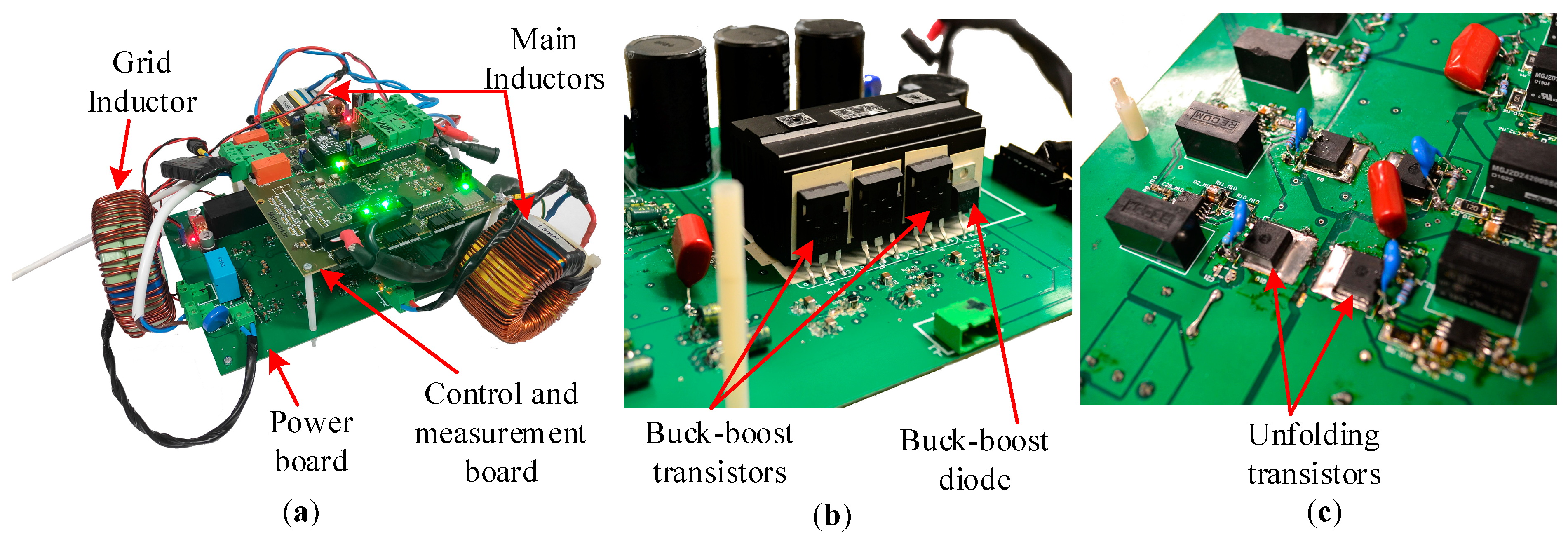
Results of experimental verification were obtained from the designed converter prototype (Figure 13). The prototype consists of the power PCB with all active and passive components, filters, driver circuits, control and measurement PCB based on the microcontroller unit (MCU) TMS320F28379 of the Texas Instruments, which provides the MPPT and MPC control algorithm. Selected MCU contains four independent cores that provide sufficient computing resources to implement a complex control system. In addition, MCU includes a fast 16-bit differential Analog to Digital Converter (ADC) block.

The control and measurement PCB contains five voltage sensor channels. Two of them provide AC voltage measurement in the range from 0 V up to 500 V. The other three sensors were designed for DC voltage measurement. The whole control circuit is galvanically isolated from the power part. The control system has the hardware and software protection items, such as a fuse, varistors, relays galvanic isolated buffers, and some software predefined limits for the measured parameters.

The inverter power PCB was designed for two parallel DC/DC cells with individual inductors, one unfolding circuit, input and output filters, and switch driver circuits. All the inductors were designed manually. Two inductances for the DC/DC stage have current limit of 10 A and the grid inductor current limit is up to 15 A. The input filter consists of three electrolytic capacitances, which are equal to 100 µF. The output filter includes an inductance of 0.3 mH.

Two different models of transistors were used for the high frequency DC stage and low frequency unfolding circuit. The main parameters of all the used active components are presented in Section 4, Table 2. DC/DC stage contains six switches UJC0650K in two parallel cells. Unfolding stage includes four transistors IPP60R060P7 (Figure 13c). The transistor S2 of the buck-boost cell is replaced by a SiC diode CREE C3D10065. All buck-boost semiconductors are placed on a common heatsink (Figure 13b). The unfolding switches have only static losses, they were placed on the power board without any heatsink.

Figure 14 demonstrates a particular case of the experimental results for the open-loop system of the buck-boost inverter based on unfolding circuit with two cells. Diagrams for the boost case are presented in Figure 14a–d and for the buck case in Figure 14e,f. The input voltage equals 190 V or 250 V for boost cases and 320 V for the buck case. The output voltage satisfies the main requirements for the grid voltage. Figure 14b,d,f shows the high-frequency ripples of the input inductor current.

The efficiency diagram is presented in Figure 15. The results for the efficiency are approximately similar to those calculated, as it was explained in Section 4. In the determination of the differences between the mathematical expressions and the experimental results, as established in the losses model, thermal changing of the parameters of the switches, such as revers recovery charge Q_rr and measurements error, were not taken into account. Consequently, theoretical assumptions were confirmed by experimental results. The efficiency was measured with the analyzer YOKOGAVA WT1800. Figure 15a shows the real efficiency along with theoretical in the boost mode. The buck case lines are shown in Figure 15b.

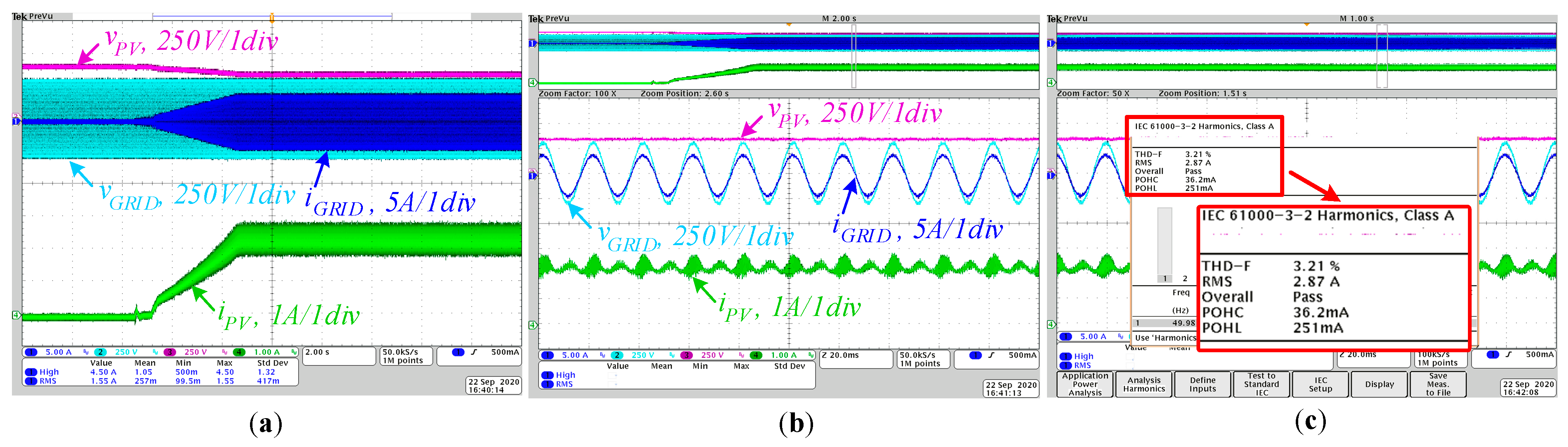
The results of the closed-loop system based on MPC are shown in Figure 16. The integral MPPT algorithm is used. The PV string contains five serial panels. The open-circuit voltage was around 410 V. The MPP voltage equaled 350 V, while the MPP current reached 2 A, as seen in Figure 16b. The system is stabilized with the THD of the grid current less than 5% (Figure 16c). The sine shape of the grid current is so good that it allowed us to tune the MPPT with no problems. As a result, the experimental results confirmed the control strategy within the efficiency theory.

7. Conclusions

The design and experimental validation of a single-stage PV string inverter with an optimal number of interleaved buck-boost cells are presented. The inverter can provide stable operation under the range of the input voltage from 100 V up to 500 V. Moreover, different PV strings can be applied for this solution. Thus, the selected topology of the inverter is suitable for PV application.

The theoretical calculation allows the estimation of real efficiency and finding the optimal number of the buck-boost cells. The theoretical dependences of the efficiency were obtained based on the parameters of the transistors UJC0650K and IPP60R060P7. The optimal number of cells depends on the cost of the inverter, on the area of the power board, on the overall energy of the inductances, and on the efficiency. The results showed that the cost and the area of the power board are increasing linearly when the additional buck-boost cell is added. The energy of inductances is also decreasing linear, so it is possible to reduce the size of the inductances with the larger number of cells. Besides, the efficiency is increasing with the higher input power. Thus, two cells were obtained as the optimal number for this research.

The real PV string characteristics with the real PV string were used in theoretical and experimental parts. The set of the 7 serial HNS-SD140 panels provided 1 kW of the input power. The real prototype was designed for the theoretical verification. The simple open-loop system was used for the efficiency measurements. The closed-loop system based on MPC provides reliable operation of the inverter in the grid-connected system.