1. Introduction
Electro-hydraulic compact drives (ECDs) represent a promising alternative to conventional valve-controlled hydraulics as well as to electro-mechanical linear drive solutions [
1,
2,
3]. By combining the robustness (including overload protection), high force density and high achievable transmission ratios of conventional hydraulic drives with the plug-and-play capabilities, better energy-efficiency and small space requirements of electro-mechanical linear drives, ECDs may be a competitive alternative in applications previously dominated by conventional technologies. As illustrated in
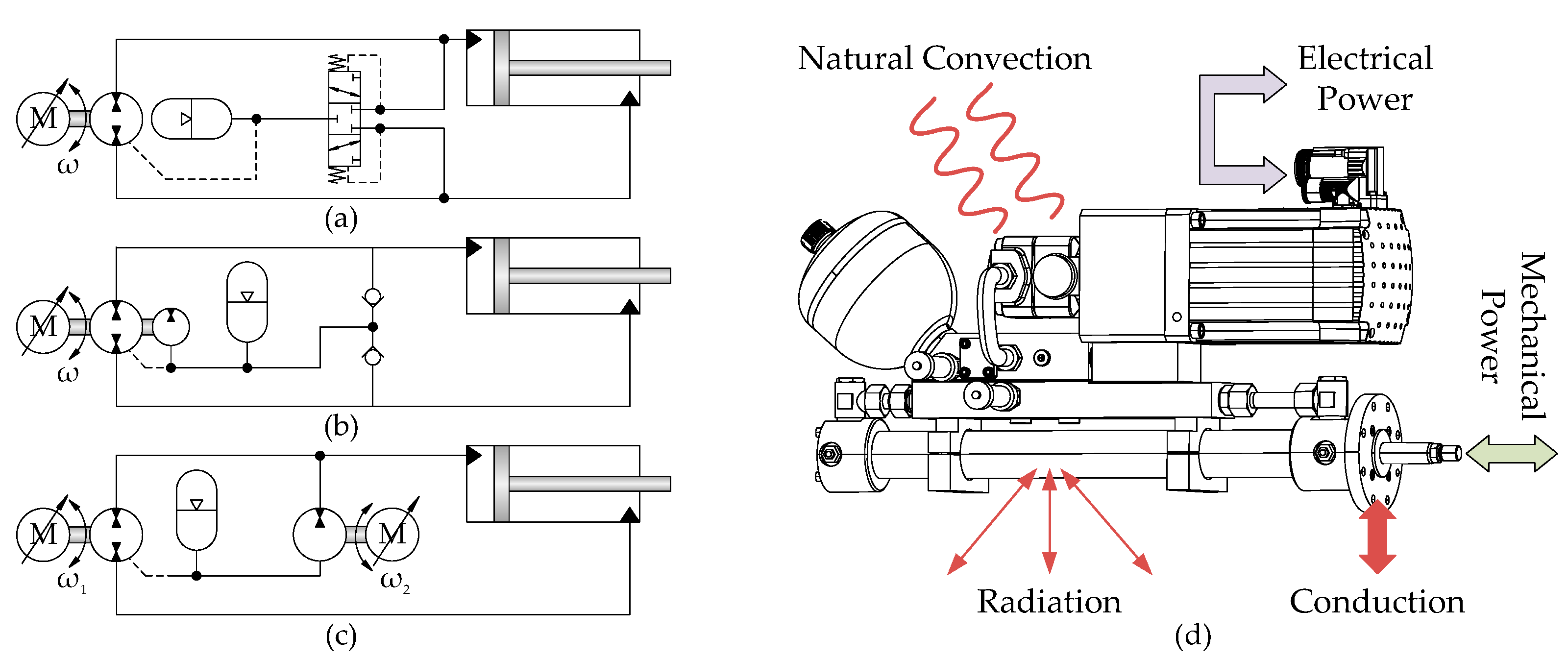
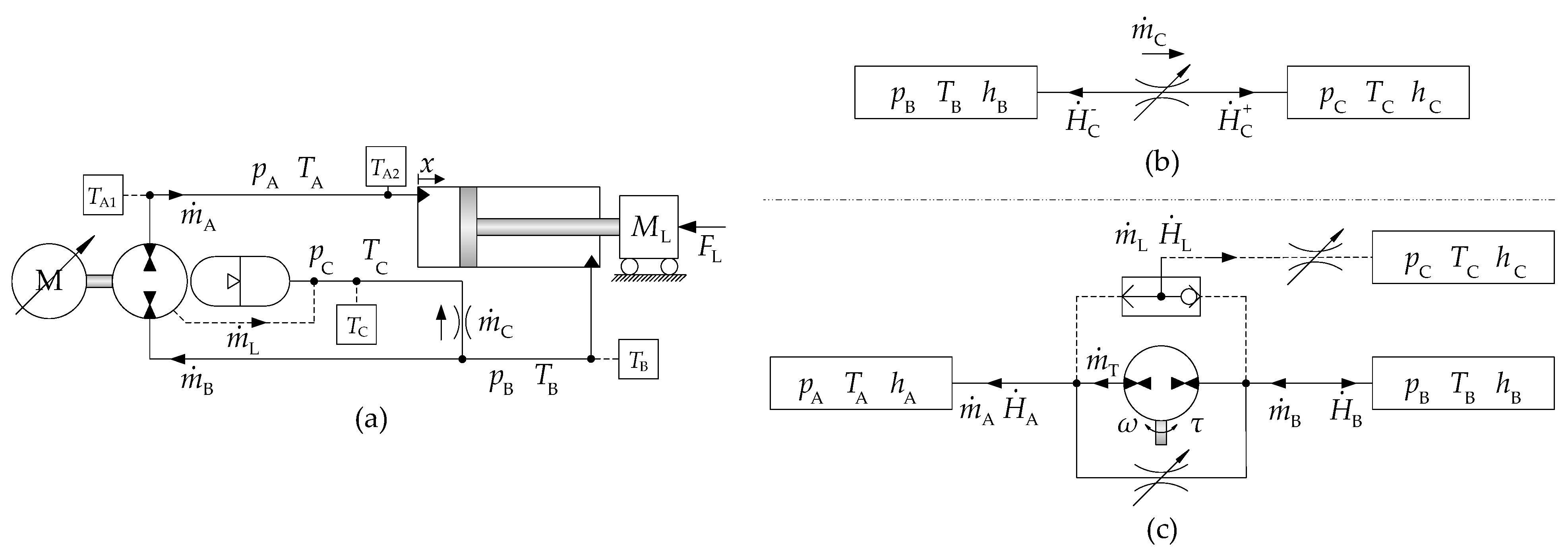
Figure 1, ECDs basically consist of a variable-speed electric motor driving a fixed-displacement hydraulic pump. The pump outlets are connected to a differential cylinder, without any throttling elements, thus avoiding the associated immense power losses and enabling ECDs to recover energy in aided load situations. To balance the asymmetric cylinder flows, a low-pressure accumulator is often utilised to ensure appropriate suction conditions for the hydraulic pump. As opposed to valve-controlled drive solutions, the energy losses of ECDs are governed by the energy efficiency of the components, as no inherent losses (i.e., valve throttling) are associated with the actuation principle.
During recent decades, the main research focus has been placed on identifying and investigating architectures that are able to connect the accumulator with the remaining circuit to facilitate operating in four quadrants. Two main topologies can be identified in research literature [
4,
5]. In valve-compensated architectures (
Figure 1a), either hydraulically or electrically actuated valves are used to connect the low pressure cylinder chamber with the accumulator [
6,
7,
8]. For pump-compensated architectures (
Figure 1b), two or more pumps are matched to the areas of the differential cylinder to balance asymmetric flow without the need of valves [
9,
10,
11,
12,
13]. To enable the ideal matching of pump displacements to the cylinder areas, independent of operating conditions, circuit architectures using two variable-speed electric motors (
Figure 1c) are also being investigated [
14,
15]. A recent review highlighting the advantages and disadvantages of the considered architectures may be found in [
16].
Some common drawbacks of the ECD technology potentially limiting its application range are currently being addressed by the research community. These include reliability and energy efficiency limitations in the low speed range of conventional hydraulic units [
17,
18,
19,
20], the challenge of incorporating load holding devices not affecting the ability of recovering energy in aided load situations [
21,
22,
23,
24,
25] and identifying alternatives to the rather bulky gas-loaded accumulator [
26,
27]. The former challenge is also addressed by designing new types of hydraulic units, such that these are capable of low-speed operation at good efficiencies. The newly introduced AX series pump from Bucher Hydraulics is an example of such [
28].
The reported energy-efficiency of ECDs ranges from 50% up to 80% [
29,
30,
31], but depends heavily on the working conditions. Nevertheless this is much higher than the energy efficiency of valve-controlled hydraulics, which features an average efficiency of 21% according to [
32]. As opposed to conventional valve-controlled hydraulics where cooling devices are needed, the improved energy efficiency of ECDs may permit these systems to rely solely on passive cooling. This is illustrated in
Figure 1d. The power losses of the system equals the passive heat transfer to the surroundings at an allowable equilibrium temperature. Passive cooling may be sufficient in the smaller power range of 5–10 kW, but for a higher power range it is unlikely that passive cooling suffices. Applications requiring larger power outputs, may among many other applications, include the actuation of large crane manipulators, where ECD architectures up to 80 kW or even bigger have been investigated by simulation studies in [
33,
34,
35]. These studies however did not include thermal considerations. In the design phase of an ECD, it would be beneficial to understand the thermal behaviour of the system and to estimate to what extent cooling efforts are needed, prior to system realization. Nevertheless, research aiming at understanding and analysing the thermal behaviour of ECDs is limited. The authors in [
36] measure and compare efficiencies of a pump-compensated ECD, showing drastically reduced efficiencies at ambient temperatures below 0 °C. In [
37,
38], a thermo-hydraulic model is formulated in the commercially available software Simulation X, but compares this with measurements for a limited period of time, making it difficult to determine the accuracy of the model. In [
39] a simple first order thermal model is proposed and used to actively control the average temperature of the system. It is unclear if the accuracy of the proposed thermal model is sufficient for system design purposes as well. In [
40,
41], a Simulation X model is formulated, and a good accuracy between measurements and simulation results is demonstrated. The parametrisation of the thermal model is elaborate, however, as a high number of solid thermal capacities are included. The current paper can be viewed as the continuation of the work in [
40,
41], as this paper investigates the trade-off between model complexity and accuracy based on the ECD system and experimental results presented in these references. The paper investigates two different thermal model complexities—the
benchmark and the
reduced model. The
benchmark model is based on a relatively fine meshed discretization of the solid thermal capacities leading to an elaborate thermal submodel. On the other hand the
reduced model features a more coarse discretization, leading to a simpler thermal model structure, making this suitable for design purposes.
The paper contributes to the research field by deriving the necessary equations, including descriptions of the fluid properties, needed to model the pressure and temperature dynamics of an ECD. Both of the considered model complexities were simulated using the equations derived in this paper to ensure comparability and full transparency. Note that the simulation results obtained in [
40,
41] are therefore not reused in this paper. To validate the derived models, these are compared to the experimental data obtained in [
40,
41].
For the mentioned references, the models are commonly based on a lumped parameter approach, which is also the case for this paper. This means that appropriate control volumes are defined assuming pressure and temperature to be homogeneous within the control volume [
42]. This approach reduces the model complexity and needed computational effort greatly compared to finite element or computational fluid dynamics (CFD) methods, which are assessed to be too elaborate for system design purposes. Note that a system designer is desiring to roughly anticipate the system temperatures, and to do this with minimal effort and prior information.
The paper is organised as follows: In
Section 2 the temperature and pressure dynamics of a lumped control volume are derived from first principles physics and in
Section 3 consistent fluid properties of the oil–air mixture are derived.
Section 4 presents the ECD prototype used for verification of the derived thermo-hydraulic model and
Section 5 formulates the two thermal model complexities of the ECD prototype denoted the
benchmark and
reduced model. In
Section 6, examples of calculating heat transfer resistances for basic geometries are given and used to parametrise the
reduced model.
Section 7 concludes the modelling part of the paper by deriving mass and enthalpy flow component models.
Section 8 finally compares the simulation results of the two model complexities with experimental data. In the Nomenclature (
Appendix A), the symbols used in the paper are listed.
2. Control Volume Dynamics
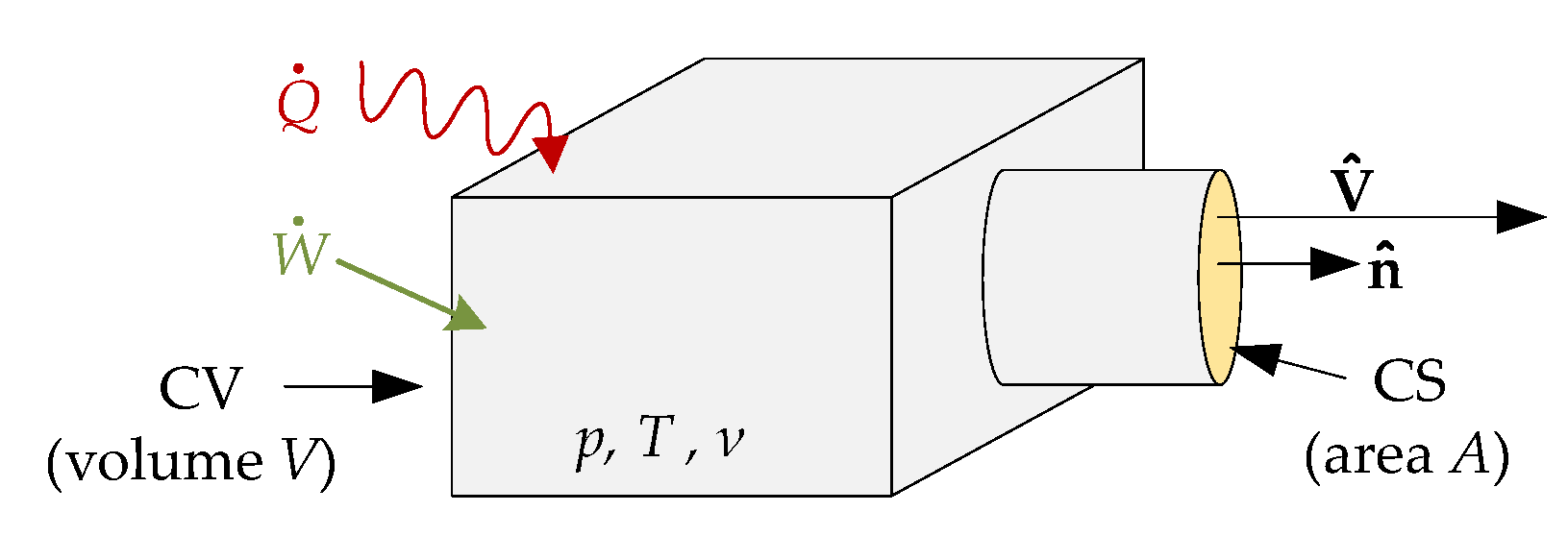
In this section, the pressure and temperature dynamics for a lumped control volume are derived from first principles physics, i.e., conservation of mass and energy. For a general control volume (CV), as seen in
Figure 2, the continuity equation and the first law of thermodynamics may be written as Equations (1) and (2), respectively [
43]:
is the fluid density, is the velocity vector of the fluid leaving the control volume across the control surface (CS) with normal vector . Thus, the mass flow leaving the control volume is positive. u is specific internal energy, and are kinetic energy and potential energy per unit mass, respectively. and are heat flow transferred to and net rate of work done on the system, respectively.
2.1. Lumped Pressure Dynamics
Consider Equation (1), and assume that the density is homogeneous in the CV and on the CS. Allowing for mass exchange to occur across multiple control surfaces leads to the following simplification of the continuity equation in Equation (1):
where
V is the volume of the CV, and the index
i is used to sum over incoming mass flows while
k denotes leaving mass flows, such that
. The density is an intensive property and may, by the state postulate, be expressed as a function of two independent intensive properties e.g., temperature and pressure. A change in density may be established by the total differential [
44]:
The partial derivatives in Equation (4) may be expressed using material properties, recognizing that the isothermal bulk modulus
and the isobaric expansion coefficient
are defined as [
45,
46]:
where
is the specific volume (
). Substituting Equation (4) into Equation (3) combined with the material properties from Equation (5), and isolating for
yield:
Hence, the pressure dynamics of a lumped control volume is given by Equation (6).
2.1.1. Mechanical Elasticity
To include mechanical elasticity, i.e., expanding hoses or pipes for increasing pressures, the volume in Equation (6) is calculated as:
where
is the volume at
, and may include a fixed volume as well as a time dependent volume, e.g., a stoke dependent volume if the control volume is a cylinder chamber.
is a tuning parameter such that a high value of
corresponds to a stiff volume, whereas a low value corresponds to an elastic volume. Inserting Equation (7) into Equation (6) yields:
where
is the effective bulk modulus, including the effect of mechanical elasticity. If
approaches infinity,
approaches
and
approaches
V, such that Equation (8) approaches Equation (6).
2.1.2. Diaphragm and Bladder Accumulators
Control volumes contained in a gas-loaded diaphragm or bladder accumulator are modelled without including mechanical elasticity. This is appropriate because nitrogen is much more compliant than the mechanical structures. For ECDs, the accumulator is operated at low pressures and room temperatures, i.e., far away from the critical point [
46], justifying nitrogen to be modelled as an ideal gas. The volume and
of the oil in the accumulator control volume are therefore found as:
where
is the accumulator volume (constant),
is the gas volume, and
is the oil volume outside the accumulator shell, which may include a fixed volume or a volume changing in time.
is the gas temperature and finally
and
, are the precharge pressure and temperature, respectively. Assuming the gas and oil pressure to be equal, and by combining Equation (10) with Equation (6) yield
as:
Note that T is the oil temperature and is the gas temperature. It can be seen that if the accumulator is removed ( = 0) Equation (11) equals Equation (6).
The gas temperature may be assumed to equal the temperature of the accumulator shell, by assuming the gas compression to be an isothermal process. However, to include temperature changes due to compression, consider the first law of thermodynamics in Equation (2). Assume the density to be homogeneous within the control volume, the kinetic and potential energies to be negligible and acknowledge that mass is not exchanged across the control surfaces:
where
U is internal energy of the gas,
is the mass of the gas and
is the isochoric specific heat. Equation (13) originates from the state postulate by taking the total differential of the internal energy as a function of pressure and volume and expressing the partial derivatives using fluid properties [
47]. For ideal gasses
and
leading to
. Recognizing the rate of work done on the gas is by compression (
) and combining Equations (12) and (13) yield the gas temperature dynamics as:
Instead of calculating the transferred heat
using the convection heat transfer coefficient
h and the surface area
A,
is modelled using a fixed thermal time constant defined as
[
48,
49,
50].
is the temperature of the accumulator shell.
2.2. Lumped Temperature Dynamics
For hydrostatic transmission systems kinetic and potential energies are small compared to internal energy and flow work (enthalpy) and thus neglected [
41,
51] in the first law of thermodynamics in Equation (2). Additionally, the assumptions given in
Section 2.1 are imposed, i.e., assuming uniform density and specific internal energy distribution in the control volume and on the control surfaces. By allowing mass transfer to occur from several control surfaces Equation (2) simplifies to:
Defining specific enthalpy as
, the term
can be rewritten to
.
is expressed as a function of temperature and pressure [
52]:
The partial derivatives are rewritten using material properties based on [
47,
52,
53]. Inserting Equation (20) into
leads to:
in Equation (18) has the form of either rate of shaft work, rate of moving boundary work (MBW) or rate of flow work [
54]:
Inserting Equations (21) and (23) in Equation (18), and isolating for the temperature derivative:
Thus, the temperature dynamic of a lumped control volume is given by Equation (26).
3. Fluid Properties
The pressure and temperature dynamics in the previous section were derived from the conservation of mass and energy. For this to be upheld during a numerical simulation, the material properties need to fulfil the relationships stated in Equation (5). One approach for doing so is to use a density description as the starting point for deriving the remaining mass/volume related properties. The oil density,
is modelled as a function of pressure and temperature and approximated by a first order Taylor series expansion:
where
and
are oil properties at
= 288.15 K and
= 101,325 Pa. Especially at low pressures, free air present in the oil affects the fluid properties. To include this, the density of the free air
is modelled as an ideal gas, compressed during a polytropic process [
46]:
where
R is the gas constant for air,
is the air temperature at the current pressure
p, assuming polytropic compression from
with polytropic coefficient
.
T is the lumped temperature of the oil–air mixture. The density of the oil–air mixture is found as:
where
,
and
are the air density and the volumes occupied by air and oil at
and
, respectively.
is defined as the volumetric ratio of air in the mixture at
and
, such that Equation (29) rewrites to:
The mixture density can thus be written as a function of pressure and temperature:
The bulk modulus
, and expansion coefficient
of the mixture are found from the definitions in Equation (
5):
The specific heat,
, is considered only for the oil due to a small mass fraction of air in the mixture. A volume fraction of air of 10% (
) at atmospheric pressure yields a mass fraction of air less than 0.2%. The specific heat is assumed to be only a function of temperature, and is given for a HLP32 oil in [
55] as:
and
are modelling parameters found in
Appendix B. The specific enthalpy of the oil–air mixture is approximated by the differential equation in Equation (19) as a finite difference [
56]:
where the notation
denotes material properties evaluated at the mean temperature and pressure. The specific enthalpy equals 0 J/kg at
=288.15 K, and
=101325 Pa.
In order to calculate the thermal resistances in
Section 6, additional fluid properties are needed, including the dynamic viscosity,
, and thermal conductivity,
k. These are modelled as oil properties, i.e., without considering the air in the mixture. The dynamic viscosity of an HM46 oil is modelled by the Vogel–Barus model [
57], and the thermal conductivity is calculated as a first order polynomial using fluid properties extracted as a function of temperature from the Equation Engineering Solver (EES, V10.836) library:
where
are modelling coefficients that are given in
Appendix B.
3.1. Temperature Independent Density
The temperature and pressure dynamics derived in
Section 2 (Equations (6) and (26)), are coupled via the thermal expansion coefficient
. As the numerical value of
is small (≈0.0007 K
), the coupling between the pressure and temperature dynamics may be neglected without sacrificing much accuracy in terms of the main dynamics [
56]. To simplify the model formulation, it is profitable to decouple pressure and temperature dynamics by assuming
= 0. However for mass to be conserved, the remaining volume and mass related properties (
and
) must be consistent with this assumption. This can be obtained by assuming the density of oil and air only being pressure dependent, such that:
where the notation
denotes properties assumed to be temperature independent. By Equation (37), the temperature independent properties can be expressed as:
The definitions in Equations (38) and (39) yield = 0, as desired.
3.2. Comparing Modelled and Measured Fluid Properties
In [
55], the density of an HLP 32 oil was measured as a function of temperature and pressure. These measurements are used to fit the parameters of
,
and
in Equation (27). In
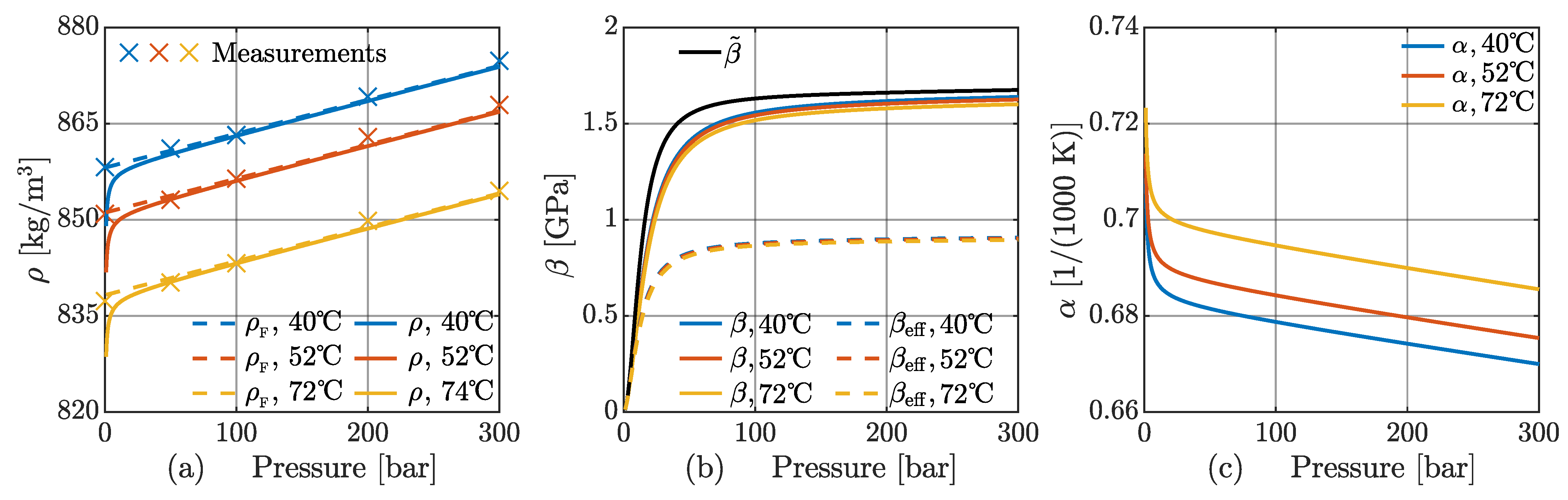
Figure 3a, a good fit between the modelled density and the measurements from [
55] is observed. In the plot, the density of the oil–air mixture is also shown. The bulk modulus and thermal expansion coefficients are shown in
Figure 3b,c.
Figure 3b includes the effective bulk modulus,
, considering mechanical elasticity, as introduced in Equation (8). Introducing mechanical elasticity lowers the bulk modulus compared to just considering the oil–air mixture.
This concludes the derivation of the lumped thermo-hydraulic model, including definition of consistent fluid properties. Models of the heat, mass and enthalpy flows entering the control volumes are defined subsequently. The ECD prototype used for experimental investigation is introduced next.
5. Thermo-Hydraulic Model Formulation
In this section, the lumped thermo-hydraulic model derived in
Section 2, is utilised to model the pressure and temperature dynamics of the ECD prototype, presented in the previous section.
Two model complexities are presented subsequently. The model denoted
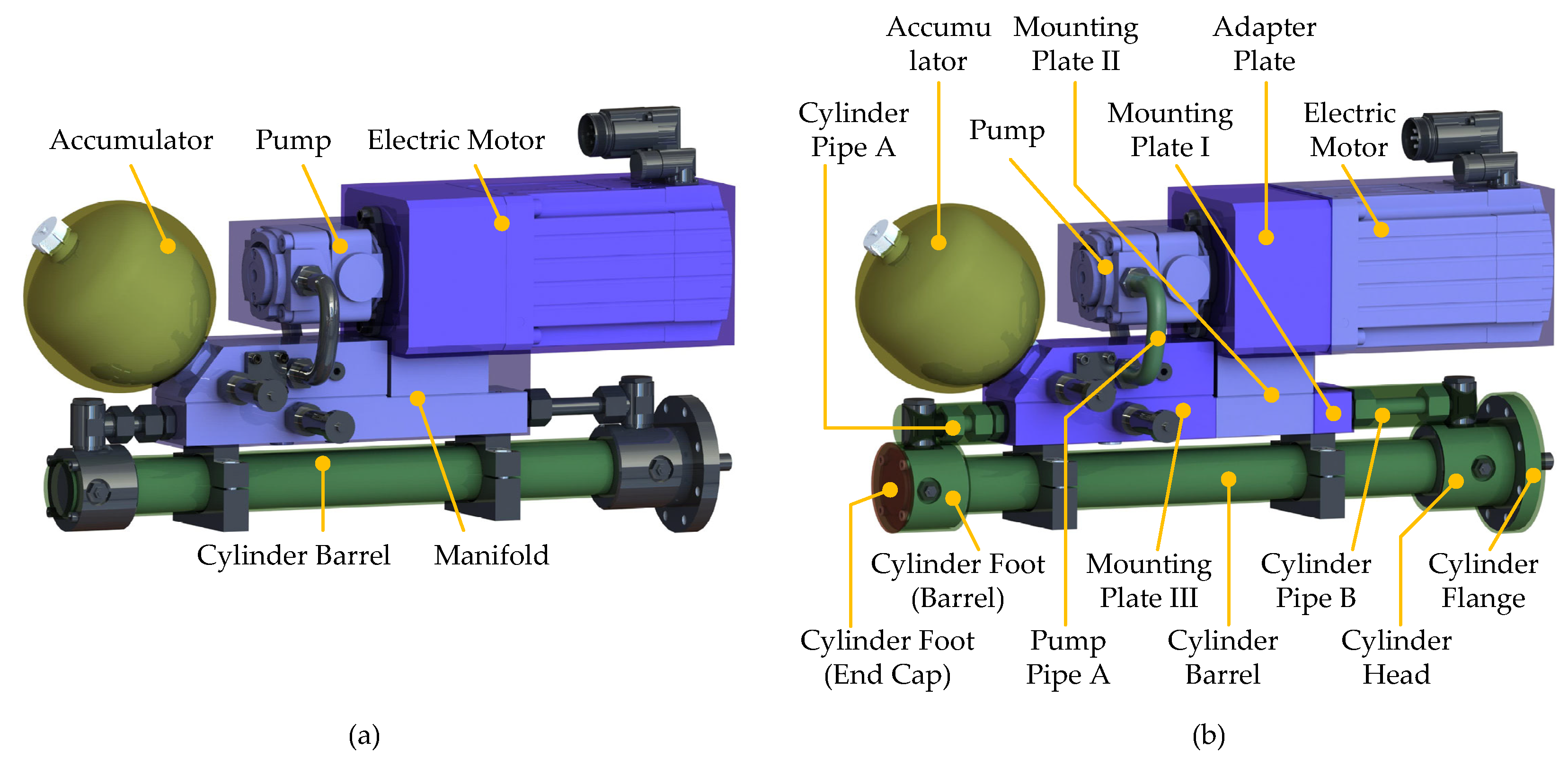
benchmark model, utilises a relatively fine meshed discretization of lumped solid thermal capacities, including all of the named components in
Figure 4. To describe the heat transfers occurring internally in the system and to the surroundings an extensive thermal resistance network is defined. This thermal network was developed in previous publications [
40,
41], and is used here as a benchmark for model validation and for comparison with a simpler model complexity, i.e., the
reduced model.
In the
reduced model, a significantly coarser discretization is utilised. In [
40,
41], the forced convection resistances were found to be negligible, as the thermal behaviour was governed by natural convection and radiation from the system to the surroundings. Therefore, the
reduced model investigates, among other things, how model accuracy is affected by neglecting forced convection resistances. Neglecting the forced convection resistances may be done in several ways. If commercial simulation software is used, arbitrary small forced convection resistances may be defined to maintain the number of lumped temperatures. Alternatively, the temperature dynamics of multiple fluid and solid control volumes may be lumped together, thus reducing the number of temperature states in the model. The latter approach is featured here. As the temperature dynamics of multiple fluid volumes are lumped together, it is beneficial to neglect the coupling between the temperature and pressure dynamics by utilising temperature independent fluid properties, as given in
Section 3.1.
Table 1 compares the two model complexities.
The reason for dealing with two model complexities is to investigate how much information and accuracy are lost when reducing the model complexity. As seen from
Table 1, the current study especially investigates the needed level of detail for the thermal submodels, including the number of thermal resistances used to model heat transfers in the system. The
benchmark model demonstrated a good ability to provide accurate temperature simulations for most of the thermal capacities in [
41]. However, parametrising the 62 thermal resistances present in the
benchmark model is both a time-consuming and tedious task. In addition, for instance, the forced convection resistances occurring in the flow channels of a custom made manifold requires detailed knowledge about the construction of this to parametrise the resistances. Such detailed information may not be available during the design phase, where a design engineer desires to estimate the operating temperature for a given ECD under some loading conditions. To address the potential challenges of the
benchmark model, a drastically reduced model, which requires limited information for parametrisation, was investigated. This includes cylinder and accumulator dimensions as well as approximate dimensions of manifold, pump and electric motor. As such, the current investigation may be regarded as a natural next step toward a simple but yet sufficiently accurate model level. The authors claim that if a thermo-hydraulic model should be useful for a design engineer, it should be relatively easy to parametrise even though this may decrease the accuracy. By the end of the day, approximate estimations or rough ideas are more useful than very accurate simulations that are never carried out due to time-consuming model development or parameters unknown during the design phase. Estimating the operating temperature is important to determine to what extent cooling is required, i.e., to obtain a proper thermal design. This may include the addition of a fan, heat pipes mounted in the manifold, an oil cooler or a water cooled manifold.
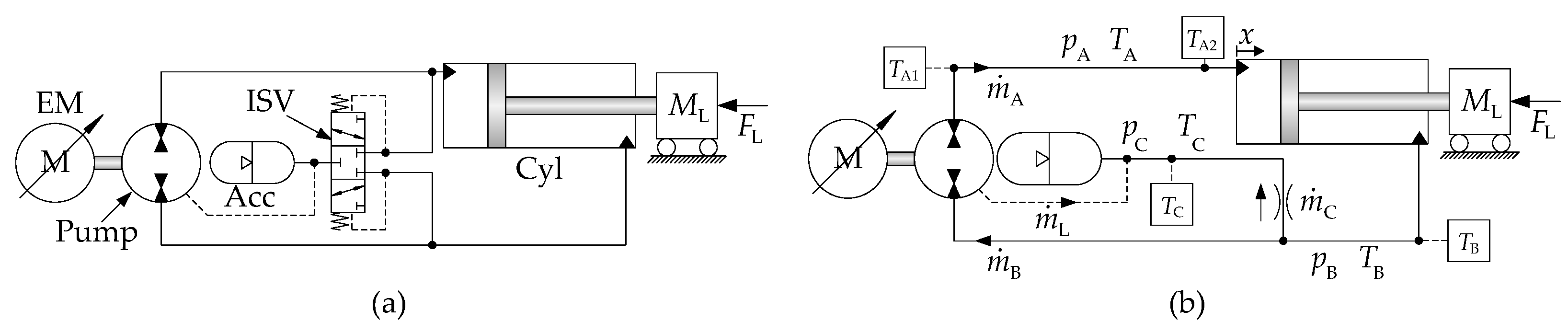
The following sections show the derivation of the two model complexities, with an offset in the system diagram in
Figure 5b.
5.1. Benchmark Model
The pressure dynamics of the
benchmark model are formulated as:
The subscripts
in Equations (40)–(42) refer to the piston chamber, the rod side chamber and the accumulator, respectively, according to
Figure 5b.
The gas temperature is modelled using Equation (14). The temperature dynamics of the oil control volumes are modelled from Equation (26) as:
where
,
and
are the sum of heat flows to the control volumes,
,
and
are the pump enthalpy flows to the control volumes.
and
are the enthalpy flow through the orifice. The enthalpy flows are modelled in
Section 7.
The
benchmark model discretises the system into 18 solid thermal capacities each associated with an individual temperature. The temperature dynamics of a solid capacity is modelled as:
where
j is indexing the 18 solid capacities and
i the heat transfer to the solid capacity.
is the net sum of heat flow into capacity
j,
is the mass of the solid capacity and
is the specific heat for the given solid material modelled as a function of the temperature. Specific heats as a function of temperature are obtained from the library of EES, and implemented as 1D lookup tables. The heat flow is described using the concept of thermal resistances,
. Analogous to an electric circuit, the temperature (voltage) may be described as the product of heat flow (current) and the thermal resistance [K/W].
is thus the sum of all heat flows through the thermal resistances connected to the capacity, and
is the temperature difference across the thermal resistance. The heat flows to oil and solid capacities may be visualised by a thermal resistance network. The resistance network for both the
benchmark and the
reduced model are presented in
Section 6.
5.2. Reduced Model
The pressure dynamics of the reduced model are similar to the dynamics from Equations (40)–(42), except that temperature independent fluid properties, and , are utilised. This entails that the temperature coupling term () vanishes.
Whereas the
benchmark model includes 18 solid thermal capacities, the
reduced model only includes five. These are the electric motor and adapter plate, the cylinder barrel, the manifold, the pump and the accumulator. In
Figure 6a, these are illustrated as basic geometries, which are used for heat transfer calculations. These include cubes (blue), horizontal cylinders (green) and spheres (yellow). For comparison,
Figure 6b shows 15 of the 18 considered solid thermal capacities approximated as basic geometries used in the
benchmark model.
As noted in [
40], the thermal behaviour of the system is governed by the natural convection and radiation resistances on the outer surfaces as these are considerably larger than the forced convection resistances between the oil and the solid materials on the inner surfaces. Taking the cylinder barrel as an example, the combined natural convection and radiation resistance is more than nine times higher than the forced convection resistance. In the
reduced model, this observation is exploited by neglecting all forced convection resistances, except the forced convection between oil and accumulator, and thus reducing the number of thermal resistances significantly.
This has the implication that all solids being in contact with oil (accumulator not included) are modelled to have the same temperature. This leads to a further simplification compared to the benchmark model, as contact and conduction resistances between solid thermal capacities are omitted. However, as a consequence, only three distinct temperatures are modelled in the reduced model. These include the oil temperature in the accumulator , the accumulator shell temperature and the lumped system temperature, , combining the thermal capacity of the oil in the A and B chamber with the cylinder barrel, pump, manifold, electric motor and adapter plate capacities. Even though the electric motor and adapter plate are not in contact with the oil, these are included in the lumped system temperature due to large contact areas with the pump and manifold, thus assuming the contact resistance to be small. All other thermal capacities, such as pipes, cylinder flanges, etc., are not included in the reduced model. This means that only approximate dimensions of the main system components are needed to parametrise the thermal resistance network.
The temperature dynamics of the three control volumes of the
reduced model are given as:
to
are heat flows through the thermal resistances defined in the next section.
and
are the mass of steel and aluminium with temperature dependent specific heats
and
, respectively.
,
and
are hydro-mechanical pump losses, cylinder friction losses and losses of the electric machine, respectively. These are modelled in
Section 7 along with the enthalpy flows
.
6. Thermal Resistance Networks
In this section, the heat flows to the control volumes and the solid capacities for both model complexities are presented. As mentioned, the heat flows are calculated based on the temperature differences across thermal resistances. This may beneficially be visualised using a thermal resistance network. The thermal resistance network for the
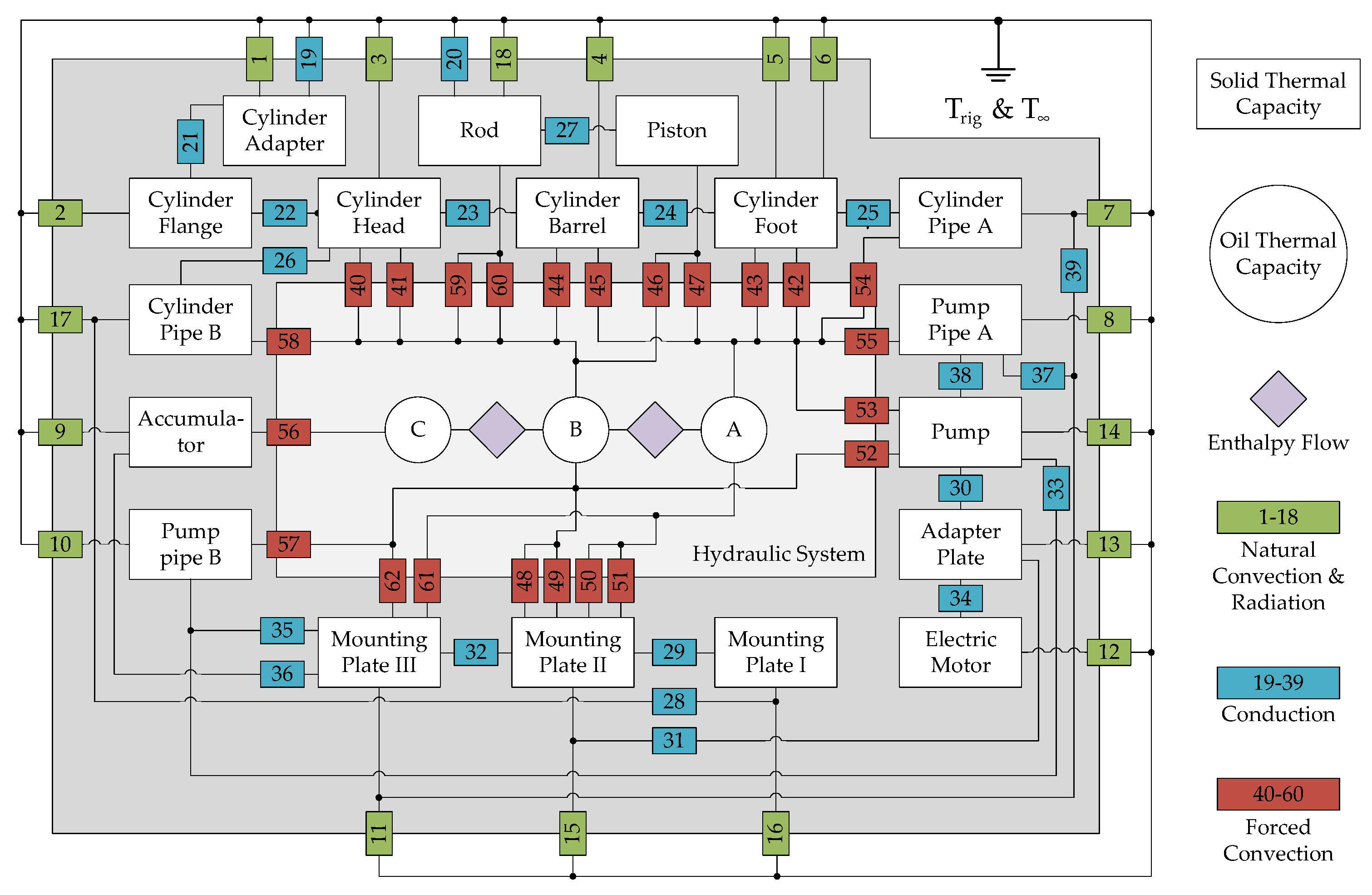
benchmark model was derived in [
41] and is shown in
Figure 7.
The 62 thermal resistances in
Figure 7 were computed in [
40,
41]. Examples of how to calculate thermal resistances for different geometries and flow conditions are given in
Section 6, when calculating resistances for the
reduced model.
In addition to heat exchanged through thermal resistances, heat is also ascribed as the consequence of energy losses of the components. The power loss due to cylinder friction is entirely added to the cylinder barrel, 25% of the pump friction losses are added to each of the oil control volumes A and B and the remaining 50% are added to the pump housing. Finally, the electric motor power losses are added to the solid capacity of the electric motor. Leakage and valve throttling losses are ascribed inherently by the enthalpy flows.
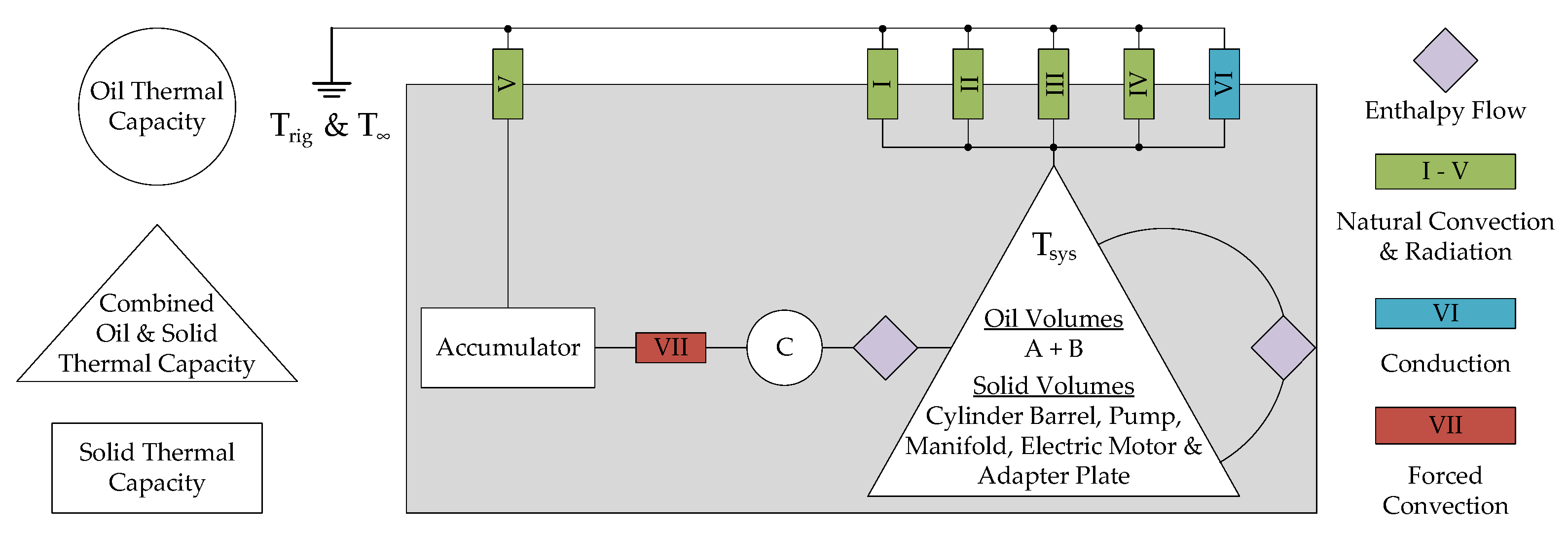
The thermal resistance network for the
reduced model is given in
Figure 8. In addition to natural convection and radiation from the five basic shapes in
Figure 6a, forced convection between oil and accumulator as well as heat conduction (contact resistance included) from the cylinder barrel through the cylinder head and flange to the test-rig are included.
The seven thermal resistances from
Figure 8 are found as either conduction, convection or radiation resistances given as [
46]:
where
is the conduction resistance (here for a plane wall example) modelling the heat transfer through a material.
L is the length of which the heat transfer occurs,
k is the thermal conductivity of the material and
A is the cross-section area.
is the contact resistance, with
being the contact conductance.
is forced or natural convection resistance. Forced convection occurs between oil and solid elements, whereas natural convection takes place at the outer surfaces of the system, as no fan is incorporated in the system.
h is the convective heat transfer coefficient.
is the surface area.
is radiation resistance, with
being the effective radiation surface area.
is the surface emissivity and
is the Stefan–Boltzmann constant.
and
are the surface temperature and the ambient temperature, respectively.
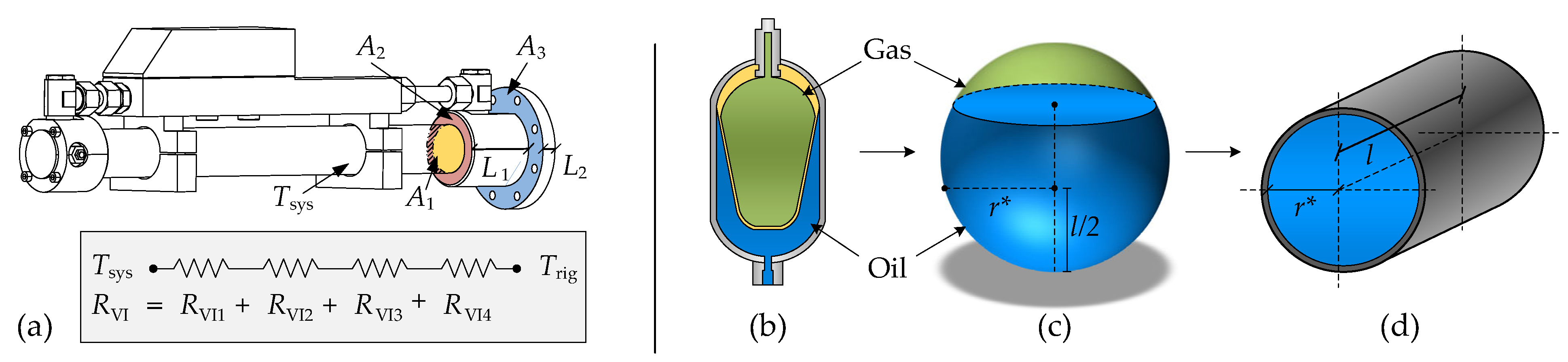
6.1. Heat Conduction
Only heat conduction from the cylinder barrel through the cylinder head and flange to the test-rig is included in the
reduced model. The test-rig is considered as a thermal reservoir, thus remaining at a constant temperature. The heat transfer is modelled as a serial connection of two conduction and two contact resistances (
and
in Equation (48)). The apparent contact areas for calculation of the contact resistances are given in
Figure 9a as
and
. The conduction resistances are modelled with areas
,
and lengths
,
.
6.2. Convection
The convective heat transfer coefficient,
h in Equation (48), may be determined from the average Nusselt number (Nu). The Nusselt number is a function of the Reynolds (Re) and Prandtl (Pr) numbers for forced convection problems, and the Rayleigh (Ra) and Prandtl numbers for natural convection problems.
where
is the geometry dependent characteristic length,
is the mean flow speed and
g is the gravitational acceleration. For natural convection problems, the fluid properties of the ambient air are calculated at the reference temperature
, i.e., at the mean temperature between surface and surroundings. Fluid properties for forced convection problems are evaluated at the lumped pressure and temperature of the oil control volume using the expressions derived in
Section 3.
The Nusselt number depends on geometry, and the methodology utilised here is to identify an appropriate approximation of the considered shape, such that well-known methodologies and formulas valid for basic shapes may be applied. This is done in
Figure 6a, where the outer surfaces of the ECD prototype is approximated using the basic shapes of a cube (electric motor and adapter plate, pump and manifold), horizontal cylinder (cylinder barrel) and sphere (accumulator).
To illustrate this approach further, consider the accumulator, which is approximated by a sphere for calculation of the natural convection resistance, as seen in
Figure 9b,c. The forced convection between the oil and the accumulator shell is modelled by approximating the flow as an internal pipe flow. The length and diameter of this pipe are updated according to the oil level in the accumulator, which is illustrated in
Figure 9c,d. The fluid height present in the virtual sphere is calculated dependent on the oil volume in the accumulator, and is used as the pipe length when calculating the Nusselt number. The pipe diameter is approximated as the diameter of the spherical cap containing the oil at half the oil height, as illustrated in
Figure 9c.
Table 2 shows the expressions for calculation of the Nusselt numbers for the geometries and flow conditions considered in the
reduced model, obtained from [
59,
60]:
The heat transfer coefficients for natural convection calculated based on the Nusselt numbers given in
Table 2 are valid for idealised conditions. In technical environments such as workshops, factories, etc., the heat transfer coefficients can be assumed to be up to 20% larger than the theoretical values, according to [
61]. This is due to ambient air flow occurring from windows, doors, people walking around, etc. In [
41], experiments identified that the ambient conditions caused the natural heat transfer coefficients to be 16% larger than the theoretical values. For a fair comparison between the
benchmark and
reduced model, all natural convection heat transfer coefficients used in this paper have been increased by 16% compared to their theoretically obtained counterparts.
6.3. Radiation
All bodies above 0 K emit thermal radiation. However, for the current study, radiation heat transfer is assumed to only occur between the solid elements and the surroundings, and not internally between the solid elements. As seen in Equation (48) the effective radiation surface, , is utilised instead of the actual surface area , acknowledging that solid elements may be shadowing each other. This means that the effective radiation area is smaller than the actual surface area. This effect is included in the benchmark model, however, the reduced model assumes , as the shadowing effect is difficult to determine without accurate knowledge of the relative placement of the solid components.
6.4. Thermal Resistances in the Reduced Model
In
Table 3, the seven thermal resistances of the
reduced model are exemplarily calculated. The resistances have been evaluated at oil and solid temperatures of 60 °C, an ambient temperature of 20 °C, fluid velocities present for a piston speed of 150 mm/s and at the initial oil level in the accumulator. As mentioned, the heat transfer coefficients have been increased by 16% compared to the idealised values to reflect the ambient flow conditions. Please note that the resistances are updated during the simulation, and the values given in
Table 3 are only given as an example to illustrate the order of magnitude.
The simple thermal resistance network and the associated numerical values of the resistances given in
Table 3 enable performing some rough estimations of the static thermal behaviour of the system. From
Figure 8, the equivalent thermal resistance to the surroundings from the lumped system components, at
, is 0.120 K/W (assuming
). If the average losses of the ECD are 450 W, this yields a static system temperature of 54 °C above the ambient temperature. Note that this is a rough estimate as the thermal resistances in
Table 2 are temperature dependent themselves.
In [
41], one of the main conclusions was that the modelled temperature was sensitive towards estimation errors of the power losses. The equivalent thermal resistance of 0.12 K/W may also be used to approximate the sensitivity towards estimation errors of the energy losses of the system or the thermal resistances. Assume the average losses to be estimated within ± 20%. This would result in estimated static temperatures in the range from 43 °C to 65 °C above ambient temperature, showing a relatively large sensitivity towards power loss estimating errors.
Furthermore,
Table 3 shows that the surface area weighted mean of the combined heat transfer coefficients for natural convection and radiation is 10.2
. Note, if the theoretical natural heat transfer coefficients are used this number would equal 9.5
. Assuming this to be the only heat transfer occurring in the system, i.e., neglecting forced convection and conduction, this may be used as an approximate number, in the early design phase of an ECD to assess if special attention is required for the thermal design. As such it may be possible for a design engineer to roughly estimate the static thermal behaviour of the ECD, if an estimate of the system losses and the outer surface area can be established.
8. Results
The ECD prototype presented in
Section 4 was tested in the laboratory by controlling it to follow a sinusoidal position reference with a frequency of 0.4 Hz (
= 2.5 s), reaching maximum cylinder and motor speeds of ±300 mm/s and
RPM, respectively. A constant load force of 5 kN is requested by the load cylinder, but due to friction and load dynamics, this is found to be varying between 3.9 kN and 5.7 kN. The test continued for a period of three hours until thermal equilibrium was reached. Oil temperatures were measured using four thermocouples (see position in
Figure 10a) with an accuracy of ±0.5 K. The surface temperatures of the prototype were monitored by a thermo-graphic camera having an accuracy of ± 1.5 K. The measured load force and the position reference were used as the simulation inputs. The derived governing equations were simulated in MatLAB Simulink using the ODE45-solver, with a maximum stepsize of 1/5000 s. Using a laptop with an Intel i7-10610 1.8 GHz processor, a 10 min simulation of the
benchmark model was completed within 20 min, whereas the simulation of the
reduced model was completed within 13 min.
8.1. Loss Behaviour
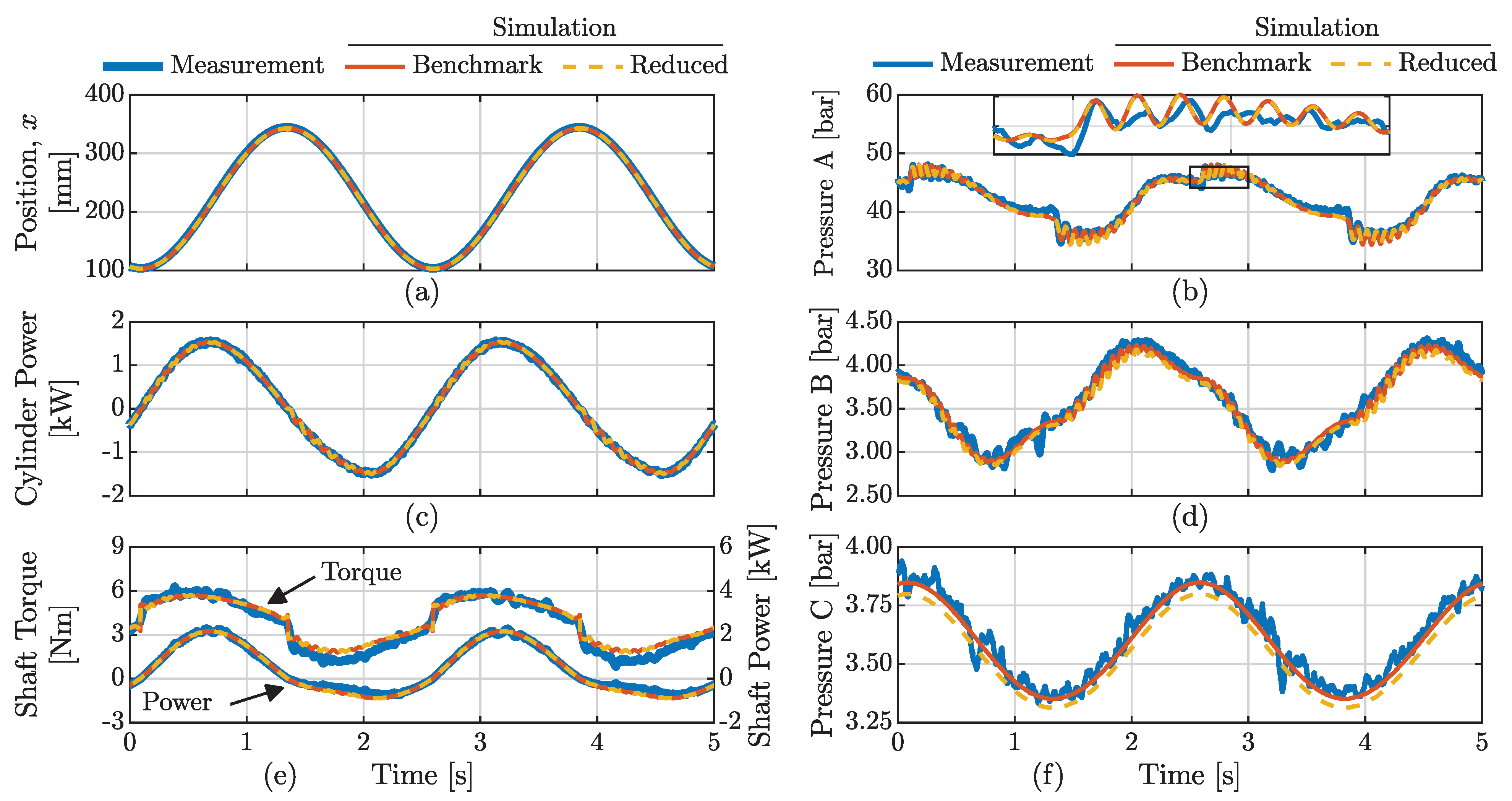
As illustrated in the previous section, the modelled temperature is rather sensitive towards inaccuracies between actual and modelled heat losses. Therefore, the simulated and measured loss behaviour is compared in
Figure 12.
Figure 12b,d,f show a good coherence between the measured and simulated pressure in all control volumes. For the pressure in the piston chamber (
), the oscillation frequency is modelled fairly accurately while the measured damping is slightly larger than the modelled damping. Interestingly, it is found that there are no noticeable differences between the pressures modelled in the
benchmark and the
reduced models, even though the dynamic pressure–temperature coupling is neglected in the
reduced model.
No noticeable differences are found between the two model complexities for any of the quantities visualised in
Figure 12, expect for the accumulator pressure. Here small deviations of approximately 0.05 bar can be seen.
Figure 12a shows a good coherence between the measured and simulated position. Combined with the accurately modelled chamber pressures, this leads to the cylinder power being modelled accurately, as seen in
Figure 12c.
Slight deviations exist between the modelled and estimated shaft torque and power during cylinder retraction, at ∼2 s and ∼4.5 s in
Figure 12e. On average, it is found that the input power to the hydraulic system and the output power are modelled with an acceptable accuracy. This means that the losses are established with a sufficient degree of accuracy for anticipating the thermal behaviour. In other words, deviations between modelled and simulated temperatures are assessed to originate from inaccurate heat transfer models rather than loss model deviations.
8.2. Static Temperatures
Even though the derived models are dynamic models, the transient temperature development is not important in some applications. If a system is going to perform the same task 24 h a day for 20 years, it is not important if static temperatures are reached after 10 min or 10 h. In this situation, only the static temperatures are relevant to ensure that the oil temperature stays within limits.
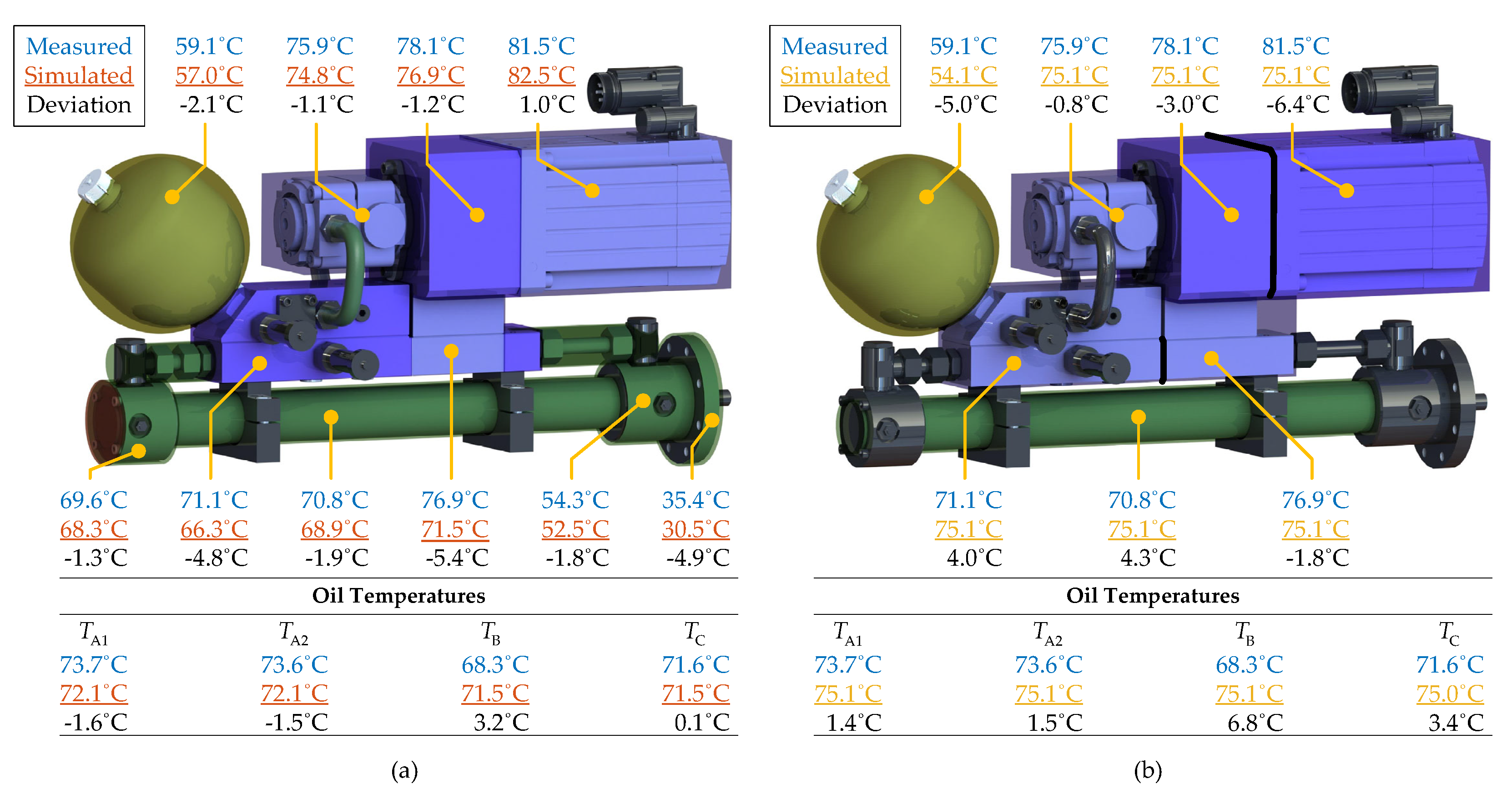
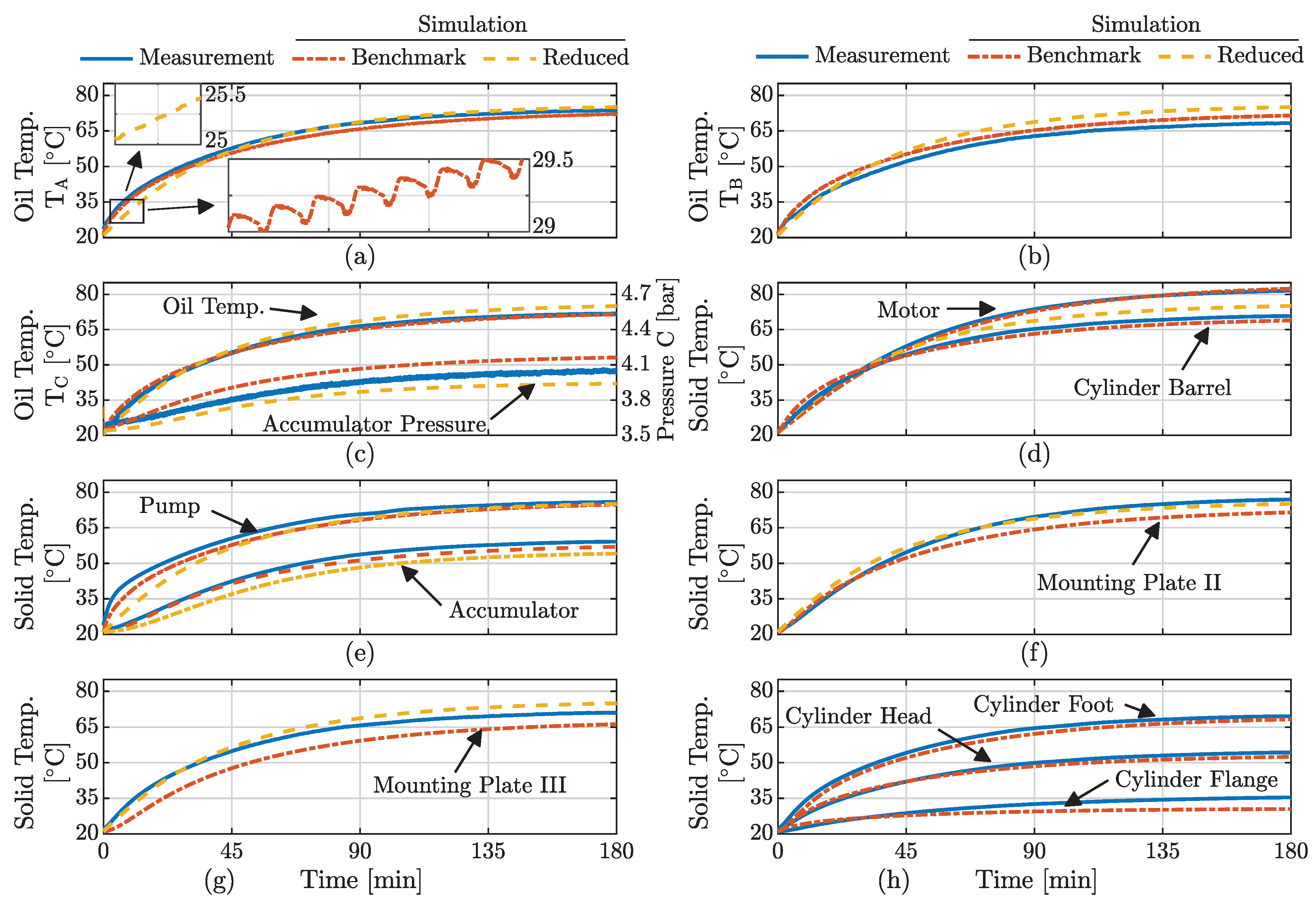
Figure 13a compares the
benchmark modelled oil and surface temperatures with the measured values. Regarding the surface temperatures, the high number of simulated thermal capacities in the
benchmark model pays off in terms of the ability to fairly accurately model the qualitative temperature distribution, e.g., the model predicts that the motor is warmer than the pump and that the cylinder head is colder than the cylinder barrel. This information is lost in the
reduced model due to the simplification of only including three thermal capacities. As seen in
Figure 13b, only two different surface temperatures are modelled, i.e., the surface temperature of the accumulator and the lumped temperature of the remaining system.
The
benchmark model in
Figure 13a models all surface temperatures within ±5.5 K. Furthermore the oil temperatures are estimated within approximately ±1.5 K, except for the oil temperature in the rod side chamber, which is overestimated with approximately 3 K. This is assessed to be satisfactorily accurate for analysis purposes, e.g., to analyse the effect of changing certain parameters such as areas and emissivities on the thermal behaviour.
As mentioned, the
reduced model in
Figure 13b is not formulated such that it is capable of predicting the individual temperature distribution of the system. This is because all system components, except the accumulator, are lumped in a single thermal capacity. This was chosen to avoid parametrising a high number of forced convection and conduction resistances. The modelled surface temperature of the system components are somewhat in-between the highest system temperature of the motor and the lowest system temperature of the cylinder barrel. Given the reduced complexity of the model, this is the expected result, but it leads to deviations up to 6.4 K, considering the surface temperatures.
In terms of the modelled oil temperatures in the
reduced model, these are overestimated by 1.4 K to 6.8 K. However, all modelled oil temperatures are larger than the measured, meaning that the simulated temperatures are conservative estimates, which is desired in terms of design tool applicability. For comparison, it can be noted that if the natural convection resistances have not been corrected for the ambient flow conditions, i.e., the idealised values are used, the modelled temperatures would be approximately 2 K larger, than the ones given in
Figure 13b.
A trade-off between modelling complexity and accuracy is identified in the comparison between the benchmark and the reduced model. Due to the simple thermal network, which may be parametrised relatively easy, this is much more applicable in the design phase, compared to the benchmark model. Furthermore, the reduced model produces reasonably accurate and conservative temperature estimates, which may be valuable to have available in the design phase. In this manner, important choices related to the thermal design of the system can be made on a fairly informed basis.
8.3. Transient Temperature
In applications where actuators are used on an on/off basis, i.e., the actuator is working for a limited time with cooling breaks in between the operating cycles, transient temperature behaviour may be relevant to optimise the thermal design.
Figure 14 compares the simulated transient temperature responses of the two model complexities and the measurements.
A general thing to observe from
Figure 14 is that the
benchmark model for most of the thermal capacities predicts the transient temperature more accurately than the
reduced model. The
reduced model heats up too slowly during the first 45 min, which can be explained by all system components being lumped together. This means that the transient temperature response is governed by the components with large heat capacities. In this case, this is the motor and the mounting plates (
Figure 14d,f,g). A reasonably transient fit is seen for these components in the
reduced model.
To illustrate how neglecting the dynamic pressure–temperature coupling in the
reduced model influences the transient temperature, consider
Figure 14a, where the oil temperature in the piston chamber,
, is shown. In the
benchmark model, temperature oscillations of ∼0.2 K are seen, and is due to pressure oscillations and the dynamic coupling by the thermal expansion coefficient
. In the
reduced model, the same pressure oscillations are present, as shown in
Figure 12b, but this does not result in any temperature oscillations, as the dynamic coupling is neglected. The temperature oscillations of the
benchmark model are, however, insignificant with respect to the dominating dynamics; thus, it is found that neglecting the dynamic coupling i.e., defining
is recommendable, as it enables a decoupled simulation of pressure and temperature dynamics.
Another difference arising as a result of neglecting the pressure–temperature coupling is visible in
Figure 14c, where the average accumulator pressure for one operating cycle is plotted. As the thermal expansion of the oil is defined as zero in the
reduced model, the accumulator pressure only increases due to thermal expansion of the gas in the accumulator. For the
benchmark model, the accumulator must contain a larger oil volume as the oil temperatures increase, resulting in a higher pressure compared to the
reduced model. However, both model complexities predicts the measured pressure within ± 0.15 bar, which is fairly accurate.
To sum up the presentation of the modelling results, it is found that there is a trade-off in terms of accuracy and thermal modelling complexity. Both model complexities, however, predict the temperature with an accuracy found to be reasonable for design purposes. Note that this is partly possible because the losses of the ECD prototype was modelled with a high degree of accuracy. For most applications, the relatively small differences in terms of modelled temperatures cannot justify the formulation of the elaborate thermal network of the benchmark model compared with the reduced model. Note that the number of resistances are reduced from 62 in the benchmark model to 7 in the reduced model. More importantly the seven resistances can be parametrised fully based on cylinder, motor, accumulator and manifold dimensions. These are available with some accuracy in the design phase of the system, thus making the reduced modelling framework a valuable tool for proper thermal design. To fully utilise the framework as a design tool, the modelling accuracy when including various heat transfer enhancing designs must be investigated. This may be the effect of including a fan, an oil cooler, heat pipes in the manifold or even a water cooled manifold.