Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview
Abstract
1. Introduction
- Modern AGC techniques in present and in future smart power systems that can incorporate renewable energy sources, different fast energy storage devices, HVDC, and FACTS devices.
- Intelligent and pattern recognition-based AGC techniques that can handle non-linearities, parametric variations, uncertain states in demand identifications, and dynamics of the different loads. Furthermore, different virtual inertial controllers (VIC), which can support and improve the inertial response of renewable energy-based AGC systems.
- AGC schemes in different configurations of microgrids including stand-alone single area and multiple area microgrids and support the integration of non-dispatchable and high intermittent distributed generation sources.
- AGC techniques in smart grids, which incorporate and improve different features including demand-side response, data forgery attacks, and two-way communications.
- Efficient AGC models in a deregulated framework that can enhance the economic efficiency and stability of the restructured power market.
- AGC techniques in conjunction with the Economic Dispatch (ED) factor to improve its economic efficiency.
- Industrial practices of different AGC models around the world to explore and analyze different issues related to its practical implementation in the field.
- The developmental history of AGC models in traditional and renewable energy power systems is explored, which considers various constraints in performing the frequency control analysis. These constraints include generation rate constraint (GRC) and governor dead band (GDB) nonlinearities, parametric variations, inertial response, time delay problems, observability of state variables, and other stability issues.
- The general concept of AGC models in a multi-area interconnected power system is explored and different objective functions, which are based on several criteria and used to eliminate the area control errors, are presented from the literature.
- A state-of-the-art study of AGC schemes, focused on classical and modern control theories, is presented for current and future smart power systems. Furthermore, various intelligent AGC schemes based on fuzzy logic and artificial neural networks are explored and various soft computing control algorithms are comprehensively analyzed. All these control methods are critically compared using the tabular method showing their merits and demerits.
- The article addresses several frequency management systems integrating small and large renewable energy sources into the power grid for frequency regulation purposes. Further, a comprehensive literature review on AGC strategies incorporating various energy storage systems (ESSs), HVDC interconnections, and FACTS devices is provided.
- A detailed overview of the AGC schemes in various microgrid configurations is presented and summarized for comparison in a tabulated form. Further, AGC approaches integrating various aspects of the smart grid are illustrated.
- The concept of a deregulated power system is addressed and the application and challenges associated with AGC implementation in different contract scenarios are presented.
- Different AGC schemes in conjunction with economic dispatch are reviewed from the literature and a detailed overview of worldwide AGC practices is provided to explore the industrial applications of AGC.
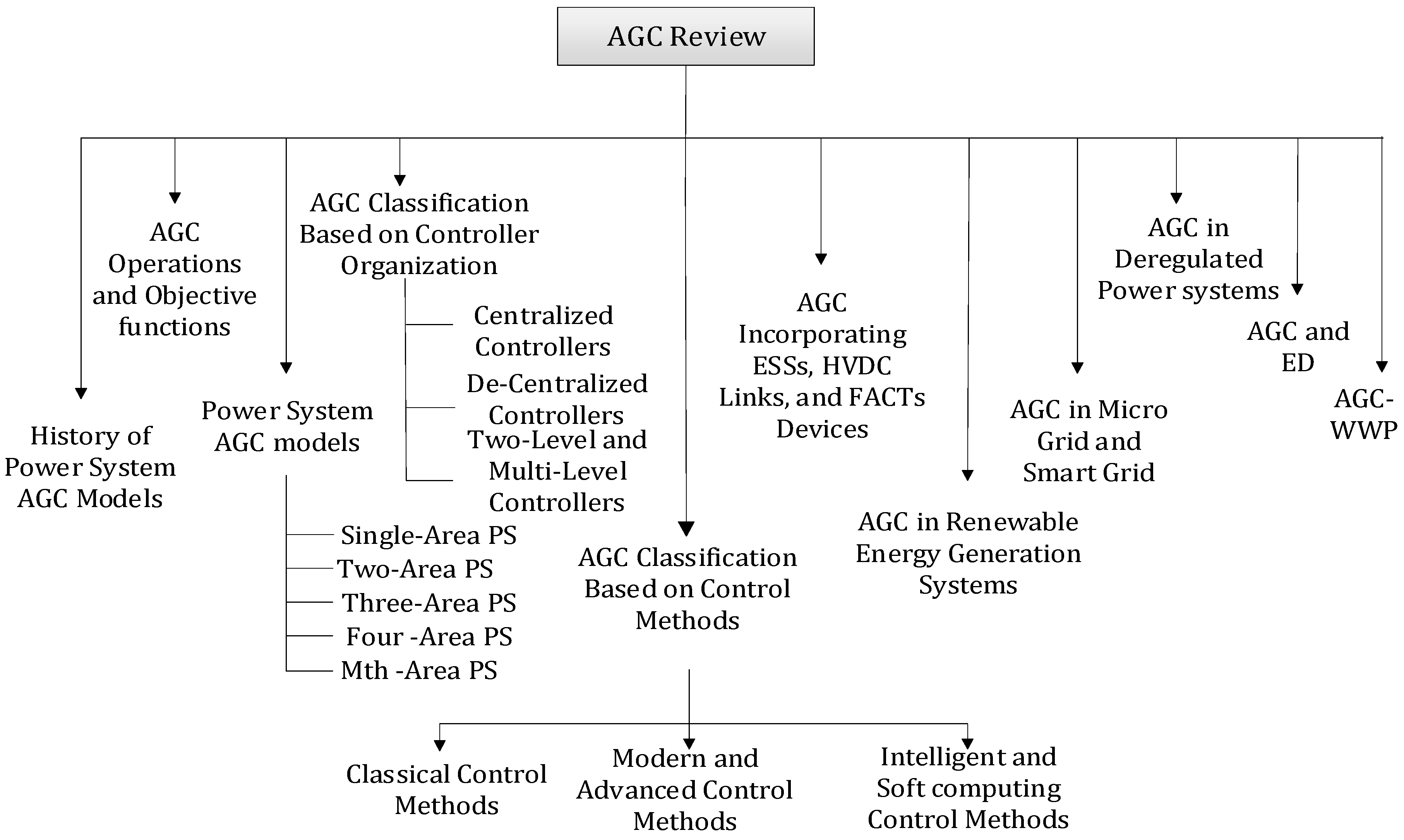
2. History of the Power System AGC Models
3. AGC Operation and Objective Functions
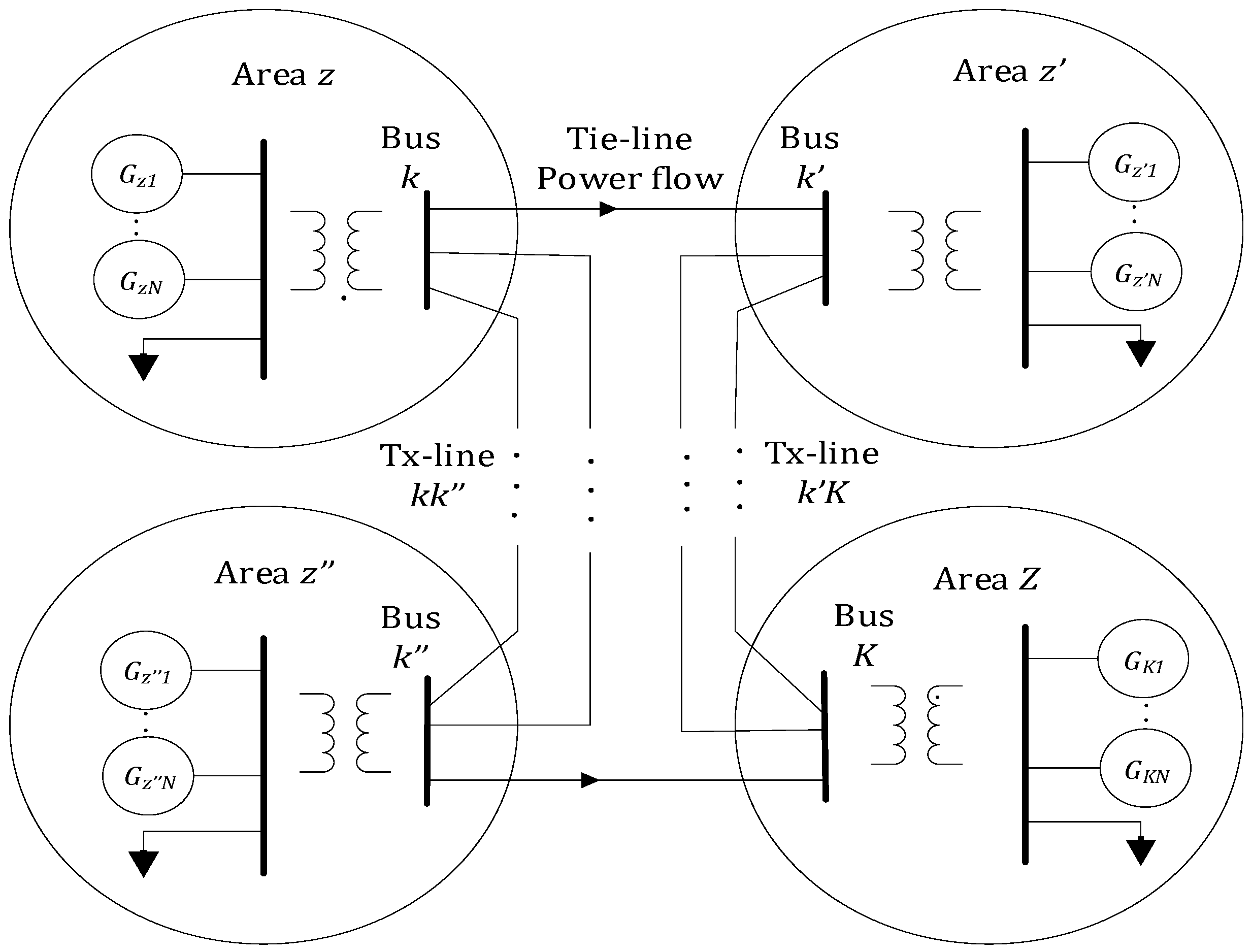
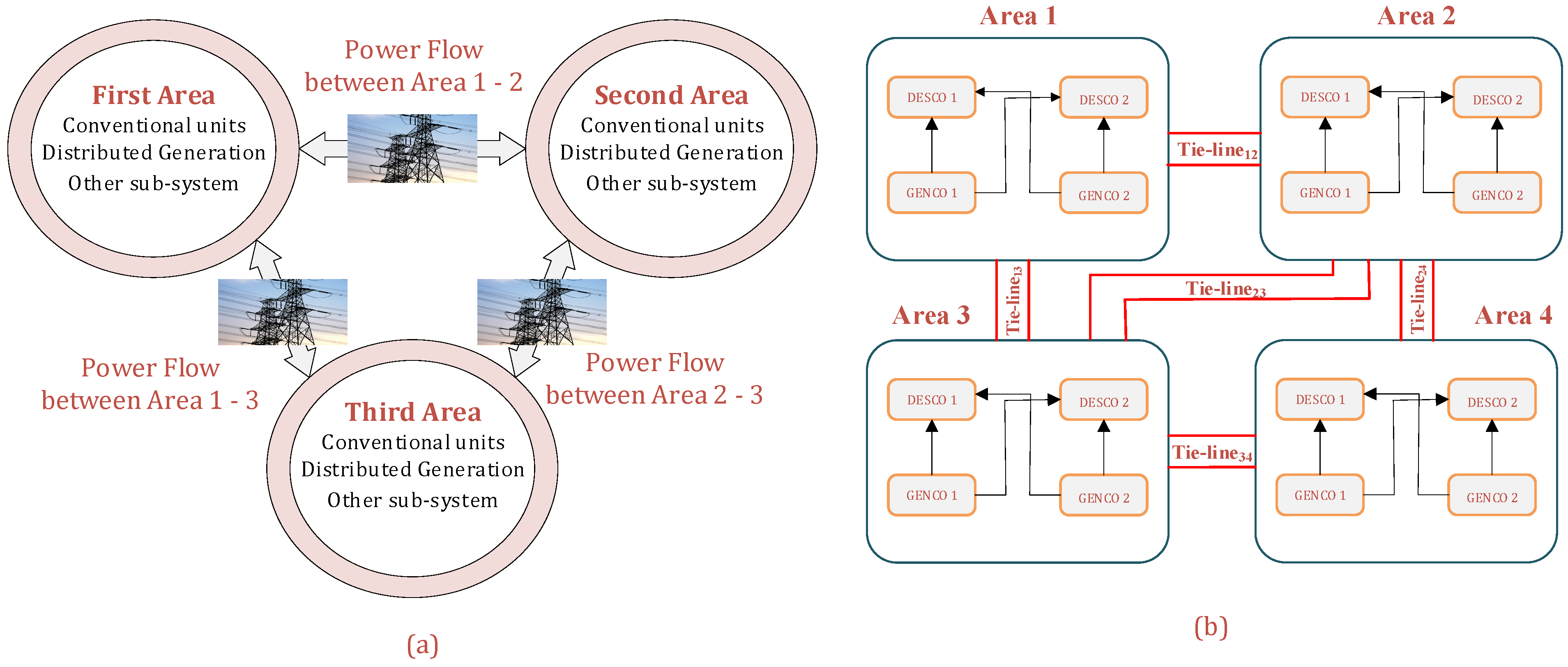
4. Power System AGC Models
4.1. Single Area Power Systems
4.2. Two Area Power Systems
4.3. Three Area Power Systems
4.4. Four Area Power Systems
4.5. M-th Area Power Systems
5. AGC Classification Based on Controller Organizations
5.1. Centralized Controllers
5.2. Decentralized Controllers
5.3. Two-Level and Multi-Level Controllers
6. AGC Classifications Based on the Control Methods
6.1. Classical Control Methods
6.2. Optimal and Suboptimal Control Methods
6.3. Adaptive, Self-Tuning, and Model Reference Control Methods
6.4. Variable Structure and Sliding Mode Control Methods
6.5. Robust Control Methods
6.6. Model Predictive Control (MPC) Methods
6.7. Digital Control Methods (DCMs)
7. Intelligent and Soft Computing Control Methods
7.1. Intelligent Control Methods
7.1.1. Fuzzy Logic Control (FLC)
7.1.2. Artificial Neural Network (ANN) Control
7.2. Soft Computing Control Methods
7.2.1. Genetic Algorithm (GA)
7.2.2. Particle Swarm Optimization (PSO)
7.2.3. Firefly Algorithm (FA)
7.2.4. Artificial Bee Colony (ABC) Algorithm
7.2.5. Differential Evolution (DE) Algorithm
7.2.6. Bacterial Foraging Optimization (BFO) Algorithm
7.2.7. Bat-Inspired Algorithm
7.2.8. Quasi Oppositional Harmony Search (QOHS) Algorithm
7.2.9. Teaching Learning-Based Optimization (TLBO)
7.2.10. Cuckoo Search Algorithm (CSA)
7.2.11. Grey Wolf Optimizer (GWO) Algorithm
7.2.12. Other Computing Control Methods
8. AGC Incorporating ESSs, FACTs Devices and HVDC Link
8.1. AGC Incorporating Energy Storage Systems (ESS)
8.2. AGC Incorporating FACTS Devices
8.3. AGC with HVDC Link
9. AGC in Renewable Energy Generation Systems
10. AGC in Microgrids and Smart Grids
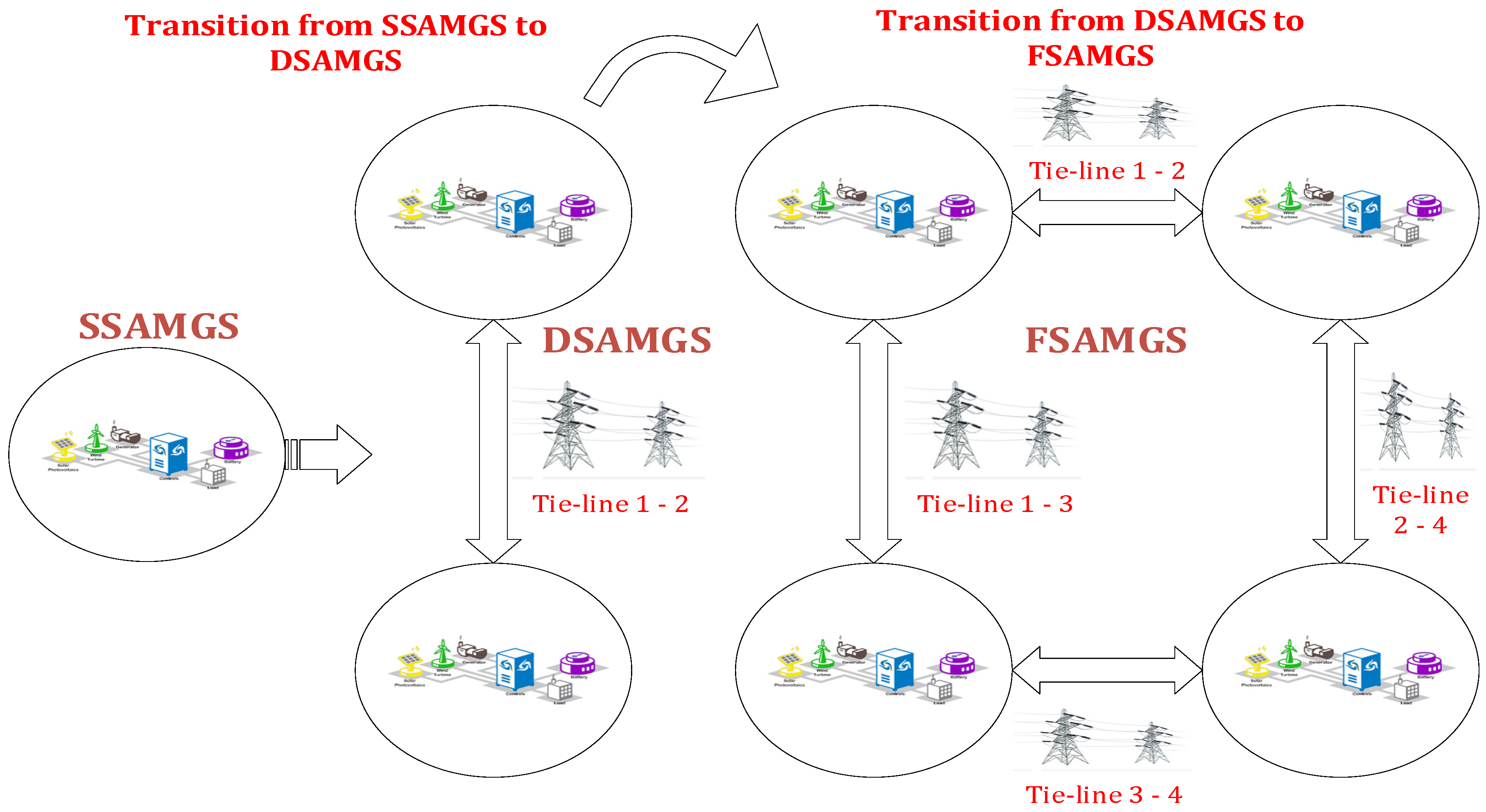
10.1. AGC in Microgrids
10.1.1. Single Area Stand-Alone MG Systems (SSAMGS)
10.1.2. Multiple Areas Stand-Alone MG Systems (MSAMGS)
10.2. AGC in Smart Grids
11. AGC in Deregulated Power Systems
12. AGC and Economic Dispatch (ED)
13. Worldwide AGC Practices
14. Future Scope of Work
- Explore AI techniques to train the AGC algorithm for activation of optimum reserves to secure the operation of the power system with large-scale integration of RESs.
- Explore and include more constraint coefficients like transmission line congestions into the objective functions to make the system more efficient in the practical scenario.
- Explore adaptive and robust control methods for the AGC to effectively handle system parametric variations.
- Explore various control techniques for AGC to perfectly predict the load and forecast the weather in large- and small-scale renewable energy-based power systems.
- An in-depth study on state estimation for AGC in real-time is required to effectively deal with the packet loss problems in the communication process.
- Susceptibilities of various AGC schemes to cyber-attacks should need to be explored further.
15. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Acronym | Definition | Acronym | Definition |
|---|---|---|---|
| AGC | Automatic generation control | FES | Flywheel energy storage |
| TSO | Transmission system operator | ISO | Independent system operator |
| AE | Aqua-electrolyzer | LTI | Linear time-invariant |
| SMES | Super magnetic energy storage system | RFC | Reliability first corporation (us) |
| RESs | Renewable energy sources | GRC | Generation rate constrains |
| BESS | Battery energy storage systems | GDB | Governor dead band |
| UPFC | Unified power flow controller | DISCOs | Distribution companies |
| MLCS | Modified load control scheme | GENCOs | Generation companies |
| DGs | Distributed generation sources | SERC | Southeastern electric reliability council (us) |
| FLC | Fuzzy logic control | TRANSCOs | Transmission companies |
| MTSA | Multiple tabu search algorithm | DPM | Disco participation matrix |
| IPFC | Interline power flow controller | ITAE | Integral time multiplied by absolute error |
| LMI | Linear matrix inequalities | AGPM | Augmented participation matrix |
| IAE | Integral of absolute error | EVs | Electrical vehicles |
| LTI | Linear time-invariant system | NPCC | Northeast power coordinating council (na) |
| GNN | Generalized neural network | SISO | Single input-single output |
References
- Kumar, P.; Kothari, D. Recent Philosophies of Automatic Generation Control Strategies in Power Systems. IEEE Trans. Power Syst. 2005, 20, 346–357. [Google Scholar]
- Shayeghi, H.; Shayanfar, H.; Jalili, A. Load frequency control strategies: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2009, 50, 344–353. [Google Scholar] [CrossRef]
- Shankar, R.; Pradhan, S.; Chatterjee, K.; Mandal, R. A comprehensive state of the art literature survey on LFC mechanism for power system. Renew. Sustain. Energy Rev. 2017, 76, 1185–1207. [Google Scholar] [CrossRef]
- Pandey, S.; Mohanty, S.; Kishor, N. A literature survey on load frequency control for conventional and distribution generation power systems. Renew. Sust. Energy. Rev. 2013, 25, 318–334. [Google Scholar] [CrossRef]
- Alhelou, H.; Hamedani-Golshan, M.-E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef]
- Zurfi, A.; Zhang, J. Exploitation of Battery Energy Storage in Load Frequency Control -A Literature Survey. Am. J. Eng. Appl. Sci. 2016, 9, 1173–1188. [Google Scholar] [CrossRef][Green Version]
- Obaid, Z.A.; Cipcigan, L.M.; Abrahim, L.; Muhssin, M.T. Frequency control of future power systems: Reviewing and evaluating challenges and new control methods. J. Mod. Power Syst. Clean Energy 2019, 7, 9–25. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 1–16. [Google Scholar] [CrossRef]
- Bevrani, H.; Hiyama, T. Intelligent Automatic Generation Control, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Veronica, A.J.; Kumar, N.S. Control strategies for frequency regulation in microgrids: A review. Wind. Eng. 2019. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control. Springer: New York, NY, USA, January 2009. [Google Scholar]
- Pappachen, A.; Fathima, A.P. Critical research areas on load frequency control issues in a deregulated power system: A state-of-the-art-of-review. Renew. Sustain. Energy Rev. 2017, 72, 163–177. [Google Scholar] [CrossRef]
- Brinda, M.D.; Suresh, A.; Rashmi, M. A literature survey on LFC in a deregulated electricity environment. World Rev. Sci. Technol. Sustain. Dev. 2018, 14, 1. [Google Scholar] [CrossRef]
- Cohn, N. Techniques for Improving the Control of Bulk Power Transfers on Interconnected Systems. IEEE Trans. Power Appar. Syst. 1971, PAS-90, 2409–2419. [Google Scholar] [CrossRef]
- Report, I. Dynamic Models for Steam and Hydro Turbines in Power System Studies. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1904–1915. [Google Scholar] [CrossRef]
- Tripathy, S.C.; Bhatti, T.S.; Jha, C.S.; Malik, O.P.; Hope, G.S. Sampled data automatic generation control analysis with reheat steam turbines and governor dead-band effects. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 1045–1051. [Google Scholar] [CrossRef]
- Malik, O.; Hope, G.; Tripathy, S.; Mital, N. Decentralized suboptimal load-frequency control of a hydro-thermal power system using the state variable model. Elecrtr. Power Syst. Res. 1985, 8, 237–247. [Google Scholar] [CrossRef]
- Bensenouci, A.; Ghany, A. Mixed H∞/H2 with pole-placement design of robust LMI-based output feedback controllers for multi-area load frequency control. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007. [Google Scholar]
- Shiva, C.K.; Mukherjee, V. Automatic generation control of multi-unit multi-area deregulated power system using a novel quasi-oppositional harmony search algorithm. IET Gener. Transm. Distrib. 2015, 9, 2398–2408. [Google Scholar] [CrossRef]
- Ross, C.; Green, T. Dynamic Performance Evaluation of a Computer Controlled Elecrtr.ric Power System. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 1158–1165. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Satsangi, P.S.; Kalra, P.K. Load frequency control: A generalised neural network approach. Int. J. Elecrtr. Rical Power Energy Syst. 1999, 21, 405–415. [Google Scholar] [CrossRef]
- Sanjeevikumar, P.; Sarojini, R.K.; Palanisamy, K.; Padmanaban, S.; Holm-Nielsen, J.B. Large Scale Renewable Energy Integration: Issues and Solutions. Energies 2019, 12, 1996. [Google Scholar]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Hongesombut, K.; Küfeoğlu, S. Virtual Inertia Control-Based Model Predictive Control for Microgrid Frequency Stabilization Considering High Renewable Energy Integration. Sustainability 2017, 9, 773. [Google Scholar] [CrossRef]
- Donde, V.; Pai, M.; Hiskens, I. Simulation and optimization in an AGC system after deregulation. IEEE Trans. Power Syst. 2001, 16, 481–489. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shayanfar, H.; Malik, O. Robust decentralized neural networks based LFC in a deregulated power system. Elecrtr. Power Syst. Res. 2007, 77, 241–251. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Dey, K.N.; Ashour, A.S.; Satapathy, S.C. Performance evaluation of objective functions in automatic generation control of thermal power system using ant colony optimization technique-designed proportional–integral–derivative controller. Elecrtr. Eng. 2008, 100, 895–911. [Google Scholar] [CrossRef]
- Saikia, L.C.; Sinha, N.; Nanda, J. Maiden application of bacterial foraging based fuzzy IDD controller in AGC of a multi-area hydrothermal system. Int. J. Elecrtr. Power. Energy Syst. 2013, 45, 98–106. [Google Scholar] [CrossRef]
- Fini, M.H.; Yousefi, G.R.; Alhelou, H.H. Comparative study on the performance of many-objective and single-objective optimisation algorithms in tuning load frequency controllers of multi-area power systems. IET Gener. Trans. Distrib. 2016, 10, 2915–2923. [Google Scholar] [CrossRef]
- Alhelou, H.; Golshan, M.; Fini, M. Wind Driven Optimization Algorithm Application to Load Frequency Control in Interconnected Power Systems Considering GRC and GDB Nonlinearities. Elecrtr. Power Compon. Syst. 2018, 46, 11–12. [Google Scholar]
- Sivaramakrlshnan, A.Y.; Hariharan, M.V.; Srisailam, M.C. Design of variable-structure load-frequency controller using pole assignment technique. Int. J. Control. 1984, 40, 487–498. [Google Scholar] [CrossRef]
- Saxena, S.; Hote, Y.V. PI Controller Based Load Frequency Control Approach for Single-Area Power System Having Communication Delay. IFAC-PapersOnLine 2018, 51, 622–626. [Google Scholar] [CrossRef]
- Barisal, A.; Mishra, S. Improved PSO based automatic generation control of multi-source nonlinear power systems interconnected by AC/DC links. Cogent Eng. 2018, 5, 1422228. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P. Evaluation of CES and DFIG unit in AGC of realistic multisource deregulated power system. Int. Trans. Elecrtr. Energy Syst. 2017, 27, e2304. [Google Scholar] [CrossRef]
- Chidembaram, I.; Paramasvam, B. Optimized load-frequency simulation in restructured power system with redox flow batteries and interline power flow controller. Int. J. Elecrtr. Power. Energy Syst. 2013, 50, 9–24. [Google Scholar] [CrossRef]
- Nayak, N.; Mishra, S.; Sharma, D.; Sahu, B.K. Application of modified sine cosine algorithm to optimally design PID/fuzzy-PID controllers to deal with AGC issues in deregulated power system. IET Gener. Transm. Distrib. 2019, 13, 2474–2487. [Google Scholar] [CrossRef]
- Dash, P.; Saikia, L.C.; Sinha, N. Comparison of performances of several FACTS devices using Cuckoo search algorithm optimized 2DOF controllers in multi-area AGC. Int. J. Elecrtr. Power Energy Syst. 2015, 65, 316–324. [Google Scholar] [CrossRef]
- Sharma, Y.; Saikia, L.C. Automatic generation control of a multi-area ST—Thermal power system using Grey Wolf Optimizer algorithm based classical controllers. Int. J. Elecrtr. Power Energy Syst. 2015, 73, 853–862. [Google Scholar] [CrossRef]
- Shiva, C.K.; Mukherjee, V. A novel quasi-oppositional harmony search algorithm for automatic generation control of power system. Appl. Soft Comput. 2015, 35, 749–765. [Google Scholar] [CrossRef]
- Vrdoljak, K.; Perić, N.; Petrović, I. Sliding mode-based load-frequency control in power systems. Elecrtr. Power Syst. Res. 2010, 80, 514–527. [Google Scholar] [CrossRef]
- Yesil, E. Interval type-2 fuzzy PID load frequency controller using Big Bang–Big Crunch optimization. Appl. Soft Comput. 2014, 15, 100–112. [Google Scholar] [CrossRef]
- Toulabi, M.; Shiroei, M.; Ranjbar, A. Robust analysis and design of power system load frequency control using the Kharitonov’s theorem. Int. J. Elecrtr. Power. Energy Syst. 2014, 55, 51–58. [Google Scholar] [CrossRef]
- Yousef, H.A.; Al-Kharusi, K.; Albadi, M.H.; Hosseinzadeh, N. Load Frequency Control of a Multi-Area Power System: An Adaptive Fuzzy Logic Approach. IEEE Trans. Power Syst. 2014, 29, 1822–1830. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Golshan, M.E.H.; Hatziargyriou, N.D. A Decentralized Functional Observer Based Optimal LFC Considering Unknown Inputs, Uncertainties, and Cyber-Attacks. IEEE Trans. Power Syst. 2019, 34, 4408–4417. [Google Scholar] [CrossRef]
- Lim, K.; Wang, Y.; Zhou, R. Robust decentralised load–frequency control of multi-area power systems. IEE Proc. Gener. Transm. Distrib. 1996, 143, 377. [Google Scholar] [CrossRef]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Kerdphol, T.; Qudaih, Y.; Bevrani, H.; Mitani, Y. Tustin’s technique based digital decentralized load frequency control in a realistic multi power system considering wind farms and communications delays. Ain Shams Eng. J. 2019, 10, 327–341. [Google Scholar] [CrossRef]
- Rahmani, M.; Sadati, N. Two-level optimal load–frequency control for multi-area power systems. Int. J. Elecrtr. Power Energy Syst. 2013, 53, 540–547. [Google Scholar] [CrossRef]
- Yang, S.; Huang, C.; Yu, Y.; Yue, N.; Xie, J. Load Frequency Control of Interconnected Power System via Multi-Agent System Method. Elecrtr. Power Compon. Syst. 2017, 45, 1–13. [Google Scholar] [CrossRef]
- Rubaai, A.; Udo, V. Self-tuning load frequency control: Multilevel adaptive approach. IEEE Proc. Gener. Trans Distrib. 1994, 141, 285–290. [Google Scholar] [CrossRef]
- Xi, K.; Lin, H.X.; Shen, C.; Van Schuppen, J.H. Multilevel Power-Imbalance Allocation Control for Secondary Frequency Control of Power Systems. IEEE Trans. Autom. Control. 2020, 65, 2913–2928. [Google Scholar] [CrossRef]
- Bengiamin, N.; Chan, W. 3-level load-frequency control of power systems interconnected by asynchronous tie lines. Proc. Inst. Elecrtr. Eng. 1979, 126, 1198. [Google Scholar] [CrossRef]
- Lee, K.; Yee, H.; Teo, C. Self-tuning algorithm for automatic generation control in an interconnected power system. Elecrtr. Power Syst. Res. 1991, 20, 157–165. [Google Scholar] [CrossRef]
- Memon, A.; Memon, L.; Shaikh, A. Pole placement design for load frequency control (LFC) of an isolated power system. J. Eng. Appl. Sci. 2002, 21, 11–16. [Google Scholar]
- Saikia, L.C.; Nanda, J.; Mishra, S. Performance comparison of several classical controllers in AGC for multi-area interconnected thermal system. Int. J. Elecrtr. Power. Energy Syst. 2001, 33, 394–401. [Google Scholar] [CrossRef]
- Arya, Y.; Kumar, N. Optimal control strategy-based AGC of Elecrtrical power systems: A comparative performance analysis. Optim. Cont. Appl. Methods. 2017, 38, 982–992. [Google Scholar] [CrossRef]
- Hasan, N.; Ibraheem; Kumar, P.; Nizamuddin. Sub-optimal automatic generation control of interconnected power system using constrained feedback control strategy. Int. J. Elecrtr. Power Energy Syst. 2012, 43, 295–303. [Google Scholar] [CrossRef]
- Sahoo, S.; Jena, N.K.; Dei, G.; Sahu, B.K. Self-adaptive fuzzy-PID controller for AGC study in deregulated Power System. Indonesian. J. Elecrtr. Eng Inform. 2019, 7, 650–663. [Google Scholar]
- Kazemi, M.H.; Karrari, M.; Menhaj, M.B. Decentralized robust adaptive-output feedback controller for power system load frequency control. Elecrtr. Eng. 2002, 84, 75–83. [Google Scholar] [CrossRef]
- Al-Hamouz, Z.; Abdel-Magid, Y. Variable structure load frequency controllers for multiarea power systems. Int. J. Elecrtr. Power Energy Syst. 1993, 15, 293–300. [Google Scholar] [CrossRef]
- Mohanty, B. TLBO optimized sliding mode controller for multi-area multi-source nonlinear interconnected AGC system. Int. J. Elecrtr. Power Energy Syst. 2015, 73, 872–881. [Google Scholar] [CrossRef]
- Hamouz, Z.; Duwaish, H.; Musabi, N. Optimal design of a sliding mode AGC controller: Application to a nonlinear interconnected model. Elecrtr. Power Syst. Res. 2011, 81, 1403–1409. [Google Scholar] [CrossRef]
- Khezri, R.; Golshannavaz, S.; Shokoohi, S.; Bevrani, H. Fuzzy logic based fine-tuning approach for robust load frequency control in a multi-area power system. Electr. Power Comp. Syst. 2016, 44, 2073–2083. [Google Scholar] [CrossRef]
- Shayeghi, H.; Jalili, A.; Shayanfar, H. Robust modified GA based multi-stage fuzzy LFC. Energy Convers. Manag. 2007, 48, 1656–1670. [Google Scholar] [CrossRef]
- Elsisi, M.; Soliman, M.; Aboelela, M.; Mansour, W. Bat inspired algorithm based optimal design of model predictive load frequency control. Int. J. Electr. Power Energy Syst. 2016, 83, 426–433. [Google Scholar] [CrossRef]
- Mc Namara, P.; Milano, F. Efficient implementation of MPC-based AGC for real-world systems with low inertia. Electr. Power Syst. Res. 2018, 158, 315–323. [Google Scholar] [CrossRef]
- Zeng, G.-Q.; Xie, X.-Q.; Chen, M.-R. An Adaptive Model Predictive Load Frequency Control Method for Multi-Area Interconnected Power Systems with Photovoltaic Generations. Energies 2017, 10, 1840. [Google Scholar] [CrossRef]
- McNamara, P.; Milano, F. Model Predictive Control-Based AGC for Multi-Terminal HVDC-Connected AC grids. IEEE Trans. Power Syst. 2017, 33, 1036–1048. [Google Scholar] [CrossRef]
- Egido, I.; Fernandez-Bernal, F.; Rouco, L. The Spanish AGC System: Description and Analysis. IEEE Trans. Power Syst. 2008, 24, 271–278. [Google Scholar] [CrossRef]
- Yesil, E.; Guzelkaya, M.; Eksin, I. Self tuning fuzzy PID type load and frequency controller. Energy Convers. Manag. 2004, 45, 377–390. [Google Scholar] [CrossRef]
- Lal, D.K.; Barisal, A.K.; Tripathy, M. Grey Wolf Optimizer Algorithm Based Fuzzy PID Controller for AGC of Multi-area Power System with TCPS. Procedia Comput. Sci. 2016, 92, 99–105. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self Adaptive Modified Bat Algorithm. Int. J. Elecrtr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Azeer, S.; Ramjug-Ballgobin, R.; Hassen, S.S. Intelligent Controllers for Load Frequency Control of Two-Area Power System. IFAC-Papers On-Line 2017, 50, 301–306. [Google Scholar] [CrossRef]
- Yin, L.; Yu, T.; Zhou, L.; Huang, L.; Zhang, X.; Zheng, B. Artificial emotional reinforcement learning for automatic generation control of large-scale interconnected power grids. IET Gener. Trans. Distrib. 2017, 11, 2305–2313. [Google Scholar] [CrossRef]
- Yin, L.; Zhao, L.; Yu, T.; Zhang, X. Deep forest reinforcement learning for preventive strategy considering automatic generation control in large-scale interconnected power systems. Appl. Sci. 2018, 8, 2185. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shayanfar, H. Application of ANN technique based on μ-synthesis to load frequency control of interconnected power system. Int. J. Elecrtr. Power Energy Syst. 2006, 28, 503–511. [Google Scholar] [CrossRef]
- Bevrani, H.; Hiyama, T.; Mitani, Y.; Tsuji, K.; Teshehlab, M. Load-frequency regulation under a bilateral LFC scheme using flexible neural networks. Eng. Intell. Syst. 2006, 14, 109–117. [Google Scholar]
- Hasan, N.; Nasirudin, I.; Farooq, S. Hybrid Taguchi Genetic Algorithm-Based AGC Controller for Multisource Interconnected Power System. Elecrtr. Power Syst. Res. 2019, 47, 101–112. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Design of a proportional-integral-derivative controller for an automatic generation control of multi-area power thermal systems using firefly algorithm. IEEE/CAA J. Autom. Sin. 2019, 6, 503–515. [Google Scholar] [CrossRef]
- Kumar, B.V. Power System loss minimization by using UPFC placed at optimal location given by Artificial Bee Colony Algorithm. Int. J. Res. Advent Technol. 2019, 7, 127–132. [Google Scholar] [CrossRef]
- Abazari, A.; Monsef, H.; Wu, B. Coordination strategies of distributed energy resources including FESS, DEG, FC and WTG in load frequency control (LFC) scheme of hybrid isolated micro-grid. Int. J. Electr. Power Energy Syst. 2019, 109, 535–547. [Google Scholar] [CrossRef]
- Mishra, S.K.P.; Sekhar, S. Modelling of Differential Evolution Based Automatic Generation Control for Two Area Interconnected Power Systems. J. Inform. Math. Sci. 2019, 11, 19–30. [Google Scholar]
- Sahu, B.K.; Pati, S.; Panda, S. Hybrid differential evolution particle swarm optimisation optimised fuzzy proportional–integral derivative controller for automatic generation control of interconnected power system. IET Gener. Transm. Distrib. 2014, 8, 1789–1800. [Google Scholar] [CrossRef]
- Sahu, B.; Pati, S.; Mohanty, P.; Panda, S. Teaching–learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system. Int. J. Elecrtr. Power Energy Syst. 2015, 27, 240–249. [Google Scholar] [CrossRef]
- Chaine, S.; Tripathy, M. Performance of CSA optimized controllers of DFIGs and AGC to improve frequency regulation of a wind integrated hydrothermal power system. Alex. Eng. J. 2019, 58, 579–590. [Google Scholar] [CrossRef]
- Sahu, B.K.; Pati, T.K.; Nayak, J.R.; Panda, S.; Kar, S.K. A novel hybrid LUS–TLBO optimized fuzzy-PID controller for load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2016, 74, 58–69. [Google Scholar] [CrossRef]
- Barik, A.K.; Das, D.C. Proficient load-frequency regulation of demand response supported bio-renewable cogeneration based hybrid microgrids with quasi-oppositional selfish-herd optimisation. IET Gener. Transm. Distrib. 2019, 13, 2889–2898. [Google Scholar] [CrossRef]
- Saha, A.; Saikia, L.C. Combined application of redox flow battery and DC link in restructured AGC system in the presence of WTS and DSTS in distributed generation unit. IET Gener. Transm. Distrib. 2018, 12, 2072–2085. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T. Frequency deviation control by coordination control of FC and double-layer capacitor in an autonomous hybrid renewable energy power generation system. Renew. Energy 2011, 36, 1741–1746. [Google Scholar] [CrossRef]
- Yan, W.; Sheng, L.; Xu, D.; Yang, W.; Liu, Q. H∞ Robust Load Frequency Control for Multi-Area Interconnected Power System with Hybrid Energy Storage System. Appl. Sci. 2018, 8, 1748. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual Inertia Control Application to Enhance Frequency Stability of Interconnected Power Systems with High Renewable Energy Penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Cantarellas, A.; Garcia, J.M.; Rodriguez, P. Modeling and sensitivity analyses of VSP based virtual inertia controller in HVDC links of interconnected power systems. Electr. Power Syst. Res. 2016, 141, 246–263. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shayanfar, H.; Jalili, A. LFC design of a deregulated power system with TCPS using PSO. Int. J. Electr. Electron. Eng. 2009, 3, 632–640. [Google Scholar]
- Ngamroo, I.; Tippayachai, J.; Dechanupaprittha, S. Robust decentralised frequency stabilisers design of static synchronous series compensators by taking system uncertainties into consideration. Int. J. Electr. Power Energy Syst. 2006, 28, 513–524. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Performance comparison of TCSC with TCPS and SSSC controllers in AGC of realistic interconnected multi-source power system. Ain Shams Eng. J. 2016, 7, 143–158. [Google Scholar] [CrossRef]
- Pathak, N.; Verma, A.; Bhatti, T.S.; Nasiruddin, I. Modeling of HVDC Tie Links and Their Utilization in AGC/LFC Operations of Multiarea Power Systems. IEEE Trans. Ind. Elecrtr. 2019, 66, 2185–2197. [Google Scholar] [CrossRef]
- Asano, H.; Yajima, K.; Kaya, Y. Influence of photovoltaic power generation on required capacity for load frequency control. IEEE Trans. Energy Convers. 1996, 11, 188–193. [Google Scholar] [CrossRef]
- Yanagawa, S.; Kato, T.; Kai, W.; Tabata, A.; Yokomizu, Y.; Okamoto, T.; Suzuoki, Y. Evaluation of LFC capacity for output fluctuation of photovoltaic power generation systems based on multi-point observation of insolation. In Proceedings of the 2001 Power Engineering Society Summer Meeting. Conference Proceedings (Cat. No.01CH37262), Vancouver, BC, Canada, 15–19 July 2001. [Google Scholar]
- Luo, H.; Hu, Z.; Zhang, H.; Chen, H. Coordinated Active Power Control Strategy for Deloaded Wind Turbines to Improve Regulation Performance in AGC. IEEE Trans. Power Syst. 2019, 34, 98–108. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshmand, P.R. Fuzzy Logic-Based Load-Frequency Control Concerning High Penetration of Wind Turbines. IEEE Syst. J. 2011, 6, 173–180. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, Z.; Fu, B.; He, L.; Fang, N. Research on Automatic Generation Control with Wind Power Participation Based on Predictive Optimal 2-Degree-of-Freedom PID Strategy for Multi-area Interconnected Power System. Energies 2018, 11, 3325. [Google Scholar] [CrossRef]
- Bhatt, P.; Ghshal, S.; Roy, R. Coordinated control of TCPS and SMES for frequency regulation of interconnected restructured power systems with dynamic participation from DFIG based wind farm. Renew. Energy 2012, 40, 40–50. [Google Scholar] [CrossRef]
- Kumar, A.; Suhag, S. Effect of TCPS, SMES, and DFIG on load frequency control of a multi-area multi-source power system using multi-verse optimized fuzzy-PID controller with derivative filter. J. Vib. Control. 2018, 24, 5922–5937. [Google Scholar] [CrossRef]
- Bagheri, A.; Jabbari, A.; Mobayen, S. An intelligent ABC-based terminal sliding mode controller for load-frequency control of islanded micro-grids. Sustain. Cities Soc. 2021, 64, 102544. [Google Scholar] [CrossRef]
- Kumar, D.; Mathur, H.D.; Bhanot, S.; Bansal, R.C. Forecasting of solar and wind power using LSTM RNN for load frequency control in isolated microgrid. Int. J. Model. Simul. 2020, 1–13. [Google Scholar] [CrossRef]
- Liu, K.; He, J.; Luo, Z.; Shen, X.; Liu, X.; Lu, T. Secondary Frequency Control of Isolated Microgrid Based on LADRC. IEEE Access 2019, 7, 53454–53462. [Google Scholar] [CrossRef]
- Safari, A.; Babaei, F.; Farrokhifar, M. A load frequency control using a PSO-based ANN for micro-grids in the presence of electric vehicles. Int. J. Ambient Energy 2019, 42, 688–700. [Google Scholar] [CrossRef]
- Fergany, A.; Hameed, M. Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimiser. IET Gener. Trans. Distrib. 2017, 11, 637–648. [Google Scholar] [CrossRef]
- Sahu, P.C.; Mishra, S.; Prusty, R.C.; Panda, S. Improved-salp swarm optimized type-II fuzzy controller in load frequency control of multi area islanded AC microgrid. Sustain. Energy Grids Netw. 2018, 16, 380–392. [Google Scholar] [CrossRef]
- Ranjan, S.; Das, D.; Latif, A.; Sinha, N. LFC for autonomous hybrid micro grid system of 3 unequal renewable areas using mine blast algorithm. Int. J. Renew. Energy 2018, 8, 1297–1308. [Google Scholar]
- Khan, M.; Sun, H.; Xiang, Y.; Shi, D. Electric vehicles participation in load frequency control based on mixed H2/H∞. Int. J. Electr. Power Energy Syst 2021, 125, 106420. [Google Scholar] [CrossRef]
- Samarakoon, K.; Ekanayake, J.; Jenkins, N. Investigation of Domestic Load Control to Provide Primary Frequency Response Using Smart Meters. IEEE Trans. Smart Grid 2012, 3, 282–292. [Google Scholar] [CrossRef]
- Bharti, K.; Singh, V.P.; Singh, S.P. Impact of Intelligent Demand Response for Load Frequency Control in Smart Grid Perspective. IETE J. Res. 2020, 1–12. [Google Scholar] [CrossRef]
- Basit, A.; Ahmad, T.; Ali, A.Y.; Ullah, K.; Mufti, G.; Hansen, A.D. Flexible Modern Power System: Real-Time Power Balancing through Load and Wind Power. Energies 2019, 12, 1710. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Load Frequency Control with Communication Topology Changes in Smart Grid. IEEE Trans. Ind. Inform. 2016, 12, 1943–1952. [Google Scholar] [CrossRef]
- Bi, W.; Zhang, K.; Chen, C. Cyber Attack Detection Scheme for a Load Frequency Control System Based on Dual-Source Data of Compromised Variables. Appl. Sci. 2021, 11, 1584. [Google Scholar] [CrossRef]
- Ghasemi-Marzbali, A. Multi-area multi-source automatic generation control in deregulated power system. Energy 2020, 201, 117667. [Google Scholar] [CrossRef]
- Arya, Y.; Kumar, N. AGC of a multi-area multi-source hydrothermal power system interconnected via AC/DC parallel links under deregulated environment. Int. J. Electr. Power Energy Syst. 2016, 75, 127–138. [Google Scholar] [CrossRef]
- Bevrani, H.; Mtani, Y.; Tsji, K.; Bevrani, H. Bilateral based robust load frequency control. Energy Conv. Mang. 2005, 46, 1129–1146. [Google Scholar] [CrossRef]
- Li, N.; Zhao, C.; Chen, L. Connecting automatic generation control and economic dispatch from an optimization view. IEEE Trans. Control Netw. Syst. 2015, 3, 254–264. [Google Scholar] [CrossRef]
- Patel, R.; Li, C.; Yu, X.; McGrath, B. Optimal Automatic Generation Control of an Interconnected Power System Under Network Constraints. IEEE Trans. Ind. Electron. 2018, 65, 7220–7228. [Google Scholar] [CrossRef]
- Patel, R.B.; Li, C.; Meegahapola, L.G.; McGrath, B.; Yu, X. Enhancing Optimal Automatic Generation Control in a Multi-Area Power System with Diverse Energy Resources. IEEE Trans. Power Syst. 2019, 34, 3465–3475. [Google Scholar] [CrossRef]
- Bacher, R.; Meeteren, H.P. Real-time optimal power flow in automatic generation control. IEEE Trans. Power Syst. 1988, 3, 1518–1529. [Google Scholar] [CrossRef]
- Eidson, D.; Ilic, M. Advanced generation control with economic dispatch. In Proceedings of the 1995 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995; Volume 4, pp. 3450–3458. [Google Scholar]
- Energinet.dk. Energinet.dk’s Ancillary Services Strategy; Energinet.dk, Doc. No. 77566/11 v1, Case No. 10/5553; Energinet.dk: Fredericia, Denmark, 2011. [Google Scholar]
- Balancing and Frequency Control—NERC. Available online: https://www.nerc.com/comm/OC/RSLandingPageDL/RelatedFiles/NERCBalancingandFrequencyControl040520111.pdf (accessed on 20 April 2021).
- Pandurangan, V.; Zareipour, H.; Malik, O. Frequency regulation services: A comparative study of select North American and European reserve markets. In Proceedings of the 2012 North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012. [Google Scholar]
- Program of Energy Research and Development Research. Available online: https://weican.ca/docs/publications/PERDPublicSummaryReport.pdf (accessed on 20 April 2021).
| Ref. | AGC-O&OF | AGC-CO | AGC-C& MCM | AGC-I&SCCM | AGC-ESS | AGC- FACTS | AGC-HVDCS | AGC-LREGS | AGC-MG & DG | AGC-SG | AGC-DPS | AGC-ED | AGC-WWP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [1] | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [2] | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [3] | ✗ | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [4] | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [5] | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [6] | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [7] | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [8] | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [9] | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ |
| [10] | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [11] | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [12] | ✗ | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [13] | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ |
| OR | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Sr. No | Control Method | Main Advantages | Drawbacks |
|---|---|---|---|
| 1 | Classical Control Methods |
|
|
| 2 | Optimal and Sub-optimal Control Methods |
|
|
| 3 | Adaptive Control Methods |
|
|
| 4 | Variable Structure Control Method |
|
|
| 5 | Robust Control Methods |
|
|
| 6 | Model Predictive control methods |
|
|
| 7 | Digital Control Methods |
|
|
| 8 | Fuzzy logic-based control methods |
|
|
| 9 | ANN-based Control Methods |
|
|
| 10 | Neuro-fuzzy based Control Methods |
|
|
| Ref. | Power System Configuration | Controller Approach | Operating Scenarios | Peak Overshoot | Settling Time | ||||
|---|---|---|---|---|---|---|---|---|---|
| [80] | Two area non-reheat thermal power system | DE based 2DOF-PID regulator | Controller comparisons with other types: | ||||||
| 2DOF-PID | 0.0144 | 0.00598 | 0.00711 | 11.1 | 7.2 | 13.8 | |||
| PID | 0.0251 | 0.0172 | 0.0083 | 24.8 | 24.1 | 23.3 | |||
| [26] | Two area non-reheat thermal power system | ACO based PID regulator | Comparisons of objective functions: | ||||||
| ISE | 1.1 × 10−6 | 0.0002 | 0.0001 | 29.62 | 37.20 | 50.41 | |||
| ITSE | 0.0016 | 0.0001 | 0.0005 | 25.69 | 25.43 | 45.54 | |||
| IAE | 3.66 × 10−6 | 0.0000 | 0.0001 | 26.29 | 32.12 | 37.64 | |||
| ITAE | 0.001 | 0.0000 | 0.0005 | 23.69 | 32.12 | 33.63 | |||
| [59] | Two area reheat thermal, hydro, gas and nuclear power plant | TLBO based AGC system with output feedback SMC | Controller comparisons with other types: | ||||||
| SMC with output feedback with TLBO | 0.001 | 2.242 × 10−4 | 2.883 × 10−5 | 1.3 | 1.46 | 1.05 | |||
| SMC with output feedback with DE | 0.0018 | 6.389 × 10−4 | 7.680 × 10−5 | 1.4 | 1.9 | 1.1 | |||
| SMC with output feedback with PSO | 0.0016 | 4.301 × 10−4 | 8.050 × 10−5 | 1.52 | 1.54 | 1.24 | |||
| [84] | Two area reheat thermal, hydro, gas and nuclear power plant | LUS-TLBO based Fuzzy PID controller | Performance evaluations: | ||||||
| Without AC-DC tie-lines | 0.000551 | 0.000219 | 0.0000826 | 5.26 | 2.96 | 2.36 | |||
| With AC-DC tie-lines | 0.000280 | 0.000208 | 0.0001353 | 1.85 | 4.14 | 2.55 | |||
| Power System Configurations | Controller Approach | Operating Scenarios | Peak Over Shoot | Settling Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three area power system with hydro-thermal sources | BFA based IDD and FDID regulator | Controller comparisons | ||||||||||||
| BFA-IDD | 0.02142 | 0.01335 | 0.01081 | 0.00113 | 0.00117 | 60.26 | 64.81 | 65.47 | 61.00 | 73.63 | ||||
| BFA-FIDD | 0.01554 | 0.01071 | 0.00742 | 0.00059 | 0.00069 | 49.75 | 52.76 | 55.21 | 51.37 | 58.75 | ||||
| Three area non-reheat thermal power system with non-linearities | CSA based 2DOF-ID controller | Use of FACTS devices | ||||||||||||
| SSSC | 0.0013 | 0.0019 | 0.0012 | 0.0002 | 0 | 0 | 33.9 | 24.28 | 30.61 | 51.12 | 40.42 | 29.12 | ||
| TCSC | 0.00004 | 0.01071 | 0.00742 | 0.0002 | 0 | 0 | 33.06 | 34.46 | 33.28 | 51.13 | 40.20 | 34.35 | ||
| TCPS | 0.0012 | 0.0013 | 0.0004 | 0 | 0 | 0 | 31.7 | 33.36 | 29.21 | 50.97 | 40.23 | 34.32 | ||
| IPFC | 0 | 0 | 0 | 0 | 0 | 0 | 28.53 | 23.37 | 26.03 | 34.56 | 40.07 | 29.12 | ||
| Three area non-reheat thermal power system with non-linearities | GWO based PID controller | Use of ESs | 0.007231 | 0.006335 | 0.006087 | 0.001814 | 0.001761 | 0.0008671 | 34.81 | 35.56 | 32.35 | 42.84 | 41.67 | 38.82 |
| With-STTP | ||||||||||||||
| Without-STTP | 0.01432 | 0.01213 | 0.006886 | 0.001026 | 0.0007518 | 0.001709 | 24.47 | 23.35 | 21.81 | 21.26 | 24.11 | 32.97 | ||
| Five- area reheat thermal power system | FFA based PID controller | Controller comparisons | ||||||||||||
| GA-PID | 0.00071 | 0.00063 | 0.0006 | 0.00089 | 0.0006 | 17.84 | 26.63 | 17.19 | 24.33 | 17.19 | ||||
| PSO-PID | 0.00042 | 0.00065 | 0.00042 | 0.00078 | 0.00042 | 16.33 | 22.7 | 16.54 | 23.23 | 16.33 | ||||
| FFA-PID | 0.00038 | 0.00075 | 0.00038 | 0.00085 | 0.00038 | 13.53 | 21.8 | 14.55 | 22.77 | 13.79 | ||||
| Ref. | Type of Power System | Areas | Energy Generation Sources | Additional Devices | Controller Approach |
|---|---|---|---|---|---|
| [32] | Traditional | 2 | Thermal, hydro, wind-Diesel | AC/DC link | IPSO based PID |
| [33] | Deregulated | 2 | Wind, hydro, thermal, gas | TCPS, CES | ISE based I |
| [34] | Deregulated | 2 | Thermal | IPFC + RFB | BFO based I and FL |
| [36] | Traditional | 3 | Thermal | TCPS, UPFC | CSA based 2DOF-IDD |
| [37] | Traditional | 3 | Solar thermal, thermal | -- | GWO based I, PI, PID |
| [38] | Traditional | 1,3,5 | Thermal | -- | QOHS based PID/IDD |
| [76] | Traditional | 2 | Thermal, wind power | -- | HTGA based PID |
| [40] | Traditional | 4 | Thermal, hydro | -- | BB-BC based IT2FPID |
| [93] | Traditional | 3 | Thermal, hydro, gas | TCSC, TCPS, SSSC | IPSO based I |
| [99] | Traditional | 3 | Wind-thermal | -- | PO-2-DOF-PID |
| [100] | Deregulated | 2 | Hydro, thermal, wind | TCPS, SMES | CRPSO based I |
| [101] | Traditional | 2 | Wind, thermal, hydro | TCPS, SMES | MWO based Fuzzy-PIDF |
| Ref. | Type of Power System | Areas | Energy Generation Sources | Additional Devices | Controller Approach |
|---|---|---|---|---|---|
| [79] | SSAMGS | 1 | DEG, WTG | FESS, FC | ABC based fuzzy-PID |
| [85] | SSAMGS & MSAMGS | 1,2 | Wind, MH, and BG, | - | NQOSO based PID |
| [87] | SSAMGS | 1 | WTG, PV | DLC, FC | GA based PID |
| [102] | SSAMGS | 1 | DEG, WT, PV, | FC, BESS, FESS | ABC based TSMC |
| [103] | SSAMGS | 1 | PV, WTG, DEG, | AE, FC, BESS | PI control |
| [104] | SSAMGS | 1 | WTG, DEG, PV | BESS, FESS | LADR control |
| [105] | SSAMGS | 1 | Wind, PV, DEG | BESS, SMES | PSO based ANN |
| [106] | MSAMGS | 2 | WTG and PV | SMES, BES | SSO based PID |
| [107] | MSAMGS | 2 | MT, PV DEG | FC, BESS | I-SSO based type-II fuzzy PID |
| [108] | MSAMGS | 3 | WTG, PV, PTC | ESS | MBA based 2DOF-PID |
| Ref. | Power System Configuration | Controller Approach | Operating Scenarios | Over Shoots | Settling Times | ||||
|---|---|---|---|---|---|---|---|---|---|
| [33] | Two area power system with thermal, hydro and gas power plants in coordination with CES/DFIG and TCPS | Integral controller | Contract scenarios: | ||||||
|
Unilateral contract
Bilateral contract Contract with violation | 0.03279 0.0756 0.07567 | 0.029 0.07932 0.079 | 0.0038 0.01114 0.01123 | 50.22 50.05 94.3 | 47.31 49.01 87.03 | 90.2 65.56 116.1 | |||
| [35] | Two area multiple units reheat thermal and, gas power plant with GRCs and GDBs | MSCA-FPID based AGC regulator | Contract scenarios: | ||||||
|
Unilateral contract
Bilateral contract Contract with violation | 0.000517 0.00291 0.004255 | 0.000471 0.004555 0.003285 | 0.000311 0 0 | 2.073 6.273 3.731 | 6.461 4.555 2.398 | 4.98 1.837 0.642 | |||
| [55] | Two area multiple units non-reheat thermal system with HVDC | WGA based SA-FPID Controller | Contract scenarios: | ||||||
|
Unilateral contract
Bilateral contract Contract with violation | 0.000135 0.0000813 0.0003905 | 0.0000662 0.0000813 0.0003529 | 0.0000329 0.0001680 0.0001680 | 0.57 2.29 2.96 | 5.07 2.29 3.47 | 3.94 5.07 5.68 | |||
| [34] | Two area multiple units reheat thermal power system with IPFC and RFB | BFO based Integral Controller | Controller comparisons: | ||||||
|
Integral controller
Integral controller with IPFC Integral controller with IPFC and RFBs | 0.321 0.204 0.148 | 0.224 0.112 0.082 | 0.081 0.059 0.042 | 16.69 6.27 4.98 | 15.48 5.47 4.72 | 14.46 7.46 6.12 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, K.; Basit, A.; Ullah, Z.; Aslam, S.; Herodotou, H. Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview. Energies 2021, 14, 2376. https://doi.org/10.3390/en14092376
Ullah K, Basit A, Ullah Z, Aslam S, Herodotou H. Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview. Energies. 2021; 14(9):2376. https://doi.org/10.3390/en14092376
Chicago/Turabian StyleUllah, Kaleem, Abdul Basit, Zahid Ullah, Sheraz Aslam, and Herodotos Herodotou. 2021. "Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview" Energies 14, no. 9: 2376. https://doi.org/10.3390/en14092376
APA StyleUllah, K., Basit, A., Ullah, Z., Aslam, S., & Herodotou, H. (2021). Automatic Generation Control Strategies in Conventional and Modern Power Systems: A Comprehensive Overview. Energies, 14(9), 2376. https://doi.org/10.3390/en14092376










