The Role of Flexibility in Photovoltaic and Battery Optimal Sizing towards a Decarbonized Residential Sector
Abstract
1. Introduction
2. Methodology
- 3D model: Required in OBJ format, it includes the buildings under study, the surfaces available for the photovoltaic installation, and the close shading objects (e.g., trees, close buildings). This information is useful to identify a suitable area where photovoltaic modules can be installed.
- Weather file: Required in EnergyPlus Weather (EPW) format, it describes the irradiation context (also considering the horizon line) and the temperature conditions needed to calculate the expected electricity generation of each photovoltaic module.
- Electricity demand: The hourly profile of the annual electric demand of the building (e.g., heat pumps and auxiliary systems, appliances, lighting system, elevators, etc.).
- Technical parameters: These include some optional indices which can affect the generated and consumed electricity profiles. The parameters are the performance ratio (PR), the PV module efficiency, the linear annual efficiency losses, and the temperature coefficient of the modules. For the battery instead, the maximum depth of discharge, round-trip efficiency, and the capacity degradation rate. A percentage for annual linear growth can be specified for the electricity demand. The time horizon to calculate the system performance is also an input.
- Economic inputs: These data include the investment and operational cost for the photovoltaic system and battery, the price of purchased and sold electricity, a possible premium related to a net billing scheme, the annual discount rate of the investment, and the linear annual growth of the price of purchased and sold electricity.
- and are the electricity of the self-consumed and injected into the grid;
- and are the price of electricity bought or sold for the final user, respectively;
- are the operating expense cost of operation and maintenance for PV system based on the installed PV nominal power ();
- are the cost of BESS replacement per BESS capacity ();
- is the sum of the investment cost for the PV and BESS system accordingly to the PV nominal power and the installed BESS capacity;
- is the discount rate.
- Self-sufficiency: Indicates the percentage of energy that can be supplied by PV and BESS.
- Normalized NPV: Is the normalized over the initial investment.
- GHG emission reduction: Indicated the reduction of GHG emission due to the adoption of PV and BESS system, compared to the reference year which is 1990.
3. Case Study
3.1. Residential Appliances
- Number of households is chosen equal to fifty according to the number of single-family houses of the district;
- Type of buildings considered is the single-family house as represented in Figure 2;
- Distribution of people considered is the one present in the default settings of LPG;
- Location chosen is the city of Bolzano, in the North-East of Italy. According to this, the Typical Meteorological Year (TMY) of the selected location has been used for the weather data [27];
- Time resolution is set equal to one hour because this is the time resolution used by the optimization tool described in Section 2.
3.2. Heat Pump Consumption Profiles
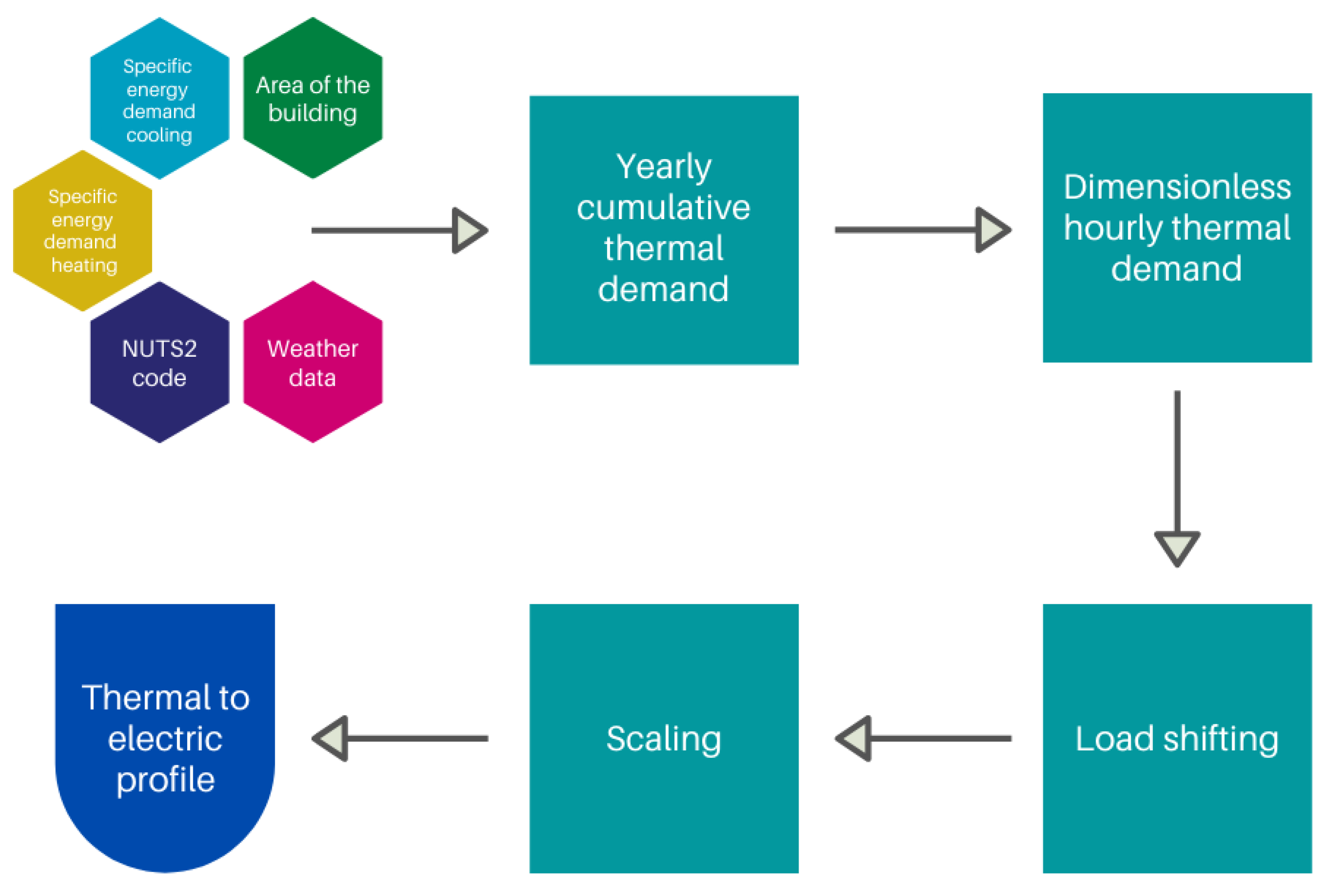
- Calculate the yearly cumulative thermal demand of the building.Within the European H2020 project 4RinEU, several dynamic simulations were performed to estimate the annual cumulative thermal demand of different buildings in different climates, before and after different renovation interventions [29] with TRNSYS [30], a well-known dynamic simulation software. We refer to the project report for the details [29]. Since the objective of this work is to consider a future scenario, it has been assumed that all the single-family houses of the district have been renovated with a standard prefabricated façade to improve thermal insulation. Simulation results suggest that for the Continental climate, the specific thermal demand of a renovated single-family house for heating and cooling is in the range of 42.1–50.7 kWh/m/y for heating and equal to 0 kWh/m/y for cooling. Thus, according to the simulation results, for each building, the specific thermal demand has been randomly selected within the given interval. The obtained value has been multiplied by the area of the building, calculated by multiplying the average area of households in the region by a coefficient to introduce variability between buildings of the district. The following formula has been used to calculate the floor area of each buildingwhere has been set equal to the country average dwelling size (93.6 m[31]) and is a coefficient used to add variability between buildings. In this case, has been considered equal to 1, since only the district aggregated profile has been used for the simulations. Finally, to calculate the annual cumulative consumption of the building i for heating and cooling, the area has been multiplied by the specific thermal demand for heating and cooling according to the following formula:
- Calculate the dimensionless hourly thermal demand of the buildings from the NUTS2 (nomenclature of territorial units for statistics, basic regions for the application of regional policies) code of the region [31], the outdoor air temperature, and the hour of the day. The relationship between the inputs and the dimensionless thermal demand was obtained in a previous study founded by the Hotmaps H2020 project from synthetic load profiles and are available at the project repository on GitLab [32]. For the details of the calculations, we refer to the project report [33].
- Apply a reduction factor during some hours of the day. This is an optional function and simulates the effect of different control logic based on the hour of the day. The reduction factor simulates a smart control and shifts part of the night thermal load during daytime hours. In practice, the thermal load during the defined hours is multiplied by a coefficient between zero and one. Two different scenarios have been considered in the current work: The scenario without demand shifting where the reduction factor has been set to zero. Conversely, for the scenario with demand shifting, the reduction factor has been considered equal to 0.5.
- Scale the modified dimensionless profile for matching the yearly cumulative thermal demand calculated at point 2. In this way, the integral of the thermal demand profile is equal to the annual cumulative thermal demand for both heating and cooling.
- Divide the thermal consumption profiles by a temperature-dependent coefficient of performance COP (heating) or by the energy efficiency ratio EER (cooling) from the performance map of a commercial reversible air to water heat pump. However, even if the detailed modeling of the heat pump is out of the scope of this work, it is important to notice that the losses of the thermal system have not been considered. In reality, shifting the electric consumption will cause an increase in thermal losses.
3.3. Electric Vehicle Charging Profiles
4. Simulation Results
4.1. Scenarios and Key Performance Indicators
- PV nominal power and BESS capacity: The optimization tool provides the cumulative nominal power for the PV energy system and the battery capacity to be installed in the considered district as the output according to the specific analyzed scenarios and the related cost functions.
- Self-sufficiency: Indicates the percentage of load that can be supplied by PV and BESS.
- Normalized NPV: Is the normalized over the initial investment.
- GHG emission reduction: Indicated the reduction of GHG emission due to the adoption of PV and BESS system compared to the reference year which is 1990.
4.2. Flexibility Impact—NPV Cost Function
4.3. Environmental Impact—LCOE Cost Function
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Renewables 2020—Analysis and Key Findings. A Report by the International Energy Agency. Available online: www.iea.org/reports/renewables-2020 (accessed on 1 March 2021).
- European Parliament. Directive 2018/2001 on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 2018, 82–209. [Google Scholar]
- Bashir, A.A.; Pourakbari Kasmaei, M.; Safdarian, A.; Lehtonen, M. Matching of Local Load with On-Site PV Production in a Grid-Connected Residential Building. Energies 2018, 11, 2409. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2020. Technical Report. 2020. Available online: https://www.iea.org/reports/world-energy-outlook-2020 (accessed on 1 March 2021).
- Mancini, F.; Nastasi, B. Energy Retrofitting Effects on the Energy Flexibility of Dwellings. Energies 2019, 12, 2788. [Google Scholar] [CrossRef]
- Reynders, G. Energy flexible buildings: An evaluation of definitions and quantification methodologies applied to thermal storage. Energy Build. 2018, 166, 372–390. [Google Scholar] [CrossRef]
- Jensen, S.O.; Marszal-Pomianowska, A.; Lollini, R.; Pasut, W.; Knotzer, A.; Engelmann, P.; Stafford, A.; Reynders, G. IEA EBC Annex 67 Energy Flexible Buildings. Energy Build. 2017, 155, 25–34. [Google Scholar] [CrossRef]
- Vigna, I.; Pernetti, R.; Pasut, W.; Lollini, R. New domain for promoting energy efficiency: Energy Flexible Building Cluster. Sustain. Cities Soc. 2018, 38, 526–533. [Google Scholar] [CrossRef]
- Barchi, G.; Pierro, M.; Moser, D. Predictive Energy Control Strategy for Peak Shaving and Shifting Using BESS and PV Generation Applied to the Retail Sector. Electronics 2019, 8, 526. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Vartiainen, E.; Masson, G.; Breyer, C. True competitiveness of solar PV—A European case study. In Proceedings of the 32th European Photovoltaic Solar Energy Conference and Exhibition Proceedings, Munich, Germany, 20–24 June 2016; pp. 12841–12851. [Google Scholar]
- Quoilin, S.; Kavvadias, K.; Mercier, A.; Pappone, I.; Zucker, A. Quantifying self-consumption linked to solar home battery systems: Statistical analysis and economic assessment. Appl. Energy 2016, 182, 58–67. [Google Scholar] [CrossRef]
- Barchi, G.; Miori, G.; Moser, D.; Papantoniou, S. A small-scale prototype for the optimization of PV generation and battery storage through the use of a building energy management system. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Sánchez Ramos, J.; Pavón Moreno, M.; Guerrero Delgado, M.; Álvarez Domínguez, S.; Cabeza, L.F. Potential of energy flexible buildings: Evaluation of DSM strategies using building thermal mass. Energy Build. 2019, 203, 109442. [Google Scholar] [CrossRef]
- Stavrakas, V.; Flamos, A. A modular high-resolution demand-side management model to quantify benefits of demand-flexibility in the residential sector. Energy Convers. Manag. 2020, 205, 112339. [Google Scholar] [CrossRef]
- Matallanas, E.; Castillo-Cagigal, M.; Gutiérrez, A.; Monasterio-Huelin, F.; Caamaño-Martín, E.; Masa, D.; Jiménez-Leube, J. Neural network controller for Active Demand-Side Management with PV energy in the residential sector. Appl. Energy 2012, 91, 90–97. [Google Scholar] [CrossRef]
- Vanhoudt, D.; Geysen, D.; Claessens, B.; Leemans, F.; Jespers, L.; Van Bael, J. An actively controlled residential heat pump: Potential on peak shaving and maximization of self-consumption of renewable energy. Renew. Energy 2014, 63, 531–543. [Google Scholar] [CrossRef]
- Fachrizal, R.; Munkhammar, J. Improved Photovoltaic Self-Consumption in Residential Buildings with Distributed and Centralized Smart Charging of Electric Vehicles. Energies 2020, 13, 1153. [Google Scholar] [CrossRef]
- Secchi, M.; Barchi, G. Peer-to-peer electricity sharing: Maximising PV self-consumption through BESS control strategies. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Genova, Italy, 10–14 June 2019; Volume 1042, pp. 1–6. [Google Scholar]
- Lovati, M.; Salvalai, G.; Fratus, G.; Maturi, L.; Albatici, R.; Moser, D. New method for the early design of BIPV with electric storage: A case study in northern Italy. Sustain. Cities Soc. 2019, 48, 101400. [Google Scholar] [CrossRef]
- Lovati, M.; Adami, J.; Dallapiccola, M.; Barchi, G.; Maturi, L.; Moser, D. From solitary pro-sumers to energy community: Quantitative assesment of the benefits of sharing electricity. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition Proceedings, Marseille, France, 9–13 September 2019; pp. 1696–1701. [Google Scholar]
- Ward, G.J. The RADIANCE lighting simulation and rendering system. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 24–29 July 1994; pp. 459–472. [Google Scholar]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Skoplaki, E.; Boudouvis, A.; Palyvos, J. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Lovati, M.; Adami, J. EnergyMatching (EM) Tool for Optimization of RES Harvesting at Building and District Scale; Technical Report. Horizon 2020 Energy Matching; 2020; Available online: https://www.energymatching.eu/results/category/public-reports?page=2 (accessed on 1 March 2021).
- Pflugradt, N. Load Profile Generator v9.5. Available online: https://www.loadprofilegenerator.de/ (accessed on 1 March 2021).
- Photovoltaic Geographical Information System (PVGIS). Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html#TMY (accessed on 1 March 2021).
- Horizon 2020 BIPVBOOST. Available online: https://bipvboost.eu (accessed on 1 March 2021).
- Pernetti, R.; Pinotti, R.; Lollini, R.; Paoletti, G.; Toledo, L. 4RinEU Project—D3.3 Deep Renovation Packages and Parametric Models in Different Geo-Clusters; Technical Report. Horizon 2020 4RinEU; 2020; Available online: https://4rineu.eu/wp-content/uploads/2021/02/4RinEU_D3.3-4RinEU-Deep-Renovation-Packages_Annex.pdf (accessed on 1 March 2021).
- Klein, S.; Beckman, W.; Mitchell, J.; Duffie, N.; Freeman, T. TRNSYS 17, Transient System Simulation Program; The Solar Energy Laboratory, University of Wisconsin-Madison: Madison, WI, USA, 1979. [Google Scholar]
- Nomenclature of Territorial Units for Statistics (NUTS2)—Eurostat. Available online: https://ec.europa.eu/eurostat (accessed on 1 March 2021).
- Horizon 2020 Hotmaps, GitLab Repository. Available online: https://gitlab.com/hotmaps/load_profile (accessed on 1 March 2021).
- Pezzuto, S.; Zambotti, S.; Croce, S.; Zambelli, P.; Garegnani, G.; Chiara, S.; Pascuas, R.P.; Zubaryeva, A.; Haas, F.; Exner, D.; et al. Hotmaps Project, D2.3 WP2 Report—Open Data Set for the EU28; Technical Report. Horizon 2020 Hotmaps; 2018; Available online: https://www.hotmaps-project.eu/wp-content/uploads/2018/03/D2.3-Hotmaps_for-upload_revised-final_.pdf (accessed on 1 March 2021)Technical Report. Horizon 2020 Hotmaps.
- Horizon 2020 HYBUILD, Grant Agreement N 768824. Available online: http://www.hybuild.eu/ (accessed on 1 March 2021).
- Lombardi, F.; Balderrama, S.; Quoilin, S.; Colombo, E. Generating high-resolution multi-energy load profiles for remote areas with an open-source stochastic model. Energy 2019, 177, 433–444. [Google Scholar] [CrossRef]
- Fischer, M.; Woodhouse, M.; Herritsch, S.; Trube, J. International Technology Roadmap for Photovoltaic (ITRPV); Technical Report; VDMA Photovoltaic Equipment: Frankfurt am Main, Germany, 2020. [Google Scholar]
- Leloux, J.; Taylor, J.; Moreton Villagrá, R.; Narvarte Fernández, L.; Trebosc, D.; Desportes, A.; Solar, S. Monitoring 30,000 PV systems in Europe: Performance, faults, and state of the art. In Proceedings of the 31th European Photovoltaic Solar Energy Conference and Exhibition Proceedings, Hamburg, Germany, 14–18 September 2015; pp. 1574–1582. [Google Scholar]
- Dash, P.; Gupta, N. Effect of temperature on power output from different commercially available photovoltaic modules. Int. J. Eng. Res. Appl. 2015, 5, 148–151. [Google Scholar]
- Prina, M.G.; Lionetti, M.; Manzolini, G.; Sparber, W.; Moser, D. Transition pathways optimization methodology through EnergyPLAN software for long-term energy planning. Appl. Energy 2019, 235, 356–368. [Google Scholar] [CrossRef]
- Gercek, C.; Devetaković, M.; Krstić-Furundžić, A.; Reinders, A. Energy Balance, Cost and Architectural Design Features of 24 Building Integrated Photovoltaic Projects Using a Modelling Approach. Appl. Sci. 2020, 10, 8860. [Google Scholar] [CrossRef]
- Kiefer, K.; Farnung, B.; Müller, B.; Reinartz, K.; Rauschen, I.; Klünter, C. Degradation in PV power plants: Theory and practice. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019; pp. 9–13. [Google Scholar]
- Jordan, D.C.; Kurtz, S.R.; VanSant, K.; Newmiller, J. Compendium of photovoltaic degradation rates. Prog. Photovoltaics Res. Appl. 2016, 24, 978–989. [Google Scholar] [CrossRef]
- Eurostat. Electricity Prices (Including Taxes) for Household Consumers, First Half 2020. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics (accessed on 1 March 2021).
- MISE. Piano Nazionale Integrato per l’Energia e il Clima; ; Ministero dello Sviluppo Economico, Ministero dell’Ambiente e della Tutela del Territorio e del Mare, Ministero delle Infrastrutture e dei Trasporti. “Piano Nazionale Integrato per l’Energia e il Clima.” Roma; 2019. Available online: https://www.mise.gov.it/images/stories/documenti/PNIEC_finale_17012020.pdf (accessed on 1 March 2021).
- Ang, B.; Su, B. Carbon emission intensity in electricity production: A global analysis. Energy Policy 2016, 94, 56–63. [Google Scholar] [CrossRef]
- Country Specific Electricity Grid Greenhouse Gas Emission Factors. Available online: https://www.carbonfootprint.com/docs/2020_07_emissions_factors_sources_for_2020_electricity_v1_3.pdf (accessed on 1 March 2021).
- de Wild-Scholten, M.M. Energy payback time and carbon footprint of commercial photovoltaic systems. Sol. Energy Mater. Sol. Cells 2013, 119, 296–305. [Google Scholar] [CrossRef]
- Hao, H.; Mu, Z.; Jiang, S.; Liu, Z.; Zhao, F. GHG Emissions from the production of lithium-ion batteries for electric vehicles in China. Sustainability 2017, 9, 504. [Google Scholar] [CrossRef]
- Misure Urgenti in Materia di Salute, Sostegno al Lavoro e All’economia, Nonché di Politiche Sociali Connesse All’emergenza Epidemiologica da COVID-19. D.L. 19 Maggio 2020, n.34. (Decreto “Rilancio”), Gazzetta Ufficiale della Repubblica Italiana, Roma. 2020. Available online: https://www.gazzettaufficiale.it/eli/id/2020/05/19/20G00052/sg (accessed on 1 March 2021).
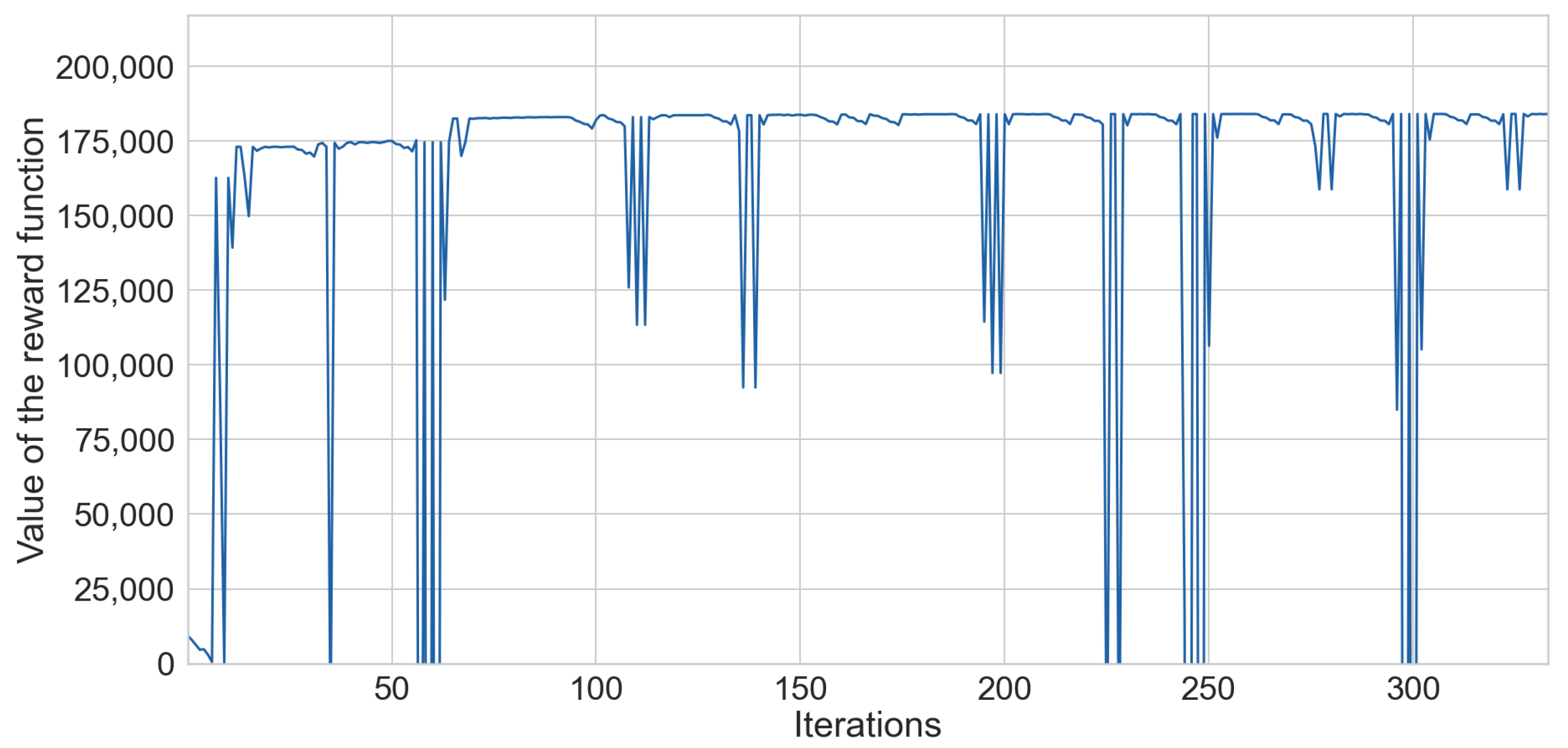

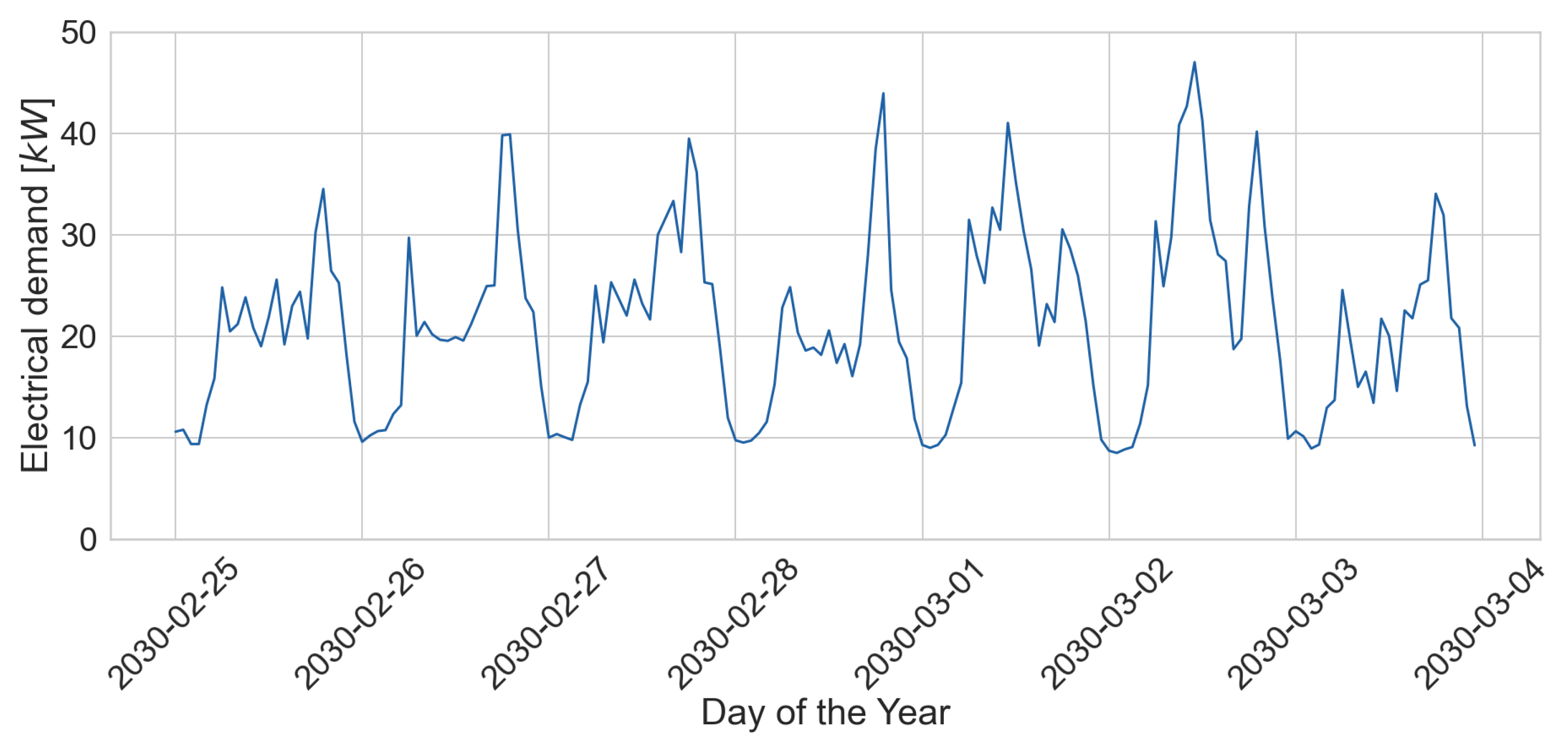
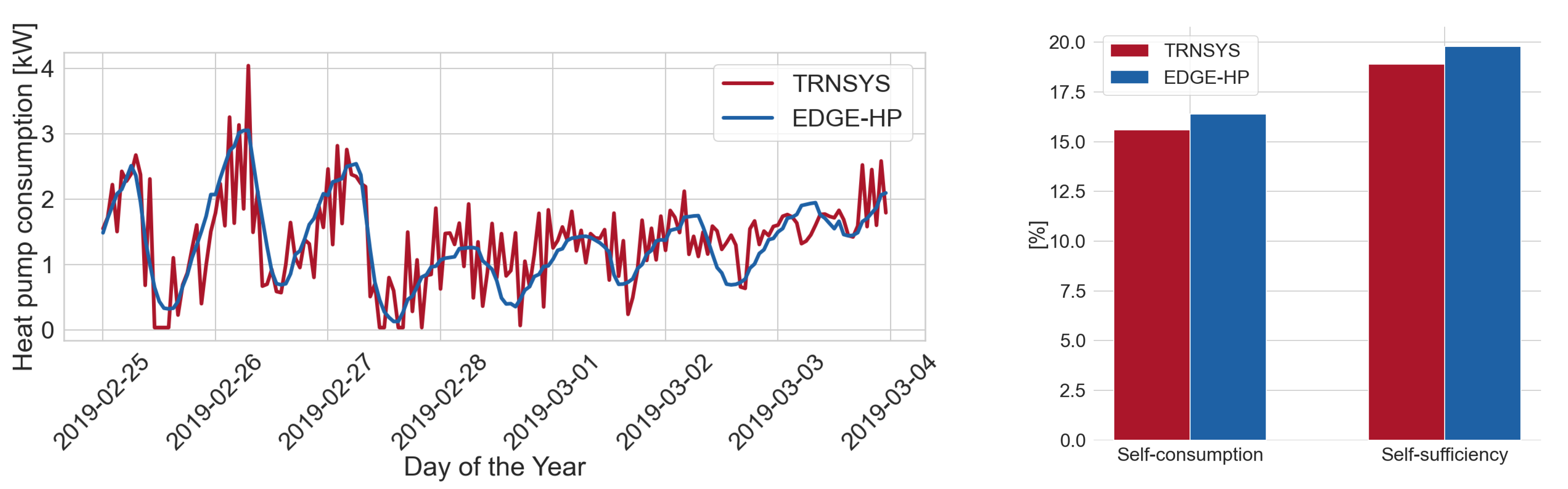
| Scenario A | Scenario B | Scenario C | Scenario D | ||
|---|---|---|---|---|---|
| EV configuration | Night charge | ✔ | |||
| RES integration | ✔ | ✔ | ✔ | ||
| HP configuration | No shifting | ✔ | ✔ | ||
| Red factor 0.5 | ✔ | ✔ | |||
| Appliances configuration | Considered | ✔ | ✔ | ✔ | |
| Not considered | ✔ |
| Parameter | Value | Unit | Reference | |
|---|---|---|---|---|
| Efficiency | 22.5 | [%] | [36] | |
| Module dimension | 0.5 × 0.5 | [m] | [-] | |
| Performance ratio | 0.8 | [-] | [37] | |
| Photovoltaic system | Temperature coefficient | −0.5 | [%/°C] | [38] |
| Cost of the system | 945 | [kWp] | [39] | |
| Annual maintenance cost * | 25–40 | [kWp/year] | [40] | |
| Linear annual efficiency losses | 0.75 | [%] | [41,42] | |
| BESS | Efficiency | 90 | [%] | [-] |
| Cost of the system | 350 | [kWh] | [39] | |
| General | Cost of the electricity | 0.2341 | [kWh] | [43] |
| Price electricity sold | 0 | [kWh] | [-] | |
| Annual discount rate * | 0–2 | [%] | [-] | |
| Time horizon | 25 | [years] | [-] |
| Scenario A | Scenario B | Scenario C | Scenario D | |
|---|---|---|---|---|
| PV power [kWp] | 83 | 179 | 166 | 78 |
| BESS capacity [kWh] | 0 | 113 | 57 | 29 |
| Self-sufficiency [%] | 19.8 | 46.8 | 42.9 | 45 |
| Normalized NPV [-] | 2.5 | 1.9 | 2.6 | 2.5 |
| PV Power [kWp] | BESS Capacity [kWh] | Self-Sufficiency [%] | LCOE [€/kWh] | N. NPV | |
|---|---|---|---|---|---|
| Scenario D | 174 | 35 | 55 | 0.072 | 0.7 |
| Scenario D S1 | Scenario D S2 | |
|---|---|---|
| PV power [kWp] | 111 | 121 |
| BESS capacity [kWh] | 110 | 91 |
| Self-sufficiency [%] | 56 | 56 |
| LCOE [€/kWh] | 0.093 | 0.086 |
| Normalized NPV [-] | 1.1 | 1.1 |
| Scenario D | Scenario D S1 | Scenario D S2 | |
|---|---|---|---|
| [%] | 46 | 56 | 55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dallapiccola, M.; Barchi, G.; Adami, J.; Moser, D. The Role of Flexibility in Photovoltaic and Battery Optimal Sizing towards a Decarbonized Residential Sector. Energies 2021, 14, 2326. https://doi.org/10.3390/en14082326
Dallapiccola M, Barchi G, Adami J, Moser D. The Role of Flexibility in Photovoltaic and Battery Optimal Sizing towards a Decarbonized Residential Sector. Energies. 2021; 14(8):2326. https://doi.org/10.3390/en14082326
Chicago/Turabian StyleDallapiccola, Mattia, Grazia Barchi, Jennifer Adami, and David Moser. 2021. "The Role of Flexibility in Photovoltaic and Battery Optimal Sizing towards a Decarbonized Residential Sector" Energies 14, no. 8: 2326. https://doi.org/10.3390/en14082326
APA StyleDallapiccola, M., Barchi, G., Adami, J., & Moser, D. (2021). The Role of Flexibility in Photovoltaic and Battery Optimal Sizing towards a Decarbonized Residential Sector. Energies, 14(8), 2326. https://doi.org/10.3390/en14082326







