A Hybrid Hilbert-Huang Method for Monitoring Distorted Time-Varying Waveforms ^†

Abstract

The electric power systems together with the entire energy sector are rapidly evolving towards a low-carbon, secure, and competitive economy facing revolutionary transformations from technical structure to economic value chain. Pathways to achieve sustainability led to the development of new technologies, accommodation of larger shares of unpredictable and stochastic electricity transfer from sources to end-users without loss of reliability, new business models and services, data management, and so on. The new technologies and incentives for local energy communities along with large development of microgrids are main forces driving the evolution of the low voltage energy sector changing the context and paradigm of rigid contractual binding between utilities and end-user customers (now progressing to flexible prosumers with generation and storage capabilities). The flexibility and operation of a prosumer can be enhanced by a non-intrusive time-frequency analysis of distorted power quality waveforms for both generation and demand at the point of common connection. Therefore, it becomes of importance to discriminate among successive quasi-steady-state operation of a given local system using only the aggregated waveforms information available in the PCC. This paper focuses on the Hilbert–Huang method with modifications such as empirical mode decomposition improved with masking signals based on the Fast Fourier Transform, Hilbert spectral analysis, and a post-processing method for separating components and their amplitudes and frequencies within distorted power signals for a low-voltage prosumer operation. The method is used for a time-frequency-magnitude representation with promising localization capabilities enabling efficient operation for prosumers.

1. Introduction

The operation of current distribution grids is impacted by the high variability of the energy transfer. For high efficiency in operation and increased power quality evaluation, awareness over the distorted waveform signals is needed, and thus, a new approximation model for its characteristic quantities (voltages, currents, power) [1,2]. Such a model is required especially to better assess the quality of existing “classical” measurements, still in use for power quality improvement. The state-of-the-art in power quality measurements and associated signal processing is also applied in emerging control algorithms dedicated to microgrids (including DC and hybrid) and energy communities [3], to overcome unprecedented operational constraints [4]. Many of those constraints are linked to measurement processes and therefore they might fail to meet the needs of the user [5,6,7] unless a careful analysis of the model uncertainties is performed. An important issue to be considered is the accuracy of estimating time-varying distorted voltage and current signals, following fast successive quasi-steady-state operation modes. It is also essential to underline the correct use of the common variable “harmonics” closely related to power quality investigations [8]. Harmonics are used to describe modes of oscillation that are stationary and linear within the investigation window and the effort in this paper is to describe higher modes of oscillations within time-varying, nonstationary, non-linear distorted waveforms. This section describes the proposed hybrid method based on Fast Fourier Transform, Improved EMD with masking signals, Hilbert Transform, and a post-processing algorithm for original signal mono-components’ amplitudes and frequencies identification.

2. Hilbert—Huang Method. A Timeline

The Hilbert transform, developed by Hilbert circa 1910, is a mathematical operator that introduces a ±π/2 phase-shift in a signal, which is useful in frequency analysis and signal processing. Circa 1998, the modification proposed to the Hilbert transform by Huang and collaborators, yielded the Hilbert–Huang transform (HHT), a powerful signal analysis tool for studying time-frequency characteristics using intrinsic mode functions and empirical decomposition [9]. The major strength of the HHT was its application to the study of non-stationary signals. Due to the overabundance of such signals and their studies, the references are too aplenty to list here. However, the HHT’s performance and accuracy were questionable when the frequency modes under study lay within an octave. It is in that regard that in 2007, Senroy et al. proposed an improvement to this method by utilizing the FFT of the signal under study as a snapshot for developing masking signals and using them with the HHT to study time-varying and closely located frequency components. In recent years, improved methods based on HHT were used for Flicker studies, Harmonics Detection, power quality studies for microgrids [10,11], and harmonic current forecasting in microgrids [12]. To study nonstationary phenomena, wavelet transform is also a powerful mathematical tool proposed to identify modes of oscillations that evolve in time [13]. Wavelets are applied to achieve a multiresolution decomposition of the original signal at different time scales, using different time resolutions to adapt to the dynamic content of the signal. Such a technique was successfully used, among others, for power quality application in [14,15]. An improved version of the wavelet transform is the S-transform [16] with better phase-frequency-time localizing properties applied also for power quality studies [17,18]. Although extensively applied to identify transient phenomena [19], the decrease of system inertia made discrimination among steady-state and dynamic regimes of a given small power system (for example, a microgrid) very difficult. Thus, based on the previous work and research in this field, the time-frequency and time-magnitude localization capabilities of the HHT method have been proven in regards to other multiresolution analysis tools for several power quality applications, signal processing analysis, but also for real-time control applications such as Transient Analysis in DC power systems [20]. In our paper, we have utilized an extension of the HHT technique to propose a monitoring method of prosumers connected to the low- and medium-voltage sections of an emerging smart electric distribution systems based on identification of quasi-steady-state time intervals. The choice was for the HHT method as this tool showed its performances in separating modes of oscillations whose frequencies lay within one octave. To avoiding repetition, the interested reader is directed to the primary source of the modified Hilbert-Huang method [21], where the comparative performances are also highlighted.

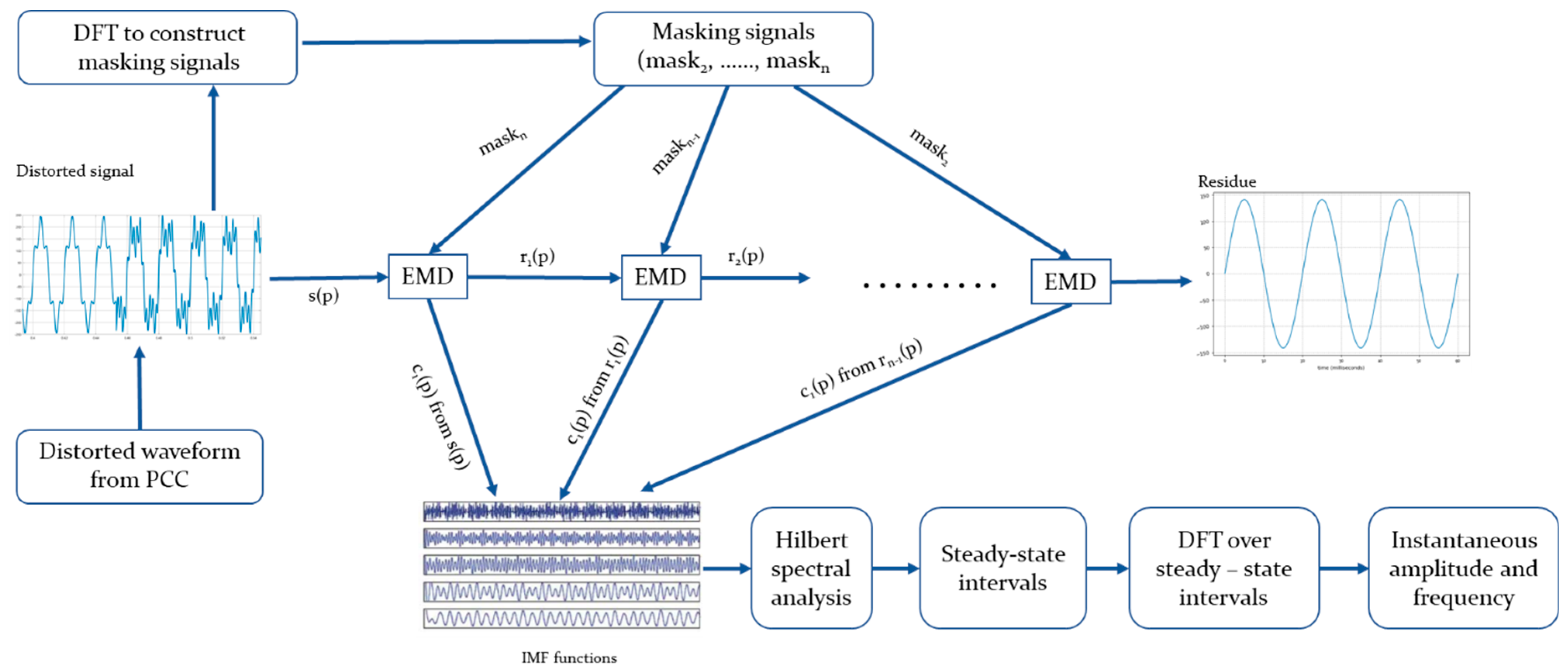
3. Hybrid Hilbert–Huang

The Hilbert–Huang method was firstly introduced in [9] as an innovative tool for the analysis of nonstationary distorted signals to identify time-frequency-magnitude behavior of the mono-components inside the original signal. The method includes Empirical Mode Decomposition (EMD) enhanced with appropriate chosen masking signals created based on the algorithm of Fast Fourier Transform, enabling this solution to generate truly mono-component intrinsic mode functions (IMFs). Even in this situation, the improved EMD with masking signals will not always guarantee mono-component functions, and a post processing algorithm is proposed after applying the Hilbert Transform over the IMFs obtained. The use of the method and the ability of separating the modes of oscillation within a distorted waveform will be demonstrated as an investigation tool for identification of events in time varying, non-stationary, non-linear waveforms specific for the energy transfer within LV prosumer environment. The monitoring and analysis will be carried out for current waveforms in the power quality framework assuming a non-steady-state system. Evolving power systems require new control algorithms and, accordingly, a measurement layer with higher dynamic performances. The non-sinusoidal time varying currents are increasingly relevant in the context of increased energy harvesting from local resources and accommodation of larger shares of unpredictable stochastic electricity transfer from sources to end-users (prosumers or not). The focus in this paper is on load patterns and how the type of household appliances and electrical vehicles chargers might highly impact them. The operation of LV distribution grids is strongly impacted by the high variability of the energy transfer through its characteristic quantities (voltages, currents) for whom the term of “harmonics” loses its meaning [9].

As described in [9], the method consists of EMD that will decompose the distorted signal into mono-component functions called intrinsic mode functions (IMFs) and then the amplitudes and frequencies will be computed using the Hilbert Transform. In this paper, before applying EMD, masking signals are created for improving the performances as in [21,22] based on a versatile Discrete Fourier Transform (DFT). A post-processing technique is proposed in this paper to obtain the frequencies and amplitudes of constituent modes inside the original signal after applying the Hilbert Transform. This section is divided by subheadings where all the steps involved in the successful implementation of the application and the authors’ contribution to each part will be highlighted and explained. The approach of the method is a continuation of the one proposed in [21] with the aim of improving its performances and expanding the area of applications involving distorted waveforms analysis and it is presented in Figure 1. The specific enhanced Hilbert-Huang method as it was described in [21] along with its performances in studying time-varying, non-stationary, non-linear signals were analyzed in contrast with the S-Transform, used as a benchmark tool. The steps involved in the definition and implementation of the new hybrid Hilbert–Huang (h H-H) method are represented by the letter “h”.

3.1. Versatile DFT and Masking Signals to Improve EMD

As acknowledged in [23], the use of masking signals is of interest as it will increase the performances of the method, essential for signal decomposition into its mono-component functions. The main point followed in the implementation of masking signals is the ability of discriminating between two neighboring modes of oscillation inside the original nonstationary distorted waveform. The role, the improvements for the EMD, and the ability to separate adjacent high-frequency components was clearly proved in [21,23]. The methodology and the analytical approach used to construct such masking signals was presented in [21], but it is now improved with the innovative versatile DFT essential for computing the parameters of the masking signals. The ground base of creating such signals is the DFT spectrum that will only be used as a starting point of the method, as the Fourier Transform approximates non-stationary, non-linear distorted waveforms modal content. The original current signal $i\left(t\right)$, subjected to the investigation window $T_w$, is digitized with proper sampling frequency $f_s$ resulting the discrete signal $i\left[p\right]$. Afterwards, the estimated frequencies and associated amplitudes will be adequately selected out of the resulting frequency spectrums, and masking signals will be created as per the following steps:

(h1)

Perform DFT over the $i\left[p\right]$ (corresponding to $i\left(t\right)$ during $T_w$) to estimate the frequencies of its components $f_1, f_2, f_3, \dots \dots , f_n$ and corresponding amplitudes $A_1, A_2, A_3, \dots \dots , A_n$, where $f_1$ is the fundamental and $f_1< f_2< f_3< \dots \dots <f_n$. The resulting spectrum is corresponding to the image of a model signal representing the stationary equivalent of the original signal over the $T_w$ window.

(h2)

Amplitudes threshold selection $A_{imp}$ for retaining the meaningful frequency components. At this stage and using this selection tools, only the components possessing more than ${\delta }_e$ percentage from the total signal energy are kept and processed. The contribution here stands for this flexible new tool capable of selecting only the meaningful components out of the DFT spectrum associated with the stationary modal equivalent of the original signal. The value of ${\delta }_e$ was set to 1% for the components’ energy to be a good compromise for the associated uncertainty of the overall chain of measurements in the distribution grids (instrument transformers, smart meters, Intelligent Electronic Devices, etc.).

(h3)

Based on the component analysis and the retained frequencies $f_k$ and their associated amplitudes, corresponding masking signals are created using the following formula:

$$mas{k}_k\left[p\right]= M_k·\sin (2\pi \left(f_k+ f_{k-1}\right)·p$$

(1)

where $M_k=5.5·amplitude\left(f_k\right)$.∙The value of 5.5 is empirical and was used based on the consideration and explanations from [21] by scaling the amplitude of the appropriate signal $f_k$ from the DFT spectrum.

3.2. Enhanced EMD with Masking Signals

Huang’s Empirical Mode Decomposition (EMD) method is underlined in this section as an essential tool capable of identifying modes of oscillation simultaneously existing inside a distorted power signal. Such time-varying, nonstationary, nonlinear waveforms are decomposed using EMD into multiple intrinsic mode functions (IMFs) that possess the well-behaved Hilbert Transform conditions. The principle of EMD lies in the concept of instantaneous frequency defined as the derivative of the phase of an analytic signal [9]. The essence of computing meaningful instantaneous frequencies is given by the Hilbert Transform [24]. For a mono-component signal, this concept uniquely defines a positive instantaneous frequency as the derivative of the phases of the signal. The situation changes when the discussions is about signals with multiple modes of oscillation within which the instantaneous frequency will have no meaningful representation. For such types of distorted waveforms, before the application of Hilbert Transform, they must be decomposed into their constituent mono-component signals to correctly compute the instantaneous frequencies. Each individual IMFs thus subtracted is defined by two main characteristics: Has its mean equal to zero and the number of local extrema equal to or different by at most 1 from the number of zero crossings. A local extremum for a random time window is defined as the point on the signal where its derivative is zero and its second derivatize is nonzero. The word local denotes that for a random observation time window, there may be multiple local extrema, while only one global extremum may be identified. Once an IMFs has it mean equal to zero, it will automatically be sifted out of the distorted signal. The original EMD technique as proposed by Huang in [9] is briefly introduced and explained using the following steps:

(a1)

Identification of local extrema (minima and maxima) for the digitized distorted signal $x\left[p\right]$.

(a2)

Perform cubic spline interpolation for the maxima and the minima to obtain the envelopes $e_{max}\left(p\right)$ and $e_{min}\left(p\right)$.

(a3)

With the new envelopes, the mean of the two is computed as:

$$m\left[p\right]=\frac{e_{max}\left[p\right]+e_{min}\left[p\right]}{2}$$

(2)

(a4)

The previous computed mean is subtracted from the original signal as

$$s_1\left[p\right]=x\left[p\right]-m\left[p\right]$$

(3)

(a5)

$s_1\left[p\right]$ is considered an IMF if its number of local extrema is equal of differs at most with one from the number of zero crossings, and the average of $s_1\left[p\right]$ is zero. If those conditions are not met, then $s_1\left[p\right]$ is not an IMF, and the steps from b1 to b4 will be subsequently repeated using $s_1\left[p\right]$ instead of $x\left[p\right]$, until the new $s_k\left[p\right]$ satisfies the conditions of an IMF.

(a6)

A residue is defined as

$$r_1\left[p\right]= x\left[p\right]-s_1\left[p\right]$$

(4)

(a7)

If this residue does not satisfy the condition of being below a threshold tolerance of error, then the method will repeat the steps from b1 to b6 for $r_1\left[p\right]$ to compute the next IMF and a new residue.

The first computed IMF is the mono-component with the highest frequency identified within the original digitized signal. The next subtracted IMFs components possess progressively lower frequencies of the distorted signal. If N IMFs mono-components are obtained based on the iterative technique described above, the original signal may be reconstructed as per the following formula:

$$x\left[p\right]={\displaystyle \sum }_{k=1}^N{s}_k\left[p\right]+r_1\left[p\right]$$

(5)

Variations, improvements, and other details of the EMD method were highlighted and underlined in [9,25,26], as well as the importance and significant contribution of the masking signals in separating two adjacent modes inside a nonstationary, nonlinear signal. The following steps are conducted towards decomposing the time-varying distorted waveform into its IMF components with the help of the masking signals previously defined:

(h4)

The next step in the overall framework of the hybrid Hilbert–Huang is performing EMD over two new signals based on the original digitized signal and the masking signals from step “(h3)”, resulting in their IMFs, based on the algorithm described from (a1) to (a7).

$$i{M}_1\left[p\right]=i\left[p\right]+mas{k}_n\left[p\right]$$

(6)

$$i{M}_2\left[p\right]=i\left[p\right]-mas{k}_n\left[p\right]$$

(7)

The computed IMFs are stored as $IM{F}_a\left[p\right]$ and $IM{F}_b\left[p\right]$. It can be then constructed:

$$s_1\left[p\right]=\frac{IM{F}_a\left[p\right]+IM{F}_b\left[p\right]}{2}$$

(8)

where $p=1\dots (T_w·f_s)$.

(h5)

$s_1\left[p\right]$ is named as the first IMF subtracted from the original digitized signal $i\left[p\right]$. For the calculated residue as for the formula in (9), the first sift stage will be applied and the first component of the signal will be identified.

$$r_1\left[p\right]= i\left[p\right]-s_1\left[p\right]$$

(9)

(h6)

The sequence (h4)–(h5) will be iteratively followed using the residues replacing the original $i\left[p\right]$ signal, until (N-1) IMFs associated with the mono-component described by the $f_n, f_{n-1}, \dots \dots , f_3,f_2$ will be computed.

As discussed above, the first IMF obtained is the mono-component with the highest frequency, the other with progressively lower frequencies. After all IMFs are identified, the original $i\left[p\right]$ can be reconstructed using Equation (5), thus the completeness of the method can be suggested as demonstrated in [9].

3.3. Post—Processing Method

For each IMF previously computed, the now Hilbert Transform is applied to calculate the amplitudes and instantaneous frequencies, as an IMFs is described as a mono-component function. Each of the IMFs extracted using the enhanced EMD with masking signal is defined by a dominant frequency and other negligible lower frequencies but still an estimate representation of the modes of oscillation that compose the original digitized signal, making the results of Hilbert Transform subject to approximations and uncertainties. As the output of the Hilbert Transform over each individual IMF is subjected to a modulated result, the authors of [21] proposed a post-processing demodulation technique to separate and extract the dominant frequency and the associated amplitude of the mono-component functions.

The study cases presented in this paper consider distorted power signals comprising of components with variable frequencies over the under-investigation time window ($T_w)$ and variable associated amplitudes. For example, a high-frequency component might occur in last part of the time window $\left(T_w\right)$. For such non-stationary, nonlinear, distorted waveforms, the approach of this paper considers a new algorithm as per the post processing part, applied over the results of the Hilbert Transform. The objective is to allow identification and segregation of quasi-steady-state subintervals within the total signal analysis window ($T_w)$. To highlight the transition between two-time intervals, a moving-average filtering technique was chosen as a simple tool for prior identification of quasi-steady-state intervals. 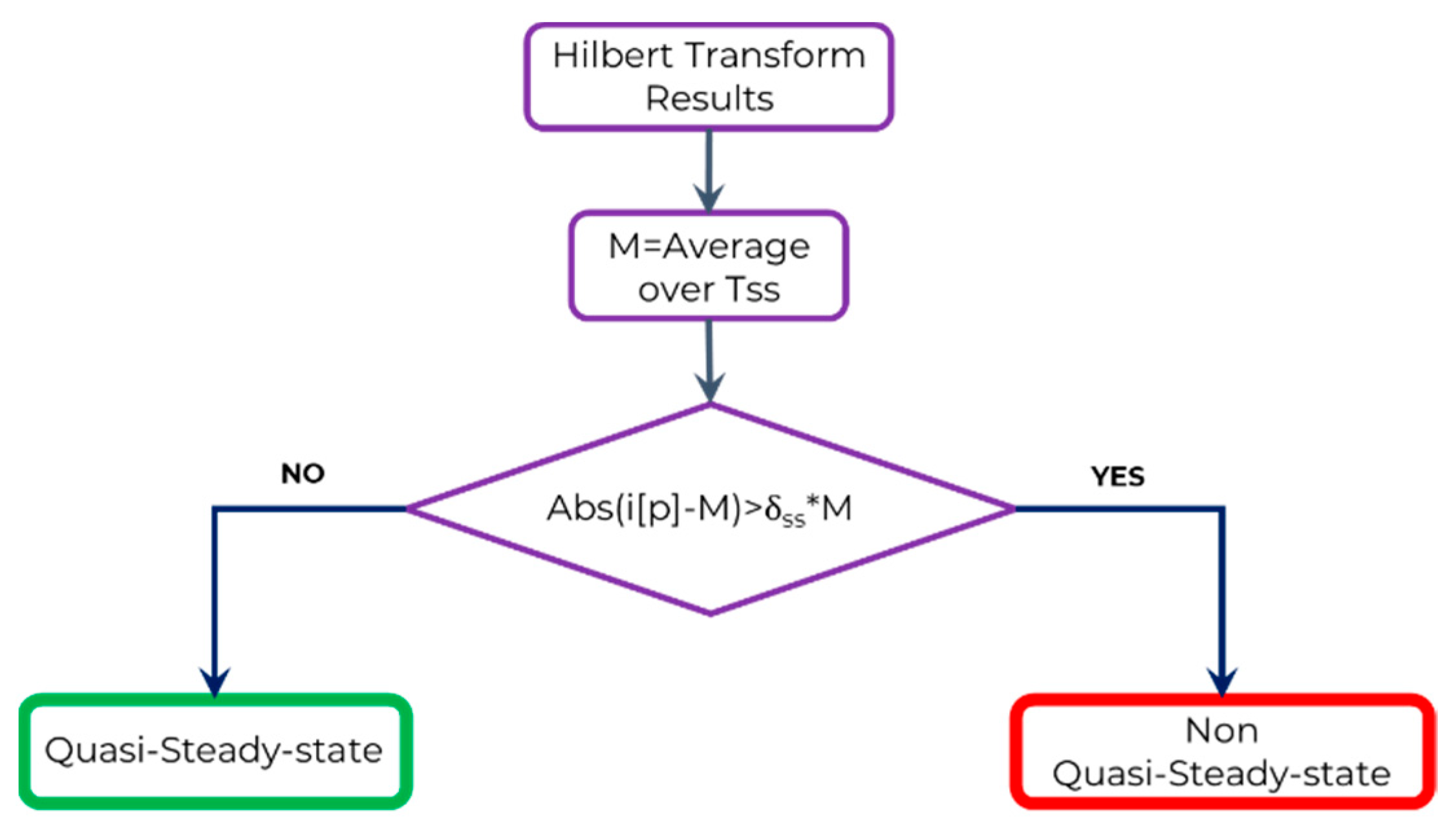The final detection of such time intervals will be conducted based on an updated version of the Rapid Voltage Changes (RVC) algorithm as defined in IEC 61000-4-30 v3.0 [8] and modified to fit into our hybrid algorithm. The updated version of the algorithm will be called Quasi-Steady-State Identification (QSSI). The final step will consist of identification of frequencies and amplitudes of the original digitized signal’s inner components, to be calculated based on a DFT algorithm executed over the identified quasi stationary intervals.

The QSSI is assessed using the methodology of the RVC event identification algorithm based on specific procedures and principles. The parameters of the algorithm are the inputs in terms of the results of Hilbert Transform over the IMFs for the $T_w$ (preliminary filtered using a moving average) and the selected time window of this procedure of $T_{SS}=200 \mathrm{ms}$ (instead of 1s as per the standard [8]). $T_{SS}$ was chosen as a multiple (at least 10 times higher) of the period for signals describing the under-investigation phenomena, in our case $10\times 20\mathrm{ms}=200 \mathrm{ms}$, based on nominal frequency of the supply. This selection is in line with PQ framework [8] and PQ analyzers [27]. A recommendation for choosing the value of $T_{SS}$ would be in the range of seconds as a good compromise between computational resources and accuracy of events’ detection. The standard [8] defines a logical signal, able to show the time intervals over which the system is assumed to operate in quasi-steady state using, as the condition for the difference between two quantities, the arithmetic mean of the values during the past $T_{SS}$ and the value at that instant, to be higher or lower than a preset threshold. If the difference is higher, then the value of the logic signal becomes “false” and stays like this until the difference between the above quantities drops below the threshold, ${\delta }_{SS}$, expressed as percentage from the signa mean value over $T_{SS}$. There is no standardized value for this threshold (as it is fully dependent on the application); however, [8] gives a couple of examples based on the values already set by other IEC standards. The amplitude threshold for discriminating quasi-steady-state intervals is application dependent, considering the expected variability of the signal amplitude and the quality of the measurement chain. In the work illustrated in this paper, we have selected ${\delta }_{SS}=5\%$. The logical diagram of the procedure on which the QSSI work is based is presented in Figure 2.

While inspired by the RVC identification algorithm, described in [8], the QSSI approach is a different application since only the starting point of such an interval is of interest and not its duration (there is no hysteresis and no evaluation feed-back.) Secondly, in [8], the RMS voltage value is used as a basis for the algorithm (i.e., information is already low-path filtered), while in the proposed algorithm here, we use the output of the improved HHT to find the inception of a new steady-state interval, defined in terms of frequency content and associated amplitudes. Additionally, the frequency estimation intervals are not predefined (as per [8] and for all the PQ analyzers such as ELSPEC [27]), nor dependent on the a-priori knowledge of the dynamic of the phenomena. The only restriction is to set the “blind” domain for the minimum duration of a steady-state, in our work this being T_b = 20 ms. This is related to achieving an “acceptable” resolution in time and frequency.

One of the applications for steady-state operation in power quality framework is related to the measurement information fusion (for example, in hybrid state estimators), when data are delivered with heterogeneous reporting rates. Another important direction for QSSI is load and generation frequency signature profiling and identification within a distribution grid with RES generation and prosumers by performing analysis at the Point of Common coupling (PCC) [28].

4. The Ability of the Method to Separate Components

Since Huang et al. proposed the modifications for the original Hilbert Transform, a lot of applications were developed in many fields of study with variations and improvements depending on the specificity of the matter. Some relevant and important findings in using the Hilbert–Huang method were in medical field, for studying parasympathetic Components of Heart Rate when using signals sampled at 256 Hz [29], for studying postural stability using signals sampled at 100 Hz [30], and the assessment of arterial distension based on Doppler wave and Hilbert–Huang processing for signals sampled at 12.8 kHz [31]. For other applications such as fault detection in a voltage source converter in HVDC systems, the distorted signals are sampled at 20 kHz [20], the same as for fault diagnosis in rolling bearing [32]. For fast detection of fault clearance in long and high-voltage transmission lines, the HHT method is used to identify sub-synchronous components that appear in the voltage waveform to detect secondary arc extinction [19], highlighting the capabilities of the HHT method in identifying time varying components with instantaneous frequencies in the range of 30 and 45 Hz. The algorithm was tested in different conditions and the results were compared with other specific methods used in detection of secondary arc extinction for real-time control based on adaptive single-phase auto-reclosure. In this section, though, we demonstrate the overall ability of the method to divide the original digitized distorted signal into mono-component and calculate the instantaneous frequencies and amplitudes based on the method of segregation the signal into quasi-steady-state intervals, using a synthetic signal. The results and the performances of the enhanced EMD with masking signals were presented in [21], showing the ability of the method to separate the modes of oscillation inside a non-stationary, nonlinear power signal and computing the instantaneous frequencies and amplitudes using demodulation algorithm over the Hilbert Transform results. In [21], a comparative analysis was performed using the S-Transform as a reference with specified parameters. Based on the previous results obtained, the aim of this paper was the identification of quasi-steady-state intervals over the moving average filtered results of the Hilbert Transform over each IMFs obtained using EMD. The steps and methodology of the hybrid HH were presented in Section 3 and Figure 1.

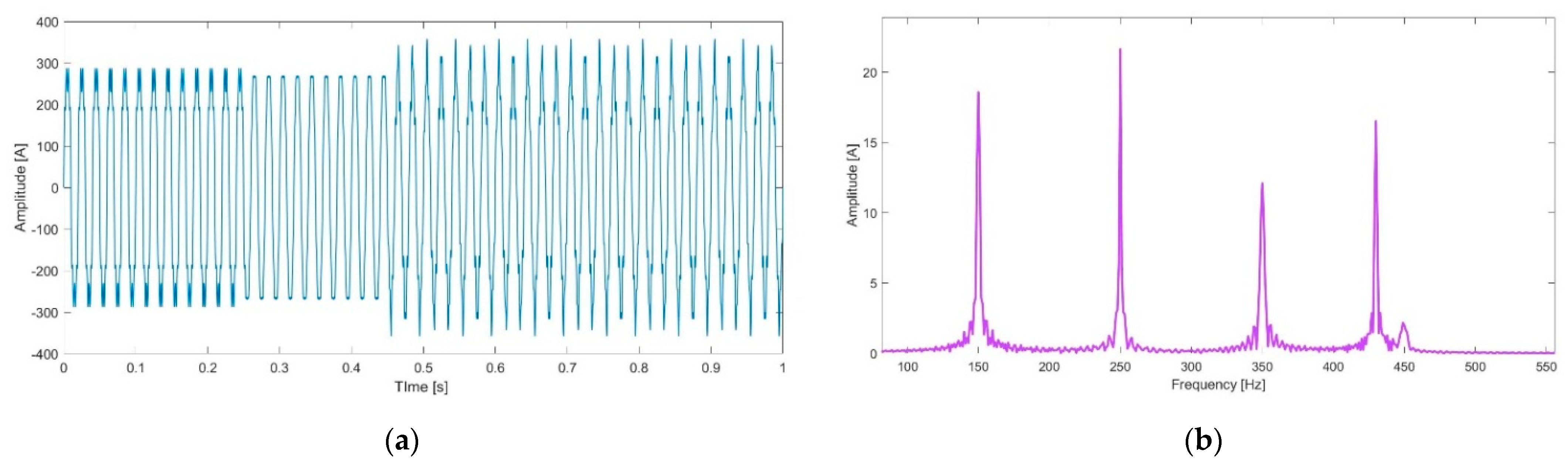
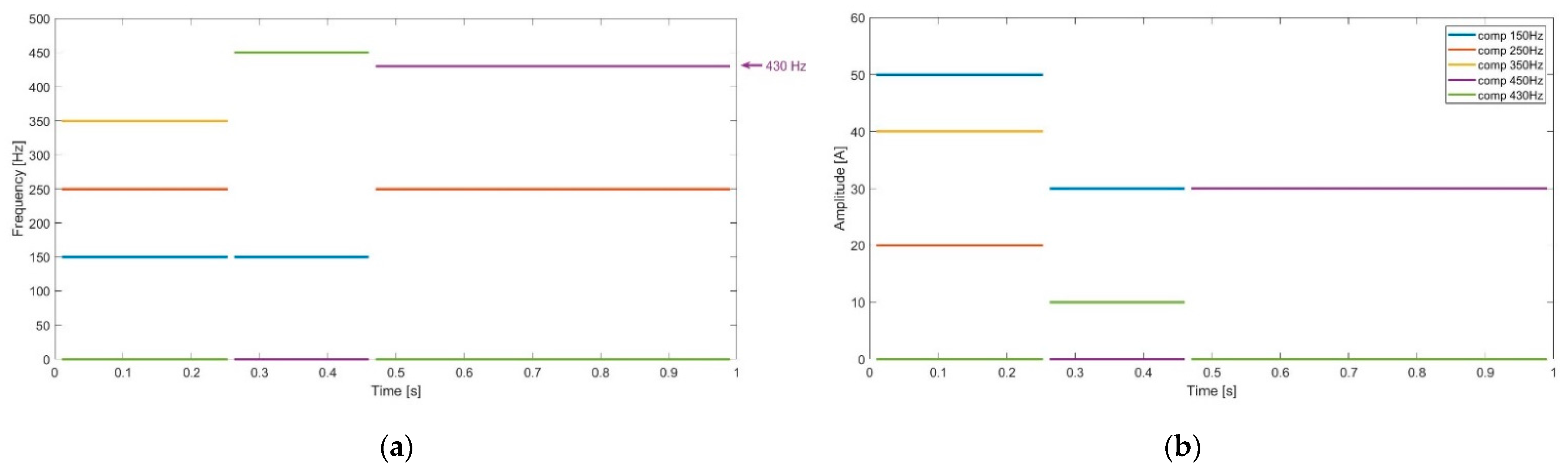
A synthetic digitized current signal is created to validate the method. A distorted signal emulating the parameters of the current in a common-coupling point for an energy community is constructed with a sampling frequency of 51.2 kHz, with a fundamental frequency of 50 Hz and multiple time-varying components as described in

Table 1. Components of the original signal under investigation.

Time [s]	Component Amplitude (% of RMS of Signal)
	150 Hz	250 Hz	350 Hz	430 Hz	450 Hz
0–0.253	23%	9%	19%	0%	0%
0.253–0.450	14%	0%	5%	0%	5%
0.450–1	0%	15%	0%	15%	0%

. For this simulation, as can be seen in the table, the components do not appear on the whole-time window $\left(T_w\right)$, but on some intervals only, their amplitudes being expressed in percentages of the RMS value of the original signal. It should be noted that each individual component has an energy higher than 1% of the total energy of the signal.

The signal as described in the table above is plotted on Figure 3a together with its DFT spectrum (Figure 3b) of the components delivered by the Fourier analysis. DFT spectrum is the first step evolved in the hybrid HH.

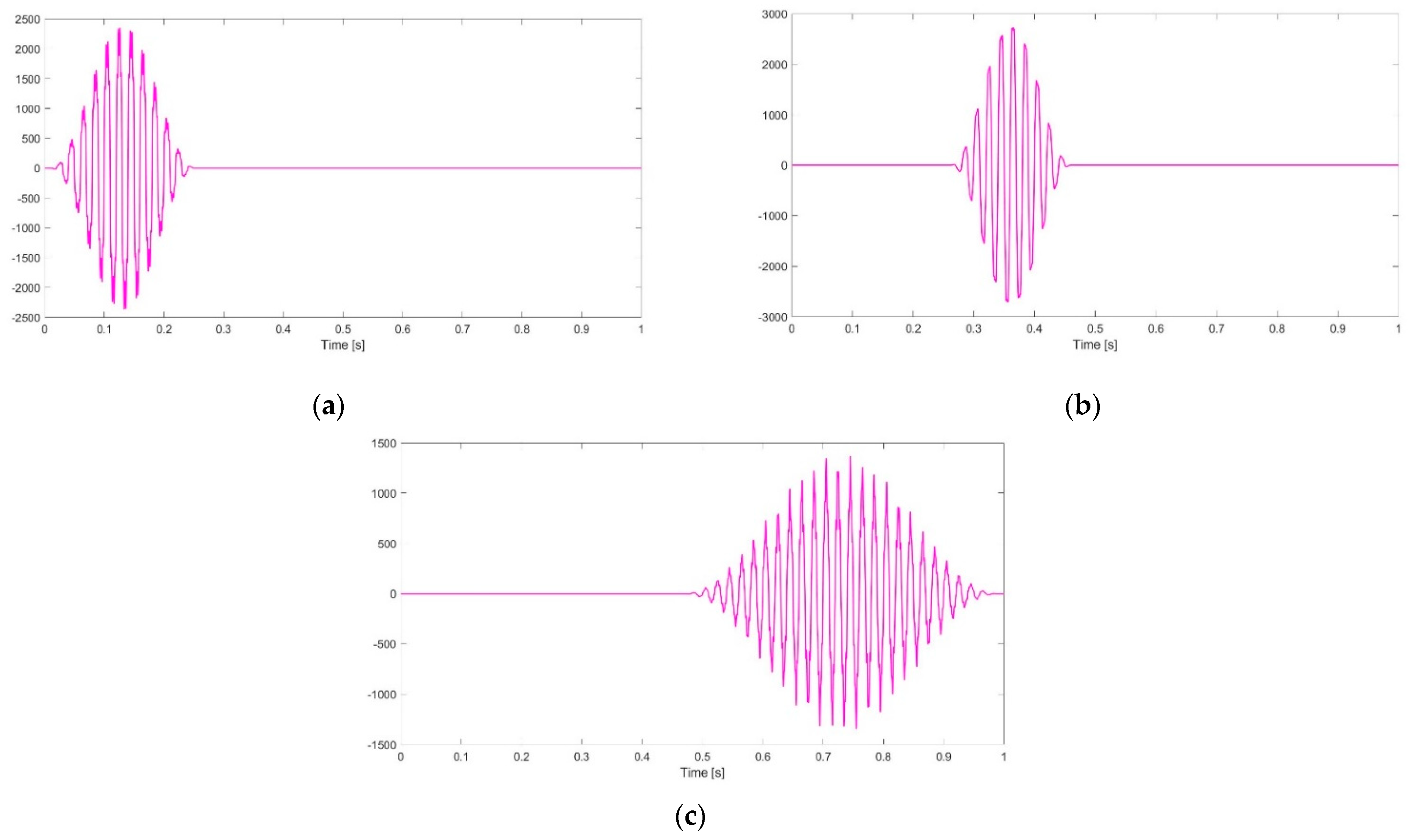
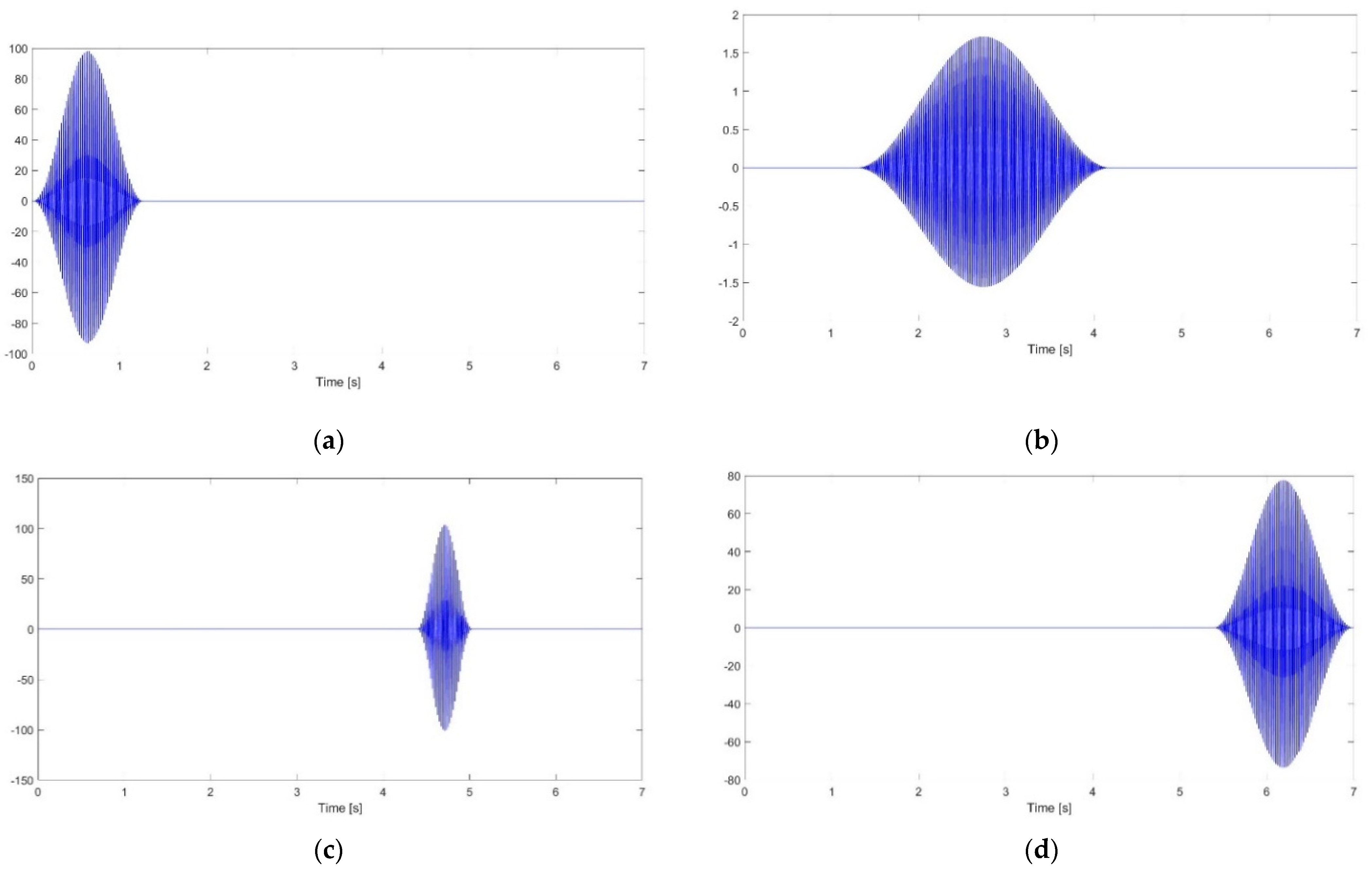
Based on the frequency information obtained from the DFT spectrum, masking signals were created to improve EMD tool and to properly extract four mono-component IMFs. Over each IMF, Hilbert Transform was applied, then a moving average filtered the results, and finally, with the help of the innovative post-processing method described in Section 3.3 three quasi-steady-state intervals were identified. One mention must be done because some parts were discarded based on the transitional aspects of the original signal, from one interval to the adjacent one and because of the artefacts at the end of the time window, $T_w$. Having obtained those time intervals, Hanning [33] windows were applied over each interval, obtaining the following signals, as can be seen in Figure 4.

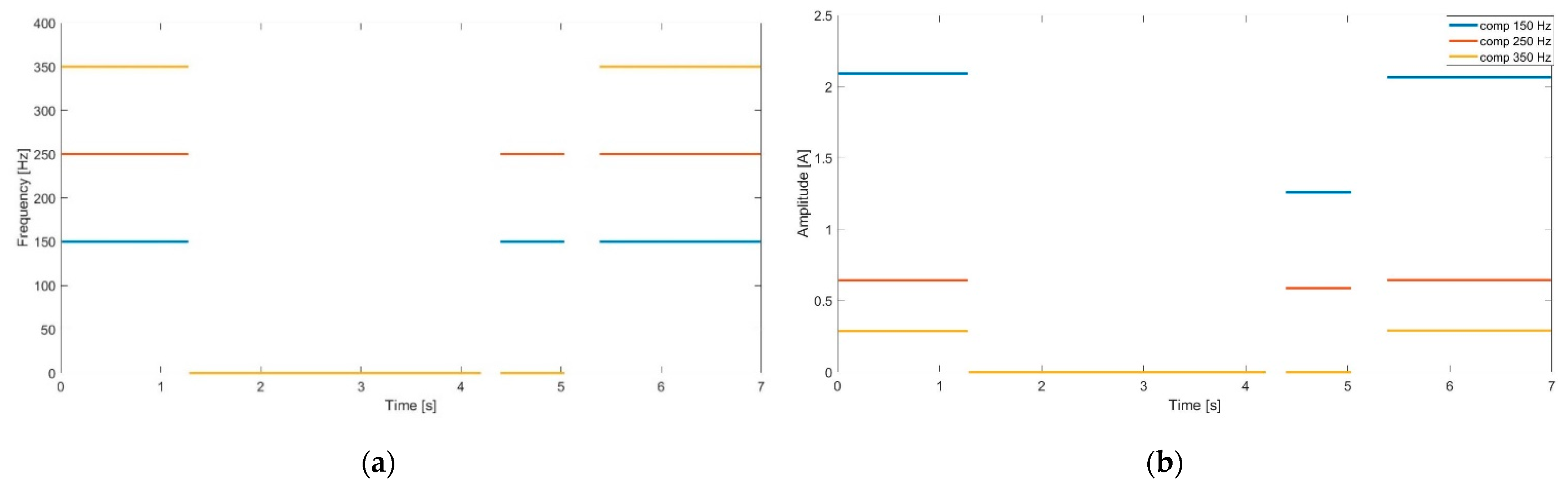
With the objective of identifying and separate the modes of oscillation inside the original distorted signal, with the quasi-steady-state intervals computed, we can now apply DFT over each of these time intervals and calculate the instantaneous frequencies and the amplitude of the inner components of the non-stationary, non-linear original signal. The final frequencies and the corresponding amplitudes are shown in Figure 5, as the method successfully traced the mono-components, identified the time intervals, and the DFT applied once again on quasi-steady-state intervals.

5. Demonstration

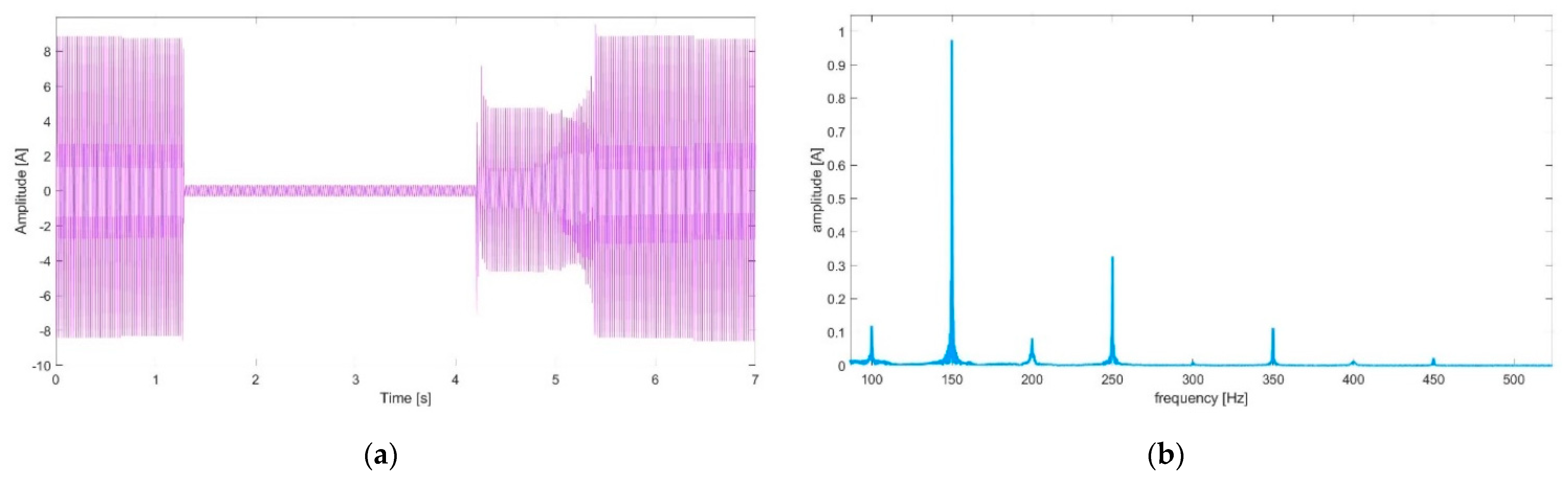
A real distorted time-varying current waveform specific for a microwave oven is used and the measurement data were provided by an ELSPEC Power Quality analyzer [27]. The current waveform digitized at a sampling rate of 1024 samples per cycle, or 51.2 kHz, was studied over a $T_w=$7 s time-window. The time window was appropriately chosen to capture the very particular cycle-based way of operating of a microwave oven. The rated input power of the under-investigation oven is 1200 W. As it will be shown in Figure 6, the current varies from approximate 8 A (peak-to-peak value) to 0.3 A and then back again to 8 A with a 1 s transition when the current reaches 4 A, peak-to-peak value. Significant 150 Hz and 250 Hz time varying components are expected to be identified within the time window, but also 100 Hz, 200 Hz, and 350 Hz. The original signal and the associated DFT spectrum are depicted in Figure 6.

The main frequencies, other than the fundamental one, are, as can be seen above, 100 Hz, 250 Hz, 200 Hz, 250 Hz, and the 350 Hz. It is to be noted that the DFT spectrum is spread over a range of frequencies thus causing the amplitude information to be subjected to a resultant uncertainty.

The first step in applying the enhanced EMD was to construct masking signals, as described in chapter 3 and in Figure 1. Based on the versatile DFT spectrum, four modes of oscillation were identified within the signal at 100 Hz, 150 Hz, 250 Hz, and 350 Hz. For those components, appropriate masking signals were constructed with 150 Hz, 250 Hz, 400 Hz, and 600 Hz.

IMF 4 will be considered negligible in amplitude and it will be discarded from the analysis, and the Hilbert Transform will be applied over the remaining IMFs. To highlight the performances of the HHT method even for lower sampling frequencies, the same signal was also digitized with 10 kHz sampling frequency. As it can be seen in Figure 7b, the components are identified, and the instantaneous amplitudes are computed with no difference to the results (Figure 7a) obtained for f_s = 50 kHz. The comparison with 10 kHz sampling frequency was made because of the computational burden associated with the EMD, and Hilbert Transform applied over non-stationary waveforms linearly decreases with a factor k, where f_s* = f_s/k. As acknowledged in [19], the computational resources associated with the method are significant, thus there was the proposition of using the method over smaller data windows, in the 1s range, and usual PQ sampling frequencies (10 kHz).

The novelty underlined within this paper in terms of quasi-steady-state time intervals identification is the next step in the intended application of the hybrid method. QSSI proves its practicality when it comes to non-stationary non-linear distorted power signals for which further investigation is required. Detection of steady-state time intervals within a distorted power waveform together with the associated frequency content is opening a wide range of potential applications such as load and generation signature profiling, power system event diagnosis, distribution transfer function estimation, etc. After filtering the results of Hilbert Transform, the algorithm for identification of quasi-steady-state intervals was enabled and four time-intervals were detected. Out of those, only three of them could be called quasi-steady state as per [8], with the remaining one to be subjected to further EMD analysis. The resulting intervals enhanced with the Hanning window are shown below in Figure 8.

The time interval in discussion, subjected to further decomposition using the hybrid HH method, is in Figure 8c, and as can be seen from the picture (and compared with the waveform of the original signal), corresponds with the transitional time interval when the distorted current signal jumps from 0.3 A to 8 A. As identified during the simulation, this interval is about 1.2 s long, and it is once again analyzed following the steps from chapter 3. The final post-processing part applied over this time interval shows a quasi-steady-state identification only for half of the total interval; for the rest we can conclude there are only transitional components, and thus discarded those artifacts. Along with the example for a synthetic signal, the edges of the observation time window were discarded, as well as the transitions between the identified time intervals. The instantaneous amplitudes and frequencies after applying post-processing algorithm and then DFT over the quasi-steady-state intervals, are shown in Figure 9. Based on the results of the improved HHT, the QSSI was achieved, thus enabling the proper use of DFT in computing instantaneous frequencies and amplitudes of the inner modes of oscillation of the original distorted power signal. DFT was applied over the entire time window $\left(T_w\right)$ under investigation but enhanced with Hanning function as per Figure 8 resulting in a 1 Hz frequency resolution. The performances of the classical DFT are well known, this tool providing a very high time-frequency resolution [34,35].

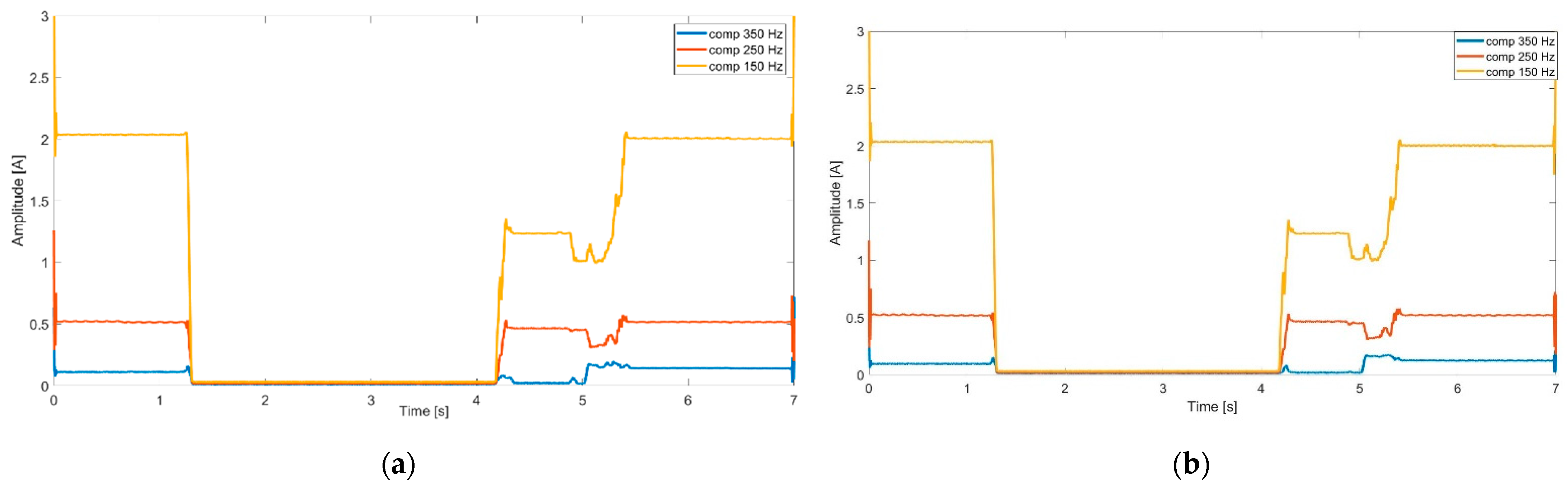
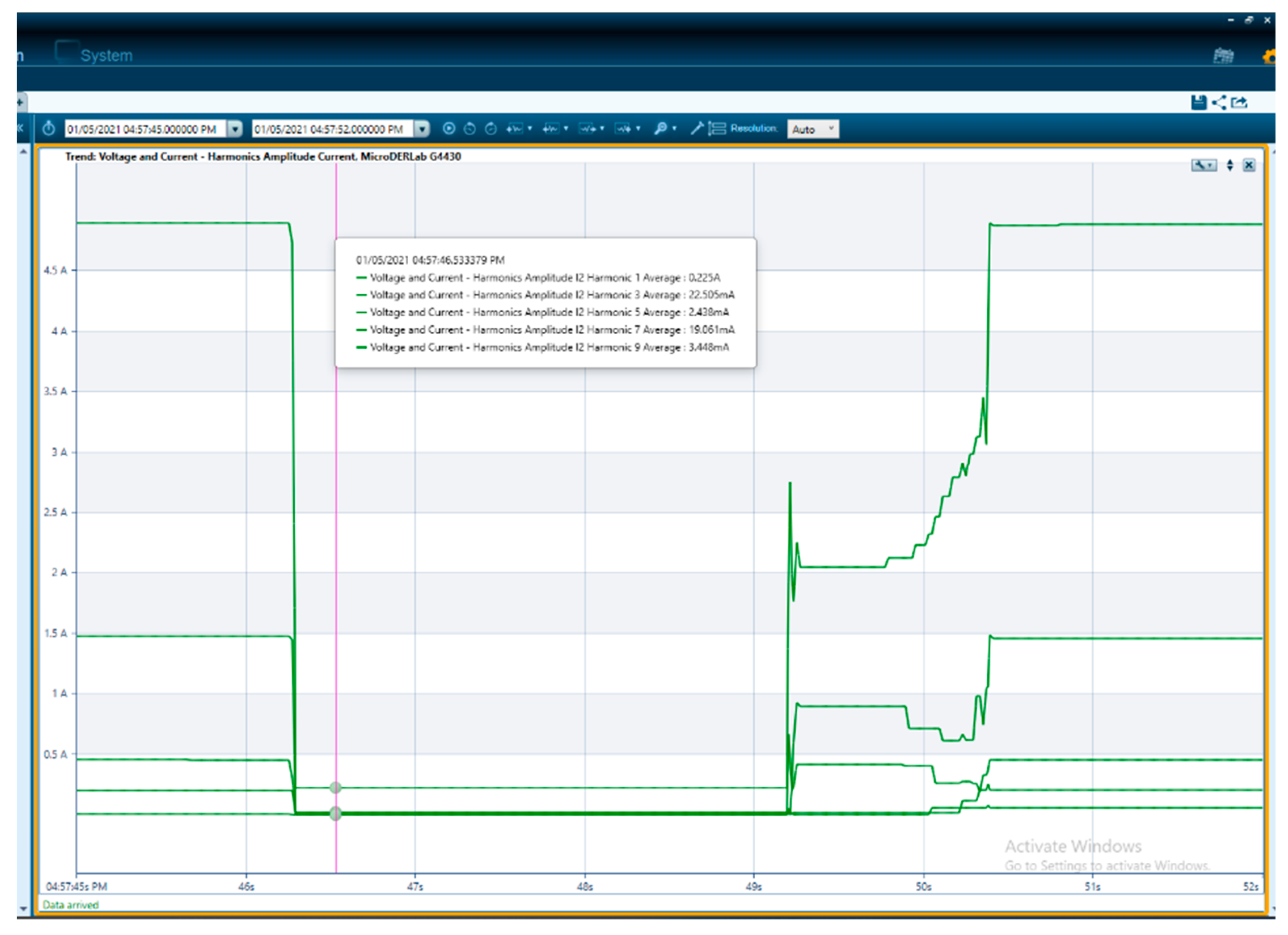
To validate the proposed hybrid algorithm, a power analyzer was used as a reference in terms of results computation, using time-varying frequency content as an input signal. A comparative analysis between the results of the hybrid Hilbert Huang method and the results of the internal algorithm of the PQ analyzer ELSPEC is assessed (Figure 10). As per [27], this equipment performs DFT every 1 cycle and can provide up to 512 harmonics of the 50Hz fundamental; it also performs DFT over a 10-cycle window, providing the frequency components with 5 Hz resolution, as per the international standard IEC 61000-4-30 [8]. These strategies not only involve a much higher computation burden for typical operation in distribution grids, which is one of the main applications of the method, but also lacks in identification of abnormal components such as the mode of oscillation with 430 Hz (as per the synthetic signal above) or 494 Hz (as per the synthetic signal analyzed in [22]).

The operation of the ELSPEC PQ analyzer is based and tied to IEC standards for harmonic computation [8]. On the other side, the hybrid method depicted in this paper has no restrictions in the analysis of distorted signals being able to identify components with 1 Hz resolution and below, depending, among others, on the selection of f_s and T_b. The final identification is not based on the Hilbert-Huang Transform but on the DFT applied over the identified steady-state time intervals. The performances of the HHT method were previously extensively studied [10,11,12,13,14,15,16,17,18,19,20,21,23,24,25,26,27,28,29,30,31] and compared with other time-frequency analysis tools such as wavelet transform, S-transform, short-time Fourier Transform. This paper uses HHT as starting point in the analysis of non-stationary, non-linear power signals for in light of the intended application: Identification of quasi-steady-state intervals using frequency domain information After the QSSI was performed over the results of Hilbert Spectrum over the entire $\left(T_w\right)$ under study, DFT will be computed over the Hanning enhanced time windows, such as in Figure 8. The results in Figure 7a show good similarity with those provided by the PQ analyzer (f_s = 50 kHz) in Figure 10 above.

6. Conclusions

The method proposed in this paper is based on two different methods that were adapted and improved: The enhanced Hilbert–Huang method based on masking signals for identification of oscillation modes existing in distorted time-varying waveform and the synthesis of a steady-state signal as presented in the QSSI algorithm.

The abilities of the original HH and of the improved versions were demonstrated for time-frequency and time-amplitude localization and the importance of masking signals to enhance EMD for power quality applications. The proposed hybrid HH showed efficiency in separation of modes of oscillation that only evolve on certain time intervals inside the investigation window. The advantages of the method were underlined and explained above, but the optimal illustration was made using signals for which the identification of change of steady state is hard to achieve. For those type of signals, unusual components (such as 430 Hz and 494 Hz) with time-varying amplitudes were added, and the method successfully identified them.

The goal of dividing the original signal into quasi-steady-state time intervals was successfully achieved as the last step of the hybrid method, giving the opportunity of achieving a detailed time–frequency description of the signal and, as such, of identifying the underlining phenomena to be further addressed by appropriate design and control schemes. Moreover, the results of QSSI can be helpful in many applications where steady-state assumption is crucial (e.g., state estimation). Another important direction for QSSI is for load and generation signature profiling by studying the distorted time-varying power waveforms at the Point of Common Coupling for low-voltage prosumers distribution grids. The method was tested on two case studies, one with a synthetic digitized waveform and the other with actual current waveform measurements specific for a microwave oven operation.

Prospective applications of the hybrid Hilbert–Huang may include load and generation frequency signature patterns and time-frequency-amplitude localization, harmonic cancellation, events detection in prosumers environment, and operation planning for microgrids at PCC, but also at prosumer level, mainly for load management based on specific har-monic patterns of targeted loads (e.g., house and office appliances, air conditioning systems, etc.).