One-Cycle Fourier Finite Position Set PLL
Abstract
1. Introduction
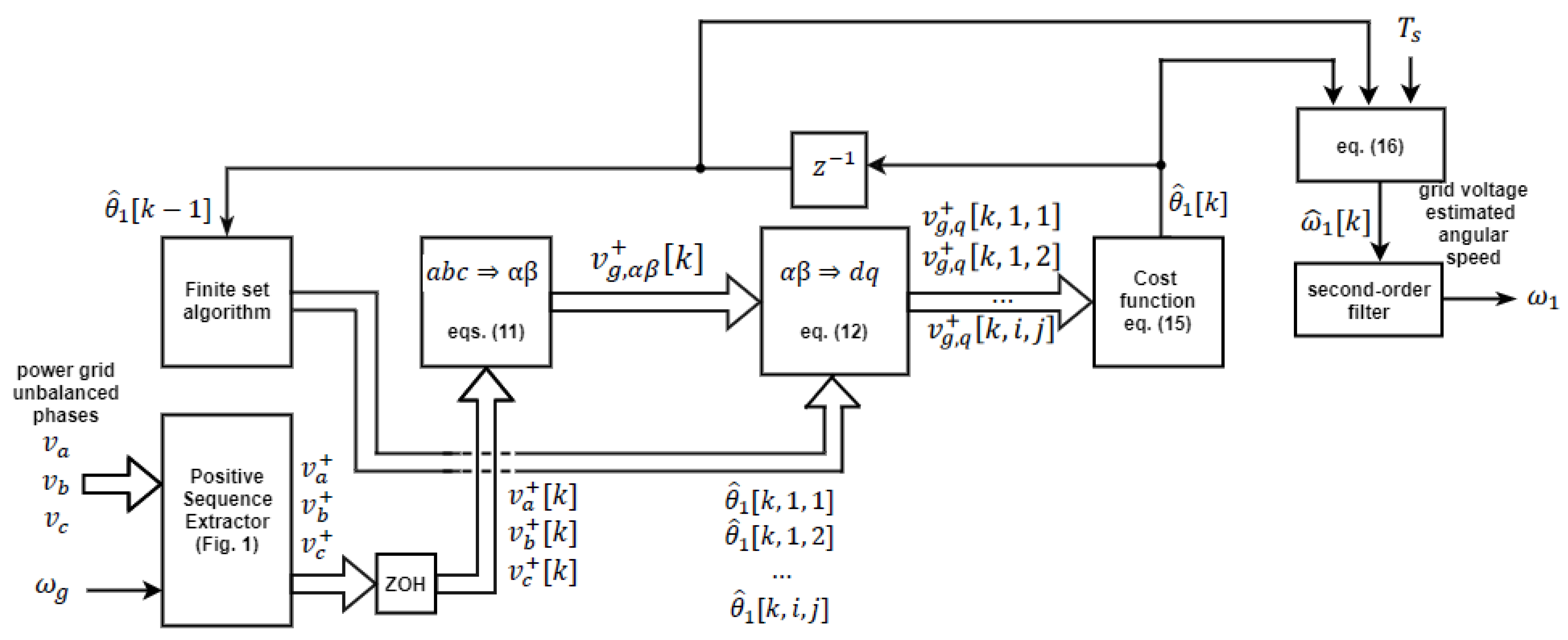
2. System Description—One-Cycle Fourier Finite Set Predictive Control PLL
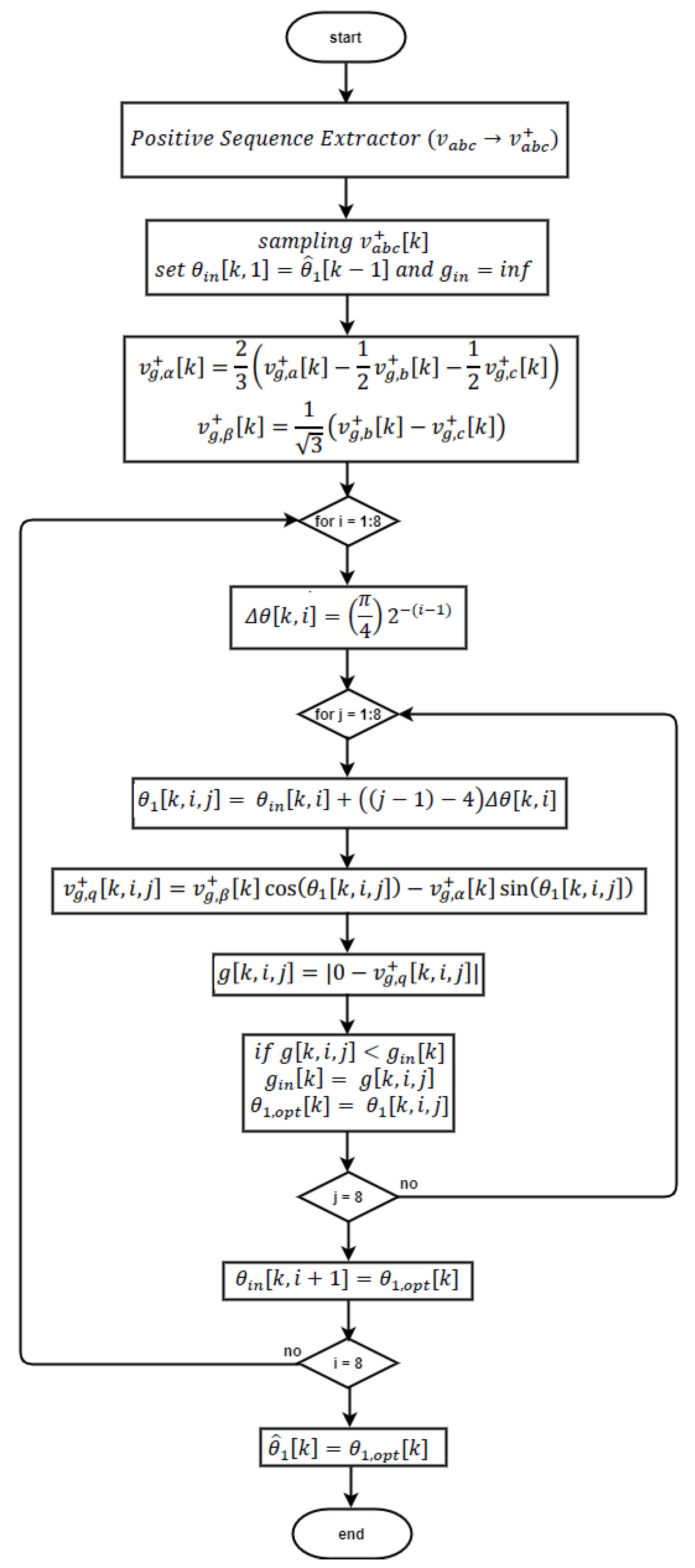
2.1. One-Cycle Fourier Algorithm
2.2. Finite Position Set
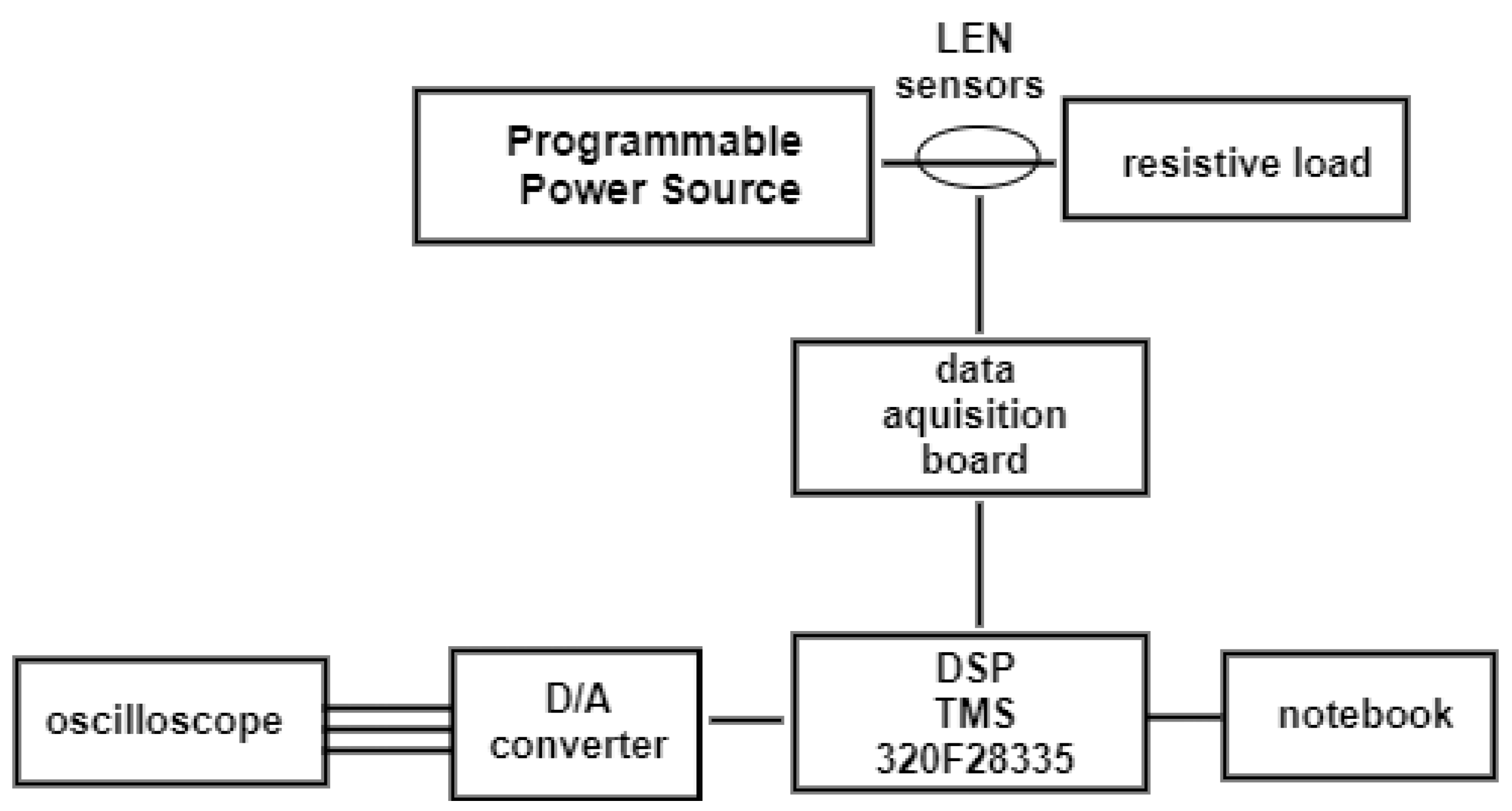
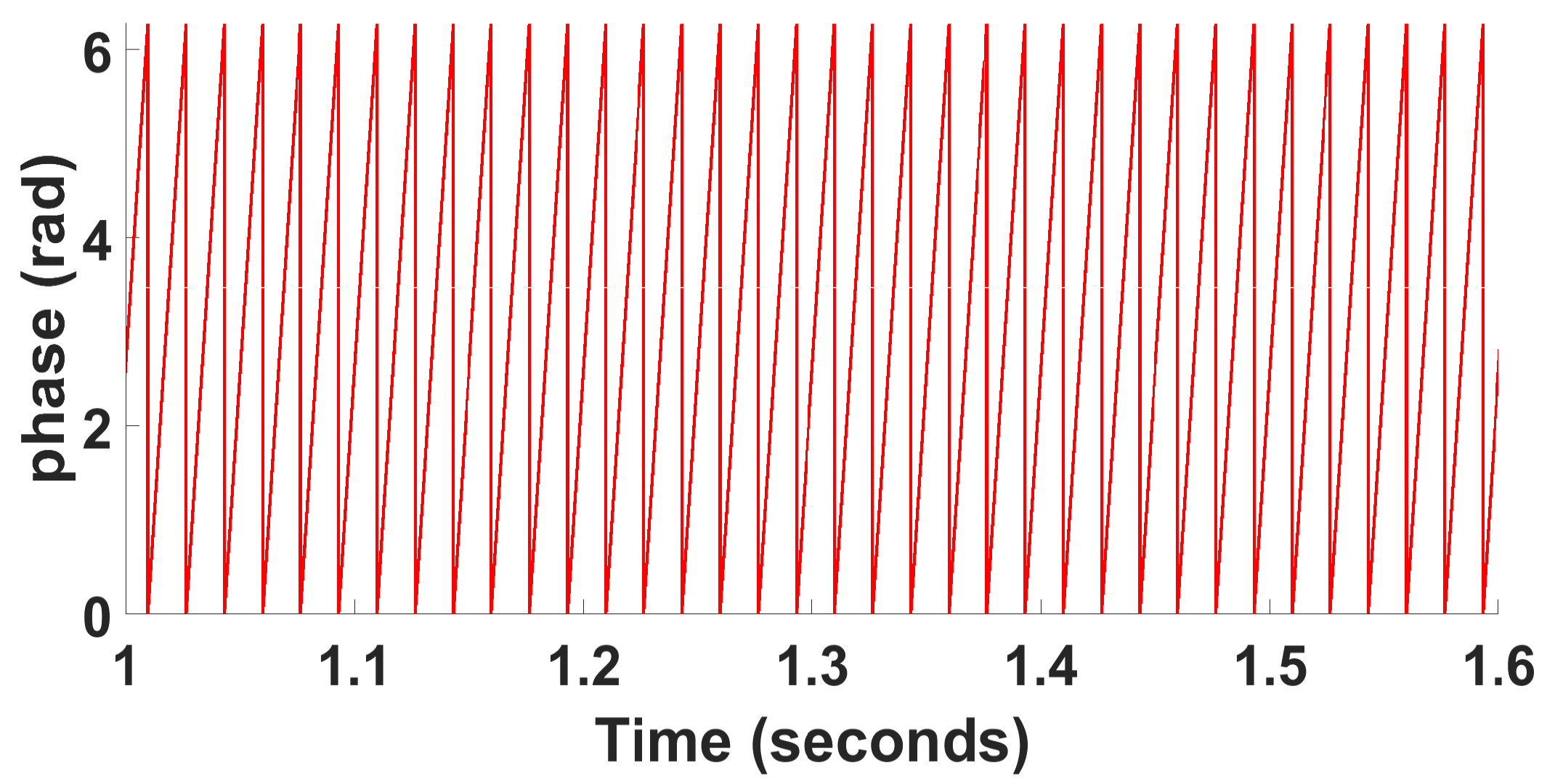
3. Experimental Results
3.1. Unbalanced Voltage with Sag in Two Phases
3.2. Balanced Grid Voltage Sag under the Presence of 5th Harmonic
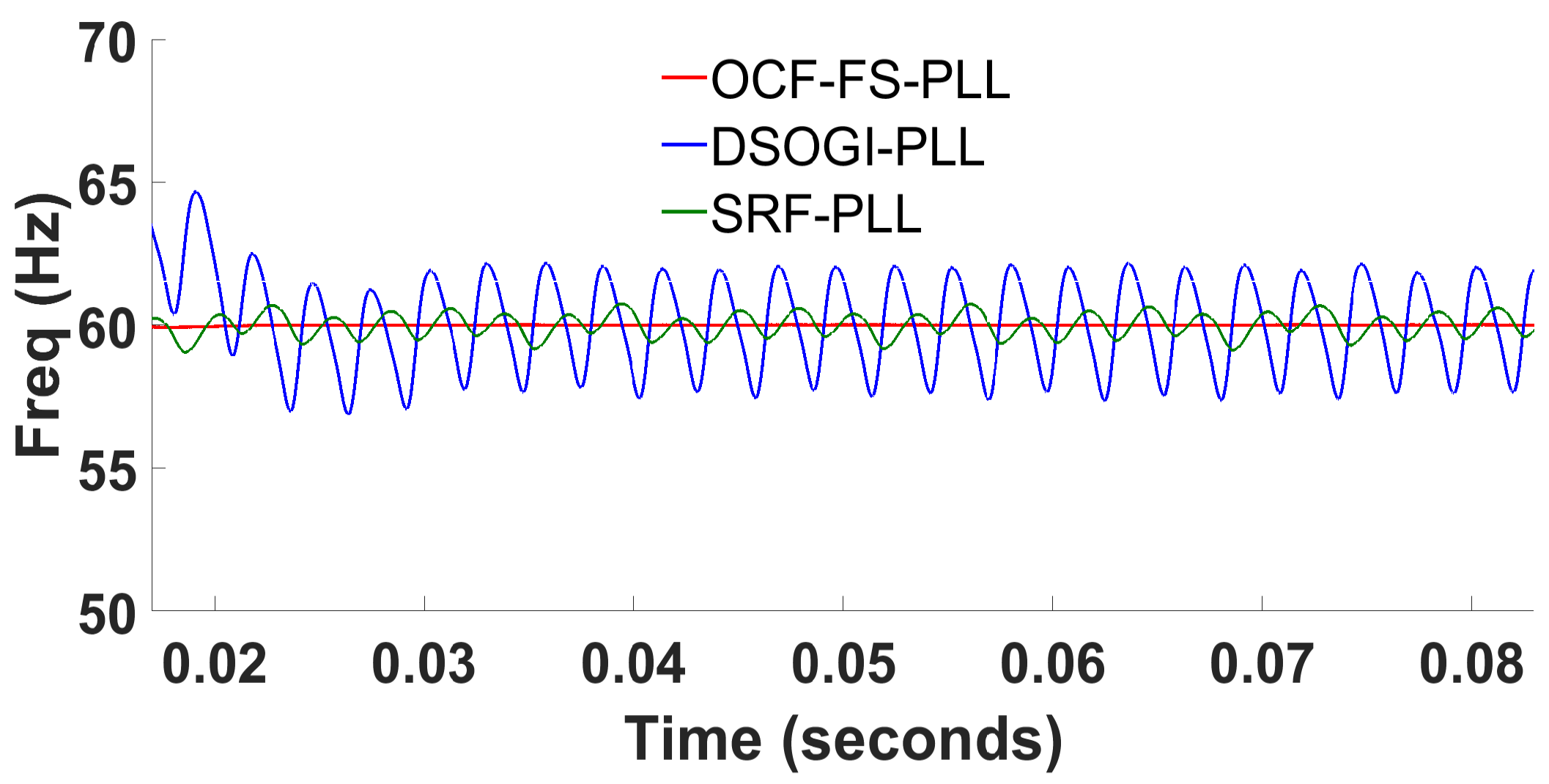
3.3. Balanced Grid Voltage Distorted by 5th, 7th, 11th, 13th, 17th and 19th Harmonics Components
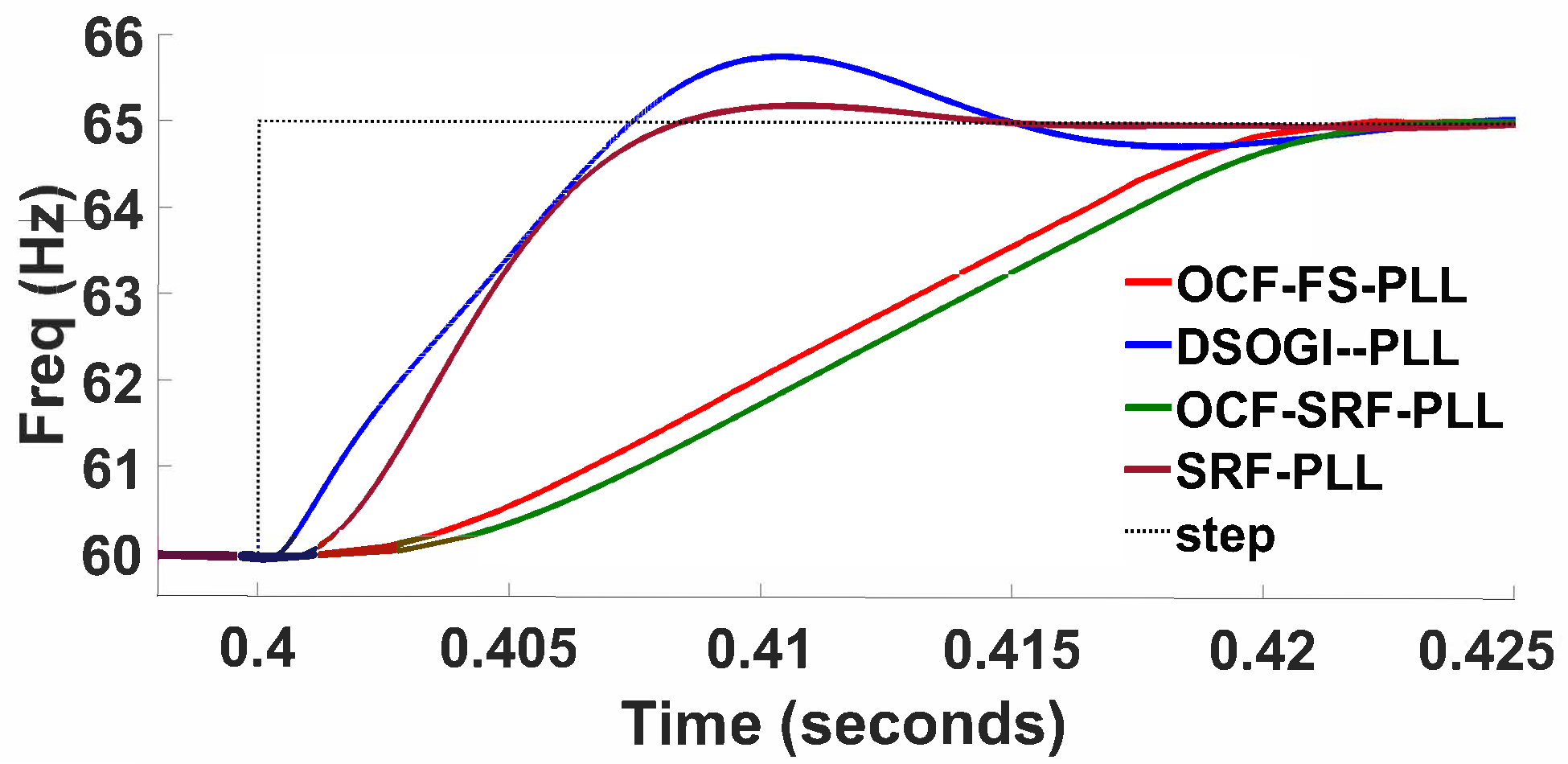
3.4. Balanced Grid Voltage with Frequency Deviation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chung, S.K. A phase tracking system for three phase utility interface inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef]
- Kaura, V.; Blasko, V. Operation of a phase locked loop under distorted utility conditions. IEEE Trans. Ind. Appl. 1997, 33, 58–63. [Google Scholar] [CrossRef]
- Rocha-Osorio, C.M.; Solís-Chaves, J.S.; Golestan, S.; Costa, F.F.; Fernandes, D.A.; Guerrero, J.M.; Alfeu, J.; Filho, S. Morphological PLL for potential applications on renewable energy. Electr. Power Syst. Res. 2018, 156, 15–23. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled double synchronous reference frame PLL for power converters control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Ghartemani, M.K.; Iravani, M.R. A method for synchronization of power electronic converters in polluted and variable-frequency environment. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar] [CrossRef]
- Ghartemani, M.K.; Karimi, H. Processing of symmetrical components in time-domain. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar]
- Rodriguez, P.; Teodorescu, R.; Candela, I.; Timbus, A.V.; Liserre, M.; Blaabjerg, F. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Bojoi, R.I.; Griva, G.; Bostan, V.; Guerrero, M.; Farina, F.; Profumo, F. Current control strategy for power conditioners using sinusoidal signal integrators in synchronous reference frame. IEEE Trans. Power Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Guerrero-Rodriguez, N.F.; Rey-Bou, A.B.; Bueno, E.J.; Ortizd, O.; Reyes-Archundiae, E. Synchronization algorithms for grid-connected renewable systems: Overview, tests and comparative analysis. Renew. Sustain. Energy Rev. 2017, 75, 629–643. [Google Scholar] [CrossRef]
- Golestan, S.; Mousazadeh, S.Y.; Guerrero, J.M.; Vasquez, J.C. A critical examination of frequency-fixed second-order generalized integrator-based phase-locked loops. IEEE Trans. Power Electron. 2017, 32, 6666–6672. [Google Scholar] [CrossRef]
- Xiao, F.; Dong, L.; Li, L.; Liao, X. A frequency-fixed SOGI-based PLL for single-phase grid-connected converters. IEEE Trans. Power Electron. 2017, 32, 1713–1719. [Google Scholar] [CrossRef]
- de Andrade, B.N.; Silva, L.H.S.; Sguarezi Filho, A.J.; Filho, S.; Costa, F.F. Enhanced SOGI-PLL by moving-average filter and one-cycle Fourier algorithm. In Proceedings of the IEEE International Conference on Renewable Energy Research and Applications, San Diego, CA, USA, 5–8 November 2017; pp. 1019–1023. [Google Scholar]
- Karimi-Ghartemani, M.; Khajehoddin, S.A.; Jain, P.K.; Bakhshai, A.; Mojiri, M. Addressing DC component in PLL and notch filter algorithms. IEEE Trans. Power Electron. 2012, 27, 78–86. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-phase PLLs: A review of recent advances. IEEE Trans. Power Electron. 2017, 32, 1825–1833. [Google Scholar] [CrossRef]
- Guo, X.; Wu, W.; Chen, Z. Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid interfaced converters in distributed utility networks. IEEE Trans. Ind. Appl. 2011, 58, 1194–1204. [Google Scholar] [CrossRef]
- Ramezani, M.; Golestan, S.; Li, S.; Guerrero, J.M. A simple approach to enhance the performance of complex-coefficient filter-based PLL in grid-connected applications. IEEE Trans. Ind. Electron. 2018, 65, 5081–5085. [Google Scholar] [CrossRef]
- Ohori, A.; Hattori, N.; Funaki, T. Phase-locked loop using complex coefficient filters for grid-connected inverter. Electr. Eng. Jpn. 2013, 189, 52–60. [Google Scholar] [CrossRef]
- Li, W.; Ruan, X.; Bao, C.; Pan, D.; Wang, X. Grid synchronization systems of threephase grid-connected power converters: A complex-vector-filter perspective. IEEE Trans. Ind. Electron. 2014, 61, 1855–1870. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Abusorrah, A.M. MAF—PLL with phase-lead compensator. IEEE Trans. Ind. Electron. 2006, 62, 3691–3695. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J.; Gao, F.; Zhang, L.; Wang, Z. A method to improve the dynamic performance of moving average filter-based PLL. IEEE Trans. Power Electron. 2015, 30, 5978–5990. [Google Scholar] [CrossRef]
- Silva, L.H.; Suarezi Filho, A.J.; Fernandesc, D.A.; Costa, F.F.; Cardoso, A.J.M. A robust phase-locked loop against fundamental frequency deviations and harmonic distortions. Electr. Power Syst. Res. 2018, 163, 338–347. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.; Kennel, R.; Quevedo, D.; Rodriguez, J. Predictive control in power electronics and drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Linder, A.; Kanchan, R.; Kennel, R.; Stolze, P. Model-Based Predictive Control of Electric Drives; Cuvillier Verlag: Gottingen, Germany, 2010. [Google Scholar]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives, 1st ed.; Wiley-IEEE: New York, NY, USA, 2012. [Google Scholar]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2004, 8, 16–31. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R. Simplified model predictive current control without mechanical sensors for variable-speed wind energy conversion systems. Electr. Eng. 2017, 99, 367–377. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Kennel, R. Fault-ride through strategy for permanent-magnet synchronous generators in variable-speed wind turbines. Energies 2016, 9, 1066. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.; Kennel, R. Finite Position Set-Phase LockedLoop for Sensorless Control of Direct-Driven Permanent-Magnet SynchronousGenerators. IEEE Trans. Power Electron. 2018, 33, 3097–3105. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R.; Rodríguez, J. Computationally Efficient Finite-Position-Set-Phase-Locked Loop for Sensorless Control of PMSGs in Wind Turbine Applications. IEEE Trans. Power Electron. 2021, 36, 3007–3016. [Google Scholar] [CrossRef]
- Dirscherl, C.; Hackl, C.; Schechner, K. Modellierung und Regelung von modernen Windkraftanlagen: Eine Einfuhrung. In Elektrische Antriebe–Regelung von Antriebssystemen; Schroder, D., Ed.; Springer: New York, NY, USA, 2015; Chapter 24; pp. 1540–1614. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]



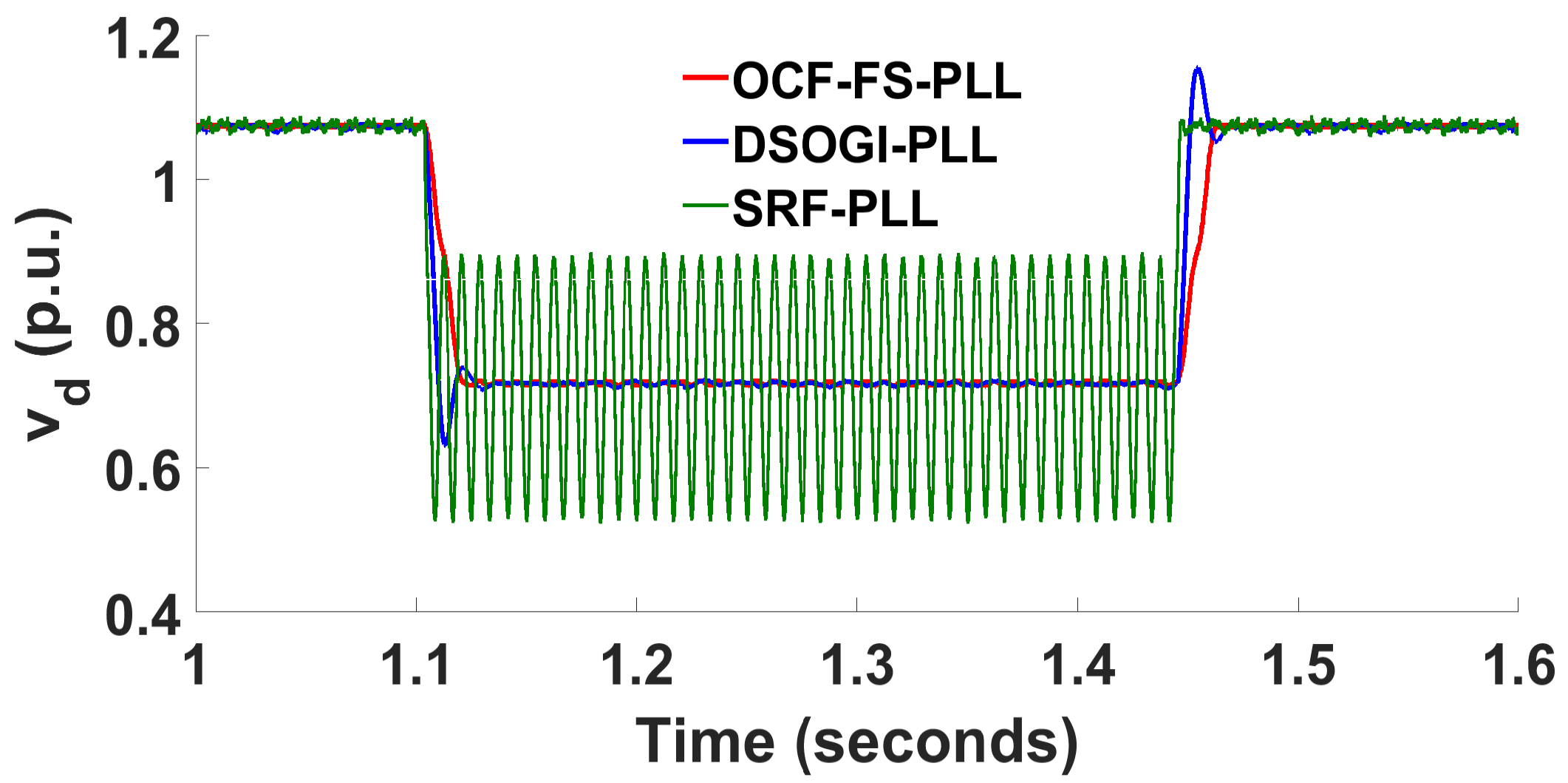
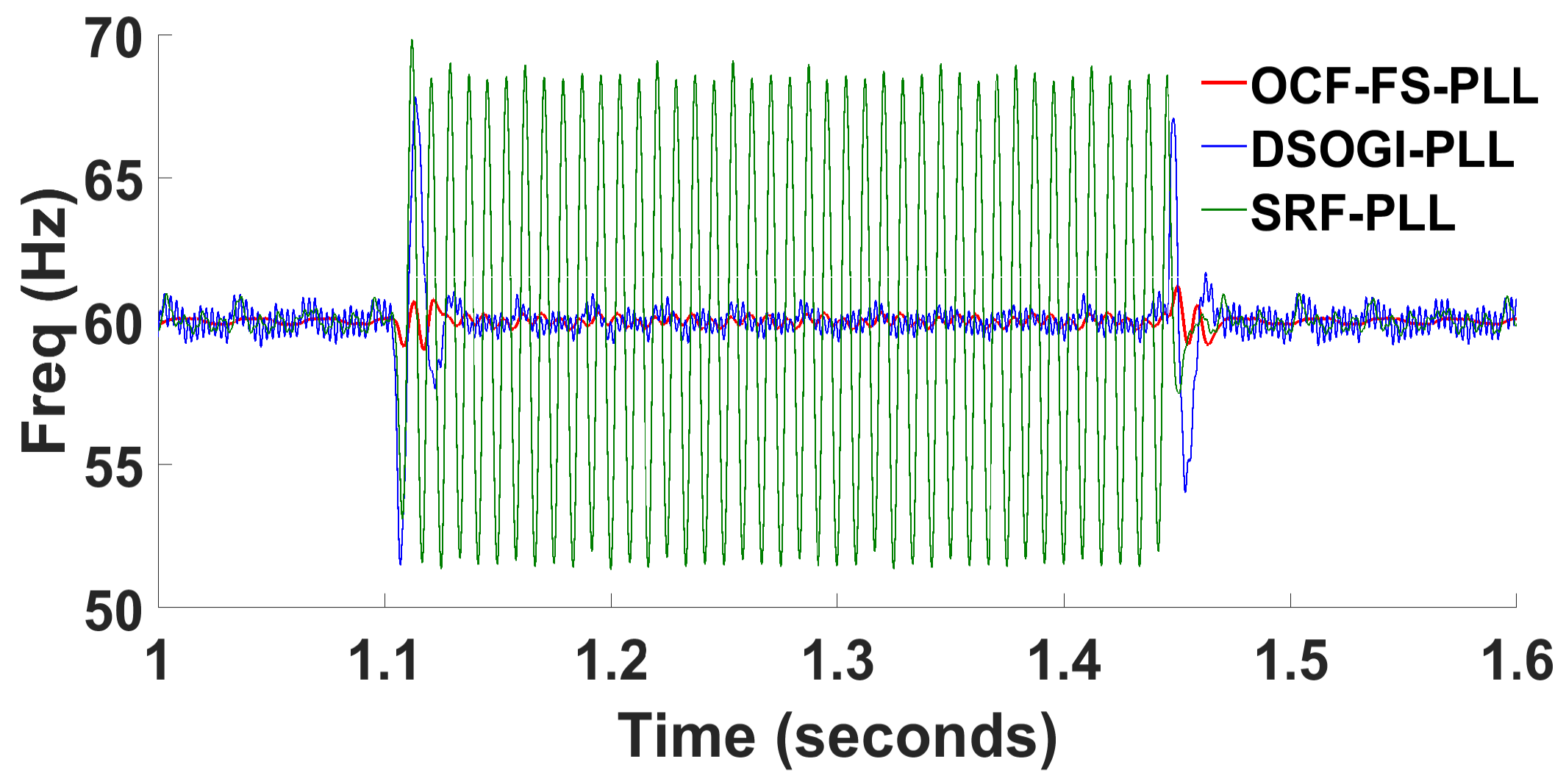
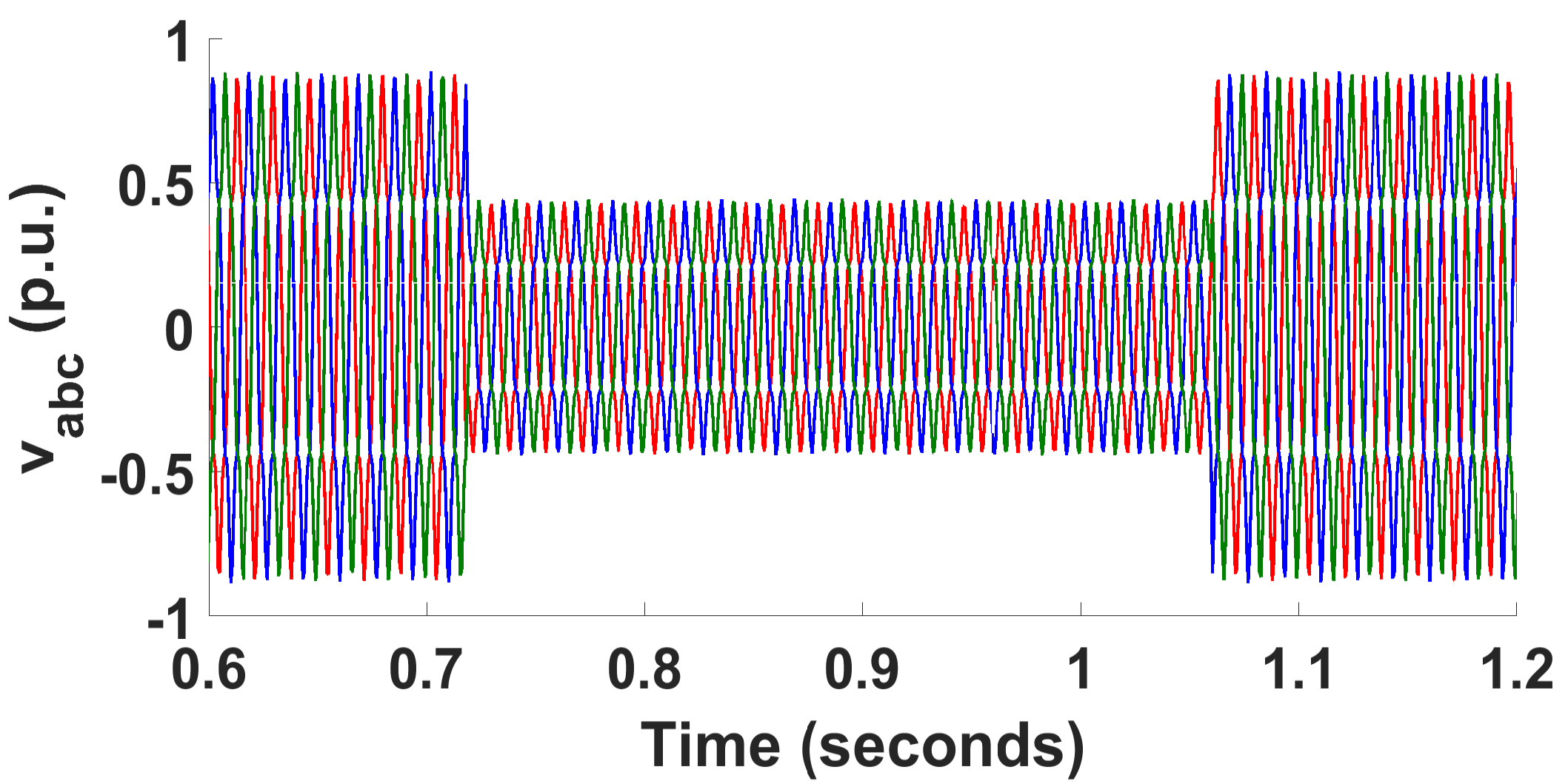
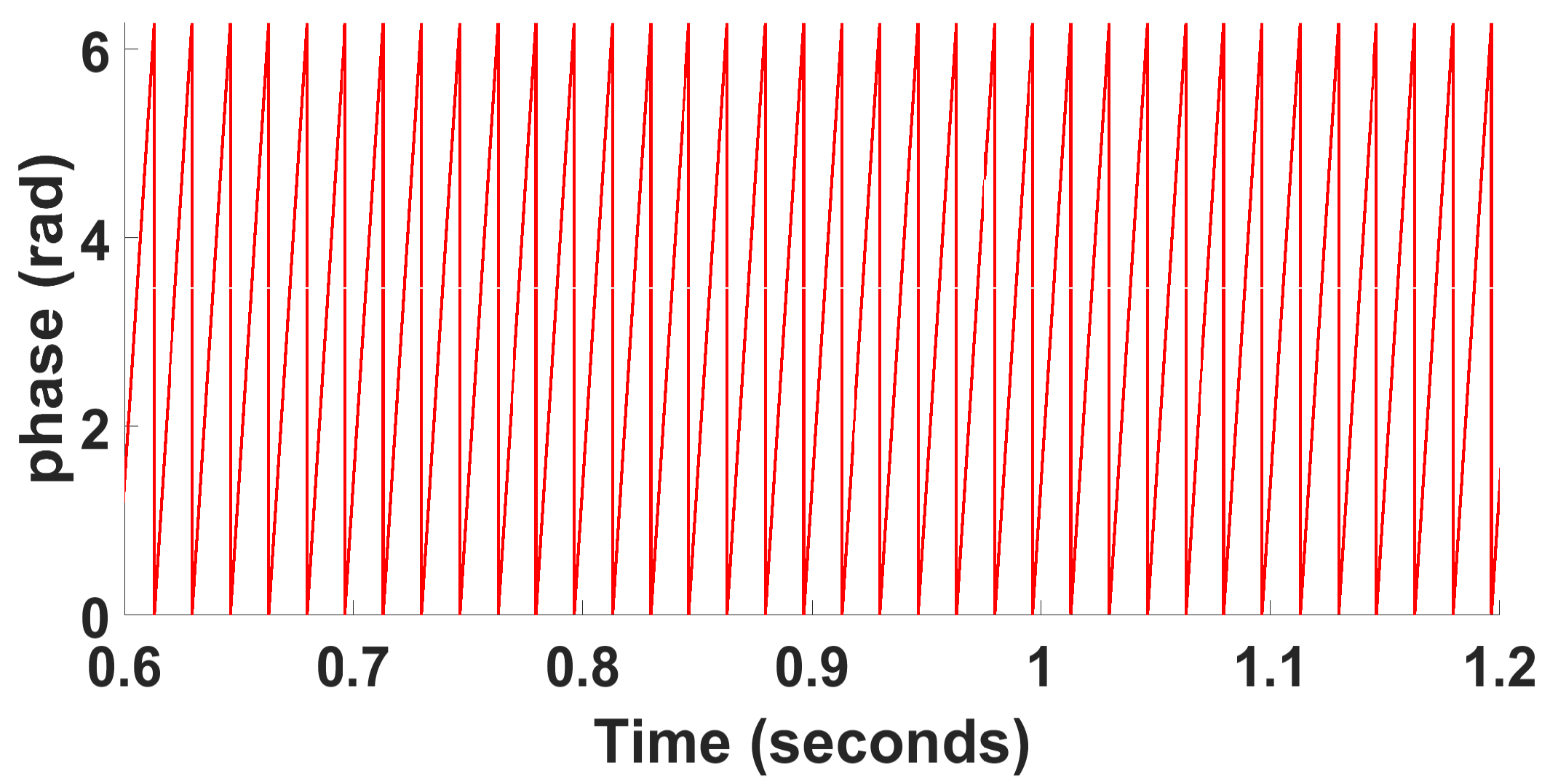
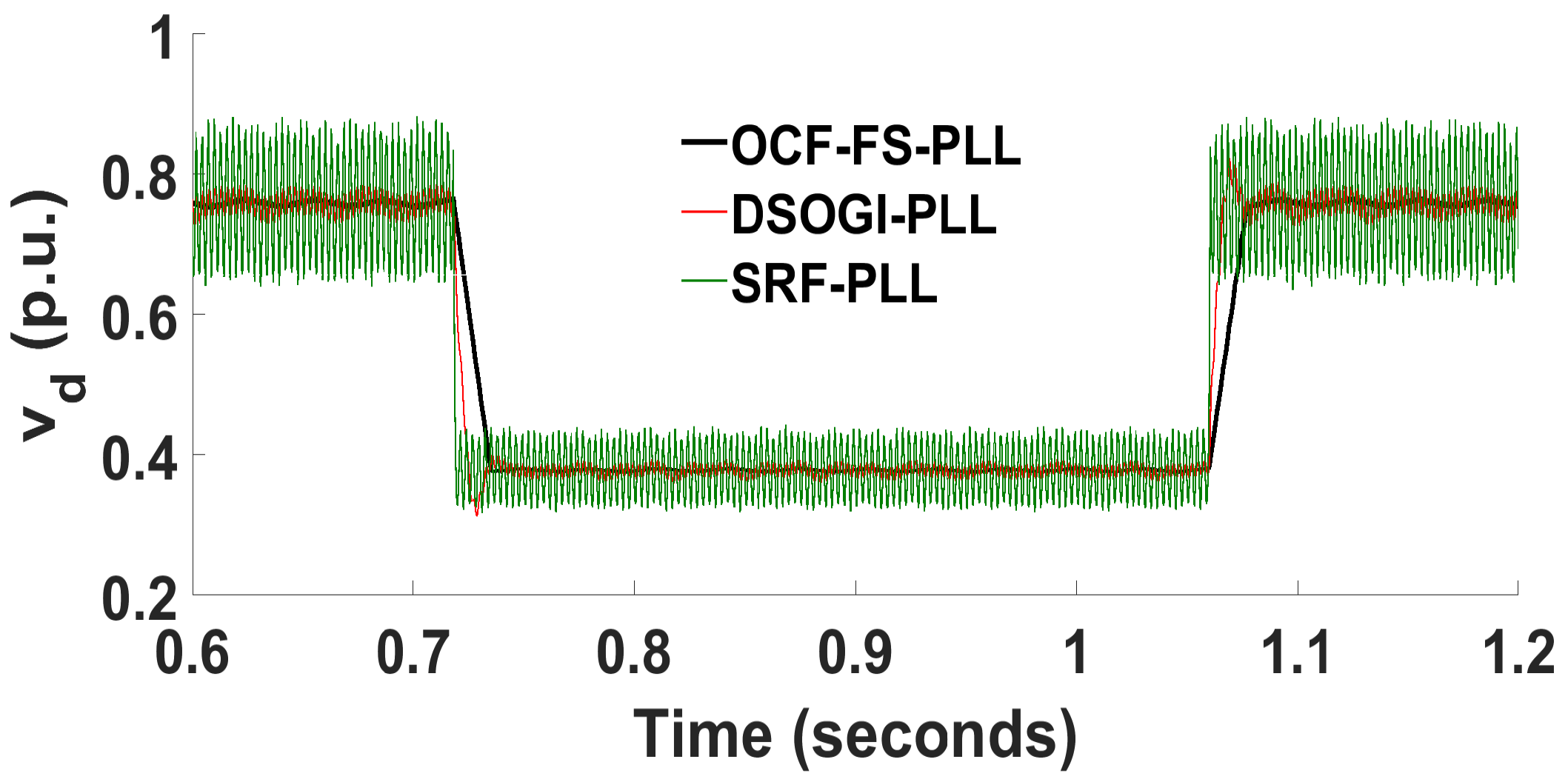
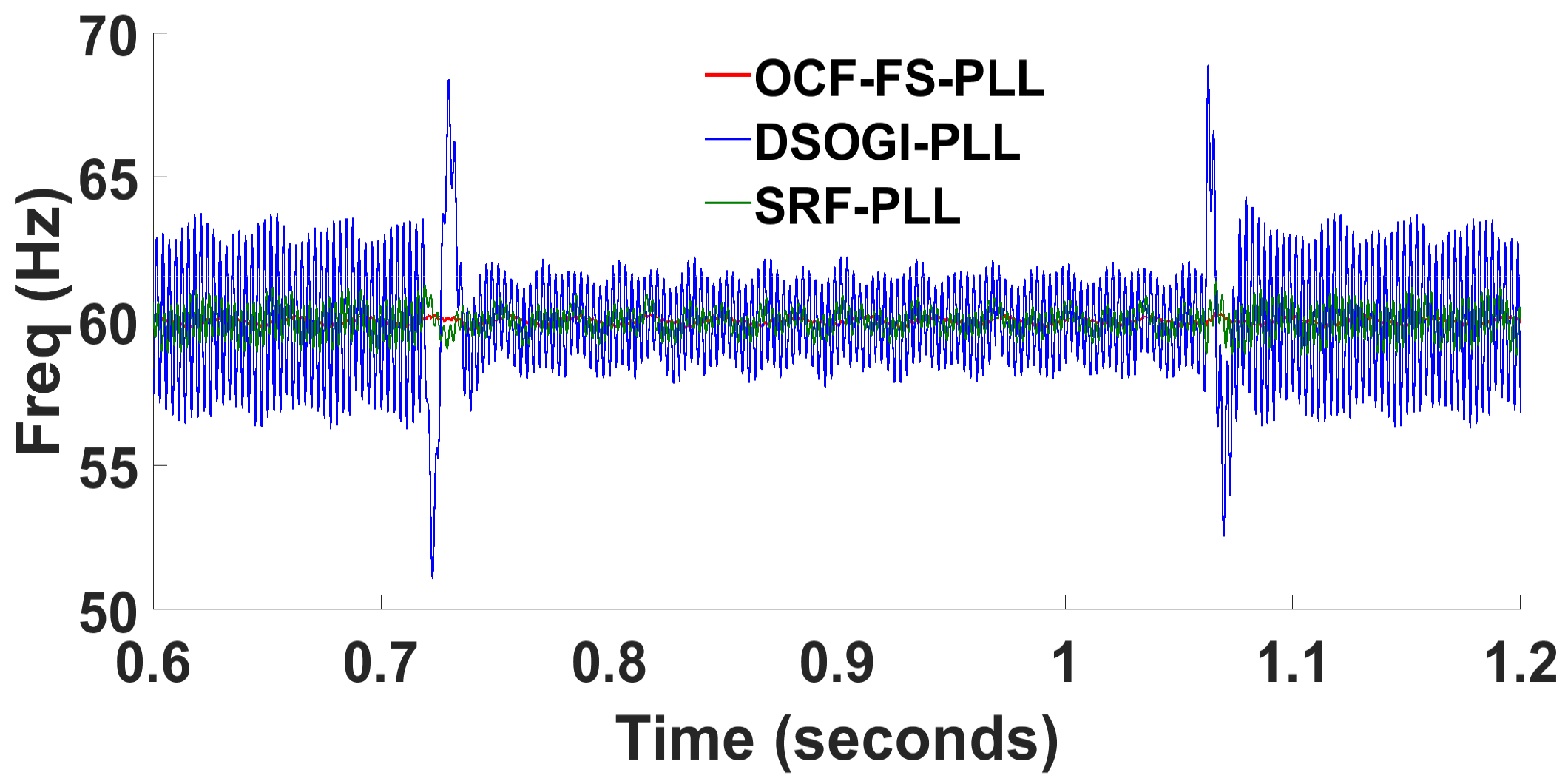

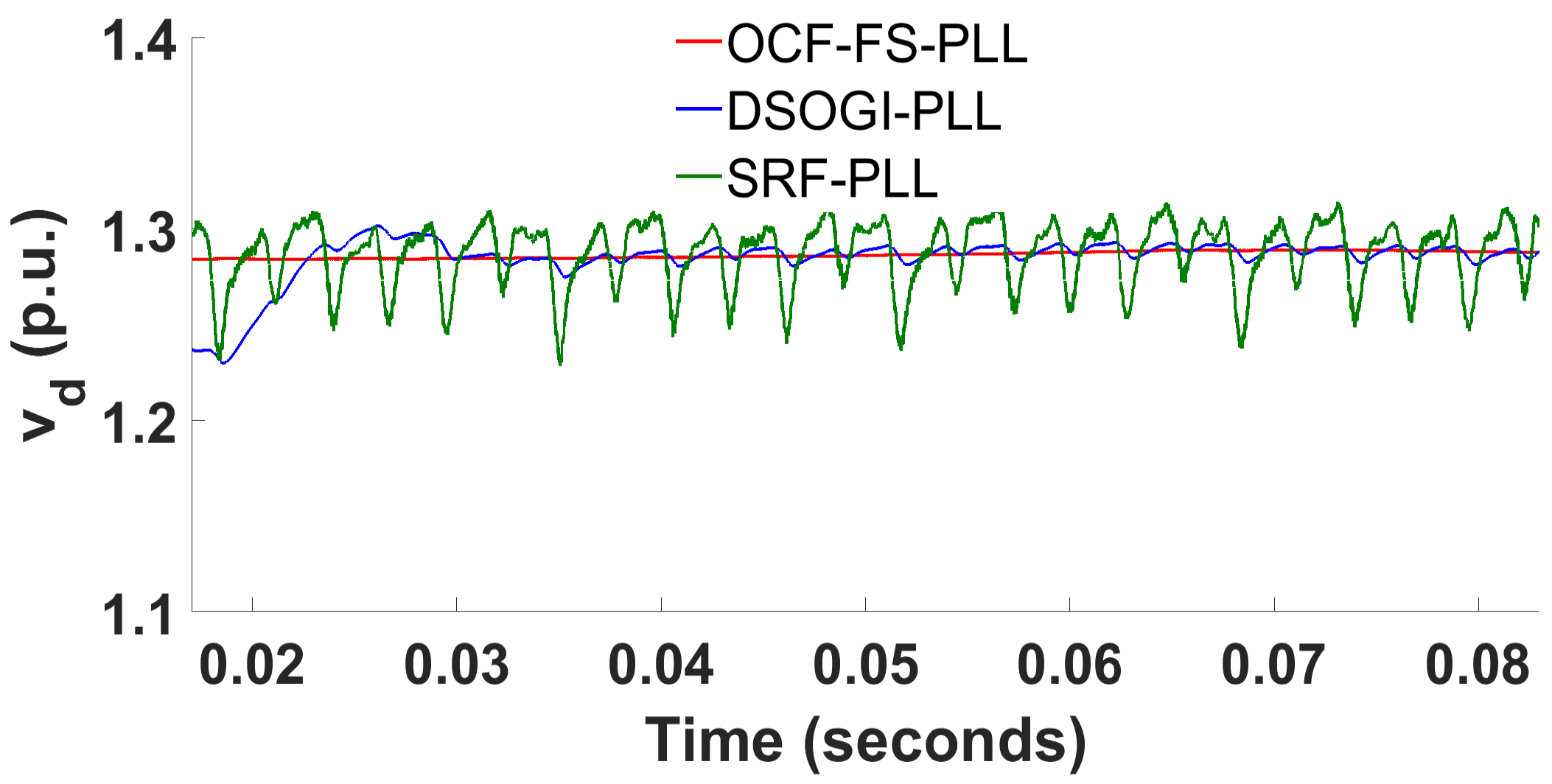



| Parameters | [%] | [ms] (freq.) | osc. [Hz] | [ms] () | [p.u.] | Need PI Controller |
|---|---|---|---|---|---|---|
| Unlanced voltage sag | ||||||
| OCF-FS-PLL | 13.06 | - | ±0.31 | 20.737 | 0.0122 | No |
| SRF-PLL | 15.81 | - | ±8.74 | 2.404 | 0.3731 | Yes |
| DSOGI-PLL | 2.08 | - | ±0.91 | 16.477 | 0.0122 | Yes |
| Balanced voltage sag with 5th harmonic | ||||||
| OCF-FS-PLL | 14.79 | - | ±0.24 | 22.639 | 0.0092 | No |
| SRF-PLL | 0.34 | - | ±0.89 | 0.001 | 0.1230 | Yes |
| DSOGI-PLL | 0.44 | - | ±2.27 | 17.172 | 0.0349 | Yes |
| Balanced voltage with 5th, 7th, 11th, 13th, 17th and 19th harmonics | ||||||
| OCF-FS-PLL | - | - | ±0.022 | - | 0.0086 | No |
| SRF-PLL | - | - | ±1.561 | - | 0.0781 | Yes |
| DSOGI-PLL | - | - | ±4.711 | - | 0.0114 | Yes |
| Frequency deviation | ||||||
| OCF-FS-PLL | 1.21 | 29.312 | ±0.02 | - | 0.0003 | No |
| SRF-PLL | 0.32 | 13.955 | ±0.04 | - | 0.0021 | Yes |
| DSOGI-PLL | 0.09 | 26.894 | ±0.04 | - | 0.0012 | Yes |
| Signal | THD [%] |
|---|---|
| Input voltage | 14.04 |
| DSOGI-PLL output voltage | 2.95 |
| OCF-FS-PLL output voltage | 0.42 |
| Signal | THD [%] |
|---|---|
| Input voltage | 4.44 |
| DSOGI-PLL output voltage | 1.02 |
| OCF-FS-PLL output voltage | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lino, F.; Assis, J.; Fernandes, D.A.; Jacomini, R.; Costa, F.F.; Sguarezi Filho, A.J. One-Cycle Fourier Finite Position Set PLL. Energies 2021, 14, 1824. https://doi.org/10.3390/en14071824
Lino F, Assis J, Fernandes DA, Jacomini R, Costa FF, Sguarezi Filho AJ. One-Cycle Fourier Finite Position Set PLL. Energies. 2021; 14(7):1824. https://doi.org/10.3390/en14071824
Chicago/Turabian StyleLino, Fernando, Jefferson Assis, Darlan A. Fernandes, Rogerio Jacomini, Fabiano F. Costa, and Alfeu J. Sguarezi Filho. 2021. "One-Cycle Fourier Finite Position Set PLL" Energies 14, no. 7: 1824. https://doi.org/10.3390/en14071824
APA StyleLino, F., Assis, J., Fernandes, D. A., Jacomini, R., Costa, F. F., & Sguarezi Filho, A. J. (2021). One-Cycle Fourier Finite Position Set PLL. Energies, 14(7), 1824. https://doi.org/10.3390/en14071824









