3.2.1. The Internal Resistance Ri Increase
As illustrated in
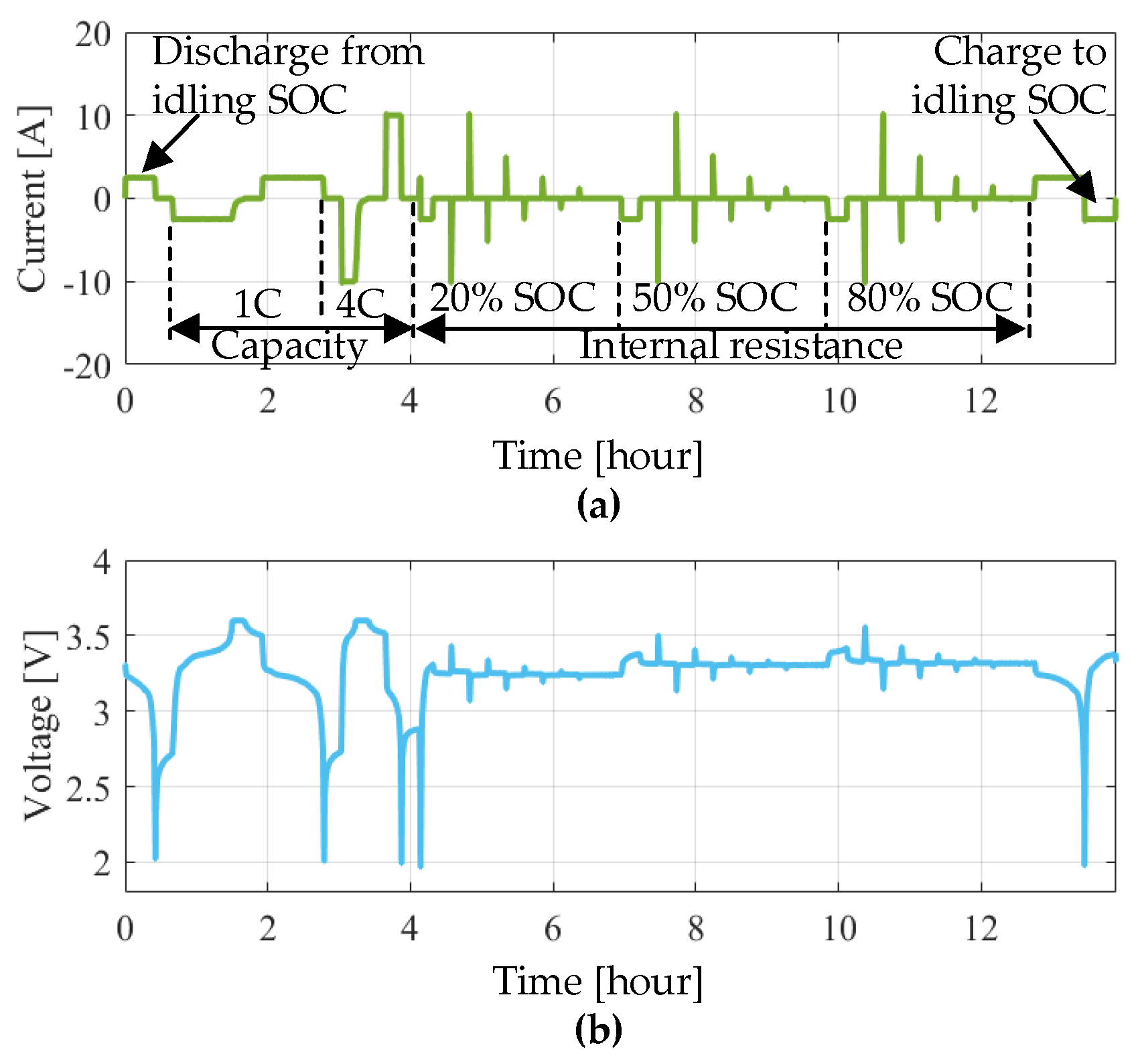
Section 2.3, a set of 18 s current pulses at three SOC levels (i.e., 20% SOC, 50% SOC and 80% SOC) were applied to the battery. Based on the analysis in [
27], a more effective state of the health indicator will be obtained when the SOC enters into the polarization zone (SOC larger than 0.8 or smaller than 20%). Hence, in this work, a discharge pulse at 80% SOC with an amplitude of 10 A (i.e., 4C-rate) was considered for calculating the internal resistance
Ri. The effect of calendar aging on the voltage drop of the LiFePO
4/C battery cells during the
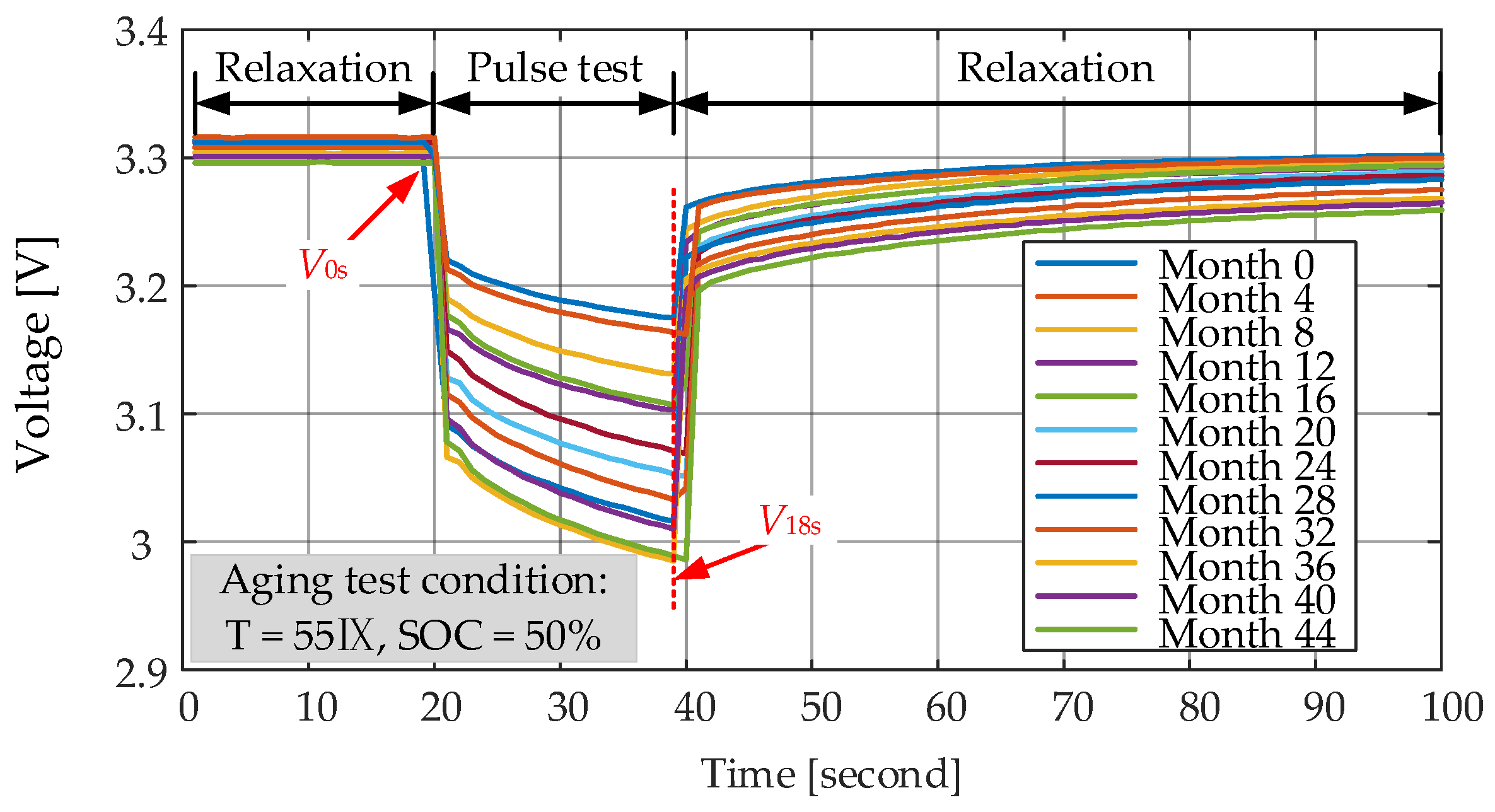
Ri measurements at different moments is presented in
Figure 13. On the basis of measured voltage and current profiles, the
Ri of the LiFePO
4/C battery cells was calculated for the five considered aging cases as
where
V0s is the voltage before applying the current pulse,
V18s represents the voltage at the end of 18s pulse and
I is the amplitude of the current. As the increase of
Ri is an important parameter to quantify the degradation behavior of LiFePO
4/C battery cells, it is calculated as
where
Ri_increase represents the increase of the resistance and
Ri_ini and
Ri_now represent the resistance of the battery cell at the beginning of life and after each reference measurement, respectively.
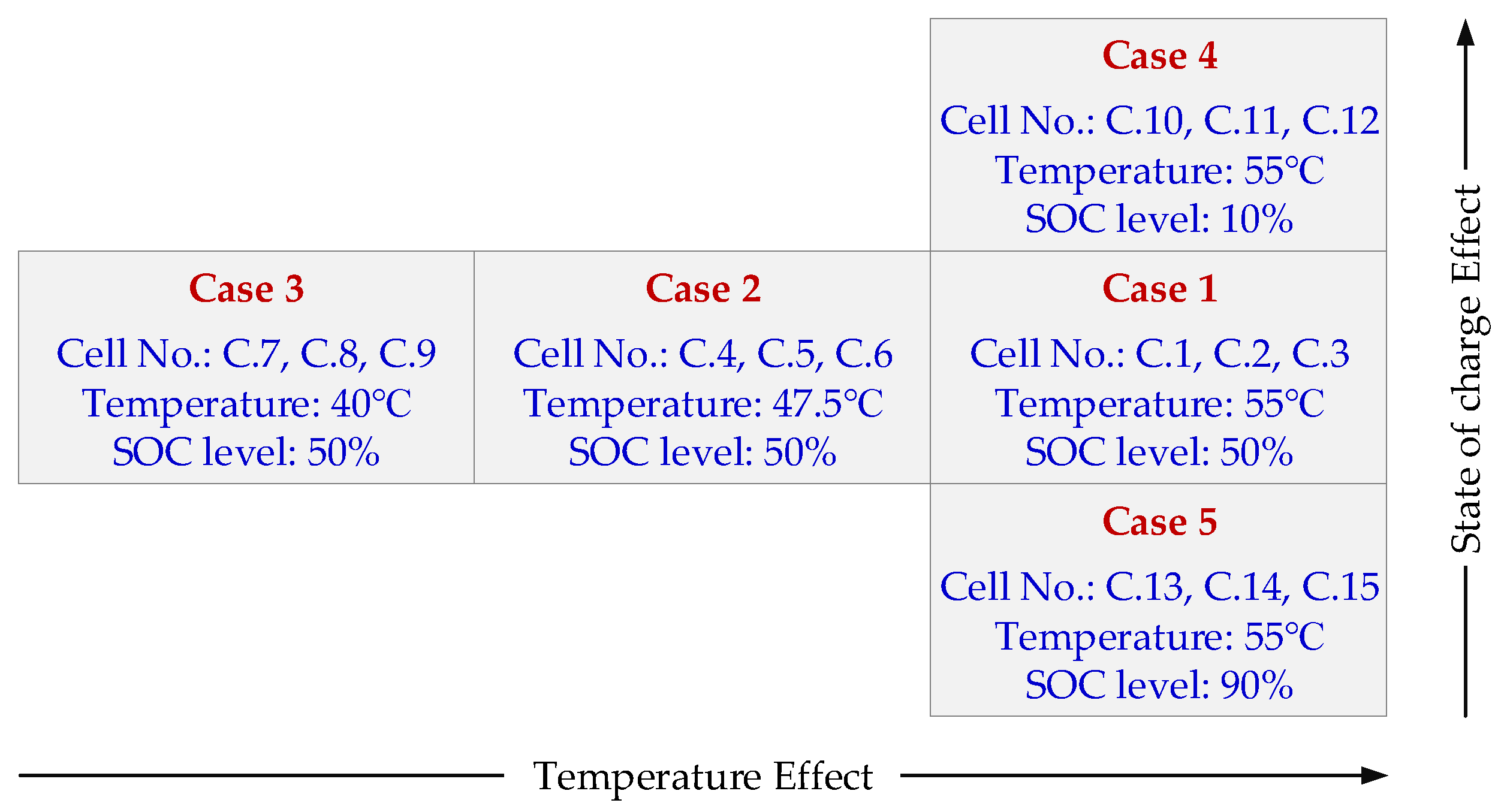
The presented procedure was used to determine the discharging
Ri and its aging behavior under the considered accelerated aging conditions, which are summarized in
Figure 1. The discharge
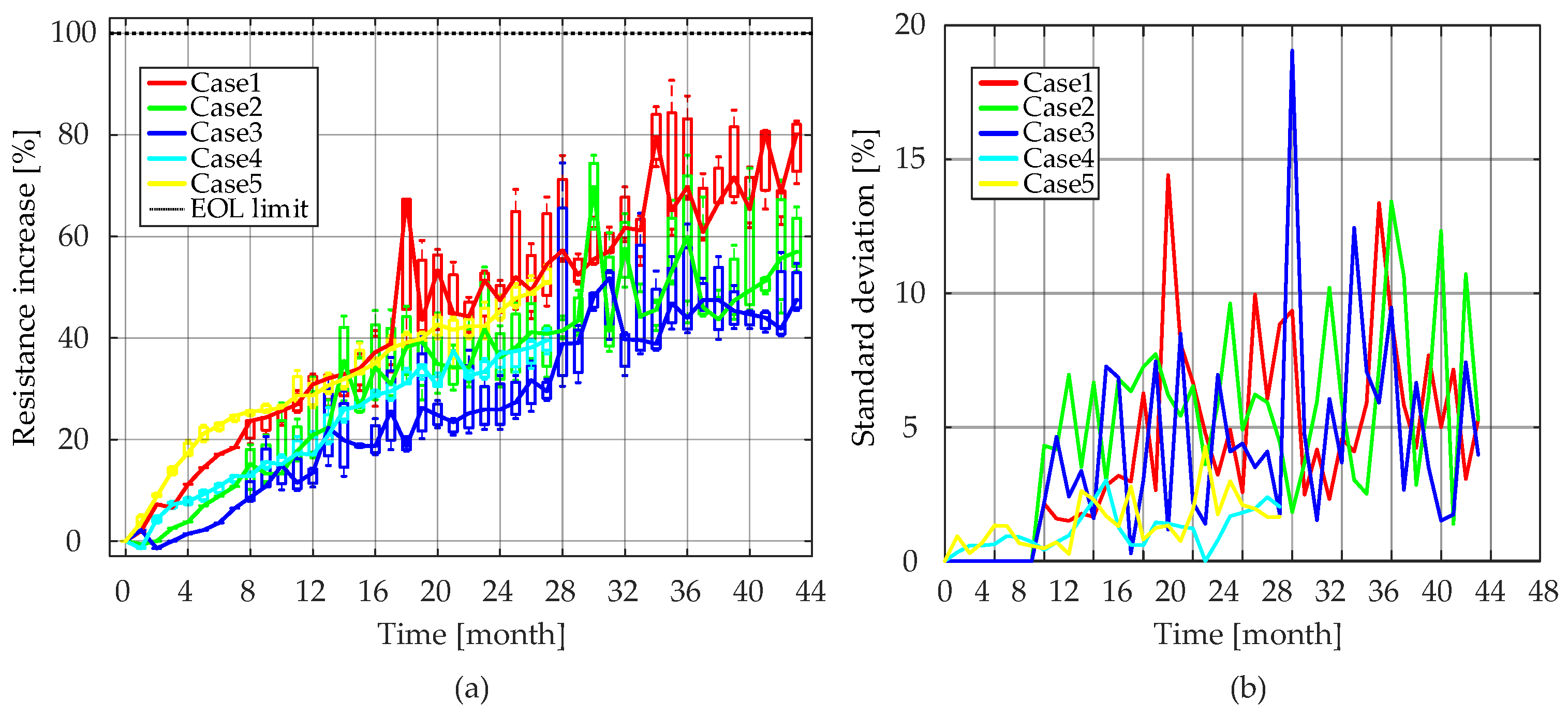
Ri values during the consecutive reference measurements throughout the accelerated calendar aging test are presented in
Figure 14, and the median values are further used to analyze the aging behavior of
Ri. As seen in
Figure 14a, for Case 4 and Case 5, the consistency between the tested three battery cells was good. However, for the other three cases, the resistance increase between cells showed an obvious inconsistency at some points. In order to reduce the effect of inconsistency between cells on model accuracy, the median value of
Ri was obtained for each calendar test condition.
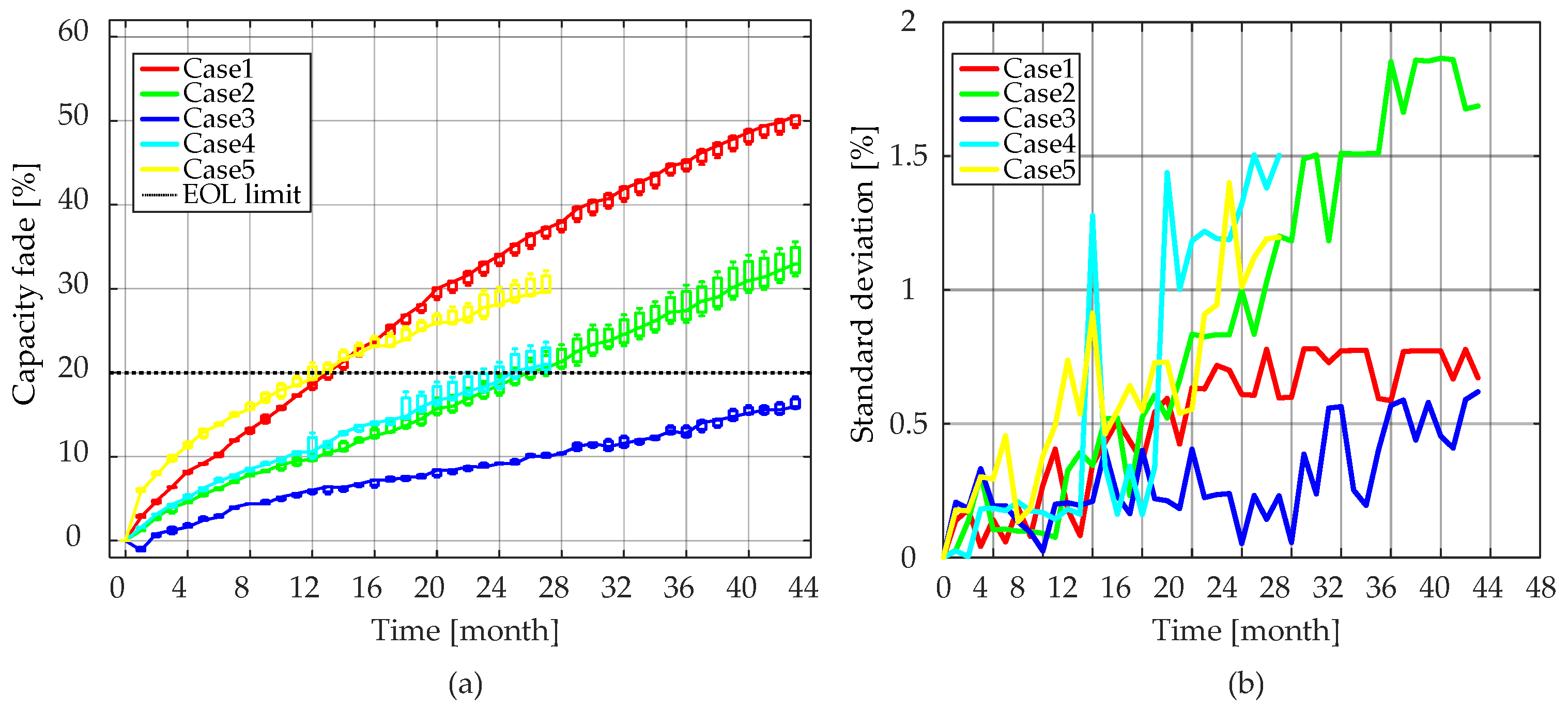
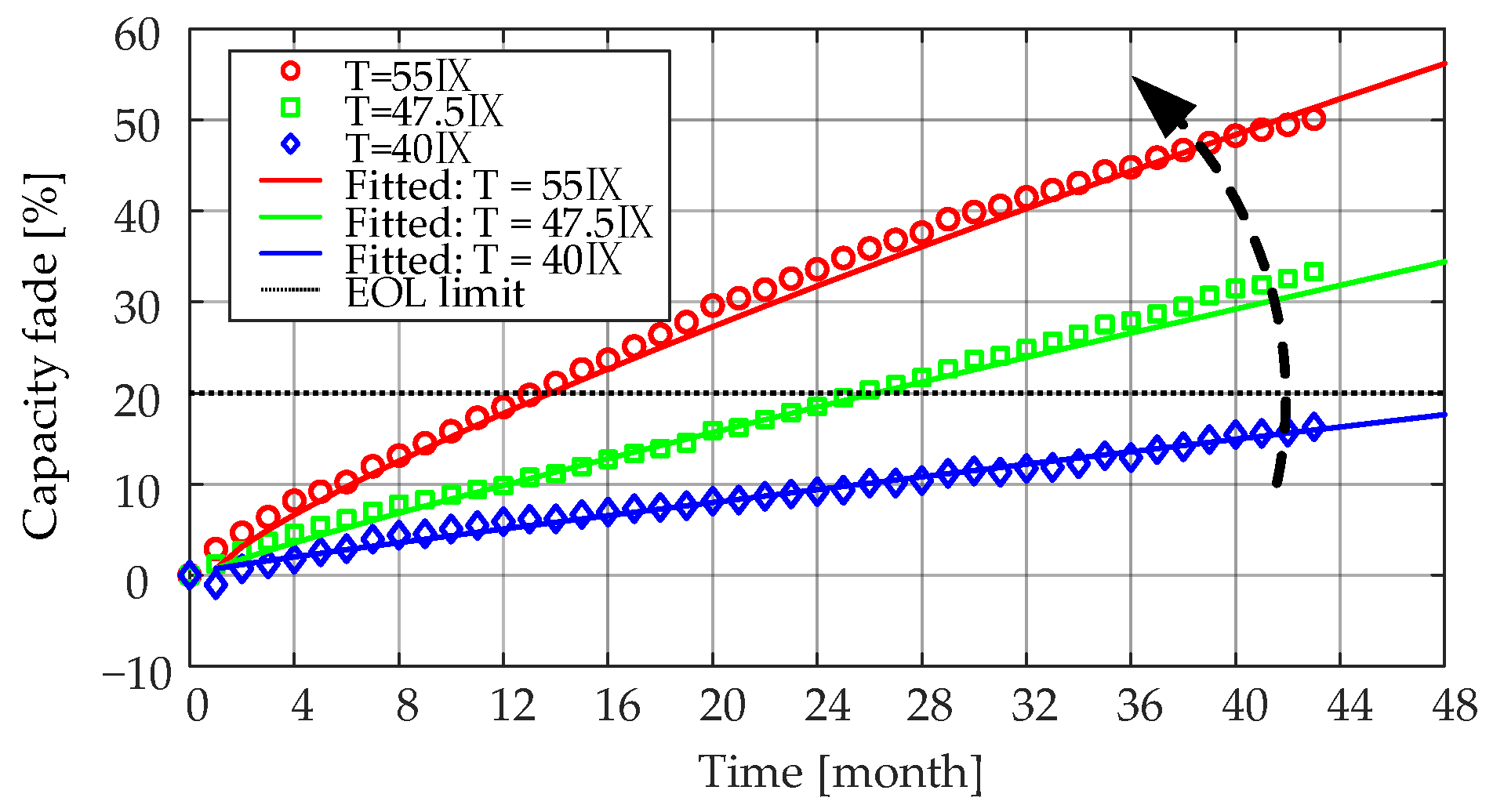
As can be seen from
Figure 5 and
Figure 14, the internal resistances of the LiFePO
4/C battery cells increased slowly relative to the rate of the capacity fade. Taking Case 4 (i.e., T = 55 °C, SOC = 50%) as an example, the LiFePO
4/C battery cells reached 20% capacity fade after 27 months of aging. At that time, the battery cells were considered to reach their EOL criterion. However, it should be stressed that for the same aging condition, there was only a 40%
Ri increase. Moreover, the
Ri increase characteristics were similar to the capacity fade. On one hand, the
Ri increased steadily during the lifetime of LiFePO
4/C cells, and on the other hand, the rate of the increase tended to slow down as the aging time increased.
3.2.2. Modeling of Ri Increase
In this subsection, the dependence of the discharge
Ri increase on the storage time, temperature and SOC level was analyzed for the values measured during the reference measurement at 80% SOC with a 4C-rate discharge pulse. The two-step fitting procedure was used as well for analyzing the aging behaviors of the LiFePO
4/C cells in terms of the
Ri increase. Thus, the dependence of the
Ri increase on the storage time for each considered test condition was studied in the first step, while in the second step, the dependence on the storage temperature and SOC level was investigated. The power function, defined in (19), was used to fit with high accuracy the measured increase of
Ri over the storage time.
where
p and
q represent the coefficients of the power function, and
t is the storage time, expressed in months.
The effects of the two stress factors on the
Ri increase were considered separately in the second step. The influence of the storage temperature could be determined based on the aging tests of Case 1, Case 2, and Case 3. For these cases, the storage temperature varied from 55 °C to 40 °C, and the SOC level was fixed to 50%. Then, the fitting function has the form of
Since the difference between the coefficients
qT obtained by fitting was very small, in order to reduce the complexity of the model, the same
qT value of 0.75 was selected at different temperatures.
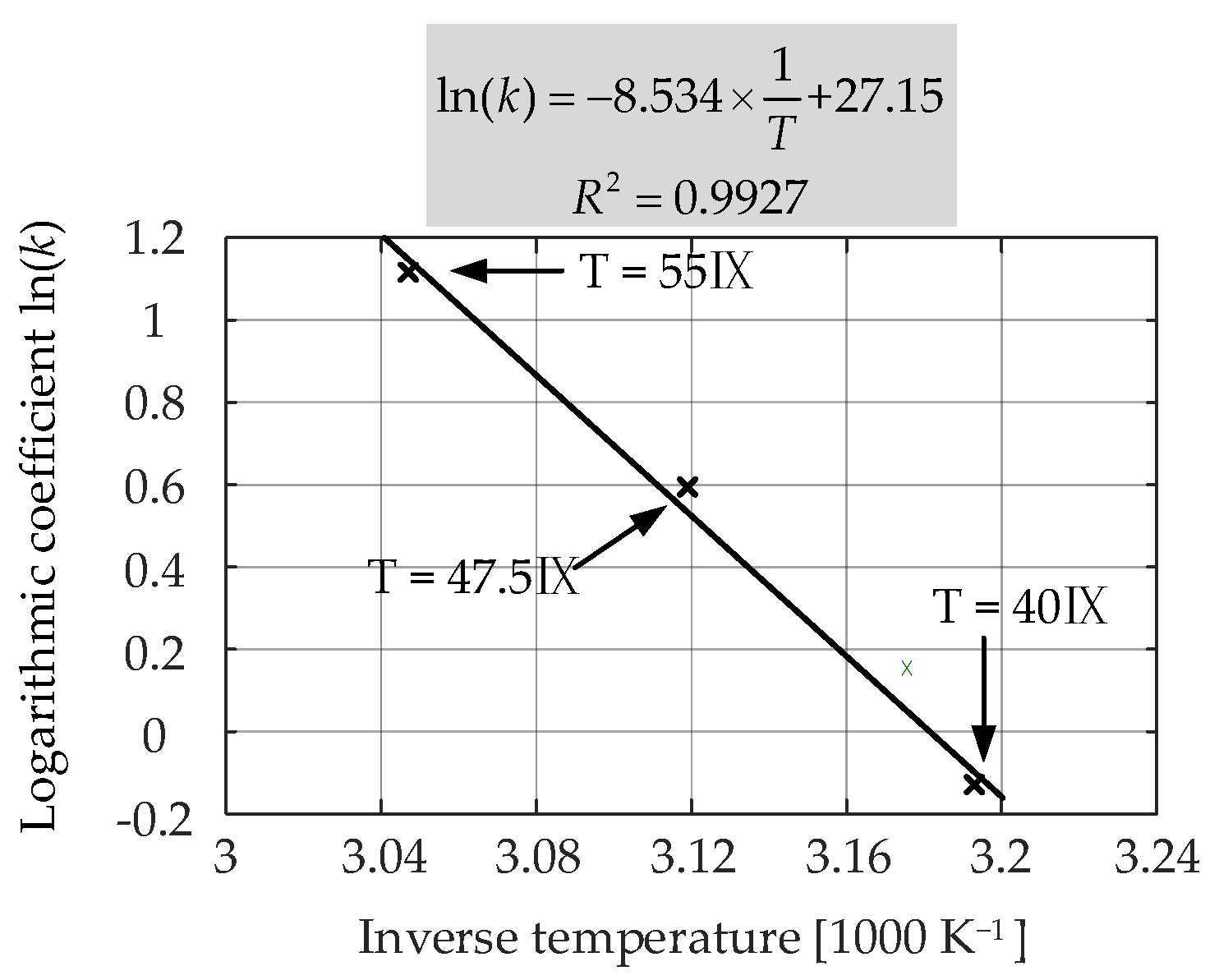
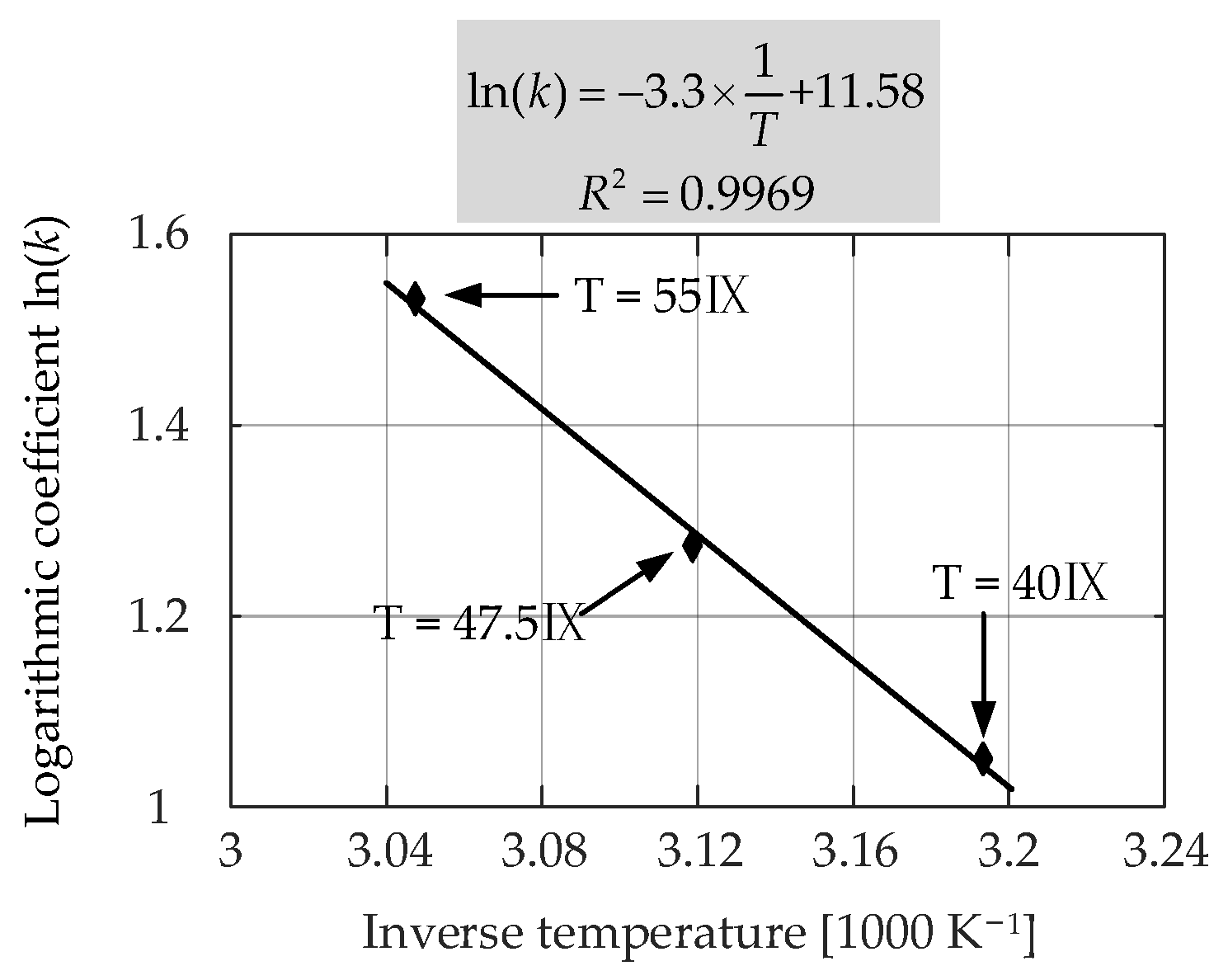
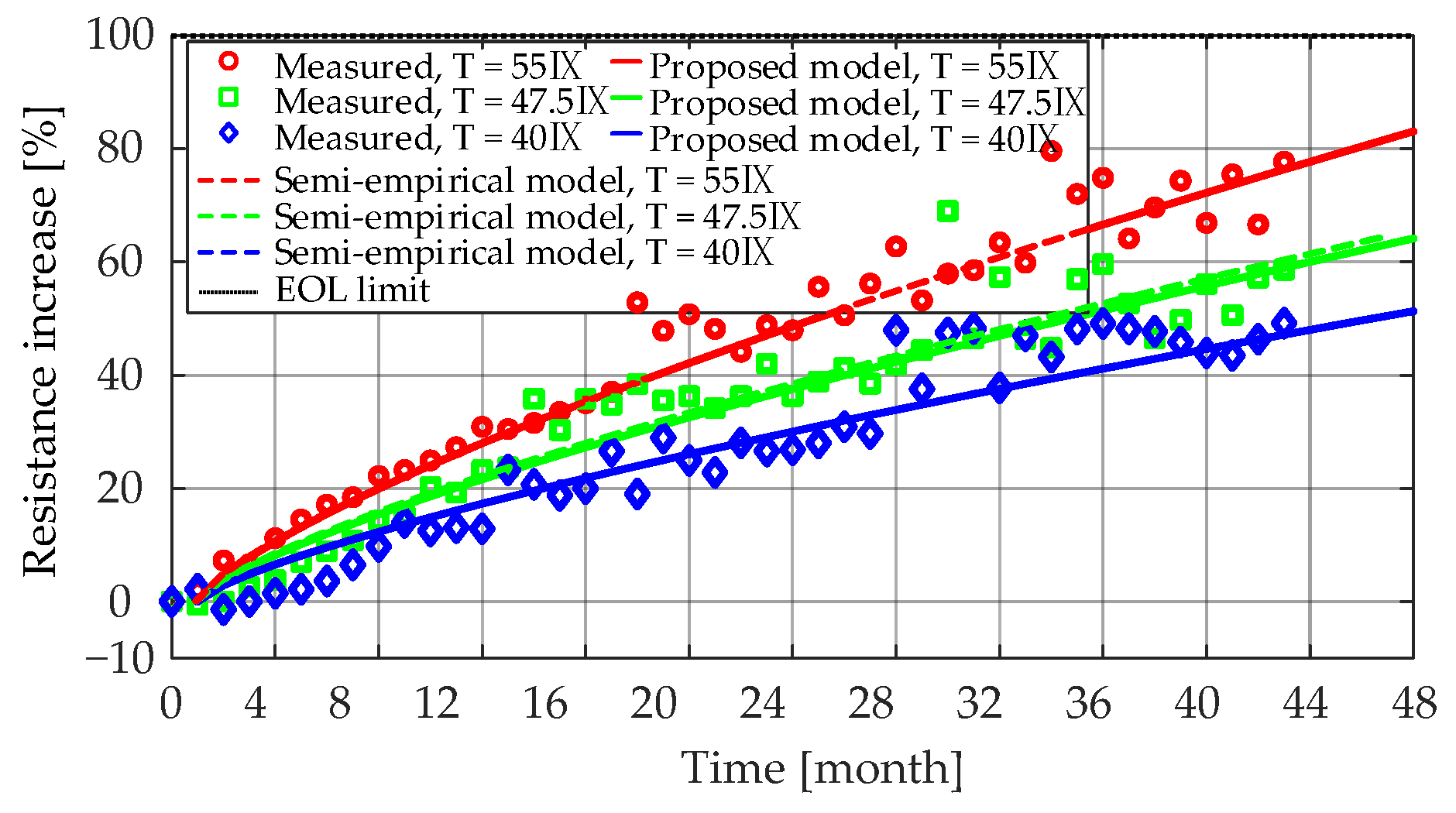
Figure 15 presents the measured and the fitted
Ri increase characteristics for the LiFePO
4/C battery cells that were aged at 50% SOC and three different temperatures (i.e., 55 °C, 47.5 °C, and 40 °C). The obtained coefficients for each case are listed in
Table 5. As can be seen from the results, the lower the storage temperature, the lower the rate of
Ri increase during the long-term calendar aging. This was due to the relatively lower rate of SEI formation and continued thickening at low SOC levels [
6].
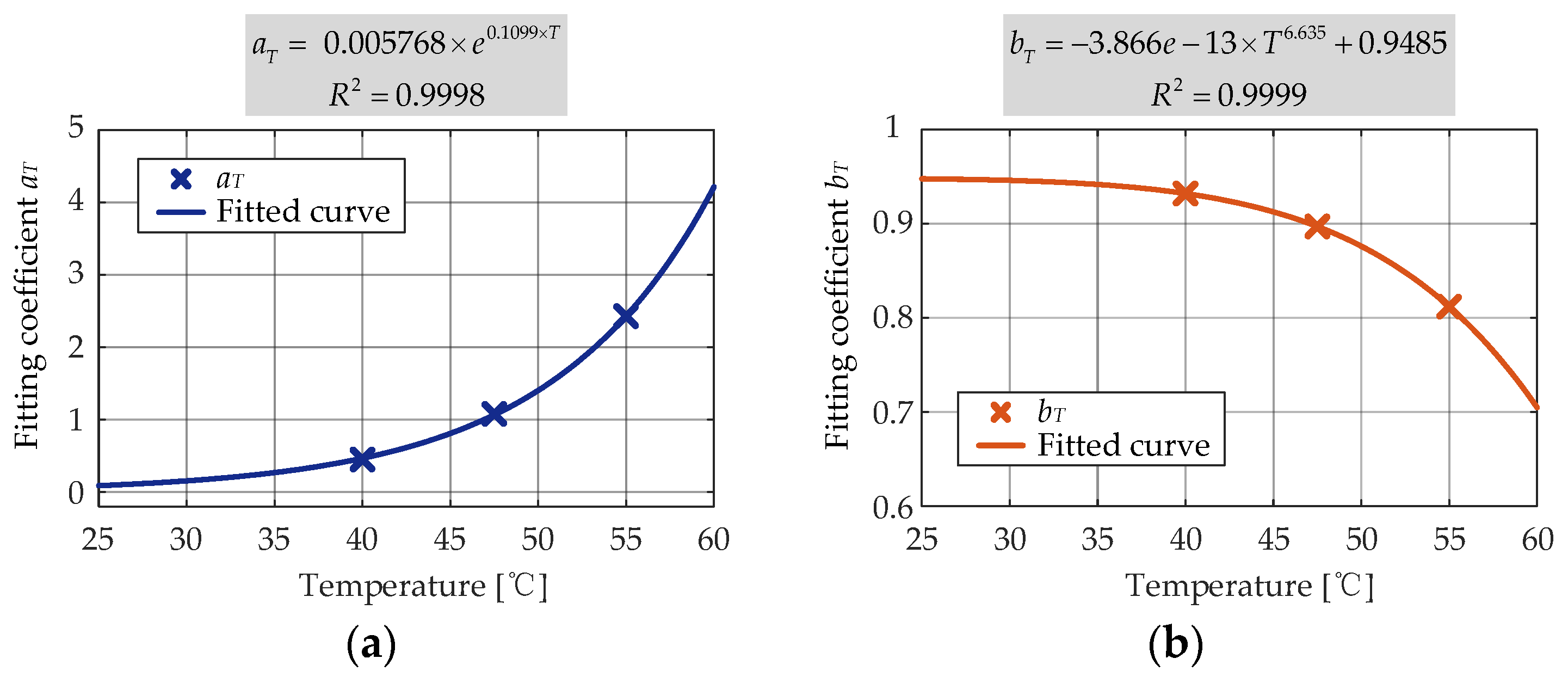
The second round of nonlinear regression was conducted to determine the dependence of
pT on the storage temperature. The exponential function given in (18) was found to be accurately correlated (
R2 = 0.9999) to the
pT obtained during the first-round fitting and the storage temperature, and the second-round curve fitting result is shown in
Figure 16.
By combining (20) and (21), a model which is able to predict the
Ri increase during storage at SOC = 50% and various temperatures (mainly, higher than 25 °C) was obtained:
where
t represents the storage time, expressed in months, and
T represents the storage temperature, expressed in degrees Celsius.
Similarly, the dependence of the
Ri increase on the SOC level at which the battery cells were stored could be modeled based on a two-step nonlinear regression procedure. First, Case 1, Case 4, and Case 5 were considered, and the objective function had the form of (23).
Next, the coefficients could be determined, which are shown in
Table 6. The measured and the fitted
Ri increase characteristics for the LiFePO
4/C battery cells stored at 55 °C and three different SOC levels (i.e., 20%, 50% and 90%) are shown in
Figure 17. The effect of the storage SOC level on the
Ri increase showed a staging behavior before
Ri of the LiFePO
4/C cells reached a 100% increase, and the doubled
Ri was usually seen as another EOL criterion. In the first stage, when the increase of
Ri is less than 30%, a higher storage SOC level made
Ri increase faster. Moreover, in the second stage (i.e., the
Ri increased by more than 30%),
Ri increased more when the battery was stored in the mid-SOC level (i.e., around 50% SOC). As discussed in
Section 3.1.2, during the first time range, the increase of the SEI film and the low anode potential will accelerate the loss of lithium ions, thereby increasing the internal resistance. After Ri increases by more than 30%, a stable SEI film is probably formed inside the battery stored at a 90% SOC level. In this case, Ri increased more and more slowly [
29].
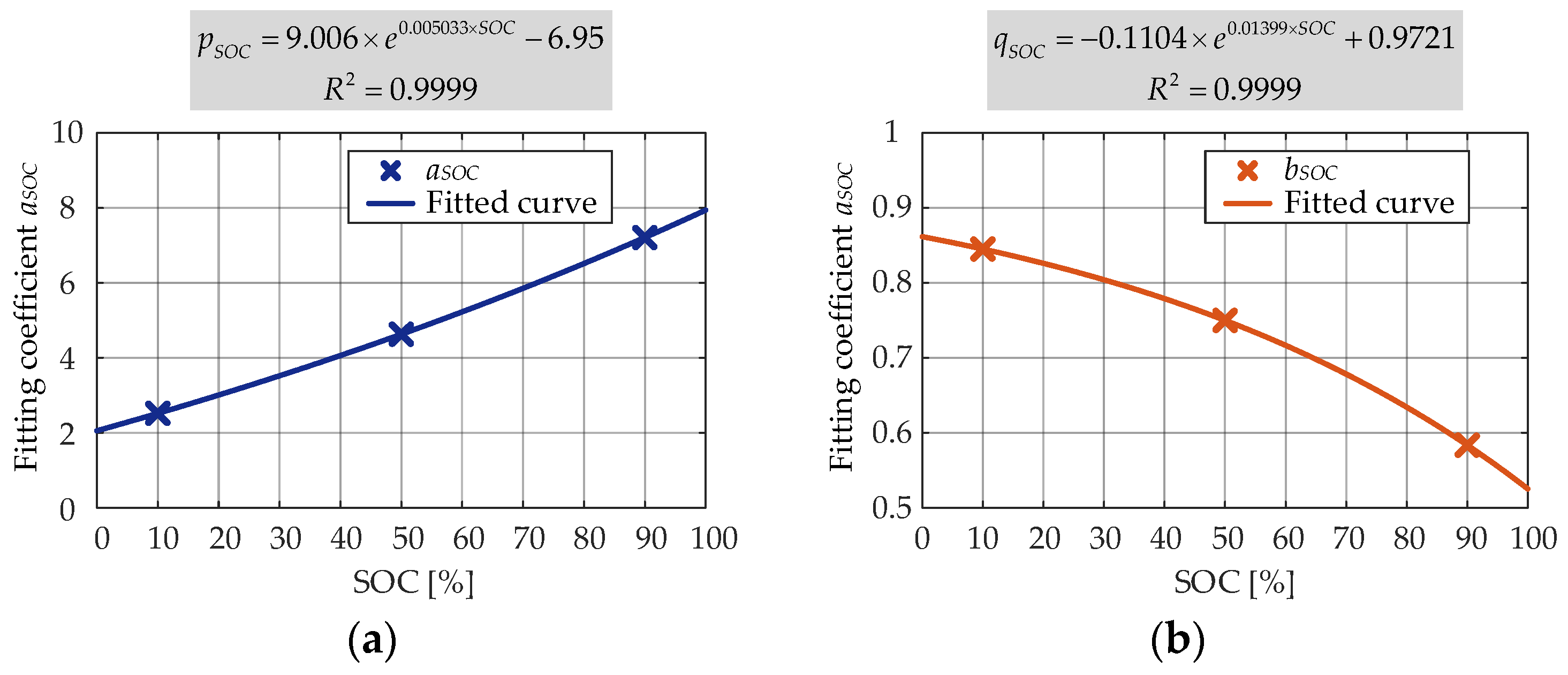
According to the results obtained in the second round of fitting, the relationship between the coefficients and SOC level was developed. As shown in
Figure 18, the coefficients
pSOC and
qSOC varied as the exponential functions. It can be seen that the SOC level influenced in a bit different manner the calendar degradation of the internal resistance (both
pSOC and
qSOC showed an exponential dependence) than the capacity (
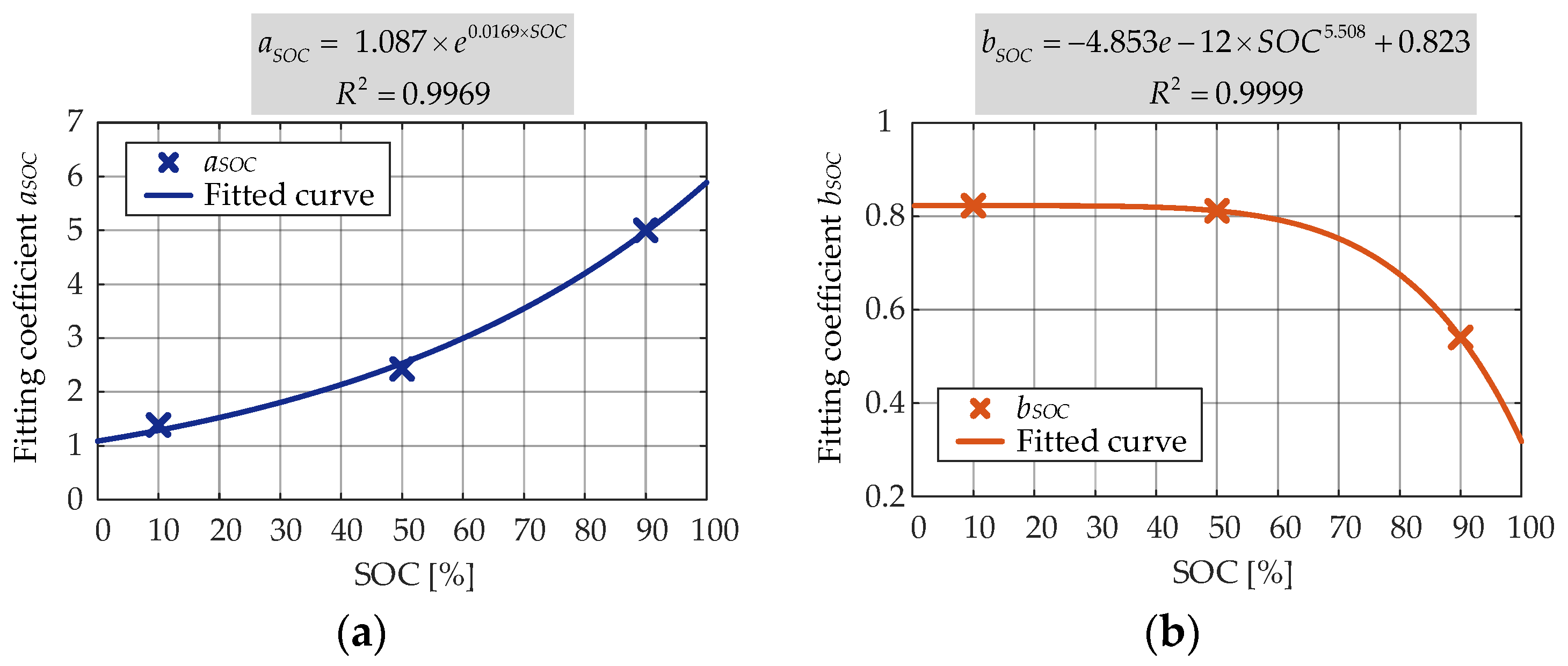
aSOC showed an exponential dependence and
bSOC showed a polynomial dependence).
By combining (23)–(25), a general model that was able to predict the
Ri increases during storage at 25 °C and different SOC levels was obtained:
where
t represents the storage time, expressed in months, and SOC represents the storage SOC level, expressed as a percentage.
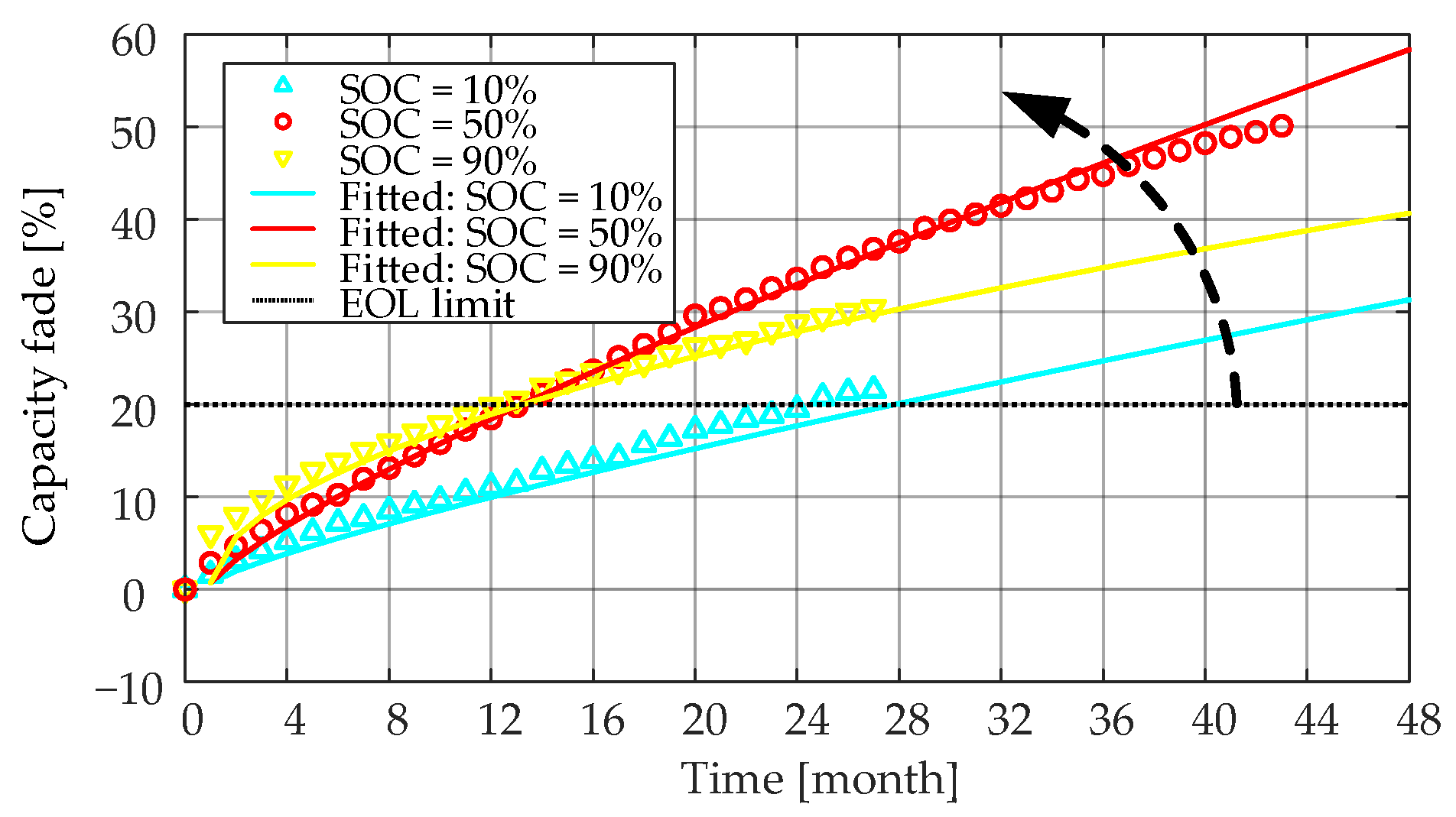
Similarly to the capacity fade, the dependences of
Ri increases to the storage temperature and to the storage SOC level were fitted separately. By combining all the considered stress factors and taking into account the interactions between them, the model that is able to predict the calendar lifetime in terms of
Ri increases is given as
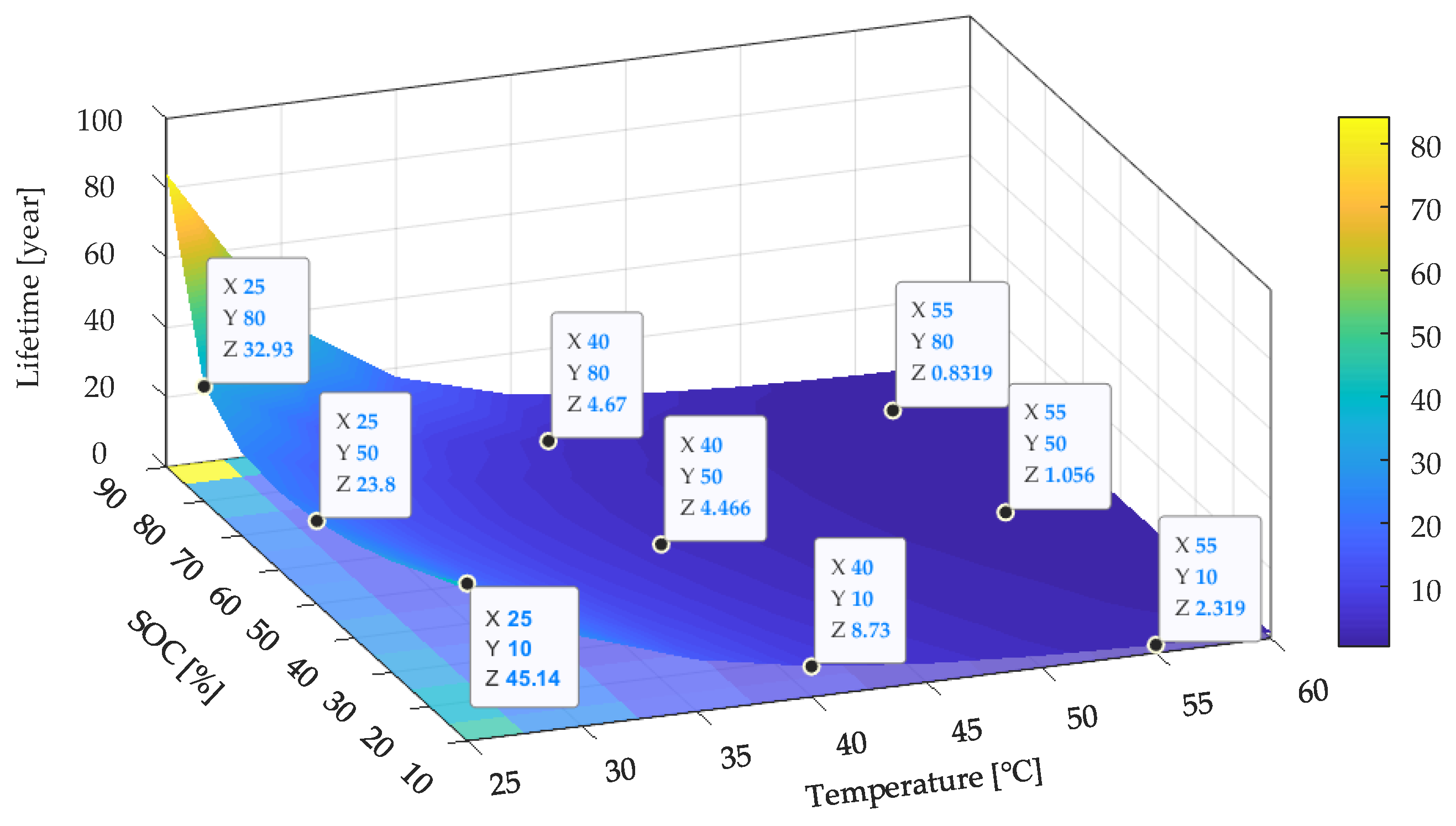
Based on the developed lifetime model (27), the
Ri increase of the LiFePO
4/C battery cells can be extrapolated to storage temperatures close to ones encountered during normal operation. The predicted lifetime based on
Ri increase model is shown in
Figure 18. It can be seen that the SOC levels at both ends (smaller than 20% SOC or larger than 80% SOC) and cooler temperatures preserved the Li-ion battery when not in use, which followed the analysis results based on the capacity fade model. Compared with the lifetime prediction results shown in
Figure 12 and
Figure 19, it can be seen that the predicted lifetime based on the
Ri increase model was longer than that based on the capacity fade model at a higher temperature (higher than 40 °C). For example, the tested battery cell can withstand approximately 5.0 years in terms of capacity if stored at 50% SOC and 55 °C. However, in terms of resistance, the batteries’ lifetimes only last for 1.1 years if they are stored under the same conditions. On the contrary, the
Ri increase model gives a shorter lifetime when the temperature decreases to 25 °C as compared with the capacity fade model. For example, the tested battery cell can withstand approximately 14.9 years in terms of capacity if stored at 50% SOC and 25 °C. However, in terms of resistance, the batteries will have 23.8 years if they are stored under the same conditions. This is because when investigating the influence of the storage temperature, the coefficient
qT in the
Ri increase model is a constant 0.75 while the coefficient
bT in the capacity fade model is an amount that varies with temperature. As the temperature decreases, the rate of capacity fate decreases exponentially, resulting in a longer predicted lifetime of the capacity-based model
In addition, by comparing the structure of models developed for predicting the calendar lifetime of the LiFePO4/C battery cells in terms of capacity (see (16)) and resistance (see (27)), it might be concluded that the degradation during storage of these two performance parameters is not caused by the same aging mechanisms. Moreover, it has to be stressed that the use of the aforementioned lifetime models for determining the aging behavior at temperatures below 25 °C might return erroneous results; this is because lifetime tests performed at lower temperatures (e.g., 15 °C, 10 °C or lower temperatures, etc.) were not considered when developing the test matrices, being outside of the scope of this paper.