Optimal Building Thermal Load Scheduling for Simultaneous Participation in Energy and Frequency Regulation Markets †
Abstract
1. Introduction
- Ramping rate: HVAC equipment can respond to frequency deviations much faster than traditional generator-side control [15];
- Efficiency loss: although prior studies reported noticeable round-trip efficiency losses during frequency regulation control of variable-speed fans [16], recent laboratory tests with controlled environments have shown negligible efficiency loss or even sensible efficiency gains when appropriate regulation control strategies are adopted [11]; in [17], it was also proved through a rigorous analysis that regulation control of HVAC equipment does not cause efficiency losses;
- Regulation performance: incorporating regulation strategies in OEM controllers could result in PJM (Pennsylvania-New Jersey-Maryland Interconnection, a regional transmission organization serving the northeast of U.S.) regulation performance scores of up to 0.98; even with an add-on (after-market) regulation control solution, regulation scores of above 0.9 were obtained consistently [11];
- Procurement cost: HVAC equipment is installed in almost every building; thus, the procurement cost is relatively lower compared to other regulation resources, such as batteries.
2. Case Study Description and Prior Results
2.1. Case Study
2.2. Prior Results
2.3. New Contributions
3. Models
3.1. Building Envelope
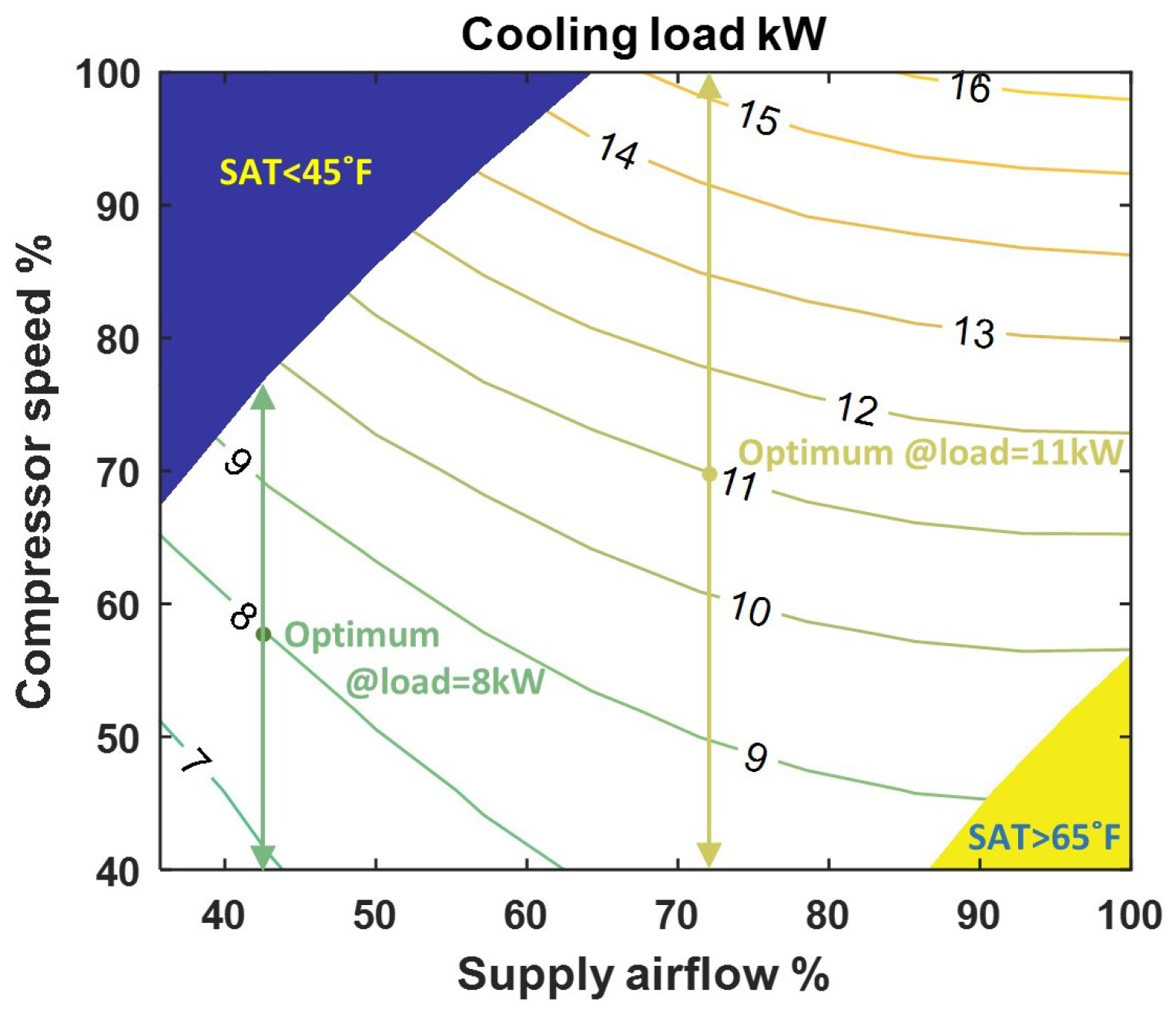
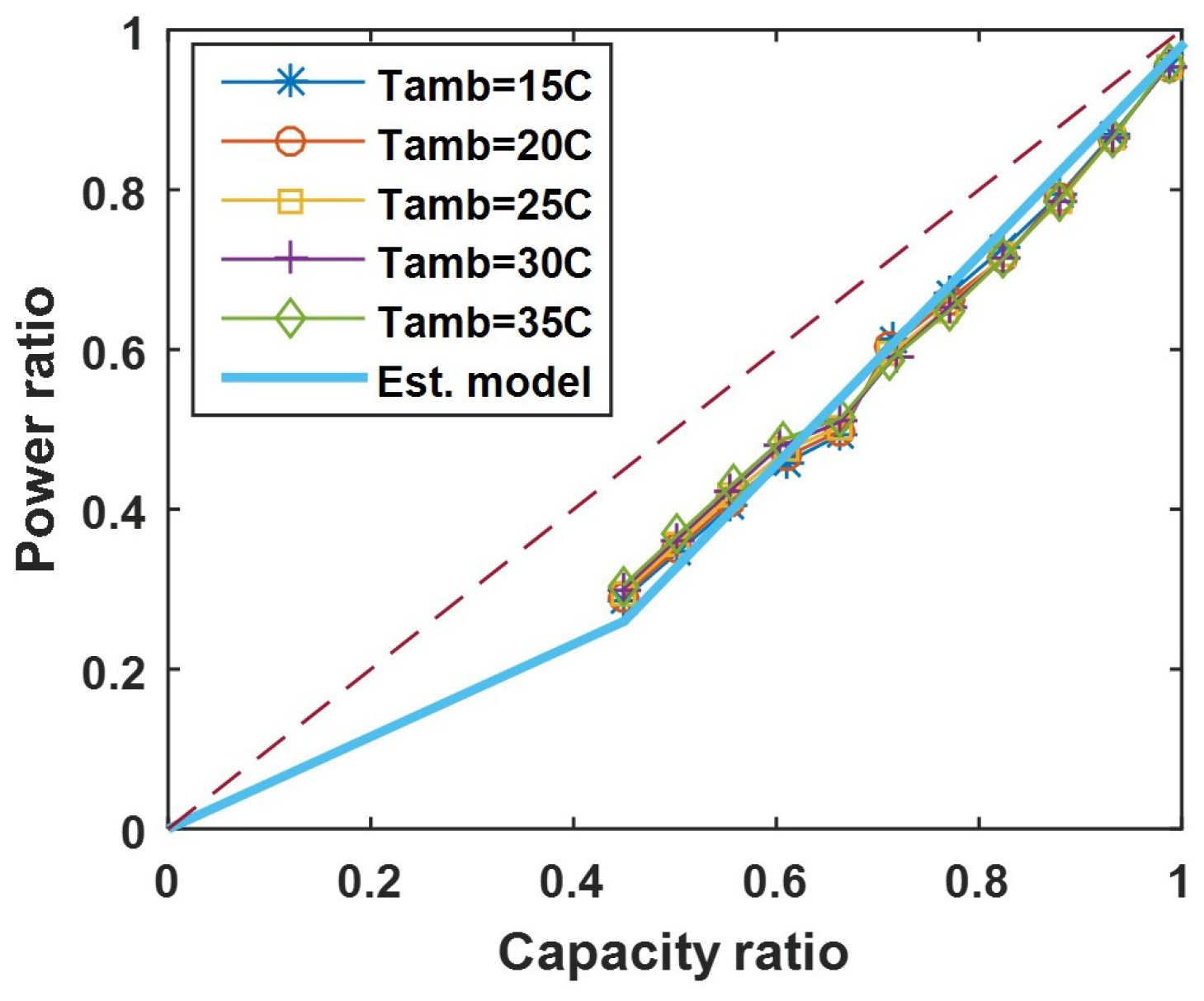
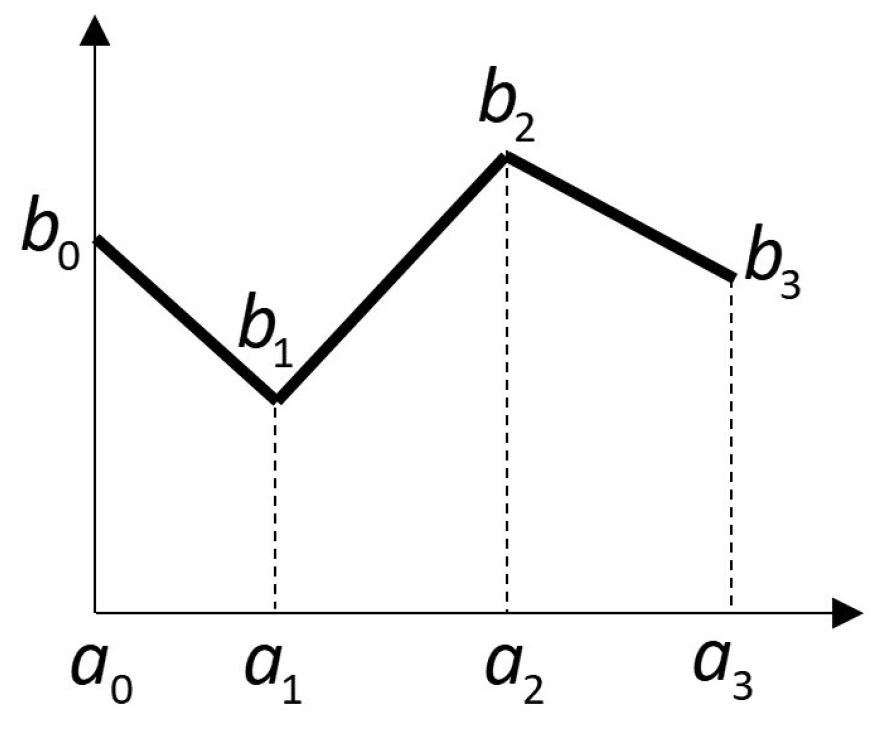
3.2. AC System
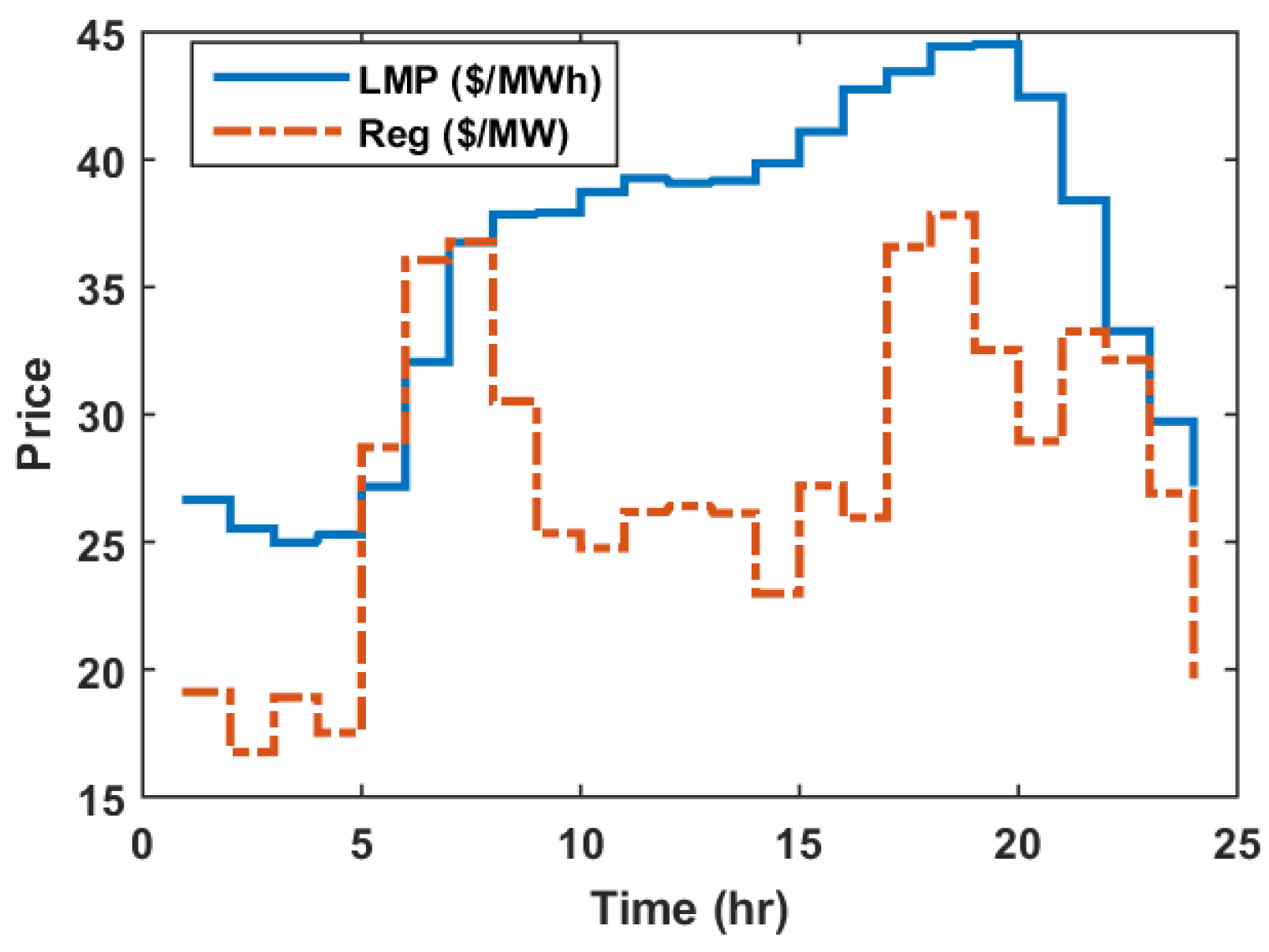
3.3. Wholesale Energy and Frequency Regulation Markets
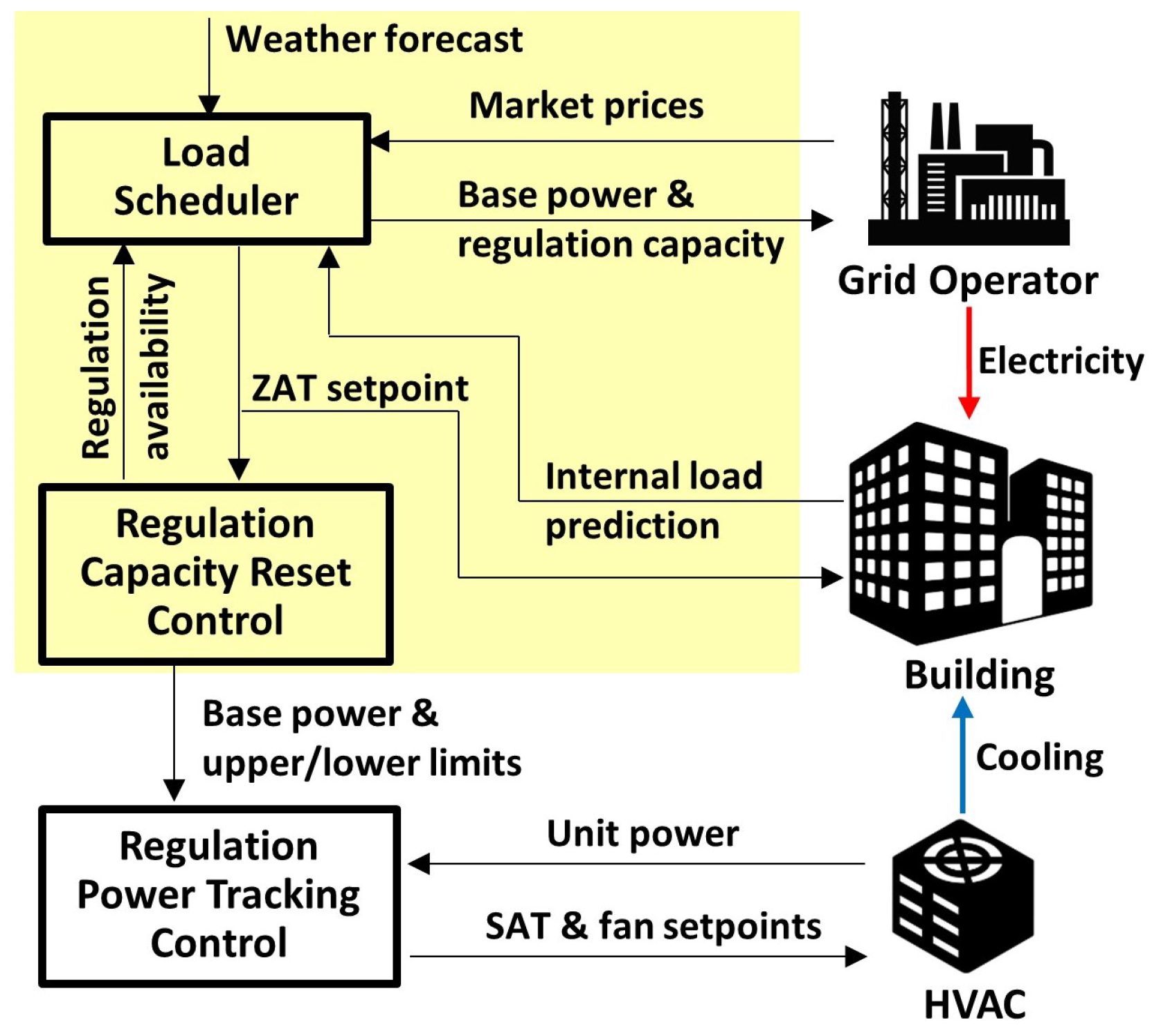
4. Bi-Market Control Strategy
4.1. Regulation Capacity Reset
4.2. Supervisory Scheduler
4.3. Baseline Control Strategies
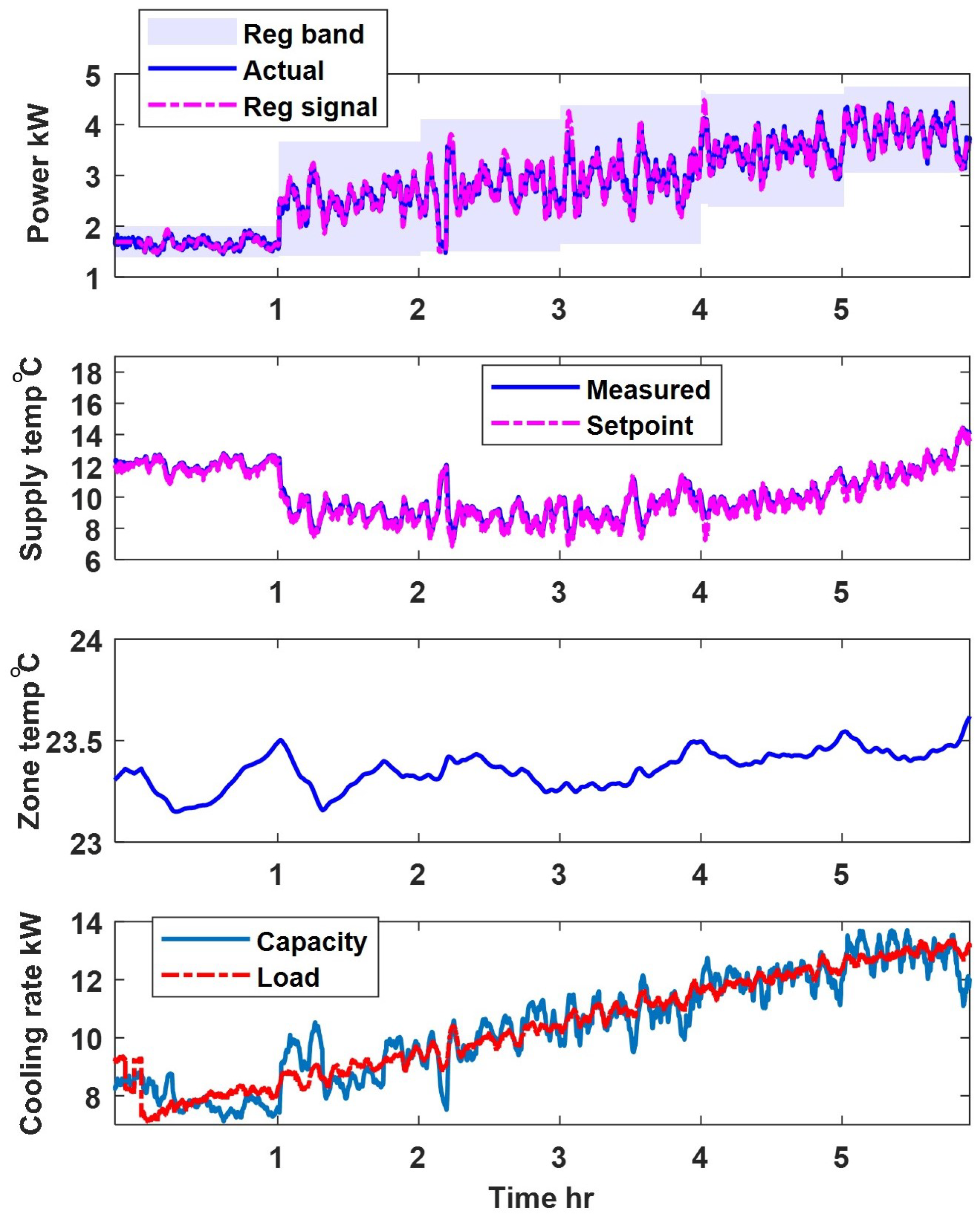
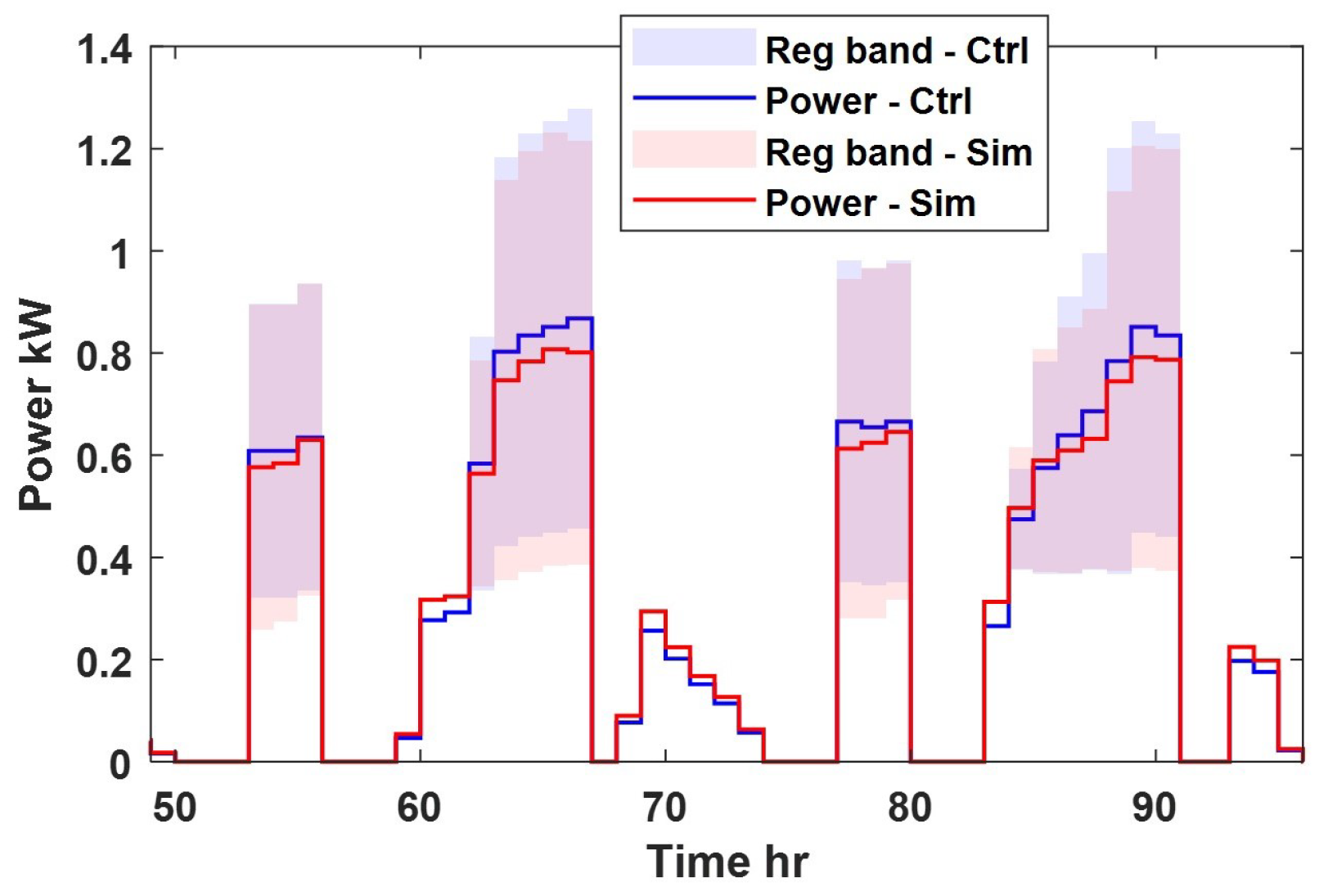
5. Case Study Results
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- What Are the Questions Raised by the UK’s Recent Blackout? Available online: https://www.theguardian.com/business/2019/aug/12/what-are-the-questions-are-raised-by-the-uks-recent-blackout (accessed on 15 September 2019).
- Zhou, Z.; Levin, T.; Conzelmann, G. Survey of US Ancillary Services Markets; Technical Report; Argonne National Lab. (ANL): Argonne, IL, USA, 2016.
- EIA, Use of Electricity Explained. Available online: https://www.eia.gov/energyexplained/index.php?page=electricity_use (accessed on 30 January 2019).
- Lin, Y.; Barooah, P.; Meyn, S.; Middelkoop, T. Experimental evaluation of frequency regulation from commercial building HVAC systems. IEEE Trans. Smart Grid 2015, 6, 776–783. [Google Scholar] [CrossRef]
- MacDonald, J. Commercial Building Loads Providing Ancillary Services in PJM; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2014. [Google Scholar]
- Fabietti, L.; Gorecki, T.T.; Qureshi, F.A.; Bitlislioğlu, A.; Lymperopoulos, I.; Jones, C.N. Experimental implementation of frequency regulation services using commercial buildings. IEEE Trans. Smart Grid 2016, 9, 1657–1666. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Tang, R. Investigation on the Use of Pumps in HVAC Systems for Providing Ancillary Services in Smart Grids. Energy Procedia 2019, 159, 219–224. [Google Scholar] [CrossRef]
- Kim, Y.J.; Fuentes, E.; Norford, L.K. Experimental study of grid frequency regulation ancillary service of a variable speed heat pump. IEEE Trans. Power Syst. 2015, 31, 3090–3099. [Google Scholar] [CrossRef]
- Motalleb, M.; Thornton, M.; Reihani, E.; Ghorbani, R. Providing frequency regulation reserve services using demand response scheduling. Energy Convers. Manag. 2016, 124, 439–452. [Google Scholar] [CrossRef]
- Su, L.; Norford, L.K. Demonstration of HVAC chiller control for power grid frequency regulation—Part 1: Controller development and experimental results. Sci. Technol. Built Environ. 2015, 21, 1134–1142. [Google Scholar] [CrossRef]
- Cai, J.; Braun, J.E. Laboratory-based assessment of HVAC equipment for power grid frequency regulation: Methods, regulation performance, economics, indoor comfort and energy efficiency. Energy Build. 2019, 185, 148–161. [Google Scholar] [CrossRef]
- Rotger-Griful, S.; Chatzivasileiadis, S.; Jacobsen, R.H.; Stewart, E.M.; Domingo, J.M.; Wetter, M. Hardware-in-the-loop co-simulation of distribution grid for demand response. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Williams, S.; Short, M.; Crosbie, T. On the use of thermal inertia in building stock to leverage decentralised demand side frequency regulation services. Appl. Therm. Eng. 2018, 133, 97–106. [Google Scholar] [CrossRef]
- Callaway, D.S. Tapping the energy storage potential in electric loads to deliver load following and regulation, with application to wind energy. Energy Convers. Manag. 2009, 50, 1389–1400. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Hu, Q.; Wang, Z. Dynamic demand control for system frequency regulation: Concept review, algorithm comparison, and future vision. Electr. Power Syst. Res. 2018, 154, 75–87. [Google Scholar] [CrossRef]
- Beil, I.; Hiskens, I.; Backhaus, S. Round-trip efficiency of fast demand response in a large commercial air conditioner. Energy Build. 2015, 97, 47–55. [Google Scholar] [CrossRef]
- Raman, N.S.; Barooah, P. On the round-trip efficiency of an HVAC-based virtual battery. IEEE Trans. Smart Grid 2019, 11, 403–410. [Google Scholar] [CrossRef]
- MacDonald, J.; Cappers, P.; Callaway, D.; Kiliccote, S. Demand response providing ancillary services: A comparison of opportunities and challenges in the US wholesale markets. In Proceedings of the Grid Interop 2012, Irving, TX, USA, 3–6 December 2012. [Google Scholar]
- Energy and Ancillary Services Market Operations. Available online: https://www.pjm.com/-/media/documents/manuals/m11.ashx?la=en (accessed on 30 January 2019).
- Balandat, M.; Oldewurtel, F.; Chen, M.; Tomlin, C. Contract design for frequency regulation by aggregations of commercial buildings. In Proceedings of the 2014 52nd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 30 September–3 October 2014; pp. 38–45. [Google Scholar]
- Vrettos, E.; Oldewurtel, F.; Andersson, G. Robust Energy-Constrained Frequency Reserves From Aggregations of Commercial Buildings. IEEE Trans. Power Syst. 2016, 31, 4272–4285. [Google Scholar] [CrossRef]
- Iria, J.; Soares, F.; Matos, M. Optimal bidding strategy for an aggregator of prosumers in energy and secondary reserve markets. Appl. Energy 2019, 238, 1361–1372. [Google Scholar] [CrossRef]
- Vrettos, E.; Andersson, G. Scheduling and Provision of Secondary Frequency Reserves by Aggregations of Commercial Buildings. IEEE Trans. Sustain. Energy 2016, 7, 850–864. [Google Scholar] [CrossRef]
- Maasoumy, M.; Rosenberg, C.; Sangiovanni-Vincentelli, A.; Callaway, D.S. Model predictive control approach to online computation of demand-side flexibility of commercial buildings HVAC systems for supply following. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 1082–1089. [Google Scholar]
- Vrettos, E.; Kara, E.C.; MacDonald, J.; Andersson, G.; Callaway, D.S. Experimental demonstration of frequency regulation by commercial buildings—Part I: Modeling and hierarchical control design. IEEE Trans. Smart Grid 2016, 9, 3213–3223. [Google Scholar] [CrossRef]
- Vrettos, E.; Kara, E.C.; MacDonald, J.; Andersson, G.; Callaway, D.S. Experimental demonstration of frequency regulation by commercial buildings—Part II: Results and performance evaluation. IEEE Trans. Smart Grid 2016, 9, 3224–3234. [Google Scholar] [CrossRef]
- Blum, D.H.; Xu, N.; Norford, L.K. A novel multi-market optimization problem for commercial heating, ventilation, and air-conditioning systems providing ancillary services using multi-zone inverse comprehensive room transfer functions. Sci. Technol. Built Environ. 2016, 22, 783–797. [Google Scholar] [CrossRef]
- Blum, D.H.; Zakula, T.; Norford, L.K. Opportunity cost quantification for ancillary services provided by heating, ventilating, and air-conditioning systems. IEEE Trans. Smart Grid 2016, 8, 1264–1273. [Google Scholar] [CrossRef]
- Pavlak, G.S.; Henze, G.P.; Cushing, V.J. Optimizing commercial building participation in energy and ancillary service markets. Energy Build. 2014, 81, 115–126. [Google Scholar] [CrossRef]
- Cai, J. A Low Cost Multi-Agent Control Approach for Building Energy System Management. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Cai, J.; Braun, J.E. A regulation capacity reset strategy for HVAC frequency regulation control. Energy Build. 2019, 185, 272–286. [Google Scholar] [CrossRef]
- Cai, J.; Braun, J. An inverse hygrothermal model for multi-zone buildings. J. Build. Perform. Simul. 2016, 9, 510–528. [Google Scholar] [CrossRef]
- Cai, J.; Braun, J.E. Assessments of variable-speed equipment for packaged rooftop units (RTUs) in the United States. Energy Build. 2018, 164, 203–218. [Google Scholar] [CrossRef]
- PJM Operating Agreement Accounting. Available online: https://www.pjm.com/-/media/documents/manuals/m28.ashx?la=en (accessed on 30 January 2019).
- The MOSEK Optimization Software. 2010. Available online: http://www.mosek.com (accessed on 1 March 2020).
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming. 2008. Available online: http://cvxr.com/cvx/ (accessed on 1 March 2020).
- Toh, K.C.; Todd, M.J.; Tütüncü, R.H. SDPT3: A MATLAB software package for semidefinite programming, version 1.3. Optim. Methods Softw. 1999, 11, 545–581. [Google Scholar] [CrossRef]


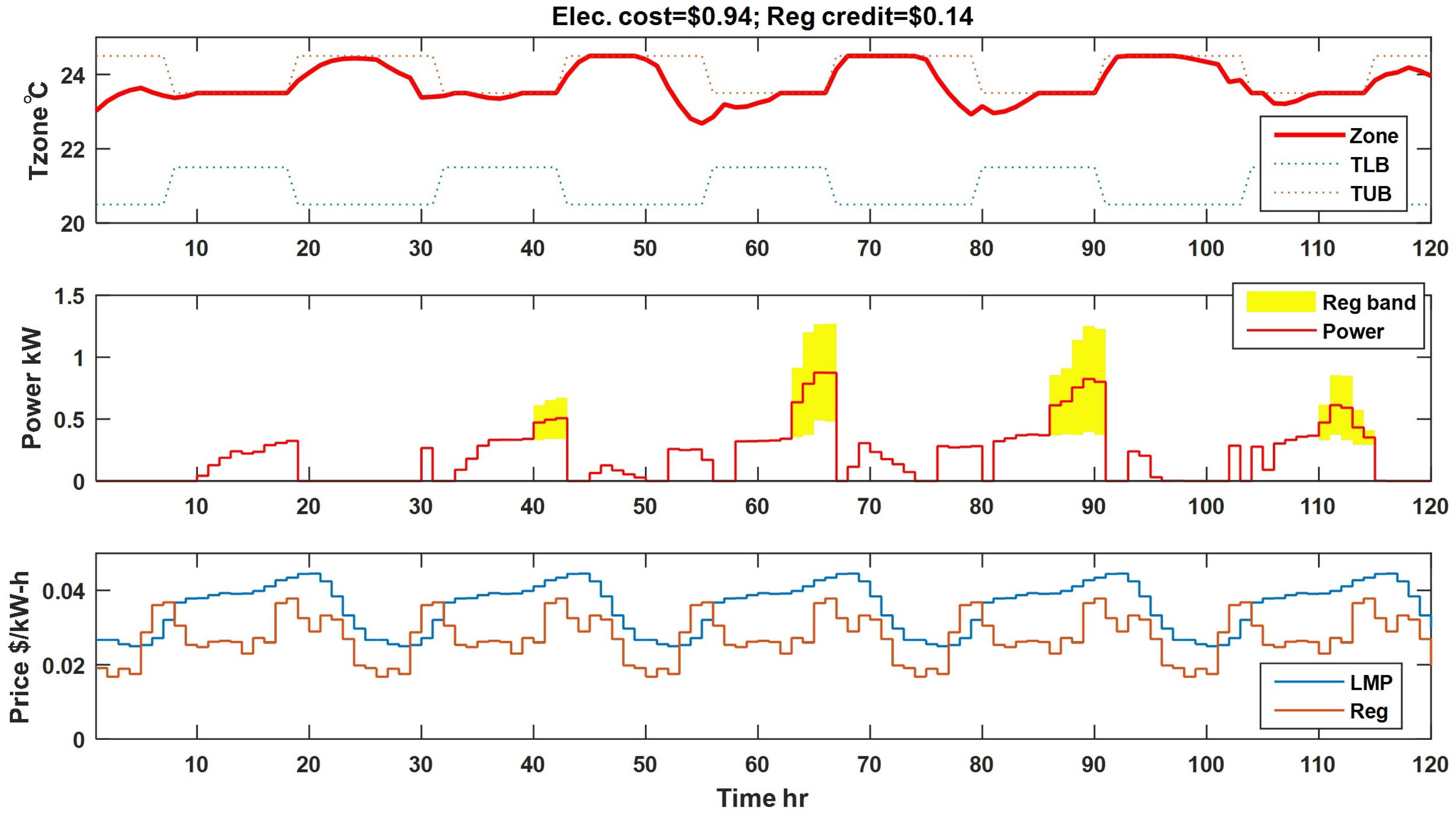
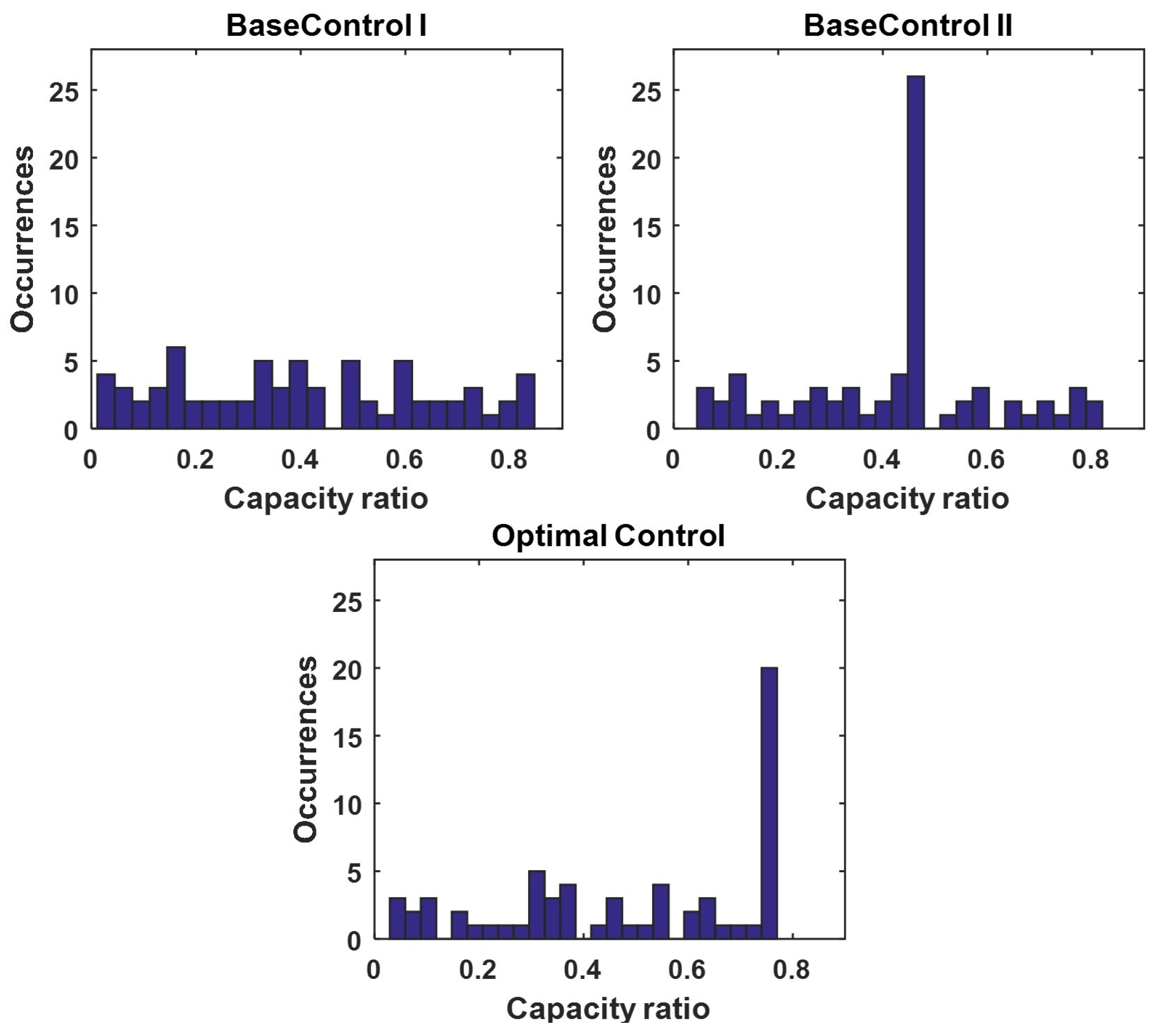

| Control Strategy | Energy Cost ($) | Reg. Credit ($) | Net Cost ($) |
|---|---|---|---|
| BaseCtrl I | 0.97 | 0.19 | 0.78 |
| BaseCtrl II | 0.94 (3%↘) | 0.14 (26.3%↘) | 0.8 (2.5%↗) |
| OptimalCtrl | 0.99 (2%↗) | 0.32 (118.6%↗) | 0.67 (14.1%↘) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J. Optimal Building Thermal Load Scheduling for Simultaneous Participation in Energy and Frequency Regulation Markets. Energies 2021, 14, 1593. https://doi.org/10.3390/en14061593
Cai J. Optimal Building Thermal Load Scheduling for Simultaneous Participation in Energy and Frequency Regulation Markets. Energies. 2021; 14(6):1593. https://doi.org/10.3390/en14061593
Chicago/Turabian StyleCai, Jie. 2021. "Optimal Building Thermal Load Scheduling for Simultaneous Participation in Energy and Frequency Regulation Markets" Energies 14, no. 6: 1593. https://doi.org/10.3390/en14061593
APA StyleCai, J. (2021). Optimal Building Thermal Load Scheduling for Simultaneous Participation in Energy and Frequency Regulation Markets. Energies, 14(6), 1593. https://doi.org/10.3390/en14061593





